1. Introduction
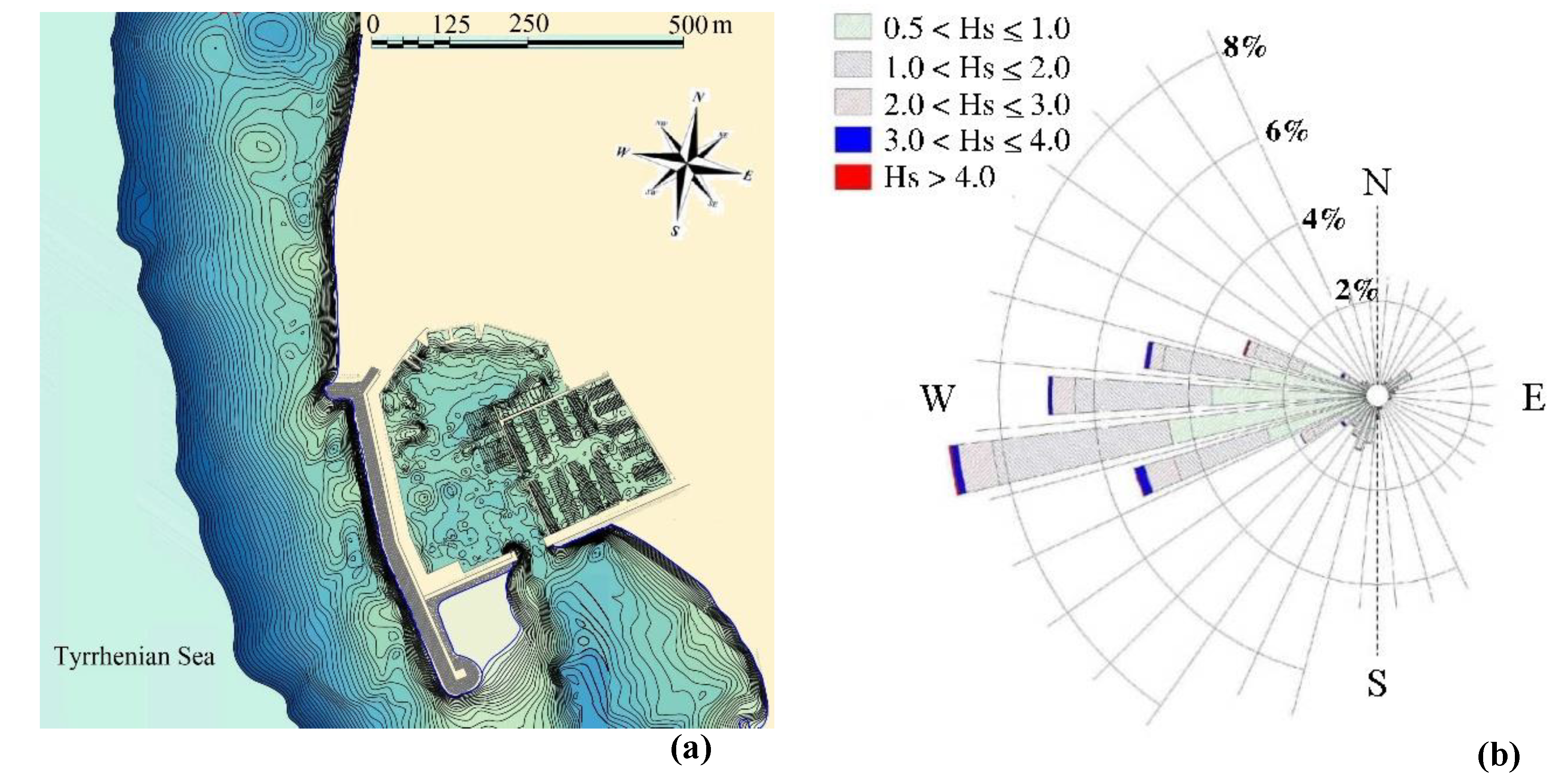
The Cetraro harbour is located in the Tyrrhenian coast of southern Italy, in a natural inlet protected by an artificial breakwater directed parallel to the coastline, approximately from North-West to South-East. The wave height directional distribution offshore Cetraro harbour highlights that the waves, in the above-mentioned coastal area, come exclusively from the sector between 250° and 290° North. Among these the most significant waves for the coastal sediment transport come from 260° North, with a wave height between 3 m and 4 m and a wave period of about 10 s. In [
1], the numerical simulations of the coastal currents, produced by the above-mentioned incoming waves in the coastal area opposite the Cetraro harbour, were carried out by a horizontal two-dimensional numerical model which is based on depth-averaged governing equations. The model used in [
1] belongs to the Boussinesq-type models that adopt a hybrid finite volume-finite difference scheme [
2]. According to this approach, in [
1] the simulation of the wave propagation from the deep-water region to the start of the surf zone is obtained by numerically integrating the Boussinesq equations [
3], while in the surf and swash zone by the Nonlinear Shallow Water Equations [
4,
5,
6]. As underlined by several authors [
7,
8,
9], in those models the presence of the dispersive terms of the Boussinesq equations allows to maintain the wave form in deep water but prevents the numerical schemes to converge to the correct solution in the surf zone, where the breaking waves exhibit steeper wave fronts. For this reason, in the surf zone, by switching off the dispersive terms, the governing equations are reduced to the Nonlinear Shallow Water Equations. As a consequence, in these Boussinesq-type models the breaking waves are represented as the weak solution (the solution that admits discontinuity) of the Nonlinear Shallow Water Equations. The main numerical drawback of this kind of models is related to the need of setting a criterion to establish when switching off the dispersive terms of the governing equations. This kind of models can be used in the case in which the three-dimensional features of the flow are negligible.
An alternative strategy to Boussinesq-type models is given by three-dimensional non-hydrostatic models that are based on the numerical integration of the Navier–Stokes equations. In this framework, a recent class of models is based on the use of a coordinate transformation along the vertical direction, called sigma coordinate transformation, and on the adoption of shock-capturing numerical schemes [
10,
11,
12,
13]. In these models, at every instant the upper boundary coincides with the free surface, therefore, on this boundary it is possible to correctly assign the dynamic pressure boundary condition, without the need for cumbersome interpolations to calculate the free surface position inside the grid cells. This strategy, accompanied by the use of shock-capturing numerical schemes, allows the above-mentioned models to exhibit good dispersive properties also by adopting a low (minor of 10) number of grid nodes along the vertical direction and allows to directly simulate the wave breaking. Recently, Cannata et al. [
14] proposed a three-dimensional nonhydrostatic model that is based on a contravariant integral form of the Navier–Stokes equations expressed in a time dependent generalized curvilinear coordinate system. These equations represent a generalization of the governing equations used in all the previous models that adopt a sigma coordinate transformation. In fact, the governing equations proposed in the models by [
10,
11,
12,
13] can be easily obtained from the ones proposed in [
14] by introducing simplifying assumptions. For example, starting from the integral contravariant form proposed in [
14], by expressing the vector and tensor quantities with respect to the Cartesian basis vectors and by taking the limit as the control volume tends to zero, the governing equations in [
14] reduce to the same differential conservative form proposed by [
10,
12], in which the differential terms are written in curvilinear coordinates but the fluid velocity vector is expressed in Cartesian components. Moreover, by introducing a further simplification consisting on the adoption of two horizontal Cartesian coordinates and by choosing as coordinate transformation the one defined by the sigma coordinate transformation, the governing equations proposed in [
14] reduce to the ones proposed in [
11,
13].
In the present paper we adopt a three-dimensional non-hydrostatic model which is based on the integral contravariant form of the Navier–Stokes equations in a time dependent curvilinear coordinate system proposed in [
14]. These governing equations are integrated in a time varying curvilinear grid which is designed to follow the geometry of irregular coastal regions and to adjust to the free surface movements. By means of a time dependent coordinate transformation, the moving irregular curvilinear grid is transformed into a fixed and regular computational one. On this fixed and regular grid, the governing equations are numerically integrated by a predictor-corrector procedure method that is different from the one proposed in [
14]. With respect to the latter, we propose two elements of originality: a modification of the procedure to update the free surface elevation and a modification of the boundary condition on the free surface. Analogously to the procedure adopted in [
14], in the predictor step an approximate velocity field (called predictor velocity field) is carried out by numerically integrating the momentum balance equations devoid of the dynamic pressure, by a shock-capturing numerical scheme in which MUSCL-TVD (Monotonic Upstream-centered Scheme for Conservation Laws–Total Variation Diminishing) reconstructions and the HLL (Harten, Lax, van Leer) approximate Riemann solver are used to obtain the point values of flow velocity and water depth at the centre of the computational cell faces; in the corrector step, the approximate velocity field is corrected by summing to it an irrotational velocity field (called corrector velocity field) obtained by numerically solving a Poisson-like equation. In [
14], the free surface elevation is calculated at the end of the corrector step, after the summation between the predictor and corrector velocity fields.
Differently from what is done in [
14], in the present paper we update the free surface elevation at the end of the predictor step (and not at the end of the corrector one). Consequently, the position of the free surface is updated by using the point values of the flow velocity and water depth directly calculated at the centre of the cell faces by the local solution of the approximate Riemann Solver.
Furthermore, we adopt a new procedure to take into account non-zero dynamic pressure at the free surface. By means of this procedure, the boundary condition for the dynamic pressure is evaluated as a function of the normal component of the turbulent stress at the free surface. These modifications improve the shock-capturing properties of the numerical procedure and allow to better simulate steep wave fronts and the wave breaking.
In this paper, the proposed three-dimensional model is applied to the numerical study of the wave induced currents that take place in the Cetraro harbour coastal area during the most significant wave event for the coastal sediment transport. By the present model, the numerical simulations are carried out in two different geometric configurations: a first one, denominated present configuration, that reproduces the geometry of the coastal defence structures currently present in the harbour area; a second one, denominated project configuration, that reproduces the presence of a breakwater designed to modify the coastal currents in the area opposite the harbour entrance during the storm events that are considered more significant for the coastal sediment transport.
The paper is structured as follows. In
Section 2, the integral and contravariant formulation of the Navier–Stokes equations in a system of time-varying curvilinear coordinates is presented. In
Section 3 the numerical procedure and new boundary condition at the free surface are proposed. In
Section 4, we validate the model against two laboratory test cases and we apply the above-mentioned model to the Cetraro harbour coastal area, in the two different geometrical configurations. Conclusions are drawn in
Section 5.
2. Governing Equations
The three-dimensional model adopted in this paper is based on governing equations that are discretized on an irregular grid that moves with the free surface. This makes it possible to obtain a computational grid where, at every instant, the top boundary coincides with the free surface and where the zero-pressure condition can be correctly assigned. As demonstrated in several papers [
11,
15,
16,
17,
18], this strategy makes it possible to obtain numerical models with good dispersive properties, also by using a small number of grid nodes (less than ten) along the vertical direction. In these models, in order to transform the irregular moving grid into a regular fixed one, the Navier–Stokes equations must be expressed in a time dependent coordinates system. In the models proposed by [
11,
15,
16,
17,
18] the horizontal coordinates are the Cartesian ones, while the vertical coordinate is a moving coordinate (usually called sigma coordinate). In this paper we adopt a boundary conforming curvilinear grid that makes it possible to reproduce the coastal region with a smaller number of grid nodes in the horizontal directions. This entails the need to express the governing equations in a generalized time dependent curvilinear coordinates system, in which all the coordinates are curvilinear. In this kind of coordinate system, the most general form of the governing equations is the contravariant one. In the literature, the correct contravariant Navier–Stokes equations in time dependent curvilinear coordinates has been proposed in two forms: a differential, not conservative, contravariant form, proposed by Luo and Bewley [
19]; an integral contravariant form proposed by Cannata et al. [
14]. The latter integral form makes it possible to derive conservative shock-capturing numerical schemes, by which the wave breaking can be treated as a discontinuity and directly simulated. For this reason, in this paper, the adopted three-dimensional model is based on the integral contravariant form of the Navier–Stokes equations in a time-dependent curvilinear coordinates system proposed in [
14].
Let
be the spatial coordinates and time in a Cartesian coordinates system; let
be the spatial coordinates and time in a moving curvilinear coordinates system. By introducing a time-dependent coordinate transformation, every Cartesian coordinate can be expressed as a function of the moving coordinates
,
. From this generic transformation (and from its inverse), the two systems of base vectors, that can be naturally defined, are the covariant base vectors,
, that are tangent to the curvilinear coordinate lines, and the contravariant base vectors
, that are normal to the curvilinear coordinate surfaces (
. With respect to these two systems of base vectors, the vector and tensor components of a generic vector
and second order tensor
are the contravariant components
,
and the covariant components
,
,
. The l
th contravariant and covariant component of the generic vector
(or tensor
are given, respectively, by the scalar product between
(or
) and the base vectors
and
[
20]. Let us define with
a control volume bounded by moving curvilinear coordinate surfaces, which at the generic instant coincides with a material volume of fluid. In a curvilinear coordinates system, in order to obtain an integral form of the governing equations, the rate of change of the momentum of a material volume and the net forces acting on it must be projected onto a direction in space that does not coincide with a coordinate line. In this coordinate system, a direction in space is identified by a vector field
whose covariant components
are not constant in space. In this paper, the vector field
that identifies the abovementioned direction in space (and that is used to obtain a contravariant integral form of the momentum equation) is the one parallel to the
lth contravariant base vector defined at the centre of the volume
. We indicate by
this base vector and by
its
kth covariant component. By following this procedure, the contravariant integral form of the Navier–Stokes equations in a time dependent curvilinear coordinate system can be expressed as:
Where and are the boundary surfaces of the control volume on which is constant and which is located at the larger and at the smaller value of respectively (indices , and are cyclic); is the Jacobian of the time-dependent coordinate transformation; is the fluid density; is the fluid velocity vector; is the stress tensor; is the body force per unit mass; is the velocity (different from the fluid velocity) of the points belonging to the moving boundary surface of the control volume .
We indicate with
the free surface elevation, with
the still water depth and with
the total water depth. The stress tensor is separated into pressure and deviatoric stress tensor and the pressure is split into hydrostatic,
and dynamic components
, where
is the gravity acceleration. In order to obtain a system of governing equations in which the conserved variables are the water depth,
and the product between the water depth and the velocity vector components,
, the following time-dependent coordinate transformation, between Cartesian and curvilinear coordinates is introduced:
As a consequence of this specific transformation, the Jacobian of the transformation can be rewritten as
, where
and
indicates the vertical unit vector. Furthermore, we define the following averages of the flow quantities over the computational grid cell:
By using the abovementioned definitions and by using the kinematic boundary condition at the free surface, the integral mass conservation equation over the water column and the integral momentum balance equation can be written in the form:
Where indicates the sum between the viscous and the turbulent stress tensor. In the present paper, the turbulent stress tensor is represented by a Smagorinsky model.
3. Numerical Procedure
Analogously to [
14], the numerical procedure for updating the cell averaged three-dimensional flow velocity field and free surface elevation is based on a predictor-corrector method in conjunction with a two-stage second order Runge–Kutta method. With respect to the numerical procedure in [
14], in the present one two elements of originality are proposed: a modification of the procedure to update the free surface elevation and a modification of the boundary condition for the dynamic pressure at the free surface. These two elements of originality entail a new procedure for the numerical solution of the flow velocity and free surface elevation that is described in this section.
1. Predictor step
At each stage of the Runge–Kutta method, the momentum Equation (6), devoid of the dynamic pressure , is numerically integrated in order to calculate a predictor velocity field (approximate velocity field). The numerical integration is carried out by a shock-capturing numerical scheme in which MUSCLE-TVD reconstructions and the HLL approximate Riemann solver are used to obtain the point values of flow velocity and water depth at the centre of the computational cell faces.
2. Updating of the free surface elevation
At the end of the predictor step, the new position of the cell averaged free surface elevation is obtained by integrating Equation (5) along the water column, starting from the point values of the water depth and flow velocity calculated at the previous step.
3. Corrector step
Using the new position of the free surface, the position of all the grid points is recalculated and the metric terms (that arise from the coordinate transformation) are updated. A Poisson-like equation Equation (7) is solved by an iterative procedure on the updated geometry in order to calculate a scalar field
. By using Equation (8), the irrotational corrector velocity field,
, is obtained. In order to produce a final non-hydrostatic divergence-free velocity field, the corrector velocity field is summed to the predictor one Equation (9).
Differently from what is done in [
14], where the free surface elevation was calculated at the end of the corrector step, in this paper we update the free surface elevation at the end of the predictor step. Consequently, the position of the free surface is updated by using the point values of the flow velocity and water depth at the centre of the cell faces that result from the local solution of the approximate Riemann Solver. This improves the shock-capturing properties of the numerical procedure and allows to better simulate steep wave fronts and the wave breaking. Further details of the numerical scheme can be found in [
14].
Surface Boundary Condition
At the free surface, the normal stresses are not equal to zero at all time: by indicating with
the physical contravariant components of generic tensor
, the physical contravariant external normal stress
is given by the atmospheric pressure
:
The total internal normal stress,
, are given by the sum between the hydrostatic pressure, the dynamic pressure
and the viscous and turbulent normal stress
. By considering that at the free surface the hydrostatic pressure is equal to the atmospheric one, we obtain:
The continuity of the normal stress reads:
By introducing Equations (10) and (11) in Equation (12) we derive the free surface boundary condition for the dynamic pressure:
The physical contravariant component of the normal stress tensor is obtained by the following scalar product between the stress tensor and the unit contravariant base vectors:
Where the viscous and turbulent stress tensor is expressed by , in which is the strain rate tensor and is the sum of the kinetic viscosity,, and the turbulent eddy viscosity, .
The physical contravariant component of the strain rate tensor
is given by:
Where indicates the tensor product between two vectors.
By introducing Equations (14) and (15) in Equation (13), on the upper face of the top computational cell, the free surface boundary condition for the dynamic pressure reads:
4. Results
The proposed model is validated thought a breaking wave test and a nearshore currents test in presence of a T-head groin. This model is used to simulate the wave propagation and wave induced currents in the coastal region of Cetraro harbour.
4.1. Breaking Wave Test Case
In this Section, in order to validate the numerical model, we numerically reproduce a wave breaking laboratory test carried out by Ting and Kirby [
21].
In the experimental tank adopted by [
21], cnoidal waves with incident height
and period
propagate towards a beach of
slope. The still water level is fixed at
in the horizontal part of the flume.
For the numerical simulations, the computational grid consists in: 13728 grid cells in the horizontal direction with spacing ; 7 grid cells in the vertical direction.
At the free surface we adopt the boundary condition described in the previous Section. At the bottom, the normal velocity component is set to zero and the tangential ones are calculated by the law of the wall. These boundary condition are assigned on the lower face of the calculation cell closest to the bottom, where the hypothesis of balance between production and dissipation of turbulent kinetic energy holds, because the dimensionless wall distance (calculated at this lower face) has a time-averaged value equal to .
In
Figure 1 the solid line shows the cross-shore distribution of the wave crest elevation obtained by the numerical simulation. The numerical result shows that the initial wave breaking point is slightly anticipated with respect to the predicted location by the experimental results (
).
By considering that a low number of grid nodes along the vertical direction is used, the numerical result is quite in good agreement with respect to the experimental one.
4.2. T-head Groin Test Case
In this Section, in order to validate the numerical model, we numerically reproduce an experimental laboratory test carried out by [
22]. T3C1 is the name of this test and it is described in the data report “LSTF Experiments Transport by Waves and Currents & Tombolo Development Behind Headland Structures” [
22].
The experimental test was carried out on a natural beach with a structure represented by a T-head groin, in which the head section was parallel to the shore, long and located offshore with respect to the shoreline. A random wave train was generated at the boundary opposite to the beach, with a significant breaking wave height, period and an initial incoming wave angle of with respect to the shoreline.
In the computational grid adopted for the numerical simulation, the number of cells in the horizontal plane is , with seven vertical layers. Random wave trains are numerically reproduced by means of a JONSWAP spectrum, with a spectral enhancement factor of .
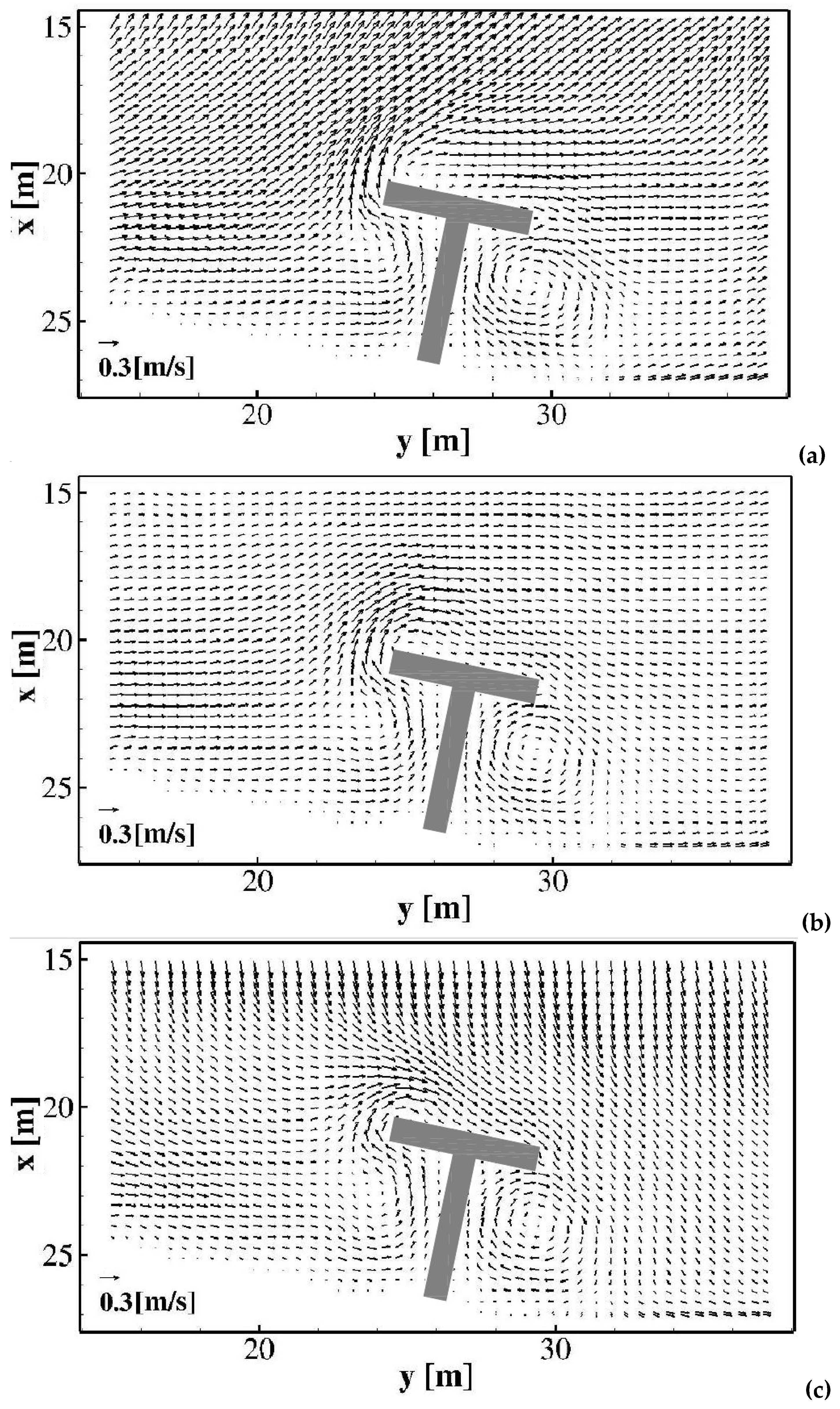
In
Figure 2, a plan view of the time-averaged velocity fields at three different position along the vertical direction (near the bottom, at an intermediate position along the vertical direction and near the free surface) is shown. The simulated velocity field is characterized by the presence of an eddy close to the structure, between
and
and between
and
.
From
Figure 2a–c, it can be noted that near the bottom the currents are more offshore-directed, while near the free surface the currents are more onshore-directed. From
Figure 2b, it can be noted that, at an intermediate position along the vertical direction, the currents are parallel to the shoreline. The different directions of the currents demonstrate the presence of the undertow current, which is offshore-directed near the bottom and onshore-directed near the free surface.
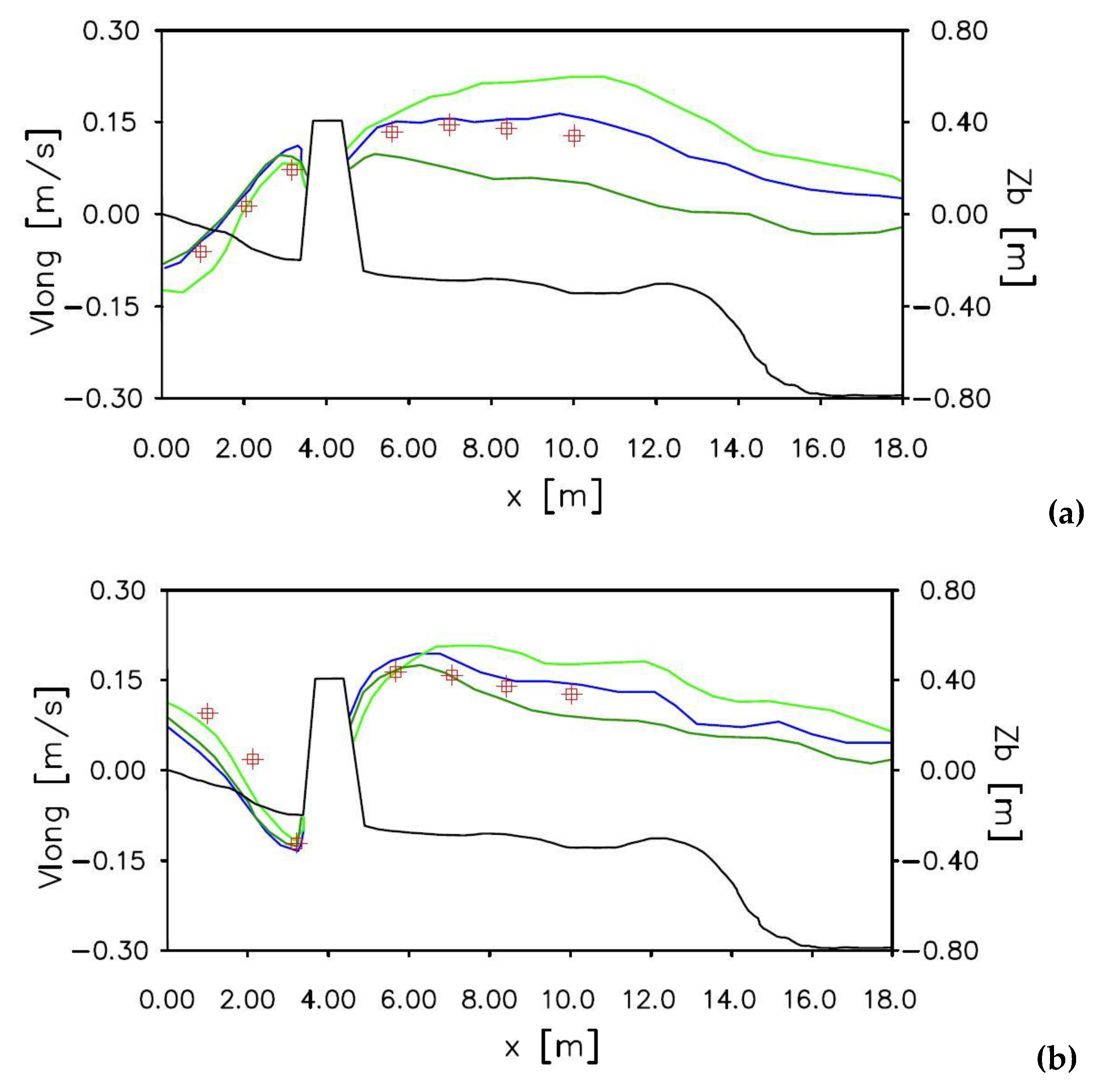
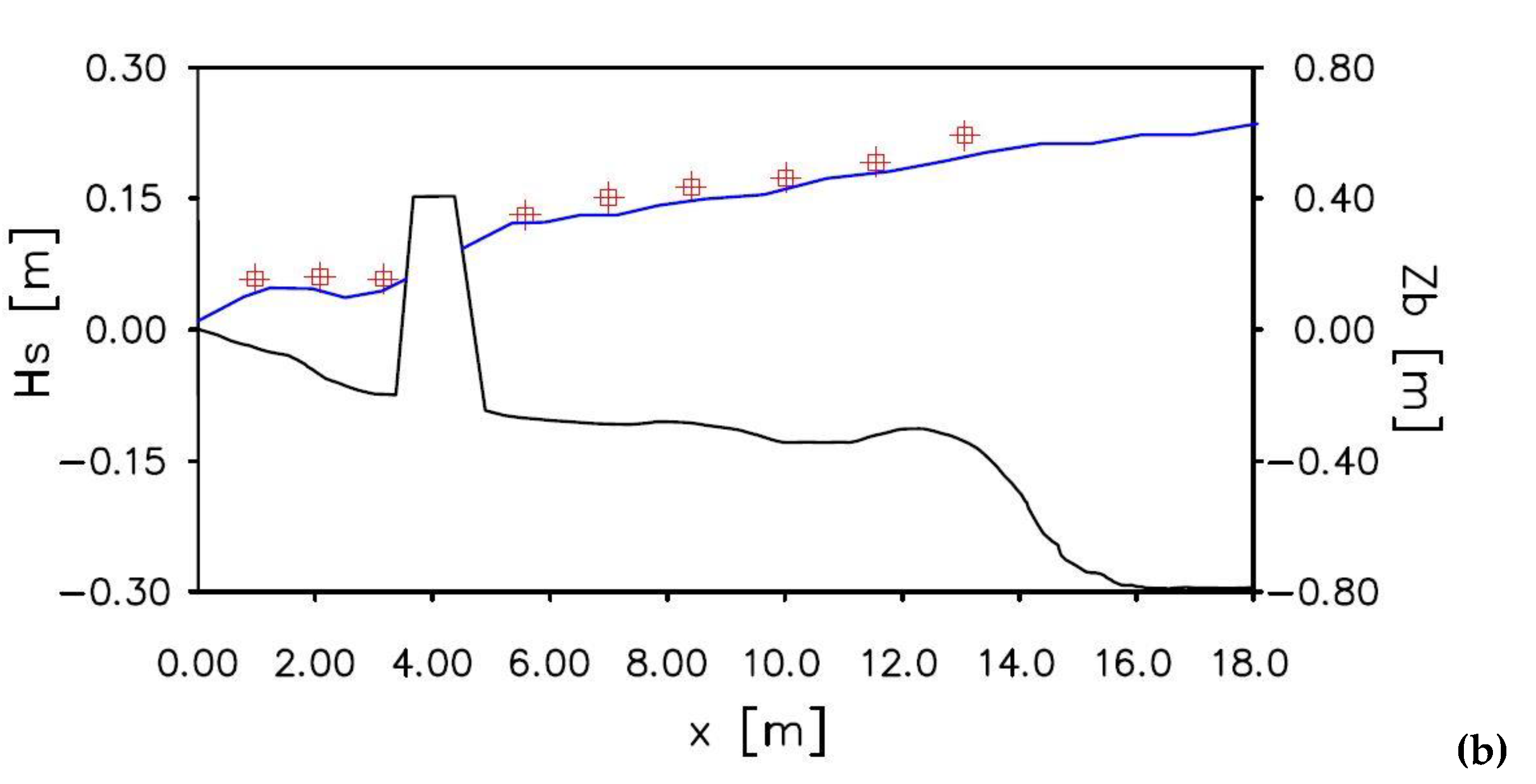
In
Figure 3, the comparison between the experimental measurements obtained by [
22] and the numerical results in terms of long-shore currents are shown in two different sections
and
. The blue lines, in
Figure 3a,b, show the depth-averaged longshore velocity compared with the experimental measurement (red square). The green lines show the velocity measured at two different position from the free surface, near the bottom
(light green line) and near the free surface
(green line).
It is possible to notice that the numerical results of the depth-averaged longshore velocity, shown in
Figure 3a, slightly overestimate the experimental measurements. From
Figure 3b it is possible to notice that the numerical results slightly underestimate the experimental measurements between the shoreline and the T-head groin, while overestimate the same measurements in the offshore zone.
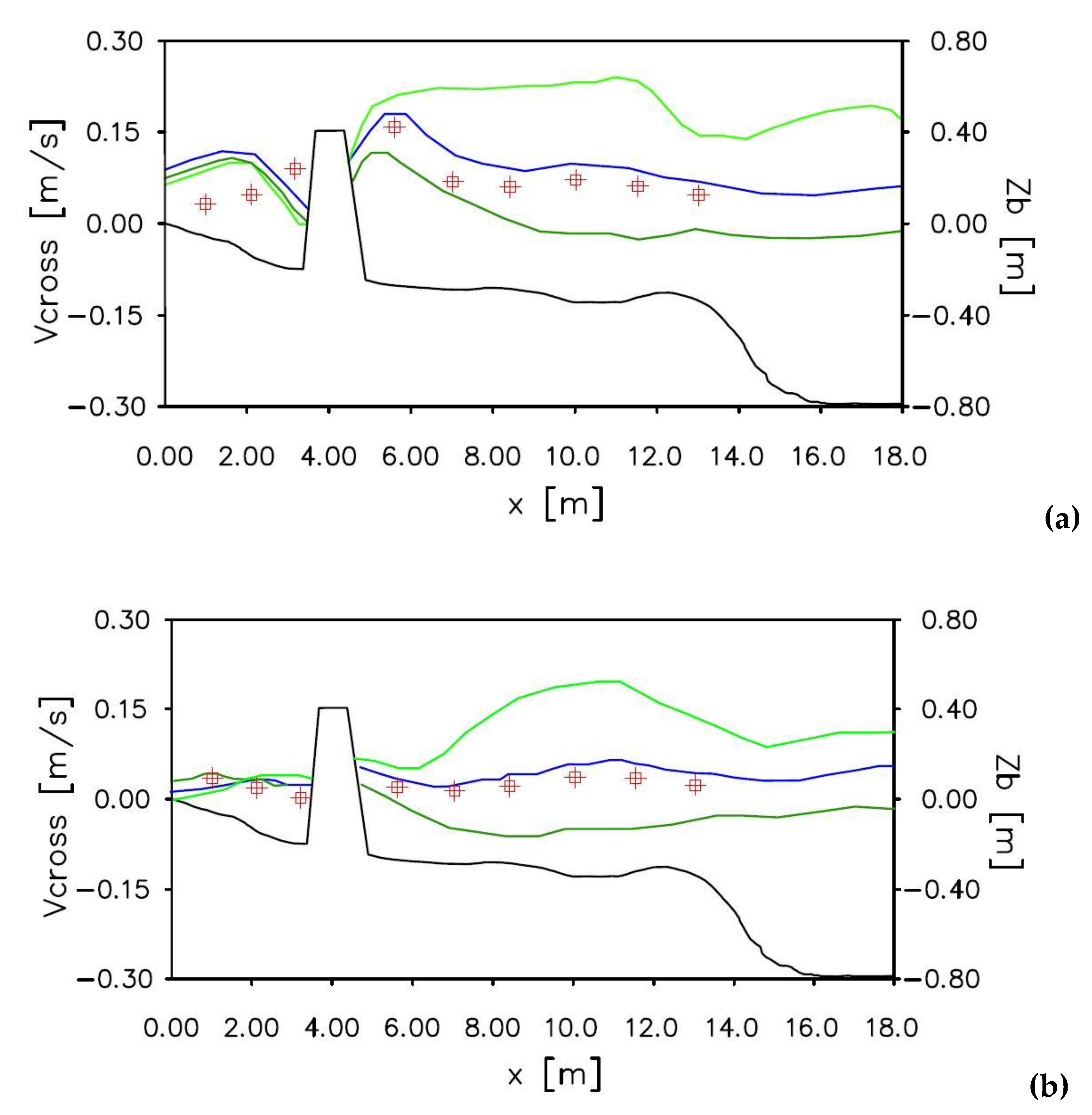
In
Figure 4 the comparison between the experimental measurements obtained by [
22] and the numerical results in terms of cross-shore currents are shown in two different sections
and
. The blue lines, in
Figure 4a,b, show the depth-averaged cross-shore velocity compared with the experimental measurements (red square). The green lines show the velocity measured at two different position from the free surface, near the bottom
(light green line) and near the free surface
(green line).
From
Figure 4a it is possible to notice that the depth-averaged cross-shore velocity is slightly overestimated by the numerical results from
to
, while from
it is slightly overestimated. From
Figure 4b it is possible to notice that the depth-averaged velocity is in quite good agreement with the numerical results.
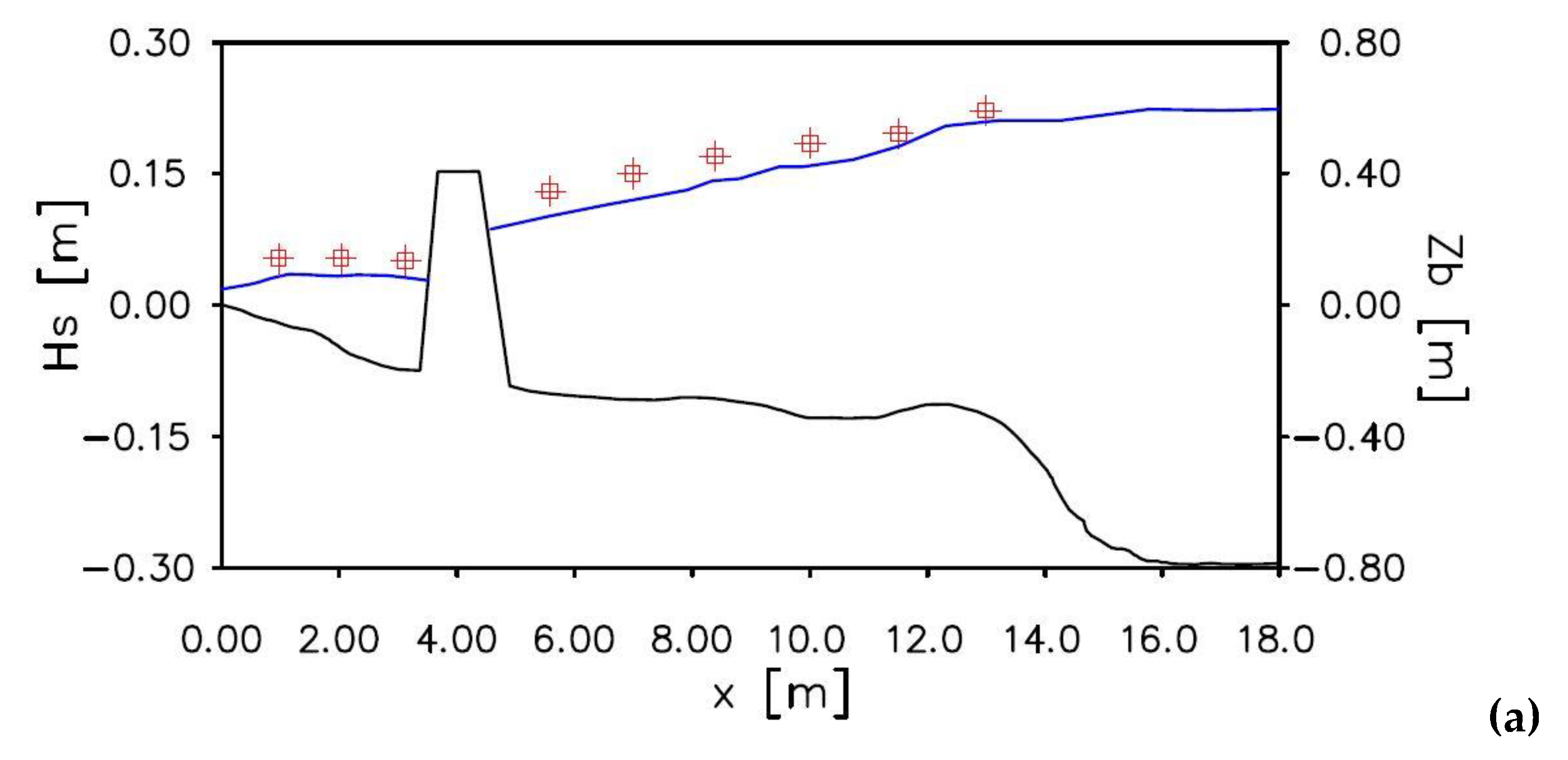
In
Figure 5 the comparison between the experimental measurements by [
22] and the numerical results in terms of the significant wave height is shown. The results obtained in the sections
and
are shown in
Figure 5a,b. Both the comparisons show that the significant wave height obtained by the numerical model is in good agreement with the experimental measurements.
4.3. Wave Induced Currents in the Cetraro Harbour (Italy)
In the present paper the proposed model is used to simulate the wave propagation and wave induced currents in the coastal region of the Cetraro harbour. A plan view of this coastal region is shown in
Figure 6a. The numerical simulations are carried out in two different geometric configurations: a first one, denominated present configuration, that reproduces the geometry of the coastal defence structures currently present in the harbour area; a second one, denominated project configuration, that reproduces the presence of a breakwater designed to modify the coastal currents in the area opposite the harbour entrance during the storm events that are considered more significant for the coastal sediment transport.
4.3.1. Wave Fields and Wave Induced Currents in the Present Configuration
As shown in
Figure 6b, in this coastal region, the most frequent waves come from
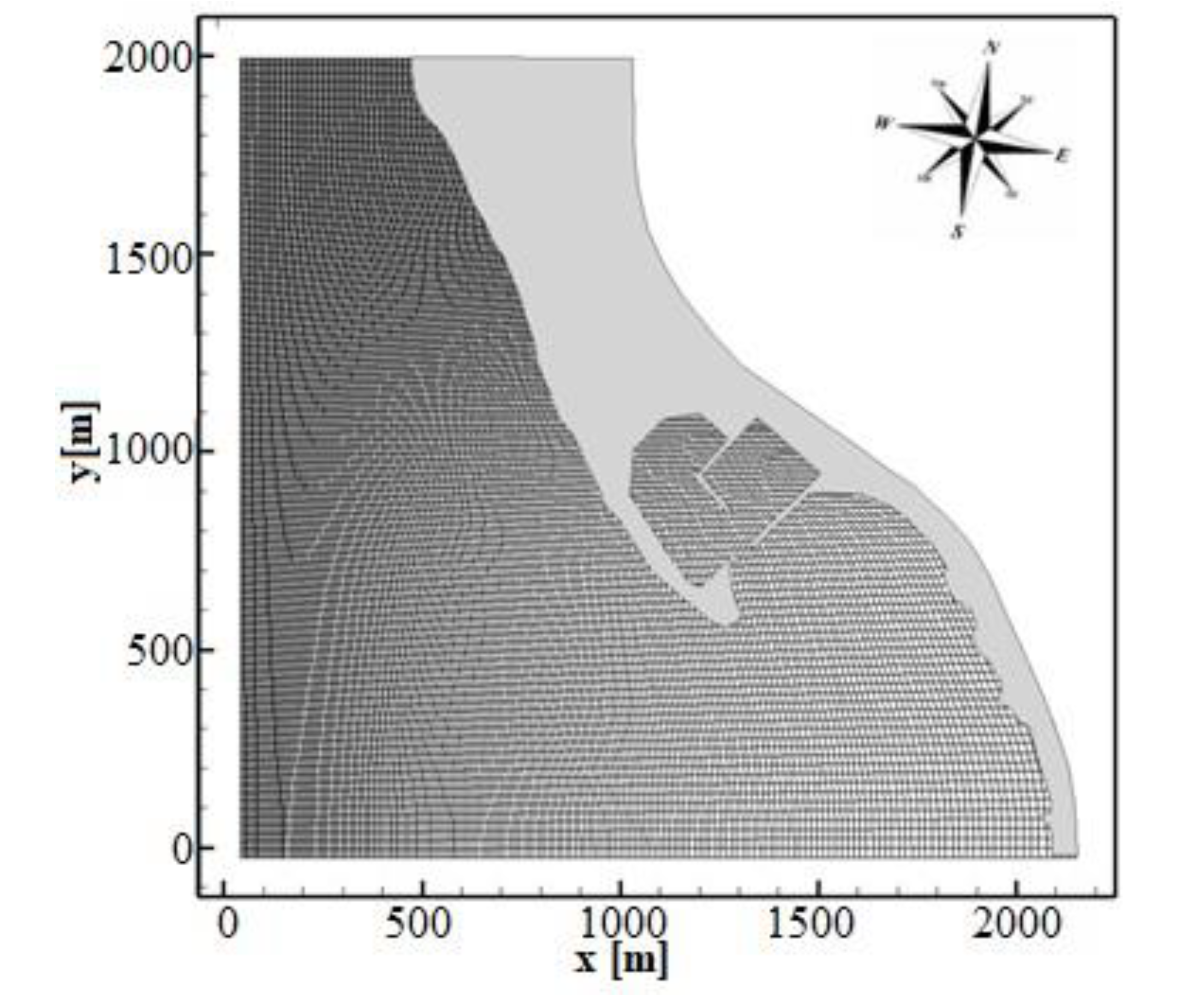
North. Among them, the most significant wave event for the coastal sediment transport has a deep-water wave height between 3 m and 4 m. In order to simulate the wave fields and currents, that affect the region of Cetraro harbour during these significant wave event, the physical domain shown in
Figure 7 is discretized by a boundary conforming curvilinear grid that reproduces approximatively
in the horizontal directions. In the present three-dimensional study, the number of grid cells in the horizontal directions are
.
A plan view of the computational grid that reproduces the present configuration is shown in
Figure 7, in which only one curvilinear coordinate line out of 6 is drawn. The spatial step of the grid in the horizontal direction ranges approximatively from
to
. For the discretization along the vertical direction, just
uniformly distributed grid cells are used. This implies a maximum spatial step in the vertical direction that, in the initial still water condition, ranges approximatively from
(in the deep-water region) to
(near the beach). The left (West) boundary of the computational grid is directed perpendicular to the direction of the significant incoming waves (
North). Thus, in all the numerical simulations the wave input is assigned on the West boundary, where random waves characterized by a JONSWAP spectrum with peak period equal to
and significant wave height equal to
are numerically generated. In the North and South open boundaries, zero gradient boundary condition for the free surface and velocity are imposed. The simulated duration of the wave event produced by the above-mentioned input wave is 1 h. By using a
nodes cluster, every simulation lasts approximately
days.
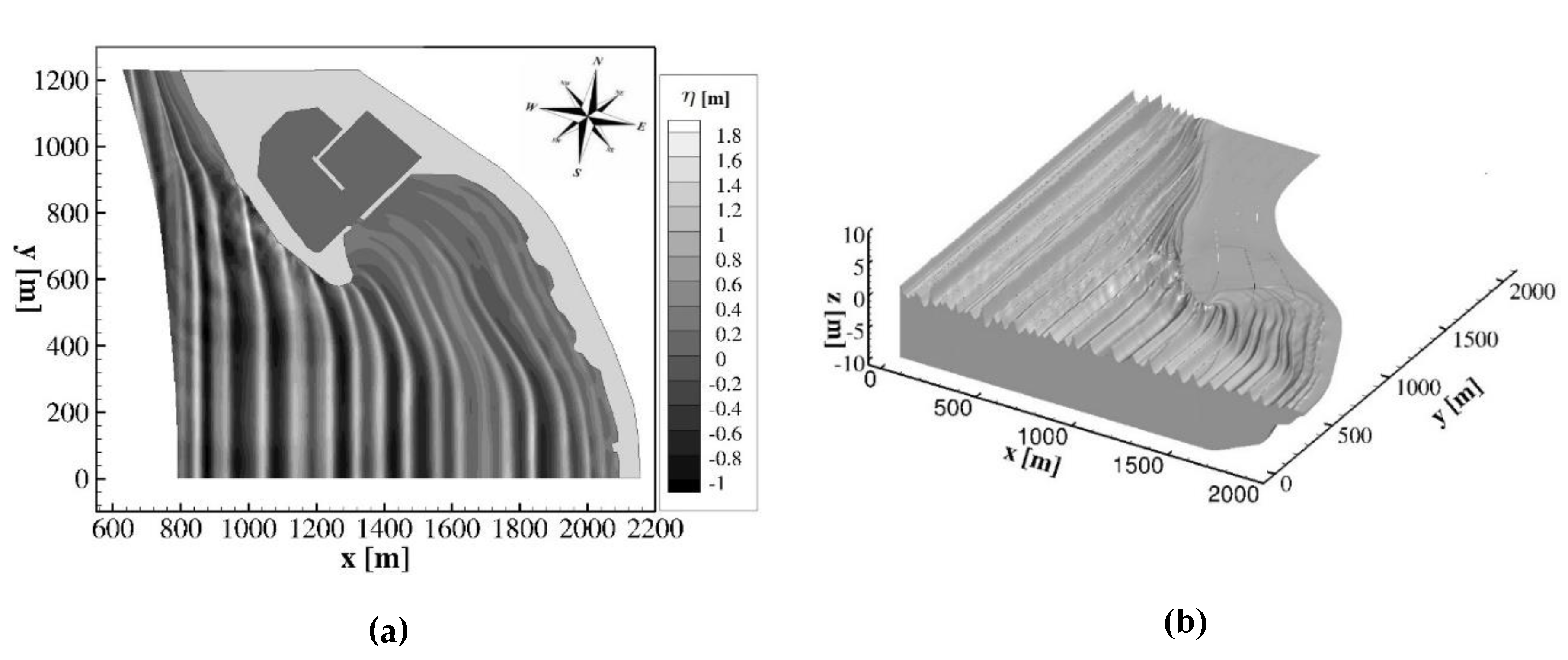
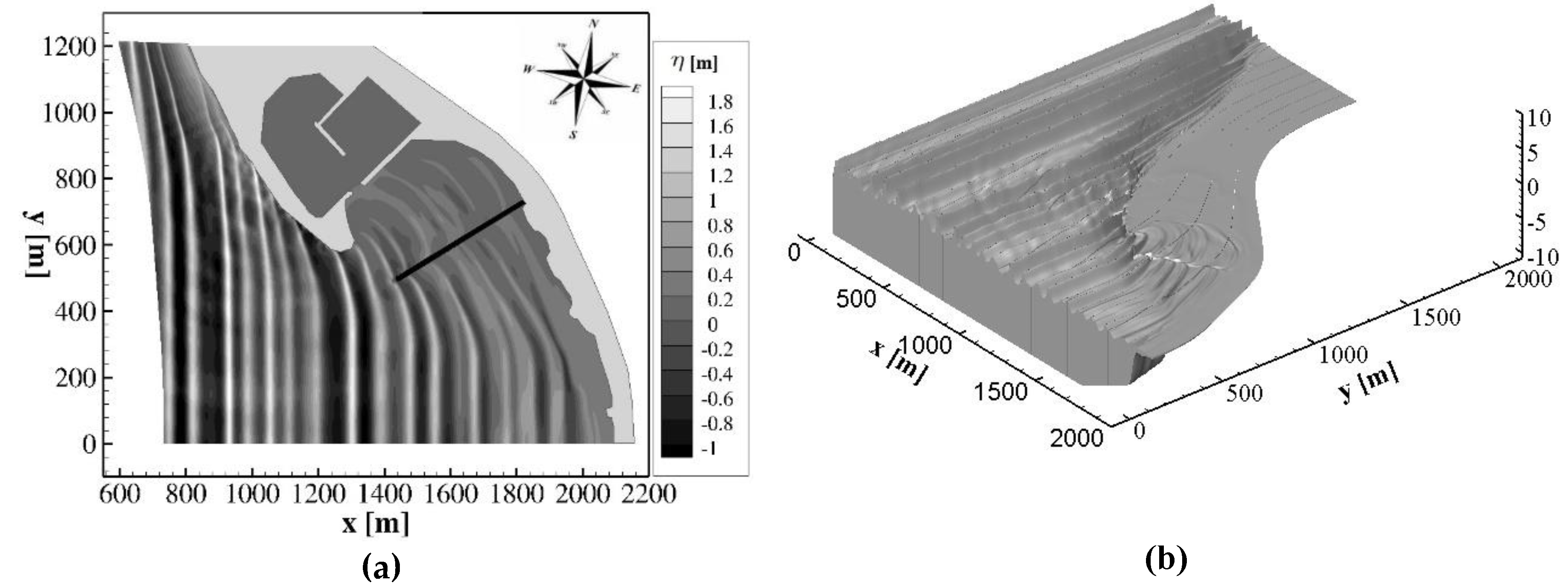
In
Figure 8a,b, respectively, a plan view and a three-dimensional view of the wave field obtained by the proposed numerical model in the coastal area of Cetraro harbour during the above-mentioned wave event are shown. From these figures it is possible to see the propagation of the wave fields from the deep water region to the coastline: it can be noted the wave reflection in correspondence of the vertical walls (
) of the existing breakwater and the wave diffraction around the southern end of it.
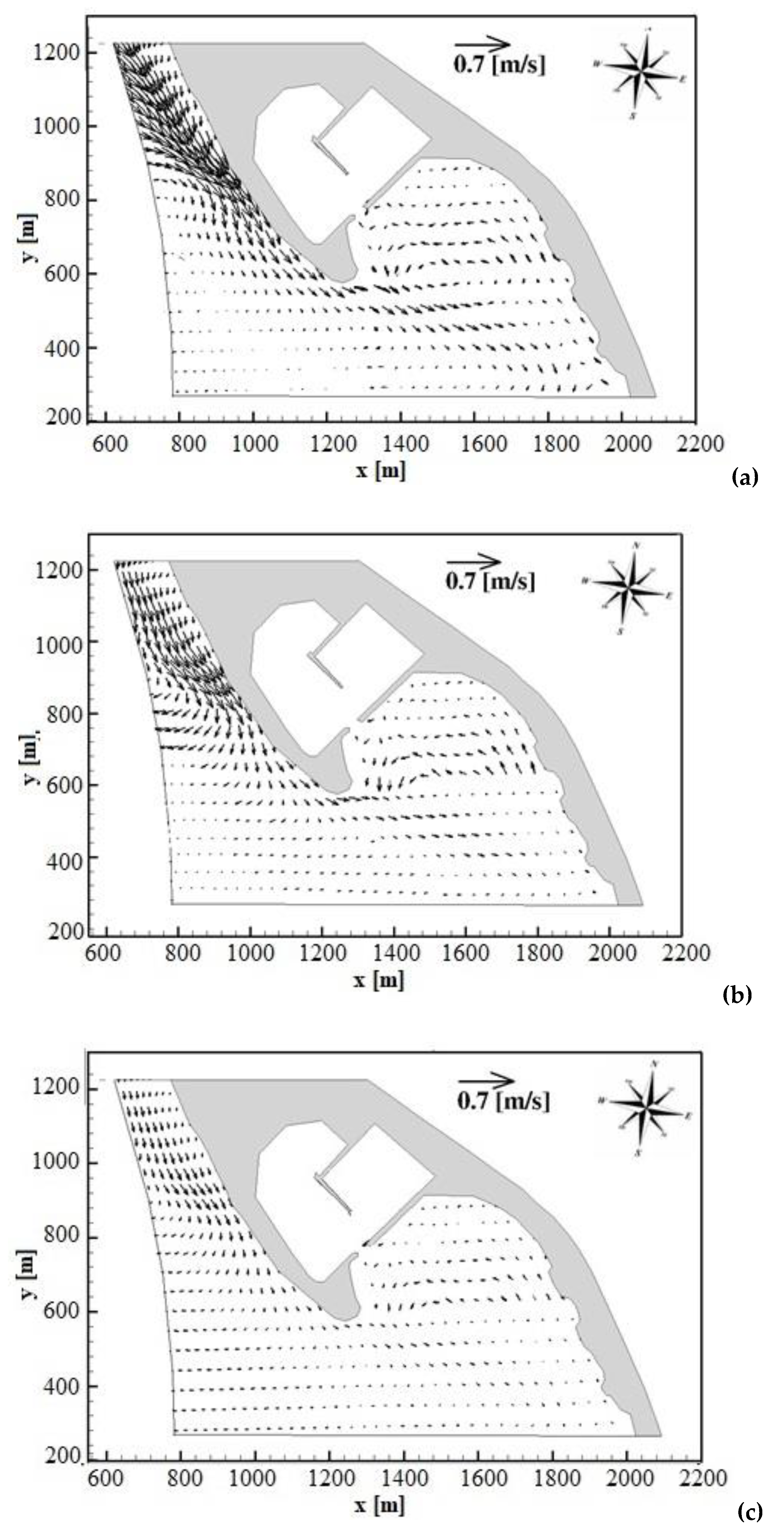
In order to calculate the coastal currents that are produced during the above-mentioned wave event in the Cetraro harbour costal region, for each simulation, after eliminated a simulated transitory period of 30 min, the instantaneous three-dimensional velocity field, obtained during the simulation, are averaged over a further simulated period of 30 min. The results are shown in
Figure 9a, where the time averaged velocity fields near the free surface are drawn by black arrows (one velocity out of
is shown). As it is possible to see from
Figure 9a, the intensity of this current decreases in the area south of the breakwater, where less steep bottom variations induce less shoaling and breaking phenomena. At the southern limit of the simulated coastal region, where the waves approach to the coastline with a minor incident angle, a smaller intense longshore current can be seen. Furthermore, from
Figure 9a it is possible to note that in the coastal area sheltered by the existing breakwater (
and
) a significant anticlockwise recirculation pattern of the coastal current occurs. In this area, a current directed from SE to NW along the coastline reaches the area opposite the Cetraro harbour entrance, where it undergoes an anticlockwise rotation.
In this figure it is possible to see that in the northern part of the simulated coastal region a significant longshore current directed from NW to SE takes place during this wave event. In this coastal area the waves approach to the shallow water near the beach with a high incidence angle and undergo a shoaling and breaking phenomenon that is highly not uniform along the y direction. This produces a significant component of the free surface gradient in the longshore direction that drives an intense current in the same direction.
In
Figure 9b the time averaged velocity field at intermediate water depth calculated during the numerical simulation is shown. In most of the simulated coastal region, this velocity field is similar to the one calculated near the free surface. The main differences with respect to the latter can be observed in the deep-water region (
) where the current at intermediate water depth shows a more intense offshore directed component.
In
Figure 9c the time averaged velocity field calculated near the bottom is shown. From this figure it can be observed that the structure of the coastal current near the bottom is similar in direction and lower in magnitude with respect to the one calculated at intermediate water. From the numerical results shown in the previous figures it can be deduced that, during the simulated wave event, in the coastal area sheltered by the existing breakwater (
and
), in correspondence of the Cetraro harbour entrance, a significant anticlockwise recirculation pattern of the coastal current occurs. Part of this recirculation pattern is due to a current that is directed along the coastline, from SE to NW, and reaches the area opposite the Cetraro harbour entrance, where it undergoes an anticlockwise rotation. In this area, where the wave energy is lower than the one previously described, the sediment picked up by the wave energy in the surf zone and transported by the currents along the coastline tends to settle. The main negative effect of this hydrodynamic process is a progressive silting that affects the area opposite the Cetraro harbour entrance.
4.3.2. Wave Fields and Wave Induced Currents in the Project Configuration
In order to modify the structure of the coastal currents, that take place in this coastal area during the significant wave event and avoid the future siltation of the Cetraro harbour entrance, a new breakwater, approximately
long, has been designed. In order to assess the effectiveness of this solution, by the proposed three-dimensional model, a numerical simulation of the wave field and wave induced currents in the project configuration is carried out by imposing the same wave input of the previous configuration, for the same simulated period. In
Figure 10a,b a plan view and a three-dimensional view of the wave field obtained by the proposed numerical model, during the above-mentioned wave event, in the Cetraro harbour project configuration is shown. In
Figure 10a it is possible to see the position of the designed breakwater (drawn in black).
From these figures (
Figure 10a,b) it is possible to see that, the wave field propagation is modified by the presence of the designed breakwater only in proximity of its offshore end, where some wave reflection occurs.
In
Figure 11, the simulated time averaged velocity fields, respectively, near the free surface, at intermediate water depth and near the bottom are drawn by black arrows (one velocity out of
is shown).
As can be seen from these figures, the presence of the designed breakwater significantly modifies the structure of the currents in the area of the harbour entrance. In the project configuration, the anticlockwise recirculation pattern that takes place in the area sheltered by the existing breakwater ( and ) is limited to the area at the SE of the designed breakwater. The presence of the designed breakwater prevents the SE–NW directed longshore current to reach the Cetraro harbour entrance. This barrier would have the positive hydrodynamic effect of preventing the accumulation of new sediment in the area opposite the Cetraro harbour entrance.