Abstract
In this study, the level set (LS) and immersed boundary (IB) methods were integrated into a Navier–Stokes equation two-phase flow solver, to investigate wave-structure interactions and induced motions of floating bodies in two dimensions. The movement of an interfacial boundary of two fluids, even with severe free-surface deformation, is tracked by using the level set method, while an immersed object inside a fluid domain is treated by the IB method. Both approaches can be implemented by solving the Navier–Stokes equations for viscous laminar flows with embedded objects in fluids. For accurate treatment of the solid–liquid phase, appropriate source terms as forcing functions to take into account the hydrodynamic effects on the body boundaries are added into the governing equations. The integrated compact interfacial tracking techniques between the interfaces of gas–liquid phase and the solid–liquid phase allow the use of a combined Eulerian Cartesian and Lagrangian grid system. Problems related to the fluid-structure interactions and induced motions of a floating body, such as (a) a dam-break wave over a dry bed; (b) a dam-break wave over either a submerged semicircular or rectangular cylinder; (c) wave decomposition process over a trapezoid breakwater; (d) a free-falling wedge into a water body; and (e) wave packet interacting with a floating body are selected to test the model performance. For all cases, the computed results are found to agree reasonably well with published experimental data and numerical solutions. For the case of modeling wave decomposition process, improved solutions are obtained. The detailed features of flow phenomena described by the physical variables of velocity, pressure and vorticity are presented and discussed. The present two-phase flow model is proved to have the advantage of simulating the cases with induced severe interfacial oscillations and coupled gas (or air) motions where the single-phase model may miss the contributions of the air motions on the interfaces. Additionally, the proposed method with uses of the LS and IB methods is demonstrated to be able to achieve the reliable predictions of complex flow fields.
1. Introduction
Obtaining solutions of a hydrodynamic model for the studies of complex two-phase flows, such as the propagation of surge fronts, movement of free-surface by a moving body, or waves pass over either completely or partially immersed structures, is an important subject in coastal and ocean engineering applications [1,2]. The key issue of modeling free-surface flows is the treatment of moving interfaces because the physical variables describing the free-surface boundary conditions are not known a priori. The aspect of solving the free-surface flow problem is mainly the description of the mesh movement, using one of the following methods: Eulerian [3,4,5,6], Lagrangian [7,8,9,10], or arbitrary Lagrangian–Eulerian [11,12,13,14].
In the Eulerian method, the coordinates of the grid points are fixed during computation. The main advantage of this method is that the two-phase flow can undergo large deformations. Notably, the significant studies of the Eulerian method are to track the fluid interfaces as the fluid moves through the meshes. The most popular method under this category is the volume of fluid (VOF) method [4], which was originally developed for finite volume method, and the marker and cell (MAC) method [4,15]. In the VOF method, the conservative principle of the volume fraction that moves in the fluid field is applied. The other methods used for tracking the free-surfaces in two-phase flow modeling include the level set method [16,17,18] and the front-tracking method [19,20,21,22]. In the Lagrangian method, it qualitatively gives accurate free-surface shapes that moves with a fluid particle. However, the numerical errors may be introduced due to the overly twisted of re-mesh. Notably, the implementation of this scheme in three dimensions would be very difficult indeed. The advantages of both the Eulerian and the Lagrangian methods are combined to yield the arbitrary Lagrangian–Eulerian (ALE) technique, in which the grid points can be moved independently of the fluid motion. As far as the ALE method is concerned, the nodes in the interior of the domain are displaced in an arbitrarily prescribed way to obtain a mesh of proper shape and thus to avoid mesh crossing. The ALE method can be considered as a moving deformable control volume problem in which the node velocity is different from the fluid velocity. However, the drawback of the ALE method is that the mesh regeneration is not an efficient technique.
While computational fluid dynamics (CFD) used for solving incompressible Navier–Stokes equations remains an important subject, the development of new and effective numerical algorithms for tackling challenging CFD problems have been observed, together with the advancement of the computer technology for simulation efficiency. Solutions for flow-structure interactions with irregular geometries is one of such significant subjects. The simplicity in generating the structured Cartesian grids finds a niche for implementing numerical formulations in comparison with other grid systems, such as body-fitted or unstructured meshes. The present study has thus selected the coordinates in the fluid domain, with the grid points to be fixed in space and time throughout the computation. The fluid can still undergo large deformations without a loss of required accuracy while using the fixed grid system. The immersed boundary (IB) method, first proposed by Peskin [23,24], involves a combined Eulerian and Lagrangian grid system approach, while all the target regions are simulated by using a Cartesian coordinate system. The effect of an immersed object can be modeled through the introduced forcing terms on the right-hand side of the Navier–Stokes equations. Notably, this method enables the application of simple orthogonal grid lines to irregular objects. This approach is particularly effective for analyzing moving objects. The IB method has been applied by various scholars [25,26,27,28,29,30,31]. This continuous forcing IB method is also implemented in the present study to solve the Navier–Stokes equations involving a fixed or moving obstacle interacting with fluids. Evidently, the usage of Cartesian grid system in the imposition of boundary conditions at an immersed boundary is complicated. As the immersed boundary can cut through the underlying Cartesian meshes in an arbitrary manner, the main challenge is to formulate a boundary treatment which does not adversely affect the accuracy and the conservation properties of the numerical solvers.
One of the contributions of the present study made to the LS and IB methods is to use a combined Eulerian Cartesian and Lagrangian grid system, to avoid the re-meshing procedure for two-phase flow model involving coupled fluid-structure interaction. A fourth-order Runge–Kutta integration in time and WENO scheme [32] in space are adopted to discretize the LS equation to track the free-surface positions with severe deformations, including wave breaking. Geometries featuring the solid obstacles in a flow domain are embedded in the Cartesian grids, with special treatments with discrete surface markers (Lagrangian grid points) to determine the force density vector at the Lagrangian points. It is a straightforward to compute the force density vector at the Eulerian grid points by using a spreading scheme involving the Lagrangian marker points. The solution with velocity and pressure variables can be easily implemented based on the finite difference method on a Cartesian grid system using a fractional-step projection method. Carrica et al. [33] used a dynamic overset grids for the analysis of hydrodynamics of ship motion. The dynamic overset mesh has a good numerical stability over ALE, as constant re-meshing of the solution domain is not necessary. The accuracy of the method lies in establishing the connections between the overset grids and the underlying grid points in the overlapping region. Later, Yang et al. [34] adopted a sharp interface method instead of the overset grids, to handle the coupling computation for solid–fluid interactions, where the interfacial flow was treated with a two-phase method. More recently, Calderer et al. [35] presented a hybrid curvilinear immersed boundary and level set approach for the simulation of air/water interaction with complex floating structures. Additionally, the present study adopts a special treatment based on the normal momentum equation with the pressure projection boundary condition method to calculate the forces on a body. Bihs and Kamath [36] used an open-source CFD code REEF3D for floating body simulations based on a six degrees of freedom (6DOF) algorithm. That model is represented with a combination of the level set method and ghost cell immersed boundary method. Notably, we present a compact and effect two-phase flow code in modeling fluid-structure interactions involving gas, liquid, and solid phases, with the use of a combined Eulerian Cartesian and Lagrangian grid system. In this study, the model is used extensively in simulating complex wave hydrodynamics and fluid-structure interactions, such as the dam-breaking flow, waves over submerged structures, and wave breaking. With a novel approach, the present model is also applied to investigate the dynamic response of a 2D floating body that can move in the three degrees of freedom (3DOF). The proposed numerical model can be comfortably extended to study three-dimensional two-phase flow problems by including a 6DOF algorithm. In this study, a numerically efficient two-phase flow model is developed to simulate two-dimensional nonlinear viscous flows including those initialized by fluid-structure interactions and the motion of floating body. The governing equations with the use of a combined LS and IB approach are solved to investigate the complex viscous free-surface flow problems. The LS method is applied to track the free-surface positions with severe deformations. Numerically, the flow equations with velocity and pressure as the physical variables are discretized over a Cartesian grid system and solved using the projection method and Adams–Bashforth time-stepping finite difference scheme. Featuring the solid bodies in a flow domain, the geometries with Lagrangian-based boundary marker points are embedded in the Cartesian grids with the imposed interpolation treatments, to ensure the accuracy of the solutions in the cut cells. Selected cases, including a uniform flow passing around a cylinder, two cylinders moving against each other in a viscous fluid, dam-break-induced surge waves, a periodic wave over a submerged trapezoidal bar, a free-falling wedge, and a wave packet interacting with a floating body, were simulated to examine the phenomena of interfacial flows involving the computations in gas–liquid and liquid–solid phases. Comparisons between the present modeling results with other published solutions are also carried out to demonstrate the robust and accuracy of the developed two-phase flow model.
2. Research Methods
The two-phase free-surface modeling is briefly described in this section. The level set (LS) and immersed boundary (IB) methods are involved to investigate wave-structure interactions and induced motions of floating bodies.
2.1. Two-Phase Flows Using Level Set Formulation
A two-phase flow model in which the interface between two fluids is captured using a level set (LS) method is developed in this study. Additionally, an immersed boundary (IB) method is adopted to obtain the hydrodynamic forces on structures after the interaction by moving fluids. The movement of the interfacial boundary between two fluids and the calculation of surface tension are based on the fixed grids assigned in the domain. Figure 1 depicts a schematic diagram showing a fixed Cartesian grid system that is used for solving the Navier–Stokes equations. Under the assumption of incompressible fluid medium and considering the effects of surface tension between two fluids and an immersed body, the governing equations for two-phase flows can be formulated as follows:
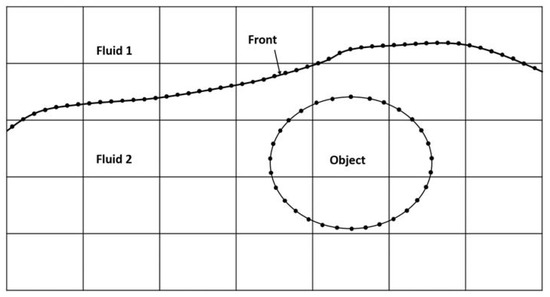
Figure 1.
Computations of flow containing two-phase, including immersed boundary. The governing equations are solved on a fixed grid, but the interface between two fluids is represented by a moving front in which it is consisting of connected marker points, and the immersed object is included in the governing equation by the immersed boundary method.
Here, the computational domain contains two different fluids, and is the Dirac delta function. is the coefficient of surface tension, k is the curvature of an interface, f denotes hydrodynamic forces induced by an immersed body, as defined later represents the wave absorbing coefficient, g is the gravitational acceleration vector, t is time, and denotes the level set function. The 2D velocity vector, describes the velocity components in x and z directions, and p is the pressure. More detailed descriptions of the physical variables given in Equation (2) can be found in Sethian and Smereka [37].
For the level set function, typically, when , it denotes the gas region, while is for the liquid region. The fluid properties, such as the density ( and viscosity can be interpolated according to the following:
where is the Heaviside function [38].
The interfacial thickness of the Heaviside function is approximately , where is a small parameter that is related to the order of the size of the mesh cells close to the interface and can be selected through the numerical tests. The density () and viscosity () with the subscripts l and represent, respectively, the corresponding properties of liquid and gas.
The level set function () describing the interface that moves with the fluid particles is governed by the transport equation:
For the numerical accuracy, a fourth-order Runge–Kutta integration in time and WENO [32] scheme in space are adopted to discretize Equation (5).
In Equation (2), the smoothed delta function can be written as follows:
Moreover, the curvature can be computed as follows:
With the consideration of a wave-absorbing region, the proposed absorbing coefficient () by Lin and Liu [39] is adopted:
where denotes the absorbing coefficient, and and are the starting position and length of the absorbing region. and are the empirical damping related coefficients. Here, the coefficients of = 200 and , as recommended by [39], are used in numerical simulations.
2.2. Numerical Formulations
The governing equations (Equations (1) and (2)) are solved by using the projection method [40], where the predicted intermediate velocity field with the known values obtained at the n (previous) time level are firstly calculated. According to the two-step calculation procedure and Adams–Bashforth time-stepping approach, the solutions of velocity vector at each intermediate (between n and n + 1) time level are determined by solving Equation (2) with the expressions of temporal difference as follows:
where t is the time step, and is the velocity vector at the n time level. The terms with the effects of convection, diffusion, surface tension, wave absorbing, and gravity are combined with a notation of RHS = :
In Equation (10), is an added term describing force density induced by the immersed bodies. Its calculation procedure, based on the IB method, is provided in the following section. With a flow passing over a rigid body, the calculation domain is separated by two phases, where one is the ordinary fluid flow surrounding the rigid body, and the other is the body phase with an inclusion of a body forcing. As can be seen in Equation (10), the velocity vectors, are first computed without considering the effect of immersed boundary. Then, the forcing term, f, is computed by a continuous forcing IB method with the computed velocity vectors, . By imposing a body force, f, in those cells, which has the property of a signed distance function near the immersed boundary, the intermediate velocity field is updated from Equation (10).
Taking the divergence of Equations (1) and (2), the pressure field can be obtained by solving the Poisson equation, which is derived by satisfying the continuity equation:
The pressure Neumann boundary conditions should be satisfied. We have the following:
Once the velocity vectors at the intermediate time level are determined, Equation (12) can be solved, using a spline alternating direction implicit method (SADI) with a standard tri-diagonal matrix solver applied for the calculations of the pressure field. Here, the SADI method is used in the z direction. The iteration consists of a sweep through the i index for each (i, k) pair, solving implicitly for the pressures in the k-index direction, where i and k represent, respectively, the grid indices along x and z directions. Then, the velocity vectors at the new (n + 1) time level can be obtained by solving the following equation:
In terms of the evaluation of the level set function () for capturing the positions of the two-phase interfaces, Equation (5), when expressed in Lagrangian description, is given as follows:
where in Equation (15) is an approximation (e.g., WENO approximation in these lecture notes). Using a uniform grid in one space dimension as an example, Equation (15) results in an ordinary differential equation (ODE) with a discrete conservative finite difference scheme.
Then, the fourth-order Runge–Kutta scheme, as shown below, is used to advance the interfaces:
where is the coordinates of the interfacial points from the previous time step, and are obtained as follows:
Here, the computed are used as the advection needed velocity field for the calculation of the level set function.
2.3. Immersed Boundary (IB) Method
The IB method basically follows the concept that the effect of an immersed structure on its surrounding flow is modeled through a force density vector (f), which is included in the Navier–Stokes equations. Figure 2 depicts an example plot showing the arrangement of the Eulerian and Lagrangian grid points used for transferring the values of variables between them through an interpolation procedure with a weighted sum of regularized Dirac delta function, . Here, the body boundary (fluid–solid interface) is distributed with discrete surface markers (Lagrangian grid points). The force density vector (f) on the right-hand side of Equation (2) can be formulated as follows:
where is the force density vector at the Lagrangian points with coordinates along the body boundary. The values at Lagrangian points are computed beforehand and then transferred into the Eulerian meshes for , using Equation (21). The discrete Dirac delta function developed by Peskin [23] is adopted in this study. The expression of for a 2D case is given as follows:
where is the regularized one-dimensional delta function. The formulations of , proposed both by Roma et al. [25] and Yang et al. [29], are as follows, respectively:
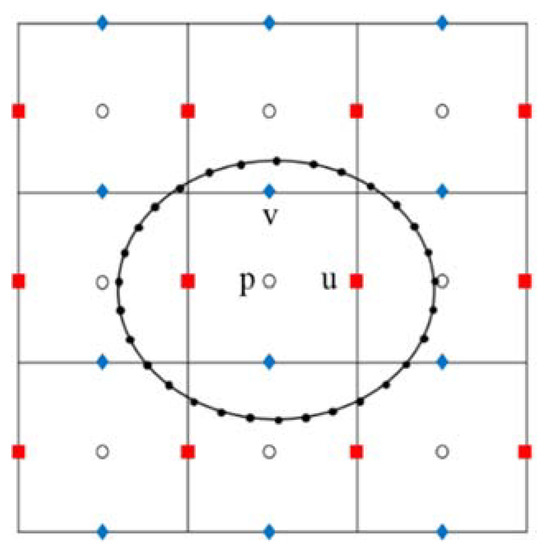
Figure 2.
Arrangements of staggered Cartesian grid and embedded interface with marker points in a two-dimensional case.
These equations are used together with the selection of the influential radius, r, to be either (Equation (23)) or (Equation (24)) for the numerical sensitivity study. The force density vector, , at the interfacial Lagrangian marker points is calculated based on the time rate change of velocity between the body velocity ( and the Lagrangian point velocity (:
where the velocity vector ( of an immersed body is determined from the equations of motion. Accordingly, the force density vector (f) at the Eulerian grid points can be calculated by using a spreading scheme involving the Lagrangian marker points as follows:
where is the control volume defined about the m-th Lagrangian marker. The resulting Eulerian force (f) from Equation (27) is then substituted into Equation (10) for solution computation.
2.4. Rigid Body Dynamics
The movements of a body subject to the external forces and moments are governed by the equations of motion for linear and angular momentum of a rigid body. In this vertical two-dimensional modeling study, the equations of motion for a body subject to external forcing can be formulated by considering the effects of inertial motion and internal mass. According to [41], the equations describing the translational and rotational motions of a moving body are expressed as follows:
Here, , , and are volume, moment of inertia, and density of the body, respectively; is the fluid density; represents the position vector relative to the body centroid, is the vector of gravitational acceleration, and the symbol denotes the cross product. and are respectively the translational and angular velocity vectors of the rigid body. In the present study, the Euler forward difference method is used to solve Equations (28) and (29) for and . The velocity vector at the surface of the rigid body can be calculated as follows:
3. Results and Discussions
Using the developed 2D two-phase flow model that integrates the approaches of level set (LS), immersed boundary (IB), and structural responses, selected fluid-structure interaction problems are investigated. The study cases include the following: (a) a uniform flow passing through a circular cylinder to verify the adopted IB methodology, (b) two cylinders moving against each other to test the moving boundary effect, (c) dam-break flows to examine the free-surface tracking capability, (d) dam-break wave flowing over a submerged structure, (e) wave decomposition process over a submerged trapezoid breakwater, (f) a free-falling wedge, and (g) wave packet interacting with a floating body. It should be noted the simulations carried out involve the interfacial conditions specified at the gas–liquid phase and the liquid–solid phase.
3.1. Flow Passing through a Cylinder
In order to verify the present IB method, cases with steady uniform flows passing through a circular cylinder are simulated for validation. The flow results are obtained at Re = 20, 40, 80, 100, and 200, where Re is the Reynolds number defined as Re = UD/υ. Here, υ denotes the kinematics viscosity of a fluid, U is the uniform flow velocity, and D denotes the diameter of the cylinder. In the test cases, a cylinder with a diameter of one unit is embedded in a 32 × 16 computational domain. Upstream flow velocity of one unit is assumed to be uniformly distributed in vertical direction. The accuracies of the predicted drag and lift coefficients, and other physical variables for the selected cases, are evaluated. For the flow conditions of Re = 20 and 40, the computed reattachment length, Lw, and drag coefficient, CD, as given in Table 1, are compared with the published experimental [42] and numerical [43,44,45,46,47] results. Additionally, to ensure the grid independence, included in Table 1 are the present results for the separately used mesh sizes of ∆h = 1/30 and ∆h = 1/40. As can be seen in Table 1 for the cases of Re = 20 and 40, the converged solutions in Lw and CD are obtained, and they are in good agreements with other published results. By refining the computational grids, it is shown to be able to improve the solutions for the flow conditions at a larger Reynolds number, such as Re = 100 or 200; this confirms the global accuracy of the present method. Comparisons between the present and other numerical results [43,46,47,48,49,50] of the drag and lift coefficients (CD and CL), and Strouhal number (St) for the cases of Re = 100 and 200 are summarized in Table 2. The present results were computed by using a refined grid size, i.e., ∆h = 1/50. It can be seen the present results are shown to have very good agreements with others given in the literature. For the cases of Re = 100 and 200, the transient solution procedure was carried out to reach the prescribed time, i.e., t = 200. Time variations of the dimensionless drag and lift coefficients at Re = 200 are presented in Figure 3. Due to the induced vortex motions, the transition processes until the CD and CL approach to the stabilized periodic variations are clearly depicted in Figure 3. Figure 4 exhibits the instantaneous distribution patterns of pressure and vorticity at t = 200 for various Reynolds numbers of 40, 80, 100, and 200. The patterns of vortex shedding for the cases of Re = 80, 100, and 200 can be clearly observed. The predicted results of vortex shedding demonstrate the proposed method can predict accurately the transient flow patterns. As can be seen, the wake triggered at the cylinder surface is asymmetric in reference to the direction of flow. The formation of vortices on either side of the flow direction does not simultaneously occur. In fact, the shedding of vortices alternates from side to side, which had been observed in experiments. Thus, the pressure distribution around the obstacle is asymmetric about the flow direction.

Table 1.
Drag coefficient and reattachment length for flow past a stationary cylinder at Re = 20 and Re = 40.

Table 2.
Drag and lift coefficients and Strouhal number for flow past a stationary cylinder at Re = 100 and Re = 200.
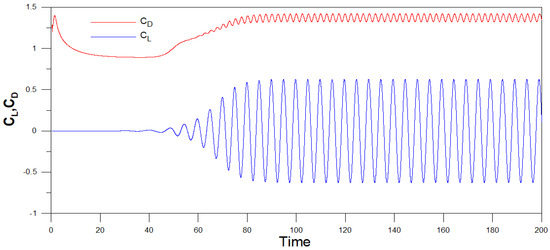
Figure 3.
Drag and lift coefficients at Re = 200.
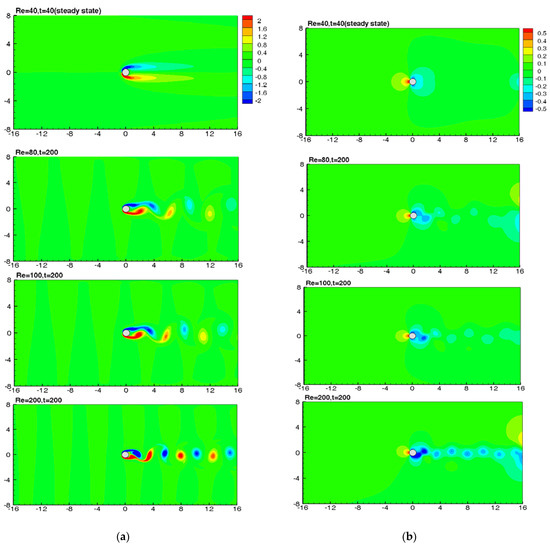
Figure 4.
Instantaneous distribution patterns of (a) vorticity and (b) pressure at t = 200 for a uniform flow past a cylinder at Re = 40, 80, 100, and 200.
3.2. Two Cylinders Moving Against Each Other in Viscous Fluid
The present model is further tested to examine the hydrodynamic effect induced by two cylinders moving in opposite directions, in a domain of viscous fluid. Again, each of the two moving cylinders has a diameter of 1 unit, and the computational domain is 32 × 16. The constant velocities of the upper and lower moving cylinders are set respectively as −1 and 1 units. As shown in Figure 5, the centers of the two cylinders are initially placed at the locations of (0, − 0.75) and (16, 0.75), separately, within the domain ranges of −8 ≤ x ≤ 24 and −8 ≤ z ≤ 8.
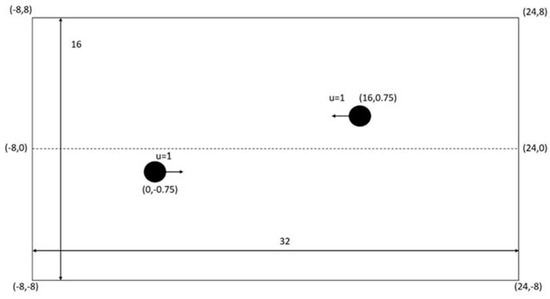
Figure 5.
Schematic diagram of two moving cylinders in a viscous fluid domain.
To test the sensitivity of the grid size on the model solutions for this moving boundary problem, the set computational grid systems include 640 × 320, 960 × 480, and 1280 × 640. The time step was selected to satisfy the Courant–Friedrichs–Lewy (CFL) condition [51]. The CFL for n-dimensional domain can be generalized as . Here, C is the Courant number, , , is the grid size in the ith dimension, which can be a varied value in a given dimension, denotes the magnitude of velocity in the ith dimension (A two-dimensional case is used here), and represents the fractional time-step. is typically set to be equal to 1. Figure 6 presents the time variations of the dimensionless lift coefficient for the upper cylinder at Re = 40. The results from Russel and Wang [44] are also included in Figure 6, for comparisons. Russel and Wang [44] presented an efficient method based on an underlying Cartesian grid for solving 2D incompressible viscous flows around multiple moving objects. It can be seen the present results agree well with those from [44], especially under the grid system of 1280 × 640 (i.e., ∆h = 1/40). The time varying drag coefficient (CD) and lift coefficient (CL) for the upper cylinder under the conditions of various Reynolds numbers are shown in Figure 7. From Figure 7, it is noted that, for all cases, the minimum values of the drag coefficient occur roughly at , where = Ut/(D/2); meanwhile, for the lift coefficient, the minimum values take place at a delayed time of around = 18. In general, the results show that the drag coefficient and the positive portion of the lift coefficient decrease with an increase in the Reynolds number. The transitions of the drag and lift coefficients become particularly pronounced at the timeframe from = 14 to = 20. In addition, to demonstrate that the present model is capable of successfully simulating the flow fields, Figure 8 depicts the instantaneous vorticity contours of two moving cylinders for Re = 100 at four selected instants. The color-coded vorticity contours range from −5 to 5. In this transient simulation study, the results of hydrodynamic effect and vortex shedding phenomena under the condition of two cylinders moving against each other in viscous fluid are found to be completely different when compared to those for a single moving body at the same Reynolds number. Due to the viscous effect within the boundary layers of the solid bodies, the moving rigid bodies are noticed to play an important role in generating the vortex flow in the immersed viscous fluid domain.
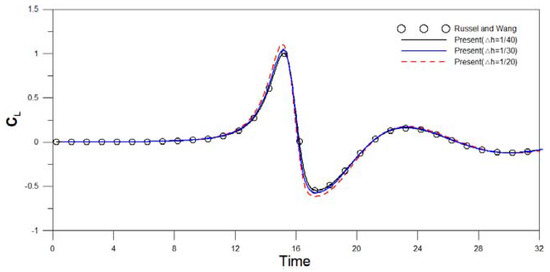
Figure 6.
Comparisons of lift coefficient on the upper cylinder at Re = 40.
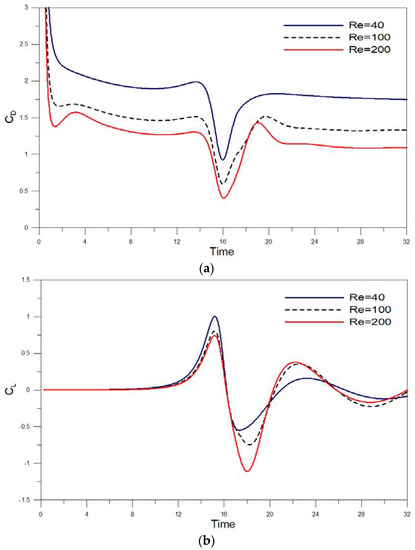
Figure 7.
Comparisons of drag and lift coefficients on upper cylinder at various Reynolds numbers: (a) drag coefficient and (b) lift coefficient.
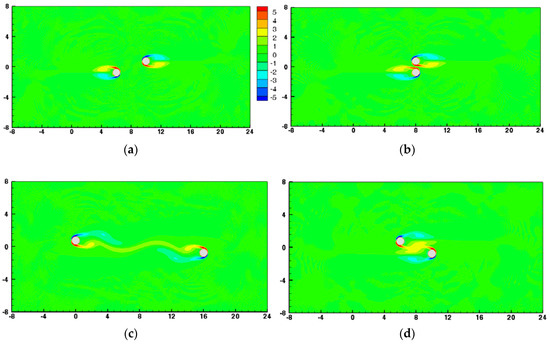
Figure 8.
Instantaneous vorticity contours of two moving cylinders at Re = 100, at different times: (a) (b) (c) (d).
3.3. Dam-Break Problems
Simulations of selected dam-break problems are used to verify the free-surface capturing approach. The first example computes the position of the leading edge of a dam-break wave and compares the results with the experimental data of Martin and Moyce [52] and numerical results from Nomeritae et al. [53]. The other cases include a dam-break wave propagating over a submerged semicircular, or a rectangular, cylinder.
Following Martin and Moyce’s [52] experimental study, the initial condition considered is a 0.057 m square water column (or H = 0.057 m) arranged behind a dam face in a 3 m long and 1 m high container. At t > 0, the dam is removed to allow the water to freely move toward downstream. Three uniform grid systems with 150 × 10 (Δx = Δz = 0.02 m), 300 × 20 (Δx = Δz = 0.01 m), and 600 × 40 grids (Δx = Δz = 0.005 m) and time step (Δt) of 5 × 10−4 sec were used to simulate the dam-break flows for the determination of the nondimensionalized leading-edge position. Figure 9 shows the comparisons between the present solutions on the time varying leading-edge position and those from measurements [52] and other numerical results [53]. For the Martin and Moyce [52] dam-break flow case, the corresponding Reynolds number was about 42,792. The computed surge front positions versus the nondimensionalized time reveal a good agreement with the data from Martin and Moyce [52] and the numerical results from Nomeritae et al. [53]. Moreover, the tests of the grid size effect indicate that the converged and nicely fit solutions are obtained when the refined grid size of Δx = Δz = 0.005 m is used.
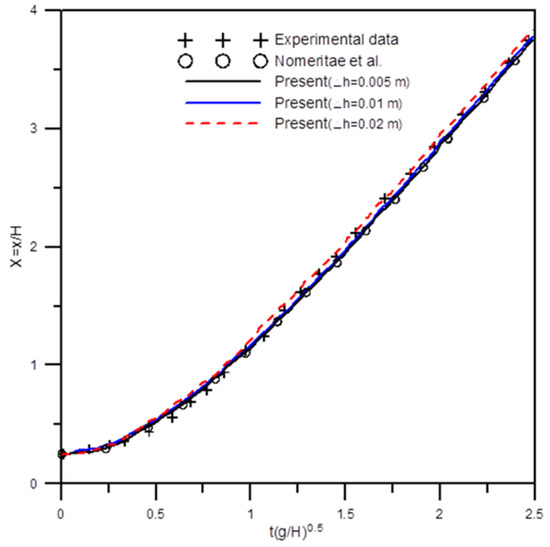
Figure 9.
Comparisons between measured [52], EISPH [53] model, and present simulated leading-edge position at different times, with initial water volume of 0.057 m in length and height.
The present two-phase flow model is also simulated for the cases with dam-break waves over a submerged structure that is placed in an enclosed channel downstream of a dam face. Illustrated in Figure 10 are the schematic diagrams of the dam-break flow problem with either a completely submerged semicircular or a rectangular cylinder. The domain of the water column upstream of the dam face is 2 m by 1 m and the downstream standing water has a depth of 0.3 m. The dimensions of the channel in length and height are, respectively, 10 and 2 m. The diameter of the semicircular cylinder is 0.4 m, and the dimensions of the rectangular cylinder are 0.4 m in length and 0.2 m in height. Two different grid sizes, Δx = Δz = Δh = 0.025 m and Δx = Δz = Δh = 0.033 m, and Δt = 0.005 s are adopted for model simulations. Here, the interfacial parameter (ε) and the influential radius (r) of the Lagrangian marker points of the IB are, respectively, 2Δh and 1.5Δh. The time varying velocities and pressures at three selected locations, namely P1 at (2 m, 0.16 m), P2 at (4 m,0.16 m), and P3 at
(5 m,0.26 m) (see Figure 10), are compared with the Flow-3D model results. The results obtained from the Flow-3D was based on the two-phase laminar flow model with the consideration of water and air phases. Figure 11 presents the comparisons between the present model results (velocity in x direction and pressure) and those from Flow-3D for the case of a submerged semicircular cylinder at point P1. The time variations of both the velocity and pressure, except at the time near the end of the interaction process, are in good agreements with the Flow-3D results. The results obtained from the arrangements of two different grid sizes reveal the consistent and reliable model predications. The comparisons of time varying pressures at points P2 and P3 under the cases of either a semicircular or a rectangular cylinder are presented in Figure 12. It is found the variation trends of the pressure at P2 and P3 under the influence of a submerged semicircular cylinder are similar to those under the case of a submerged rectangular cylinder. However, due to a more severe geometry change that appeared in the rectangular cylinder, the pressures at P2 and P3 under the case of a submerged rectangular cylinder are greater than those with a semicircular cylinder after the surge waves impact on the cylinders.
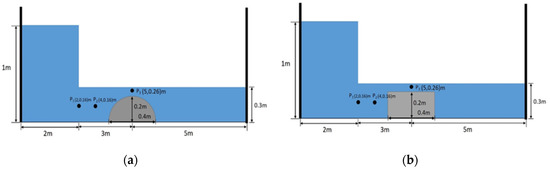
Figure 10.
Schematic diagram of dam-break waves over a submerged structure: (a) semicircular cylinder and (b) rectangular cylinder.
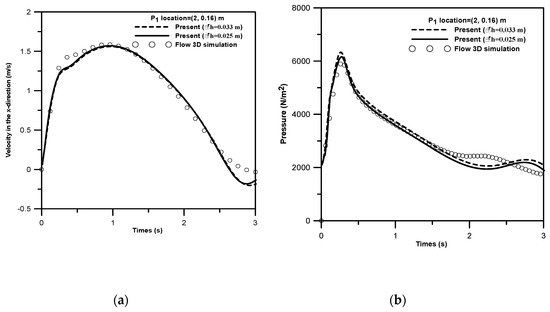
Figure 11.
Comparisons between results (velocity and pressure) from the present model and Flow 3D simulations for the case of semicircular cylinder at point P1: (a) velocity and (b) pressure.
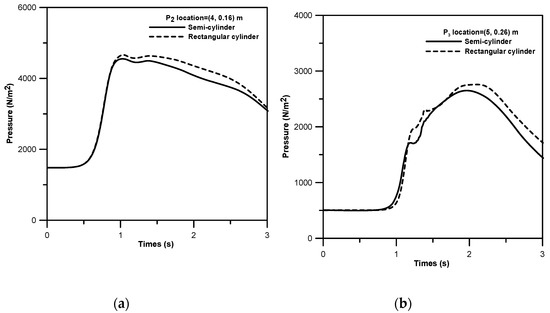
Figure 12.
Comparisons of pressure variations for a dam-break flow over a semicircular and a rectangular cylinder at fixed points of (a) P2 at (4 m, 0.16 m) and (b) P3 at (5 m, 0.26 m).
In terms of force computations from IB approach, the time variations of drag forces acting respectively on a semicircular or a rectangular cylinder are presented in Figure 13. As a model verification, the present results for the case of a submerged rectangular cylinder are also compared with those obtained from the Flow-3D in Figure 13b. As indicated in Figure 13a, the maximum force induced by the leading surge wave on a semicircular cylinder (600 N) is less than that on a rectangular cylinder (850 N). For the case of a dam-break wave over a rectangular cylinder, as shown in Figure 13b, the predicted maximum in-line force from IB calculations is found to be slightly greater than that from the Flow-3D model. In addition, although the variation pattern is similar, the present model predicts higher values of the forces caused by the follow-up waves due to the slightly higher water-surface level predicted (See Figure 14). Regarding the case of a dam-break wave over a submerged rectangular cylinder, the sensitivity tests for force computation, using thee different input conditions, namely ε = Δh, r = 1.5Δh; ε = 2Δh, r = 1.5Δh; and ε = 2Δh, r = 2Δh, are presented in Figure 13b. Apparently, the difference of forces computed for cases of ε = 2Δh, r = 1.5Δh and ε = 2Δh, r= 2Δh is insignificant. In other words, the influential radius has reached its required converged value on the numerical simulation. However, the force predications have a noticeable difference when using two different interfacial thickness, i.e., ε = Δh and ε = 2Δh, between two fluids. From results shown in Figure 13, it is evident that the values of hydrodynamic force are highly affected by the shape of the cylinder. Due to its smooth shape, the semicircular cylinder is subject to a relatively smaller hydrodynamic force than that to a rectangular cylinder. Figure 14 presents the spatial variations of the free-surface elevations at t = 0.5 s and t = 2.0 s, with the results obtained from both the present model and Flow-3D. Good agreement is noticed from the comparison plots. Due to the presence of a submerged structure, the predicted higher nonlinear growth of the free-surface flows has resulted in a more complex flow field with steep velocity gradient within the region of boundary layer.
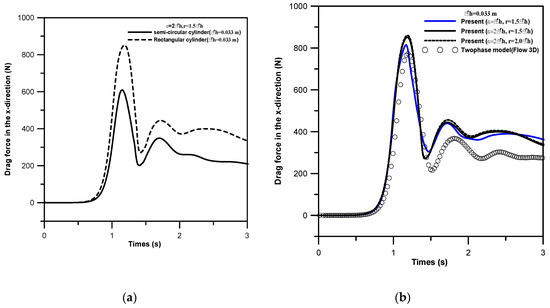
Figure 13.
Time variations of drag force (N): (a) semicircular cylinder vs. rectangular cylinder and (b) rectangular cylinder.
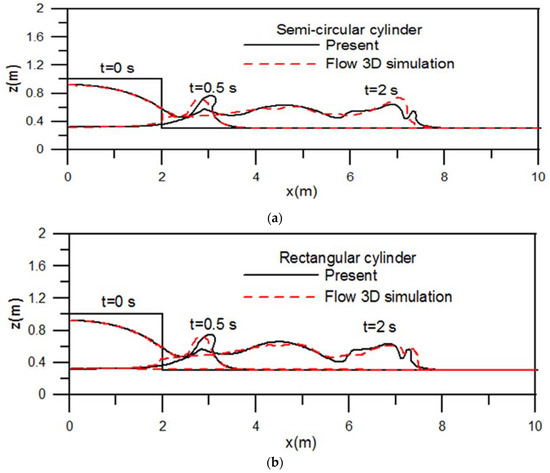
Figure 14.
Comparisons of free-surface elevation at t = 0.5 s and t = 2.0 s: (a) semicircular cylinder and (b) rectangular cylinder.
In order to compare the flow patterns induced by either a submerged semicircular cylinder or a rectangular cylinder, the evolutions of density distributions of showing the water surface levels at various times are illustrated in Figure 15. Notably, a very similar variation trend of the free-surface elevation in cases with two tested submerged cylinders can be observed. Figure 16 presents the velocity vectors of a dam-break wave passing over the submerged structures of either a semicircular cylinder or a rectangular cylinder. The two-phase flow patterns between air and water phases are plotted particularly to show the motion of the vortices, which are generated during the process of wave-structure interaction. As seen in Figure 16, the plots also illustrate the local velocity distribution near the free-surface and around the submerged structures. The results obtained from the present two-phase flow model indicate that the shape of submerged rigid bodies has a noticeable effect on the vortex motion of the gas-phase fluid above the interface of the advancing waves. It should be noted that the results presented above for the dam-break wave problems were obtained from the simulations of the present two-phase flow model, involving the interfacial handing techniques between the air–water phase and liquid–solid phase that allow uniquely the use of a Cartesian-coordinate based mesh system. Though the single-phase flow model can be used to resolve the free-surface boundary condition of the Navier–Stokes equations, the numerical procedure adds further complexity for modeling free-surface flow problems.
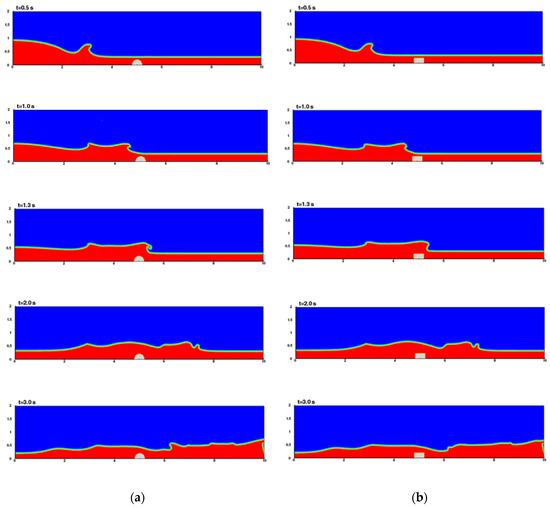
Figure 15.
Density distributions of a dam-break wave over submerged structures at different times: (a) semicircular cylinder and (b) rectangular cylinder.
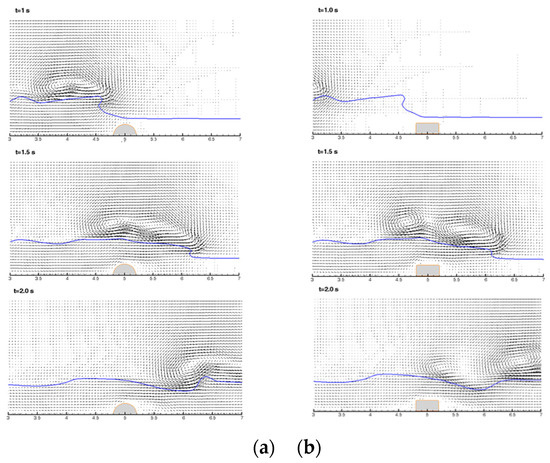
Figure 16.
Velocity distributions of a dam-break wave over submerged structures at different times: (a) semicircular cylinder and (b) rectangular cylinder.
3.4. Wave Decomposition Process over a Submerged Trapezoid Breakwater
The model application is further extended to simulate wave generation, propagation, and interacting with a submerged trapezoidal bar. This case has been experimentally investigated by Beji and Battjes [54], where the measurements were performed in a 36 m long flume with a set water depth of 0.4 m. The numerical simulation was performed in a computational flume (or domain), which is 36 m long and 0.6 m high, and the water depth is 0.4 m. The spatial domain in this numerical wave tank (NWT) is divided into three zones: the wave generation zone, the wave propagation region, and the wave-absorbing layer. The length of wave generation zone is one wavelength long, and the center of the zone is located at x = 10.5 m. The numerical wave-absorbing layers are located in both the upstream and downstream domains with the ranges of 0 < x < 8 m and 28 < x < 36 m, respectively. The length of bar base is 11 m (between x = 14 m and x = 25 m), and its height is 0.3 m. The slopes of the inclined front and rear faces of the trapezoid breakwater are, respectively, 1/20 and 1/10.
The simulations start with a state of rest in water body subject to hydrostatic pressure. The free-surface elevation and velocity component for the incoming Stokes waves are specified at the inlet of the upstream boundary as the inflow conditions [55]. Separately, a total of 360,000 and 450,000 grid points together with Δt = 0.002 s were used in the numerical calculations. The mesh sizes ∆x and ∆z for 360,000 grid points are, respectively, 0.01 and 0.005 m, whereas, for cases using 450,000 grid points, they are ∆x = 0.01 m and ∆z = 0.004 m. In the experimental study by Beji and Battjes [54], an incident wave train with a wave height, H = 2 cm, a wave period of T = 2.02 s, and a wavelength of 3.73 m was generated to propagate over a submerged trapezoidal bar. The free-surface elevations computed with the same input conditions are compared with the measurements to demonstrate the performance of the developed model.
Presented in Figure 17 are comparison plots showing the time varying free-surface elevations at the locations of six gauges, identified as a, b, c, d, e, and f, with positions at x = 18.5 m, 20.5 m, 21.5 m, 22.5 m, 23.5 m, and 25.5 m, respectively. The results in Figure 17 exhibit the temporal free-surface evolution and the wave transformation processes due to the shoaling effect along the region of non-constant water depth. Because the decrease of the water depth along the upward slope of the bar, the wave elevation is shown to deform with a steepened wave amplitude and sawtoothed-like profile at x = 20.5 m and 21.5 m (See Figure 17b,c). Additionally, as shown in Figure 17d, high and sharp wave crests are formed over the bar crest at x = 22.5 m due to the wave shoaling and nonlinear interaction between waves and a submerged bar. Figure 17e reveals the decomposition of the wave with the development of higher harmonic components at regions from x = 23.5 m onward, as the wave propagates over and past the back face of the bar. It is noticed that the wave elevations obtained from the present model at the six-gauge locations match nicely with the experimental measurements [54] and the Flow-3D results. The simulated results of Flow-3D are based on a single phase with either laminar or turbulent () flow model. The comparisons of the present and Flow-3D wave elevations indicate that both results are well predicted when compared with the measurements at the gauge locations during the period from t = 33 s to t = 39 s. However, relatively, the results from the present model are shown to have slightly better agreements with the experimental measurements than those from the Flow-3D, considering either the laminar or the turbulent () flow module. It again demonstrates that the present two-phase flow model that combines LS and IB methods can be implemented with reasonable predictions for the study of hydrodynamic interactions between waves and structures.
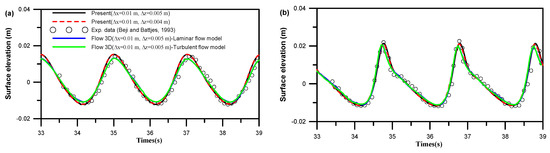
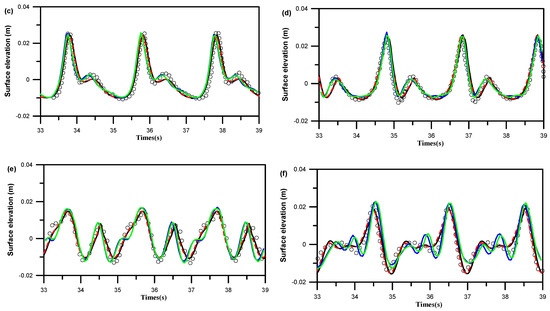
Figure 17.
Free surface elevations on six wave gauges (a) x = 18.5 m; (b) x = 20.5 m; (c) x = 21.5 m; (d) x = 22.5 m; (e) x = 23.5 m; (f) x = 25.5 m.
3.5. Free Falling Wedge
In this section, with the added effect of the dynamic response of a moving solid body, a two-dimensional free-falling wedge that is subject to the motions of three degrees of freedom (DOF) after its entering a fluid domain is investigated with the developed numerical model. A solid symmetric wedge with a density of ρb = 466.6 kg/m3 is selected for model simulations. It is positioned with its vertex of the obtuse angle pointing downward. The length of the wedge base is 1.2 m, and the side angle is 25°. The computational results in terms of the position of wedge’s bottom vertex and its velocity are compared with the experimental data collected by Yettou et al. [56]. A 2D computational domain is considered, in which the length of the domain is 20 m and the height is 4 m, including a fluid domain with water depth of 1 m. Following the experimental setup, initially, the distance from the tip of the bottom vertex to the free-surface is 1.3 m. The wedge is suddenly released into the 20 m long tank. Two grid sizes as Δh = 0.04 m and Δh = 0.02 m are used for the numerical simulations. Figure 18 shows the induced velocity fields of the fluid domains at nine selected instants under the action of a free-falling wedge and its impact on the free surface. The variations of the interface also reflect the motions of the free-surface. The induced severe interfacial oscillations and coupled air motions after the wedge entering the water body can be observed. As the present numerical approaches treats more closely the two-phase flow conditions as a process of fully nonlinear fluid-structure interaction, it is believed more accurate and physically fitted results can be generated by the present model when compared to other models considering only the single-phase flow conditions without the inclusion of the effect of air phase. The use of orthogonal mesh system is highly essential to capture the vortex generation at the regions near or around a solid structure in the cases involving the interactions of air/water/solid. The comparisons between the simulated results and measured data from Yettou et al. [56] in terms of the time varying vertical position in z coordinate and vertical velocity of the bottom vertex for a free-falling wedge described above are presented in Figure 19a,b, respectively. The results obtained by using either the grid size of Δh = 0.04 m or Δh = 0.02 m are concluded to have nearly identical values, confirming the converged solutions. In terms of the model performance, the present results are shown to have good agreements with the published numerical solutions [36] and experimental data [56]. The maximum vertical velocity reaches 4.8 m/s at t = 0.56 s. This computational case demonstrates the model’s capability in simulating the coupled motions between the dynamic responses of a free-falling wedge and the induced free-surface waves.

Figure 18.
Velocity vector of free-falling wedge; the contour shows the density distribution of two-phase at different times: (a) t = 0 s; (b) t = 0.3 s; (c) t = 0.5 s; (d) t = 0.55 s; (e) t = 0.65 s; (f) t = 0.8 s; (g) t = 1.2 s; (h) t = 1.4 s; (i) t = 2 s.
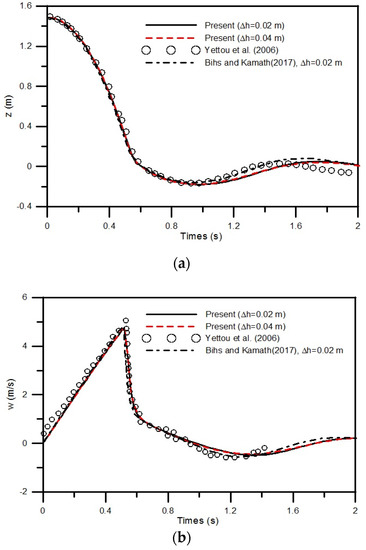
Figure 19.
Motion of a free-falling wedge: (a) vertical position of the bottom vertex; (b) vertical velocity of the bottom vertex.
3.6. Wave Packet Interacting with a Floating Body
As an extension of the modeling study given in Section 3.5, a case considering a wave-packet interacting with a floating body is numerically investigated. In this case, the numerical setup follows the experimental study performed by Hadzic et al. [57] in a small towing tank of the Berlin University of Technology. The tested floating object was a rectangular prism with the dimensions of 10 cm in length (along the x direction), 29 cm in width (along y direction), and 5 cm in high (along z direction). The density of the body was 680 kg/m3, and the mass of the body was 0.986 kg. As shown in Figure 20, the center of the body was situated at a distance of 2.11 m away from the wavemaker. The computational domain is set as a 13 m long and 0.8 m high channel (water depth = 0.4 m). In Hadzic et al.’s [57] experiments, a flap-type wavemaker was controlled to produce a wave packet with a focusing point at the original location of the object. The grid sizes of Δx = 0.02 m and Δz = 0.005 m were used for the 2D numerical computations. Temporal variations of the body motions in three DOFs are computed during the interaction process between the wave packet and the floating body. Figure 21 depicts the time-based changes of the oscillating angle of the flap wavemaker that generate a wave packet. The simulated time varying wave elevations at the locations of x = 1.65 m and x = 2.66 m during the evolution of the wave packet are presented in Figure 22. The experimentally measured data from Hadzic et al. [57] are also included in Figure 22 for comparisons. The simulated wave packet is shown to fit nicely with the measured data. The maximum values of the wave elevation occur roughly at t = 5.8 s and t = 7.7 s at the locations of x = 1.65 m and x = 2.66 m, respectively. In general, the results show the increasing trend of the wave elevation until t = 5.8 s at the location of x = 1.65 but delayed to t = 7.7 s at the location of x = 2.66 m. Afterward, the wave elevation is shown to have a trend of periodic decay with time.
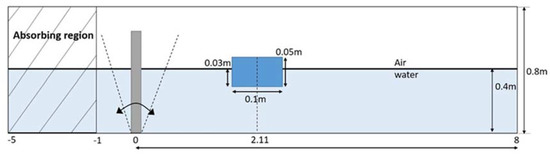
Figure 20.
Layout of the freely floating box interacting with a wave packet.
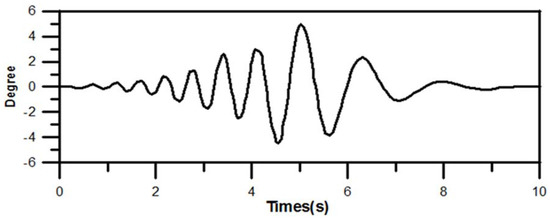
Figure 21.
Time-based variations of the flap wavemaker angle used for the generation of a wave packet.
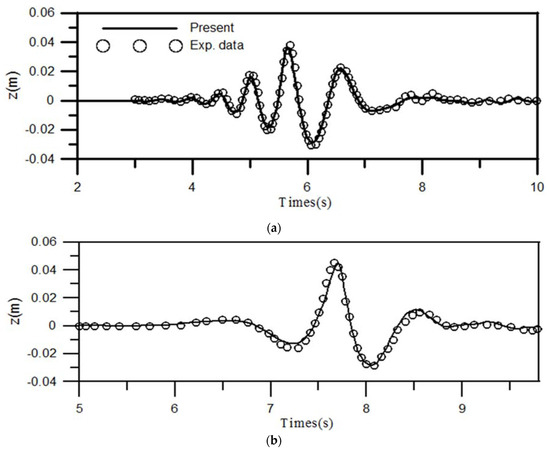
Figure 22.
Time-based variations of wave elevation during the evolution of the wave packet at (a) x = 1.65 m and (b) x = 2.66 m.
In terms of the three DOF motions of a floating body, it is generally defined that the rotational motion that is referenced to its longest axis (in this case, the body width in y direction) as the rolling motion. Then, in this study, the translational motion along the x direction is defined as the sway motion. The vertical motion is as usual the heave motion. The time variations of computed sway, heave, and rolling motions with values referenced to its original body center location are plotted together with the measured data from Hadzic et al. [57] in Figure 23. The comparisons suggest that the predicted body motions in 3DOFs are in reasonably good agreements with measured ones. As shown in Figure 23a, the floating body’s sway motion reaches the maximum value of 0.11 m at t = 7.6 s. The observed oscillatory heave motion is indicated in Figure 23b, where the motion varies within the range of −0.04 to 0.04 m, until it damps out at roughly t = 8.5 s. Figure 23c shows the time-based variations of the rolling angles of the floating body motion in which the angle of rolling motion ranges approximately from −20° to 20°. Finally, two snapshots showing the free-surface deformation and fluid velocity vectors surrounding the floating body at t = 7.2 s and t = 7.6 s are presented in Figure 24. Overall, the good matched comparisons between the simulated fluid and body motions with the experimental measurements demonstrate, again, that the developed two-phase viscous flow model can provide reasonable predictions on waves interacting with a floating body.
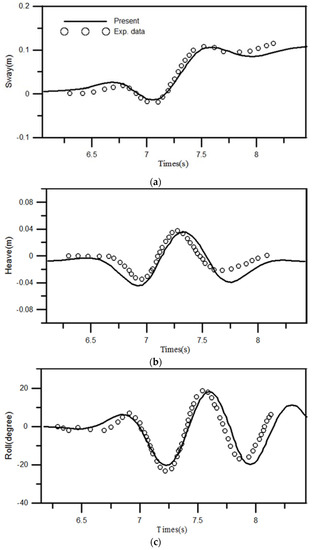
Figure 23.
Time-based variations of the floating body motions during the interaction with the wave packet (a) sway, (b) heave, and (c) roll.
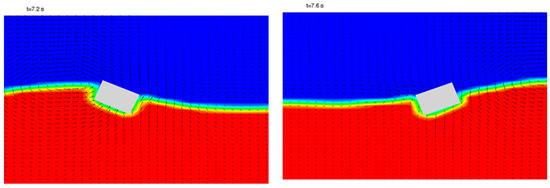
Figure 24.
Density distributions and velocity vectors of floating body at t = 7.2 s (left) and t = 7.6 s (right).
The promising results obtained from the present 2D two-phase flow model suggest that the numerical approaches presented in this study can be extended to the development of a 3D model to study the three-dimensional two-phase flow problems. By using similar methodologies as those proposed in the present study, the Navier–Stokes-equations-based projection method, the LS method, and the IB approach can be extended to the domain of three dimension, including using a combined Eulerian Cartesian and Lagrangian grid system. Certainly, the complexity of the problems arises from modeling the induced 3D motions of a floating body, where six degrees of freedom should be considered. The movements of a rigid body subject to the external forces and moments will be governed by the equations of motion covering three linear translational and three rotational motions. Following the similar procedure of using a combined Cartesian and Lagrangian grid system, the movements of the 3D interfacial boundaries and the dynamic responses of a moving body can be simulated. As a future research direction, the present research group plans to extend the developed 2D two-phase free-surface flow model to an applicable 3D model for solving the 3D problems.
4. Conclusions
A compact interfacial method by solving the Navier–Stokes equations with added source terms of external forces from immersed bodies for modeling two-phase flow problems is presented in this study. The treatments of the moving free-surface and the immersed bodies with separately using the LS and IB methods are included in the developed model. It can be noted that the present study uses a combined Eulerian Cartesian and Lagrangian grid system to avoid the re-meshing procedure for two-phase flow modeling involving coupled fluid-structure interactions. A higher-order Runge–Kutta integration in time and WENO scheme in space are included to discretize the LS equation to track the interfacial positions with severe free-surface deformations. The proposed numerical technique does not require the conformation of the grid lines onto the boundary of an immersed object, and at the same time, the effect of an immersed object can be implemented through the right-hand side source term of the Navier–Stokes equations.
The study cases include both the moving objects in a viscous fluid and interfacial two-phase flows, such as dam-break flows and wave motions over a submerged structure and the motions of a floating body. Good accuracy of the computed results, as confirmed by the comparisons with published results in calculating the variations of velocity/pressure/vorticity field and the hydrodynamic forces, was achieved. It is demonstrated that the present numerical model can simulate reasonably well for the cases of a dam-break flow passing over either a submerged semicircular or a rectangular cylinder. The model was also tested successfully to simulate the periodic waves propagating over a coastal bar, where the predicted free-surface elevations reflect an improved resolution by comparing to the Flow-3D simulations, using the same grid size. The predicted results are shown to have slightly better agreements with the experimental measurements when comparing to those from Flow-3D, using either the laminar or turbulent () flow module. Moreover, the use of an interfacial method in this study is capable of capturing directly the vortex formulations at the recirculation zone downstream of a submerged structure. With detailed calculations of the free-surface deformation, the present model can provide a better estimation of the free-surface elevation and flow patterns for strongly nonlinear interaction between waves and structures. It is concluded with certainty that the two-phase free-surface flow model developed in this study is able to successfully simulate nonlinear water wave problems, including the accurate predictions of severe wave deformation processes.
For cases with dynamic responses of moving bodies, the present model is also extended to compute with good comparison results the motions of a free-falling wedge as it is entering a water body and wave packet interacting with a 2D floating body. The results obtained from the present study suggest that a two-phase flow model with a coupled immersed body calculation can be recommended for the investigation of nonlinear water waves interacting with structures, and with the integration of equations of motion, to predict the responses of a floating body. Our findings also support the conclusions that the present model is an effective numerical tool for free-surface flow computations in a domain including gas, liquid, and solid phases, with the use of a combined Eulerian Cartesian and Lagrangian grid system.
Author Contributions
D.-C.L. and K.-H.W. devised the experimental strategy and carried out this numerical experiment; D.-C.L. wrote the manuscript, and K.-H.W. contributed to the revisions; T.-W.H. partially contributed to the experiment and analysis of the data. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan, grant number No. MOST 107-2221-E-992-020.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| English Symbols | |
| k | curvature of an interface |
| f | hydrodynamic forces |
| wave absorbing coefficient | |
| g | gravitational acceleration vector |
| t | Time |
| velocity vectors | |
| P | Pressure |
| starting position of the absorbing region | |
| length of the absorbing region | |
| velocity vectors at each of the intermediate (between n and n+1) time level | |
| velocity vectors without considering the effect of immersed boundary | |
| force density vector at the Lagrangian points | |
| Lagrangian points with coordinates | |
| Lagrangian point velocity of body | |
| translational velocity vectors of body | |
| body volume | |
| body moment of inertia | |
| position vector relative to the body centroid | |
| D | cylinder diameter |
| U | uniform flow velocity |
| CD | drag coefficient |
| CL | lift coefficient |
| St | Strouhal numbers |
| Greek | |
| Symbols | |
| Dirac delta function | |
| surface tension coefficient | |
| level set function | |
| Heaviside function | |
| fluid density | |
| fluid viscosity | |
| interfacial thickness | |
| control volume defined about the m-th Lagrangian marker | |
| body density | |
| body angular velocity vectors | |
| Re | Reynolds number |
| υ | fluid kinematics viscosity |
References
- Koo, W.; Kim, M.-H. Freely floating-body simulation by a 2D fully nonlinear numerical wave tank. Ocean. Eng. 2004, 31, 2011–2046. [Google Scholar] [CrossRef]
- Finnegan, W.; Goggins, J. Numerical simulation of linear water waves and wave–structure interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar] [CrossRef]
- Halow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface. Phys. Fluids 1965, 12, 2182–2189. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nicholas, B.D. Volume of fluid method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Anbarsooz, M.; Passandideh-Fard, M.; Moghiman, M. Fully nonlinear viscous wave generation in numerical wave tanks. Ocean Eng. 2013, 59, 73–85. [Google Scholar] [CrossRef]
- Kang, L.; Jing, Z. Depth-averaged non-hydrostatic hydrodynamic model using a new multithreading parallel computing method. Water 2017, 9, 184. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Ramaswamy, B.; Kawahara, M. Lagrangian finite element analysis applied to viscous free surface flow. Int. J. Num. Meth. Fluids 1987, 7, 953–984. [Google Scholar] [CrossRef]
- Hansbo, P. Lagrangian incompressible flow computations in three dimensions by use of space-time finite elements. Int. J. Num. Meth. Fluids 1995, 20, 989–1001. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Hirt, C.W.; Amsden, A.A.; Cook, J.L. An arbitrary Lagrangian Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Chan, R.K.C. A generalized arbitrary Lagrangian-Eulerian method for incompressible flows with sharp interfaces. J. Comput. Phys. 1975, 17, 311–331. [Google Scholar] [CrossRef]
- Pracht, W.E. Calculating three-dimensional fluid flows at all speeds with an Eulerian-Lagrangian computing mesh. J. Comput. Phys. 1975, 17, 132–159. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Liu, W.K.; Zimmerman, T.K. Lagrangian Eulerian finite element formulation for incompressible viscous flows. Comput. Meth. Appl. Mech. Eng. 1981, 29, 329–349. [Google Scholar] [CrossRef]
- Hieu, P.D.; Tanimoto, K. Verification of a VOF-based two-phase flow model for wave breaking and wave-structure interaction. Ocean Eng. 2006, 33, 1565–1588. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations (PDF). J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level set methods: An overview and some recent results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level Set Methods and Dynamic Implicit Surfaces; Springer: Berlin, Germany, 2002. [Google Scholar]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Agresar, G.; Linderman, J.J.; Tryggvason, G.; Powell, , K.G. An adaptive, Cartesian, front tracking method for the motion, deformation and adhesion of circulating cells. J. Comput. Phys. 1998, 43, 346–380. [Google Scholar] [CrossRef]
- Bunner, B.; Tryggvason, G. Direct Numerical simulations of three-dimensional bubbly flows. Phys. Fluids 1999, 11, 1967–1969. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, C.; Al-Rawahi, N.; Tauber, W.; Han, J.; Nas, S.; Jan, Y.-J. A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Peskin, C.S. Numerical-analysis of blood-flow in heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Roma, A.M.; Peskin, C.S.; Berger, M.J. An adaptive version of the immersed boundary method. J. Comput. Phys. 1999, 153, 509–534. [Google Scholar] [CrossRef]
- Iaccarino, G.; Verzicoo, R. Immersed boundary technique for turbulent flow simulations. Appl. Mech. Rev. 2003, 56, 331–347. [Google Scholar] [CrossRef]
- Tseng, Y.-H.; Ferziger, J.H. A ghost-cell immersed boundary method for flow in complex geometry. J. Comput. Phys. 2003, 192, 593–623. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, X.; Li, Z.; He, G.-W. A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations. J. Comput. Phys. 2009, 228, 7821–7836. [Google Scholar] [CrossRef]
- Simon, G.; Thomas, B.; Dominique, A. A coupled volume-of-fluid/immersed method for the study of propagating waves over complex-shaped bottom: Application to the solitary wave. Comput. Fluids 2016, 131, 56–65. [Google Scholar]
- Lo, D.C.; Lee, C.-P.; Lin, I.-F. An efficient immersed boundary method for fluid flow simulations with moving boundaries. Appl. Math. Comput. 2018, 328, 312–337. [Google Scholar] [CrossRef]
- Liu, X.-D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Carrica, P.M.; Wilson, R.V.; Noack, R.W.; Stern, F. Ship motions using single-phase level set with dynamic overset grid. Comput. Fluids 2007, 36, 1415–1433. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Stern, F. Sharp interface immersed-boundary/level-set method for wave-body interactions. J. Comput. Phys. 2009, 228, 6590–6616. [Google Scholar] [CrossRef]
- Calderer, A.; Kang, S.; Sotiropoulos, F. Level set immersed boundary method for coupled simulation of air/water interaction with complex floating structures. J. Comput. Phys. 2014, 277, 201–227. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A. A combined level set/ghost cell immersed boundary representation for floating body simulations. Int. J. Num. Meth. Fluids 2017, 83, 905–916. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.F. Discussion of vertical variation of the flow across the surf zone. Coast. Eng. 2004, 50, 161–164. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problem. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Suzuki, K.; Inamuro, T. Effect of internal mass in the simulation of a moving body by the immersed boundary method. Comput. Fluids 2011, 49, 173–187. [Google Scholar]
- Tritton, D.J. Experiments on the flow past a circular cylinder at low Reynolds number. J. Fluid Mech. 1959, 6, 547–567. [Google Scholar] [CrossRef]
- Calhoun, D.A. Cartesian grid method for solving the two-dimensional streamfunction-vorticity equations in irregular regions. J. Comput. Phys. 2002, 176, 231–275. [Google Scholar] [CrossRef]
- Russel, D.; Wang, Z.J. A Cartesian grid method for modeling multiple moving objects in 2D incompressible viscous flow. J. Comput. Phys. 2003, 191, 177–205. [Google Scholar] [CrossRef]
- Silva, A.A.; Neto, S.; Damasceno, J.J.R. Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method. J. Comput. Phys. 2003, 189, 351–370. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.J. An immersed interface method for simulating the interaction of a fluid with moving immersed boundaries. J. Comput. Phys. 2006, 216, 454–493. [Google Scholar] [CrossRef]
- Kolahdouz, E.M.; Bhalla, A.P.S.; Craven, B.A.; Griffith, B.E. An immersed interface method for discrete surfaces. J. Comput. Phys. 2020, 400, 1–37. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Sheng, X.; Sung, C.H. Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 1998, 139, 35–57. [Google Scholar] [CrossRef]
- Choi, J.I.; Oberoi, R.C.; Edwards, J.R.; Rosati, J.A. An immersed boundary method for complex incompressible flow. J. Comput. Phys. 2007, 224, 757–784. [Google Scholar] [CrossRef]
- Griffith, B.E.; Luo, X.Y. Hybrid finite difference/finite element version of the immersed boundary method. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2888. [Google Scholar] [CrossRef]
- Courant, R.; Fredrichs, K.O.; Lewy, H. Über die partiellen differenzengleichungen der mathematischen physik. Math. Ann. 1928, 100, 32. [Google Scholar] [CrossRef]
- Martin, J.; Moyce, W. Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philos. R. Soc. London. A Math. Phys. Eng. Sci. 1952, 244, 312–324. [Google Scholar]
- Nomeritae; Edoardo, D.; Stefania, G.; Ha, H.B. Explicit incompressible SPH algorithm for free-surface flow modelling: A comparison with weakly compressible schemes. Adv. Water Resour. 2016, 97, 156–167. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J.A. Experimental investigation of wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1984. [Google Scholar]
- Yettou, E.M.; Desrochers, Y.; Champoux, Y. Experimental study on the water impact of a symmetrical wedge. Fluid Dyn. Res. 2006, 38, 47–66. [Google Scholar] [CrossRef]
- Hadzic, I.; Hennig, J.; Peric, M.; Xing-Kaeding, Y. Computation of flow induced motion of floating bodies. Appl. Math. Model. 2005, 29, 1196–1210. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).