Abstract
This paper aims at evaluating the wave overtopping discharge over the pavement of “Piazza S. Marco” (Venice) in order to select the best option to mitigate the risk of flooding of the Piazza and to protect the monuments and historic buildings, e.g., the “Basilica S. Marco”. In fact, the MO.S.E. (MOdulo Sperimentale Elettromeccanico) system is designed to keep the water level below a certain value, for the safety of the lagoon, but it does not guarantee the defence of the Piazza, where flooding is still possible, being its pavement locally much lower than the maximum expected water level. To completely defend the Piazza, specific additional works are planned to prevent the back-flow through the natural drainage system (now the primary pathway) or by filtration or by overtopping. This paper investigates on the overtopping mechanism, under conditions compatible with a fully operational MO.S.E. system, through 2-D experiments. The pavement of the Piazza is gently sloping towards the masonry quay which, in some parts is formed by 5 descending steps, and in some other parts, is just a vertical wall. Close to the “Marciana” Library, a critical part is present, with a slightly lower crest freeboard. In total, three cross-sections were examined in the 36 m long wave flume of the Padova University. The test programme includes 10 irregular wave attacks and three different water levels. The test results differ considerably from the results of the available formulas, since the investigated cross-sections by far exceed their range of applicability. The presence of the steps affects only the reflection coefficient rather than the overtopping discharges. In general, if the waves incident to the Piazza are higher than 40 cm, which is a possible scenario, some other adaptation works must be considered, such as the pavement rise, temporary barriers or the reduction of the waves impacting the quay through, for instance, floating breakwaters.
1. Introduction
In order to cope with the expected sea-level rise Cazenave at al. [1] and subsidence Tosi et al. [2], and the consequent increasing frequency of flooding of Venice Lionello [3], the well-known MO.S.E. (MOdulo Sperimentale Elettromeccanico, www.mosevenezia.eu) system is designed to keep the water level below a certain value, thus preserving the people mobility and the economic activities. In particular, the maximum expected water level in Venice when the barriers are closed is +1.10 m relative to the local tidal reference (named ZMPS, Zero Mareografico Punta Salute). Obviously, in order to guarantee this maximum level, the MO.S.E. gates will close when the mean water level at the inlets is much below this value, in order to anticipate the predicted wind set-up, rainfall contribution, etc. Rinaldo et al. [4]. However, the gates are not intended to specifically protect “Piazza S. Marco”, that needs additional works to avoid its flooding, e.g., regulation of the drainage system to avoid the water entry from the sewer drains and from seepage. In fact, the mean elevation of the square is ~0.95 m ZMPS, with some areas in front of the S. Marco church lower than 0.7 m ZMPS.
Another adaptation measure could be the reduction of the possible wave overtopping from the S. Marco Basin. In fact, waves generated by boats or by wind blowing from South-East can overtop the quay (named “Riva S. Marco”, Figure 1). The evaluation of this discharge is not straightforward due to the complex topography of the site and to the uncertainties of the boundary conditions and forcing (water levels, wind velocities and directions). In particular, the Riva S. Marco is characterized by a natural stone pavement mildly sloping toward the vertical wall or, in some parts, toward a vertical wall with descending steps in front. In case of very high-water level inside the lagoon, the pavement is completely inundated.
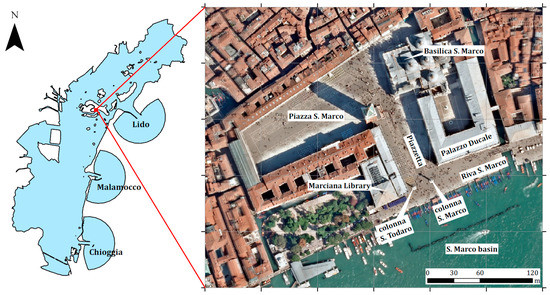
Figure 1.
Location and orthophoto of the study site: Piazza S. Marco, Venice, Italy.
Wave overtopping is widely investigated in the literature since its evaluation is crucial for structures that protect the inland against flooding. There are many simple predictive tools such as the Goda’s design charts [5], the “Overtopping of Seawalls: Design and Assessment Manual 2” [6], the “Coastal Engineering Manual” [7], and the EurOtop 2018 manual [8]. Almost all the empirical formulae proposed by these guidelines are derived from large datasets of laboratory and field measurements and take into account three types of structures: (i) sloping sea dikes; (ii) armoured rubble slopes and mounds; (iii) vertical walls. The experimental dataset address by the CLASH European project is described by Van der Meer et al. [9]. Recently, van Gent et al. [10] and Zanuttigh et al. [11] developed neural network systems that predict the overtopping for complicated structure geometries and variable wave conditions, on the basis of a homogeneous and wide database of measurements that trains the network Verhaeghe et al. [12].
The mildly sloping pavement over the quay in Piazza S. Marco could be assimilated to a promenade placed behind a vertical wall. However, the existing studies usually consider the presence of a promenade over smooth dikes. For instance, Van Doorslaer et al. [13] examined the typical defence structures of the Belgian coasts, characterized by smooth dikes, with a long and mildly sloping promenade above the still water level. From this study, the first set of formulae were established to parametrize the combined effect of crown wall, bullnose and promenades into a reduction coefficient γ* to be included in the EurOtop formulae [8] for the prediction of the overtopping discharge. Pullen et al. [14] investigated, through field and laboratory measurements, the overtopping discharge at Samphire Hoe. The structure is a composite vertical wall comprising a rock toe berm and, on the top, a parapet and a 23 m large promenade, that during severe overtopping events, is completely inundated. Conversely to the S. Marco case, most of the discharge in Samphire Hoe fall in the area directly behind the parapet wall.
The particular geometry that characterizes the “Riva S. Marco” has never been investigated and it is out of the range of validity of the γ* coefficient relative to the promenade effect. The present study aims at evaluating the wave overtopping, considering three representative cross-sections and several forcing conditions. The results are compared to the EurOtop formula for vertical wall and an influence factor accounting for the presence of the sloping pavement of the S. Marco quay is proposed. The investigation could be useful to select an appropriate adaptation measure that reduces overtopping, minimizing the impact and considering the historic and architectural constraints of the city of Venice. Among the measures and solutions that reduce the amount of overtopping, those that may be considered are, for instance, the addition of structural elements to the quay wall such as berms Burcharth et al. [15], crown walls Van Doorslaer et al. [13], Formentin et al. [16], steps Kerpen et al. [17], McCabe et al. [18], bullnoses Pearson et al. [19], Martinelli et al. [20]; the promenade upgrades Van Doorslaer et al. [21], De Finis et al. [22] combined to the addition of stilling wave basins Geeraerts et al. [23], Kisacik et al. [24] or overspill basin Grossi et al. [25], Cappietti et al. [26]; the reduction of the waves incident the quay by floating breakwaters Ruol et al. [27].
In order to meet the aims, physical model tests were performed in the wave flume (2D) of the Padova University.
In addition to this introduction, this paper includes two main sections and a concluding paragraph. The first section describes the study site, the laboratory facility, the tested configurations, the test programme and the types of analysis carried out. The second section presents the results in terms of waves and overtopping discharges, discussing the effect of the geometry of the quay and of the steps in front of the vertical quay. Lastly, conclusions useful for design purposes are drawn.
2. Materials and Methods
2.1. Study Site
The Venice lagoon is a shallow brackish water body (area ~550 km2), located in the Northern part of the Adriatic Sea. The morphology consists of small islands, tidal flats, marshes and a complex network of channels and it is connected to the sea through three large inlets: Lido, Malamocco and Chioggia. The lagoon is characterized by a semidiurnal tidal regime with a spring tidal range of about 1 m D’Alpaos et al. [28] and the storm surge is an additional relevant component. The highest surge ever measured was on 4 November 1966 when the sea level rose approximately 194 cm above ZMPS and persisted above the 120 cm level for more than 15 h Canestrelli et al. [29]. More recently, on 29 October 2018 at 13 UTC, the fifth highest historical level was recorded in Venice (since 1872, starting year of the measurements) with a maximum sea level of 1.56 m ZMPS. A second peak (1.48 m ZMPS) followed this maximum, with an estimated storm surge of 1.30 m, that “luckily” was not in phase with the astronomical tide so that it was not reached a much more severe flooding Cavaleri et al. [30]. Very recently, on 12 November 2019 at 22.50 UTC, the water level reached 1.87 m ZMPS, the second highest value ever measured, due to an “unlucky” combination of an astronomical tidal peak with a severe storm surge generated by a strong wind (up to 30 m/s) and a sudden pressure drop down to 987 h Pa.
The North Adriatic Sea, and consequently the Venice lagoon, is characterized by two prevailing wind regimes, the Bora and the Scirocco, which blow from North-East and South-East respectively Ruol et al. [31]. The Scirocco wind regime (SE) is responsible for the highest storm surge in front of the Piazza S. Marco Mel et al. [32]. For instance, the direction measured during the 29 October 2018 storm was approximately from 100° N to 150° N and the direction during 12 November 2019 quickly turned from 100° N to 230° N.
The MO.S.E. was designed to mitigate the effect of the increasing number of high tide conditions Trincardi et al. [33] and to maintain the water level in front of Venice below a certain threshold (1.10 m ZMPS in extreme cases, more frequently in the range 0.9 m–1.0 m ZMPS).
The “Piazza S. Marco”, constructed in the ninth century as a small square, was significantly enlarged in 1174 and it is dominated at its eastern end by the “Basilica S. Marco”. The “Piazzetta” S. Marco is an extension of the Piazza towards S. Marco basin in its South-East border (Figure 1). The Piazzetta lies between the “Palazzo Ducale” (on the east side) and the “Marciana” library (West). The Piazza was paved in the late 12th century with bricks and in 1723 the bricks were replaced with masonry blocks, named “masegni”.
The “Riva S. Marco” (historic quay of Venice—Figure 2) is characterized by a pavement mildly sloping toward the lagoon. The quay can be subdivided into three portions, hereafter named A, B and C (Figure 2), characterized by different cross-sections. To describe these cross-sections, three distinctive points are defined: z1 is the edge of the quay, z2 is the point where the pavement height is equal to 1.1 m ZMPS (maximum expected level with MO.S.E. gates in operation) and z3 is the crest height (highest point of the cross-section). Type A and B have a vertical wall (Figure 3a). Type A cross-section, placed in proximity of the “Marciana” library is the most critical since the crest height (z3) is 1.10 m ZMPS, distant 5 m from the edge. Type B, placed between the “Colonna San Todaro” and “Colonna San Marco”, has a crest at height z3 = 1.17 m ZMPS, distant 20 m from the edge. Type C (Figure 3b) is characterized by 5 descending steps, 15 cm high. The crest and its distance from the edge are the same of type B cross-section. Table 1 summarizes the characteristics of the three cross-sections. In front of the quay, a small floating breakwater is placed in a water depth of 3.5 m, that attenuates the waves generated by small boats and protects the “gondole”, docked at the Riva. This structure is not intended to be efficient for wind waves (longer period).
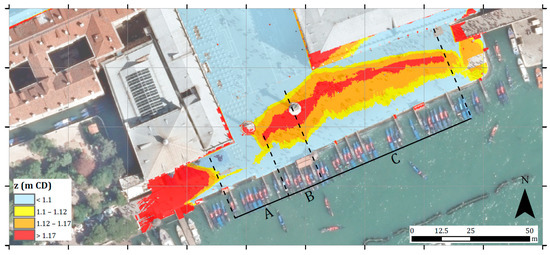
Figure 2.
Location and orthophoto of the study site: Piazza S. Marco, Venice, Italy.
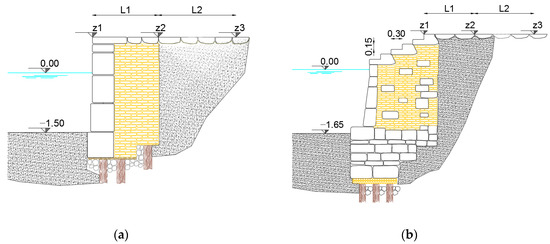
Figure 3.
Cross-section of the quay at Riva S. Marco, in correspondence of the vertical wall (a) and of the descending steps (b). The water depths are referred to ZMPS.

Table 1.
Summary of the cross-section types that characterize the Riva S. Marco.
A dataset of waves relative to 2003–2013 measured at the “Punta della Salute” station (situated approximately in front of the square) by the “Centro Previsioni e Segnalazioni Maree—CPSM” institution, allows to analyse the typical wave characteristics in the S. Marco basin. In the same station, a very long dataset of sea level is also available. The wave dataset includes: significant wave height Hs (m), maximum wave height HMAX (m), mean period Tm (s), peak period Ts (s) and water level z (m ZMPS). Moreover, the CPSM institution collected, since 1983, wind and sea level data both inside and outside the lagoon Mel et al. [32].
It was found that the waves approaching the quay (generated both from ships and from winds) are characterized by significant wave heights in the range 0.1–0.5 m and peak periods in the range 1.5–3.5 s. Figure 4 shows an example of measurements during an extreme event occurred in February 2012, when the wind speed at the Lido inlet remained over 15 m/s for 24 h, reaching a maximum of 25.5 m/s. This event was characterized by a SE direction (Scirocco), generating waves up to 38 cm in front of the Piazza. This value is considered to have a return period of approximately one year. The maximum water level in the S. Marco basin was 0.76 m ZMPS. The plot of Hs shows also the daily average. This value is obtained by averaging the wave heights at the same hour of every day, considering all the available measurements. The trend highlights that, during the night, the waves are characterized by lower Hs than during the daytime hours since the ship traffic is less intense.
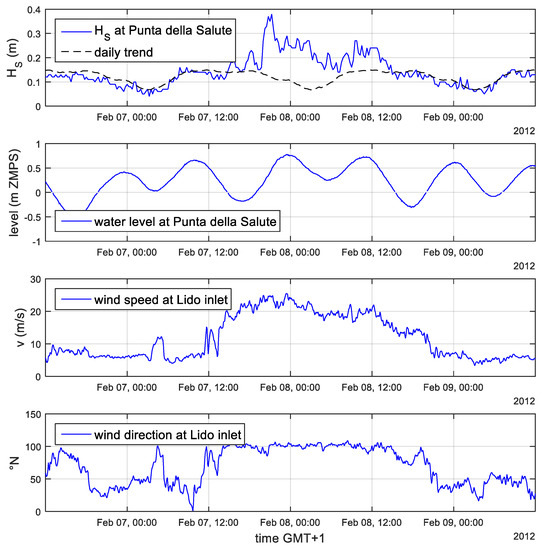
Figure 4.
Example of measurements (February 2012), from top to bottom: significant wave height (m), sea level (m ZMPS), wind speed (m/s) and wind direction (°N).
In general, if the wind blows with a speed of 15 m/s from South-East (100° N–140° N), i.e., the directions of the maximum fetch in front of the square, waves higher than 30 cm are generated in the lagoon and therefore they can easily overtop the quay. In order to statistically characterise the occurrence probability of the waves, a statistical analysis of the winds measured at the Lido inlet was carried out. Winds blowing from SE with intensity 15 m/s were observed three times per year.
2.2. Experimental Set-Up and Test Programme
Physical model tests were performed in the wave flume of the Padova University, that is 36.0 m long, 1.0 m wide and 1.30 m deep (Figure 5), and is equipped with a dual piston-flap type wavemaker, capable of generating regular and irregular waves, with active wave absorption. A series of thin metallic plates, parallel to the side walls, are placed in front of the wavemaker to avoid transverse oscillations. The bed is made of lean concrete and the sides are glass made. A recirculation system is present.

Figure 5.
Wave flume and test setup with wave gauges and structure positions.
In this study, the bottom of the model is fixed and non-erodible and reproduces a simplified bathymetry. The bed is horizontal, except for the zone in front of the structure that has a slope of 1:10. The piston-type mode was used.
Tests were carried out in geometrical scale 1:5, according to Froude similarity. The three cross-sections previously described were tested and their geometries were accurately reproduced (Figure 6). A vertical structure simulates the vertical wall of the “Riva S. Marco” and 4 plastic plates were placed behind it, to mimic the presence of the pavement over the quay (Figure 7). During the tests for the cross-section C, 5 metallic descending steps were added in front of the vertical wall. The distance of the model structure from the wave generator was 22.7 m.
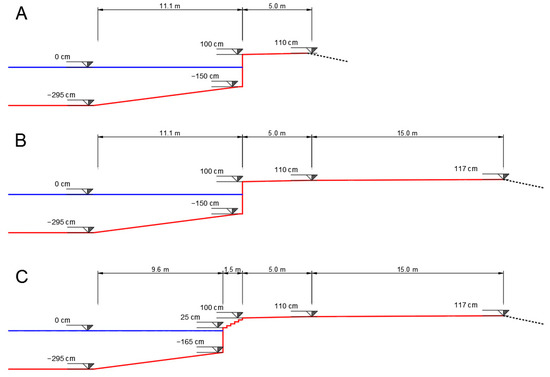
Figure 6.
Geometries of the tested sections: type A, B and C.

Figure 7.
Front view of two tested types of cross-section: vertical wall type B (a), and wall with steps type C (b).
Two arrays of four wave gauges were used to measure the incident and reflected waves in the offshore and nearshore zones, and with a sampling frequency of 100 Hz. The offshore array is placed at 10.45 m from the wave generator and the nearshore one is placed at 19.15 m (Figure 5). In both arrays, the intervals between wave gauges are, from offshore to onshore: 19 cm, 11 cm and 53 cm.
The test programme (Table 2) includes irregular wave attack characterized by 5 significant wave heights Hs ranging from 0.2 to 0.75 m, 2 wave steepness (Hs/L = 0.048 and 0.063) and three different tidal levels (+0.9 m, +1.0 m and +1.1 m ZMPS). A more detailed investigation of the effect of the wave steepness was not carried out, after observing that the effect of this variable did not affect significantly the results to have practical design value. All the 28 Wave States (WS given in Table 1) are generated for each of the three cross-sections, reaching a total of 84 tests. The white noise filter method was used to generate the irregular wave attacks, lasting ~15 min (i.e., number of waves for each test ~1000), aiming at reproducing JONSWAP spectra with standard peak enhancement factor = 3.3. The random seed used to test the different sections is common for the same wave attack.

Table 2.
Test programme repeated for each tested cross-section.
Due to the high wave reflection induced by the vertical wall, the efficiency of the wavemaker absorption system is critical. The hardware system used in the laboratory is a consolidated active wave absorption from HR Wallingford. The system efficiency was proven during the phase of transfer function calibration. For the tests under analysis, it was simply verified that the incident wave field is stationary even for long runs.
The overtopping discharge was measured for all the configurations. Three different setups were used, each appropriately sized to collect the maximum expected volume of overtopped water preserving an accuracy of at least 1%. The first setup was a tray that redirected the overtopping flow to a large bucket, and the volume was measured at the end of the test. The second was similar, but with a narrower tray width (10 cm), so that only the fraction at mid-section (considered representative of the full width) was collected. The last, suited to very large discharges, also comprised a pumping system, placed in the bucket, a flowmeter, and a non-return valve along the outlet pipe.
2.3. Analysis Methods
The same analysis methods described in Martinelli et al. [20] was used. In short, the water elevation signals were band-pass filtered in the range 0.1–20 Hz to remove the average and possible noise. Incident and reflected waves were identified using the method described in Zelt et al. [34]. Typical time-domain analysis were carried out to find the significant (Hs) and maximum (Hmax) values of the wave height and the significant (Ts) and mean (Tm) wave period. Spectral analysis allowed to find the peak wave period Tp and the estimate of the significant wave height Hm0.
The measured value of the mean overtopping discharge was obtained by dividing the accumulated overtopping volume by the test duration and by the collecting tray width, so to obtain unit values. The measurements were compared to the predictions of the formula (Equation (1)) given by the EurOtop Manual [8]. This equation is relative to a vertical wall considering non-impulsive conditions and influencing foreshore, since the bed in the laboratory in front of the breakwater has a slope of 1:10.
where γ takes into account the presence of a berm, oblique waves, a crown wall, etc. The effect of the presence of a sloping pavement at the top of the vertical wall can be assimilated to a promenade and its effect could be included using an influence factor γprom given by the EurOtop Manual (Equation (2)).
where the Lm−1,0 is the deepwater wavelength and Gc is the promenade width, valid in the range GC/Lm−1,0 = 0.05–0.5.
At S. Marco quay, Gc is equal to (L1 + L2) for the tests with 0.9 m and 1.0 m ZMPS water levels and Gc is equal to L2 for tests with 1.1 m ZMPS water level (L1 and L2 are defined in Figure 3 and in Table 1). However, the coefficient γprom is not applicable for this investigation, since the ratio between GC and Lm−1,0 is largely outside the range of application, GC/Lm−1,0 = 0.6–4, and the formula gives inaccurate or even negative results. Therefore, in the following, a new coefficient is proposed that fits the measures, in order to have a simple tool for the prediction of the overtopping within the experimentally investigated range.
3. Results
The results are given in terms of reflection coefficients and mean overtopping discharges. Comparisons with available formulas are also proposed that enhanced the need for physical model tests for the analyzed geometries.
3.1. Waves
This sub-section presents the main results in terms of incident and reflected wave characteristics, summarized in Table 3, Table 4 and Table 5. Figure 8 shows the wave reflection coefficient kR (ratio between reflected and incident Hs) for the three cross-sections (A, B and C) against the wave period. In the figure, crosses (x) are relative to the wave steepness Sop = 0.063 and circles (o) are relative to Sop = 0.048.

Table 3.
Test results for cross-section type A.

Table 4.
Test results for cross-section type B.

Table 5.
Test results for cross-section type C.
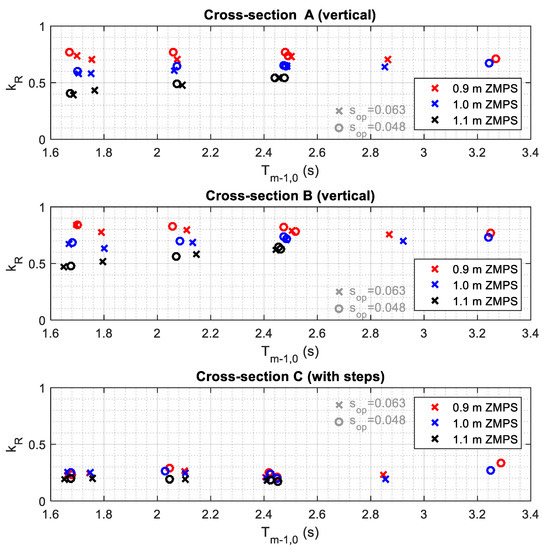
Figure 8.
Wave reflection coefficient for the three cross-sections, from top to bottom: type A, B and C.
For the vertical wall sections (A and B), kR decreases with the water level, due to the increasing overflow. For the lowest water level (i.e., 0.9 m ZMPS, red symbols), the promenade does not play a relevant role and kR is very close to 1.0 and independent from Hs and Tp, since all the tested waves are almost completely reflected by the wall. For the highest water level 1.1 m ZMPS (black symbols), at rest, the promenade is partially submerged. The smaller/shorter waves run up the promenade and the resulting kR is only ~0.5; the higher/longer waves are more effectively reflected (kR ~ 0.8) by the vertical wall below the mean sea level. Therefore, in this case, kR increases with wave height/period. The case with water level = 1.0 m ZMPS (blue symbols) is intermediate: at rest, the still water level reaches the edge of the promenade, and the reflection is not affected by Hs or Tp since the vertical wall and the promenade affect in the same measure all the waves.
For the third analysed cross-section (type C, with steps) kR is significantly lower (kR ~ 0.3). In fact, the presence of the 5 steps can be compared to a “rough slope” that diminishes the reflection and facilitates the run-up over the quay. Clearly, the number of steps, as well as their dimensions, influence the energy dissipation. This agrees with the results of Kerpen et al. [17]. The pictures in Figure 9 give a qualitative description of the wave-structure interaction at the quay border. The same wave is selected from the videos of test no. 7 for two configurations, with and without steps.

Figure 9.
Snapshot of the same wave approaching two different cross-sections: type B (a), type C (b).
3.2. Mean Overtopping Discharge
The mean overtopping discharge was measured for all the tests and all the cross-sections. Figure 10 shows the wave overtopping results for the three tested cross-sections against the measured significant wave height.
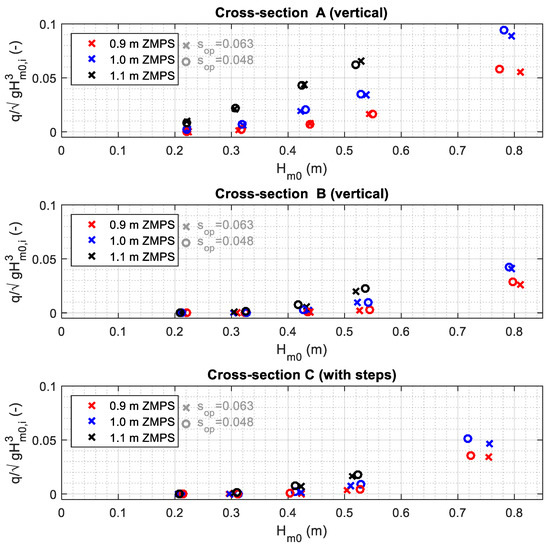
Figure 10.
Wave overtopping results for the three tested cross-sections, from top to bottom: type A, type B and type C.
As anticipated, the cross-section A represents a critical issue since the maximum level of the pavement is only 5 m apart the quay and its elevation is only 10 cm higher than the border (Figure 6A). In this section, with the highest water level, almost all the waves cause overtopping. Therefore, this portion of the quay requires a specific design to reduce flooding considering multiple mitigation strategies, e.g., provisional barriers to be temporarily placed on the pavement to reduce overtopping volumes, and/or the installation of an efficient floating breakwater to reduce the incident wave heights. Moreover, in this area, a significant rise of the pavement is not feasible since the slope between the crest of the quay and the square cannot be too steep.
Focusing on the cross-sections B and C, for which the maximum level of the pavement is about 20 m apart the quay and its elevation is 17 cm higher than the border, it was found that only the waves higher than 0.3 m are responsible for considerable discharges over the quay, and therefore can cause, or exacerbate, the flooding of Piazza S. Marco. The differences in terms of overtopping between sections B and C (without and with the steps) are negligible. In fact, the vertical wall (B) causes a high reflection that almost doubles the wave height increasing the overtopping, whereas the series of small steps (C) behaves more or less like a ramp that facilitates run-up and consequently the overtopping. Both these behaviours were observed to provide quantitatively similar results.
Figure 11a, Figure 12a and Figure 13a compare the measured dimensionless overtopping discharge to the EurOtop [8] prediction using Equation (1), without any influence factor. As expected, the predictions largely overestimate the results, since the presence of the promenade is ignored. Moreover, for the type A under the highest water level condition, the formula gives a single result since the freeboard is zero.
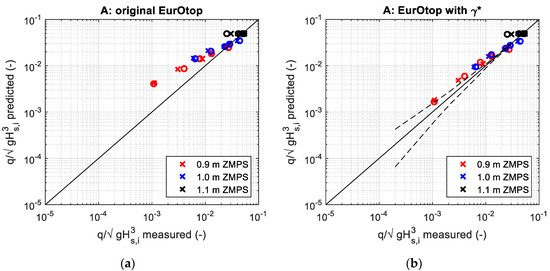
Figure 11.
Measured overtopping and predictions for the cross-sections A: according to EurOtop (a), applying γ* (b). Crosses (x) are relative to Sop = 0.063, circles (o) are relative to Sop = 0.048. Dashed lines are the upper and lower 95% prediction bounds.
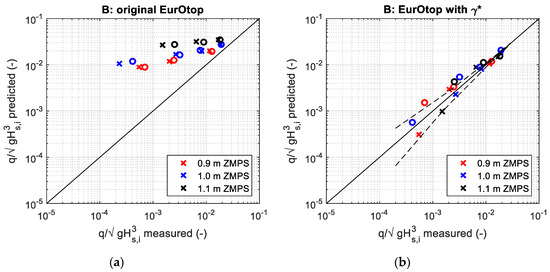
Figure 12.
Measured overtopping and predictions for the cross-sections B: according to EurOtop (a), applying γ* (b). Crosses (x) are relative to Sop = 0.063, circles (o) are relative to Sop = 0.048. Dashed lines are the upper and lower 95% prediction bounds.
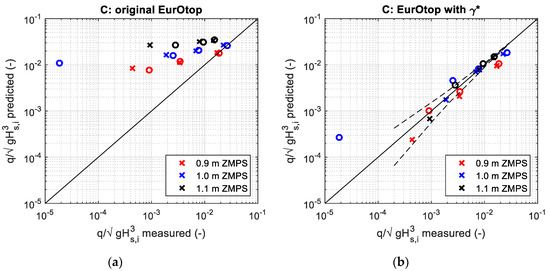
Figure 13.
Measured overtopping and predictions for the cross-sections C: according to EurOtop (a), applying γ* (b). Crosses (x) are relative to Sop = 0.063, circles (o) are relative to Sop = 0.048. Dashed lines are the upper and lower 95% prediction bounds.
To overcome this issue, a new influence factor accounting for the presence of a mildly sloping pavement is proposed. The presence of the steps is ignored since it has a minor and uncertain influence on the measured overtopping discharge. The reduction effect found by Kerpen et al. [17] is relative to a stepped revetment that continues down to the bottom with no vertical wall, i.e., a geometry significantly different from section C.
The formulation (Equation (3)) follows the one proposed by the EurOtop manual, i.e., taking into account the dimensionless promenade width (GC/Lm−1,0).
The best fit of experimental data was achieved through the least-squares method, obtaining b equal to 0.2251 (with 95% confidence bounds = [0.2128–0.2374]). The a coefficient takes into account the wall slope at the free surface (α) and it was set equal to a = (a1 + α/180°), where a1 is equal to 0.5 (with 95% confidence bounds = [0.4513–0.5487]). For the S. Marco quay, α is 90° for water levels equal to 0.9 and 1.0 m (i.e., a ~1) and α is ~0° for the water level 1.1 m, i.e., a ~a1 when the promenade is partially submerged. The investigated range for Equation (3) is GC/Lm−1,0 = 0.6–4.
Figure 11b, Figure 12b and Figure 13b compare the measured dimensionless overtopping discharges with the EurOtop prediction using (Equation (1)), introducing the new proposed influence factor (Equation (3)). These figures show also an empirical indication of the upper and lower 95% prediction bounds, based on the coefficient variability. The prediction bounds are numerically obtained through a MonteCarlo simulation that randomly samples the coefficients, assumed to be Gaussian distributed. The 95% bounds are evaluated for a limited set of conditions. Since different conditions give potentially the same expected overtopping but different confidence intervals, an average value is assumed. Finally, the curve is smoothed.
It may be observed that the structure of the γ-formula proposed by the Eurotop Manual (Equation (2)) is effective also for the prediction of the overtopping measurements of this investigation, although a different calibration of the parameter (Equation (3)) is necessary to achieve a good agreement with the results. Clearly, γ cannot effectively represent the effect of the promenade when Rc tends to zero, since the overtopping in Equation (1) becomes independent from. Therefore, as expected, for cross-section A the tests with water level equal to 1.1 m ZMPS (Rc = 0) remain in disagreements with the predictions.
To assess the quality of the estimates, three performance metrics were calculated (Table 6): the coefficient of efficiency NSE Nash et al. [35], the index of agreement D Willmott et al. [36] and the square of the correlation coefficient r2. Complete disagreement is described by D = 0, r2 = 0 and negative NSE. All indexed are = 1 for perfect agreement. Applying the original EurOtop formula (Equation (1)), the NSE is equal to 0.7488, D is equal to 0.9336 and r2 is equal to 0.8632. Considering the new influence factor γ*, the NSE reaches the value of 0.9471, D is equal to 0.9847 and r2 is equal to 0.9655.

Table 6.
Test results for cross-section type C.
4. Conclusions
This paper discusses the wave overtopping that can flood the “Piazza S. Marco”, Venice, under particular combinations of water level and incident wave height. Currently, the inundation may be caused by several factors: the water inlet from the sewer drains, the seepage, the overflow from the bounds and the wave overtopping over the “Riva S. Marco” border. Today, the first mechanism is dominant.
The MO.S.E. system is expected to guarantee that the water level remains below 1.1 m ZMPS in the whole lagoon, but the “Piazza S. Marco” would be slightly flooded in these conditions. Works are planned to completely defend the “Piazza”, avoiding the back-flow through the drainage system, and reducing the overflow and overtopping volumes.
The first problem will be solved using special devices, operated by motorized sluice gates, able to close the drainage network towards the lagoon when necessary. The overflow from the lower boundaries along the smaller channels (not affected by waves) will be avoided with a local increase of the pavements. In light of this, the major problem remains the estimate of the overtopping volumes entering “Piazza S.Marco” from its quay (Riva San Marco) caused by the wave action.
This phenomenon was faced up by means of physical model tests, performed in the wave flume of Padova University: 84 tests have been carried out, considering 3 water levels, 2 wave steepness and up to five wave heights. Three representative cross-sections have been analyzed to represent the dis-homogeneity of the quay. EurOtop empirical formula can describe the effect of the mildly sloping pavements through the promenade influence factor. However, the range of validity of the formula does not include the investigated case. The structure of the γ-formula was found to be still effective also for our case, although a different calibration of the coefficient is necessary (Equation (3)). The coefficients and their confidence interval are given. The obtained formula is a useful design tool able to predict the overtopping for the S. Marco quay, under a wide range of wave heights and water levels.
In general, the experiments show that, under waves higher than 30 cm (an event that is expected to occur a few times per year), the overtopping is significant for all the tested water levels. For rare case of waves higher than 40 cm, the overtopping is critical and some mitigation measure is required since the discharge alone exceeds the limits of the drainage system envisaged for the rainfall.
One of the possible mitigation measures consists of an efficient floating breakwater, to be placed in front of the “Piazza”, able to significantly reduce the transmitted waves. The quay in front of the “Marciana” library needs a specific solution, e.g., a temporary barrier, since its crest freeboard may fall below the level in the lagoon, even when the MO.S.E. is operating.
Author Contributions
Conceptualization, P.R., C.F., M.V. and L.M.; methodology, P.R., C.F., M.V. and L.M.; formal analysis, C.F., M.V. and L.M.; investigation, M.V.; writing—original draft preparation, C.F.; writing—review and editing, C.F. and L.M.; supervision, P.R. and L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The fruitful discussion with the colleagues of ICEA Department, Consorzio Venezia Nuova, Thetis, Konstructiva, and Mate Eng., regarding the flood protection of Piazza San Marco, is greatly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cazenave, A.; Cozannet, G.L. Sea level rise and its coastal impacts. Earth’s Future 2014, 2, 15–34. [Google Scholar] [CrossRef]
- Tosi, L.; Strozzi, T.; Da Lio, C.; Teatini, P. Regional and local land subsidence at the Venice coastland by TerraSAR-X PSI. Proc. Int. Assoc. Hydrol. Sci. 2015, 372, 199–205. [Google Scholar] [CrossRef]
- Lionello, P. The climate of the Venetian and North Adriatic region: Variability, trends and future change. Phys. Chem. Earth. Parts A/B/C 2012, 40, 1–8. [Google Scholar] [CrossRef]
- Rinaldo, A.; Nicótina, L.; Celegon, E.A.; Beraldin, F.; Botter, G.; Carniello, L.; Cecconi, G.; Defina, A.; Settin, T.; Uccelli, A.; et al. Sea level rise, hydrologic runoff, and the flooding of Venice. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co Pte Ltd.: Singapore, 2010. [Google Scholar]
- Environment Agency. Wave Overtopping of Seawalls, Design and Assessment Manual; R&D Technical Report W178; HR Wallingford Ltd.: Wallingford, UK, 1999.
- US Army Corps of Engineers. Coastal Engineering Manual-Part VI; USACE: Washington, DC, USA, 2002.
- van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schuuttrumpf, H.; Troch, P.; Zanuttigh, B. EurOtop: Manual on Wave Overtopping of Sea Defences and Related Structures. Available online: www.overtopping-manual.com. (accessed on 28 December 2018).
- Van Der Meer, J.W.; Verhaeghe, H.; Steendam, G.J. The new wave overtopping database for coastal structures. Coastal Eng. 2009, 56, 108–120. [Google Scholar] [CrossRef]
- Van Gent, M.R.; Boogaard, H.F.V.D.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Formentin, S.M.; Van Der Meer, J.W. Prediction of extreme and tolerable wave overtopping discharges through an advanced neural network. Ocean Eng. 2016, 127, 7–22. [Google Scholar] [CrossRef]
- Verhaeghe, H.; Van Der Meer, J.W.; Steendam, G.-J.; Besley, P.; Franco, L.; Van Gent, M. Wave Overtopping Database As the Starting Point for a Neural Network Prediction Method. In Proceedings of the Coastal Structures, Portland, OR, USA, 26–30 August 2003; pp. 418–430. [Google Scholar]
- Van Doorslaer, K.; De Rouck, J.; Audenaert, S.; Duquet, V. Crest modifications to reduce wave overtopping of non-breaking waves over a smooth dike slope. Coast. Eng. 2015, 101, 69–88. [Google Scholar] [CrossRef]
- Pullen, T.; Allsop, W.; Bruce, T.; Pearson, J. Field and laboratory measurements of mean overtopping discharges and spatial distributions at vertical seawalls. Coast. Eng. 2009, 56, 121–140. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Andersen, T.L.; Lara, J.L. Upgrade of coastal defence structures against increased loadings caused by climate change: A first methodological approach. Coast. Eng. 2014, 87, 112–121. [Google Scholar] [CrossRef]
- Formentin, S.M.; Zanuttigh, B. A Genetic Programming based formula for wave overtopping by crown walls and bullnoses. Coast. Eng. 2019, 152, 103529. [Google Scholar] [CrossRef]
- Kerpen, N.B.; Schoonees, T.; Schlurmann, T. Wave Overtopping of Stepped Revetments. Water 2019, 11, 1035. [Google Scholar] [CrossRef]
- McCabe, M.; Stansby, P.; Apsley, D. Random wave runup and overtopping a steep sea wall: Shallow-water and Boussinesq modelling with generalised breaking and wall impact algorithms validated against laboratory and field measurements. Coast. Eng. 2013, 74, 33–49. [Google Scholar] [CrossRef]
- Pearson, J.; Bruce, T.; Allsop, W.; Kortenhaus, A.; Van Der Meer, J.; Smith, J.M. Effectiveness of recurve walls in reducing wave overtopping on seawalls and breakwaters. Coast. Eng. 2004, 4, 4404–4416. [Google Scholar]
- Martinelli, L.; Ruol, P.; Volpato, M.; Favaretto, C.; Castellino, M.; De Girolamo, P.; Franco, L.; Romano, A.; Sammarco, P. Experimental investigation on non-breaking wave forces and overtopping at the recurved parapets of vertical breakwaters. Coast. Eng. 2018, 141, 52–67. [Google Scholar] [CrossRef]
- Van Doorslaer, K.; Romano, A.; De Rouck, J.; Kortenhaus, A. Impacts on a storm wall caused by non-breaking waves overtopping a smooth dike slope. Coast. Eng. 2017, 120, 93–111. [Google Scholar] [CrossRef]
- De Finis, S.; Romano, A.; Bellotti, G. Numerical and laboratory analysis of post-overtopping wave impacts on a storm wall for a dike-promenade structure. Coast. Eng. 2020, 155, 103598. [Google Scholar] [CrossRef]
- Geeraerts, J.; De Rouck, J.; Beels, C.; Gysens, S.; De Wolf, P.; Smith, J.M. Reduction of wave overtopping at seadikes: stilling wave basin (SWB). Coast. Eng. 2006, 5, 4680–4691. [Google Scholar]
- Kisacik, D.; Tarakcioglu, G.O.; Baykal, C. Stilling wave basins for overtopping reduction at an urban vertical seawall—The Kordon seawall at Izmir. Ocean Eng. 2019, 185, 82–99. [Google Scholar] [CrossRef]
- Grossi, A.; Kortenhaus, A.; Romano, A.; Franco, L. Wave Overtopping Prediction for Sloping Coastal Structures with Overspill Basins at the Crest. In Proceedings of the Coastal Structures and Solutions to Coastal Disasters, Boston, MA, USA, 9–11 September 2015; pp. 743–753. [Google Scholar]
- Cappietti, L.; Aminti, P.L. Laboratory investigation on the effectiveness of an overspill basin in reducing wave overtopping on marina breakwaters. Coast. Eng. Proc. 2012, 1, 20. [Google Scholar] [CrossRef]
- Ruol, P.; Martinelli, L.; Pezzutto, P. Formula to Predict Transmission for π-Type Floating Breakwaters. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 1–8. [Google Scholar] [CrossRef]
- D’Alpaos, A.; Carniello, L.; Rinaldo, A. Statistical mechanics of wind wave-induced erosion in shallow tidal basins: Inferences from the Venice Lagoon. Geophys. Res. Lett. 2013, 40, 3402–3407. [Google Scholar] [CrossRef]
- Canestrelli, P.; Mandich, M.; Pirazzoli, P.A.; Tomasin, A. Wind, Depression and Seiches: Tidal Perturbations in Venice (1951–2000). Centro Previsioni e Segnalazioni Maree. Comune Venezia 2001. pp. 1–104. Available online: http://93.62.201.235/maree/DOCUMENTI/Venti_depressioni_e_sesse.pdf (accessed on 19 November 2018).
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Davolio, S.; Ferrarin, C.; Magnusson, L.; et al. The October 29, 2018 storm in Northern Italy—An exceptional event and its modeling. Prog. Oceanogr. 2019, 178, 102178. [Google Scholar] [CrossRef]
- Ruol, P.; Martinelli, L.; Favaretto, C. Vulnerability Analysis of the Venetian Littoral and Adopted Mitigation Strategy. Water 2018, 10, 984. [Google Scholar] [CrossRef]
- Mel, R.; Carniello, L.; D’Alpaos, L. Addressing the effect of the MO. SE barriers closure on wind setup within the Venice lagoon. Estuar. Coast. Shelf Sci. 2019, 225, 106249. [Google Scholar] [CrossRef]
- Trincardi, F.; Barbanti, A.; Bastianini, M.; Benetazzo, A.; Cavaleri, L.; Chiggiato, J.; Papa, A.; Pomaro, A.; Sclavo, M.; Tosi, L.; et al. The 1966 Flooding of Venice: What Time Taught Us for the Future. Oceanography 2016, 29, 178–186. [Google Scholar] [CrossRef]
- Zelt, J.A.; Skjelbreia, J.E. Estimating incident and reflected wave fields using an arbitrary number of wave gauges. In Proceedings of the 23rd International Conference on Coastal Engeering, Venice, Italy, 4–9 October 1992; pp. 777–789. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River Flow forecasting through conceptual models-Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; LeGates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Space Phys. 1985, 90, 8995. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).