Automated Mapping of Water Table for Cranberry Subirrigation Management: Comparison of Three Spatial Interpolation Methods
Abstract
:1. Introduction
2. Materials and Methods
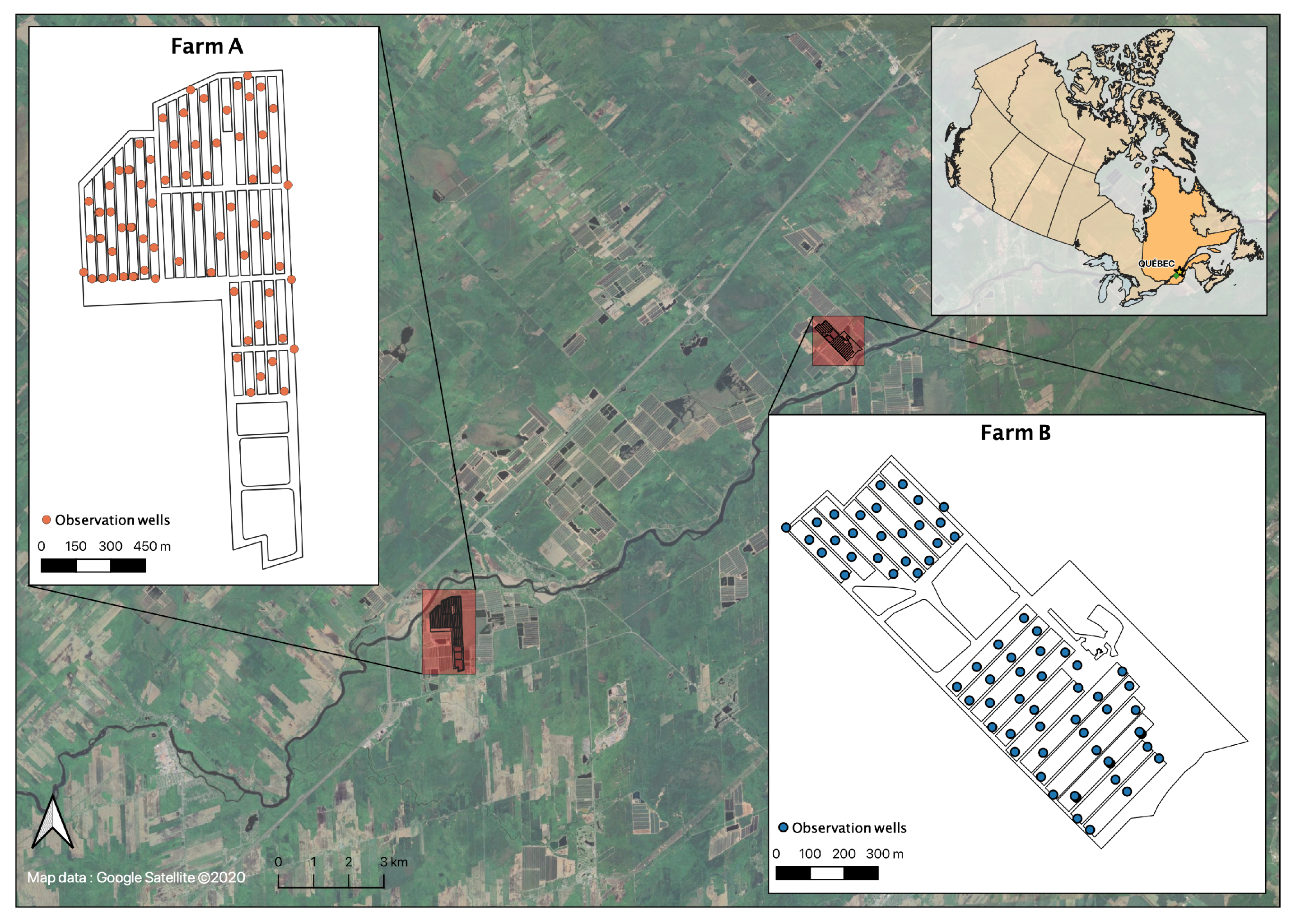
2.1. Study Sites
2.2. Observed Data
2.2.1. Water Table Depth
2.2.2. Precipitation
2.2.3. Yields
2.3. Spatial Interpolation Methods
2.3.1. Inverse Distance Weighting (IDW)
2.3.2. Thin Plate Splines (TPS)
2.3.3. Kriging
2.4. Evaluation Criteria of Method Performance
2.5. Sensitivity of Interpolation Methods to Spatial Sampling Density
3. Results and Discussion
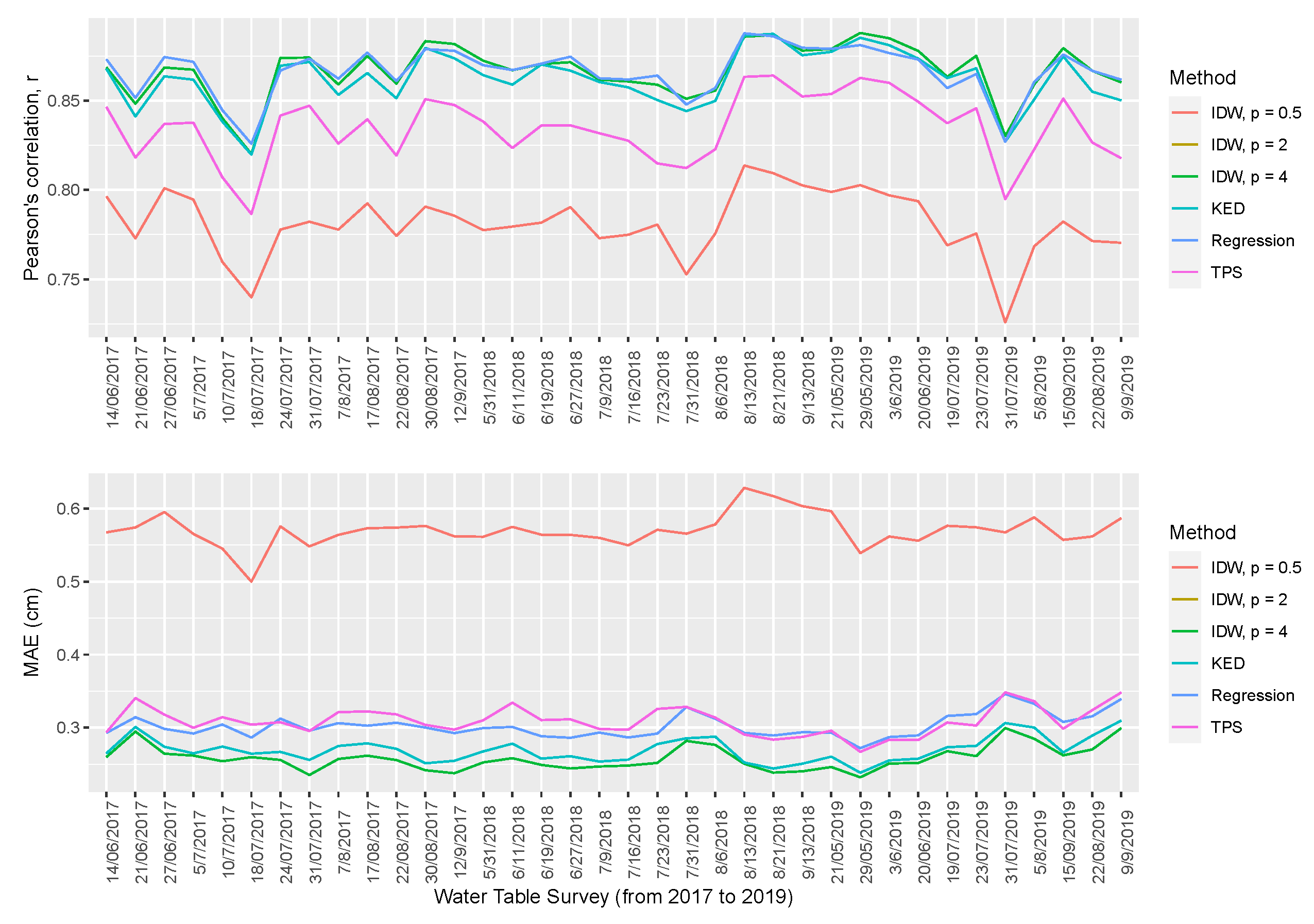
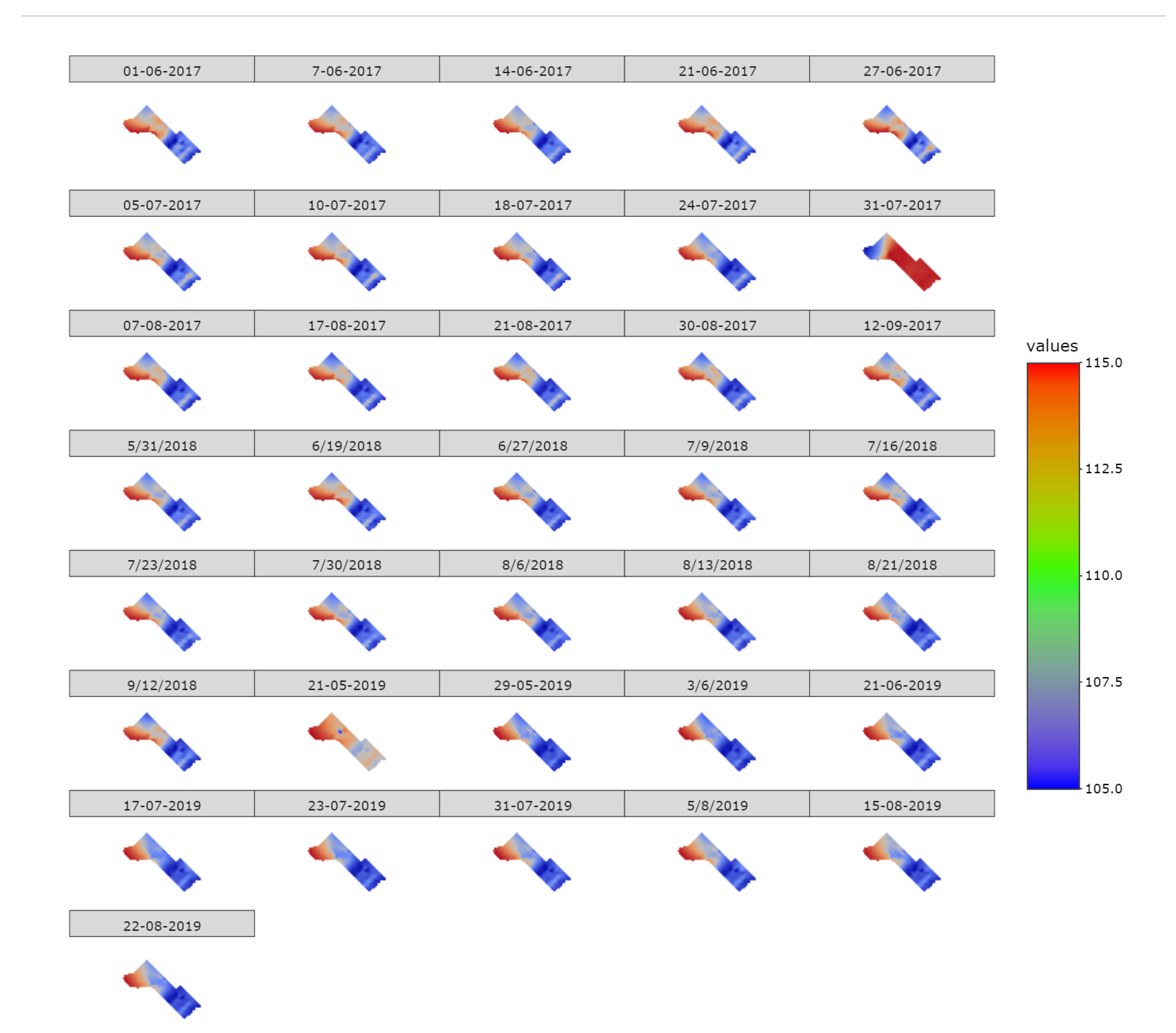
3.1. Performance of the Studied Interpolation Methods
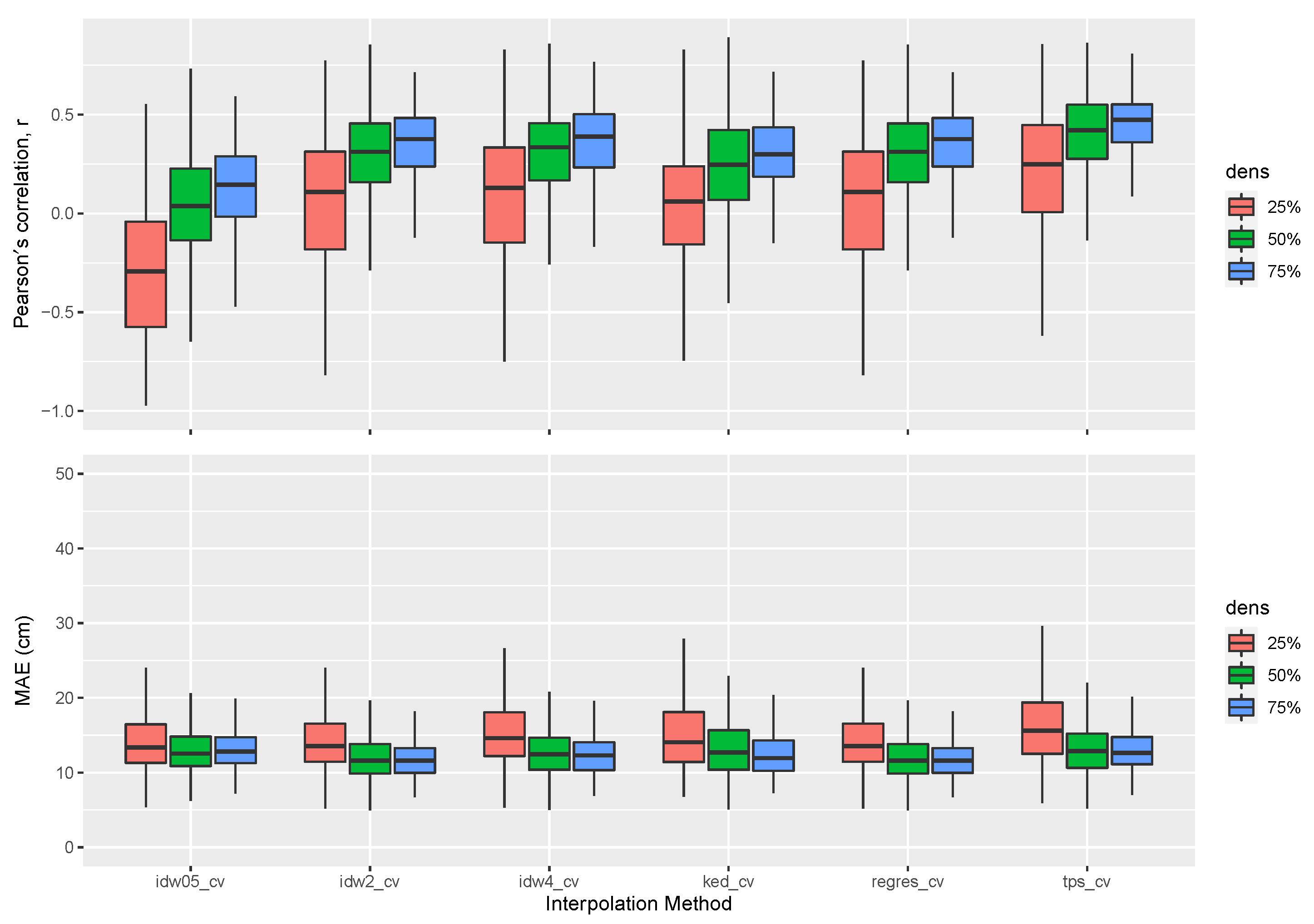
3.2. Effects of Spatial Sampling Density on Interpolation Metrics
3.3. Water Table and Cranberry Yield Response to Precipitation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IDW | Inverse distance weighting |
| KED | Kriging with external drift |
| KRG | Kriging |
| MAE | Mean absolute error |
| ME | Mean error |
| MSE | Mean squared error |
| RSME | Root mean squared error |
| TPS | Thin plate splines |
| WTD | Water table depth |
References
- Rodriguez-Galiano, V.; Mendes, M.P.; Garcia-Soldado, M.J.; Chica-Olmo, M.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total Environ. 2014, 476–477, 189–206. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Hamm, S.-Y.; Jang, S.; Cheong, J.-Y.; Kim, G.-B. Relationship between groundwater and climate change in South Korea. Geosci. J. 2014, 18, 209–218. [Google Scholar] [CrossRef]
- Ghose, D.K.; Panda, S.S.; Swain, P.C. Prediction of water table depth in western region, Orissa using BPNN and RBFN neural networks. J. Hydrol. 2010, 394, 296–304. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Lefebvre, A.; Eilers, W.; Chunn, B. Environmental Sustainability of Canadian Agriculture: Agri-Environmental Indicator Report Series–Report # 2; Agriculture and Agri-Food Canada: Ottawa, ON, Canada, 2005.
- MAPAQ. Portrait-Diagnostic Sectoriel de la Canneberge au Québec; Ministère de l’Agriculture, des Pêcheries et de l’Alimentation du Québec (MAPAQ), Gouvernement du Québec: Quebec City, QC, Canada, 2018; ISBN 978-2-550-81047-6.
- Vanderleest, C.P.L.; Caron, J.; Bland, W.L. Water table level management as an irrigation strategy for cranberry (Vaccinium macrocarpon Aiton) 1. Can. J. Soil Sci. 2016, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, C.; Jeranyama, P.; Alverson, N. Agricultural water requirements for commercial production of cranberries. Can. J. Soil Sci. 2017, 97, 38–45. [Google Scholar] [CrossRef]
- Samson, M.E.; Fortin, J.; Pepin, S.; Caron, J. Impact of potassium sulfate salinity on growth and development of cranberry plants subjected to overhead and subirrigation. Can. J. Soil Sci. 2016, 97, 20–30. [Google Scholar]
- Caron, J.; Bonin, S.; Pepin, S.; Kummer, L.; Vanderleest, C.; Bland, W.L. Determination of irrigation set points for cranberries from soil-and plant-based measurements. Can. J. Soil Sci. 2016, 96, 37–50. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, V.; Gallich, J.; Gumiere, S.; Pepin, S.; Caron, J. Water table control for increasing yield and saving water in cranberry production. Sustainability 2015, 7, 10602–10619. [Google Scholar] [CrossRef] [Green Version]
- Elmi, A.; Madramootoo, C.H.; Yside, P.; Dodds, G. Water requirements and subirrigation technology design criteria for cranberry production in Quebec. Canada. Can. Biosyst. Eng. 2010, 52, 1.1–1.8. [Google Scholar]
- Sun, Y.; Kang, S.; Li, F.; Zhang, L. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Environ. Model. Softw. 2009, 24, 1163–1170. [Google Scholar] [CrossRef]
- Adhikary, P.P.; Dash, C.J. Comparison of deterministic and stochastic methods to predict spatial variation of groundwater depth. Appl. Water Sci. 2017, 7, 339–348. [Google Scholar] [CrossRef] [Green Version]
- Oiro, S.; Comte, J.C.; Soulsby, C.; Walraevens, K. Using stable water isotopes to identify spatio-temporal controls on groundwater recharge in two contrasting East African aquifer systems. Hydrol. Sci. J. 2018, 63, 862–877. [Google Scholar] [CrossRef]
- Varouchakis, E.A.; Hristopulos, D.T. Comparison of stochastic and deterministic methods for mapping groundwater level spatial variability in sparsely monitored basins. Environmental Monitoring and Assessment. Environ. Monit. Assess. 2013, 185, 1–19. [Google Scholar] [CrossRef]
- Reed, P.; Minsker, B.; Valocchi, A.J. Cost-effective long-term groundwater monitoring design using a genetic algorithm and global mass interpolation. Water Resour. Res. 2000, 36, 3731–3741. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, S.H.; Sedghamiz, A. Geostatistical analysis of spatial and temporal variations of groundwater level. Environ. Monit. Assess. 2007, 129, 277–294. [Google Scholar] [CrossRef]
- Buchanan, S.; Triantafilis, J. Mapping water table depth using geophysical and environmental variables. Groundwater 2009, 47, 80–96. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Lafond, J.A.; Hallema, D.W.; Périard, Y.; Caron, J.; Gallich, J. Mapping soil hydraulic conductivity and matric potential for water management of cranberry: Characterisation and spatial interpolation methods. Biosyst. Eng. 2014, 128, 29–40. [Google Scholar] [CrossRef]
- Lafond, J.A.; Gumiere, S.J.; Hallema, D.W.; Périard, Y.; Jutras, S.; Caron, J. Spatial distribution patterns of soil water availability as a tool for precision irrigation management in Histosols: Characterization and spatial interpolation. Vadose Zone J. 2015, 14, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bier, V.A.; de Souza, E.G. Interpolation selection index for delineation of thematic maps. Comput. Electron. Agric. 2017, 136, 202–209. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Pelletier, V.; Gallich, J.; Caron, J.; Jutras, S.; March, S. Critical irrigation threshold and cranberry yield components. Agric. Water Manag. 2015, 148, 106–112. [Google Scholar] [CrossRef]
- Pozdnyakova, L.; Giménez, D.; Oudemans, P.V. Spatial analysis of cranberry yield at three scales. Agron. J. 2005, 97, 49–57. [Google Scholar] [CrossRef]
- Brédy, J.; Gallich, J.; Celicourt, P.; Gumiere, S.J. Water table depth forecasting in cranberry fields using two decision-tree-modeling approaches. Agric. Water Manag. 2020, 233, 106090. [Google Scholar]
- QGIS Development Team. QGIS Geographic Information System. Available online: http://qgis.osgeo.org (accessed on 10 August 2020).
- Nychka, D.; Furrer, R.; Paige, J.; Sain, S. Fields: Tools for Spatial Data. R Package Version 11.6. 2017. Available online: https://github.com/NCAR/Fields (accessed on 7 May 2020). [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. Available online: https://www.r-project.org (accessed on 7 May 2020).
- Schuenemeyer, J.H.; Drew, L.J. Statistics for Earth and Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.; Stein, A. Comparison of Kriging with External Drift and Regression Kriging; ITC: Enschede, The Netherlands, 2003.
- Hiemstra, P.H.; Pebesma, E.J.; Twenhöfel, C.J.; Heuvelink, G.B. Real-time automatic interpolation of ambient gamma dose rates from the Dutch radioactivity monitoring network. Comput. Geosci. 2009, 35, 1711–1721. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Yao, L.; Huo, Z.; Feng, S.; Mao, X.; Kang, S.; Chen, J.; Steenhuis, T.S. Evaluation of spatial interpolation methods for groundwater level in an arid inland oasis, northwest China. Environ. Earth Sci. 2014, 71, 1911–1924. [Google Scholar] [CrossRef]
- Sadat-Noori, M.; Ebrahimi, K.; Liaghat, A.M.; Hoorfar, A.H. Comparison of different geostatistical methods to estimate groundwater level at different climatic periods. Water Environ. J. 2013, 27, 10–19. [Google Scholar] [CrossRef]
- Caruso, C.; Quarta, F. Interpolation methods comparison. Comput. Math. Appl. 1998, 35, 109–126. [Google Scholar] [CrossRef] [Green Version]
- Ohmer, M.; Liesch, T.; Goeppert, N.; Goldscheider, N. On the optimal selection of interpolation methods for groundwater contouring: An example of propagation of uncertainty regarding inter-aquifer exchange. Adv. Water Resour. 2017, 109, 121–132. [Google Scholar] [CrossRef]
- Hosseini, E.; Gallich, J.; Caron, J. Comparison of several interpolators for smoothing hydraulic conductivity data in South West Iran. Trans. ASAE 1993, 36, 1687–1693. [Google Scholar] [CrossRef]
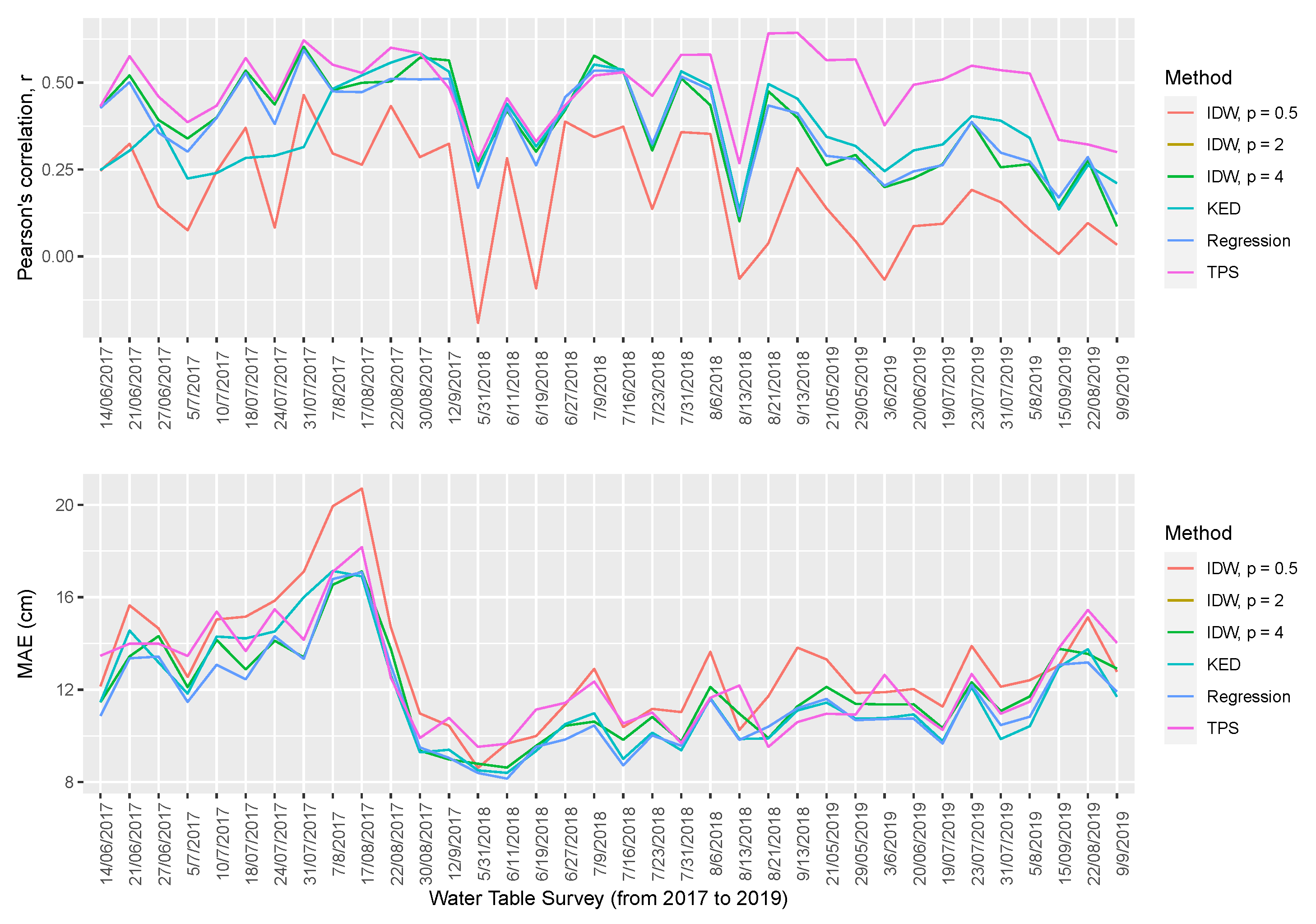





| Interpolation metrics for Farm A from 2017 to 2019 | |||||||
| Interpolation Methods | ME | MAE | Correlation (Observed vs Interpolated) | Correlation (Interpolated vs Residual) | RMSE | RMSE SD | URMSE |
| IDW (p = 0.5) | 0.44 | 13.00 | 0.01 | −0.06 | 18.88 | 0.99 | 18.86 |
| IDW (p = 2) | 1.22 | 11.89 | 0.29 | −0.13 | 18.14 | 0.95 | 18.06 |
| IDW (p = 4) | 1.20 | 12.58 | 0.30 | −0.35 | 19.20 | 1.01 | 19.09 |
| KED | 0.27 | 13.45 | 0.24 | −0.19 | 20.74 | 1.09 | 20.70 |
| Regression | 1.22 | 11.89 | 0.29 | −0.13 | 18.14 | 0.95 | 18.06 |
| TPS | 0.74 | 13.30 | 0.38 | −0.43 | 19.27 | 1.02 | 19.21 |
| Interpolation metrics for Farm B from 2017 to 2019 | |||||||
| Interpolation Methods | ME | MAE | Correlation (Observed vs Interpolated) | Correlation (Interpolated vs Residual) | RMSE | RMSE SD | URMSE |
| IDW (p = 0.5) | 0.01 | 0.58 | 0.41 | 0.65 | 0.68 | 0.86 | 0.68 |
| IDW (p = 2) | −0.04 | 0.32 | 0.59 | 0.26 | 0.43 | 0.55 | 0.43 |
| IDW (p = 4) | −0.02 | 0.28 | 0.60 | −0.07 | 0.42 | 0.53 | 0.49 |
| KED | −0.01 | 0.39 | 0.55 | −0.02 | 0.50 | 0.64 | 0.49 |
| Regression | −0.05 | 0.32 | 0.59 | 0.26 | 0.43 | 0.55 | 0.43 |
| TPS | 0.00 | 0.33 | 0.59 | −0.26 | 0.47 | 0.59 | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celicourt, P.; Gumiere, S.J.; Lafond, J.A.; Gumiere, T.; Gallichand, J.; Rousseau, A.N. Automated Mapping of Water Table for Cranberry Subirrigation Management: Comparison of Three Spatial Interpolation Methods. Water 2020, 12, 3322. https://doi.org/10.3390/w12123322
Celicourt P, Gumiere SJ, Lafond JA, Gumiere T, Gallichand J, Rousseau AN. Automated Mapping of Water Table for Cranberry Subirrigation Management: Comparison of Three Spatial Interpolation Methods. Water. 2020; 12(12):3322. https://doi.org/10.3390/w12123322
Chicago/Turabian StyleCelicourt, Paul, Silvio Jose Gumiere, Jonathan A. Lafond, Thiago Gumiere, Jacques Gallichand, and Alain N. Rousseau. 2020. "Automated Mapping of Water Table for Cranberry Subirrigation Management: Comparison of Three Spatial Interpolation Methods" Water 12, no. 12: 3322. https://doi.org/10.3390/w12123322






