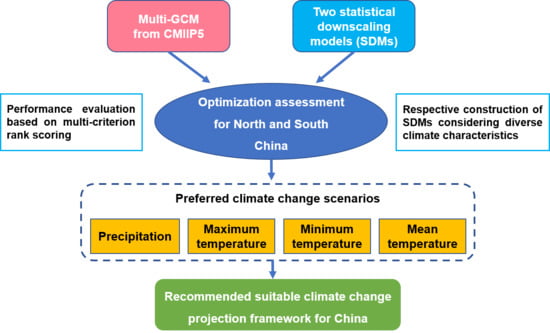
Optimization Assessment of Projection Methods of Climate Change for Discrepancies between North and South China
Abstract
1. Introduction
2. Materials and Methods
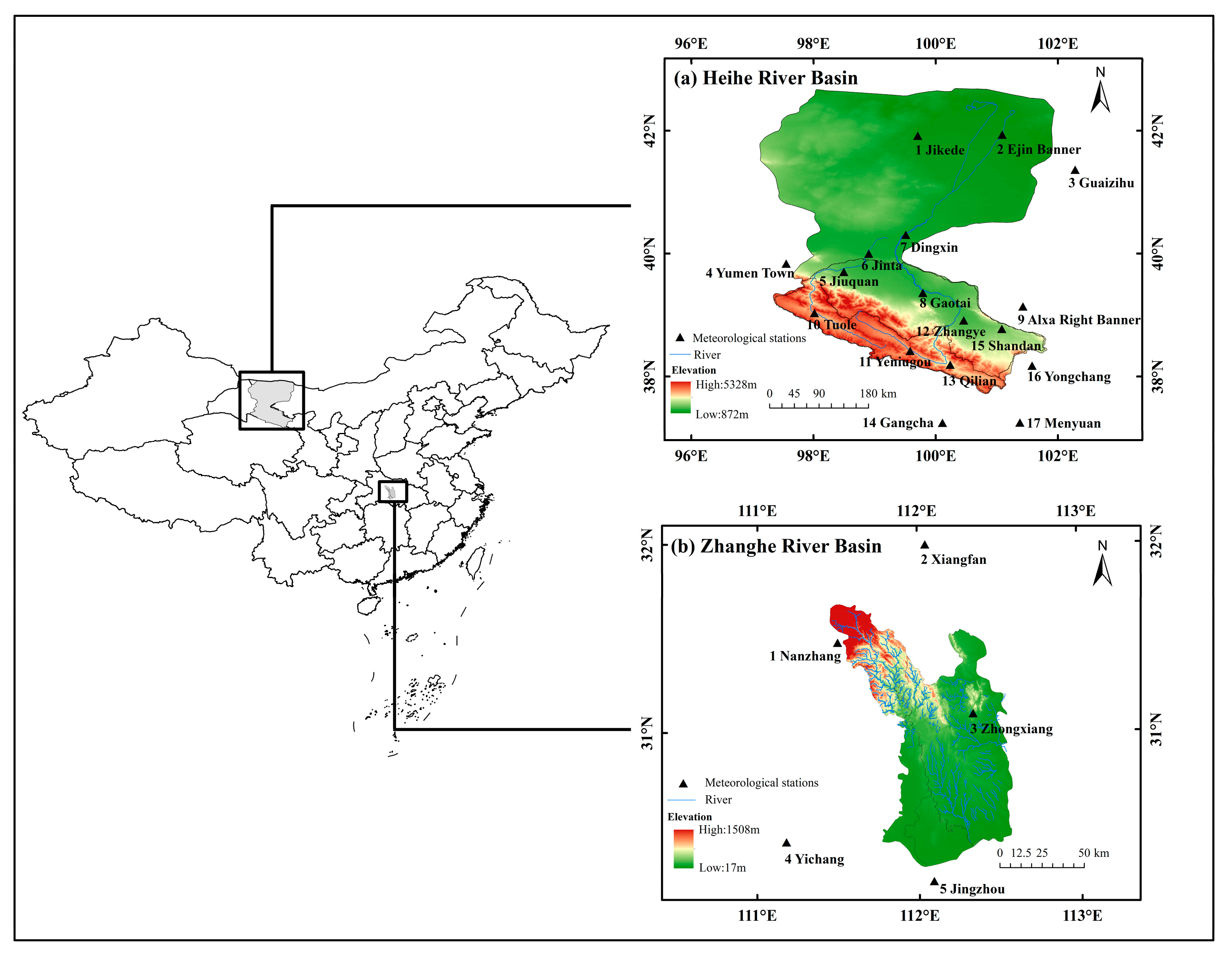
2.1. Study Area
2.1.1. Heihe River Basin
2.1.2. Zhanghe River Basin
2.2. Data
2.2.1. Observed Data
2.2.2. GCM Data
2.2.3. ERA-40 Reanalysis Data
2.3. Methods
2.3.1. Performance Evaluation of Multi-GCMs
Score-Based Method
2.3.2. Statistical Downscaling Methods
SDSM
MOS
Daily Translation (DT)
Daily Bias Correction (DBC)
2.3.3. Evaluation Metrics for Model Calibration and Validation
3. Results and Discussion
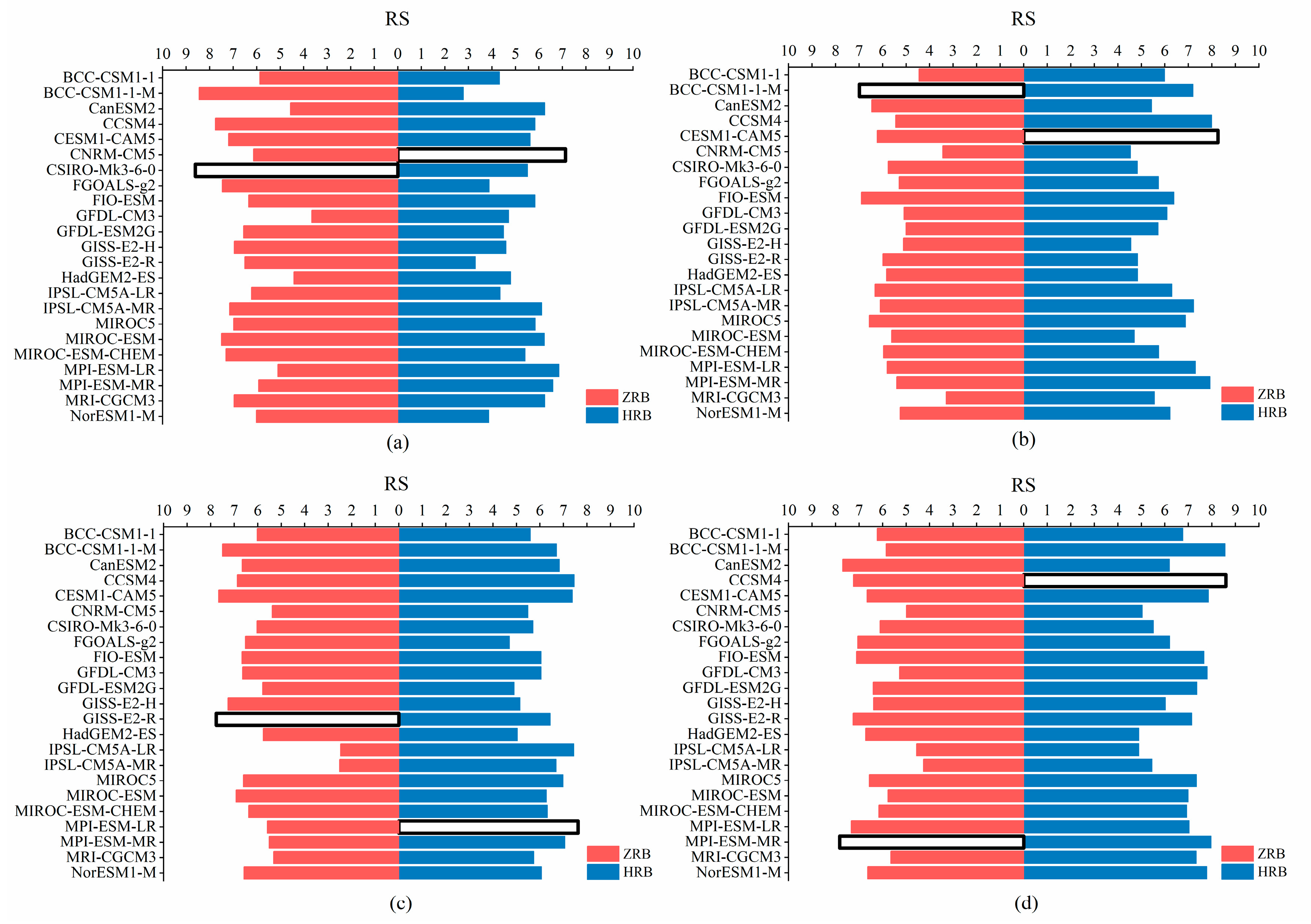
3.1. Performance Evaluation of GCMs
3.1.1. Rank Scoring of Different Climate Variables
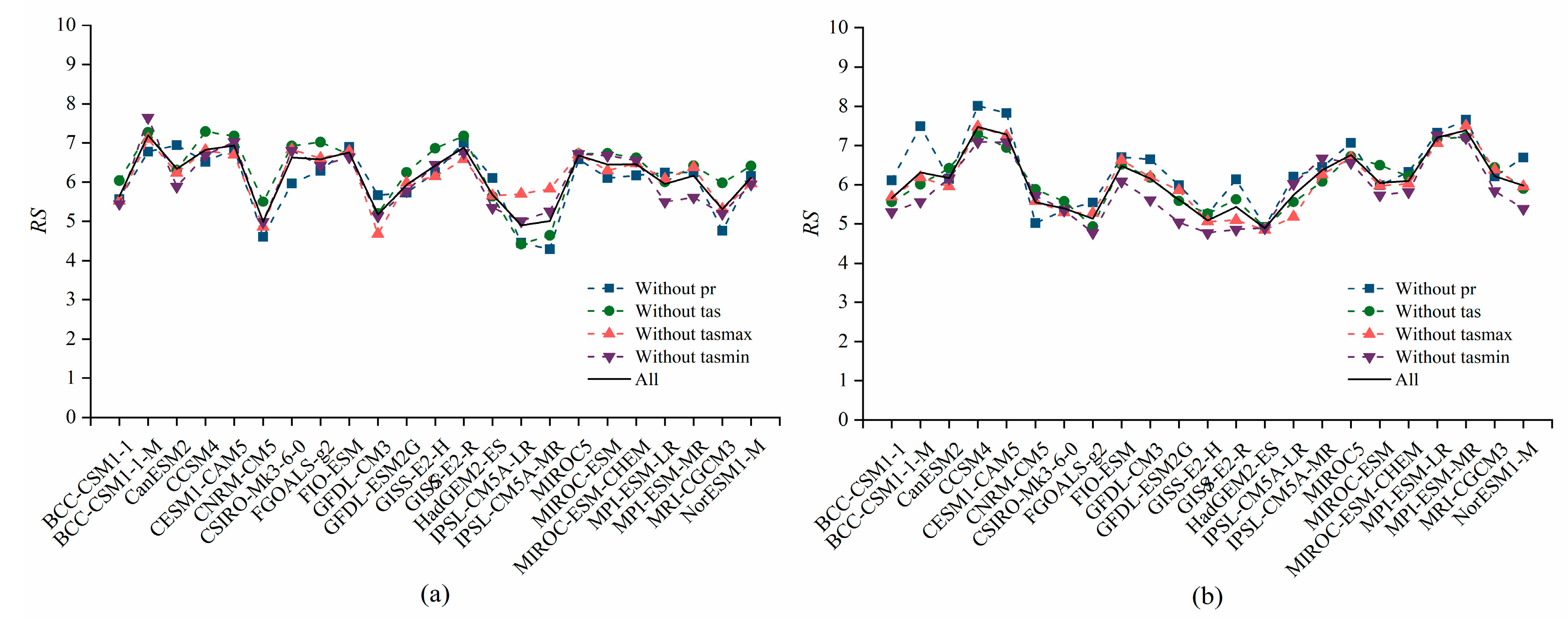
3.1.2. Sensitivity Analysis of the Multi-Criterion Score-Based Method
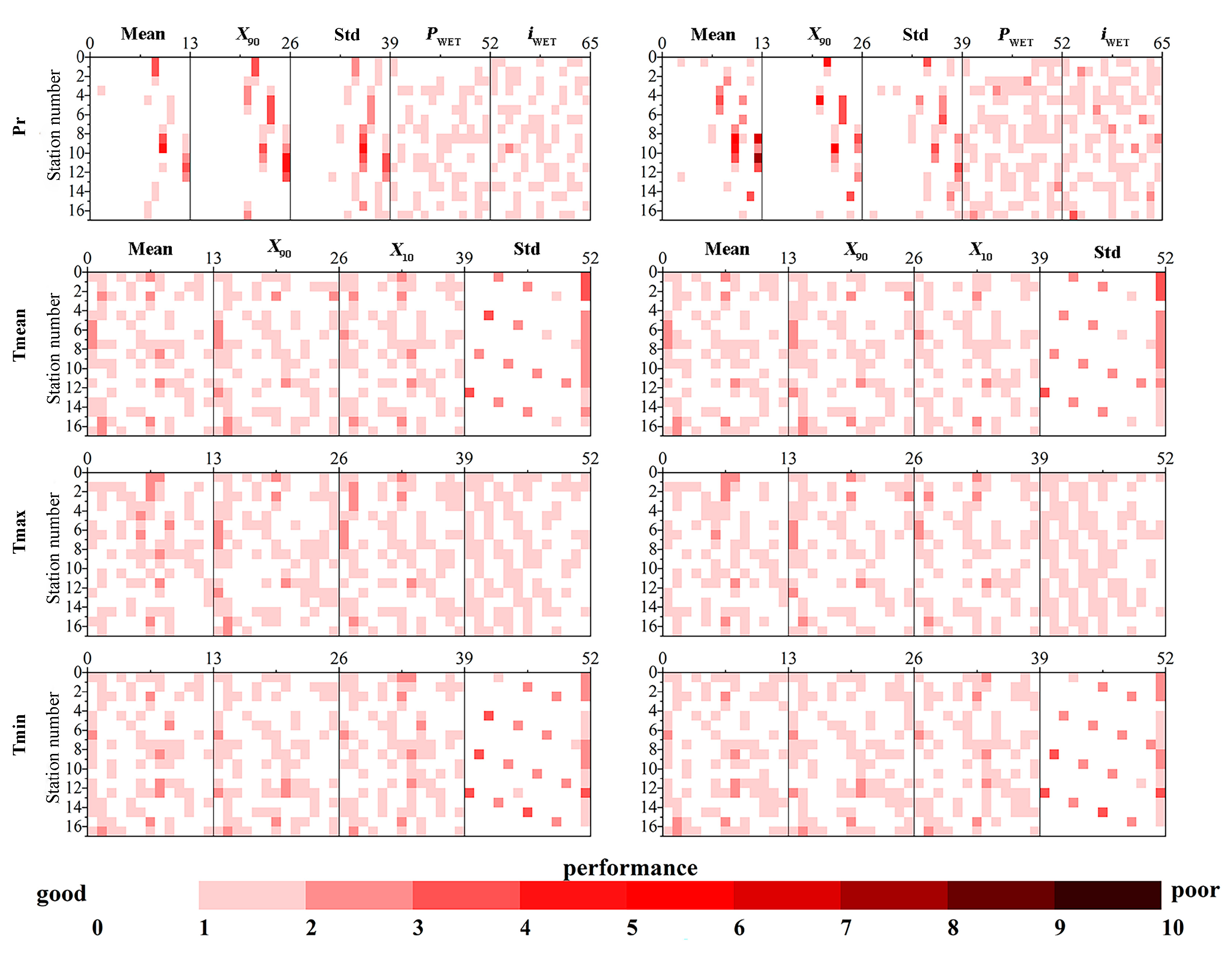
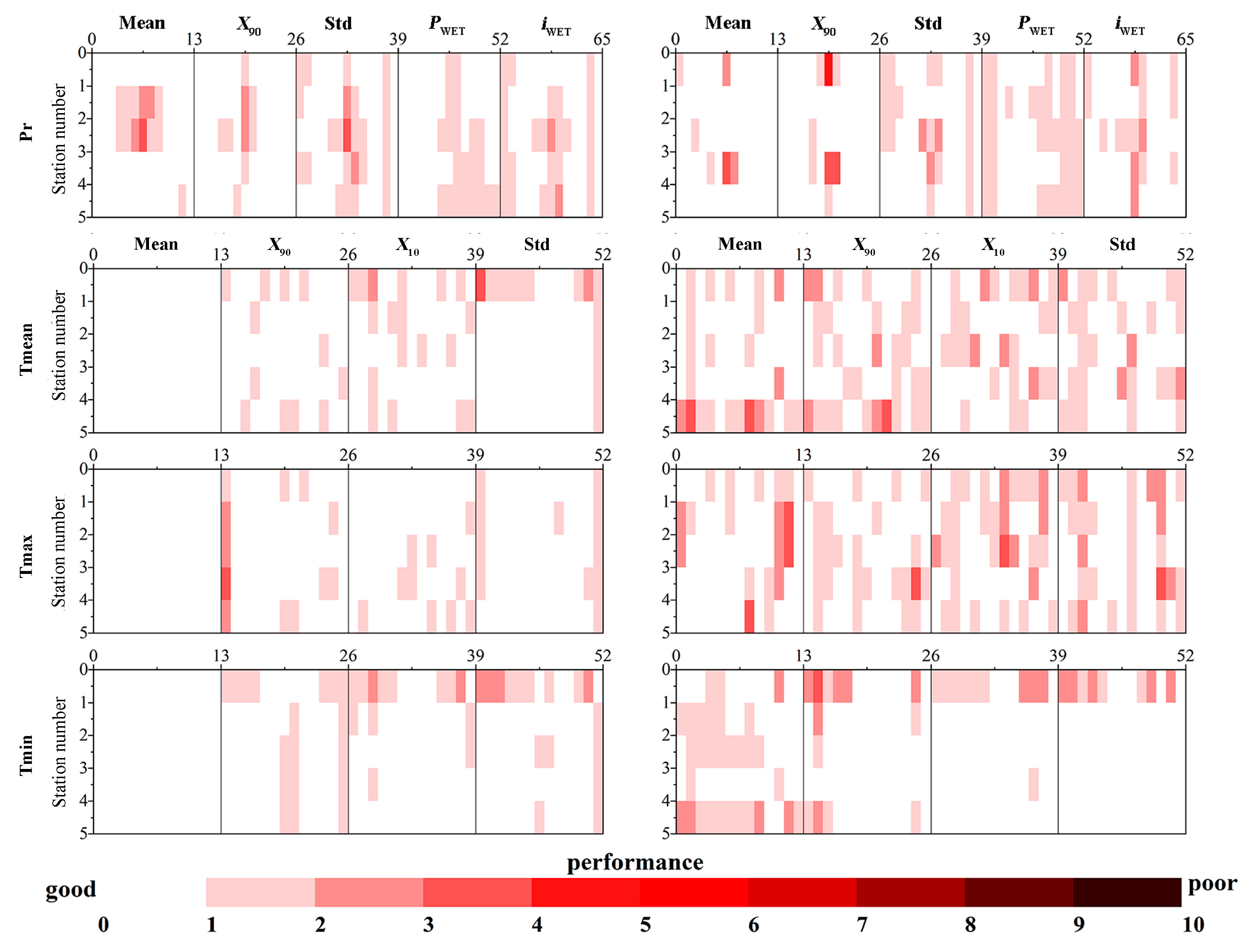
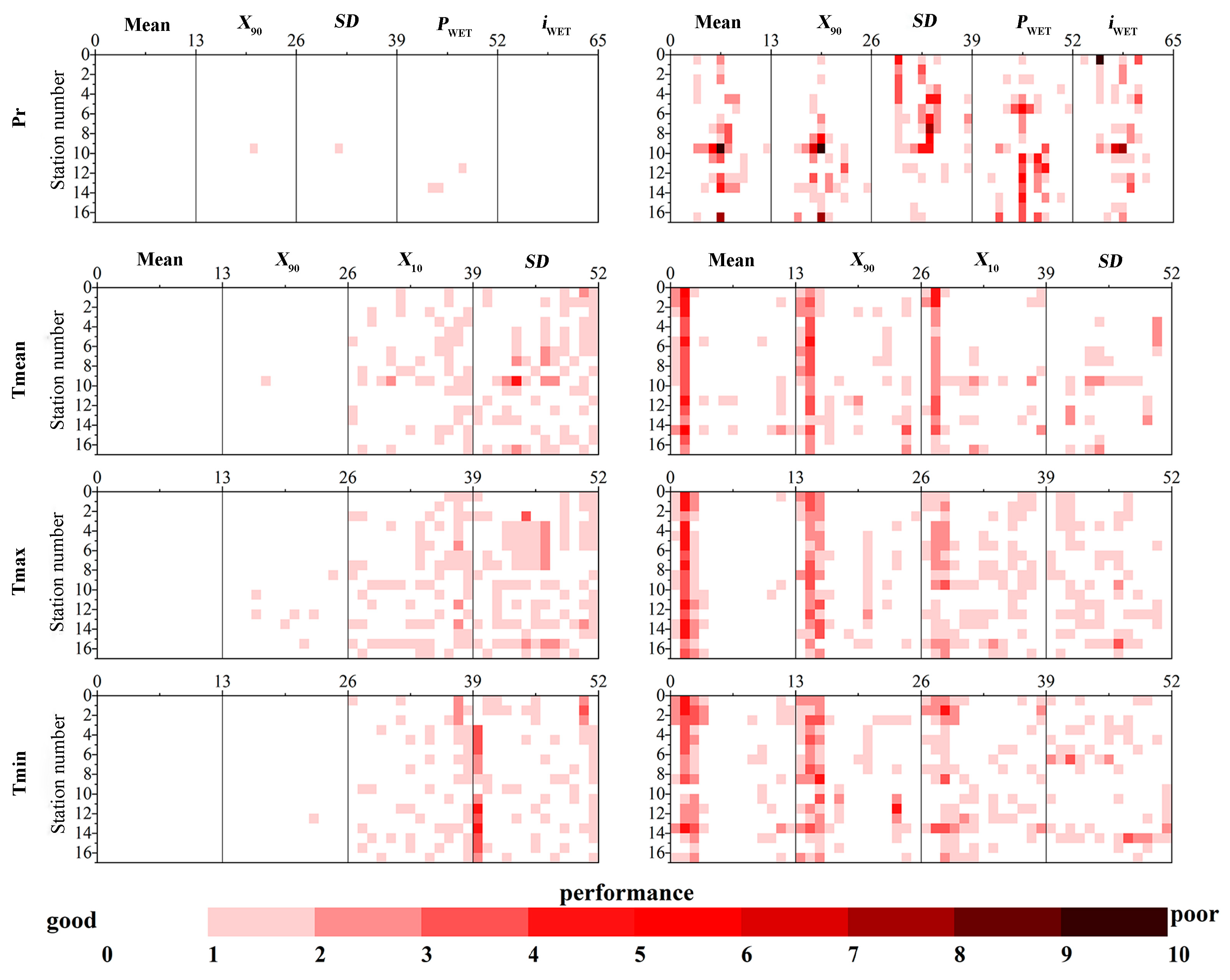
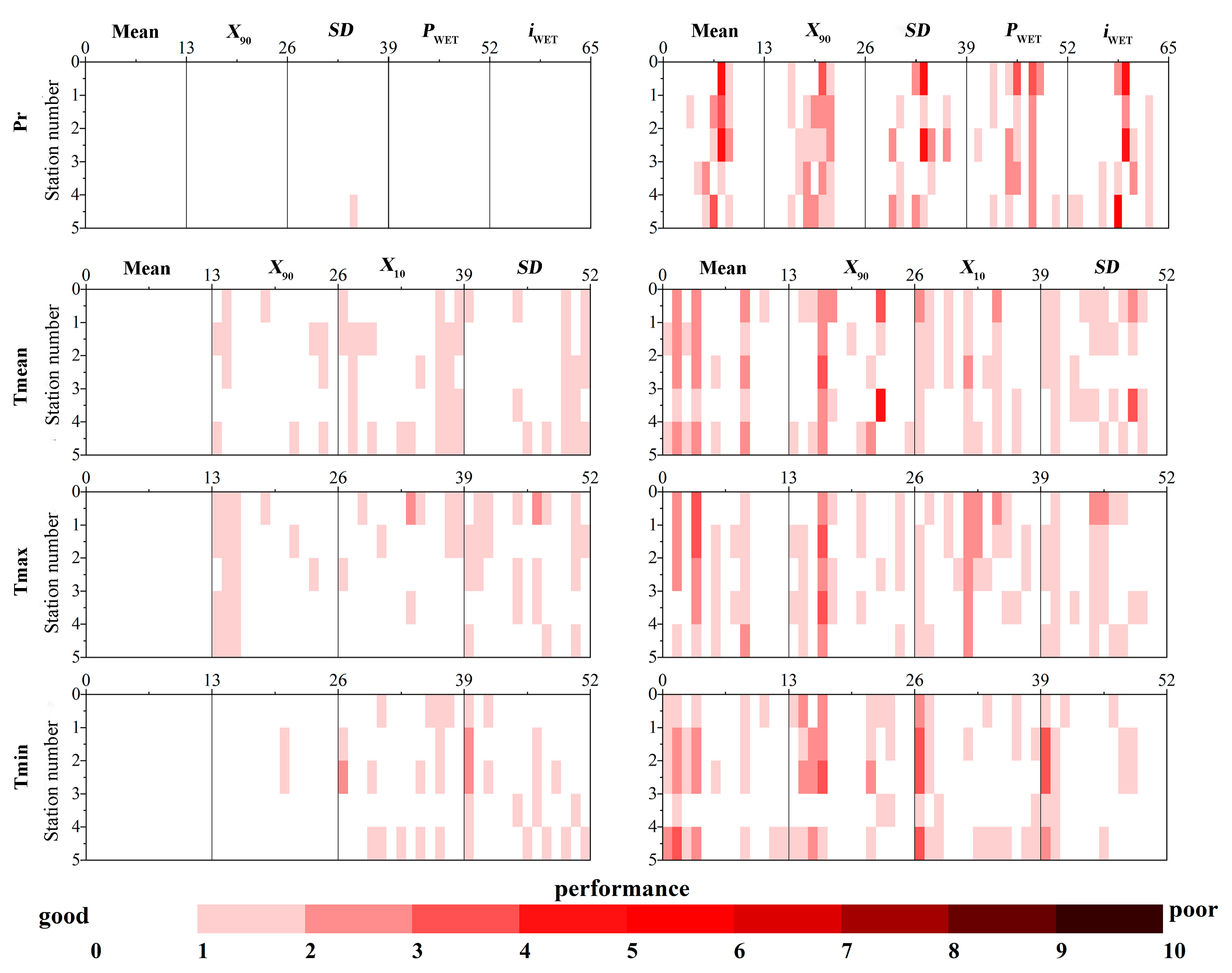
3.2. Calibration and Validation of Downscaling Models
3.2.1. SDSM Model
The Heihe River Basin
The Zhanghe River Basin
3.2.2. MOS Model
The Heihe River Basin
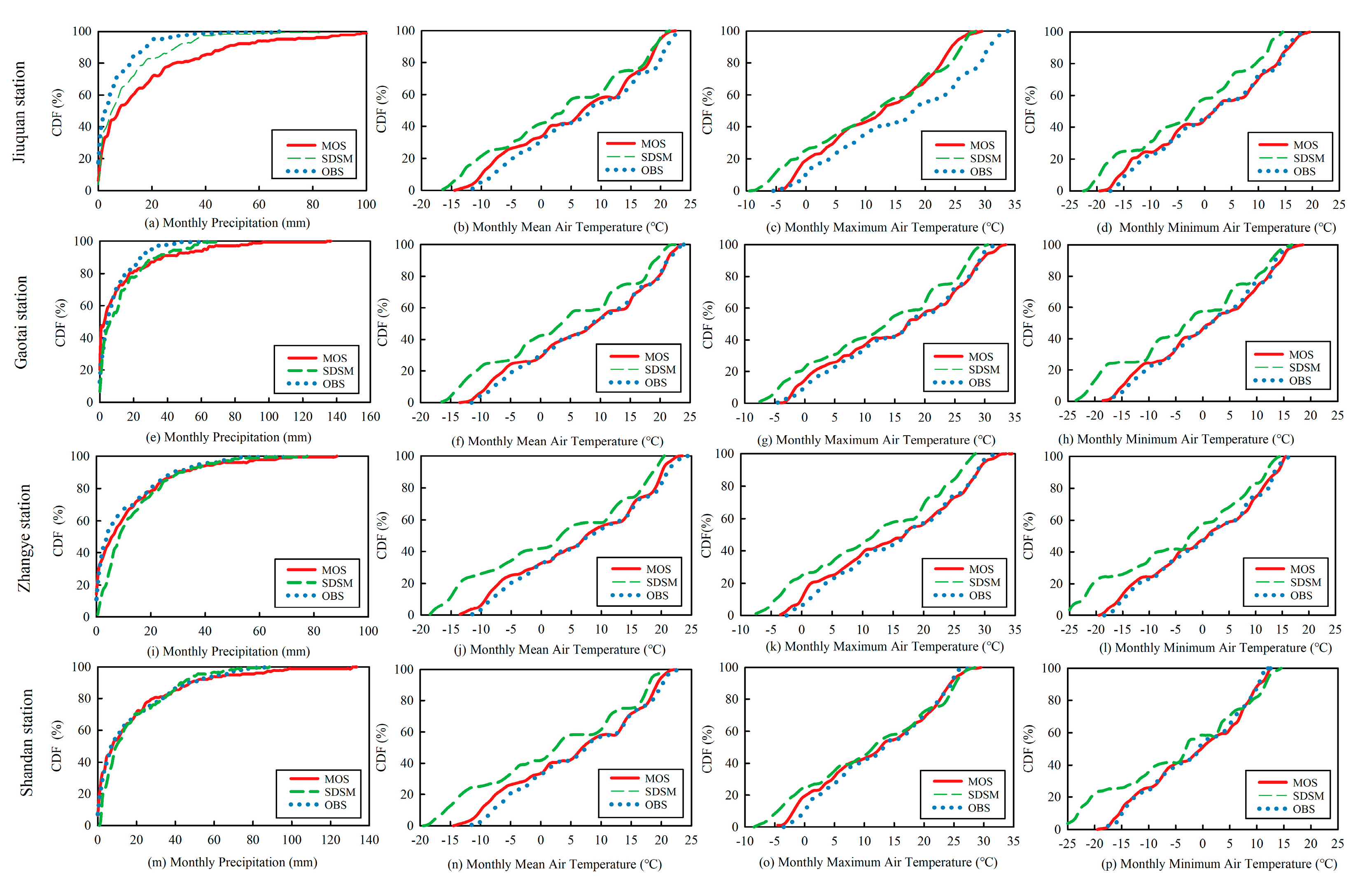
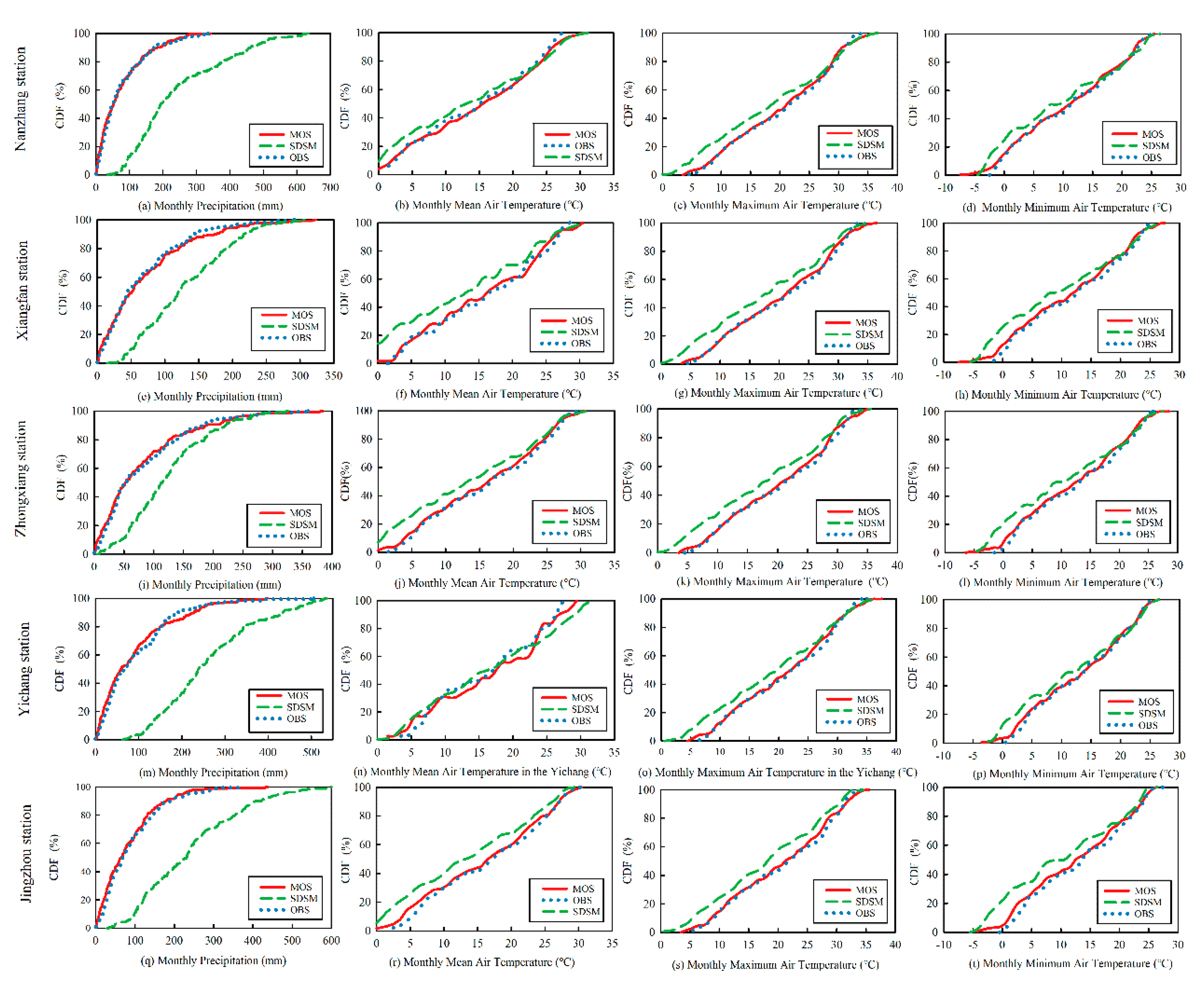
3.3. Optimization Assessment of SDSM and MOS for the Two Basins
3.3.1. Assessment of the HRB
3.3.2. Assessment in the ZRB
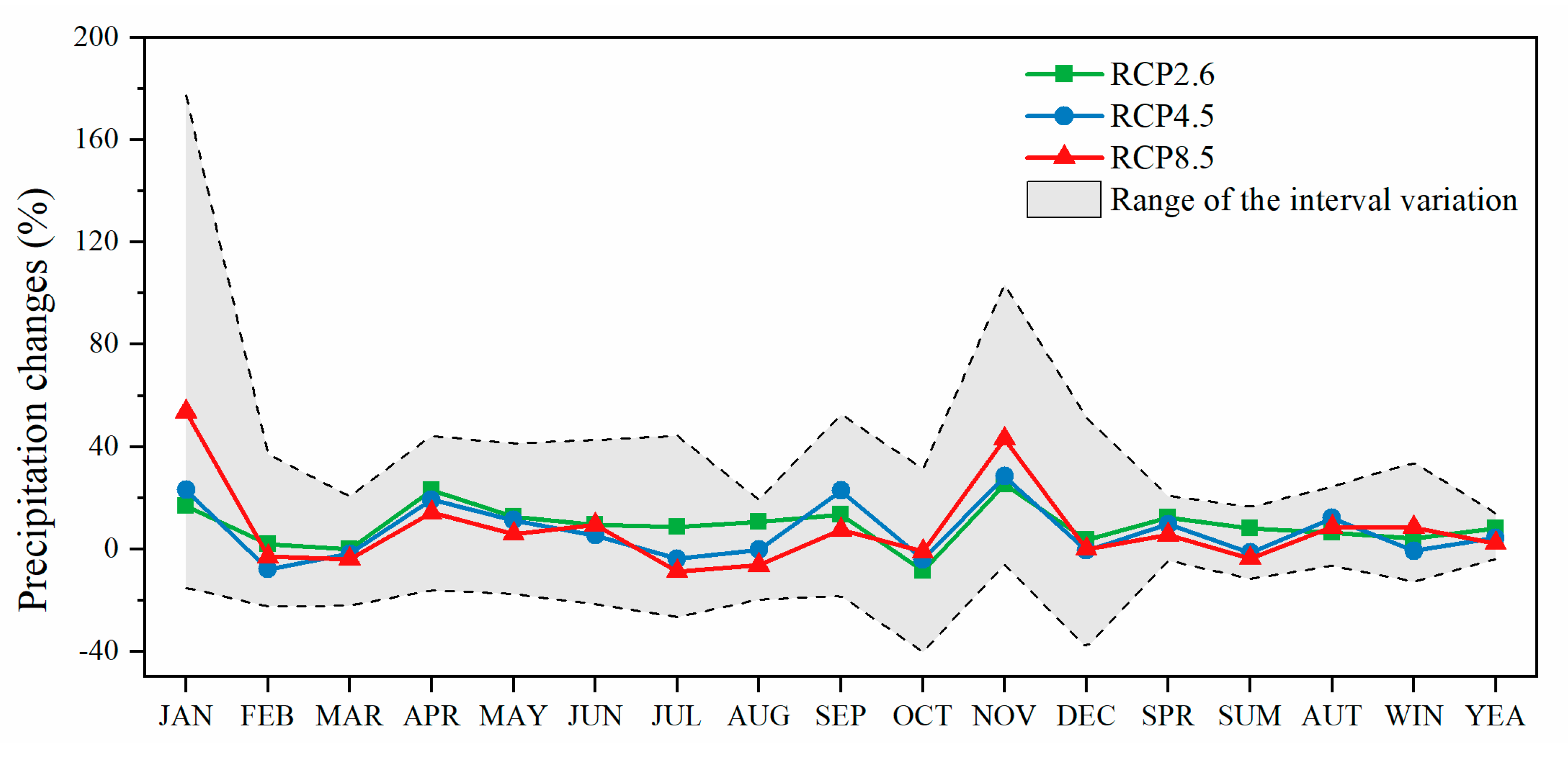
3.4. Climate Change Projections
3.4.1. Precipitation Scenarios
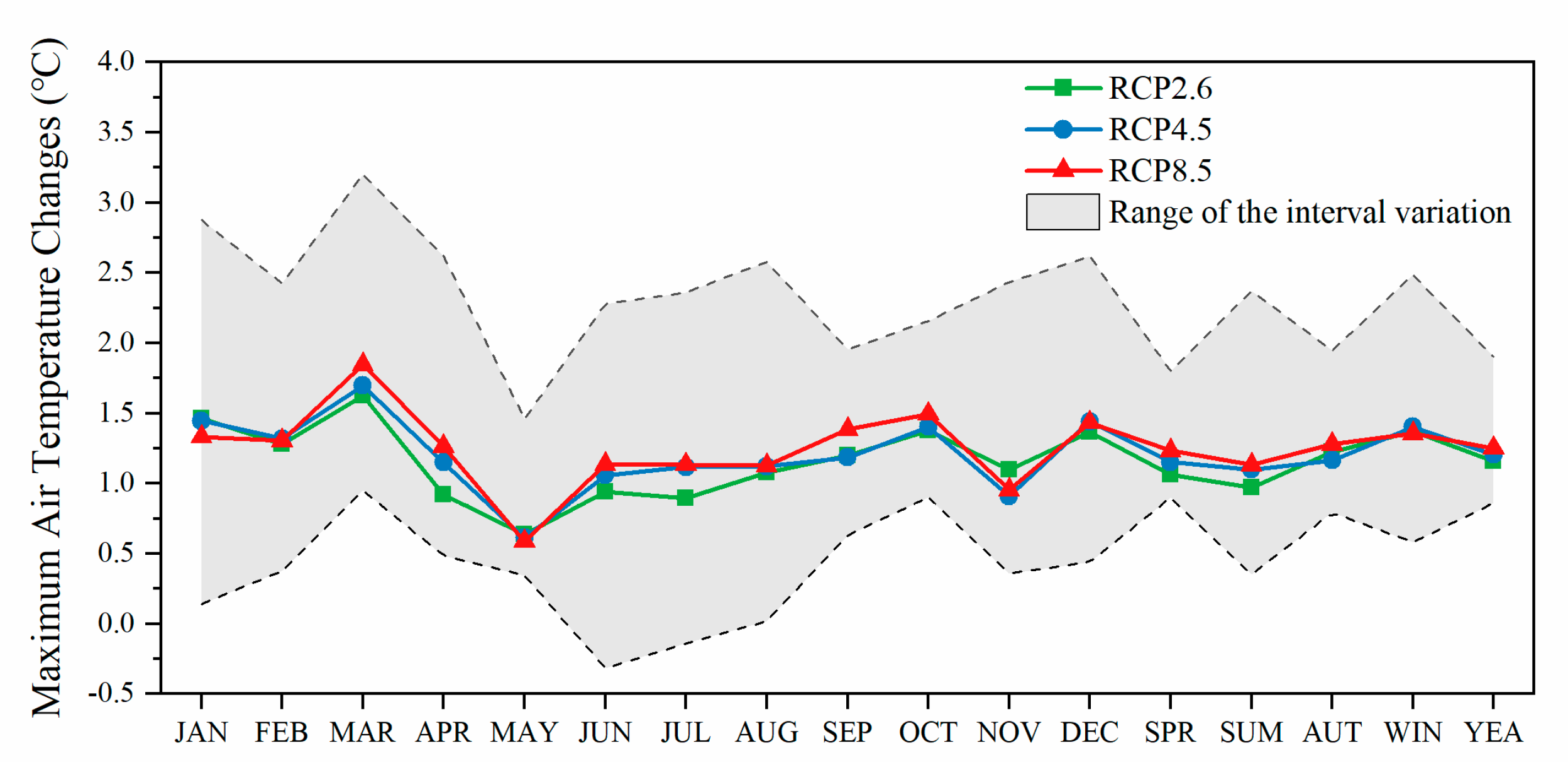
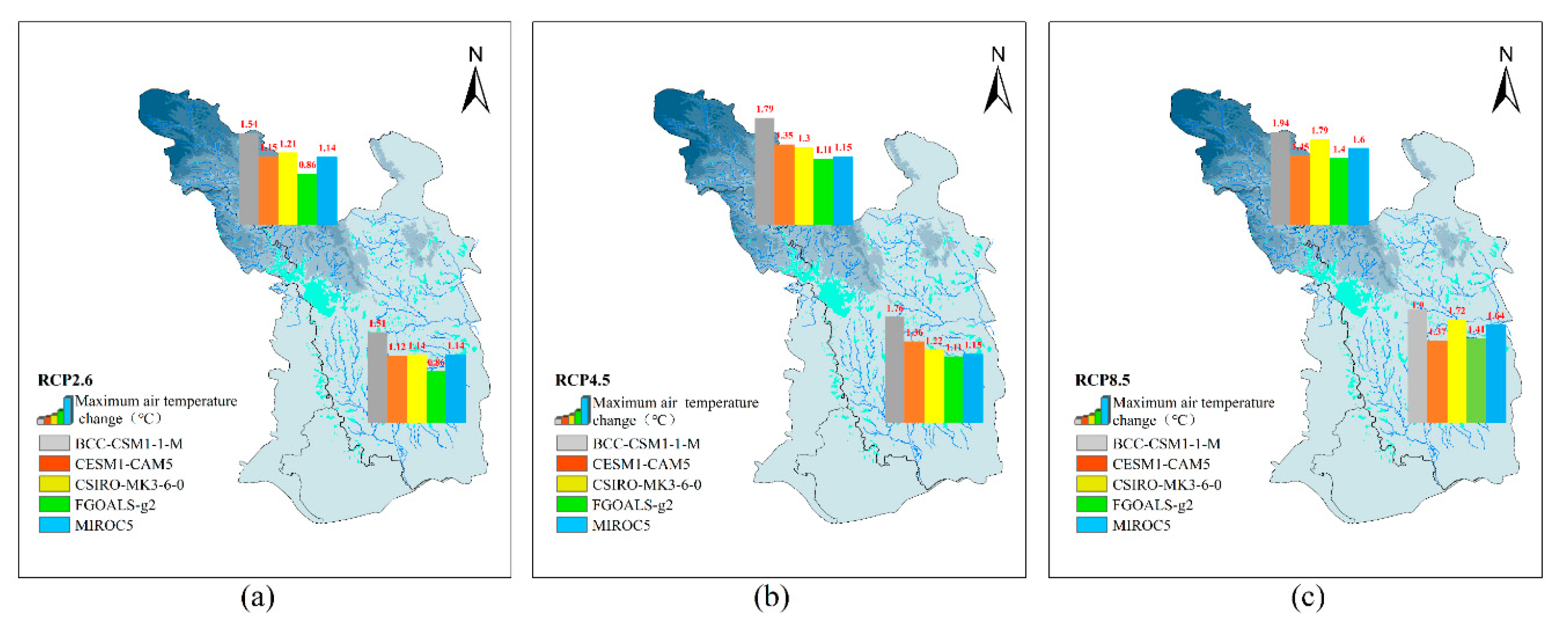
3.4.2. Maximum Air Temperature Scenarios
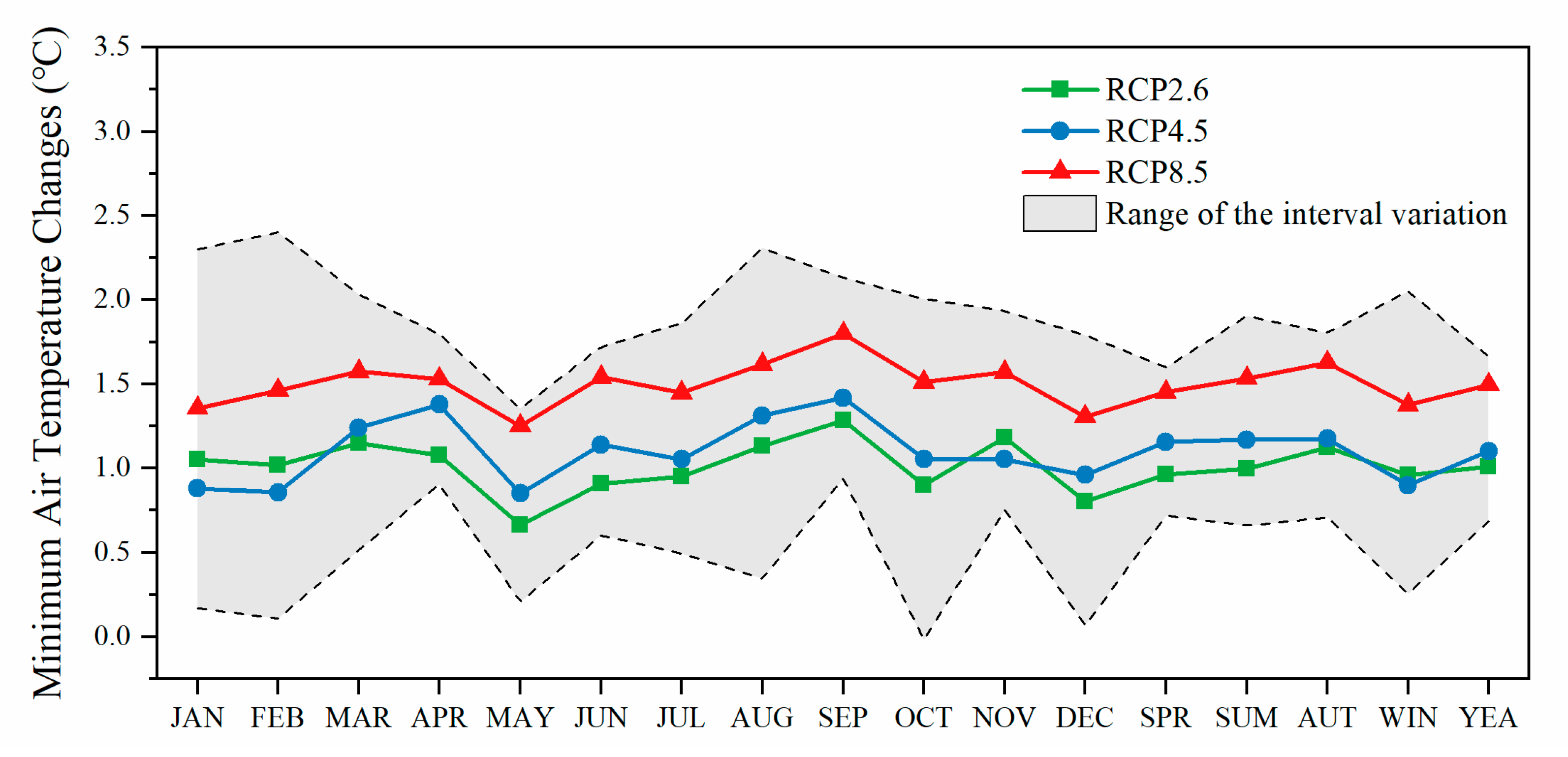
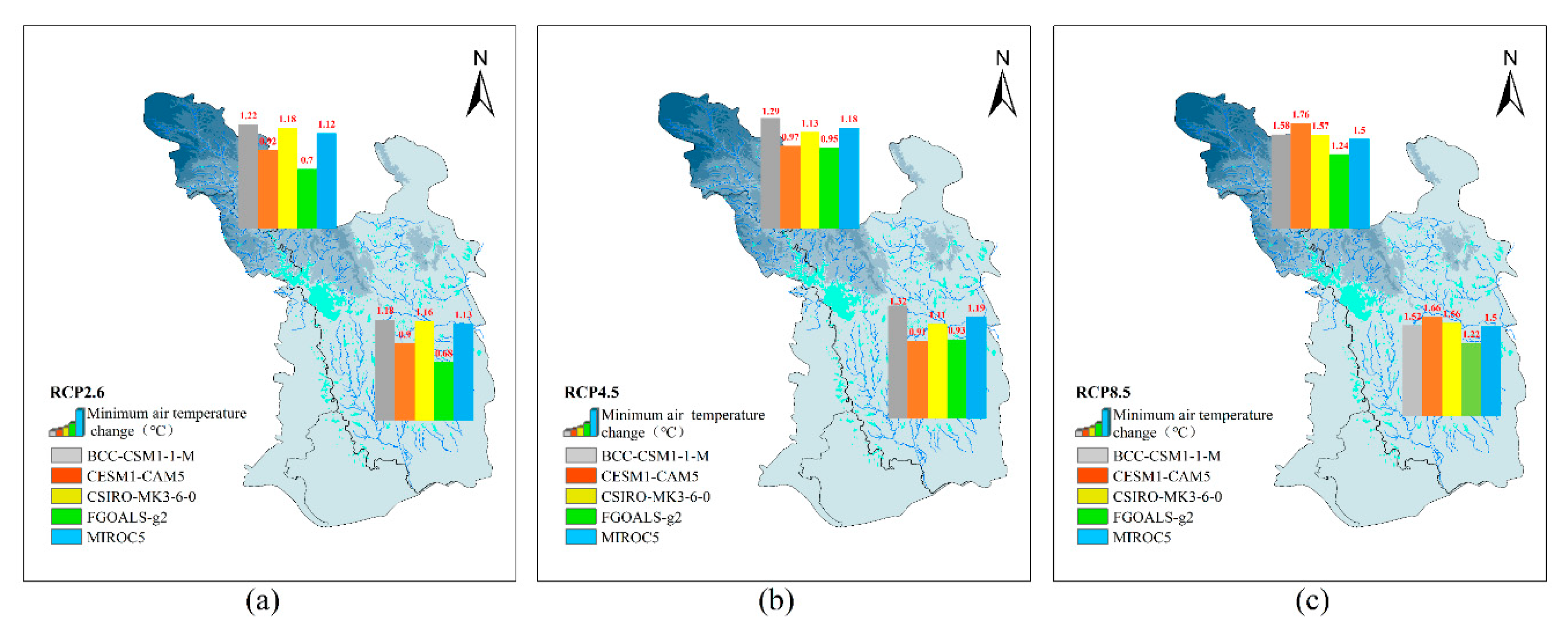
3.4.3. Minimum Air Temperature Scenarios
4. Conclusions
- (1)
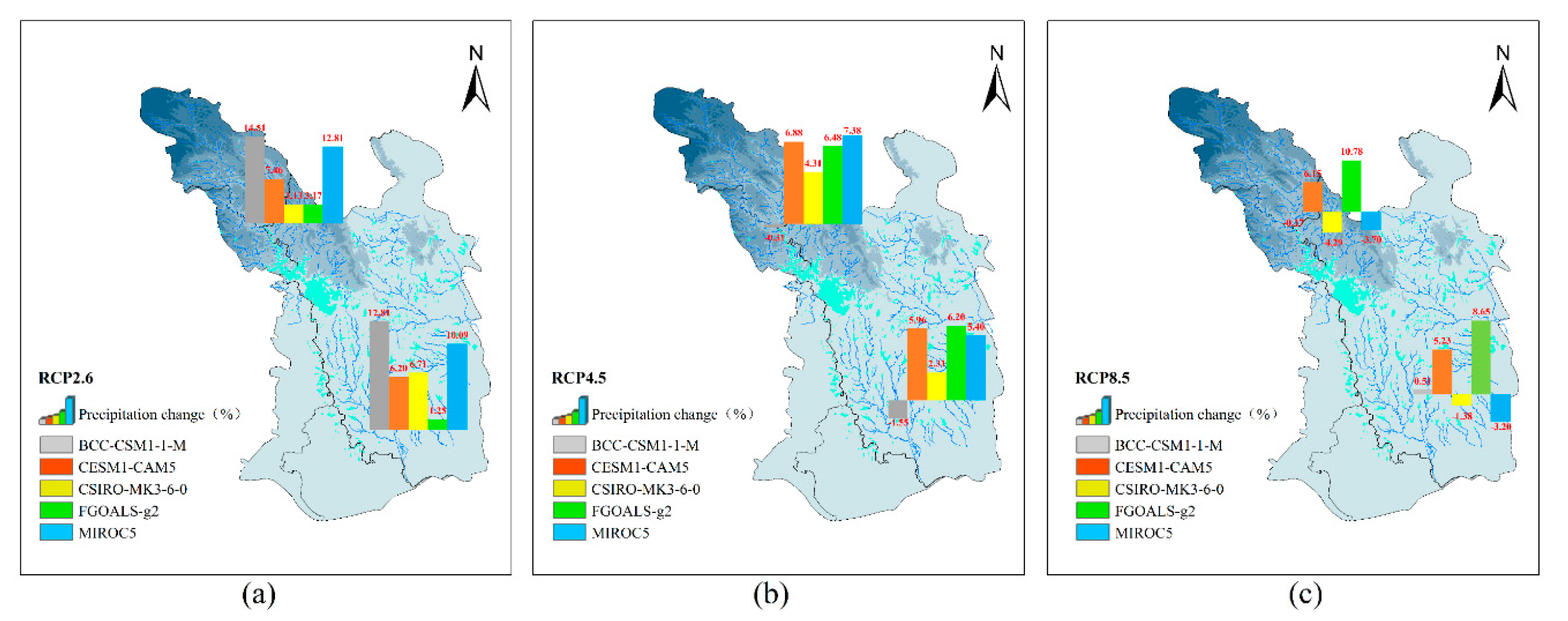
- According to the results of the score-based method and sensitivity analysis, five optimal GCMs were selected for each basin: CNRM-CM5, MPI-ESM-LR, MPI-ESM-MR, MRI-CGCM3, and CANESM2 were suitable for the HRB (arid climate) in North China; BCC-CSM1-1-M, CESM1-CAM5, MIROC5, CSIRO-MK3-6-0, and FGOALS-g2 were more appropriate for the ZRB (humid climate) in South China.
- (2)
- For different climate variables, SDSM and MOS showed superiority in different climatic basins. In the HRB, the performance of SDSM in downscaling precipitation was better than that of MOS, whereas MOS performed better in downscaling the temperature variables. In the ZRB, for both precipitation and temperature, MOS performed better than SDSM.
- (3)
- As indicated by the cumulative distribution functions (CDFs), MOS better captured the precipitation distribution characteristics in the humid region, but not in the arid region, implying that the climate characteristics of a specific region significantly impact the selection of the downscaling method, which is critical to the reliability of future climate change projections.
- (4)
- In the HRB, which is characterized as an inland arid climate, the multi-GCM-projected mean annual precipitation under the three RCP scenarios showed a decreasing trend, ranging between −12.3% and 4.4%. The most significant decrease appeared in the upstream [33]. In the ZRB, located in the middle reaches of the Yangtze River, the projected mean annual precipitation mostly exhibited an upward tendency ranging between −3.9% and 13.8%. The air temperature was projected to consistently increase in the HRB and ZRB, and the increase in the maximum air temperature was slightly larger than that of the minimum air temperature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Area | Stations | Tmax | Tmin | Tmean | Precipitation |
|---|---|---|---|---|---|
| HRB | 1 Jikede | mslp, p5ta, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu, p8hu | mslp, p5ta, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu |
| 2 Ejin Banner | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu, p8hu | mslp, p5ta, p7ta, p8ta, ta2m | lspr, p7ta, p8ta, ta2m, p5hu, p7hu, p8hu | |
| 3 Guaizihu | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m | mslp, p7ta, p8ta, ta2m | lspr, p7ta, p8ta, ta2m, p5hu, p7hu, p8hu | |
| 4 Yumen Town | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 5 Jiuquan | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 6 Jinta | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu, p8hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 7 Dingxin | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m, p7hu, p8hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 8 Gaotai | mslp, p7ta, p8ta, ta2m | p5ta, p8ta, ta2m, p7hu, p8hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 9 Alxa Right Banner | mslp, p7ta, p8ta, ta2m | mslp, p5ta, p7ta, p8ta, ta2m | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 10 Tuole | mslp, p5ta, p7ta, p8ta, ta2m | p5ta, ta2m, p8hu | p5ta, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p8hu | |
| 11 Yeniugou | mslp, p5ta, p7ta, p8ta, ta2m | p5ta, ta2m, p5hu, p7hu, p8hu | p5ta, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 12 Zhangye | mslp, p7ta, p8ta, ta2m | p5ta, ta2m, p5hu, p7hu, p8hu | mslp, p5ta, p7tap8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 13 Qilian | mslp, p5ta, p7ta, p8ta, ta2m | ta2m, p5hu, p7hu, p8hu | mslp, p5ta, p7tap8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 14 Gangcha | mslp, p5ta p7ta, p8ta, ta2m | p5ta, ta2m, p5hup7hu, p8hu | p5ta, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 15 Shandan | mslp, p7ta, p8ta, ta2m | p5ta, p8ta, ta2m, p5hu, p7hup8hu | mslp, p5ta, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 16 Yongchang | mslp, p7ta, p8ta, ta2m | p5ta, p8ta, ta2m, p5hu, p7hu, p8hu | mslp, p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| 17 Menyuan | mslp, p5ta, p7ta, p8ta, ta2m | p5ta, ta2m, p5hu, p7hu, p8hu | mslp, p5ta p7ta, p8ta, ta2m | lspr, mslp, p7ta, p8ta, ta2m, p7hu, p8hu | |
| ZRB | 1 Nanzhang | mslp, p500, p5ta, p8ta, ta2m | mslp, p5_u, p500, p5ta, p850, p8ta, ta2m | mslp, p500, p5ta, p8ta, ta2m | mslp, p500, p5ta, p7_u, p850, p8ta, va10 |
| 2 Xiangfan | mslp, p5_u, p500, p5ta, p8ta, ta2m | mslp, p5_u, p500, p5ta, p850, p8ta, ta2m | mslp, p500, p5ta, p8ta, ta2m | mslp, p500, p5ta, p850, p8ta, va10 | |
| 3 Zhongxiang | mslp, p5_u, p500, p5ta, p8ta, ta2m | mslp, p5_u, p500, p5ta, p850, p8ta, ta2m | mslp, p500, p5ta, p8ta, ta2m | mslp, p500, p5ta, p850, p8ta | |
| 4 Yichang | mslp, p5_u, p500, p5ta, p8ta, ta2m | mslp, p5_u, p500p5ta, p850, p8ta, ta2m | mslp, p500, p5ta, p5_u, p8ta ta2m | mslp, p500, p5ta, p850, p8ta, ta2m | |
| 5 Jingzhou | mslp, p5_u, p500, p5ta, p850, p8ta, ta2m | mslp, p5_u, p500, p5ta, p850, p8ta, ta2m | mslp, p500, p5ta, p5_u, p8tata2m | mslp, p500, p5ta, p850, p8ta |
| ID | Model Name | Source | Horizontal Resolution (lat × lon) |
|---|---|---|---|
| 1 | BCC-CSM 1.1 | Beijing Climate Center, China Meteorological Administration, China | 2.7906° × 2.8125° |
| 2 | BCC-CSM1.1-M | Beijing Climate Center, China Meteorological Administration, China | 1.1215° × 1.125° |
| 3 | CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada | 2.7906° × 2.8125° |
| 4 | CCSM4 | National Center for Atmospheric Research (NCAR), USA | 0.9424° × 1.25° |
| 5 | CESM1-CAM5 | National Center for Atmospheric Research (NCAR) Boulder, CO, USA | 0.9424° × 1.25° |
| 6 | CNRM-CM5 | Centre National de Recherches Meteorologiques, Meteo-France, France | 1.4007° × 1.4063° |
| 7 | CSIRO-Mk3.6.0 | Australian Commonwealth Scientific and Industrial Research Organization, Australia | 1.8653° × 1.875° |
| 8 | FGOALS-g2 | Institute of Atmospheric Physics, Chinese Academy of Sciences, China | 2.7906° × 2.8125° |
| 9 | FIO-ESM | The First Institute of Oceanography, SOA, China | 2.7906° × 2.8125° |
| 10 | GFDL-CM3 | Geophysical Fluid Dynamics Laboratory, USA | 2° × 2.5° |
| 11 | GFDL-ESM2G | Geophysical Fluid Dynamics Laboratory, USA | 2° × 2.5° |
| 12 | GISS-E2-H | NASA Goddard Institute for Space Studies, USA | 2° × 2.5° |
| 13 | GISS-E2-R | NASA Goddard Institute for Space Studies, USA | 2° × 2.5° |
| 14 | HadGEM2-ES | Met Office Hadley Centre, UK | 1.25° × 1.875° |
| 15 | IPSL-CM5A-LR | Institut Pierre-Simon Laplace, France | 1.8947° × 3.75° |
| 16 | IPSL-CM5A-MR | Institut Pierre-Simon Laplace, France | 1.2676° × 2.5° |
| 17 | MIROC5 | Atmosphere and Ocean Research Institute (The University of Tokyo),National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 1.4005° × 1.4063° |
| 18 | MIROC-ESM | Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 2.7906° × 2.8125° |
| 19 | MIROC-ESM-CHEM | Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 2.7906° × 2.8125° |
| 20 | MPI-ESM-LR | Max Planck Institute for Meteorology, Germany | 1.8653° × 1.875° |
| 21 | MPI-ESM-MR | Max Planck Institute for Meteorology, Germany | 1.8653° × 1.875° |
| 22 | MRI-CGCM3 | Meteorological Research Institute, Japan | 1.1215° × 1.125° |
| 23 | NorESM1-M | Norwegian Climate Centre, Norway | 1.8947° × 2.5° |
| Long Name | Short Name | Long Name | Short Name |
|---|---|---|---|
| Large-scale precipitation | lspr | Specific humidity at 850 hPa | p8hu |
| Mean sea level pressure | mslp | Temperature at 500 hPa | p5ta |
| Mean temperature at 2 m | ta2m | Temperature at 700 hPa | p7ta |
| 10 m meridional velocity | va10 | Temperature at 850 hPa | p8ta |
| 10 m zonal velocity | ua10 | 500 hPa meridional velocity | p5_v |
| 500 hPa geopotential height | p500 | 700 hPa meridional velocity | p7_v |
| 700 hPa geopotential height | p700 | 850 hPa meridional velocity | p8_v |
| 850 hPa geopotential height | p850 | 500 hPa zonal velocity | p5_u |
| Specific humidity at 500 hPa | p5hu | 700 hPa zonal velocity | p7_u |
| Specific humidity at 700 hPa | p7hu | 850 hPa zonal velocity | p8_u |
| Evaluation Indices | Mean | X90 | X10 | SD | PWET | iWET | |||
|---|---|---|---|---|---|---|---|---|---|
| Variables | P | T | P | T | T | P | T | P | P |
| January | 1 | 1 | 14 | 14 | 27 | 27 | 40 | 40 | 53 |
| February | 2 | 2 | 15 | 15 | 28 | 28 | 41 | 41 | 54 |
| March | 3 | 3 | 16 | 16 | 29 | 29 | 42 | 42 | 55 |
| April | 4 | 4 | 17 | 17 | 30 | 30 | 43 | 43 | 56 |
| May | 5 | 5 | 18 | 18 | 31 | 31 | 44 | 44 | 57 |
| June | 6 | 6 | 19 | 19 | 32 | 32 | 45 | 45 | 58 |
| July | 7 | 7 | 20 | 20 | 33 | 33 | 46 | 46 | 59 |
| August | 8 | 8 | 21 | 21 | 34 | 34 | 47 | 47 | 60 |
| September | 9 | 9 | 22 | 22 | 35 | 35 | 48 | 48 | 61 |
| October | 10 | 10 | 23 | 23 | 36 | 36 | 49 | 49 | 62 |
| November | 11 | 11 | 24 | 24 | 37 | 37 | 50 | 50 | 63 |
| December | 12 | 12 | 25 | 25 | 38 | 38 | 51 | 51 | 64 |
| Daily average precipitation/temperature | 13 | 13 | 26 | 26 | 39 | 39 | 52 | 52 | 65 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 84.46 | 0.87 | −0.09 | 0.0003 | 0.5 | −0.015 | ||||||
| BCC-CSM 1.1 | 111.16 | 0.67 | 1.19 | 0.45 | −0.91 | −0.10 | −0.0014 | 0.5 | 0.016 | 0.011 | 0.69 | 5.87 |
| BCC-CSM1-1-M | 63.6 | 0.91 | 1.11 | 0.35 | 0.98 | 0.01 | 0.0013 | 0.5 | −0.030 | 0.004 | 0.82 | 8.45 |
| CanESM2 | 132.65 | 0.64 | 1.53 | 0.26 | 0.87 | 0.43 | 0.0114 | 0.5 | −0.038 | 0.012 | 0.68 | 4.56 |
| CCSM4 | 120.23 | 0.83 | 1.23 | 0.47 | 0.75 | −0.71 | −0.0113 | 0.5 | −0.028 | 0.005 | 0.79 | 7.76 |
| CESM1-CAM5 | 121.05 | 0.76 | 1.3 | 0.52 | 0.5 | −0.45 | −0.0079 | 0.5 | −0.005 | 0.007 | 0.77 | 7.19 |
| CNRM-CM5 | 82.16 | 0.68 | 1.34 | 0.39 | 0.41 | 0.1 | 0.0046 | 0.49 | 0.024 | 0.008 | 0.75 | 6.14 |
| CSIRO-MK3-6-0 | 86.24 | 0.86 | 1.06 | 0.47 | 0.78 | −0.58 | −0.0063 | 0.5 | −0.019 | 0.007 | 0.76 | 8.61 |
| FGOALS-g2 | 86.24 | 0.73 | 1.02 | 0.48 | −0.54 | 0.22 | 0.0039 | 0.5 | −0.006 | 0.008 | 0.73 | 7.47 |
| FIO-ESM | 136.86 | 0.7 | 1.42 | 0.55 | 0.61 | −0.19 | −0.0026 | 0.5 | −0.034 | 0.009 | 0.7 | 6.34 |
| GFDL-CM3 | 107.08 | 0.6 | 1.32 | 0.26 | 0.91 | −1.90 | −0.0338 | 0.5 | −0.021 | 0.015 | 0.62 | 3.66 |
| GFDL-ESM2G | 91.68 | 0.82 | 1.17 | 0.4 | −0.36 | −1.12 | −0.0176 | 0.5 | 0 | 0.007 | 0.74 | 6.55 |
| GISS-E2-H | 108.82 | 0.67 | 1.13 | 0.49 | 0.36 | −0.66 | −0.0103 | 0.5 | −0.014 | 0.008 | 0.75 | 6.95 |
| GISS-E2-R | 112.02 | 0.64 | 1.13 | 0.49 | 0.4 | −0.53 | −0.0082 | 0.5 | 0.001 | 0.01 | 0.72 | 6.51 |
| HadGEM2-ES | 106.79 | 0.84 | 1.29 | 0.47 | 0.9 | −2.03 | −0.0333 | 0.48 | −0.138 | 0.009 | 0.75 | 4.42 |
| IPSL-CM5A-LR | 82.12 | 0.71 | 1.02 | 0.46 | −0.36 | −1.46 | −0.0195 | 0.5 | 0.005 | 0.009 | 0.72 | 6.22 |
| IPSL-CM5A-MR | 77.26 | 0.78 | 1.08 | 0.43 | 0.02 | −1.15 | −0.0141 | 0.5 | 0.038 | 0.006 | 0.78 | 7.15 |
| MIROC5 | 128.75 | 0.7 | 1.35 | 0.52 | 0.96 | −0.39 | −0.0068 | 0.5 | −0.018 | 0.007 | 0.75 | 6.98 |
| MIROC-ESM | 79.84 | 0.87 | 1.13 | 0.4 | −1.00 | 0.3 | 0.0056 | 0.5 | 0.013 | 0.005 | 0.79 | 7.5 |
| MIROC-ESM-CHEM | 82.88 | 0.83 | 1.09 | 0.44 | −0.99 | 0.62 | 0.0107 | 0.5 | 0.007 | 0.005 | 0.78 | 7.31 |
| MPI-ESM-LR | 123.54 | 0.68 | 1.35 | 0.4 | 0.78 | −0.50 | 0.0029 | 0.5 | 0.003 | 0.011 | 0.66 | 5.1 |
| MPI-ESM-MR | 126.05 | 0.68 | 1.35 | 0.45 | 0.7 | 0.35 | 0.0089 | 0.5 | 0.001 | 0.01 | 0.69 | 5.91 |
| MRI-CGCM3 | 57.04 | 0.82 | 1.15 | 0.25 | 0.21 | −0.30 | −0.0019 | 0.5 | −0.001 | 0.007 | 0.76 | 6.97 |
| NorESM1-M | 122.14 | 0.74 | 1.38 | 0.43 | −0.54 | 0.04 | 0.0031 | 0.5 | 0.004 | 0.008 | 0.72 | 6.02 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 16.22 | 0.53 | 0.66 | 0.0015 | 0.5 | 0.014 | ||||||
| BCC-CSM 1.1 | 12.29 | 0.78 | 0.54 | 0.98 | 0.78 | 0.58 | 0.0017 | 0.5 | −0.006 | 0.007 | 0.67 | 4.45 |
| BCC-CSM1-1-M | 13.88 | 0.68 | 0.39 | 0.97 | 0.82 | 0.56 | 0.0014 | 0.5 | 0.01 | 0.006 | 0.71 | 6.99 |
| CanESM2 | 13.86 | 0.7 | 0.4 | 0.97 | 0.75 | 0.79 | 0.002 | 0.5 | 0.002 | 0.005 | 0.74 | 6.46 |
| CCSM4 | 13.63 | 0.71 | 0.41 | 0.98 | 0.59 | 1.01 | 0.0022 | 0.5 | −0.002 | 0.008 | 0.67 | 5.45 |
| CESM1-CAM5 | 13.78 | 0.63 | 0.37 | 0.98 | 0.58 | 0.62 | 0.0013 | 0.5 | −0.003 | 0.007 | 0.68 | 6.23 |
| CNRM-CM5 | 12.73 | 0.69 | 0.49 | 0.98 | 0.37 | −0.07 | 0.0001 | 0.5 | 0.007 | 0.009 | 0.64 | 3.44 |
| CSIRO-MK3-6-0 | 14.7 | 0.69 | 0.37 | 0.97 | 0.32 | 0.66 | 0.0017 | 0.5 | −0.007 | 0.008 | 0.66 | 5.77 |
| FGOALS-g2 | 12.88 | 0.73 | 0.47 | 0.98 | 0.88 | 0.85 | 0.0021 | 0.5 | −0.003 | 0.006 | 0.72 | 5.29 |
| FIO-ESM | 14.29 | 0.59 | 0.34 | 0.97 | 0.74 | 0.69 | 0.0015 | 0.5 | −0.005 | 0.004 | 0.76 | 6.91 |
| GFDL-CM3 | 12.04 | 0.76 | 0.56 | 0.97 | 0.75 | 0.24 | 0.0007 | 0.5 | −0.012 | 0.006 | 0.7 | 5.09 |
| GFDL-ESM2G | 13.6 | 0.58 | 0.41 | 0.96 | 0.93 | 0.74 | 0.0017 | 0.5 | −0.011 | 0.01 | 0.62 | 5 |
| GISS-E2-H | 14.69 | 0.49 | 0.34 | 0.97 | 0.64 | −0.31 | −0.0004 | 0.5 | −0.003 | 0.005 | 0.73 | 5.12 |
| GISS-E2-R | 14.76 | 0.47 | 0.35 | 0.97 | 0.69 | 0.24 | 0.0006 | 0.5 | −0.007 | 0.006 | 0.71 | 5.99 |
| HadGEM2-ES | 13.23 | 0.66 | 0.42 | 0.98 | 0.5 | 0.71 | 0.0017 | 0.5 | 0.014 | 0.008 | 0.71 | 5.84 |
| IPSL-CM5A-LR | 14.13 | 0.66 | 0.38 | 0.97 | 0.78 | 0.98 | 0.0021 | 0.5 | −0.009 | 0.004 | 0.75 | 6.32 |
| IPSL-CM5A-MR | 15.03 | 0.64 | 0.33 | 0.97 | 0.56 | 1.1 | 0.0026 | 0.5 | 0.003 | 0.007 | 0.7 | 6.1 |
| MIROC5 | 15.85 | 0.55 | 0.26 | 0.98 | 0.39 | 0.28 | 0.0007 | 0.5 | −0.001 | 0.008 | 0.67 | 6.57 |
| MIROC-ESM | 16.33 | 0.54 | 0.27 | 0.97 | 0.81 | 0.38 | 0.0009 | 0.5 | −0.002 | 0.011 | 0.6 | 5.62 |
| MIROC-ESM-CHEM | 16.04 | 0.55 | 0.28 | 0.97 | 0.82 | 0.68 | 0.0014 | 0.5 | −0.002 | 0.011 | 0.61 | 5.96 |
| MPI-ESM-LR | 14.5 | 0.56 | 0.33 | 0.97 | 0.63 | 0.83 | 0.0019 | 0.5 | −0.015 | 0.006 | 0.72 | 5.81 |
| MPI-ESM-MR | 14.53 | 0.56 | 0.32 | 0.97 | 0.65 | 1.32 | 0.003 | 0.5 | 0.016 | 0.005 | 0.73 | 5.4 |
| MRI-CGCM3 | 13.78 | 0.74 | 0.45 | 0.97 | 0.32 | 0.12 | 0.0006 | 0.5 | −0.01 | 0.009 | 0.64 | 3.3 |
| NorESM1-M | 12.23 | 0.79 | 0.54 | 0.98 | 0.75 | 0.59 | 0.0013 | 0.5 | −0.01 | 0.006 | 0.72 | 5.25 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 20.99 | 0.41 | 0.29 | 0.0008 | 0.5 | 0.005 | ||||||
| BCC-CSM 1.1 | 16.81 | 0.61 | 0.61 | 0.96 | 0.34 | 0.55 | 0.0018 | 0.5 | −0.004 | 0.006 | 0.72 | 6.03 |
| BCC-CSM1-1-M | 18.99 | 0.54 | 0.44 | 0.96 | 0.9 | 0.53 | 0.0017 | 0.5 | −0.008 | 0.004 | 0.76 | 7.5 |
| CanESM2 | 18.58 | 0.54 | 0.46 | 0.96 | 0.13 | 0.57 | 0.0016 | 0.5 | −0.002 | 0.001 | 0.72 | 6.66 |
| CCSM4 | 19.77 | 0.43 | 0.35 | 0.96 | −0.01 | 0.88 | 0.0021 | 0.5 | 0.003 | 0.006 | 0.71 | 6.86 |
| CESM1-CAM5 | 19.34 | 0.4 | 0.39 | 0.96 | −0.15 | 0.45 | 0.0011 | 0.5 | −0.006 | 0.005 | 0.73 | 7.66 |
| CNRM-CM5 | 18.31 | 0.48 | 0.49 | 0.95 | −0.35 | −0.12 | −0.0008 | 0.5 | 0.001 | 0.01 | 0.64 | 5.38 |
| CSIRO-MK3-6-0 | 19.51 | 0.51 | 0.42 | 0.95 | −0.27 | 0.71 | 0.002 | 0.5 | 0.012 | 0.005 | 0.72 | 6.03 |
| FGOALS-g2 | 17.26 | 0.57 | 0.55 | 0.96 | 0.65 | 0.79 | 0.0023 | 0.5 | −0.004 | 0.004 | 0.76 | 6.52 |
| FIO-ESM | 18.61 | 0.45 | 0.42 | 0.95 | 0.31 | 0.78 | 0.0018 | 0.5 | −0.011 | 0.005 | 0.73 | 6.67 |
| GFDL-CM3 | 16.15 | 0.61 | 0.66 | 0.96 | 0.25 | 0.25 | 0.0009 | 0.5 | 0.014 | 0.004 | 0.76 | 6.65 |
| GFDL-ESM2G | 17.2 | 0.46 | 0.55 | 0.95 | 0.74 | 0.81 | 0.002 | 0.5 | 0.012 | 0.008 | 0.67 | 5.79 |
| GISS-E2-H | 18.28 | 0.39 | 0.47 | 0.95 | 0.04 | −0.38 | −0.0006 | 0.5 | 0.007 | 0.004 | 0.77 | 7.26 |
| GISS-E2-R | 18.39 | 0.38 | 0.47 | 0.95 | 0.17 | 0.21 | 0.0006 | 0.5 | 0.011 | 0.005 | 0.75 | 7.76 |
| HadGEM2-ES | 17.47 | 0.5 | 0.51 | 0.96 | −0.59 | 0.26 | 0.0001 | 0.5 | −0.015 | 0.005 | 0.75 | 5.77 |
| IPSL-CM5A-LR | 26.53 | 0.27 | 0.77 | 0.91 | 0.3 | 1.23 | 0.0021 | 0.5 | 0.021 | 0.007 | 0.68 | 2.47 |
| IPSL-CM5A-MR | 27.72 | 0.28 | 0.88 | 0.93 | −0.10 | 1.11 | 0.0022 | 0.5 | 0.017 | 0.007 | 0.68 | 2.52 |
| MIROC5 | 20.55 | 0.44 | 0.35 | 0.96 | −0.29 | 0.01 | 0.0003 | 0.5 | −0.007 | 0.006 | 0.71 | 6.61 |
| MIROC-ESM | 21.84 | 0.41 | 0.39 | 0.94 | 0.31 | 0.27 | 0.0007 | 0.5 | −0.004 | 0.009 | 0.64 | 6.92 |
| MIROC-ESM-CHEM | 21.32 | 0.42 | 0.39 | 0.94 | 0.34 | 0.7 | 0.0017 | 0.5 | −0.003 | 0.008 | 0.66 | 6.39 |
| MPI-ESM-LR | 18.75 | 0.42 | 0.43 | 0.94 | 0.04 | 0.83 | 0.0018 | 0.5 | −0.010 | 0.005 | 0.72 | 5.59 |
| MPI-ESM-MR | 18.8 | 0.41 | 0.42 | 0.95 | 0.1 | 1.25 | 0.003 | 0.5 | 0.014 | 0.005 | 0.74 | 5.51 |
| MRI-CGCM3 | 18.85 | 0.56 | 0.48 | 0.96 | −0.43 | −0.06 | 0.0002 | 0.5 | −0.005 | 0.007 | 0.69 | 5.32 |
| NorESM1-M | 17.7 | 0.49 | 0.48 | 0.96 | 0.2 | 0.47 | 0.0011 | 0.5 | −0.012 | 0.006 | 0.71 | 6.58 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 12.46 | 0.68 | 1.15 | 0.0024 | 0.5 | −0.0067 | ||||||
| BCC-CSM 1.1 | 8.1 | 1.17 | 0.58 | 0.98 | 0.83 | 0.56 | 0.0015 | 0.5 | 0.006 | 0.006 | 0.72 | 6.18 |
| BCC-CSM1-1-M | 9.3 | 0.98 | 0.44 | 0.98 | 0.8 | 0.76 | 0.0015 | 0.5 | 0.0096 | 0.009 | 0.64 | 5.81 |
| CanESM2 | 9.18 | 1.09 | 0.5 | 0.98 | 0.85 | 1.04 | 0.0025 | 0.5 | −0.0045 | 0.005 | 0.72 | 7.6 |
| CCSM4 | 8.97 | 1.14 | 0.51 | 0.98 | 0.76 | 1.01 | 0.0021 | 0.5 | 0.0058 | 0.006 | 0.72 | 7.16 |
| CESM1-CAM5 | 9.46 | 1 | 0.43 | 0.98 | 0.78 | 0.71 | 0.0015 | 0.5 | 0.0032 | 0.007 | 0.69 | 6.61 |
| CNRM-CM5 | 8.4 | 1.05 | 0.54 | 0.98 | 0.61 | 0.13 | 0.0005 | 0.5 | 0.0054 | 0.007 | 0.69 | 4.97 |
| CSIRO-MK3-6-0 | 10.1 | 1.01 | 0.42 | 0.98 | 0.51 | 0.69 | 0.0015 | 0.5 | −0.0028 | 0.008 | 0.67 | 6.05 |
| FGOALS-g2 | 8.77 | 1.06 | 0.5 | 0.98 | 0.89 | 0.84 | 0.002 | 0.5 | 0.0022 | 0.006 | 0.71 | 6.98 |
| FIO-ESM | 10.39 | 0.85 | 0.35 | 0.97 | 0.79 | 0.57 | 0.7893 | 0.5 | 0.0013 | 0.004 | 0.76 | 7.05 |
| GFDL-CM3 | 7.69 | 1.15 | 0.63 | 0.97 | 0.83 | 0.26 | 0.0007 | 0.5 | 0.0065 | 0.006 | 0.7 | 5.25 |
| GFDL-ESM2G | 9.83 | 0.84 | 0.42 | 0.96 | 0.91 | 0.71 | 0.0016 | 0.5 | 0.0078 | 0.008 | 0.67 | 5.83 |
| GISS-E2-H | 11.02 | 0.71 | 0.29 | 0.98 | 0.79 | −0.18 | −0.0002 | 0.5 | −0.0014 | 0.005 | 0.73 | 6.37 |
| GISS-E2-R | 11.02 | 0.68 | 0.3 | 0.98 | 0.81 | 0.31 | 0.0007 | 0.5 | −0.0060 | 0.006 | 0.72 | 7.21 |
| HadGEM2-ES | 9.41 | 0.94 | 0.42 | 0.98 | 0.81 | 0.18 | 0.0006 | 0.5 | 0.0115 | 0.006 | 0.71 | 6.7 |
| IPSL-CM5A-LR | 3.06 | 3.7 | 1.19 | 0.96 | 0.81 | 0.7 | 0.0021 | 0.5 | −0.0019 | 0.005 | 0.73 | 4.49 |
| IPSL-CM5A-MR | 3.83 | 3.1 | 1.1 | 0.97 | 0.72 | 0.56 | 0.0017 | 0.5 | −0.0005 | 0.007 | 0.7 | 4.2 |
| MIROC5 | 11.99 | 0.74 | 0.23 | 0.98 | 0.64 | 0.58 | 0.0011 | 0.5 | −0.0041 | 0.008 | 0.66 | 6.52 |
| MIROC-ESM | 12.07 | 0.75 | 0.24 | 0.98 | 0.88 | 0.3 | 0.0006 | 0.5 | −0.0006 | 0.011 | 0.61 | 5.76 |
| MIROC-ESM-CHEM | 11.94 | 0.75 | 0.26 | 0.98 | 0.88 | 0.49 | 0.0009 | 0.5 | 0.0003 | 0.009 | 0.64 | 6.13 |
| MPI-ESM-LR | 10.86 | 0.77 | 0.29 | 0.98 | 0.79 | 0.88 | 0.0018 | 0.5 | 0.0174 | 0.007 | 0.7 | 7.28 |
| MPI-ESM-MR | 10.83 | 0.77 | 0.3 | 0.98 | 0.79 | 1.32 | 0.0029 | 0.5 | 0.0155 | 0.005 | 0.74 | 7.75 |
| MRI-CGCM3 | 9.2 | 1.09 | 0.49 | 0.98 | 0.59 | 0.3 | 0.0009 | 0.5 | 0.0055 | 0.009 | 0.64 | 5.63 |
| NorESM1-M | 8 | 1.29 | 0.63 | 0.98 | 0.85 | 0.68 | 0.0016 | 0.5 | −0.0090 | 0.006 | 0.7 | 6.57 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 11.31 | 1.64 | 0.136 | 2.03 × 10−4 | 0.229 | −0.140 | ||||||
| BCC-CSM 1.1 | 32.06 | 0.67 | 1.14 | 0.56 | 0.88 | 0.32 | 5.44 × 10−5 | 0.275 | −0.181 | 0.296 | 0.357 | 4.33 |
| BCC-CSM1-1-M | 23.44 | 0.71 | 1.16 | 0.53 | 0.92 | −0.489 | −4.32 × 10−5 | 0.264 | 0.186 | 0.265 | 0.388 | 2.79 |
| CanESM2 | 30.48 | 1.15 | 1.12 | 0.79 | 0.83 | 0.385 | 5.43 × 10−5 | 0.279 | 0.13 | 0.077 | 0.7 | 6.25 |
| CCSM4 | 26.36 | 0.93 | 1.14 | 0.74 | 0.92 | 0.572 | 8.88 × 10−5 | 0.272 | −0.175 | 0.197 | 0.529 | 5.83 |
| CESM1-CAM5 | 25.75 | 1.06 | 1.14 | 0.75 | 0.92 | −0.401 | −3.54 × 10−5 | 0.268 | 0.054 | 0.101 | 0.662 | 5.62 |
| CNRM-CM5 | 20.43 | 1.35 | 1.16 | 0.77 | 0.99 | 0.133 | 2.06 × 10−5 | 0.224 | 0.108 | 0.028 | 0.793 | 7.13 |
| CSIRO-MK3-6-0 | 19.49 | 1.06 | 1.16 | 0.75 | 0.87 | 1.053 | 9.62 × 10−5 | 0.235 | 0.085 | 0.127 | 0.629 | 5.51 |
| FGOALS-g2 | 30.78 | 0.54 | 1.14 | 0.52 | 0.93 | 1.369 | 1.77 × 10−4 | 0.275 | −0.182 | 0.298 | 0.341 | 3.88 |
| FIO-ESM | 26.36 | 0.93 | 1.14 | 0.74 | 0.92 | 0.572 | 8.88 × 10−5 | 0.272 | −0.175 | 0.197 | 0.529 | 5.83 |
| GFDL-CM3 | 26.44 | 0.88 | 1.15 | 0.64 | 0.9 | −0.480 | −5.06 × 10−5 | 0.262 | −0.197 | 0.186 | 0.531 | 4.71 |
| GFDL-ESM2G | 23.41 | 0.9 | 1.16 | 0.54 | 0.92 | 0.551 | 4.97 × 10−5 | 0.248 | 0.188 | 0.124 | 0.584 | 4.49 |
| GISS-E2-H | 52 | 0.64 | 1.08 | 0.64 | 0.65 | 0.236 | 5.92 × 10−5 | 0.311 | −0.098 | 0.298 | 0.333 | 4.6 |
| GISS-E2-R | 41.05 | 0.55 | 1.11 | 0.57 | 0.73 | 1.428 | 1.72 × 10−4 | 0.319 | −0.082 | 0.301 | 0.284 | 3.3 |
| HadGEM2-ES | 25.3 | 1.04 | 1.15 | 0.57 | 0.94 | 0.478 | 6.68 × 10−5 | 0.281 | 0.168 | 0.134 | 0.61 | 4.8 |
| IPSL-CM5A-LR | 20.41 | 0.72 | 1.16 | 0.58 | 0.89 | 0.253 | 2.94 × 10−5 | 0.269 | −0.171 | 0.241 | 0.414 | 4.35 |
| IPSL-CM5A-MR | 24.31 | 0.9 | 1.16 | 0.72 | 0.94 | 0.752 | 8.39 × 10−5 | 0.222 | −0.037 | 0.1 | 0.616 | 6.12 |
| MIROC5 | 31.86 | 0.82 | 1.13 | 0.74 | 0.93 | 0.037 | 2.37 × 10−5 | 0.276 | −0.104 | 0.212 | 0.52 | 5.84 |
| MIROC-ESM | 42.15 | 0.85 | 1.09 | 0.8 | 0.9 | 0.084 | 2.35 × 10−5 | 0.301 | −0.129 | 0.248 | 0.484 | 6.23 |
| MIROC-ESM-CHEM | 41.18 | 0.84 | 1.1 | 0.78 | 0.91 | 0.419 | 9.45 × 10−5 | 0.298 | 0.137 | 0.264 | 0.453 | 5.41 |
| MPI-ESM-LR | 22.32 | 1.37 | 1.16 | 0.69 | 0.93 | −0.047 | 7.90 × 10−6 | 0.251 | −0.159 | 0.064 | 0.723 | 6.85 |
| MPI-ESM-MR | 23.34 | 1.32 | 1.15 | 0.68 | 0.94 | −0.236 | −1.59 × 10−5 | 0.255 | −0.164 | 0.058 | 0.737 | 6.6 |
| MRI-CGCM3 | 11.48 | 1.19 | 1.18 | 0.73 | 0.98 | 0.55 | 3.72 × 10−5 | 0.214 | 0.029 | 0.04 | 0.757 | 6.25 |
| NorESM1-M | 27.28 | 0.83 | 1.13 | 0.69 | 0.84 | −0.200 | −9.32 × 10−6 | 0.282 | 0.172 | 0.259 | 0.458 | 3.86 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 5.88 | −0.17 | 1.272 | 0.003 | 0.33 | −0.044 | ||||||
| BCC-CSM 1.1 | 2 | 27.41 | 0.44 | 0.98 | 0.99 | 0.855 | 0.002 | 0.332 | −0.029 | 0.015 | 0.542 | 5.99 |
| BCC-CSM1-1-M | 3.65 | −0.19 | 0.3 | 0.98 | 0.98 | 0.994 | 0.003 | 0.33 | −0.046 | 0.013 | 0.595 | 7.2 |
| CanESM2 | 1.83 | 3.25 | 0.42 | 0.98 | 0.95 | 1.441 | 0.003 | 0.331 | −0.033 | 0.015 | 0.566 | 5.44 |
| CCSM4 | 4.25 | 0.79 | 0.28 | 0.98 | 0.97 | 0.985 | 0.003 | 0.329 | −0.050 | 0.009 | 0.678 | 7.99 |
| CESM1-CAM5 | 5.24 | 0.54 | 0.25 | 0.99 | 0.98 | 0.805 | 0.002 | 0.33 | −0.048 | 0.008 | 0.698 | 8.25 |
| CNRM-CM5 | 1.23 | 3.51 | 0.47 | 0.98 | 0.98 | −0.152 | 0 | 0.332 | −0.023 | 0.01 | 0.655 | 4.54 |
| CSIRO-MK3-6-0 | 2.18 | 3.74 | 0.38 | 0.99 | 0.92 | 0.614 | 0.002 | 0.329 | −0.051 | 0.017 | 0.526 | 4.83 |
| FGOALS-g2 | −0.17 | 28.3 | 0.57 | 0.97 | 0.95 | 0.964 | 0.003 | 0.331 | −0.037 | 0.013 | 0.579 | 5.73 |
| FIO-ESM | 4.16 | 3.71 | 0.37 | 0.98 | 0.98 | 0.907 | 0.002 | 0.332 | −0.023 | 0.011 | 0.618 | 6.38 |
| GFDL-CM3 | 2.93 | 1.38 | 0.34 | 0.98 | 0.96 | 0.892 | 0.002 | 0.331 | −0.038 | 0.013 | 0.583 | 6.09 |
| GFDL-ESM2G | 3.98 | 4.38 | 0.31 | 0.98 | 0.91 | 0.919 | 0.002 | 0.331 | −0.037 | 0.014 | 0.572 | 5.71 |
| GISS-E2-H | 4.7 | −3.96 | 0.41 | 0.97 | 0.94 | 0.171 | 0 | 0.331 | −0.023 | 0.014 | 0.606 | 4.56 |
| GISS-E2-R | 3.27 | −0.40 | 0.64 | 0.85 | 0.97 | 1.271 | 0.003 | 0.328 | −0.056 | 0.015 | 0.578 | 4.84 |
| HadGEM2-ES | 3.27 | −0.40 | 0.64 | 0.85 | 0.97 | 1.271 | 0.003 | 0.328 | −0.056 | 0.015 | 0.578 | 4.84 |
| IPSL-CM5A-LR | 1.22 | −0.36 | 0.48 | 0.98 | 0.95 | 1.022 | 0.003 | 0.331 | −0.035 | 0.01 | 0.669 | 6.3 |
| IPSL-CM5A-MR | 1.05 | 4.81 | 0.52 | 0.98 | 0.99 | 1.448 | 0.003 | 0.33 | −0.037 | 0.009 | 0.704 | 7.22 |
| MIROC5 | 6.44 | 0.34 | 0.24 | 0.99 | 0.96 | 0.932 | 0.002 | 0.33 | −0.045 | 0.015 | 0.555 | 6.87 |
| MIROC-ESM | 3.69 | 3.5 | 0.36 | 0.97 | 0.99 | 0.51 | 0.001 | 0.331 | 0.039 | 0.017 | 0.536 | 4.71 |
| MIROC-ESM-CHEM | 3.61 | 3.9 | 0.37 | 0.97 | 0.99 | 1.025 | 0.003 | 0.331 | 0.036 | 0.015 | 0.57 | 5.74 |
| MPI-ESM-LR | 6 | 2.28 | 0.25 | 0.98 | 0.95 | 0.967 | 0.002 | 0.33 | −0.050 | 0.013 | 0.614 | 7.3 |
| MPI-ESM-MR | 5.78 | 3.57 | 0.25 | 0.99 | 0.94 | 1.291 | 0.003 | 0.33 | −0.047 | 0.012 | 0.642 | 7.92 |
| MRI-CGCM3 | 3 | 2.12 | 0.35 | 0.98 | 0.97 | 0.508 | 0.001 | 0.332 | −0.031 | 0.014 | 0.605 | 5.56 |
| NorESM1-M | 3.26 | −1.04 | 0.37 | 0.99 | 0.97 | 0.866 | 0.002 | 0.332 | −0.032 | 0.012 | 0.607 | 6.22 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | 14.07 | 0.85 | 0.937 | 0.002 | 0.327 | 0.062 | ||||||
| BCC-CSM 1.1 | 7.4 | 1.58 | 0.62 | 0.98 | 0.99 | 0.736 | 0.002 | 0.332 | −0.033 | 0.014 | 0.541 | 5.59 |
| BCC-CSM1-1-M | 9.72 | 1.41 | 0.47 | 0.98 | 0.97 | 0.887 | 0.003 | 0.33 | −0.050 | 0.012 | 0.618 | 6.7 |
| CanESM2 | 10.24 | 1.41 | 0.45 | 0.98 | 0.97 | 1.196 | 0.003 | 0.33 | 0.041 | 0.014 | 0.58 | 6.82 |
| CCSM4 | 10.02 | 3.52 | 0.47 | 0.98 | 0.95 | 0.853 | 0.002 | 0.328 | −0.057 | 0.011 | 0.635 | 7.45 |
| CESM1-CAM5 | 11.02 | 1.88 | 0.39 | 0.98 | 0.96 | 0.713 | 0.002 | 0.329 | −0.055 | 0.011 | 0.648 | 7.38 |
| CNRM-CM5 | 13.64 | 1.41 | 0.35 | 0.98 | 0.9 | −0.209 | 0 | 0.331 | −0.043 | 0.014 | 0.605 | 5.49 |
| CSIRO-MK3-6-0 | 8.14 | 3.15 | 0.61 | 0.98 | 0.95 | 0.477 | 0.001 | 0.329 | −0.052 | 0.016 | 0.558 | 5.7 |
| FGOALS-g2 | 5.15 | 2.51 | 0.83 | 0.97 | 0.93 | 0.851 | 0.002 | 0.331 | −0.040 | 0.013 | 0.573 | 4.7 |
| FIO-ESM | 8.56 | 1.22 | 0.54 | 0.98 | 0.99 | 0.814 | 0.002 | 0.332 | −0.030 | 0.013 | 0.572 | 6.05 |
| GFDL-CM3 | 7.46 | 2.56 | 0.64 | 0.98 | 0.97 | 0.876 | 0.002 | 0.33 | −0.044 | 0.014 | 0.573 | 6.04 |
| GFDL-ESM2G | 7.96 | 1.59 | 0.59 | 0.98 | 0.87 | 0.85 | 0.002 | 0.331 | −0.038 | 0.013 | 0.582 | 4.9 |
| GISS-E2-H | 8.84 | 1.54 | 0.59 | 0.97 | 0.97 | 0.128 | 0 | 0.331 | −0.020 | 0.015 | 0.596 | 5.15 |
| GISS-E2-R | 10.29 | 0.98 | 0.47 | 0.97 | 0.95 | 0.586 | 0.001 | 0.33 | −0.040 | 0.011 | 0.647 | 6.43 |
| HadGEM2-ES | 9.42 | 1.46 | 0.72 | 0.85 | 0.98 | 1.008 | 0.003 | 0.328 | −0.059 | 0.013 | 0.602 | 5.04 |
| IPSL-CM5A-LR | 13.32 | 0.89 | 0.32 | 0.97 | 0.96 | 1.172 | 0.003 | 0.331 | −0.042 | 0.009 | 0.673 | 7.43 |
| IPSL-CM5A-MR | 13.21 | −0.67 | 0.42 | 0.97 | 0.97 | 1.477 | 0.004 | 0.328 | −0.053 | 0.01 | 0.676 | 6.68 |
| MIROC5 | 12.05 | 1.2 | 0.33 | 0.98 | 0.97 | 0.818 | 0.002 | 0.33 | −0.045 | 0.014 | 0.571 | 6.98 |
| MIROC-ESM | 9.15 | 1.61 | 0.55 | 0.97 | 0.99 | 0.415 | 0.001 | 0.33 | 0.041 | 0.016 | 0.562 | 6.28 |
| MIROC-ESM-CHEM | 9.07 | 1.63 | 0.56 | 0.97 | 0.99 | 0.902 | 0.002 | 0.33 | 0.041 | 0.018 | 0.524 | 6.32 |
| MPI-ESM-LR | 12.29 | 0.95 | 0.3 | 0.98 | 0.97 | 0.941 | 0.002 | 0.329 | −0.054 | 0.012 | 0.637 | 7.62 |
| MPI-ESM-MR | 12.05 | 0.98 | 0.31 | 0.98 | 0.97 | 1.183 | 0.003 | 0.329 | −0.052 | 0.013 | 0.613 | 7.06 |
| MRI-CGCM3 | 9.41 | 0.27 | 0.54 | 0.98 | 0.98 | 0.407 | 0.001 | 0.33 | −0.043 | 0.013 | 0.615 | 5.74 |
| NorESM1-M | 8.56 | 1.56 | 0.56 | 0.99 | 0.96 | 0.875 | 0.002 | 0.331 | −0.035 | 0.013 | 0.592 | 6.07 |
| Model | Mean | CV | NRMSE | rtom | rspa | M-K | EOF1 | EOF2 | RS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zc | β | SB | SS | |||||||||
| Observation | −1.42 | 6.71 | 1.754 | 0.004 | 0.331 | −0.033 | ||||||
| BCC-CSM 1.1 | −3.67 | −3.06 | 0.41 | 0.98 | 0.98 | 0.897 | 0.002 | 0.333 | −0.020 | 0.012 | 0.584 | 6.76 |
| BCC-CSM1-1-M | −2.53 | 1.68 | 0.29 | 0.98 | 0.97 | 1.086 | 0.003 | 0.331 | −0.038 | 0.009 | 0.66 | 8.56 |
| CanESM2 | −5.60 | −2.47 | 0.46 | 0.98 | 0.89 | 1.557 | 0.004 | 0.333 | −0.020 | 0.012 | 0.61 | 6.19 |
| CCSM4 | −1.44 | 25.09 | 0.26 | 0.98 | 0.96 | 1.159 | 0.003 | 0.329 | −0.040 | 0.01 | 0.673 | 8.6 |
| CESM1-CAM5 | −0.68 | −0.24 | 0.27 | 0.98 | 0.97 | 0.815 | 0.002 | 0.331 | −0.038 | 0.013 | 0.623 | 7.85 |
| CNRM-CM5 | −7.85 | −2.10 | 0.63 | 0.98 | 0.96 | 0.038 | 0 | 0.333 | −0.006 | 0.01 | 0.665 | 5.04 |
| CSIRO-MK3-6-0 | −3.98 | −5.33 | 0.34 | 0.99 | 0.9 | 0.765 | 0.002 | 0.33 | −0.045 | 0.016 | 0.545 | 5.52 |
| FGOALS-g2 | −6.02 | −1.97 | 0.53 | 0.97 | 0.87 | 1.047 | 0.003 | 0.331 | −0.035 | 0.012 | 0.643 | 6.2 |
| FIO-ESM | −0.78 | 11.99 | 0.36 | 0.98 | 0.98 | 0.963 | 0.002 | 0.333 | −0.017 | 0.01 | 0.647 | 7.66 |
| GFDL-CM3 | −2.66 | 23.6 | 0.3 | 0.98 | 0.92 | 0.792 | 0.002 | 0.332 | −0.030 | 0.01 | 0.65 | 7.8 |
| GFDL-ESM2G | −0.86 | 1.12 | 0.29 | 0.98 | 0.92 | 0.982 | 0.002 | 0.332 | −0.034 | 0.012 | 0.604 | 7.36 |
| GISS-E2-H | 0.51 | 1.46 | 0.46 | 0.96 | 0.91 | 0.14 | 0 | 0.332 | −0.023 | 0.011 | 0.658 | 6.02 |
| GISS-E2-R | 1.23 | 0.2 | 0.5 | 0.97 | 0.92 | 0.921 | 0.002 | 0.331 | −0.027 | 0.009 | 0.69 | 7.14 |
| HadGEM2-ES | −3.28 | −5.85 | 0.65 | 0.85 | 0.94 | 1.544 | 0.004 | 0.33 | −0.049 | 0.014 | 0.556 | 4.89 |
| IPSL-CM5A-LR | −10.79 | −1.17 | 0.91 | 0.95 | 0.91 | 0.655 | 0.002 | 0.332 | −0.025 | 0.009 | 0.67 | 4.89 |
| IPSL-CM5A-MR | −11.28 | −1.29 | 0.96 | 0.95 | 0.98 | 1.07 | 0.003 | 0.332 | −0.021 | 0.01 | 0.642 | 5.46 |
| MIROC5 | 0.65 | 10.69 | 0.31 | 0.98 | 0.95 | 0.908 | 0.002 | 0.33 | −0.040 | 0.013 | 0.581 | 7.34 |
| MIROC-ESM | −1.55 | −2.17 | 0.34 | 0.97 | 0.99 | 0.626 | 0.002 | 0.332 | −0.027 | 0.015 | 0.551 | 6.99 |
| MIROC-ESM-CHEM | −1.66 | −52.70 | 0.35 | 0.97 | 0.99 | 1.088 | 0.003 | 0.332 | −0.026 | 0.013 | 0.598 | 6.93 |
| MPI-ESM-LR | 0.42 | −1.04 | 0.32 | 0.98 | 0.91 | 1.124 | 0.002 | 0.33 | −0.045 | 0.012 | 0.635 | 7.03 |
| MPI-ESM-MR | 0.25 | −0.13 | 0.31 | 0.98 | 0.91 | 1.433 | 0.003 | 0.331 | −0.041 | 0.01 | 0.686 | 7.97 |
| MRI-CGCM3 | −2.80 | 0.09 | 0.29 | 0.98 | 0.96 | 0.652 | 0.002 | 0.332 | −0.021 | 0.011 | 0.666 | 7.33 |
| NorESM1-M | −2.32 | 21.3 | 0.34 | 0.99 | 0.95 | 0.891 | 0.002 | 0.332 | −0.032 | 0.013 | 0.593 | 7.79 |
References
- Chen, J.; Xu, C.; Guo, S.; Chen, H. Progress and challenge in statistically downscaling climate model outputs. J. Water Resour. Res. 2016, 5, 299–313. [Google Scholar] [CrossRef]
- Gooré Bi, E.; Gachon, P.; Vrac, M.; Monette, F. Which downscaled rainfall data for climate change impact studies in urban areas? Review of current approaches and trends. Theor. Appl. Climatol. 2017, 127, 685–699. [Google Scholar] [CrossRef]
- Tong, S.; Berry, H.L.; Ebi, K.; Bambrick, H.; Hu, W.; Green, D.; Hanna, E.; Wang, Z.; Butler, C.D. Climate change, food, water and population health in China. B. World Health Organ. 2016, 94, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, L.; Yang, X. Study on extreme climate events and drought/flood disasters: Review and prospect. China Flood Drought Manag. 2017, 27, 66–74. [Google Scholar]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Wang, L.; Ranasinghe, R.; Maskey, S.; van Gelder, P.H.A.J.; Vrijling, J.K. Comparison of empirical statistical methods for downscaling daily climate projections from CMIP5 GCMs: A case study of the Huai River Basin, China. Int. J. Climatol. 2016, 36, 145–164. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, J.; Xiong, Z.; Wang, S.; Yuan, J. An intercomparison of multiple statistical downscaling methods for daily precipitation and temperature over China: Present climate evaluations. Clim. Dynam. 2019, 53, 4629–4649. [Google Scholar] [CrossRef]
- Dai, A.; Rasmussen, R.M.; Ikeda, K.; Liu, C. A new approach to construct representative future forcing data for dynamic downscaling. Clim. Dynam. 2020, 55, 315–323. [Google Scholar] [CrossRef]
- Mascaro, G.; Viola, F.; Deidda, R. Evaluation of Precipitation from EURO-CORDEX Regional Climate Simulations in a Small-Scale Mediterranean Site. J. Geophys. Res. Atmos. 2018, 123, 1604–1625. [Google Scholar] [CrossRef]
- Zou, L.; Zhou, T.; Peng, D. Dynamical downscaling of historical climate over CORDEX East Asia domain: A Comparison of regional ocean-atmosphere coupled model to stand-alone RCM simulations. J. Geophys. Res. Atmos. 2016, 121, 1442–1458. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- Suzuki-Parker, A.; Kusaka, H.; Takayabu, I.; Dairaku, K.; Ishizaki, N.N.; Ham, S. Contributions of GCM/RCM Uncertainty in Ensemble Dynamical Downscaling for Precipitation in East Asian Summer Monsoon Season. Sola 2018, 14, 97–104. [Google Scholar] [CrossRef]
- Abiodun, B.J.; Omar, S.A.; Lennard, C.; Jack, C. Using regional climate models to simulate extreme rainfall events in the Western Cape, South Africa. Int. J. Climatol. 2016, 36, 689–705. [Google Scholar] [CrossRef]
- Cao, X.; Tang, R.; Wang, W.; Xue, J. Precipitation projection of the Luanhe River Basin based on two statistical downscaling models. J. Yangzhou Univ. (Nat. Sci. Ed.) 2016, 19, 28–32. [Google Scholar]
- Fan, L.; Fu, C.; Chen, D. Estimation of local temperature change scenarios in North China using statistical downscaling method. Chin. J. Atmos. Sci. 2007, 31, 887–897. [Google Scholar]
- Liu, Y.; Guo, W.; Feng, J.; Zhang, K. A summary of methods for statistical downscaling of meteorological data. Adv. Earth Sci. 2011, 26, 837–847. [Google Scholar]
- Stennett-Brown, R.K.; Jones, J.J.P.; Stephenson, T.S.; Taylor, M.A. Future Caribbean temperature and rainfall extremes from statistical downscaling. Int. J. Climatol. 2017, 37, 4828–4845. [Google Scholar] [CrossRef]
- Tang, J.; Niu, X.; Wang, S.; Gao, H.; Wang, X.; Wu, J. Statistical downscaling and dynamical downscaling of regional climate in China: Present climate evaluations and future climate projections. J. Geophys. Res. Atmos. 2016, 121, 2110–2129. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Kirono, D.G.C.; Kent, D.M.; Frost, A.J.; Charles, S.P.; Timbal, B.; Nguyen, K.C.; Fu, G. Comparison of runoff modelled using rainfall from different downscaling methods for historical and future climates. J. Hydrol. 2010, 387, 10–23. [Google Scholar] [CrossRef]
- Cheng, C.S.; Auld, H.; Li, Q.; Li, G. Possible impacts of climate change on extreme weather events at local scale in south-central Canada. Clim. Chang. 2012, 112, 963–979. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Hundecha, Y.; Lawrence, D.; Madsen, H.; Willems, P.; Martinkova, M.; Vormoor, K.; Bürger, G.; Hanel, M.; Kriaučiūnienė, J.; et al. Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 1827–1847. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Z.; Charles, S.P.; Fu, G.; Liu, L. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China. Int. J. Climatol. 2011, 31, 2006–2020. [Google Scholar] [CrossRef]
- Hu, Y.; Maskey, S.; Uhlenbrook, S. Downscaling daily precipitation over the Yellow River source region in China: A comparison of three statistical downscaling methods. Theor. Appl. Climatol. 2013, 112, 447–460. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Zhang, Z.; Xu, C.; Wang, B.; Yao, J. Estimation of future precipitation change in the Yangtze River basin by using statistical downscaling method. Stoch. Env. Res. Risk Assess. 2011, 25, 781–792. [Google Scholar] [CrossRef]
- Liu, W.; Fu, G.; Liu, C.; Charles, S.P. A comparison of three multi-site statistical downscaling models for daily rainfall in the North China Plain. Theor. Appl. Climatol. 2013, 111, 585–600. [Google Scholar] [CrossRef]
- Rana, A.; Moradkhani, H. Spatial, temporal and frequency based climate change assessment in Columbia River Basin using multi downscaled-scenarios. Clim. Dynam. 2016, 47, 579–600. [Google Scholar] [CrossRef]
- San-Martín, D.; Manzanas, R.; Brands, S.; Herrera, S.; Gutiérrez, J.M. Reassessing model uncertainty for regional projections of precipitation with an ensemble of statistical downscaling methods. J. Clim. 2017, 30, 203–223. [Google Scholar] [CrossRef]
- Zelazowski, P.; Huntingford, C.; Mercado, L.M.; Schaller, N. Climate pattern-scaling set for an ensemble of 22 GCMs—Adding uncertainty to the IMOGEN version 2.0 impact system. Geosci. Model. Dev. 2018, 11, 541–560. [Google Scholar] [CrossRef]
- Kusangaya, S.; Warburton Toucher, M.L.; van Garderen, E.A. Evaluation of uncertainty in capturing the spatial variability and magnitudes of extreme hydrological events for the uMngeni catchment, South Africa. J. Hydrol. 2018, 557, 931–946. [Google Scholar] [CrossRef]
- Tegegne, G.; Melesse, A.M.; Worqlul, A.W. Development of multi-model ensemble approach for enhanced assessment of impacts of climate change on climate extremes. Sci. Total Environ. Sci. 2020, 704, 135357. [Google Scholar] [CrossRef]
- Das, L.; Dutta, M.; Mezghani, A.; Benestad, R.E. Use of observed temperature statistics in ranking CMIP5 model performance over the Western Himalayan Region of India. Int. J. Climatol. 2018, 38, 554–570. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Babovic, V. Projections of Future Climate Change in Singapore Based on a Multi-Site Multivariate Downscaling Approach. Water 2019, 11, 2300. [Google Scholar] [CrossRef]
- Wang, R.; Cheng, Q.; Liu, L.; Yan, C.; Huang, G. Multi-model projections of climate change in different RCP scenarios in an arid inland region, Northwest China. Water 2019, 11, 347. [Google Scholar] [CrossRef]
- Fu, G.; Liu, Z.; Charles, S.P.; Xu, Z.; Yao, Z. A score-based method for assessing the performance of GCMs: A case study of southeastern Australia. J. Geophysi. Res. Atmos. 2013, 118, 4154–4167. [Google Scholar] [CrossRef]
- Li, F.; Xu, Z.; Liu, X.; Li, X.; Liu, Z. Assessment on performance of different general circulation models in Songhuajiang River basin. Hydrology 2011, 31, 24–31. [Google Scholar]
- Liu, L.; Guo, Z.; Huang, G.; Wang, R. Water productivity evaluation under multi-GCM projections of climate change in oases of the Heihe River basin, northwest China. Int. J. Environ. Res. Public Health 2019, 16, 1706. [Google Scholar] [CrossRef]
- Zhang, A.; Zheng, C.; Wang, S.; Yao, Y. Analysis of streamflow variations in the Heihe River Basin, northwest China: Trends, abrupt changes, driving factors and ecological influences. J. Hydrol. Reg. Stud. 2015, 3, 106–124. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. Roy. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Chen, J.; St-Denis, B.G.; Brissette, F.P.; Lucas-Picher, P. Using Natural Variability as a Baseline to Evaluate the Performance of Bias Correction Methods in Hydrological Climate Change Impact Studies. J. Hydrometeorol. 2016, 17, 2155–2174. [Google Scholar] [CrossRef]
- Shu, Q.; Wang, Q.; Song, Z.; Qiao, F.; Zhao, J.; Chu, M.; Li, X. Assessment of Sea Ice Extent in CMIP6 with Comparison to Observations and CMIP5. Geophys. Res. Lett. 2020, 47, e2020GL087965. [Google Scholar] [CrossRef]
- Kudo, R.; Yoshida, T.; Masumoto, T. Uncertainty analysis of impacts of climate change on snow processes: Case study of interactions of GCM uncertainty and an impact model. J. Hydrol. 2017, 548, 196–207. [Google Scholar] [CrossRef]
- Rosenberg, E.A.; Keys, P.W.; Booth, D.B.; Hartley, D.; Burkey, J.; Steinemann, A.C.; Lettenmaier, D.P. Precipitation extremes and the impacts of climate change on stormwater infrastructure in Washington State. Clim. Chang. 2010, 102, 319–349. [Google Scholar] [CrossRef]
- Vetter, T.; Reinhardt, J.; Floerke, M.; van Griensven, A.; Hattermann, F.; Huang, S.; Koch, H.; Pechlivanidis, I.G.; Ploetner, S.; Seidou, O.; et al. Evaluation of sources of uncertainty in projected hydrological changes under climate change in 12 large-scale river basins. Clim. Chang. 2017, 141, 419–433. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Z.; Li, F.; Qiu, L. GCM performance on simulating climatological factors in Yarlung Zangbo river basin based on a ranked score method. J. Beijing Normal Univ. (Nat. Sci.) 2013, 49, 304–311. [Google Scholar]
- Boehnisch, A.; Ludwig, R.; Leduc, M. Using a nested single-model large ensemble to assess the internal variability of the North Atlantic Oscillation and its climatic implications for central Europe. Earth Syst. Dynam. 2020, 11, 617–640. [Google Scholar] [CrossRef]
- Borges, P.D.A.; Barfus, K.; Weiss, H.; Bernhofer, C. Extended predictor screening, application and added value of statistical downscaling of a CMIP5 ensemble for single-site projections in Distrito Federal, Brazil. Int. J. Climatol. 2017, 37, 46–65. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H. Monotonic trend and step changes in Japanese precipitation. J. Hydrol. 2003, 279, 144–150. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. Forest Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Mtongori, H.I.; Stordal, F.; Benestad, R.E. Evaluation of Empirical Statistical Downscaling Models’ Skill in Predicting Tanzanian Rainfall and Their Application in Providing Future Downscaled Scenarios. J. Clim. 2016, 29, 3231–3252. [Google Scholar] [CrossRef]
- Frazier, A.G.; Timm, O.E.; Giambelluca, T.W.; Diaz, H.F. The influence of ENSO, PDO and PNA on secular rainfall variations in Hawai’i. Clim. Dynam. 2018, 51, 2127–2140. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Mullan, D.; Chen, J.; Zhang, X.J. Validation of non-stationary precipitation series for site-specific impact assessment: Comparison of two statistical downscaling techniques. Clim. Dynam. 2016, 46, 967–986. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Statistically downscaled climate dataset for East Africa. Sci. Data 2019, 6, 1–8. [Google Scholar] [CrossRef]
- Tavakol-Davani, H.; Nasseri, M.; Zahraie, B. Improved statistical downscaling of daily precipitation using SDSM platform and data-mining methods. Int. J. Climatol. 2013, 33, 2561–2578. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmos. Res. 2016, 178–179, 521–534. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M.S. Evaluation of SDSM developed by annual and monthly sub-models for downscaling temperature and precipitation in the Jhelum basin, Pakistan and India. Theor. Appl. Climatol. 2013, 113, 27–44. [Google Scholar] [CrossRef]
- Meenu, R.; Rehana, S.; Mujumdar, P.P. Assessment of hydrologic impacts of climate change in Tunga-Bhadra river basin, India with HEC-HMS and SDSM. Hydrol. Process. 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, J.; Zhao, Y.; Tang, J.; Jia, Z. Assessment of future climate change impacts on nonpoint source pollution in snowmelt period for a cold area using SWAT. Sci Rep. 2018, 8, 2402. [Google Scholar] [CrossRef]
- González-Rojí, S.J.; Wilby, R.L.; Sáenz, J.; Ibarra-Berastegi, G. Harmonized evaluation of daily precipitation downscaled using SDSM and WRF+WRFDA models over the Iberian Peninsula. Clim. Dynam. 2019, 53, 1413–1433. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, Z.; Zhang, W.; Gujree, I. Long-Term Perspective Changes in Crop Irrigation Requirement Caused by Climate and Agriculture Land Use Changes in Rechna Doab, Pakistan. Water 2019, 11, 1567. [Google Scholar] [CrossRef]
- Phuong, D.N.D.; Duong, T.Q.; Liem, N.D.; Tram, V.N.Q.; Cuong, D.K.; Loi, N.K. Projections of Future Climate Change in the Vu Gia Thu Bon River Basin, Vietnam by Using Statistical DownScaling Model (SDSM). Water 2020, 12, 755. [Google Scholar] [CrossRef]
- Wilby, R.L.; Tomlinson, O.J.; Dawson, C.W. Multi-site simulation of precipitation by conditional resampling. Clim. Res. 2003, 23, 183–194. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W. The statistical downscaling model: Insights from one decade of application. Int. J. Climatol. 2013, 33, 1707–1719. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.; Wang, X. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Chung, E.; bin Ismail, T. Projection of spatial and temporal changes of rainfall in Sarawak of Borneo Island using statistical downscaling of CMIP5 models. Atmos. Res. 2017, 197, 446–460. [Google Scholar] [CrossRef]
- Salimun, E.; Tangang, F.; Juneng, L.; Zwiers, F.W.; Merryfield, W.J. Skill evaluation of the CanCM4 and its MOS for seasonal rainfall forecast in Malaysia during the early and late winter monsoon periods. Int. J. Climatol. 2016, 36, 439–454. [Google Scholar] [CrossRef]
- Turco, M.; Quintana-Seguí, P.; Llasat, M.C.; Herrera, S.; Gutiérrez, J.M. Testing MOS precipitation downscaling for ENSEMBLES regional climate models over Spain. J. Geophys. Res. 2011, 116, D18. [Google Scholar] [CrossRef]
- Turco, M.; Llasat, M.C.; Herrera, S.; Gutierrez, J.M. Bias correction and downscaling of future RCM precipitation projections using a MOS-Analog technique. J. Geophys. Res. Atmos. 2017, 122, 2631–2648. [Google Scholar] [CrossRef]
- Mpelasoka, F.S.; Chiew, F.H.S. Influence of rainfall scenario construction methods on runoff projections. J. Hydrometeorol. 2009, 10, 1168–1183. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrotra, R.; Sharma, A. Correcting for systematic biases in GCM simulations in the frequency domain. J. Hydrol. 2016, 538, 117–126. [Google Scholar] [CrossRef]
- Meher, J.K.; Das, L.; Akhter, J.; Benestad, R.E.; Mezghani, A. Performance of CMIP3 and CMIP5 GCMs to Simulate Observed Rainfall Characteristics over the Western Himalayan Region. J. Clim. 2017, 30, 7777–7799. [Google Scholar] [CrossRef]
- Worku, G.; Teferi, E.; Bantider, A.; Dile, Y.T. Statistical bias correction of regional climate model simulations for climate change projection in the Jemma sub-basin, upper Blue Nile Basin of Ethiopia. Theor. Appl. Climatol. 2020, 139, 1569–1588. [Google Scholar] [CrossRef]
- Aloysius, N.R.; Sheffield, J.; Saiers, J.E.; Li, H.; Wood, E.F. Evaluation of historical and future simulations of precipitation and temperature in central Africa from CMIP5 climate models. J. Geophys. Res. Atmos. 2016, 121, 130–152. [Google Scholar] [CrossRef]
- Yang, X.; Wood, E.F.; Sheffield, J.; Ren, L.; Zhang, M.; Wang, Y. Bias Correction of Historical and Future Simulations of Precipitation and Temperature for China from CMIP5 Models. J. Hydrometeorol. 2018, 19, 609–623. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, Z.; Xu, C.; Sun, P.; Hu, P.; He, C. A new statistical downscaling approach for global evaluation of the CMIP5 precipitation outputs: Model development and application. Sci. Total Environ. 2019, 690, 1048–1067. [Google Scholar] [CrossRef]
| Evaluation Metric | Method |
|---|---|
| Mean | Relative Error (%) |
| Coefficient of variation | Relative Error (%) |
| Temporal variation | Normalized root mean square error (NRMSE) [44] |
| Monthly distribution | Pearson correlation coefficient [45,46] |
| Spatial distribution | Pearson correlation coefficient |
| Trend and its magnitude | Mann–Kendall Z test [47] |
| Mann–Kendall β test [48] | |
| Space–time variability | The first eigenvector of empirical orthogonal functions (EOF1) [49,50] |
| The second eigenvector of empirical orthogonal functions (EOF2) | |
| Probability density functions (PDFs) | Brier score (BS) [51] |
| Skill score (Sscore) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lun, Y.; Liu, L.; Wang, R.; Huang, G. Optimization Assessment of Projection Methods of Climate Change for Discrepancies between North and South China. Water 2020, 12, 3106. https://doi.org/10.3390/w12113106
Lun Y, Liu L, Wang R, Huang G. Optimization Assessment of Projection Methods of Climate Change for Discrepancies between North and South China. Water. 2020; 12(11):3106. https://doi.org/10.3390/w12113106
Chicago/Turabian StyleLun, Yurui, Liu Liu, Ruotong Wang, and Guanhua Huang. 2020. "Optimization Assessment of Projection Methods of Climate Change for Discrepancies between North and South China" Water 12, no. 11: 3106. https://doi.org/10.3390/w12113106
APA StyleLun, Y., Liu, L., Wang, R., & Huang, G. (2020). Optimization Assessment of Projection Methods of Climate Change for Discrepancies between North and South China. Water, 12(11), 3106. https://doi.org/10.3390/w12113106