Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand
Abstract
1. Introduction
- The employment of 10 climatic factors over 16 years to assess the impact of climate change on urban water demand.
- Development and analysis of a new hybrid algorithm SMA-ANN for the water demand optimisation problem, and choosing the optimal hyperparameters of the ANN approach.
- The application of two hybrid algorithms, MVO-ANN and BSA-ANN, for analysing and validating the proposed SMA-ANN algorithm.
- Using the novel methodology, which contains data pre-processing techniques (EMD and tolerance) and hybrid SMA-ANN algorithm, to simulate the monthly stochastic pattern of water demand based on the best scenario of climatic factors over 16 years.
- Minimising the uncertainty by applying three metaheuristic algorithms for more validation, and using the ANN (stand-alone) to confirm the results of the SMA-ANN model. Additionally, employing 10 climatic factors that give scientific insight (i.e., to what extent climate change has driven water demand) for policymakers to achieve sustainability.
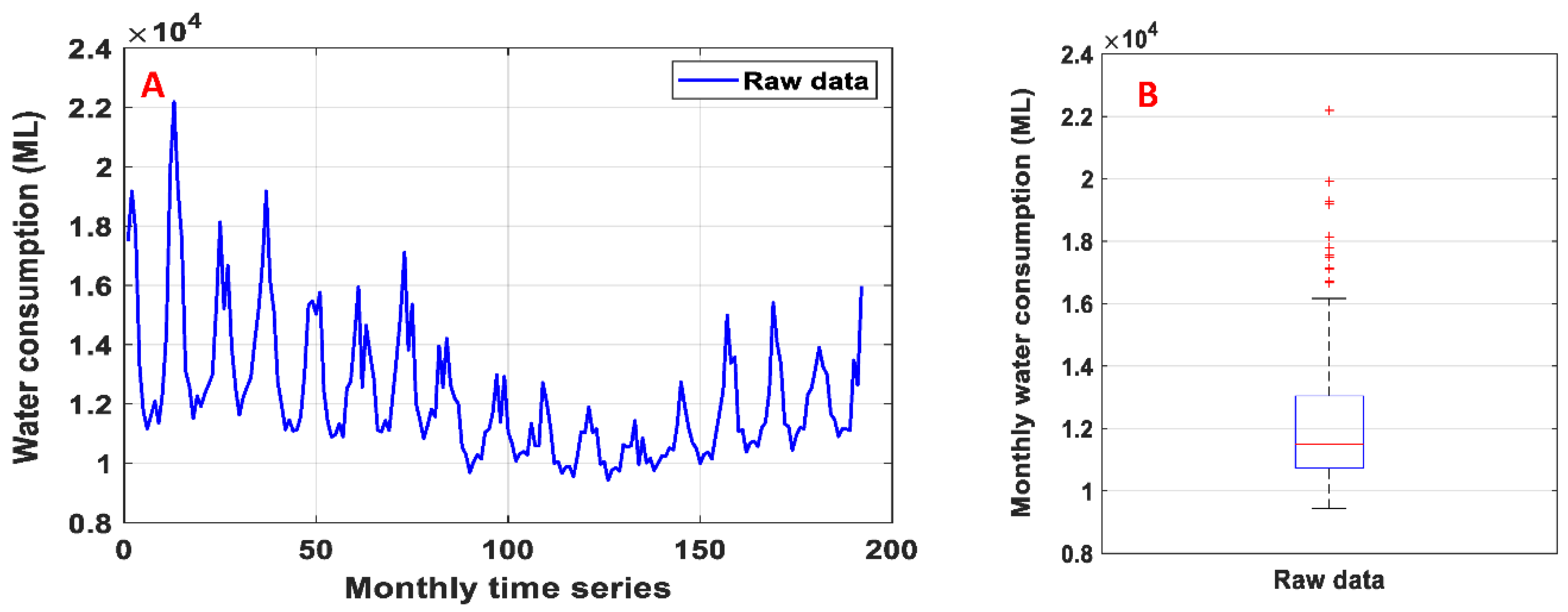
2. Case Study and Data Used
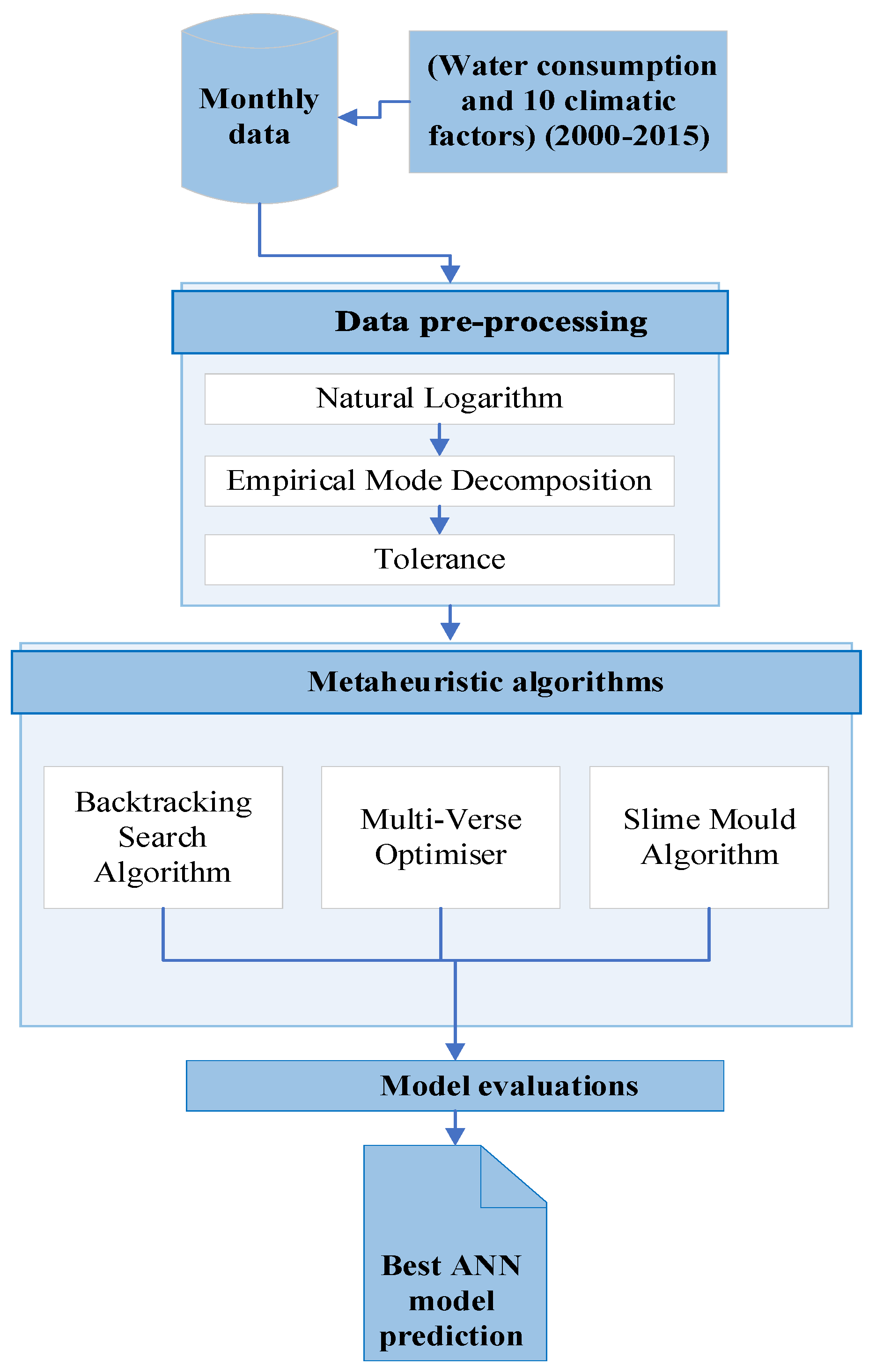
3. Proposed Methodology
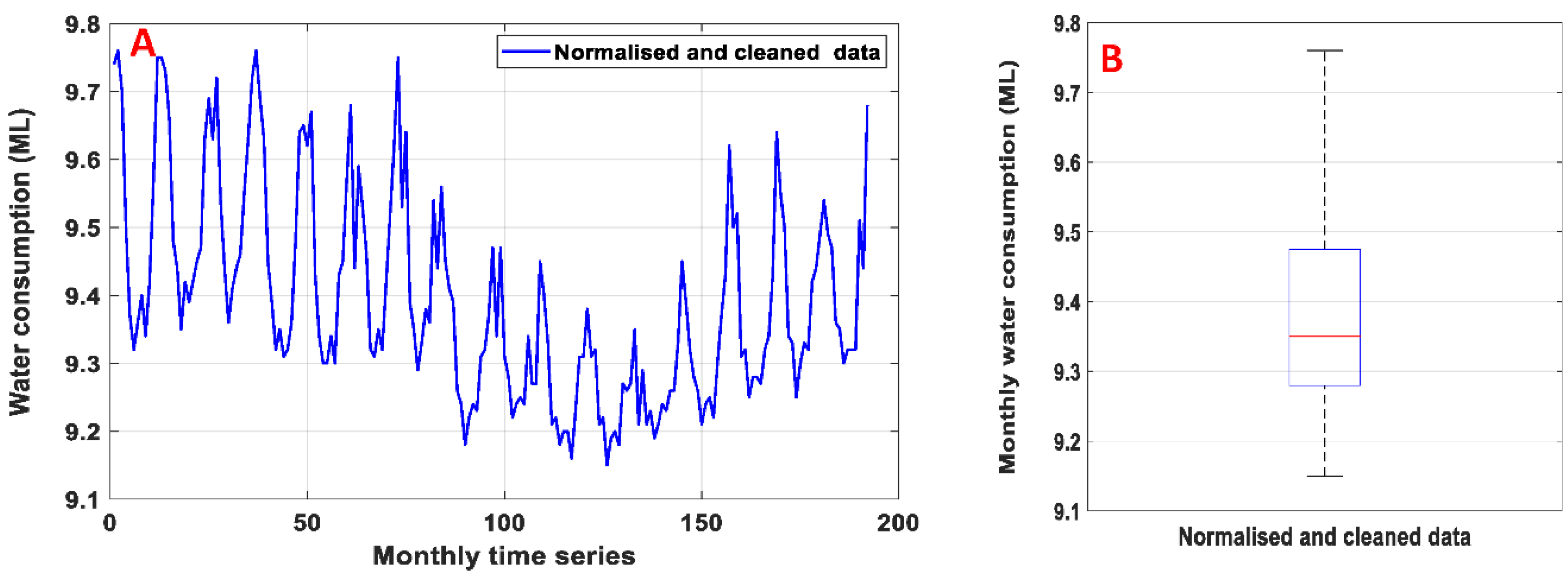
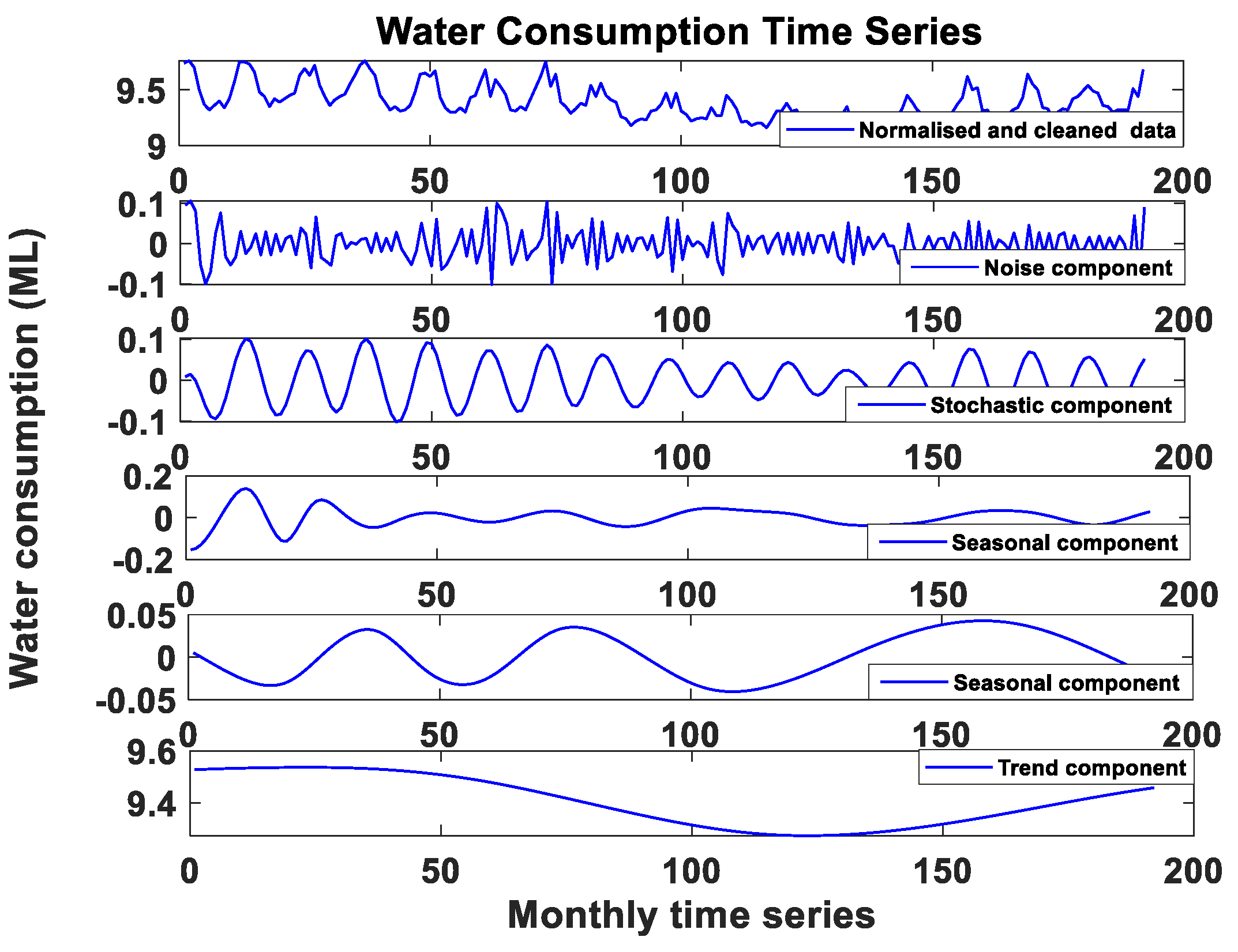
3.1. Data Pre-Processing
- The maximum difference between the number of local maxima and minima is one.
- The mean value of an IMF is zero.
- Assume hk − 1(t) = x(t), and hi,k − 1(t) = x(t), where i and k refer to the IMF number and the iteration number for finding the accurate ith IMF, respectively.
- Identify all the maxima and minima points of the series hi,k − 1(t).
- Connect the maxima points by cubic spline interpolation and do the same thing for the minima points. The linked maxima points are called the upper envelope, Ui,k − 1(t), while the linked minima points are called the lower envelope, Li,k − 1(t).
- The mean of the upper and lower envelopes is found using this formula: mi,k − 1(t) = (Ui,k − 1(t) − Li,k − 1(t))/2.
- Form the following formula: hi,k(t): = hi,k − 1(t) − mi,k − 1(t). The component hi,k(t) is primarily described as the first IMF. To determine the first IMF accurately, the hi,k(t) is considered as a new signal, and the mean of upper envelope, lower envelope and the mean (i.e., UI,k(t), Li,k − 1(t) and mi,k of the hi,k(t)) are calculated. The new component hi,k(t) is checked to see whether it has IMF properties or not. If it does, then it (i.e., hk(t)) is identified as an IMF. If not, the process will be repeated until IMF properties are obtained. The number of the repetitions to identify an IMF is called iterations and is notated by k, while the IMF number is notated by i.
- When the ith IMF is obtained, the residue is obtained: resi = hi,k − 1 − IMFi.
- The residue resi is now treated as the signal hi+1,k − 1 and the same steps 2–6 are repeated until no more IMFs can be extracted.
3.2. Slime Mould Algorithm (SMA)
- a.
- Approaching food
- b.
- Warp food
3.3. Artificial Neural Network (ANN)
3.4. Hybrid Metaheuristic Algorithm-Based Artificial Neural Network
3.5. Model Evaluation
4. Results and Discussion
4.1. Preparation of Dependent and Independent Variables
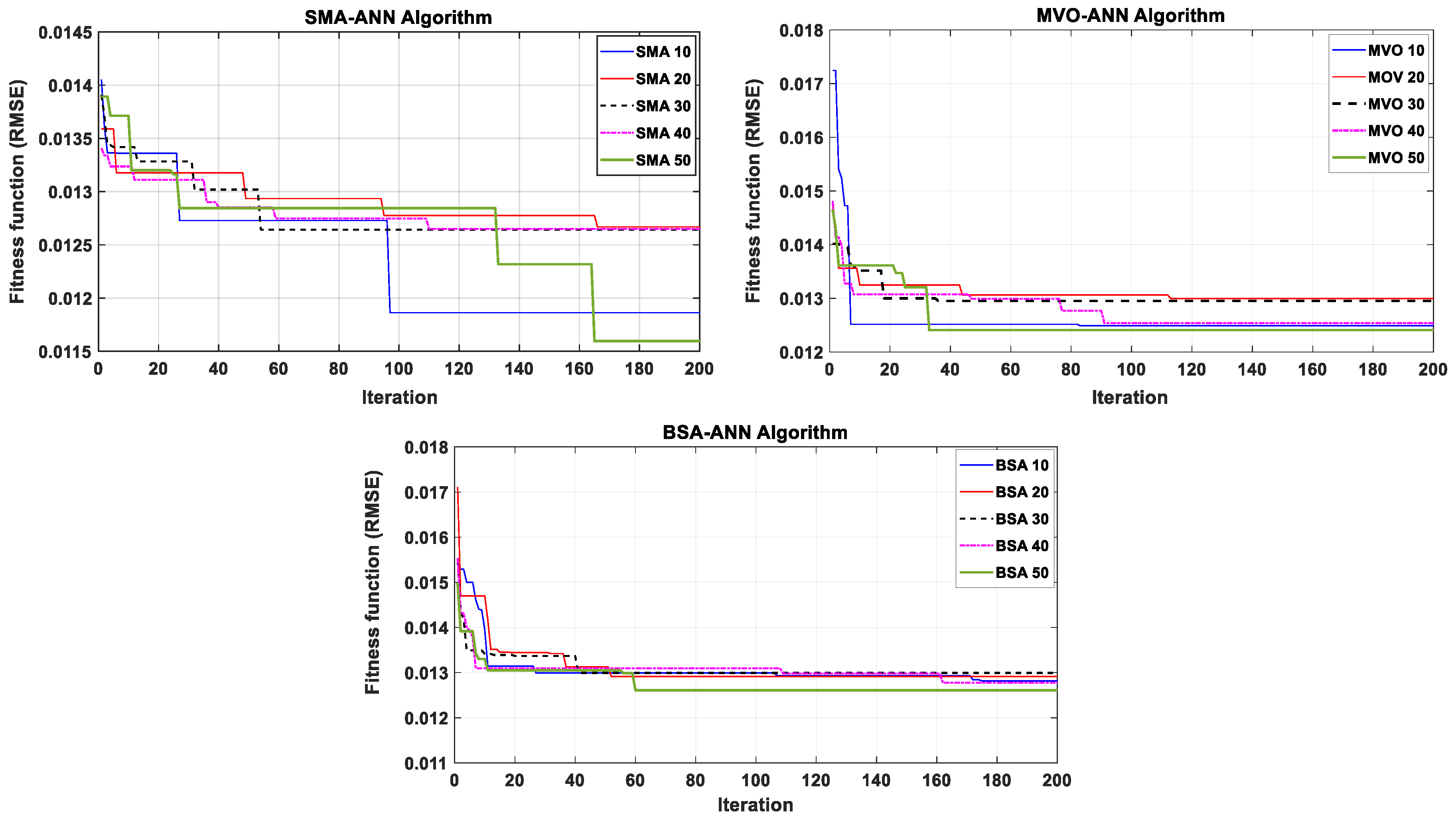
4.2. Model Configuration
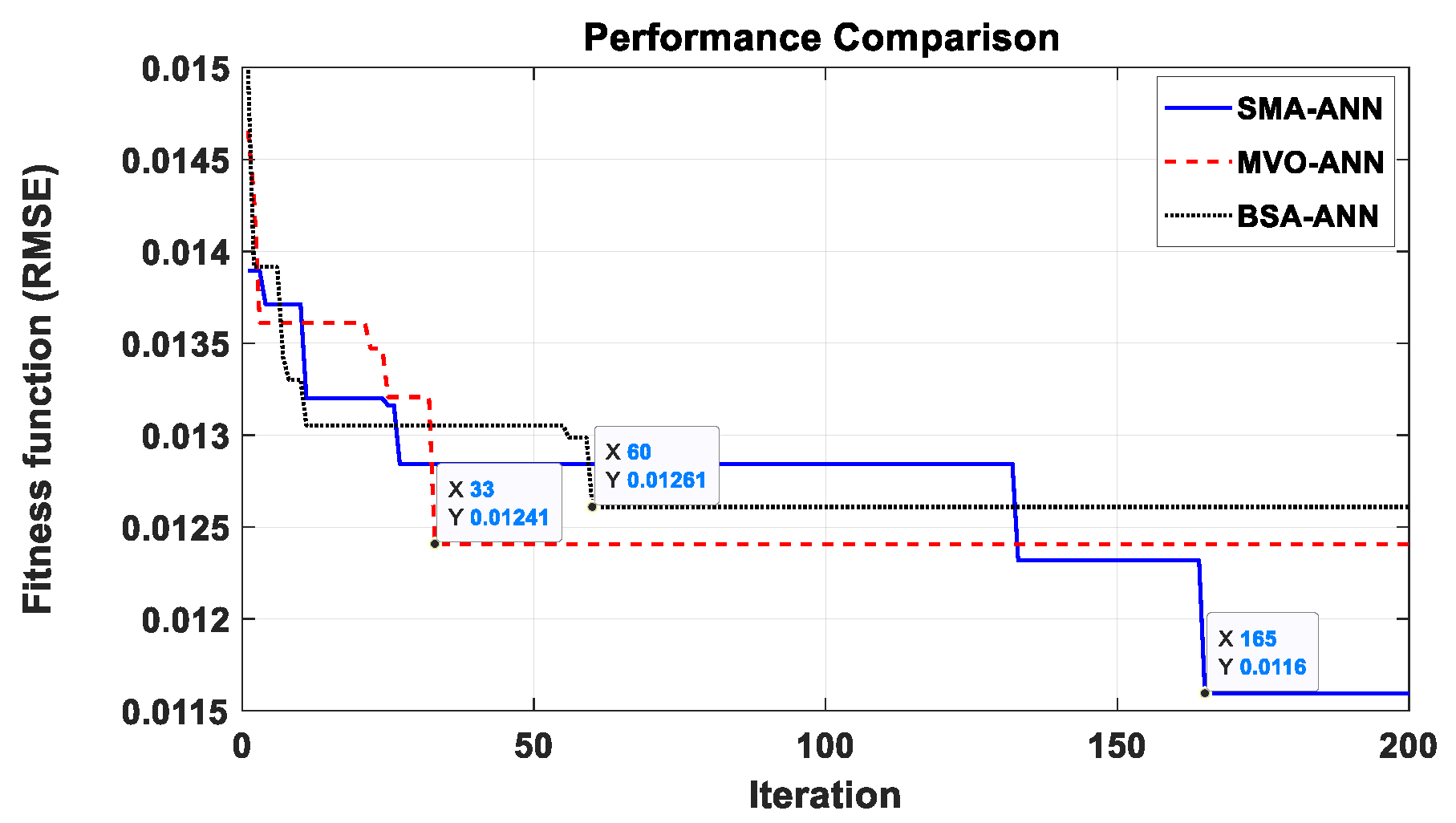
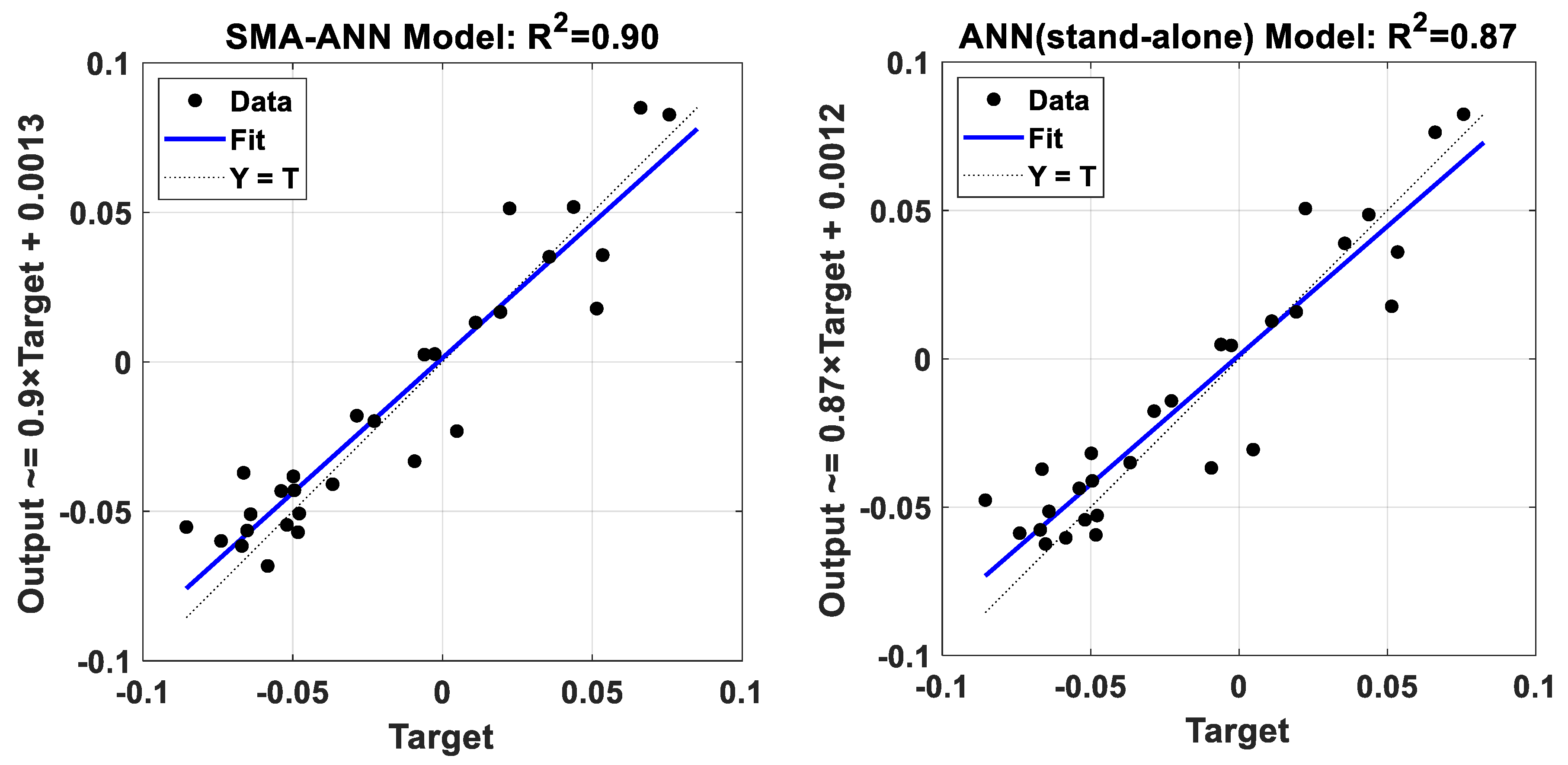
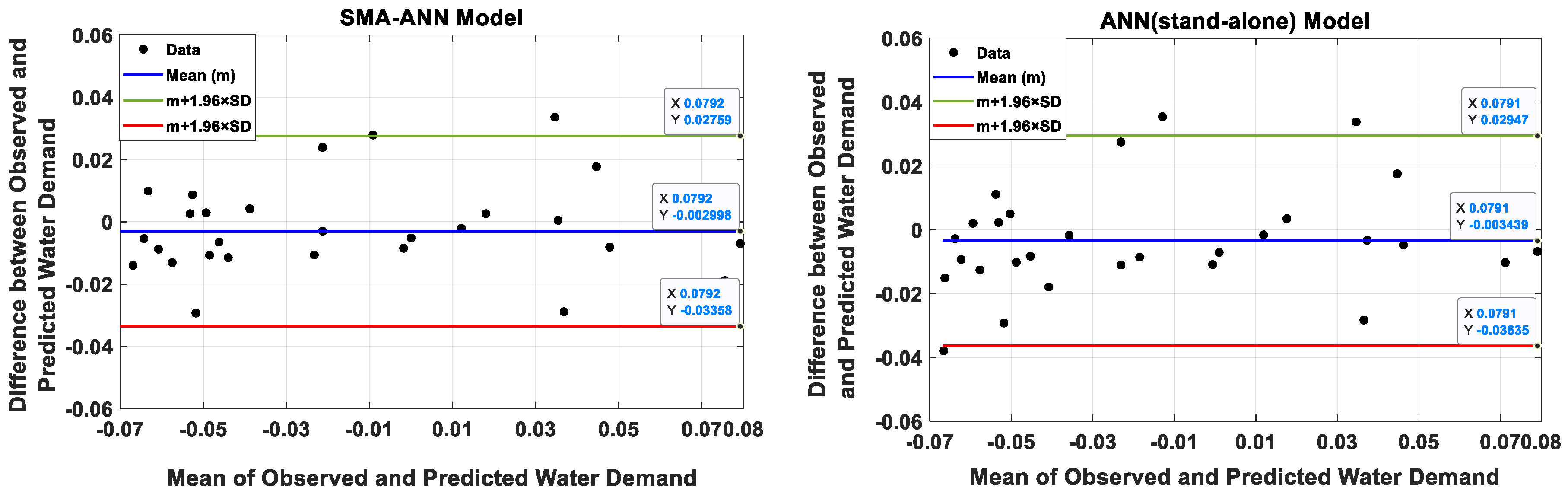
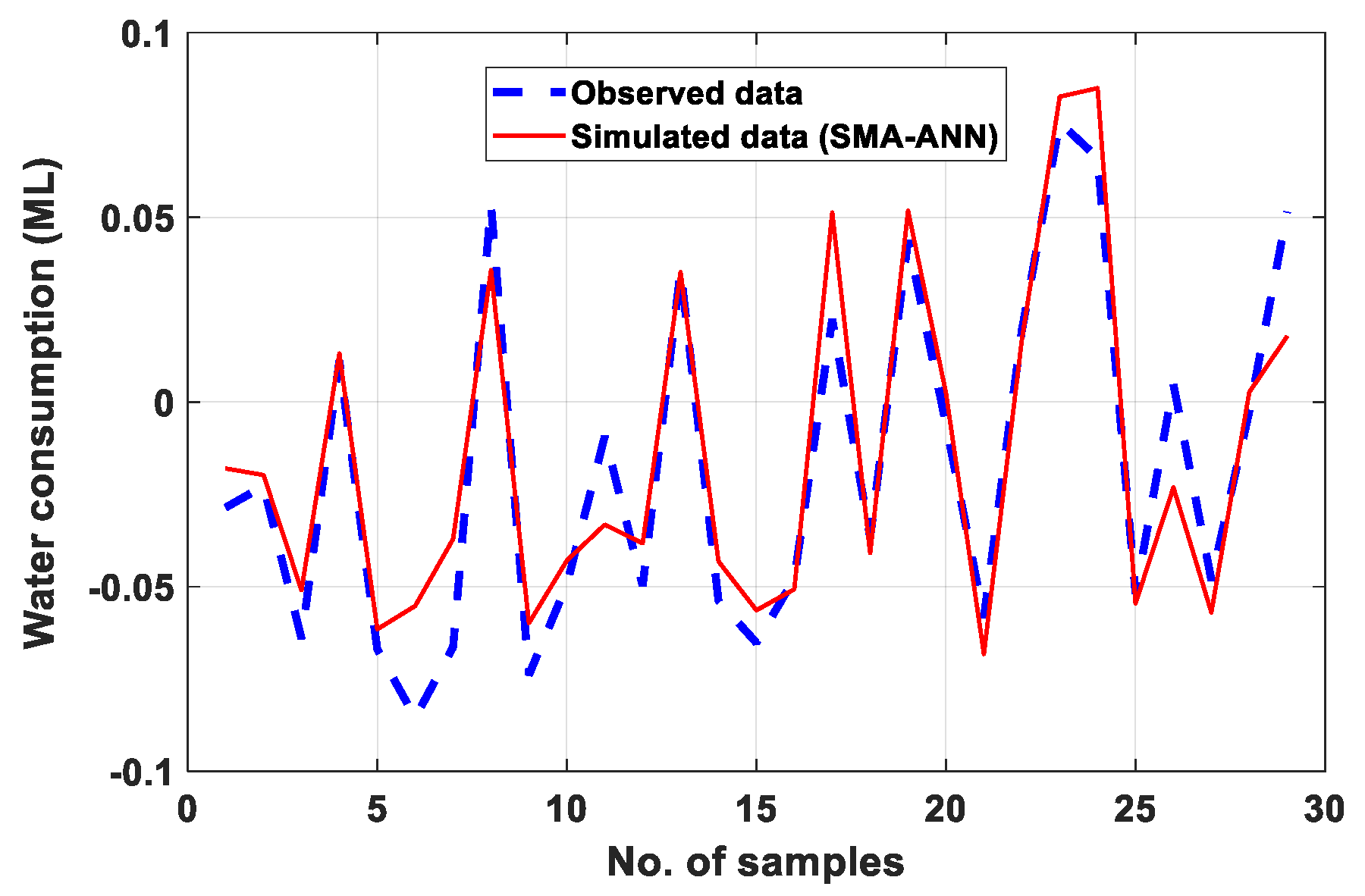
4.3. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Farhan, S.L.; Abdelmonem, M.G.; Nasar, Z.A. The Urban Transformation of Traditional City Centres: Holy Karbala as a Case Study. Int. J. Archit. Res. ArchNet-IJAR 2018, 12, 53–67. [Google Scholar] [CrossRef]
- Farhan, S.L.; Jasim, I.A.; Al-Mamoori, S.K. The transformation of the city of Najaf, Iraq: Analysis, reality and future prospects. J. Urban. Regen. Renew. 2019, 13, 160–171. [Google Scholar]
- Zubaidi, S.L.; Kot, P.; Hashim, K.; Alkhaddar, R.; Abdellatif, M.; Muhsin, Y.R. Using LARS–WG model for prediction of temperature in Columbia City, USA. IOP Conf. Ser. Mater. Sci. Eng. 2019, 584, 1–9. [Google Scholar] [CrossRef]
- Hashim, K.S.; Kot, P.; Zubaidi, S.L.; Alwash, R.; Al Khaddar, R.; Shaw, A.; Al-Jumeily, D.; Aljefery, M.H. Energy Efficient Electrocoagulation Using Baffle-Plates Electrodes for Efficient Escherichia Coli Removal from Wastewater. J. Water Process. Eng. 2020, 33, 1–7. [Google Scholar] [CrossRef]
- Rahim, M.S.; Nguyen, K.A.; Stewart, R.A.; Giurco, D.; Blumenstein, M. Machine Learning and Data Analytic Techniques in Digital Water Metering: A Review. Water 2020, 12, 294. [Google Scholar] [CrossRef]
- Hemati, A.; Rippy, M.A.; Grant, S.B.; Davis, K.; Feldman, D. Deconstructing Demand: The Anthropogenic and Climatic Drivers of Urban Water Consumption. Environ. Sci. Technol. 2016, 50, 12557–12566. [Google Scholar] [CrossRef]
- Roy, U.; Majumder, M. Vulnerability of Watersheds to Climate Change Assessed by Neural Network and Analytical Hierarchy Process; Springer: New York, NY, USA, 2016; Volume 3, p. 97. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Gharghan, S.K.; Ahmed, M.S.; Hashim, K. A Method for Predicting Long-Term Municipal Water Demands Under Climate Change. Water Resour. Manag. 2020, 34, 1265–1279. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Monthly water demand prediction using wavelet transform, first-order differencing and linear detrending techniques based on multilayer perceptron models. Urban Water J. 2018, 15, 177–181. [Google Scholar] [CrossRef]
- Rasifaghihi, N.; Li, S.S.; Haghighat, F. Forecast of urban water consumption under the impact of climate change. Sustain. Cities Soc. 2020, 52. [Google Scholar] [CrossRef]
- Ebrahim Banihabib, M.; Mousavi-Mirkalaei, P. Extended linear and non-linear auto-regressive models for forecasting the urban water consumption of a fast-growing city in an arid region. Sustain. Cities Soc. 2019, 48. [Google Scholar] [CrossRef]
- Pacchin, E.; Alvisi, S.; Franchini, M. A Short-Term Water Demand Forecasting Model Using a Moving Window on Previously Observed Data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.H.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Resour. Planing Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A., II; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- De Souza Groppo, G.; Costa, M.A.; Libânio, M. Predicting water demand: A review of the methods employed and future possibilities. Water Supply 2019. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Firat, M.; Turan, M.E.; Yurdusev, M.A. Comparative analysis of fuzzy inference systems for water consumption time series prediction. J. Hydrol. 2009, 374, 235–241. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple Random Forests Modelling for Urban Water Consumption Forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Monthly Water Consumption Prediction Using Season Algorithm and Wavelet Transform–Based Models. J. Water Resour. Plan. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Mouatadid, S.; Adamowski, J. Using extreme learning machines for short-term urban water demand forecasting. Urban. Water J. 2016, 14, 630–638. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2015, 27, 495–513. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Uthansakul, P.; Riaz, M.; Khan, M.N.; Lloret, J. Exploiting Multi-Verse Optimization and Sine-Cosine Algorithms for Energy Management in Smart Cities. Appl. Sci. 2020, 10, 2095. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.-S.; Chu, S.-C. A Parallel Multi-Verse Optimizer for Application in Multilevel Image Segmentation. IEEE Access 2020, 8, 32018–32030. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Al-Bugharbee, H.; Olier, I.; Hashim, K.S.; Gharghan, S.K.; Kot, P.; Alkhaddar, R.M. Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water 2020, 12, 1885. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Zhao, X.; Yang, Q.J. Backtracking search algorithm with Lévy flight for estimating parameters of photovoltaic models. Energy Convers. Manag. 2020, 208, 112615. [Google Scholar] [CrossRef]
- Mehmood, A.; Shi, P.; Raja, M.A.Z.; Zameer, A.; Chaudhary, N.I. Design of backtracking search heuristics for parameter estimation of power signals. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Futur. Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Ghafil, H.N.; Jármai, K. Dynamic differential annealed optimization: New metaheuristic optimization algorithm for engineering applications. Appl. Soft Comput. 2020, 93, 106392. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris Hawk Optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Zanella-Calzada, L.A.; Oliva, D.; Heidari, A.A.; Zaldivar, D.; Pérez-Cisneros, M.; Foong, L.K. An Efficient Harris Hawks-inspired Image Segmentation Method. Exert Syst. Appl. 2020, 155, 113428. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H. Short-Term Water Demand Prediction in Residential Complexes: Case Study in Columbia City, USA. In Proceedings of the 2018 11th International Conference on Developments in eSystems Engineering (DeSE), Cambridge, UK, 2–5 September 2018; pp. 31–35. [Google Scholar]
- Zubaidi, S.L.; Al-Bugharbee, H.; Muhsen, Y.R.; Hashim, K.; Alkhaddar, R.M.; Hmeesh, W.H. The Prediction of Municipal Water Demand in Iraq: A Case Study of Baghdad Governorate. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 274–277. [Google Scholar]
- Campisi-Pinto, S.; Adamowski, J.; Oron, G. Forecasting Urban Water Demand Via Wavelet-Denoising and Neural Network Models. Case Study: City of Syracuse, Italy. Water Resour. Manag. 2012, 26, 3539–3558. [Google Scholar] [CrossRef]
- Seo, Y.; Kwon, S.; Choi, Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology 2018, 5, 54. [Google Scholar] [CrossRef]
- Vecchio, A.; Anzidei, M.; Serpelloni, E.; Florindo, F. Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100. Water 2019, 11, 1480. [Google Scholar] [CrossRef]
- Chu, T.-Y.; Huang, W.-C. Application of Empirical Mode Decomposition Method to Synthesize Flow Data: A Case Study of Hushan Reservoir in Taiwan. Water 2020, 12, 927. [Google Scholar] [CrossRef]
- Gedefaw, M.; Hao, W.; Denghua, Y.; Girma, A.; Khamis, M.I. Variable selection methods for water demand forecasting in Ethiopia: Case study Gondar town. Cogent Environ. Sci. 2018, 4. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Leng, G.; Yang, Y.; Gao, Q.; Fan, Y.; Luo, J. The Potential Utility of Satellite Soil Moisture Retrievals for Detecting Irrigation Patterns in China. Water 2018, 10, 1505. [Google Scholar] [CrossRef]
- Kim, K.; Joo, H.; Han, D.; Kim, S.; Lee, T.; Kim, H.S. On Complex Network Construction of Rain Gauge Stations Considering Nonlinearity of Observed Daily Rainfall Data. Water 2019, 11, 1578. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]
- MW. Corporate Plan 2016/17 to 2020/21; MW: Victoria, Australia, 2017; p. 39. [Google Scholar]
- SEW. South East Water Annual Report 2015-16; Including the Financial Report; SEW: Queensland, Australia, 2016. [Google Scholar]
- Araghinejad, S. Data-Driven Modeling: Using MATLAB® in Water Resources and Environmental Engineering; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, Sixth ed.; Pearson Education, Inc.: New York, NY, USA, 2013. [Google Scholar]
- Bailey, O.; Zlatanovic, L.; van der Hoek, J.P.; Kapelan, Z.; Blokker, M.; Arnot, T.; Hofman, J. A Stochastic Model to Predict Flow, Nutrient and Temperature Changes in a Sewer under Water Conservation Scenarios. Water 2020, 12, 1187. [Google Scholar] [CrossRef]
- Tabrizi, A.A.; Al-Bugharbee, H.; Trendafilova, I.; Garibaldi, L. A cointegration-based monitoring method for rolling bearings working in time-varying operational conditions. Meccanica 2017, 52, 1201–1217. [Google Scholar] [CrossRef]
- Abdou, A.D.; Ngom, N.F.; Sidibé, S.; Niang, O.; Thioune, A.; Ndiaye, C.H. Neural networks for biomedical signals classification based on empirical mode decomposition and principal component analysis. In Innovation and Interdisciplinary Solutions for Underserved Areas; Springer: New York, NY, USA, 2017; pp. 267–278. [Google Scholar]
- Zeiler, A.; Faltermeier, R.; Keck, I.R.; Tomé, A.M.; Puntonet, C.G.; Lang, E.W. Empirical mode decomposition-an introduction. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Pallant, J. SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS; Open University Press/McGraw-Hill: London, UK, 2016. [Google Scholar]
- Bayatvarkeshi, M.; Mohammadi, K.; Kisi, O.; Fasihi, R. A new wavelet conjunction approach for estimation of relative humidity: Wavelet principal component analysis combined with ANN. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Al-Bugharbee, H.; Ortega-Martorell, S.; Gharghan, S.K.; Olier, I.; Hashim, K.S.; Al-Bdairi, N.S.S.; Kot, P. A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro-Fuzzy Inference System Approach. Water 2020, 12, 1628. [Google Scholar] [CrossRef]
- González Perea, R.; Camacho Poyato, E.; Montesinos, P.; Rodríguez Díaz, J.A. Optimisation of water demand forecasting by artificial intelligence with short data sets. Biosyst. Eng. 2019, 177, 59–66. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
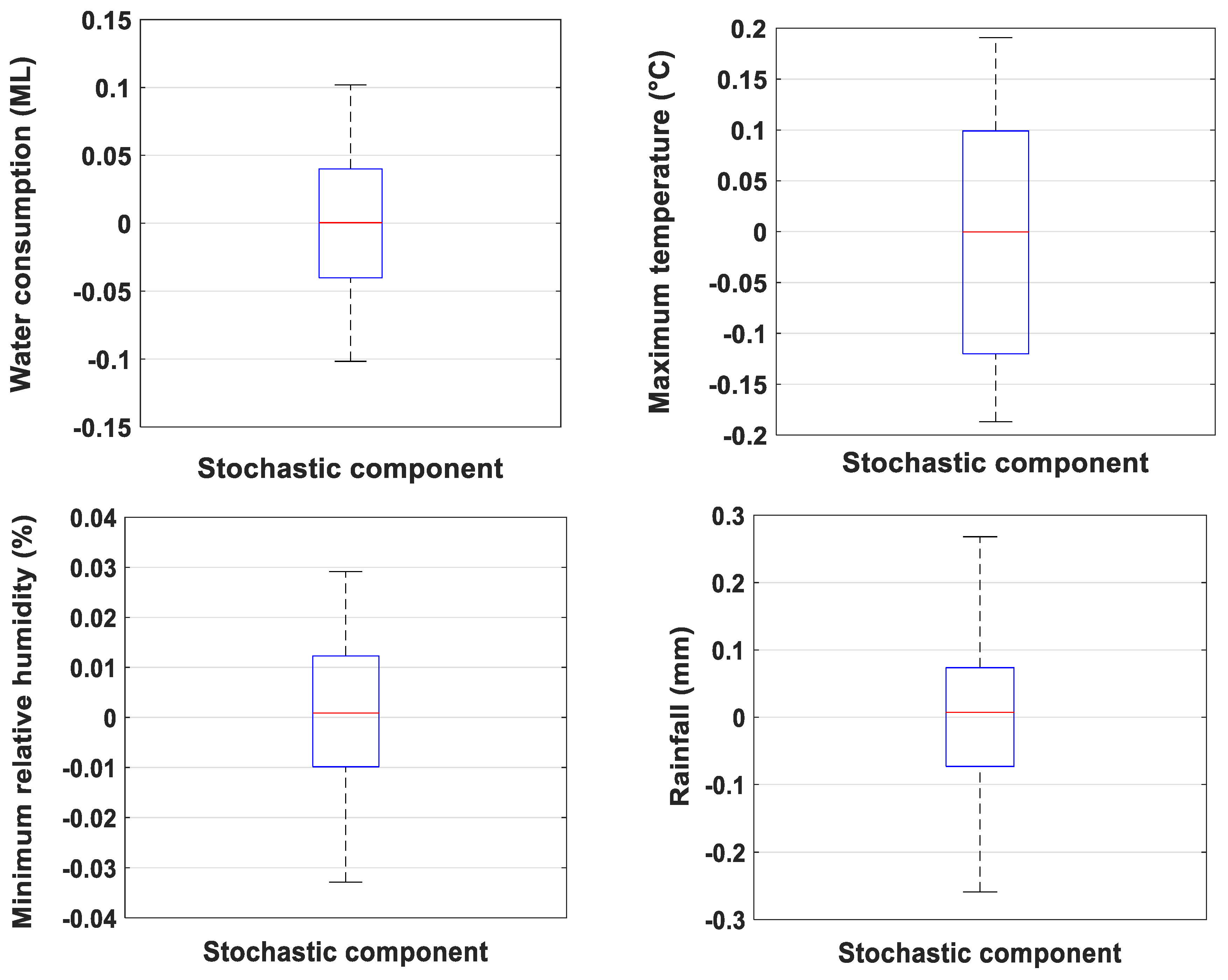
| Data | Tmax | Tmin | Tmean | Rain | Eva | Srad | VP | RHmax | RHmin | FA-O56 |
|---|---|---|---|---|---|---|---|---|---|---|
| Raw | 0.63 | 0.61 | 0.62 | −0.10 | 0.61 | 0.60 | 0.55 | −0.59 | −0.54 | 0.63 |
| Stochastic | 0.93 | 0.91 | 0.92 | −0.53 | 0.88 | 0.83 | 0.88 | −0.89 | −0.75 | 0.88 |
| Climatic Factors | Tolerance Value |
|---|---|
| Tmax | 0.322 |
| RHmin | 0.344 |
| Rain | 0.867 |
| Models | MAE | RMSE | MARE |
|---|---|---|---|
| SMA-ANN | 0.012 | 0.015 | 0.001 |
| ANN | 0.013 | 0.017 | 0.015 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubaidi, S.L.; Abdulkareem, I.H.; Hashim, K.S.; Al-Bugharbee, H.; Ridha, H.M.; Gharghan, S.K.; Al-Qaim, F.F.; Muradov, M.; Kot, P.; Al-Khaddar, R. Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand. Water 2020, 12, 2692. https://doi.org/10.3390/w12102692
Zubaidi SL, Abdulkareem IH, Hashim KS, Al-Bugharbee H, Ridha HM, Gharghan SK, Al-Qaim FF, Muradov M, Kot P, Al-Khaddar R. Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand. Water. 2020; 12(10):2692. https://doi.org/10.3390/w12102692
Chicago/Turabian StyleZubaidi, Salah L., Iqbal H. Abdulkareem, Khalid S. Hashim, Hussein Al-Bugharbee, Hussein Mohammed Ridha, Sadik Kamel Gharghan, Fuod F. Al-Qaim, Magomed Muradov, Patryk Kot, and Rafid Al-Khaddar. 2020. "Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand" Water 12, no. 10: 2692. https://doi.org/10.3390/w12102692
APA StyleZubaidi, S. L., Abdulkareem, I. H., Hashim, K. S., Al-Bugharbee, H., Ridha, H. M., Gharghan, S. K., Al-Qaim, F. F., Muradov, M., Kot, P., & Al-Khaddar, R. (2020). Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand. Water, 12(10), 2692. https://doi.org/10.3390/w12102692











