SPH Modeling of Water-Related Natural Hazards
Abstract
1. Introduction
2. Two-Phase Coupled Dynamics
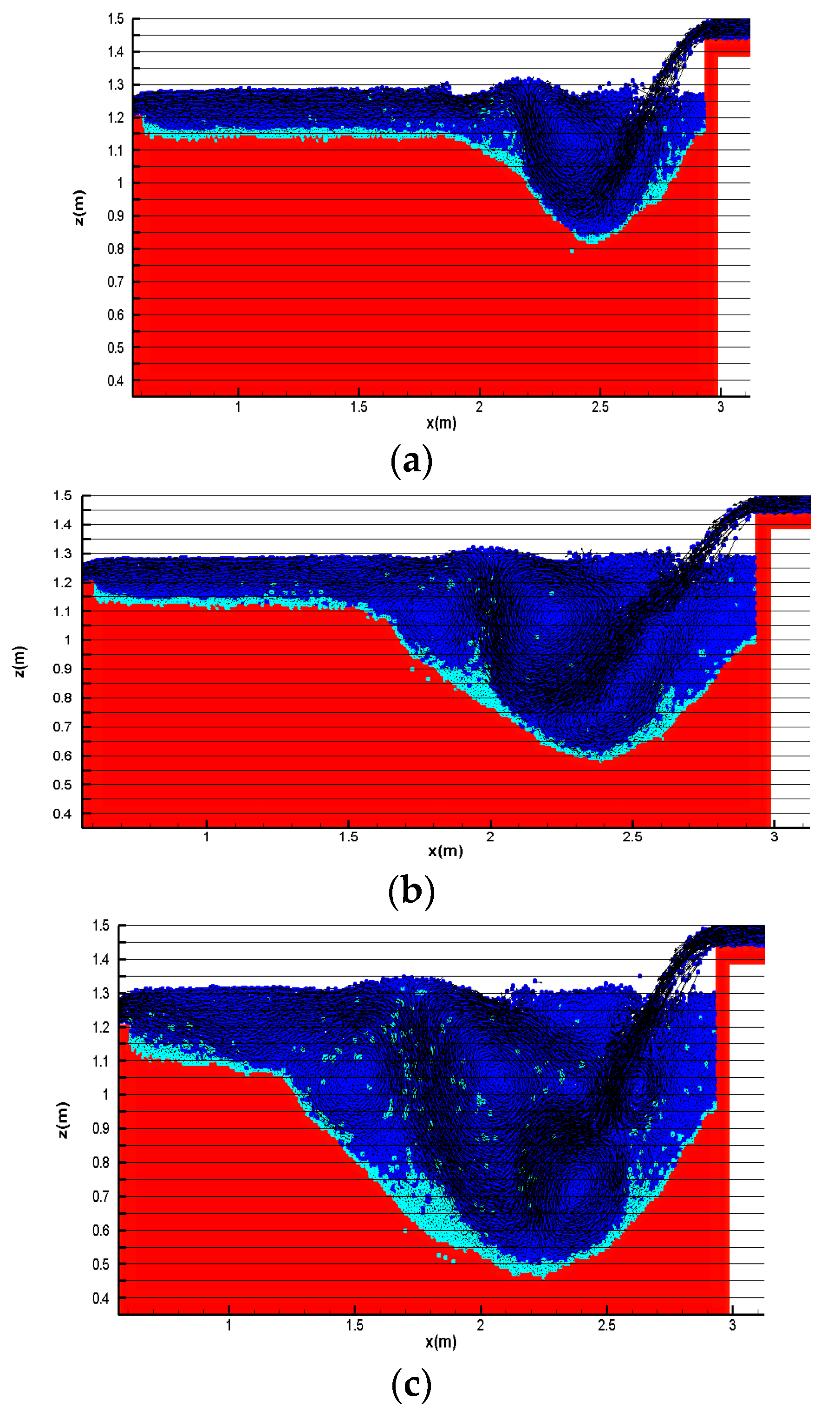
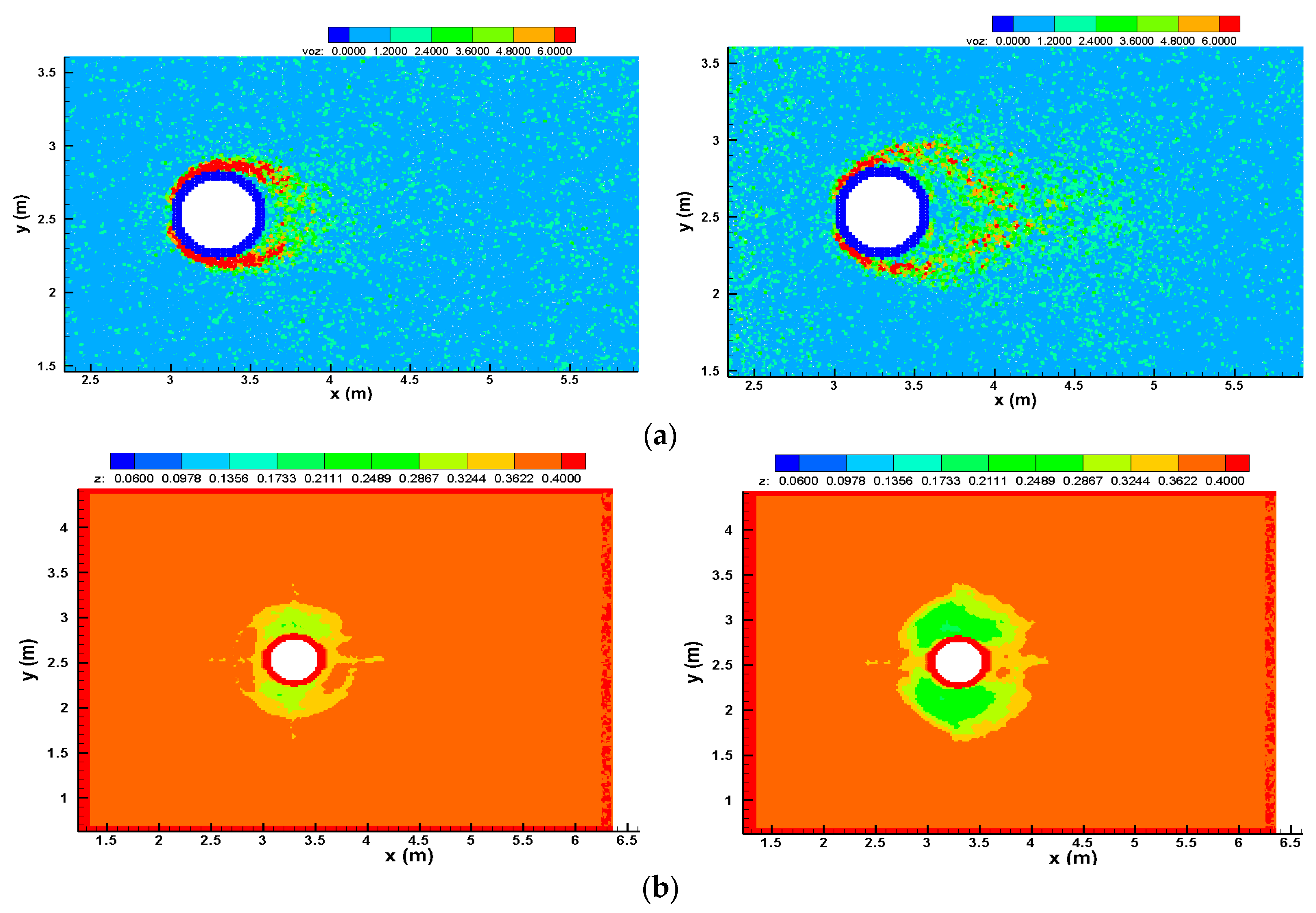
2.1. Scouring and Sediment Transport
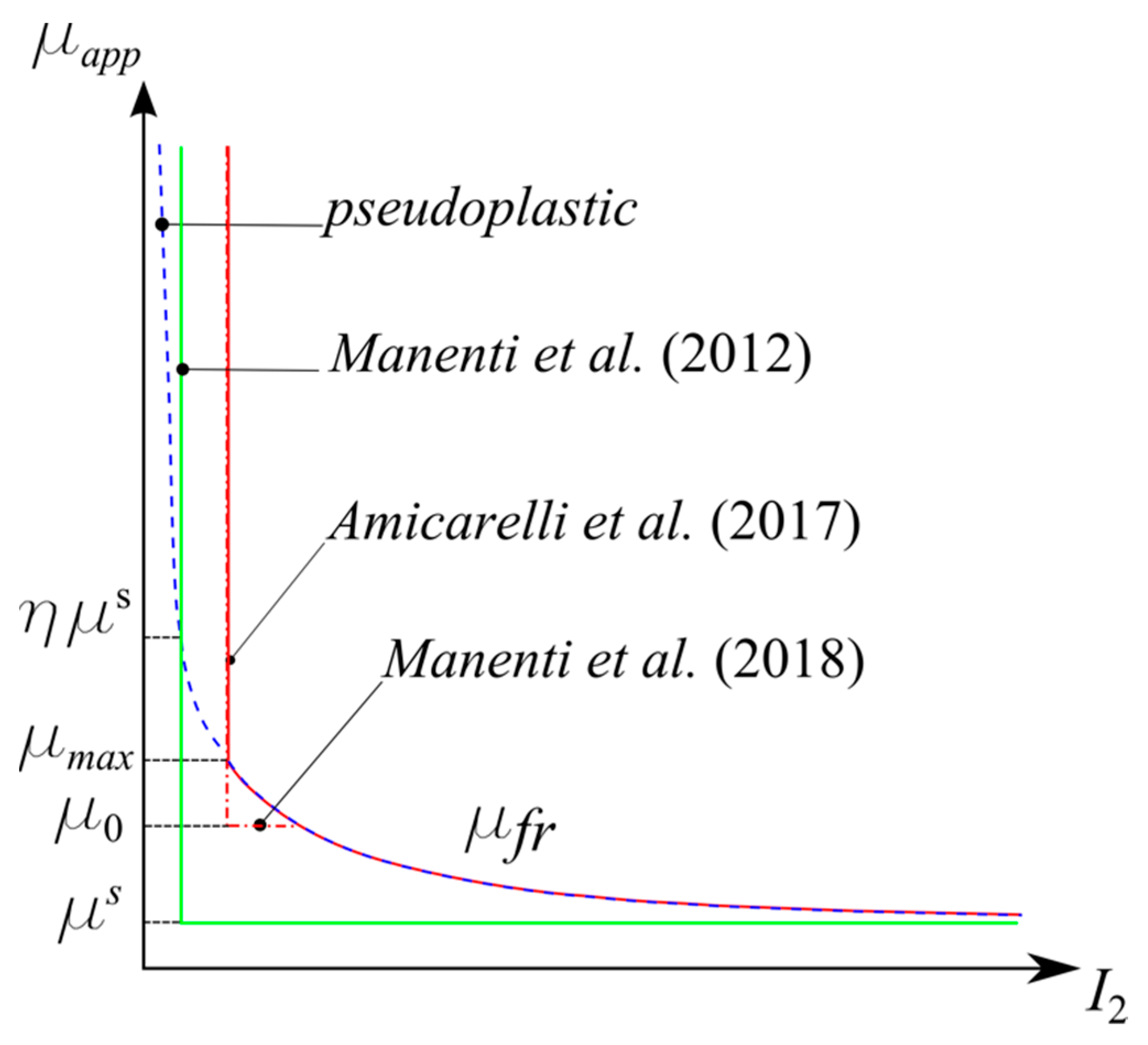
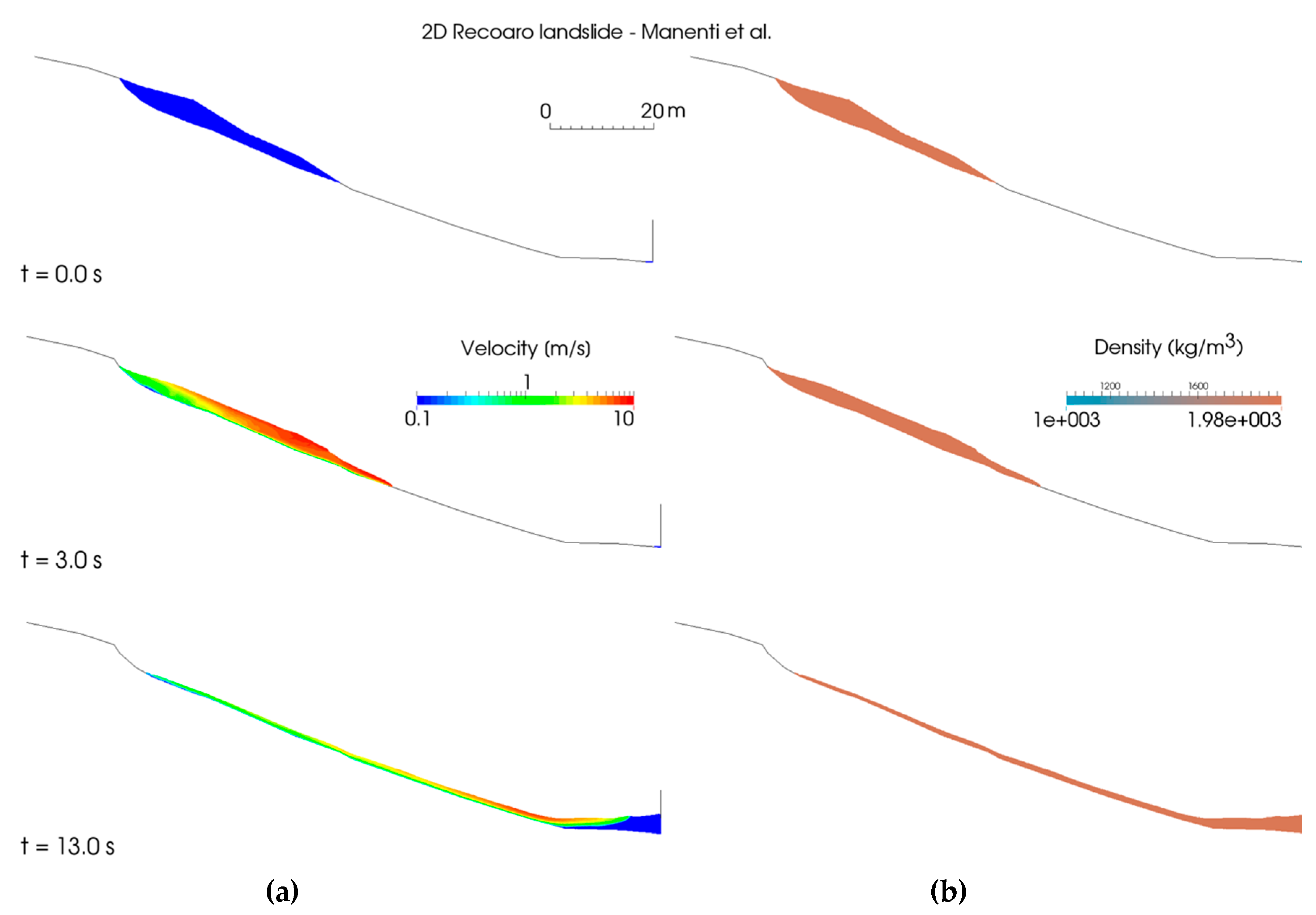
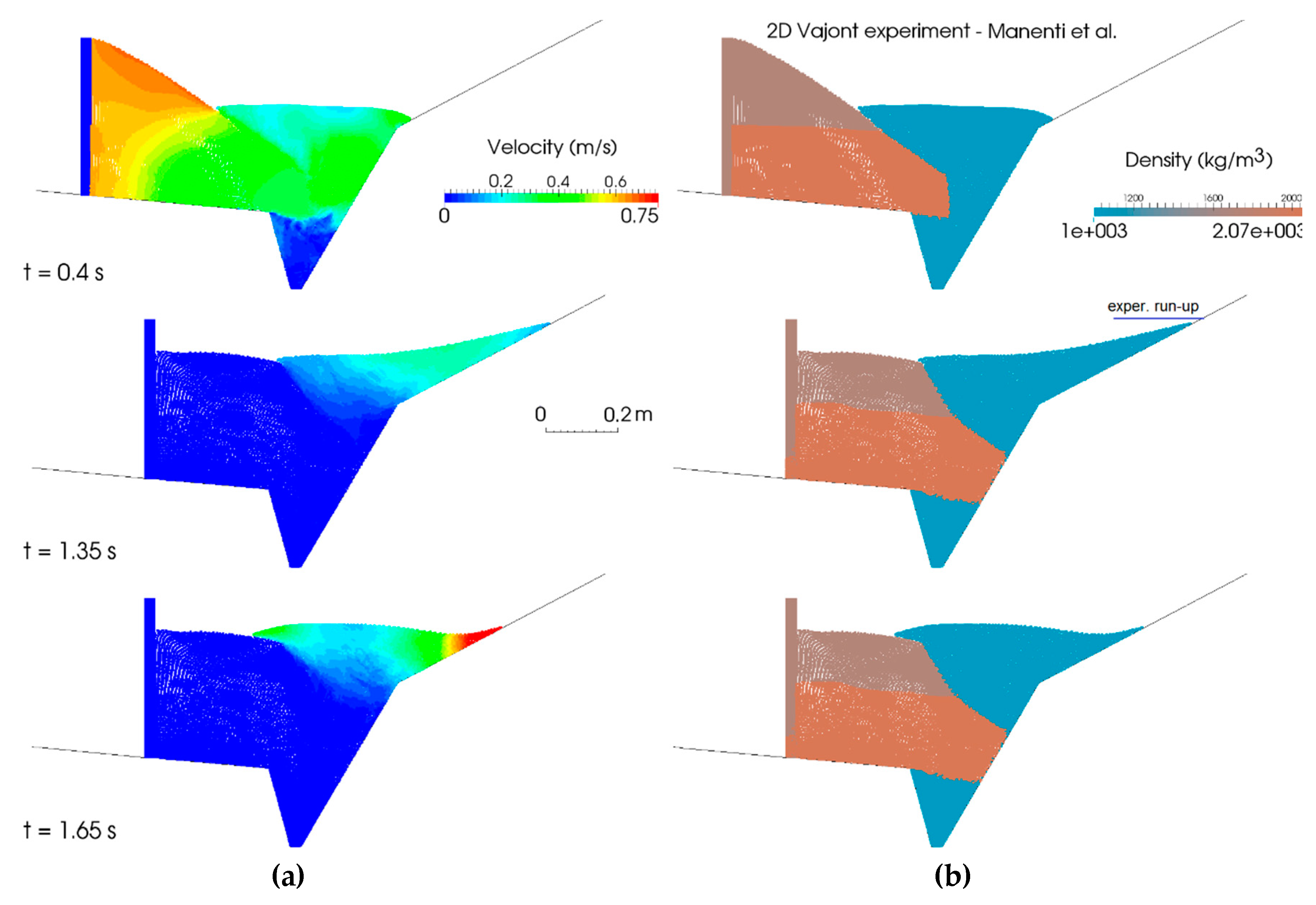
2.2. Fast Landslides and Dense Granular Flows Interacting with Water
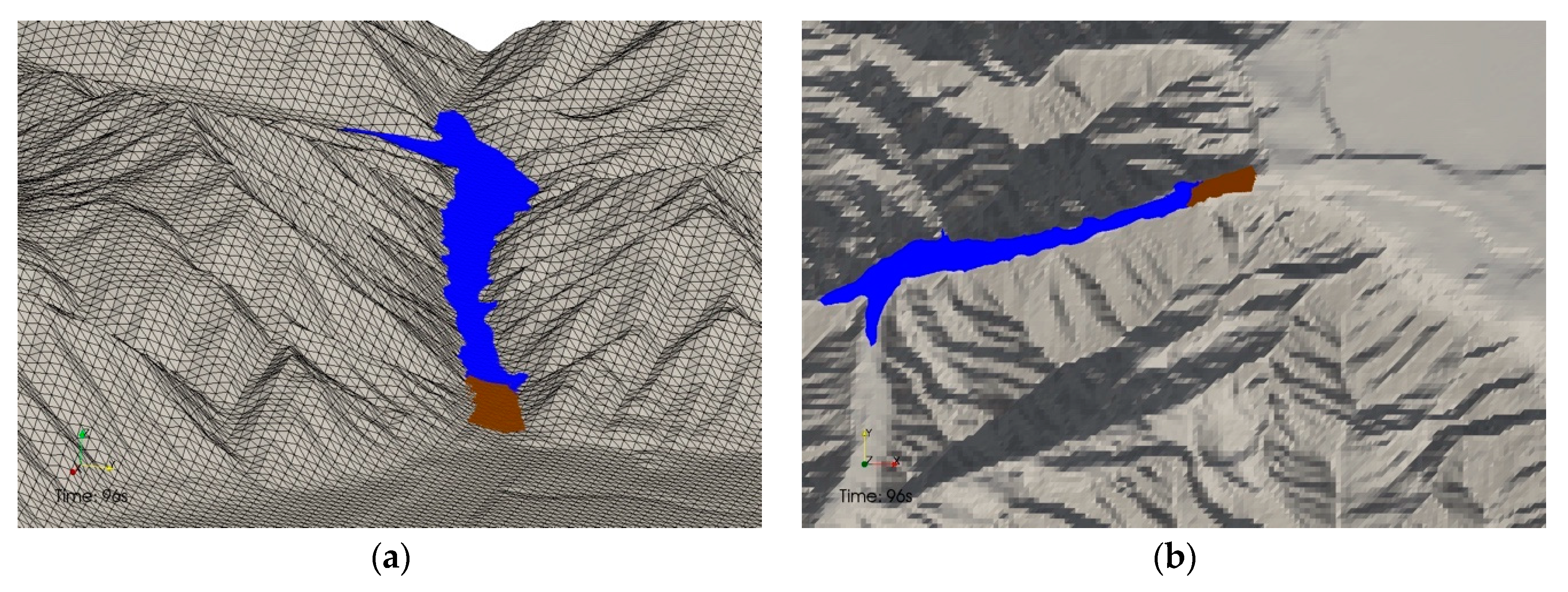
3. Flooding in Complex Topography with the Transport of Sediments
4. High Performance Computing Solutions for Complex Hydraulic Engineering Problems
5. Conclusions and Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, D.; Shao, S.; Li, S.; Shi, Y.; Arikawa, T.; Zhang, H. 3D ISPH erosion model for flow passing a vertical cylinder. J. Fluids Struct. 2018, 78, 374–399. [Google Scholar] [CrossRef]
- Wang, D.; Shaowu, L.; Arikawa, T.; Gen, H. ISPH Simulation of Scour Behind Seawall Due to Continuous Tsunami Overflow. Coast. Eng. J. 2016, 58, 1650014. [Google Scholar] [CrossRef]
- Wang, C.; Peng, C.; Meng, X. Smoothed Particle Hydrodynamics Simulation of Water-Soil Mixture Flows. J. Hydraul. Eng. 2016, 142, 04016032. [Google Scholar] [CrossRef]
- Guandalini, R.; Agate, G.; Manenti, S.; Sibilla, S.; Gallati, M. SPH Based Approach toward the Simulation of Non-cohesive Sediment Removal by an Innovative Technique Using a Controlled Sequence of Underwater Micro-explosions. Procedia IUTAM 2015, 18, 28–39. [Google Scholar] [CrossRef][Green Version]
- Guandalini, R.; Agate, G.; Manenti, S.; Sibilla, S.; Gallati, M. Innovative numerical modeling to investigate local scouring problems induced by fluvial structures. In Proceedings of the Sixth International Conference on Bridge Maintenance, Safety and Management (IABMAS 2012), Stresa, Italy, 8–12 July 2012; pp. 3110–3116. [Google Scholar]
- Zubeldia, E.H.; Fourtakas, G.; Rogers, B.D.; Farias, M.M. Multi-phase SPH model for simulation of erosion and scouring by means of the shields and Drucker–Prager criteria. Adv. Water Resour. 2018, 117, 98–114. [Google Scholar] [CrossRef]
- Manenti, S.; Sibilla, S.; Gallati, M.; Agate, G.; Guandalini, R. SPH simulation of sediment flushing induced by a rapid water flow. J. Hydraul. Eng. 2012, 138, 272–284. [Google Scholar] [CrossRef]
- Amicarelli, A.; Kocak, B.; Sibilla, S.; Grabe, J. A 3D smoothed particle hydrodynamics model for erosional dam-break floods. Int. J. Comput. Fluid Dyn. 2017, 31, 413–434. [Google Scholar] [CrossRef]
- Manenti, S.; Amicarelli, A.; Todeschini, S. WCSPH with Limiting Viscosity for Modeling Landslide Hazard at the Slopes of Artificial Reservoir. Water 2018, 10, 515. [Google Scholar] [CrossRef]
- Tan, H.; Chen, S. A hybrid DEM-SPH model for deformable landslide and its generated surge waves. Adv. Water Resour. 2017, 108, 256–276. [Google Scholar] [CrossRef]
- Shi, C.; An, Y.; Wu, Q.; Liu, Q.; Cao, Z. Numerical simulation of landslide-generated waves using a soil–water coupling smoothed particle hydrodynamics model. Adv. Water Resour. 2016, 92, 130–141. [Google Scholar] [CrossRef]
- Viroulet, S.; Sauret, A.; Kimmoun, O.; Kharif, C. Granular collapse into water: Toward tsunami landslides. J. Vis. 2013, 16, 189–191. [Google Scholar] [CrossRef]
- Capone, T.; Panizzo, A.; Monaghan, J.J. SPH modeling of water waves generated by submarine landslides. J. Hydraul. Res. 2010, 48, 80–84. [Google Scholar] [CrossRef]
- Bordoni, M.; Meisina, C.; Valentino, R.; Bittelli, M.; Chersich, S. Site-specific to local-scale shallow landslides triggering zones assessment using TRIGRS. Nat. Hazards Earth Syst. Sci. 2015, 15, 1025–1050. [Google Scholar] [CrossRef]
- Zizioli, D.; Meisina, C.; Valentino, R.; Montrasio, L. Comparison between different approaches to modeling shallow landslide susceptibility: A case history in Oltrepo Pavese, Northern Italy. Nat. Hazards Earth Syst. Sci. 2013, 13, 559–573. [Google Scholar] [CrossRef]
- Ray, R.; Deb, K.; Shaw, A. Pseudo-Spring smoothed particle hydrodynamics (SPH) based computational model for slope failure. Eng. Anal. Bound. Elem. 2019, 102, 139–148. [Google Scholar] [CrossRef]
- Gu, S.; Zheng, X.; Ren, L.; Xie, H.; Huang, Y.; Wei, J.; Shao, S. SWE-SPHysics Simulation of Dam Break Flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef]
- Barreiro, A.; Domínguez, J.M.; Crespo, A.J.C.; González-Jorge, H.; Roca, D.; Gómez-Gesteira, M. Integration of UAV photogrammetry and SPH modeling of fluids to study runoff on real terrains. PLoS ONE 2014, 9, e111031. [Google Scholar] [CrossRef]
- Vacondio, R.; Mignosa, P.; Pagani, S. 3D SPH numerical simulation of the wave generated by the Vajont rock slide. Adv. Water Res. 2013, 59, 146–156. [Google Scholar] [CrossRef]
- Qiu, L.C.; Liu, Y.; Han, Y. A 3D Simulation of a Moving Solid in Viscous Free-Surface Flows by Coupling SPH and DEM. Math. Probl. Eng. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Albano, R.; Sole, A.; Mirauda, D.; Adamowski, J. Modeling large floating bodies in urban area flash-floods via a Smoothed Particle Hydrodynamics model. J. Hydrol. 2016, 541, 344–358. [Google Scholar] [CrossRef]
- Amicarelli, A.; Albano, R.; Mirauda, D.; Agate, G.; Sole, A.; Guandalini, R. A smoothed particle hydrodynamics model for 3D solid body transport in free surface flows. Comput. Fluids 2015, 116, 205–228. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Hillslope Hydrology and Stability; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Inam, A.; Adamowski, J.; Prasher, S.; Halbe, J.; Malard, J.; Albano, R. Coupling of a distributed stakeholder-built system dynamics socio-economic model with SAHYSMOD for sustainable soil salinity management—Part 1: Model development. J. Hydrol. 2017, 55, 596–618. [Google Scholar] [CrossRef]
- Shao, S. Incompressible smoothed particle hydrodynamics simulation of multi-fluid flows. Int. J. Numer. Meth. Fluids 2012, 69, 1715–1735. [Google Scholar] [CrossRef]
- Manenti, S. Standard WCSPH for free-surface multi-phase flows with a large density ratio. Int. J. Ocean Coast. Eng. 2018, 1. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial ows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Hu, X.Y.; Adams, N.A. An incompressible multi-phase SPH method. J. Comput. Phys. 2007, 227, 264–278. [Google Scholar] [CrossRef]
- Grenier, N.; Antuono, M.; Colagrossi, A.; le Touzé, D.; Alessandrini, B. An Hamiltonian interface SPH formulation for multi-fluid and free-surface flows. J. Comput. Phys. 2009, 228, 380–393. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Ashkan, R. A simple SPH algorithm for multi-fluid ow with high density ratios. Int. J. Numer. Methods Fluids 2013, 71, 537–561. [Google Scholar] [CrossRef]
- Bouscasse, B.; Colagrossi, A.; Marrone, S.; Souto-Iglesias, A. SPH modelling of viscous flow past a circular cylinder interacting with a free surface. Comput. Fluids 2017, 146, 190–212. [Google Scholar] [CrossRef]
- Hamill, L. Bridge Hydraulics; E&FN Spon: New York, NY, USA, 1999. [Google Scholar]
- Persi, E.; Petaccia, G.; Fenocchi, A.; Manenti, S.; Ghilardi, P.; Sibilla, S. Hydrodynamic coefficients of yawed cylinders in open-channel flow. Flow Meas. Instrum. 2019, 65, 288–296. [Google Scholar] [CrossRef]
- Dordoni, S.; Malerba, P.; Sgambi, L.; Manenti, S. Fuzzy reliability assessment of bridge piers in presence of scouring. In Proceedings of the 5th International Conference on Bridge Maintenance, Safety and Management, Philadelphia, PA, USA, 11–15 July 2010; pp. 1388–1395. [Google Scholar]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment; Advanced Series on Ocean Engineering; World Scientific Publishing Company: Singapore, 2002; Volume 17. [Google Scholar]
- Whitehouse, R.J.S. Scour at Marine Structures; Thomas Telford: London, UK, 1998. [Google Scholar]
- Wang, D.; Arikawa, T.; Li, S.W.; Gen, H. Numerical Simulation on Scour behind Seawall due to Tsunami Overflow. In Proceedings of the Coastal Structures & Solutions to Coastal Disasters Joint Conference, Boston, MA, USA, 9–11 September 2015; ASCE: Reston, VA, USA, 2015. [Google Scholar]
- Li, S.W.; Wang, D. Tsunami occurrences in China and numerical simulation of a supposed tsunami process in Bohai Sea. In Proceedings of the China Ocean Engineering, Dailian, China, August 2013; pp. 490–496. Available online: http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HYGC201308001076.htm (accessed on 30 August 2013).
- Sugano, T.; Nozu, A.; Kohama, E.; Shimosako, K.; Kikuchi, Y. Damage to coastal structures. Soils Found. 2014, 54, 883–901. [Google Scholar] [CrossRef]
- Takahashi, H.; Sassa, S.; Morikawa, Y.; Takano, D.; Maruyama, K. Stability of caisson-type breakwater foundation under tsunami-induced seepage. Soils Found. 2014, 54, 789–805. [Google Scholar] [CrossRef]
- Nakamura, T.; Mizutani, N. Sediment Transport Calculation Considering Laminar and Turbulent Resistance Forces Caused by Infiltration/Exfiltration and its Application to Tsunami-induced Local Scouring. J. Offshore Mech. Arct. Eng. 2013, 136, 011105. [Google Scholar] [CrossRef]
- Oie, T.; Dong, W.; Takatani, T.; Araki, K.; Shaowu, L.; Goto, H.; Arikawa, T. Numerical simulation of scouring behind the seawall caused by tsunami overflow with accurate ISPH method. Jpn. Soc. Civ. Eng. 2015, 71, 253–258. (In Japanese) [Google Scholar]
- Ettema, R.; Kirkil, G.; Muste, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. Comput. Phys. Commun. 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, P.; Ming, F. An SPH modeling of bubble rising and coalescing in three dimensions. Comput. Methods Appl. Mech. Eng. 2015, 294, 189–209. [Google Scholar] [CrossRef]
- Ming, F.R.; Sun, P.N.; Zhang, A.M. Numerical investigation of rising bubbles bursting at a free surface through a multiphase SPH model. Meccanica 2017, 52, 2665–2684. [Google Scholar] [CrossRef]
- Ran, Q.; Tong, J.; Shao, S.; Fu, X.; Xu, Y. Incompressible SPH scour model for movable bed dam break flows. Adv. Water Resour. 2015, 82, 39–50. [Google Scholar] [CrossRef]
- Gotoh, H.; Ikari, H.; Memita, T.; Sakai, T. Lagrangian Particle Method for Simulation of Wave Overtopping on a Vertical Seawall. Coast. Eng. J. 2005, 47, 157–181. [Google Scholar] [CrossRef]
- Ulrich, C.; Leonardi, M.; Rung, T. Multi-physics SPH simulation of complex marine-engineering hydrodynamic problems. Ocean Eng. 2013, 64, 109–121. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on smoothed particle hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Fourtakas, G.; Rogers, B.D. Modeling multi-phase liquid-sediment scour and resuspension induced by rapid flows using Smoothed Particle Hydrodynamics (SPH) accelerated with a Graphics Processing Unit (GPU). Adv. Water Resour. 2016, 92, 186–199. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of solutions and suspensions. I. Theory. J. Phys. Colloid Chem. 1948, 52, 277–299. [Google Scholar] [CrossRef] [PubMed]
- Todeschini, S. Trends in long daily rainfall series of Lombardia (Northern Italy) affecting urban stormwater control. Int. J. Climatol. 2012, 32, 900–919. [Google Scholar] [CrossRef]
- Todeschini, S.; Papiri, S.; Ciaponi, C. Placement Strategies and Cumulative Effects of Wet-weather Control Practices for Intermunicipal Sewerage Systems. Water Resour. Manag. 2018, 32, 2885–2900. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Peres, D.J.; Cancelliere, A.; Foti, E. A combined triggering-propagation modeling approach for the assessment of rainfall induced debris flow susceptibility. J. Hydrol. 2017, 550, 130–143. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A FORTRAN Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; U.S. Geological Survey: Reston, VA, USA, 2008.
- O’Brien, J. Flo-2d User’s Manual, version 2006.01; flo-2d Software. Inc.: Nutrioso, AZ, USA, 2006. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Pastor, M.; Haddad, B.; Sorbino, G.; Cuomo, S.; Drempetic, V. A depth-integrated, coupled SPH model for flow-like landslides and related phenomena. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 143–172. [Google Scholar] [CrossRef]
- Pastor, M.; Quecedo, M.; González, E.; Herreros, I.; Merodo, J.A.F.; Mira, P. A simple approximation to bottom friction for Bingham fluid depth integrated models. J. Hydraul. Eng. 2004, 130, 149–155. [Google Scholar] [CrossRef]
- Rendina, I.; Viccione, G.; Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dyn. 2019, 33, 107–123. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y.M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Albano, R.; Craciun, I.; Mancusi, L.; Sole, A.; Ozunu, A. Flood damage assessment and uncertainity analysis: the case study of 2006 flood in Ilisua Basin in Romania. Carpath. J. Earth. Environ. Sci. 2017, 2, 12. [Google Scholar]
- Di Risio, M.; Bellotti, G.; Panizzo, A.; de Girolamo, P. Three-dimensional experiments on landslide generated waves at a sloping coast. Coast. Eng. 2009, 56, 659–671. [Google Scholar] [CrossRef]
- Panizzo, A.; de Girolamo, P.; di Risio, M.; Maistri, A.; Petaccia, A. Great landslide events in Italian artificial reservoirs. Nat. Hazards Earth Syst. Sci. 2005, 5, 733–740. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.E. Lituya Bay case: Rockslide impact and wave run-up. Sci. Tsunami Hazards 2001, 19, 3–22. [Google Scholar]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Heinrich, P. Nonlinear water waves generated by submarine and aerial landslides. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 249–266. [Google Scholar] [CrossRef]
- Xu, W.J.; Dong, X.Y.; Ding, W.T. Analysis of fluid-particle interaction in granular materials using coupled SPH-DEM method. Powder Technol. 2019, 353, 459–472. [Google Scholar] [CrossRef]
- Canelas, R.B.; Dominiguez, J.M.; Crespo, A.J.C.; Gomez-Gesteira, M.; Ferreira, R.M.L. Resolved Simulation of a granular-fluid flow with a coupled SPH-DCDEM model. J. Hydraul. Eng. 2017, 143, 6017012. [Google Scholar] [CrossRef]
- Zago, V.; Bilotta, G.; Hérault, A.; Dalrymple, R.A.; Fortuna, L.; Cappello, A.; Ganci, G.; del Negro, C. Semi-implicit 3D SPH on GPU for lava flows. J. Comp. Phys. 2018, 375, 854–870. [Google Scholar] [CrossRef]
- Manenti, S.; Pierobon, E.; Gallati, M.; Sibilla, S.; D’Alpaos, L.; Macchi, E.; Todeschini, S. Vajont Disaster: Smoothed Particle Hydrodynamics Modeling of the Postevent 2D Experiments. J. Hydraul. Eng. 2016, 142, 5015007. [Google Scholar] [CrossRef]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v.9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2019. submitted. [Google Scholar]
- SPHERA v.9.0.0 (RSE SpA). Available online: https://github.com/AndreaAmicarelliRSE/SPHERA (accessed on 21 February 2019).
- Aristodemo, F.; Merignolo, D.D.; Groenenboom, P.; Schiavo, A.L.; Veltri, P.; Veltri, M. Assessment of Dynamic Pressures at Vertical and Perforated Breakwaters through Diffusive SPH Schemes. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Chauchat, J.; Médale, M. A three-dimensional numerical model for incompressible two-phase flow of a granular bed submitted to a laminar shearing flow. Comput. Methods Appl. Mech. Eng. 2010, 199, 439–449. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Capart, H.; Zech, Y. A Godunov method for the computation of erosional shallow water transients. Int. J. Numer. Meth. Fluids 2003, 41, 951–976. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Zech, Y. Experimental study of dam-break flow against an isolated obstacle. J. Hydraul. Res. 2007, 45 (Suppl. 1), 27–36. [Google Scholar] [CrossRef]
- Lin, P.; Wu, Y.; Bai, J.; Lin, Q. A numerical study of dam-break flow and sediment transport from a quake lake. J. Earthq. Tsunami 2011, 5, 401–428. [Google Scholar] [CrossRef]
- Wu, W.; Jiang, E.; China, P.R.; Wang, S.S. Depth-averaged 2-D calculation of flow and sediment transport in the lower Yellow River. Int. J. River Basin Manag. 2004, 2, 51–59. [Google Scholar] [CrossRef]
- Armstrong, L.; Gu, S.; Luo, K. Study of wall-to-bed heat transfer in a bubbling fluidised bed using the kinetic theory of granular flow. Int. J. Heat Mass Transf. 2010, 53, 4949–4959. [Google Scholar] [CrossRef]
- GDAL (OSGEO). Available online: https://github.com/OSGeo/gdal (accessed on 16 April 2019).
- DEM2xyz (RSE SpA). Available online: https://github.com/AndreaAmicarelliRSE/DEM2xyz (accessed on 16 April 2019).
- Paraview (Kitware). Available online: https://github.com/Kitware/ParaView (accessed on 16 April 2019).
- Grid Interpolator (RSE SpA). Available online: https://github.com/AndreaAmicarelliRSE/Grid_Interpolator (accessed on 16 April 2019).
- SRTM3/DTED1 (USGS). Available online: http://earthexplorer.usgs.gov/ (accessed on 16 April 2019).
- Baker, M.; Buyya, R. Cluster Computing at a Glance. In High Performance Cluster Computing—Architectures and Systems; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999; pp. 3–47. [Google Scholar]
- Nickolls, J.; Buck, I.; Garland, M.; Skadron, K. Scalable Parallel Programming with CUDA. Queue GPU Comput. 2008, 6, 40–53. [Google Scholar] [CrossRef]
- Nickolls, J.; Dally, W.J. The GPU computing era. IEEE Micro 2010, 30, 56–69. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Ann. Rev. Astronom. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving Particle Semi-Implicit Method for Fragmentation of Incompressible Fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Viccione, G.; Bovolin, V.; Carratelli, E.P. Defining and optimizing algorithms for neighbouring particle identification in SPH fluid simulations. Int. J. Numer. Methods Fluids 2008, 58, 625–638. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M.; Marongiu, J.C. Neighbour lists in smoothed particle hydrodynamics. Int. J. Numer. Methods Fluids 2011, 67, 2026–2042. [Google Scholar] [CrossRef]
- Winkler, D.; Rezavand, M.; Rauch, W. Neighbour lists for smoothed particle hydrodynamics on GPUs. Comput. Phys. Commun. 2018, 225, 140–148. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, Y.; Shao, S. Efficient Implementation of Smoothed Particle Hydrodynamics (SPH) with Plane Sweep Algorithm. Commun. Comput. Phys. 2016, 19, 770–800. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q. A GPU-accelerated smoothed particle hydrodynamics (SPH) model for the shallow water equations. Environ. Model. Softw. 2016, 75, 28–43. [Google Scholar] [CrossRef]
- Gonnet, P. Efficient and Scalable Algorithms for Smoothed Particle Hydrodynamics on Hybrid Shared/Distributed-Memory Architectures. SIAM J. Sci. Comput. 2014, 37, C95–C121. [Google Scholar] [CrossRef]
- Joselli, M.; Junior, J.R.d.; Clua, E.W.; Montenegro, A.; Lage, M.; Pagliosa, P. Neighborhood grid: A novel data structure for fluids animation with GPU computing. J. Parallel Distrib. Comput. 2015, 75, 20–28. [Google Scholar] [CrossRef]
- Wenbo, C.; Yao, Y.; Zhang, Y. Performance analysis of parallel smoothed particle hydrodynamics on multi-core CPUs. In Proceedings of the 2014 International Conference on Cloud Computing and Internet of Things, Changchun, China, 13–14 December 201.
- Nishiura, D.; Furuichi, M.; Sakaguchi, H. Computational performance of a smoothed particle hydrodynamics simulation for shared-memory parallel computing. Comput. Phys. Commun. 2015, 194, 18–32. [Google Scholar] [CrossRef]
- Ferrari, A.; Dumbser, M.; Toro, E.F.; Armanini, A. A new 3D parallel SPH scheme for free surface flows. Comput. Fluids 2009, 38, 1203–1217. [Google Scholar] [CrossRef]
- Cherfils, J.M.; Pinon, G.; Rivoalen, E. JOSEPHINE: A parallel SPH code for free-surface flows. Comput. Phys. Commun. 2012, 183, 1468–1480. [Google Scholar] [CrossRef]
- Oger, G.; Le Touzé, D.; Guibert, D.; De Leffe, M.; Biddiscombe, J.; Soumagne, J.; Piccinali, J.-G. On distributed memory MPI-based parallelization of SPH codes in massive HPC context. Comput. Phys. Commun. 2016, 200, 1–14. [Google Scholar] [CrossRef]
- Egorova, M.S.; Dyachkov, S.A.; Parshikov, A.N.; Zhakhovsky, V.V. Parallel SPH modeling using dynamic domain decomposition and load balancing displacement of Voronoi subdomains. Comput. Phys. Commun. 2019, 234, 112–125. [Google Scholar] [CrossRef]
- Yeylaghi, S.; Moa, B.; Oshkai, P.; Buckham, B.; Crawford, C. ISPH modeling for hydrodynamic applications using a new MPI-based parallel approach. J. Ocean Eng. Mar. Energy 2017, 3, 35–50. [Google Scholar] [CrossRef]
- Guo, X.; Rogers, B.D.; Lind, S.; Stansby, P.K. New massively parallel scheme for Incompressible Smoothed Particle Hydrodynamics (ISPH) for highly nonlinear and distorted flow. Comput. Phys. Commun. 2018, 233, 16–28. [Google Scholar] [CrossRef]
- Fleissner, F.; Eberhard, P. Parallel load-balanced simulation for short-range interaction particle methods with hierarchical particle grouping based on orthogonal recursive bisection. Int. J. Numer. Methods Eng. 2008, 74, 531–553. [Google Scholar] [CrossRef]
- Harada, T.; Koshizuka, S.; Kawaguchi, Y. Smoothed particle hydrodynamics on GPUs. In Proceedings of the Computer Graphics International Conference, Petròpolis, Brazil, 30 March 2007; pp. 63–70. Available online: https://pdfs.semanticscholar.org/a132/6b93316e7ce4d2580bd5e3928ce6ff24e386.pdf (accessed on 21 February 2019).
- Crespo, A.C.; Dominguez, J.M.; Barreiro, A.; Gómez-Gesteira, M.; Rogers, B.D. GPUs, a new tool of acceleration in CFD: Efficiency and reliability on smoothed particle hydrodynamics methods. PLoS ONE 2011, 6, e20685. [Google Scholar] [CrossRef] [PubMed]
- Hérault, A.; Bilotta, G.; Vicari, A.; Rustico, E.; del Negro, C. Numerical simulation of lava flow using a GPU SPH model. Ann. Geophys. 2011, 54. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K.; Domínguez, J.M. Multi-phase SPH modeling of violent hydrodynamics on GPUs. Comput. Phys. Commun. 2015, 196, 304–316. [Google Scholar] [CrossRef]
- Winkler, D.; Meister, M.; Rezavand, M.; Rauch, W. gpuSPHASE—A shared memory caching implementation for 2D SPH using CUDA. Comput. Phys. Commun. 2017, 213, 165–180. [Google Scholar] [CrossRef]
- Cercos-Pita, J.L. AQUAgpusph, a new free 3D SPH solver accelerated with OpenCL. Comput. Phys. Commun. 2015, 192, 295–312. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Qiu, L.C. OpenCL-Based GPU Acceleration of ISPH Simulation for Incompressible Flows. Appl. Mech. Mater. 2014, 444, 380–384. [Google Scholar] [CrossRef]
- Nie, X.; Chen, L.; Xiang, T. Real-Time Incompressible Fluid Simulation on the GPU. Int. J. Comput. Games Technol. 2015, 2015, 417417. [Google Scholar] [CrossRef]
- Chow, A.D.; Rogers, B.D.; Lind, S.J.; Stansby, P.K. Incompressible SPH (ISPH) with fast Poisson solver on a GPU. Comput. Phys. Commun. 2018, 226, 81–103. [Google Scholar] [CrossRef]
- Hori, C.; Gotoh, H.; Ikari, H.; Khayyer, A. GPU-acceleration for Moving Particle Semi-Implicit method. Comput. Fluids 2011, 51, 174–183. [Google Scholar] [CrossRef]
- Kakuda, K.; Nagashima, T.; Hayashi, Y.; Obara, S.; Toyotani, J.; Miura, S. Three-dimensional fluid flow simulations using GPU-based particle method. Comput. Model. Eng. Sci. 2013, 95, 363–376. [Google Scholar]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Sætra, M.L.; Altinakar, M. Efficient shallow water simulations on GPUs: Implementation, visualization, verification, and validation. Comput. Fluids 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Vacondio, R.; Palù, A.D.; Mignosa, P. GPU-enhanced finite volume shallow water solver for fast flood simulations. Environ. Model. Softw. 2014, 57, 60–75. [Google Scholar] [CrossRef]
- García-Feal, O.; González-Cao, J.; Gómez-Gesteira, M.; Cea, L.; Domínguez, J.M.; Formella, A. An accelerated tool for flood modeling based on Iber. Water 2018, 10, 1459. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Li, G. Fast simulation of large-scale floods based on GPU parallel computing. Water 2018, 10, 589. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Metod. Numer. Calc. Disen. Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Wolfe, M.; Lee, S.; Kim, J.; Tian, X.; Xu, R.; Chapman, B.; Chandrasekaran, S. The OpenACC data model: Preliminary study on its major challenges and implementations. Parallel Comput. 2018, 78, 15–27. [Google Scholar] [CrossRef]
- Hérault, A.; Zhang, H.; Dalrymple, R.A.; Yang, R.; Wu, J. Numerical modeling of dam-break flood through intricate city layouts including underground spaces using GPU-based SPH method. J. Hydrodyn. 2014, 25, 818–828. [Google Scholar]
- Liang, Q.; Xia, X.; Hou, J. Efficient urban flood simulation using a GPU-accelerated SPH model. Environ. Earth Sci. 2015, 74, 7285–7294. [Google Scholar] [CrossRef]
- Dickson, N.G.; Karimi, K.; Hamze, F. Importance of explicit vectorization for CPU and GPU software performance. J. Comput. Phys. 2011, 230, 5383–5398. [Google Scholar] [CrossRef][Green Version]
- Lee, V.W.; Kim, C.; Chhugani, J.; Deisher, M. Debunking the 100X GPU vs. CPU Myth: An Evaluation of Throughput Computing on CPU and GPU. ACM SIGARCH Comput. Arch. News 2010, 38, 451–460. [Google Scholar] [CrossRef]
- Valdez-Balderas, D.; Domínguez, J.M.; Rogers, B.D.; Crespo, A.J.C. Towards accelerating smoothed particle hydrodynamics simulations for free-surface flows on multi-GPU clusters. J. Parallel Distrib. Comput. 2013, 73, 1483–1493. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Valdez-Balderas, D.; Rogers, B.D.; Gómez-Gesteira, M. New multi-GPU implementation for smoothed particle hydrodynamics on heterogeneous clusters. Comput. Phys. Commun. 2013, 184, 1848–1860. [Google Scholar] [CrossRef]
- Rustico, E.; Bilotta, G.; Herault, A.; del Negro, C.; Gallo, G. Advances in multi-GPU smoothed particle hydrodynamics simulations. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 43–52. [Google Scholar] [CrossRef]
- Ji, Z.; Xu, F.; Takahashi, A.; Sun, Y. Large scale water entry simulation with smoothed particle hydrodynamics on single- and multi-GPU systems. Comput. Phys. Commun. 2016, 209, 1–12. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manenti, S.; Wang, D.; Domínguez, J.M.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. https://doi.org/10.3390/w11091875
Manenti S, Wang D, Domínguez JM, Li S, Amicarelli A, Albano R. SPH Modeling of Water-Related Natural Hazards. Water. 2019; 11(9):1875. https://doi.org/10.3390/w11091875
Chicago/Turabian StyleManenti, Sauro, Dong Wang, José M. Domínguez, Shaowu Li, Andrea Amicarelli, and Raffaele Albano. 2019. "SPH Modeling of Water-Related Natural Hazards" Water 11, no. 9: 1875. https://doi.org/10.3390/w11091875
APA StyleManenti, S., Wang, D., Domínguez, J. M., Li, S., Amicarelli, A., & Albano, R. (2019). SPH Modeling of Water-Related Natural Hazards. Water, 11(9), 1875. https://doi.org/10.3390/w11091875






