Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: a Numerical and Experimental Analysis
Abstract
1. Introduction
2. Mathematical Model
2.1. Assumptions
- The filling water column is modeled using a rigid column model.
- The air–water interface is considered perpendicular to the main direction of a single pipeline.
- The friction factor is constant over the transient event.
- A polytropic model describes the air phase.
2.2. Formulations
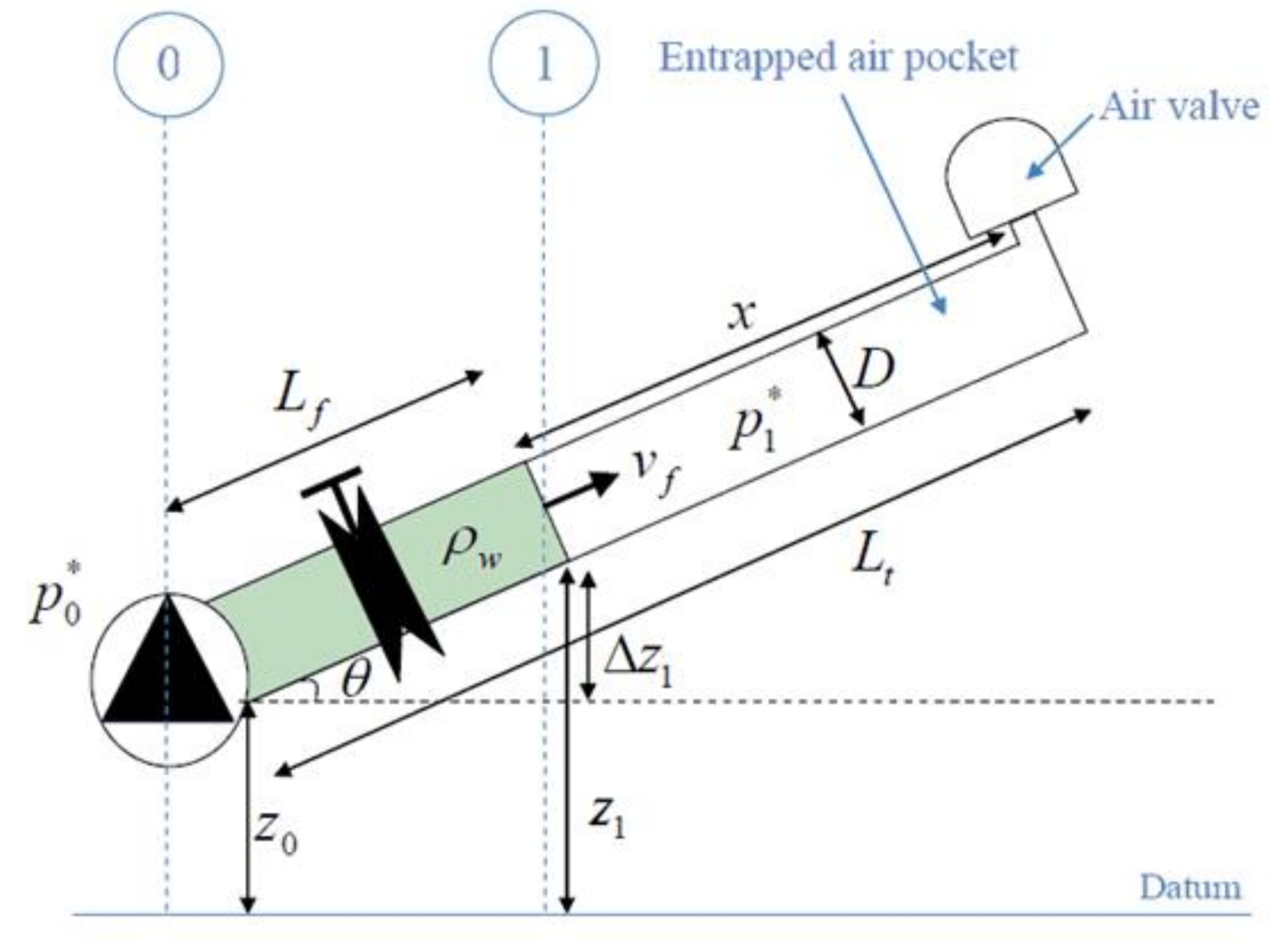
- This equation represents the water movement adequately since in transient flows with trapped air, the compressibility of the air is much higher compared to the water and pipe system:where = water velocity, = initial pressure supplied by tank or pump, = air pocket pressure, = length of the filling column, = time, = internal pipe diameter, = resistance coefficient of the regulating valve, = friction factor, = water density, = gravity acceleration, = difference elevation, and = cross-sectional area. The relation (named as gravity term) is calculated for single pipelines as , where represents the pipe slope.
- A piston flow model is considered to represent the interface position, which is applicable in inclined piping installations:
- The polytropic model of the air phase [30]:This formulation shows the evolution of the air pocket pressure over time by relating the compression of an air pocket ) to the quantity of the expelled air by an air valve ():where = polytropic coefficient, = air pocket volume, = air density, and = air pocket mass.
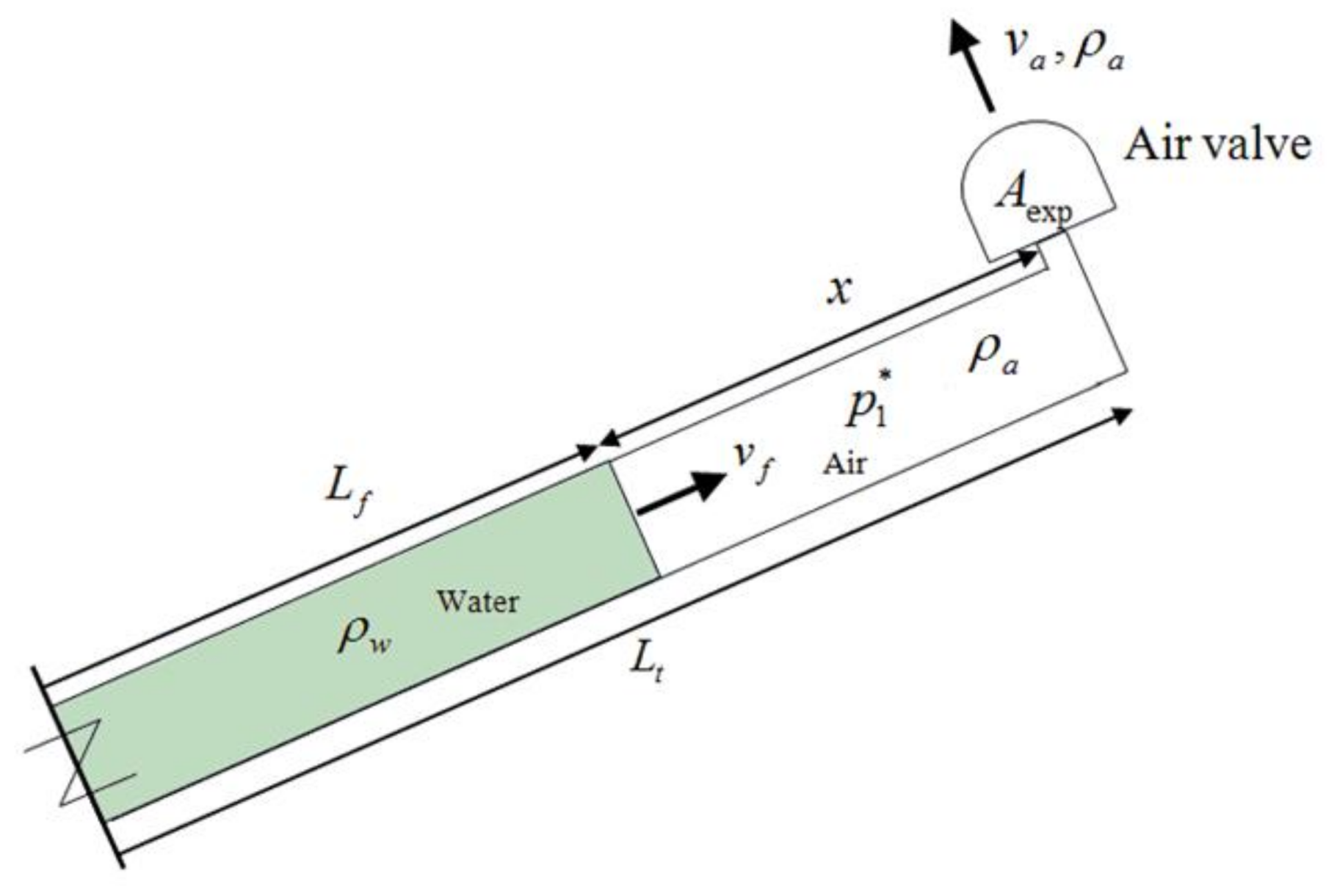
- The air mass equation [28]:where = cross-sectional area of an air valve for expelling conditions, and = air velocity.Here the air pocket density () inside of a pipe system is identical to the air density expelled by an air valve and considering , thus:Based on the variables and parameters shown in Figure 2, then:where = air pocket size, and = total length of the pipe.And deriving the Formulation (6), then:Plugging Formulations (6) and (7) into (5), then:
- The air valve characterization:Subsonic conditions are required to perform an adequate filling process according to recommendations given by the American Water Works Association (AWWA) [32], thus:where = atmospheric pressure, = outflow discharge coefficient, = air constant, and = air temperature.
2.3. System Equations and Resolution
2.4. Initial and Boundary Conditions
3. Numerical Validation
3.1. Experimental Facility and Instrumentation
3.2. Experimental Test
3.3. Model Verification
3.4. Comparisons Without Air Valve
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Cross-sectional area of pipe (m2) | |
| Cross-sectional area of outlet orifice in an air valve (m2) | |
| Outflow discharge coefficient an air valve (−) | |
| Internal pipe diameter (m) | |
| Friction factor (−) | |
| Polytropic coefficient (−) | |
| Gravity acceleration (m/s2) | |
| Length of the filling column (m) | |
| Total length of pipe (m) | |
| Air mass (kg) | |
| Atmospheric pressure (Pa) | |
| Absolute pressure supplied by an energy source (Pa) | |
| Air pocket pressure (Pa) | |
| Gas constant (287 J/kg/ K) | |
| Resistance coefficient of the regulating valve (m s2/m6) | |
| Air temperature ( K) | |
| Time (s) | |
| Peak time (s) | |
| Air volume (m3) | |
| Air velocity (m/s) | |
| Water velocity (m/s) | |
| Air pocket size (m) | |
| Difference elevation (m) | |
| Air density (kg/m3) | |
| Water density (kg/m3) | |
| BV | Electro-pneumatic ball valve |
| HT | Hydro-pneumatic tank |
References
- Abreu, J.; Cabrera, E.; Izquierdo, J.; García-Serra, J. Flow Modeling in Pressurized Systems Revisited. J. Hydraul. Eng. 1999, 125, 1154–1169. [Google Scholar] [CrossRef]
- Azoury, P.H.; Baasiri, M.; Najm, H. Effect of Valve-Closure Schedule on Water Hammer. J. Hydraul. Eng. 1986, 112, 890–903. [Google Scholar] [CrossRef]
- Himr, D. Investigation and Numerical Simulation of a Water Hammer with Column Separation. J. Hydraul. Eng. 2015, 141, 04014080. [Google Scholar] [CrossRef]
- Simpson, A.R.; Wylie, E.B. Large Water-Hammer Pressures for Column Separation in Pipelines. J. Hydraul. Eng. 1991, 117, 1310–1316. [Google Scholar] [CrossRef]
- Saemi, S.; Raisee, M.; Cervantes, M.J.; Nourbakhsh, A. Computation of two- and three-dimensional water hammer flows. J. Hydraul. Res. 2019, 57, 386–404. [Google Scholar] [CrossRef]
- Karney, B.W.; Simpson, A.R. In-line check valves for water hammer control. J. Hydraul. Res. 2007, 45, 547–554. [Google Scholar] [CrossRef]
- Triki, A. Water-Hammer Control in Pressurized-Pipe Flow Using a Branched Polymeric Penstock. J. Pipeline Syst. Eng. Pract. 2017, 8, 04017024. [Google Scholar] [CrossRef]
- Triki, A.; Fersi, M. Further investigation on the water-hammer control branching strategy in pressurized steel-piping systems. Int. J. Press. Vessel. Pip. 2018, 165, 135–144. [Google Scholar] [CrossRef]
- Stephenson, D. Simple Guide for Design of Air Vessels for Water Hammer Protection of Pumping Lines. J. Hydraul. Eng. 2002, 128, 792–797. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Ramos, H.M. The Effect of Water Hammer on a Confined Air Pocket Towards Flow Energy Storage System. J. Water Supply: Res. Technol.-AQUA. 2016, 65, 116–126. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Aalami, M.T.; Ramos, H.M. Study of a Compressed Air Vessel for Controlling the Pressure Surge in Water Networks: CFD and Experimental Analysis. Water Resour. Manag. 2016, 30, 2687–2702. [Google Scholar] [CrossRef]
- Besharat, M.; Viseu, M.T.; Ramos, H.M. Experimental Study of Air Vessel Sizing to either Store Energy or Protect the System in the Water Hammer Occurrence. Water 2017, 9, 63. [Google Scholar] [CrossRef]
- Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučkovič, S.; Hou, Q.; van’t Westende, J.M.C. Emptying of Large-Scale Pipeline by Pressurized Air. J. Hydraul. Eng. 2012, 138, 1090–1100. [Google Scholar] [CrossRef]
- Tijsseling, A.; Hou, Q.; Bozkus, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Backflow Air and Pressure Analysis in Emptying Pipeline Containing Entrapped Air Pocket. Urban Water J. 2018, 15, 769–779. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric Pressure in a Water Draining Pipeline with an Air Pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Computational Fluid Dynamics for Sub-Atmospheric Pressure Analysis in Pipe Drainage. J. Hydraul. Res. 2019, 1–13. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Wright, S.J. Rapid Flow Startup in Filled Horizontal Pipelines. J. Hydraul. Eng. 2008, 134, 984–992. [Google Scholar] [CrossRef]
- Trindade, B.C.; Vasconcelos, J.G. Modeling of Water Pipeline Filling Events Accounting for Air Phase Interactions. J. Hydraul. Eng. 2013, 139, 921–934. [Google Scholar] [CrossRef]
- Malekpour, A.; Karney, B.; Nault, J. Physical understanding of sudden pressurization of pipe systems with entrapped air: Energy auditing approach. J. Hydraul. Eng. 2015, 142, 04015044. [Google Scholar] [CrossRef]
- Apollonio, C.; Balacco, G.; Fontana, N.; Giugni, M.; Marini, G.; Piccinni, A.F. Hydraulic Transients Caused by Air Expulsion during Rapid Filling of Undulating Pipelines. Water 2016, 8, 25. [Google Scholar] [CrossRef]
- Wang, L.; Wang, F.; Karney, B.; Malekpour, A. Numerical Investigation of Rapid Filling in Bypass Pipelines. J. Hydraul. Res. 2017, 55, 647–656. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. CFD and 1D Simulation of Transient Flow Effect on Air Vessel. In Proceedings of the 13th International Conference on Pressure Surges, Bordeaux, France, 14–16 November 2018; BHR Group: Bordeaux, France, 2018. [Google Scholar]
- Ramezani, L.; Karney, B.; Malekpour, A. The Challenge of Air Valves: A Selective Critical Literature Review. J. Water Resour. Plan. Manag. 2016, 141, 04015017. [Google Scholar] [CrossRef]
- Balacco, G.; Apollonio, C.; Piccinni, A.F. Experimental Analysis of Air Valve Behaviour During Hydraulic Transients. J. Appl. Water Eng. Res. 2015, 3, 3–11. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Iglesias-Rey, P.L.; Mora-Melia, D. Transient Phenomena during the Emptying Process of a Single Pipe with Water-Air Interaction. J. Hydraul. Res. 2019, 57, 318–326. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Experimental and Numerical Analysis of a Water Emptying Pipeline Using Different Air Valves. Water 2017, 9, 98. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. A Parametric Sensitivity Analysis of Numerically Modelled Piston-Type Filling and Emptying of an Inclined Pipeline with an Air Valve. In Proceedings of the 13th International Conference on Pressure Surges, Bordeaux, France, 14–16 November 2018; BHR Group: Bordeaux, France, 2018. [Google Scholar]
- American Water Works Association (AWWA). Manual of Water Supply Practices-M51: Air-Release, Air-Vacuum, and Combination Air Valves, 1st ed.; American Water Works Association: Denver, CO, USA, 2001. [Google Scholar]






| Test No. | (bar) | 1 (Pa) | |
|---|---|---|---|
| 1 | 0.20 | 120060 | 0.96 |
| 2 | 0.20 | 120060 | 1.36 |
| 3 | 0.50 | 150075 | 0.96 |
| 4 | 0.50 | 150075 | 1.36 |
| 5 | 0.75 | 175087 | 0.96 |
| 6 | 0.75 | 175087 | 1.36 |
| 7 | 1.25 | 225112 | 0.96 |
| 8 | 1.25 | 225112 | 1.36 |
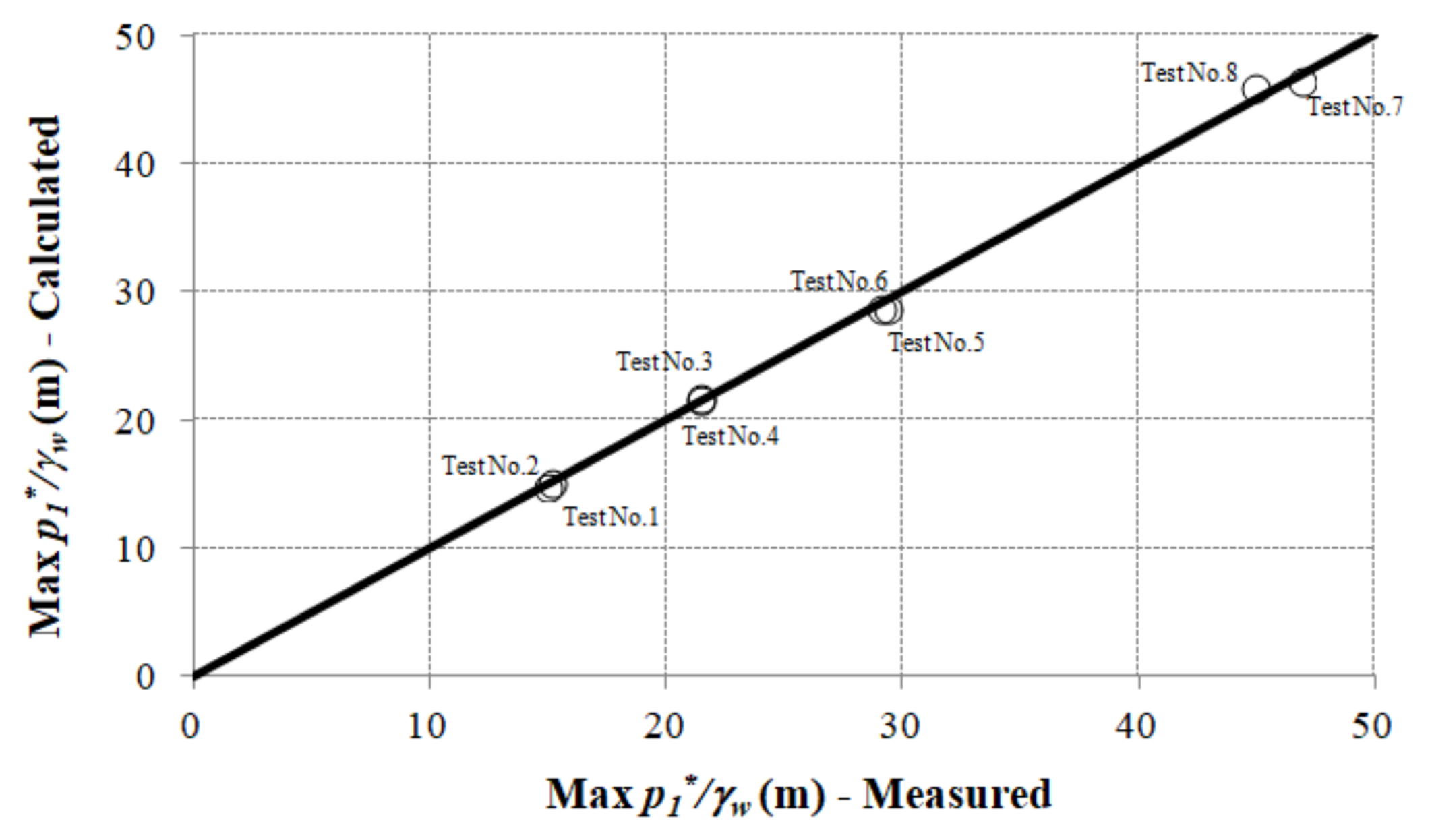
| Test No. | Maximum Value of Air Pocket Pressure Head (m) | tpeak (s) | |
|---|---|---|---|
| 1 | 15.0 | 0.96 | 0.55 |
| 2 | 15.0 | 1.36 | 0.58 |
| 3 | 21.4 | 0.96 | 0.50 |
| 4 | 21.4 | 1.36 | 0.52 |
| 5 | 29.3 | 0.96 | 0.46 |
| 6 | 29.1 | 1.36 | 0.49 |
| 7 | 46.9 | 0.96 | 0.40 |
| 8 | 44.9 | 1.36 | 0.44 |
| Test No. | Air Pocket Pressure Head (M) | Peak Reduction Percentage (%) | |
|---|---|---|---|
| Without Air Vale | Using the Air Valve S050 | ||
| 1 | 15.9 | 15.0 | 5 |
| 2 | 16.0 | 15.0 | 6 |
| 3 | 23.6 | 21.4 | 9 |
| 4 | 23.1 | 21.4 | 7 |
| 5 | 32.2 | 29.3 | 9 |
| 6 | 31.4 | 29.1 | 7 |
| 7 | 51.1 | 46.9 | 8 |
| 8 | 47.4 | 44.9 | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Hernández, Ó.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: a Numerical and Experimental Analysis. Water 2019, 11, 1814. https://doi.org/10.3390/w11091814
Coronado-Hernández ÓE, Besharat M, Fuertes-Miquel VS, Ramos HM. Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: a Numerical and Experimental Analysis. Water. 2019; 11(9):1814. https://doi.org/10.3390/w11091814
Chicago/Turabian StyleCoronado-Hernández, Óscar E., Mohsen Besharat, Vicente S. Fuertes-Miquel, and Helena M. Ramos. 2019. "Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: a Numerical and Experimental Analysis" Water 11, no. 9: 1814. https://doi.org/10.3390/w11091814
APA StyleCoronado-Hernández, Ó. E., Besharat, M., Fuertes-Miquel, V. S., & Ramos, H. M. (2019). Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: a Numerical and Experimental Analysis. Water, 11(9), 1814. https://doi.org/10.3390/w11091814








