Physical Parameterization of IDF Curves Based on Short-Duration Storms
Abstract
1. Introduction
2. Materials and Methods
2.1. Sherman Parameterization
- rainfall intensity, in mm/h
- T return period, in years
- d storm duration, in minutes
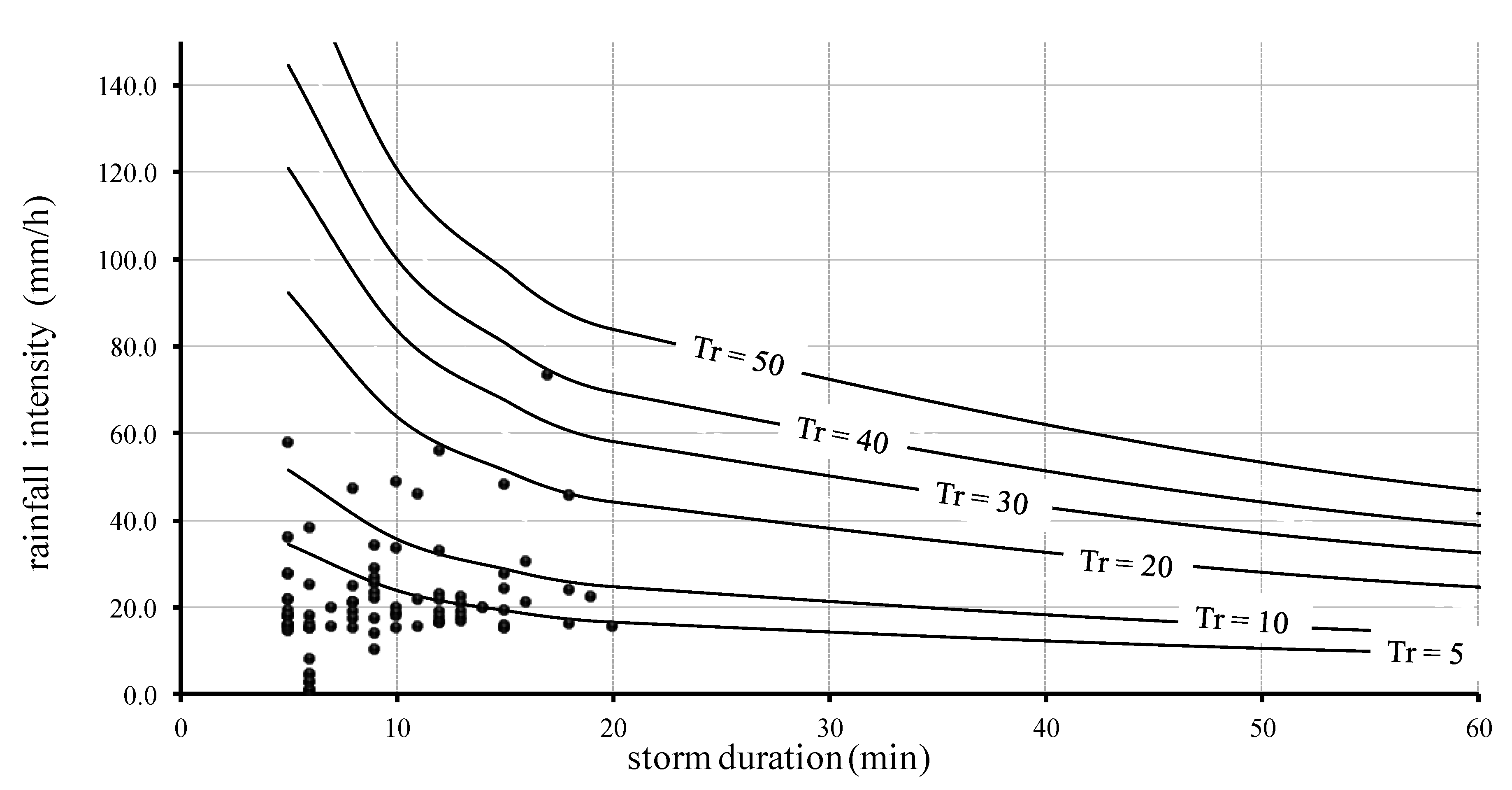
“The Montana curve showed significant deviations at the lower time scales (for durations from 0 to 10 min), although giving a good representation of the decay of expected maximum rainfall intensities for larger durations (see Figure 1). The limitation of this formula is obvious, since it estimates rainfall intensities tending to infinity when time approaches to 0, and therefore a resulting overestimation of rainfall intensities for low t values”[22], p. 676.
2.2. Traditional Methodologies for Estimating IDF Curves
2.3. Proposed Methodologies for Estimating IDF Curves
2.4. Queretaro Hydrometeorological Network
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Shrestha, A.; Babel, M.; Weesakul, S.; Vojinovic, Z. Developing Intensity–Duration–Frequency (IDF) Curves under Climate Change Uncertainty: The Case of Bangkok, Thailand. Water 2017, 9, 145. [Google Scholar] [CrossRef]
- Hershfield, D. Extreme rainfall relationships. ASCE J. Hydraul. Div. 1962, 88, 73–92. [Google Scholar]
- Vivekanandan, N. Analysis of hourly rainfall data for the development of IDF relationships using the order statistics approach of probability distributions. Int. J. Manag. Sci. Eng. Manag. 2013, 8, 283–291. [Google Scholar] [CrossRef]
- Dunkerley, D. Identifying individual rain events from pluviograph records: A review with analysis of data from an Australian dryland site. Hydrol. Process. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
- Dunkerley, D. Rain event properties in nature and in rainfall simulation experiments: A comparative review with recommendations for increasingly systematic study and reporting. Hydrol. Process. 2008, 22, 4415–4435. [Google Scholar] [CrossRef]
- Dunkerley, D. How do the rain rates of sub-event intervals such as the maximum 5- and 15-min rates (I5orI30) relate to the properties of the enclosing rainfall event? Hydrol. Process. 2010, 24, 2425–2439. [Google Scholar] [CrossRef]
- Van de Vyver, H. A multiscaling-based intensity–duration–frequency model for extreme precipitation. Hydrol. Process. 2018, 32, 1635–1647. [Google Scholar] [CrossRef]
- Hosseinzadehtalaei, P.; Tabari, H.; Willems, P. Precipitation intensity–duration–frequency curves for central Belgium with an ensemble of EURO-CORDEX simulations, and associated uncertainties. Atmos. Res. 2018, 200, 1–12. [Google Scholar] [CrossRef]
- Adamowski, K.; Bougadis, J. Detection of trends in annual extreme rainfall. Hydrol. Process. 2003, 17, 3547–3560. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K. Scaling model of a rainfall intensity–duration–frequency relationship. Hydrol. Process. 2006, 20, 3747–3757. [Google Scholar] [CrossRef]
- Cunderlik, J.; Ouarda, T. Regional flood–rainfall duration-frequency modeling at small ungaged sites. J. Hydrol. 2007, 345, 61–69. [Google Scholar] [CrossRef]
- Adamowski, J.; Adamowski, K.; Bougadis, J. Influence of trend on short duration design storms. Water Resour. Manag. 2009, 24, 401–413. [Google Scholar] [CrossRef]
- Burn, D.; Taleghani, A. Estimates of changes in design rainfall values for Canada. Hydrol. Process. 2013, 27, 1590–1599. [Google Scholar] [CrossRef]
- Burn, D. A framework for regional estimation of intensity–duration–frequency (IDF) curves. Hydrol. Process. 2014, 28, 4209–4218. [Google Scholar] [CrossRef]
- Soulis, E.; Sarhadi, A.; Tinel, M.; Suthar, M. Extreme precipitation time trends in Ontario, 1960–2010. Hydrol. Process. 2016, 30, 4090–4100. [Google Scholar] [CrossRef]
- Harremoës, P.; Mikkelsen, P. Properties of extreme point rainfall I: Results from a rain gauge system in Denmark. Atmos. Res. 1995, 37, 277–286. [Google Scholar] [CrossRef]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P. Update of regional intensity–duration–frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- Olsson, J.; Niemczynowicz, J.; Berndtsson, R.; Larson, M. An analysis of the rainfall time structure by box counting—Some practical implications. J. Hydrol. (Amst.) 1992, 137, 261–277. [Google Scholar] [CrossRef]
- Bengtsson, L.; Milloti, S. Extreme storms in Malmö, Sweden. Hydrol. Process. 2010, 24, 3462–3475. [Google Scholar] [CrossRef]
- Olsson, J.; Willen, U.; Kawamura, A. Downscaling extreme short-term regional climate model precipitation for urban hydrological applications. Hydrol. Res. 2012, 43, 341–351. [Google Scholar] [CrossRef]
- Garcia-Bartual, R.; Schneider, M. Estimating Maximum Expected Short-Duration Rainfall Intensities from Extreme Convective Storms. Phys. Chem. Earth Part B 2001, 26, 675–681. [Google Scholar] [CrossRef]
- Salas, L.; Fernandez, J. “In-site” regionalization to estimate an intensity—Duration—Frequency law: A solution to scarce spatial data in Spain. Hydrol. Process. 2007, 21, 3507–3513. [Google Scholar] [CrossRef]
- Garcia-Marin, A.; Ayuso-Muñoz, J.; Jimenez-Hornero, F.; Estevez, J. Selecting the best IDF model by using the multifractal approach. Hydrol. Process. 2012, 27, 433–443. [Google Scholar] [CrossRef]
- Yu, P.; Chen, C. Potential of extending the rainfall intensity–duration–frequency relationship to non-recording rain gauges. Hydrol. Process. 1997, 11, 377–390. [Google Scholar] [CrossRef]
- Yu, P.; Cheng, C. Incorporating uncertainty analysis into a regional IDF formula. Hydrol. Process. 1998, 12, 713–726. [Google Scholar] [CrossRef]
- Lee, K.; Ho, J. Design Hyetograph for Typhoon Rainstorms in Taiwan. J. Hydrol. Eng. 2008, 13, 647–651. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H. Extending the Rational Method for assessing and developing sustainable urban drainage systems. Water Res. 2018, 144, 112–125. [Google Scholar] [CrossRef]
- Chang, K.; Lai, S.; Faridah, O. RainIDF: Automated derivation of rainfall intensity–duration–frequency relationship from annual maxima and partial duration series. J. Hydroinform. 2013, 15, 1224–1233. [Google Scholar] [CrossRef][Green Version]
- Liew, S.; Raghavan, S.; Liong, S. How to construct future IDF curves, under changing climate, for sites with scarce rainfall records? Hydrol. Process. 2013, 28, 3276–3287. [Google Scholar] [CrossRef]
- Knighton, J.; Walter, M. Critical rainfall statistics for predicting watershed flood responses: Rethinking the design storm concept. Hydrol. Process. 2016, 30, 3788–3803. [Google Scholar] [CrossRef]
- Pizarro, R.; Garcia-Chevesich, P.; Valdes, R.; Dominguez, F.; Hossain, F.; Folliott, P.; Olivares, C.; Morales, C.; Balocchi, F.; Bro, P. Inland water bodies in Chile can locally increase rainfall intensity. J. Hydrol. 2013, 481, 56–63. [Google Scholar] [CrossRef]
- Pizarro, R.; Aravena, D.; Macaya, K.; Abarza, A.; Cornejo, M.; Labra, M.; Pavez, M.; Roman, L. Curvas Intensidad-Duracion-Frecuencia Para la Zona Centro sur de Chile. Talca, Chile; Programa Hidrologico Internacional de UNESCO (PHI) para America Latina y el Caribe. PHI-VI/Documento Tecnico N° 7. Montevideo, Uruguay, 2007. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000228195 (accessed on 1 April 2019).
- Pizarro, R.; Valdes, R.; Garcia-Chevesich, P.; Vallejos, C.; Sangüesa, C.; Morales, C.; Balocchi, F.; Abarza, A.; Fuentes, R. Latitudinal Analysis of Rainfall Intensity and Mean Annual Precipitation in Chile. Chil. J. Agric. Res. 2012, 72, 252–261. [Google Scholar] [CrossRef]
- Puricelli, M. Rainfall extremes modeling under shortage of data and uncertainty in the Pampean region (Argentina). Cuad. Investig. Geogr. 2018, 44, 719. [Google Scholar] [CrossRef]
- Pizarro, R.; Sangüesa, C.; Bro, P.; Ingram, B.; Vera, M.; Vallejos, C.; Morales, C.; Olivares, C.; Balocchi, F.; Fuentes, R.; et al. Curvas Intensidad Duracion Frecuencia Para las Regiones Metropolitana, Maule y Biobio. Intensidades Desde 15 Minutos a 24 Horas; Programa Hidrologico Internacional de UNESCO (PHI) para America Latina y el Caribe. PHI-VII/Documento Tecnico N° 29; Universidad de Talca: Montevideo, Uruguay, 2013; 129p. [Google Scholar]
- Silveira, L.; Usera, G.; Alonso, J.; Scavone, M.; Chreties, C.; Perera, G.; Gonzalez, M. Nuevas curvas intensidad-duracion-frecuencia de precipitacion para el departamento de Montevideo, Uruguay. Agrociencia Urug. 2014, 18, 113–125. [Google Scholar]
- Pereyra-Diaz, D.; Perez-Sesma, J.; Gomez-Romero, L. Ecuaciones que estiman las curvas intensidad-duracion-periodo de retorno de la lluvia. GEOS 2004, 24, 46–56. [Google Scholar]
- Sherman, C.W. Frequency and Intensity of Excessive Rainfall at Boston, Mass. Trans. Am. Soc. Civil Eng. 1931, 95, 951–960. [Google Scholar]
- Bernard, M.M. Formulas for rainfall intensities of long durations. Trans. Am. Soc. Civil Eng. 1932, 96, 592–606. [Google Scholar]
- Chow, V.; Maidment, D.; Mays, L. Hidrologia Aplicada; Mc Graw-Hill: Santa Fe de Bogota, CO, USA, 1994; 584p. [Google Scholar]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity–duration–frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Campos, D.; Gomez, R. Procedimiento para obtener curvas IDT a partir de registros pluviometricos. Ing. Hidraul. Mex. 1990, 5, 39–52. [Google Scholar]
- Campos, D. Intensidades maximas de lluvia para diseño hidrologico urbano en la republica mexicana. Ing. Investig. Technol. 2010, 11, 179–188. [Google Scholar]
- Bell, F. Generalized rainfall-duration-frequency relationships. ASCE J. Hydraul. Div. 1969, 95, 311–327. [Google Scholar]
- Chen, C. Rainfall intensity–duration–frequency formulas. J. Hydraul. Div. Am. Soc. Civ. Eng. 1983, 109, 1603–1621. [Google Scholar] [CrossRef]
- Chocat, B. Encyclopedie de L’hydrologie Urbaine et de L’assainissement; Collection: Eaux Pluviales Lavoisier: Paris, France, 1997; 1136p. [Google Scholar]
- Notaro, V.; Liuzzo, L.; Freni, G.; La Loggia, G. Uncertainty Analysis in the Evaluation of Extreme Rainfall Trends and Its Implications on Urban Drainage System Design. Water 2015, 7, 6931–6945. [Google Scholar] [CrossRef]
- Da Silva, C.; Schardong, A.; Garcia, J.; Oliveira, C. Climate Change Impacts and Flood Control Measures for Highly Developed Urban Watersheds. Water 2018, 10, 829. [Google Scholar] [CrossRef]
- Sanches Fernandes, L.; Pereira, M.; Morgado, S.; Macario, E. Influence of Climate Change on the Design of Retention Basins in Northeastern Portugal. Water 2018, 10, 743. [Google Scholar] [CrossRef]
- Svensson, C.; Clarke, R.; Jones, D. An experimental comparison of methods for estimating rainfall intensity–duration–frequency relations from fragmentary records. J. Hydrol. 2007, 341, 79–89. [Google Scholar] [CrossRef]
- Seong, K. Deriving a practical form of IDF formula using transformed rainfall intensities. Hydrol. Process. 2014, 28, 2881–2896. [Google Scholar] [CrossRef]
- Asikoglu, O.; Benzeden, E. Simple generalization approach for intensity–duration–frequency relationships. Hydrol. Process. 2012, 28, 1114–1123. [Google Scholar] [CrossRef]
- Lopcu, Y. Modeling the Intensity–Duration–Frequency Relationships of Annual Maximum Storms. Master’s Thesis, Civil Engineering, Dokuz Eylul University, Izmir, Turkey, 2007. [Google Scholar]
- Sane, Y.; Panthou, G.; Bodian, A.; Vischel, T.; Lebel, T.; Dacosta, H.; Quantin, G.; Wilcox, C.; Ndiaye, O.; Diongue-Niang, A.; et al. Intensity–duration–frequency (IDF) rainfall curves in Senegal. Nat. Hazard. Earth Syst. 2018, 18, 1849–1866. [Google Scholar] [CrossRef]
- Linsley, R.; Kohler, M.; Paulhus, J. Applied Hydrology; Mc Graw-Hill: New York, NY, USA, 1949; 689p. [Google Scholar]
- Wenzel, H. 1982. Rainfall for urban stormwater design. In Urban Storm Water Hydrology; Water Resources Monograph 7; American Geophysical Union: Washington, DC, USA, 1982; pp. 35–67. [Google Scholar]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Elsebaie, I. Developing rainfall intensity–duration–frequency relationship for two regions in Saudi Arabia. J. King Saud Univ. Eng. Sci. 2012, 24, 131–140. [Google Scholar] [CrossRef]
- Mendoza, C.; Trasviña, J.; Gutierrez-Lopez, A. Empleo del algoritmo GRG Nonlinear en el calculo de intensidades de lluvia. Revista NTHE 2018, 24, 11–15. [Google Scholar]
- Sumner, G. The prediction of short-duration storm rainfall intensity maxima. J. Hydrol. 1978, 37, 91–100. [Google Scholar] [CrossRef]
- Gutierrez-Lopez, M.; Barragan, R. Ajuste de curvas IDF a partir de tormentas de corta duración. Tecnol. Cienc. Agua 2019, 10. [Google Scholar] [CrossRef]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden. Atmos. Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Cheng, K.; Wei, C.; Cheng, Y.; Yeh, H. Effect of spatial variation characteristics on contouring of design storm depth. Hydrol. Process. 2003, 17, 1755–1769. [Google Scholar] [CrossRef]
- Minh Nhat, L.; Tachikawa, Y.; Takara, K. Establishment of Intensity–Duration–Frequency Curves for Precipitation in the Monsoon Area of Vietnam. Annu. Disas. Prev. Res. Inst. Kyoto Univ. 2006, 49, 93–103. [Google Scholar]
- Gupta, H.; Wagener, T.; Liu, Y. Reconciling theory with observations: Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Euser, T.; Winsemius, H.; Hrachowitz, M.; Fenicia, F.; Uhlenbrook, S.; Savenije, H. A framework to assess the realism of model structures using hydrological signatures. Hydrol. Earth Syst. Sci. 2013, 17, 1893–1912. [Google Scholar] [CrossRef]
- Jehn, F.; Chamorro, A.; Houska, T.; Breuer, L. Trade-offs between parameter constraints and model realism: A case study. Sci. Rep. 2019, 9, 10729. [Google Scholar] [CrossRef] [PubMed]
- Hershfield, D. Rainfall Frequency Atlas of the United States for Durations from 30 Min to 24 H and Return Periods from 1 to 100 Years; Pap. No. 40; U.S. Dep. Commerce, Weather Bur. Tech.: Washington, DC, USA, 1961; 115p. [Google Scholar]
- Hershfield, D. Rainfall Input for Hydrologie Models. In Geochemistry, Precipitation, Evaporation, Soil-Moisture, Hydrometry; Reports and Discussions. Publication (78); General Assembly of Bern; International Association of Scientific Hydrology (IASH): Gentbrugge, Belgium, 1968; pp. 177–188. [Google Scholar]

| Formulation Known As | k | m | n | C | |
|---|---|---|---|---|---|
| Law of Montana [47] | - | - | 0 | - | - |
| Sherman [39] | - | - | - | 1 | - |
| Bernard [40] | - | 0 | 1 | 1 | 0 |
| Talbot/Linsley [56] 1 | - | 0 | 1 | 1 | - |
| Wenzel/Kimijima [57] | - | 0 | 1 | - | - |
| Chow [41] | - | - | 1 | 1 | - |
| Koutsoyiannis [42] 2 | - | - | - | 1 | - |
| Seong [52] | - | 1 | 1 | - |
| Duration of the Storm (minutes) | TST | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 18 | 20 | |
| C-01 | 9 | 5 | 1 | 5 | 8 | 4 | 2 | 3 | 0 | 1 | 3 | 4 | 1 | 2 | 48 |
| B-02 | 7 | 14 | 2 | 3 | 4 | 10 | 7 | 5 | 6 | 4 | 3 | 1 | 4 | 3 | 73 |
| CH-03 | 14 | 11 | 7 | 6 | 6 | 2 | 3 | 6 | 4 | 2 | 4 | 2 | 2 | 0 | 69 |
| CC-04 | 10 | 1 | 0 | 6 | 3 | 5 | 0 | 3 | 1 | 0 | 3 | 0 | 1 | 0 | 33 |
| C-05 | 7 | 10 | 7 | 8 | 7 | 6 | 2 | 5 | 2 | 0 | 4 | 7 | 3 | 3 | 71 |
| ER-06 | 26 | 11 | 0 | 6 | 9 | 7 | 1 | 4 | 1 | 2 | 5 | 2 | 1 | 2 | 77 |
| M-07 | 13 | 16 | 7 | 6 | 10 | 5 | 6 | 2 | 4 | 2 | 7 | 2 | 2 | 0 | 82 |
| RP-08 | 10 | 2 | 7 | 2 | 1 | 3 | 4 | 0 | 2 | 3 | 1 | 1 | 2 | 1 | 39 |
| SJA-09 | 4 | 4 | 4 | 1 | 6 | 3 | 2 | 2 | 2 | 2 | 0 | 1 | 0 | 0 | 31 |
| - | 100 | 74 | 35 | 43 | 54 | 45 | 27 | 30 | 22 | 16 | 30 | 20 | 16 | 11 | 523 |
| Station ID | Method-a (min) | Method-b (min) | Method-c (min) | Method-d (min) | ||
|---|---|---|---|---|---|---|
| C-01 | 48(5) | 18.0 | 13.55 | 9.85 | 10.0 | 14.85 |
| B-02 | 73(6) | 15.0 | 21.02 | 11.00 | 16.0 | 17.00 |
| CH-03 | 69(5) | 15.6 | 12.50 | 8.88 | 10.5 | 13.88 |
| CC-04 | 33(5) | 15.0 | 12.00 | 11.18 | 12.5 | 16.18 |
| C-05 | 71(6) | 15.0 | 13.03 | 10.98 | 8.0 | 16.98 |
| ER-06 | 77(5) | 15.6 | 12.07 | 7.70 | 13.0 | 12.70 |
| M-07 | 82(6) | 18.0 | 18.01 | 11.09 | 17.5 | 17.09 |
| RP-08 | 39(5) | 15.6 | 15.42 | 11.07 | 12.5 | 16.07 |
| SJA-09 | 31(9) | 15.0 | 13.51 | 11.29 | 12.5 | 20.29 |
| Typical Storm (In Situ) | C = 0 | (M-a) C= 12.5 | (M-b) C = 10.5 | (M-c) 1 C = 8.88 | (M-d) 2 C = 13.88 | |
|---|---|---|---|---|---|---|
| 20 | 36.09 | 16.50 | 12.75 | 13.19 | 13.58 | 12.48 |
| 15 | 26.60 | 19.21 | 13.93 | 14.50 | 15.02 | 13.58 |
| 10 | 23.50 | 23.82 | 15.50 | 16.28 | 17.01 | 15.02 |
| 5 | 16.96 | 34.39 | 17.71 | 18.88 | 20.02 | 17.01 |
| Tr | C = 0 | (M-a) = 12.5 | (M-b) = 10.5 | (M-c) = 8.88 | (M-d) = 13.88 |
|---|---|---|---|---|---|
| 20 | 74.4 | 48.4 | 50.9 | 53.1 | 46.9 |
| 10 | 51.6 | 33.5 | 35.2 | 36.8 | 32.5 |
| 5 | 35.7 | 23.2 | 24.4 | 25.5 | 22.5 |
| Fact | Values | Reference |
|---|---|---|
| “the rainfall time series that allows the correct transfer to the model is 30 min” | The storm duration using in this study for IDF curves is 35 min. | [63], p.374 |
| “the storm index associated with the precipitation depth for design storms lasts 60 min” | The IDF equation presented is of type [42] where C = 55 | [64], p.16 |
| “The parameter C varies between 0 and” their data vary between 0.083 h (5 min) and 0.167 h (10 min). The results of his work present two IDF equations. | C for the IDF curves were C = 0.189 (5 min) and C = 0.143 (10 min). The parameters of these equations are obtained by L-moments and an optimization routine. | [42], p.129 |
| “IDF curves for precipitation in the Monsoon area of Vietnam, identifies ratios 60-min rainfall intensity and duration for same return period” | The ratios were fitted by Sherman’s equation with C = 76.31 | [65], p.100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutierrez-Lopez, A.; Jimenez Hernandez, S.B.; Escalante Sandoval, C. Physical Parameterization of IDF Curves Based on Short-Duration Storms. Water 2019, 11, 1813. https://doi.org/10.3390/w11091813
Gutierrez-Lopez A, Jimenez Hernandez SB, Escalante Sandoval C. Physical Parameterization of IDF Curves Based on Short-Duration Storms. Water. 2019; 11(9):1813. https://doi.org/10.3390/w11091813
Chicago/Turabian StyleGutierrez-Lopez, Alfonso, Sergio Bernardo Jimenez Hernandez, and Carlos Escalante Sandoval. 2019. "Physical Parameterization of IDF Curves Based on Short-Duration Storms" Water 11, no. 9: 1813. https://doi.org/10.3390/w11091813
APA StyleGutierrez-Lopez, A., Jimenez Hernandez, S. B., & Escalante Sandoval, C. (2019). Physical Parameterization of IDF Curves Based on Short-Duration Storms. Water, 11(9), 1813. https://doi.org/10.3390/w11091813






