A New Technical Concept for Water Management and Possible Uses in Future Water Systems

Abstract

A new degree of freedom in water management is presented here. This is obtained by displacing water, and in this paper is conceptually explained by two methods: using an excavated cavern as a container for compressed air to displace water, and using inflatable balloons. The concepts might have a large impact on a variety of water management applications, ranging from mitigating discharge fluctuation in rivers to flood control, energy storage applications and disease-reduction measures. Currently at a low technological readiness level, the concepts require further research and development, but the authors see no technical challenges related to these concepts. The reader is encouraged to use the ideas within this paper to find new applications and to continue the out-of-the-box thinking initiated by the ideas presented in this paper.

1. Introduction

Fresh water is a paramount part of any human life and a prerequisite for a developed society and high quality of life. Apart from the obvious use of drinking it, water can provide many services for both society and environments, either in a natural or modified system. The IPCC 2011 climate report (chapter five) has an extensive section (on services and characteristics of Hydro Power Plant (HPP) projects, but transferrable to the general case as well) in which energy and water management services as well as their main environmental and societal characteristics are identified.

For society, these services might be the following: transportation and recreation (riverboats and barges); irrigation; fisheries; energy storage and power production (hydropower production (at HPP)); electric energy storage (Pumped Hydro Storage, (PHS)); waste management; fertilization of farmland (sedimentation by flooding); protection of shorelines (sediments settling in estuaries and river mouths dampening waves and tidal erosion); flood protection (dams and natural lakes reduce flood intensity); and groundwater stabilization.

For environments, the services might be as follows: providing habitat and reproduction areas for living organisms ranging from the smallest protozoa and algae to plants, fish, birds and mammals; the cleaning of river beds during floods; bringing nutrients in the form of sediments to coastal regions; and the settling of sediments to protect ocean shorelines and thus habitats.

The availability of fresh water varies between different parts of the world. Consequently, the use and management of water also vary between countries and continents. Climate changes are predicted to result in changing weather systems, altering the intensity and distribution of precipitation around the globe. The effect of this on the watercourses on a regional and local scale is difficult to predict, as global models must be downscaled into climatic data for use in models of catchments areas [1]. An overall trend seems to be captured in Figure 1, however, which represents the median of 12 climate model projections using the A1B scenario, “A balanced emphasis on all energy sources”, from the Special Report on Emissions Scenario by the Intergovernmental Panel on Climate Change (IPCC) [2]. “Climate change has large direct impacts on several aspects of the hydrological cycle—in particular, increases in extremes—making managing and using water resources more challenging” [3].

Current water management systems and infrastructures have been established based on historical data, typically before anthropogenic climate changes were even theorized as being possible. The systems represent large investments and, quite often, incremental additions and/or modifications are not possible, or at least are very expensive. Utilizing the infrastructure to the fullest or even increasing their capacity without modifying the systems is important. When developing the ideas presented in this paper, reusing existing infrastructure has been a guiding principle. The applications presented here are at a low technological readiness level (TRL). As such, cost has not been given any weight in this paper, although it is likely that cost is strongly related to any installation derived from the ideas presented. Hence, a cost–benefit analysis is of course necessary in the long term, but if the benefits are large enough, funding is often available. To put things into perspective, following the 2008 financial crisis, the aid to the financial sector from EU member states was 1400 billion US$ [4], whereas the worldwide government spending on low-carbon Research and Development (R&D) in 2017 was just above 20 billion US$ [5]. This means that close to 70 years of global low-carbon R&D funding was used to keep the EU financial system afloat. This strongly indicates that, where there is a governmental and political will, funding is available.

This paper will present novel ideas on how to achieve a new degree of freedom for topics related to water management. This freedom is linked to the active control of the displacement of water by compressed air in different configurations. The objective of this paper is to present the concepts and to get engineers and scientists to “think outside the box”, and in this way stimulate ingenuity and the emergence of new technical solutions. The motivation of the authors is stimulate the development of new technical solutions that will provide water management services to society in the future.

The authors acknowledge that part of this paper has the characteristics of a popular scientific publication more than a technical science publication. However, to be able to bring the concepts in focus to a higher TRL, they need to be presented to a technical audience. Furthermore, the actual ways of implementing the concepts might vary depending on the needs of the services required, so a high degree of tailor-made solutions are likely to be needed. This also suggests that presenting something with a high level of technical detail will not aid the objective of this paper, namely to present the concept and induce creativity within the technical community.

2. New Technical Concepts; Method

The new concepts are based on displacement of water as a method to obtain a new degree of freedom to operate and manage water bodies and flows. Both concepts make use of air as the medium to displace water, but the configurations for obtaining the displacements are different. Problems related to not being able to provide the new degree of freedom are numerous and will be presented in more detail in later sections which will more specifically explain the problems and how displacement can resolve them.

In the next section, the proof for displacement as a method for obtaining a new level of freedom is presented based on first principles. If this proof is not needed from the reader’s point of view, this section can be omitted with no loss of continuity.

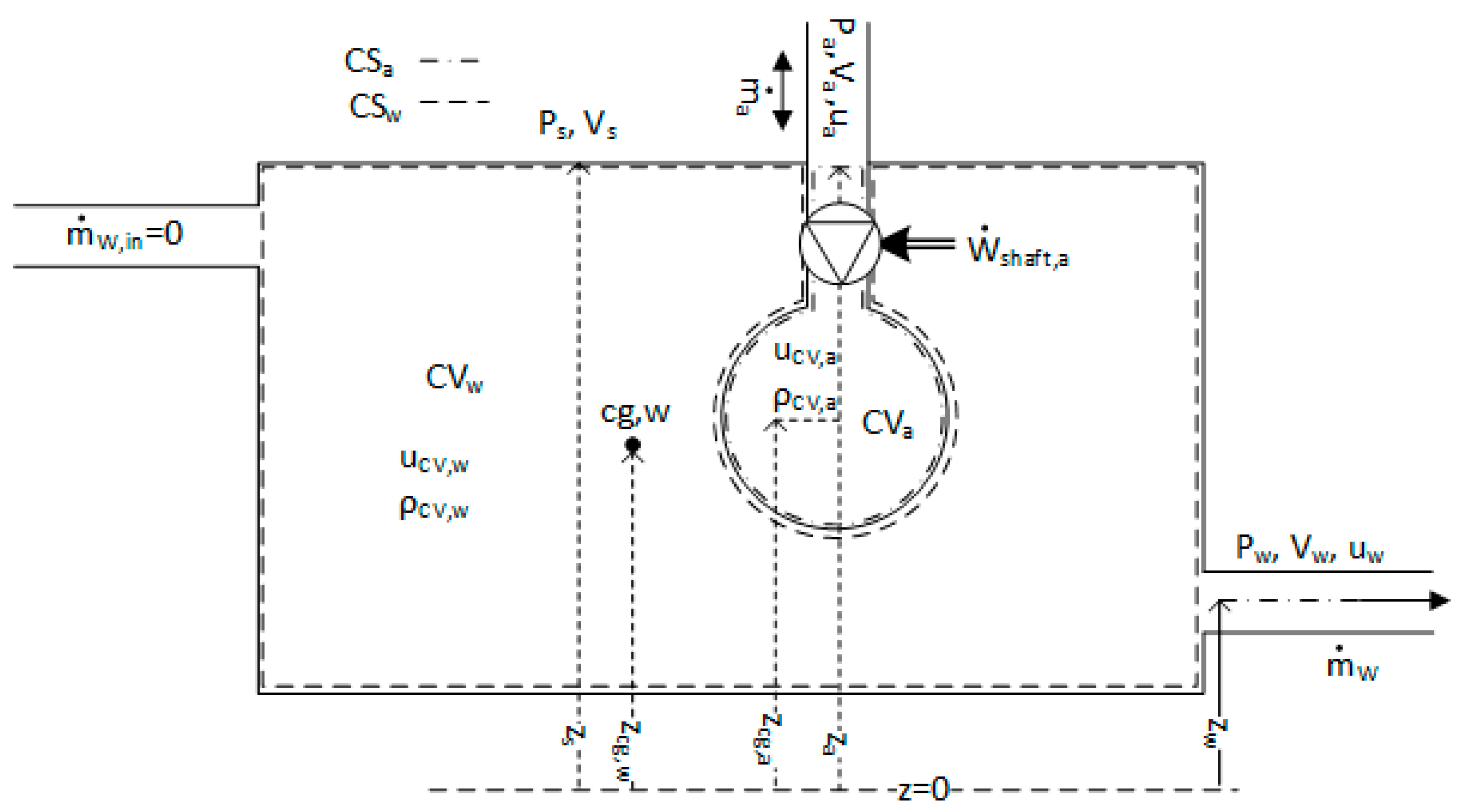
2.1. Displacing Water Using Compressed Air

Water is, for all practical purposes, incompressible, meaning that a given mass will have a fixed volume. Decoupling water volume and levels means that a portion of the volume must be moved to a different location. This is called displacement and is what the compressed air is claimed to be able to do in the concepts presented.

Although rather intuitive, in the end, it can be shown mathematically to be true as well. This can be done by utilization of the Reynolds Transport Theorem. This theorem can be applied to any extensive property, such as energy, momentum and mass. It basically describes a control volume (CV) which has inlets and outlets crossing a control surface (CS) and formulates that the rate at which an extensive property B_sys is produced/consumed in the system must be equal to the sum of the net flow of B through the CS, and the change of the amount of B within the CV according to [6]

$$\begin{array}{c}\frac{d{B}_{sys}}{dt}=\frac{d}{dt}{\displaystyle {\int }_{CV}^{}}\rho bdV+{\displaystyle {\int }_{CS}^{}}\rho b(\overrightarrow{V_r}·\overrightarrow{n})dA,\end{array}$$

(1)

where ρ (kg/m³) is the density of the fluid carrying the property B; b = B/m (B/kg) is the intensive property linked to the extensive property; and ${\overrightarrow{V}}_r$ (m/s) and $\overrightarrow{n}$ (-) are the relative velocity vector between the fluid and the local CS and the normal vector of the local CS, respectively. Consider two such systems, one for air (subscript a) contained within another one for water (subscript w), as shown in Figure 2:

The interphase between the water and air is intended to be flexible—like a balloon—so that it is free to expand or collapse. The quantities ${\dot{m}}_{w,in}$ and ${\dot{m}}_{w,out}$ are the mass flow of water in and out of the CV, respectively, while ${\dot{m}}_a$ is the mass flow of air (positive or negative) through the air inlet.

Two versions of Equation (1) can be constructed, considering that no air or water is produced or consumed ($\frac{D{B}_a}{Dt}=0;\frac{D{B}_w}{Dt}=0$); using B₁ = m_a; b₁ = m_a/m_a = 1; B₂ = m_w; b₂ = m_w/m_w = 1;

$$\begin{array}{c}\frac{d}{dt}{\displaystyle {\int }_{CV,w}^{}}{\rho }_{w}dV=-{{\displaystyle \int }}_{CS,w}^{}{\rho }_w(\overrightarrow{V_r}·\overrightarrow{n})dA={\dot{m}}_{w,in}-{\dot{m}}_{w, out},\end{array}$$

(2)

$$\begin{array}{c}\frac{d}{dt}{\displaystyle {\int }_{CV,a}^{}}{\rho }_{a}dV=-{{\displaystyle \int }}_{CS,a}^{}{\rho }_a(\overrightarrow{V_r}·\overrightarrow{n})dA={\dot{m}}_a.\end{array}$$

(3)

Assuming the densities to be constant (which holds for low-pressure water, and is a slight simplification for low-pressure air), the densities can be removed in the respective equations, and adding the resulting equations together yields

$$\begin{array}{c}\frac{d}{dt}\left({\displaystyle {\int }_{CV,a}^{}}dV+{\displaystyle {\int }_{CV,w}^{}}dV\right)=Q_a+Q_{w,in}-Q_{w, out},\end{array}$$

(4)

where $Q$ is the volume flow (or discharge) of water or air, corresponding to the mass flows. The left-hand side of Equation (4) describes the rate of change of the combined volume of air and water. The right-hand side considers the sum of the discharge through the inlets and outlets. Imagine that a volume of air is submerged in a balloon in a water reservoir (as shown in Figure 2) and for some reason the water level in the reservoir is not allowed to change. This means that the combined volume should be constant, and Equation (4) is simplified to

$$Q_a=Q_{w,out}-Q_{w,in}.$$

(5)

If no air volume exists, as is the case for existing reservoirs, Equation (5) reduces to $Q_{w,out}=Q_{w,in}$, meaning that the discharge of water into and out of the reservoir must be identical. Thus, Equation (5) show that the presence of the air displacement makes it possible to decouple the water out of and into the reservoir, obtaining the new degree of freedom.

Energy Considerations

Even if a new degree of freedom is obtained, some insight into the energy cost of this is appropriate. Using energy E (kJ) as the extensive property under investigation in Equation (1), a starting point for an energy analysis of the system can be defined. After divisions of energy into heat (which will be neglected) and work, and further dividing work into work added to the system by a component and pressure work added by the surroundings on the inlets and outlets [6], we get

$${\dot{W}}_{shaft}=\frac{d}{dt}{\displaystyle {\int }_{CV}^{}}\rho edV+{\displaystyle {\int }_{CS}^{}}\rho \left(\frac{P}{\rho }+e\right)(\overrightarrow{V_r}·\overrightarrow{n})dA,$$

(6)

where ${\dot{W}}_{shaft}$ (kJ/s) is the power added or extracted by the component(s); $e=u+\frac{V^2}{2}+gz$, where the right-hand side terms are internal, kinetic and potential specific energies, respectively (kJ/kg). This system can be set-up for the water and air configuration in Figure 2, considering the case where the water level must be maintained at a constant level while providing environmental flow $Q_{w,out}$ while there is no inflow, $Q_{w,in}=0$. The water system has no component that can add (pump) or extract (turbine) power to or from the flow, so there in no ${\dot{W}}_{shaft}$-term in this system. However, for the air system, a term ${\dot{W}}_{shaft,a}$ appears to represent the power added to inflate it. The development of the equations can be found in Appendix A, yielding

$$\begin{array}{c}{\dot{W}}_{shaft,a}=g({\rho }_w-{\rho }_a)(z_s-z_{cg, a})Q_{w,out},\end{array}$$

(7)

where $z_s$ is the elevation of the reservoir surface and $z_{cg,a}$ is the elevation of the centre of gravity (COG) of the air body. Further realising that the density of air is much lower than the water density, the term related to the air system will in practise be negligible; consequently,

$$\begin{array}{c}{\dot{W}}_{shaft,a}=g{\rho }_w(z_s-z_{cg, a})Q_{w,out}.\end{array}$$

(8)

This is the power needed to provide the necessary displacement of water by the air system. Scrutinizing Equation (8), it is recognized that the term represents the power needed to bring the flow from atmospheric pressure to the pressure at the COG of the air body. Another case can be investigated by setting the discharge $Q_{w,out}$ to a negative value. This case is one in which the water level must be kept constant, and there is an inflow (negative outflow), but no outflow. In this case, the term ${\dot{W}}_{shaft,a}$ will change sign, indicating power will go in the opposite direction. This means that regeneration of power is possible when the air is released from the system. For a full cycle, we thus only must pay the price of energy losses, because the inflation/deflating process is an energy storage process.

2.2. Examples of Use of the New Capabilities

There are several examples that can be used to highlight some uses of the new capabilities obtained by this decoupling. First, we assume that the water level at its maximum in a reservoir used for hydropower, for instance. The combined volume cannot be increased, because water would be spilled over the dam or through spillways, and it can be assumed that this must be avoided, perhaps due to safety issues or economical concerns. If the draining of water, ${\dot{V}}_{w,out}$, due to capacity issues is smaller than the inflow of water, ${\dot{V}}_{w,in}$, releasing air from the balloon (having negative ${\dot{V}}_a$) will keep the volume constant. The volume of air in the CV will decrease, allowing for the water volume to increase, but keeping the sum of the two fixed. For this to be possible, air must be present in the volume prior to this incident occurring. However, the reservoir levels and weather forecast should give an indication of such an incident occurring, and the draining of water can be kept higher than the inflow while air is added to the volume in the hours before the incident. Alternatively, some air volume could be present as a default safety margin. If such air volume—in this case, in the form of a balloon—does not exist, there is no possibility at all of avoiding water to be spilled, and safety is no longer ensured.

The opposite case is if the water is at the minimum allowed level; for example, near the end of the dry season. If the need for water downstream supplied by the draining of water, ${\dot{V}}_{w,out}$, is larger than the inflow of water, ${\dot{V}}_{w,in}$, this is made possible by adding air to the balloon, having a positive ${\dot{V}}_a$. Then, the inflating balloon would displace water volume as the water was drained and the level would be kept constant. If such a balloon did not exist, the needed water could not be supplied because this would cause the level to go below the minimum allowable level. Supplying the needed water can, for instance, be of paramount importance to avoid the stranding of fish, [7]. Keeping the level constant can also be of importance for benthic fauna [8].

Both cases above assume that the combined volume should be constant, but the flexibility provided by the displacement can also be used to increase or reduce the combined volume as well, effectively changing the water levels more than what would be the case for mass balance in and out of the reservoirs. Such applications will be discussed later in the paper.

Obtaining the desired displacement can be done in several ways. In principle, a crane could be used to submerge a solid body with a density higher than the water and thus displace a water volume corresponding to the volume of the body. With no indications of these being the only appropriate ways of achieving displacement, two other configurations are considered in this paper; they use an underground cavern and inflatable balloons, respectively. The reasons for choosing these are the fact that much of the infrastructure and components needed are available from other applications existing today and that a gas—in this case, air—is relatively easy to handle. This will be explained in the sections describing the two configurations.

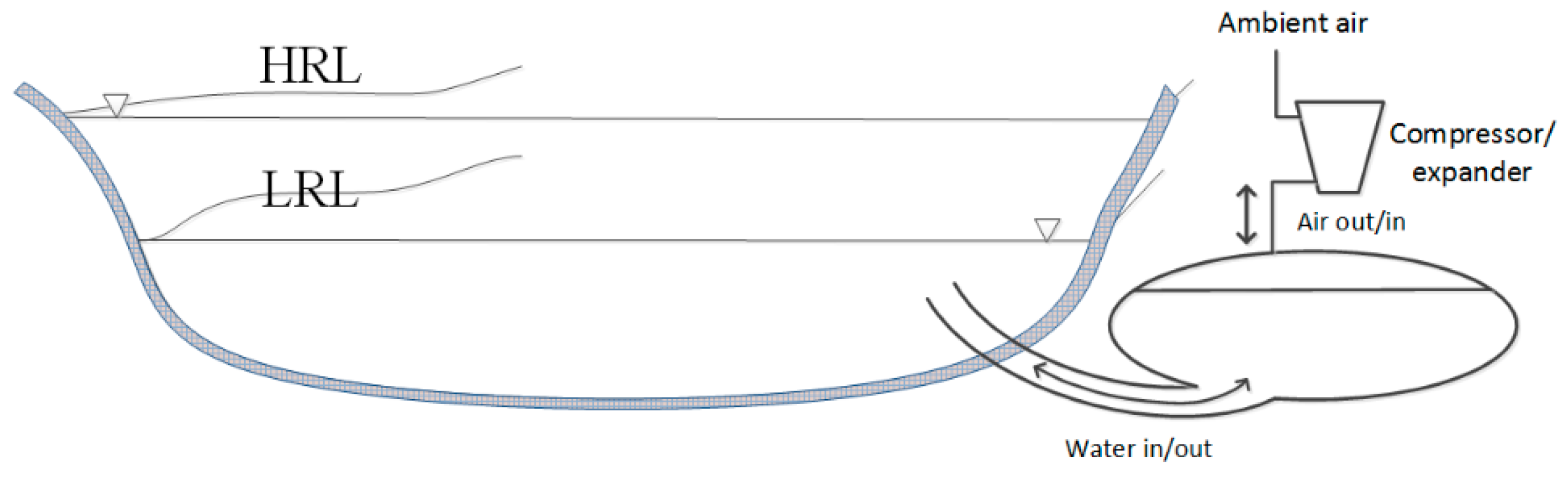
2.2.1. Inflatable Balloons

Displacing water by inflating balloons anchored to the bottom of the water body is the first configuration discussed in this paper. It can be seen in Figure 3.

The principle is intuitively understood and identical to the example used to prove the concept in the section above. Using compressed air to inflate the balloons will displace water, giving the flexibility to operate with a new degree of freedom. Using balloons, the need arises to have strong foundation for the balloons as they experience large buoyancy forces. Although used for a slightly different purpose (compressed air energy storage at great ocean depths), balloons of the type considered appropriate for this configuration have been made and tested in a laboratory [9].

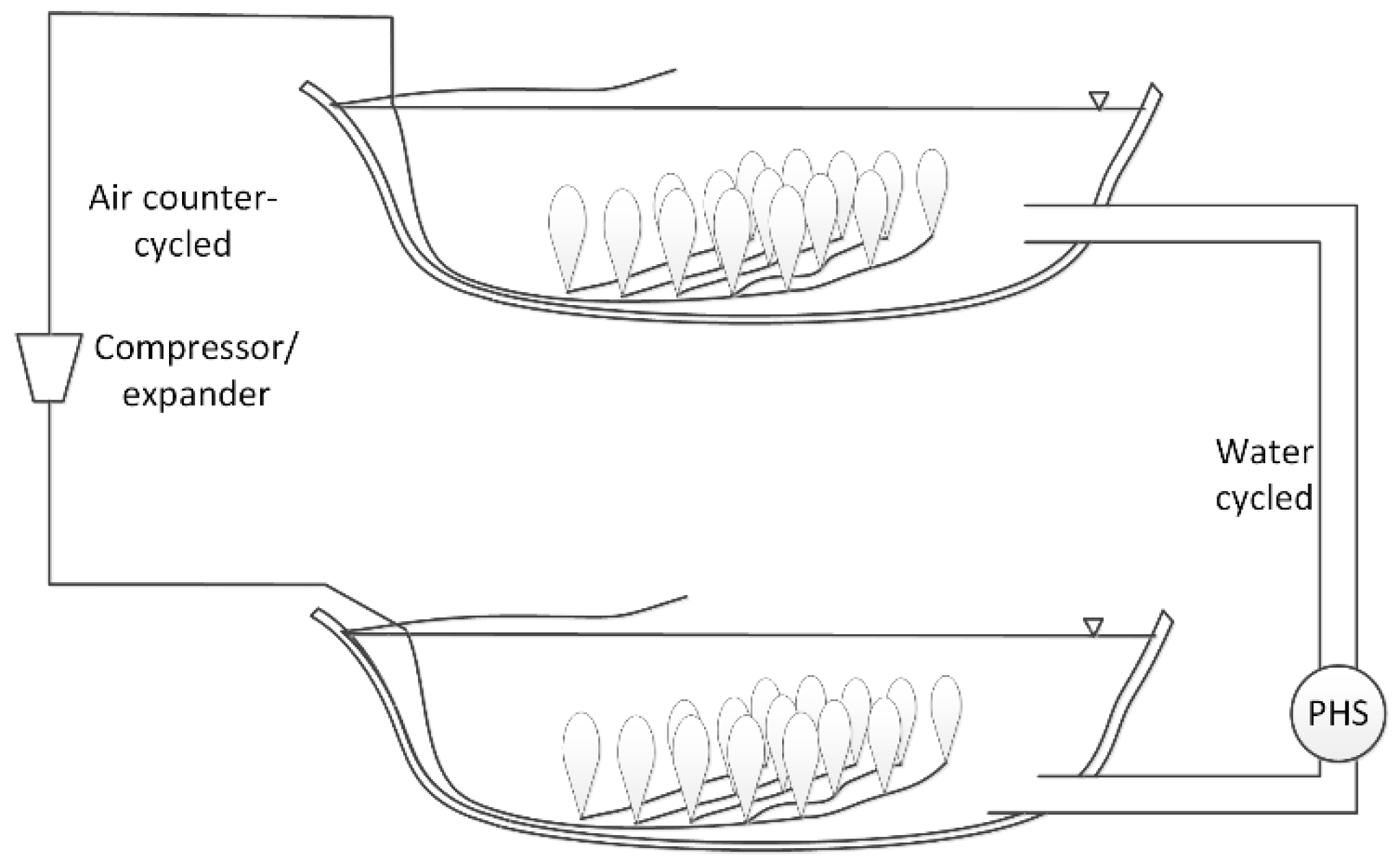
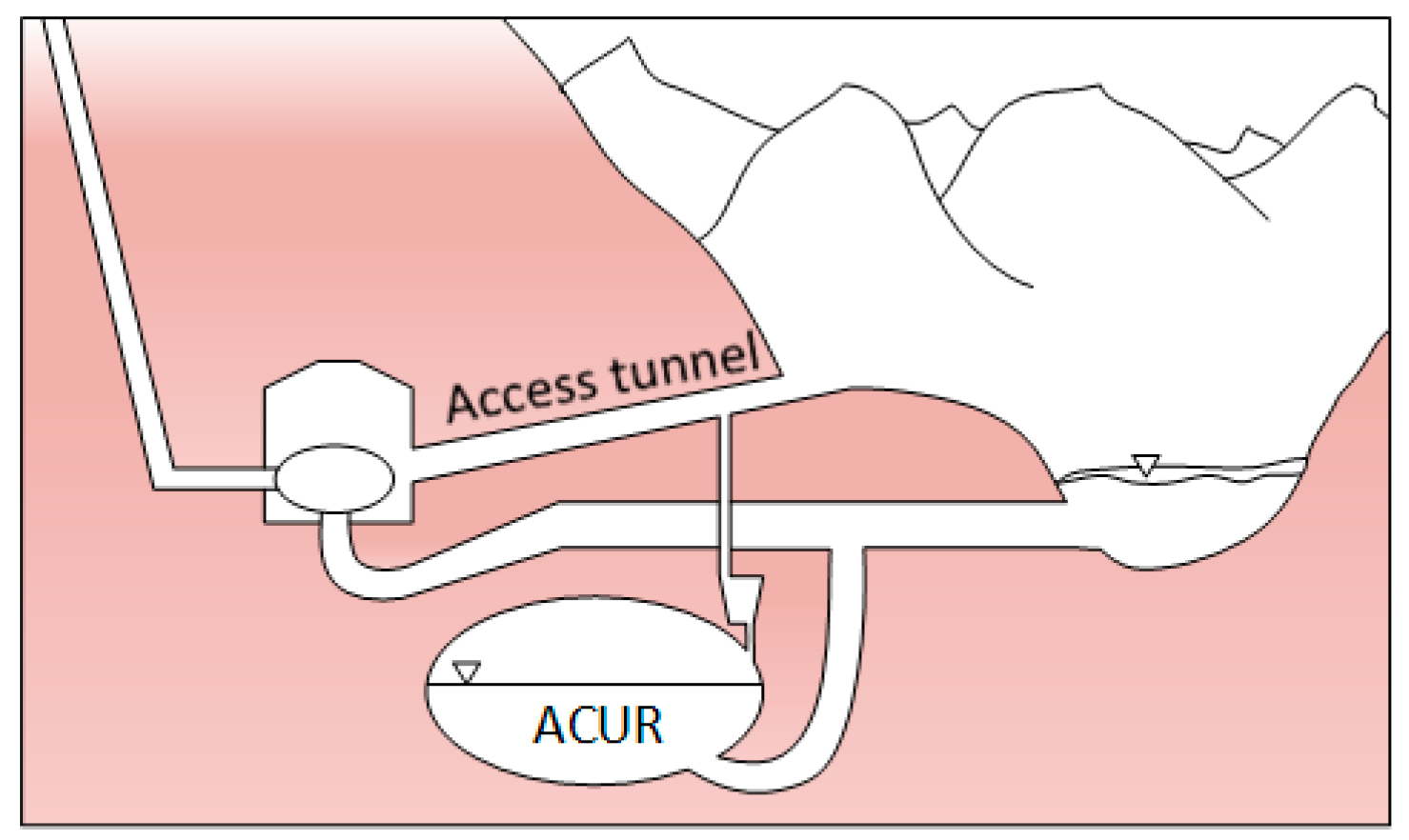
2.2.2. Air Cushion Underground Cavern (ACUR)

ACUR is an underground cavern excavated for retaining air near a water surface. It can be seen sketched in Figure 4.

The tunnel allowing water to go in or out of the ACUR element is connected to an adjacent water reservoir. Displacing water in ACUR by admitting compressed air will give an addition to the water volume of the adjacent reservoir; vice versa, expanding air from ACUR will allow for water entering it, removing the same water volume from the adjacent water body. ACUR is simply an additional volume in which water can be stored. However, the flexibility obtained by using air to displace water is what gives the possibility of the manipulation of water levels.

Subject to acceptable ground conditions, making ACUR water and air-tight might be a challenge. ACUR must be as close to the water level of the adjacent water body as possible, and this will make the pressure inside ACUR quite low—not significantly higher that atmospheric pressure. There is a resemblance between ACUR and a high-pressure component present in a hydropower plant, called air cushion surge chambers. They are chambers in the rock hydraulically connected to the penstock of power plants and are used where a surge shaft cannot be installed due to the local geographical conditions. They are partially filled with water and air, and the purpose of the surge chamber is to improve the governing stability and reduce retardation pressures when stopping the flow through the power plant, either for regulation of power or shutting down the power plant. The fact that these installations can provide sufficient air and water-tightness despite high pressures indicates that it should be possible to make ACUR air and water-tight as well.

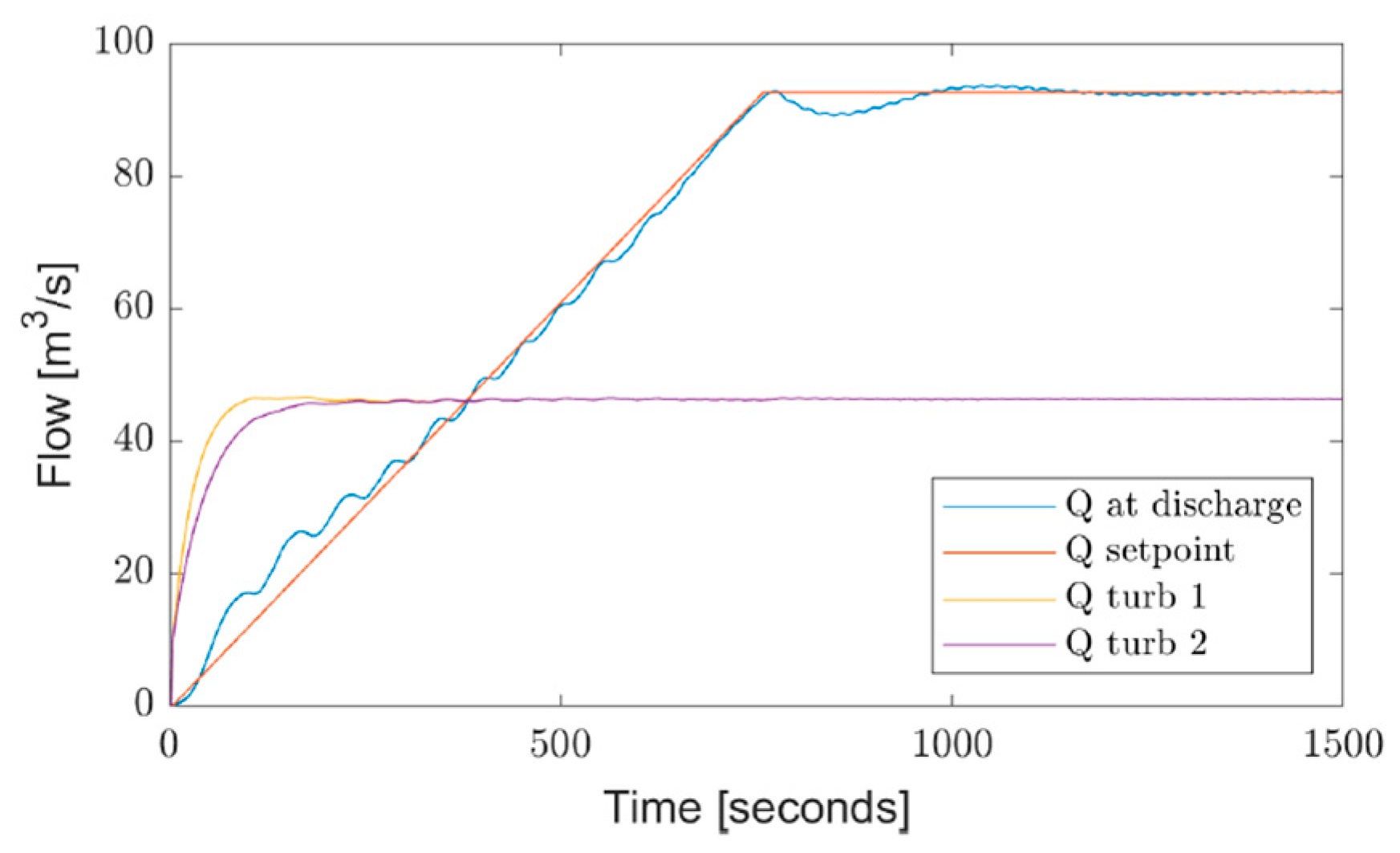
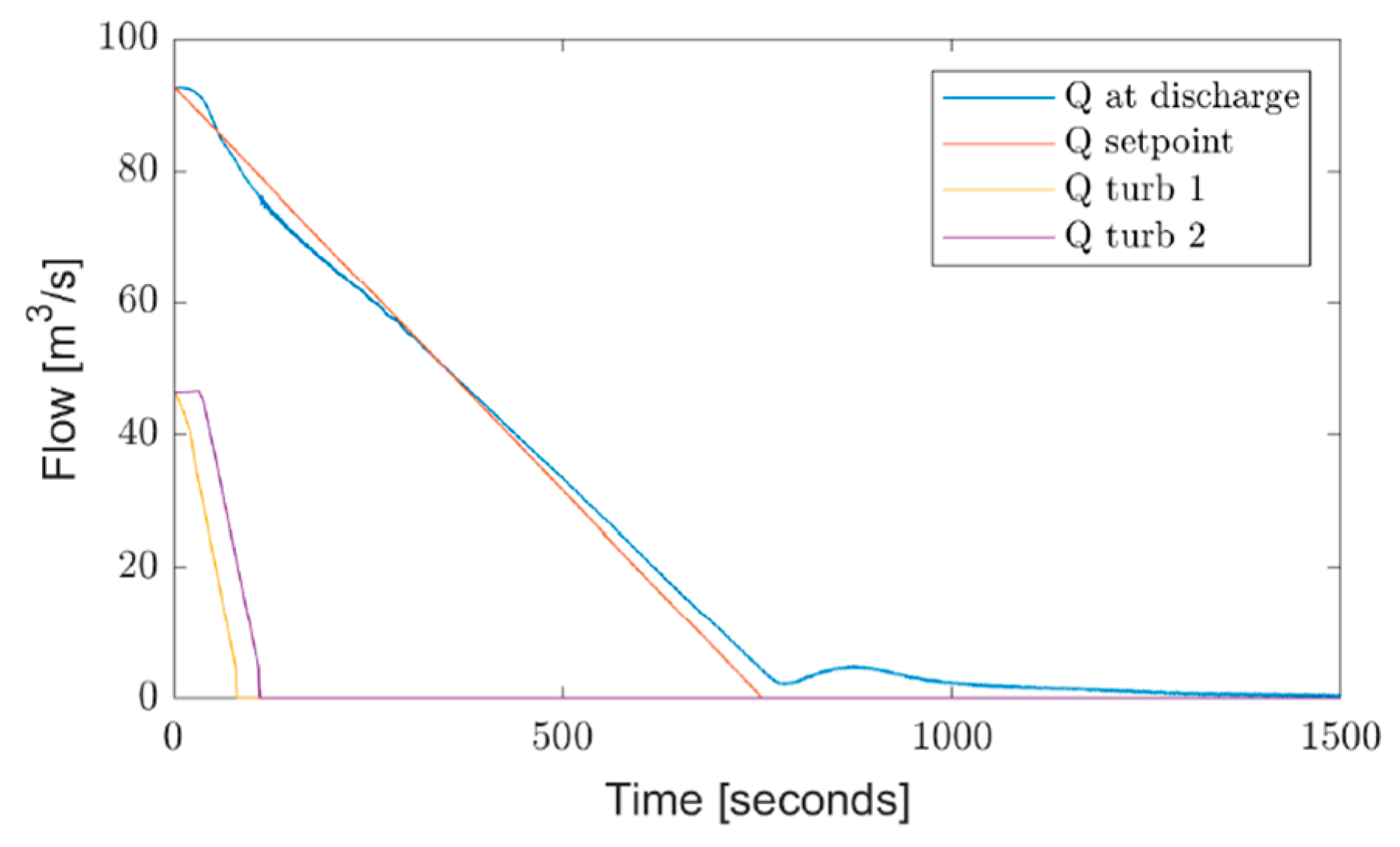
3. Applications

There are different applications that can be imagined for these concepts. The balloons clearly need a water volume of some size to work, since they are positioned within the water volume. ACUR provides an additional hidden volume and can be constructed adjacent to small rivers and where no significant volume is present, as well as connected to reservoirs. In addition to flow in regulated rivers, as presented below, the configurations may be used in cities where flooding is a main issue [10]. Watersheds such as rivers, channels, lakes, pools and ponds may be equipped with balloons as shown in Figure 3 to keep the water surfaces at a proper level. During heavy rains, air is released from the balloons, creating a large volume for the water to fill. Once the weather conditions become stable, air can be pumped into the balloons at a slow speed, letting the water leave the city in a controlled fashion.

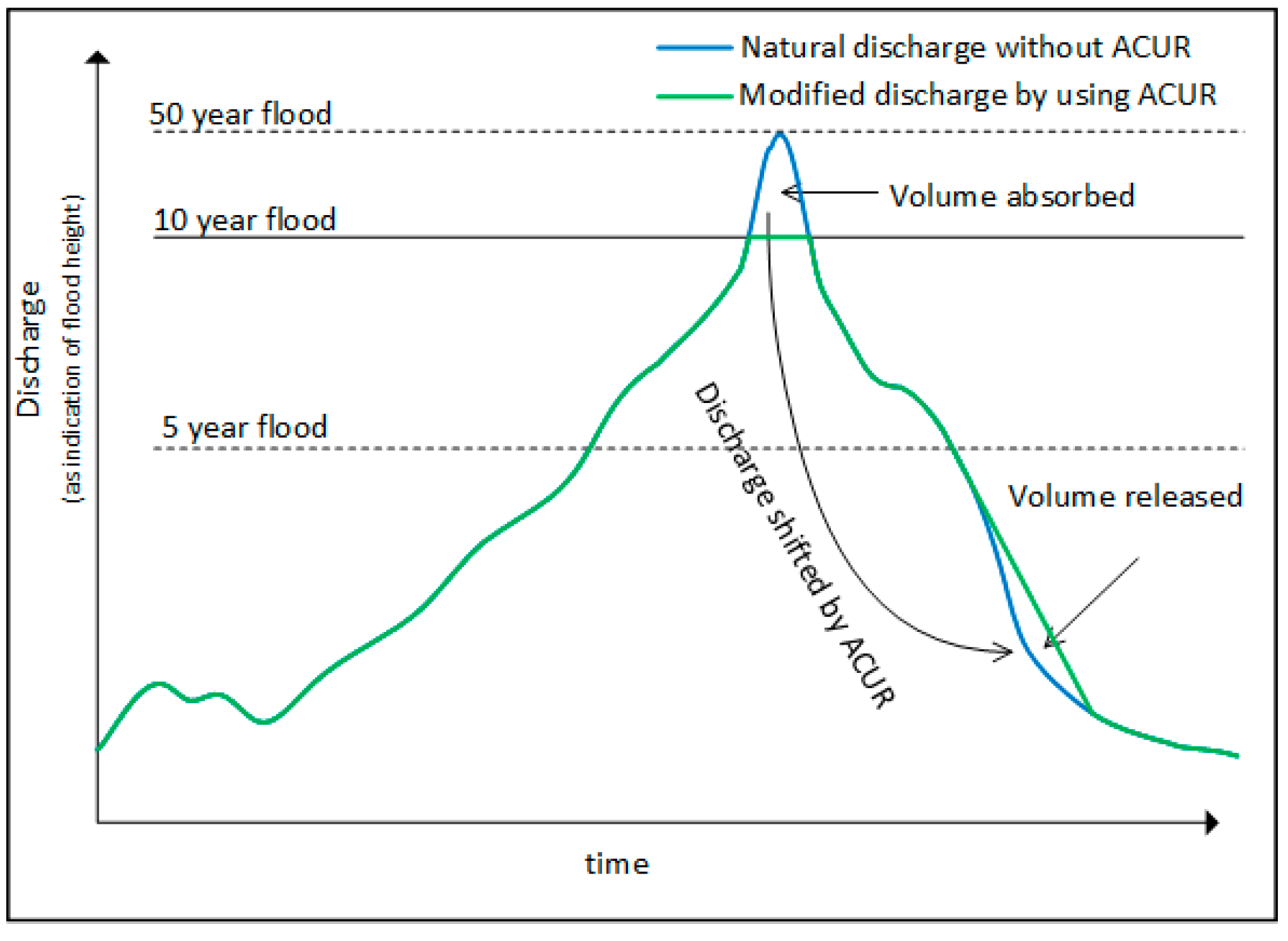
3.1. Floods, Droughts and Discharge Fluctuation Manipulations

As Figure 1 shows, run-off is expected to change significantly for most of the planet in the future. Floods and droughts are thus likely to intensify. Since simulations have shown that the ACUR configuration can be used to both mitigate and mimic floods [11], it has a potential to be implemented for rivers and used to dampen the magnitude of the discharge in flood incidents. Destructive floods are ones that are so big that they rarely occur, named by the amount of years between their statistical appearance. A 50-year flood is thus more severe than a 10-year flood. Furthermore, it is the flood peak that is responsible for the level of destruction. Hence, by allowing some of the discharge to enter ACUR, the peak flood discharges can be reduced, making the flood less dangerous. Such a scenario is illustrated in Figure 5.

The volume needed to turn a 50-year flood into a 10-year flood is of course dependent on the flood characteristics. The duration of the flood peaks tends to be short, so it is not far-fetched to imagine a feasible volume for ACUR being able to relieve the situation. Furthermore, the periods of a flood incident in which the water retrieves rapidly might also be a concern, because an overly high hydro morphological pressure in river embankments might cause landslides. The water stored at the peak flood event could be stored and released to prevent water levels falling too rapidly, hence reducing the risk of landslides. In rivers with many tributaries, ACUR can be used to shift the time of the occurrence of the peak flow of the individual tributaries so that the flood peaks from the tributaries do not all add to the main river flood peak.

In periods of drought, stored water in ACUR can be used for periods where a river flow is at critical levels. The water in the cavern would be subjected to little evaporation, as it is kept away from solar radiation and winds.

Some natural phenomena are triggered by flood-like discharge events. This is might be migratory events for fish in rivers. As an example, the Atlantic salmon migrate from the river as salmon fry in the springtime snow-melt floods [12]. At the other end of the salmon life cycle, the salmon run up the river at high-discharge periods to easily get to the spawning grounds. Mimicking local flood-like events is, for instance, a perfect method to supply water to channels used to attract fish to fish-ways [13,14]. Active use of ACUR could thus facilitate these natural migrations.

In heavily regulated rivers, natural floods have been reduced and silt and sediments have settled in the gravel, which are used by fish as a substrate for hiding fertilized eggs. This has been found to be the case for white sturgeon in the Kootenai River downstream Libby Dam, where the relative rarity of very high flows due to the regulation by the dam is partially responsible for the lack of successful spawning [15]. Therefore, there might be cases in which a regulated river would benefit from a flood-like discharge event. ACUR could be used to provide this as well, by storing water and releasing it when the natural river flow is high, artificially creating a flood-like peak in the discharge. Simply releasing additional high-value water from the reservoir in such a case can be an alternative but carries a high cost. The water stored in ACUR has already given its energy to the generators of the hydroelectric plant and thus has a lower value. The cost of pushing water out of the cavern and into the river would be the cost of operating the compressors providing the pressurized air. In fact, in electrical sub-systems dominated by intermittent energy sources, energy prices have been negative, due to the cost of shutting down wind turbines. Future systems will be dominated by intermittent energy sources, and it is completely feasible that mitigating floods by running compressors will be a net income incident for power companies in the future.

3.2. Energy Storage and Power Production

ACUR provides an additional volume for storage of water, and at some locations, this additional volume might be very useful. The world is in dire need of reliable, large-scale and fast electrical energy storage technologies. Currently, the best technology by far to provide this is Pumped Storage Power plants (PSP) in addition to large reservoirs. The PSPs are, however, dependent on having both water available as well as a steep terrain with the possibility to construct a reservoir with high elevation. Such locations are not found everywhere, and the best locations have already been developed. The expansion of the power capacity at existing PHS sites has been performed at several locations. This is simply a matter of adding units between the existing upper and lower reservoir. This increases the power that can be produced, but emptying the upper reservoir will then go faster, since the energy storage capacity has not been increased. At some point, the expansion of power at the PSP might be limited by the rate of water level decrease, because a too high rate might introduce too much sediment into the water, or landslides might occur. Installing and operating ACUR to reduce the rate of water level decrease by displacing water into the main reservoir might provide the possibility to add more power by working around this limitation. A suggested position of ACUR in conjunction to the reservoir can be seen in Figure 6.

Installing and operating ACUR thus gives the possibility to install more capacity than otherwise possible. Furthermore, the added volume of ACUR represents a novel way of increasing the energy storage capacity at reservoirs. The conventional way of doing this is not easy, because this will in most cases imply that the height of the dam must be increased, and this is not possible in most cases because the additional forces on the construction void the structural integrity of the existing dam (in Europe, this is still possible at several locations due to the high safety factor used when designing the dams due to the cold war). One project in which the dam height was increased due to energy storage increase considerations is at Vianden PHS [16]; however, this dam is not representative of the majority of dams. ACUR represents the possibility of increasing the energy storage at an existing power plant without the need to replace the existing dam.

The position of ACUR below the lowest reservoir level (LRL) in Figure 6 is intentional, and the interested reader can find reasons for this in a previous paper by one of the authors [17]. In that same paper, the ACUR configuration is theoretically demonstrated, showing that the reduction in the efficiency of a pump–turbine cycle due to losses in the compressed air system is small, and that the relative reduction decreases with the increasing head of the PHS.

Water bodies that are currently off-limits for use as reservoirs for pumped storage power plants due to water level limitations might also be allowed for this kind of operation. Imagine two water bodies close to each other with an elevation difference that makes them suitable for pumped hydro; constructing a pumped hydro plant operating between the two water bodies and water displacement capabilities at both bodies would make it possible to operate the plant without any water level changes to either water body by the opposite operation of the displacement capabilities at the two reservoirs. As water is pumped from the lower body, displacement by air would make the level constant. At the upper water body, air would have to be evacuated to make place for the pumped water. Actually, the air could be a closed cycle as well, in which air from the upper part is moved to the lower part simultaneously as water is pumped, counter-cycled to the water. This can be seen in Figure 6, where inflatable balloons are used. ACUR could also be used, but for both applications, the storage is limited to the volume of ACUR/balloons. This might very well be suited for intra-day and hydraulic short-circuit operation for grid stability issues close to a large concentration of energy consumers. In fact, it could be possible to make existing Run-of-River (ROR) power plants operate in a less ROR-like manner. With little or no power production in the power plant, the water level effect of the inflow of water in the upper reservoir could be compensated for by removing the air from the balloons in this reservoir. The same air could be added to the balloons downstream of the powerplant, displacing water and maintaining the flow to the downstream river sections, as seen in Figure 7. When power is needed, the power plant can be ramped up or brought on-line, producing large amounts of power as the air is cycled back again, mitigating any water level and the discharge fluctuations of the reservoir and river. This would change the merit order of the power plant and provide a much-needed addition to the flexibility of the electrical system, allowing the higher penetration of intermittent renewable energy sources into the system.

For hydropower plants (without pumping capabilities), there might be limitations on their operation due to restrictions on the allowed water level in the reservoirs. This is the case for several Nordic hydropower plants, in which the restrictions are typically linked to the summer water level due to fish migration, recreation, transport, etc. The power production capabilities are thus greatly reduced because the level is linked to the volume, and the production of power reduces the volume and thus reduce the level. In such cases, using compressed air to displace volume would lift or ease the restriction, and the installed capacity would be available for a duration corresponding to the available maximum volume of air. Interestingly, this volume of air is then also available as a volume for flood damping, as the overflow of water can be avoided as the air is expanded, storing the flood. Flood reduction by hydropower reservoirs has great potential socio-economic value; in Norway, as one example, conservative estimates on some waterways estimate several hundreds of million Euros could be saved by the flood dampening capabilities of such reservoirs [18]. As precipitation is expected to be more intense, the capabilities for flood damping by existing hydropower reservoirs might not be sufficient. Furthermore, the Norwegian Water Resources and Energy Directorate has stated that, in a phase where concessions are being renewed, environmental and recreational concerns will be given more weight and will lead to less flexibility due to stronger water level restrictions. This has made Statkraft—the biggest producer of renewable energy in Europe—raise concerns about the future capability of flood protection in Norway [19].

Another possible use of ACUR is at storage hydropower plants with outlets to rivers. Storage power plants are very important for the balancing of the grid because they have the energy storage and power capacity needed to balance baseload generation, intermittent generation and consumption via market mechanisms. This is typically referred to as “hydropeaking” [20]. However, outlets to rivers are often problematic because the discharge to the river can violently fluctuate according to the hydropeaking of the power plant. This is a serious environmental problem because it significantly alters the natural dynamic characteristics of the river flow, affecting the ecology in a negative and often unacceptable way [21]. There are ways of reducing the effect of hydropeaking, and retention/compensation basins are examples of constructional measures [22]. However, there are limitations concerning the flexibility enabled by such basins as well, and additional measures are likely to increase the flexibility further. Using ACUR as a temporary water storage volume and compressed air as an active measure to control the flow out of ACUR will make it possible to smoothen the discharge transients at large operational changes, starts and stops. The layout of this can be seen in Figure 8.

This application of ACUR is currently being investigated in the EU Horizon 2020 project HydroFlex, and the findings are that ACUR is able to smoothen the discharge well, providing the possibility of much faster ramp up/start up and ramp down/shut down of the power plants within current environmental restrictions. This can be seen in Figure 9 and Figure 10, respectively. These results are obtained from a simulation of the power plant Bratsberg [23], which has two identical units. The “Q setpoint” is the target for the governor, which is implemented to control the compressor providing an active use of the ACUR element and represents current limitations due to environmental restrictions. “Q at discharge” is the discharge into the downstream river that results from the operation of the ACUR element. As can be seen, the start-up and shut-down of the units can be performed much faster than the targeted flow due to the presence of the governed ACUR element. The ACUR technique significantly increasing the flexibility of the units. The analysis corresponds to TRL3 and is regarded as proof of concept by the authors.

3.3. Environmental Operation

Several of the applications already described might be categorized as being initiated by environmental concerns. However, other operations might give additional environmental benefits. In large hydropower and irrigation reservoirs, water can become stagnant and result in an increase in parasitic diseases [24] and other organisms associated with human illness [25]. In such cases, a grid of balloons could be used (a minimum of two if the overall water level is to be kept constant) to circulate water by inflating some balloons with a volume rate of air and at the same time deflating some balloons with the same rate. In this way, water is set in motion within the reservoir. This would contribute to preventing negative effects from occurring due to stagnant water, simply because it would be less stagnant. Such systems are not limited to rivers and power production and can be of interest for the storage of water in general. As a final remark on this, it is noted that most of the undeveloped hydropower potential is in Africa, South America and Asia [26], in climates where there are challenges associated with these kinds of problems.

4. Discussion

The authors recognize that the concepts described in this paper are far from being deployed, and much research and development is needed before the concepts reach a TRL which make it ready for field-testing. However, the authors see no major technological challenges related to these concepts. Compressors exist today that move large volumes of air against low pressures. The compression heat and subsequent energy loss is not very high for low pressures, if energy recovery from the compressed air is necessary. Constructing caverns and trapping air is understood and has been successfully applied, even at high pressures. Balloons have been made which are intended to be inflated/deflated by air, even at high pressures. Anchoring balloons to the bottom of a reservoir should be a matter of dimensioning.

5. Conclusions

Climate change is expected to make the task of future water management more difficult. The presented concepts represent a new degree of freedom, which might facilitate this task and make better use of existing infrastructure. The high degree of conceptuality presented in this paper, along with no indication of cost, makes conclusions on an applicable level difficult. However, the intention of the paper is to stimulate out-of-the-box thinking and the assessment of possible applications among engineers and researchers throughout the community. No technical challenges have been identified that makes the concepts unfeasible, but further research and development must be performed.