Quantifying the Uncertainty Related to Climate Change in the Assessment of Urban Flooding—A Case Study
Abstract
1. Introduction
2. Materials and Methods
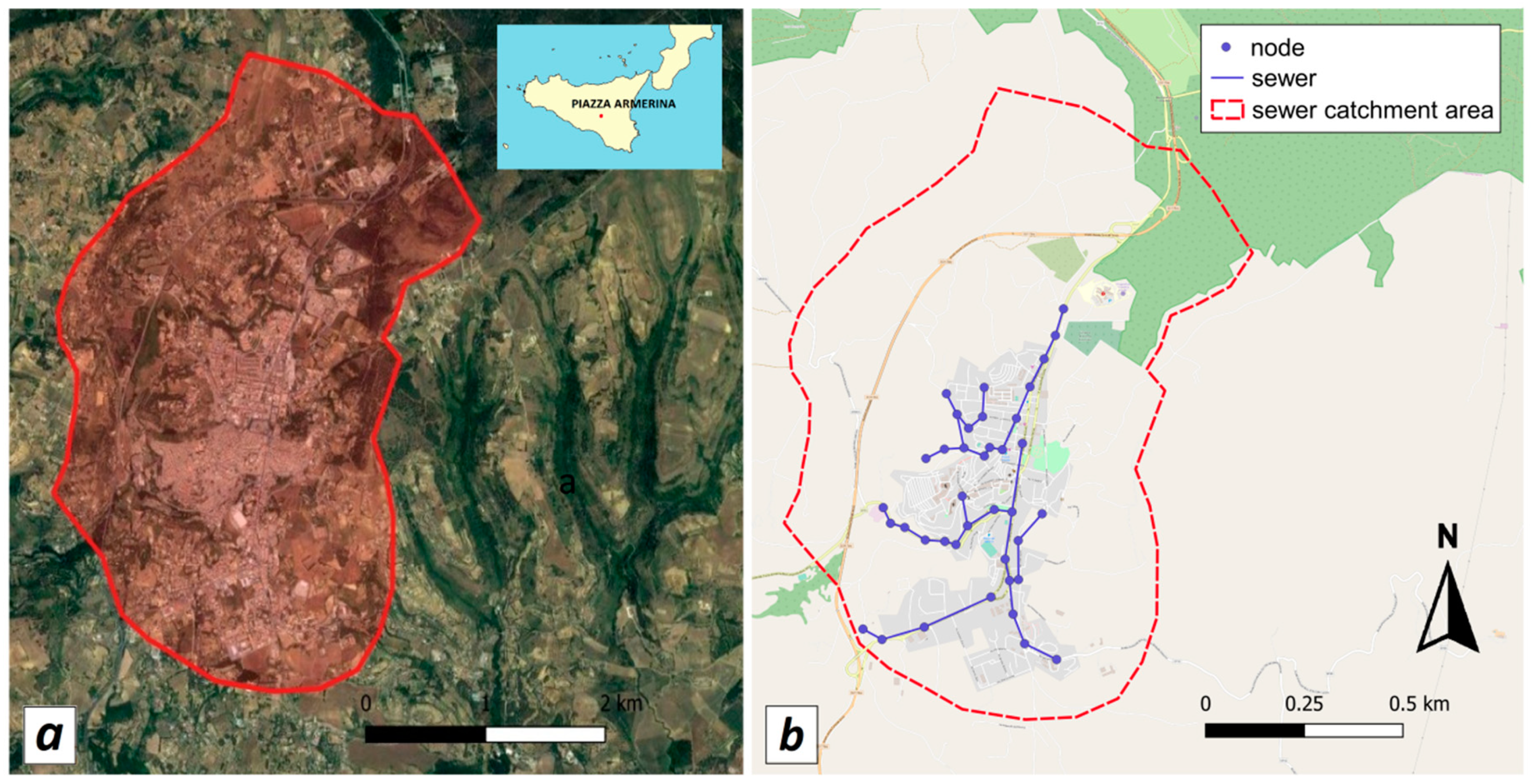
2.1. Case Study and Dataset
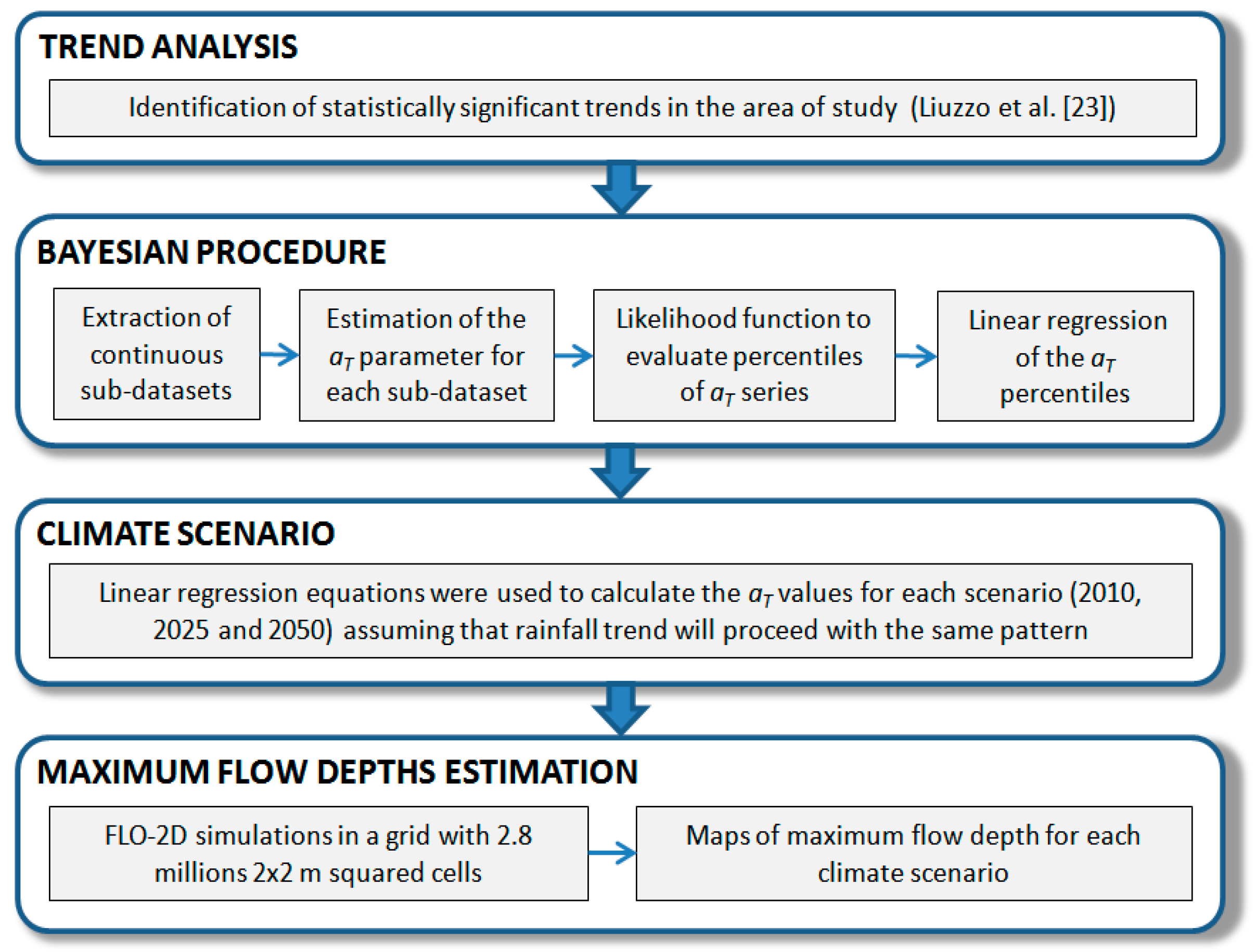
2.2. Estimation of DDF Curve Parameters in Climate Change Scenarios
- From the original dataset, several continuous sub-datasets with different ending years and lengths were extracted. Specifically, starting from a minimum of 15 years, the length of each sub-dataset was increased by one, up to a maximum of 35 years. This choice was based on the evidence that an intensification of the hydrological cycle occurred in the last 30–35 years [27]. Moreover, this assumption is furtherly supported by the evidence of a statistically significant increase of the average annual rainfall during the last 30 years in Sicily [28];
- The aT parameter was estimated for each of the above-mentioned sub-datasets;
- The likelihood function was used to evaluate the 95th, 50th, and 5th percentiles of each aT series.
2.3. The Hydraulic Model: FLO-2D
3. Results
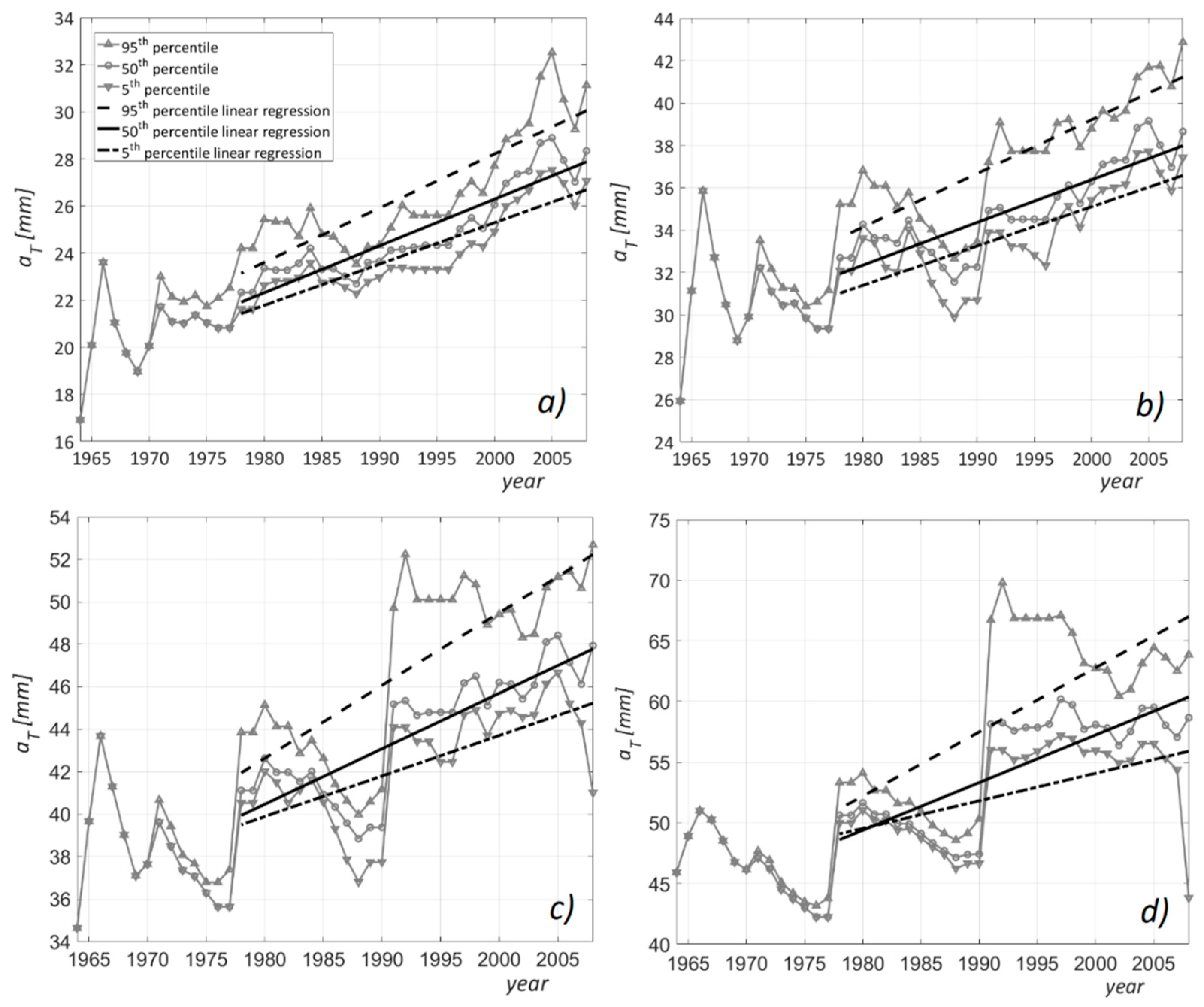
3.1. DDF Curves Parameters
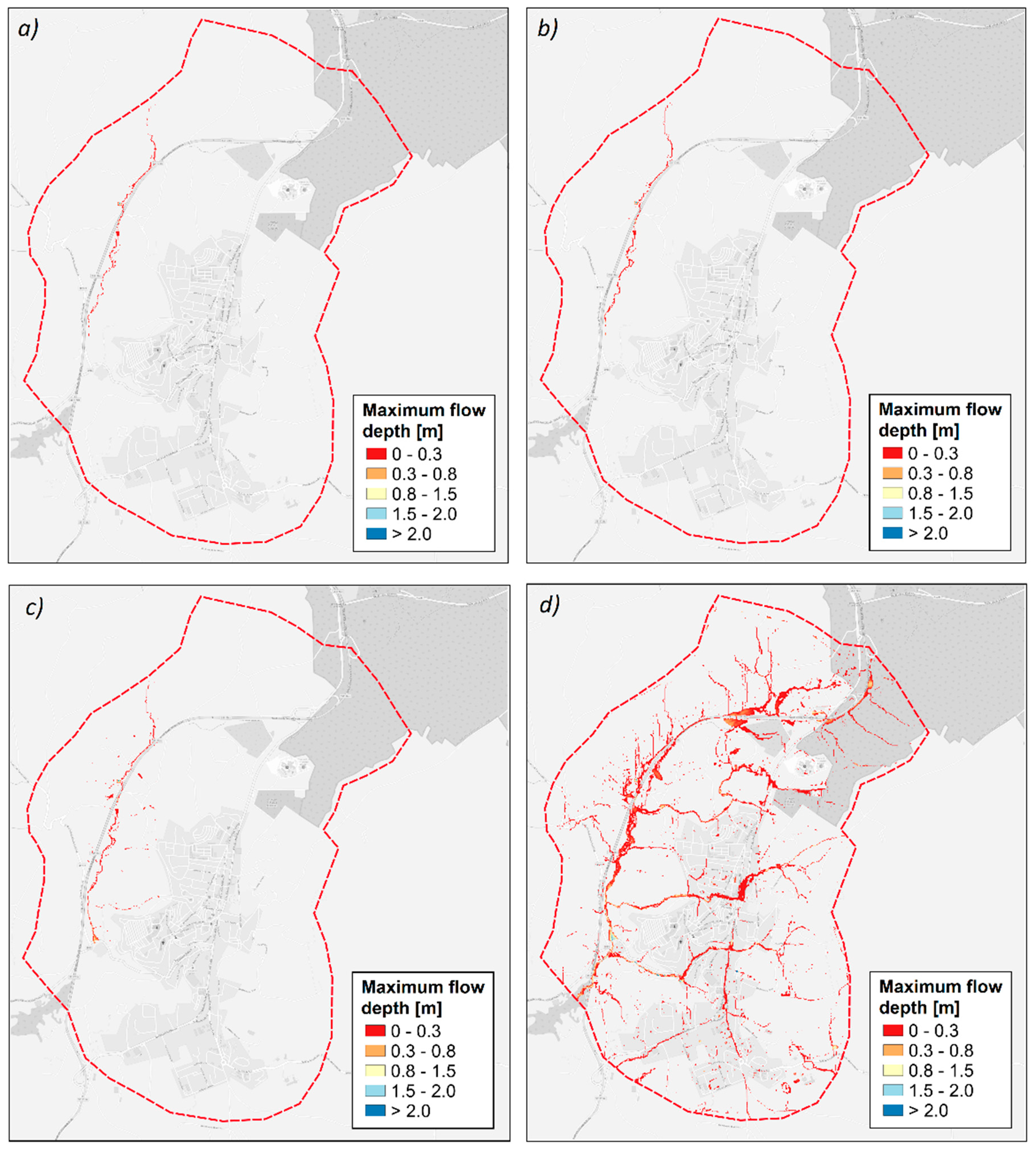
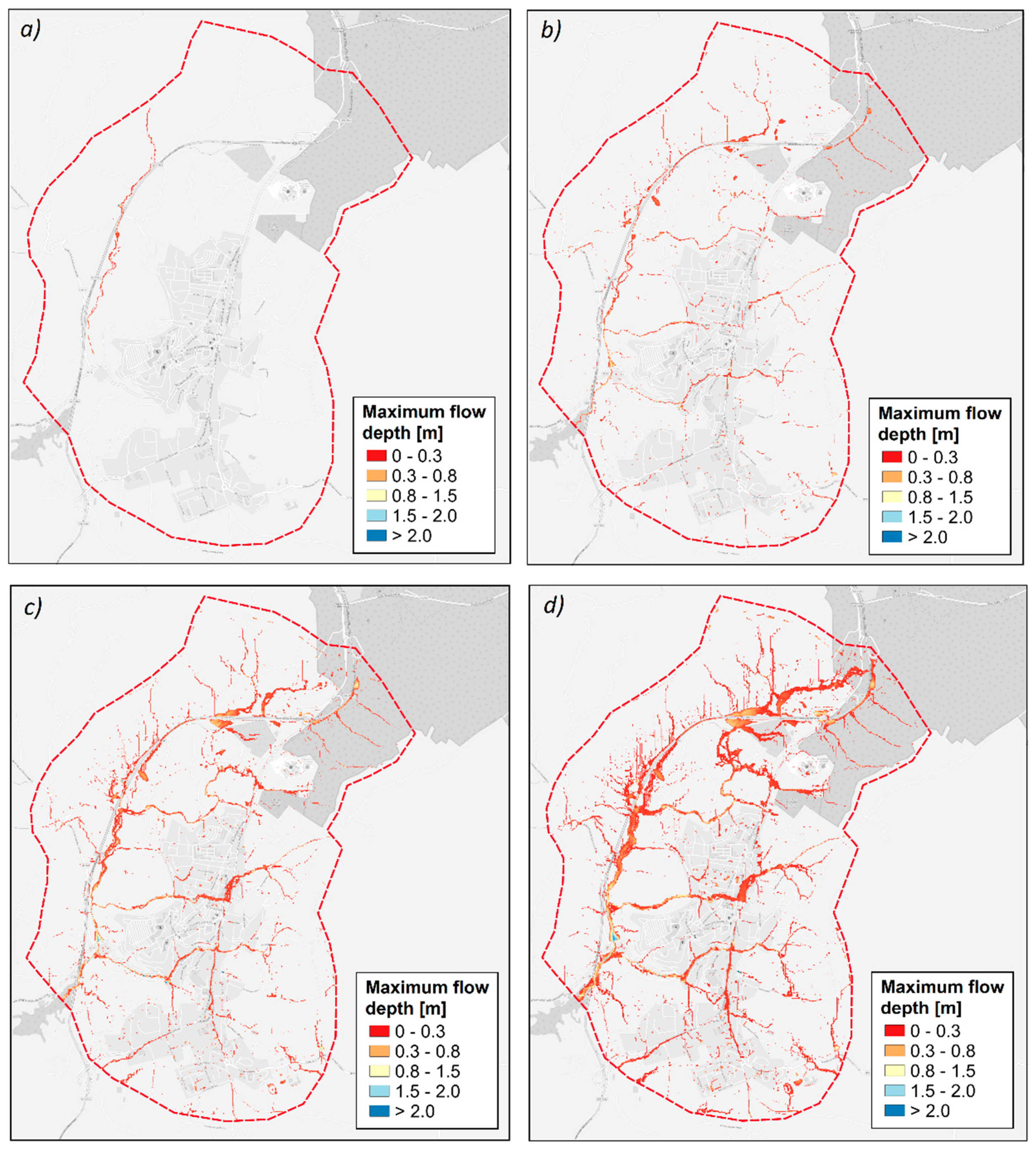
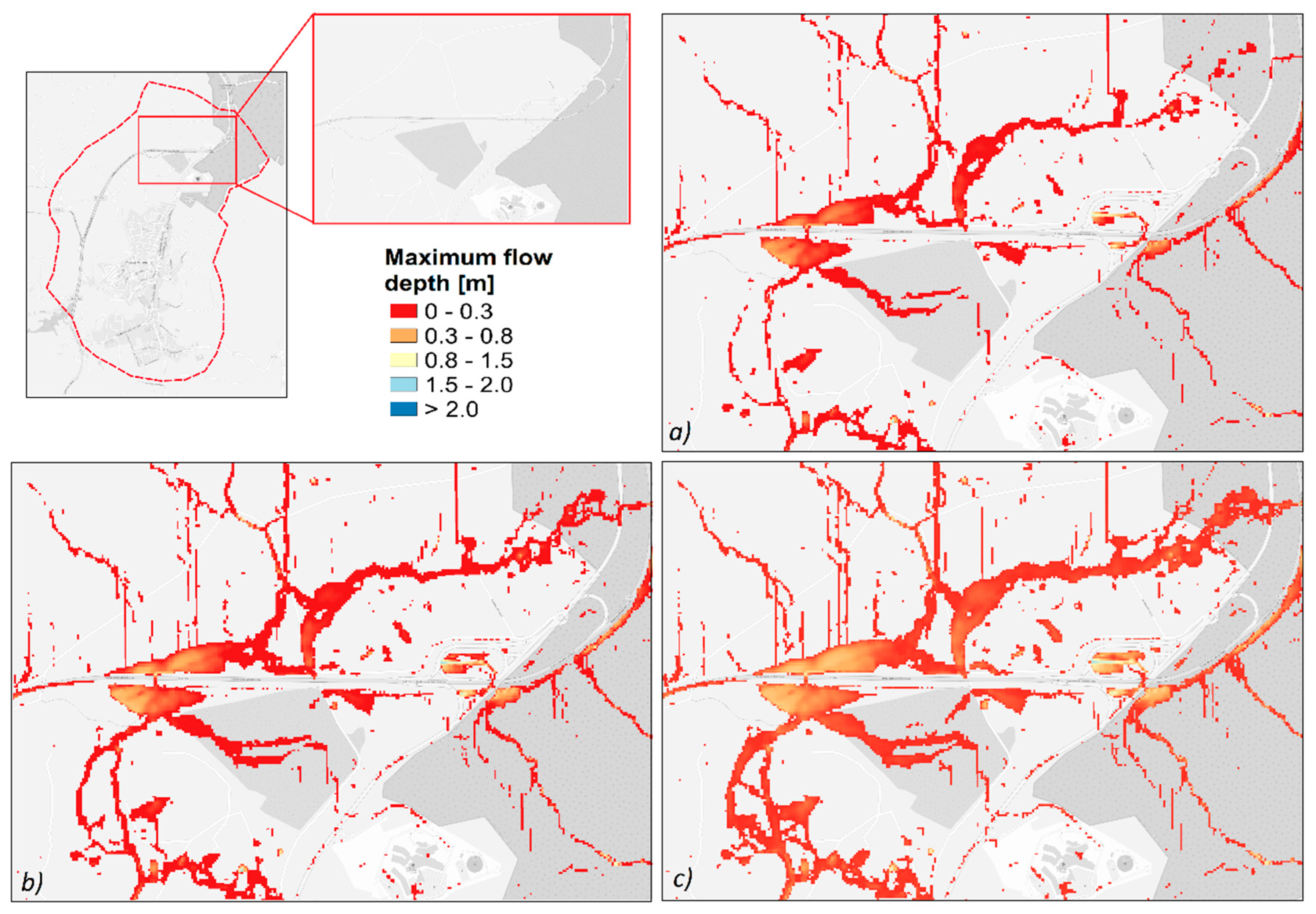
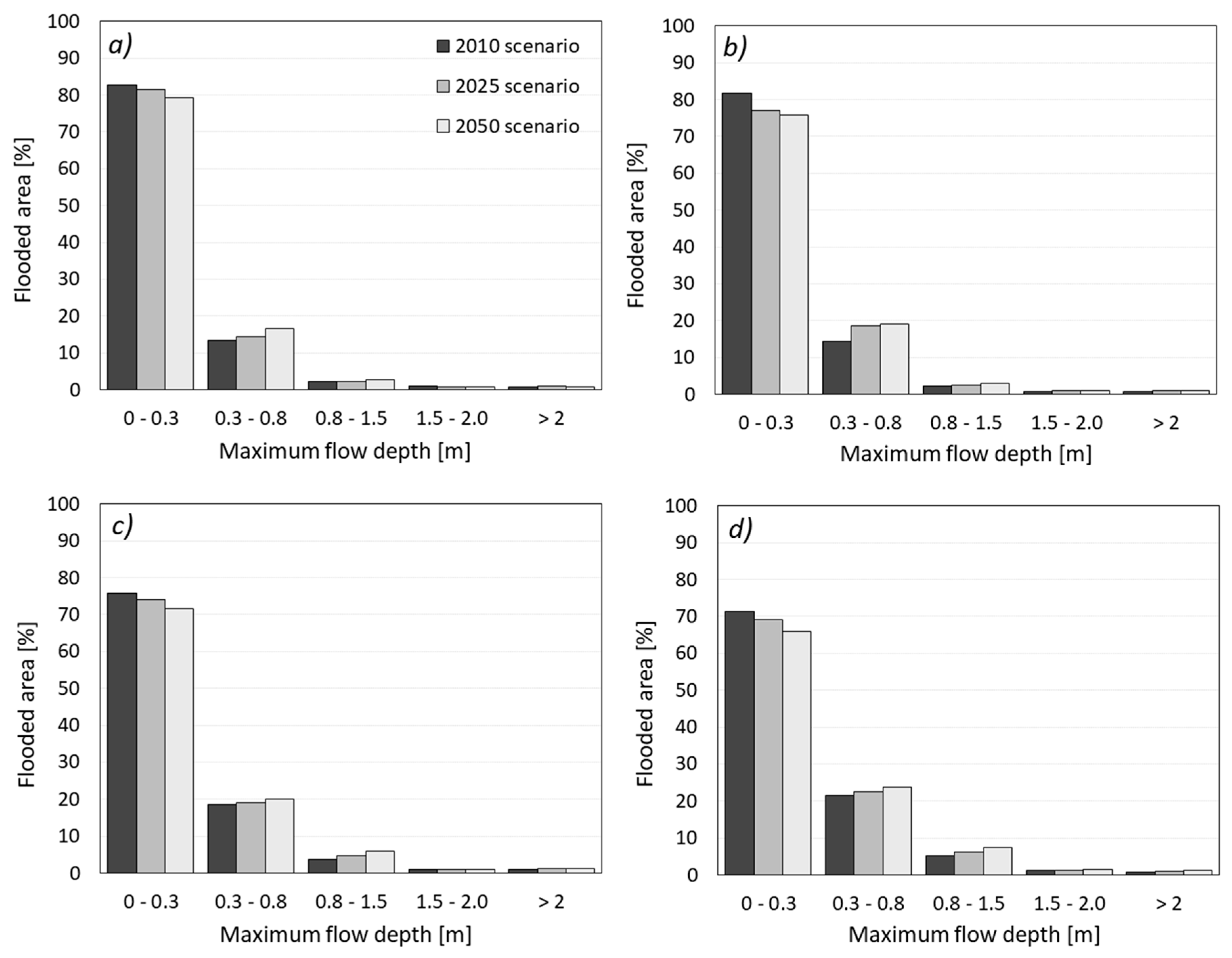
3.2. Maps of Maximum Flow Depths
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Portmann, R.W.; Solomon, S.; Hegerl, G.C. Spatial and seasonal patterns in climate change, temperatures, and precipitation across the United States. Proc. Natl. Acad. Sci. USA 2009, 106, 7324–7329. [Google Scholar] [CrossRef] [PubMed]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Hewitson, B. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global increasing trends in annual maximum daily precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Arisz, H.; Burrell, B.C. Urban drainage infrastructure planning and design considering climate change. In Proceedings of the 2006 IEEE EIC Climate Change Conference, Ottawa, ON, Canada, 10–12 May 2006. [Google Scholar]
- Arnbjerg-Nielsen, K.; Fleischer, H.S. Feasible adaptation strategies for increased risk of flooding in cities due to climate change. Water Sci. Technol. 2009, 60, 273–281. [Google Scholar] [CrossRef] [PubMed]
- Freni, G.; La Loggia, G.; Notaro, V. Uncertainty in urban flood damage assessment due to urban drainage modelling and depth-damage curve estimation. Water Sci. Technol. 2010, 61, 2979–2993. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Bülow Gregersen, I.; Madsen, H.; Nguyen, V.-T.-V. Impacts of climate change on rainfall extremes and urban drainage systems: A review. Water Sci. Technol. 2013, 68, 16–28. [Google Scholar] [CrossRef]
- Schreider, S.Y.; Smith, D.I.; Jakeman, A.J. Climate change impacts on urban flooding. Clim. Chang. 2000, 47, 91–115. [Google Scholar] [CrossRef]
- Denault, C.; Millar, R.G.; Lence, B.J. Assessment of possible impacts of climate change in an urban catchment. J. Am. Water Res. Assoc. 2006, 42, 685–697. [Google Scholar] [CrossRef]
- Markus, M.; Wuebbles, D.J.; Liang, X.Z.; Hayhoe, K.; Kristovich, D.A. Diagnostic analysis of future climate scenarios applied to urban flooding in the Chicago metropolitan area. Clim. Chang. 2012, 111, 879–902. [Google Scholar] [CrossRef]
- Huong, H.T.L.; Pathirana, A. Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol. Earth Syst. Sci. 2013, 17, 379–394. [Google Scholar] [CrossRef]
- Zhou, Q.; Leng, G.; Huang, M. Impacts of future climate change on urban flood volumes in Hohhot in northern China: Benefits of climate change mitigation and adaptations. Hydrol. Earth Syst. Sci. 2018, 22, 305–316. [Google Scholar] [CrossRef]
- Da Silva, C.; Schardong, A.; Garcia, J.; Oliveira, C. Climate change impacts and flood control measures for highly developed urban watersheds. Water 2018, 10, 829. [Google Scholar] [CrossRef]
- Andimuthu, R.; Kandasamy, P.; Mudgal, B.V.; Jeganathan, A.; Balu, A.; Sankar, G. Performance of urban storm drainage network under changing climate scenarios: Flood mitigation in Indian coastal city. Sci. Rep. 2019, 9, 7783. [Google Scholar] [CrossRef] [PubMed]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden. Atmos Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Kaspersen, P.S.; Ravn, N.H.; Arnbjerg-Nielsen, K.; Madsen, H.; Drews, M. Influence of urban land cover changes and climate change for the exposure of European cities to flooding during high-intensity precipitation. Proc. IAHS 2015, 370, 21–27. [Google Scholar] [CrossRef]
- Ashley, R.; Tait, S.; Cashman, A.; Blanksby, J.; Hurley, A.L.; Sandlands, L.; Saul, A. 21st Sewerage Design; Full Report, UKWIR Report 06/WM07/7; UK Water Industry Research: London, UK, 2006. [Google Scholar]
- Abdellatif, M.; Atherton, W.; Alkhaddar, R.; Osman, Y. Flood risk assessment for urban water system in a changing climate using artificial neural network. Nat Hazards 2015, 79, 1059–1077. [Google Scholar] [CrossRef]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V.T.V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Archetti, R.; Bolognesi, A.; Casadio, A.; Maglionico, M. Development of flood probability charts for urban drainage network in coastal areas through a simplified joint assessment approach. Hydrol. Earth Syst. Sci. 2011, 15, 3115–3122. [Google Scholar] [CrossRef]
- Krasovskaia, I.; Gottschalk, L. Stability of river flow regimes. Hydrol. Res. 1992, 23, 137–154. [Google Scholar] [CrossRef]
- Notaro, V.; Liuzzo, L.; Freni, G.; La Loggia, G. Uncertainty analysis in the evaluation of extreme rainfall trends and its implications on urban drainage system design. Water 2015, 7, 6931–6945. [Google Scholar] [CrossRef]
- Liuzzo, L.; Notaro, V.; Freni, G. Uncertainty related to climate change in the assessment of the DDF curve parameters. Environ. Model. Softw. 2017, 96, 1–13. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two-Dimensional Water Flood and Mudflow Simulation. J. Hydraul. Eng. 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Liuzzo, L.; Freni, G. Analysis of extreme rainfall trends in Sicily for the evaluation of depth-duration-frequency curves in climate change scenarios. J. Hydrol. Eng. 2015, 20, 04015036. [Google Scholar] [CrossRef]
- Notaro, V.; Fontanazza, C.M.; Freni, G.; La Loggia, G. Assessment of Modelling Structure and Data Availability Influence on Urban Flood Damage Modelling Uncertainty. Procedia Eng. 2014, 89, 788–795. [Google Scholar] [CrossRef][Green Version]
- Vose, R.S.; Easterling, D.R.; Gleason, B. Maximum and minimum temperature trends for the globe: An update through 2004. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Glantz, M. Societal Responses to Climate Change: Forecasting by Analogy, No. 35; Westview Press: Boulder, CO, USA, 1988. [Google Scholar]

| T (Years) | Scenario | nT | aT (mm) | ||
|---|---|---|---|---|---|
| 95th Percentile | 50th Percentile | 5th Percentile | |||
| 2 | 2010 | 0.27 | 30.5 | 28.3 | 27.0 |
| 2025 | 0.27 | 34.0 | 31.3 | 29.7 | |
| 2050 | 0.27 | 39.7 | 36.2 | 34.1 | |
| 5 | 2010 | 0.32 | 41.7 | 38.4 | 37.0 |
| 2025 | 0.32 | 45.5 | 41.4 | 39.7 | |
| 2050 | 0.32 | 51.9 | 46.4 | 44.4 | |
| 10 | 2010 | 0.29 | 52.9 | 48.3 | 45.6 |
| 2025 | 0.29 | 58.1 | 52.2 | 48.5 | |
| 2050 | 0.29 | 66.6 | 58.8 | 53.2 | |
| 20 | 2010 | 0.29 | 68.0 | 61.1 | 56.3 |
| 2025 | 0.29 | 76.0 | 67.0 | 59.7 | |
| 2050 | 0.29 | 89.2 | 76.8 | 65.4 | |
| Scenario | Return Period (Years) | Flooded Area (km2) | ||
|---|---|---|---|---|
| 95th Percentile | 50th Percentile | 5th Percentile | ||
| 2010 | 2 | 0.020 | 0.019 | 0.018 |
| 5 | 0.042 | 0.021 | 0.020 | |
| 10 | 0.274 | 0.034 | 0.025 | |
| 20 | 0.788 | 0.603 | 0.441 | |
| 2025 | 2 | 0.021 | 0.020 | 0.019 |
| 5 | 0.164 | 0.029 | 0.024 | |
| 10 | 0.507 | 0.243 | 0.094 | |
| 20 | 0.788 | 0.764 | 0.556 | |
| 2050 | 2 | 0.023 | 0.022 | 0.021 |
| 5 | 0.472 | 0.225 | 0.111 | |
| 10 | 0.750 | 0.523 | 0.276 | |
| 20 | 1.258 | 0.970 | 0.719 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liuzzo, L.; Freni, G. Quantifying the Uncertainty Related to Climate Change in the Assessment of Urban Flooding—A Case Study. Water 2019, 11, 2072. https://doi.org/10.3390/w11102072
Liuzzo L, Freni G. Quantifying the Uncertainty Related to Climate Change in the Assessment of Urban Flooding—A Case Study. Water. 2019; 11(10):2072. https://doi.org/10.3390/w11102072
Chicago/Turabian StyleLiuzzo, Lorena, and Gabriele Freni. 2019. "Quantifying the Uncertainty Related to Climate Change in the Assessment of Urban Flooding—A Case Study" Water 11, no. 10: 2072. https://doi.org/10.3390/w11102072
APA StyleLiuzzo, L., & Freni, G. (2019). Quantifying the Uncertainty Related to Climate Change in the Assessment of Urban Flooding—A Case Study. Water, 11(10), 2072. https://doi.org/10.3390/w11102072






