Large Scale Flood Hazard Analysis by Including Defence Failures on the Dutch River System
Abstract
1. Introduction
1.1. Load Interdependencies
1.2. Spatial Aspects of Load Interdependencies
2. Load Interdependencies in The Netherlands
3. Methodology
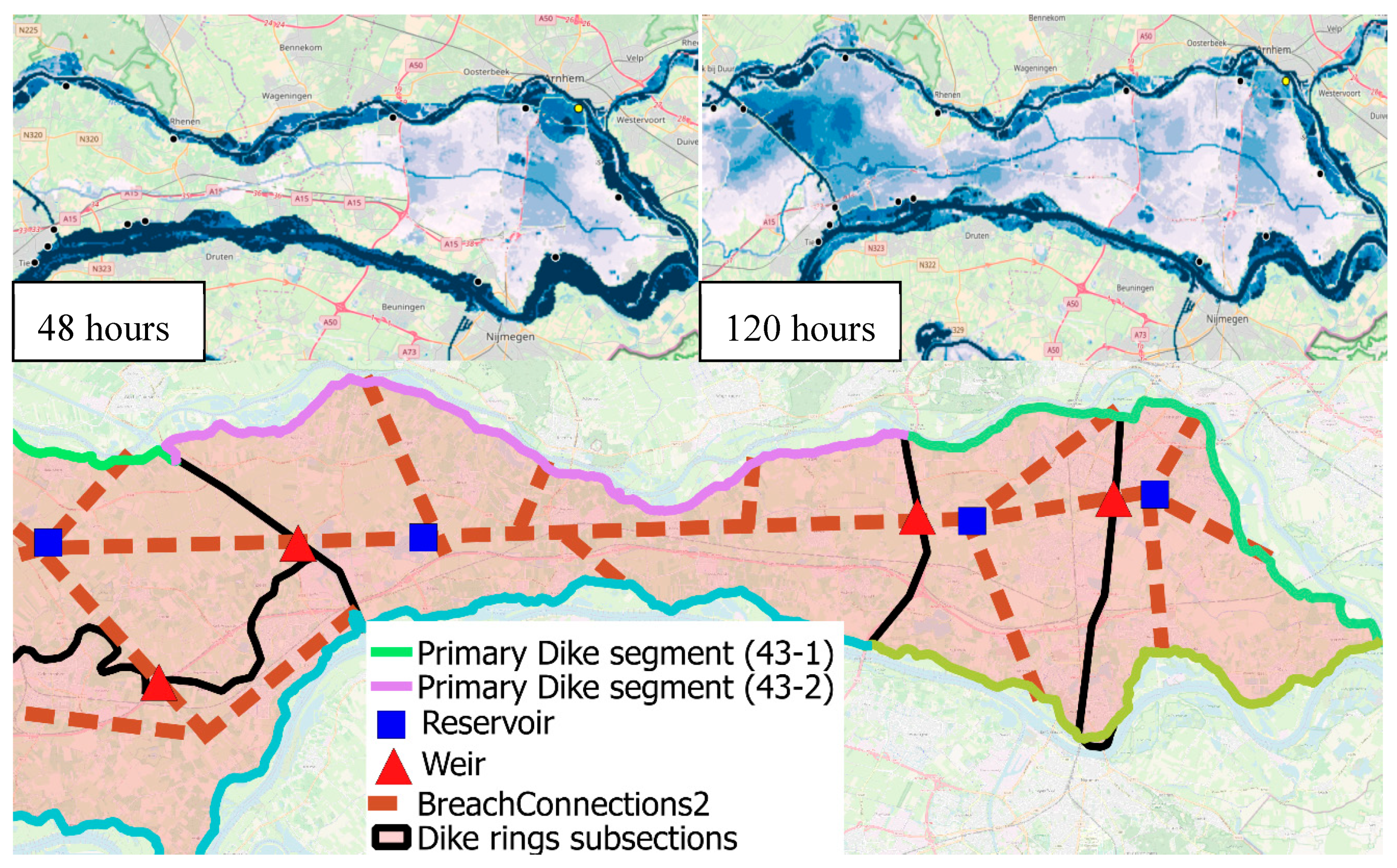
3.1. Case Study
3.2. Computational Framework and Scenarios
4. Results and Discussion
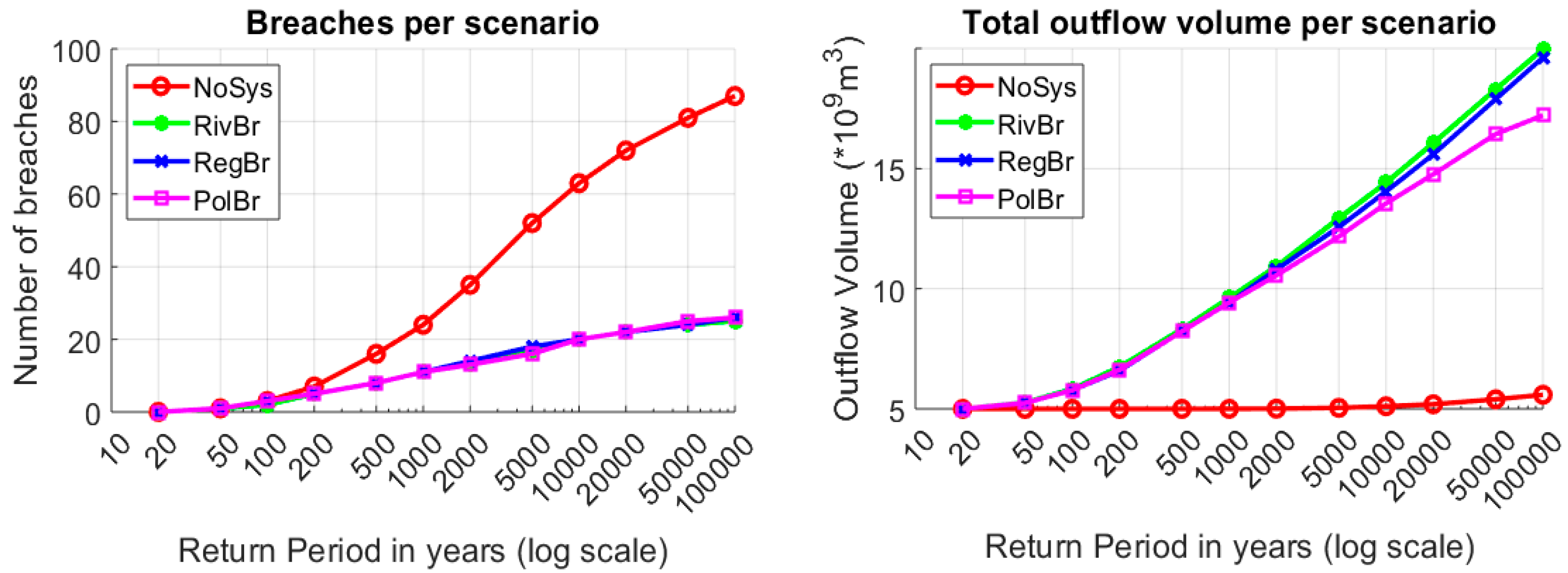
4.1. Overall System
4.2. A: Dike Ring 43
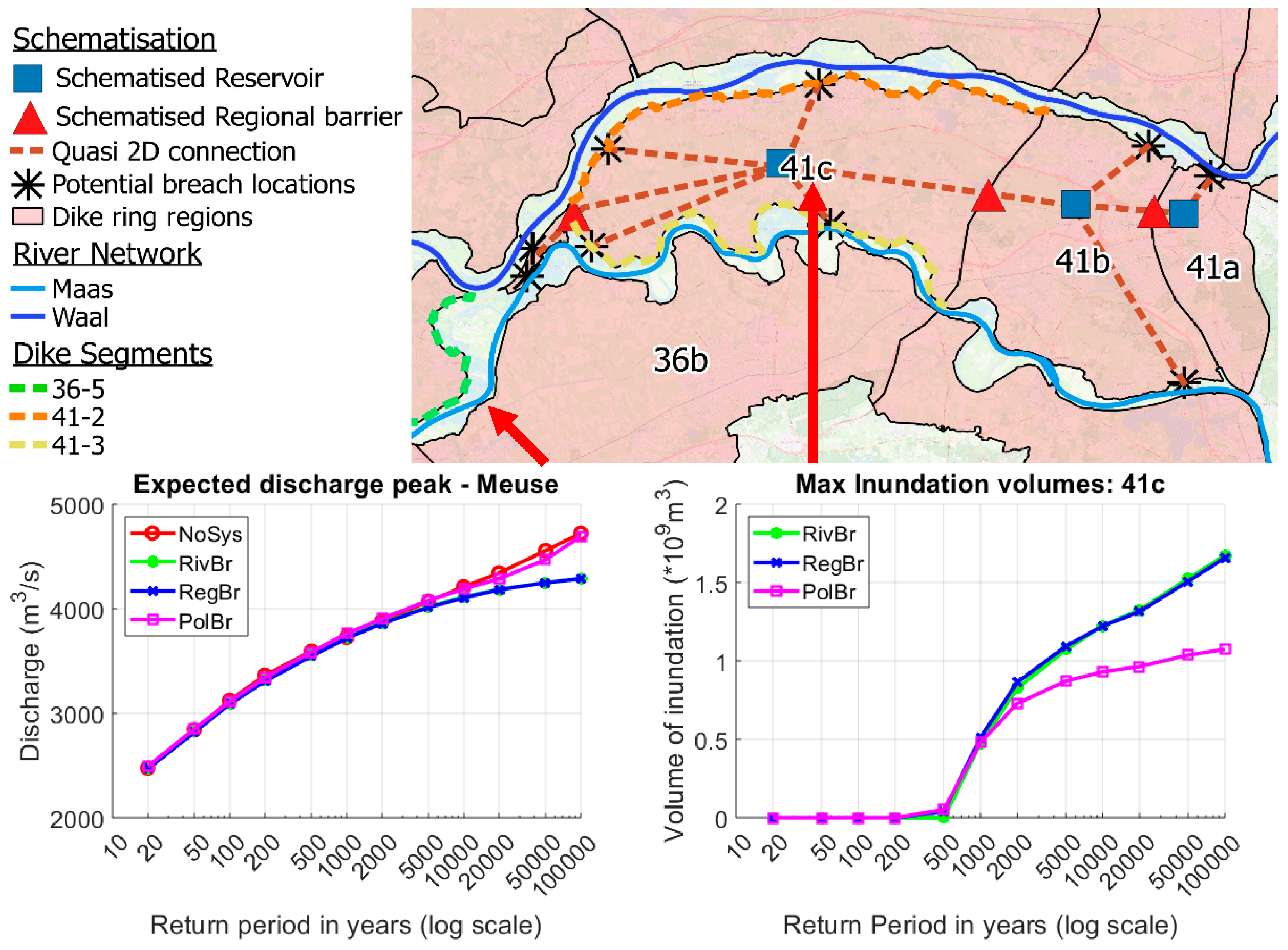
4.3. B: Dike Ring 41
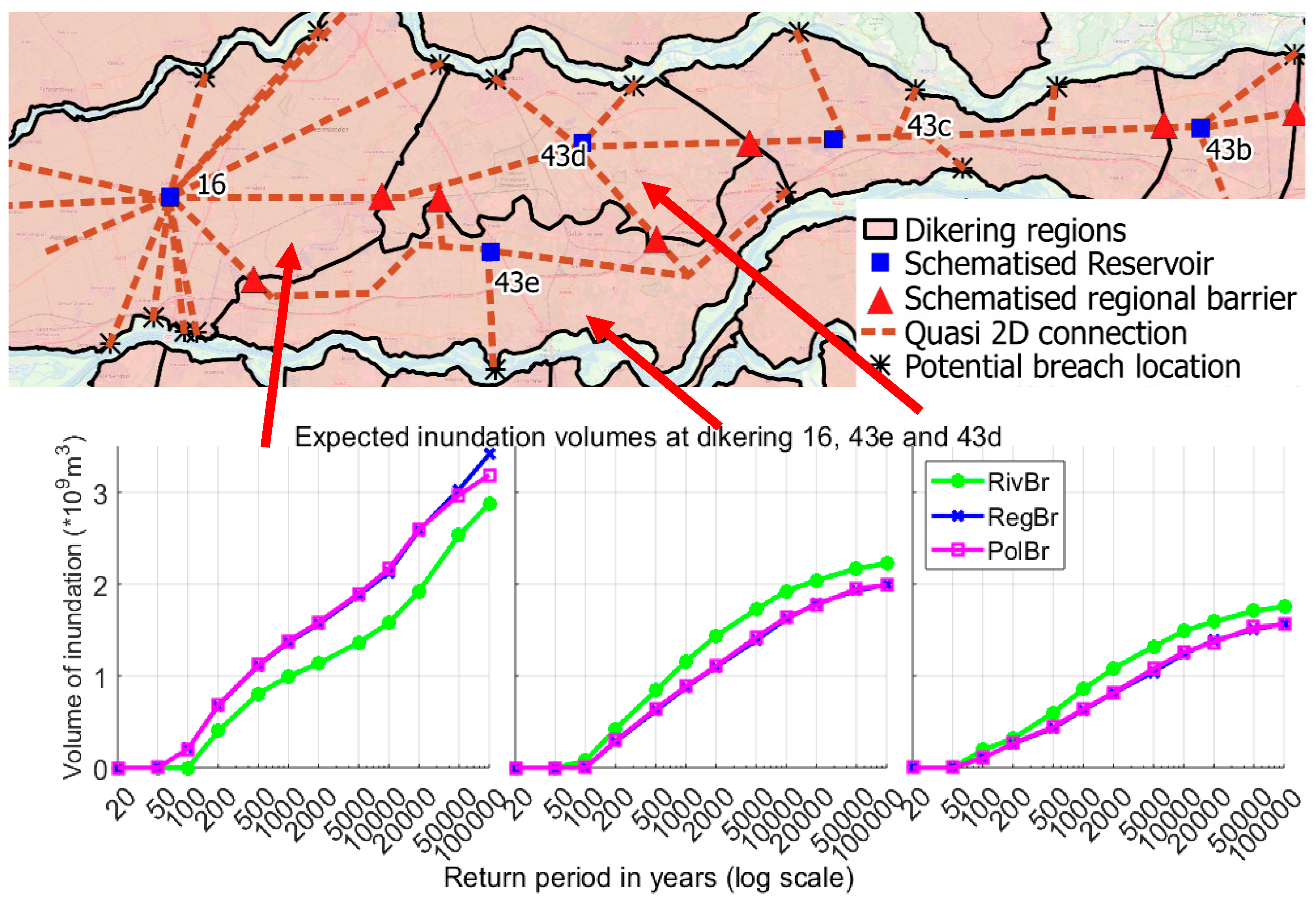
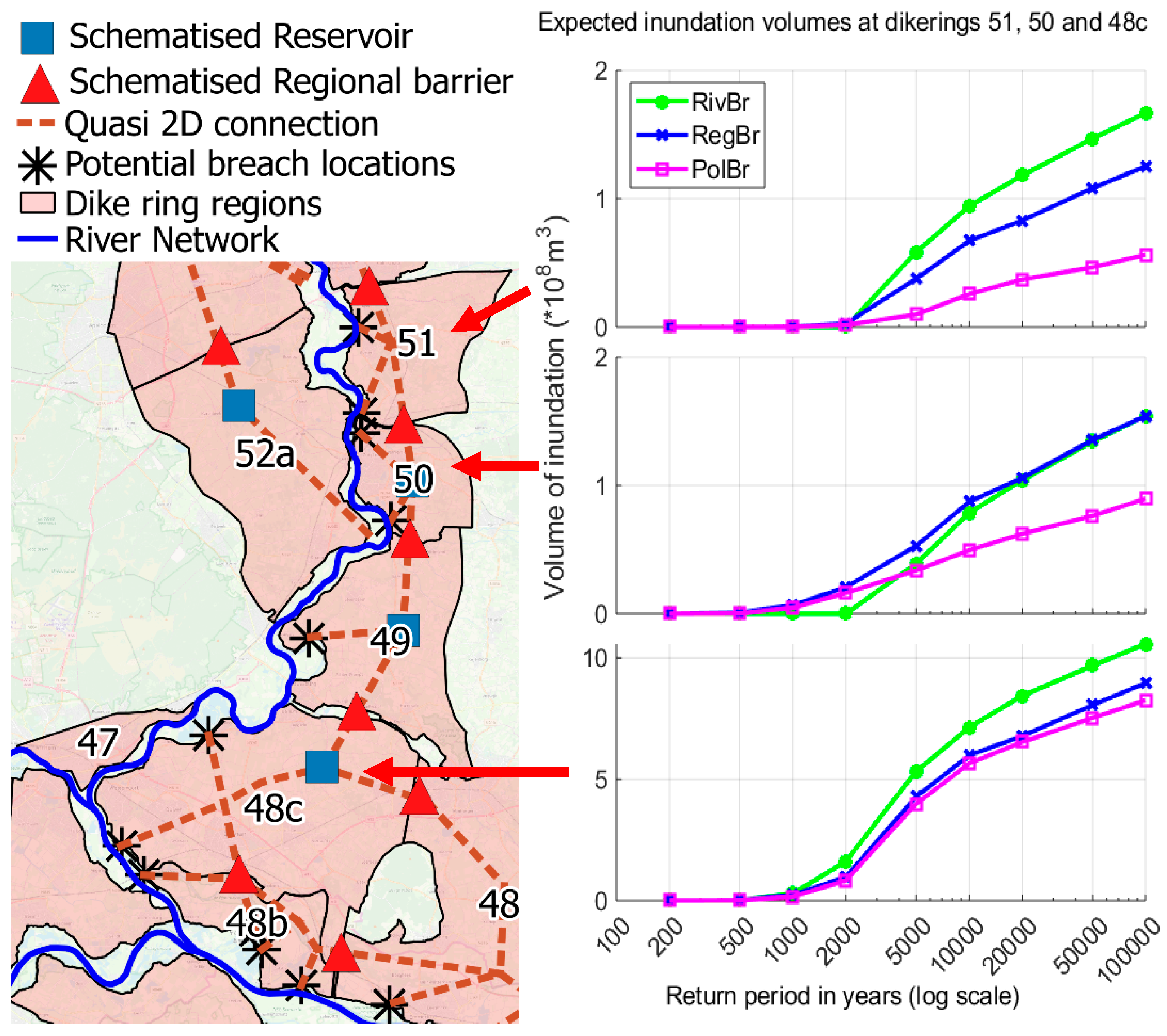
4.4. IJssel Valley
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Klerk, W.J. Load Interdependencies of Flood Defences. Master’s Thesis, TU Delft Faculty of Civil Engineering and Geosciences, Delft, The Netherlands, 2013. [Google Scholar]
- Van Mierlo, M.C.L.M.; Vrouwenvelder, A.C.W.M.; Calle, E.O.F.; Vrijling, J.K.; Jonkman, S.N.; de Bruijn, K.M.; Weerts, A.H. Assessment of flood risk accounting for river system behaviour. Int. J. River Basin Manag. 2010, 5, 93–104. [Google Scholar] [CrossRef]
- De Bruijn, K.M.; Diermanse, F.L.M.; Beckers, J.V.L. An advanced method for flood risk analysis in river deltas, applied to societal flood fatality risk in the Netherlands. Nat. Hazards Earth Syst. Sci. 2014, 14, 2767–2781. [Google Scholar] [CrossRef]
- Gouldby, B.; Lhomme, J.; Mcgahey, C.; Panzeri, M.; Hassan, M.; Burgada, N.K.; Magaña Orue, C.; Jamieson, S.; Wright, G.; Van Damme, M.; et al. A flood system risk analysis model with dynamic sub-element 2D inundation model, dynamic breach growth and life-loss. In Proceedings of the 2nd European Conference on Flood Risk Management, FLOODrisk2012, Rotterdam, The Netherlands, 19–23 November 2012. [Google Scholar]
- Vorogushyn, S.; Bates, P.D.; De Bruijn, K.; Castellarin, A.; Kreibich, H.; Priest, S.; Schröter, K.; Bagli, S.; Blöschl, G.; Domeneghetti, A.; et al. Evolutionary leap in large-scale flood risk assessment needed. Wiley Interdiscip. Rev. Water 2017, 5, e1266. [Google Scholar] [CrossRef]
- Ciullo, A.; De Bruijn, K.M.; Kwakkel, J.H.; Klijn, F. Accounting for the uncertain effects of hydraulic interactions in optimising embankments heights: Proof of principle for the IJssel River. J. Flood Risk Manag. 2019, e12532. [Google Scholar] [CrossRef]
- Dupuits, E.J.C.; Bruijn, K.M.D.; Diermanse, F.L.M.; Kok, M. Economically optimal safety targets for riverine flood defence systems. In Proceedings of the FLOODrisk 2016—3rd European Conference on Flood Risk Management, Lyon, France, 17–21 October 2016. [Google Scholar] [CrossRef]
- Dupuits, E.J.C.; Klerk, W.J.; Schweckendiek, T.; de Bruijn, K.M. Impact of including interdependencies between multiple riverine flood defences on the economically optimal flood safety levels. Reliab. Eng. Syst. Saf. 2019, 191, 106475. [Google Scholar] [CrossRef]
- De Bruijn, K.; Beckers, J.; Van Der Most, H. Casualty risks in the discussion on new flood protection standards in The Netherlands. WIT Trans. Ecol. Environ. 2010, 133, 73–83. [Google Scholar]
- Assteerawatt, A.; Tsaknias, D.; Azemar, F.; Ghosh, S.; Hilberts, A. Large-scale and High-resolution Flood Risk Model for Japan. In Proceedings of the FLOODrisk 2016—3rd European Conference on Flood Risk Management, Lyon, France, 17–21 October 2016; p. 11009. [Google Scholar]
- Dunn, C.; Baker, P.; Fleming, M. Flood risk management with HEC-WAT and the FRA compute option. In Proceedings of the FLOODrisk 2016—3rd European Conference on Flood Risk Management, Lyon, France, 17–21 October 2016; p. 11006. [Google Scholar] [CrossRef]
- Apel, H.; Merz, B.; Thieken, A.H. Influence of dike breaches on flood frequency estimation. Comput. Geosci. 2009, 35, 907–923. [Google Scholar] [CrossRef]
- Kiss, T.; Fehérváry, I.; Fiala, K. Modelling the Hydrological Effects of a Levee Failure on the Lower Tisza River. J. Environ. Geogr. 2015, 8, 31–38. [Google Scholar] [CrossRef]
- Diermanse, F.L.M.; Carroll, D.G.; Beckers, J.V.L.; Ayre, R.; Schuurmans, J.M. A Monte Carlo framework for the Brisbane River catchment flood study. In Hydrology and Water Resources Symposium 2014; Engineers Australia: Barton, Australia, 2014; p. 62. [Google Scholar]
- Curran, A.; De Bruijn, K.M.; Kok, M. Influence of water level duration on dike breach triggering, focusing on system behaviour hazard analyses in lowland rivers. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2018, 1–15. [Google Scholar] [CrossRef]
- Wojciechowska, K.; Pleijter, G.; Zethof, M.; Havinga, F.J.; Van Haaren, D.H.; Ter Horst, W.L.A. Application of Fragility Curves in Operational Flood Risk Assessment. Geotech. Saf. Risk V 2015, 524–529. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Vorogushyn, S.; Castellarin, A.; Merz, B.; Brath, A. Probabilistic flood hazard mapping: Effects of uncertain boundary conditions. Hydrol. Earth Syst. Sci. 2013, 17, 3127–3140. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Merz, B.; Lindenschmidt, K.-E.; Apel, H. A new methodology for flood hazard assessment considering dike breaches. Water Resour. Res. 2010, 46, 1–17. [Google Scholar] [CrossRef]
- Jongejan, R.; Maaskant, B.; Horst, W.; Havinga, F.J.; Roode, N.; Stefess, H. The VNK2-project: A fully probabilistic risk analysis for all major levee systems in the Netherlands. IAHS 2013, 357, 75–85. [Google Scholar]
- Diermanse, F.; Roscoe, K.; Ijmker, J.; Mens, M. Hydra-Ring: A computational framework to combine failure probabilities. EGU Gen. Assem. Conf. Abstr. 2013, 15, 11112. [Google Scholar]
- De Bruijn, K.M.; Diermanse, F.L.M.; Doef, M.; van der Doef, M.; Klijn, F. Hydrodynamic system behaviour: Its analysis and implications for flood risk management. E3S Web Conf. 2016, 7, 11001. [Google Scholar] [CrossRef]
- Verheij, H.J.; der Knaap, F.C.M. Modification breach growth model in HIS-OM. WL|Delft Hydraul. Q 2002, 3299, 2002. [Google Scholar]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Bhuyian, M.N.M.; Kalyanapu, A. Impact of spatial resolution on downstream flood hazard due to dam break events using probabilistic flood modeling. In Proceedings of the Dam Safety Conference, ASDSO, Providence, RI, USA, 8–12 September 2013. [Google Scholar]
- Bates, P.D.; De Roo, A.P.J. A simple raster based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Lhomme, J.; Sayers, P.; Gouldby, B.; Samuels, P.; Wills, M.; Mulet-marti, J. Recent development and application of a rapid flood spreading method. In Proceedings of the Flood Risk Management-Research and Practice, FLOODrisk 2008, Oxford, UK, 30 September–2 October 2008. [Google Scholar]
- Falter, D. A Novel Approach for Large-Scale Flood Risk Assessments: Continuous and Long-Term Simulation of the full Flood Risk Chain. Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2016; p. 96. [Google Scholar]
- De Bruijn, K.M. Resilience of the lowland part of the Mekong River. In NCR-days 2004; Research for Managing Rivers: Present and Future Issues; Netherlands Centre for River Studies: Delft, The Netherlands, 2005. [Google Scholar]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Dhondia, J.F.; Stelling, G.S. SOBEK one dimensional—Two dimensional integrated hydraulic model for flood simulation—Its capabilities and features explained. In Hydroinformatics; World Scientific: Hackensack, NJ, USA, 2004; pp. 1867–1874. [Google Scholar]
- Driessen, A.M.A.J. Watersnood Tussen Maas en Waal: Overstromingsrampen in Het Rivierengebied Tussen 1780 en 1810; Walburg Pers Zutphen: Zutphen, The Netherlands, 1994. [Google Scholar]
- De Moel, H.; Aerts, J.C.J.H.; Koomen, E. Development of flood exposure in the Netherlands during the 20th and 21st century. Glob. Environ. Chang. 2011, 21, 620–627. [Google Scholar] [CrossRef]
- Slomp, R. Implementing Risk Based Flood Defence Standards; Rijkswaterstaat: Rotterdam, The Netherlands, 2016. [Google Scholar]
- Jongejan, R.B.; Maaskant, B. Quantifying flood risks in the Netherlands. Risk Anal. 2015, 35, 252–264. [Google Scholar] [CrossRef] [PubMed]
- Ter Horst, W.L.A. Veiligheid Nederland in Kaart 2: Overstromingsrisico van dijkringgebieden 14, 15 en 44. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwju59DR1JDkAhVhxYsBHcrRCKMQFjAAegQIARAC&url=https%3A%2F%2Fwww.helpdeskwater.nl%2Fpublish%2Fpages%2F131662%2Fsysteemwerking_dijkringen_14-15-44.pdf&usg=AOvVaw0IZiORtQ1blVbw1FmI71lm (accessed on 20 August 2019).
- Van Mierlo, M.C.L.M.; Vrouwenvelder, A.C.W.M.; Calle, E.O.F.; Vrijling, J.K.; Jonkman, S.N.; de Bruijn, K.; Weerts, A.H. Effects of River System Behaviour on Flood Risk. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwjUkLjc1pDkAhV6JaYKHRoHDccQFjAAegQIABAC&url=https%3A%2F%2Fpdfs.semanticscholar.org%2Fed50%2Fa44882872f127b55e39f5b0cc0be7eb04388.pdf&usg=AOvVaw3HnZc1DTnMQd-RyhPbdQd_ (accessed on 20 August 2019).
- Wagenaar, D.J.; De Bruijn, K.M.; Bouwer, L.M.; De Moel, H. Uncertainty in flood damage estimates and its potential effect on investment decisions. Nat. Hazards Earth Syst. Sci. 2016, 16, 1–14. [Google Scholar] [CrossRef]
- Kolen, B.; Kok, M.; Helsloot, I.; Maaskant, B. EvacuAid: A Probabilistic Model to Determine the Expected Loss of Life for Different Mass Evacuation Strategies during Flood Threats. Risk Anal. 2013, 33, 1312–1333. [Google Scholar] [CrossRef] [PubMed]
- Klijn, F.; Asselman, N.; Van Der Most, H. Compartmentalisation: Flood consequence reduction by splitting up large polder areas. J. Flood Risk Manag. 2010, 3, 3–17. [Google Scholar] [CrossRef]
- Van der Most, H.; Klijn, F. De werking van het waterkeringsysteem: de dijkring voorbij? Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwjKzLzg15DkAhXjJaYKHdFPCzsQFjAAegQIABAC&url=http%3A%2F%2Fpublications.deltares.nl%2F1206262_015.pdf&usg=AOvVaw2MJxmoEzvKc6yRhQitLoRD (accessed on 27 June 2013).
- Courage, W.; Vrouwenvelder, T.; van Mierlo, T.; Schweckendiek, T. System behaviour in flood risk calculations. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2013, 7, 62–76. [Google Scholar] [CrossRef]
- Bomers, A.; Schielen, R.M.J.; Hulscher, S.J.M.H. How dike breaches affect discharges in a complex river system. Accept. Publ. Nat. Hazards 2019. [Google Scholar] [CrossRef]
- Hegnauer, M.; Beersma, J.J.; van den Boogaard, H.F.P.; Buishand, T.A.; Passchier, R.H. Generator of Rainfall and Discharge Extremes (GRADE) for the Rhine and Meuse Basins; Final Report of GRADE 2.0.; Deltares: Delft, The Netherlands, 2014; p. 84. [Google Scholar]
- Duits-Nederlandse Werkgroep Hoogwater. Risicoanalyse Grensoverschrijdende dijk-Ringen Niederrhein Risikoanalyse für die Grenzüberschreitenden Deichringe am Niederrhein Hoofdrapport fase 1 en 2 (In Dutch); Duits-Nederlandse Werkgroep Hoogwater: Arnhem, Nederland, 2009. [Google Scholar]
- Ververs, M.; Klijn, F. Werken noodoverloopgebieden? Wat leert ons de overstroming van 1926. Geografie 2004, 7, 14–17. [Google Scholar]
- Hesselink, A.W.; Stelling, G.S.; Kwadijk, J.C.J.; Middelkoop, H. Inundation of a Dutch river polder, sensitivity analysis of a physically based inundation model using historic data. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Lizard Flooding Repository. Available online: https://flooding.lizard.net/ (accessed on 15 July 2019).
- Kreibich, H.; Piroth, K.; Seifert, I.; Maiwald, H.; Kunert, U.; Schwarz, J.; Merz1, B.; Thieken, A.H. Is flow velocity a significant parameter in flood damage modelling? Nat. Hazards Earth Syst. Sci. 2009, 9, 1679–1692. [Google Scholar] [CrossRef]
- Dang, N.M.; Babel, M.S.; Luong, H.T. Evaluation of food risk parameters in the Day River Flood Diversion Area, Red River Delta, Vietnam. Nat. Hazards 2011, 56, 169–194. [Google Scholar] [CrossRef]
- Diermanse, F.L.M.; (Deltares, The Netherlands). Memo: Samenvallen hoogwaters Rijn en Maas. Personal Communication, 2002. (In Dutch). [Google Scholar]
- Levelt, O.; van Vuren, S.; Pol, J.; van der Meij, R.; Nugroho, D.; ter Horst, W.; Koopmans, R.; van der Scheer, P.; Kruif, A.; de Grave, P. Beleidsstudie Kostenreductie Dijkversterking door Rivierverruiming; Deltares: Delft, The Netherlands, 2017. [Google Scholar]
| Scenario Name | River Breach | Regional Breach | Polder-Side Breach |
|---|---|---|---|
| NoSys | ✗ | ✗ | ✗ |
| RivBr | ✓ | ✗ | ✗ |
| RegBr | ✓ | ✓ | ✗ |
| PolBr | ✓ | ✓ | ✓ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curran, A.; de Bruijn, K.M.; Klerk, W.J.; Kok, M. Large Scale Flood Hazard Analysis by Including Defence Failures on the Dutch River System. Water 2019, 11, 1732. https://doi.org/10.3390/w11081732
Curran A, de Bruijn KM, Klerk WJ, Kok M. Large Scale Flood Hazard Analysis by Including Defence Failures on the Dutch River System. Water. 2019; 11(8):1732. https://doi.org/10.3390/w11081732
Chicago/Turabian StyleCurran, Alex, Karin M. de Bruijn, Wouter Jan Klerk, and Matthijs Kok. 2019. "Large Scale Flood Hazard Analysis by Including Defence Failures on the Dutch River System" Water 11, no. 8: 1732. https://doi.org/10.3390/w11081732
APA StyleCurran, A., de Bruijn, K. M., Klerk, W. J., & Kok, M. (2019). Large Scale Flood Hazard Analysis by Including Defence Failures on the Dutch River System. Water, 11(8), 1732. https://doi.org/10.3390/w11081732






