Scour at Bridge Foundations in Supercritical Flows: An Analysis of Knowledge Gaps
Abstract
1. Introduction
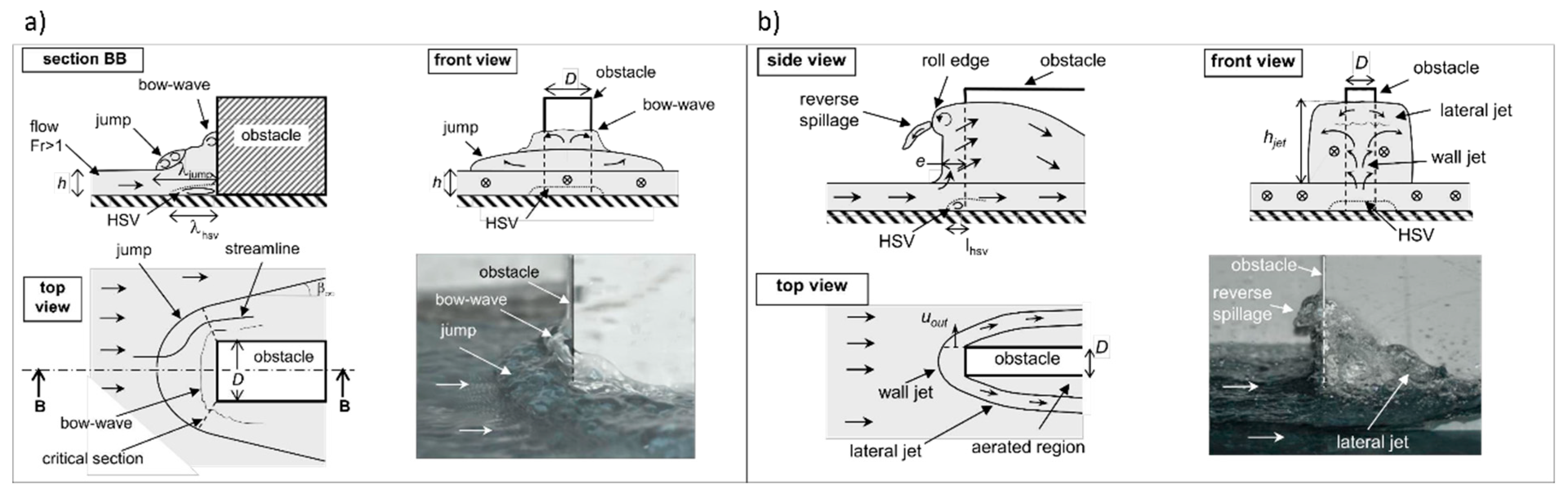
2. Flow Patterns around Bridge Foundations
2.1. Surface Mounted Emerging Obstacles on Flat Beds
2.1.1. Subcritical Flows
2.1.2. Supercritical Flows
2.2. Foundations with Scour Hole
2.2.1. Subcritical Flows
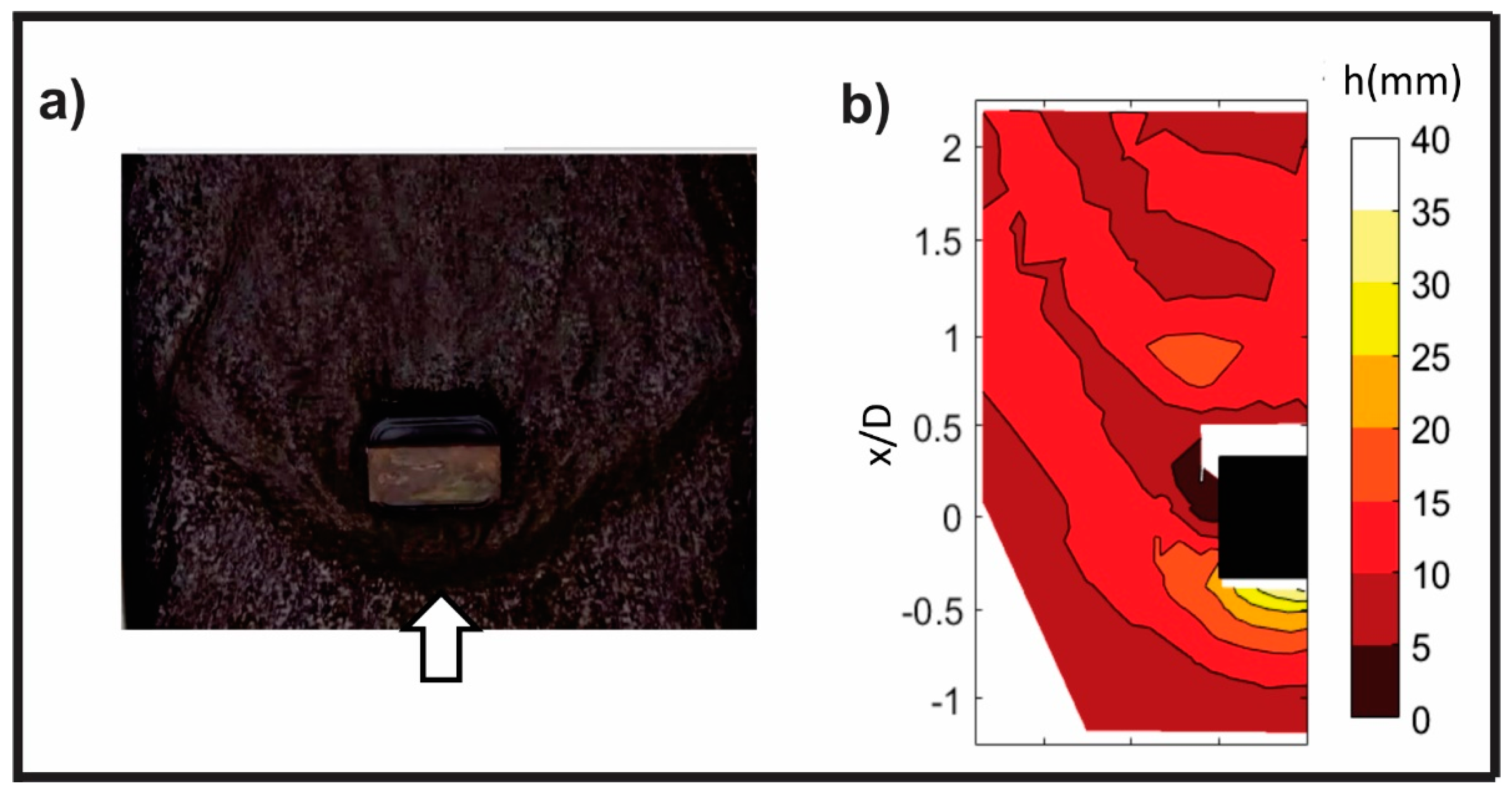
2.2.2. Supercritical Flows
3. Scour around Bridge Foundations
3.1. Subcritical Flows
3.2. Supercritical Flows
4. Recommended Methods for the Study of Flow and Scour in Supercritical Flows
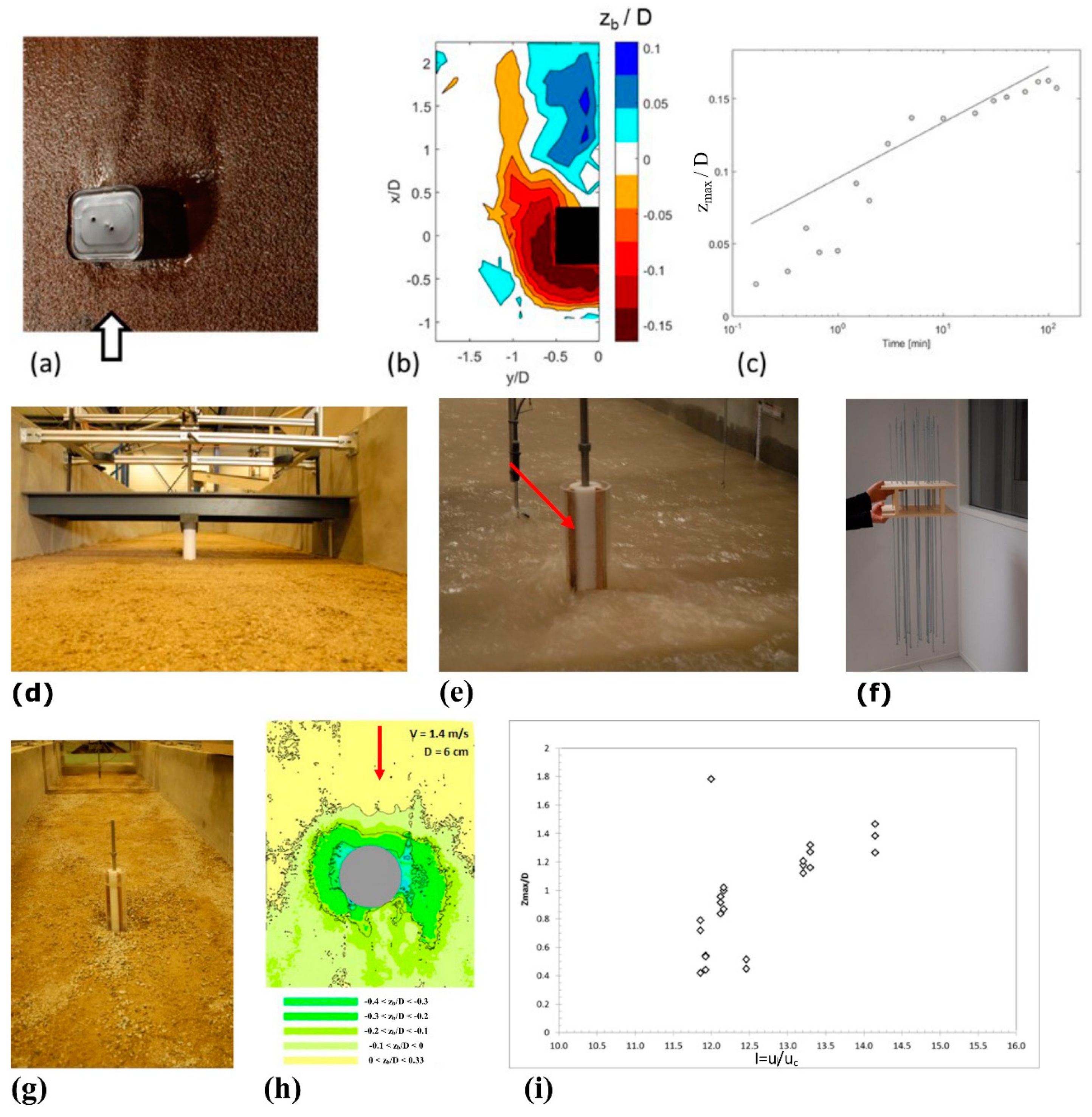
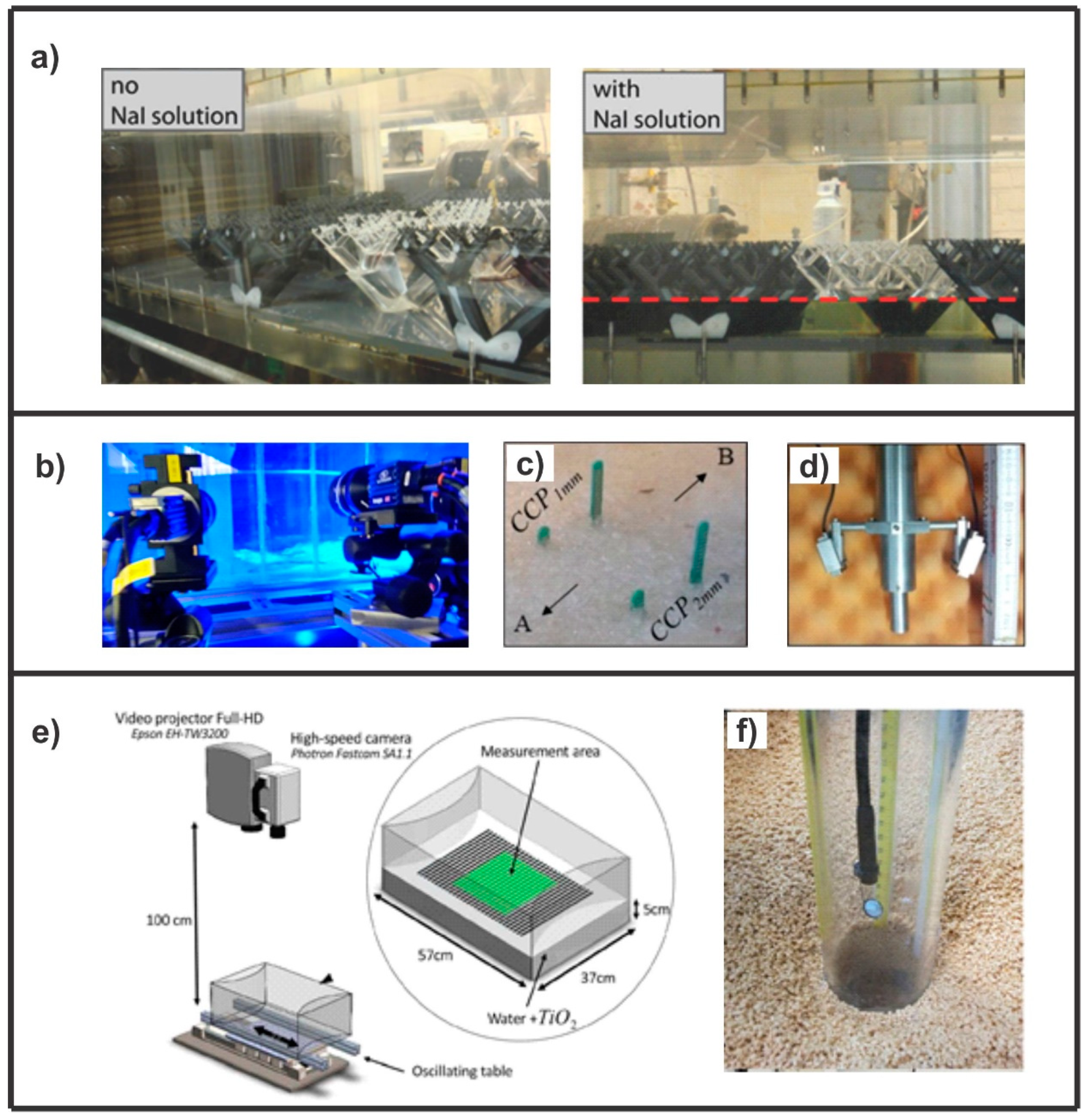
4.1. Laboratory Techniques for Flow and Scour Dynamics
4.1.1. Standard Velocimetry
4.1.2. Advanced Measurement of Hydrodynamic Processes
4.1.3. Image-Based Reconstruction of a Free Surface
4.1.4. Distance Sensors for Scour Measurement
4.1.5. Image-Based Reconstruction of Scour during Running Experiments
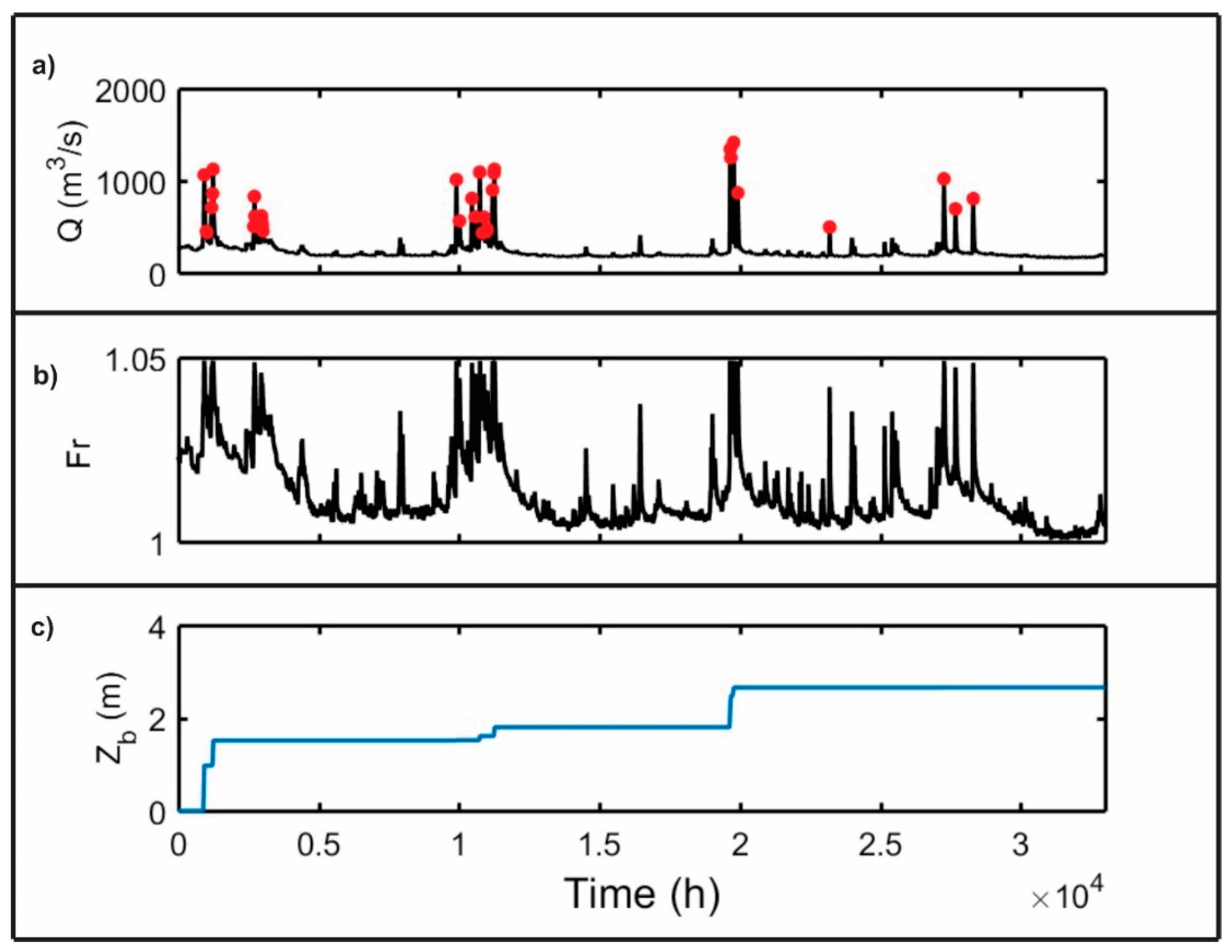
4.2. Field Techniques for Flow and Scour Dynamics
4.2.1. Approaching Flow Measurements
4.2.2. Bed Level Measurements
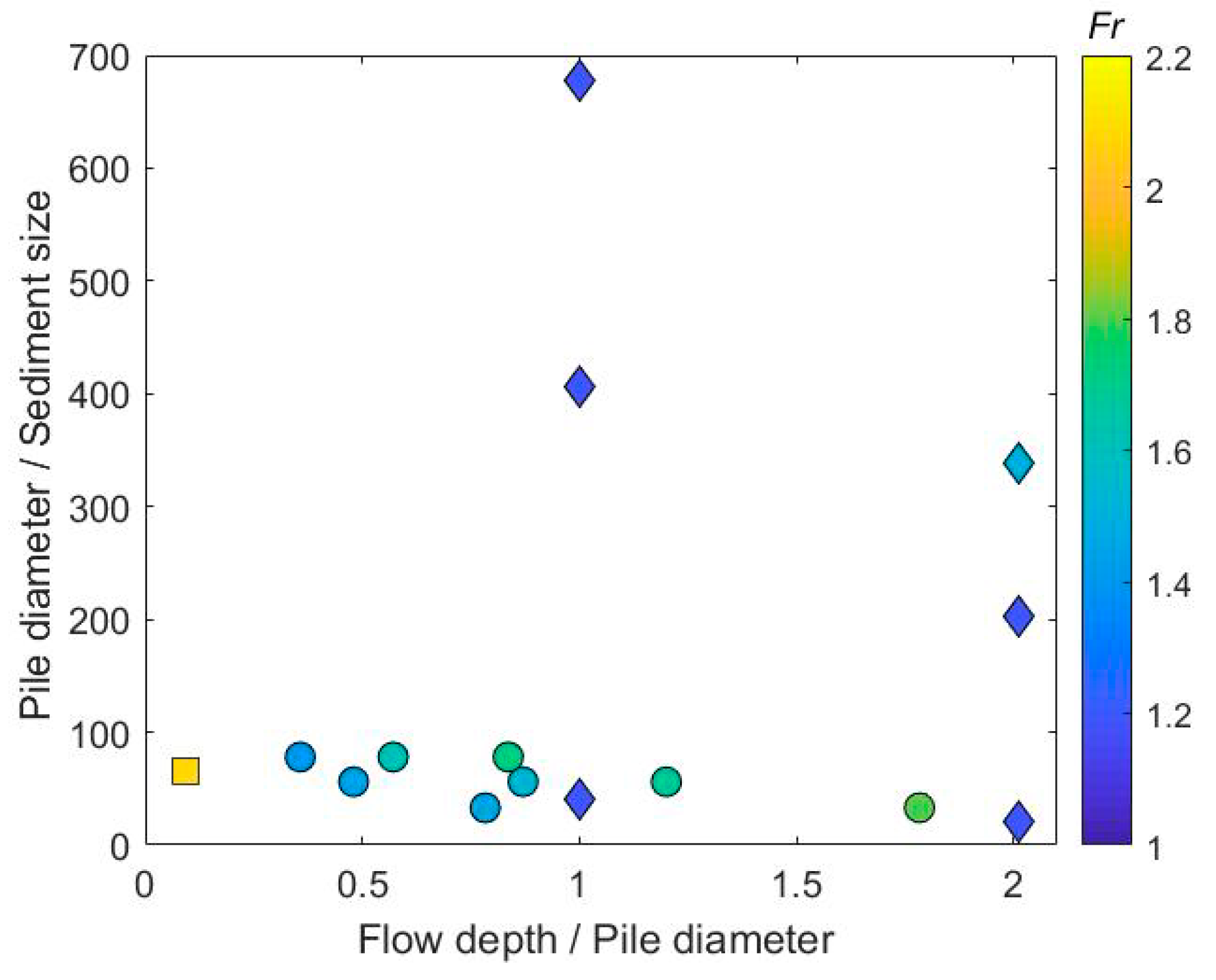
4.3. Physical Scale Models of Scour at Bridge Foundations
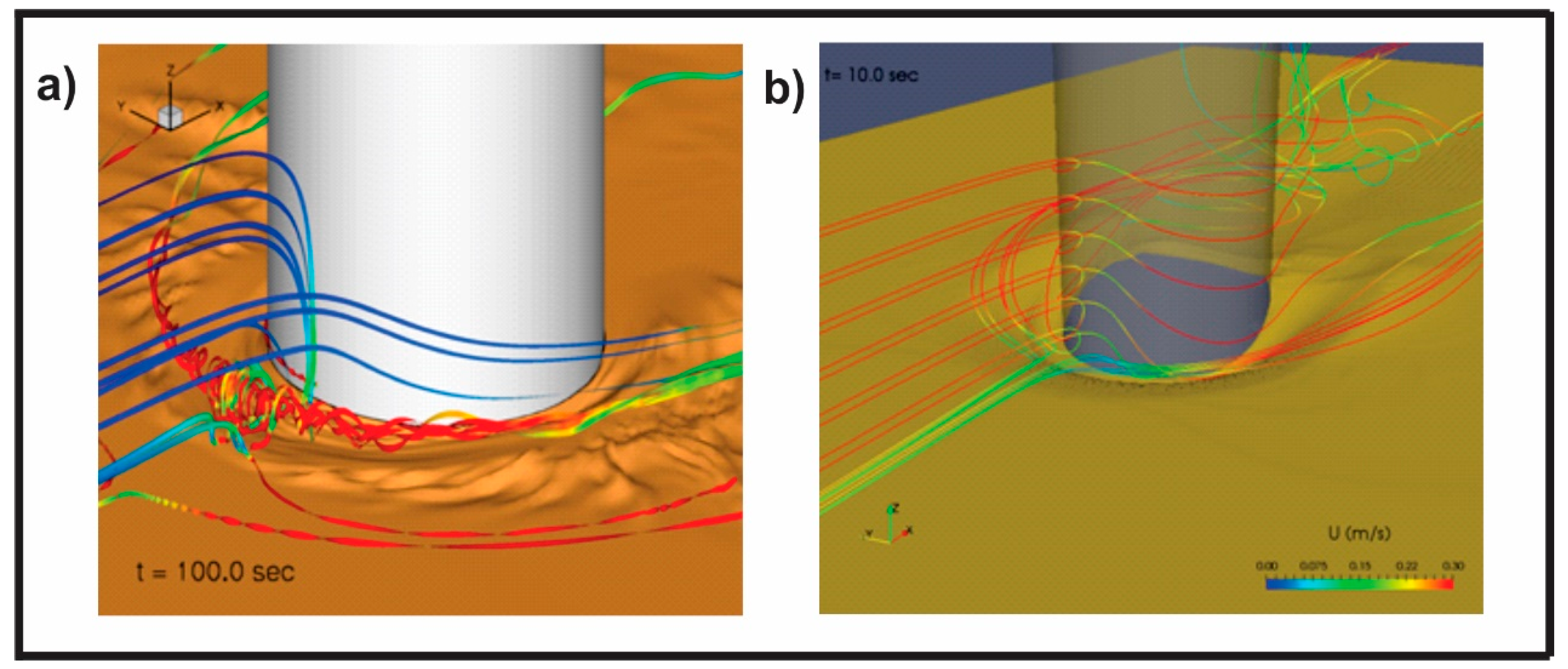
4.4. Advanced Numerical Tools for Simulation of Scour in Supercritical Flows
4.4.1. Coupled Hydrodynamics and Sediment Transport Approach
4.4.2. Multi-Phase Flow Approach
4.5. Moving from the Local Scale Phenomena Up to Long Term Dynamics
5. Discussion and Conclusions
5.1. Measuring Techniques for Flow in the Laboratory
5.2. Measuring Techniques for Scour in the Laboratory
5.3. Measuring Techniques for Flow in the Field
5.4. Measuring Techniques for Scour in the Field
5.5. Physical Modeling of Scour in Supercritical Flows
5.6. Numerical Modeling of Scour in Supercritical Flows
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges, 5th ed.; FHWA-HIF-12-003, HEC-18; Books Express Publishing: Berkshire, UK, 2012. [Google Scholar]
- Melville, B.; Coleman, S. Bridge Scour; Water Resources: Littleton, CO, USA, 2000. [Google Scholar]
- Ettmer, B.; Bleck, M.; Broich, K.; Link, O.; Meyering, H.; Pfleger, F.; Stahlmann, A.; Unger, J.; Weichert, R.; Werth, K.; et al. Scour Around Piers; Merkblatt DWA-M529; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e.V. DWA: Hennef (Sieg), Germany, 2016. (In German) [Google Scholar]
- MOP. Highways Design Manual; Chilean Ministry of Public Works: Santiago, Chile, 2000. (In Spanish)
- Lu, J.Y.; Hong, J.H.; Su, C.C.; Wang, C.Y.; Lai, J.S. Field measurements and simulation of bridge scour depth variations during floods. J. Hydraul. Eng. 2008, 134, 810–821. [Google Scholar] [CrossRef]
- Roux, S.; Misset, C.; Romieu, P. Construction of a New Bridge over the Rivière des Galets; Study on physical model; phase 1—tests on abutment scour; Technical Report CNR: Lyon, France, 2015. [Google Scholar]
- Yang, H.C.; Su, C.C. Real-time river bed scour monitoring and synchronous maximum depth data collected during Typhoon Soulik in 2013. Hydrol. Proc. 2015, 29, 1056–1068. [Google Scholar] [CrossRef]
- Camenen, B.; Dugué, V.; Proust, S.; Le Coz, J.; Paquier, A. Formation of standing waves in a mountain river and its consequences on gravel bar morphodynamics. In Proceedings of the 6th IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Santa Fe, Argentina, 21–25 September 2009; Volume I, pp. 65–72. [Google Scholar]
- Fruchart, F.; Delphin, G.; Reynaud, S.; Séraphine, C.; Cadudal, J.; Bonnet, P.; Lemahieu, H. Rivière des Galets Reunion Island—20 year experience of risk management. In Proceedings of the 12th Congress Interpraevent 2012, Grenoble, France, 23–26 April 2012. [Google Scholar]
- Dargahi, B. The turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Devenport, W.J.; Simpson, R.L. Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction. J. Fluid Mech. 1990, 210, 23–55. [Google Scholar] [CrossRef]
- Paik, J.; Escauriaza, C.; Sotiropoulos, F. On the bimodal dynamics of the turbulent horseshoe vortex system in a wing-body junction. Phys. Fluids 2007, 19, 045107. [Google Scholar] [CrossRef]
- Apsilidis, N.; Diplas, P.; Dancey, C.L.; Bouratsis, P. Time-resolved flow dynamics and Reynolds number effects at a wall–cylinder junction. J. Fluid Mech. 2015, 776, 475–511. [Google Scholar] [CrossRef]
- Schanderl, W.; Manhart, M. Reliability of wall shear stress estimations of the flow around a wall-mounted cylinder. Comput. Fluids 2016, 128, 16–29. [Google Scholar] [CrossRef]
- Schanderl, W.; Jenssen, U.; Manhart, M. Near-wall stress balance in front of a wall-mounted cylinder. Flow Turbul. Combust. 2017, 99, 665–684. [Google Scholar] [CrossRef]
- Schanderl, W.; Jenssen, U.; Strobl, C.; Manhart, M. The structure and budget of turbulent kinetic energy in front of a wall-mounted cylinder. J. Fluid Mech. 2017, 827, 285–321. [Google Scholar] [CrossRef]
- Paik, J.; Escauriaza, C.; Sotiropoulos, F. Coherent structure dynamics in turbulent flows past in-stream structures: Some insights gained via numerical simulation. J. Hydraul. Eng. 2010, 136, 981–993. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Reynolds number effects on the coherent dynamics of the turbulent horseshoe vortex. Flow Turbul. Combust. 2011, 86, 231–262. [Google Scholar] [CrossRef]
- Dey, S. Sediment pick-up for evolving scour near circular cylinders. Appl. Math. Model. 1996, 20, 534–539. [Google Scholar] [CrossRef]
- Rivière, N.; Vouillat, G.; Launay, G.; Mignot, E. Emerging obstacles in supercritical open-channel flows: Detached hydraulic jump versus wall-jet-like bow wave. J. Hydraul. Eng. 2017, 143, 04017011. [Google Scholar] [CrossRef]
- Mignot, E.; Rivière, N. Bow-wave-like hydraulic jump and horseshoe vortex around an obstacle in a supercritical open channel flow. Phys. Fluids 2010, 22, 117105. [Google Scholar] [CrossRef]
- Gond, L.; Perret, G.; Mignot, E.; Riviere, N. Analytical prediction of the hydraulic jump detachment length in front of mounted obstacles in supercritical open-channel flows. Phys. Fluids 2019, 31, 045101. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Lagrangian model of bed-load transport in turbulent junction flows. J. Fluid Mech. 2011, 666, 36–76. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Initial stages of erosion and bed form development in a turbulent flow around a cylindrical pier. J. Geophys. Res. Earth Surf. 2011, 116, 1–24. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Characteristics of horseshoe vortex in developing scour holes at piers. J. Hydraul. Eng. 2007, 133, 399–413. [Google Scholar] [CrossRef]
- Kumar, A.; Kothyari, U.C.; Raju, K.G.R. Flow structure and scour around circular compound bridge piers–A review. J. Hydro Environ. Res. 2012, 6, 251–265. [Google Scholar] [CrossRef]
- Mignot, E.; Moyne, T.; Doppler, D.; Rivière, N. Clear-water scouring process in a flow in supercritical regime. J. Hydraul. Eng. 2016, 142, 04015063. [Google Scholar] [CrossRef]
- Breusers, H.N.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Debnath, K.; Chaudhuri, S. Bridge pier scour in clay-sand mixed sediments at near-threshold velocity for sand. J. Hydraul. Eng. 2010, 136, 597–609. [Google Scholar] [CrossRef]
- Link, O.; Klischies, K.; Montalva, G.; Dey, S. Effects of bed compaction on scour at a bridge pier in sandy clay mixtures. J. Hydraul. Eng. 2013, 139, 1013–1019. [Google Scholar] [CrossRef]
- Ng, K.W.; Chakradhar, R.; Ettema, R.; Kempema, E.W. Geotechnical considerations in hydraulic modeling of bridge abutment scour. J. Appl. Water Eng. Res. 2015, 3, 132–142. [Google Scholar] [CrossRef]
- Harris, J.M.; Whitehouse, R.J. Scour development around large-diameter monopiles in cohesive soils: Evidence from the field. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 04017022. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Clear-water scour at abutments in thinly armored beds. J. Hydraul. Eng. 2004, 130, 622–634. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Raikar, R.V.; Dey, S. Clear-water scour at bridge piers in fine and medium gravel beds. Can. J. Civ. Eng. 2005, 32, 775–781. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V. Clear-water scour at piers in sand beds with an armor layer of gravels. J. Hydraul. Eng. 2007, 133, 703–711. [Google Scholar] [CrossRef]
- Diab, R.; Link, O.; Zanke, U. Geometry of developing and equilibrium scour holes at bridge piers in Gravel. Can. J. Civ. Eng. 2010, 37, 544–552. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K. Experimental investigation of clear-water temporal scour variation around bridge pier in gravel. Environ. Fluid Mech. 2018, 18, 871–890. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Ranga Raju, K.G. Scour around spur dikes and bridge abutments. J. Hydraul. Res. 2001, 39, 367–374. [Google Scholar] [CrossRef]
- Coleman, S.E.; Lauchlan, C.S.; Melville, B.W. Clear-water scour development at bridge abutments. J. Hydraul. Res. 2003, 41, 521–531. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Flow Field at a Vertical-Wall Abutment. J. Hydraul. Eng. 2005, 131, 1126–1135. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng. 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Ettema, R.E. Scour at Bridge Piers. Ph.D. Thesis, The University of Auckland, Auckland, New Zealand, 1980. [Google Scholar]
- Raudkivi, A.J. Functional Trends of Scour at Bridge Piers. J. Hydraul. Eng. 1986, 112, 1–13. [Google Scholar] [CrossRef]
- Dargahi, B. Controlling mechanism of local scouring. J. Hydraul. Eng. 1990, 116, 1197–1214. [Google Scholar] [CrossRef]
- Gobert, C.; Link, O.; Manhart, M.; Zanke, U. Discussion of coherent structures in the flow field around a circular cylinder with scour hole by G. Kirkil, S.G. Constantinescu and R. Ettema. J. Hydraul. Eng. 2010, 119, 82–84. [Google Scholar] [CrossRef]
- Ettmer, B.; Orth, F.; Link, O. Live-bed scour at bridge piers in a lightweight polystyrene bed. J. Hydraul. Eng. 2015, 1491–1495. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Morphological evolution of dune-like bed forms generated by bridge scour. J. Hydraul. Eng. 2014, 140, 06014009. [Google Scholar] [CrossRef]
- Lachaussée, F.; Bertho, Y.; Morize, C.; Sauret, A.; Gondret, P. Competitive dynamics of two erosion patterns around a cylinder. Phys. Rev. Fluids 2018, 3, 012302. [Google Scholar] [CrossRef]
- Jain, S.C.; Fischer, E.E. Scour around bridge piers at high velocities. J. Hydraul. Div. 1980, 106, 1827–1842. [Google Scholar]
- Oliveto, G.; Hager, W. Temporal evolution of clear-water pier and abutment scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Revil-Baudard, T.; Chauchat, J.; Hurther, D.; Barraud, P.-A. Investigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements. J. Fluid Mech. 2015, 767, 1–30. [Google Scholar] [CrossRef]
- Brevis, W.; Niño, Y.; Jirka, G.H. Integrating cross-correlation and relaxation algorithms for particle tracking velocimetry. Exp. Fluids 2011, 50, 135–147. [Google Scholar] [CrossRef]
- Wise, D.J.; Brevis, W. Experimental and numerical assessment of turbulent flows through arrays of multi-scale, surface mounted cubes. In Proceedings of the Inaugural UK Fluid Conference, Imperial College London, London, UK, 7–9 September 2016. [Google Scholar]
- Auel, C.; Albayrak, I.; Boes, R.M. Turbulence characteristics in supercritical open channel flows: Effects of Froude number and aspect ratio. J. Hydraul. Eng. 2014, 140, 04014004. [Google Scholar] [CrossRef]
- Wiederseiner, S.; Andreini, N.; Epely-Chauvin, G.; Ancey, C. Refractive-index and density matching in concentrated particle suspensions: A review. Exp. Fluids 2011, 50, 1183–1206. [Google Scholar] [CrossRef]
- Bai, K.; Katz, J.; Meneveau, C. Turbulent flow structure inside a canopy with complex multi-scale elements. Bound. Layer Meteorol. 2015, 155, 435–457. [Google Scholar] [CrossRef]
- Fromant, G.; Mieras, R.S.; Revil-Baudard, T.; Puleo, J.A.; Hurther, D.; Chauchat, J. On bed load and suspended load measurement performances in sheet flows using acoustic and conductivity profilers. JGR 2018, 123, 2546–2562. [Google Scholar]
- Aubourg, Q.; Mordant, N. Investigation of resonances in gravity-capillary wave turbulence. Phys. Rev. Fluids 2016, 1, 023701. [Google Scholar] [CrossRef]
- Nichols, A.; Rubinato, M. Remote sensing of environmental processes via low-cost 3d free-surface mapping. In Proceedings of the 4th IAHR Europe Congress, Liege, Belgium, 27–29 July 2016. [Google Scholar]
- Cobelli, P.J.; Maurel, A.; Pagneux, V.; Petitjeans, P. Global measurement of water waves by Fourier transform profilometry. Exp. Fluids 2009, 46, 1037. [Google Scholar] [CrossRef]
- Link, O. Untersuchung der Kolkung an Einem Schlanken Zylindrischen pfeiler in sandigem boden. Ph.D. Thesis, Institut für Wasserbau und Wasserwirtschaft, Technische Universität, Darmstadt, German, 2006. [Google Scholar]
- Link, O.; Pfleger, F.; Zanke, U. Characteristics of developing scour-holes at a sand-embedded cylinder. International, J. Sediment Res. 2008, 23, 258–266. [Google Scholar] [CrossRef]
- Lanckriet, T.; Puleo, J.A.; Waite, N. A conductivity concentration profiler for sheet flow sediment transport. IEEE J. Ocean. Eng. 2013, 38, 55–70. [Google Scholar] [CrossRef]
- Bouratsis, P.P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. High-resolution 3-D monitoring of evolving sediment beds. Water Resour. Res. 2013, 49, 977–992. [Google Scholar] [CrossRef]
- Bouratsis, P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. Quantitative spatio-temporal characterization of scour at the base of a cylinder. Water 2017, 9, 227. [Google Scholar] [CrossRef]
- Chang, W.Y.; Lai, J.S.; Yen, C.L. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Link, O.; Castillo, C.; Pizarro, A.; Rojas, A.; Ettmer, B.; Escauriaza, C.; Manfreda, S. A model of bridge pier scour during flood waves. J. Hydraul. Res. 2017, 55, 310–323. [Google Scholar] [CrossRef]
- Wallerstein, N.P. Dynamic model for constriction scour caused by large woody debris. Earth Surf. Process. Landf. 2003, 28, 49–68. [Google Scholar] [CrossRef]
- Welber, M.; Le Coz, J.; Laronne, J.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 52, 1108–1126. [Google Scholar] [CrossRef]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in Hydraul. Eng. Appl. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef]
- Dramais, G.; Le Coz, J.; Camenen, B.; Hauet, A. Advantages of a mobile LSPIV method for measuring flood discharges and improving stage–discharge curves. J. Hydro Environ. Res. 2011, 5, 301–312. [Google Scholar] [CrossRef]
- Su, C.C.; Lu, J.Y. Measurements and prediction of typhoon-induced short-term general scours in intermittent rivers. Nat. Hazards 2013, 66, 671–687. [Google Scholar] [CrossRef]
- Hong, J.H.; Guo, W.D.; Chiew, Y.M.; Chen, C.H. A new practical method to simulate flood-induced bridge pier scour—A case study of Mingchu bridge piers on the Cho-Shui River. Water 2016, 8, 238. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Gavin, K. A review of bridge scour monitoring techniques. J. Rock Mech. Geotech. Eng. 2014, 6, 138–149. [Google Scholar] [CrossRef]
- Bao, T.; Liu, Z. Vibration-based bridge scour detection: A review. Struct. Control Health Monit. 2017, 24, e1937. [Google Scholar] [CrossRef]
- McNamara, J.P.; Borden, C. Observations on the movement of coarse gravel using implanted motion-sensing radio transmitters. Hydrol. Process. 2004, 18, 1871–1884. [Google Scholar] [CrossRef]
- Ettema, R.; Melville, B.; Barkdoll, B. Scale effect in pier-scour experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Ettema, R.; Kirkil, G.; Muste, M. Similitude of large-scale turbulence in experiments on local scour at cylinders. J. Hydraul. Eng. 2006, 132, 33–40. [Google Scholar] [CrossRef]
- Lee, S.; Sturm, T. Effect of sediment size scaling on physical modeling of bridge pier scour. J. Hydraul. Eng. 2009, 135, 793–802. [Google Scholar] [CrossRef]
- Link, O.; Henríquez, S.; Ettmer, B. Physical scale modeling of scour around bridge piers. J. Hydraul. Res. 2019, 57, 227–237. [Google Scholar] [CrossRef]
- Pizarro, A.; Ettmer, B.; Manfreda, S.; Rojas, A.; Link, O. Dimensionless effective flow work for estimation of pier scour caused by flood waves. J. Hydraul. Eng. 2017, 143, 06017006. [Google Scholar] [CrossRef]
- Escauriaza, C.; Paola, C.; Voller, V.R. Computational models of flow, sediment transport and morphodynamics in rivers. In Gravel-Bed Rivers: Processes and Disasters, 1st ed.; Tsutsumi, D., Laronne, J.B., Eds.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Olsen, N.R.; Melaaen, M.C. Three-dimensional calculation of scour around cylinders. J. Hydraul. Eng. 1993, 119, 1048–1054. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Sumer, M.B. Mathematical modeling of scour: A review. J. Hydraul. Res. 2007, 45, 723–735. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical investigation of flow and scour around a vertical circular cylinder. Philos. Trans. R. Soc. A 2015, 373, 20140104. [Google Scholar] [CrossRef]
- Quezada, M.; Tamburrino, A.; Niño, Y. Numerical simulation of scour around circular piles due to unsteady currents and oscillatory flows. Eng. Appl. Comput. Fluid Mech. 2018, 12, 354–374. [Google Scholar] [CrossRef]
- Link, O.; González, C.; Maldonado, M.; Escauriaza, C. Coherent structure dynamics and sediment motion around a cylindrical pier in developing scour holes. Acta Geophys. 2012, 60, 1689–1719. [Google Scholar] [CrossRef]
- Zhou, L. Numerical Modeling of Scour in Steady Flows. Ph.D. Thesis, École centrale de Lyon, Lyon, France, 2017. Available online: https://tel.archives-ouvertes.fr/tel-01598600/document (accessed on 9 August 2018).
- Nagel, T. Numerical Study of Multi-Scale Flow Sediment, Structure Interactions Using a Multiphase Approach. Ph.D. Thesis, Université de Grenoble-Alpes, Grenoble, France, 2018. [Google Scholar]
- Jenkins, J.T.; Hanes, D.M. Collisional sheet flows of sediment driven by a turbulent fluid. J. Fluid Mech. 1998, 370, 29–52. [Google Scholar] [CrossRef]
- Chauchat, J.; Cheng, Z.; Nagel, T.; Bonamy, C.; Hsu, T.-J. Sedfoam- 2.0: A 3-D two-phase flow numerical model for sediment transport. Geosci. Model Dev. 2017, 10, 4367–4392. [Google Scholar] [CrossRef]
- Cheng, Z.; Hsu, T.-J.; Chauchat, J. An eulerian two-phase model for steady sheet flow using large-eddy simulation methodology. Adv. Water Resour. 2018, 111 (Suppl. C), 205–223. [Google Scholar] [CrossRef]
- Kim, Y.; Cheng, Z.; Hsu, T.-J.; Chauchat, J. A numerical study of sheet flow under monochromatic non-breaking waves using a free surface resolving Eulerian two-phase flow model. J. Geophys. Res. Oceans 2018, 123, 4693–4719. [Google Scholar] [CrossRef]
- Juez, C.; Lacasta, A.; Murillo, J.; García-Navarro, P. An efficient GPU implementation for a faster simulation of unsteady bed-load transport. J. Hydraul. Res. 2016, 54, 275–288. [Google Scholar] [CrossRef]
- Flint, M.M.; Fringer, O.; Billington, S.L.; Freyberg, D.; Diffenbaugh, N.S. Historical analysis of hydraulic bridge collapses in the continental United States. J. Infrastruct. Syst. 2017, 23, 04017005. [Google Scholar] [CrossRef]
- Tubaldi, E.; Macorini, L.; Izzuddin, B.A.; Manes, C.; Laio, F. A framework for probabilistic assessment of clear-water scour around bridge piers. Struct. Saf. 2017, 69, 11–22. [Google Scholar] [CrossRef]
- Fischer, E.M.; Knutti, R. Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Chang. 2016, 6, 986. [Google Scholar] [CrossRef]
- Grayson, R.; Blöschl, G. Spatial Patterns in Catchment Hydrology: Observations and Modeling; CUP Archive: Cambridge, UK, 2001. [Google Scholar]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses; models to advance the science of hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Manfreda, S.; Mita, L.; Dal Sasso, S.F.; Samela, C.; Mancusi, L. Exploiting the use of physical information for the calibration of a lumped hydrological model. Hydrol. Process. 2017, 32, 1420–1433. [Google Scholar] [CrossRef]
- Pizarro, A.; Samela, C.; Fiorentino, M.; Link, O.; Manfreda, S. BRISENT: An entropy-based model for bridge-pier scour estimation under complex hydraulic scenarios. Water 2017, 9, 889. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W. and Friedrich, H. Live-bed scour at submerged weirs. J. Hydraul. Eng. 2014, 141, 04014071. [Google Scholar] [CrossRef]
- Fox, J.F.; Papanicolaou, A.N.; Hobbs, B.; Kramer, C.; Kjos, L. Fluid-sediment dynamics around a barb: An experimental case study of a hydraulic structure for the Pacific Northwest. Can. J. Civil Eng. 2005, 32, 853–867. [Google Scholar] [CrossRef]
- Fox, J.F.; Papanicolaou, A.N.; Kjos, L. Eddy taxonomy methodology around a submerged barb obstacle within a fixed rough bed. J. Eng. Mech. 2005, 131, 1082–1101. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Bressan, F.; Fox, J.; Kramer, C.K.; Kjos, L. Role of structure submergence on scour evolution in gravel bed rivers: Application to slope-crested structures. J. Hydraul. Eng. 2018, 144, 03117008. [Google Scholar] [CrossRef]
- Duan, J.G.; He, L.; Fu, X.; Wang, Q. Mean flow and turbulence around experimental spur dike. Adv. Water Resour. 2009, 32, 1717–1725. [Google Scholar] [CrossRef]
- Kondolf, G.M. Hungry water: Effects of dams and gravel mining on river channels. Environ. Manag. 1997, 21, 533–551. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Link, O.; Mignot, E.; Roux, S.; Camenen, B.; Escauriaza, C.; Chauchat, J.; Brevis, W.; Manfreda, S. Scour at Bridge Foundations in Supercritical Flows: An Analysis of Knowledge Gaps. Water 2019, 11, 1656. https://doi.org/10.3390/w11081656
Link O, Mignot E, Roux S, Camenen B, Escauriaza C, Chauchat J, Brevis W, Manfreda S. Scour at Bridge Foundations in Supercritical Flows: An Analysis of Knowledge Gaps. Water. 2019; 11(8):1656. https://doi.org/10.3390/w11081656
Chicago/Turabian StyleLink, Oscar, Emmanuel Mignot, Sebastien Roux, Benoit Camenen, Cristián Escauriaza, Julien Chauchat, Wernher Brevis, and Salvatore Manfreda. 2019. "Scour at Bridge Foundations in Supercritical Flows: An Analysis of Knowledge Gaps" Water 11, no. 8: 1656. https://doi.org/10.3390/w11081656
APA StyleLink, O., Mignot, E., Roux, S., Camenen, B., Escauriaza, C., Chauchat, J., Brevis, W., & Manfreda, S. (2019). Scour at Bridge Foundations in Supercritical Flows: An Analysis of Knowledge Gaps. Water, 11(8), 1656. https://doi.org/10.3390/w11081656






