A Framework for Improving Reliability of Water Distribution Systems Based on a Segment-Based Minimum Cut-Set Approach
Abstract
1. Introduction
2. Methods
2.1. WDS Reliability Assessment Using A Segment-Based Minimum Cut-Set Approach
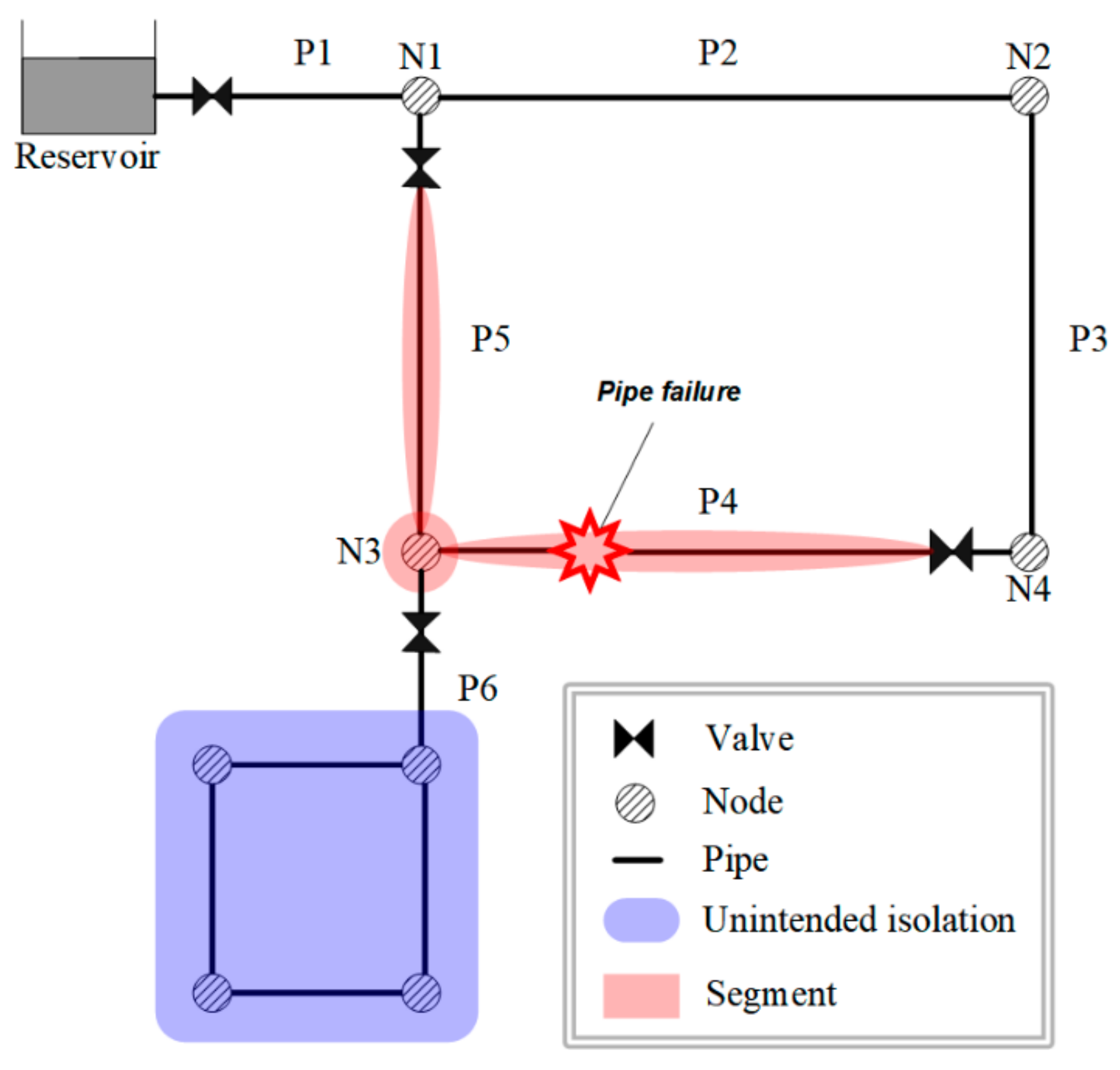
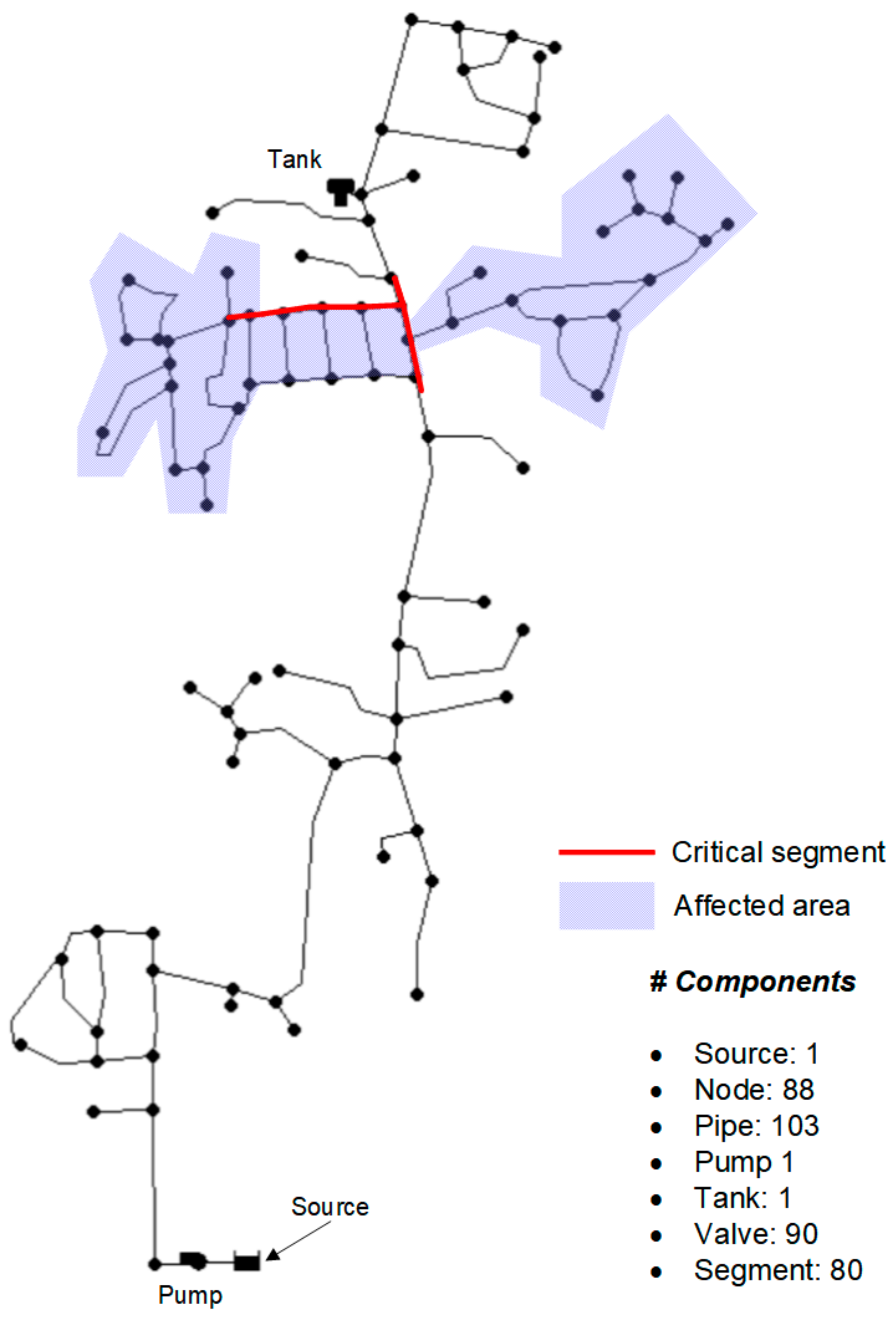
2.1.1. Unintended Isolation
2.1.2. Minimum Cut-Sets
- What: suspension of water supply and/or low pressure at any node
- Where: node(s), segment(s) and unintended isolation(s)
- When: a pipe failure
2.1.3. Success Mode Approach
2.2. Proposed Framework for Improving WDS Reliability
2.2.1. General Criteria for Installing Valves and Increasing Pipe Durability
- The WDS reliability increases by replacing existing pipes in the minimum cut-sets with more durable (i.e., larger diameters) ones represented by even with the same construction cost.
- Even though the WDS reliability linearly increases in proportion to the construction cost, the increasing rate is not significant. It means that structural modification or installing additional valves to the WDS is required to efficiently improve the WDS reliability.
- It is not necessary to install valves on a pipe which does not belong to minimum cut-sets. This is because the pipe does not cause any top events when broken.
- Even though some nodes can be free from a suspension of water by installing valve(s) around a broken pipe, in case the pipe breaking still causes any top event in the system, it is better to increase the durability of the pipe than installing valves.
- For a segment consisting of two or more pipes, valves should be installed for the weakest pipe. However, if the pipe with the additional valve is broken, no top event should occur in the system. If the top event still occurs due to the pipe breakage, the durability of the pipe should be increased rather than installing the valves.
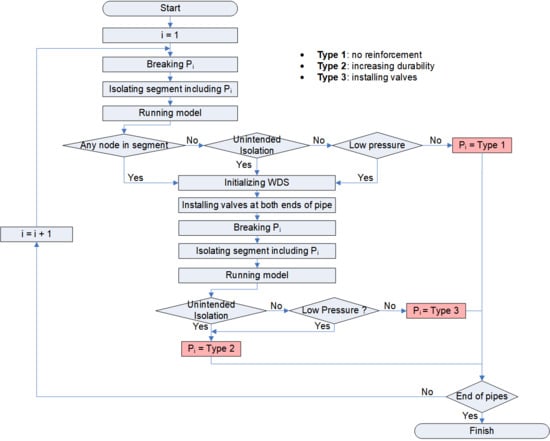
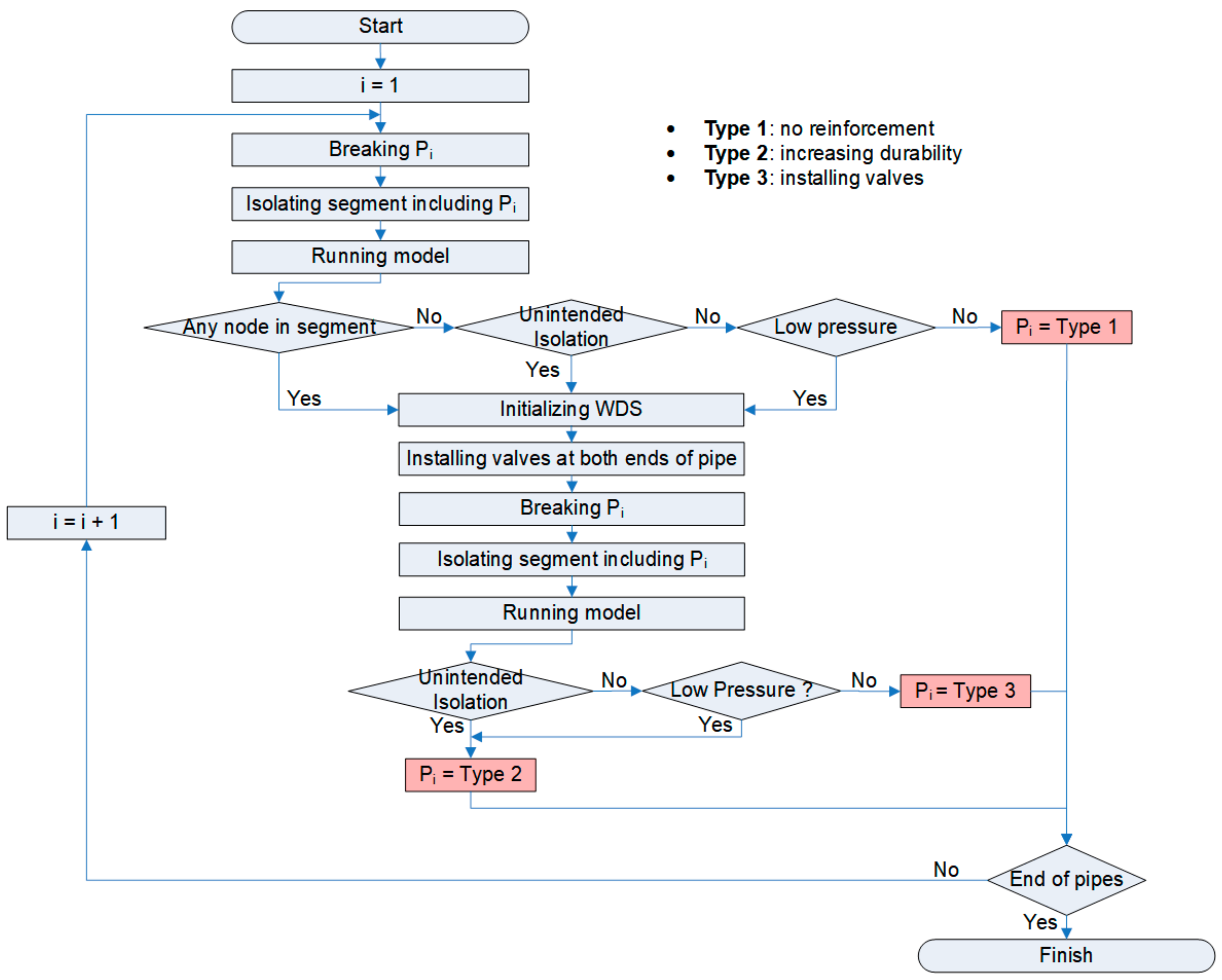
2.2.2. Proposed Framework for Improving WDS Reliability
Proposed Three Types of Reinforcement
Proposed Rules for Improving WDS Reliability
3. Results and Discussion
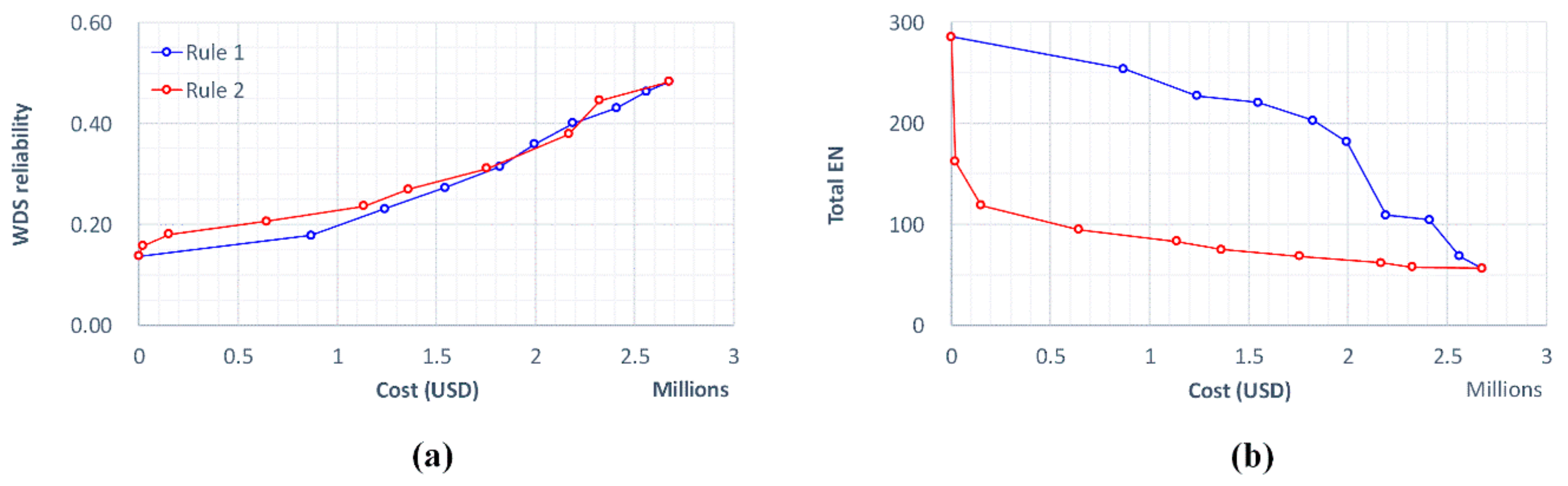
3.1. Application Results of Rules 1 and 2
3.2. Caveats and Follow-Up Studies
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mays, L.W. Water Distribution Systems Handbook; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Walski, T.M.; Chase, D.V.; Savic, D.A.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modeling and Management; Bentley Institute Press: Crewe, UK, 2003. [Google Scholar]
- Andreou, S.A.; Marks, D.H.; Clark, R.M. A new methodology for modelling break failure patterns in deteriorating water distribution systems: Theory. Adv. Water Resour. 1987, 10, 2–10. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Seismic Hazard Assessment Model for Urban Water Supply Networks. J. Water Resour. Plan. Manag. 2015, 142, 04015055. [Google Scholar] [CrossRef]
- Su, Y.; Mays, L.W.; Duan, N.; Lansey, K.E. Reliability-Based Optimization Model for Water Distribution Systems. J. Hydraul. Eng. 1987, 113, 1539–1556. [Google Scholar] [CrossRef]
- Ostfeld, A. Reliability analysis of regional water distribution systems. Urban Water 2001, 3, 253–260. [Google Scholar] [CrossRef]
- World Health Organization. Operation and Maintenance of Urban Water Supply and Sanitation Systems: A Guide for Managers; World Health Organization: Geneva, Switzerland, 1994. [Google Scholar]
- Gheisi, A.; Forsyth, M.; Naser, G. Water Distribution Systems Reliability: A Review of Research Literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Mays, L.W. Review of Reliability Analysis of Water Distribution Systems; Proc. Symposium: Mackay, Australia, 1996. [Google Scholar]
- Tung, Y.K. Evaluation of Water Distribution Network Reliability; Water Research Cent: Laramie, WY, USA, 1985. [Google Scholar]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Analytical Methods. J. Water Resour. Plan. Manag. 1988, 114, 253–275. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 16111. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Jun, H.D.; Park, J.I.; Baek, C.W.; Kim, J.H. A Segment-based Minimum Cutset Method for Estimating the Reliability of Water Distribution Systems. J. Korea Water Resour. Assoc. 2007, 40, 735–742. [Google Scholar] [CrossRef]
- Walski, T.M. Water distribution valve topology for reliability analysis. Reliab. Eng. Syst. Saf. 1993, 42, 21–27. [Google Scholar] [CrossRef]
- PieTrucha-urbaniK, K.; Studziński, A. Case Study of Failure Simulation of Pipelines Conducted in Chosen Water Supply System. Eksploat. Niezawodn. 2017, 19, 317–323. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Studziński, A. Qualitative analysis of the failure risk of water pipes in terms of water supply safety. Eng. Fail. Anal. 2019, 95, 371–378. [Google Scholar] [CrossRef]
- Studziński, A.; Katarzyna, P.U. Failure Risk Analysis of Water Distributions Systems Using Hydraulic Models on Real Field Data. Ekon. Śr. 2019, 1, 152–165. [Google Scholar]
- Gupta, R.; Bhave, P.R. Comparison of Methods for Predicting Deficient-Network Performance. J. Water Resour. Plan. Manag. 1996, 122, 214–217. [Google Scholar] [CrossRef]
- Jun, H.; Loganathan, G.V.; Deb, A.K.; Grayman, W.; Snyder, J. Valve Distribution and Impact Analysis in Water Distribution Systems. J. Environ. Eng. 2007, 133, 790–799. [Google Scholar] [CrossRef]
- Jun, H.D.; Kim, S.H.; Yoo, D.G.; Kim, J.H. Evaluation of the Reliability Improvement of a Water Distribution System by Changing Pipe. J. Korea Water Resour. Assoc. 2009, 42, 505–511. [Google Scholar] [CrossRef][Green Version]
- Yannopoulos, S.; Mike, S. Water Distribution System Reliability Based on Minimum Cut Set Approach and the Hydraulic Availability. Water Resour. Manag. 2013, 27, 1821–1836. [Google Scholar] [CrossRef]
- Rossman, L.A. Epanet 2: Users Manual; United States Environmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Jun, H.; Loganathan, G.V.; Kim, J.H.; Park, S. Identifying Pipes and Valves of High Importance for Efficient Operation and Maintenance of Water Distribution Systems. Water Resour. Manag. 2008, 22, 719–736. [Google Scholar] [CrossRef]
- Fard, N.S. Determination of minimal cut sets of a complex fault tree. Comput. Ind. Eng. 1997, 33, 59–62. [Google Scholar] [CrossRef]
- Blischke, W.R.; Murthy, D.P. Reliability: Modeling, Prediction, and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mays, L.W. Water Supply Systems Security; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Maupin, M.A.; Kenny, J.F.; Hutson, S.S.; Lovelace, J.K.; Barber, N.L.; Linsey, K.S. Estimated Use of Water in the United States in 2010; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar]
- The Korea Water Resources Corporation. Development of Decision-Support System for Water Pipeline Rehabilitation (Korean); The Korea Water Resources Corporation: Daejeon, Korea, 1995. [Google Scholar]
- Gupta, R.; Baby, A.; Arya, P.; Ormsbee, L. Upgrading Reliability of Water Distribution Networks Recognizing Valve Locations. Procedia Eng. 2014, 89, 370–377. [Google Scholar] [CrossRef]
- Jun, H.; Loganathan, G.V. Valve-Controlled Segments in Water Distribution Systems. J. Water Resour. Plan. Manag. 2007, 133, 145–155. [Google Scholar] [CrossRef]
- Shuang, Q.; Liu, Y.; Tang, Y.; Liu, J.; Shuang, K. System Reliability Evaluation in Water Distribution Networks with the Impact of Valves Experiencing Cascading Failures. Water 2017, 9, 413. [Google Scholar] [CrossRef]
- Baek, C.W.; Jun, H.D.; Kim, J.H. Development of a PDA model for water distribution systems using harmony search algorithm. KSCE J. Civ. Eng. 2010, 14, 613–625. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savić, D.; Kapelan, Z. Pressure-Driven Demand and Leakage Simulation for Water Distribution Networks. J. Hydraul. Eng. 2008, 134, 626–635. [Google Scholar] [CrossRef]
- Lee, H.M.; Yoo, D.G.; Kim, D.Y.; Kim, J.H. Development and Application of Pressure Driven Analysis Model based on EPANET. J. Korean Soc. Hazard Mitig. 2013, 13, 121–129. [Google Scholar] [CrossRef]
- Ozger, S.S.; Mays, L.W. A Semi-Pressure-Driven Approach to Reliability Assessment of Water Distribution Networks; Arizona State University: Phoenix, AZ, USA, 2003. [Google Scholar]
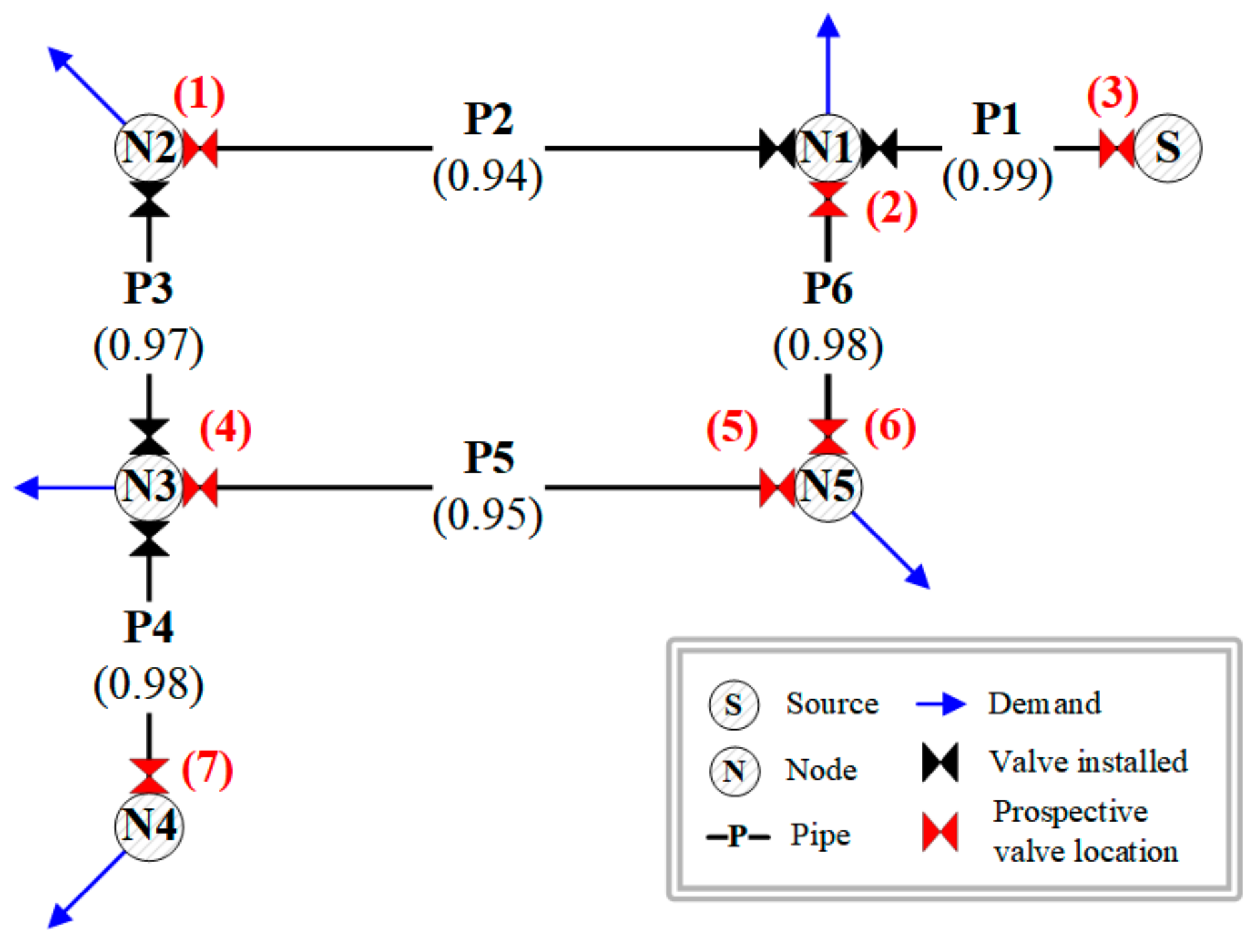
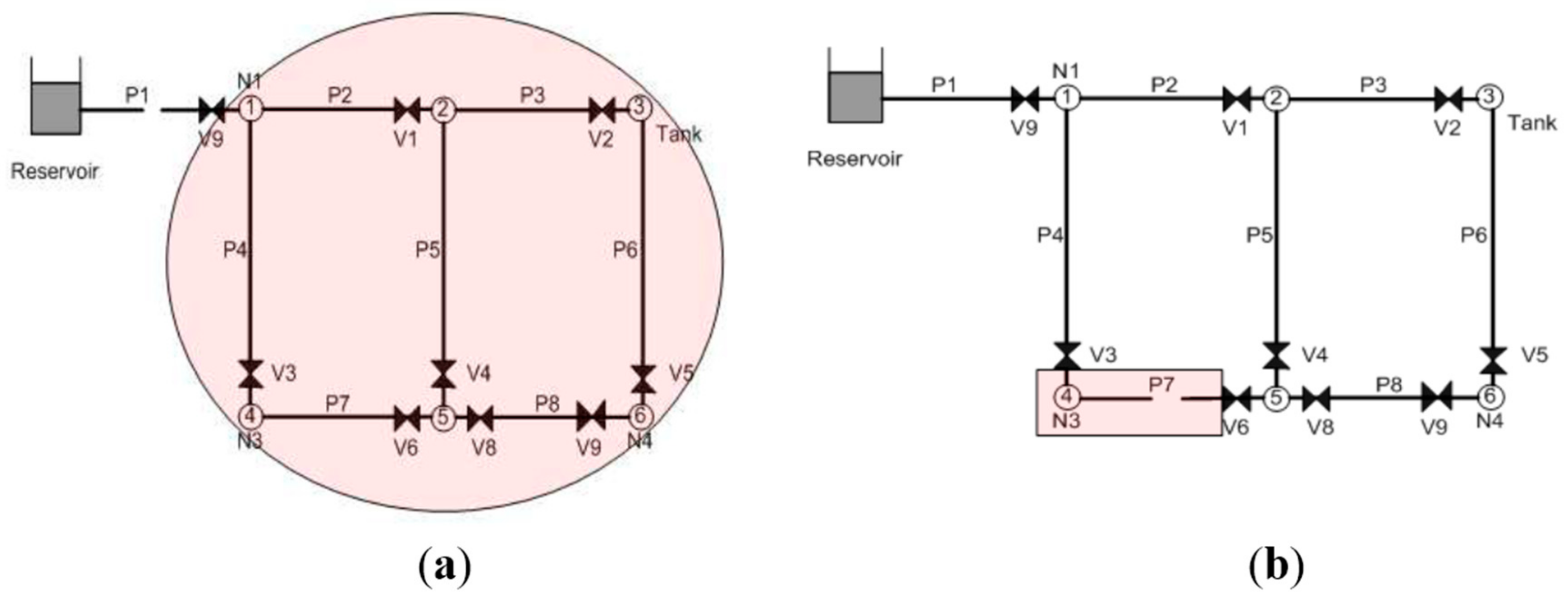
| Case | Install Location | Pipes in Minimum Cut-Sets | WDS Reliability | Total Cost |
|---|---|---|---|---|
| 1 | × | P1, P2, P4, P5, P6 | 0.849 | 0 |
| 2 | (1) | P1, P4, P5, P6 | 0.903 | 1 |
| 3 | (2), (6) | P1, P2, P4, P5 | 0.866 | 2 |
| 4 | (3) | P1, P2, P4, P5, P6 | 0.849 | 1 |
| 5 | (4), (5) | P1, P2, P4, P6 | 0.894 | 2 |
| 6 | (7) | P1, P2, P4, P5, P6 | 0.849 | 1 |
| Rule | Case | WDS Reliability | Number of Pipes in MC | Number of Segments | Number of Valves Installed | Cost (USD, ×106) | Total EN |
|---|---|---|---|---|---|---|---|
| - | Initial | 0.137 | 90 | 80 | - | - | 286 |
| 1 | 1 | 0.178 | 86 | 86 | 6 | 0.868 | 254 |
| 2 | 0.231 | 80 | 94 | 8 | 0.371 | 227 | |
| 3 | 0.273 | 74 | 101 | 7 | 0.305 | 221 | |
| 4 | 0.314 | 68 | 108 | 7 | 0.279 | 203 | |
| 5 | 0.359 | 61 | 118 | 10 | 0.170 | 182 | |
| 6 | 0.401 | 55 | 127 | 9 | 0.197 | 109 | |
| 7 | 0.431 | 51 | 131 | 4 | 0.220 | 105 | |
| 8 | 0.463 | 45 | 140 | 9 | 0.152 | 68 | |
| 9 | 0.483 | 40 | 149 | 9 | 0.112 | 57 | |
| 2 | 1 | 0.157 | 80 | 98 | 18 | 0.020 | 162 |
| 2 | 0.181 | 73 | 111 | 13 | 0.130 | 119 | |
| 3 | 0.206 | 69 | 116 | 5 | 0.492 | 95 | |
| 4 | 0.236 | 65 | 121 | 5 | 0.492 | 83 | |
| 5 | 0.269 | 58 | 130 | 9 | 0.226 | 75 | |
| 6 | 0.311 | 54 | 135 | 5 | 0.394 | 69 | |
| 7 | 0.379 | 49 | 140 | 5 | 0.412 | 62 | |
| 8 | 0.446 | 42 | 147 | 7 | 0.156 | 58 | |
| 9 | 0.483 | 40 | 149 | 2 | 0.351 | 57 | |
| - | - | 69 | 2.674 |
| Item | From | To | |
|---|---|---|---|
| Rule-Based | Practical | ||
| Cost (USD, ×106) | - | 2.674 | 0.549 |
| WDS reliability | 0.137 | 0.483 | 0.423 |
| Total EN | 286 | 57 | 64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jun, H.D.; Yoo, D.G.; Kim, J.H. A Framework for Improving Reliability of Water Distribution Systems Based on a Segment-Based Minimum Cut-Set Approach. Water 2019, 11, 1524. https://doi.org/10.3390/w11071524
Kim S, Jun HD, Yoo DG, Kim JH. A Framework for Improving Reliability of Water Distribution Systems Based on a Segment-Based Minimum Cut-Set Approach. Water. 2019; 11(7):1524. https://doi.org/10.3390/w11071524
Chicago/Turabian StyleKim, Seokhyeon, Hwan Don Jun, Do Guen Yoo, and Joong Hoon Kim. 2019. "A Framework for Improving Reliability of Water Distribution Systems Based on a Segment-Based Minimum Cut-Set Approach" Water 11, no. 7: 1524. https://doi.org/10.3390/w11071524
APA StyleKim, S., Jun, H. D., Yoo, D. G., & Kim, J. H. (2019). A Framework for Improving Reliability of Water Distribution Systems Based on a Segment-Based Minimum Cut-Set Approach. Water, 11(7), 1524. https://doi.org/10.3390/w11071524