Criticality Analysis of a Water Distribution System Considering Both Economic Consequences and Hydraulic Loss Using Modern Portfolio Theory
Abstract
:1. Introduction
2. Methodology
2.1. ECLIPS (Economic Consequence Linked to Interruption in Providing Service)
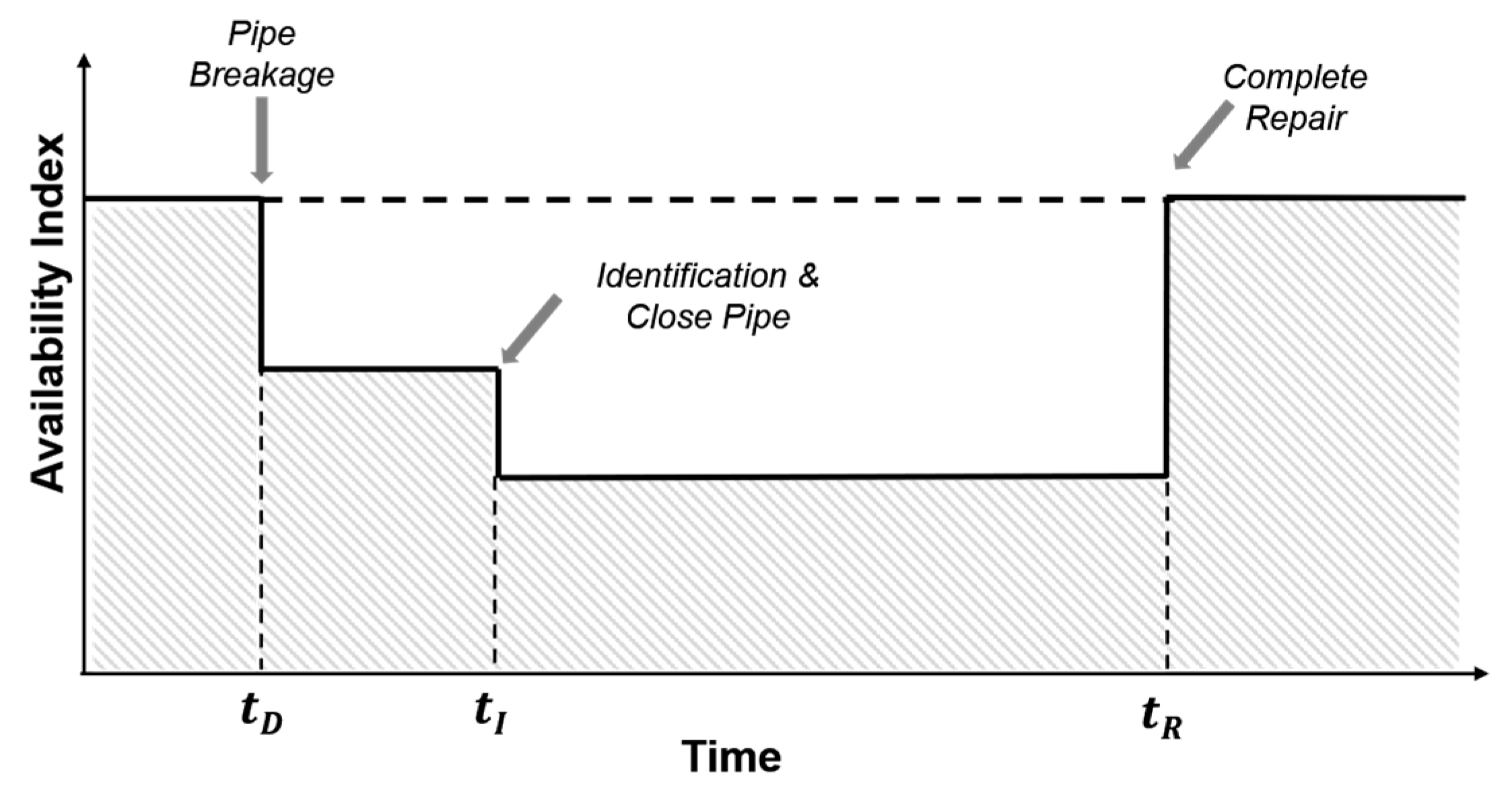
2.2. Resilience Measures
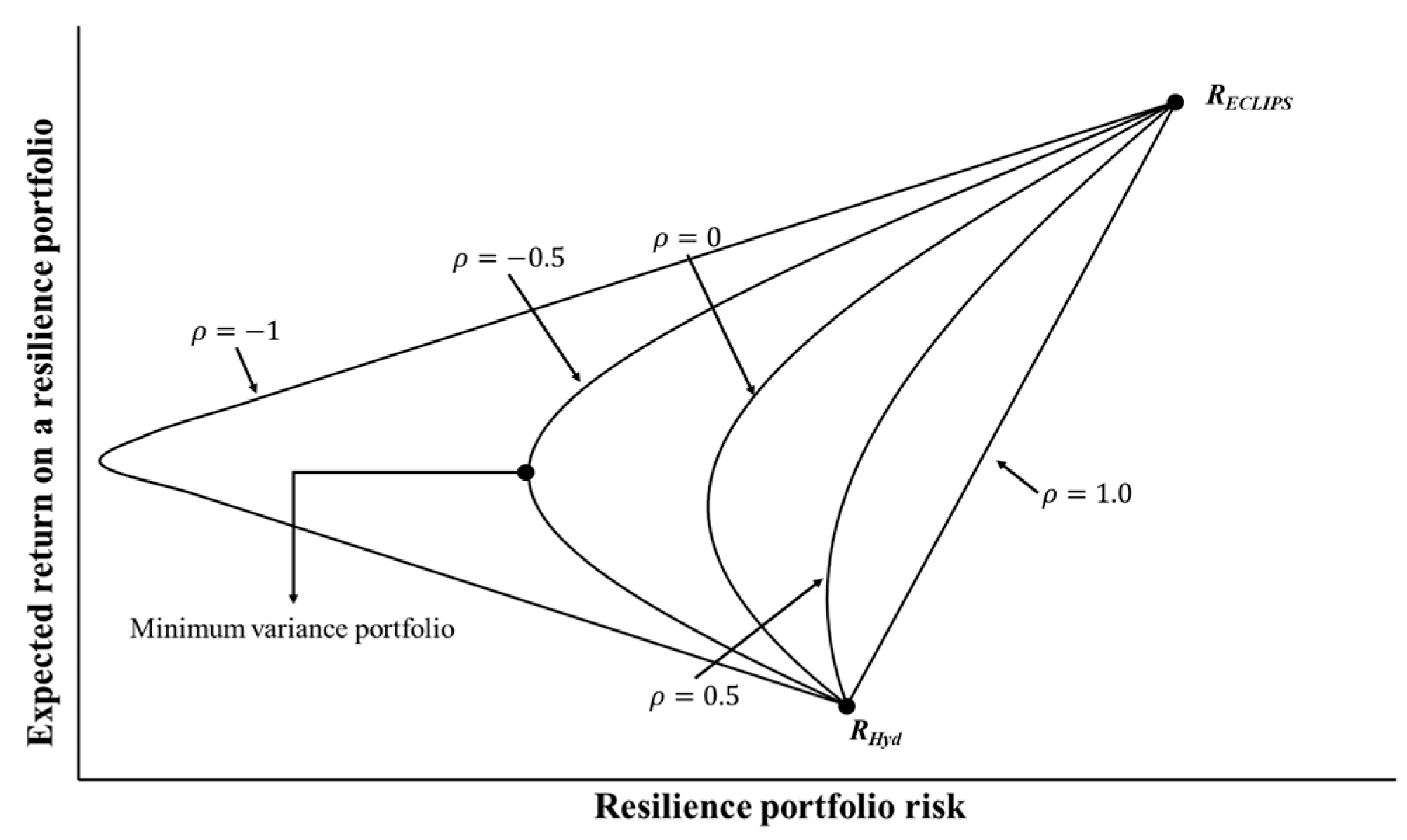
2.3. Modern Portfolio Theory
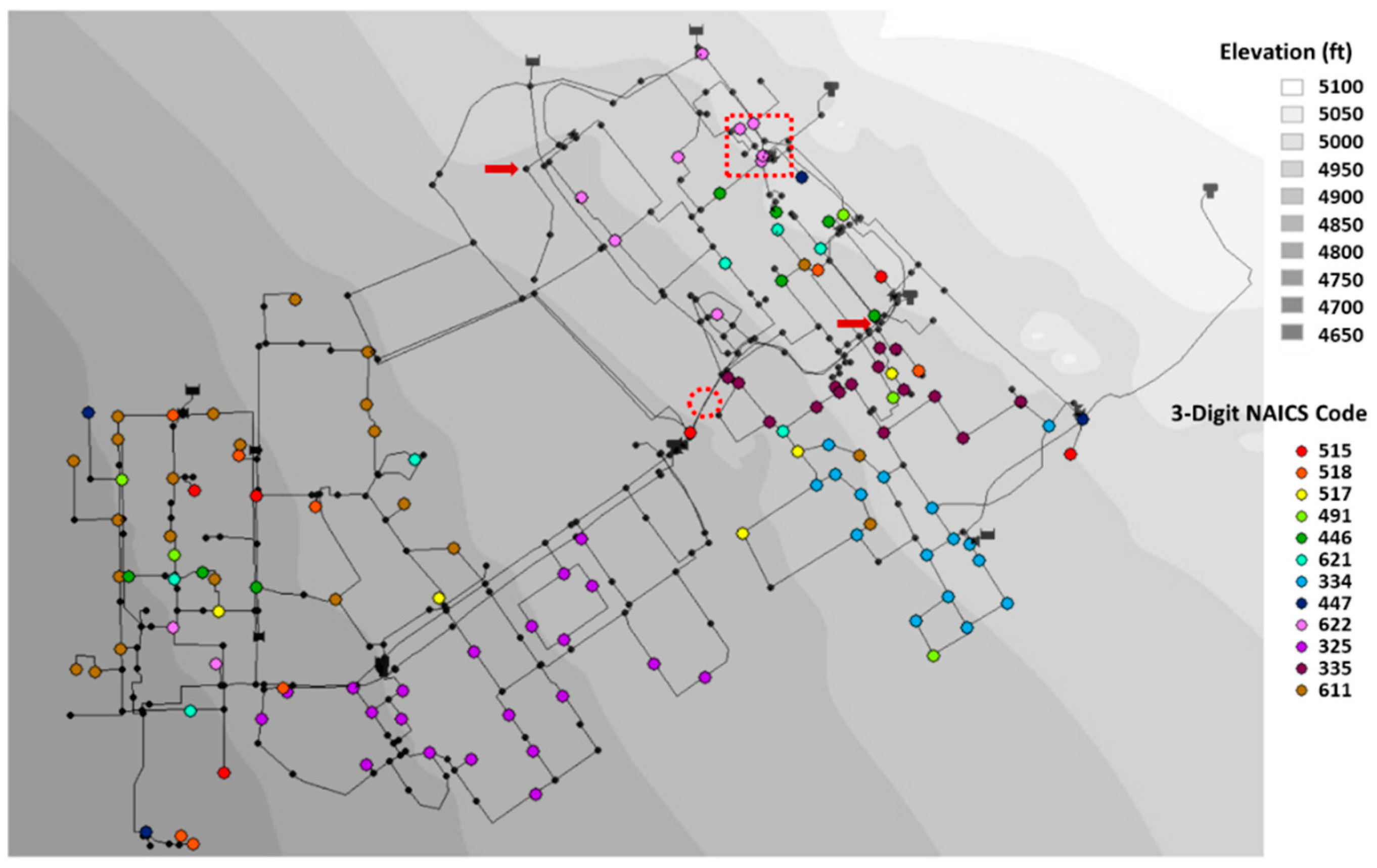
2.4. Study Network Description
2.5. Demonstrations
3. Results and Discussion
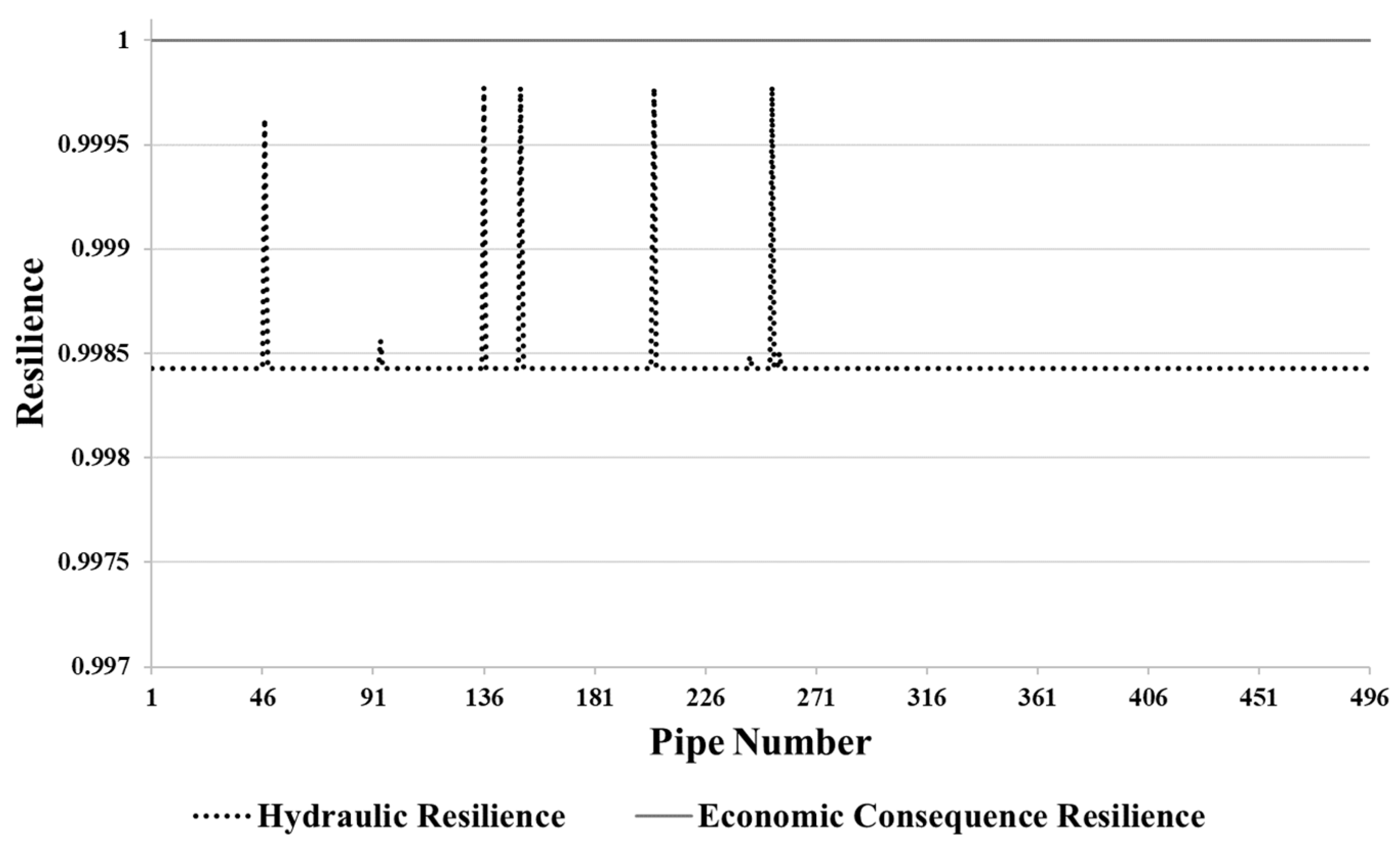
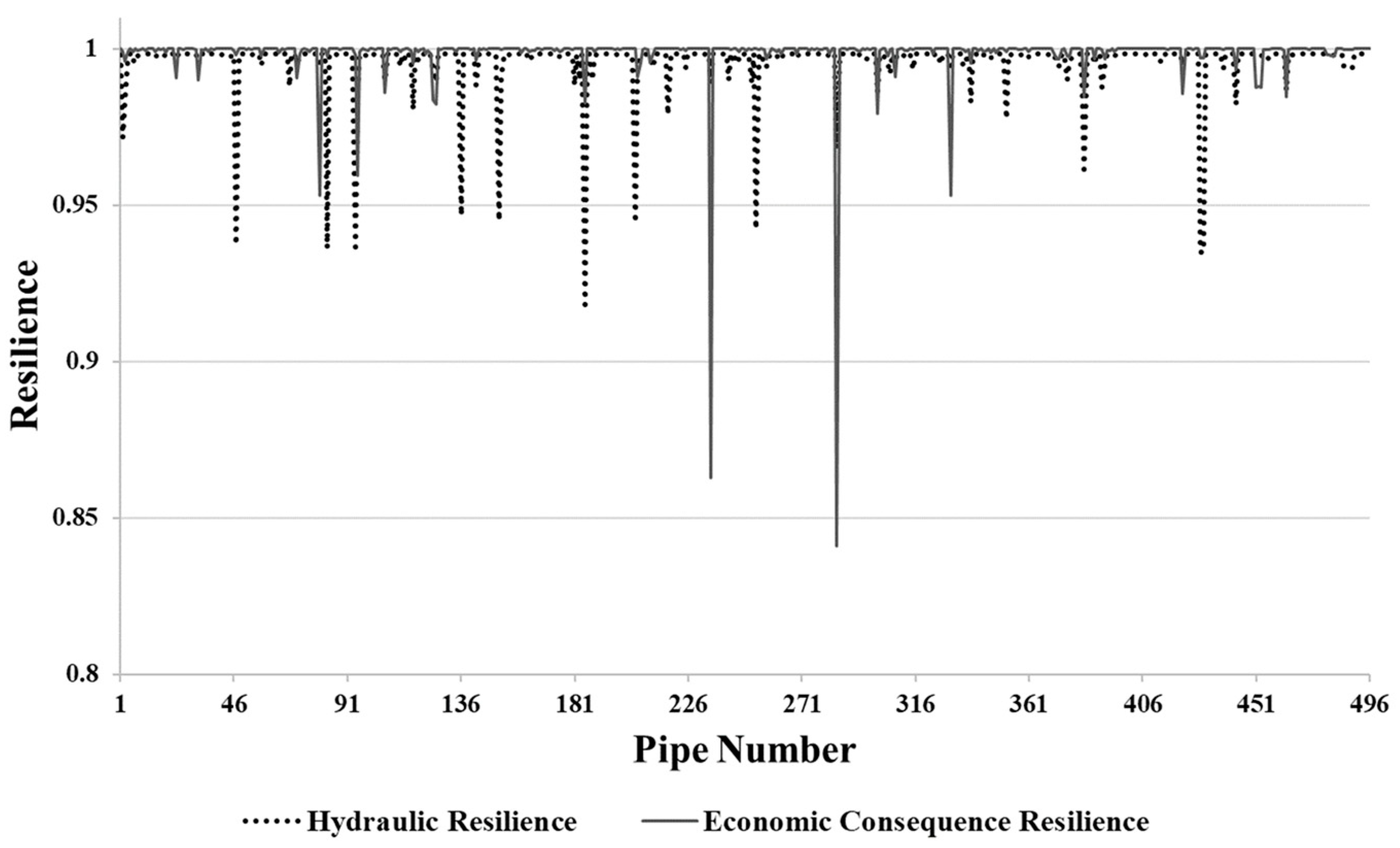
3.1. Assessment of Differences Between and for Identifying Pipes Critical for Replacement
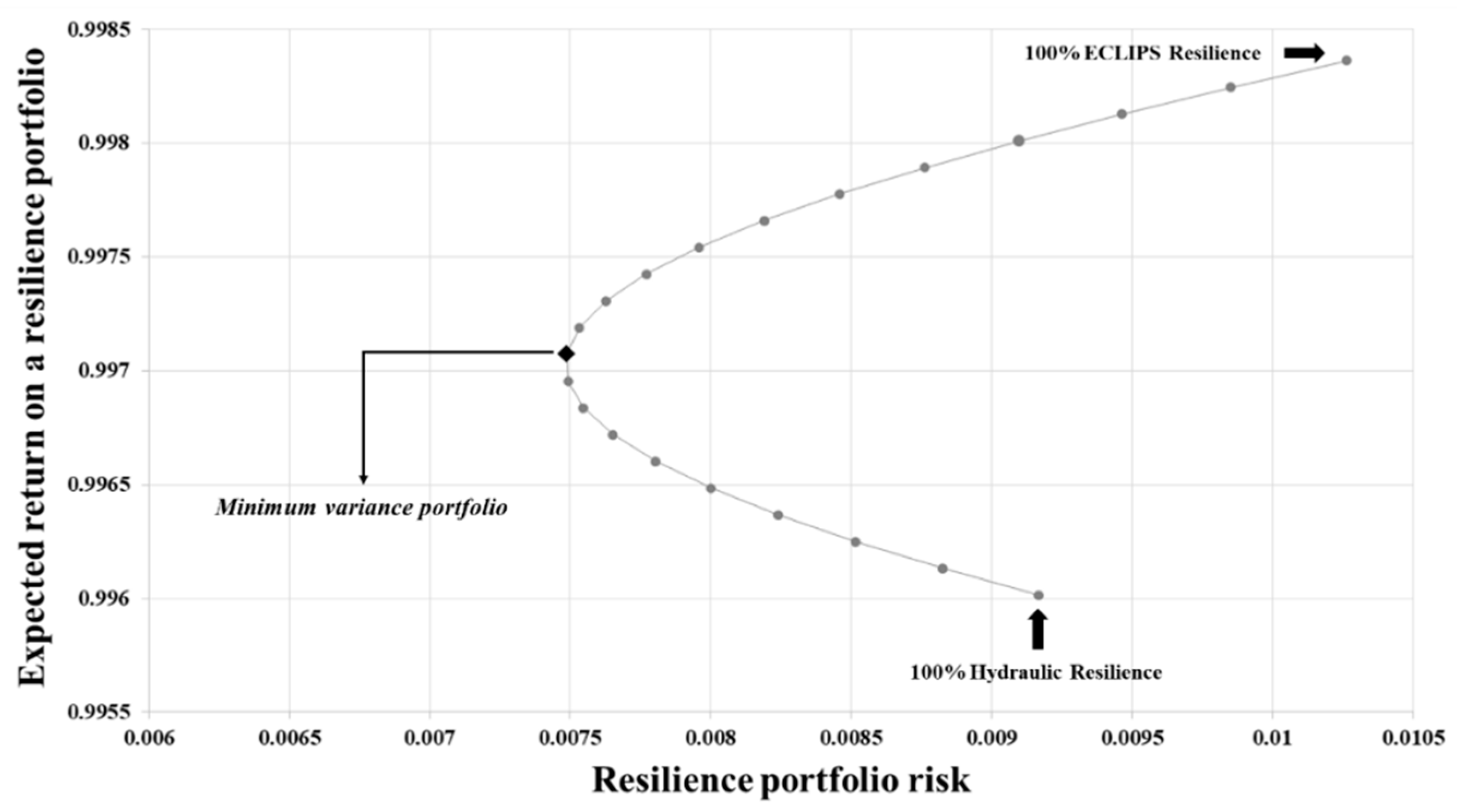
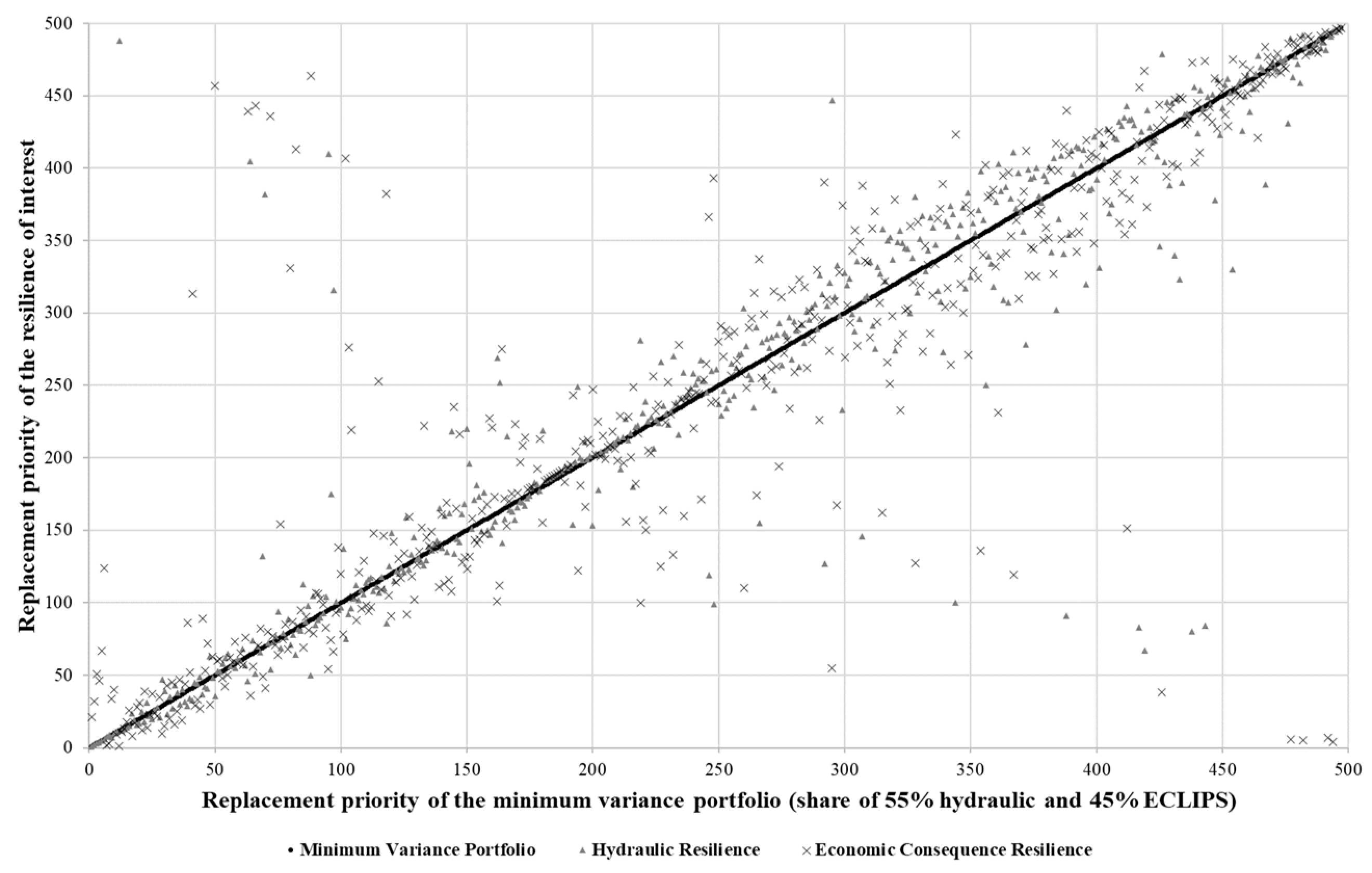
3.2. Applying Modern Portfolio Theory to Identify Minimum Combined Risk for and
4. Conclusions and Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- American Water Works Association. The State of Water Loss Control in Drinking Water Utilities; White Paper; American Water Works Association: Denver, CO, USA, 2014. [Google Scholar]
- Solley, W.B.; Pierce, R.R.; Perlman, H.A. Estimated Use of Water in the United States in 1995; US Geological Survey: Reston, VA, USA, 1998.
- American Society of Civil Engineers. Failure to Act: Closing the Infrastructure Investment Gap for America’s Economic Future; American Society of Civil Engineers: Reston, VA, USA, 2016. [Google Scholar]
- American Society of Civil Engineers. 2017 Report Card for America’s Infrastructure; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]
- Little, R.G. Controlling cascading failure: Understanding the vulnerabilities of interconnected infrastructures. J. Urban Technol. 2002, 9, 109–123. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Asset Management: A Best Practices Guide; EPA 816-F-08-014; U.S. Environmental Protection Agency: Washington, DC, USA, 2008.
- Boulos, P.F. Optimal Scheduling of Pipe Replacement. J. Am. Water Works Assoc. 2017, 109, 42–46. [Google Scholar] [CrossRef]
- Piratla, K.R.; Ariaratnam, S.T. Criticality analysis of water distribution pipelines. J. Pipeline Syst. Eng. Pract. 2011, 2, 91–101. [Google Scholar] [CrossRef]
- Luong, H.T.; Nagarur, N.N. Optimal maintenance policy and fund allocation in water distribution networks. J. Water Resour. Plan. Manag. 2005, 131, 299–306. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Near-optimal rehabilitation scheduling of water distribution systems based on a multi-objective genetic algorithm. Civ. Eng. Environ. Syst. 2006, 23, 143–160. [Google Scholar] [CrossRef]
- Giustolisi, O.; Berardi, L. Prioritizing pipe replacement: From multiobjective genetic algorithms to operational decision support. J. Water Resour. Plan. Manag. 2009, 135, 484–492. [Google Scholar] [CrossRef]
- Roshani, E.; Filion, Y. Event-based approach to optimize the timing of water main rehabilitation with asset management strategies. J. Water Resour. Plan. Manag. 2013, 140, 04014004. [Google Scholar] [CrossRef]
- Neelakantan, T.; Suribabu, C.; Lingireddy, S. Optimisation procedure for pipe-sizing with break-repair and replacement economics. Water SA 2008, 34, 217–224. [Google Scholar]
- Suribabu, C.; Neelakantan, T. Sizing of water distribution pipes based on performance measure and breakage-repair-replacement economics. ISH J. Hydraul. Eng. 2012, 18, 241–251. [Google Scholar] [CrossRef]
- Shamir, U.; Howard, C.D. Reliability and risk assessment for water supply systems. In Proceedings of the Computer Applications in Water Resources, Buffalo, NY, USA, 10–12 June 1985; pp. 1218–1228. [Google Scholar]
- Moglia, M.; Burn, S.; Meddings, S. Decision support system for water pipeline renewal prioritisation. J. Inf. Technol. 2006, 11, 237–256. [Google Scholar]
- Shin, S.; Lee, S.; Judi, D.R.; Parvania, M.; Goharian, E.; McPherson, T.; Burian, S.J. A Systematic Review of Quantitative Resilience Measures for Water Infrastructure Systems. Water 2018, 10, 164. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Jin, H.; Piratla, K.R. A resilience-based prioritization scheme for water main rehabilitation. J. Water Supply Res. Technol. 2016, 65, 307–321. [Google Scholar] [CrossRef]
- Chang, S.E.; Svekla, W.D.; Shinozuka, M. Linking infrastructure and urban economy: Simulation of water-disruption impacts in earthquakes. Environ. Plan. B Plan. Des. 2002, 29, 281–301. [Google Scholar] [CrossRef]
- Lee, S.; Shin, S.; Judi, D.; McPherson, T.; Burian, S. Water Distribution System Recovery Strategies Considering Economic Consequences from Business Loss. In Proceedings of the CCWI2017, Sheffield, UK, 5–7 September 2017. [Google Scholar]
- Rossman, L.A. EPANET 2: Users Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2000.
- Judi, D.R.; McPherson, T.N. Development of Extended Period Pressure-Dependent Demand Water Distribution Models; Los Alamos National Lab.(LANL): Los Alamos, NM, USA, 2015.
- Heflin, C.; Jensen, J.; Miller, K. Understanding the economic impacts of disruptions in water service. Eval. Program Plan. 2014, 46, 80–86. [Google Scholar] [CrossRef]
- Pagsuyoin, S.A.; Santos, J.R.; Chua, L.; Irvine, K. Modeling the effects of drought in urban economies using regional input-output analysis. Int. J. Environ. Clim. Chang. 2015, 5, 134–146. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Hazard Mitigation Assistance Unified Guidance; Federal Emergency Management Agency: Washington, DC, USA, 2010.
- U.S. Department of the Interior Bureau of Reclamation. Cataloguing Commercial, Industrial, and Institutional Customer Classes. 2009; Volume 2 of 5. Available online: https://www.usbr.gov/lc/socal/reports/weep/Vol2CIIcustomers.pdf (accessed on 08 October 2018).
- Zhuang, B.; Lansey, K.; Kang, D. Resilience/availability analysis of municipal water distribution system incorporating adaptive pump operation. J. Hydraul. Eng. 2012, 139, 527–537. [Google Scholar] [CrossRef]
- Lee, S.; Shin, S.; Judi, D.; McPherson, T.; Burian, S. Detectability-Based Resilience of Water Distribution System Using Failure Finger Print. In Proceedings of the WDSA/CCWI Joint Conference 2018, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Walski, T.M.; Pelliccia, A. Economic analysis of water main breaks. J. Am. Water Works Assoc. 1982, 74, 140–147. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Aerts, J.C.; Botzen, W.W.; Werners, S.E. Portfolios of adaptation investments in water management. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 1247–1265. [Google Scholar] [CrossRef]
- Shin, S.; Park, H. Achieving cost-efficient diversification of water infrastructure system against uncertainty using modern portfolio theory. J. Hydroinform. 2018, 20, 739–750. [Google Scholar] [CrossRef]
- Paydar, Z.; Qureshi, M. Irrigation water management in uncertain conditions—Application of Modern Portfolio Theory. Agric. Water Manag. 2012, 115, 47–54. [Google Scholar] [CrossRef]
- Kidson, R.; Haddad, B.; Zheng, H. Improving water supply reliability through portfolio management: Case study from Southern California. In Proceedings of the 4th WEAS International Conference in Water Resources, Hydrology and Hydraulics, Cambridge, UK, 24–26 February 2009; pp. 24–26. [Google Scholar]
- Kang, D.; Lansey, K. Multiperiod planning of water supply infrastructure based on scenario analysis. J. Water Resour. Plan. Manag. 2012, 140, 40–54. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Scenario-based robust optimization of regional water and wastewater infrastructure. J. Water Resour. Plan. Manag. 2012, 139, 325–338. [Google Scholar] [CrossRef]
- Elton, E.J.; Gruber, M.J.; Brown, S.J.; Goetzmann, W.N. Modern Portfolio Theory and Investment Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sharp, W.W.; Walski, T.M. Predicting internal roughness in water mains. J. Am. Water Works Assoc. 1988, 80, 34–40. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Seismic hazard assessment model for urban water supply networks. J. Water Resour. Plan. Manag. 2015, 142, 04015055. [Google Scholar] [CrossRef]
| 3-Digit NAICS | Description | ECLIPS (M$/Gal) | Number of Nodes | Demand (GPM) |
|---|---|---|---|---|
| 515 | Broadcasting (except Internet) | 0.028257 | 6 | 179.71 |
| 518 | Internet Service Providers, Web Search Portals, and Data Processing Services | 0.006780 | 8 | 313.08 |
| 517 | Telecommunications | 0.005268 | 5 | 41.04 |
| 491 | Postal Service | 0.002229 | 5 | 69.33 |
| 446 | Health and Personal Care Stores | 0.001925 | 8 | 354.23 |
| 621 | Ambulatory Health Care Services | 0.001254 | 7 | 134.96 |
| 334 | Computer and Electronic Product Manufacturing | 0.000956 | 16 | 303.98 |
| 447 | Gasoline Stations | 0.000922 | 4 | 18.44 |
| 622 | Hospitals | 0.000819 | 11 | 762.87 |
| 325 | Chemical Manufacturing | 0.000663 | 21 | 428.10 |
| 335 | Electrical Equipment, Appliance, and Component Manufacturing | 0.000521 | 15 | 317.18 |
| 611 | Educational Services | 0.000080 | 23 | 649.27 |
| 000 | Landscape Irrigation or Other Non-Revenue Generating Use | 0.000000 | 303 | 1524.00 |
| Pipe | MVP * | Pipe | MVP * | ||||
|---|---|---|---|---|---|---|---|
| 136 | 1 | 1 | 343 | 347 | 11 | 9 | 473 |
| 205 | 2 | 2 | 459 | 185 | 12 | 18 | 12 |
| 151 | 3 | 3 | 448 | 75 | 13 | 21 | 3 |
| 253 | 4 | 4 | 487 | 256 | 14 | 11 | 484 |
| 47 | 5 | 5 | 75 | 349 | 15 | 27 | 7 |
| 31 | 6 | 471 | 1 | 118 | 16 | 43 | 4 |
| 247 | 7 | 6 | 17 | 244 | 17 | 12 | 481 |
| 260 | 8 | 8 | 24 | 32 | 18 | 58 | 6 |
| 200 | 9 | 10 | 23 | 309 | 19 | 31 | 9 |
| 94 | 10 | 7 | 84 | 285 | 20 | 427 | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Shin, S.; Judi, D.R.; McPherson, T.; Burian, S.J. Criticality Analysis of a Water Distribution System Considering Both Economic Consequences and Hydraulic Loss Using Modern Portfolio Theory. Water 2019, 11, 1222. https://doi.org/10.3390/w11061222
Lee S, Shin S, Judi DR, McPherson T, Burian SJ. Criticality Analysis of a Water Distribution System Considering Both Economic Consequences and Hydraulic Loss Using Modern Portfolio Theory. Water. 2019; 11(6):1222. https://doi.org/10.3390/w11061222
Chicago/Turabian StyleLee, Seungyub, Sangmin Shin, David R. Judi, Timothy McPherson, and Steven J. Burian. 2019. "Criticality Analysis of a Water Distribution System Considering Both Economic Consequences and Hydraulic Loss Using Modern Portfolio Theory" Water 11, no. 6: 1222. https://doi.org/10.3390/w11061222
APA StyleLee, S., Shin, S., Judi, D. R., McPherson, T., & Burian, S. J. (2019). Criticality Analysis of a Water Distribution System Considering Both Economic Consequences and Hydraulic Loss Using Modern Portfolio Theory. Water, 11(6), 1222. https://doi.org/10.3390/w11061222






