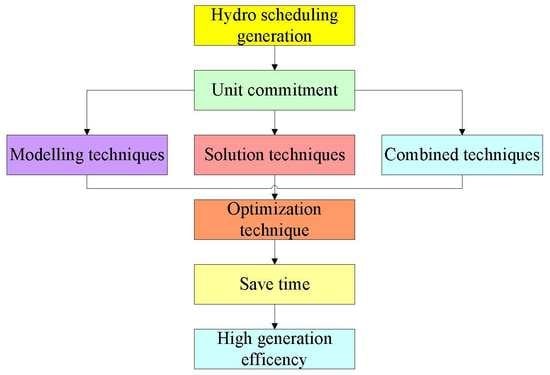
Modeling and Solution Techniques Used for Hydro Generation Scheduling
Abstract
1. Introduction
2. Hydro Constraints
3. Different Modelling and Solution Techniques
3.1. Modelling Techniques
3.1.1. Mixed Integer Programming
3.1.2. Dynamic Programming
3.1.3. Nonlinear Approach
3.1.4. Stochastic Modelling
3.1.5. Successive Linear Programming
3.2. Solution Techniques
3.2.1. Lagrange Relaxation
- First step is initialization; estimate the initial value of λ. For obtaining a better estimate, time dependent constraints are neglected and for each hour there is a value of u and λ.
- Second step is minor iteration, which is used to find the optimal solution. The accurate solution is obtained by fixing u as zero for the initial estimate. Implementation of two update schemes is done. Initially the feasibility is obtained by a sub gradient method with step size control. The u’s are fixed after obtaining the optimal solution and they are fixed till a small change will make the solution infeasible. The overall set of individual sub problems have to be solved for each set of u’s.
- Third step is of large major, it is known that whenever optimal solution is achieved, a new measurement of economic dispatch is done, in this way λ is updated. After doing this, step (b) is repeated.
- Fourth step focuses on the solution of the individual unit. Time is the state variable and for this unit is adjusted to be on/off. This is termed as minimum up time which shows a positive value; it means when unit is up it gives positive value and when unit is down it gives negative value and it is called minimum. Down time is based on discretized hourly interval. The problem is with down time as it takes a long time to cool the unit so it is compulsory to keep track of negative values of unit. Further, the state space influences the time of execution so it is not required to enhance the start-up costs, which depends on minimum up/down times.
- To confirm solution in general, several major iterations are done. The criteria which is used to check the result is known as stopping and it is very crucial to understand it. The most influential strategy is natural criterion, which is the distinction between dual and primal objectives as a fraction. This is better for large systems as compared to small ones. However, a minute variation in u gives the change in output between optimality and inaccuracy of the solution instead of knowing this, consider that the result is obtained. However, meeting the criteria does not guarantee the optimum solution.
- Sixth step deals with the same units and makes a group of similar units and places them in a given set of λ, u. To ensure that such units are distinct, adjust heat rate data slightly.
- Seventh step deals with the generalization of start-up constraints related to system and plant by unit groups. Basically, in a group all the units of the plants are placed and units in a group are just placed randomly. One unit at a given hour is started and if units are require to be excluded from the group are simply not assigned to that group. It is also possible that units can be grouped in more than one group. In the algorithm of dynamic programming, unit is a member of a group and is started up at any time. If at a given hour a unit of a group is committed, then the algorithm does not permit another unit to be started up.
- Eighth step focuses on the reserve for security purpose, it is allowed with area reserve constraints which do not affect the overall computational time because areas are sets of units which are user defined.
- The last step emphasized the reserve constraint which must be satisfied in economic dispatch calculation. There is enough strength committed to fulfill the reserve within the dynamic program. On a strictly economic basis, the generation allocation is done but it cannot satisfy the total reserve constraint because each unit gives maximum contribution to reserve. For fulfilling the need of reserve requirement, a new step called post-dispatch is added in the economic dispatch. From the most expensive unit to the cheapest unit, the post-dispatch works in transferring the generation when it is required.
3.2.2. Bender Decomposition Approach
3.2.3. Linear Quadratic Penalty Approach
3.2.4. Genetic Algorithm
- In initial population, production of genotypes (initial binary coded solutions) like (say M = 500) is done by binding all units. After this, units are turning away from commitment by some probability in an irregular manner. Checking of schedules for demand, minimum up and down unit of time, and spinning reserve constraints should be done. While fulfilling the requirement of all constraints, a term fitness score is introduced which specified the main aim of solution. Lambda iteration technique economically dispatches the hourly load; in this way it calculates the main goal related with every solution. The ranking of solution is done in descending order and it depends on the fitness values for every solution and solutions which are best are known as parents. Moreover, each solution is concerned with fitness score. D () = whole cost of fuel + cost of shut down/start up.
- Reproduction is a prime selection operator. Roulette wheel parent selection algorithm is used to select two genotypes. The specialty of this algorithm is that while remaining in the population it chooses a genotype which corresponding to relative fitness of genotypes. A two primary genetic operator’s mutation and crossover are helpful in producing a new offspring genotype.
- The current samples of genetic strings are obtained throughout the process of evolution. Crossover operation has two stages, i.e., unit stage and population stage. With fixed probability of 0.7, both types of crossover are done.
- For better planning, it is required to exchange the scheduling periods within the genotype. There is no fitness function value of partial string of genotype, the selection process is accomplished in an irregular manner with some certain probability. There are two stages of unit crossover and they are dealing with strings first half and second half with randomly chosen units in order to find suitable planning, therefore, the first stage is about maintaining the first half and interchanging the second half of the strings. While the second stage is about maintaining the second half and interchanging the first half of the strings.
- Certain probability is implemented on this operator. The implementation of this certain probability has some advantage, the combination of the parent genotypes results in a new genotype which inherent the properties of both parents. The offspring are an identical replication of their parents. Roulette wheel parent selection gives parent genotypes and there is crossover between these parent genotypes. The scheme of crossover is using single point crossover.
- The other step is mutation which deals with producing a new genetic material into gene at a low rate. The bits of genotypes’ offspring change from ‘0’ to ‘1’ because they are randomly selected with a minute probability.
- In this manipulator, based on the overall load, units are ranked and arranged in descending order. Here, the net heat rate of fuel cost is calculated at full load times. To calculate the average production cost of full load, the status of ith and jth units are exchanged. The units give status of ON and OFF, if the production cost of ith unit is lesser than the production cost of jth unit at full load. To avoid local convergence and reducing overall cost, this process is done by some probability for every scheduled hour.
- Repairing up/down time manipulator indicate is concerned with repairing the solution which is not optimal related to constraints of minimum up and down time. It explains the state of a unit for hour ‘0’. The state ON and OFF is updated and revised when constraint of minimum up/down time in a given time t is violated.
- Concerning spinning reserve and demand constraints, this manipulator approximates the solution which is not optimal. These constraints are checked every hour and if the schedule is not satisfied for that special hour it is maintained from the last generation which is also an optimal result.
- In descending order, the whole population is organized and it includes parents and offspring. The basis of the next generation is formed when the best k solutions are transcribed. In order to obtain the best scheduling results of UC, it is necessary to calculate fuel cost for every interval including flow line losses.
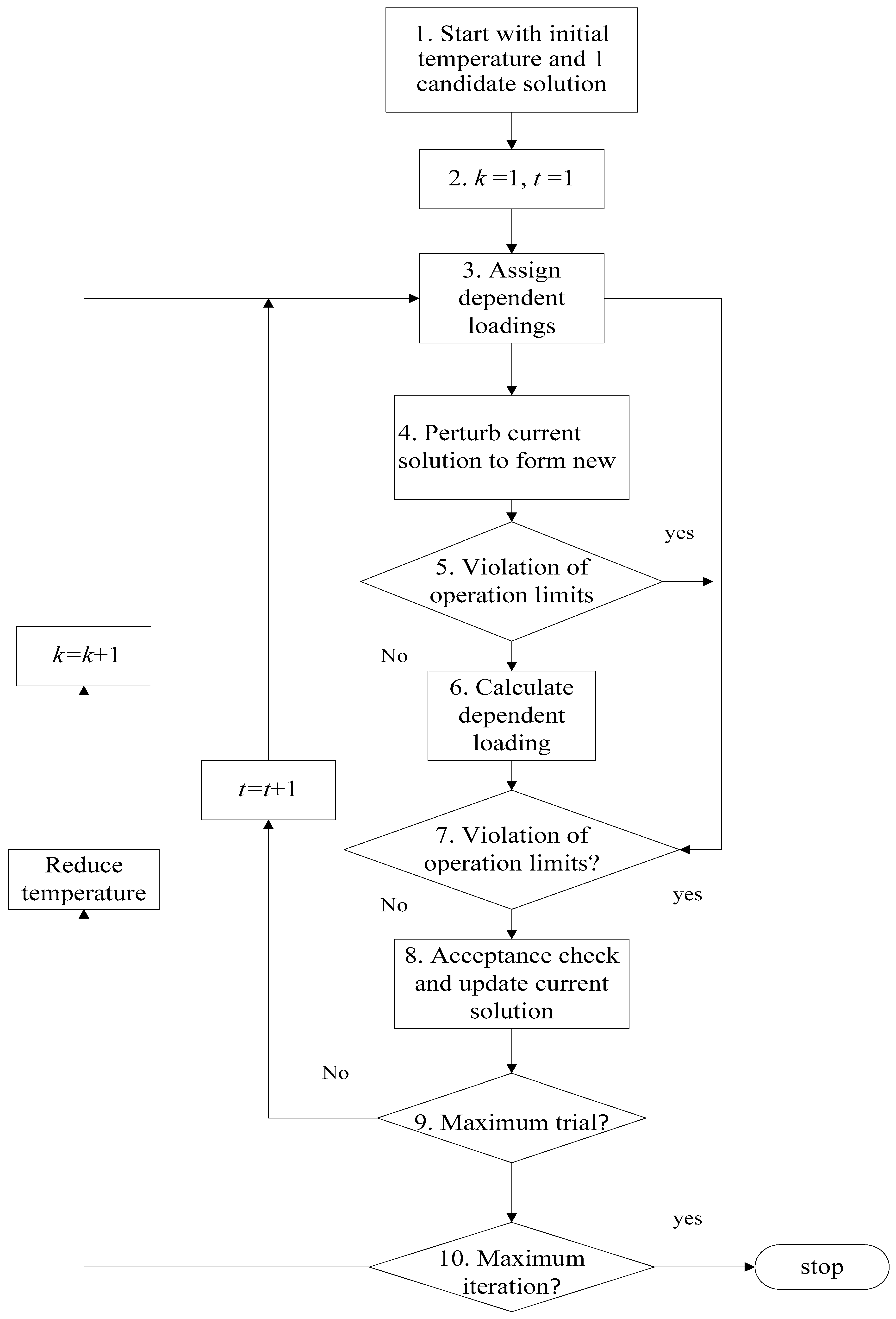
3.2.5. Enhanced Simulated Annealing
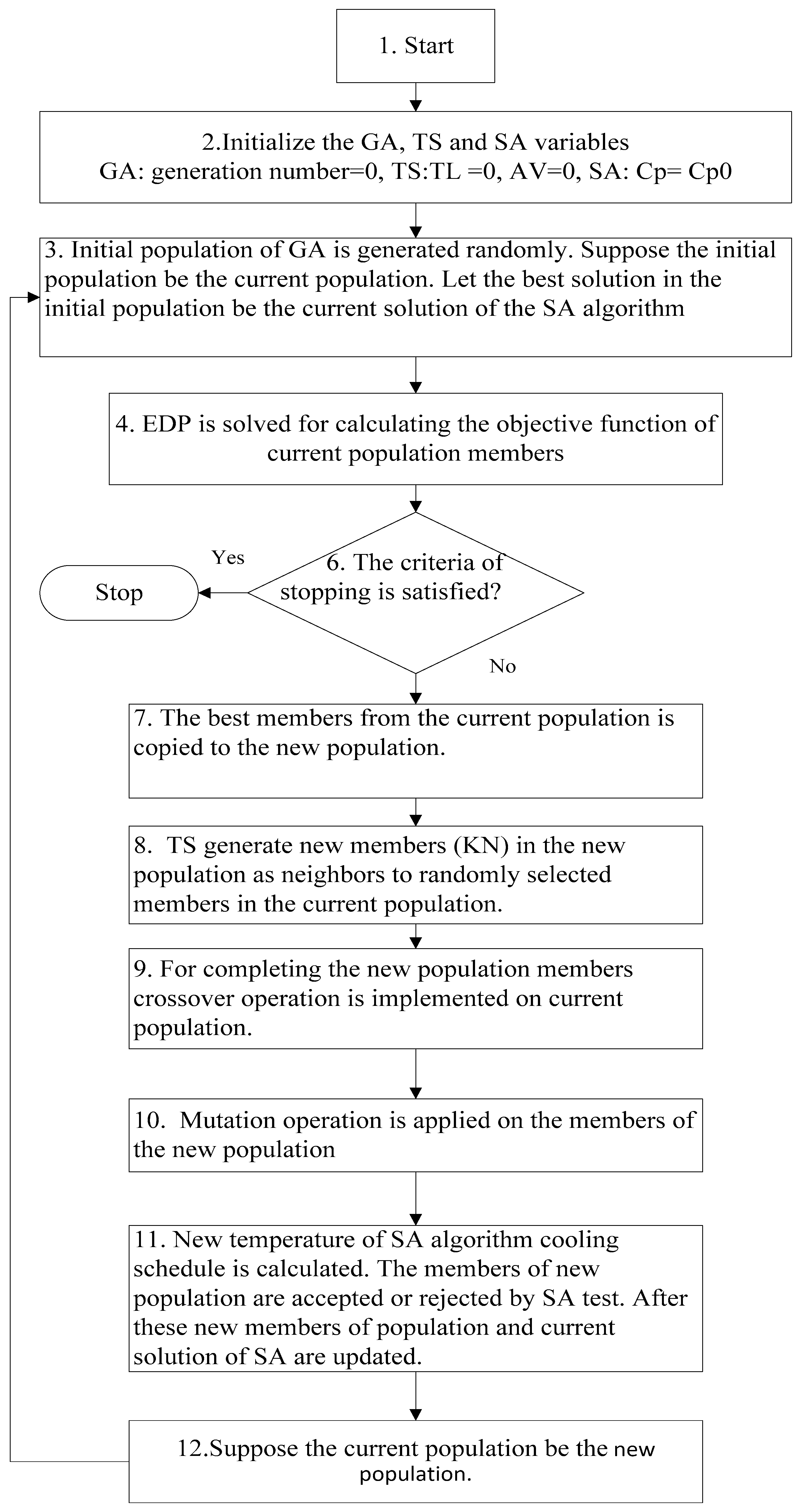
3.2.6. Genetic Algorithm, Tabu Search and Simulated Annealing
3.2.7. Heuristic Algorithms
3.3. Combination of Modeling and Solution Techniques
3.3.1. Combined Method
3.3.2. Dynamic Programming with Heuristic Techniques
3.4. Advantages and Disadvantages
4. Discussion
4.1. Summary of Modelling Techniques
4.2. Summary of Solution Techniques
5. Conclusions and Prospective Outlook
5.1. Conclusions
5.2. Prospective Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Output of electric power of unit j in plant k at time t (MW) | |
| Flow of water in hydro plant k (m3/s) | |
| ON/OFF generating status of unit j at time t in plant k (binary) | |
| ON/OFF pumping status of unit j in time t within plant k (binary) | |
| Load demand at time t (MW) | |
| High operating limits for unit j in plant k (MW) | |
| Spinning reserve requirement in time t | |
| Volume of water in jth reservoir in time t | |
| Water discharge rate jth reservoir | |
| Maximum number of online units in plant k in time t | |
| Minimum number of online units in plant k in time t | |
| Shutdown status of hydro unit j of plant k in time t | |
| Startup status of hydro unit j of plant k in time t | |
| Cost function of unit j (Rs/h) |
References
- Séguin, S.; Côté, P.; Audet, C. Self-scheduling short-term unit commitment and loading problem. IEEE Trans. Power Syst. 2016, 31, 133–142. [Google Scholar] [CrossRef]
- Shen, J.J.; Shen, Q.Q.; Wang, S.; Lu, J.Y.; Meng, Q.X. Generation Scheduling of a Hydrothermal System Considering Multiple Provincial Peak-Shaving Demands. IEEE Access 2019, 7, 46225–46239. [Google Scholar] [CrossRef]
- Carpentier, P.L.; Gendreau, M.; Bastin, F. Long-term management of a hydroelectric multireservoir system under uncertainty using the progressive hedging algorithm. Water Resour. Res. 2013, 49, 2812–2827. [Google Scholar] [CrossRef]
- Shen, J.J.; Zhang, X.F.; Wang, J.; Cao, R.; Wang, S.; Zhang, J. Optimal operation of interprovincial Hydropower System Including Xiluodu and Local Plants in Multiple Recipient Regions. Energies 2019, 12, 144. [Google Scholar] [CrossRef]
- Fosso, O.B.; Gjelsvik, A.; Haugstad, A.; Mo, B.; Wangensteen, I. Generation scheduling in a deregulated system. The Norwegian case. IEEE Trans. Power Syst. 1999, 14, 75–81. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic optimization for unit commitment—A review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Glotić, A.; Zamuda, A. Short-term combined economic and emission hydrothermal optimization by surrogate differential evolution. Appl. Energy 2015, 141, 42–56. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Dinh, B.H. An effectively adaptive selective cuckoo search algorithm for solving three complicated short-term hydrothermal scheduling problems. Energy 2018, 155, 930–956. [Google Scholar] [CrossRef]
- Taktak, R.; D’Ambrosio, C. An overview on mathematical programming approaches for the deterministic unit commitment problem in hydro valleys. Energy Syst. 2017, 8, 57–79. [Google Scholar] [CrossRef]
- Sahraoui, Y.; Bendotti, P.; D’Ambrosio, C. Real-world hydro-power unit-commitment: Dealing with numerical errors and feasibility issues. Energy 2017. [Google Scholar] [CrossRef]
- Shiddehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power System; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Patra, S.; Goswami, S.; Goswami, B. Fuzzy and simulated annealing based dynamic programming for the unit commitment problem. Expert Syst. Appl. 2009, 36, 5081–5086. [Google Scholar] [CrossRef]
- Doherty, R.; O’malley, M. A new approach to quantify reserve demand in systems with significant installed wind capacity. IEEE Trans. Power Syst. 2005, 20, 587–595. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Sun, N.; Jia, B.; Qin, H. Integrated scheduling of hydro, thermal and wind power with spinning reserve. Energy Procedia 2019, 158, 6302–6308. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, J.; Wu, X. Hydro unit commitment with a head-sensitive reservoir and multiple vibration zones using MILP. IEEE Trans. Power Syst. 2016, 31, 4842–4852. [Google Scholar] [CrossRef]
- Carrión, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Wang, J.; Guo, M.; Liu, Y. Hydropower unit commitment with nonlinearity decoupled from mixed integer nonlinear problem. Energy 2018, 150, 839–846. [Google Scholar] [CrossRef]
- Razavi, S.-E.; Nezhad, A.E.; Mavalizadeh, H.; Raeisi, F.; Ahmadi, A. Robust hydrothermal unit commitment: A mixed-integer linear framework. Energy 2018, 165, 593–602. [Google Scholar] [CrossRef]
- Senjyu, T.; Shimabukuro, K.; Uezato, K.; Funabashi, T. A fast technique for unit commitment problem by extended priority list. IEEE Trans. Power Syst. 2003, 18, 882–888. [Google Scholar] [CrossRef]
- Burns, R. Optimization of priority lists for a unit commitment program. In Proceedings of the Proc. IEEE Power Engineering Society Summer Meeting, San Francisco, CA, USA, 20–25 July 1975. [Google Scholar]
- Chang, G.W.; Aganagic, M.; Waight, J.G.; Medina, J.; Burton, T.; Reeves, S.; Christoforidis, M. Experiences with mixed integer linear programming based approaches on short-term hydro scheduling. IEEE Trans. Power Syst. 2001, 16, 743–749. [Google Scholar] [CrossRef]
- Conejo, A.J.; Arroyo, J.M.; Contreras, J.; Villamor, F.A. Self-scheduling of a hydro producer in a pool-based electricity market. IEEE Trans. Power Syst. 2002, 17, 1265–1272. [Google Scholar] [CrossRef]
- Jia, J.; Guan, X. MILP formulation for short-term scheduling of cascaded reservoirs with head effects. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengleng, China, 8–10 August 2011; pp. 4061–4064. [Google Scholar]
- Tong, B.; Zhai, Q.; Guan, X. An MILP based formulation for short-term hydro generation scheduling with analysis of the linearization effects on solution feasibility. IEEE Trans. Power Syst. 2013, 28, 3588–3599. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Yang, D. Improved dynamic programming for hydropower reservoir operation. J. Water Resour. Plan. Manag. 2012, 140, 365–374. [Google Scholar] [CrossRef]
- Amado, S.M.; Ribeiro, C.C. Short-term generation scheduling of hydraulic multi-reservoir multi-area interconnected systems. IEEE Trans. Power Syst. 1987, 2, 758–763. [Google Scholar] [CrossRef]
- Lyra, C.; Ferreira, L.R.M. A multiobjective approach to the short-term scheduling of a hydroelectric power system. IEEE Trans. Power Syst. 1995, 10, 1750–1755. [Google Scholar] [CrossRef]
- Arce, A.; Ohishi, T.; Soares, S. Optimal dispatch of generating units of the Itaipú hydroelectric plant. IEEE Trans. Power Syst. 2002, 17, 154–158. [Google Scholar] [CrossRef]
- Snyder, W.L.; Powell, H.D.; Rayburn, J.C. Dynamic programming approach to unit commitment. IEEE Trans. Power Syst. 1987, 2, 339–348. [Google Scholar] [CrossRef]
- Van den Bosch, P.; Honderd, G. A solution of the unit commitment problem via decomposition and dynamic programming. IEEE Trans. Power Appar. Syst. 1985, 1684–1690. [Google Scholar] [CrossRef]
- Håberg, M. Fundamentals and recent developments in stochastic unit commitment. Int. J. Electr. Power Energy Syst. 2019, 109, 38–48. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Cheng, C.-T.; Wu, X.-Y. Optimization of large-scale hydropower system peak operation with hybrid dynamic programming and domain knowledge. J. Clean. Prod. 2018, 171, 390–402. [Google Scholar] [CrossRef]
- Zhuang, F.; Galiana, F. Unit commitment by simulated annealing. IEEE Trans. Power Syst. 1990, 5, 311–318. [Google Scholar] [CrossRef]
- Kothari, D.; Ahmad, A. An expert system approach to the unit commitment problem. Energy Convers. Manag. 1995, 36, 257–261. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Rudolf, A.; Bayrleithner, R. A genetic algorithm for solving the unit commitment problem of a hydro-thermal power system. IEEE Trans. Power Syst. 1999, 14, 1460–1468. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evaluation of genetic algorithms for optimal reservoir system operation. J. Water Resour. Plann. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Yu, B.; Yuan, X.; Wang, J. Short-term hydro-thermal scheduling using particle swarm optimization method. Energy Convers. Manag. 2007, 48, 1902–1908. [Google Scholar] [CrossRef]
- Ruzic, S.; Rajakovic, N. A new approach for solving extended unit commitment problem. IEEE Trans. Power Syst. 1991, 6, 269–277. [Google Scholar] [CrossRef]
- Peterson, W.L.; Brammer, S.R. A capacity based Lagrangian relaxation unit commitment with ramp rate constraints. IEEE Trans. Power Syst. 1995, 10, 1077–1084. [Google Scholar] [CrossRef]
- Ghaddar, B.; Naoum-Sawaya, J.; Kishimoto, A.; Taheri, N.; Eck, B. A Lagrangian decomposition approach for the pump scheduling problem in water networks. Eur. J. Oper. Res. 2015, 241, 490–501. [Google Scholar] [CrossRef]
- Petcharaks, N.; Ongsakul, W. Hybrid enhanced Lagrangian relaxation and quadratic programming for hydrothermal scheduling. Electr. Power Compon. Syst. 2007, 35, 19–42. [Google Scholar] [CrossRef]
- Redondo, N.J.; Conejo, A. Short-term hydro-thermal coordination by Lagrangian relaxation: Solution of the dual problem. IEEE Trans. Power Syst. 1999, 14, 89–95. [Google Scholar] [CrossRef]
- Xi, E.; Guan, X.; Li, R. Scheduling hydrothermal power systems with cascaded and head-dependent reservoirs. IEEE Trans. Power Syst. 1999, 14, 1127–1132. [Google Scholar]
- Glover, F. Artificial intelligence, heuristic frameworks and tabu search. Manag. Decis. Econ. 1990, 11, 365–375. [Google Scholar] [CrossRef]
- Glover, F.; Taillard, E. A user’s guide to tabu search. Ann. Oper. Res. 1993, 41, 1–28. [Google Scholar] [CrossRef]
- Victorie, T.; Jeyakumar, A. Unit commitment by a Tabu-search-based hybrid-optimization technique. IEE Proc. Gener. Transm. Distrib. 2005, 152, 563–574. [Google Scholar] [CrossRef]
- Ikura, Y.; Gross, G. Efficient large-scale hydro system scheduling with forced spill conditions. IEEE Trans. Power Appar. Syst. 1984, 3502–3520. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Mariano, S.J.P.S.; Mendes, V.M.F.; Ferreira, L.A.F.M. Nonlinear optimization method for short-term hydro scheduling considering head-dependency. Eur. Trans. Electr. Power 2008, 20, 172–183. [Google Scholar] [CrossRef]
- Illerhaus, S.; Verstege, J. Optimal operation of industrial CHP-based power systems in liberalized energy markets. In Proceedings of the PowerTech Budapest 99. Abstract Records.(Cat. No. 99EX376), Budapest, Hungary, 29 August–2 September 1999; p. 210. [Google Scholar]
- Ryan, S.M.; Wets, R.J.-B.; Woodruff, D.L.; Silva-Monroy, C.; Watson, J.-P. Toward scalable, parallel progressive hedging for stochastic unit commitment. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Ordoudis, C.; Pinson, P.; Zugno, M.; Morales, J.M. Stochastic unit commitment via progressive hedging—Extensive analysis of solution methods. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Rachunok, B.; Staid, A.; Watson, J.-P.; Woodruff, D.L.; Yang, D. Stochastic Unit Commitment Performance Considering Monte Carlo Wind Power Scenarios. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Gade, D.; Hackebeil, G.; Ryan, S.M.; Watson, J.-P.; Wets, R.J.-B.; Woodruff, D.L. Obtaining lower bounds from the progressive hedging algorithm for stochastic mixed-integer programs. Math. Program. 2016, 157, 47–67. [Google Scholar] [CrossRef]
- Cheung, K.; Gade, D.; Silva-Monroy, C.; Ryan, S.M.; Watson, J.-P.; Wets, R.J.-B.; Woodruff, D.L. Toward scalable stochastic unit commitment. Energy Syst. 2015, 6, 417–438. [Google Scholar] [CrossRef]
- Scuzziato, M.R.; Finardi, E.C.; Frangioni, A. Comparing spatial and scenario decomposition for stochastic hydrothermal unit commitment problems. IEEE Trans. Sustain. Energy 2018, 9, 1307–1317. [Google Scholar] [CrossRef]
- Aravena, I.; Papavasiliou, A. A distributed asynchronous algorithm for the two-stage stochastic unit commitment problem. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Papavasiliou, A.; Oren, S.; Rountree, B. Applying high performance computing to transmission-constrained stochastic unit commitment for renewable penetration. IEEE Trans. Power Syst. 2015, 30, 1690–1701. [Google Scholar] [CrossRef]
- López-Salgado, C.J.; Ano, O.; Ojeda-Esteybar, D.M. Stochastic Unit Commitment and Optimal Allocation of Reserves: A Hybrid Decomposition Approach. IEEE Trans. Power Syst. 2018, 33, 5542–5552. [Google Scholar] [CrossRef]
- Vatanpour, M.; Yazdankhah, A.S. The impact of energy storage modeling in coordination with wind farm and thermal units on security and reliability in a stochastic unit commitment. Energy 2018, 162, 476–490. [Google Scholar] [CrossRef]
- Nasri, A.; Kazempour, S.J.; Conejo, A.J.; Ghandhari, M. Network-constrained AC unit commitment under uncertainty: A Benders’ decomposition approach. IEEE Trans. Power Syst. 2016, 31, 412–422. [Google Scholar] [CrossRef]
- Mehrtash, M.; Raoofat, M.; Mohammadi, M.; Zareipour, H. Fast stochastic security-constrained unit commitment using point estimation method. Int. Trans. Electr. Energy Syst. 2016, 26, 671–688. [Google Scholar] [CrossRef]
- Vatanpour, M.; Sadeghi Yazdankhah, A. Application of Benders decomposition in stochastic scheduling of thermal units with coordination of wind farm and energy storage system considering security constraint. J. Energy Manag. Technol. 2018, 2, 9–17. [Google Scholar]
- Du, E.; Zhang, N.; Kang, C.; Xia, Q. Scenario Map Based Stochastic Unit Commitment. IEEE Trans. Power Syst. 2018, 33, 4694–4705. [Google Scholar] [CrossRef]
- Valinejad, J.; Oladi, Z.; Barforoshi, T.; Parvania, M. Stochastic unit commitment in the presence of demand response program under uncertainties. IJE Trans. B Appl. 2017, 30, 1134–1143. [Google Scholar]
- Uçkun, C.; Botterud, A.; Birge, J.R. An improved stochastic unit commitment formulation to accommodate wind uncertainty. IEEE Trans. Power Syst. 2015, 31, 2507–2517. [Google Scholar] [CrossRef]
- Abbaspourtorbati, F.; Zima, M. The Swiss reserve market: Stochastic programming in practice. IEEE Trans. Power Syst. 2016, 31, 1188–1194. [Google Scholar] [CrossRef]
- Asensio, M.; Contreras, J. Stochastic unit commitment in isolated systems with renewable penetration under CVaR assessment. IEEE Trans. Smart Grid 2015, 7, 1356–1367. [Google Scholar] [CrossRef]
- Gomes, I.; Laia, R.; Pousinho, H.; Melício, R.; Mendes, V. Aggregation Platform for Wind-PV-Thermal Technology in Electricity Market. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 799–804. [Google Scholar]
- Jiang, R.; Guan, Y.; Watson, J.-P. Cutting planes for the multistage stochastic unit commitment problem. Math. Program. 2016, 157, 121–151. [Google Scholar] [CrossRef]
- Analui, B.; Scaglione, A. A dynamic multistage stochastic unit commitment formulation for intraday markets. IEEE Trans. Power Syst. 2018, 33, 3653–3663. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Liao, X.; Qin, H. Study on unit commitment problem considering pumped storage and renewable energy via a novel binary artificial sheep algorithm. Appl. Energy 2017, 187, 612–626. [Google Scholar] [CrossRef]
- Shahbazitabar, M.; Abdi, H. A novel priority-based stochastic unit commitment considering renewable energy sources and parking lot cooperation. Energy 2018, 161, 308–324. [Google Scholar] [CrossRef]
- Jo, K.-H.; Kim, M.-K. Stochastic unit commitment based on multi-scenario tree method considering uncertainty. Energies 2018, 11, 740. [Google Scholar] [CrossRef]
- Norouzi, M.R.; Ahmadi, A.; Nezhad, A.E.; Ghaedi, A. Mixed integer programming of multi-objective security-constrained hydro/thermal unit commitment. Renew. Sustain. Energy Rev. 2014, 29, 911–923. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aghaei, J.; Shayanfar, H.A.; Rabiee, A. Mixed integer programming of multiobjective hydro-thermal self scheduling. Appl. Soft Comput. 2012, 12, 2137–2146. [Google Scholar] [CrossRef]
- Esmaeily, A.; Ahmadi, A.; Raeisi, F.; Ahmadi, M.R.; Nezhad, A.E.; Janghorbani, M. Evaluating the effectiveness of mixed-integer linear programming for day-ahead hydro-thermal self-scheduling considering price uncertainty and forced outage rate. Energy 2017, 122, 182–193. [Google Scholar] [CrossRef]
- Borghetti, A.; D’Ambrosio, C.; Lodi, A.; Martello, S. An MILP approach for short-term hydro scheduling and unit commitment with head-dependent reservoir. IEEE Trans. Power Syst. 2008, 23, 1115–1124. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Wei, J.; Wang, G.; Yeh, W.W.-G. Hydro unit commitment via mixed integer linear programming: A case study of the three gorges project, China. IEEE Trans. Power Syst. 2014, 29, 1232–1241. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.; Simonovic, S.P. Short-term operation model for coupled hydropower reservoirs. J. Water Resour. Plan. Manag. 2000, 126, 98–106. [Google Scholar] [CrossRef]
- Lowery, P. Generating unit commitment by dynamic programming. IEEE Trans. Power Appar. Syst. 1966, 422–426. [Google Scholar] [CrossRef]
- Catalão, J.; Mariano, S.; Mendes, V.; Ferreira, L. Scheduling of head-sensitive cascaded hydro systems: A nonlinear approach. IEEE Trans. Power Syst. 2008, 24, 337–346. [Google Scholar] [CrossRef]
- Takriti, S.; Birge, J.R.; Long, E. A stochastic model for the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 1497–1508. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, T. Stochastic security-constrained unit commitment. IEEE Trans. Power Syst. 2007, 22, 800–811. [Google Scholar] [CrossRef]
- Fosso, O.B.; Belsnes, M.M. Short-term hydro scheduling in a liberalized power system. In Proceedings of the 2004 International Conference on Power System Technology, Singapore, 21–24 November 2004; pp. 1321–1326. [Google Scholar]
- Wang, S.; Shahidehpour, S.; Kirschen, D.S.; Mokhtari, S.; Irisarri, G. Short-term generation scheduling with transmission and environmental constraints using an augmented Lagrangian relaxation. IEEE Trans. Power Syst. 1995, 10, 1294–1301. [Google Scholar] [CrossRef]
- Frangioni, A.; Gentile, C.; Lacalandra, F. Sequential Lagrangian-MILP approaches for unit commitment problems. Int. J. Electr. Power Energy Syst. 2011, 33, 585–593. [Google Scholar] [CrossRef]
- Orero, S.; Irving, M. A combination of the genetic algorithm and Lagrangian relaxation decomposition techniques for the generation unit commitment problem. Electr. Power Syst. Res. 1997, 43, 149–156. [Google Scholar] [CrossRef]
- Beltran, C.; Heredia, F.J. Unit commitment by augmented lagrangian relaxation: Testing two decomposition approaches. J. Optim. Theory Appl. 2002, 112, 295–314. [Google Scholar] [CrossRef]
- Virmani, S.; Adrian, E.C.; Imhof, K.; Mukherjee, S. Implementation of a Lagrangian relaxation based unit commitment problem. IEEE Trans. Power Systems 1989, 4, 1373–1380. [Google Scholar] [CrossRef]
- Gröwe-Kuska, N.; Kiwiel, K.; Nowak, M.; Römisch, W.; Wegner, I. Power management under uncertainty by Lagrangian relaxation. In Proceedings of the 6th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Madeira, Spain, 17 August 2000. [Google Scholar]
- Baldick, R. The generalized unit commitment problem. IEEE Trans. Power Syst. 1995, 10, 465–475. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Pardalos, P.M.; Guan, Y. A decomposition approach to the two-stage stochastic unit commitment problem. Ann. Oper. Res. 2013, 210, 387–410. [Google Scholar] [CrossRef]
- Franco, P.; Carvalho, M.; Soares, S. A network flow model for short-term hydro-dominated hydrothermal scheduling problems. IEEE Trans. Power Syst. 1994, 9, 1016–1022. [Google Scholar] [CrossRef]
- Leite, P.T.; Carneiro, A.A.F.M.; Carvalho, A. Energetic operation planning using genetic algorithms. IEEE Trans. Power Syst. 2002, 17, 173–179. [Google Scholar] [CrossRef]
- Kazarlis, S.A.; Bakirtzis, A.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Ahmed, J.A.; Sarma, A.K. Genetic algorithm for optimal operating policy of a multipurpose reservoir. Water Resour. Manag. 2005, 19, 145–161. [Google Scholar] [CrossRef]
- Wong, S.Y.W. An enhanced simulated annealing approach to unit commitment. Int. J. Electr. Power Energy Syst. 1998, 20, 359–368. [Google Scholar] [CrossRef]
- Mantawy, A.; Abdel-Magid, Y.L.; Selim, S.Z. Integrating genetic algorithms, tabu search, and simulated annealing for the unit commitment problem. IEEE Trans. Power Syst. 1999, 14, 829–836. [Google Scholar] [CrossRef]
- Kjeldsen, N.H.; Chiarandini, M. Heuristic solutions to the long-term unit commitment problem with cogeneration plants. Comput. Oper. Res. 2012, 39, 269–282. [Google Scholar] [CrossRef]
- Johannesen, A.; Gjelsvik, A.; Fosso, O.; Flatabo, N. Optimal short term hydro scheduling including security constraints. IEEE Trans. Power Syst. 1991, 6, 576–583. [Google Scholar] [CrossRef]
- Su, C.-C.; Hsu, Y.-Y. Fuzzy dynamic programming: an application to unit commitment. IEEE Trans. Power Syst. 1991, 6, 1231–1237. [Google Scholar]
- Frangioni, A.; Gentile, C.; Lacalandra, F. Solving unit commitment problems with general ramp constraints. Int. J. Electr. Power Energy Syst. 2008, 30, 316–326. [Google Scholar] [CrossRef]
- Li, T.; Shahidehpour, M. Price-based unit commitment: A case of Lagrangian relaxation versus mixed integer programming. IEEE Trans. Power Syst. 2005, 20, 2015–2025. [Google Scholar] [CrossRef]
- Schulze, T.; Grothey, A.; McKinnon, K. A stabilised scenario decomposition algorithm applied to stochastic unit commitment problems. Eur. J. Oper. Res. 2017, 261, 247–259. [Google Scholar] [CrossRef]
- Catalão, J.P.d.S.; Pousinho, H.M.I.; Mendes, V.M.F. Scheduling of head-dependent cascaded reservoirs considering discharge ramping constraints and start/stop of units. Int. J. Electr. Power Energy Syst. 2010, 32, 904–910. [Google Scholar] [CrossRef]
- Finardi, E.C.; da Silva, E.L. Sagastizábal, C. Solving the unit commitment problem of hydropower plants via Lagrangian relaxation and sequential quadratic programming. Comput. Appl. Math. 2005, 24, 317–342. [Google Scholar] [CrossRef]
- Finardi, E.C.; da Silva, E.L. Solving the hydro unit commitment problem via dual decomposition and sequential quadratic programming. IEEE Trans. Power Syst. 2006, 21, 835–844. [Google Scholar] [CrossRef]
- Nowak, M.P.; Römisch, W. Stochastic Lagrangian relaxation applied to power scheduling in a hydro-thermal system under uncertainty. Ann. Oper. Res. 2000, 100, 251–272. [Google Scholar] [CrossRef]
- Su, C.; Cheng, C.; Wang, P. An MILP Model for Short-Term Peak Shaving Operation of Cascaded Hydropower Plants Considering Unit Commitment. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–5. [Google Scholar]
- Chen, Y.; Liu, F.; Liu, B.; Wei, W.; Mei, S. An efficient MILP approximation for the hydro-thermal unit commitment. IEEE Trans. Power Syst. 2016, 31, 3318–3319. [Google Scholar] [CrossRef]
- Cerisola, S.; Baíllo, Á.; Fernández-López, J.M.; Ramos, A.; Gollmer, R. Stochastic power generation unit commitment in electricity markets: A novel formulation and a comparison of solution methods. Oper. Res. 2009, 57, 32–46. [Google Scholar] [CrossRef]
- Valenzuela, J.; Mazumdar, M. Commitment of electric power generators under stochastic market prices. Oper. Res. 2003, 51, 880–893. [Google Scholar] [CrossRef]
- Philpott, A.; Schultz, R. Unit commitment in electricity pool markets. Math. Program. 2006, 108, 313–337. [Google Scholar] [CrossRef]
- Garver, L.L. Power generation scheduling by integer programming-development of theory. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1962, 81, 730–734. [Google Scholar] [CrossRef]
- Muckstadt, J.A.; Wilson, R.C. An application of mixed-integer programming duality to scheduling thermal generating systems. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1968–1978. [Google Scholar] [CrossRef]
- Dillon, T.S.; Edwin, K.W.; Kochs, H.-D.; Taud, R. Integer programming approach to the problem of optimal unit commitment with probabilistic reserve determination. IEEE Trans. Power Appar. Syst. 1978, 6, 2154–2166. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Haghrah, A. Optimal short-term generation scheduling of hydrothermal systems by implementation of real-coded genetic algorithm based on improved Mühlenbein mutation. Energy 2017, 128, 77–85. [Google Scholar] [CrossRef]
- Simab, M.; Javadi, M.S.; Nezhad, A.E. Multi-objective programming of pumped-hydro-thermal scheduling problem using normal boundary intersection and VIKOR. Energy 2018, 143, 854–866. [Google Scholar] [CrossRef]
- Tan, Z.; Ju, L.; Li, H.; Qin, C.; Peng, D. Multiobjective CVaR optimization model and solving method for hydrothermal system considering uncertain load demand. Math. Probl. Eng. 2015, 2015, 741379. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P. Fast evolutionary programming techniques for short-term hydrothermal scheduling. IEEE Trans. Power Syst. 2003, 18, 214–220. [Google Scholar] [CrossRef]
- Estahbanati, M. Hybrid probabilistic-harmony search algorithm methodology in generation scheduling problem. J. Exp. Theor. Artif. Intell. 2014, 26, 283–296. [Google Scholar] [CrossRef]
- Kang, C.; Guo, M.; Wang, J. Short-term hydrothermal scheduling using a two-stage linear programming with special ordered sets method. Water Resour. Manag. 2017, 31, 3329–3341. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Zhang, Y.; Fang, N.; Zhang, R. Short term hydrothermal scheduling using multi-objective differential evolution with three chaotic sequences. Int. J. Electr. Power Energy Syst. 2013, 47, 85–99. [Google Scholar] [CrossRef]
- Selvakumar, A.I. Civilized swarm optimization for multiobjective short-term hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2013, 51, 178–189. [Google Scholar] [CrossRef]
- Zhou, J.; Liao, X.; Ouyang, S.; Zhang, R.; Zhang, Y. Multi-objective artificial bee colony algorithm for short-term scheduling of hydrothermal system. Int. J. Electr. Power Energy Syst. 2014, 55, 542–553. [Google Scholar] [CrossRef]
- de Queiroz, A.R. Stochastic hydro-thermal scheduling optimization: An overview. Renew. Sustain. Energy Rev. 2016, 62, 382–395. [Google Scholar] [CrossRef]
- Chaudhry, F.; Amin, M.; Iqbal, M.; Khan, R.; Khan, J. A novel chaotic differential evolution hybridized with quadratic programming for short-term hydrothermal coordination. Neural Comput. Appl. 2018, 30, 3533–3544. [Google Scholar] [CrossRef]
- Espinosa, S.; Cazco, D.A.; Salcedo, M.Y. Economic dispatch hydrothermal system with CO2 emissions constraints. IEEE Lat. Am. Trans. 2017, 15, 2090–2096. [Google Scholar] [CrossRef]
- Takriti, S.; Birge, J.R. Using integer programming to refine Lagrangian-based unit commitment solutions. IEEE Trans. Power Syst. 2000, 15, 151–156. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Cheng, C.-T.; Wu, X.-Y. Optimization of hydropower system operation by uniform dynamic programming for dimensionality reduction. Energy 2017, 134, 718–730. [Google Scholar] [CrossRef]
- Georgakakos, A.P.; Yao, H.; Yu, Y. Control model for hydroelectric energy-value optimization. J. Water Resour. Plan. Manag. 1997, 123, 30–38. [Google Scholar] [CrossRef]
- Naresh, R.; Sharma, J. Hydro system scheduling using ANN approach. IEEE Trans. Power Syst. 2000, 15, 388–395. [Google Scholar] [CrossRef]
- Kumar, V.S.; Mohan, M. Solution to security constrained unit commitment problem using genetic algorithm. Int. J. Electr. Power Energy Syst. 2010, 32, 117–125. [Google Scholar] [CrossRef]
- Juste, K.; Kita, H.; Tanaka, E.; Hasegawa, J. An evolutionary programming solution to the unit commitment problem. IEEE Trans. Power Syst. 1999, 14, 1452–1459. [Google Scholar] [CrossRef]
- Archibald, T.; McKinnon, K.; Thomas, L. An aggregate stochastic dynamic programming model of multireservoir systems. Water Resour. Res. 1997, 33, 333–340. [Google Scholar] [CrossRef]
- Borges, C.L.; Pinto, R.J. Small hydro power plants energy availability modeling for generation reliability evaluation. IEEE Trans. Power Syst. 2008, 23, 1125–1135. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Sule, B.F.; Loucks, D.P. Stochastic dynamic programming models for reservoir operation optimization. Water Resour. Res. 1984, 20, 1499–1505. [Google Scholar] [CrossRef]
- Aghaei, J.; Ahmadi, A.; Shayanfar, H.; Rabiee, A. Mixed integer programming of generalized hydro-thermal self-scheduling of generating units. Electr. Eng. 2013, 95, 109–125. [Google Scholar] [CrossRef]
- Barros, M.T.; Tsai, F.T.; Yang, S.-L.; Lopes, J.E.; Yeh, W.W. Optimization of large-scale hydropower system operations. J. Water Resour. Plan. Manag. 2003, 129, 178–188. [Google Scholar] [CrossRef]
- Soares, S.; Carneiro, A.A. Optimal operation of reservoirs for electric generation. IEEE Trans. Power Deliv. 1991, 6, 1101–1107. [Google Scholar] [CrossRef]
- Shawwash, Z.K.; Siu, T.K.; Russel, S. The BC Hydro short term hydro scheduling optimization model. In Proceedings of the 21st International Conference on Power Industry Computer Applications. Connecting Utilities. PICA 99. To the Millennium and Beyond (Cat. No. 99CH36351), Santa Clara, CA, USA, 21 May 1999; pp. 183–189. [Google Scholar]
- Yoo, J.-H. Maximization of hydropower generation through the application of a linear programming model. J. Hydrol. 2009, 376, 182–187. [Google Scholar] [CrossRef]
- Le Ngo, L.; Madsen, H.; Rosbjerg, D. Simulation and optimisation modelling approach for operation of the Hoa Binh reservoir, Vietnam. J. Hydrol. 2007, 336, 269–281. [Google Scholar] [CrossRef]
- Mo, B.; Gjelsvik, A.; Grundt, A.; Karesen, K. Optimisation of hydropower operation in a liberalised market with focus on price modelling. In Proceedings of the 2001 IEEE Porto Power Tech Proceedings (Cat. No. 01EX502), Porto, Portugal, 10–13 September 2001; p. 6. [Google Scholar]
- Aslan, Y.; Arslan, O.; Yasar, C. A sensitivity analysis for the design of small-scale hydropower plant: Kayabogazi case study. Renew. Energy 2008, 33, 791–801. [Google Scholar] [CrossRef]
- Mahmoud, M.; Dutton, K.; Denman, M. Dynamical modelling and simulation of a cascaded reserevoirs hydropower plant. Electr. Power Syst. Res. 2004, 70, 129–139. [Google Scholar] [CrossRef]
- Chang, S.-C.; Chen, C.-H.; Fong, I.-K.; Luh, P.B. Hydroelectric generation scheduling with an effective differential dynamic programming algorithm. IEEE Trans. Power Syst. 1990, 5, 737–743. [Google Scholar] [CrossRef]
- Mariño, M.A.; Mohammadi, B. Reservoir operation by linear and dynamic programming. J. Water Resour. Plan. Manag. 1983, 109, 303–319. [Google Scholar] [CrossRef]
- Jacoby, H.D.; Loucks, D.P. Combined use of optimization and simulation models in river basin planning. Water Resour. Res. 1972, 8, 1401–1414. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Wilhelmi, J.R.; Arévalo, L.A. Optimal short-term operation schedule of a hydropower plant in a competitive electricity market. Energy Convers. Manag. 2010, 51, 2955–2966. [Google Scholar] [CrossRef]
- Finardi, E.C.; Scuzziato, M.R. Hydro unit commitment and loading problem for day-ahead operation planning problem. Int. J. Electr. Power Energy Syst. 2013, 44, 7–16. [Google Scholar] [CrossRef]
- Duckstein, L.; Opricovic, S. Multiobjective optimization in river basin development. Water Resour. Res. 1980, 16, 14–20. [Google Scholar] [CrossRef]
- Kuby, M.J.; Fagan, W.F.; ReVelle, C.S.; Graf, W.L. A multiobjective optimization model for dam removal: An example trading off salmon passage with hydropower and water storage in the Willamette basin. Adv. Water Resour. 2005, 28, 845–855. [Google Scholar] [CrossRef]
- Singal, S.; Saini, R.; Raghuvanshi, C. Analysis for cost estimation of low head run-of-river small hydropower schemes. Energy Sustain. Dev. 2010, 14, 117–126. [Google Scholar] [CrossRef]
- Sharif, M.; Wardlaw, R. Multireservoir systems optimization using genetic algorithms: Case study. J. Comput. Civ. Eng. 2000, 14, 255–263. [Google Scholar] [CrossRef]
- Jalali, M.; Afshar, A.; Marino, M. Reservoir operation by ant colony optimization algorithms. Iran. J. Sci. Technol. Trans. B Eng. 2006, 30, 107–117. [Google Scholar]
- Jalali, M.; Afshar, A.; Marino, M. Multi-colony ant algorithm for continuous multi-reservoir operation optimization problem. Water Resour. Manag. 2007, 21, 1429–1447. [Google Scholar] [CrossRef]
- Iqbal, M.; Azam, M.; Naeem, M.; Khwaja, A.; Anpalagan, A. Optimization classification, algorithms and tools for renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 39, 640–654. [Google Scholar] [CrossRef]
| Groups | Techniques |
|---|---|
| Heuristic | Genetic algorithm, differential evolution, bacterial foraging algorithm, simulated annealing, artificial bee colony algorithm, harmony search algorithm, particle swarm optimization and imperialistic competition algorithm. |
| Mathematical programming | Mixed integer linear programming, priority list approach, branch and bound approach, lagrange relaxation, linear programming, successive quadratic linear programming, nonlinear approach, bender decomposition, dynamic programming, stochastic programming, model predictive control, value function approximation, generation method, column-constraint, nested CG, state-space approximation and stabilized LR. |
| Hybrid techniques | Artificial neural network, genetic algorithm, tabu search and dynamic programming. |
| Modelling Techniques | Authors | Remarks |
|---|---|---|
| Mixed Integer programming-constraint method | Ahmadi, Aghaei, Shayanfar and Rabiee [77] | This method gives more profit rather than emission generation |
| Mixed integer linear programming | Borghetti, D’Ambrosio, Lodi and Martello [79] | This method is effective for solving large scale complex multi-unit commitment. |
| MILP | Li, Li, Wei, Wang and Yeh [80] | By adopting parallel version speed is improved |
| Stochastic programming | Gröwe-Kuska, Kiwiel, Nowak, Römisch and Wegner [92] | It gives guaranteed accuracy bounds |
| Nonlinear Approach | Catalão, Mariano, Mendes and Ferreira [50] | As the Binary variables are large, Computational burden increases. |
| Mixed integer nonlinear programming | Teegavarapu and Simonovic [81] | This method is computationally efficient. |
| Stochastic dynamic programming | Archibald et al. [137], Borges and Pinto [138], Stedinger et al. [139] | It focused on energy availability and reliability with random inflow and availability of generating the units. It is also good in solving the problem easily as it divides the original problem into independent, low dimensional sub-problems. Stochastic dynamic programming models, either stationary or non-stationary, are good in finding the policies which are helpful in operating the reservoirs. |
| Mixed integer programming | Aghaei et al. [140], Norouzi, Ahmadi, Nezhad and Ghaedi [76] and Ahmadi, Aghaei, Shayanfar and Rabiee [77] | It controls the emissions of Hydrothermal plants. It also helps in computational requirement. This method deals with security constraints effectively. It also studies the effect of prohibited operating zones and valve loading effect |
| Nonlinear programming | Barros et al. [141] | For better operation of real time nonlinear programming, this is the better choice. |
| Stochastic programming | Soares and Carneiro [142] | This method deals with both cascaded and single reservoirs with high head for optimal operation. |
| Linear programming | Shawwash et al. [143], Yoo [144] | It finds the generation on hourly basis. It is computationally fast. |
| Simulation model | Le Ngo et al. [145] | For increasing the production of hydropower plant, it maintains the level of reservoir high. |
| Stochastic dual dynamic programming | Mo et al. [146] | It focused on price as well operation of plant. |
| Sensitivity analysis, Dynamic programming SIMULINK | Aslan et al. [147] Mahmoud et al. [148] | It finds the ideal configuration by using the flow rates when they are higher and also finds the key element of plant efficiency is head loss. |
| Differential dynamic programming | Chang et al. [149] | It works better for small tail and high head reservoir plants. |
| Mixed integer linear programming | Carrión and Arroyo [17] | It minimizes the curse of dimensionality |
| Dynamic programming | Lowery [82], Mariño and Mohammadi [150], [151,152] | It is good in determining the optimum way of k + 1 units instead of k unit. It is also worthy in giving maximum power, when head and discharge changes. Multi-reservoirs have no impact on DP. It works in investigating the optimization models analytically. |
| Solution Techniques | Authors | Remarks |
|---|---|---|
| Augmented Lagrange Relaxation | Wang, Shahidehpour, Kirschen, Mokhtari and Irisarri [87] | New algorithm was developed which is fast, efficient and robust in practical size systems. |
| Sequential Lagrange-mixed integer linear programming | Frangioni, Gentile and Lacalandra [88] | Efficiency is improved by the sequential process of these two techniques. Here, mixed integer programming is a modelling technique and sequential lagrange is a solution technique. |
| Lagrange Relaxation decomposition, Genetic Algorithm | Orero and Irving [89] | This combined method handles both discrete and continuous parameters. |
| Augmented Lagrange relaxation ALR, Decomposition techniques (Auxiliary problem principle APP and Block coordinate descent BCD) | Beltran and Heredia [90] | Augmented Lagrange Relaxation method becomes a local and global optimizer by using Auxiliary problem principle (APP) and Block coordinated descent (BCD). The comparison of APP and BCD shows that BCD is faster as compared to APP. |
| Lagrange relaxation | Virmani, Adrian, Imhof and Mukherjee [91], Norouzi, Ahmadi, Nezhad and Ghaedi [76] and Finardi and Scuzziato [153] | The linear variability is involved between the time of execution and time stages. This method gives efficient results and it is more capable in precision and execution time for large level systems. It also considers the turbine losses. |
| Combined LP and heuristic technique | Johannesen et al. [102] | It handles multi-objectives more easily. |
| Linear-quadratic penalty approach | Franco et al. [150] | It solves general problems directly, but it does not give good quality results. |
| Lagrangian decomposition | Baldick [95] | It considers the effect of head change in single function. |
| Fuzzy and simulated annealing with dynamic programming | Patra, Goswami and Goswami [93] | The computation time is good. |
| Artificial Neural network | Naresh and Sharma [134] | This approach deals with the optimization of hydropower system which is interconnected |
| Multi objective optimization | Duckstein and Opricovic [154], Kuby et al. [155] | This helps in decision making process and also evaluates the trade-offs based on economics and ecology. |
| Regression method | Singal et al. [156] | The correlations are developed for finding the project cost and compare it with current project cost |
| Genetic Algorithm | Sharif and Wardlaw [157] Oliveira and Loucks [36] | This is used for any reservoir and it also considers the real vectors. |
| Ant-colony, multi-colony Ant algorithm | Jalali et al. [158,159] | The work of ant colony method is to provide good results while multi colony deals with probability of reducing the domain of global optimality. |
| Different optimization techniques | Iqbal et al. [160] | Suggested different optimization techniques for different users. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parvez, I.; Shen, J.; Khan, M.; Cheng, C. Modeling and Solution Techniques Used for Hydro Generation Scheduling. Water 2019, 11, 1392. https://doi.org/10.3390/w11071392
Parvez I, Shen J, Khan M, Cheng C. Modeling and Solution Techniques Used for Hydro Generation Scheduling. Water. 2019; 11(7):1392. https://doi.org/10.3390/w11071392
Chicago/Turabian StyleParvez, Iram, Jianjian Shen, Mehran Khan, and Chuntian Cheng. 2019. "Modeling and Solution Techniques Used for Hydro Generation Scheduling" Water 11, no. 7: 1392. https://doi.org/10.3390/w11071392
APA StyleParvez, I., Shen, J., Khan, M., & Cheng, C. (2019). Modeling and Solution Techniques Used for Hydro Generation Scheduling. Water, 11(7), 1392. https://doi.org/10.3390/w11071392