Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools
Abstract
1. Introduction
2. Methods
- Infected bathers shed pathogens at a specific shedding rate.
- Pathogens in the water are inactivated by the active disinfectant (HOCl) and have natural die-off.
- Pathogens are mixed/dispersed via turbulent diffusion from the infected bathers to other bathers.
- Bathers ingest surviving pathogens and are infected according to a dose-response model.
2.1. Cyanurate Chemistry
2.2. Effect of Cyanurate on Disinfection Kinetics
2.3. Pathogen Selection
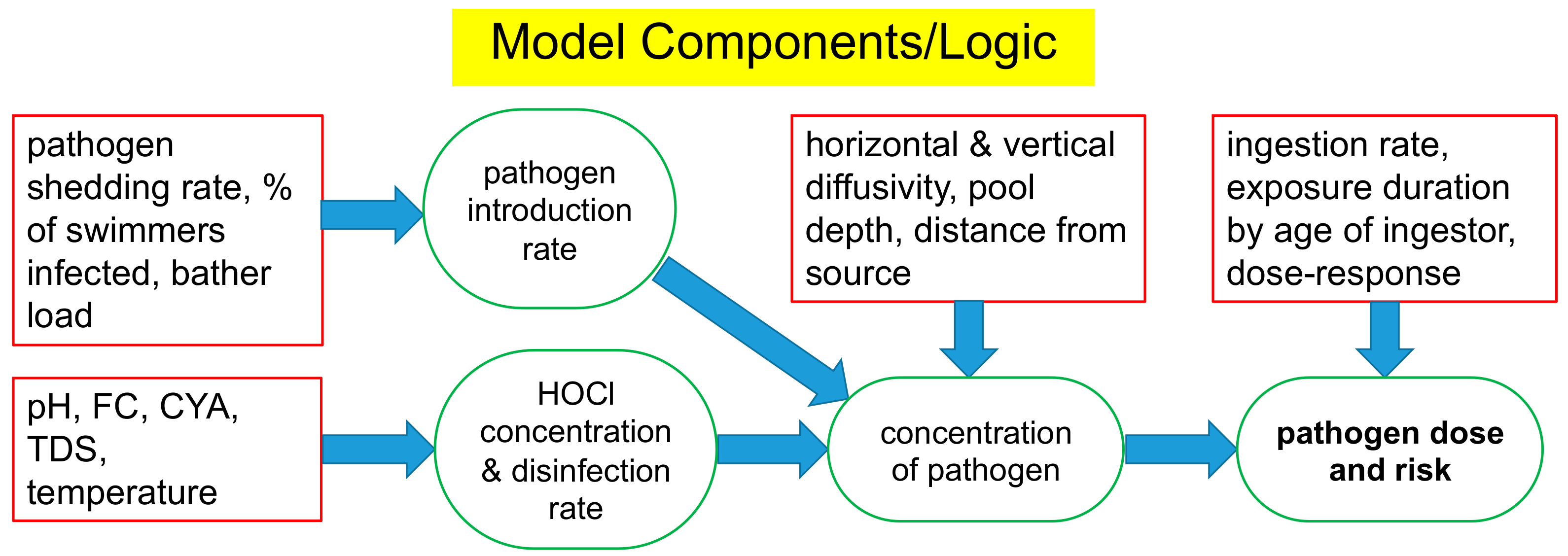
2.4. Steady-State Model of Pathogen Risk
2.4.1. Simulation of Bather Shedding Pathogens
2.4.2. Simulation of Subject Pathogen Inactivation and Natural Die-Off
2.4.3. Simulation of Pathogen Mixing/Dispersion
2.4.4. Simulation of Dose-Response Infection Risk
2.4.5. Model Limitations
3. Results
3.1. Cyanurate Chemistry
3.1.1. HOCl vs. CYA and pH
3.1.2. HOCl vs. CYA/FC Ratio
3.1.3. HOCl Range in Regulatory Code
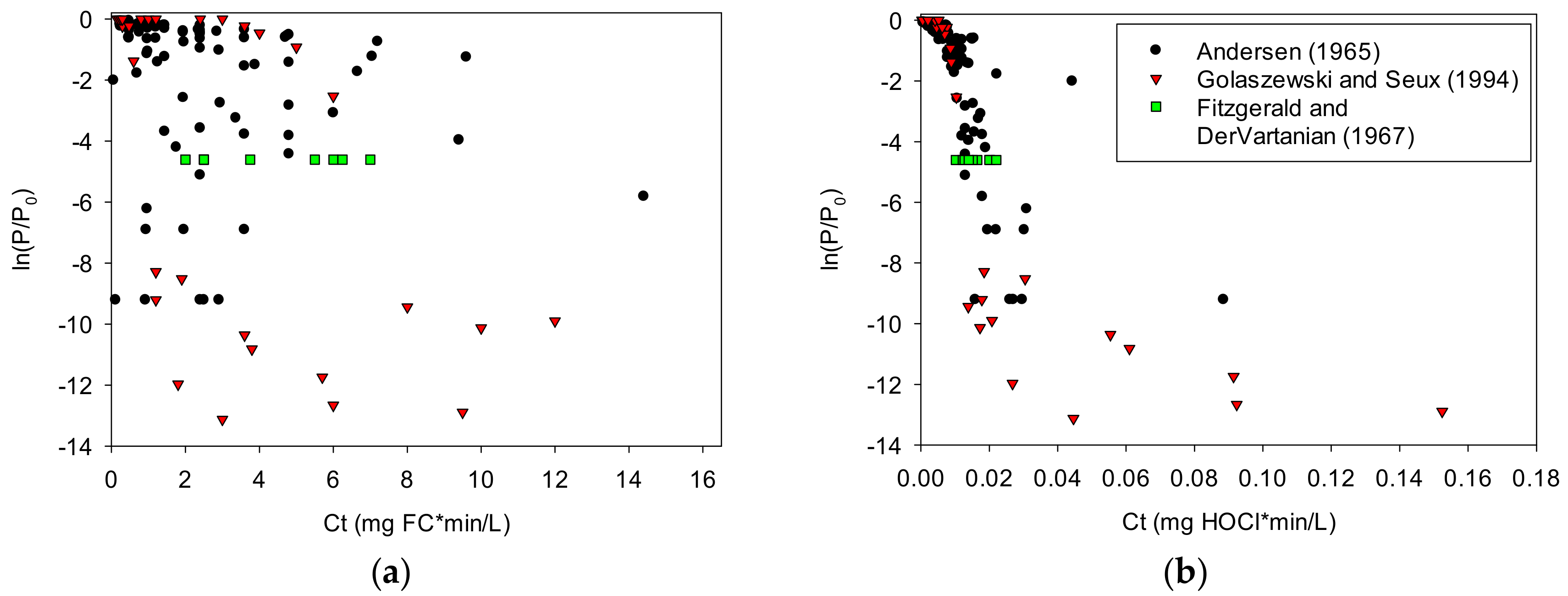
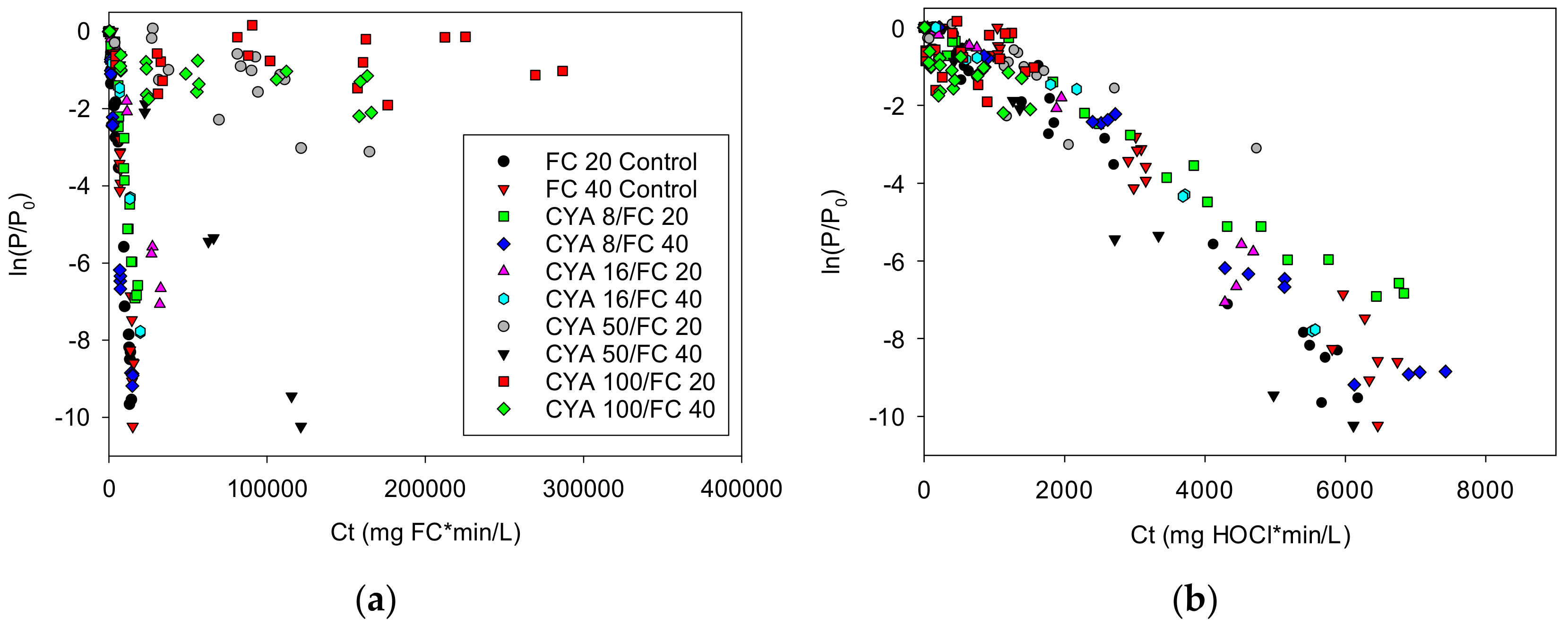
3.2. Effect of Cyanurate on Disinfection Kinetics
3.3. Steady-State Model of Pathogen Risk
3.3.1. Model Accuracy
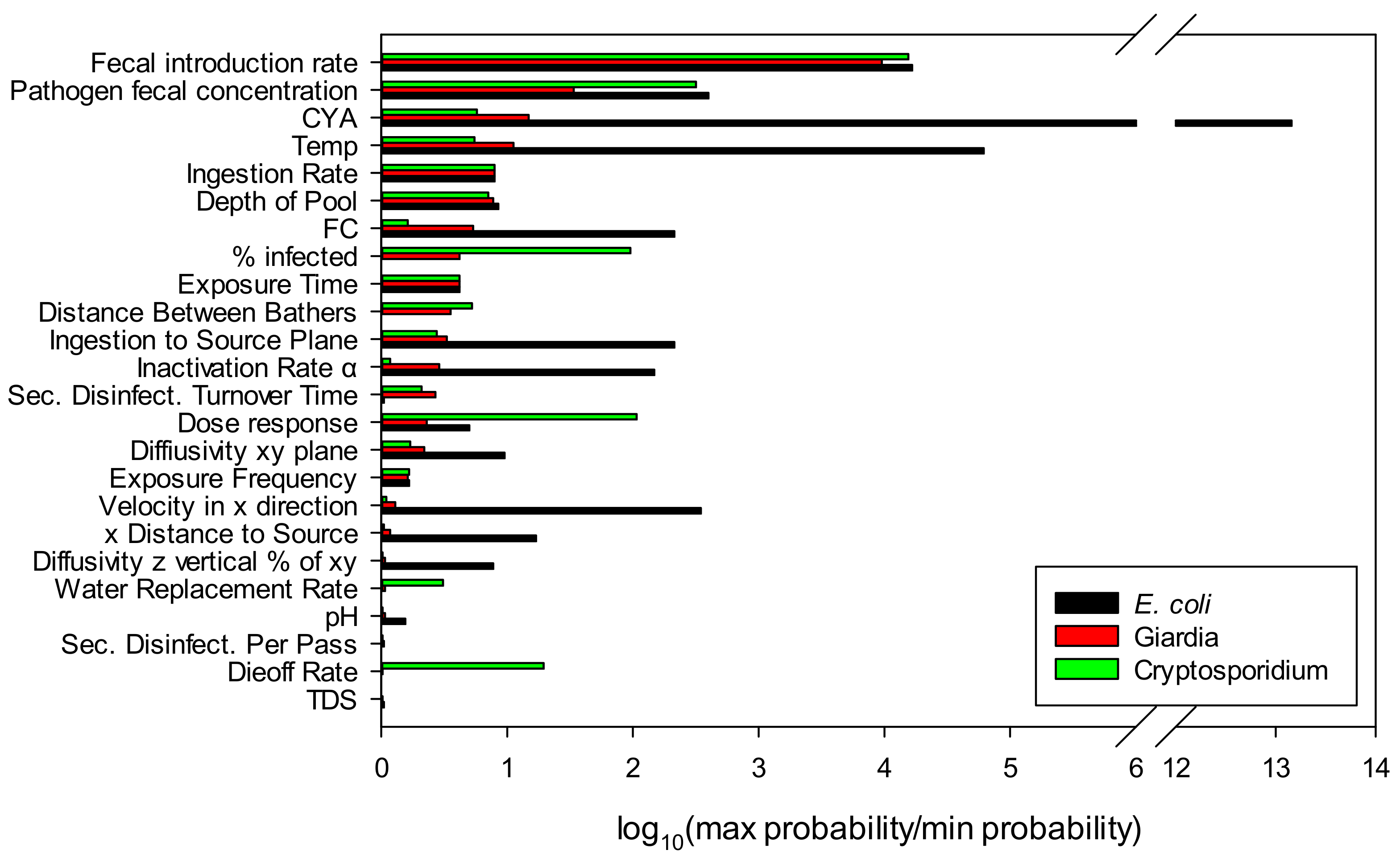
3.3.2. Model Sensitivity
3.3.3. Effect of Diffusivity on Risk
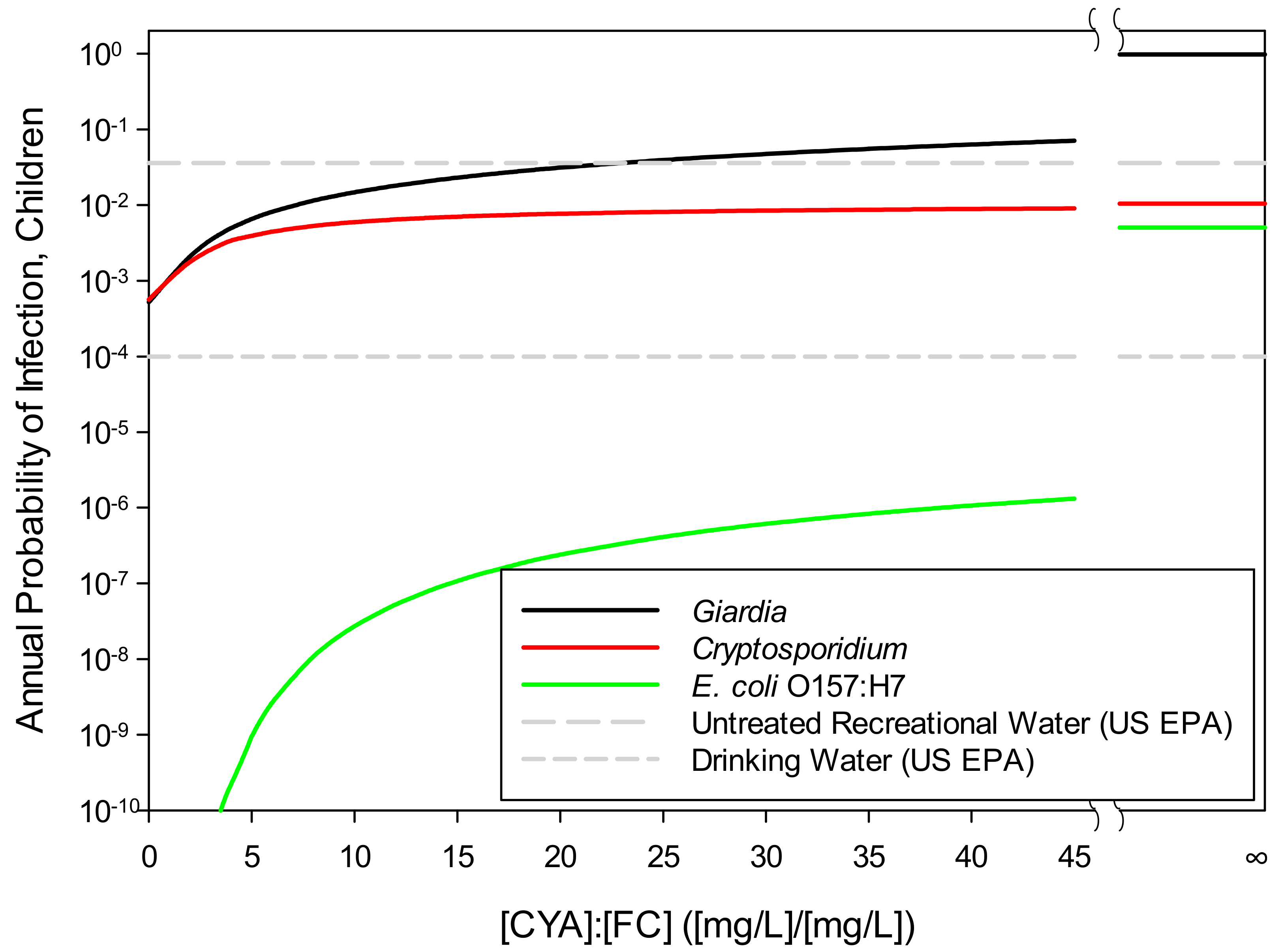
3.3.4. Probability of Infection Risk vs. CYA/FC Ratio
3.3.5. Model Validation
4. Discussion
4.1. Previous Studies
4.2. Use of CYA/FC Ratio
4.3. Risk Assessment
4.4. Setting a Standard
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- CDC. Model Aquatic Health Code, 3rd Edition. Available online: https://www.cdc.gov/mahc/index.html (accessed on 23 June 2019).
- O’Brien, J.E.; Morris, J.C.; Butler, J.N. Equilibria in Aqueous Solutions of Chlorinated Isocyanurate. In Chemistry of Water Supply, Treatment, and Distribution; Rubin, A.J., Ed.; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1974; pp. 333–358. ISBN 0-250-40036-7. [Google Scholar]
- Wahman, D.G. First acid ionization constant of the drinking water relevant chemical cyanuric acid from 5 to 35 °C. Environ. Sci. Water Res. Technol. 2018, 4, 1522–1530. [Google Scholar] [CrossRef] [PubMed]
- Wahman, D.G.; Alexander, M.T. A Drinking Water Relevant Water Chemistry Model for the Free Chlorine and Cyanuric Acid System from 5°C to 35°C. Environ. Eng. Sci. 2019, 36, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Wajon, J.E.; Morris, J.C. The analysis of free chlorine in the presence of nitrogenous organic compounds. Environ. Int. 1980, 3, 41–47. [Google Scholar] [CrossRef]
- Andersen, J.R. A Study of the Influence of Cyanuric Acid on the Bactericidal Effectiveness of Chlorine. Am. J. Public Health 1965, 55, 1629–1637. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fitzgerald, G.P.; DerVartanian, M.E. Factors Influencing the Effectiveness of Swimming Pool Bactericides. Appl. Microbiol. 1967, 15, 504–509. [Google Scholar] [PubMed]
- Golaszewski, G.; Seux, R. The Kinetics of the Action of Chloroisocyanurates on Three Bacteria: Pseudomonas aeruginosa, Streptococcus faecalis and Staphylococcus aureus. Water Res. 1994, 28, 207–217. [Google Scholar] [CrossRef]
- Murphy, J.L.; Arrowood, M.J.; Lu, X.; Hlavsa, M.C.; Beach, M.J.; Hill, V.R. Effect of Cyanuric Acid on the Inactivation of Cryptosporidium parvum under Hyperchlorination Conditions. Environ. Sci. Technol. 2015, 49, 7348–7355. [Google Scholar] [CrossRef]
- Shields, J.M.; Arrowood, M.J.; Hill, V.R.; Beach, M.J. The effect of cyanuric acid on the disinfection rate of Cryptosporidium parvum in 20-ppm free chlorine. J. Water Health 2009, 7, 109–114. [Google Scholar] [CrossRef]
- Yamashita, T.; Sakae, K.; Ishihara, Y.; Isomura, S.; Inoue, H. Virucidal effect of chlorinated water containing cyanuric acid. Epidemiol. Infect. 1988, 101, 631–639. [Google Scholar] [CrossRef]
- Saita, K.; Tachikawa, M.; Tezuka, M.; Sawamura, R. Effects of Isocyanuric Acid on the Poliovirus Inactivation with Hypochlorous Acid. Jpn. J. Toxicol. Environ. Heal. 1998, 44, 442–450. [Google Scholar] [CrossRef][Green Version]
- Sommerfeld, M.R.; Adamson, R.P. Influence of stabilizer concentration on effectiveness of chlorine as an algicide. Appl. Environ. Microbiol. 1982, 43, 497–499. [Google Scholar] [PubMed]
- Engel, J.P.; Rubin, A.J.; Sproul, O.J. Inactivation of Naegleria gruberi cysts by Chlorinated Cyanurates. Appl. Environ. Microbiol. 1983, 46, 1157–1162. [Google Scholar] [PubMed]
- Black, A.P.; Keirn, M.A.; Smith, J.U., Jr.; Dykes, G.M.; Harlan, W.E. The Disinfection of Swimming Pool Water Part II. A Field Study of the Disinfection of Public Swimming Pools. Am. J. Public Health 1970, 60, 740–750. [Google Scholar] [CrossRef] [PubMed]
- Kowalski, X.; Hilton, T.B. Comparison of Chlorinated Cyanurates with Other Chlorine Disinfectants. Public Health Rep. 1966, 81, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Le Guyader, M.; Grateloup, I. Relative Weight of Bacteriological Parameters in Swimming Pool Water Treated by Hypochlorite or Chloroisocyanurates. J. Fr. Hydrol. 1988, 19, 241–250. [Google Scholar] [CrossRef]
- Butterfield, C.T.; Wattie, E.; Megregian, S.; Chambers, C.W. Influence of pH and Temperature on the Survival of Coliforms and Enteric Pathogens When Exposed to Free Chlorine. Public Heal. Rep. 1943, 58, 1837–1866. [Google Scholar] [CrossRef]
- Hlavsa, M.C.; Roberts, V.A.; Kahler, A.M.; Hilborn, E.D.; Mecher, T.F.; Beach, M.J.; Wade, T.J.; Yoder, J.S. Outbreaks of Illness Associated with Recreational Water—United States, 2011–2012. Morb. Mortal. Wkly. Rep. 2015, 64, 668–672. [Google Scholar]
- Hlavsa, M.C.; Roberts, V.A.; Kahler, A.M.; Hilborn, E.D.; Wade, T.J.; Backer, L.C.; Yoder, J.S. Recreational Water–Associated Disease Outbreaks—United States, 2009–2010. Morb. Mortal. Wkly. Rep. 2014, 63, 1–5. [Google Scholar]
- Hlavsa, M.C.; Roberts, V.A.; Anderson, A.R.; Hill, V.R.; Kahler, A.M.; Orr, M.; Garrison, L.E.; Hicks, L.A.; Newton, A.; Hilborn, E.D.; et al. Surveillance for Waterborne Disease Outbreaks and Other Health Events Associated with Recreational Water—United States, 2007–2008 and Surveillance for Waterborne Disease Outbreaks Associated with Drinking Water—United States, 2007–2008. Morb. Mortal. Wkly. Rep. 2011, 60, 38–68. [Google Scholar]
- Yoder, J.S.; Hlavsa, M.C.; Craun, G.F.; Hill, V.; Yu, P.A.; Hicks, L.A.; Alexander, N.T.; Calderon, R.L.; Roy, S.L.; Beach, M.J. Surveillance for Waterborne Disease and Outbreaks Associated with Recreational Water Use and Other Aquatic Facility-Associated Health Events—United States, 2005–2006. Morb. Mortal. Wkly. Rep. Surveill. Summ. 2008, 57, 1–38. [Google Scholar]
- Dziuban, E.; Liang, J.; Craun, G.; Hill, V.; Yu, P.; Painter, J.; Moore, M.; Calderon, R.; Roy, S.; Beach, M. Surveillance for Waterborne Disease and Outbreaks Associated with Recreational Water—United States, 2003–2004. Morb. Mortal. Wkly. Rep. Surveill. Summ. 2006, 55, 31–65. [Google Scholar]
- Gould, L.H.; Demma, L.; Jones, T.F.; Hurd, S.; Vugia, D.J.; Smith, K.; Shiferaw, B.; Segler, S.; Palmer, A.; Zansky, S.; et al. Hemolytic Uremic Syndrome and Death in Persons with Escherichia coli O157:H7 Infection, Foodborne Diseases Active Surveillance Network Sites, 2000–2006. Clin. Infect. Dis. 2009, 49, 1480–1485. [Google Scholar] [CrossRef] [PubMed]
- CDC. National Enteric Disease Surveillance: Shiga Toxin-Producing Escherichia coli (STEC) Annual Report, 2011. Available online: https://www.cdc.gov/ncezid/dfwed/PDFs/national-stec-surv-summ-2011-508c.pdf (accessed on 23 June 2019).
- CDC. National Enteric Disease Surveillance: Shiga Toxin-Producing Escherichia coli (STEC) Annual Report, 2012. Available online: https://www.cdc.gov/ncezid/dfwed/PDFs/national-stec-surv-summ-2012-508c.pdf (accessed on 23 June 2019).
- World Health Organization. Quantitative Microbial Risk Assessment: Application for Water Safety Management, WHO Press: Geneva, Switzerland, 2016; ISBN 978 92 4 156537 0.
- Van Lier, A.; McDonald, S.A.; Bouwknegt, M.; Kretzschmar, M.E.; Havelaar, A.H.; Mangen, M.-J.J.; Wallinga, J.; de Melker, H.E. Disease burden of 32 infectious diseases in the Netherlands, 2007–2011. PLoS ONE 2016, 11, e0153106. [Google Scholar] [CrossRef] [PubMed]
- CDC. Prevalence of parasites in fecal material from chlorinated swimming pools—United States, 1999. Morb. Mortal. Wkly. Rep. 2001, 50, 410–412. [Google Scholar]
- Shields, J.M.; Gleim, E.R.; Beach, M.J. Prevalence of Cryptosporidium spp. and Giardia intestinalis in swimming pools, Atlanta, Georgia. Emerg. Infect. Dis. 2008, 14, 948–950. [Google Scholar] [CrossRef] [PubMed]
- Painter, J.E.; Gargano, J.W.; Collier, S.A.; Yoder, J.S. Giardiasis Surveillance—United States, 2011–2012. Morb. Mortal. Wkly. Rep. Surveill. Summ. 2015, 64, 15–25. [Google Scholar]
- Hlavsa, M.C.; Cikesh, B.L.; Roberts, V.A.; Kahler, A.M.; Vigar, M.; Hilborn, E.D.; Wade, T.J.; Roellig, D.M.; Murphy, J.L.; Xiao, L.; et al. Outbreaks Associated with Treated Recreational Water—United States, 2000–2014. Morb. Mortal. Wkly. Rep. 2018, 67, 547–551. [Google Scholar] [CrossRef] [PubMed]
- Ishii, S.; Sadowsky, M. Escherichia coli in the Environment: Implications for Water Quality and Human Health. Microbes Environ. 2008, 23, 101–108. [Google Scholar] [CrossRef]
- Guandalini, S.; Frye, R.E.; Tamer, M.A. Diarrhea. Available online: https://emedicine.medscape.com/article/928598-overview (accessed on 23 June 2019).
- Pintar, K.D.M.; Fazil, A.; Pollari, F.; Charron, D.F.; Waltner-Toews, D.; McEwen, S.A. A risk assessment model to evaluate the role of fecal contamination in recreational water on the incidence of cryptosporidiosis at the community level in Ontario. Risk Anal. 2010, 30, 49–64. [Google Scholar] [CrossRef]
- Schets, F.; Engels, G.; Evers, E. Cryptosporidium and Giardia in swimming pools in the Netherlands. J. Water Health 2004, 2, 191–200. [Google Scholar] [CrossRef][Green Version]
- Schets, F.M.; Schijven, J.F.; de Roda Husman, A.M. Exposure assessment for swimmers in bathing waters and swimming pools. Water Res. 2011, 45, 2392–2400. [Google Scholar] [CrossRef]
- Suppes, L.M.; Canales, R.A.; Gerba, C.P.; Reynolds, K.A. Cryptosporidium risk from swimming pool exposures. Int. J. Hyg. Environ. Health 2016, 219, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Cloteaux, A.; Gérardin, F.; Midoux, N. Influence of Swimming Pool Design on Hydraulic Behavior: A Numerical and Experimental Study. Engineering 2013, 5, 511–524. [Google Scholar] [CrossRef][Green Version]
- Lewis, L.; Chew, J.; Woodley, I.; Colbourne, J.; Pond, K. The application of computational fluid dynamics and small-scale physical models to assess the effects of operational practices on the risk to public health within large indoor swimming pools. J. Water Health 2015, 13, 939–952. [Google Scholar] [CrossRef] [PubMed]
- Karch, H.; Rüssmann, H.; Schmidt, H.; Schwarzkopf, A.; Hessemann, J. Long-Term Shedding and Clonal Turnover of Enterohemorrhagic Escherichia coli O157 in Diarrheal Diseases. J. Clin. Microbiol. 1995, 33, 1602–1605. [Google Scholar] [PubMed]
- Danciger, M.; Lopez, M. Numbers of Giardia in the Feces of Infected Children. Am. J. Trop. Med. Hyg. 1975, 24, 237–242. [Google Scholar] [CrossRef] [PubMed]
- Chappell, C.L.; Okhuysen, P.C.; Sterling, C.R.; DuPont, H.L. Cryptosporidium parvum: Intensity of infection and oocyst excretion patterns in healthy volunteers. J. Infect. Dis. 1996, 173, 232–236. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rendtorff, R.C.; Kashgarian, M. Stool patterns of healthy adult males. Dis. Colon Rectum 1967, 10, 222–228. [Google Scholar] [CrossRef] [PubMed]
- Keuten, M. (Delft University of Technology, Delft, The Netherlands). Personal communication, 2017.
- Keuten, M.G.A.; Schets, F.M.; Schijven, J.F.; Verberk, J.Q.J.C.; van Dijk, J.C. Definition and quantification of initial anthropogenic pollutant release in swimming pools. Water Res. 2012, 46, 3682–3692. [Google Scholar] [CrossRef]
- Gerba, C.P. Assessment of enteric pathogen shedding by bathers during recreational activity and its impact on water quality. Quant. Microbiol. 2000, 2, 55–68. [Google Scholar] [CrossRef]
- Elmir, S.M.; Wright, M.E.; Abdelzaher, A.; Solo-Gabriele, H.M.; Fleming, L.E.; Miller, G.; Rybolowik, M.; Shih, M.-T.P.; Pillai, S.P.; Cooper, J.A.; et al. Quantitative evaluation of bacteria released by bathers in a marine water. Water Res. 2007, 41, 3–10. [Google Scholar] [CrossRef]
- Zhao, T.; Doyle, M.P.; Zhao, P.; Blake, P.; Wu, F.-M. Chlorine inactivation of Escherichia coli O157:H7 in water. J. Food Prot. 2001, 64, 1607–1609. [Google Scholar] [CrossRef]
- U.S. EPA. LT1ESWTR Disinfection Profiling and Benchmarking Technical Guidance Manual; National Service Center for Environmental Publications: Washington, DC, USA, 2003.
- Shields, J.M.; Hill, V.R.; Arrowood, M.J.; Beach, M.J. Inactivation of Cryptosporidium parvum under chlorinated recreational water conditions. J. Water Health 2008, 6, 513–520. [Google Scholar] [CrossRef]
- Karim, M.R.; Manshadi, F.D.; Karpiscak, M.M.; Gerba, C.P. The persistence and removal of enteric pathogens in constructed wetlands. Water Res. 2004, 38, 1831–1837. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Murphy, T.; Holden, N.M. Evaluation of the effect of temperature on the die-off rate for Cryptosporidium parvum oocysts in water, soils, and feces. Appl. Environ. Microbiol. 2008, 74, 7101–7107. [Google Scholar] [CrossRef]
- Socolofsky, S.A.; Jirka, G.H. Environmental Fluid Mechanics Part I: Mass Transfer and Diffusion; Engineering Lectures. Available online: http://www.ifh.uni-karlsruhe.de/lehre/envflu_I/Downloads/course_script/ed2/script_ed2.pdf (accessed on 23 June 2019).
- Majowicz, S.E.; Scallan, E.; Jones-Bitton, A.; Sargeant, J.M.; Stapleton, J.; Angulo, F.J.; Yeung, D.H.; Kirk, M.D. Global incidence of human Shiga toxin-producing Escherichia coli infections and deaths: A systematic review and knowledge synthesis. Foodborne Pathog. Dis. 2014, 11, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Hellard, M.E.; Sinclair, M.I.; Hogg, G.G.; Fairley, C.K. Prevalence of enteric pathogens among community based asymptomatic individuals. J. Gastroenterol. Hepatol. 2000, 15, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Haas, C.N.; Rose, J.B.; Gerba, C.; Regli, S. Risk Assessment of Radon in Drinking Water; National Academies Press: Washington, DC, USA, 1993; Volume 13, ISBN 978-0-309-06292-3. [Google Scholar]
- Nilsen, V.; Wyller, J. QMRA for Drinking Water: 1. Revisiting the Mathematical Structure of Single-Hit Dose-Response Models. Risk Anal. 2016, 36, 145–162. [Google Scholar] [CrossRef]
- Rose, J.B.; Gerba, C.P. Use of Risk Assessment for Development of Microbial Standards. Water Sci. Technol. 1991, 24, 29–34. [Google Scholar] [CrossRef]
- Cornick, N.A.; Helgerson, A.F. Transmission and Infectious Dose of Escherichia coli O157:H7 in Swine. Appl. Environ. Microbiol. 2004, 70, 5331–5335. [Google Scholar] [CrossRef]
- Rendtorff, R.C. The Experimental Transmission of Human Intestinal Protozoan Parasites II. Giardia Lamblia Cysts Given in Capsules. Am. J. Epidemiol. 1954, 59, 209–222. [Google Scholar] [CrossRef]
- Messner, M.J.; Chappell, C.L.; Okhuysen, P.C. Risk Assessment for Cryptosporidium: A Hierarchical Bayesian Analysis of Human Dose Response Data. Water Res. 2001, 35, 3934–3940. [Google Scholar] [CrossRef]
- Behnke, S.; Parker, A.E.; Woodall, D.; Camper, A.K. Comparing the chlorine disinfection of detached biofilm clusters with those of sessile biofilms and planktonic cells in single- and dual-species cultures. Appl. Environ. Microbiol. 2011, 77, 7176–7184. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, G.P.; DerVartanian, M.E. Pseudomonas aeruginosa for the evaluation of swimming pool chlorination and algicides. Appl. Microbiol. 1969, 17, 415–421. [Google Scholar] [PubMed]
- O’Brien, J.E. Hydrolytic and Ionization Equilibria of Chlorinated Isocyanurate in Water; Harvard University: Cambridge, MA, USA, 1972. [Google Scholar]
- U.S. EPA. Use of Micobial Risk Assessment in Setting EPA Drinking Water Standards; National Service Center for Environmental Publications: Washington, DC, USA, 1992.
- U.S. EPA. Recreational Water Quality Criteria; National Service Center for Environmental Publications: Washington, DC, USA, 2012.
- Xiao, S.; Yin, P.; Zhang, Y.; Hu, S. Occurrence of cryptosporidium and giardia and the relationship between protozoa and water quality indicators in swimming pools. Korean J. Parasitol. 2017, 55, 129–136. [Google Scholar] [CrossRef] [PubMed]
- Canelli, E. Chemical, Bacteriological, and Toxicological Properties of Cyanuric Acid and Chlorinated Isocyanurates as Applied to Swimming Pool Disinfection. Am. J. Public Heal. 1974, 64, 155–162. [Google Scholar] [CrossRef]
- U.S. EPA. Guidance Manual for Compliance with the Filtration and Disinfection Requirements for Public Water Systems Using Surface Water Sources; National Service Center for Environmental Publications: Washington, DC, USA, 1991.
- Rose, L.J.; Rice, E.W.; Jensen, B.; Murga, R.; Peterson, A.; Donlan, R.M.; Arduino, M.J. Chlorine inactivation of bacterial bioterrorism agents. Appl. Environ. Microbiol. 2005, 71, 566–568. [Google Scholar] [CrossRef]
- Rose, L.J.; Rice, E.W.; Hodges, L.; Peterson, A.; Arduino, M.J. Monochloramine inactivation of bacterial select agents. Appl. Environ. Microbiol. 2007, 73, 3437–3439. [Google Scholar] [CrossRef]
- O’Connell, H.A.; Rose, L.J.; Shams, A.; Bradley, M.; Arduino, M.J.; Rice, E.W. Variability of Burkholderia pseudomallei strain sensitivities to chlorine disinfection. Appl. Environ. Microbiol. 2009, 75, 5405–5409. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Safe Recreational Water Environments—Volume 2: Swimming Pools and Similar Environments; WHO Press: Geneva, Switzerland, 2006; ISBN 92 4 154680 8. [Google Scholar]


| Pathogen (Units) | Low | Mean | High |
|---|---|---|---|
| Escherichia coli O157 a (CFU/g) | |||
| Giardiab (cysts/g) | |||
| Cryptosporidium parvumc (oocysts/g) |
| Model Source | Age Group | Low | Mean | High |
|---|---|---|---|---|
| [46] | All a | 0.04 | 0.70 | 3.5 |
| [47] | Children b | 0.67 | 21.1 c | 667 |
| [47] | Adult | 0.0067 | 0.21 c | 6.67 |
| CYA (mg/L) | FC (mg/L Cl2) | HOCl (mg/L Cl2) |
|---|---|---|
| 20 | 1.0 | 0.01962 |
| 30 | 1.5 | 0.01991 |
| 40 | 2.0 | 0.02006 |
| 50 | 2.5 | 0.02015 |
| 60 | 3.0 | 0.02021 |
| 70 | 3.5 | 0.02025 |
| 80 | 4.0 | 0.02029 |
| 90 | 4.5 | 0.02031 |
| Parameter (Units) | Selected | Min | Max |
|---|---|---|---|
| FC (mg/L) | 2 | 1 | 10 |
| CYA (mg/L) | 90 | 0 | 100 |
| pH | 7.5 | 7.2 | 7.8 |
| Temp (°C) | 25 | 20 | 40 |
| TDS (mg/L) | 1000 | 500 | 5000 |
| Sec. disinfect. per pass (%/pass) | 99.9 | 90 | 99.9 |
| Sec. disinfect. turnover time (min) | 0 | 30 | 360 |
| Water replacement rate (L/bather) | 0 | 0 | 30 |
| Diffusivity xy plane (cm2/min) | 500 | 100 | 5000 |
| Diffusivity z vertical % of xy (%) | 100 | 20 | 100 |
| Velocity in x direction (cm/min) | 0 | 0 | 10,000 |
| Depth of pool (cm) | 91.44 | 30.48 | 250 |
| Distance between bathers (cm) | 118.05 | 80 | 240 |
| Ingestion to source plane (cm) | 45.72 | 0 | 90 |
| x distance to source (cm) | 45.72 | 30 | 90 |
| Ingestion rate (ml/hr) | 24.2 | 6.3 | 50 |
| Exposure time (hrs/visit) | 1.9 | 1.2 | 5 |
| Exposure frequency (visits/year) | 72.9 | 72.6 | 120 |
| Fecal introduction rate (g/bather/min) | 0.0007 | 0.00004 | 0.666667 |
| Parameter (Inits) | Pathogen | Selected | Min | Max |
|---|---|---|---|---|
| % infected (%) | E. coli Giardia Cryptosporidium | 0.0935 4.4 0.4 | 0 0 0 | 10 10 10 |
| Inactivation Rate α (/ppm min) | E. coli Giardia Cryptosporidium | |||
| Die-off Rate Constant, (/min) | E. coli Giardia Cryptosporidium | 0 0 0 | ||
| Dose response (/Infective unit) | E. coli [60] Giardia [61] Cryptosporidium [62] | 2.65 |
| Pathogen (Units) | Low | Mean | High |
|---|---|---|---|
| Escherichia coli O157 (CFU/bather/min) | |||
| Giardia (cysts/bather/min) | |||
| Cryptosporidium parvum (oocysts/bather/min) |
| Pathogen/Per-Visit Risk a | FC | CYA/FC Ratio | FC, no CYA | |||
|---|---|---|---|---|---|---|
| 0 mg/L | 90/2 = 45 | 40/2 = 20 | 20/2 = 10 | 10/2 = 5 | 2 mg/L | |
| Escherichia coli O157 | ||||||
| Giardia | ||||||
| Cryptosporidium parvum | ||||||
| Pathogen/Annual Risk b | 0 mg/L | 90/2 = 45 | 40/2 = 20 | 20/2 = 10 | 10/2 = 5 | 2 mg/L |
| Escherichia coli O157 | ||||||
| Giardia | ||||||
| Cryptosporidium parvum | ||||||
| Microorganism | Units | Swimming Pools [68] | Model a | |||
|---|---|---|---|---|---|---|
| % pos. | Mean ± SD | Near Bather b | In-Between c | Well-Mixed | ||
| Total coliforms d | MPN/L | 36.7 | 2.7 ± 5.7 | 0.057 | ||
| Giardia | cysts/10L | 15.0 | 0.27 ± 0.71 | 1.9 | 0.023 | 0.28 |
| Cryptosporidium | oocysts/10L | 16.7 | 0.30 ± 0.79 | 0.14 | 0.058 | 0.067 |
| CYA (ppm) | Min. FC (ppm) |
|---|---|
| 20 | 1.0 |
| 30 | 1.5 |
| 40 | 2.0 |
| 50 | 2.5 |
| 60 | 3.0 |
| 70 | 3.5 |
| 80 | 4.0 |
| 90 | 4.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falk, R.A.; Blatchley, E.R., III; Kuechler, T.C.; Meyer, E.M.; Pickens, S.R.; Suppes, L.M. Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools. Water 2019, 11, 1314. https://doi.org/10.3390/w11061314
Falk RA, Blatchley ER III, Kuechler TC, Meyer EM, Pickens SR, Suppes LM. Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools. Water. 2019; 11(6):1314. https://doi.org/10.3390/w11061314
Chicago/Turabian StyleFalk, Richard A., Ernest R. Blatchley, III, Thomas C. Kuechler, Ellen M. Meyer, Stanley R. Pickens, and Laura M. Suppes. 2019. "Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools" Water 11, no. 6: 1314. https://doi.org/10.3390/w11061314
APA StyleFalk, R. A., Blatchley, E. R., III, Kuechler, T. C., Meyer, E. M., Pickens, S. R., & Suppes, L. M. (2019). Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools. Water, 11(6), 1314. https://doi.org/10.3390/w11061314






