Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors
Abstract
1. Introduction
- reduction in inauspicious consequences of contamination (both accidental and intentional) in terms of limitation of contaminated areas (direct action);
- optimal placement of quality sensors (indirect action).
2. Materials and Methods
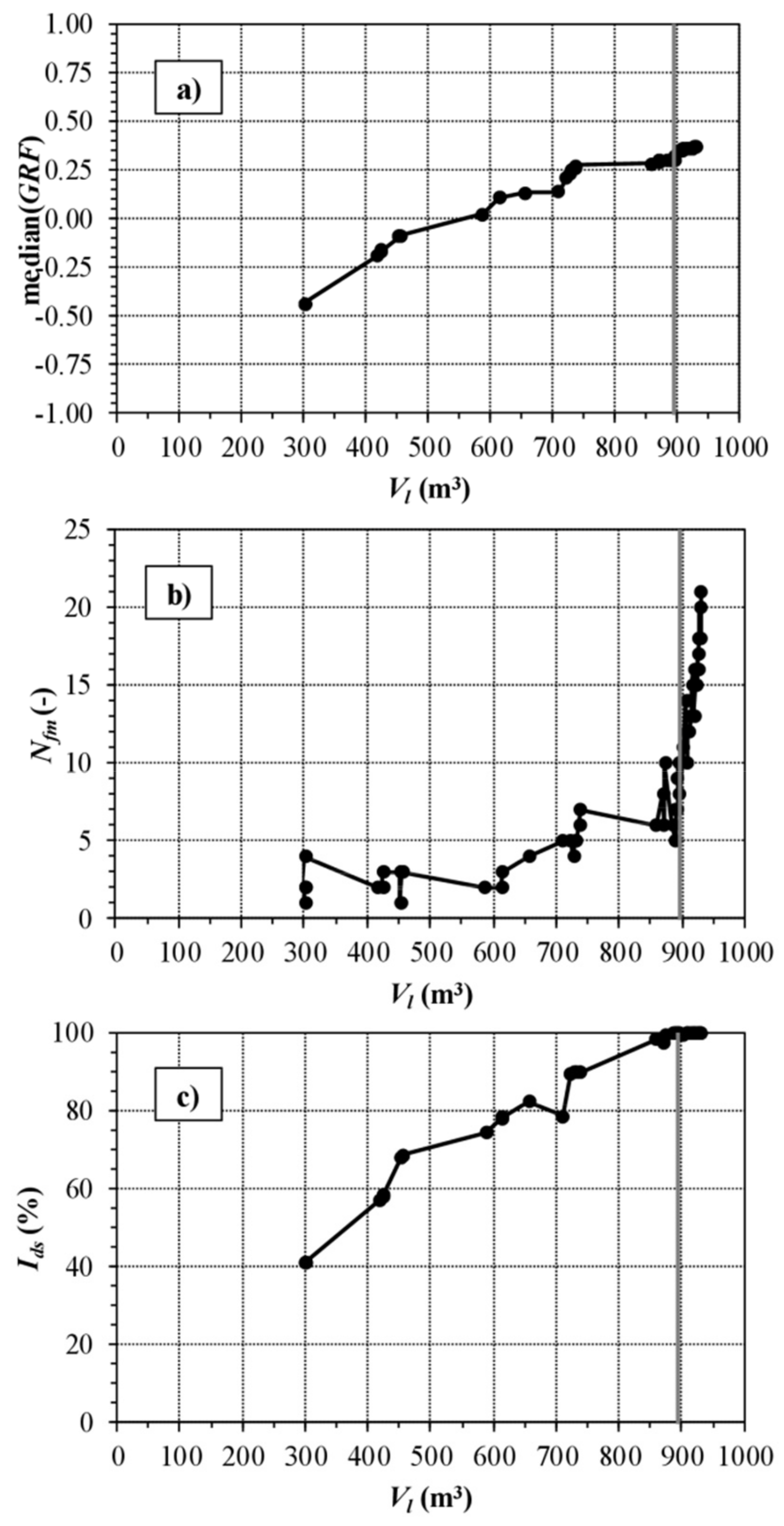
2.1. Procedure 1—WNP
2.2. Procedure 2—Optimal Sensor Placement
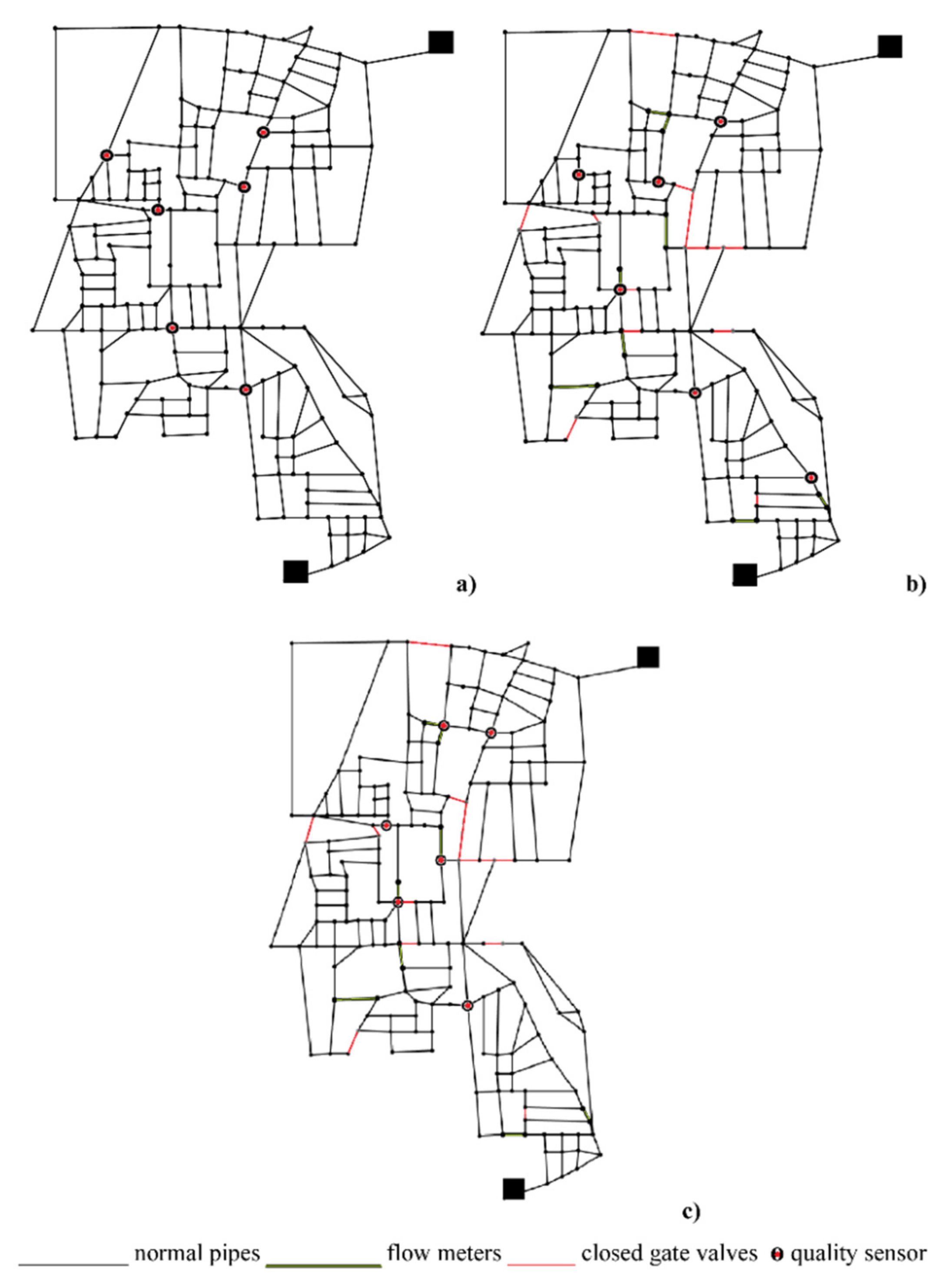
- Option 1, sensors can be installed at all nodes (typical greedy approach);
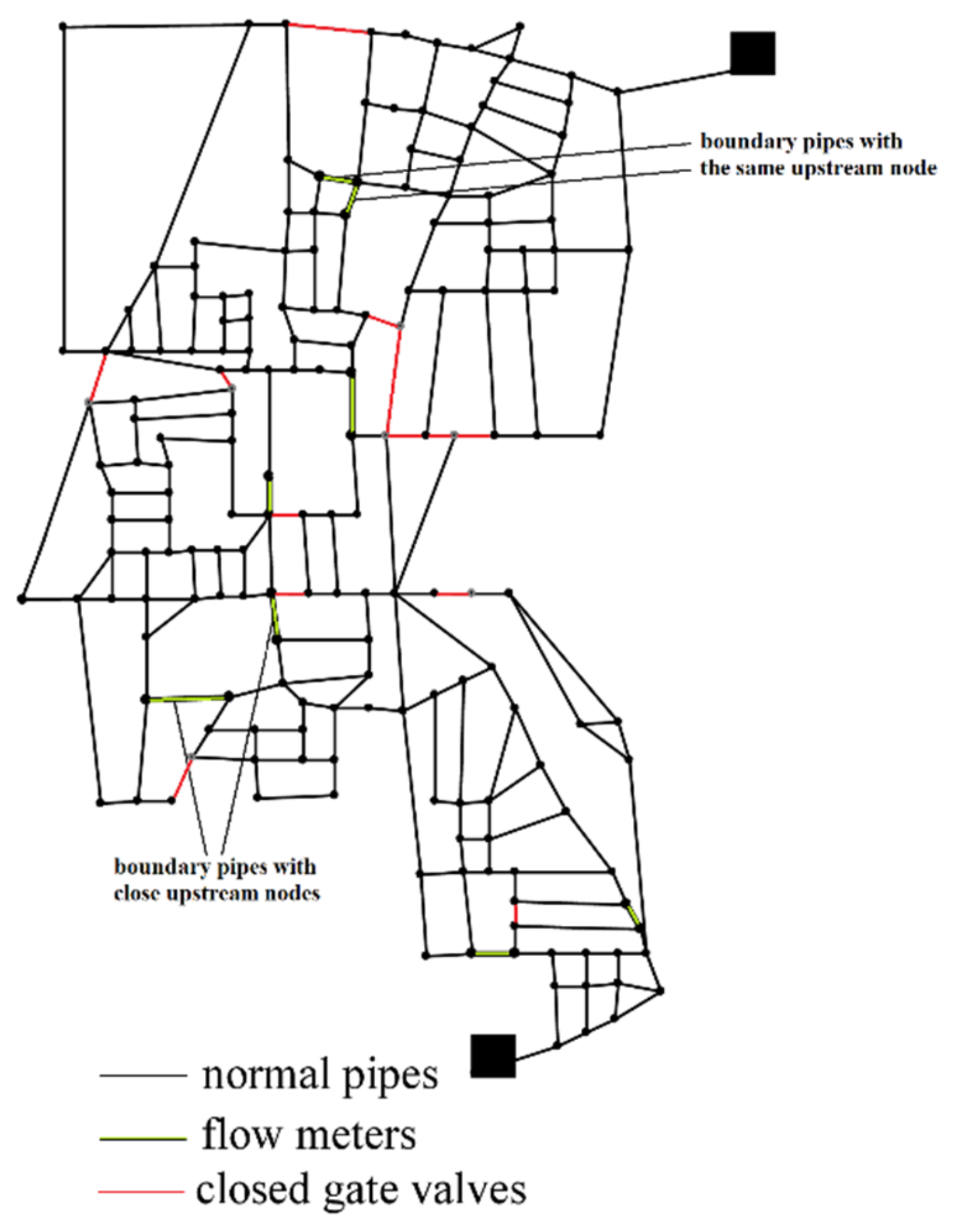
- Option 2, sensors can be installed only at the hydraulically upstream nodes of the boundary pipes;
- Option 3, sensors can be installed at the most central nodes of each district, identified through topological considerations;
- Option 4, sensors can be installed at the hydraulically upstream nodes of the boundary pipes and at the most central nodes of each district.
2.3. Procedure 3—Comparison of Sensor Placement Solutions
3. Case Study
4. Results and Discussions
- all the 182 demanding nodes were considered to be potential locations for contaminant injection;
- 24 possible contamination times in the day (hour 0, 1, 2, …, 22, 23);
- single value of the mass injection rate equal to 350 g/min;
- single value of the injection duration equal to 60 min.
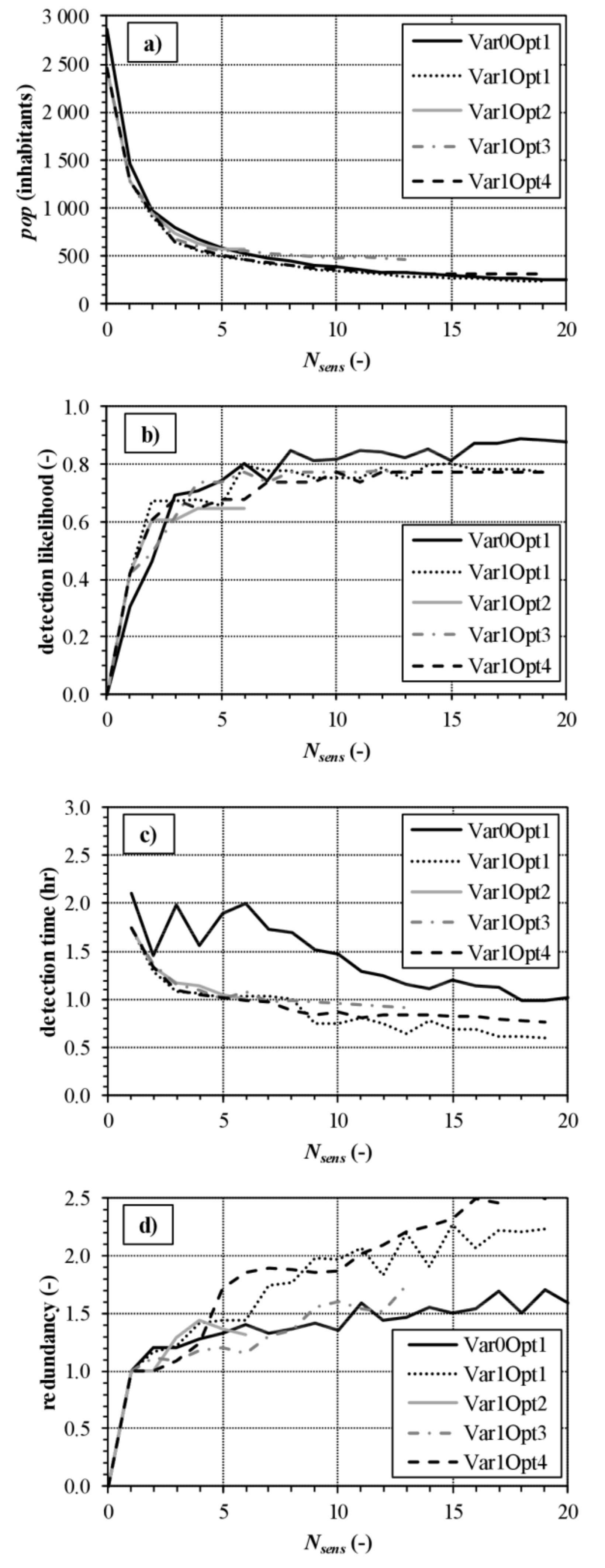
- Var1Op1: Optimal sensor placement on the partitioned WDN allowing sensor installation on all nodes (182 potential locations);
- Var1Opt2: Optimal sensor placement on the partitioned WDN allowing sensor installation only on the nodes hydraulically upstream from the flowmeter fitted boundary pipes (8 potential locations);
- Var1Opt3: Optimal sensor placement on the partitioned WDN allowing sensor installation only on the most central nodes of each district (15 potential locations, i.e., three locations for each district, which feature a much higher betweenness centrality value than the other nodes);
- Var1Opt4: Optimal sensor placement on the partitioned WDN allowing sensor installation on the nodes hydraulically upstream from the flowmeter fitted boundary pipes and on the most central nodes of each district (23 scenarios).
5. Conclusions
- almost identical performance in terms of WDN monitoring, compared to the option of considering all nodes as potential locations;
- money savings thanks to the possibility of sharing some electronical components for data acquisition, sharing, and transmission;
- easiness of access to the sensors for maintenance;
- reduction in the search space and, therefore, in the computational complexity in the optimizations for optimal sensor placement;
- easier identification of the area from which the contamination starts with the subsequent possibility of isolating the district, assuring a higher resilience of the system to the spreading of the contamination.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kroll, D.J. Securing Our Water Supply: Protecting a Vulnerable Resource; PennWell Books: Tulsa, OK, USA, 2006. [Google Scholar]
- Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water 2018, 10, 579. [Google Scholar] [CrossRef]
- Che, H.; Liu, S.; Smith, K. Performance evaluation for a contamination detection method using multiple water quality sensors in an early warning system. Water 2015, 7, 1422–1436. [Google Scholar] [CrossRef]
- Lee, B.H.; Deininger, R.A. Optimal locations of monitoring stations in water distribution system. J. Environ. Eng. 1992, 118, 4–16. [Google Scholar] [CrossRef]
- Kumar, A.; Kansal, M.L.; Arora, G. Identification of monitoring stations in water distribution system. J. Environ. Eng. 1997, 123, 746–752. [Google Scholar] [CrossRef]
- Watson, J.-P.; Greenberg, H.J.; Hart, W.E. A multiple-objective analysis of sensor placement optimization in water networks. In Proceedings of the World Water and Environmental Resources Congress 2004, Salt Lake City, UT, USA, 27 June–1 July 2004; pp. 1–10. [Google Scholar]
- Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.-P. Scalability of integer programming computations for sensor placement in water networks. In Proceedings of the World Water and Environmental Resources Congress 2004, Anchorage, AK, USA, 15–19 May 2005; pp. 1–13. [Google Scholar]
- Ostfeld, A.; Salomons, E. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Uber, J.; Janke, R.; Murray, R.; Meyer, P. Greedy heuristic methods for locating water quality sensors in distribution systems. In Proceedings of the World Water and Environmental Resources Congress 2004, Salt Lake City, UT, USA, 27 June–1 July 2004; pp. 1–9. [Google Scholar]
- Kessler, A.; Ostfeld, A.; Sinai, G. Detecting accidental contaminations in municipal water networks. J. Water Resour. Plan. Manag. 1998, 124, 192–198. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Securing water distribution systems using online contamination monitoring. J. Water Resour. Plan. Manag. 2005, 131, 402–405. [Google Scholar] [CrossRef]
- Berry, J.; Carr, R.D.; Hart, W.E.; Leung, V.J.; Phillips, C.A.; Watson, J.-P. Designing contamination warning systems for municipal water networks using imperfect sensors. J. Water Resour. Plan. Manag. 2009, 135, 253–263. [Google Scholar] [CrossRef]
- McKenna, S.A.; Hart, D.B.; Yarrington, L. Impact of sensor detection limits on protecting water distribution systems from contamination events. J. Water Resour. Plan. Manag. 2006, 132, 305–309. [Google Scholar] [CrossRef]
- Dorini, G.; Jonkergouw, P.; Kapelan, Z.; Di Pierro, F.; Khu, S.T.; Savic, D. An efficient algorithm for sensor placement in water distribution systems. In Proceedings of the Eighth Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–13. [Google Scholar]
- Huang, J.; McBean, E.A.; James, W. Multiobjective optimization for monitoring sensor placement in water distribution systems. In Proceedings of the 8th Annual Symposium on Water Distribution Systems Analysis, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Propato, M.; Piller, O. Battle of the water sensor networks. In Proceedings of the Annual Symposium on Water Distribution Systems Analysis, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Wu, Z.Y.; Walski, T. Multiobjective optimization of sensor placement in water distribution systems. In Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Hart, W.E.; Murray, R. Review of sensor placement strategies for contamination warning systems in drinking water distribution systems. J. Water Resour. Plan. Manag. 2010, 136, 611–619. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R.; Ormsbee, L. A review of sensor placement objective metrics for contamination detection in water distribution networks. Water Supply 2015, 15, 898–917. [Google Scholar] [CrossRef]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.-P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z.; et al. The battle of the water sensor networks (BWSN): A design challenge for engineers and algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef]
- Xu, X.; Lu, Y.; Huang, S.; Xiao, Y.; Wang, W. Incremental sensor placement optimization on water network. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Berlin, Germany, 23–27 September 2013; pp. 467–482. [Google Scholar]
- Krause, A.; Leskovec, J.; Guestrin, C.; VanBriesen, J.; Faloutsos, C. Efficient sensor placement optimization for securing large water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 516–526. [Google Scholar] [CrossRef]
- Sankary, N.; Ostfeld, A. Inline mobile sensors for contaminant early warning enhancement in water distribution systems. J. Water Resour. Plan. Manag. 2016, 143, 04016073. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R.; Kamble, S.; Sargaonkar, A. Risk-based analysis for contamination event selection and optimal sensor placement for intermittent water distribution network security. Water Resour. Manag. 2016, 30, 2671–2685. [Google Scholar] [CrossRef]
- Zheng, F.; Du, J.; Diao, K.; Zhang, T.; Yu, T.; Shao, Y. Investigating effectiveness of sensor placement strategies in contamination detection within water distribution systems. J. Water Resour. Plan. Manag. 2018, 144, 06018003. [Google Scholar] [CrossRef]
- Deuerlein, J.W. Decomposition model of a general water supply network graph. J. Hydraul. Eng. 2008, 134, 822–832. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C.; Deuerlein, J.W. A graph decomposition-based approach for water distribution network optimization. Water Resour. Res. 2013, 49, 2093–2109. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Topological clustering for water distribution systems analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Perelman, L.S.; Allen, M.; Preisc, A.; Iqbal, M.; Whittle, A.J. Multi-level automated sub-zoning of water distribution systems. In Proceedings of the 7th International Congress on Environmental Modelling and Software, San Diego, CA, USA, 18 June 2014. [Google Scholar]
- Galdiero, E.; De Paola, F.; Fontana, N.; Giugni, M.; Savic, D. Decision support system for the optimal design of district metered areas. J. Hydroinf. 2016, 18, 49–61. [Google Scholar] [CrossRef]
- Hajebi, S.; Roshani, E.; Cardozo, N.; Barrett, S.; Clarke, A.; Clarke, S. Water distribution network sectorisation using graph theory and many-objective optimisation. J. Hydroinf. 2016, 18, 77–95. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I.; Fernandez, M.H. A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Weighted spectral clustering for water distribution network partitioning. Stud. Comput. Intell. Complex Netw. Their Appl. V 2016, 693, 797–807. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.F.; Tzatchkov, V.G.; Varela, J.M.R.; Yamanaka, V.H.A. Economic and Energy Criteria for District Meter Areas Design of Water Distribution Networks. Water 2017, 9, 463. [Google Scholar] [CrossRef]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Montalvo, I. Multi-agent adaptive boosting on semi-supervised water supply clusters. Adv. Eng. Softw. 2012, 50, 131–136. [Google Scholar] [CrossRef]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Ilaya-Ayza, A.; Pérez-García, R.; Tavera, M. A flexible methodology to sectorize water supply networks based on social network theory concepts and multiobjective optimization. J. Hydroinf. 2015, 18, 62–76. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-based procedure for partitioning water distribution systems into independent districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J.; Huang, Y.; Zhao, H. Automatic Partitioning of Water Distribution Networks Using Multiscale Community Detection and Multiobjective Optimization. J. Water Resour. Plan. Manag. 2017, 143, 4017057. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Optimal Sensor Placement in a Partitioned Water Distribution Network for the Water Protection from Contamination. Proceedings 2018, 2, 670. [Google Scholar] [CrossRef]
- Perelman, L.S.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated sub-zoning of water distribution systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized Cuts and Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Water Distribution Network Clustering: Graph Partitioning or Spectral Algorithms? Stud. Comput. Intell. Complex Netw. Their Appl. VI 2018, 689, 1197–1209. [Google Scholar]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological taxonomy of water distribution networks. Water 2018, 10, 444. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratapm, A.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak Analysis in Pipeline System by Means of Optimal Value Regulation. J. Hydraul. Eng. 1999, 125, 277–285. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Todini, E. Generalized resilience and failure indices for use with pressure driven modeling and leakage. J. Water Resour. Plan. Manag. 2016, 142, 4016019. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Templeman, A.B. Seamless pressure-deficient water distribution system model. J. Water Manag. 2010, 163, 389–396. [Google Scholar] [CrossRef]
- Ciaponi, C.; Franchioli, L.; Murari, E.; Papiri, S. Procedure for Defining a Pressure-Outflow Relationship Regarding Indoor Demands in Pressure-Driven Analysis of Water Distribution Networks. Water Resour. Manag. 2014, 29, 817–832. [Google Scholar] [CrossRef]
- Tinelli, S.; Creaco, E.; Ciaponi, C. Sampling significant contamination events for optimal sensor placement in water distribution systems. J. Water Resour. Plan. Manag. 2017, 143, 4017058. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET2 Users Manual; United States Environmental Protection Agency: Washington, DC, USA, 2000.
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Savic, D. Simplified Approach to Water Distribution System Management via Identification of a Primary Network. J. Water Resour. Plan. Manag. 2017, 144, 1–9. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Multiobjective contaminant sensor network design for water distribution systems. J. Water Resour. Plan. Manag. 2008, 134, 366–377. [Google Scholar] [CrossRef]
- Tinelli, S.; Creaco, E.; Ciaponi, C. Impact of objective function selection on optimal placement of sensors in water distribution networks. Ital. J. Eng. Geol. Environ. 2018, 173–178. [Google Scholar] [CrossRef]
| Option | Variant 0 (Un-Partitioned) | Variant 1 (Partitioned) |
|---|---|---|
| 1 (all nodes) | Var0Opt1 | Var1Opt1 |
| 2 (only boundary nodes) | - | Var1Opt2 |
| 3 (only central nodes) | - | Var1Opt3 |
| 4 (boundary nodes + central nodes) | - | Var1Opt4 |
| Nsens | Var0Opt1 | Var1Opt1 | Var1Opt2 | Var1Opt3 | Var1Opt4 |
|---|---|---|---|---|---|
| 0 | 2806 | 2458 | 2458 | 2458 | 2458 |
| 1 | 1438 | 1274 | 1274 | 1274 | 1274 |
| 2 | 982 | 919 | 953 | 974 | 953 |
| 3 | 789 | 648 | 741 | 679 | 653 |
| 4 | 667 | 559 | 638 | 598 | 569 |
| 5 | 589 | 500 | 572 | 561 | 515 |
| 6 | 514 | 462 | 564 | 548 | 472 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water 2019, 11, 1315. https://doi.org/10.3390/w11061315
Ciaponi C, Creaco E, Di Nardo A, Di Natale M, Giudicianni C, Musmarra D, Santonastaso GF. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water. 2019; 11(6):1315. https://doi.org/10.3390/w11061315
Chicago/Turabian StyleCiaponi, Carlo, Enrico Creaco, Armando Di Nardo, Michele Di Natale, Carlo Giudicianni, Dino Musmarra, and Giovanni Francesco Santonastaso. 2019. "Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors" Water 11, no. 6: 1315. https://doi.org/10.3390/w11061315
APA StyleCiaponi, C., Creaco, E., Di Nardo, A., Di Natale, M., Giudicianni, C., Musmarra, D., & Santonastaso, G. F. (2019). Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water, 11(6), 1315. https://doi.org/10.3390/w11061315









