Model Uncertainty Analysis Methods for Semi-Arid Watersheds with Different Characteristics: A Comparative SWAT Case Study
Abstract
1. Introduction
2. Materials
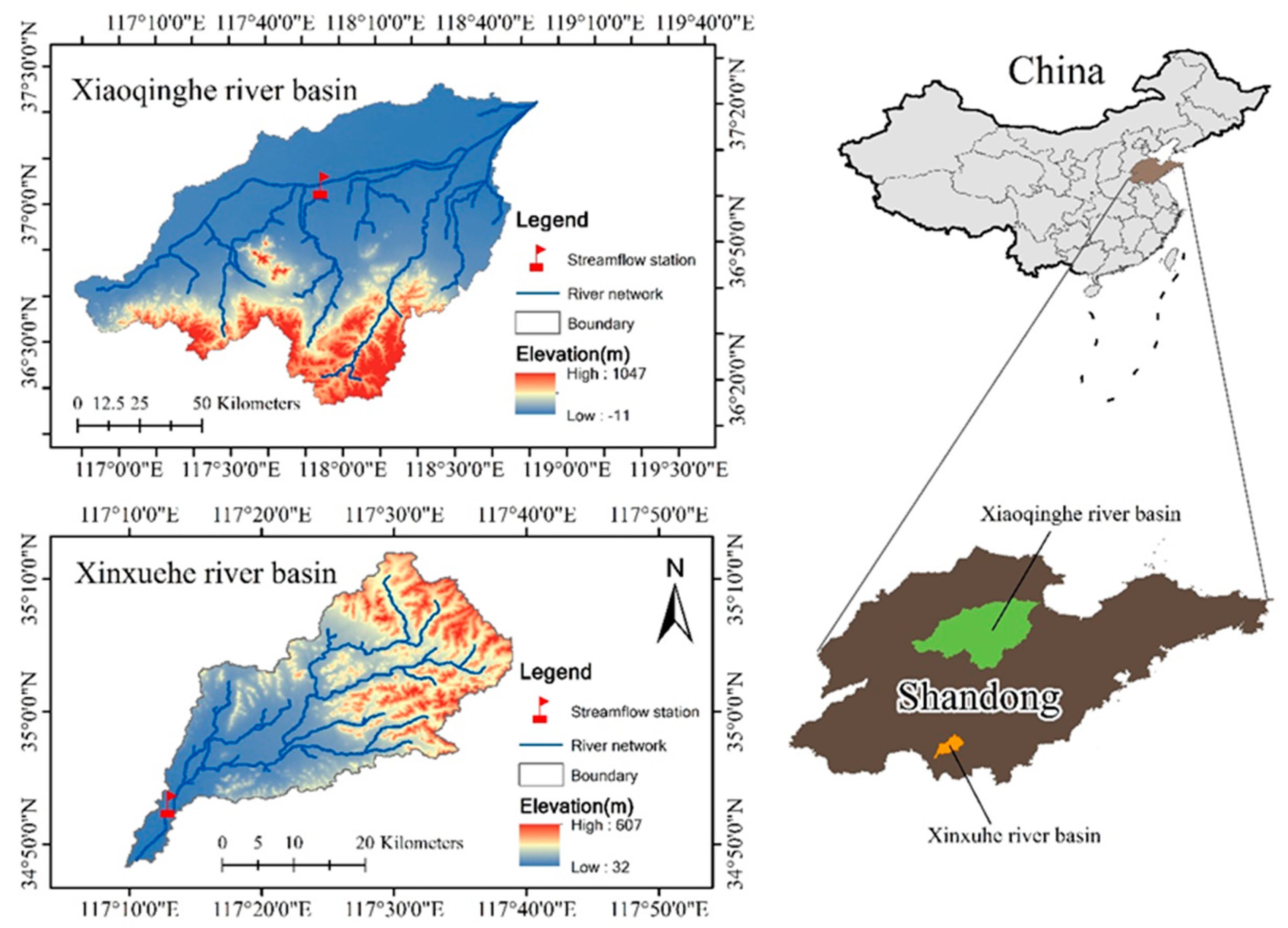
2.1. Overview of Research Area
2.2. Data Source
3. Method
3.1. Overview of SWAT Model
3.2. Principles and Procedures of the SUFI-2 Method
3.3. Principles and Procedures of the GLUE Method
3.4. Evaluation Criteria for Calibration and Uncertainty Analysis Results
4. Results Analysis
4.1. Uncertainty Analysis of Xiaoqing River Basin
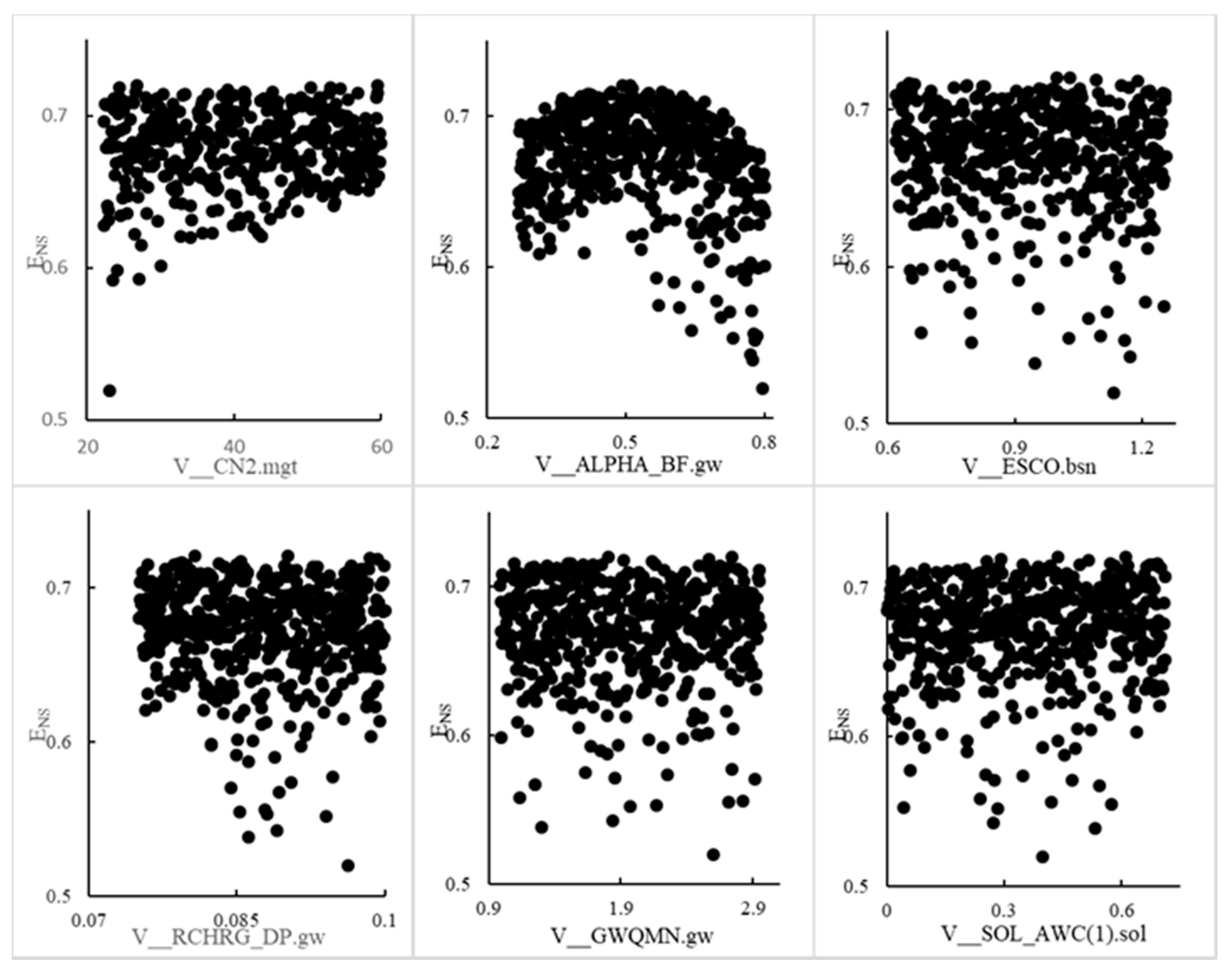
4.1.1. Parameter Selection and Range Determination
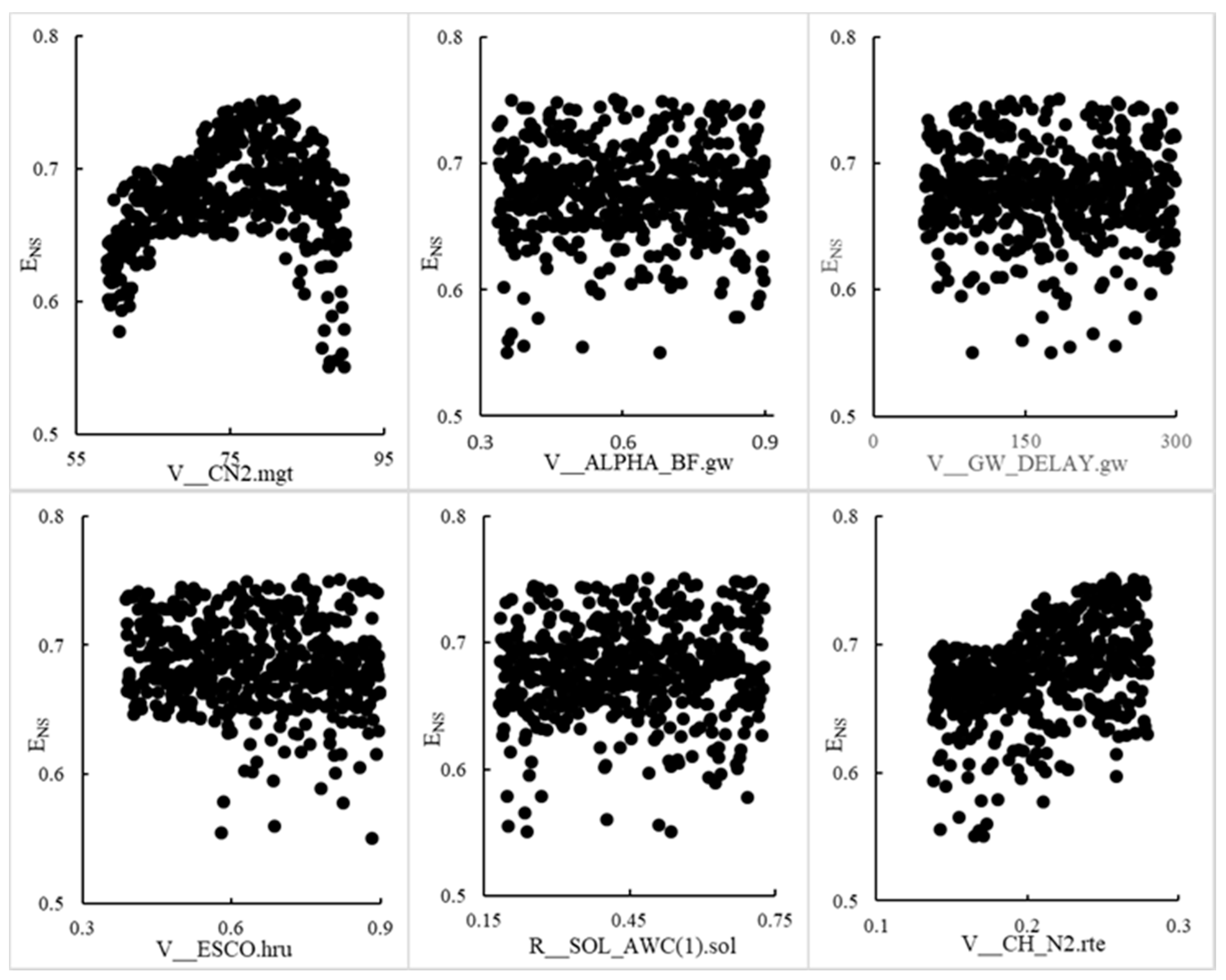
4.1.2. Parameter Uncertainty Analysis of the Two Methods in the Xiaoqing River Basin
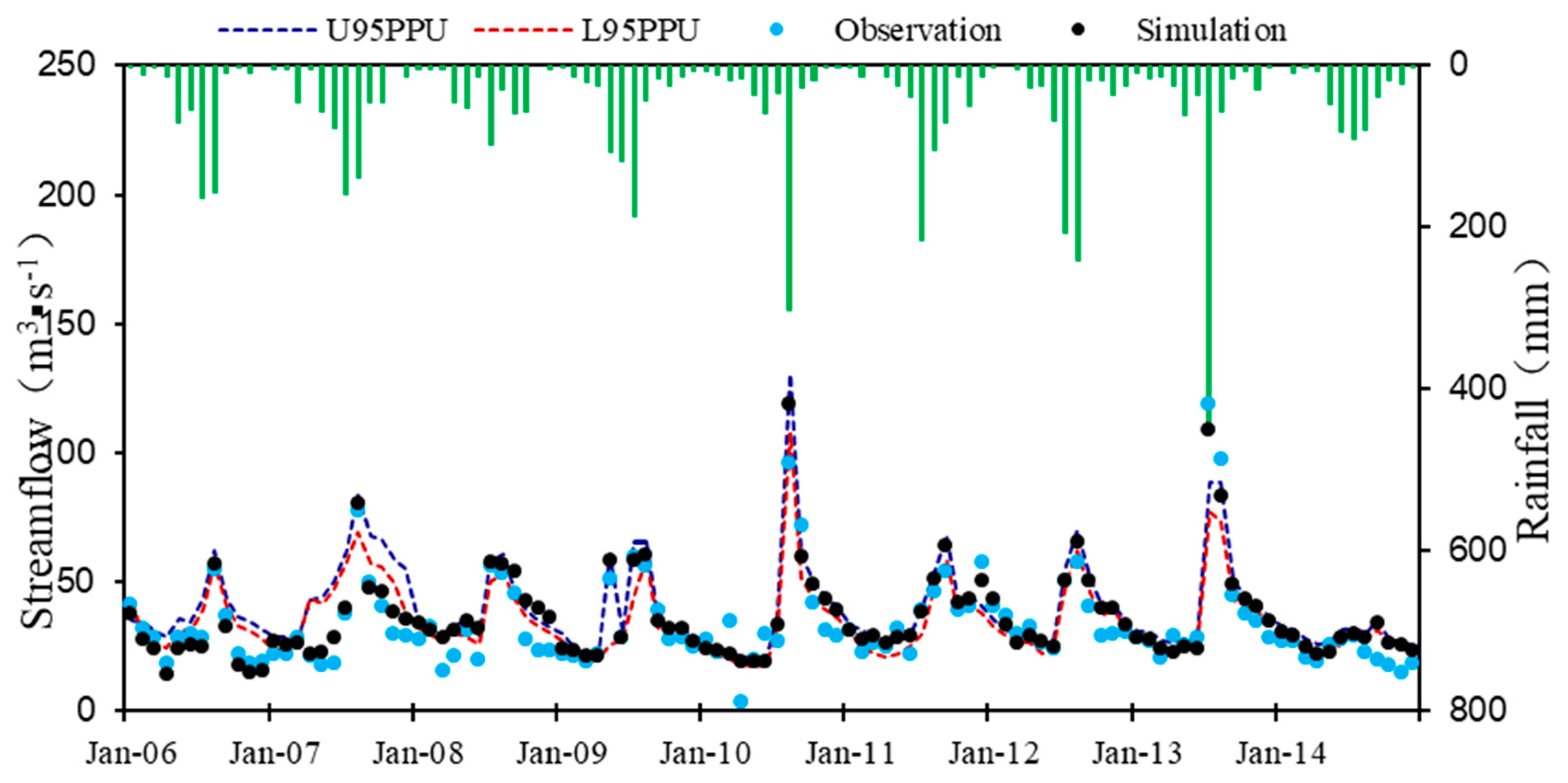
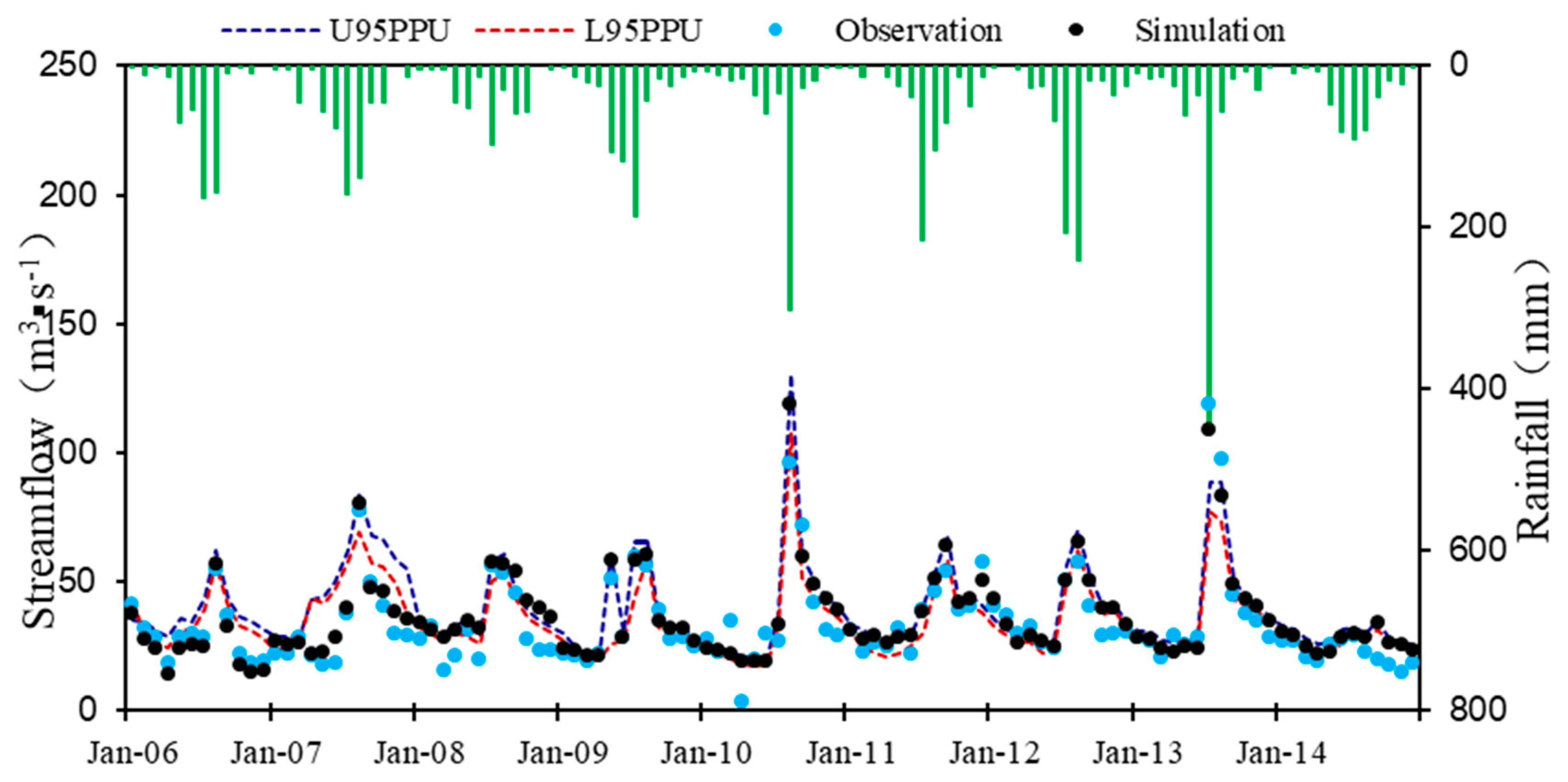
4.1.3. Analysis of Uncertainty of Model Simulation
4.2. Uncertainty Analysis of the Xinxue River
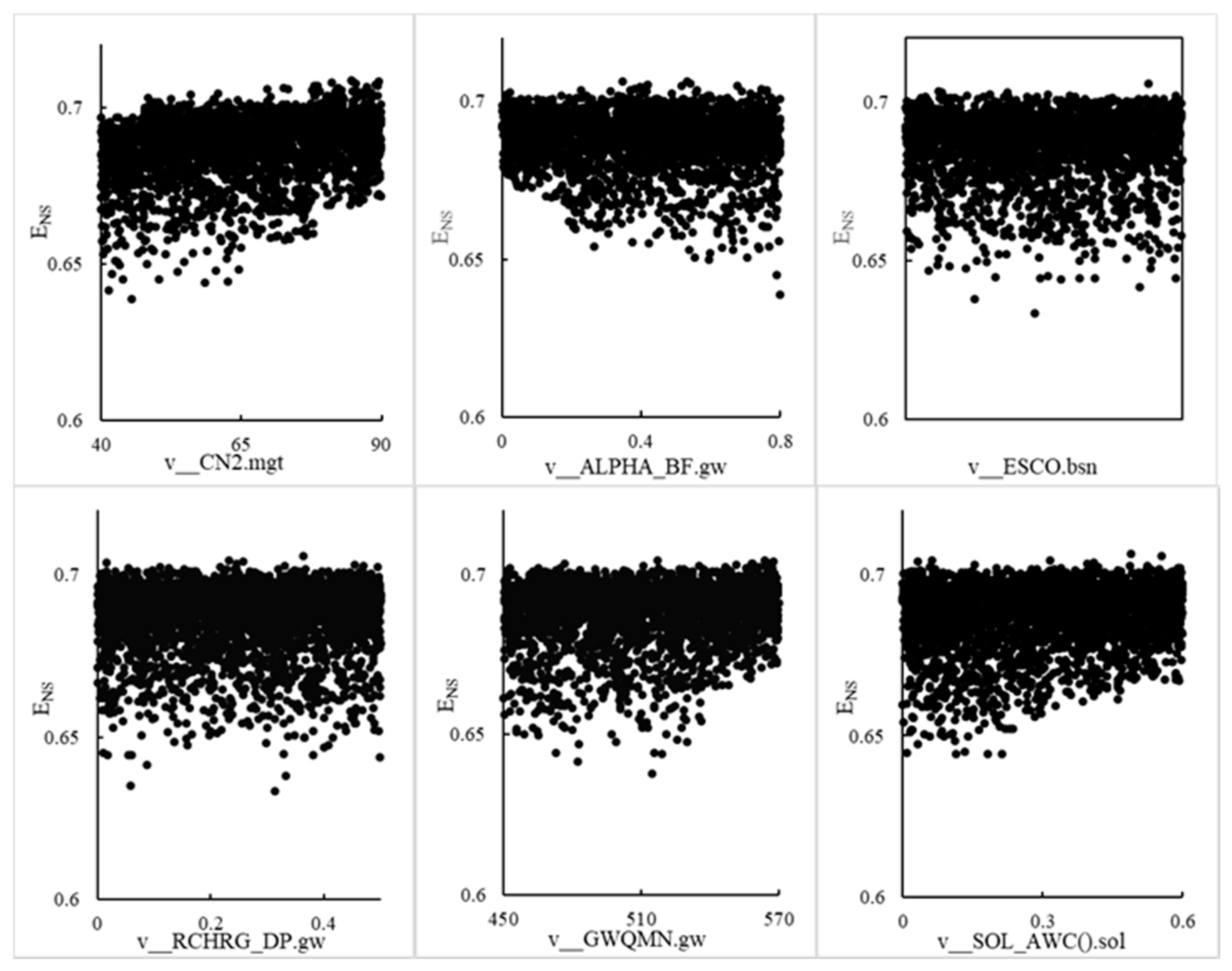
4.2.1. Parameter Selection and Scale Determination
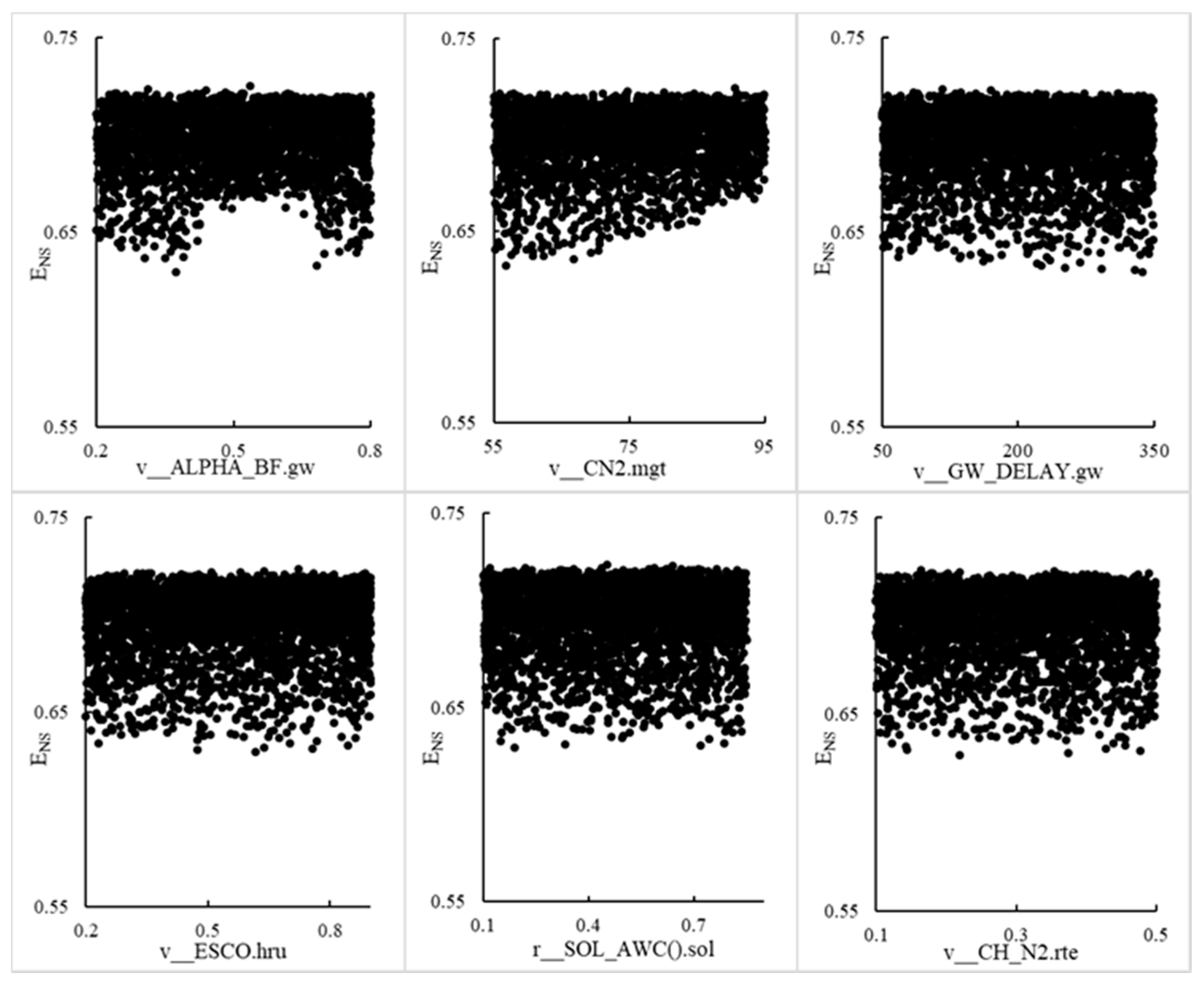
4.2.2. Uncertainty Analysis of Model Parameter
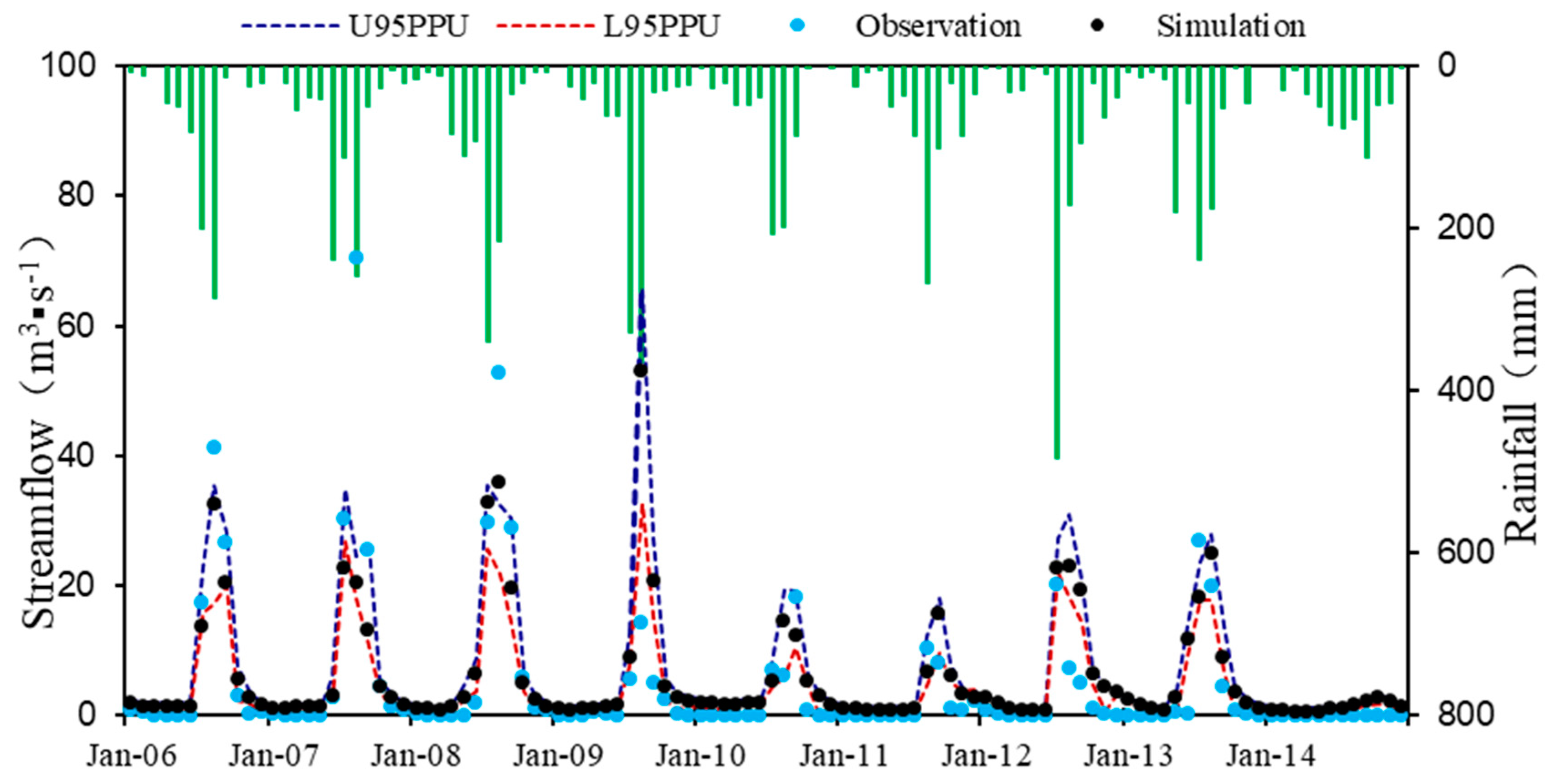
4.2.3. Uncertainty Analysis of Model Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Singh, V.P. Hydrologic modeling: Progress and future directions. Geosci. Lett. 2018, 5. [Google Scholar] [CrossRef]
- Pohlert, T.; Huisman, J.A.; Breuer, L.; Frede, H.G. Integration of a detailed biogeochemical model into SWAT for improved nitrogen predictions—Model development, sensitivity, and GLUE analysis. Ecol. Model. 2007, 203, 215–228. [Google Scholar] [CrossRef]
- Bronstert, A.; Bárdossy, A. Uncertainty of runoff modelling at the hillslope scale due to temporal variations of rainfall intensity. Phys. Chem. Earth Parts A/B/C 2003, 28, 283–288. [Google Scholar] [CrossRef]
- Deflandre, A.; Williams, R.J.; Elorza, F.J.; Mira, J.; Boorman, D.B. Analysis of the QUESTOR water quality model using a Fourier amplitude sensitivity test (FAST) for two UK rivers. Sci. Total Environ. 2006, 360, 290–304. [Google Scholar] [CrossRef] [PubMed]
- Deb, P.; Kiem, A.S.; Willgoose, G. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Pandey, V.K.; Panda, S.N.; Sudhakar, S. Modelling of an Agricultural Watershed using Remote Sensing and a Geographic Information System. Biosyst. Eng. 2005, 90, 331–347. [Google Scholar] [CrossRef]
- Stonefelt, M.D.; Fontaine, T.A.; Hotchkiss, R.H. Impacts of climate change on water yield in the upper wind river basin. J. Am. Water Resour. Assoc. 2000, 36, 321–336. [Google Scholar] [CrossRef]
- Wang, G.; Li, J.; Sun, W.; Xue, B.; A, Y.; Liu, T. Non-point source pollution risks in a drinking water protection zone based on remote sensing data embedded within a nutrient budget model. Water Res. 2019, 157, 238–246. [Google Scholar] [CrossRef]
- Her, Y.G.; Jeong, J.; Bieger, K.; Rathjens, H.; Arnold, J.; Srinivasan, R. Implications of conceptual channel representation on SWAT streamflow and sediment modeling. J. Am. Water Resour. Assoc. 2017, 53, 725–747. [Google Scholar] [CrossRef]
- Ruan, H.; Zou, S.; Yang, D.; Wang, Y.; Yin, Z.; Lu, Z.; Li, F.; Xu, B. Runoff Simulation by SWAT Model Using High-Resolution Gridded Precipitation in the Upper Heihe River Basin, Northeastern Tibetan Plateau. Water 2017, 9, 866. [Google Scholar] [CrossRef]
- Xie, H.; Lian, Y. Uncertainty-based evaluation and comparison of SWAT and HSPF applications to the Illinois River Basin. J. Hydrol. 2013, 481, 119–131. [Google Scholar] [CrossRef]
- Li, Z.L.; Shao, Q.X.; Xu, Z.X.; Cai, X.T. Analysis of parameter uncertainty in semi-distributed hydrological models: Using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Yesuf, H.M.; Melesse, A.M.; Zeleke, G.; Alamirew, T. Streamflow prediction uncertainty analysis and verification of SWAT model in a tropical watershed. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 4, 279–298. [Google Scholar] [CrossRef]
- Caflisch, R.E. Monte carlo and quasi-monte carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef]
- Gilks, W.R. Markov Chain Monte Carlo; John Wiley & Sons. Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Schuol, J.; Abbspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T. Methods to quantify and identify the sources of uncertainty for river basin water quality models. Water Sci. Technol. 2015, 53, 51–59. [Google Scholar] [CrossRef]
- Ashraf Vaghefi, S.; Mousavi, S.J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Analyses of the impact of climate change on water resources components, drought and wheat yield in semiarid regions: Karkheh River Basin in Iran. Hydrol. Process. 2014, 28, 2018–2032. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling pesticide diuron loading from the San Joaquin watershed into the Sacramento-San Joaquin Delta using SWAT(Article). Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Xu, G.H.; Wang, Y.G.; Engel, B.A.; Peng, H.; Zhang, W.S.; Cheng, M.L.; Dai, M.L. Modelling hydrology and water quality processes in the Pengxi River basin of the Three Gorges Reservoir using the soil and water assessment tool. Agric. Water Manag. 2017, 182, 24–38. [Google Scholar] [CrossRef]
- Hollaway, M.J.; Beven, K.J.; Benskin, C.M.H.; Collins, A.L.; Evans, R.; Falloon, P.D.; Forber, K.J.; Hiscock, K.M.; Kahana, R.; Macleod, C.J.A.; et al. The challenges of modelling phosphorus in a headwater catchment: Applying a ‘limits of acceptability’ uncertainty framework to a water quality model. J. Hydrol. 2017, 558, 607–624. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, C.Y.; Chen, X.W.; Xu, Y.P.; Yin, Y.X.; Gao, L.; Liu, M.B. Uncertainty in simulation of land-use change impacts on catchment runoff with multi-timescales based on the comparison of the HSPF and SWAT models. J. Hydrol. 2019, 573, 486–500. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, R.; Men, C.; Guo, L.; Miao, Y. Effects of dynamic land use inputs on improvement of SWAT model performance and uncertainty analysis of outputs. J. Hydrol. 2018, 563, 874–886. [Google Scholar] [CrossRef]
- Notter, B.; Hurnil, H.; Wiesmann, U.; Abbaspour, K.C. Modelling water provision as an ecosystem service in a large East African river basin. Hydrol. Earth Syst. Sci. 2012, 16, 69–86. [Google Scholar] [CrossRef]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R. Assessment of Future Climate Change Impacts on Water Resources of Upper Sind River Basin, India Using SWAT Model. Water Resour. Manag. 2013, 27, 3647–3662. [Google Scholar] [CrossRef]
- Delsman, J.R.; Oude Essink, H.P.; Beven, K.J.; Stuyfzand, P.J. Uncertainty estimation of end-member mixing using generalized likelihood uncertainty estimation (GLUE), applied in a lowland catchment. Water Resour. Res. 2013, 49, 4792–4806. [Google Scholar] [CrossRef]
- Sun, N.; Hong, B.; Hall, M. Assessment of the SWMM model uncertainties within the generalized likelihood uncertainty estimation (GLUE) framework for a high-resolution urban sewershed. Hydrol. Process. 2014, 28, 3018–3034. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of Eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
- Shivhare, N.; Dikshit, P.K.S.; Dwivedi, S.B. A Comparison of SWAT Model Calibration Techniques for Hydrological Modeling in the Ganga River Watershed. Engineering 2018, 4, 643–652. [Google Scholar] [CrossRef]
- Zhao, F.B.; Wu, Y.P.; Qiu, L.J.; Sun, Y.Z.; Sun, L.Q.; Li, Q.L.; Niu, J.; Wang, G.Q. Parameter Uncertainty Analysis of the SWAT Model in a mountain-loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Su, Q.; Peng, C.; Yi, L.; Huang, H.; Liu, Y.; Xu, X.; Chen, G.; Yu, H. An improved method of sediment grain size trend analysis in the Xiaoqinghe Estuary, southwestern Laizhou Bay, China. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Han, D.; Wang, G.; Liu, T.; Xue, B.-L.; Kuczera, G.; Xu, X. Hydroclimatic response of evapotranspiration partitioning to prolonged droughts in semiarid grassland. J. Hydrol. 2018, 563, 766–777. [Google Scholar] [CrossRef]
- Xie, Y.L.; Huang, G.H.; Li, W.; Li, J.B.; Li, Y.F. An inexact two-stage stochastic programming model for water resources management in Nansihu Lake Basin, China. J. Environ. Manag. 2013, 127, 188–205. [Google Scholar] [CrossRef] [PubMed]
- Arnold, J.G.; Williams, J.R.; Nicks, A.D.; Sammons, N.B. SWRRB: A Basin Scale Simulation Model for Soil and Water Resources Management; Texas A&M Press: College Station, TX, USA, 1990. [Google Scholar]
- Knisel, W.G. CREAMS: A Field Scale Model for Chemicals, Runoff, and Erosion from Agricultural Management Systems; Conservation Research Report No. 26; U.S. Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1980.
- Leonard, R.S.; Knisel, W.G.; Still, D.A. GLEAMS: Groundwater Loading Effects of Agricultural Management Systems. Trans. Am. Soc. Agric. Eng. 1987, 30, 1403–1418. [Google Scholar] [CrossRef]
- Williams, J.R.; Jones, C.A.; Dyke, P.T. A modelling approach to determining the relationship between erosion and soil productivity. Trans.-Am. Soc. Agric. Eng. 1984, 27, 129–144. [Google Scholar] [CrossRef]
- Arnold, J.G.; Williams, J.R.; Maidment, D.R. Continuous-time water and sediment-routing model for large basins. J. Hydraul. Eng.—ASCE 1995, 121, 171–183. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Technical Report No. 406; Texas Water Resources Institute, Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Jodar-Abellan, A.; Valdes-Abellan, J.; Pla, C.; Gomariz-Castillo, F. Impact of land use changes on flash flood prediction using a sub-daily SWAT model in five Mediterranean ungauged watersheds (SE Spain). Sci. Total Environ. 2019, 657, 1578–1591. [Google Scholar] [CrossRef] [PubMed]
- Kidane, M.; Tolessa, T.; Bezie, A.; Kessete, N.; Endrias, M. Evaluating the impacts of climate and land use/land cover (LU/LC) dynamics on the Hydrological Responses of the Upper Blue Nile in the Central Highlands of Ethiopia. Spat. Inf. Res. 2019, 27, 151–167. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Koch, K. Monte Carlo methods. GEM-Int. J. Geomath. 2018, 9, 117–143. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Chang, J.; Guo, A.; Li, Z. Investigating the Dynamic Influence of Hydrological Model Parameters on Runoff Simulation Using Sequential Uncertainty Fitting-2-Based Multilevel-Factorial-Analysis Method. Water 2018, 9, 1177. [Google Scholar] [CrossRef]
- Yaduvanshi, A.; Srivastava, P.; Worqlul, A.; Sinha, A. Uncertainty in a Lumped and a Semi-Distributed Model for Discharge Prediction in Ghatshila Catchment. Water 2018, 4, 381. [Google Scholar] [CrossRef]
- Wang, G.Q.; Liu, S.M.; Liu, T.X.; Fu, Z.Y.; Yu, J.S.; Xue, B.L. Modelling above-ground biomass based on vegetation indexes: A modified approach for biomass estimation in semi-arid grasslands. Int. J. Remote Sens. 2018, 40, 3835–3854. [Google Scholar] [CrossRef]
- A, Y.L.; Wang, G.Q.; Liu, T.X.; Xue, B.L.; Kuczera, G. Spatial variation of correlations between vertical soil water and evapotranspiration and their controlling factors in a semi-arid region. J. Hydrol. 2019, 574, 53–63. [Google Scholar] [CrossRef]
- Sisay, E.; Halefom, A.; Khare, D.; Singh, L.; Worku, T. Hydrological modelling of ungauged urban watershed using SWAT model. Model. Earth Syst. Environ. 2017, 3, 693–702. [Google Scholar] [CrossRef]
- Deb, P.; Babel, M.S.; Denis, A.F. Multi-GCMs approach for assessing climate change impact on water resources in Thailand. Model. Earth Syst. Environ. 2018, 4, 825–839. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Dantas, J.C.; Beltrão, J.D.A.; Santos, C.A. Hydrological simulation in a tropical humid basin in the Cerrado blome using the SWAT model. Hydrol. Res. 2018, 49, 908–923. [Google Scholar] [CrossRef]
- Hu, X.; Mcisaac, G.F.; David, M.B.; Louwers, C.A. Modeling riverine nitrate export from an East-Central Illinois watershed using SWAT. J. Environ. Qual. 2007, 36, 996–1005. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.Y.; Chen, L.; Chen, T. The influence of parameter distribution uncertainty on hydrological and sediment modeling: A case study of SWAT model applied to the Daning watershed of the Three Gorges Reservoir Region, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 235–251. [Google Scholar]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R.; Singh, S.K.; Srivastava, P.K. SWAT Model Calibration and Uncertainty Analysis for Streamflow Prediction in the Kunwari River Basin, India, Using Sequential Uncertainty Fitting. Environ. Process. 2015, 2, 79–95. [Google Scholar] [CrossRef]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Fang, Q.; Wang, G.Q.; Liu, T.X.; Xue, B.L.; A, Y.L. Controls of carbon flux in a semi-arid grassland ecosystem experiencing wetland loss: Vegetation patterns and environmental variables. Agric. For. Meteorol. 2018, 259, 196–210. [Google Scholar] [CrossRef]
- Fang, Q.; Wang, G.; Xue, B.; Liu, T.; Kiem, A. How and to what extent does precipitation on multi-temporal scales and soil moisture at different depths determine carbon flux responses in a water-limited grassland ecosystem? Sci. Total Environ. 2018, 635, 1255–1266. [Google Scholar] [CrossRef] [PubMed]
- Wilcke, W.; Yasin, S.; Schmitt, A.; Valarezo, C.; Zech, W. Soils along the altitudinal transect and in catchments. In Ecological Studies 198, Gradients in a Tropical Mountain Ecosystem of Ecuador; Chapter 9; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the spatial prediction of soil texture—Comparison of regression tree and random forest models. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
- Briak, H.; Moussadek, R.; Aboumaria, K.; Mrabet, R. Assessing sediment yield in Kalaya gauged watershed (Northern Morocco) using GIS and SWAT model. Int. Soil Water Conserv. Res. 2016, 4, 177–185. [Google Scholar] [CrossRef]

| Parameter | Parameter Meaning | Initial Value Interval | Affected Object and Process |
|---|---|---|---|
| CN2 | SCS runoff curve coefficient | 35–98 | Surface runoff |
| ALPHA_BF | Base flow alpha coefficient | 0–1 | groundwater |
| ESCO | Soil evaporation compensation coefficient | 0.01–1 | Soil evaporation |
| RCHRG_DP | Permeability coefficient of deep aquifer | 0–1 | Groundwater process |
| GWQMN | Runoff coefficient of deep groundwater | 0–5000 | Soil moisture |
| SOL_AWC | Available soil water | 0–1 | Soil moisture |
| Method | Simulation | P-factor | R-factor | ENS | R2 |
|---|---|---|---|---|---|
| SUFI-2 | calibration period | 0.77 | 0.75 | 0.71 | 0.72 |
| validation period | 0.73 | 0.73 | 0.74 | 0.76 | |
| GLUE | calibration period | 0.84 | 0.80 | 0.71 | 0.75 |
| validation period | 0.81 | 0.75 | 0.71 | 0.76 |
| Parameter | Parameter Meaning | Range of Initial Value | Influenced Object & Process |
|---|---|---|---|
| CN2 | SCS Runoff Coefficient | 35–98 | Surface Runoff |
| ALPHA_BF | Base Flow Coefficient α | 0–1 | Subterranean Water |
| GW_DELAY | Subterranean Water Lag Coefficient | 0–500 | Process of Subterranean Water |
| ESCO | Soil Evaporation Compensation Coefficient | 0.01–1 | Soil Evaporation |
| SOL_AWC | Available Water in Soil | 0–1 | Soil Moisture |
| CH_N2 | Drainage Line Manning Coefficient | −0.01–0.3 | Concentration of Channel |
| Method | Simulation | P-factor | R-factor | ENS | R2 |
|---|---|---|---|---|---|
| SUFI-2 | calibration period | 0.74 | 0.87 | 0.71 | 0.73 |
| validation period | 0.73 | 0.75 | 0.73 | 0.75 | |
| GLUE | calibration period | 0.76 | 0.90 | 0.72 | 0.72 |
| validation period | 0.73 | 0.83 | 0.73 | 0.74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xue, B.; Yan, Y.; Wang, G.; Sun, W.; Li, Z.; Yu, J.; Xie, G.; Shi, H. Model Uncertainty Analysis Methods for Semi-Arid Watersheds with Different Characteristics: A Comparative SWAT Case Study. Water 2019, 11, 1177. https://doi.org/10.3390/w11061177
Zhang L, Xue B, Yan Y, Wang G, Sun W, Li Z, Yu J, Xie G, Shi H. Model Uncertainty Analysis Methods for Semi-Arid Watersheds with Different Characteristics: A Comparative SWAT Case Study. Water. 2019; 11(6):1177. https://doi.org/10.3390/w11061177
Chicago/Turabian StyleZhang, Lufang, Baolin Xue, Yuhui Yan, Guoqiang Wang, Wenchao Sun, Zhanjie Li, Jingshan Yu, Gang Xie, and Huijian Shi. 2019. "Model Uncertainty Analysis Methods for Semi-Arid Watersheds with Different Characteristics: A Comparative SWAT Case Study" Water 11, no. 6: 1177. https://doi.org/10.3390/w11061177
APA StyleZhang, L., Xue, B., Yan, Y., Wang, G., Sun, W., Li, Z., Yu, J., Xie, G., & Shi, H. (2019). Model Uncertainty Analysis Methods for Semi-Arid Watersheds with Different Characteristics: A Comparative SWAT Case Study. Water, 11(6), 1177. https://doi.org/10.3390/w11061177







