Abstract
The morphological evolution of tidal flats has been widely investigated in recent years as it represents a very important topic which is highly related to the climate-driven environmental changes. The period over which geomorphological changes can be noted is a multi-year up to pluri-decennial time scale, defined as medium-long period. This work presents a new conceptual model which is able to predict and estimate a limit depth between an erosion condition and a no-erosion condition for tidal flats. The domains of applicability are shallow and confined basins, where tidal flats are characterized by near-horizontal topography, as occurs inside lagoons. The theoretical approach provides a general equation which relates the limit depth of tidal flats to current velocity and critical erosion shear stress. The procedure, followed through to its development, takes into account the important role of the bottom friction dissipation in wind wave generation process for shallow water. The relationship between tidal flat depth, current velocity and critical shear stress is provided in three different configurations, depending on the direction of the wave motion compared to the current. The limit depth compared to the measured depth can suggest if tidal flats tend or not towards an erosion state over a medium-long period. In this sense, the conceptual model provides a relevant contribution to the comprehension of morphodynamics of these important environments. This approach has been validated with its application to a real context and the results are provided in the paper.
1. Introduction
Tidal flat landforms in coastal and estuarine systems include a great variety of environments, which are constantly shaped by complex physical and biological factors [1,2]. As transitional environments, tidal flats are periodically submerged and exposed under tide and wave driven processes which deeply affect the sediment transport mechanisms [3,4,5,6,7,8,9]. Moreover, sediment supply and fluvial inflow as well as organic and anthropic activities can alter their morphology [10,11,12,13]. According to Friedrichs [5], sediment transport mechanisms induced by tides and waves also involve the gradual morphological transition beyond low tide level. For this reason, in this paper the term “tidal flats” is used in its dynamic meaning, which includes both the actual tidal-flats, in the strict sense, and the sub-tidal flats.
Due to their particular nature, tidal flats are fundamental to estuarine and lagoon morphodynamics and their ecological and socio-economic importance is widely recognized [14,15,16]. At the same time, the fragile balance of these environments can interfere with human-induced changes, such as shoreline protection intervention or dredging operations for the maintenance of waterways navigability. Within this context, the possible configurations of tidal flats over a medium-long period, become an essential element for the management and sustainability of coastal areas [17]. The term “medium-long” refers to a multi-year up to a pluri-decennial time scale over which the geomorphological changes can be noted.
Many studies have investigated morphological changes over a medium-long period occurring in coastal lagoon and tidal flat environments, in order to assess the erosional/accretionary pattern, and the relative sediment budget. These studies consider geomatics techniques based on historical cartography, photogrammetry, topography [18,19,20,21,22] or on the satellite image processing [23]. Direct measurements and monitoring of bed level changes in tidal flats are quite difficult to carry out, due to the complexity of the environment and the lack of appropriate measuring equipment and methods [24]. Only recent studies have provided detailed quantification of high-resolution short-term (from daily to seasonal time scale) bed level dynamics, coupled with hydrodynamic data [24,25,26,27].
In order to improve understanding and predicting of how a tidal flat can evolve over a medium-long time scale, theoretical and numerical approaches have been developed, which need monitoring and measurement data in order to be applied. This research is based on a proper definition of an equilibrium pattern which can lead to a stable morphology [4,5,7,28,29,30,31]. In fact, tides, wind and wave climate operate over a wide range of scales, from that of a storm, to the semidiurnal or diurnal cycle to seasonal, annual or decade long periods. In this sense, the concept of quasi-equilibrium [4] or dynamic equilibrium [5,28,29,30] is preferred as opposed to an unrealistic static condition in which no sediment is transported. Equivalently, this means that erosion is balanced by deposition at each point of the tidal flat, when considered over a suitably long period [4,30].
Starting from this assumption, the cross-shore profile shapes of tidal flats exposed to the sea, typical of estuarine environments, have been widely investigated through experimental observations [32,33,34], and numerical solutions [4,5,17,35,36,37]. Given the complexity of the processes involved, the results obtained are generally only qualitative and strongly conditioned by the necessary simplifications that have been made.
Among the first studies, Friedrichs and Aubrey [38] proposed the dynamic equilibrium theory, based on a simplified analytical approach, useful to explain the morphological responses of intertidal systems. This method assumes that the cross-shore profile of a tidal flat is stable when the maximum bed shear stress during a tidal cycle is uniform over space, ensuring no net deposition or erosion anywhere in the system. Taking into account annual or longer time scales, the profile approximates a concave shape if it is purely wave-dominated, while it results convex if the tide is prevailing in the overall balance. If a shorter timescale is considered, tidal flat morphology can evolve dynamically between these two configurations depending on the bed shear stress variability.
Subsequent and more complex models [4,8,35,39] have been used to simulate the mudflat profile shapes in the 2D-vertical plane, finding results which qualitatively agree with those of Friedrichs and Aubrey [38]. Hu et al. [28] have extended the dynamic equilibrium theory by explicitly taking into account a spatiotemporal bed shear stress variation to predict tidal flat morphodynamics. In this sense, the developed model overcomes the limit of the original analytical solution of Friedrichs and Aubrey [38] that is based on the assumption of a uniform bed shear stress distribution that may not occur in reality.
A similar choice of a reference shear stress for long-term modeling is also followed by Mariotti and Fagherazzi [40] who proposed a dynamic model to study the morphological evolution of fetch-limited basins or lagoons. The analyzed configuration is typical of tidal flats which are sheltered from the sea by barrier islands. In these cases, tidal flats are inherently horizontal with a very small slope and such that they can be characterized in a sufficient area by a uniform depth value. Moreover, the wave motion is locally generated here and it presents lower periods and wave heights [41,42,43,44,45]. Mariotti and Fagherazzi [46] feature the non–monotonic relationship between wave shear stress and depth, which represents the focus point of a previous conceptual model, which was proposed by Fagherazzi et al. [47]. This non-monotonic distribution of the bed shear stress with depth is then compared to a critical erosion threshold for cohesive sediments and a fixed deposition rate. The conceptual approach has been subsequently improved taking into account the effects of a collinear current shear stress and different sediment inputs [48]. Starting from similar assumptions some numerical applications to the Venice Lagoon have been conducted with the aim to describe the morphological evolutionary trend through hypsometry, which corresponds to frequency area distribution related to bottom elevation [18,49].
A recent line of research deals with the role played both by bottom friction and wave period on the wave bottom shear stress, which is fundamental in coastal morphodynamics [45,50]. It has been numerically shown that the bottom friction dissipation can severely limit the wave field with the consequence that the relative curve of bed shear stress loses the bell shape, tending instead to decrease monotonically with the water depth [45]. In this sense, the wave motion is able to induce sediment transport only when very strong winds are considered, which are however rare. Experimental findings [29] support this outcome, that necessarily leads to reviewing the processes that drive sediment transport over a tidal cycle or a longer time scale, in order to identify the conditions for the morphodynamic equilibrium of tidal flats. For these reasons, the conceptual model briefly recalled can be revised and extended.
In the present paper a new theoretical approach is proposed with the aim of providing a reasonable morphodynamic trend over a medium-long period for tidal flats in sheltered environments. This method gives the equation to derive a limit depth value that can suggest if the tidal flat tends, or not towards an erosion state. The maximum shear stress caused both by the wave motion and the current field is compared to the critical threshold of erosion which represents the resistance of the bottom to sediment mobilization. The wave shear stress is numerically computed by means of a generation process with a morphologically representative wind speed and a proper representation of bottom dissipation. The relationship between tidal flat depth, current velocity and critical shear stress is provided in three different configurations, depending on the direction of the wave motion compared to the current.
With the aim of validating the new conceptual model, an application to the Marano and Grado lagoon in the Northern Adriatic Sea (Italy) has been conducted, starting from two bathymetries detected 45 years apart and numerical data obtained from a previous application by means of a spectral–morphodynamic coupled model [51].
2. Tidal Flat Morphodynamics: Some Preliminary Considerations
Within lagoons and sheltered areas, tidal currents are undoubtedly dominant for sediment transport close to tidal inlets and inside the main channels, where higher current velocities can profoundly incise the bed [52,53,54,55,56,57,58]. On the other hand, wave motion is decisive in the resuspension of sediments from the tidal flats bottom, where shallow depths limit current velocities and the corresponding values of shear stress [3,9,40,48,51,54,55]. Even the small waves generated by local moderate winds can contribute to morphological stability in the long-term period, the wave orbital motion being able to penetrate down to the water depth [3,7,9].
The generation process of wind waves on shallow depths leads to quite different characteristics from offshore waves developed on deep waters, as the friction dissipation severely restricts the maximum value that wave heights and periods can reach [3,45]. This particular aspect has been verified both experimentally and numerically and it has led to a set of equations formulated for wave forecasting in shallow water [43,59]. However, the growth curves, extensively used in many applications [40,46,55,60], may not be exhaustive in order to correctly interpret the wave field. In fact, they have been determined by adopting a low friction factor, generally representative of very smooth, homogenous and flat beds.
In the presence of a more irregular bottom, characterized by bedforms (uneven granulometry with coexistence of sand and mud, and vegetation), the wave friction factor can considerably increase. This result was achieved by the authors in a previous study [45], performing a numerical generation process by means of the third generation spectral model SWAN [61], based on the complete wave action balance equation.
A regular computational grid has been chosen to reproduce the generation process in a microtidal limited-fetch environment, where the tidal flats are characterized by near-horizontal topography, such the Marano and Grado or the Venice lagoons mapped in Figure 1.
Figure 1.
Venice lagoon and Marano and Grado lagoon depicted in the (a) European context and (b) in the Northern Adriatic Sea.
Several configurations of depth, wind speed and bed roughness have been set to establish the role played by bottom friction and to identify the spectral approach that better reproduces the energy dissipation of locally generated waves. The comparison between the available formulations in SWAN, has outlined that the Madsen model [62] is more suitable to be applied in such coastal and transitional environments. The previously mentioned study by Pascolo et al. [45] has verified that an equivalent roughness of a few centimeters is sufficient to considerably limit the wave orbital velocity Uw computed at the bottom.
As depicted in Figure 2a for different wind speed values, these wave velocities tend to follow an almost constant trend on the tidal flat depths, herein indicated as d, commonly included in the range 0.5–2 m below still water level.
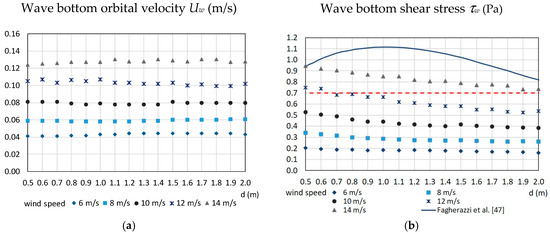
Figure 2.
(a) Root mean square value of the maxima of the bottom orbital velocity and (b) wave bed shear stress computed on different depths d by means SWAN [61]. The equivalent roughness height is 0.05 m. The dashed line indicates the critical erosion threshold adopted by Fagherazzi et al. [47] and is evaluated as a mean value for the tidal flats of the Venice lagoon [63,64], while the continuous line is the non-monotonic curve that the same authors proposed for a wind speed equal to 8 m/s.
Pascolo et al. [45] have also shown that the shallow water generation process is substantially independent from the fetch length, as the fully developed sea state can be reached on very short distances, less than 5 km.
The more relevant consequence, decisive for morphodynamic processes, is the considerable reduction of the wave bottom shear stress acting on the sediment grains. The wave bottom shear stress depends on the wave velocity according to the following quadratic law:
where ρ is the water density, fw is the friction factor and Uw the maximum wave bottom orbital velocity. The friction factor is evaluated by means of the Soulsby formulation [65]:
A = UwT/2π being one half of the horizontal orbital excursion, T the wave period, z0 = KN/30, and KN the equivalent Nikuradse roughness. This last parameter is generally taken as a function of the median diameter if the bed is composed of coarse grains, while for fine cohesive grains or mud-beds, KN can be set equal to a few millimeters as an approximation of the mud protrusions height [66].
Figure 2b highlights how the bed shear stress computed assuming KN = 0.005 m, tends to be quite flat and homogeneous for the analyzed depths. These trends are very different from the non-monotonic curve suggested by Fagherazzi et al. [47] for a wind speed of 8 m/s, as already discussed by Pascolo et al. [45]. The reason could be attributable to the assumptions of a KN value equal to 5 × 10−5 m and above all monochromatic wind waves, generated with an imposed constant wave period.
The dashed line refers to a critical shear stress for cohesive sediments of 0.7 Pa evaluated as a mean value for the tidal flats of the Venice lagoon [63,64]. The same value has been adopted successfully in several applications in some coastal environments of the North Adriatic Sea [47,48,51,54,67]. It can be noticed that the non-monotonic curve derived by Fagherazzi et al. [47] exceeds the critical shear stress over the whole analyzed domain. On the other hand, the wave stress component on rougher bed, is sufficient to resuspend sediments from the bottom only for high wind speeds and therefore extreme events. This means that the current velocity becomes truly decisive in triggering the transport process in presence of moderate winds, which are considered representative for the morphological evolution over timescale longer than that of a storm [5,40]. The new conceptual model, which is proposed in the present paper, is precisely based on these assumptions.
3. Conceptual Model
The conceptual model starts from the computation of the maximum total bed shear stress due to the non-linear interaction of wave and current shear stresses, as suggested by Soulsby [65]:
where the mean bottom shear stress τm and the current contribution τc are respectively equal to:
Uc being the absolute value of the current velocity, φ the angle between the wave motion direction and the current, g the gravity acceleration, n the Manning coefficient, and d the water depth.
The wave bed shear stress component τw, is computed through the Equations (1) and (2), where the wave friction factor derives from an equivalent Nikuradse roughness of 0.005 m and the wave bottom velocity is the result of the numerical generation process achieved performing SWAN in stationary mode on a regular grid. In Table 1, a summary has been reported of the main applied source terms and their relative formulation references and set parameters. The wind speed range, chosen for the wave generation, is from 6 m/s to 14 m/s as deduced from data collected inside the Marano and Grado lagoon [51]. This range is coherent with values observed inside the Venice lagoon [47,48,54], the Virginia Coast Reserve in Virginia [55] and the Willapa Bay in Washington State [46], taken as examples.

Table 1.
Summary of the source terms used in SWAN simulation for the wind wave generation process and their relative formulation references and set parameters.
Once the wave bottom shear stress has been determined on all the considered tidal flats depths, the maximum bed shear stress is computed adding the current contribution by means of Equation (5) for different current velocity values. In the present study the Manning coefficient n, representative of the bed resistance to the flow field inside tidal channels and over tidal flats, is taken equal to 0.0285 s/m1/3. This value has been calibrated in a previous hydrodynamic modeling study of the Marano and Grado lagoon [51]. The current velocity is assumed variable in an appropriate range, taking into account that generally it rarely exceeds 0.25 m/s on the tidal flats in shallow and confined basins [3,9,46,48].
Figure 3 shows the effects of the combination of waves and current under three different scenarios between the flow direction and the wave rays, and suggests current velocities which lead to maximum shear stress greater than the chosen critical threshold. The wave component in this case is relative to a wind speed of 10 m/s.
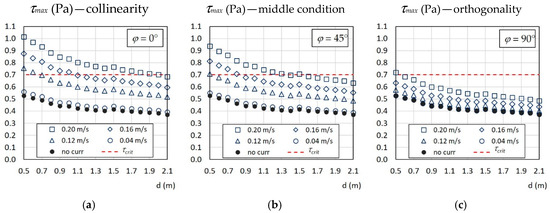
Figure 3.
Comparison between the erosion critical threshold (dashed red line) and the maximum total bed shear stress due to the combination of the wave contribution obtained from a wind speed of 10 m/s and different values of current velocity as a function of depth d. The angle between waves and current direction is respectively equal to: (a) 0°, (b) 45°and (c) 90°.
The analyzed configurations refer to the limit conditions of respectively collinearity and orthogonality between waves and current, with the addition of the middle angle of 45°. The presence of the flow field enhances the bottom shear stress, shifting the wave component upwards. When a collinearity is considered, even low velocities of the order of 0.10–0.20 m/s can give a shear stress component with magnitude comparable to the wave motion. The existence of an angle between the two components attenuates the resultant forcing until considerably reducing it in a condition close to the orthogonality, for which the current contribution is much lower.
From another point of view, it is possible to compute the depth at which the maximum bottom shear stress achieves the assigned critical threshold, at varying currents. In this way, the conceptual model provides a depth value which can be compared to the actual depth of a tidal flat in order to determine if it tends to deepen or to remain stable. The procedure followed to establish this limit depth value is illustrated in the flow chart in Figure 4.
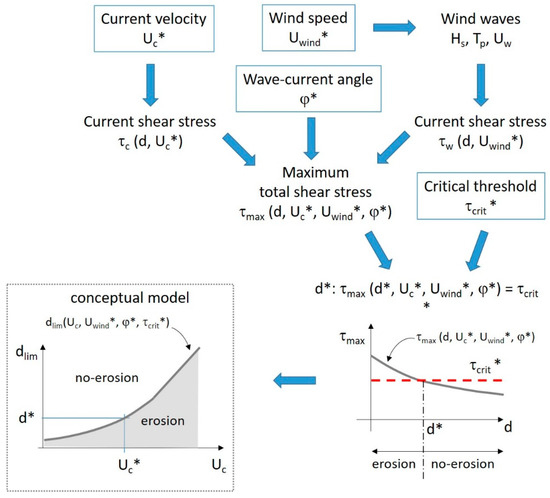
Figure 4.
Scheme of the conceptual model, which provides the limit depth value dlim between an erosion condition and a no-erosion condition. The limit depth is a function of the current velocity Uc, the wind speed Uwind, the angle φ between generated wind waves and the current flow, and the critical erosion shear stress τcrit. The asterisked variables inside the rectangles represent the values assigned as input to the model.
The asterisked variables inside the rectangles represent the values which the conceptual model requires as input. The maximum total bed shear stress can be computed at varying depth once the current velocity Uc*, the wind speed Uwind* and the angle φ* between the resultant wind waves and tidal current, have been established. The depth d* corresponds to the value for which this maximum shear stress is equal to the critical erosion threshold τcrit*. In this manner, a limit depth separates two conditions: an erosion condition for depths lower than d* and a no-erosion condition for depths greater than d*. The conceptual model provides the theoretical curve of this limit depth dlim(Uc, Uwind*, φ*, τcrit*) at varying current velocities and for different assigned values of Uwind*, φ*, τcrit*.
For a better comprehension of this procedure, first the example with a wind speed of 10 m/s and a critical shear stress of 0.7 Pa is followed. Figure 5a shows the discrete values of the limit depth in the three cases of vector composition between waves and current, i.e., for angles of respectively 0°, 45°, and 90°.
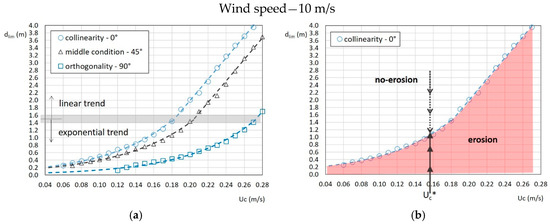
Figure 5.
(a) Limit water depth obtained by the conceptual model with a wind speed of 10 m/s and the critical erosion shear stress is 0.7 Pa. (b) Case of collinearity between waves and current. The dashed lines are regression curves. The arrows indicate the tidal flat tendency to deepen or to be filled if sediments supply is available.
Observing the dashed lines, which represent the regression curves of the obtained points, two different trends can be clearly recognized: the former exponential and the latter linear. The transition between these two conditions is placed around a depth of about 1.5 m.
The applicability of the conceptual model becomes clearer from Figure 5b where the collinearity curve is taken as an example. The curve subdivides the plane into two zones: the lower represents conditions for which depths tend to deepen; the upper one indicates depths which can be considered dynamically stable or under a depositional trend if sediment supply is available. This latter condition, for which the bed tends to fill up, can go on until it reaches the limit depth on the curve, given the current speed value Uc*. Therefore, the continuous arrows direction shows the tendency of the flat bed to deepen, while the dotted arrows suggest the depth can be reduced by a potential deposition.
This procedure has been performed by computing the total bed shear stress for different wind speeds and comparing it with some values of the erosion critical shear stress, among those proposed in literature [63,64,65,66]. In this manner, many curves representative of the limit depths between erosion conditions and not, have been obtained. In all these cases, the three angles of 0°, 45° and 90° between waves and current directions have been analyzed.
Figure 6 shows the results for a critical shear stress equal to 0.7 Pa and a wind speed respectively of 8 m/s and 12 m/s.
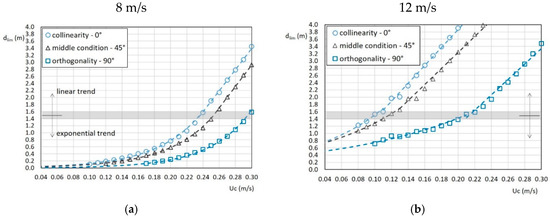
Figure 6.
Water depth d corresponding to the maximum bed shear stress equal to the critical threshold of 0.7 Pa obtained for different values of the current velocity Uc and angles between the wave motion and the flow direction. The wave field is generated by a wind speed of (a) 8 m/s and (b) 12 m/s. The dashed lines are regression curves.
Both the wind speeds of 6 m/s and 14 m/s cannot be considered representative for a morphological evolution over a medium-long period, the former being too low while the latter is quite high but rare.
As shown by the grey band, the exponential trends for depths lower than about 1.5 m and the linear ones for greater values are confirmed, suggesting substantial independence from the wind conditions, at least among those examined.
The regression curves can be expressed in a dimensional form by the following equations:
dlim_exp and dlim_lin being respectively the limit depth given by the exponential and the linear trends, for which the relative coefficients Ai and Bi with i = 1, 2 can be computed by means of the least squares method.
These dimensional equations provide a quantitative estimate of the limit depth for a critical shear stress of 0.7 Pa and for the analysed wind speeds. In Table 2 the values of the coefficients for the different cases are summarized.

Table 2.
Summary of the parameters entering in the Equations (6) and (7) for the specified wind speed and angles between the flow direction and the wave motion.
Both the exponential and the linear trends are also found if the critical erosion shear stress is left as varying while the wind speed remains set equal to 10 m/s. This substantial independence also from the erosion threshold, as well as from the wind speed, corroborates the general validity of the approach.
The results are presented in two forms as discussed below. The curves indicated as “actual” in Figure 7(a1,b1,c1) refer to water depths derived by imposing the maximum bed shear stress equal to different critical thresholds, here taken from 0.5 Pa up to 1.0 Pa.
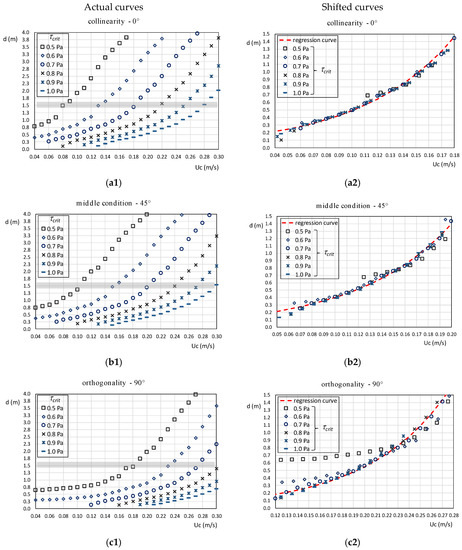
Figure 7.
Water depth d corresponding to the maximum bed shear stress equal to different critical thresholds and current velocities Uc. The wave field is generated by a wind speed of 10 m/s. The angles between the wave motion and the flow direction are specified above each graph. (a1) Original curves in the condition of collinearity; (a2) shifted curves in the condition of collinearity; (b1) original curves in the middle condition; (b2) shifted curves in the middle condition; (c1) original curves in the condition of orthogonality; (c2) shifted curves in the condition of orthogonality.
Observing the arrangement of these curves, it is noted that they can be horizontally shifted towards each other until an almost perfect overlapping is obtained as shown in Figure 7(a2,b2,c2), with the exception of the orthogonal configuration for which there are some discrepancies. These curves are indicated as “shifted”.
The amount by which the curves are shifted can be related to the corresponding value of the critical shear stress. These quantities have therefore been fit through polynomial curves in order to provide a general equation that can give a quantitative estimate of the limit depth of erosion for a tidal flat inside shallow lagoons, if the current velocity and the erosion threshold are known.
By limiting the analysis only to the exponential component, the limit depth can be so expressed as:
C, D and E being the coefficients deriving from the polynomial regression, the values of which are reported in Table 3 depending on the angle between the wave rays and the flow direction.

Table 3.
Summary of the parameters within the Equations (8) for the specified wind speed and angle between the flow direction and the wave motion.
To test the applicability of the present conceptual model to a real context, the Marano and Grado lagoon is taken as a case study, since the topographical differences of various portions of its tidal flats, evaluated over a period of 45 years, are available. The 1964 hydrographic map edited by the Magistrato alle Acque of Venice [71] has been compared to the more recent bathymetric data surveyed in 2009 [72], making it possible to carry out morphological evaluations over the long term.
4. Study Site
The Marano and Grado lagoon is depicted in Figure 8. Together with the Venice lagoon, it is one of the two most important coastal systems in the North East of Italy and is located between the low Friuli Venezia Giulia plain and the Northern Adriatic Sea.
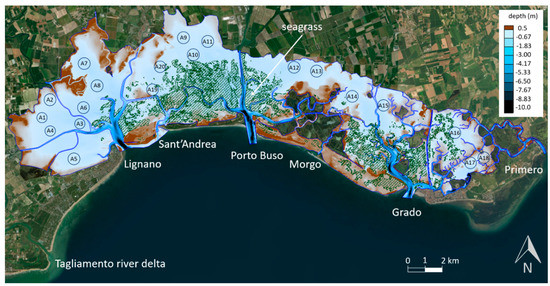
Figure 8.
Marano and Grado lagoon, Italy. The six tidal inlets, the main channels and the seagrass distribution are highlighted. The contour refers to the more recent bathymetric data surveyed in 2009. Circles represent tidal flats that have been considered for the application of the developed conceptual model.
Its extension roughly covers an area of 160 km2 and it is bordered by the delta systems of the two main rivers that cross Friuli Venezia Giulia: the Tagliamento on the west and the Isonzo on the east. On the sea side, the lagoon area is bounded by a series of barrier islands alternating with six tidal inlets. The shoreline develops from the western tidal inlet of Lignano to the eastern inlet of Primero for an overall length of about 32 km.
Petti et al. [51] have recently investigated the sediment transport processes of the Marano and Grado lagoon over an annual period, by means of a morphodynamic spectral coupled model. This study required the analyses of a large amount of wind and tide data to define a representative sequence of waves and water levels. The mean tidal range, given by the difference between the mean high water level (MHWL) and the mean low water level (MLWL) is about 0.76 m as resulting from the zero-crossing technique, carried out over 24 years of recording of the Grado tide gauge [51]. The mean range increases up to about 1.05 m during the spring tides and it is reduced to 0.22 m in the neap tides [20,73]. The annual average tidal signal, depicted in Figure 9, consists of three main astronomical components, the two principal semidiurnal, solar and lunar, and the lunar diurnal. It has a resultant periodicity of 12.5 days and is consistent with the tidal ranges specified above [51].
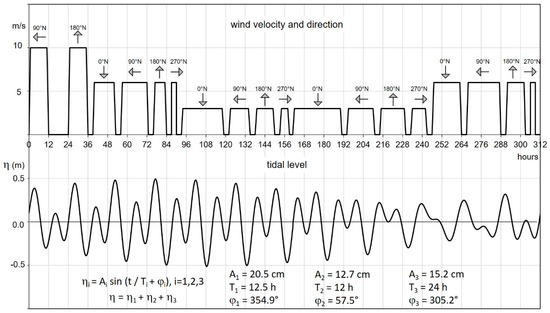
Figure 9.
Representative sequence of winds and water levels acting over an annual period, as deduced from data collected inside the Marano and Grado lagoon and subsequent analyses [51]. The tidal level variation is the sum of three main harmonic components which are defined by the respective amplitude Ai, period Ti and phase φi.
In order to derive also an annual average anemometric characterization, the extensive field of wind data collected inside the lagoon area has been subdivided into appropriate classes. These classes, of both wind speed and direction, have been combined with the tide sequence as shown in Figure 9. The so determined hydrodynamic conditions have been used to perform the morphodynamic numerical simulations of the lagoon bottom evolution over a period of an average year.
The comparison between the final and initial bed levels confirms that the interaction between tidal currents and waves governs the sediment transport mechanism inside the entire lagoon area. In particular, the most of the erosion areas are concentrated precisely on the tidal flats and near the saltmarshes, due to the shallower depths. The wind speed of 10 m/s, corresponding to the 90th percentile value as deduced from the duration curve, contributes significantly to cohesive sediment resuspension from tidal flats. The following transport inside internal channels provides 75% of their annual filling, as deduced from the simulated deposited volumes [51]. These results are in agreement with the flattening trend of the bottom topography which has been observed in the last decades with a net loss of fine sediments and saltmarshes surface [20].
The tidal flat composition is prevalently characterized by fine and cohesive sediments, even if sand content progressively increases towards the tidal inlets. An extended vegetal cover by seagrass is present in the central lagoon [74], and in the eastern portion along the main channel departing from the Grado inlet, as depicted in Figure 8. Seagrass has an important stabilizing effect on sediment resuspension from the bottom, as roots increase the critical erosion shear stress that can reach quite considerable values [63], while vegetation biomass favors mineral sediment trapping and promotes belowground organic production [36]. Moreover, the presence of vegetation can greatly affect the hydrodynamic field, decreasing both wave heights and current velocities, and consequently the corresponding bed shear stress.
On the contrary, some areas in the two extreme lateral portion of the lagoon, respectively on the west and east sides, are characterized by a greater mobility of the cohesive sediments due to several factors, among them shellfish farming. Trawl nets and dredges produce disturbances which lead to sediment resuspension comparable to that induced by the wave motion during storm conditions [75,76]. The different resistance degree of the bed to erosion has been taken into account in the morphodynamic modelling, setting a spatially variable critical threshold by the comparison with the morphologies of the Venice lagoon, for which measured values are available.
On the basis of these considerations, twenty tidal flats picked out in Figure 8 by the circles and an identification number have been chosen as test cases for the developed conceptual model. Their arrangement is as distributed as possible throughout the overall lagoon area, except for the portion covered by seagrass as it deeply affects the morphodynamic balance, which therefore cannot be considered representative for a medium-long period evolution.
5. Results
The morphological evolution of the Marano and Grado lagoon in 45 years can be shown by the comparison between two different hypsometric distributions. These curves have been obtained respectively from the digitalized and reconstructed bathymetry from 1964 and the one deriving from the more recent survey of 2009. The area subtended by the curve up to a given depth represents the percentage of the lagoon surface that was at a greater or equal depth. The shifting between the two curves reported in Figure 10a, underlines the deepening trend of the lagoon with a loss of area at depths shallower than 0.8 m compared to a consistent increase of greater depths from 0.9 m up to about 1.7 m.
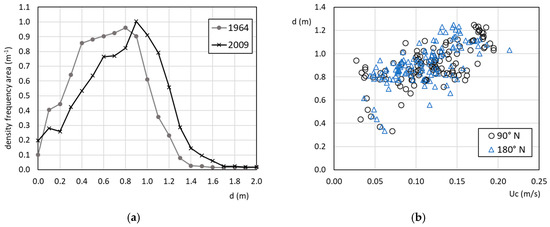
Figure 10.
(a) Density frequency area distributions as a function of bottom elevation d obtained from the two available bathymetries respectively in 1964 and 2009. Depth accuracy is about 0.05 m [20,71,72]. (b) Characterization of the points taken inside the selected areas in term of maximum current velocities Uc during wind events of 10 m/s blowing from respectively 90° N and 180° N, and actual depth d.
The peak of the tidal flat distributions has remained fairly constant, moving in the small range of 0.8–0.9 m, which in fact characterizes the average depth of the greatest number of points taken as samples in the selected areas. Nowadays, more than 80% of the lagoon area is represented by tidal flats up to 2 m deep, while only the tidal channels are deeper, and occupy 5% of the global area. In detail, only 25% of the tidal flats are shallower than 0.5 m and the remaining part is subtidal, confined up to 1.5 m, rarely reaching 2.0 m. In the western and the central part of the lagoon, tidal flats extend as intertidal talus of the fringing salt marshes and gently deepen up to becoming subtidal, towards the secondary channels; flat beds around the bifurcation between main and secondary channels, as in Lignano and Porto Buso, are always subtidal. In the eastern part of the lagoon, influenced by the Grado inlet, tidal flats are variably distributed according to the complex morphological systems, consisting of saltmarshes, islands, fish farms and channels.
In order to apply the new conceptual model, the hydrodynamic conditions are needed for each of the analyzed points, taken as samples in the selected areas. In particular, the model requires the representative current velocity value, its vector composition with the wind direction and the critical erosion shear stress. These features have been deduced from the morphodynamic application of Petti et al. [51]. As the current magnitude varies during a tidal cycle, the maximum value simulated during wind events of 10 m/s blowing from respectively 90° N and 180° N has been chosen, according to other applications in similar contexts [5,40,55]. These values are plotted in Figure 10b together with the corresponding depth, and they are all less than 0.25 m/s. This result confirms the choices made in the development of the model. The list of the preliminary parameters necessary for the use of the conceptual model within each area is shown in Table 4.

Table 4.
The list of the preliminary parameters for the conceptual model within each area, referring to the wind condition which leads to the maximum value of the bed shear stress.
They refer to the wind and current conditions which lead to the maximum value of the bed shear stress and they are obtained as average values on the set of selected points.
The wave-current angle has been established according to the wind direction and that of the tidal flow at the maximum velocity instant and it has been associated with one of the three examined configurations of 0°, 45° or 90°. Given that the orthogonality between waves and current leads to much lower values of bed shear stress compared to the other two configurations, it does not figure among the chosen settings.
Most areas are characterized by a critical shear stress of 0.7 Pa with the exception of the tidal flats belonging to A4 and A5 located in the western portion and to A16–A18 in the eastern part of the lagoon, which have a shear stress of 0.5 Pa, as justified above.
Both the wind directions contribute to the morphological evolution of the lagoon, and not only the direction that maximizes the fetch length or that is collinear with the current field, as is usually assumed in similar studies [48,49]. These particular features depend on the generation process of wind waves in shallow and confined waters and on the bi-dimensional nature of the flow field. In light of this, it is important to consider an omnidirectional distribution of winds [51] and also to check the vector composition in relation to the current, as the present conceptual model allows us to do.
The summarized data can be combined through the Equation (8), taking into account the different parameters specified in Table 3 according to the wave-current configuration. The conceptual model provides the limit depth between the erosion state and the no-erosion state, as highlighted in Figure 5b. In this way, it is possible to compare the conceptual erosion state with the measured one, making it possible to validate the model. The results are reported in Table 5.

Table 5.
Validation of the conceptual model. Symbol x is used when the difference between the depths are negative, suggesting an erosion state. The compared depths are those measured in 1964 (d1964) and 2009 (d2009) and the limit depth (dlim) provided by the conceptual model.
The measured erosion state can be defined by the comparison between the 1964 and the 2009 depths, respectively indicated as d1964 and d2009. If the difference d1964 − d2009 is negative, an erosion trend will have been verified over the 45 years. The limit depths provided by the conceptual model have been compared to both the measured depth in 1964 and that surveyed in 2009. Similarly, a negative difference d1964 − dlim means that a deepening trend should have happened over the 45 years, while the difference d2009 − dlim suggests if the depth measured in 2009 is still under an erosion trend or not. In all these cases, the symbol “x” is used to identify an erosion condition.
The agreement between the measured erosion states and those predicted by the conceptual model is substantial over almost all the selected areas, referring to both the erosion trend or not. This correspondence corroborates and validates the described procedure and the determined analytical solution making it therefore suitable to predict the medium-long term morphological evolution of tidal flats in sheltered coastal environments.
It is noticeable that the stable areas are all located along the northern internal edge of the lagoon, and they are characterized by an average depth close to the interval of 0.8–0.9 m, which effectively corresponds to the peaks of density frequency area distributions in Figure 10a. At the same time the current velocities do not exceed 0.13 m/s, which is a rather low value, thus ensuring both dynamic stability and the possibility for sediments to be deposited if available. Zones A12 and A13 are an exception because, despite having the same bottom resistance, the erosion processes are triggered by higher current velocities. The southern portion of the lagoon is characterized by the presence of fishing valleys which are bounded by embankments and for this reason hydraulically impermeable. This condition produces an effect similar to that of a cross-section narrowing on the flow between the eastern and the western part of the lagoon, with a consequent increasing of current velocities near the zones A12 and A13.
In the western part of the lagoon area connected to the Lignano inlet, an important deepening of the seabed toward depths approaching 1.5 m can be recognized. In particular, tidal flats A3, A6 and A8 are close to main channels characterized by higher values of depth and current velocities, while A4 and A5 are concession areas for shellfish farming since 2006. This intended use can make the bottom more exposed to erosive mechanisms, due to the destabilization of sediment structures by fishing gear, which cause an increased likelihood of renewed suspension during natural storms [75,76]. The mismatch between the measured and theoretical state for the tidal flat A5 can be ascribed to its less intensive use, which therefore does not significantly alter the critical shear stress. In fact, if a 0.7 Pa is taken as threshold, the resulting limit depth would be equal to 0.91 m which is much closer to the real depth.
Also the tidal flats in the eastern lagoon area tend to reach a depth of around 0.8–0.9 m, but on the contrary in this case there is a significant erosive tendency with respect to the bathymetric data of 1964. This condition happens even though the Primero basin is sheltered, with very small extensions on all the directions and shallower depths than the rest of the lagoon, leading to limited wave field and a maximum current velocities range which does not exceed 0.06 m/s, as can be seen from Table 4. This case represents an example of how important it is to consider the strong interaction between local wind waves and current, whose respective low values are sufficient, only if taken together, to overcome the bed resistance.
Two of the examined areas, A14 and A20, located in the central area outside the surface covered by seagrass, have deepened over time, despite the conceptual model missing this trend, providing limit depths very similar to the original ones. The reason can be sought in a different bottom critical shear stress or hydrodynamic condition, since area A20 is close to a channel that over time has been filled and has disappeared.
6. Discussion
The considerations and results presented in the previous section corroborate the procedure followed to define the conceptual model. The proposed approach is able to adequately address the question of estimating a limit depth for the morphological evolution of tidal flats, and it can suggest if they undergo an erosion trend or not over a medium-long period.
The model can be applied to shallow and confined basins, such as the coastal lagoon taken as a case study; in these contexts, tidal flats are characterized by a very small slope and they can be considered sufficiently uniform in depth. Their depth variation is related to the distribution of the total bed shear stress resulting from the complex interaction between currents and local wind waves. A methodology widely used to investigate the hydrodynamic and morphodynamic processes, consists in applying a dedicated numerical modelling. In particular, this is usually done by coupling different modules, as in the study of Petti et al. [51]: a hydrodynamic model to reproduce the flow field, a wind wave model, and a morphodynamic model to compute the bed evolution. This approach is certainly more complete because it takes into account the variability of the phenomena both on the vertical section and on the horizontal plane. However, it requires great computational effort especially in very large domains, and it needs proper calibration and validation processes to be performed. Moreover, from a morphodynamic point of view, it is possible to provide an estimation of the evolution trend only for reduced time scales, at most an annual period or just over.
In order to predict tidal flats morphology for medium-long periods, such as the 45 years considered in the analyzed case study, more simplified approaches are needed. This is the focus of many analytical methods and theories, developed around the dynamic equilibrium of the cross-shore profile shapes, as reported in the introduction. The present model starts from similar assumptions but it provides a quantitative estimation in the morphological evolution of tidal flats, and not only a qualitative one as in the dynamic model by Friedrichs and Aubrey [38]. Moreover, it extends the study proposed by Fagherazzi et al. [47], considering the variability of the wind speed and the current velocity, and also adding their vector composition through the angle φ. In this sense, the conceptual model takes into account the effects on the bottom shear stress induced by the interaction between waves and current velocities on the horizontal plane. Recent outcomes for the generation process in shallow water show that it is deeply affected by the role played by bed roughness and the variability of the wave period [45,50]. The consequence is an important reduction in the main wave parameters, above all in the wave orbital velocity and in the resulting wave bottom shear stress which tends to assume low values, especially on the tidal flat shallow depths. In the present model, the evaluation of the total maximum bed shear stress takes into account all of these issues.
The wind speed, the current velocity, the angle between their directions and the critical erosion shear stress are required as input values by the model. These parameters can be quite easily deduced from direct measurements, literature suggestions or as results from more simplified numerical modeling. More details about the choice of these parameters are given below.
Wave motion is undoubtedly the dominant factor in tidal flats evolution, because the wave-induced bed shear stress is often the main factor that controls the suspended-sediment concentration [7]. However, current velocity cannot be neglected as it can drag and move away sediments, which would otherwise only be resuspended. To evaluate erosion mechanisms over the medium-long period, it is important to choose morphologically representative values of both wind speed and current velocity to be used in the conceptual model, similarly to Fagherazzi et al. [47].
In particular, the required values should account for both the characteristic magnitude of the hydrodynamic forcing as well as the duration in which this forcing is strong enough [29]. The astronomical tide component does not vary significantly in time, giving a current field that periodically repeats alternating flood and ebb phases. In this sense, the tidal velocity oscillates from a minimum to a maximum value over every cycle. On the other hand, the wave motion is strongly linked to wind speed and its frequency, i.e., lower but more frequent wind speeds generate a weak wave motion, as opposed to stronger but extreme events. A useful scale widely adopted for evaluating coastal morphologies [5,30] is the 90th percentile velocity, in analogy to the procedure followed in the application to the case study of the Marano and Grado lagoon.
Generally, the tidal flow direction is linked to level changes inside the basin and to the tidal channel geometry, while the wave direction can be taken substantially coincident to that of the wind, as only sheltered environments and locally generated waves are herein considered. These evidences suggest the proper angle between current velocities and waves to be set.
The last input parameter is the critical threshold of bed resistance, which is a key factor to interpreting the morphological evolution of tidal flats. In fact, erosion processes are triggered when the resultant bed shear stress exceeds the critical erosion shear stress [45,46]. However, this important parameter does not have a unique definition in literature, because it can take on very different values within a wide range both from a spatial and a temporal point of view [63,64]. In this sense, it is the most sensitive parameter which can also lead to quite important differences in the results provided by the conceptual model, as can be observed in Figure 7.
Equation (8), which is derived from the depicted curves, represents the main outcome of the conceptual model and its validity is general if within the limits recommended for its application, i.e., shallow depths and confined environments. The investigated ranges of both tidal flat depths and current velocities are in fact quite short and they are compatible with the typical values of many shallow lagoons. This is the case for example of the lagoons cited in the present paper [46,47,51,55], which have all been the subject of morphodynamic studies to understand the relative role of waves and current motion. In these contexts, the average depth of tidal flats is around 1 m where current velocities are rather low and within the range 0.1–0.3 m/s.
Furthermore, the equation is the result of the regression of the points below the grey band that establishes the upper limit of the exponential part, as outlined in Figure 5, Figure 6 and Figure 7. This band indicates a different relationship between the limit depth and the maximum bed shear stress and it can reflect the prevailing of waves or current in the erosion mechanism. In particular, for intermediate wind speeds both wind waves and tidal currents are relevant in the erosive process on shallow depths, even if the major role is however played by the wave motion, as the current velocities are quite low. Depths greater than about a few meters are reached only inside the lagoon channels where the flow is more concentrated and it is able to engrave the seabed. In these conditions, where the hydrodynamics are more energetic, the current is certainly the dominant forcing, but for this reason they are not suitable for the conceptual model.
A further consideration concerns the dynamic equilibrium, which is defined as the balance condition between erosion and deposition, so that no net sediment transport occurs. If the erosion mechanism is relatively simple to define by comparing it with the critical stress for sediment resuspension, this is not the same for the deposition process. In fact, this latter term is associated not only with a relative shear stress, but also with the sediments supply, which can have a strong variability both over time and in space [63,64]. For these reasons and given the complexity and the uncertainty in quantifying the deposition rate, the herein presented conceptual model does not distinguish a morphologically stable condition from a deposition one.
7. Conclusions
In this paper a new simple conceptual model has been proposed in order to investigate the dynamic equilibrium of a tidal flat over a medium-long period. The theoretical approach provides a quantitative estimation of a limit depth, which separates an erosion condition from a no-erosion condition for tidal flats in sheltered basins. These contexts are generally characterized by shallow and quite flat bottoms, continuously reshaped by the currents deriving from the periodic sea water level variations, and the local wind waves. In particular, the wave field is deeply affected by bottom friction dissipations, differently from the offshore generation process, leading to much lower bed shear stress.
In this sense, the contribution of the tidal current becomes fundamental in triggering the erosion processes and the subsequent transport of sediments, until the limit depth, for which this mechanism stops, is reached. If deposition and sediment supply are not considered, this limit depth corresponds to the condition that makes the assigned erosion threshold equal to the maximum shear stress resulting from the interaction between waves and current.
The limit depth is expressed by means of a dimensional equation which requires as input the values of the critical shear stress, the current velocity and the angle between the flow and the wind direction. This equation is related to an assigned wind speed and it gives an exponential trend of the limit depth at varying current velocity, up to depth values of about 1.5 m. For values greater than this, the dependence becomes linear and it involves current velocities higher than 0.2–0.3 m/s, that exceed the range considered in the development of the present conceptual model. In this sense, its application is suitable to provide a realistic estimation of the limit depth for the morphological evolution of a tidal flats belonging to shallow and limited-fetch environments.
It has been furthermore verified that the vector composition of the current flow in relation to the wave rays can deeply affect the erosion mechanism, configuring itself as an important additional variable that must be taken into account. To this purpose, three angle configurations between the waves and the current direction have been considered: collinearity, orthogonality and a middle condition. In particular, this last case which considers a generic angle of 45° does not actually lead to a condition so different from the collinear case, while the curve of the limit depth tends to significantly decrease if orthogonality is realized.
To validate the conceptual model, its application to a real context has been performed. The Marano and Grado lagoon has been taken as a case study, starting from hydrodynamic data deriving from a previous numerical modeling and two bathymetries surveyed 45 years apart. The comparison between the measured erosion states and the ones theoretically predicted, gives encouraging results in support of the usefulness of this new conceptual model. As a next step, the authors plan to determine the analytical expression of the limit erosion depth for a tidal flat, in a dimensionless form, to generalize its applicability as far as possible.
Author Contributions
M.P., S.P. and S.B. have conceived and developed the conceptual model. M.P., S.P., S.B., A.B. and G.F. have performed the application of the conceptual model to the case study.
Funding
This research has been carried out with the financial support by the partnership agreement “Studio di assetto morfologico ambientale della laguna di Marano e Grado” among the Regione Autonoma Friuli Venezia Giulia, The University of Udine and the University of Trieste.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fan, D.; Wang, Y.; Liu, M. Classifications, sedimentary features and facies associations of tidal flats. J. Palaeogeogr. 2013, 2, 66–80. [Google Scholar] [CrossRef]
- Dalrymple, R.W.; Choi, K. Morphologic and facies trends through the fluvial–marine transition in tide-dominated depositional systems: A schematic framework for environmental and sequence-stratigraphic interpretation. Earth-Sci. Rev. 2007, 81, 135–174. [Google Scholar] [CrossRef]
- Le Hir, P.; Roberts, W.; Cazaillet, O.; Christie, M.; Bassoullet, P.; Bacher, C. Characterization of intertidal flat hydrodynamics. Cont. Shelf Res. 2000, 20, 1433–1459. [Google Scholar] [CrossRef]
- Roberts, W.; Le Hir, P.; Whitehouse, R.J.S. Investigation using simple mathematical models of the effect of tidal currents and waves on the profile shape of intertidal mudflats. Cont. Shelf Res. 2000, 20, 1079–1097. [Google Scholar] [CrossRef]
- Friedrichs, C.L. Tidal flat morphodynamics: A synthesis. In Treatise on Estuarine and Coastal Science, Estuarine and Coastal Geology and Geomorphology; Hansom, J.D., Fleming, B.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 3, pp. 137–170. [Google Scholar]
- Coco, G.; Zhou, Z.; van Maanen, B.; Olabarrieta, M.; Tinoco, R.; Townend, I. Morphodynamics of tidal networks: Advances and challenges. Mar. Geol. 2013, 346, 1–16. [Google Scholar] [CrossRef]
- Green, M.O.; Coco, G. Review of wave-driven sediment resuspension and transport in estuaries. Rev. Geophys. 2014, 52, 77–117. [Google Scholar] [CrossRef]
- Zhou, Z.; Coco, G.; van der Wegen, M.; Gong, Z.; Zhang, C.; Townend, I. Modeling sorting dynamics of cohesive and non-cohesive sediments on intertidal flats under the effect of tides and wind waves. Cont. Shelf Res. 2015, 104, 76–91. [Google Scholar] [CrossRef]
- Zhu, Q.; van Prooijen, B.C.; Wang, Z.B.; Yang, S.L. Bed-level changes on intertidal wetland in response to waves and tides: A case study from the Yangtze River Delta. Mar. Geol. 2017, 385, 160–172. [Google Scholar] [CrossRef]
- Corenblit, D.; Baas, A.C.W.; Bornette, G.; Darrozes, J.; Delmotte, S.; Francis, R.A.; Gurnell, A.M.; Julien, F.; Naiman, R.J.; Steiger, J. Feedbacks between geomorphology and biota controlling Earth surface processes and landforms: A review of foundation concepts and current understandings. Earth-Sci. Rev. 2011, 106, 307–331. [Google Scholar] [CrossRef]
- Murray, A.B.; Knaapen, M.A.F.; Tal, M.; Kirwan, M.L. Biomorphodynamics: Physical-biological feedbacks that shape landscapes. Water Resour. Res. 2008, 44, W11301. [Google Scholar] [CrossRef]
- Wang, Z.B.; Van Maren, D.S.; Ding, P.X.; Yang, S.L.; Van Prooijen, B.C.; De Vet, P.L.M.; Winterwerp, J.C.; De Vriend, H.J.; Stive, M.J.F.; He, Q. Human impacts on morphodynamic thresholds in estuarine systems. Cont. Shelf Res. 2015, 111, 174–183. [Google Scholar] [CrossRef]
- De Vet, P.L.M.; van Prooijen, B.C.; Wang, Z.B. The differences in morphological development between the intertidal flats of the Eastern and Western Scheldt. Geomorphology 2017, 281, 31–42. [Google Scholar] [CrossRef]
- Dyer, K.R.; Christie, M.C.; Wright, E.W. The classification of intertidal mudflats. Cont. Shelf Res. 2000, 20, 1039–1060. [Google Scholar] [CrossRef]
- Kirby, R. Practical implications of tidal flat shape. Cont. Shelf Res. 2000, 20, 1061–1077. [Google Scholar] [CrossRef]
- Van Maren, D.S.; Winterwerp, J.C. The role of flow asymmetry and mud properties on tidal flat sedimentation. Cont. Shelf Res. 2013, 60, S71–S84. [Google Scholar] [CrossRef]
- Maan, D.C.; Prooijen, B.C.; Wang, Z.B.; De Vriend, H.J. Do intertidal flats ever reach equilibrium? J. Geophys. Res. Earth Surf. 2015, 120, 2406–2436. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Morphological evolution of the Venice lagoon: Evidence from the past and trend for the future. J. Geophys. Res. 2009, 114, F04002. [Google Scholar] [CrossRef]
- Sarretta, A.; Pillon, S.; Molinaroli, E.; Guerzoni, S.; Fontolan, G. Sediment budget in the Lagoon of Venice, Italy. Cont. Shelf Res. 2010, 8, 934–949. [Google Scholar] [CrossRef]
- Fontolan, G.; Pillon, S.; Bezzi, A.; Villalta, R.; Lipizer, M.; Triches, A.; D’Aietti, A. Human impact and the historical transformation of saltmarshes in the Marano and Grado Lagoon, northern Adriatic Sea. Estuar. Coast. Shelf Sci. 2012, 113, 41–56. [Google Scholar] [CrossRef]
- Wang, C.; Temmerman, S. Does biogeomorphic feedback lead to abrupt shifts between alternative landscape states?: An empirical study on intertidal flats and marshes. J. Geophys. Res. Earth Surf. 2013, 118, 229–240. [Google Scholar] [CrossRef]
- De Sanjosé Blasco, J.J.; Gómez-Lende, M.; Sánchez-Fernández, M.; Serrano-Cañadas, E. Monitoring Retreat of Coastal Sandy Systems Using Geomatics Techniques: Somo Beach (Cantabrian Coast, Spain, 1875–2017). Remote Sens. 2018, 10, 1500. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Jin, S.; Sun, C.; Wei, X. Evolution of the topography of tidal flats and sandbanks along the Jiangsu coast from 1973 to 2016 observed from satellites. ISPRS J. Photogramm. Remote Sens. 2019, 150, 27–43. [Google Scholar] [CrossRef]
- Belliard, J.P.; Silinski, A.; Meire, D.; Kolokythas, G.; Levy, Y.; Van Braeckel, A.; Bouma, T.J.; Temmerman, S. High-resolution bed level changes in relation to tidal and wave forcing on a narrow fringing macrotidal flat: Bridging intra-tidal, daily and seasonal sediment dynamics. Mar. Geol. 2019, 412, 123–138. [Google Scholar] [CrossRef]
- Christiansen, C.; Vølund, G.; Lund-Hansen, L.C.; Bartholdy, J. Wind influence on tidal flat sediment dynamics: Field investigations in the Ho Bugt, Danish Wadden Sea. Mar. Geol. 2006, 235, 75–86. [Google Scholar] [CrossRef]
- Hu, Z.; Yao, P.; van der Wal, D.; Bouma, T.J. Patterns and drivers of daily bed-level dynamics on two tidal flats with contrasting wave exposure. Sci. Rep. 2017, 7, 7088. [Google Scholar] [CrossRef]
- Shi, B.; Cooper, J.R.; Li, J.; Yang, Y.; Yang, S.L.; Luo, F.; Yu, Z.; Wang, Y.P. Hydrodynamics, erosion and accretion of intertidal mudflats in extremely shallow waters. J. Hydrol. 2019, 573, 31–39. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, Z.B.; Zitman, T.J.; Stive, M.J.F.; Bouma, T.J. Predicting long-term and short-term tidal flat morphodynamics using a dynamic equilibrium theory. J. Geophys. Res. Earth Surf. 2015, 120, 1803–1823. [Google Scholar] [CrossRef]
- Hu, Z.; van der Wal, D.; Cai, H.; van Belzen, J.; Bouma, T.J. Dynamic equilibrium behaviour observed on two contrasting tidal flats from daily monitoring of bed-level changes. Geomorphology 2018, 311, 114–126. [Google Scholar] [CrossRef]
- Zhou, Z.; Coco, G.; Townend, I.; Olabarrieta, M.; van der Wegen, M.; Gong, Z.; D’Alpaos, A.; Gao, S.; Jaffe, B.E.; Gelfenbaum, G.; et al. Is “Morphodynamic Equilibrium” an oxymoron? Earth-Sci. Rev. 2017, 165, 257–267. [Google Scholar] [CrossRef]
- Woodroffe, C.D. Coasts: Form, Process and Evolution; Cambridge University Press: Cambridge, UK, 2002; 640p. [Google Scholar]
- Fan, D.; Guo, Y.; Wang, P.; Shi, J.Z. Cross-shore variations in morphodynamic processes of an open-coast mudflat in the Changjiang Delta, China: With an emphasis on storm impacts. Cont. Shelf Res. 2006, 26, 517–538. [Google Scholar] [CrossRef]
- Green, M.O. Very small waves and associated sediment resuspension on an estuarine intertidal flat. Estuar. Coast. Shelf Sci. 2011, 93, 449–459. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Ma, Y. Intra-tidal sedimentary processes associated with combined wave–current action on an exposed, erosional mudflat, southeastern Yangtze River Delta, China. Mar. Geol. 2014, 347, 95–106. [Google Scholar] [CrossRef]
- Pritchard, D.; Hogg, A.J.; Roberts, W. Morphological modelling of intertidal mudflats: The role of cross-shore tidal currents. Cont. Shelf Res. 2002, 22, 1887–1895. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. A numerical model for the coupled long-term evolution of salt marshes and tidal flats. J. Geophys. Res. 2010, 115, F01004. [Google Scholar] [CrossRef]
- Hunt, S.; Bryan, K.R.; Mullarney, J.C. The influence of wind and waves on the existence of stable intertidal morphology in meso-tidal estuaries. Geomorphology 2015, 228, 158–174. [Google Scholar] [CrossRef]
- Friedrichs, C.T.; Aubrey, D.G. Uniform Bottom Shear Stress and Equilibrium Hyposometry of Intertidal Flats. In Coastal and Estuarine Studies; Pattiaratchi, C., Ed.; AGU: Washington, DC, USA, 1996; Volume 50, pp. 405–429. [Google Scholar]
- Pritchard, D.; Hogg, A.J. Cross-shore sediment transport and the equilibrium morphology of mudflats under tidal currents. J. Geophys. Res. 2003, 108, 3313. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. A two-point dynamic model for the coupled evolution of channels and tidal flats. J. Geophys. Res. Earth Surf. 2013, 118, 1387–1399. [Google Scholar] [CrossRef]
- Hsiao, S.V.; Shemdin, O.H. Bottom Dissipation in Finite-Depth Water Waves. Coast. Eng. 1978, 24, 434–448. [Google Scholar] [CrossRef]
- Vincent, C.L.; Hughes, S.A. Wind Wave Growth in Shallow Water. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 765–770. [Google Scholar] [CrossRef]
- Young, I.R.; Verhagen, L.A. The growth of fetch limited waves in water of finite depth. 1. Total energy and peak frequency. Coast. Eng. 1996, 29, 47–78. [Google Scholar] [CrossRef]
- Shi, B.; Cooper, J.R.; Pratolongo, P.D.; Gao, S.; Bouma, T.J.; Li, G.; Li, C.; Yang, S.L.; Wang, Y.P. Erosion and accretion on a mudflat: The importance of very shallow-water effects. J. Geophys. Res. Oceans 2017, 122, 9476–9499. [Google Scholar] [CrossRef]
- Pascolo, S.; Petti, M.; Bosa, S. On the Wave Bottom Shear Stress in Shallow Depths: The Role of Wave Period and Bed Roughness. Water 2018, 10, 1348. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. Wind waves on a mudflat: The influence of fetch and depth on bed shear stresses. Cont. Shelf Res. 2013, 60, S99–S110. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Carniello, L.; D’Alpaos, L.; Defina, A. Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes. Proc. Natl. Acad. Sci. USA 2006, 103, 8337–8341. [Google Scholar] [CrossRef] [PubMed]
- Fagherazzi, S.; Palermo, C.; Rulli, M.C.; Carniello, L.; Defina, A. Wind waves in shallow microtidal basins and the dynamic equilibrium of tidal flats. J. Geophys. Res. 2007, 112, F02024. [Google Scholar] [CrossRef]
- Defina, A.; Carniello, L.; Fagherazzi, S.; D’Alpaos, L. Self-organization of shallow basins in tidal flats and salt marshes. J. Geophys. Res. 2007, 112, F03001. [Google Scholar] [CrossRef]
- Pascolo, S.; Petti, M.; Bosa, S. Wave–Current Interaction: A 2DH Model for Turbulent Jet and Bottom-Friction Dissipation. Water 2018, 10, 392. [Google Scholar] [CrossRef]
- Petti, M.; Bosa, S.; Pascolo, S. Lagoon Sediment Dynamics: A Coupled Model to Study a Medium-Term Silting of Tidal Channels. Water 2018, 10, 569. [Google Scholar] [CrossRef]
- Allen, J.R.L.; Duffy, M.J. Medium-term sedimentation on high intertidal mudflats and salt marshes in the Severn Estuary, SW Britain: The role of wind and tide. Mar. Geol. 1998, 150, 1–27. [Google Scholar] [CrossRef]
- Cappucci, S.; Amos, C.L.; Hosoe, T.; Umgiesser, G. SLIM: A numerical model to evaluate the factors controlling the evolution of intertidal mudflats in Venice Lagoon, Italy. J. Mar. Syst. 2004, 51, 257–280. [Google Scholar] [CrossRef]
- Umgiesser, G.; Sclavo, M.; Carniel, S.; Bergamasco, A. Exploring the bottom shear stress variability in the Venice Lagoon. J. Mar. Syst. 2004, 51, 161–178. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Wiberg, P.L. Importance of wind conditions, fetch, and water levels on wave-generated shear stresses in shallow intertidal basins. J. Geophys. Res. 2009, 114, F03022. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Bouma, T.J.; Klaassen, P.; van der Wal, D.; Stive, M.J.F.; Herman, P.M.J. Hydrodynamic forcing on salt-marsh development: Distinguishing the relative importance of waves and tidal flows. Estuar. Coast. Shelf Sci. 2010, 89, 73–88. [Google Scholar] [CrossRef]
- Carniello, L.; Defina, A.; D’Alpaos, L. Modeling sand-mud transport induced by tidal currents and wind waves in shallow microtidal basins: Application to the Venice Lagoon (Italy). Estuar. Coast. Shelf Sci. 2012, 102, 105–115. [Google Scholar] [CrossRef]
- Shi, B.W.; Yang, S.L.; Wang, Y.P.; Bouma, T.J.; Zhu, Q. Relating accretion and erosion at an exposed tidal wetland to the bottom shear stress of combined current–wave action. Geomorphology 2012, 138, 380–389. [Google Scholar] [CrossRef]
- CERC. Shore Protection Manual; U.S. Army Coastal Engineering Research Center: Washington, DC, USA, 1984; Volume 1. [Google Scholar]
- Carniello, L.; D’Alpaos, A.; Defina, A. Modeling wind waves and tidal flows in shallow micro-tidal basins. Estuar. Coast. Shelf Sci. 2011, 92, 263–276. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I, Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Madsen, O.S.; Poon, Y.-K.; Graber, H.C. Spectral wave attenuation by bottom friction: Theory. In Proceedings of the 21th International Conference Coastal Engineering, ASCE, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 492–504. [Google Scholar]
- Amos, C.L.; Bergamasco, A.; Umgiesser, G.; Cappucci, S.; Cloutier, D.; Denat, L.; Flindt, M.; Bonardi, M.; Cristante, S. The stability of tidal flats in Venice Lagoon—The results of in-situ measurements using two benthic, annular flumes. J. Mar. Syst. 2004, 51, 211–241. [Google Scholar] [CrossRef]
- Amos, C.L.; Umgiesser, G.; Ferrarin, C.; Thompson, C.E.L.; Whitehouse, R.J.S.; Sutherland, T.F.; Bergamasco, A. The erosion rates of cohesive sediments in Venice lagoon, Italy. Cont. Shelf Res. 2010, 30, 859–870. [Google Scholar] [CrossRef]
- Soulsby, R.L. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford Publications: London, UK, 1997; p. 249. [Google Scholar]
- Whitehouse, R.J.S.; Soulsby, R.L.; Roberts, W.; Mitchener, H.J. Dynamics of Estuarine Muds; Technical Report; Thomas Telford: London, UK, 2000. [Google Scholar]
- Bosa, S.; Petti, M.; Pascolo, S. Numerical Modelling of Cohesive Bank Migration. Water 2018, 10, 961. [Google Scholar] [CrossRef]
- Cavaleri, L.; Rizzoli, P.M. Wind wave prediction in shallow water: Theory and applications. J. Geophys. Res. 1981, 86, 10961–10973. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Dorigo, L. La Carta Idrografica Della Laguna di Grado e Marano; Magistrato alle Acque-Ufficio Idrografico: Venezia, Italy, 1966. [Google Scholar]
- Triches, A.; Pillon, S.; Bezzi, A.; Lipizer, M.; Gordini, E.; Villalta, R.; Fontolan, G.; Menchini, G. Carta Batimetrica Della Laguna di Marano e Grado; Arti Grafiche Friulane; Imoco spa: Udine, Italy, 2011; p. 39. ISBN 978-88-95980-02-7. [Google Scholar]
- Dorigo, L. La Laguna di Grado e le sue Foci. Ricerche e Rilievi Idrograficil; Magistrato alle Acque-Ufficio Idrografico: Venezia, Italy, 1965. [Google Scholar]
- Boscutti, F.; Marcorin, I.; Sigura, M.; Bressan, E.; Tamberlich, F.; Vianello, A.; Casolo, V. Distribution modeling of seagrasses in brackish waters of Grado-Marano lagoon (Northern Adriatic Sea). Estuar. Coast. Shelf Sci. 2015, 164, 183–193. [Google Scholar] [CrossRef]
- Pranovi, F.; Da Ponte, F.; Raicevich, S.; Giovanardi, O. A multidisciplinary study of the immediate effects of mechanical clam harvesting in the Venice Lagoon. ICES J. Mar. Sci. 2004, 61, 43–52. [Google Scholar] [CrossRef]
- Black, K.; Parry, G. Entrainment, dispersal, and settlement of scallop dredge sediment plumes: Field measurements and numerical modelling. Can. J. Fish. Aquat. Sci. 2011, 56, 2271–2281. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).