A New Digital Lake Bathymetry Model Using the Step-Wise Water Recession Method to Generate 3D Lake Bathymetric Maps Based on DEMs
Abstract
1. Introduction
- Airborne observation: This method uses airborne gravity data to determine the lake bottom shape with the assumed density of sediment [11]. The advantage of this method is that it can generate the sediment layer due to the density variance; the disadvantage is the high cost of airborne equipment for large-scale observations [11].
- Passive imaging method: This method is widely applicable to shallow turbid water bodies by the different reflectances of different wave bands [12]. There are two main ways to establish the relationship between the depth and reflectance (i.e., the equation fitting method) [13] and the machine learning method, such as ANN (artificial neural network) [14]. However, a necessary condition for this method is that the water must be shallow enough; it does not work for large and deep lakes [15].
- Empirical equation methods: These methods establish a formula for estimating the average depth with the lake area based on a large number of real average-depth data to calibrate the parameters [16]. Some other method even takes more information into account such as surrounding average slope [1]. However, they cannot generate bathymetric maps or derive the volume-depth and area-depth curves for single lakes.
- Similar volume–area (V–A) curve method: This method is based on the regional similarity of volume–area relationships. The method chooses several similar valleys as virtual reservoirs and then simulates the process of water filling and regression. It may be successful for researching small mountainous lakes, but for medium and large lakes, similar valleys are always lacking [17].
- Lake bathymetric map simulation method: This method uses the surrounding digital elevation model (DEM) data to estimate the lake bottom shape. For example, Messager et al. tested a GIS-based method based on power functions in which the depth is derived as ((the distance from shore)^α × tan(slope)) using different values of the exponent α [1]. We reproduced this method and found that the model result cannot maintain continuity, which is the most challenging barrier in the model proposed in this study. We finally overcame this problem by proposing a water recession method (WRM).
- The area–elevation combined methods: These methods use optical satellite imagery such as Landsat [18] or MODIS [19,20] to derive lake-surface area series; meanwhile, they use satellite altimetry such as ICESat/GLAS and ENVISAT [18,19] to generate surface elevation. The area and surface elevation series are then combined to calculate relative lake volume estimates. These methods are widely acceptable since they are based on simple and direct mathematical logics. However, the lack and disconnection of lake level data from satellite altimetry is a key issue that limits the applications of the abovementioned methods [18,21]. Besides, these methods can achieve accurate results of relative lake volume rather than absolute volume or bathymetry.
- Other interpolating methods and derivative spline methods: These methods basically use the control points in the calculation area and the control conditions of boundaries to generate the whole bathymetric map for water bodies, such as Kriging [22] or spline interpolation [23]. There are many successful researches about rivers because of the regularity of the river bathymetry [24,25], and there are even some mature methods in ArcGIS tools [26], but the common point is that they need field survey results as input data. We admit the measured data is indispensable for high accurate research, and more uniform distribution of the input data will lead to more accurate results. However, in considering the big cost of large-scale in-situ data [5], it is still important to develop remote sensing methods without these data. This is also the starting point of our method.
2. Data and Model Development
2.1. Input Data
2.2. Assumptions
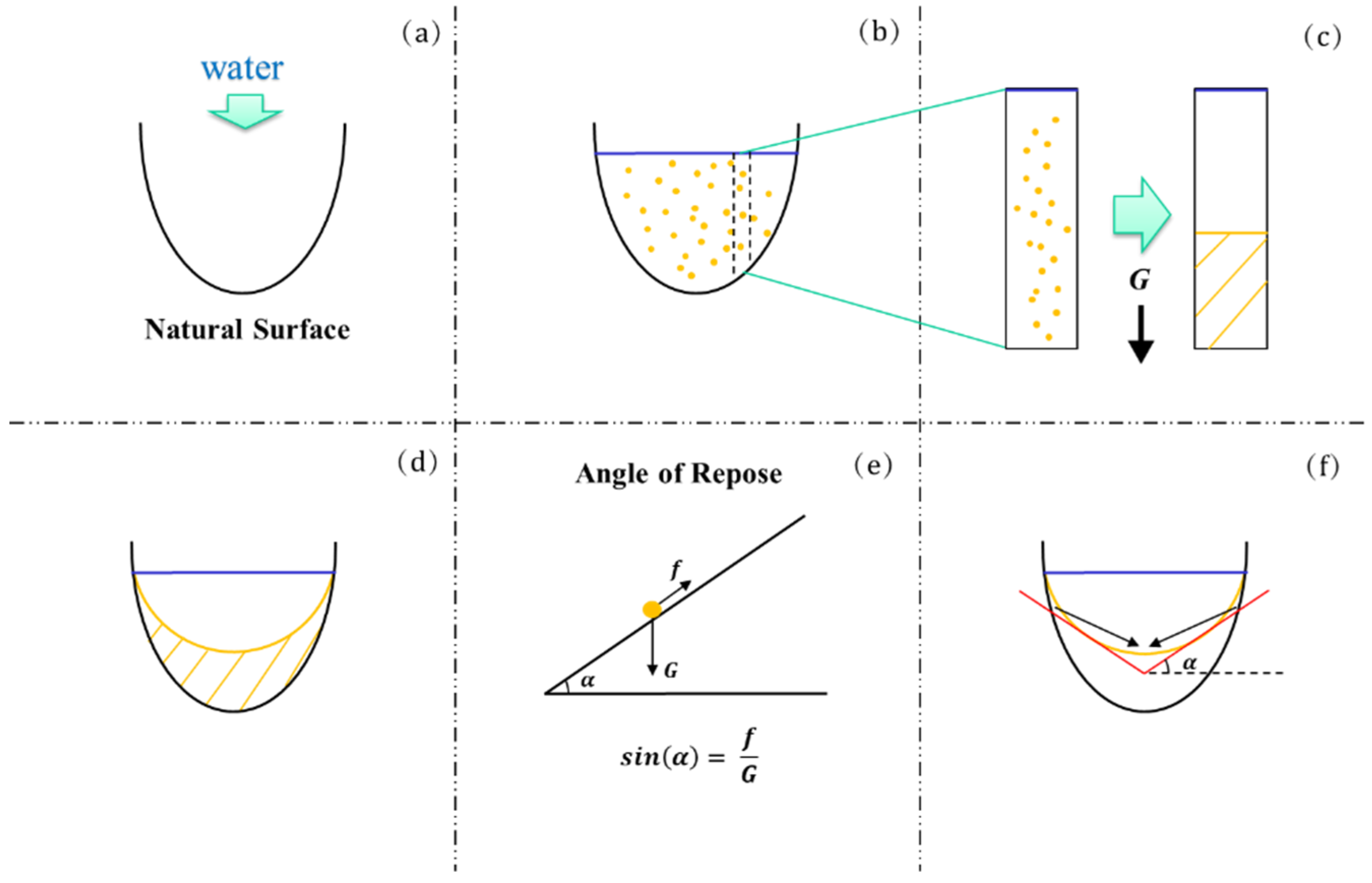
- The natural surface of the lake’s bathymetry is typically formed and shaped by geophysical processes similar to those that shaped its surrounding landmass.
- The agent rate of water is uniform throughout the whole lake.
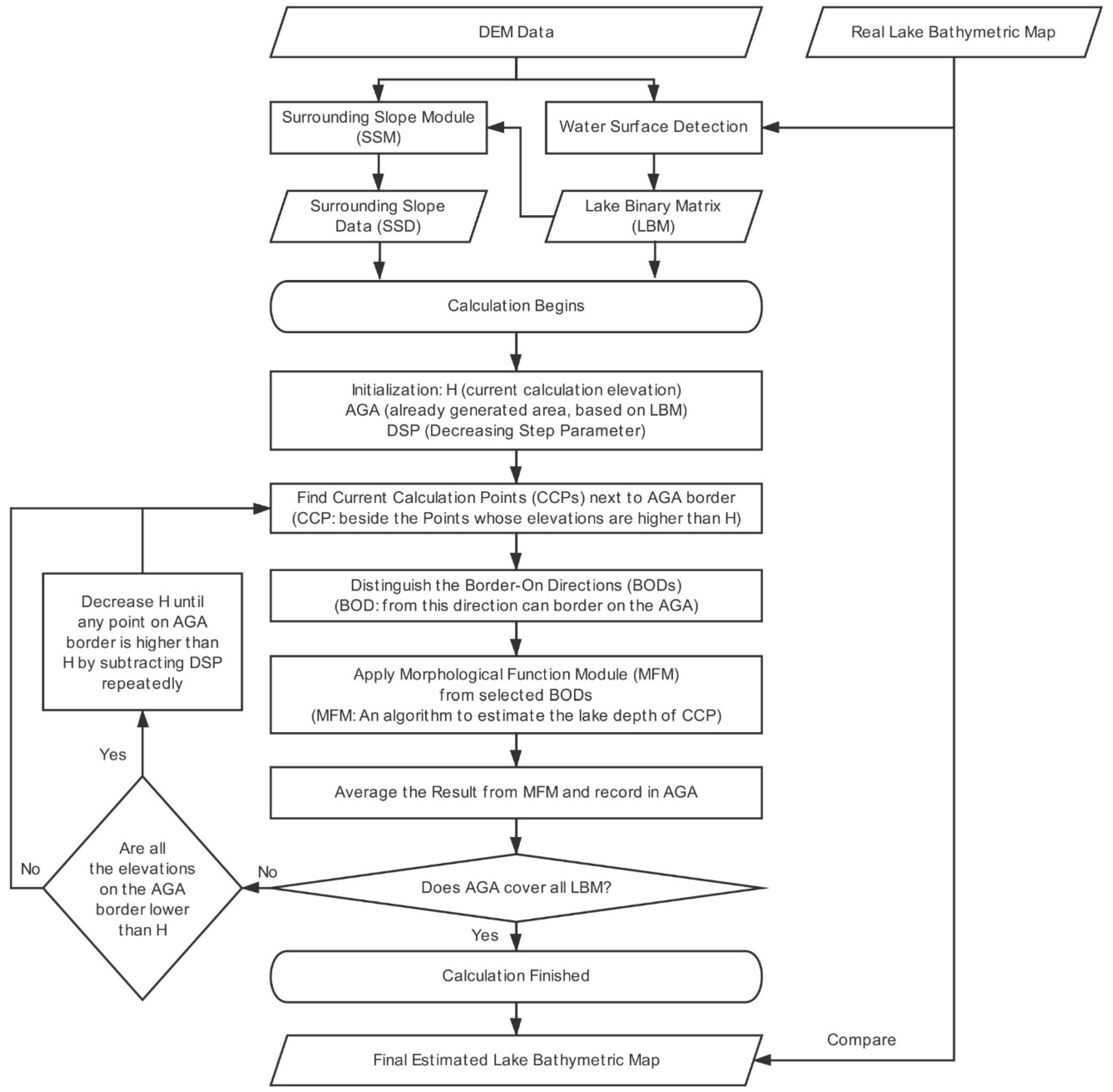
2.3. Model Procedure
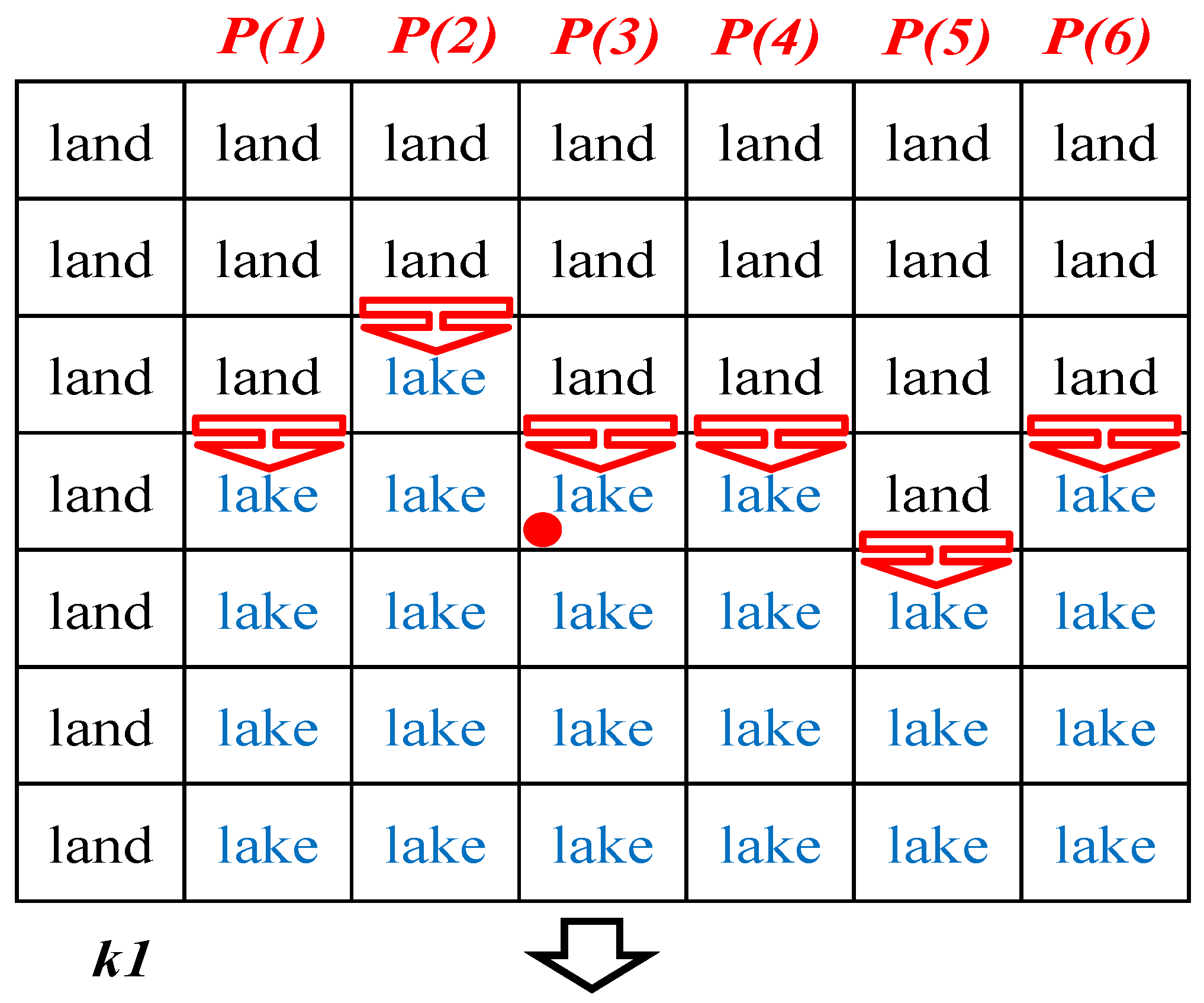
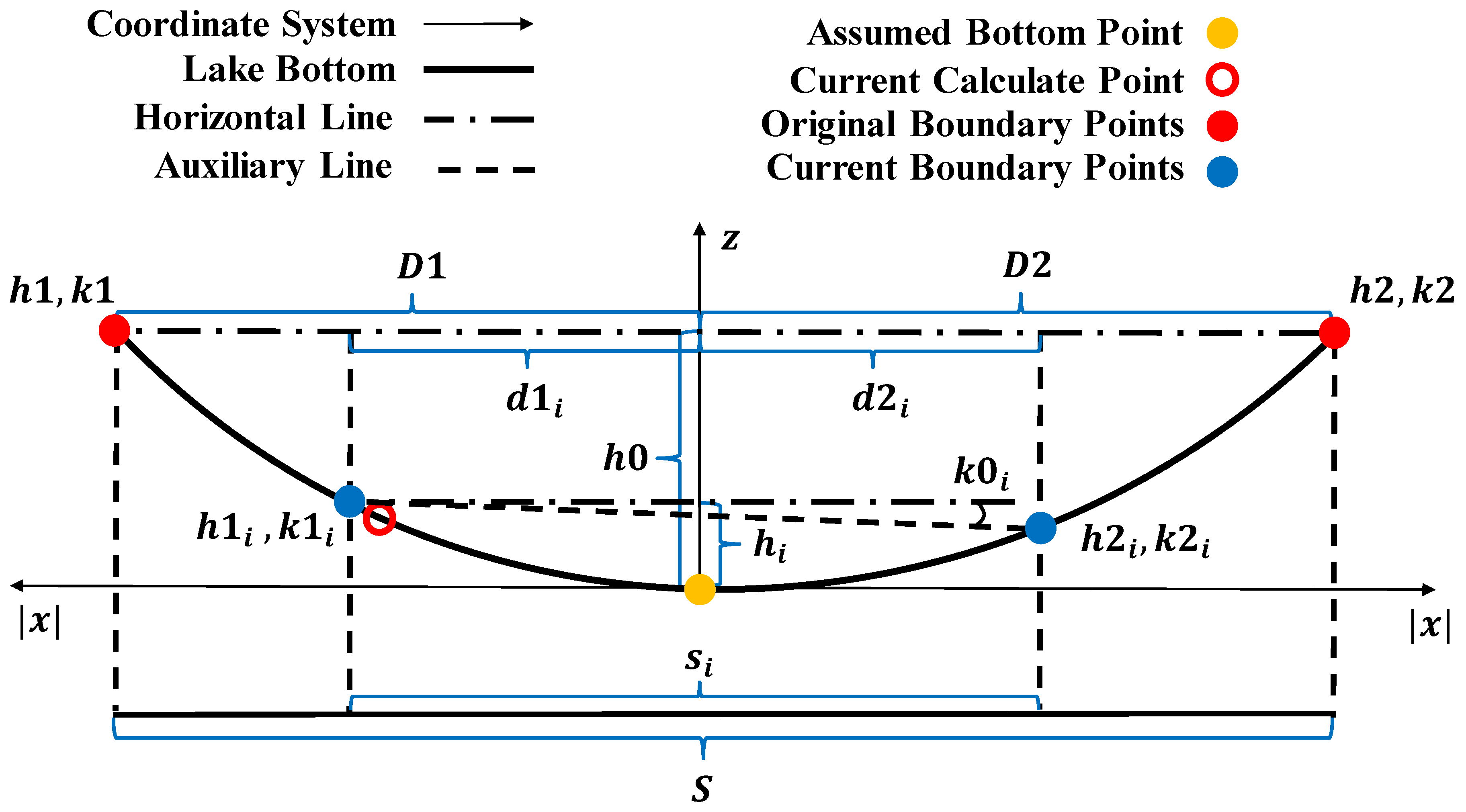
- Finding CCPs: The current calculation points (CCPs) are found through a circulation step by (1) drawing the AGA border adjacent to the uncalculated side, (2) finding the pixels whose values are higher than the H, and (3) defining the pixels that are in the uncalculated area but next to the pixels found in step 2 as the CCPs. For example, the hollow red point in Figure 3 is a CCP ready for calculation. Note that the CCP is the pixel that is calculated during each circulation interval.
- Determining BOD of CCPs: After the CCPs are found, we need to calculate each CCP based on the same AGA. For one CCP, before we apply the calculation formula, we need to distinguish the border-on directions (BODs), defined as the directions on which we can find a border-on AGA pixel. There are four potential directions (north, west, south, and east) for each CCP, and the BODs are defined as the directions on which we can find a border-on AGA pixel. As shown in Figure 3, the north and west directions are the BODs for this CCP. The reason for finding the BODs is based on the inverse distance weighted interpolation method [39], meaning that the influencing power decreases as the distance increases. In this model, we consider that the far coast has little influence on nearshore pixels, so the pixel elevation is only decided from the BODs. Obviously, the last pixel should have four BODs, while most cases have one to three BODs.
- Estimating the depth value of CCPs by the MFM: After the BODs are determined, we use the morphologic function module (MFM) to calculate the estimated pixel elevation from all BODs and then average the results (please see Section 2.5 for more details). This step iterates until the following situation is met.
- After obtaining the value of the CCPs, by now, all CCPs are assigned an estimated value in this iteration, the AGA and H will be updated to the next iteration. For the AGA, the position of the CCPs in this iteration will turn to “calculated” from “uncalculated”. As for H, after step 3, if all elevations of the AGA boundary drop below H, we then need to decrease H to make the calculation continue by a predefined decreasing step parameter (DSP); if not, it will do another iteration using the same H. In the former case, the new H equals the original H minus the DSP, and this process is continued until any CCP occurs. The DSP has a low sensitivity when it is small enough, but it also influences the efficiency of the program if it is too small. In this study, we set the DSP as 1 m in all tests with the same vertical resolution as the SRTM data. The H and DSP changing mechanism are the core of the WRM, and it makes the calculation progress relying on the water surface decrease rather than simply shrink the geometry boundary; this is better since the WRM imitates a natural process that makes the calculated surface almost horizontal rather than irregular.
2.4. Surrounding Slope Module (SSM)
2.5. Morphologic Function Module (MFM)
3. Model Validation
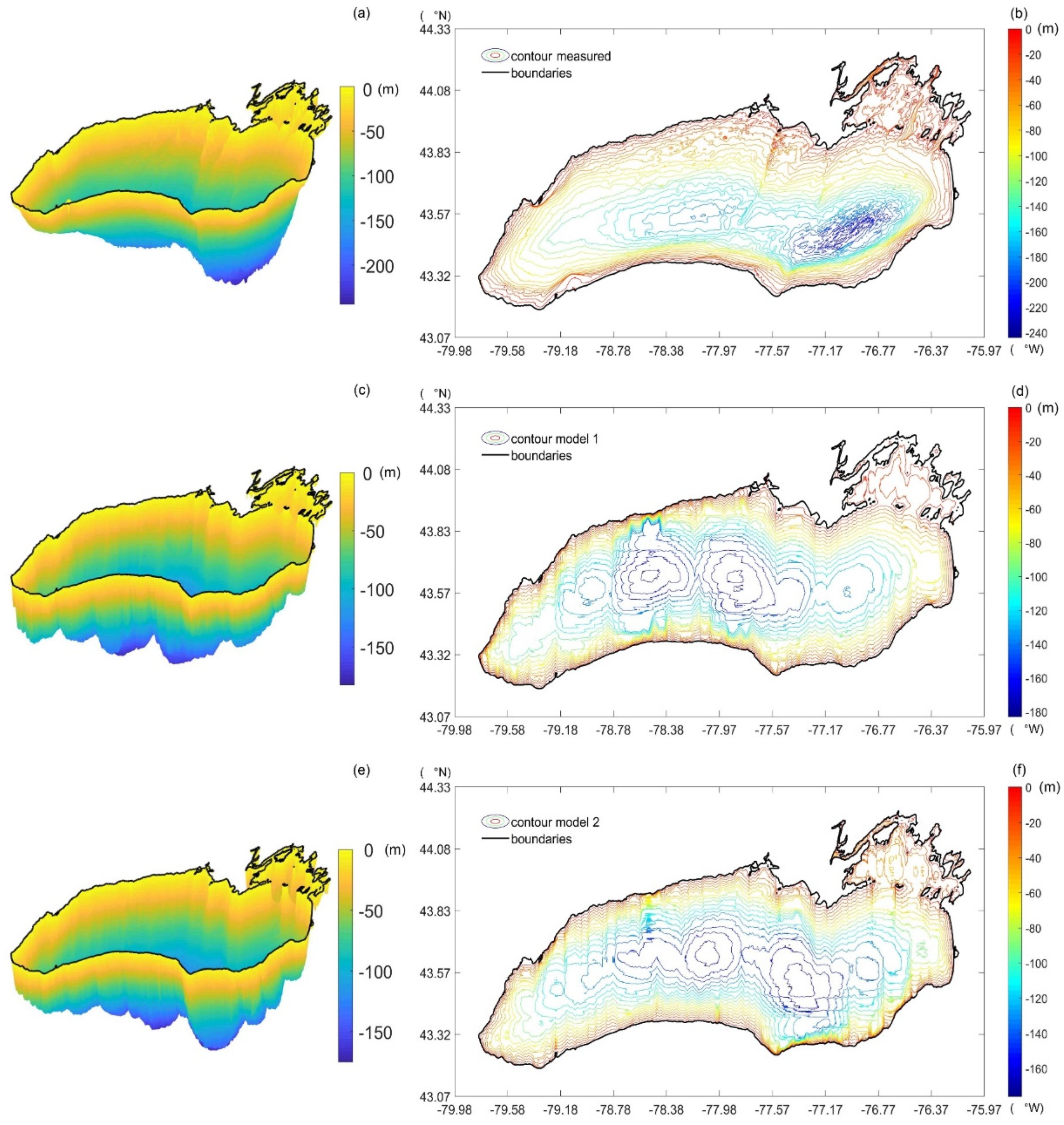
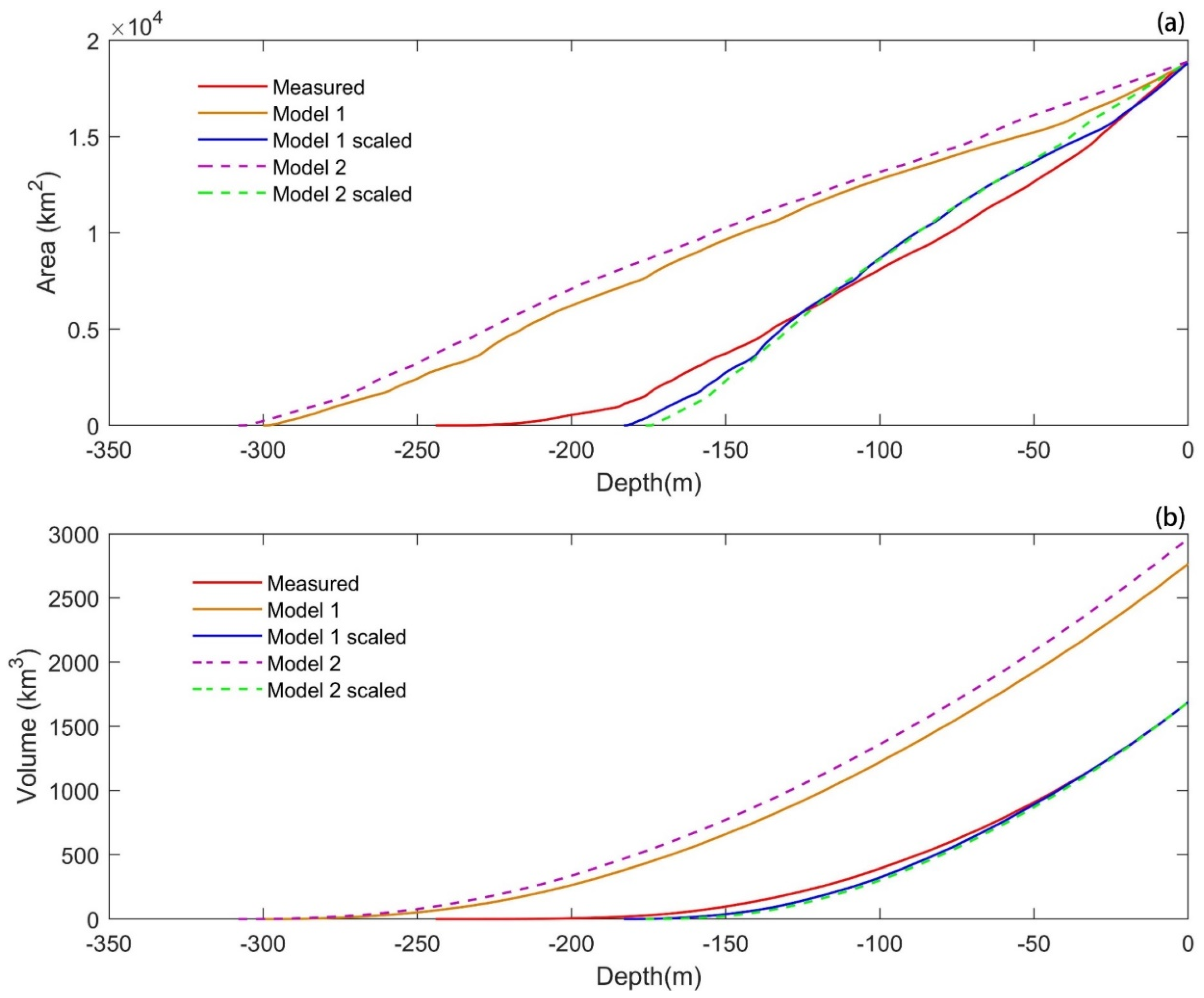
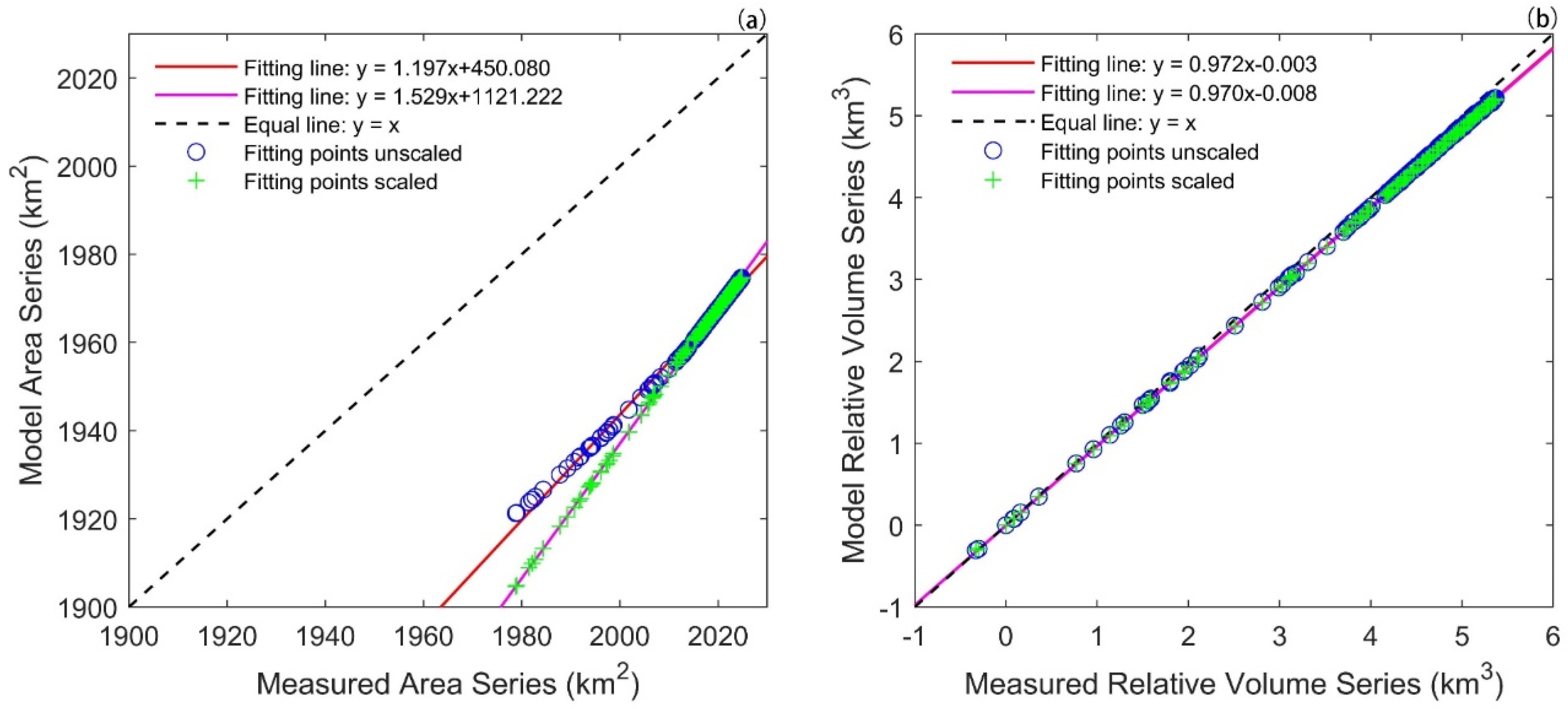
3.1. Analysis of Lake Ontario
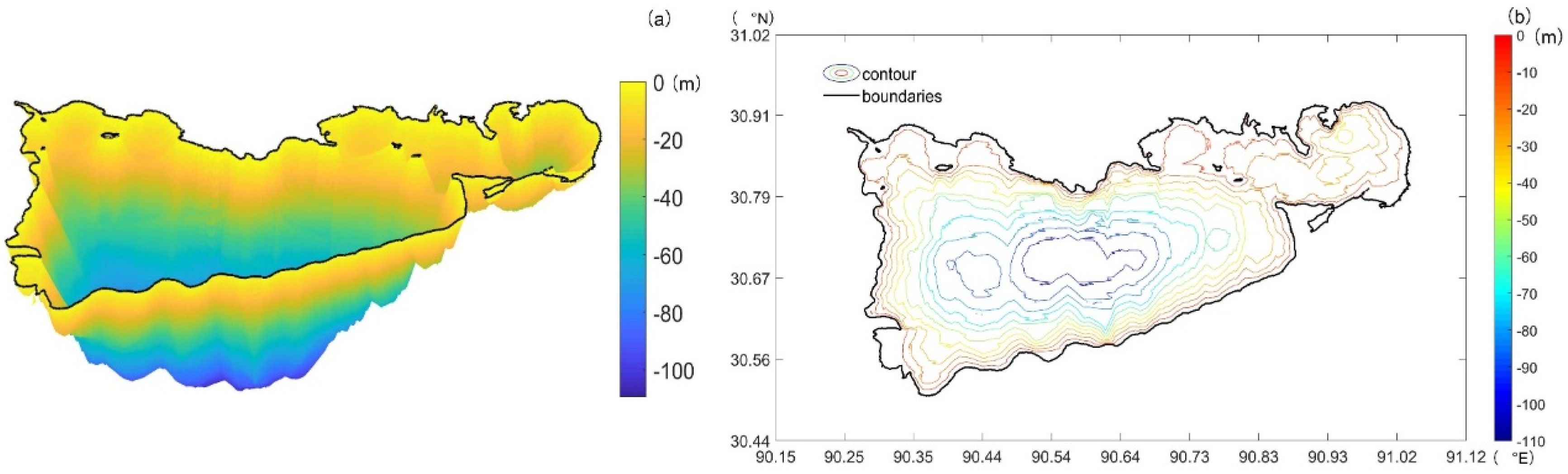
3.2. Analysis of Lake Namco
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Hollister, J.W.; Milstead, W.B.; Urrutia, M.A. Predicting maximum lake depth from surrounding topography. PLOS ONE 2011, 6, 1–6. [Google Scholar] [CrossRef]
- Tibor, G.; Sade, R.; Hall, J.K.; Ben-Avraham, Z.; Nishri, A. Lake Bathymetry and Bottom Morphology; Springer: Dordrecht, Netherlands, 2014; pp. 59–68. [Google Scholar]
- Moses, S.A.; Janaki, L.; Joseph, S.; Justus, J.; Vimala, S.R. Influence of lake morphology on water quality. Environ. Monit. Assess. 2011, 182, 443–454. [Google Scholar] [CrossRef]
- Khattab, M.F.O.; Abo, R.K.; Al-Muqdadi, S.W.; Merkel, B.J. Generate Reservoir Depths Mapping by Using Digital Elevation Model: A Case Study of Mosul Dam Lake, Northern Iraq. Adv. Remote Sens. 2017, 6, 15. [Google Scholar] [CrossRef]
- Lyzenga, D. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 2010, 2, 71–82. [Google Scholar] [CrossRef]
- Elfes, A. Sonar-based real-world mapping and navigation. IEEE J. Rob. Autom. 1987, 3, 249–265. [Google Scholar] [CrossRef]
- Dost, R.J.J.; Mannaerts, C.M.M. Generation of lake bathymetry using SONAR, satellite imagery and GIS. In Proceedings of the 2008 ESRI International User Conference: GIS, Geography in Action, San Diego, FL, USA, 4–8 August 2008; pp. 1–5. [Google Scholar]
- Filina, I.; Lukin, V.; Masolov, V.; Blankenship, D. Unconsolidated sediments at the bottom of Lake Vostok from seismic data. Usgs Prof. Pap. 2007, 31, 1–5. [Google Scholar] [CrossRef]
- Palethorpe, B.; Hayes-Gill, B.; Crowe, J.; Sumner, M.; Crout, N.; Foster, M.; Reid, T.; Benford, S.; Greenhalgh, C.; Laybourn-Parry, J. Real-time physical data acquisition through a remote sensing platform on a polar lake. Limnol. Oceanogr. Methods 2004, 2, 191–201. [Google Scholar] [CrossRef]
- Filina, I.; Blankenship, D.; Lukin, V.; Masolov, V.; Sen, M. New Bathymetry Model of Lake Vostok from Airborne Gravity Data; USGS: Reston, VA, USA, 2007.
- Foody, G.M.; Muslim, A.M.; Atkinson, P.M. Super-resolution mapping of the waterline from remotely sensed data. Int. J. Remote Sens. 2005, 26, 5381–5392. [Google Scholar] [CrossRef]
- Ma, R.; Duan, H.; Liu, Q.; Loiselle, S.A. Approximate bottom contribution to remote sensing reflectance in Taihu Lake, China. J. Great Lakes Res. 2011, 37, 18–25. [Google Scholar] [CrossRef]
- Moses, S.A.; Janaki, L.; Joseph, S.; Gomathi, J.P.; Joseph, J. Lake bathymetry from Indian Remote Sensing (P6-LISS III) satellite imagery using artificial neural network model. Lakes Reservoirs Res. Manag. 2013, 18, 145–153. [Google Scholar] [CrossRef]
- Stumpf, R.; Holderied, K.; Robinson, J. Mapping Water Depths in Clear Water from Space. In Proceedings of the 13th Biennial Coastal Zone Conference, Baltimore, MD, USA, 13–17 July 2003; pp. 13–17. [Google Scholar]
- Cael, B.B.; Heathcote, A.J.; Seekell, D.A. The volume and mean depth of Earth’s lakes. Geophys. Res. Lett. 2017, 44, 209–218. [Google Scholar] [CrossRef]
- Bemmelen, C.W.T.; Mann, M.; Ridder, M.P.; Rutten, M.M.; Giesen, N.C. Determining water reservoir characteristics with global elevation data. Geophys. Res. Lett. 2016, 43, 11–278. [Google Scholar] [CrossRef]
- Kropacek, J.; Braun, A.; Kang, S.; Feng, C.; Ye, Q.; Hochschild, V. Analysis of lake level changes in Nam Co in central Tibet utilizing synergistic satellite altimetry and optical imagery. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 3–11. [Google Scholar] [CrossRef]
- Song, C.; Bo, H.; Ke, L. Inter-annual changes of alpine inland lake water storage on the Tibetan Plateau: Detection and analysis by integrating satellite altimetry and optical imagery. Hydrol. Processes 2014, 28, 2411–2418. [Google Scholar] [CrossRef]
- Keys, T.A.; Scott, D.T. Monitoring volumetric fluctuations in tropical lakes and reservoirs using satellite remote sensing. Lake Reservoir Manage. 2018, 34, 154–166. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Calmant, S.; Rio, R.A.D.; Kouraev, A.; Bergé-Nguyen, M.; Maisongrande, P. Lakes Studies from Satellite Altimetry; Springer: Heidelberg, Berlin, 2011; pp. 509–533. [Google Scholar]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Catmull, E.; Clark, J. Recursively generated B-spline surfaces on arbitrary topological meshes. Comput. Aided Des. 1978, 10, 350–355. [Google Scholar] [CrossRef]
- Hu, P.; Hou, J.H.; Zhi, Z.; Bingyao, L.; Guo, K. An Improved Method Constructing 3D River Channel for Flood Modeling. Water 2019, 11, 403. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W. Modeling the Influence of River Cross-Section Data on a River Stage Using a Two-Dimensional/Three-Dimensional Hydrodynamic Model. Water 2017, 9, 203. [Google Scholar] [CrossRef]
- Dysarz, T. Development of RiverBox—An ArcGIS Toolbox for River Bathymetry Reconstruction. Water 2018, 10, 1266. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geog. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4; CGIAR Consortium for Spatial Information: Washington, DC, USA, 2008. [Google Scholar]
- Schumm, S.A.; Lichty, R.W. Time, space, and causality in geomorphology. Am. J. Sci. 1965, 263, 110–119. [Google Scholar] [CrossRef]
- Wilkinson, B.H.; Mcelroy, B.J. The impact of humans on continental erosion and sedimentation. Geol. Soc. Am. Bull. 2007, 119, 140–156. [Google Scholar] [CrossRef]
- Falanruw, M.C. Traditional adaptation to natural processes of erosion and sedimentation on Yap Island. In Proceedings of the Symposium: Research Needs and Applications to Reduce Erosion and Sedimentation in Tropical Steeplands, Suva, Fiji, 11–15 June 1990; pp. 231–237. [Google Scholar]
- Cole, J.J. Multiple approaches to estimating air-water gas exchange in small lakes. Limnol. Oceanogr. Methods 2010, 8, 285–293. [Google Scholar] [CrossRef]
- LeBlanc, L.R.; Mayer, L.; Rufino, M.; Schock, S.G.; King, J. Marine sediment classification using the chirp sonar. J. Acoust. Soc. Am. 1992, 91, 107–115. [Google Scholar] [CrossRef]
- Vos, J.A. Testing compost as an anti wind erosion agent in a win tunnel. Soil Technol. 1996, 9, 209–221. [Google Scholar] [CrossRef]
- Seppala, M. Wind as a Geomorphic Agent in Cold Climates; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- József, T. Groundwater as a geologic agent: An overview of the causes, processes, and manifestations. Hydrogeol. J. 1999, 7, 1–14. [Google Scholar]
- Morales-Marin, L.A.; French, J.R.; Burningham, H.; Battarbee, R.W. Three-dimensional hydrodynamic and sediment transport modeling to test the sediment focusing hypothesis in upland lakes. Limnol. Oceanogr. 2017, 63, S156–S176. [Google Scholar] [CrossRef]
- Hayes, F.R.; Anthony, E.H. Lake water and sediment VI The standing crop of bacteria in lake sediments and its place in the classification of lakes. Limnol. Oceanogr. 1959, 4, 299–315. [Google Scholar] [CrossRef]
- Watson, D.F. A refinement of inverse distance weighted interpolation. Geo-Processing 1985, 2, 315–327. [Google Scholar]
- Annoni, P.; Brüggemann, R. The dualistic approach of FCA: A further insight into Ontario Lake sediments. Chemosphere 2008, 70, 2025–2031. [Google Scholar] [CrossRef] [PubMed]
- Botts, L.; Krushelnicki, B. The Great Lakes. An Environmental Atlas and Resource Book; Great Lakes National Program Office: Toronto, ON, Canada, 1987; Volume 32. [Google Scholar]
- Moorman, B.J.; Michel, F.A. Bathymetric mapping and sub-bottom profiling through lake ice with ground-penetrating radar. J. Paleolimnol. 1997, 18, 61–73. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Schütt, B.; Berking, J.; Frechen, M.; Yi, C. Late Pleistocene Lake Level Fluctuations of the Nam Co, Tibetan Plateau, China. Zeitschrift für Geomorphol. 2008, 52, 57–75. [Google Scholar] [CrossRef]
- Townshend, J.; Short, N.M. The Landsat Tutorial Workbook: Basics of Satellite Remote Sensing by Nicholas M. Short. Geog. J. 1984, 150, 283–284. [Google Scholar] [CrossRef]
- Cohen, W.B.; Goward, S.N. Landsat’s Role in Ecological Applications of Remote Sensing. Bioscience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Wan, W.; Long, D.; Hong, Y.; Ma, Y.; Yuan, Y.; Xiao, P.; Duan, H.; Han, Z.; Gu, X. A lake data set for the Tibetan Plateau from the 1960s, 2005, and 2014. Sci. Data 2016, 3, 160039. [Google Scholar] [CrossRef]
- Zhu, S.; Wan, W.; Xie, H.; Liu, B.; Li, H.; Hong, Y. An Efficient and Effective Approach for Georeferencing AVHRR and GaoFen-1 Imageries Using Inland Water Bodies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2491–2500. [Google Scholar] [CrossRef]
- Cook, R.D. Detection of Influential Observation in Linear Regression. Technometrics 2000, 42, 65–68. [Google Scholar] [CrossRef]
- Larson, G.; Schaetzl, R. Origin and Evolution of the Great Lakes. J.Great Lakes Res. 2001, 27, 518–546. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Zhu, L.; Wang, L.; Yi, C. Distribution and formation of monohydrocalcite from surface sediments in Nam Co Lake, Tibet. Quat. Int. 2012, 263, 85–92. [Google Scholar] [CrossRef]
- Jaeger, H.M.; Liu, C.H.; Nagel, S.R. Relaxation at the Angle of Repose. Phys. Rev. Lett. 1989, 62, 40–43. [Google Scholar] [CrossRef] [PubMed]
- Webster, A.G. On the Angle of Repose of Wet Sand. Proc. Natl. Acad. Sci. USA 1919, 5, 263–265. [Google Scholar] [CrossRef] [PubMed]


| Abbreviation | Full name | Definition |
|---|---|---|
| WRM | Water Recession Method | It is a process simulating the water recession. In this process, the water keeps decreasing and land appears gradually. |
| SSM | Surrounding Slope Module | It is a program module designed for calculating the surrounding slope of four directions |
| SSD | Surrounding Slope Data | It is the result of the SSM recorded by a matrix. The value is slope, m and n represent position, and 4 represents direction. |
| LBM | Lake Binary Matrix | It is a binary matrix to record water and land by 1 and 0, and it has the same size with input from the digital elevation model (DEM). |
| H | Height | It is the current calculation of elevation, as well as the assumed water surface height in the WRM. |
| AGA | Already Generated Area | It is a binary matrix to record the calculated and uncalculated pixels, and it has the same format as that of the LBM. |
| DSP | Decreasing Step Parameter | It is the decreasing height of every single iteration and it controls the decreasing speed of the water surface in the WRM. |
| CCP | Current Calculation Point | The pixel which will be assigned to an estimated value in this present iteration. |
| BOD | Border-On Direction | In this direction, the CCP is adjacent to the water pixel rather than the land pixel. |
| MFM | Morphologic Function Module | It is a program module designed to calculate the estimated value of the CCP by mathematical function and input information. |
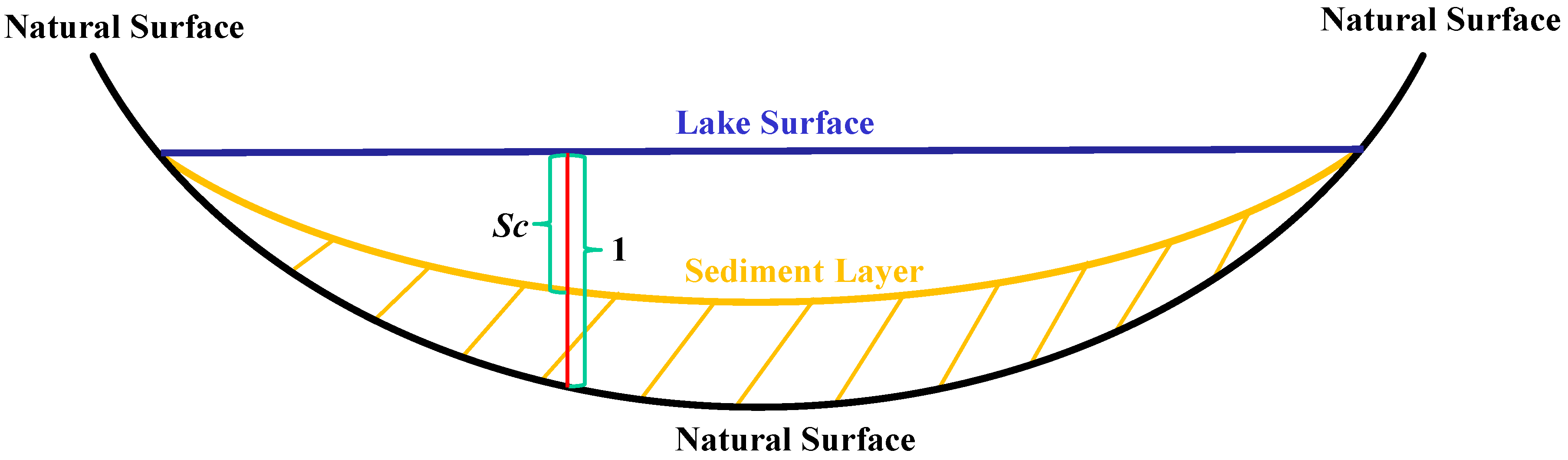
| Sc | Sediment coefficient | It is a correction factor serving for this model based on the two assumptions. |
| Model | MAE | RMSE | R-squared of A 1 | R-squared of V 1 |
|---|---|---|---|---|
| 1 | 24.232 m | 33.957 m | 0.982 | 0.993 |
| 2 | 22.076 m | 29.312 m | 0.973 | 0.988 |
| Model | Area | Volume |
|---|---|---|
| Unscaled | 53.669 | 0.123 |
| Scaled | 55.896 | 0.135 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Liu, B.; Wan, W.; Xie, H.; Fang, Y.; Chen, X.; Li, H.; Fang, W.; Zhang, G.; Tao, M.; et al. A New Digital Lake Bathymetry Model Using the Step-Wise Water Recession Method to Generate 3D Lake Bathymetric Maps Based on DEMs. Water 2019, 11, 1151. https://doi.org/10.3390/w11061151
Zhu S, Liu B, Wan W, Xie H, Fang Y, Chen X, Li H, Fang W, Zhang G, Tao M, et al. A New Digital Lake Bathymetry Model Using the Step-Wise Water Recession Method to Generate 3D Lake Bathymetric Maps Based on DEMs. Water. 2019; 11(6):1151. https://doi.org/10.3390/w11061151
Chicago/Turabian StyleZhu, Siyu, Baojian Liu, Wei Wan, Hongjie Xie, Yu Fang, Xi Chen, Huan Li, Weizhen Fang, Guoqing Zhang, Mingwei Tao, and et al. 2019. "A New Digital Lake Bathymetry Model Using the Step-Wise Water Recession Method to Generate 3D Lake Bathymetric Maps Based on DEMs" Water 11, no. 6: 1151. https://doi.org/10.3390/w11061151
APA StyleZhu, S., Liu, B., Wan, W., Xie, H., Fang, Y., Chen, X., Li, H., Fang, W., Zhang, G., Tao, M., & Hong, Y. (2019). A New Digital Lake Bathymetry Model Using the Step-Wise Water Recession Method to Generate 3D Lake Bathymetric Maps Based on DEMs. Water, 11(6), 1151. https://doi.org/10.3390/w11061151










