Wake Effect Assessment in Long- and Short-Crested Seas of Heaving-Point Absorber and Oscillating Wave Surge WEC Arrays
Abstract
1. Introduction
2. MILDwave-NEMOH Coupled Model
2.1. Basis of the MILDwave-NEMOH Coupled Model
- A first simulation is performed in MILDwave to obtain the incident wave field in the time-domain, without any floating structure in the numerical basin. The wave characteristics at the coupling location are computed and used as input values for NEMOH.
- A second simulation is performed in NEMOH to calculate the perturbed wave field around the floating structure at the coupling location in the frequency-domain.
- A third simulation is performed in MILDwave to obtain the perturbed wave field in the time-domain. The perturbed wave field from NEMOH is transformed from the frequency-domain to the time-domain and coupled into MILDwave by prescribing an internal wave generation boundary.
- Finally, the total wave field is obtained as the combination of the incident and perturbed wave fields calculated in MILDwave in the time-domain.
2.2. The Wave Propagation Model MILDwave
2.3. The Wave-Structure Interaction Solver, NEMOH
- The flow is inviscid.
- The flow is irrotational.
- The fluid is incompressible.
- The motion amplitudes of the modelled floating bodies are much smaller than the wavelength.
- The sea bottom is flat.
2.4. Generation of the Incident Wave Field
2.5. Calculation of the Perturbed Wave Field
2.6. Calculation of the Total Wave Field
3. Numerical Framework
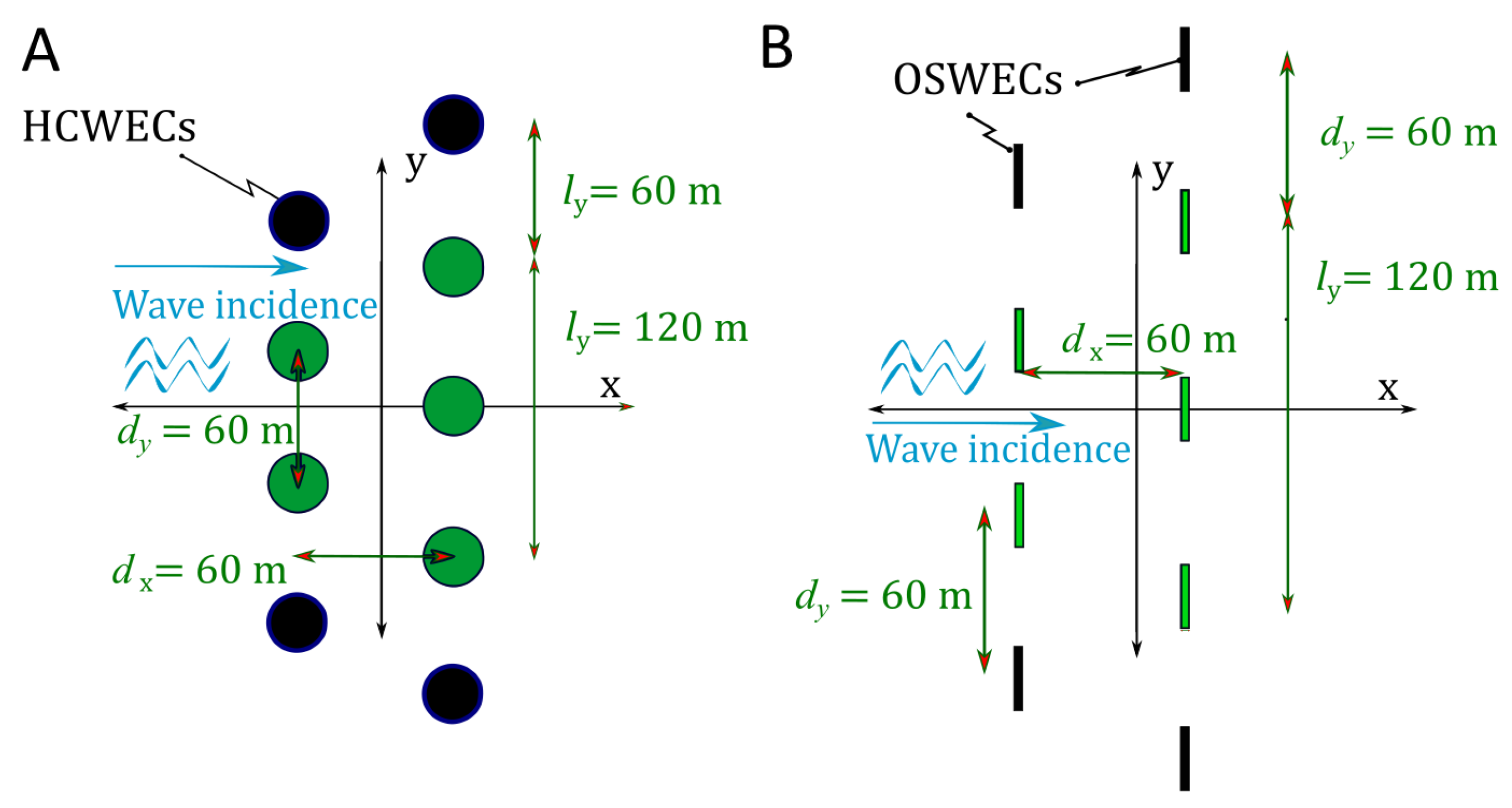
3.1. Modelled WECs and Array Layout
- Heaving Cylindrical Wave Energy Converter (HCWEC): is a disc shaped heaving buoy WEC with a diameter, ∅, of 20.0 m, a height, , of 4.0 m, and a draft, , of 2.0 m. HCWECs are designed to be deployed at water depths of around 30.0 m.
- Oscillating Wave Surge Wave Energy Converter (OSWEC): the second WEC chosen is a bottom-fixed pitching flap driven by the surge motion of the waves. OSWECs are designed to be deployed in shallow water at depths of 10.0–20.0 m. The simulated OSWEC has dimensions of 20.0 m width, , 1.0 m thickness, , and 12.0 m height, . It is hinged at the seabed with pitching motion about its bottom end.
3.2. Wave Conditions
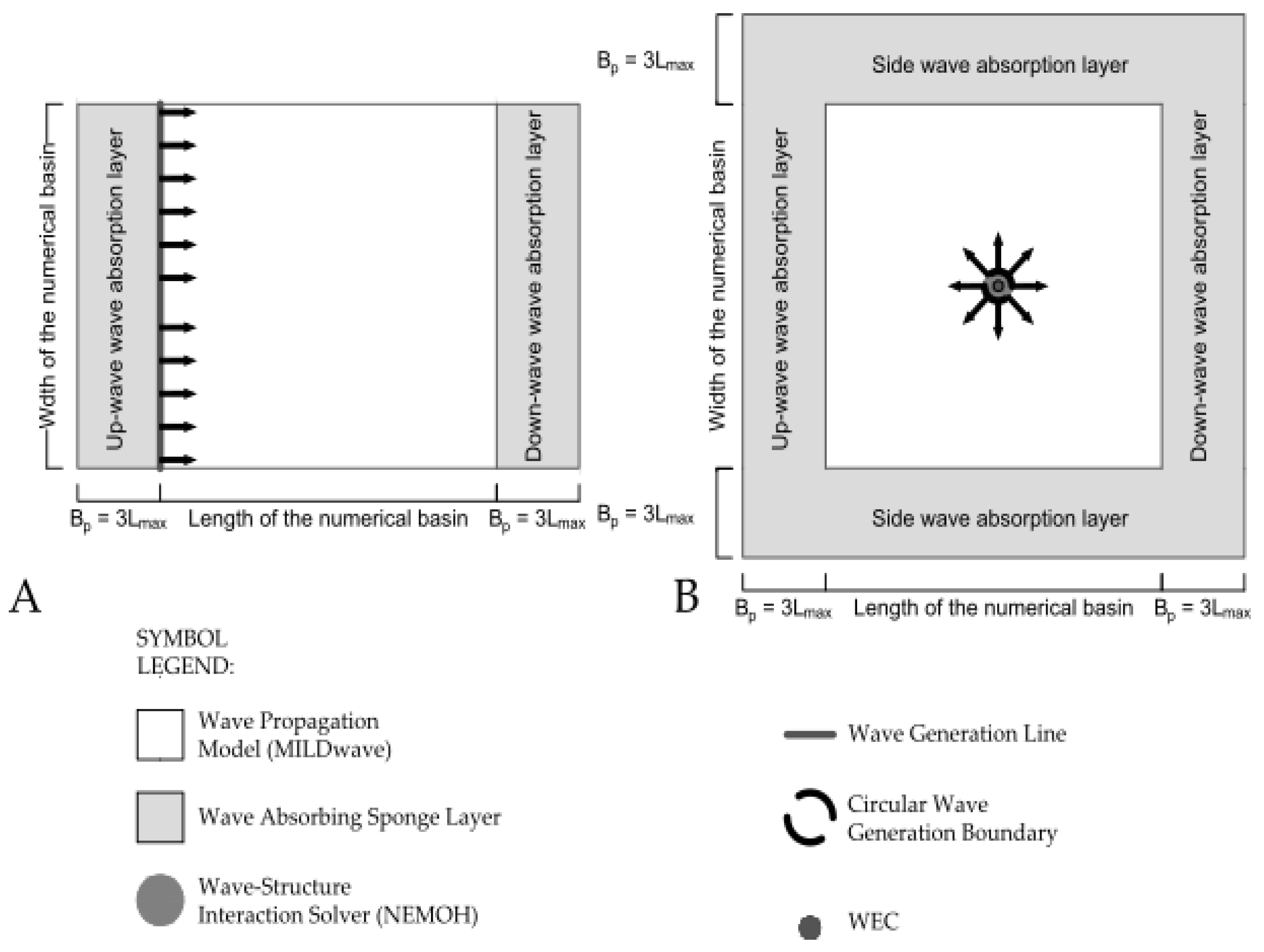
3.3. Numerical Set-Up
3.4. Test Cases
4. Results
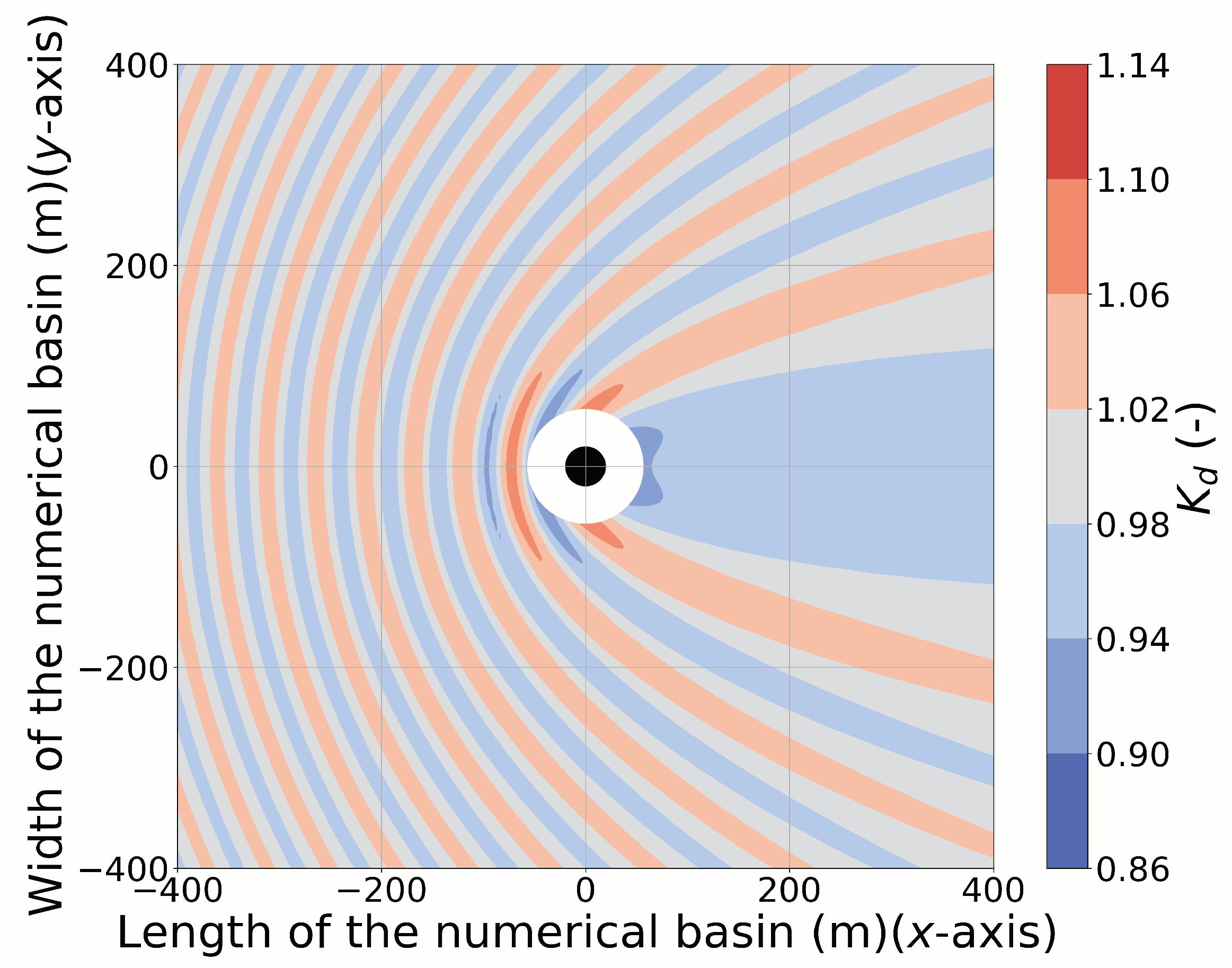
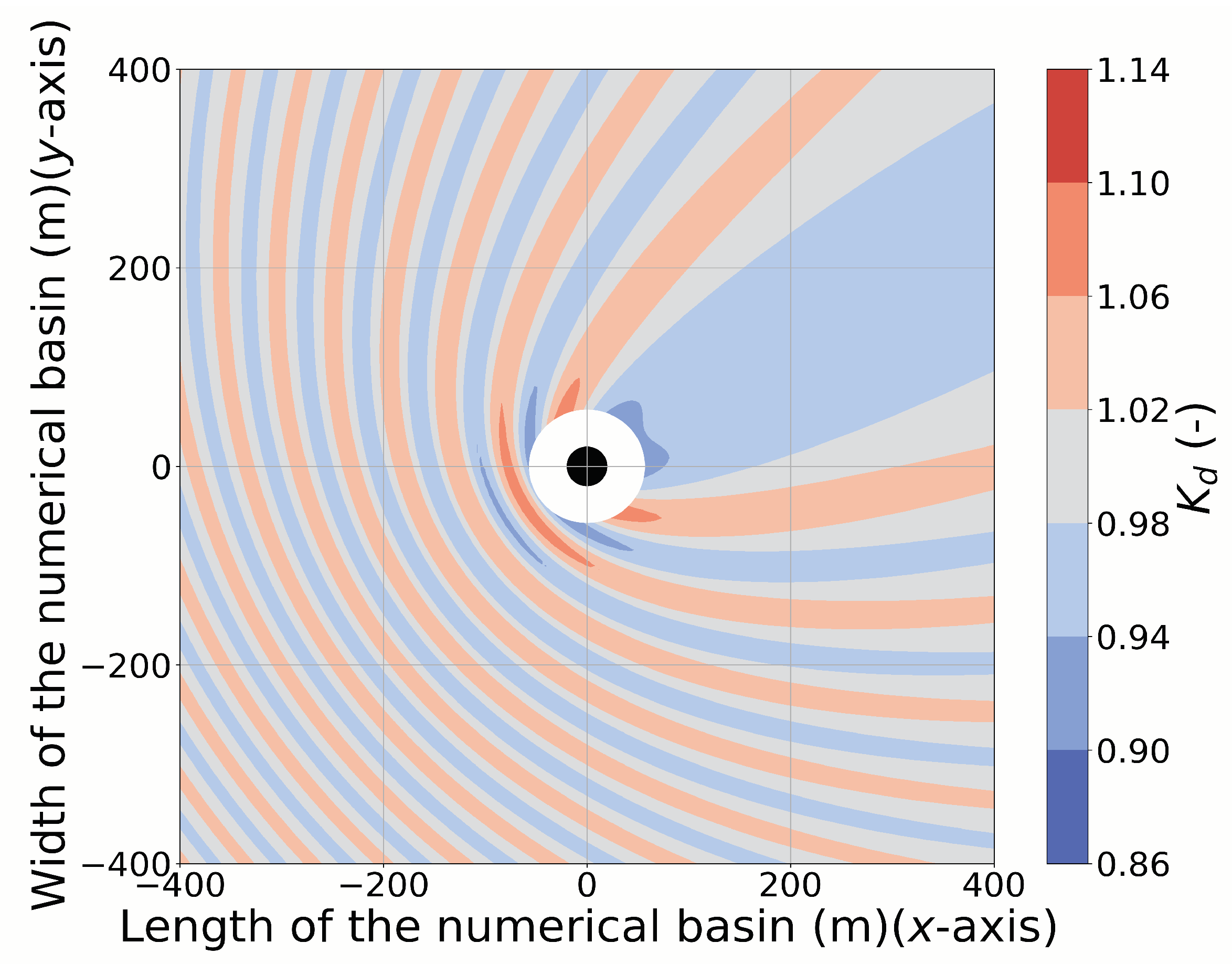
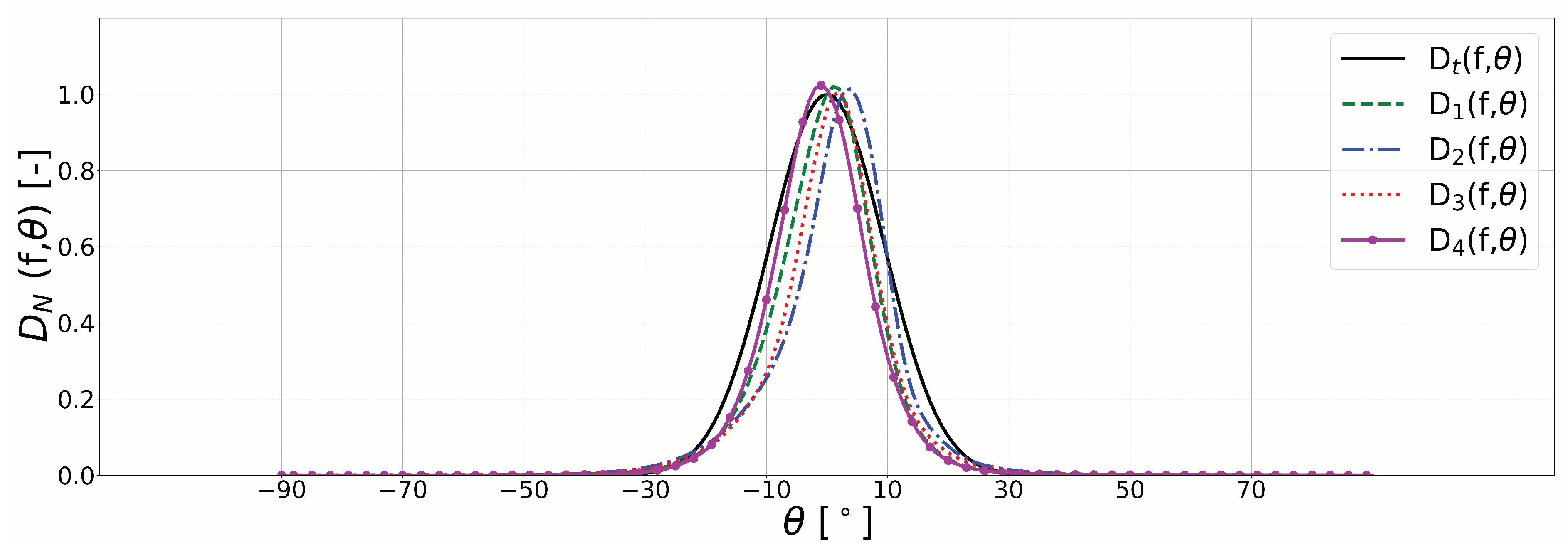
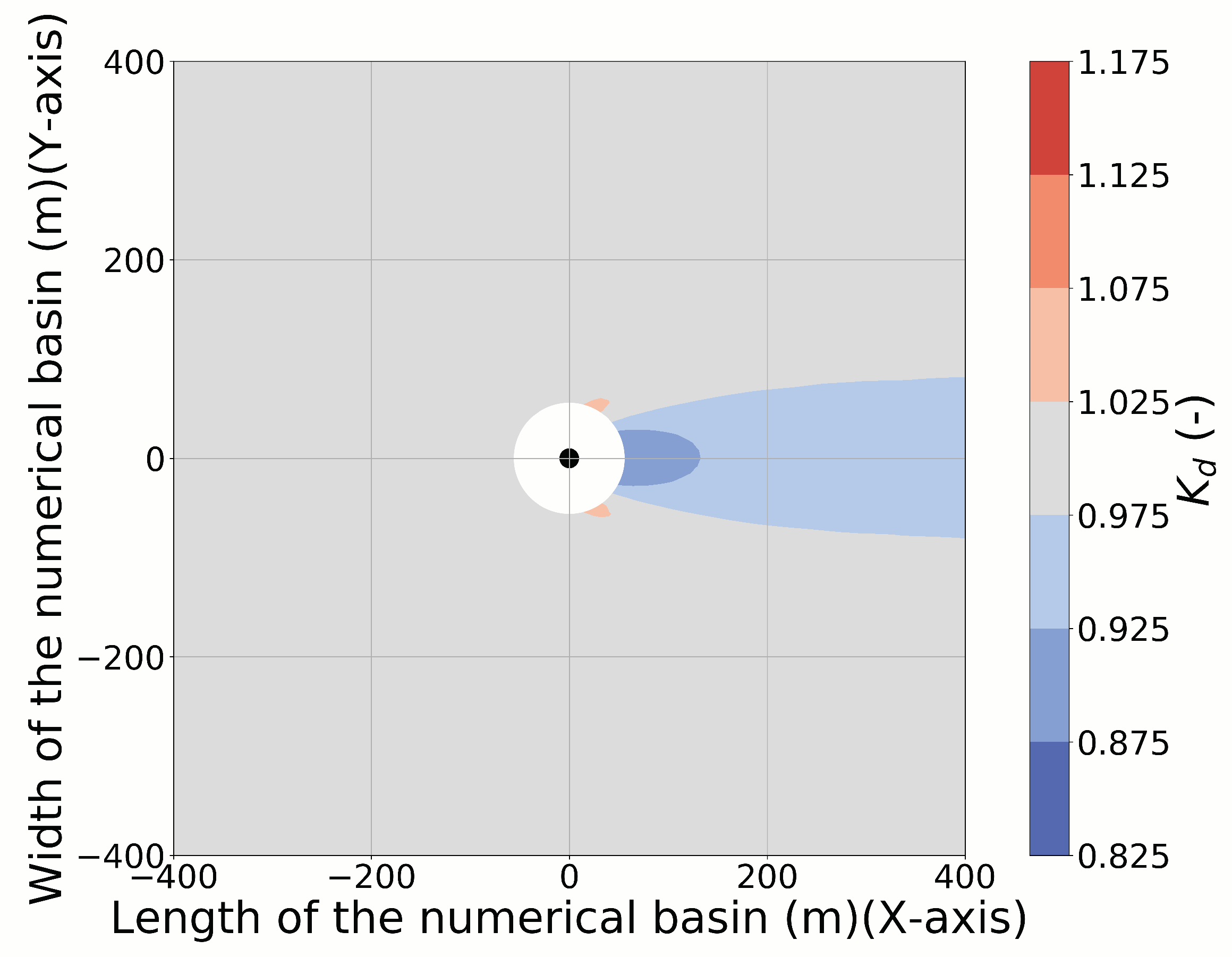
4.1. Disturbance Coefficient for Short-Crested Irregular Waves
4.2. 9-OSWEC Array
4.3. 9-HCWEC Array
4.4. Comparison Summary
4.5. Computational Time
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| BEM | Boundary Element Method |
| PTO | Power Take-Off |
| RAO | Response Amplitude Operator |
| P-M | Pierson–Moskowitz |
| DOF | Degree of freedom |
| HCWEC | Heaving Cylindrical Wave Energy Converter |
| OSWEC | Oscillating Wave Surge Wave Energy Converter |
References
- Greaves, D.; Iglesias, G. Wave and Tidal Energy; John Wiley & Sons: New York, NY, USA, 2018. [Google Scholar]
- European Marine Energy Centre (EMEC) Ltd. Wave Developers Database. Available online: http://www.emec.org.uk/marine-energy/wave-developers/ (accessed on 13 November 2018).
- Millar, D.L.; Smith, H.C.M.; Reeve, D.E. Modelling analysis of the sensitivity of shoreline change to a wave farm. Ocean. Eng. 2007, 34, 884–901. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G. Wave farm impact based on realistic wave-WEC interaction. Energy 2013, 51, 216–229. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave farm impact: The role of farm-to-coast distance. Renew. Energy 2014, 69, 375–385. [Google Scholar] [CrossRef]
- Abanades, J.; Greaves, D.; Iglesias, G. Wave farm impact on the beach profile: A case study. Coast. Eng. 2014, 86, 36–44. [Google Scholar] [CrossRef]
- Venugopal, V.; Smith, G. Wave Climate Investigation for an Array of Wave Power Devices. In Proceedings of the 7th European Wave and Tidal Energy Conference, orto, Portugal, 11–13 September 2007; p. 10. [Google Scholar]
- Chang, G.; Ruehl, K.; Jones, C.; Roberts, J.; Chartrand, C. Numerical modeling of the effects of wave energy converter characteristics on nearshore wave conditions. Renew. Energy 2016, 89, 636–648. [Google Scholar] [CrossRef]
- Stokes, C.; Conley, D.C. Modelling Offshore Wave farms for Coastal Process Impact Assessment: Waves, Beach Morphology, and Water Users. Energies 2018, 11, 2517. [Google Scholar] [CrossRef]
- Folley, M. Phase-Averaging Wave Propagation Array Models. In Numerical Modelling of Wave Energy Converters; Elsevier: Amsterdam, The Netherlands, 2016; pp. 221–225. [Google Scholar]
- Smith, H.C.; Pearce, C.; Millar, D.L. Further analysis of change in nearshore wave climate due to an offshore wave farm: An enhanced case study for the Wave Hub site. Renew. Energy 2012, 40, 51–64. [Google Scholar] [CrossRef]
- Beels, C.; Troch, P.; De Backer, G.; Vantorre, M.; De Rouck, J. Numerical implementation and sensitivity analysis of a wave energy converter in a time-dependent mild-slope equation model. Coast. Eng. 2010, 57, 471–492. [Google Scholar] [CrossRef]
- Stratigaki, V.; Vanneste, D.; Troch, P.; Gysens, S.; Willems, M. Numerical Modelling of Wave Penetration in Ostend Harbour. Coast. Eng. Proc. 2011, 1, 42. [Google Scholar] [CrossRef]
- Troch, P.; Stratigaki, V. Phase-Resolving Wave Propagation Array Models. In Numerical Modelling of Wave Energy Converters; Folley, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 10; pp. 191–216. [Google Scholar]
- Tuba Özkan-Haller, H.; Haller, M.C.; Cameron McNatt, J.; Porter, A.; Lenee-Bluhm, P. Analyses of Wave Scattering and Absorption Produced by WEC Arrays: Physical/Numerical Experiments and Model Assessment. In Marine Renewable Energy: Resource Characterization and Physical Effects; Yang, Z., Copping, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 71–97. [Google Scholar]
- Stratigaki, V. Experimental Study and Numerical Modelling of Intra-Array Interactions and Extra-Array Effects of Wave Energy Converter Arrays. Ph.D. Thesis, Ghent University, Belgium, Brussel, 2014. [Google Scholar]
- Verbrugghe, T.; Stratigaki, V.; Troch, P.; Rabussier, R.; Kortenhaus, A. A comparison study of a generic coupling methodology for modeling wake effects of wave energy converter arrays. Energies 2017, 10, 1697. [Google Scholar] [CrossRef]
- Verao Fernandez, G.; Balitsky, P.; Stratigaki, V.; Troch, P. Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry. Energies 2018, 11, 2899. [Google Scholar] [CrossRef]
- Verao Fernandez, G.; Stratigaki, V.; Troch, P. Irregular Wave Validation of a Coupling Methodology for Numerical Modelling of Near and Far Field Effects of Wave Energy Converter Arrays. Energies 2019, 12, 538. [Google Scholar] [CrossRef]
- Balitsky, P.; Verao Fernandez, G.; Stratigaki, V.; Troch, P. Assessment of the Power Output of a Two-Array Clustered WEC Farm Using a BEM Solver Coupling and a Wave-Propagation Model. Energies 2018, 11, 2907. [Google Scholar] [CrossRef]
- Engsig-Karup, A.; Bingham, H.; Lindberg, O. An efficient flexible-order model for 3D nonlinear water waves. J. Comput. Phys. 2009, 228, 2100–2118. [Google Scholar] [CrossRef]
- Troch, P. MILDwave—A Numerical Model for Propagation and Transformation of Linear Water Waves; Technical Report, Internal Report; Department of Civil Engineering, Ghent University: Ghent, Belgium, 1998. [Google Scholar]
- Tomey-Bozo, N.; Babarit, J.M.A.; Troch, P.; Lewis, T.; Thomas, G. Wake Effect Assesment of a flap-type wave energy converter farm using a coupling methodology. In Proceedings of the ASME 36th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2017), Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Tomey-Bozo, N.; Murphy, J.; Troch, P.; Lewis, T.; Thomas, G. Modelling of a flap-type wave energy converter farm in a mild-slope equation model for a wake effect assessment. IET Renew. Power Gener. 2017, 11, 1142–1152. [Google Scholar] [CrossRef]
- Tomey-Bozo, N.; Babarit, A.; Murphy, J.; Stratigaki, V.; Troch, P.; Lewis, T.; Thomas, G. Wake effect assessment of a flap type wave energy converter farm under realistic environmental conditions by using a numerical coupling methodology. Coast. Eng. 2018, 143, 96–112. [Google Scholar] [CrossRef]
- Göteman, M.; McNatt, C.; Giassi, M.; Engström, J.; Isberg, J. Arrays of Point-Absorbing Wave Energy Converters in Short-Crested Irregular Waves. Energies 2018, 11, 964. [Google Scholar] [CrossRef]
- Stratigaki, V.; Troch, P.; Forehand, D. A fundamental coupling methodology for modelling near-field and far-field wave effects of floating structures and wave energy devices. Renew. Energy 2019, in press. [Google Scholar] [CrossRef]
- WAMIT Inc. User Manual, Versions 6.4, 6.4 PC, 6.3, 6.3S-PC; WAMIT: Boston, MA, USA, 2006. [Google Scholar]
- Balitsky, P.; Verao Fernandez, G.V.; Troch, P. Coupling methodology for modelling the near-field and far-field effects of a Wave Energy Converter. In Proceedings of the ASME 36th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2017), Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Radder, A.C.; Dingemans, M.W. Canonical equations for almost periodic, weakly nonlinear gravity waves. Wave Motion 1985, 7, 473–485. [Google Scholar] [CrossRef]
- Lee, C.; Suh, K.D. Internal generation of waves for time-dependent mild-slope equations. Coast. Eng. 1998, 34, 35–57. [Google Scholar] [CrossRef]
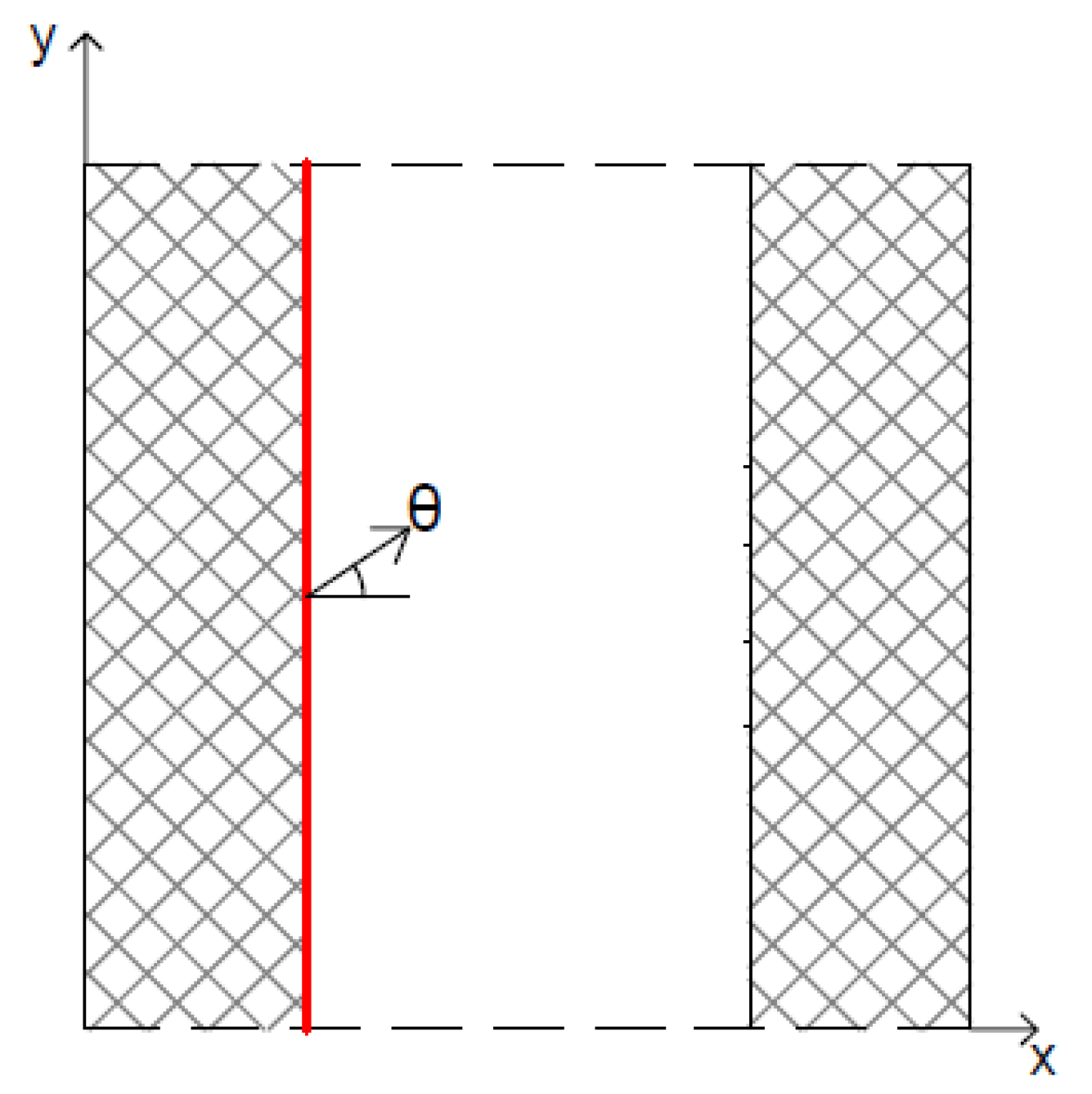
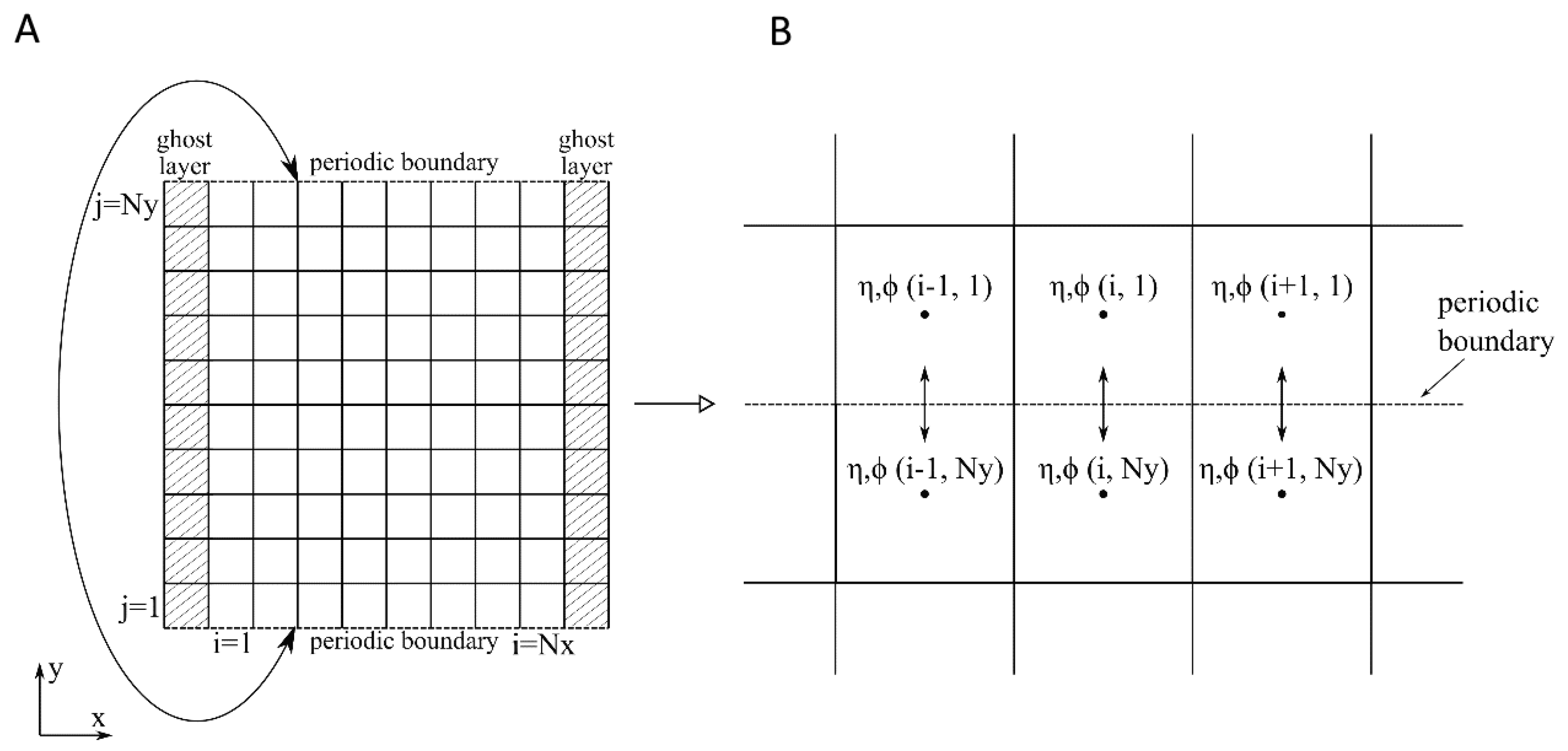
- Vasarmidis, P.; Stratigaki, V.; Troch, P. Accurate and Fast Generation of Irregular Short Crested Waves by Using Periodic Boundaries in a Mild-Slope Wave Model. Energies 2019, 12, 785. [Google Scholar] [CrossRef]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver {NEMOH}. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Alves, M. Wave Energy Converter modelling techniques based on linear hydrodynamic theory. In Numerical Modelling of Wave Energy Converters; Folley, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 1; pp. 11–65. [Google Scholar]
- Penalba, M.; Touzón, I.; Lopez-Mendia, J.; Nava, V. A numerical study on the hydrodynamic impact of device slenderness and array size in wave energy farms in realistic wave climates. Ocean. Eng. 2017, 142, 224–232. [Google Scholar] [CrossRef]
- Penalba, M.; Kelly, T.; Ringwood, J. Using NEMOH for Modelling Wave Energy Converters: A Comparative Study with WAMIT. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC 2017), Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Sand, S.E.; Mynett, A.E. Directional Wave Generation and Analysis. In Proceedings of the IAHR Seminar on Wave Analysis and Generation in Laboratory Basins, Lausanne, Switzerland, 1–3 September 1987; pp. 363–376. [Google Scholar]
- Frigaard, P.; Helm-Petersen, J.; Klopman, G.; Standsberg, C.; Benoit, M.; Briggs, M.; Miles, M.; Santas, J.; Schäffer, H.; Hawkes, P. IAHR List of Sea Parameters: An update for multidirectional waves. In Proceedings of the 27th IAHR Congress, San Francisco, CA, USA, 10–15 August 1997; Mansard, E., Ed.; Canadian Government Publishing: Ottawa, ON, Canada, 1997. 11p. [Google Scholar]
- J Cargo, C.; Plummer, A.; Hillis, A.; Schlotter, M. Determination of optimal parameters for a hydraulic power take-off unit of a wave energy converter in regular waves. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 98–111. [Google Scholar] [CrossRef]
- Borgman, L.; Panicker, N. Design Study for a Suggested Wave Gage Array off Point Mugu, California; Technical Report (University of California, Berkeley. Hydraulic Engineering Laboratory) HEL; University of California, Hydraulic Engineering Laboratory: Berkeley, CA, USA, 1970. [Google Scholar]

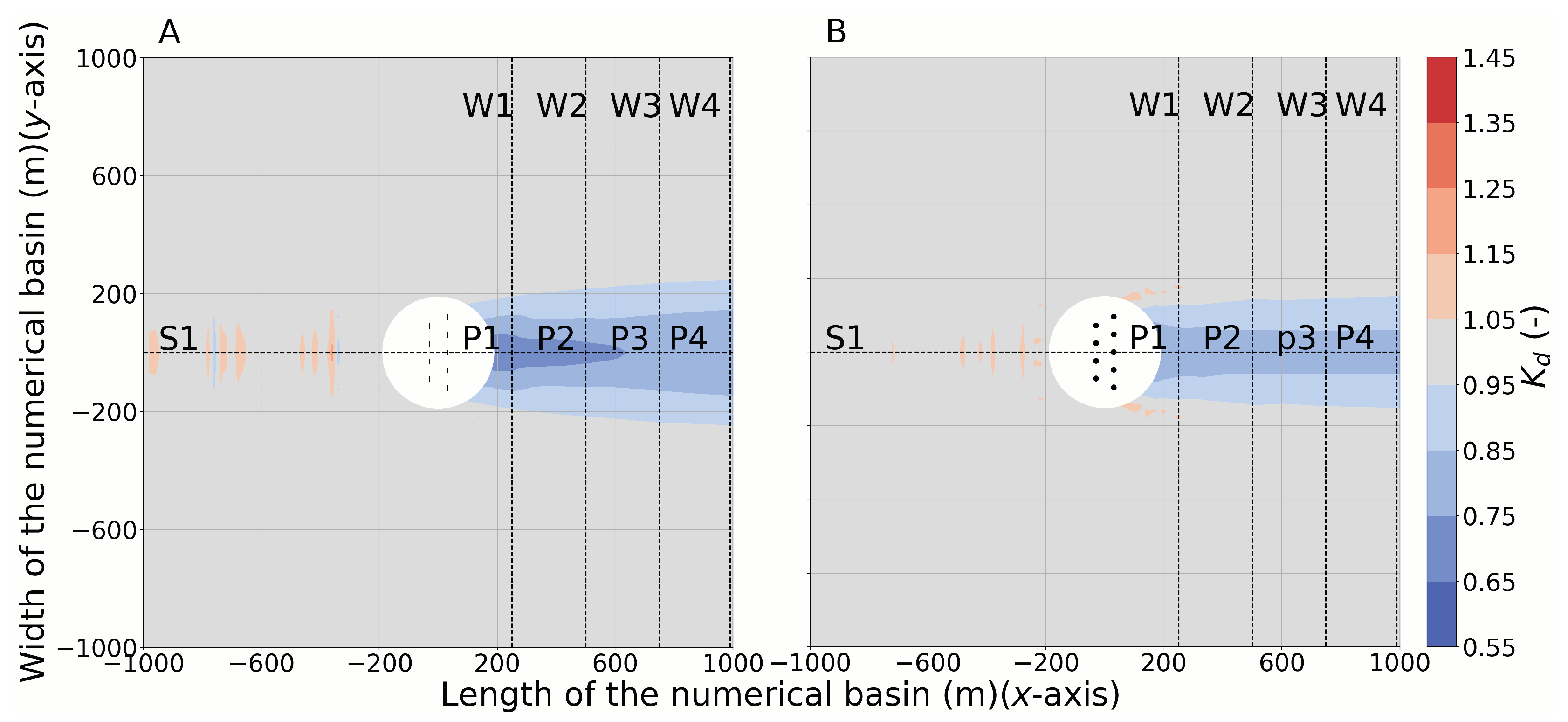
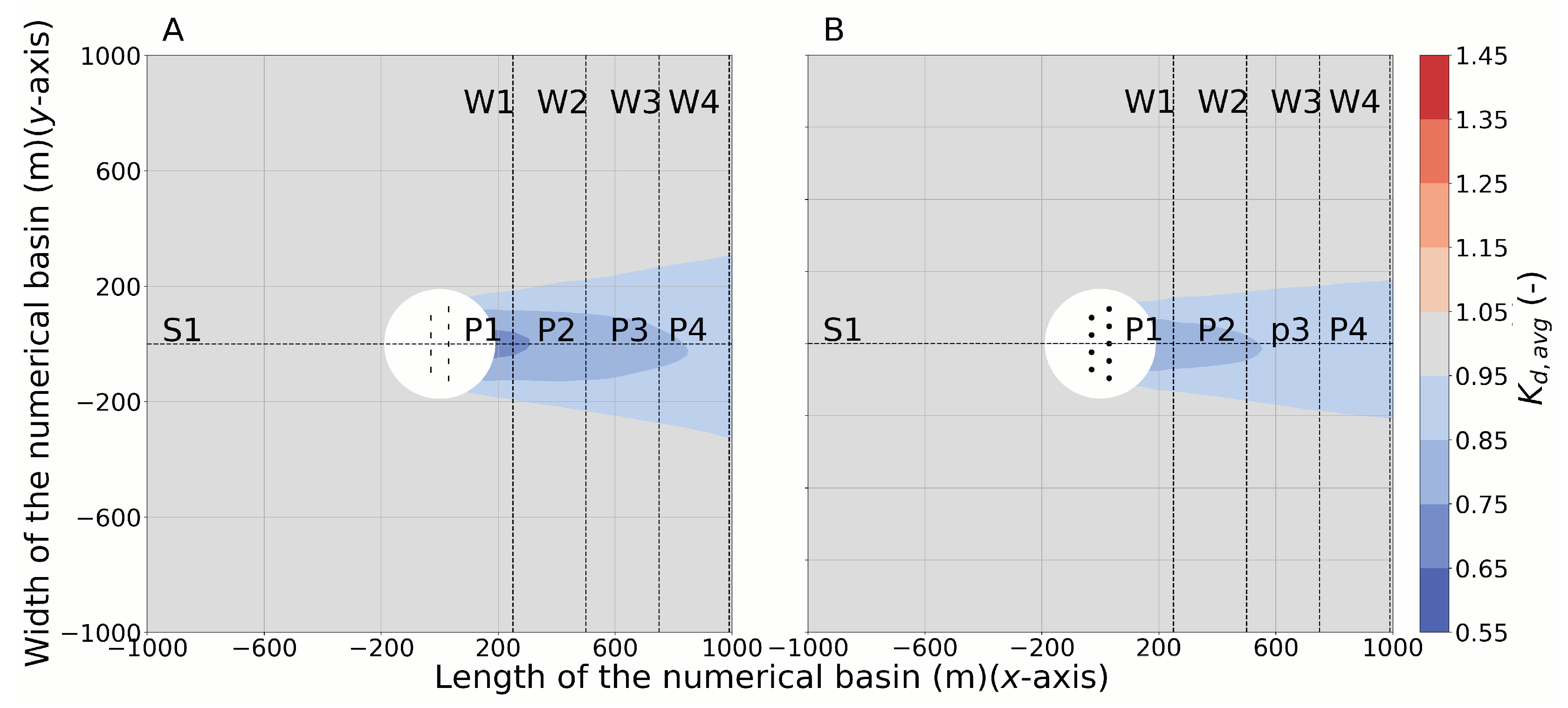

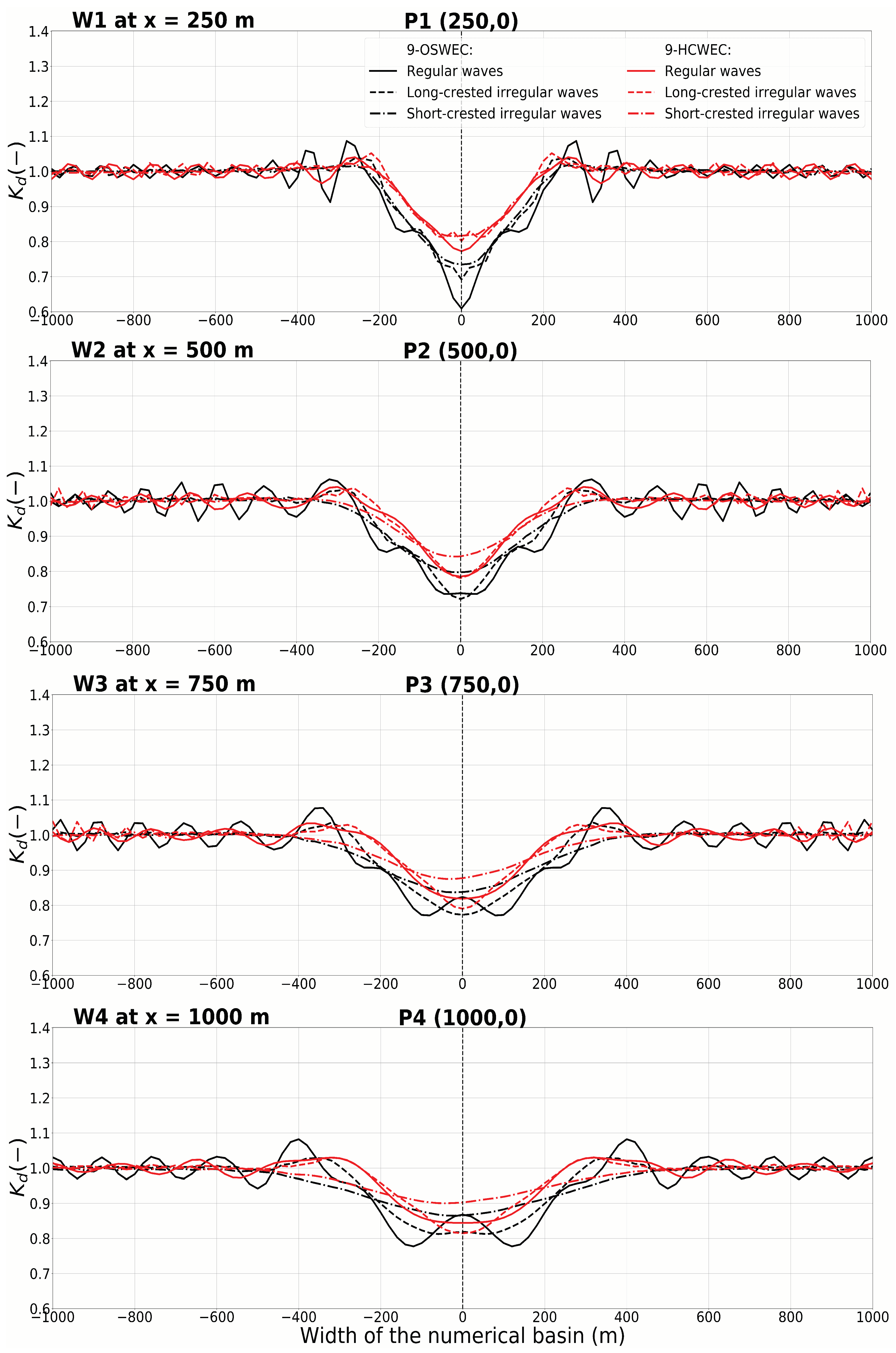
| Regular Waves | Long-Crested Irregular Waves | Short-Crested Irregular Waves |
|---|---|---|
| H = m | m | = m |
| s | s | = s |
| = 2000.0 m | = 2000.0 m | = 2000.0 m |
| = 2000.0 m | = 2000.0 m | = 2000.0 m |
| - | Pierson–Moskowitz Spectrum | Pierson–Moskowitz Spectrum |
| - | = 20 | = 50 |
| - | = 0.0 | = 15.8 |
| = L/30 = 3.0 m | = /30 = 3.0 m | = /30 = 3.0 m |
| = L/30 = 3.0 m | = /30 = 3.0 m | = /30 = 3.0 m |
| = 600 s | = 4000 s | = 5000 s |
| = 0.4 s | = 0.4 s | = 0.4 s |
| Regular Waves | Long-Crested Irregular Waves | Short-Crested Irregular Waves |
|---|---|---|
| H = m | m | = m |
| s | s | = s |
| = 400.0 m | = 400.0 m | = 400.0 m |
| = 400.0 m | = 400.0 m | = 400.0 m |
| - | Pierson–Moskowitz Spectrum | Pierson–Moskowitz Spectrum |
| - | = 20 | = 50 |
| - | = 0.0 | = 15.8 |
| = L/30 = 3.0 m | = /30 = 3.0 m | = /30 = 3.0 m |
| = L/30 = 3.0 m | = /30 = 3.0 m | = /30 = 3.0 m |
| Test Case | Wave Type | WEC (array) |
|---|---|---|
| 1 | Regular | Single HCWEC |
| 2 | Regular | H1 array layout |
| 3 | Regular | H2 array layout |
| 4 | Regular | Single OSWEC |
| 5 | Regular | O1 array layout |
| 6 | Regular | O2 array layout |
| 7 | Irregular long-crested | Single HCWEC |
| 8 | Irregular long-crested | H1 array layout |
| 9 | Irregular long-crested | H2 array layout |
| 10 | Irregular long-crested | Single OSWEC |
| 11 | Irregular long-crested | O1 array layout |
| 12 | Irregular long-crested | O2 array layout |
| 13 | Irregular short-crested | Single HCWEC |
| 14 | Irregular short-crested | H1 array layout |
| 15 | Irregular short-crested | H2 array layout |
| 16 | Irregular short-crested | Single OSWEC |
| 17 | Irregular short-crested | O1 array layout |
| 18 | Irregular short-crested | O2 array layout |
| P1(250,0) | P2(500,0) | P3(750,0) | P4(1000,0) | |
|---|---|---|---|---|
| 1 HCWEC | ||||
| Regular waves | −3.11 | −2.15 | −1.77 | −1.54 |
| Long-crested irregular waves | −4.7 | −3.24 | −2.66 | −2.31 |
| Short-crested irregular waves | −4.92 | −3.01 | −2.37 | −2.03 |
| 1 OSWEC | ||||
| Regular waves | −7.87 | −5.74 | −4.74 | −4.15 |
| Long-crested irregular waves | −7.53 | −5.28 | −4.42 | −3.90 |
| Short-crested irregular waves | −5.21 | −3.39 | −2.87 | −2.85 |
| 5 HCWEC | ||||
| Regular waves | −17.99 | −12.19 | −9.89 | −8.53 |
| Long-crested irregular waves | −21.21 | −14.93 | −11.96 | −10.23 |
| Short-crested irregular waves | −16.69 | −10.66 | −7.91 | −6.12 |
| 5 OSWEC | ||||
| Regular waves | −22.12 | −20.67 | −18.87 | −17.50 |
| Long-crested irregular waves | −23.52 | −16.50 | −15.08 | −14.06 |
| Short-crested irregular waves | −20.37 | −13.63 | −10.42 | −8.64 |
| 9 HCWEC | ||||
| Regular waves | −22.75 | −21.51 | −18.12 | −15.75 |
| Long-crested irregular waves | −19.82 | −21.90 | −21.72 | −18.71 |
| Short-crested irregular waves | −18.49 | −15.80 | −12.50 | −10.17 |
| 9 OSWEC | ||||
| Regular waves | −39.08 | −26.15 | −22.67 | −22.48 |
| Long-crested irregular waves | −30.81 | −27.83 | −22.72 | −18.90 |
| Short-crested irregular waves | −26.55 | −20.28 | −16.23 | −13.59 |
| Computational Time (h) | |||||
|---|---|---|---|---|---|
| Test Case | J, Number | NEMOH | MILDwave | MILDwave | Total |
| Number | of Bodies [-] | Perturbed Wave | Incident Wave | Perturbed Wave | Computational |
| Simulation | Simulation | Simulation | Time | ||
| 1 | 1 | 0.00 | 0.18 | 0.22 | 0.40 |
| 2 | 5 | 0.03 | 0.18 | 0.22 | 0.43 |
| 3 | 9 | 0.08 | 0.18 | 0.22 | 0.48 |
| 7 | 1 | 0.21 | 0.5 | 0.77 | 1.48 |
| 8 | 5 | 0.41 | 0.5 | 0.77 | 1.68 |
| 9 | 9 | 1.51 | 0.5 | 0.77 | 2.78 |
| 10 | 1 | 0.08 | 1.18 | 1.21 | 2.47 |
| 11 | 5 | 0.75 | 1.18 | 1.21 | 4.14 |
| 12 | 9 | 4.16 | 1.18 | 1.21 | 6.63 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verao Fernandez, G.; Stratigaki, V.; Vasarmidis, P.; Balitsky, P.; Troch, P. Wake Effect Assessment in Long- and Short-Crested Seas of Heaving-Point Absorber and Oscillating Wave Surge WEC Arrays. Water 2019, 11, 1126. https://doi.org/10.3390/w11061126
Verao Fernandez G, Stratigaki V, Vasarmidis P, Balitsky P, Troch P. Wake Effect Assessment in Long- and Short-Crested Seas of Heaving-Point Absorber and Oscillating Wave Surge WEC Arrays. Water. 2019; 11(6):1126. https://doi.org/10.3390/w11061126
Chicago/Turabian StyleVerao Fernandez, Gael, Vasiliki Stratigaki, Panagiotis Vasarmidis, Philip Balitsky, and Peter Troch. 2019. "Wake Effect Assessment in Long- and Short-Crested Seas of Heaving-Point Absorber and Oscillating Wave Surge WEC Arrays" Water 11, no. 6: 1126. https://doi.org/10.3390/w11061126
APA StyleVerao Fernandez, G., Stratigaki, V., Vasarmidis, P., Balitsky, P., & Troch, P. (2019). Wake Effect Assessment in Long- and Short-Crested Seas of Heaving-Point Absorber and Oscillating Wave Surge WEC Arrays. Water, 11(6), 1126. https://doi.org/10.3390/w11061126






