1. Introduction
Runoff forecasting, especially medium- and long-term runoff forecasting, plays an important role in the comprehensive development, utilization, scientific management and optimization of water resources [
1,
2,
3,
4]. Extreme floods, which seem to occur more frequently in recent years (due to climate change), cause immense human suffering and result in enormous economic losses every year worldwide. Therefore, it is necessary to accurately predict the time and size of peak flow before a flood event [
5]. Accurate prediction of medium- and long-term runoff is an important prerequisite for guiding the comprehensive development and utilization of water resources, scientific management, and optimal dispatch. Over the past decades, massive runoff forecasting methods and application studies have been carried out at home and abroad. In terms of methods, they can be roughly divided as: data driven model and process driven model. A data-driven model refers to the optimal mathematical relationship between a forecast object (such as annual average runoff) and a predictor (such as the circulation index) based on historical data, regardless of the physical mechanism of the hydrological process. These mathematical relationships can be used to predict future hydrological variables [
6]. Traditional methods used to establish mathematical relations include linear regression, stepwise regression [
7], local regression, artificial neural networks [
8,
9,
10], and support vector machines [
11,
12,
13]. Meanwhile, a process-driven model requires a hydrological model that can reflect the characteristics of runoff, and future medium- and long-term rainfall information is used as model input to obtain changes in the forecast object [
14]. The ensemble streamflow prediction (ESP) method proposed by American scholar Day [
15] is a process-driven model and researchers have used this method to study medium- and long-term runoff forecasting in many watersheds. As the mechanism of hydrological process has not been fully elucidated, the applicability of this model is limited [
16,
17,
18,
19,
20]. Therefore, a data-driven model, especially the runoff prediction model based on neural networks, has become a focused topic for [
21,
22,
23,
24] the application of back propagation (BP) neural networks to medium- and long-term hydrological forecasting [
25]. In [
26,
27,
28], the application of wavelet neural networks to runoff forecasting was investigated. In [
29], the application of gray self-memory based on a BP network model to runoff forecasting was examined. However, these neural network models have two drawbacks: easy fall into local minima and slow convergence [
30]. SHAO Yue-hong et al. [
31] further evaluate and compare the performance of ENN and land surface hydrological model (TOPX) in the study region.
At present, the commonly used methods for medium and long-term runoff forecasting are based on statistical methods, that is, forecasting is realized by looking for the statistical relationship between the forecasted objects and forecasted factors.
There are three problems in the current statistical methods for medium- and long-term runoff forecasting: First, the hydrological process is complex, and there is a non-linear relationship between the forecasting factors and the forecasting objects, in addition to a linear relationship. Second, principal component analysis (PCA), which is used for noise reduction and redundancy elimination of primary factors, is essentially a linear mapping method, and the principal components obtained are generated by linear mapping. This method ignores the correlation between data higher than the second order, so the extracted principal components are not optimal. Third, the model is used to establish the optimal mathematical relationship between the forecast object and the forecast factor. The commonly used multiple regression is actually a linear fitting, which cannot reflect the nonlinear relationship between the forecast object and the forecast factor. Compared to other models, artificial neural networks for good robustness, strong nonlinear mapping and self-learning ability in long-term runoff forecast has been widely used, but neural network model parameter uncertainty may influence the accuracy of the forecast; there are certain differences in the results with each forecast.
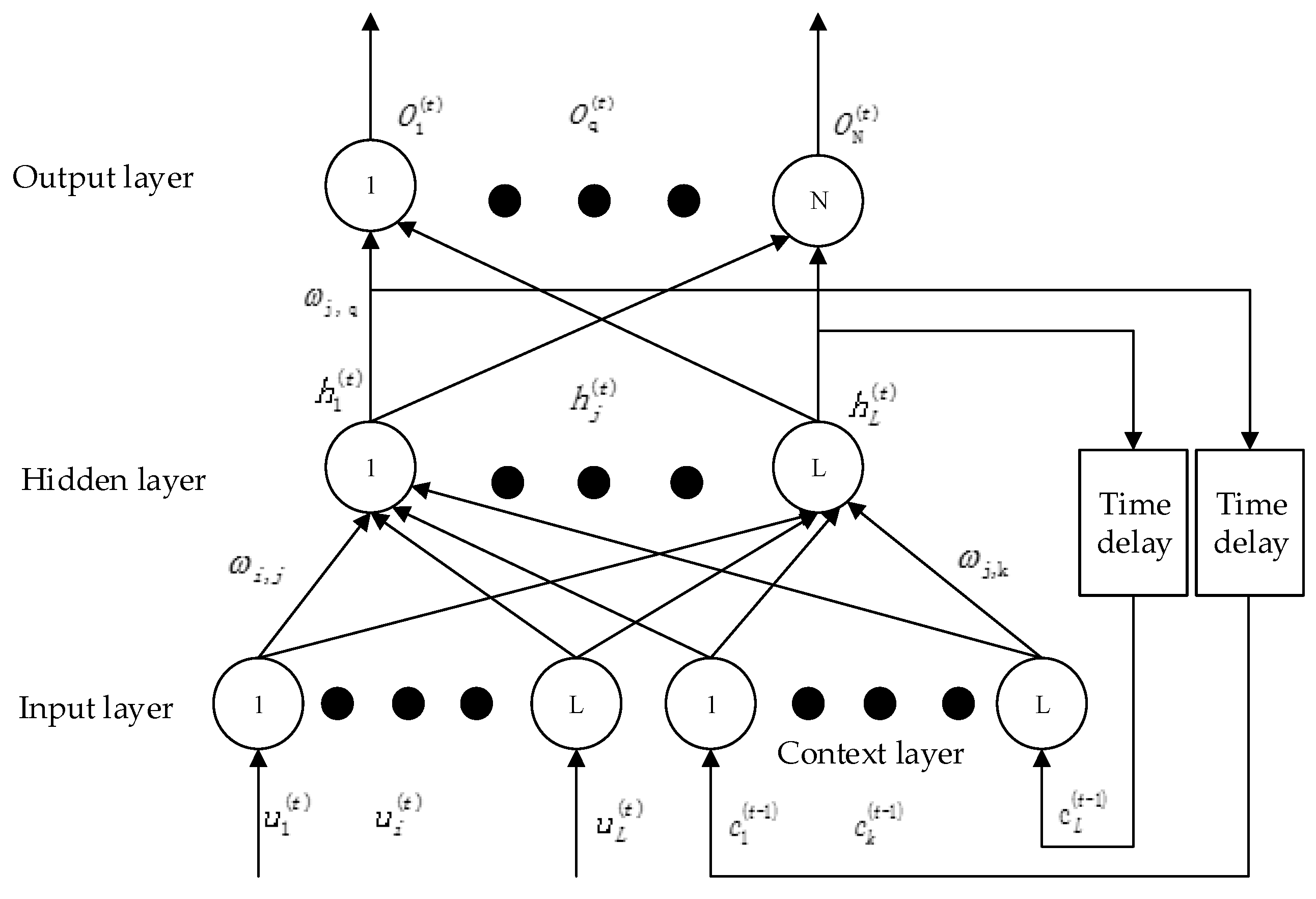
In 1990, Elman proposed the Elman Neural Network and used it to address the voice processing problem [
32]. The Elman network is a recurrent neural network with the ability to adapt to time-varying characteristics. Unlike a positive feedback neural network, it has feedback connections originating from the outputs of the hidden layer neurons to its input layer. The state of its neuron depends not only on the current input signal, but also on the previous states of the neuron [
33]. Thus, the Elman Neural Network can maintain a sort of state, allowing it to perform tasks such as sequence-prediction [
34]. However, relevant research within the domain of medium- and long-term runoff forecasting is very limited.
Compared with previous methods, the main contributions and problems solved in this paper are presented as:
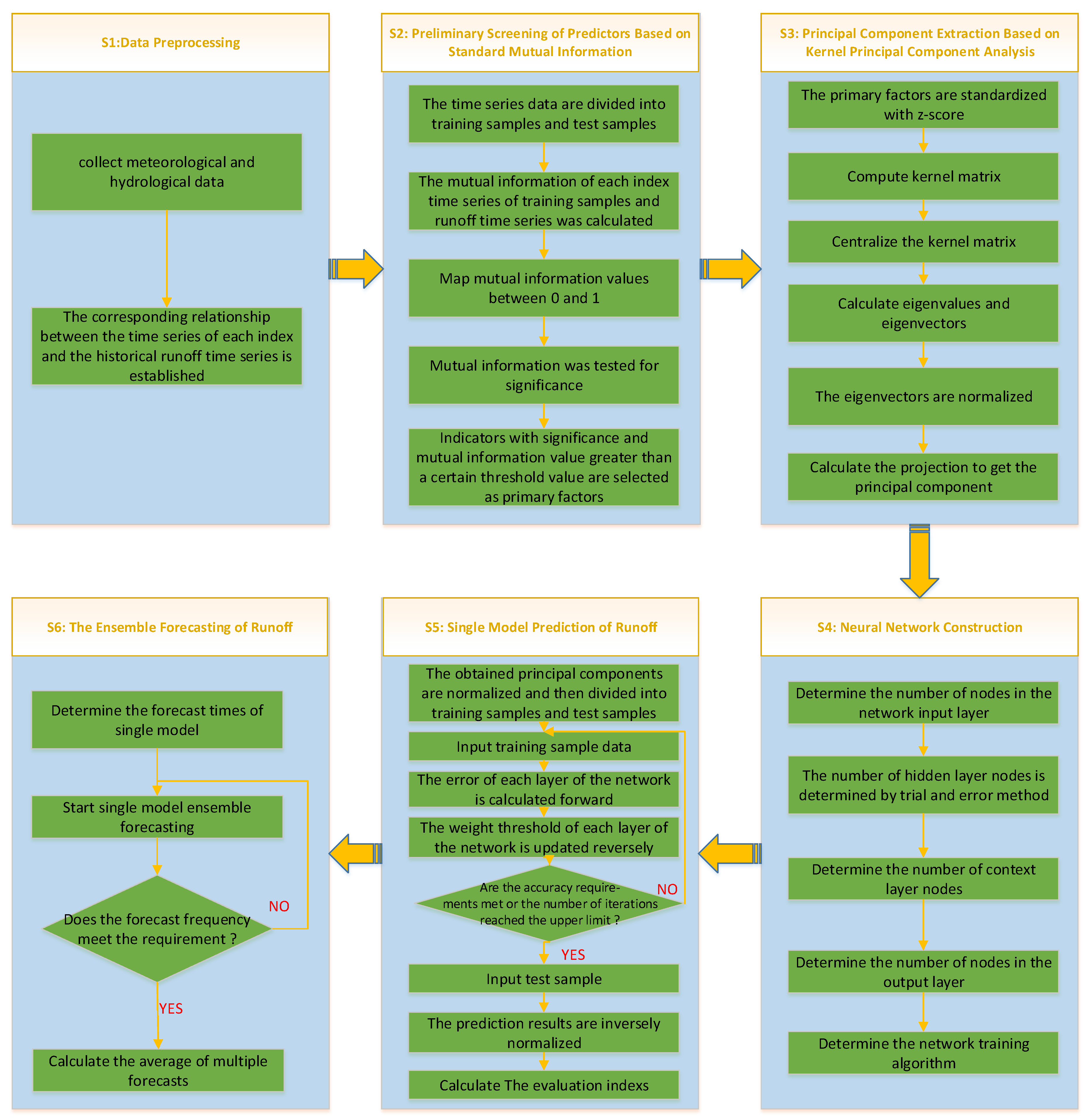
(1) Due to the non-linear relationship of experimental data, we adopted the primary prediction factor method based on NMI, which could not only reflect the nonlinear relationship between variables, but also reflect the nonlinear relationship between variables. NMI overcomes the defect of traditional linear correlation analysis.
(2) KPCA is the nonlinear extension of PCA, that is, the original vector is mapped to the high-dimensional feature space F by mapping function Φ, and PCA analysis is carried out in F. The data in the original space, which are linearly indivisible, are almost linearly separable in the high dimensional feature space. In this instance, PCA is done in a high-dimensional space, and extracted principal components are more represented. Therefore, the feature extraction method based on KPCA greatly improves the processing capacity of nonlinear data and has more advantages than the traditional feature extraction method based on PCA. In addition, the principal components extracted by KPCA are orthogonal to each other, and the data are de-noised and de-redundant, which can well prevent the overfitting of the neural network and improve the generalization ability of the network.
(3) With good robustness, nonlinear mapping, and strong self-learning ability, the artificial neural network can mine the internal relations between the prediction factors and the prediction objects. The Elman neural network selected in this paper is a typical dynamic regression network, which has additional context layers compared with commonly used forward neural networks (such as BP neural network). The context layer can record information from the last network iteration as input to the current iteration, making the Elman network more suitable for prediction of time series data [
35]. In addition, the neural network has parameter uncertainty. In order to reduce the uncertainty of prediction, the method of multi-model set prediction is adopted to improve prediction accuracy.
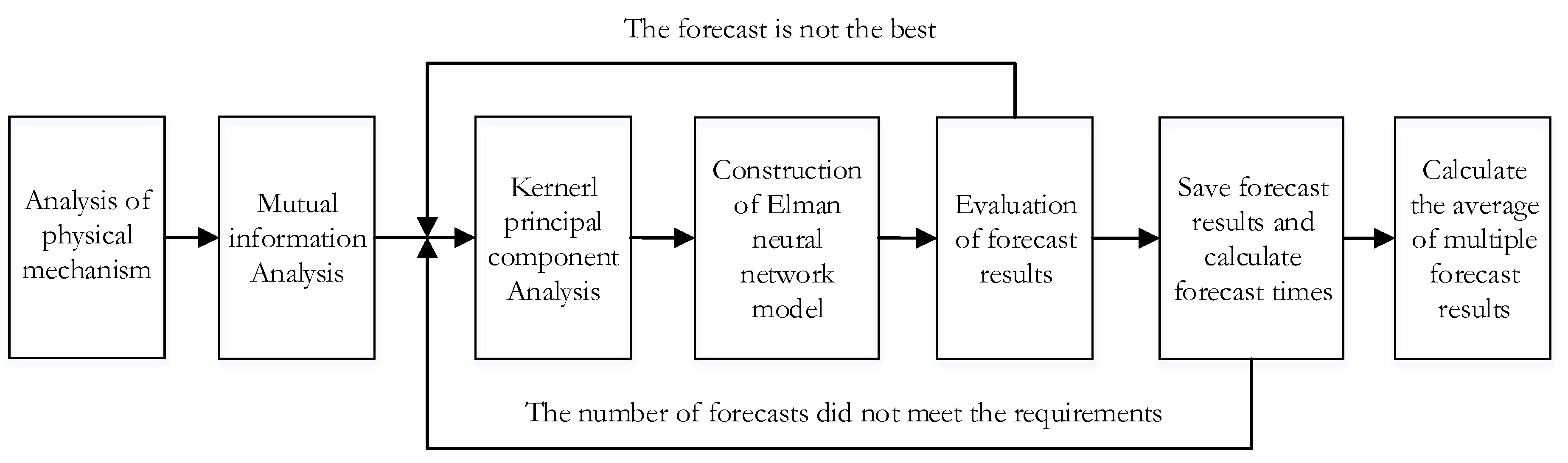
In conclusion, NMI, KPCA and Elman neural network used in this paper have the ability to process non-linear data, except linear data. In addition, the processed data can be de-noised and de-redundant to prevent overfitting of the neural network and improve the generalization ability of the network. The combination of the above three methods overcomes the limitation of traditional methods and improves the stability and accuracy of model prediction. The main purpose of this paper is to build an adaptive data driven runoff forecast [
36,
37] model, by using the normalized mutual information method to automatically select predictors, and then use the KPCA method to extract features from the selected factors; finally, based on the above, a cyclic neural network model is constructed for runoff prediction. Through the analysis and evaluation of the experimental results, the accuracy of the prediction [
38] is improved, and the average annual runoff predicted by a single model. Multiple models are realized based on the Elman neural network, which provides a reference for medium- and long-term runoff prediction [
39].