A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources
Abstract
1. Introduction
2. Random Forests
2.1. How Random Forests Work
2.1.1. Supervised Learning
2.1.2. Classification and Regression Trees
2.1.3. Bagging
2.1.4. Random Forests
2.2. Properties of Random Forests
2.3. Variable Importance Metrics
2.4. Parameters
2.5. Variable Selection
2.6. Interactions
2.7. Uncertainty, Time Series Forecasting, Spatial and Spatiotemporal Modeling
2.8. What to Expect and Not Expect from Random Forests
2.8.1. Twenty Two Reasons towards the Use of Random Forests
- 1.1.
- 1.2.
- They can capture non-linear dependencies between predictor and dependent variables (see e.g., Boulesteix et al. [16]).
- 1.3.
- They are non-parametric; i.e., no parametric statistical model needs to be defined for their use (see e.g., Boulesteix et al. [16]).
- 1.4.
- They are fast compared to other machine learning algorithms (see e.g., Ziegler and König [17]) and, also, they can operate in parallel computing mode.
- 1.5.
- They can be applied to large-scale problems (see e.g., Biau and Scornet [2]).
- 1.6.
- 1.7.
- They do not overfit (see e.g., Díaz-Uriarte and De Andres [80]).
- 1.8.
- 1.9.
- The number of model parameters is small, and the default values in corresponding software implementations are properly set and the algorithm is robust to changes of the parameters (see Section 2.4, and Biau and Scornet [2], Díaz-Uriarte and De Andres [80]).
- 1.10.
- They are robust to the inclusion of noisy predictor variables (see e.g., Díaz-Uriarte and De Andres [80]).
- 1.11.
- 1.12.
- They can operate successfully when interactions (see Section 2.6) are present (see e.g., Boulesteix et al. [16], Ziegler and König [17], Díaz-Uriarte and De Andres [80], Boulesteix et al. [83]).
- 1.13.
- 1.14.
- They permit ranking of the relative significance of predictor variables, through variable importance metrics (VIMs; see Section 2.3 and Biau and Scornet [2], Ziegler and König [17], Díaz-Uriarte and De Andres [80]).
- 1.15.
- Variable selection procedures, based on VIMs, can be combined with other machine learning algorithms (see e.g., Ziegler and König [17]).
- 1.16.
- They can effectively handle small sample sizes (see e.g., Biau and Scornet [2]).
- 1.17.
- 1.18.
- They can simultaneously incorporate continuous and categorical variables (see e.g., Díaz-Uriarte and De Andres [80]).
- 1.19.
- They can be used to solve problems with many classes of the response variable (see e.g., Díaz-Uriarte and De Andres [80]).
- 1.20.
- They are invariant to monotone transformations of the predictor variables (see e.g., Díaz-Uriarte and De Andres [80]).
- 1.21.
- They can effectively handle missing data (see e.g., Biau and Scornet [2]).
- 1.22.
- There exist free software implementations of RF algorithms (see e.g., Díaz-Uriarte and De Andres [80]), with most variants and extensions been available as contributed packages in the R programming language.
2.8.2. Why the Practicing Hydrologist Should Use Random Forests with Caution
- 2.1.
- The theoretical properties of random forests are not fully understood, and they are usually interpreted based on simplified/stylized versions of the algorithm (see e.g., Biau and Scornet [2], Ziegler and König [17], and Section 2.2).
- 2.2.
- Random forests cannot extrapolate outside the training range; see Hengl et al. [47] for an example.
- 2.3.
- 2.4.
- Random forests are harder to interpret/understand compared to single trees (see e.g., Ziegler and König [17]).
- 2.5.
- The automation of random forests may result in a slight decrease of their predictive performance compared to e.g., highly parameterized tree-based boosting (see e.g., Efron and Hastie [3], p. 324).
- 2.6.
- They cannot adequately model datasets with imbalanced data (i.e., datasets in which the number of observations of the response variable belonging to one class differs significantly compared to other classes, [91]).
- 2.7.
3. Random Forest Variants
4. R Software
5. Random Forests in a Published Case Study
6. Application of Random Forests and Related Algorithms in Water Sciences
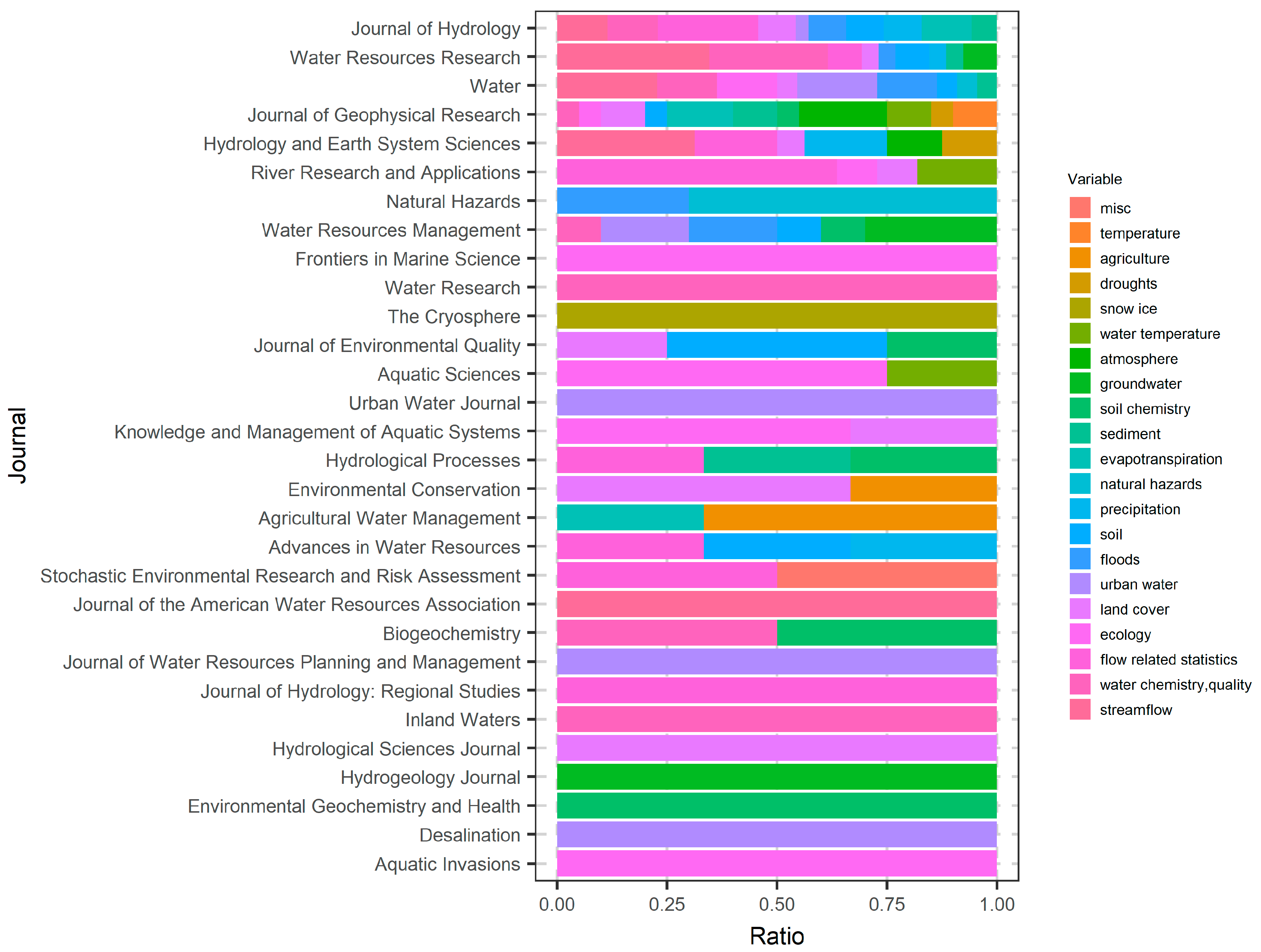
6.1. Literature Search Results
6.2. More in-Depth Analysis on the Use of Random Forests
- Ability to model non-linear relationships (reason 1.2), and ability to model interactions (reason 1.12).
- Speed (reason 1.4), and small number of parameters (reason 1.9).
- Simplicity (reason 1.6), and small number of parameters (reason 1.9).
- Flexibility of the algorithm (reason 1.13), and reliability of VIMs (reason 2.3).
- Ability to process small samples (reason 1.16), and free software implementation (reason 1.22).
- Ability to solve problems with many classes (reason 1.19), and free software implementation (reason 1.22).
7. Concluding Remarks and Take-Home Considerations
- Contrary to the general class of data-driven models, which focus mostly on forecasting and prediction over interpretation and understanding, random forests allow for explicit interpretation of the obtained results through variable importance metrics (VIMs); see Introduction.
- Important considerations regarding the implementation of data-driven models in water science, such as splitting of the dataset into training and testing periods, preprocessing of variables, and variable selection, are explicitly dealt with by random forests. For example, tuning of the algorithm is commonly performed using OOB (out-of-bag) data (see Section 2.1.4 and Section 2.5), preprocessing has generally small influence on the predictive performance of the algorithm (see reason 1.20 in Section 2.8.1), while there are many automatic variable selection procedures based on VIMs (see reason 1.15 in Section 2.8.1).
- In 33% of the reviewed water-related studies (i.e., 67 out of 203) random forests were not the algorithm of focus but, rather, they were used to complement other modeling approaches to improve inference. This highlights their usefulness in water science.
- The role of random forests as a useful complementary tool in water resources applications is related to their benchmarking nature (see e.g., the comment by Efron and Hastie [3] (pp. 347, 348) in Section 2.8.1, and reason 1.1), as well as their simplicity and ease of use (see Section 2.8.1). Other important properties of RF algorithms are their speed, and the fact that little (or no) tuning of their parameters is required to reach an acceptable predictive performance; see Section 6.1.
- While some attractive properties of random forests are also shared by other data-driven methods (e.g., non-linear and non-parametric modeling), their selection is driven mostly by their increased predictive performance, their capability to capture non-linear dependencies and interactions of variables, as well as their speed, parsimonious parameterization, ease of use, and ability to handle big datasets; see Section 6.1 and Section 6.2, and Figure 8. The use of VIMs for interpretation and variable selection is also noteworthy, as they are not commonly implemented by data-driven models other than random forests.
- The large potential of random forests in water resources applications has been exploited only to a small degree. Perhaps, this is related to the fact that many RF-variants were introduced very recently, while the properties of the algorithm are not fully understood; see Section 6.1. Thus, the potential for further uses and improvements is large, including variants specializing in clustering, modeling of interactions, heteroscedasticity, survival analysis, computation of VIMs and more. The added value of random forests is also confirmed by a wide range of applications in diverse areas of research, such as streamflow modeling, imputation of missing values, water quality, hydrological signatures, ecology, land cover, urban water, floods, and soil properties among other applications; see Section 6.1 for further details.
- Another important aspect is that most RF-variants have been implemented in the R programming language, and are freely available; see Table 3. This facilitates reproducibility of the results, research advancements, as well as further uses of the algorithm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Biau, G.Ã.Š.; Scornet, E. A random forest guided tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T. Computer Age Statistical Inference, 1st ed.; Cambridge University Press: New York, NY, USA, 2016; ISBN 9781107149892. [Google Scholar]
- Liakos, K.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.L. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Granger, J.; Amani, M.; Brisco, B.; Huang, W. Remote sensing for wetland classification: A comprehensive review. GISci. Remote Sens. 2018, 55, 623–658. [Google Scholar] [CrossRef]
- Chen, X.; Wang, M.; Zhang, H. The use of classification trees for bioinformatics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, B.A.; Polley, E.C.; Briggs, F.B.S. Random forests for genetic association studies. Stat. Appl. Genet. Mol. Biol. 2011, 10, 32. [Google Scholar] [CrossRef]
- Chen, X.; Ishwaran, H. Random forests for genomic data analysis. Genomics 2012, 99, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Cherkasov, A.; Muratov, E.N.; Fourches, D.; Varnek, A.; Baskin, I.I.; Cronin, M.; Dearden, J.; Gramatica, P.; Martin, Y.C.; Todeschini, R.; et al. QSAR modeling: Where have you been? Where are you going to? J. Med. Chem. 2014, 57, 4977–5010. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.M.; Schwender, H.; Keith, J.; Nunkesser, R.; Mengersen, K.; Macrossan, P. Methods for identifying SNP interactions: A review on variations of logic regression, random forest and Bayesian logistic regression. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 1580–1591. [Google Scholar] [CrossRef] [PubMed]
- Criminisi, A.; Shotton, J.; Konukoglu, E. Decision forests: A unified framework for classification, regression, density estimation, manifold learning and semi-supervised learning. Found. Trends Comput. Graph. Vis. 2011, 7, 81–227. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 493–507. [Google Scholar] [CrossRef]
- Ziegler, A.; König, I.R. Mining data with random forests: Current options for real-world applications. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 55–63. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinformatics 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological modelling using artificial neural networks. Prog. Phys. Geogr. Earth Environ. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Jain, A.; Maier, H.R.; Dandy, G.C.; Sudheer, K.P. Rainfall runoff modelling using neural networks: State-of-the-art and future research needs. ISH J. Hydraul. Eng. 2009, 15 (Suppl. S1), 52–74. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Aguilera, P.A.; Fernández, A.; Fernández, R.; Rumí, R.; Salmerón, A. Bayesian networks in environmental modelling. Environ. Model. Softw. 2011, 26, 1376–1388. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.W.; Mount, N.J.; See, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.L. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. Earth Environ. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–artificial intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Raghavendra, S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Afshar, A.; Massoumi, F.; Afshar, A.; Mariño, M.A. State of the art review of ant colony optimization applications in water resource management. Water Resour. Manag. 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Choong, S.M.; El-Shafie, A. State-of-the-art for modelling reservoir inflows and management optimization. Water Resour. Manag. 2015, 29, 1267–1282. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Afan, H.A.; El-shafie, A.; Mohtar, W.H.M.W.; Yaseen, Z.M. Past, present and prospect of an Artificial Intelligence (AI) based model for sediment transport prediction. J. Hydrol. 2016, 541, 902–913. [Google Scholar] [CrossRef]
- Phan, T.D.; Smart, J.C.R.; Capon, S.J.; Hadwen, W.L.; Sahin, O. Applications of Bayesian belief networks in water resource management: A systematic review. Environ. Model. Softw. 2016, 85, 98–111. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Sudheer, K.P. Methods used for quantifying the prediction uncertainty of artificial neural network based hydrologic models. Stoch. Environ. Res. Risk Assess. 2017, 31, 1659–1670. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V.; Kahya, E.; Hrnjica, B.; Sattar, A.M.A.; Yaseen, Z.M. Genetic programming in water resources engineering: A state-of-the-art review. J. Hydrol. 2018, 566, 643–667. [Google Scholar] [CrossRef]
- Shen, C. A trans-disciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate streamflow forecasting using commonly used data-driven models: Literature review and case study. Hydrol. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 1st ed.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Olshen, R. A conversation with Leo Breiman. Stat. Sci. 2001, 16, 184–198. [Google Scholar] [CrossRef]
- Iorgulescu, I.; Beven, K.J. Nonparametric direct mapping of rainfall-runoff relationships: An alternative approach to data analysis and modeling? Water Resour. Res. 2004, 40, W08403. [Google Scholar] [CrossRef]
- Cox, D.R.; Efron, B. Statistical thinking for 21st century scientists. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Schmid, M. Machine learning versus statistical modeling. Biom. J. 2014, 56, 588–593. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D. 50 years of data science. J. Comput. Graph. Stat. 2017, 26, 745–766. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C.; Villa-Vialaneix, N. Random forests for big data. Big Data Res. 2017, 9, 28–46. [Google Scholar] [CrossRef]
- Cox, D.R.; Kartsonaki, C.; Keogh, R.H. Big data: Some statistical issues. Stat. Probab. Lett. 2018, 136, 111–115. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L. Recent advance in earth observation big data for hydrology. Big Earth Data 2018, 2, 86–107. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Binder, H.; Abrahamowicz, M.; Sauerbrei, W.; Simulation Panel of the STRATOS Initiative. On the necessity and design of studies comparing statistical methods. Biom. J. 2018, 60, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Boulesteix, A.L.; Hable, R.; Lauer, S.; Eugster, M.J.A. A statistical framework for hypothesis testing in real data comparison studies. Am. Stat. 2015, 69, 201–212. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Janitza, S.; Hornung, R.; Probst, P.; Busen, H.; Hapfelmeier, A. Making complex prediction rules applicable for readers: Current practice in random forest literature and recommendations. Biom. J. 2018. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Chang, Q. Feature selection methods for big data bioinformatics: A survey from the search perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef]
- Athey, S. Beyond prediction: Using big data for policy problems. Science 2017, 355, 483–485. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling, 1st ed.; Springer-Verlag: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Biau, G.Ã.Š.; Devroye, L.; Lugosi, G.Ã.Ą. Consistency of random forests and other averaging classifiers. J. Mach. Learn. Res. 2008, 9, 2015–2033. [Google Scholar]
- Scornet, E.; Biau, G.Ã.Š.; Vert, J.P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Scornet, E. On the asymptotics of random forests. J. Multivar. Anal. 2016, 146, 72–83. [Google Scholar] [CrossRef]
- Genuer, R. Variance reduction in purely random forests. J. Nonparametric Stat. 2012, 24, 543–562. [Google Scholar] [CrossRef]
- Biau, G.Ã.Š. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Grömping, U. Variable importance in regression models. Wiley Interdiscip. Rev. Comput. Stat. 2015, 7, 137–152. [Google Scholar] [CrossRef]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining data with random forests: A survey and results of new tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application and characteristics of classification and regression trees, bagging and random forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed]
- Janitza, S.; Tutz, G.; Boulesteix, A.L. Random forest for ordinal responses: Prediction and variable selection. Comput. Stat. Data Anal. 2016, 96, 57–73. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Bender, A.; Bermejo, J.L.; Strobl, C. Random forest Gini importance favours SNPs with large minor allele frequency: Impact, sources and recommendations. Brief. Bioinform. 2012, 13, 292–304. [Google Scholar] [CrossRef]
- Nicodemus, K.K.; Malley, J.D.; Strobl, C.; Ziegler, A. The behaviour of random forest permutation based variable importance measures under predictor correlation. BMC Bioinform. 2010, 11, 110. [Google Scholar] [CrossRef]
- Hapfelmeier, A.; Hothorn, T.; Ulm, K.; Strobl, C. A new variable importance measure for random forests with missing data. Stat. Comput. 2014, 24, 21–34. [Google Scholar] [CrossRef]
- Janitza, S.; Celik, E.; Boulesteix, A.L. A computationally fast variable importance test for random forests for high-dimensional data. Adv. Data Anal. Classif. 2016. [Google Scholar] [CrossRef]
- Scornet, E. Tuning parameters in random forests. ESAIM Proc. Surv. 2017, 60, 144–162. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.L. To tune or not to tune the number of trees in random forest. J. Mach. Learn. Res. 2018, 18, 1–18. [Google Scholar]
- Díaz-Uriarte, R.; De Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Heinze, G.; Wallisch, C.; Dunkler, D. Variable selection—A review and recommendations for the practicing statistician. Biom. J. 2018, 60, 431–449. [Google Scholar] [CrossRef] [PubMed]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Boulesteix, A.L.; Janitza, S.; Hapfelmeier, A.; Van Steen, K.; Strobl, C. Letter to the Editor: On the term ‘interaction’ and related phrases in the literature on Random Forests. Brief. Bioinform. 2015, 16, 338–345. [Google Scholar] [CrossRef]
- Wager, S.; Hastie, T.; Efron, B. Confidence intervals for random forests: The Jackknife and the infinitesimal Jackknife. J. Mach. Learn. Res. 2014, 15, 1625–1651. [Google Scholar] [PubMed]
- Meinshausen, N. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Tyralis, H.; Papacharalampous, G. Variable selection in time series forecasting using random forests. Algorithms 2017, 10, 114. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. One-step ahead forecasting of geophysical processes within a purely statistical framework. Geosci. Lett. 2018, 5, 12. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 481–514. [Google Scholar] [CrossRef]
- Athey, S.; Tibshirani, J.; Wager, S. Generalized random forests. Ann. Stat. 2019, 47, 1148–1178. [Google Scholar] [CrossRef]
- Wolpert, D.H. The lack of a priori distinctions between learning algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Schubach, M.; Re, M.; Robinson, P.N.; Valentini, G. Imbalance-aware machine learning for predicting rare and common disease-associated non-coding variants. Sci. Rep. 2017, 7, 2959. [Google Scholar] [CrossRef]
- Wager, S.; Athey, S. Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Tripoliti, E.E.; Fotiadis, D.I.; Manis, G. Modifications of the construction and voting mechanisms of the Random Forests Algorithm. Data Knowl. Eng. 2013, 87, 41–65. [Google Scholar] [CrossRef]
- Chipman, H.A.; George, E.I.; McCulloch, R.E. BART: Bayesian Additive Regression Trees. Ann. Appl. Stat. 2010, 4, 266–298. [Google Scholar] [CrossRef]
- Pratola, M.; Chipman, H.A.; George, E.I.; McCulloch, R.E. Heteroscedastic BART using multiplicative regression trees. arXiv, 2018; arXiv:1709.07542v2. [Google Scholar]
- Schlosser, L.; Hothorn, T.; Stauffer, R.; Zeileis, A. Distributional regression forests for probabilistic precipitation forecasting in complex terrain. arXiv, 2018; arXiv:1804.02921v1. [Google Scholar]
- Segal, M.; Xiao, Y. Multivariate random forests. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 80–87. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 3, 841–860. [Google Scholar] [CrossRef]
- Nowozin, S.; Rother, C.; Bagon, S.; Sharp, T.; Yao, B.; Kohli, P. Decision tree fields. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar] [CrossRef]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased recursive partitioning: A conditional inference framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Shah, R.D.; Meinshausen, N. Random intersection trees. J. Mach. Learn. Res. 2014, 15, 629–654. [Google Scholar]
- Basu, S.; Kumbier, K.; Brown, J.B.; Yu, B. Iterative random forests to discover predictive and stable high-order interactions. Proc. Natl. Acad. Sci. USA 2018, 115, 1943–1948. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Amaratunga, D.; Cabrera, J.; Lee, Y.S. Enriched random forests. Bioinformatics 2008, 24, 2010–2014. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Augustin, T. Unbiased split selection for classification trees based on the Gini index. Comput. Stat. Data Anal. 2007, 52, 483–501. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Yang, F.; Wang, J.; Fan, G. Kernel induced survival forests. arXiv, 2010; arXiv:1008.3952v1. [Google Scholar]
- Ishwaran, H.; Kogalur, U.B.; Chen, X.; Minn, A.J. Random survival forests for high-dimensional data. Stat. Anal. Data Min. 2011, 4, 115–132. [Google Scholar] [CrossRef]
- Saffari, A.; Leistner, C.; Santner, J.; Godec, M.; Bischof, H. On-line random forests. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009. [Google Scholar] [CrossRef]
- Yi, Z.; Soatto, S.; Dewan, M.; Zhanm, Y. Information forests. In Proceedings of the 2012 Information Theory and Applications Workshop, San Diego, CA, USA, 5–10 February 2012. [Google Scholar] [CrossRef]
- Denil, M.; Matheson, D.; Freitas, N. Consistency of online random forests. Proc. Mach. Learn. Res. 2013, 28, 1256–1264. [Google Scholar]
- Lakshminarayanan, B.; Roy, D.M.; Teh, Y.W. Mondrian forests: Efficient online random forests. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: New York, NY, USA, 2014; pp. 3140–3148. [Google Scholar]
- Clémençon, S.; Vayatis, N. Tree-based ranking methods. IEEE Trans. Inf. Theory 2009, 55, 4316–4336. [Google Scholar] [CrossRef]
- Clémençon, S.; Depecker, M.; Vayatis, N. Ranking forests. J. Mach. Learn. Res. 2013, 14, 39–73. [Google Scholar]
- Ozuysal, M.; Calonder, M.; Lepetit, V.; Fua, P. Fast keypoint recognition using random ferns. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 448–461. [Google Scholar] [CrossRef] [PubMed]
- Meinshausen, N. Node harvest. Ann. Appl. Stat. 2010, 4, 2049–2072. [Google Scholar] [CrossRef]
- Montillo, A.; Shotton, J.; Winn, J.; Iglesias, J.E.; Metaxas, D.; Criminisi, A. Entangled decision forests and their application for semantic segmentation of CT images. In Information Processing in Medical Imaging. IPMI 2011; Lecture Notes in Computer Science; Székely, G., Hahn, H.K., Eds.; Springer: Berlin/Heidelberg, Germany; Volume 6801, pp. 184–196. [CrossRef]
- Pauly, O.; Mateus, D.; Navab, N. STARS: A new ensemble partitioning approach. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011. [Google Scholar] [CrossRef]
- Bernard, S.; Adam, S.; Heutte, L. Dynamic random forests. Pattern Recognit. Lett. 2012, 33, 1580–1586. [Google Scholar] [CrossRef]
- Ellis, N.; Smith, S.J.; Pitcher, C.R. Gradient forests: Calculating importance gradients on physical predictors. Ecology 2012, 93, 156–168. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G. Feature selection via regularized trees. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G. Gene selection with guided regularized random forest. Pattern Recognit. 2013, 46, 3483–3489. [Google Scholar] [CrossRef]
- Yan, D.; Chen, A.; Jordan, M.I. Cluster forests. Comput. Stat. Data Anal. 2013, 66, 178–192. [Google Scholar] [CrossRef]
- Winham, S.J.; Freimuth, R.R.; Biernacka, J.M. A weighted random forests approach to improve predictive performance. Stat. Anal. Data Min. 2013, 6, 496–505. [Google Scholar] [CrossRef] [PubMed]
- Rahman, R.; Otridge, J.; Pal, R. IntegratedMRF: Random forest-based framework for integrating prediction from different data types. Bioinformatics 2017, 33, 1407–1410. [Google Scholar] [CrossRef] [PubMed]
- Denisko, D.; Hoffman, M.M. Classification and interaction in random forests. Proc. Natl. Acad. Sci. USA 2018, 115, 1690–1692. [Google Scholar] [CrossRef]
- Friedberg, R.; Tibshirani, J.; Athey, S.; Wager, S. Local linear forests. arXiv, 2018; arXiv:1807.11408v2. [Google Scholar]
- Biau, G.Ã.Š.; Scornet, E.; Welbl, J. Neural random forests. Sankhya A 2018. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. Ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Evaluation of random forests and Prophet for daily streamflow forecasting. Adv. Geosci. 2018, 45, 201–208. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner’s Guide in Atmospheric Science, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Ada, M.; San, B.T. Comparison of machine-learning techniques for landslide susceptibility mapping using two-level random sampling (2LRS) in Alakir catchment area, Antalya, Turkey. Nat. Hazards 2018, 90, 237–263. [Google Scholar] [CrossRef]
- Addor, N.; Nearing, G.; Prieto, C.; Newman, A.J.; LeVine, N.; Clark, M.P. A ranking of hydrological signatures based on their predictability in space. Water Resour. Res. 2018, 54, 8792–8812. [Google Scholar] [CrossRef]
- Anderson, G.J.; Lucas, D.D.; Bonfils, C. Uncertainty analysis of simulations of the turn-of-the-century drought in the Western United States. J. Geophys. Res. Atmos. 2018, 123, 13219–13237. [Google Scholar] [CrossRef]
- Asare-Kyei, D.; Forkuor, G.; Venus, V. Modeling flood hazard zones at the sub-district level with the rational model integrated with GIS and remote sensing approaches. Water 2015, 7, 3531–3564. [Google Scholar] [CrossRef]
- Asim, K.M.; Martínez-Álvarez, F.; Basit, A.; Iqbal, T. Earthquake magnitude prediction in Hindukush region using machine learning techniques. Nat. Hazards 2017, 85, 471–486. [Google Scholar] [CrossRef]
- Bachmair, S.; Svensson, C.; Hannaford, J.; Barker, L.J.; Stahl, K. A quantitative analysis to objectively appraise drought indicators and model drought impacts. Hydrol. Earth Syst. Sci. 2016, 20, 2589–2609. [Google Scholar] [CrossRef]
- Bachmair, S.; Weiler, M. Hillslope characteristics as controls of subsurface flow variability. Hydrol. Earth Syst. Sci. 2012, 16, 3699–3715. [Google Scholar] [CrossRef]
- Bae, M.J.; Park, Y.S. Diversity and distribution of endemic stream insects on a nationwide scale, South Korea: Conservation perspectives. Water 2017, 9, 833. [Google Scholar] [CrossRef]
- Balázs, B.; Bíró, T.; Dyke, G.; Singh, S.K.; Szabó, S. Extracting water-related features using reflectance data and principal component analysis of Landsat images. Hydrol. Sci. J. 2018, 63, 269–284. [Google Scholar] [CrossRef]
- Baudron, P.; Alonso-Sarría, F.; García-Aróstegui, J.L.; Cánovas-García, F.; Martínez-Vicente, D.; Moreno-Brotóns, J. Identifying the origin of groundwater samples in a multi-layer aquifer system with random forest classification. J. Hydrol. 2013, 499, 303–315. [Google Scholar] [CrossRef]
- Behnia, P.; Blais-Stevens, A. Landslide susceptibility modelling using the quantitative random forest method along the northern portion of the Yukon Alaska Highway Corridor, Canada. Nat. Hazards 2018, 90, 1407–1426. [Google Scholar] [CrossRef]
- Berezowski, T.; Chybicki, A. High-resolution discharge forecasting for snowmelt and rainfall mixed events. Water 2018, 10, 56. [Google Scholar] [CrossRef]
- Berryman, E.M.; Vanderhoof, M.K.; Bradford, J.B.; Hawbaker, T.J.; Henne, P.D.; Burns, S.P.; Frank, J.M.; Birdsey, R.A.; Ryan, M.G. Estimating soil respiration in a subalpine landscape using point, terrain, climate, and greenness data. J. Geophys. Res. Biogeosci. 2018, 123, 3231–3249. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef]
- Birkel, C.; Soulsby, C.; Ali, G.; Tetzlaff, D. Assessing the cumulative impacts of hydropower regulation on the flow characteristics of a large Atlantic salmon river system. River Res. Appl. 2014, 30, 456–475. [Google Scholar] [CrossRef]
- Boisramé, G.; Thompson, S.; Stephens, S. Hydrologic responses to restored wildfire regimes revealed by soil moisture-vegetation relationships. Adv. Water Resour. 2018, 112, 124–1246. [Google Scholar] [CrossRef]
- Bond, N.R.; Kennard, M.J. Prediction of hydrologic characteristics for ungauged catchments to support hydroecological modeling. Water Resour. Res. 2017, 53, 8781–8794. [Google Scholar] [CrossRef]
- Booker, D.J.; Snelder, T.H. Comparing methods for estimating flow duration curves at ungauged sites. J. Hydrol. 2012, 434–435, 78–94. [Google Scholar] [CrossRef]
- Booker, D.J.; Whitehead, A.L. Inside or outside: Quantifying extrapolation across river networks. Water Resour. Res. 2018, 54, 6983–7003. [Google Scholar] [CrossRef]
- Booker, D.J.; Woods, R.A. Comparing and combining physically-based and empirically-based approaches for estimating the hydrology of ungauged catchments. J. Hydrol. 2014, 508, 227–239. [Google Scholar] [CrossRef]
- Boyle, J.S.; Klein, S.A.; Lucas, D.D.; Ma, H.Y.; Tannahill, J.; Xie, S. The parametric sensitivity of CAM5′s MJO. J. Geophys. Res. Atmos. 2015, 120, 1424–1444. [Google Scholar] [CrossRef]
- Brentan, B.M.; Meirelles, G.L.; Manzi, D.; Luvizotto, E. Water demand time series generation for distribution network modeling and water demand forecasting. Urban Water J. 2018, 15, 150–158. [Google Scholar] [CrossRef]
- Brunner, M.I.; Furrer, R.; Sikorska, A.E.; Viviroli, D.; Seibert, J.; Favre, A.C. Synthetic design hydrographs for ungauged catchments: A comparison of regionalization methods. Stoch. Environ. Res. Risk Assess. 2018, 32, 1993–2023. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Nampak, H.; Bui, Q.T.; Tran, Q.A.; Nguyen, Q.P. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibilitgy modeling in a high-frequency tropical cyclone area using GIS. J. Hydrol. 2016, 540, 317–330. [Google Scholar] [CrossRef]
- Cabrera, P.; Carta, J.A.; González, J.; Melián, G. Wind-driven SWRO desalination prototype with and without batteries: A performance simulation using machine learning models. Desalination 2018, 435, 77–96. [Google Scholar] [CrossRef]
- Cancela, J.J.; Fandiño, M.; Rey, B.J.; Dafonte, J.; González, X.P. Discrimination of irrigation water management effects in pergola trellis system vineyards using a vegetation and soil index. Agric. Water Manag. 2017, 183, 70–77. [Google Scholar] [CrossRef]
- Carlisle, D.M.; Falcone, J.; Wolock, D.M.; Meador, M.R.; Norris, R.H. Predicting the natural flow regime: Models for assessing hydrological alteration in streams. River Res. Appl. 2010, 26, 118–136. [Google Scholar] [CrossRef]
- Carvalho, G.; Amado, C.; Brito, R.S.; Coelho, S.T.; Leitão, J.P. Analysing the importance of variables for sewer failure prediction. Urban Water J. 2018, 15, 338–345. [Google Scholar] [CrossRef]
- Castelletti, A.; Galelli, S.; Restelli, M.; Soncini-Sessa, R. Tree-based reinforcement learning for optimal water reservoir operation. Water Res. Res. 2010, 46, W09507. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple random forests modelling for urban water consumption forecasting. Water Resour. Manag. 2017, 31, 4715–4729. [Google Scholar] [CrossRef]
- Chen, K.; Guo, S.; He, S.; Xu, T.; Zhong, Y.; Sun, S. The value of hydrologic information in reservoir outflow decision-making. Water 2018, 10, 1372. [Google Scholar] [CrossRef]
- Chenar, S.S.; Deng, Z. Development of genetic programming-based model for predicting oyster norovirus outbreak risks. Water Res. 2018, 128, 20–37. [Google Scholar] [CrossRef]
- Darrouzet-Nardi, A.; Reed, S.C.; Grote, E.E.; Belnap, J. Observations of net soil exchange of CO2 in a dryland show experimental warming increases carbon losses in biocrust soils. Biogeochemistry 2015, 126, 363–378. [Google Scholar] [CrossRef]
- De Paul Obade, V.; Lal, R.; Moore, R. Assessing the accuracy of soil and water quality characterization using remote sensing. Water Resour. Manag. 2014, 28, 5091–5109. [Google Scholar] [CrossRef]
- Dhungel, S.; Tarboton, D.G.; Jin, J.; Hawkins, C.P. Potential effects of climate change on ecologically relevant streamflow regimes. River Res. Appl. 2016, 32, 1827–1840. [Google Scholar] [CrossRef]
- Diesing, M.; Kröger, S.; Parker, R.; Jenkins, C.; Mason, C.; Weston, K. Predicting the standing stock of organic carbon in surface sediments of the North–West European continental shelf. Biogeochemistry 2017, 135, 183–200. [Google Scholar] [CrossRef]
- Dubinsky, E.A.; Butkus, S.R.; Andersen, G.L. Microbial source tracking in impaired watersheds using PhyloChip and machine-learning classification. Water Res. 2016, 105, 56–64. [Google Scholar] [CrossRef]
- Erechtchoukova, M.G.; Khaiter, P.A.; Saffarpour, S. Short-term predictions of hydrological events on an urbanized watershed using supervised classification. Water Resour. Manag. 2016, 30, 4329–4343. [Google Scholar] [CrossRef]
- Fang, K.; Kou, D.; Wang, G.; Chen, L.; Ding, J.; Li, F.; Yang, G.; Qin, S.; Liu, L.; Zhang, Q.; et al. Decreased soil cation exchange capacity across Northern China’s grasslands over the last three decades. J. Geophys. Res. Biogeosci. 2017, 122, 3088–3097. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Feng, L.; Nowak, G.; O’Neill, T.J.; Welsh, A.H. CUTOFF: A spatio-temporal imputation method. J. Hydrol. 2014, 519, 3591–3605. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier—A case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Gong, D.; Zhang, Q.; Zhao, L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric. Water Manag. 2017, 193, 163–173. [Google Scholar] [CrossRef]
- Fouad, G.; Skupin, A.; Tague, C.L. Regional regression models of percentile flows for the contiguous United States: Expert versus data-driven independent variable selection. J. Hydrol. Reg. Stud. 2018, 17, 64–82. [Google Scholar] [CrossRef]
- Francke, T.; López-Tarazón, J.A.; Schröder, B. Estimation of suspended sediment concentration and yield using linear models, random forests and quantile regression forests. Hydrol. Process. 2008, 22, 4892–4904. [Google Scholar] [CrossRef]
- Fukuda, S.; Spreer, W.; Yasunaga, E.; Yuge, K.; Sardsud, V.; Müller, J. Random Forests modelling for the estimation of mango (Mangifera indica L. cv. Chok Anan) fruit yields under different irrigation regimes. Agric. Water Manag. 2013, 116, 142–150. [Google Scholar] [CrossRef]
- Fullerton, A.H.; Torgersen, C.E.; Lawler, J.J.; Steel, E.A.; Ebersole, J.L.; Lee, S.Y. Longitudinal thermal heterogeneity in rivers and refugia for coldwater species: Effects of scale and climate change. Aquat. Sci. 2018, 80, 3. [Google Scholar] [CrossRef] [PubMed]
- Gage, E.; Cooper, D.J. The influence of land cover, vertical structure, and socioeconomic factors on outdoor water use in a western US city. Water Resour. Manag. 2015, 29, 3877–3890. [Google Scholar] [CrossRef]
- Gagné, T.O.; Hyrenbach, K.D.; Hagemann, M.; Bass, O.L.; Pimm, S.L.; MacDonald, M.; Peck, B.; Van Houtan, K.S. Seabird trophic position across three ocean regions tracks ecosystem differences. Front. Mar. Sci. 2018, 5, 317. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Assessing the predictive capability of randomized tree-based ensembles in streamflow modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2669–2684. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Tree-based iterative input variable selection for hydrological modeling. Water Res. Res. 2013, 49, 4295–4310. [Google Scholar] [CrossRef]
- Gao, M.; Li, H.Y.; Liu, D.; Tang, J.; Chen, X.; Chen, X.; Blöschl, G.; Leunge, L.R. Identifying the dominant controls on macropore flow velocity in soils: A meta-analysis. J. Hydrol. 2018, 567, 590–604. [Google Scholar] [CrossRef]
- Gegiuc, A.; Similä, M.; Karvonen, J.; Lensu, M.; Mäkynen, M.; Vainio, J. Estimation of degree of sea ice ridging based on dual-polarized C-band SAR data. Cryosphere 2018, 12, 343–364. [Google Scholar] [CrossRef]
- Gerlitz, L.; Vorogushyn, S.; Apel, H.; Gafurov, A.; Unger-Shayesteh, K.; Merz, B. A statistically based seasonal precipitation forecast model with automatic predictor selection and its application to central and south Asia. Hydrol. Earth Syst. Sci. 2016, 20, 4605–4623. [Google Scholar] [CrossRef]
- Giglio, D.; Lyubchich, V.; Mazloff, M.R. Estimating oxygen in the Southern Ocean using argo temperature and salinity. J. Geophys. Res. Oceans 2018, 123, 4280–4297. [Google Scholar] [CrossRef]
- Gmur, S.J.; Vogt, D.J.; Vogt, K.A.; Suntana, A.S. Effects of different sampling scales and selection criteria on modelling net primary productivity of Indonesian tropical forests. Environ. Conserv. 2014, 41, 187–197. [Google Scholar] [CrossRef]
- Gong, W.; Duan, Q.; Li, J.; Wang, C.; Di, Z.; Dai, Y.; Ye, A.; Miao, C. Multi-objective parameter optimization of common land model using adaptive surrogate modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2409–2425. [Google Scholar] [CrossRef]
- González-Ferreras, A.M.; Barquín, J. Mapping the temporary and perennial character of whole river networks. Water Res. Res. 2017, 53, 6709–6724. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Seneviratne, S.I. Towards observation-based gridded runoff estimates for Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2859–2879. [Google Scholar] [CrossRef]
- Hamel, P.; Guswa, A.J.; Sahl, J.; Zhang, L. Predicting dry-season flows with a monthly rainfall–runoff model: Performance for gauged and ungauged catchments. Hydrol. Process. 2017, 31, 3844–3858. [Google Scholar] [CrossRef]
- Händel, F.; Engelmann, C.; Klotzsch, S.; Fichtner, T.; Binder, M.; Graeber, P.W. Evaluation of decentralized, closely-spaced precipitation water and treated wastewater infiltration. Water 2018, 10, 1460. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Res. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- He, Y.; Gui, Z.; Su, C.; Chen, X.; Chen, D.; Lin, K.; Bai, X. Response of sediment load to hydrological change in the upstream part of the Lancang-Mekong river over the past 50 years. Water 2018, 10, 888. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Hoshino, E.; van Putten, E.I.; Girsang, W.; Resosudarmo, B.P.; Yamazaki, S. Fishers’ perceived objectives of community-based coastal resource management in the Kei Islands, Indonesia. Front. Mar. Sci. 2017, 4, 141. [Google Scholar] [CrossRef]
- Huang, P.; Zhu, N.; Hou, D.; Chen, J.; Xiao, Y.; Yu, J.; Zhang, G.; Zhang, H. Real-time burst detection in district metering areas in water distribution system based on patterns of water demand with supervised learning. Water 2018, 10, 1765. [Google Scholar] [CrossRef]
- Huang, Z.; Siwabessy, J.; Heqin, C.; Nichol, S. Using multibeam backscatter data to investigate sediment-acoustic relationships. J. Geophys. Res. Oceans 2018, 123, 4649–4665. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Aler-Mur, R.; Galvan-Leon, I.; Pozo-Vázquez, D. Automatic cloud-type classification based on the combined use of a sky camera and a ceilometer. J. Geophys. Res. Atmos. 2017, 122, 11045–11061. [Google Scholar] [CrossRef]
- Ibarra-Berastegi, G.; Saénz, J.; Ezcurra, A.; Elías, A.; Argandoña, J.D.; Errasti, I. Downscaling of surface moisture flux and precipitation in the Ebro Valley (Spain) using analogues and analogues followed by random forests and multiple linear regression. Hydrol. Earth Syst. Sci. 2011, 15, 1895–1907. [Google Scholar] [CrossRef]
- Jacoby, J.; Burghdoff, M.; Williams, G.; Read, L.; Hardy, F.J. Dominant factors associated with microcystins in nine midlatitude, maritime lakes. Inland Waters 2015, 5, 187–202. [Google Scholar] [CrossRef]
- Jakubčinová, K.; Haruštiaková, D.; Števove, B.; Švolíková, K.; Makovinská, J.; Kováč, V. Distribution patterns and potential for further spread of three invasive fish species (Neogobius melanostomus, Lepomis gibbosus and Pseudorasbora parva) in Slovakia. Aquat. Invasions 2018, 13, 513–524. [Google Scholar] [CrossRef]
- Jing, W.; Song, J.; Zhao, X. Validation of ECMWF multi-layer reanalysis soil moisture based on the OzNet hydrology network. Water 2018, 10, 1123. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, P.; Zhao, X. Reconstructing monthly ECV global soil moisture with an improved spatial resolution. Water Resour. Manag. 2018, 32, 2523–2537. [Google Scholar] [CrossRef]
- Keto, A.; Aroviita, J.; Hellsten, S. Interactions between environmental factors and vertical extension of helophyte zones in lakes in Finland. Aquat. Sci. 2018, 80, 41. [Google Scholar] [CrossRef]
- Kim, H.K.; Kwon, Y.S.; Kim, Y.J.; Kim, B.H. Distribution of epilithic diatoms in estuaries of the Korean Peninsula in relation to environmental variables. Water 2015, 7, 6702–6718. [Google Scholar] [CrossRef]
- Kim, J.; Grunwald, S. Assessment of carbon stocks in the topsoil using random forest and remote sensing images. J. Environ. Qual. 2016, 45, 1910–1918. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Hassanlourad, M.; Ardakani, A. Evaluation of liquefaction potential based on CPT data using random forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Laakso, T.; Kokkonen, T.; Mellin, I.; Vahala, R. Sewer condition prediction and analysis of explanatory factors. Water 2018, 10, 1239. [Google Scholar] [CrossRef]
- Leasure, D.R.; Magoulick, D.D.; Longing, S.D. Natural flow regimes of the Ozark-Ouachita interior highlands region. River Res. Appl. 2016, 32, 18–35. [Google Scholar] [CrossRef]
- Lee, Y.J.; Park, C.; Lee, M.L. Identification of a contaminant source location in a river system using random forest models. Water 2018, 10, 391. [Google Scholar] [CrossRef]
- Li, R.; Zhao, S.; Zhao, H.; Xu, M.; Zhang, L.; Wen, H.; Sheng, Q. Spatiotemporal assessment of forest biomass carbon sinks: The relative roles of forest expansion and growth in Sichuan Province, China. J. Environ. Qual. 2018, 46, 64–71. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X.; et al. Intercomparison of six upscaling evapotranspiration methods: From site to the satellite pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Liao, X.; Zheng, J.; Huang, C.; Huang, G. Approach for evaluating LID measure layout scenarios based on random forest: Case of Guangzhou—China. Water 2018, 10, 894. [Google Scholar] [CrossRef]
- Lima, A.R.; Cannon, A.J.; Hsieh, W.W. Forecasting daily streamflow using online sequential extreme learning machines. J. Hydrol. 2016, 537, 431–443. [Google Scholar] [CrossRef]
- Lin, Y.P.; Lin, W.C.; Wu, W.Y. Uncertainty in various habitat suitability models and its impact on habitat suitability estimates for fish. Water 2015, 7, 4088–4107. [Google Scholar] [CrossRef]
- Loos, M.; Elsenbeer, H. Topographic controls on overland flow generation in a forest – An ensemble tree approach. J. Hydrol. 2011, 409, 94–103. [Google Scholar] [CrossRef]
- Loosvelt, L.; De Baets, B.; Pauwels, V.R.N.; Verhoest, N.E.C. Assessing hydrologic prediction uncertainty resulting from soft land cover classification. J. Hydrol. 2014, 517, 411–424. [Google Scholar] [CrossRef]
- Lorenz, R.; Herger, N.; Sedláček, J.; Eyring, V.; Fischer, E.M.; Knutti, R. Prospects and caveats of weighting climate models for summer maximum temperature projections over North America. J. Geophys. Res. Atmos. 2018, 123, 4509–4526. [Google Scholar] [CrossRef]
- Lu, X.; Ju, Y.; Wu, L.; Fan, J.; Zhang, F.; Li, Z. Daily pan evaporation modeling from local and cross-station data using three tree-based machine learning models. J. Hydrol. 2018, 566, 668–684. [Google Scholar] [CrossRef]
- Lutz, S.R.; Krieg, R.; Müller, C.; Zink, M.; Knöller, K.; Samaniego, L.; Merz, R. Spatial patterns of water age: Using young water fractions to improve the characterization of transit times in contrasting catchments. Water Res. Res. 2018, 54, 4767–4784. [Google Scholar] [CrossRef]
- Maheu, A.; Poff, N.L.; St-Hilaire, A. A classification of stream water temperature regimes in the conterminous USA. River Res. Appl. 2016, 32, 896–906. [Google Scholar] [CrossRef]
- Maloney, K.O.; Cole, J.C.; Schmid, M. Predicting thermally events in rivers with a strategy to evaluate management alternatives. River Res. Appl. 2016, 32, 1428–1437. [Google Scholar] [CrossRef]
- Markonis, Y.; Moustakis, Y.; Nasika, C.; Sychova, P.; Dimitriadis, P.; Hanel, M.; Máca, P.; Papalexiou, S.M. Global estimation of long-term persistence in annual river runoff. Adv. Water Resour. 2018, 113, 1–12. [Google Scholar] [CrossRef]
- McGrath, D.; Sass, L.; O’Neel, S.; McNeil, C.; Candela, S.G.; Baker, E.H.; Marshall, H.P. Interannual snow accumulation variability on glaciers derived from repeat, spatially extensive ground-penetrating radar surveys. Cryosphere 2018, 12, 3617–3633. [Google Scholar] [CrossRef]
- McManamay, R.A. Quantifying and generalizing hydrologic responses to dam regulation using a statistical modeling approach. J. Hydrol. 2014, 519, 1278–1296. [Google Scholar] [CrossRef]
- Meador, M.R.; Carlisle, D.M. Relations between altered streamflow variability and fish assemblages in Eastern USA streams. River Res. Appl. 2012, 28, 1359–1368. [Google Scholar] [CrossRef]
- Menberu, M.W.; Marttila, H.; Tahvanainen, T.; Kotiaho, J.S.; Hokkanen, R.; Kløve, B.; Ronkanen, A.K. Changes in pore water quality after peatland restoration: Assessment of a large-scale, replicated before-after-control-impact study in Finland. Water Res. Res. 2017, 53, 8327–8343. [Google Scholar] [CrossRef]
- Meyers, G.; Kapelan, Z.; Keedwell, E. Short-term forecasting of turbidity in trunk main networks. Water Res. 2017, 124, 67–76. [Google Scholar] [CrossRef]
- Midekisa, A.; Senay, G.B.; Wimberly, M.C. Multisensor earth observations to characterize wetlands and malaria epidemiology in Ethiopia. Water Res. Res. 2014, 50, 8791–8806. [Google Scholar] [CrossRef]
- Miller, M.P.; Carlisle, D.M.; Wolock, D.M.; Wieczorek, M. A database of natural monthly streamflow estimates from 1950 to 2015 for the conterminous United States. J. Am. Water Resour. Assoc. 2018, 54, 1258–1269. [Google Scholar] [CrossRef]
- Mitsopoulos, I.; Mallinis, G. A data-driven approach to assess large fire size generation in Greece. Nat. Hazards 2017, 88, 1591–1607. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-flood forecasting in an Andean mountain catchment—Development of a step-wise methodology based on the random forest algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Näschen, K.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Seregina, L.S.; Thonfeld, F.; van der Linden, R. Hydrological modeling in data-scarce catchments: The Kilombero floodplain in Tanzania. Water 2018, 10, 599. [Google Scholar] [CrossRef]
- Nateghi, R.; Guikema, S.D.; Quiring, S.M. Forecasting hurricane-induced power outage durations. Nat. Hazards 2014, 74, 1795–1811. [Google Scholar] [CrossRef]
- Navares, R.; Díaz, J.; Linares, C.; Aznarte, J.L. Comparing ARIMA and computational intelligence methods to forecast daily hospital admissions due to circulatory and respiratory causes in Madrid. Stoch. Environ. Res. Risk Assess. 2018, 32, 2849–2859. [Google Scholar] [CrossRef]
- Nelson, J.A.; Carvalhais, N.; Cuntz, M.; Delpierre, N.; Knauer, J.; Ogée, J.; Migliavacca, M.; Reichstein, M.; Jung, M. Coupling water and carbon fluxes to constrain estimates of transpiration: The TEA algorithm. J. Geophys. Res. Biogeosci. 2018, 123, 3617–3632. [Google Scholar] [CrossRef]
- Núñez, J.; Hallack-Alegría, M.; Cadena, M. Resolving regional frequency analysis of precipitation at large and complex scales using a bottom-up approach: The Latin America and the Caribbean drought Atlas. J. Hydrol. 2016, 538, 515–538. [Google Scholar] [CrossRef]
- Oczkowski, A.; Kreakie, B.; McKinney, R.A.; Prezioso, J. Patterns in stable isotope values of nitrogen and carbon in particulate matter from the Northwest Atlantic continental shelf, from the Gulf of Maine to Cape Hatteras. Front. Mar. Sci. 2016, 3, 252. [Google Scholar] [CrossRef]
- Olaya-Marín, E.J.; Martínez-Capel, F.; Vezza, P. A comparison of artificial neural networks and random forests to predict native fish species richness in Mediterranean rivers. Knowl. Manag. Aquat. Syst. 2013, 409, 7. [Google Scholar] [CrossRef]
- Olson, J.R.; Hawkins, C.P. Predicting natural base-flow stream water chemistry in the western United States. Water Res. Res. 2012, 48, W02504. [Google Scholar] [CrossRef]
- O’Neil, G.L.; Goodall, J.L.; Watson, L.T. Evaluating the potential for site-specific modification of LiDAR DEM derivatives to improve environmental planning-scale wetland identification using random forest classification. J. Hydrol. 2018, 559, 192–208. [Google Scholar] [CrossRef]
- Park, H.; Chung, S. pCO2 dynamics of stratified reservoir in temperate zone and CO2 pulse emissions during turnover events. Water 2018, 10, 1347. [Google Scholar] [CrossRef]
- Parker, J.; Epifanio, J.; Casper, A.; Cao, Y. The effects of improved water quality on fish assemblages in a heavily modified large river system. River Res. Appl. 2016, 32, 992–1007. [Google Scholar] [CrossRef]
- Parkhurst, D.F.; Brenner, K.P.; Dufour, A.P.; Wymer, L.J. Indicator bacteria at five swimming beaches—analysis using random forests. Water Res. 2005, 39, 1354–1360. [Google Scholar] [CrossRef]
- Peñas, F.J.; Barquín, J.; Álvarez, C. Sources of variation in hydrological classifications: Time scale, flow series origin and classification procedure. J. Hydrol. 2016, 538, 487–499. [Google Scholar] [CrossRef]
- Peñas Silva, F.J.; Barquín Ortiz, J.; Snelder, T.H.; Booker, D.J.; Álvarez, C. The influence of methodological procedures on hydrological classification performance. Hydrol. Earth Syst. Sci. 2014, 18, 3393–3409. [Google Scholar] [CrossRef]
- Pesántez, J.; Mosquera, G.M.; Crespo, P.; Breuer, L.; Windhorst, D. Effect of land cover and hydro-meteorological controls on soil water DOC concentrations in a high-elevation tropical environment. Hydrol. Process. 2018, 32, 2624–2635. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; Samson, R.; Verhoest, N.E.C. Modelling groundwater-dependent vegetation patterns using ensemble learning. Hydrol. Earth Syst. Sci. 2008, 12, 603–613. [Google Scholar] [CrossRef]
- Petty, T.R.; Dhingra, P. Streamflow Hydrology Estimate using Machine Learning (SHEM). J. Am. Water Resour. Assoc. 2018, 54, 55–68. [Google Scholar] [CrossRef]
- Piniewski, M. Classification of natural flow regimes in Poland. River Res. Appl. 2017, 33, 1205–1218. [Google Scholar] [CrossRef]
- Povak, N.A.; Hessburg, P.F.; McDonnell, T.C.; Reynolds, K.M.; Sullivan, T.J.; Salter, R.B.; Cosby, B.J. Machine learning and linear regression models to predict catchment-level base cation weathering rates across the southern Appalachian Mountain region, USA. Water Res. Res. 2014, 50, 2798–2814. [Google Scholar] [CrossRef]
- Povak, N.A.; Hessburg, P.F.; Reynolds, K.M.; Sullivan, T.J.; McDonnell, T.C.; Salter, R.B. Machine learning and hurdle models for improving regional predictions of stream water acid neutralizing capacity. Water Res. Res. 2013, 49, 3531–3546. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Du, X.; Tang, X. Prediction of open stope hangingwall stability using random forests. Nat. Hazards 2018, 92, 1179–1197. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R. Identification of critical flood prone areas in data-scarce and ungauged regions: A comparison of three data mining models. Water Resour. Manag. 2017, 31, 1473–1487. [Google Scholar] [CrossRef]
- Rattray, A.; Ierodiaconou, D.; Womersley, T. Wave exposure as a predictor of benthic habitat distribution on high energy temperate reefs. Front. Mar. Sci. 2015, 2, 8. [Google Scholar] [CrossRef]
- Redo, D.J.; Aide, T.M.; Clark, M.L.; Andrade-Núñez, M.J. Impacts of internal and external policies on land change in Uruguay, 2001–2009. Environ. Conserv. 2012, 39, 122–131. [Google Scholar] [CrossRef]
- Revilla-Romero, B.; Thielen, J.; Salamon, P.; De Groeve, T.; Brakenridge, G.R. Evaluation of the satellite-based Global Flood Detection System for measuring river discharge: Influence of local factors. Hydrol. Earth Syst. Sci. 2014, 18, 4467–4484. [Google Scholar] [CrossRef]
- Reyes Rojas, L.A.; Adhikari, K.; Ventura, S.J. Projecting soil organic carbon distribution in central Chile under future climate scenarios. J. Environ. Qual. 2018, 47, 735–745. [Google Scholar] [CrossRef]
- Reynolds, L.V.; Shafroth, P.B.; Poff, N.L.R. Modeled intermittency risk for small streams in the Upper Colorado River Basin under climate change. J. Hydrol. 2015, 523, 768–780. [Google Scholar] [CrossRef]
- Robinson, G.; Moutari, S.; Ahmed, A.A.; Hamill, G.A. An advanced calibration method for image analysis in laboratory-scale seawater intrusion problems. Water Resour. Manag. 2018, 32, 3087–3102. [Google Scholar] [CrossRef]
- Rossel, S.; Martínez Arbizu, P. Effects of sample fixation on specimen identification in biodiversity assemblies based on proteomic data (MALDI-TOF). Front. Mar. Sci. 2018, 5, 149. [Google Scholar] [CrossRef]
- Rossi, P.M.; Marttila, H.; Jyväsjärvi, J.; Ala-aho, P.; Isokangas, E.; Muotka, T.; Kløve, B. Environmental conditions of boreal springs explained by capture zone characteristics. J. Hydrol. 2015, 531, 992–1002. [Google Scholar] [CrossRef]
- Roubeix, V.; Daufresne, M.; Argillier, C.; Dublon, J.; Maire, A.; Nicolas, D.; Raymond, J.C.; Danis, P.A. Physico-chemical thresholds in the distribution of fish species among French lakes. Knowl. Manag. Aquat. Syst. 2017, 418, 41. [Google Scholar] [CrossRef]
- Rowden, A.A.; Anderson, O.F.; Georgian, S.E.; Bowden, D.A.; Clark, M.R.; Pallentin, A.; Miller, A. High-resolution habitat suitability models for the conservation and management of vulnerable marine ecosystems on the Louisville seamount chain, South Pacific Ocean. Front. Mar. Sci. 2017, 4, 335. [Google Scholar] [CrossRef]
- Rozema, P.D.; Kulk, G.; Veldhuis, M.P.; Buma, A.G.J.; Meredith, M.P.; van de Poll, W.H. Assessing drivers of coastal primary production in Northern Marguerite Bay, Antarctica. Front. Mar. Sci. 2017, 4, 184. [Google Scholar] [CrossRef]
- Sadler, J.M.; Goodall, J.L.; Morsy, M.M.; Spencer, K. Modeling urban coastal flood severity from crowd-sourced flood reports using Poisson regression and random forest. J. Hydrol. 2018, 559, 43–55. [Google Scholar] [CrossRef]
- Sahoo, M.; Kasot, A.; Dhar, A.; Kar, A. On Predictability of groundwater level in Shallow Wells using satellite observations. Water Resour. Manag. 2018, 32, 1225–1244. [Google Scholar] [CrossRef]
- Salo, J.A.; Theobald, D.M. A multi-scale, hierarchical model to map riparian zones. River Res. Appl. 2016, 32, 1709–1720. [Google Scholar] [CrossRef]
- Santos, P.; Amado, C.; Coelho, S.T.; Leitão, J.P. Stochastic data mining tools for pipe blockage failure prediction. Urban Water J. 2017, 14, 343–353. [Google Scholar] [CrossRef]
- Schnieders, J.; Garbe, C.S.; Peirson, W.L.; Smith, G.B.; Zappa, C.J. Analyzing the footprints of near-surface aqueous turbulence: An image processing-based approach. J. Geophys. Res. Oceans 2013, 118, 1272–1286. [Google Scholar] [CrossRef]
- Schnier, S.; Cai, X. Prediction of regional streamflow frequency using model tree ensembles. J. Hydrol. 2014, 517, 298–309. [Google Scholar] [CrossRef]
- Schwarz, K.; Weathers, K.C.; Pickett, S.T.A.; Lathrop, R.G., Jr.; Pouyat, R.V. A comparison of three empirically based, spatially explicit predictive models of residential soil Pb concentrations in Baltimore, Maryland, USA: Understanding the variability within cities. Environ. Geochem. Health 2013, 35, 495–510. [Google Scholar] [CrossRef] [PubMed]
- Seibert, M.; Merz, B.; Apel, H. Seasonal forecasting of hydrological drought in the Limpopo basin: A comparison of statistical methods. Hydrol. Earth Syst. Sci. 2017, 21, 1611–1629. [Google Scholar] [CrossRef]
- Shchur, A.; Bragina, E.; Sieber, A.; Pidgeon, A.M.; Radelof, V.C. Monitoring selective logging with Landsat satellite imagery reveals that protected forests in Western Siberia experience greater harvest than non-protected forests. Environ. Conserv. 2017, 44, 191–199. [Google Scholar] [CrossRef]
- Shiri, J. Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J. Hydrol. 2018, 561, 737–750. [Google Scholar] [CrossRef]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Karimi, S.; Iturraran-Viveros, U. Modeling soil bulk density through a complete data scanning procedure: Heuristic alternatives. J. Hydrol. 2017, 549, 592–602. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D. Public health and pipe breaks in water distribution systems: Analysis with internet search volume as a proxy. Water Res. 2014, 53, 26–34. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Sidibe, M.; Dieppois, B.; Mahé, G.; Paturel, J.E.; Amoussou, E.; Anifowose, B.; Lawler, D. Trend and variability in a new, reconstructed streamflow dataset for West and Central Africa, and climatic interactions, 1950–2005. J. Hydrol. 2018, 561, 478–493. [Google Scholar] [CrossRef]
- Sieg, T.; Vogel, K.; Merz, B.; Kreibich, H. Tree-based flood damage modeling of companies: Damage processes and model performance. Water Res. Res. 2017, 53, 6050–6068. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Singh, N.K.; Emanuel, R.E.; Nippgen, F.; McGlynn, B.L.; Miniat, C.F. The relative influence of storm and landscape characteristics on shallow groundwater responses in forested headwater catchments. Water Res. Res. 2018, 54, 9883–9900. [Google Scholar] [CrossRef]
- Smith, A.; Sterba-Boatwright, B.; Mott, J. Novel application of a statistical technique, random forests, in a bacterial source tracking study. Water Res. 2010, 44, 4067–4076. [Google Scholar] [CrossRef] [PubMed]
- Snelder, T.; Ortiz, J.B.; Booker, D.; Lamouroux, N.; Pella, H.; Shankar, U. Can bottom-up procedures improve the performance of stream classifications? Aquat. Sci. 2012, 74, 45–59. [Google Scholar] [CrossRef]
- Snelder, T.H.; Booker, D.J. Natural Flow Regime classifications are sensitive to definition processes. River Res. Appl. 2013, 29, 822–838. [Google Scholar] [CrossRef]
- Snelder, T.H.; Datry, T.; Lamouroux, N.; Larned, S.T.; Sauquet, E.; Pella, H.; Catalogne, C. Regionalization of patterns of flow intermittence from gauging station records. Hydrol. Earth Syst. Sci. 2013, 17, 2685–2699. [Google Scholar] [CrossRef]
- Speich, M.J.R.; Lischke, H.; Zappa, M. Testing an optimality-based model of rooting zone water storage capacity in temperate forests. Hydrol. Earth Syst. Sci. 2018, 22, 4097–4124. [Google Scholar] [CrossRef]
- Stephan, P.; Hendricks, S.; Ricker, R.; Kern, S.; Rinne, E. Empirical parametrization of Envisat freeboard retrieval of Arctic and Antarctic sea ice based on CryoSat-2: Progress in the ESA climate change initiative. Cryosphere 2018, 12, 2437–2460. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Yan, X.H. Retrieving temperature anomaly in the global subsurface and deeper ocean from satellite observations. J. Geophys. Res. Oceans 2018, 123, 399–410. [Google Scholar] [CrossRef]
- Sui, Y.; Fu, D.; Wang, X.; Su, F. Surface water dynamics in the North America Arctic based on 2000–2016 Landsat data. Water 2018, 10, 824. [Google Scholar] [CrossRef]
- Sultana, Z.; Sieg, T.; Kellermann, P.; Müller, M.; Kreibich, H. Assessment of business interruption of flood-affected companies using random forests. Water 2018, 10, 1049. [Google Scholar] [CrossRef]
- Taormina, R.; Galelli, S.; Tippenhauer, N.O.; Salomons, E.; Ostfeld, A.; Eliades, D.G.; Aghashahi, M.; Sundararajan, R.; Pourahmadi, M.; Banks, M.K.; et al. Battle of the attack detection algorithms: Disclosing cyber attacks on water distribution networks. J. Water Resour. Plan. Manag. 2018, 144, 04018048. [Google Scholar] [CrossRef]
- Tesfa, T.K.; Tarboton, D.G.; Chandler, D.G.; McNamara, J.P. Modeling soil depth from topographic and land cover attributes. Water Res. Res. 2009, 45, W10438. [Google Scholar] [CrossRef]
- Tesoriero, A.J.; Gronberg, J.A.; Juckem, P.F.; Miller, M.P.; Austin, B.P. Predicting redox-sensitive contaminant concentrations in groundwater using random forest classification. Water Res. Res. 2017, 53, 7316–7331. [Google Scholar] [CrossRef]
- Tillman, F.D.; Anning, D.W.; Heilman, J.A.; Buto, S.G.; Miller, M.P. Managing salinity in Upper Colorado river basin streams: Selecting catchments for sediment control efforts using watershed characteristics and random forests models. Water 2018, 10, 676. [Google Scholar] [CrossRef]
- Tongal, H.; Booij, M.J. Simulation and forecasting of streamflows using machine learning models coupled with base flow separation. J. Hydrol. 2018, 564, 266–282. [Google Scholar] [CrossRef]
- Trancoso, R.; Larsen, J.R.; McAlpine, C.; McVicar, T.R.; Phinn, S. Linking the Budyko framework and the Dunne diagram. J. Hydrol. 2016, 535, 581–597. [Google Scholar] [CrossRef]
- Tudesque, L.; Gevrey, M.; Lek, S. Links between stream reach hydromorphology and land cover on different spatial scales in the Adour-Garonne Basin (SW France). Knowl. Manag. Aquat. Syst. 2011, 403. [Google Scholar] [CrossRef]
- Tyralis, H.; Dimitriadis, P.; Koutsoyiannis, D.; O’Connell, P.E.; Tzouka, K.; Iliopoulou, T. On the long-range dependence properties of annual precipitation using a global network of instrumental measurements. Adv. Water Resour. 2018, 111, 301–318. [Google Scholar] [CrossRef]
- Umar, M.; Rhoads, B.L.; Greenberg, J.A. Use of multispectral satellite remote sensing to assess mixing of suspended sediment downstream of large river confluences. J. Hydrol. 2018, 556, 325–338. [Google Scholar] [CrossRef]
- Vågen, T.G.; Winowiecki, L.A.; Twine, W.; Vaughan, K. Spatial gradients of ecosystem health indicators across a human-impacted semiarid savanna. J. Environ. Qual. 2018, 47, 746–757. [Google Scholar] [CrossRef]
- Van der Heijden, S.; Haberlandt, U. A fuzzy rule based metamodel for monthly catchment nitrate fate simulations. J. Hydrol. 2015, 531, 863–876. [Google Scholar] [CrossRef]
- Vaughan, A.A.; Belmont, P.; Hawkins, C.P.; Wilcock, P. Near-channel versus watershed controls on sediment rating curves. J. Geophys. Res. Earth Surf. 2017, 122, 1901–1923. [Google Scholar] [CrossRef]
- Veettil, A.V.; Konapala, G.; Mishra, A.K.; Li, H.Y. Sensitivity of drought resilience-vulnerability- exposure to hydrologic ratios in contiguous United States. J. Hydrol. 2018, 564, 294–306. [Google Scholar] [CrossRef]
- Vezza, P.; Parasiewicz, P.; Calles, O.; Spairani, M.; Comoglio, C. Modelling habitat requirements of bullhead (Cottus gobio) in Alpine streams. Aquat. Sci. 2014, 76, 1–15. [Google Scholar] [CrossRef]
- Wang, B.; Hipsey, M.R.; Ahmed, S.; Oldham, C. The impact of landscape characteristics on groundwater dissolved organic nitrogen: Insights from machine learning methods and sensitivity analysis. Water Res. Res. 2018, 54, 4785–4804. [Google Scholar] [CrossRef]
- Wang, P.; Bai, X.; Wu, X.; Yu, H.; Hao, Y.; Hu, B. GIS-based random forest weight for rainfall-induced landslide susceptibility assessment at a humid region in Southern China. Water 2018, 10, 1019. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Wanik, D.W.; Anagnostou, E.N.; Hartman, B.M.; Frediani, M.E.B.; Astitha, M. Storm outage modeling for an electric distribution network in Northeastern USA. Nat. Hazards 2015, 79, 1359–1384. [Google Scholar] [CrossRef]
- Wanyama, I.; Rufino, M.C.; Pelster, D.E.; Wanyama, G.; Atzberger, C.; van Asten, P.; Verchot, L.V.; Butterbach-Bahl, K. Land-use, land-use history and soil type affect soil greenhouse gas fluxes from agricultural landscapes of the East African highlands. J. Geophys. Res. Biogeosci. 2018, 123, 976–990. [Google Scholar] [CrossRef]
- Waugh, S.M.; Ziegler, C.L.; MacGorman, D.R. In situ microphysical observations of the 29–30 May 2012 Kingfisher, OK, Supercell with a balloon-borne video disdrometer. J. Geophys. Res. Atmos. 2018, 123, 5618–5640. [Google Scholar] [CrossRef]
- Wright, N.C.; Polashenski, C.M. Open-source algorithm for detecting sea ice surface features in high-resolution optical imagery. Cryosphere 2018, 12, 1307–1329. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Dong, Z.; Tang, Q.; Lv, X.; Dong, G. Analysis of natural streamflow variation and its influential factors on the Yellow River from 1957 to 2010. Water 2018, 10, 1155. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, B.; Gong, Z. Real-time identification of urban rainstorm waterlogging disasters based on Weibo big data. Nat. Hazards 2018, 94, 833–842. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z. Evaluating different machine learning methods for upscaling evapotranspiration from Flux Towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J.; Ye, M.; Liang, F. Quantifying model structural error: Efficient Bayesian calibration of a regional groundwater flow model using surrogates and a data-driven error model. Water Res. Res. 2017, 53, 4084–4105. [Google Scholar] [CrossRef]
- Yamazaki, K.; Rowlands, D.J.; Aina, T.; Blaker, A.T.; Bowery, A.; Massey, N.; Miller, J.; Rye, C.; Tett, S.F.B.; Williamson, D.; et al. Obtaining diverse behaviors in a climate model without the use of flux adjustments. J. Geophys. Res. Atmos. 2013, 118, 2781–2793. [Google Scholar] [CrossRef]
- Yang, G.; Guo, S.; Liu, P.; Li, L.; Xu, C. Multiobjective reservoir operating rules based on cascade reservoir input variable selection method. Water Resour. Res. 2017, 53, 3446–3463. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Sorooshian, S.; Li, X. Simulating California reservoir operation using the classification and regression-tree algorithm combined with a shuffled cross-validation scheme. Water Resour. Res. 2016, 52, 1626–1651. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Zhang, Y.; Chen, J.; Jia, K.; Zhang, X.; Fisher, J.B.; Wang, X.; Zhang, L.; et al. Estimation of high-resolution terrestrial evapotranspiration from Landsat data using a simple Taylor skill fusion method. J. Hydrol. 2017, 553, 508–526. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Chen, S.Y.; Kuo, C.M.; Tseng, H.W. Comparison of random forests and support vector machine for real-time radar-derived rainfall forecasting. J. Hydrol. 2017, 552, 92–104. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Ye, M.; Che, T.; Zhang, G. Estimating daily air temperatures over the Tibetan Plateau by dynamically integrating MODIS LST data. J. Geophys. Res. Atmos. 2016, 121, 11425–11441. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, C.; Xia, J.; Zhang, Y.; Yu, Q.; Eamus, D. Recognition of key regions for restoration of phytoplankton communities in the Huai River basin, China. J. Hydrol. 2012, 420–421, 292–300. [Google Scholar] [CrossRef]
- Zhao, D.; Wu, Q.; Cui, F.; Xu, H.; Zeng, Y.; Cao, Y.; Du, Y. Using random forest for the risk assessment of coal-floor water inrush in Panjiayao Coal Mine, northern China. Hydrogeol. J. 2018, 26, 2327–2340. [Google Scholar] [CrossRef]
- Zhao, W.; Sánchez, N.; Lu, H.; Li, A. A spatial downscaling approach for the SMAP passive surface soil moisture product using random forest regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Zheng, Z.; Kirchner, P.B.; Bales, R.C. Topographic and vegetation effects on snow accumulation in the southern Sierra Nevada: A statistical summary from lidar data. Cryosphere 2016, 10, 257–269. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction. Nat. Hazards 2015, 79, 291–316. [Google Scholar] [CrossRef]
- Zhu, J.; Pierskalla, W.R., Jr. Applying a weighted random forests method to extract karst sinkholes from LiDAR data. J. Hydrol. 2016, 533, 343–352. [Google Scholar] [CrossRef]
- Zimmermann, A.; Francke, T.; Elsenbeer, H. Forests and erosion: Insights from a study of suspended-sediment dynamics in an overland flow-prone rainforest catchment. J. Hydrol. 2012, 428–429, 170–181. [Google Scholar] [CrossRef]
- Zimmermann, B.; Zimmermann, A.; Turner, B.L.; Francke, T.; Elsenbeer, H. Connectivity of overland flow by drainage network expansion in a rain forest catchment. Water Resour. Res. 2014, 50, 1457–1473. [Google Scholar] [CrossRef]
- Zscheischler, J.; Fatichi, S.; Wolf, S.; Blanken, P.D.; Bohrer, G.; Clark, K.; Desai, A.R.; Hollinger, D.; Keenan, T.; Novick, K.A.; et al. Short-term favorable weather conditions are an important control of interannual variability in carbon and water fluxes. J. Geophys. Res. Biogeosci. 2016, 121, 2186–2198. [Google Scholar] [CrossRef] [PubMed]
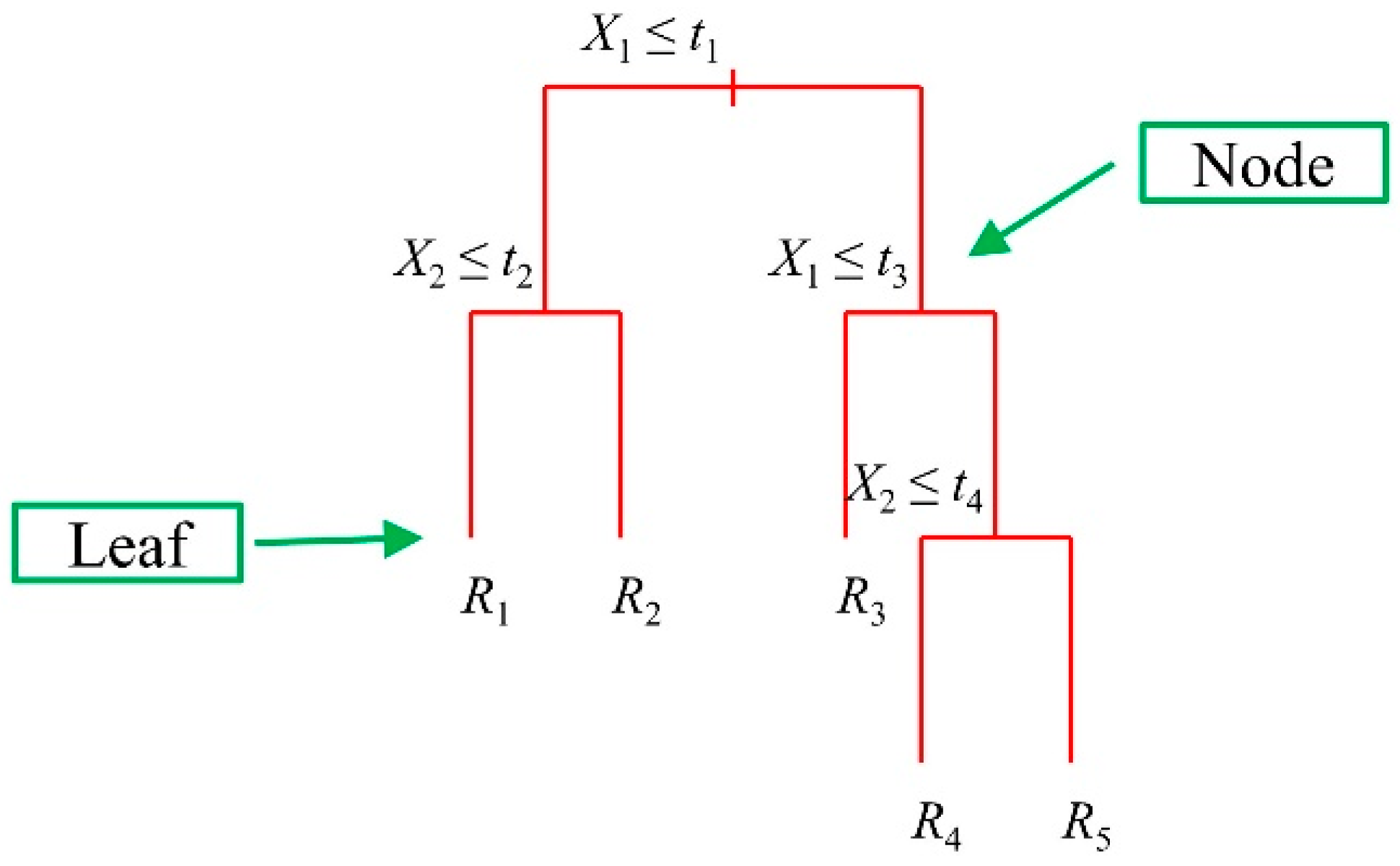
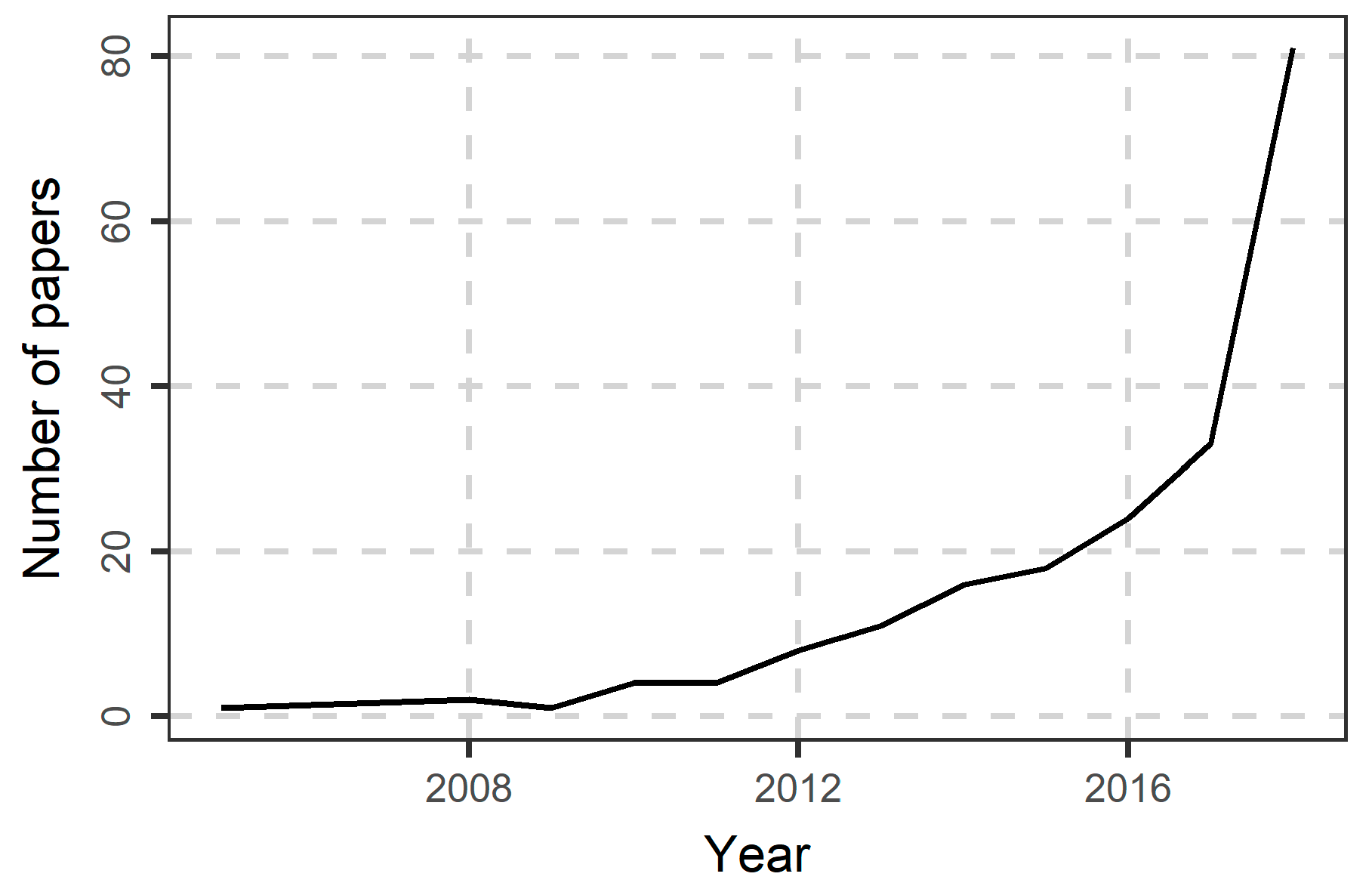
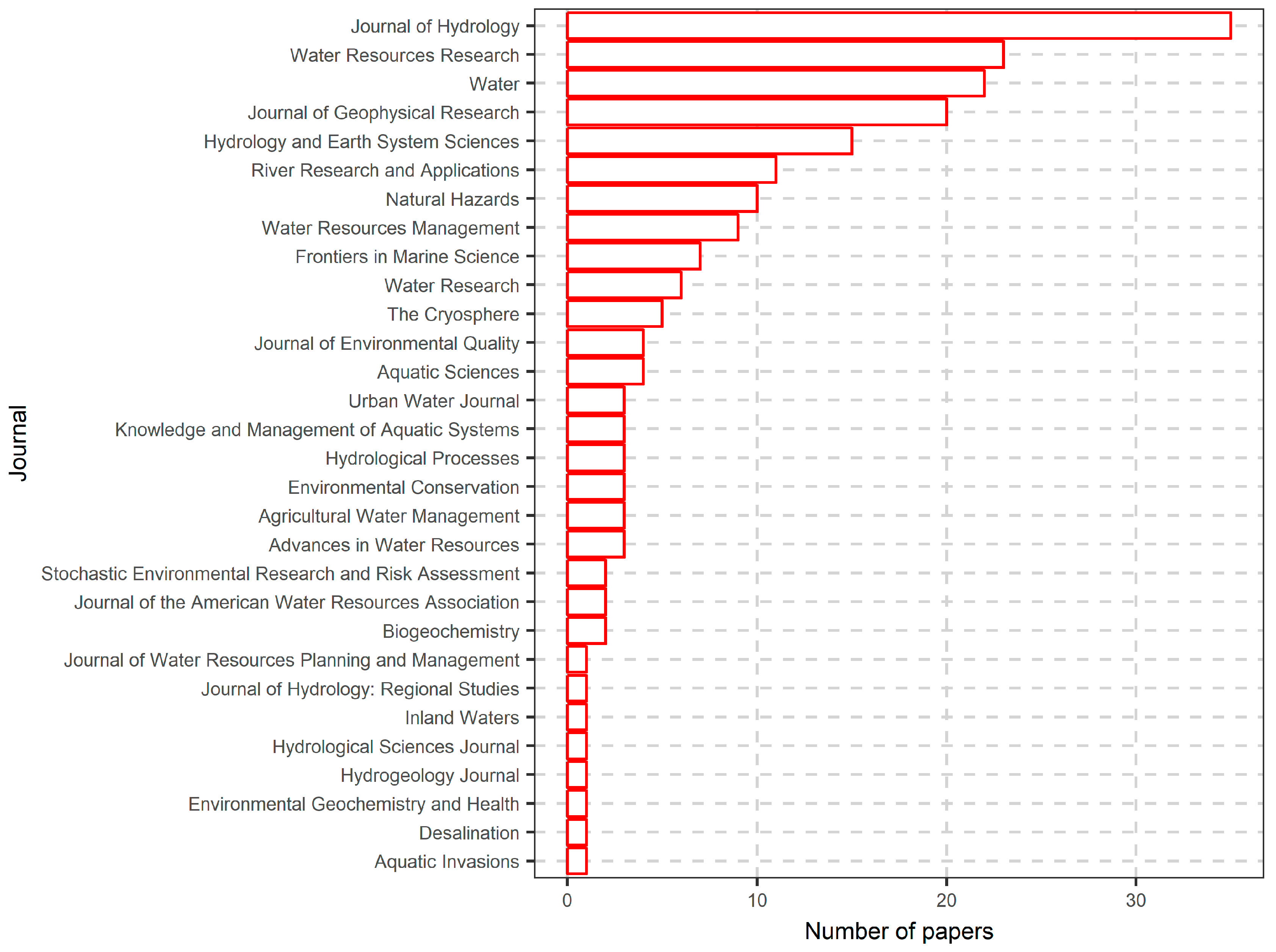
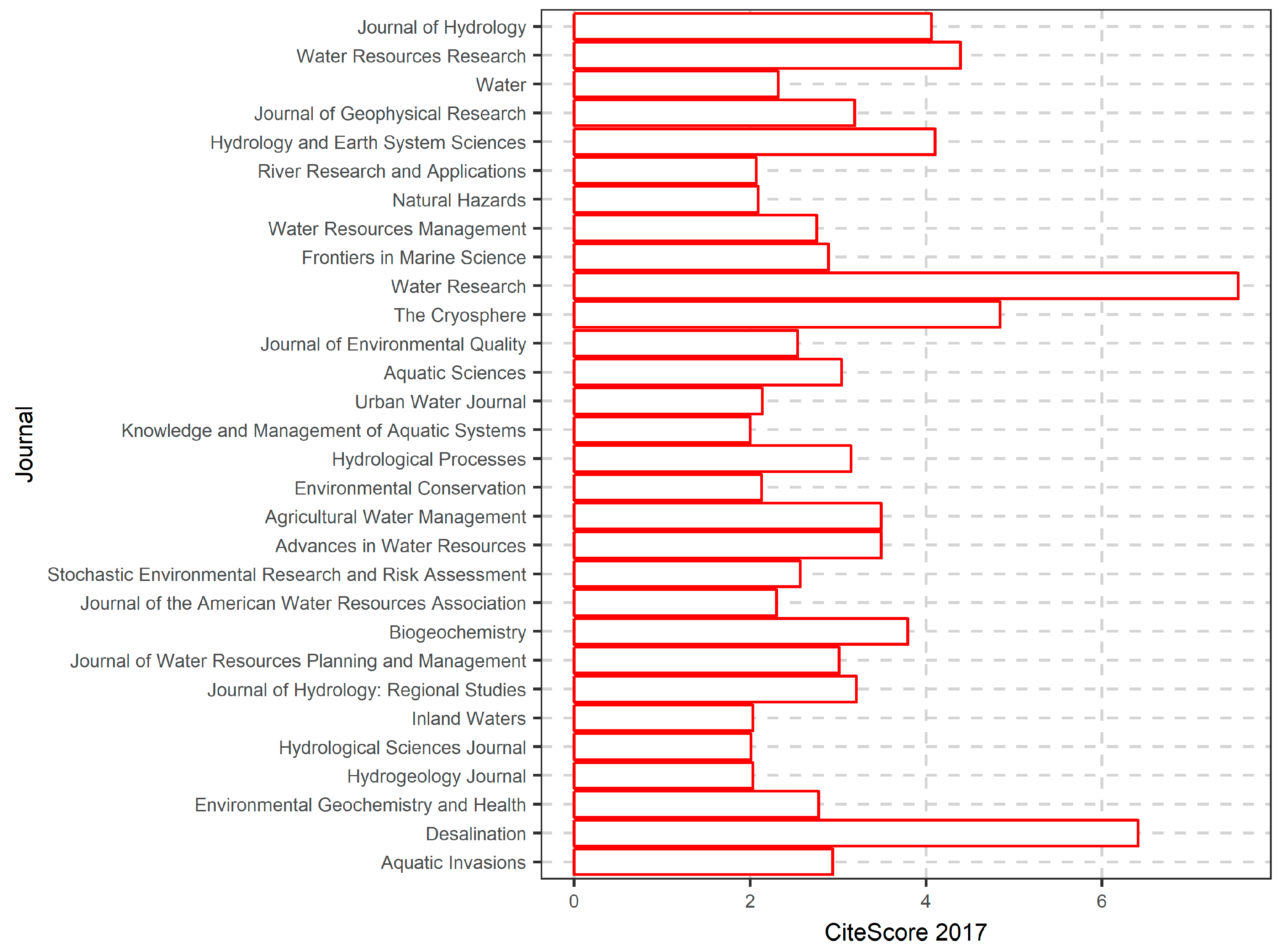
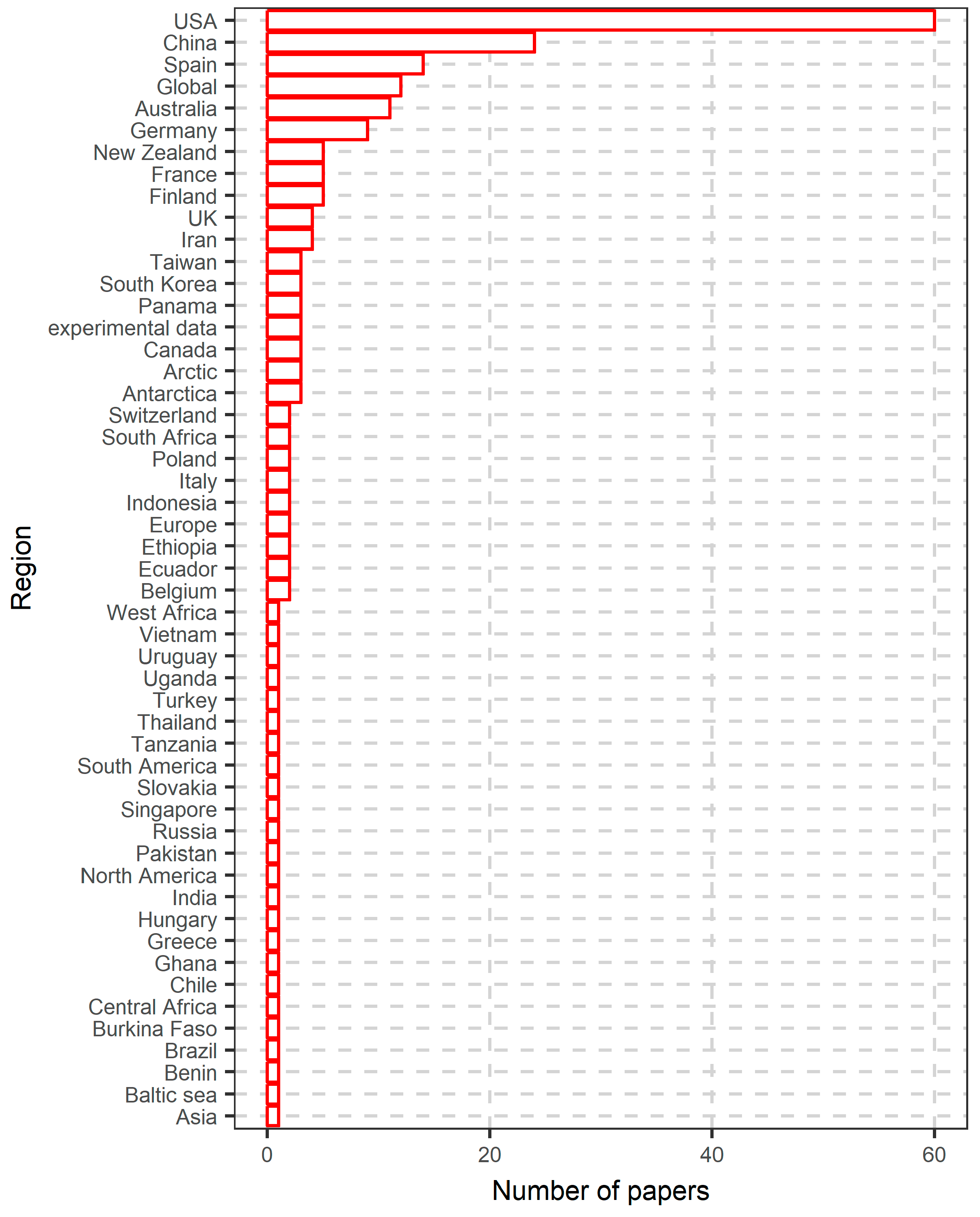
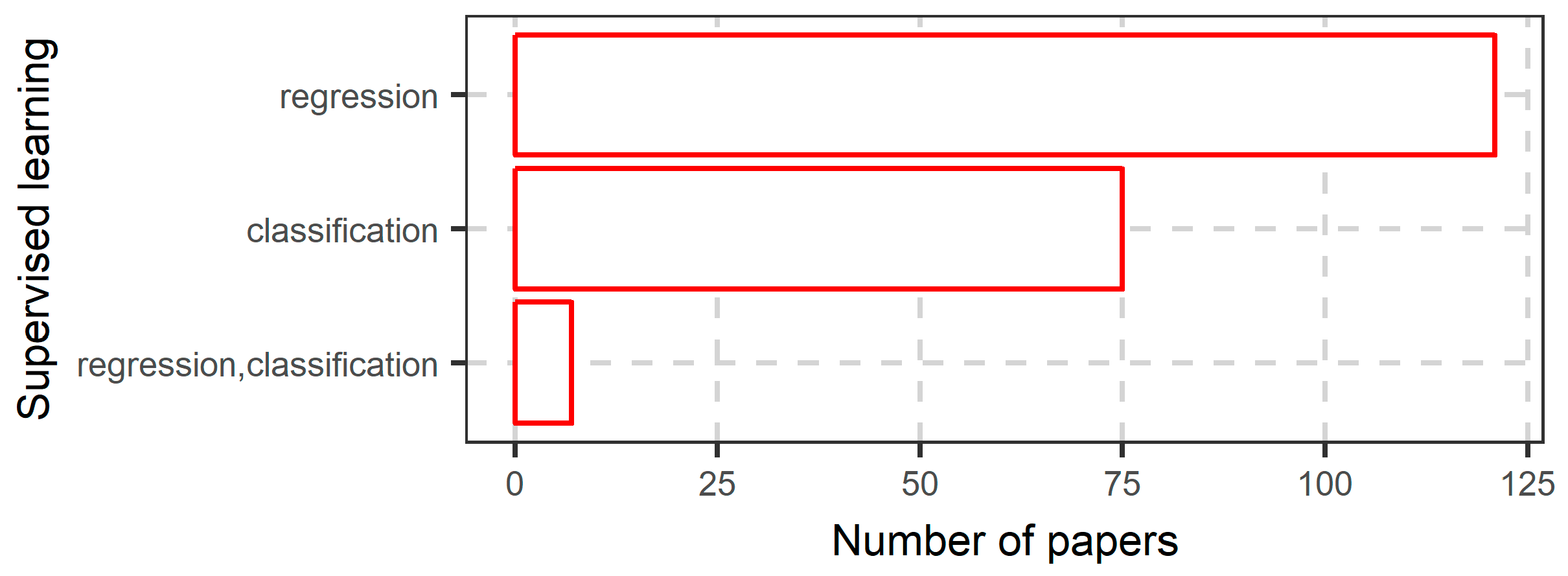
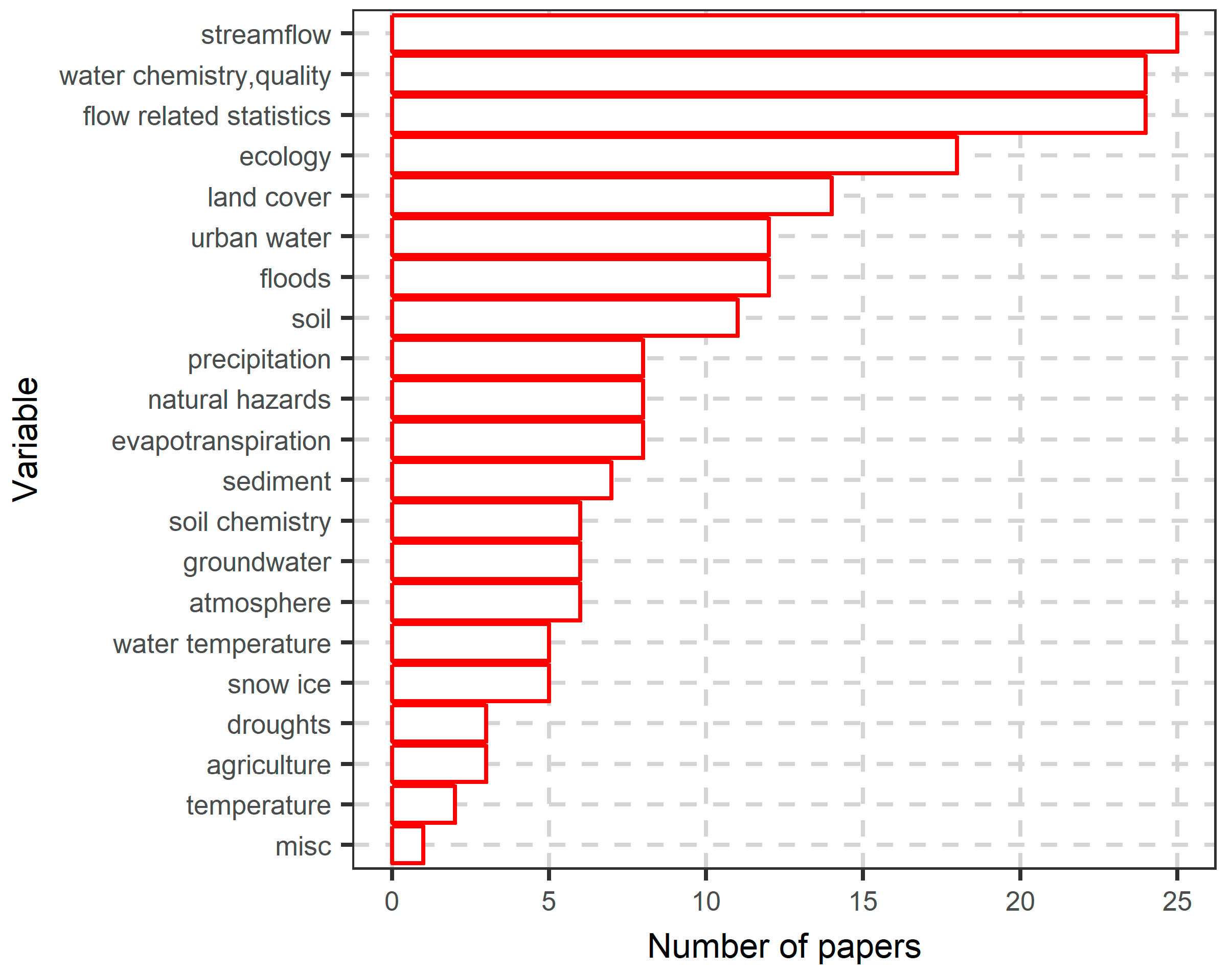
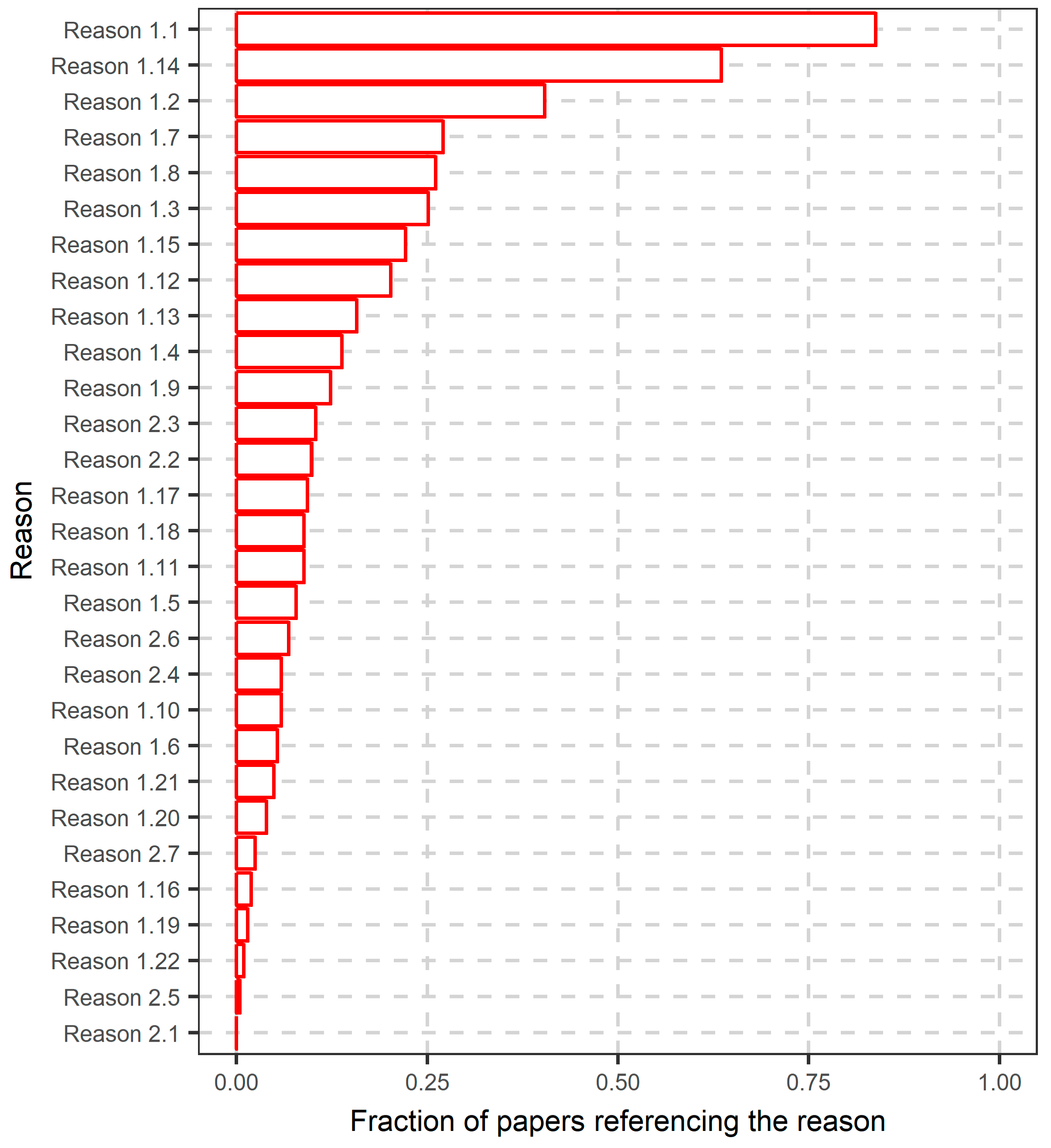
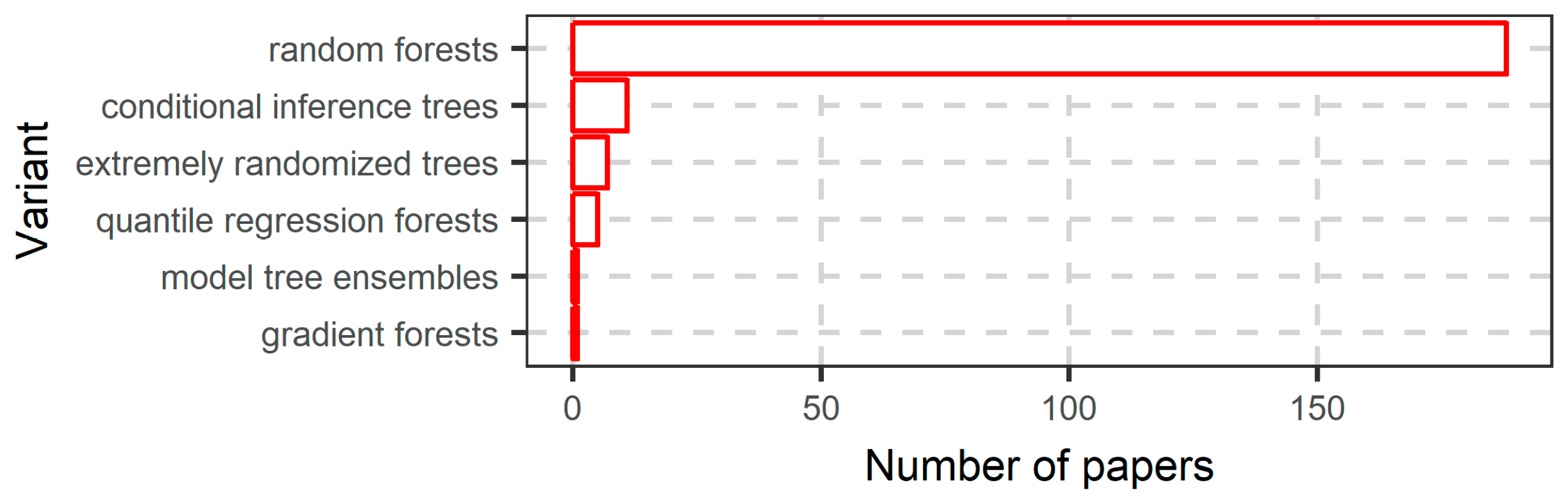
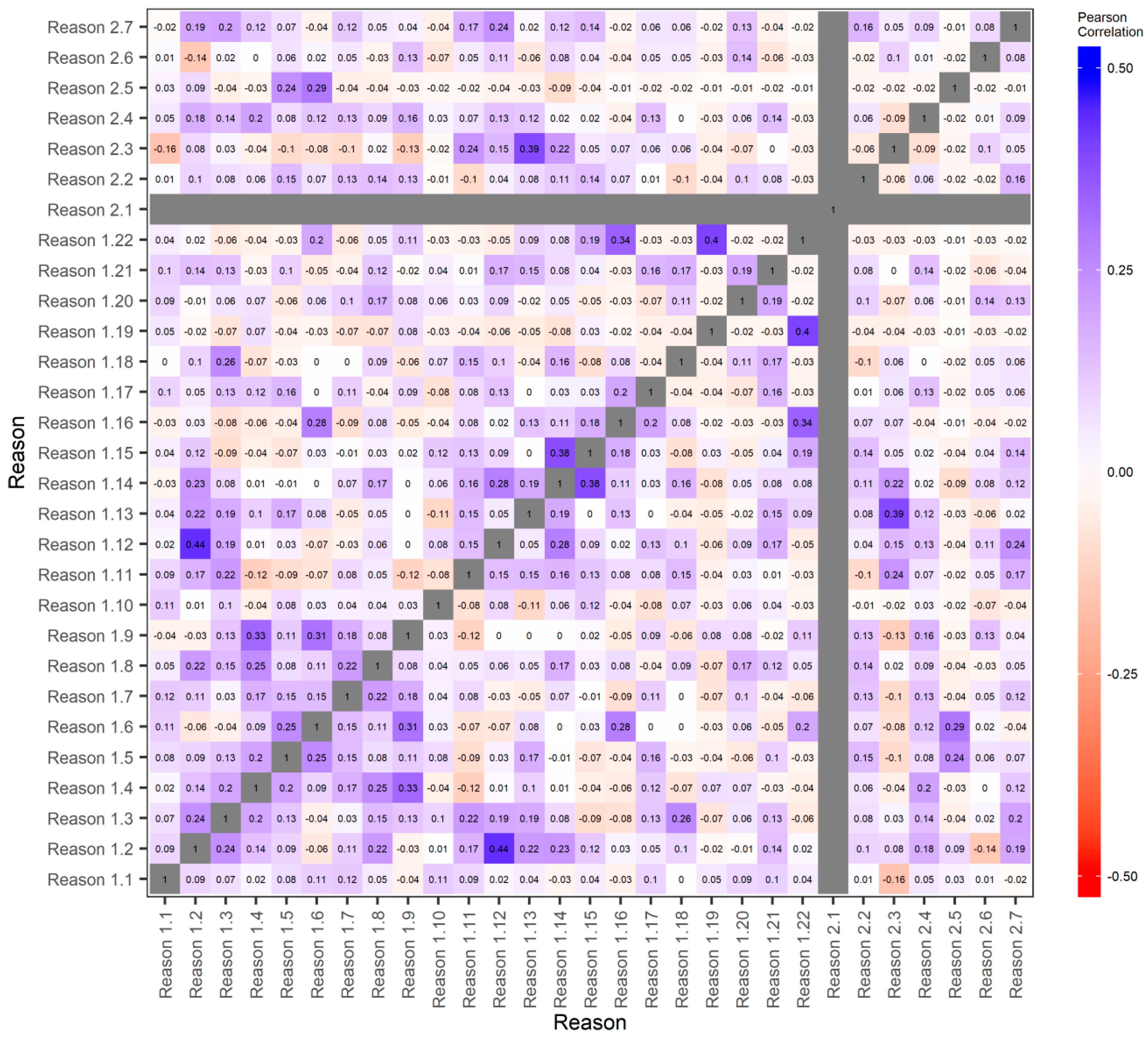
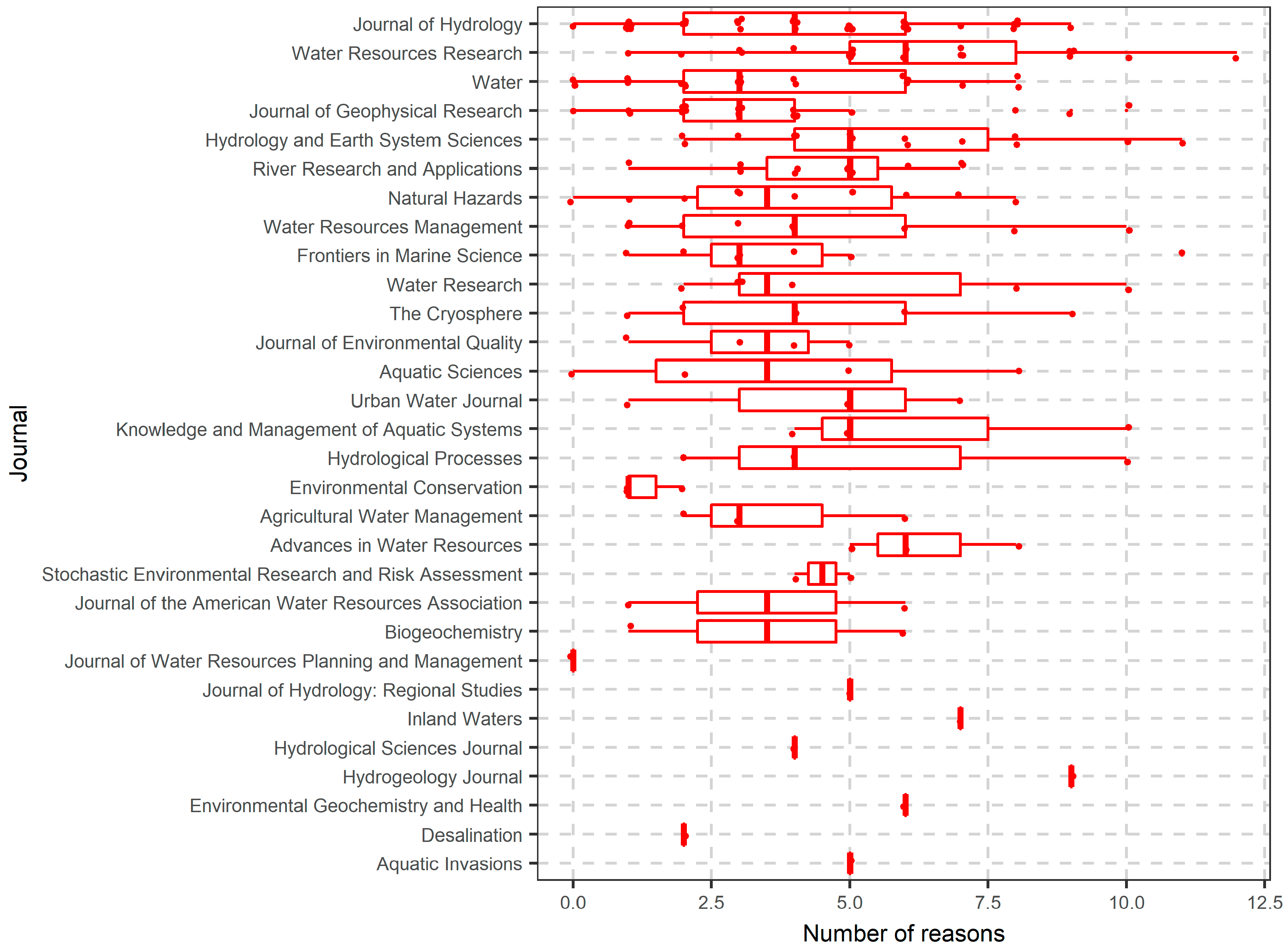
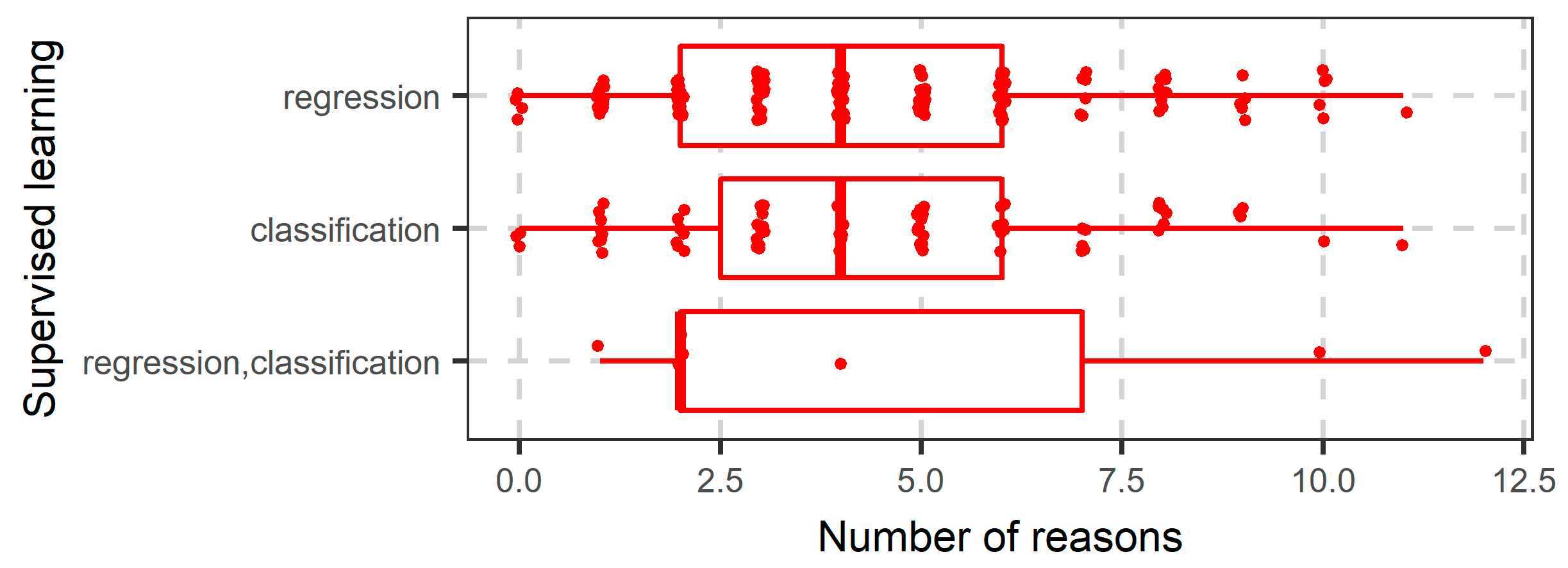
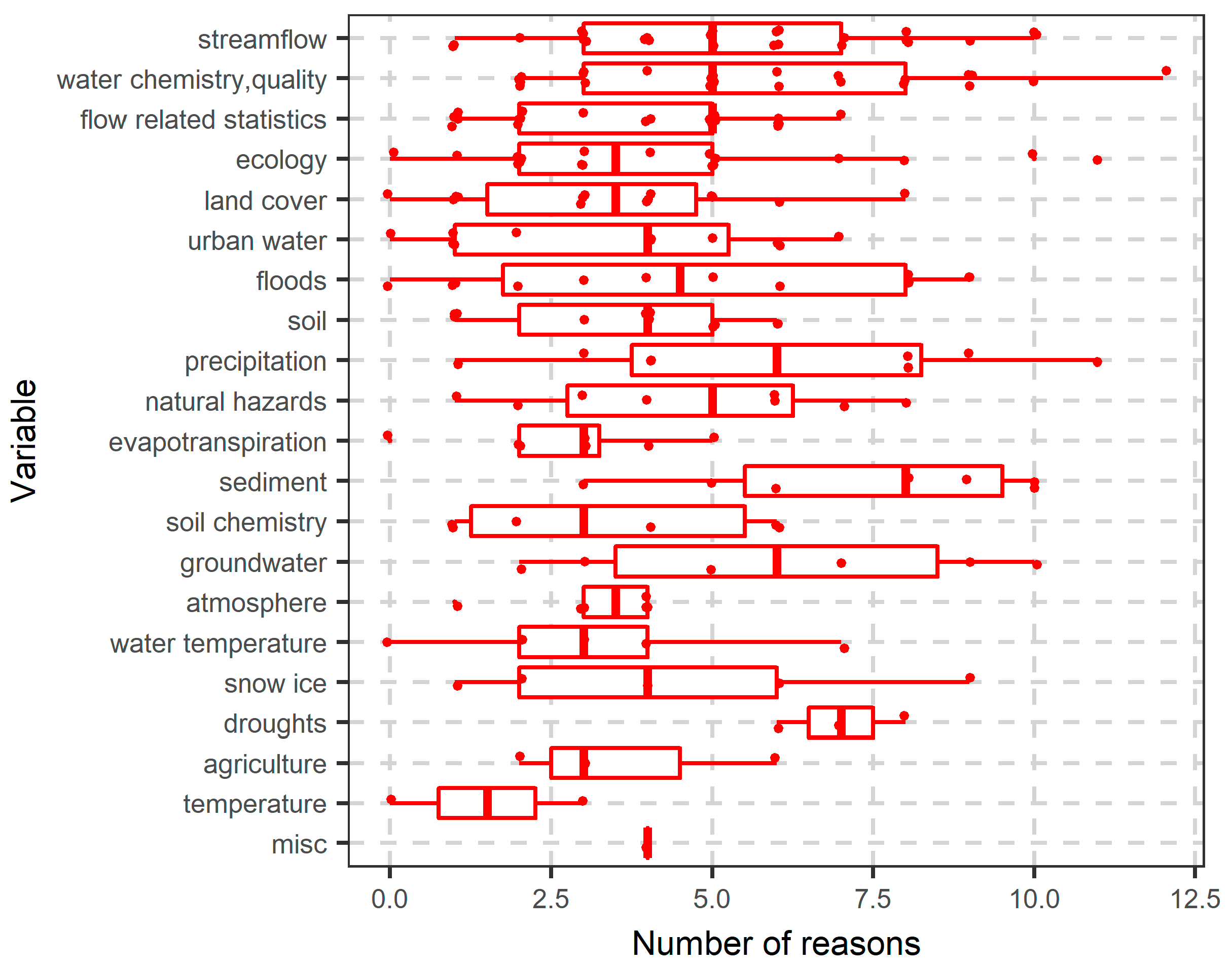
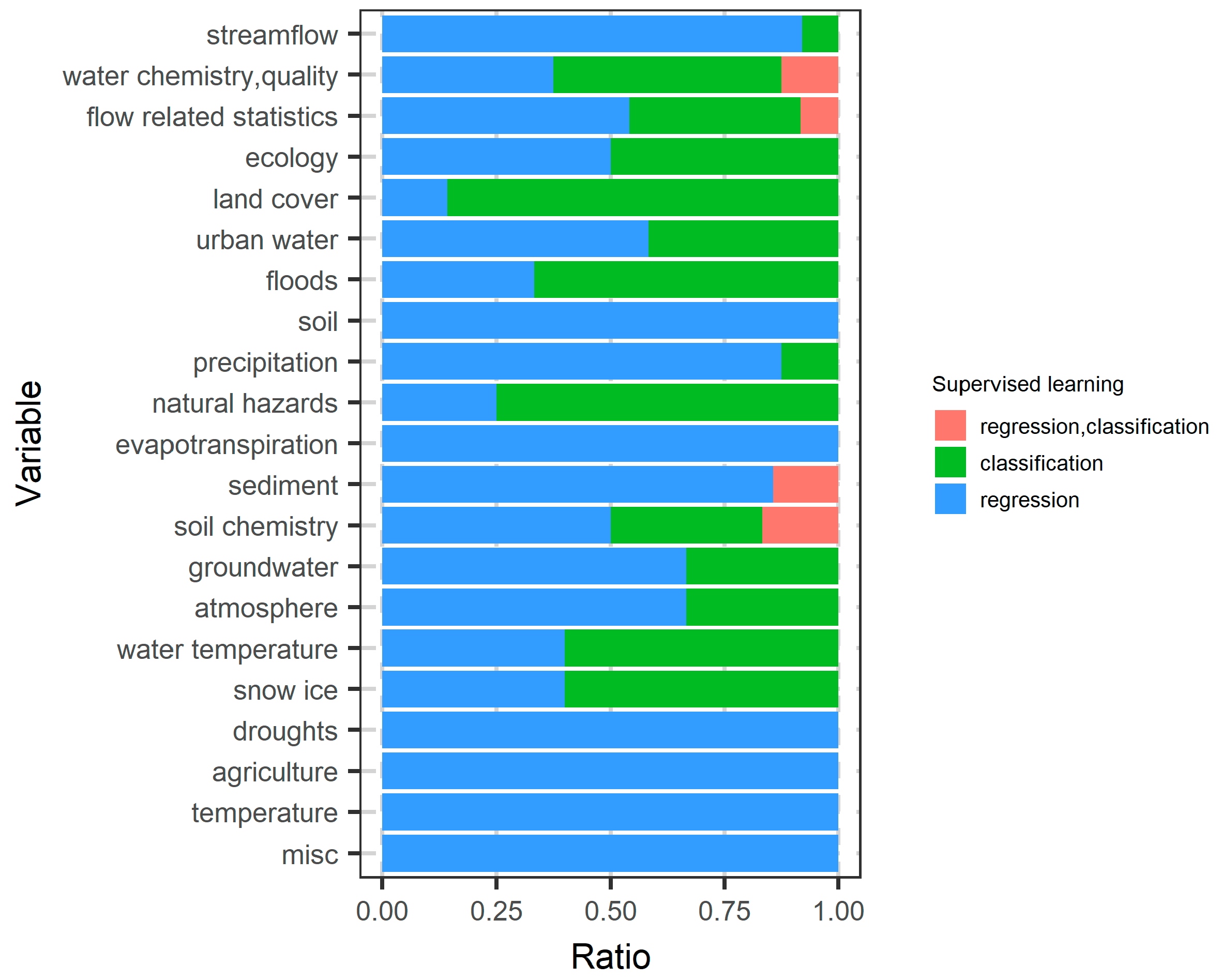
| Paper | Algorithms | General Theme | Topics Examined |
|---|---|---|---|
| [21] | Artificial neural networks | Rainfall-runoff modeling and flood forecasting | Preprocessing, variable selection, training, testing, modeling practices |
| [22,23] | Artificial neural networks | Water resources applications | Methods for variable selection |
| [20] | Artificial neural networks, genetic programming, evolutionary regression, fuzzy-rule based systems, support vector machines, chaos theory, instance-based learning, regression trees | River flow forecasting, river basin flow prediction, contaminant transport | Testing, human expertise, uncertainty estimation, hybrid models |
| [24] | Artificial neural networks | Rainfall-runoff modeling | Variable selection, training, testing, hybrid models, extrapolation |
| [25] | Artificial neural networks | Flow, salinity, level, nitrate, SO4, drought index, sediment, volume, turbidity, specific conductance, DO, pH, water temperature, concentration of tracer, runoff, river discharge, Secchi depth, Chl a, phosphorus, ammonia, fecal coliform, water supply, debris flow, dam inflow | Variable selection, training, testing, model architecture |
| [26] | Bayesian networks | Environmental modeling | Preprocessing, training, testing, software |
| [27] | Artificial neural networks | Rainfall-runoff, river flow forecasting | Model architecture, preprocessing, variable selection, training, testing, physical interpretation, modular solutions, ensemble learning, hybrid models, benchmark datasets, diagnostics, operational models, uncertainty estimation |
| [28] | Wavelet-Artificial intelligence models | Precipitation modeling, flow forecasting, rainfall-runoff modeling, sediment modeling, groundwater modeling, hydroclimatologic applications | Reviews of data-driven models, testing, usefulness of hybrid wavelet-based models |
| [29] | Support vector machine | Rainfall forecasting, runoff forecasting, streamflow forecasting, sediment yield forecasting, evaporation and evapotranspiration forecasting, lake and water level forecasting, flood forecasting, drought forecasting, groundwater level forecasting, soil moisture estimation, groundwater quality assessment | Mostly comparison of studies |
| [30] | Ant colony optimization | Optimization, reservoir operation and surface water management, water distribution systems, drainage and wastewater engineering, groundwater systems including remediation, monitoring, and management, Environmental and Watershed Management Problems, other applications | Analysis of the literature |
| [31] | Artificial neural networks, fuzzy logic networks, genetic algorithms, genetic programming, particle swarm optimization, honey-bee mating, artificial bee colony | Inflow forecasting, reservoir management optimization | General evaluation of the algorithms |
| [32] | Artificial neural networks, support vector machine, fuzzy logic, evolutionary computing, wavelet-artificial intelligence model | Streamflow forecasting | General evaluation of the algorithms |
| [33] | Artificial neural networks, adaptive neuro fuzzy inference system, other algorithms, wavelet-artificial intelligence model | Sediment transport | General evaluation of the algorithms |
| [34] | Bayesian belief networks | Environmental applications | Geographic distribution of papers, data sources, testing, climate change related issues, water resources management, integration with other models |
| [35] | Artificial neural networks | Forecasting of water related variables, uncertainty estimation | General evaluation of methods for uncertainty estimation, testing |
| [36] | Genetic programming | Rainfall-runoff modeling, streamflow forecasting, water quality variables modeling, groundwater modeling, soil properties modeling, sediment transport, reservoir flow prediction, pipeline flow prediction, open channel flow, wave height prediction, statistical downscaling, precipitation, evaporation, evapotranspiration, solar radiation, drought forecasting, temperature | Evaluation of the applications, selection of parameters |
| [37] | Deep learning | Water resources related problems | General discussion |
| [38] | ARIMA, ARMAX, linear regression, support vector machine, genetic programming, fuzzy logic, hybrid models | Univariate streamflow forecasting | General evaluation of the algorithms |
| Variant | Reference | Characteristic |
|---|---|---|
| Quantile regression forests | [85] | Quantile regression |
| Extremely randomized trees | [103] | They split nodes by choosing cut-points fully at random and use the full learning sample to grow the trees. It corresponds to a lower parametric version of random forests |
| Enriched random forests | [104] | Weighted random selection of predictor variables as candidates for splitting. |
| Rotation forests | [105] | Combines splitting of the predictor variables set with principal component analysis for improved accuracy |
| Conditional inference forests | [71,100,106,107,108] | Unbiased variable importance measures in the case of correlated or mixed type (i.e., continuous and categorical) predictor variables. |
| Random survival forests | [98,109,110] | Survival analysis. |
| Online forests, Mondrian forests. information forests | [111,112,113,114] | Handles training data arriving sequentially or continuously, changing the underlying distribution. |
| Ranking forests | [115,116] | Ranking problems |
| Random ferns | [117] | Same test parameters are used in all nodes of the same tree level. It corresponds to a lower parametric version of random forests. |
| Bayesian additive regression trees | [94] | Aggregation of trees, but inference and fitting is accomplished using Bayesian methods. Conditional means and quantiles can be computed. |
| Node harvest | [118] | Multiple single nodes. |
| Density forests | [15] | Density estimation of unlabeled data. |
| Manifold forests | [15] | Manifold learning (dimensionality reduction). |
| Semi-supervised forests | [15] | Semi-supervised learning. |
| Entangled forests | [119] | Entanglement of the tests applied at each tree node with other nodes in the forest. |
| Decision tree fields | [99] | Combination of random forests and random fields. |
| STAR model | [120] | They can be seen as single nodes equipped with one random projection and multiple decision thresholds |
| Multivariate random forests | [97] | Predicts multiple dependent variables. |
| Dynamic random forests | [121] | Inclusion of trees in the ensemble learner depending on previous outputs. |
| Gradient forests | [122] | Use of alternative importance measures. |
| Regularized random forests | [123,124] | Improvements on variable selection within trees. |
| Cluster forests | [125] | Appropriate for clustering (unsupervised learning). |
| Weighted random forests | [126] | Incorporates tree-level weights for more accurate prediction and computation of variable importance. |
| Random intersection trees | [101] | High-order interaction discovery. |
| Hyper-Ensemble Smote Undersampled Random Forests | [91] | Undersampling of the majority class and oversampling of the minority class to learn from highly imbalanced data. |
| Integrated multivariate random forests | [127] | Integrated different data subtypes. |
| Generalized random forests | [89] | Generalization of random forests for adaptive, local estimation. |
| Iterative random forests | [102,128] | High-order interaction discovery. |
| Heteroscedastic Bayesian additive regression trees | [95] | Bayesian additive regression trees for modeling heteroscedastic data. |
| Local linear forests | [129] | They model smooth signals and fix boundary bias issues. They build on generalized random forests. |
| Distributional regression forests | [96] | Version of generalized additive models for location, scale, and shape parameters (GAMLSS), using trees. |
| Causal forests | [92] | Estimation of heterogeneous treatment effects. They can be used for statistical inference. |
| Neural random forests | [130] | Reformulation of random forests in a neural network setting. |
| R Package | Characteristics |
|---|---|
| abcrf | Combined with other methods |
| AUCRF | Variable selection |
| bartMachine | Variant |
| Boruta | Variable selection |
| CALIBERrfimpute | Imputation |
| caret | Of general use |
| edarf | Utilities |
| extendedForest | Utilities |
| forestControl | Variable selection |
| forestFloor | Utilities |
| funbarRF | Application |
| ggRandomForests | Utilities |
| gradientForest | Variant |
| grf | Variant |
| hyperSMURF | Variant |
| IntegratedMRF | Variant |
| IPMRF | Variable importance |
| iRafNet | Variant |
| iRF | Variant |
| JRF | Variant |
| m2b | Application |
| MAVTgsa | Application |
| metaforest | Application |
| missForest | Imputation |
| mlr | Of general use |
| mobForest | Application |
| ModelMap | Utilities |
| MultivariateRandomForest | Variant |
| obliqueRF | Variant |
| OOBCurve | Utilities |
| ParallelForest | Better programmed |
| party | Variant |
| partykit | Variant |
| pRF | Variable importance |
| quantregForest | Variant |
| randomForest | Variant |
| randomForestExplainer | Variable importance |
| randomForestSRC | Variant |
| ranger | Better programmed |
| Rborist | Better programmed |
| RFgroove | Variable importance |
| RFmarkerDetector | Application |
| rfPermute | Variable importance |
| rfUtilities | Utilities |
| roughrf | Imputation |
| RRF | Variant |
| snpRF | Variant |
| Sstack | Application |
| SuperLearner | Of general use |
| trimTrees | Variant |
| tuneRanger | Utilities |
| varSelRF | Variable selection |
| vita | Variable importance |
| VSURF | Variable selection |
| wsrf | Variant |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. https://doi.org/10.3390/w11050910
Tyralis H, Papacharalampous G, Langousis A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water. 2019; 11(5):910. https://doi.org/10.3390/w11050910
Chicago/Turabian StyleTyralis, Hristos, Georgia Papacharalampous, and Andreas Langousis. 2019. "A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources" Water 11, no. 5: 910. https://doi.org/10.3390/w11050910
APA StyleTyralis, H., Papacharalampous, G., & Langousis, A. (2019). A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water, 11(5), 910. https://doi.org/10.3390/w11050910





