Probabilistic Hydrological Post-Processing at Scale: Why and How to Apply Machine-Learning Quantile Regression Algorithms

Abstract

We conduct a large-scale benchmark experiment aiming to advance the use of machine-learning quantile regression algorithms for probabilistic hydrological post-processing “at scale” within operational contexts. The experiment is set up using 34-year-long daily time series of precipitation, temperature, evapotranspiration and streamflow for 511 catchments over the contiguous United States. Point hydrological predictions are obtained using the Génie Rural à 4 paramètres Journalier (GR4J) hydrological model and exploited as predictor variables within quantile regression settings. Six machine-learning quantile regression algorithms and their equal-weight combiner are applied to predict conditional quantiles of the hydrological model errors. The individual algorithms are quantile regression, generalized random forests for quantile regression, generalized random forests for quantile regression emulating quantile regression forests, gradient boosting machine, model-based boosting with linear models as base learners and quantile regression neural networks. The conditional quantiles of the hydrological model errors are transformed to conditional quantiles of daily streamflow, which are finally assessed using proper performance scores and benchmarking. The assessment concerns various levels of predictive quantiles and central prediction intervals, while it is made both independently of the flow magnitude and conditional upon this magnitude. Key aspects of the developed methodological framework are highlighted, and practical recommendations are formulated. In technical hydro-meteorological applications, the algorithms should be applied preferably in a way that maximizes the benefits and reduces the risks from their use. This can be achieved by (i) combining algorithms (e.g., by averaging their predictions) and (ii) integrating algorithms within systematic frameworks (i.e., by using the algorithms according to their identified skills), as our large-scale results point out.

1. Introduction

Issuing useful hydrological predictions (e.g., river flow predictions) is one of the most important challenges in hydrology. Dealing with this challenge involves answering numerous research questions, but also putting research into practice by exploiting research advancements in operational contexts. This additional consideration introduces some extra requirements for prediction methodologies, mostly related to their appropriateness for what we call prediction “at scale”. Issuing hydrological predictions “at scale” is a major theme in the present study. The term “at scale” is used here according to Taylor and Letham [1], i.e., to imply several notions of scale, mostly (i) a large number of required predictions, and (ii) a large variety of prediction problems to be solved. The latter are created, e.g., under different climate and catchment conditions.

Also importantly, the present study is principally founded upon the premise that (operational) hydrological predictions can be most useful when expressed in probabilistic terms (see, e.g., references [2,3,4,5,6]), i.e., in terms of probability distribution function (PDF) [4] (see also references [7,8]) or in terms of prediction intervals (or predictive quantiles). Delivering probabilistic hydrological predictions is a relatively new practice [6,9] considering the much longer history of hydrological modelling, comprehensively summarized by Todini [4]. This practice is also referred to in the related literature as “global uncertainty” quantification (see, e.g., reference [9]) or “predictive uncertainty” quantification (see, e.g., reference [4]), and its technical implications are under consideration and ongoing discussions (see, e.g., references [3,10,11,12,13]).

The background of the present study lies in the tremendous and growing progress made in two distinct research fields, the advancements of which can be exploited in hydrological contexts for predictive modelling (contrasted to explanatory and descriptive modelling in Shmueli [14]). These are the field of “process-based” hydrological modelling (term used here as defined in Montanari and Koutsoyiannis [6]; see, e.g., references [15,16,17,18,19,20,21,22]) and the field of machine-learning (see, e.g., references [23,24,25,26]). The former includes various modelling approaches spanning from distributed to lumped conceptual approaches, which also aim (besides prediction) at supporting some sort of “physical interpretation” of the catchment-scale hydrological phenomena [4] and describing the catchment’s behavior as a whole [16], respectively. Moreover, the machine-learning field includes a large variety of multi-purpose algorithmic techniques, potentially useful in various applied fields, such as hydrology. Among its latest advancements are ensemble learning methods (e.g., the bagging by Breiman [27] and random forests by Breiman [28]), i.e., methods that combine the results of individual learning algorithms [29]. Machine-learning algorithms are often referred to in the hydrological literature under the more general term “data-driven models”.

Process-based hydrological models and data-driven algorithmic approaches are regarded as two different “streams of thought” in predictive hydrological modelling which need to be harmonized “for the sake of hydrology” [4]. In fact, machine-learning techniques can be perceived as manifestations of the algorithmic modelling culture, a statistical modelling culture that is grounded on the premise that the mechanism behind the data generation is completely unknown and, therefore, obtaining predictions by exploiting the data does not require its prior description through an analytical model [30]. This culture fundamentally deviates from what is called “process-based modelling”.

Often perceived to represent tradition, experience and lessons-learnt knowledge (from a “physical process-oriented” modeller’s point of view) [4], process-based models are mostly preferred by hydrological modellers and hydro-meteorological forecasters [31]. Among the plethora of the currently available process-based hydrological models, few exemplary ones are more trustable than others (e.g., the Génie Rural—GR hydrological models by Perrin et al. [16], Mouelhi et al. [17], and others, which are also available in open source by Coron et al. [32,33]), as it is evident from the literature that they are the result of decades of continuous and labor-intensive hydrological research focusing on better overall prediction, better prediction of low and high flows, and model parsimony, among others (see, e.g., the related comments in Perrin et al. [16]).

On the other hand, “engineering-oriented” modellers report on (unexploited) opportunities for high predictive performance stemming from the use of data-driven hydrological models [4]. Machine-learning regression algorithms are regularly implemented in the data-driven hydrological literature for solving a vast amount of technical problems, and for building confidence in predictive and explanatory modelling (see, e.g., references [34,35,36,37,38,39,40]). Yet, their potential has been realized and exploited only to a limited extent, and mostly for obtaining “point” predictions (term used here as opposed to “probabilistic”). Nonetheless, this potential includes the possibility of delivering probabilistic hydrological predictions (including forecasts; see, e.g., the relevant practical suggestions for using random forests in water-related applications by Tyralis et al. [41]), in spite of the widespread misconception existing in the minds of hydrologists that machine-learning algorithms are by nature deterministic (i.e., not statistical). Actually, machine-learning methods are all statistical (therefore, “machine-learning” and “statistical learning” are terms interchangeably used beyond hydrology), and some of them (e.g., the quantile regression ones, on which this study focuses) are ideal for predictive uncertainty quantification.

Advancing the implementation of machine-learning regression algorithms by conducting large-sample (and in-depth) hydrological investigations has been gaining prominence recently (see, e.g., references [42,43,44,45,46]), perhaps following a more general tendency for embracing large-scale hydrological analyses and model evaluations (see, e.g., references [47,48,49,50,51]). The key significance of such studies in improving the modelling of hydrological phenomena, especially when the modelling is data-driven, has been emphasized by several experts in the field (see, e.g., references [16,52,53,54,55]).

In the present study, we exploit a large dataset for advancing the use of machine-learning algorithms within broader methodological approaches for quantifying the predictive uncertainty in hydrology. The hydrological modelling and hydro-meteorological forecasting literatures include a large variety of such methodologies (see, e.g., references [45,46,56,57,58,59,60,61,62,63,64,65,66,67,68,69]), reviewed in detail by Montanari [9] and Li et al. [70]. Deterministic “process-based” hydrological models are usually and preferably a core ingredient of probabilistic approaches of this family. In this context, statistical models are applied to convert the point predictions provided by hydrological models to probabilistic predictions. Such methodologies are hereafter referred to under the term “probabilistic hydrological post-processing” methodologies.

We are explicitly interested in probabilistic hydrological post-processing methodologies whose models are estimated sequentially in more than one stage (see also Section 2.1; hereafter referred to as “multi-stage probabilistic hydrological post-processing methodologies”) and machine-learning quantile regression algorithms, since the former can accommodate the latter naturally and effectively. The effectiveness of this accommodation has already been proven, for example, with the large-scale results by Papacharalampous et al. [45] and Tyralis et al. [46] for the monthly and daily timescales, respectively. Aiming at combining the advantages from both the above-outlined “streams of thought” in predictive hydrological modelling, these studies and a few earlier ones (to the best of our knowledge, those mentioned in

Table 1. List of statistical models implemented within multi-stage hydrological post-processing methodologies.

Statistical Model	Classification	Studies
Meta-Gaussian bivariate distribution model	Parametric; conditional distribution	References [6,61,62]
Generalized additive models (GAMLSS)	Parametric; machine-learning	References [71,72]
Quantile regression	Non-parametric; machine-learning; quantile regression	References [45,46,64,65,69,73]
Quantile regression forests		References [46,74]
Quantile regression neural networks		References [66,67,75]

) have integrated process-based hydrological models and data-driven algorithmic approaches (spanning from conditional distribution modelling approaches to regression algorithms) within multi-stage probabilistic hydrological post-processing methodologies for predictive uncertainty quantification purposes.

As summarized in Table 1, multi-stage (mostly two-stage) probabilistic hydrological post-processing has been implemented both using parametric and non-parametric statistical models. Machine-learning quantile regression algorithms do not make assumptions about the probability distribution function (PDF) of the predictand; therefore, they fall into the broader class of non-parametric techniques. Their output is a set of predictive quantiles of selected levels (e.g., the predictive quantiles of levels α/2 and 1 − α/2, which form the (1 − α) 100% central prediction interval), instead of predictive PDFs of the hydrological processes of interest. While (three) algorithms from this category have already been incorporated into multi-stage probabilistic hydrological post-processing methodologies (mostly for solving technical problems within case studies; see Table 1), there is no extensive study focusing on formalizing and framing this incorporation. We aspire to fill this gap by conducting the largest and most systematic assessment of machine-learning algorithms for probabilistic post-processing in hydrology.

We aim at answering the following research question: Why and how to apply machine-learning quantile regression algorithms for probabilistic hydrological post-processing? As implied by our aim, our contribution in the literature includes the inspection and appraisal of both quantitative and qualitative aspects of the application of the algorithms. Although our benchmark experiment holds a prominent position in this study, the theoretical and practical information on the proposed methodologies and framework, also provided herein, are rather equally important for answering the above-stated research question. Specifically, we:

• Explore, through benchmark tests, the modelling possibilities provided by the integration of process-based models and machine-learning quantile regression algorithms for probabilistic hydrological modelling. This exploration encompasses the:

  ✓

  comparative assessment of a representative sample set of machine-learning quantile regression algorithms in two-stage probabilistic hydrological post-processing with emphasis on delivering probabilistic predictions “at scale” (an important aspect within operational settings);

  ✓

  identification of the properties of these algorithms, as well as the properties of the broader algorithmic approaches, by investigating their performance in delivering predictive quantiles and central prediction intervals of various levels; and

  ✓

  exploration of the performance of these algorithms for different flow magnitudes, i.e., in conditions characterized by different levels (i.e., magnitudes) of predictability.

• Explore, through benchmark tests, the modelling possibilities provided by simple quantile averaging. Simple quantile averaging is the simplest way to combine multiple quantile predictions (by averaging them), but also “hard to beat in practice” [76,77].
• Formulate practical recommendations and technical advice on the implementation of the algorithms for solving the problem of interest (and other problems of technical nature). An important remark to be made is that these recommendations are not meant in any case to be limited to selecting a single algorithm for all tasks and under all conditions. Each algorithm has its strengths and limitations, which have to be identified so that it finds its place within a broader framework (provided that the algorithm is a good fit for solving the problem of interest). This point of view is in accordance with the ‘‘no free lunch theorem’’ by Wolpert [78].
• Justify and interpret key aspects of the developed methodological framework and its high appropriateness for progressing our understanding on how machine-learning quantile regression algorithms should be used to maximize benefits and minimize risks from their implementation.

Preliminary works on the above can be found in Papacharalampous et al. [79], while Papacharalampous et al. [45,69] (studies built on the work by Montanari and Koutsoyiannis [6]) and Tyralis et al. [46] focus on ensemble learning probabilistic hydrological post-processing methodologies that can accommodate the algorithms assessed herein. Ensemble learning methods combining the predictions obtained by multiple learning algorithms (e.g., the equal-weight combiner tested herein) are increasingly adopted in many engineering and applied science fields, since they frequently provide improved predictive performance with respect to each of the individual learning algorithms (see, e.g., the review by Sagi and Rokach [29]). The results of the present study also advocate the value of ensemble learning for probabilistic hydrological post-processing.

2. Background on Methodologies, Models and Algorithms

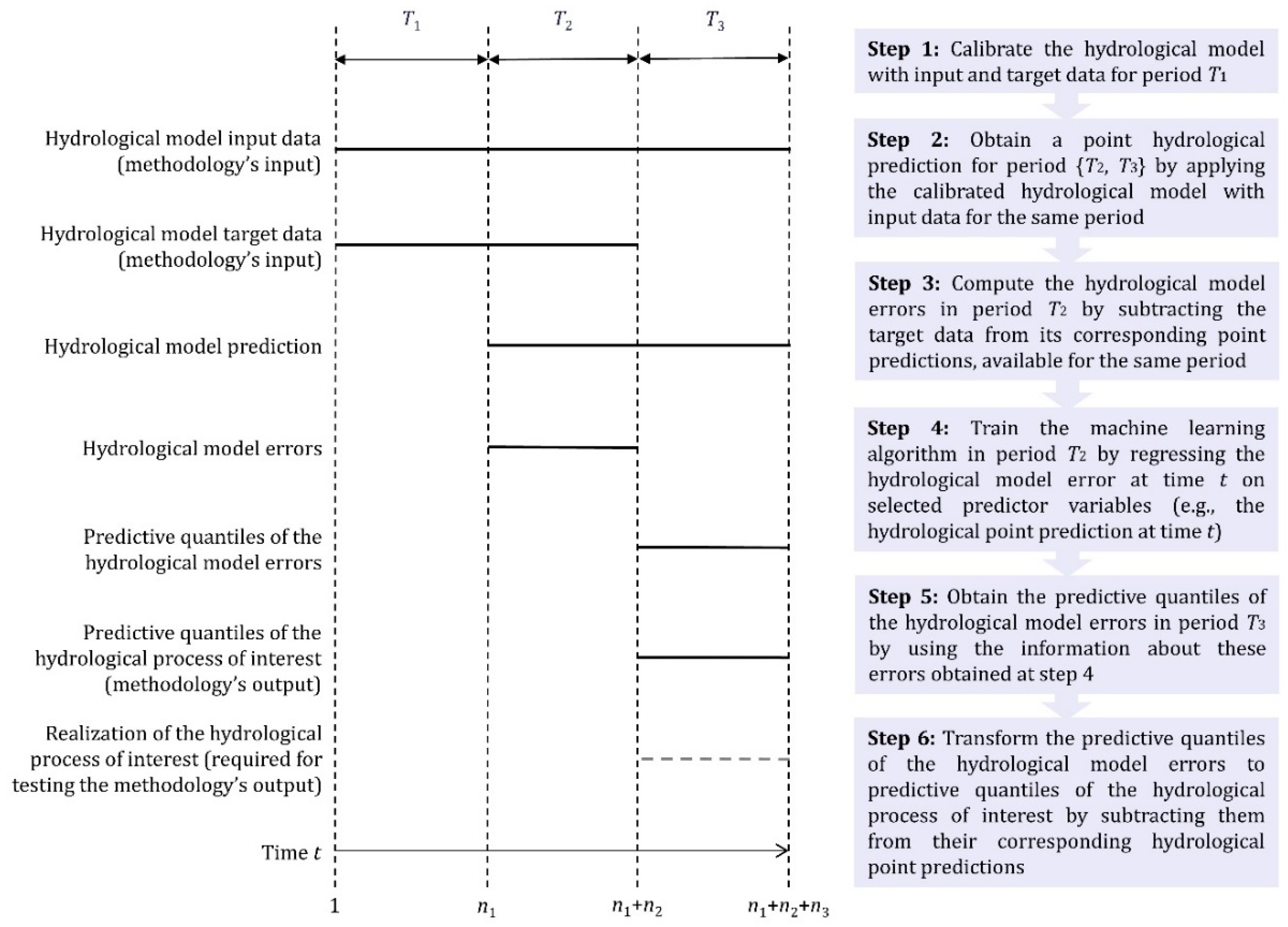
2.1. Multi-Stage Probabilistic Hydrological Post-Processing

This section is devoted to outlining the main procedures carried out within multi-stage probabilistic hydrological post-processing methodologies and how the latter can accommodate machine-learning quantile regression algorithms. For this outline, we assume a historical rainfall-runoff dataset, a process-based hydrological model and at least one machine-learning quantile regression algorithm. The key idea implemented is to use point predictions provided by the hydrological model as predictor variables within a quantile regression setting. This implies the division of the historical dataset into two independent segments; the first is used to calibrate the hydrological model, while the second is used to apply the calibrated hydrological model and to form the regression training set. The information encompassed in the latter is finally exploited by the machine-learning quantile regression algorithm(s). A commonly adopted response variable in the regression is the hydrological model error. The latter is defined as the deviation of a target value from the point prediction provided by the hydrological model.

In this context, the regression problem to be solved is summarized as follows. We are interested in modelling the changes of selected quantiles of the hydrological model error at time t with the changes of the predictor variables, typically a set of hydrological model predictions (e.g., the hydrological model predictions at times t − 1 and t). These predictions can be obtained by using the hydrological model either in simulation or in forecasting mode, i.e., by either using observations or using forecasts as inputs, respectively (see reference [80]). In Figure 1, we present a typical two-stage probabilistic hydrological post-processing methodology using a machine-learning quantile regression algorithm for modelling the hydrological model errors. The predictions provided by multiple machine-learning quantile regression algorithms can be further combined, for example, via simple quantile averaging through an equal-weight combiner. Optimal prediction combinations with respect to one or more scores would require a third stage at which the combiner is trained (see, e.g., reference [46]).

2.2. Implemented Hydrological Model

We implement the Génie Rural à 4 paramètres Journalier (GR4J) model by Perrin et al. [16], a four-parameter conceptual hydrological model. This model is widely applied in the literature (see, e.g., references [46,53,68,81,82,83,84,85,86,87,88]), while its reliability is well-supported by large-sample empirical results (see reference [16]). It was developed by using as starting point the Génie Rural à 3 paramètres Journalier (GR3J) model by Edijatno et al. [89], i.e., a three-parameter conceptual hydrological model. A large-sample investigation of the latter can be found in Perrin et al. [15]. GR4J was proposed as an improved (but still parsimonious) version of its precursor model, selected through extensive computational tests among 235 (preliminary) modifications of the latter. Its four parameters are the maximum capacity of the production store (expressed in mm), the groundwater exchange coefficient (expressed in mm), the one-day ahead maximum capacity of the routing store (expressed in mm) and the time base of the unit hydrograph (expressed in days). Its inputs are daily precipitation and potential evapotranspiration, while its output is daily streamflow. For its mathematical formulation, the reader is referred to Perrin et al. [16]. We note that the implementation of this hydrological model is auxiliary herein. Specifically, this model is used to form the regression problem solved by the machine-learning algorithms, as explained in Section 2.1. Therefore, while possible, the implementation of other hydrological models is out of the scope of the study.

2.3. Assessed Machine-Learning Quantile Regression Algorithms

2.3.1. Theoretical Background and List of Algorithms

Quantile regression algorithms are explained from an applied perspective in the tutorial article of Waldmann [90], while a review with up-to-date progress in the field is available in Koenker [91]. Quantile regression algorithms quantify the relationship (within a regression setting) between the predictor variables x (input to the algorithm) and a conditional quantile of the dependent variable y. The quantile q_τ(y) of random variable y at level τ ∈ (0, 1) is defined as:

$$q_{\tau }(y):=F_y^{-1}(\tau )$$

(1)

where F_y denotes the cumulative distribution function (CDF) of y. Moreover, the respective conditional quantile q_τ(y|x) is defined by

$$q_{\tau }(y|\mathit{x}):=F_{y|x}^{-1}(\tau |\mathit{x})=y_{\tau }(\mathit{x})$$

(2)

where F_y|x denotes the CDF of y conditional on x. Quantile regression is equivalent to standard regression, with the difference that the former focuses on modelling conditional quantiles instead of modelling conditional means. Most quantile regression algorithms are based on minimization of the average quantile score (or average pinball loss) over all observations. The quantile score (QS_τ; see, e.g., references [92,93]) is defined by Equations (3) and (4).

QS_τ(u) := (τ − Ι{u < 0}) u

(3)

u := y_τ(x) − y

(4)

In Equation (3), I{∙} denotes the indicator function. When the average quantile score is minimized, observations of the dependent variable are divided approximately to two groups including 100 × τ% and 100 × (1 − τ)% of the data. This observation has been theoretically confirmed (see reference [91]).

According to Waldmann [90], quantile regression is appropriate when: (a) the interest is in events at the limit of probability; (b) the conditional distribution of the dependent variable is not known or is hard to deduce; (c) there are numerous outliers among the observations of the dependent variable; and (d) heteroscedasticity needs to be modelled. Drawbacks of quantile regression algorithms are also enumerated by Waldmann [90]. A main drawback, shared by most algorithms from this category due to separately estimating different quantiles, is quantile crossing. Furthermore, parameter estimation is harder in quantile regression than in standard regression.

In the following subsections, we outline the main properties of the quantile regression algorithms assessed in the present study. The reader is also referred to the specialized literature for further information. The assessed algorithms and their abbreviations used herein are listed in

Table 2. Machine-learning quantile regression algorithms assessed in this study. Their software implementation is detailed in Appendix A.

S/n	Primal Machine-Learning Algorithm	Abbreviation	Section
1	Quantile regression	qr	2.3.2
2	Generalized random forests for quantile regression	qrf	2.3.3
3	Generalized random forests for quantile regression emulating quantile regression forests	qrf_meins	2.3.3
4	Gradient boosting machine with trees as base learners	gbm	2.3.4
5	Model-based boosting with linear models as base learners	mboost_bols	2.3.4
6	Quantile regression neural networks	qrnn	2.3.5
7	Equal-weight combiner of the above six algorithms implemented with the same predictor variables	ensemble	-

. The predictand and predictor variables in the regression are defined in Section 3.3.

2.3.2. Quantile Regression

Quantile regression was introduced by Koenker and Bassett [94], following the exploration of quantile estimation problems by Koenker and colleagues in the 1970s (see reference [91]). It is the linear variant of quantile regression algorithms and its role is similar to that of standard linear regression. Intuitively, quantile regression is performed by fitting a linear model and bisecting the data so that 100 × τ% lie below the predicted values of the fitted model. In practice, this is performed by fitting a linear model to the data and minimizing the average quantile score. Quantile regression and its variants are extensively analyzed in Koenker [95]. The method uses similar techniques to linear regression, to estimate the quantiles of a dependent variable, conditional upon selected predictor variables.

2.3.3. Quantile Regression Forests and Generalized Random Forests

Quantile regression forests were introduced by Meinshausen [96]. They are based on Breiman’s [28] random forests, which have been extensively used in hydrology (see the review by Tyralis et al. [41]). Practically, random forests are regression algorithms that average an ensemble of decision trees (see a review on ensemble learning by Sagi and Rokach [29]). The ensemble is created by bagging (abbreviation for bootstrap aggregation [27]) regression trees using an additional randomization process. With this additional randomization, the splitting in the nodes of the regression tree is conducted by randomly selecting a fixed number of predictor variables. An extensive description of the procedure for training decision trees and random forests can be found in Hastie et al. [23] (pp. 587–604).

While regression forests can approximate the conditional mean of the dependent variable, quantile regression forests approximate its conditional quantiles. Diverging from other quantile regression algorithms (see Section 2.3.2, Section 2.3.4 and Section 2.3.5), quantile regression forests are not based on the minimization of the quantile score. While random forests estimate the conditional mean by averaging the outcomes of the individual decision trees, quantile regression forests average the indicator functions of the event that the outcome of the decision tree in the test set is lower than q_τ.

Generalized random forests [97] and their related quantile prediction algorithms differ from random forests in the implemented partitioning mechanism in the nodes of the decision trees. Due to this procedure, they are theoretically more suitable to model heterogeneities in the observed data compared to quantile regression forests.

Some important properties of random forests and their variants, as summarized in Tyralis et al. [41], are that: (a) they have high predictive performance; (b) they are non-linear and non-parametric; (c) they are fast compared to other machine-learning algorithms; (d) they are straightforward, easy-to-use and require little tuning of the parameters (default values of the parameters are of high predictive performance); and (e) they are stable and robust to the inclusion of noisy predictor variables. An important drawback of random forests is that they do not extrapolate beyond the range of the training dataset.

2.3.4. Gradient Boosting Machine and Model-Based Boosting

A general view of boosting methods can be found in Mayr et al. [98]. The concept behind boosting is to iteratively improve (boost) weak learners (i.e., algorithms of low predictive ability) to form a strong learner. A particular type of boosting algorithms, introduced by Friedman [99], is gradient boosting machine. It is described as an “off-the-shelf” method by Hastie et al. [23] (p. 352). Gradient boosting algorithms minimize a loss function via steepest gradient descent in function space. The main idea is to fit the weak learner to the negative gradient vector of the loss function evaluated at the previous iteration [98]. In plain language, boosting is an ensemble learning method in which new models are added to the ensemble sequentially. In particular, at each iteration the new model is trained to minimize the error of the ensemble learnt up until now [100]. The weak learners used in our case are decision trees. The loss function (i.e., error that has to be minimized) used is the quantile score.

While many of the random forests’ properties are shared by gradient boosting machine since both use decision trees as base learners, a major difference is that gradient boosting machine is theoretically expected to perform better due to being highly parameterized [101] (p. 324). However, in practice, random forests often perform better, because optimization required for boosting algorithms is not trivial, and it also depends on how accustomed the user is to using the particular algorithm. On the contrary, random forests are easy-to-use and perform very well with little tuning.

The most critical parameter in gradient boosting is the number of iterations performed to fit the algorithm. Too few iterations may result in sub-optimal fitting and too many may result in overfitting. While there are different approaches to optimize the parameters of the algorithm [100], these approaches are computationally costly in big datasets. Other drawbacks of gradient boosting machine are: (a) that they are memory-consuming due to a large number of iterations; (b) their evaluation speed; and (c) that they are slower to learn compared to random forests.

In addition to decision trees, we also boost linear base learners using the quantile loss function. The relevant theory and implementation are presented by Bühlmann and Hothorn [102], Hothorn et al. [103], and Hofner et al. [104].

2.3.5. Quantile Regression Neural Networks

Artificial neural networks are perhaps the most widespread machine-learning algorithm in hydrology (see, e.g., the review by Maier et al. [105]). The main concept of neural networks is to extract linear combinations of the predictor variables as derived features. The dependent variable is then modelled as a nonlinear function of these features [23] (p. 389). The main reasons for using artificial neural networks are their high predictive performance and their ability to extract linear combinations of features [23] (p. 351). Some of their drawbacks are that: (a) they are prone to overfitting; (b) the inclusion of too many predictor variables can decrease the predictive performance (unlike, for example, random forests); (c) they perform sub-optimally when needed to extrapolate beyond the range of the training set; (d) there are many model structures and architectures to choose from (albeit this can be viewed as an advantage due to offering higher flexibility); (e) appropriate optimization of the model hyperparameters can be important for improving their predictive performance [105]; and (f) they are computationally slow [23] (p. 351).

Artificial neural networks can predict conditional quantiles if they are fitted by minimizing the quantile score. This approach was proposed by Taylor [75], termed as “quantile regression neural networks”. An improved version of quantile regression neural networks by Cannon [106] is implemented in the present study. This version uses the standard multilayer perceptron artificial neural networks.

3. Experimental Data and Methodology

In this section, we present the experimental data and methodology adopted in the study. Statistical software information is summarized in Appendix A.

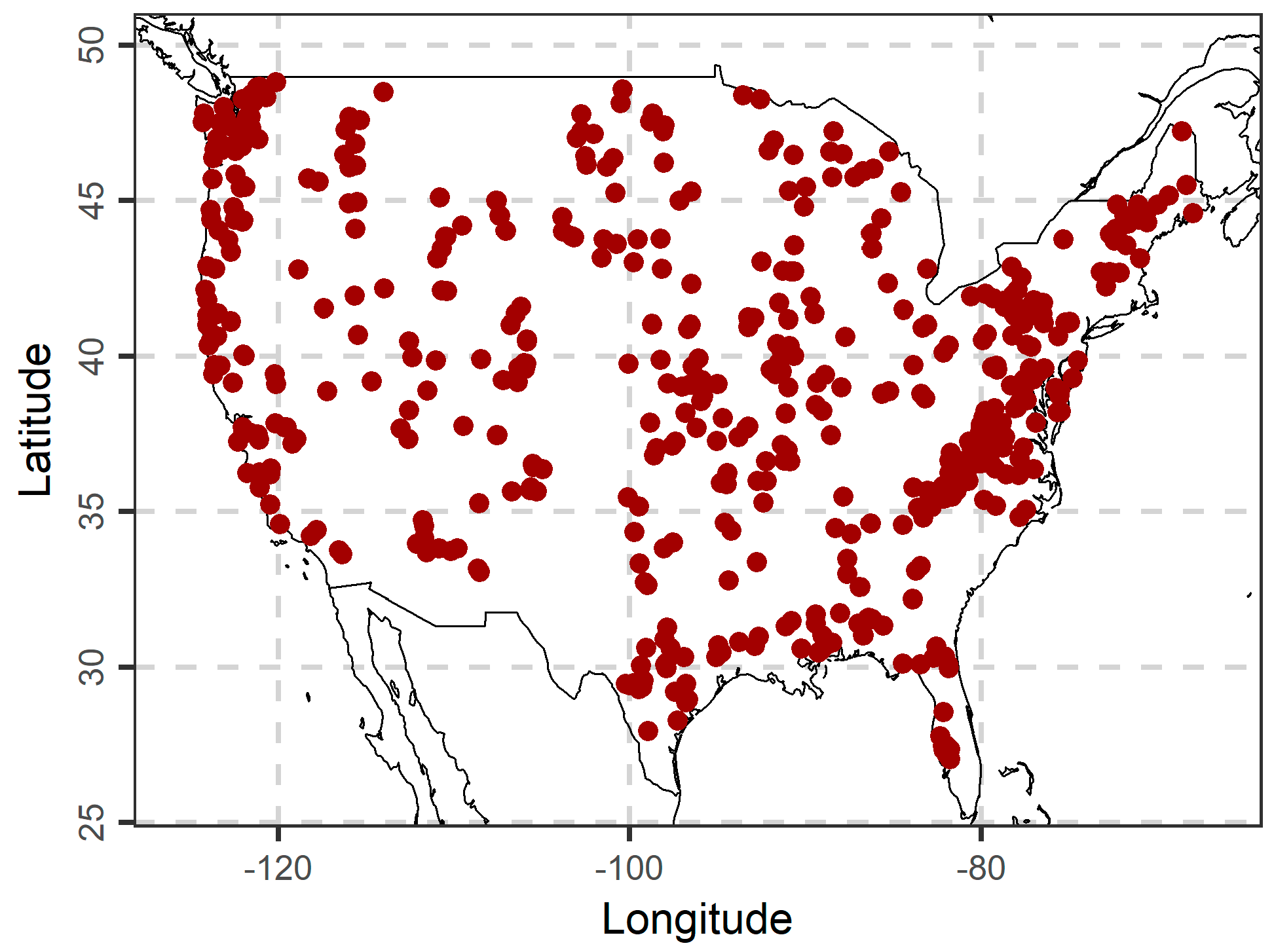
3.1. Rainfall-Runoff Data and Time Periods

We use data originating from 511 catchments in the contiguous United States. The locations of the stations are presented in Figure 2. These catchments are minimally affected by human activities. The data are sourced from the Catchment Attributes and MEteorology for Large sample Studies (CAMELS) dataset [107,108], which is fully documented in Newman et al. [109] and Addor et al. [110]. The dataset includes complete daily precipitation, temperature and streamflow information over a 34-year period of 1980−2013. Daily precipitation and temperature data were originally made available by Thornton et al. [111]. We estimate daily potential evapotranspiration using the formula by Oudin et al. [82] and temperature data.

We divide the entire 34-year time period Τ = {1980-01-01, ..., 2013-12-31} into sub-periods T₀ = {1980-01-01, ..., 1980-12-31} (1-year period), T₁ = {1981-01-01, ..., 1991-12-31} (11-year period), T₂ = {1992-01-01, ..., 2002-12-31} (11-year period) and T₃ = {2003-01-01, ..., 2013-12-31} (11-year period). We use data from these sub-periods as detailed in Section 3.2, Section 3.3 and Section 3.4 (see also Section 2.1).

3.2. Application of the Hydrological Model

We apply the GR4J hydrological model (see Section 2.2) to obtain a point prediction of daily streamflow for each catchment through the following steps:

• Data from period T₀ are used to warm up the hydrological model.
• Data from period T₁ are used to calibrate the hydrological model. For the calibration, we implement the optimization algorithm by Michel [112] for maximizing the Nash–Sutcliffe efficiency criterion [113]. The latter is a well-established criterion for hydrological model calibration. While possible, the implementation of other optimization algorithms and objective functions is out of the scope of the study.
• The calibrated hydrological model is used with daily precipitation and potential evapotranspiration data from period {T₂, T₃} to predict daily streamflow for the same period.

3.3. Solved Regression Problem and Assessed Configurations

The hydrological model predictions for period T₂ are used together with their respective target values to obtain the hydrological model errors for the same period. For each catchment, the hydrological model errors and the hydrological model predictions for period T₂ are used to train each of the assessed machine-learning algorithms in predicting the quantiles of level τ ∈ {0.005, 0.0125, 0.025, 0.05, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 0.95, 0.975, 0.9875, 0.995} of the hydrological model errors. The response variable of the regression is the hydrological model error at time t, and the predictor variables are presented in

Table 3. Configurations of the machine-learning quantile regression algorithms assessed in this study. The primal algorithms are presented in Section 2.3.

Abbreviations of Assessed Configurations	Predictor Variables of the Regression
qr_2, qrf_2, qrf_meins_2, gbm_2, mboost_bols_2, qrnn_2, ensemble_2	Hydrological model predictions at times t − 1 and t
qr_3, qrf_3, qrf_meins_3, gbm_3, mboost_bols_3, qrnn_3, ensemble_3	Hydrological model predictions at times t − 2, t − 1 and t
qr_4, qrf_4, qrf_meins_4, gbm_4, mboost_bols_4, qrnn_4, ensemble_4	Hydrological model predictions at times t − 3, t − 2, t − 1 and t

, together with the assessed configurations of the machine-learning algorithms that they define. We do not try configurations using a single predictor variable (specifically the hydrological model prediction at time t only), because some of the machine-learning algorithms (e.g., the generalized random forests for quantile regression) do not work without a second predictor. While possible, we also do not try configurations using precipitation and/or evapotranspiration (or temperature) variables, because (i) such variables are already considered by the hydrological model, and (ii) their consideration is less common in the literature than the consideration of hydrological model predictions.

3.4. Performance Assessment

The predictive quantiles of the hydrological model errors are transformed to predictive quantiles of daily streamflow for period T₃ (hereafter referred to as “predictive quantiles of interest”) by being subtracted from their corresponding hydrological model predictions. The predictive quantiles of interest are processed using the following subsequent steps: (i) Negative values of predictive quantiles of level 0.005 are censored to zero; and (ii) quantile crossing is handled in an ad hoc manner (if present), i.e., by replacing predictive quantiles of level τ_k+1 (where k is the sequential number of the quantile levels of interest starting from 1 for quantile level 0.005) with the predictive quantiles of level τ_k delivered by the same algorithm for the same target random variable, if the former predictive quantiles are predicted to be smaller than the latter predictive quantiles.

We assess the quality of the processed predictive quantiles of interest using daily streamflow data for period T₃. The performance assessment is made by computing the scores presented in

Table 4. Scores computed for assessing a prediction interval of level (1 − α), 0 < α < 1, or a predictive quantile of level τ, 0 < τ < 1.

Score	Definition	Units	Possible Values	Preferred Values	Criterion/Criteria
Reliability score (RSα)	Equation (5)	-	[0, 1]	Smaller |RSα – (1 – α)|	Reliability
Average width (AWα)	Equation (6)	mm/day	[0, +∞)	Smaller AWα	Sharpness
Average interval score (AISα)	Equation (7)	mm/day	[0, +∞)	Smaller AISα	Reliability, sharpness
Average quantile score (AQSτ)	Equation (8)	mm/day	[0, +∞)	Smaller AQSτ	Reliability, sharpness

. For this assessment, the following remarks are useful (see, e.g., references [93,114,115]):

• The goal of probabilistic modelling is to maximize sharpness subject to reliability.
• Reliability refers to the statistical consistency between the probabilistic predictions and the observations.
• Sharpness refers to the narrowness of the prediction intervals.

For a specific prediction interval of level (1 − α), 0 < α < 1, formed by the predictive quantiles {w_t, t ∊ T₃} and {l_t, t ∊ T₃}, where w_t and l_t are the upper and lower quantiles, respectively, at time t, the reliability score (RS_α), average width (AW_α) and average interval score (AIS_α) are defined, respectively, as:

RS_α := ∑_t(I{l_t < y_t < w_t})/|T₃|

(5)

AW_α := ∑_t(w_t − l_t)/|T₃|

(6)

AIS_α(l_t, w_t; y_t) := ∑_t((w_t − l_t) + (2/α) (l_t − y_t) I{y_t < l_t} + (2/α) (y_t − w_t) I{y_t > w_t})/|T₃|

(7)

In these equations, y_t is the targeted observation at time t ∊ T₃ and |T₃| is the number of the target data points included in period T₃. The origins of the interval score (see, e.g., reference [93]) trace back to Dunsmore [116] and Winkler [117]. For a predictive quantile of level τ, 0 < τ < 1, the average quantile score (AQS_τ) is defined by (see also Equations (3) and (4)):

AQS_τ(y_τ(x_t); y_t) := ∑_t ((τ − Ι{(y_t − y_τ(x_t)) < 0}) (y_t − y_τ(x_t)))/|T₃|

(8)

Some remarks should be made on the appropriateness of the computed scores. Reliability is an important criterion for assessing the usefulness of probabilistic predictions. This criterion can be assessed by measuring the coverage of the delivered prediction intervals, i.e., the percentage of data points included in these intervals; see Equation (5). For engineering applications, narrower prediction intervals are also preferred to avoid excessively precautionary design or decisions. AIS_α and AQS_τ provide an objective co-assessment of these two important criteria, and they are suggested as “proper scores” in Gneiting and Raftery [93]. In this view, smaller values of these scores indicate more useful probabilistic predictions.

Note that computing point prediction performance metrics (e.g., the root mean square error; RMSE) is irrelevant to the targeted assessment and, therefore, out of the scope of this study. Nevertheless, the information provided by the average quantile score, when this score is computed for the predictive quantiles of level 0.5, is equivalent to the information provided by the mean absolute error (MAE).

For the overall assessment of the algorithms, we compute (a) the four scores (RS_α, AW_α, AIS_α and AQS_τ) conditional upon the algorithm and the catchment; and (b) the relative decreases provided by all algorithms in terms of AW_α, AIS_α and AQS_τ with respect to qr_2 (benchmark). We compute the relative decreases instead of the relative increases, since the former can be interpreted as relative improvements (see Table 4). Moreover, for each 34-year-long time series of daily streamflow (i.e., from 511 catchments), we define 100 quantile ranges corresponding to 100 quantile level ranges of equal size, i.e., levels (0, 0.01), [0.01, 0.02), …, [0.99, 1), to also compute the employed scores conditional upon the algorithm, the catchment and the range of observed flow quantiles, and the corresponding relative decreases in terms of AW_α, AIS_α and AQS_τ with respect to qr_2. These latter computations allow us to inspect the performance of the algorithms for different flow magnitudes.

As stemming from the above-outlined methodological information, the quantile regression algorithm has been selected as the reference algorithm in the experiment. Since this algorithm is linear in parameters (see Section 2.3.2), fast to implement and already exploited in the literature to a significant extent for solving the problem of interest (see Table 1), it is a befitting benchmark for non-linear, more computationally demanding and rarely or never-used before (for the problem of interest) algorithms. A last remark to be highlighted concerning the performance assessment is that, while benchmarking is undoubtedly the only available means for characterizing an algorithm as “good enough” in terms of any score, the AW_α, AIS_α and AQS_τ values can only be properly interpreted when presented comparatively (using benchmarking). In fact, the widths of the prediction intervals (and the related components in the interval and quantile scores) largely depend on the flow magnitude, in contrast to the RS_α values that are bounded within the range [0, 1].

4. Experimental Results and Interpretations

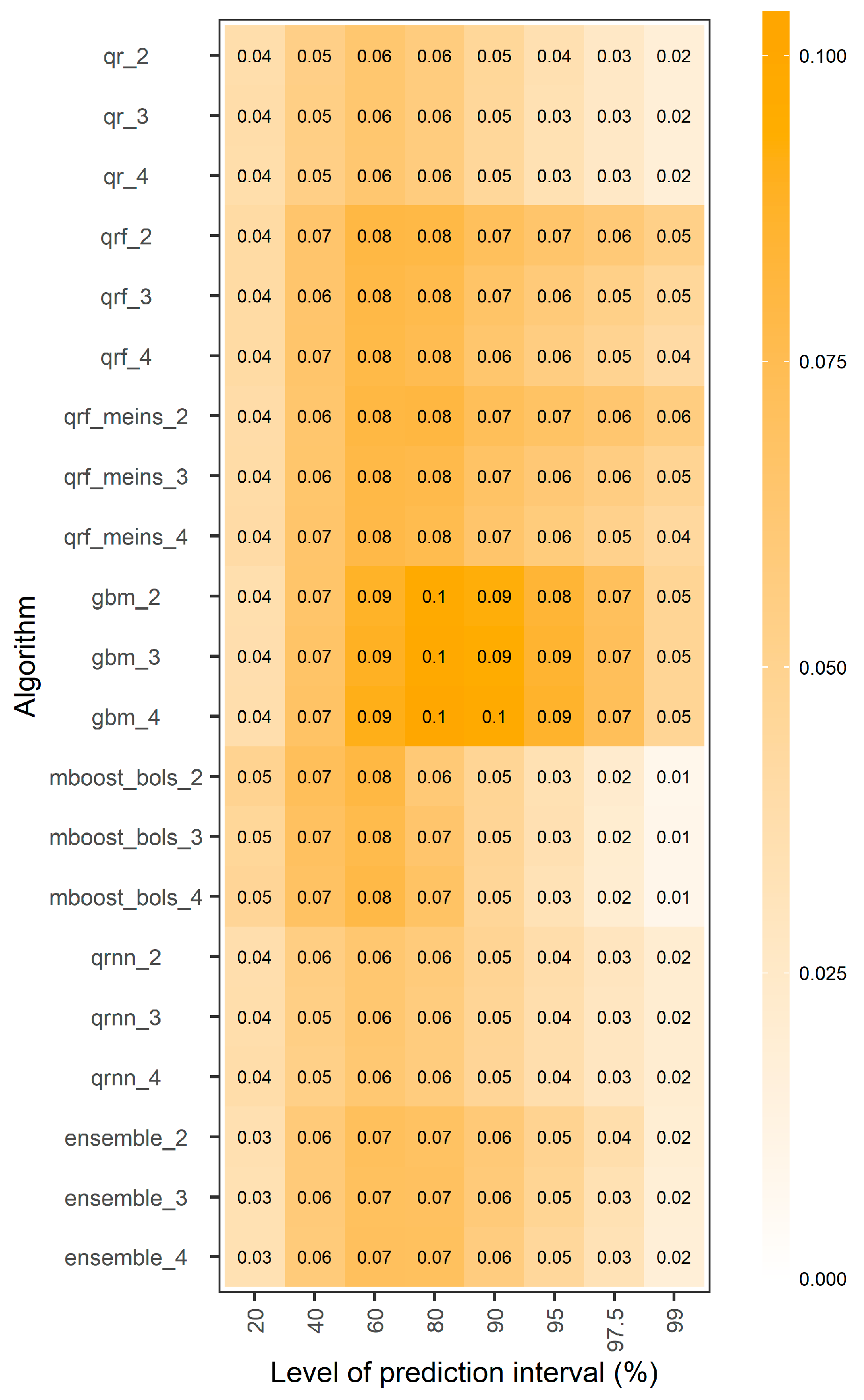
4.1. Overall Assessment of the Machine-Learning Aalgorithms

In this section, we present and discuss summary results of the overall assessment of the machine-learning algorithms, when these algorithms are accommodated within two-stage probabilistic hydrological post-processing methodologies. The assessment refers to how well the algorithms deliver various central prediction intervals and predictive quantiles of several levels, and here it is collectively made for all observed flow magnitudes. Some additional visualizations, resulted for the same investigations, are available in Papacharalampous et al. [118]. In these visualizations, the interested reader can find information about differences in predictive performance from catchment to catchment and related patterns revealed for the machine-learning algorithms through the investigations of the study. This information is herein omitted for reasons of brevity.

A comparison of the machine-learning algorithms with respect to their average-case reliability (i.e., the average coverage across all catchments) when delivering the 20%, 40%, 60%, 80%, 90%, 95%, 97.5% and 99% central prediction intervals is well-supported by Figure 3. In Figure 3, we present the mean absolute deviations of the reliability scores from their nominal values, as computed conditionally on the algorithm and the prediction interval. This figure can be interpreted according to the following example: A mean absolute deviation equal to 0.05 for the 90% prediction intervals means that the absolute deviation of the 511 reliability scores (computed for the 511 catchments) from 0.90 (nominal value for the 90% prediction intervals) is on average equal to 0.05. This mean absolute deviation could, for instance, be computed for the case in which the absolute deviations (always positive or zero) are equal to 0.02 for 255 catchments, equal to 0.05 for one catchment and equal to 0.08 for 255 catchments, since (0.02 × 255 + 0.05 × 1 + 0.08 × 255)/511 = (5.1 + 0.05 + 20.4)/511 = 0.05. In summary, qr and qrnn are found to mostly perform on average better than the remaining algorithms. For the 95%, 97.5% and 99% prediction intervals, mboost_bols also stands out because of its good average-case performance. With respect to the same criterion, the worst performing algorithm is mostly gbm. For the 60%, 80%, 90%, 95% and 97.5% prediction intervals, all gbm configurations exhibit the smallest average-case reliability. The ensemble learner, i.e., the equal-weight combiner of all the algorithms (when these algorithms are implemented with the same predictor variables), exhibits performance that could be characterized similar or even better (for the 20% prediction intervals) than the performance of the individual algorithms combined. Another remark to be highlighted here is that the mean absolute deviations can be less informative about the quality of the outer prediction intervals (e.g., for the 95%, 97.5%, and 99% prediction intervals). In fact, even an algorithm that always produces prediction intervals from −∞ to +∞, would offer mean absolute deviations equal to 0.05, 0.025 and 0.01 for these intervals, respectively.

Furthermore, as opposed to the whole picture, only relatively small average-case differences in reliability (differences up to 0.01) are observed across the various configurations of the same algorithms. Larger differences are observed from one algorithm to the other (differences up to 0.05) and for the various prediction intervals of the same algorithm (differences up to 0.06). The interpretation of this observation is straightforward: the two additional predictors do not add as much information as switching from one algorithm to another does, and the predictive performance also largely depends on the prediction task. It is relevant and important to note that, even when we focus on a single criterion (here the average-case reliability), we cannot identify a best performing algorithm for all tasks, i.e., we cannot identify a best performing algorithm in delivering all prediction intervals. For example, if we were only interested in delivering the four outer prediction intervals (i.e., 90%, 95%, 97.5% and 99%), mboost_bols would be the safest choice.

The degree of sharpness characterizing the delivered prediction intervals is also relevant when we are interested in applying the machine-learning algorithms for technical purposes. In Figure 4, we present the median relative decreases (i.e., the median values of relative decreases computed across all catchments) in terms of the average width of the prediction intervals provided by each of the assessed algorithms with respect to qr_2. In more precise terms, these median relative decreases can be interpreted according to the following example: A median relative decrease in terms of average width equal to 9.25%, provided by the gbm_3 algorithm for the 90% prediction intervals, means that the gbm_3 algorithm produces 90% prediction intervals that are, in the median case across the 511 catchments, narrower than the 90% prediction intervals provided by qr_2 by 9.25%. The median relative decreases are mostly positive, i.e., the algorithms provide narrower prediction intervals compared to the benchmark. Only mboost_bols delivers wider prediction intervals at the 97.5% and 99% prediction levels. Overall, the sharpest prediction intervals are the ones delivered by gbm, followed by those delivered by qrf and qrf_meins. Regarding the behavior of the various algorithms from a comparative perspective, different patterns characterize the displayed relative decreases for the various algorithms.

We should note here again that relatively sharp prediction intervals are only desired when accompanied by a good performance in terms of reliability, and vice versa. Therefore, some interesting observations could be drawn from Figure 3 and Figure 4. For instance, qrf and qrf_meins seem to exhibit comparable average-case reliability with qr for the 20% prediction intervals, and at the same time to be offering a larger degree of sharpness. Moreover, qrnn and ensemble offer significant median-case decreases in terms of average widths with respect to the benchmark, and they are also quite reliable compared to it. Such observations are important for gaining insight on how the algorithms behave in comparison to one another while solving the problem of interest. Nevertheless, from a practical point of view, we are most interested in collectively assessing reliability and sharpness in an objective manner.

This objective co-assessment with respect to reliability and sharpness is herein allowed by Figure 5 and Figure 6, which display the median relative decreases (which can be interpreted as median relative improvements) with respect to qr_2 in terms of average interval score and average quantile score, respectively. In more precise terms, these median relative decreases can be interpreted according to the following example: A median relative decrease in terms of average interval score (average quantile score) equal to 1.58% (2.54%) is provided by the ensemble_2 algorithm for the 99% prediction intervals (quantiles of level 0.995). This result means that the ensemble_2 algorithm delivers prediction intervals (predictive quantiles) that are, in the median case across the 511 catchments, better than those delivered by qr_2 by 1.58% (2.54%) in terms of average interval score (average quantile score). The following observations are important:

• More predictor variables result in mostly improved performance for the tree-based methods (qrf, qrf_meins, gbm) and the equal-weight combiner of all algorithms, and slightly less pronounced improvements for qrnn.
• The performance of qr and mboost_bols is found to not be significantly affected by the number of predictor variables.
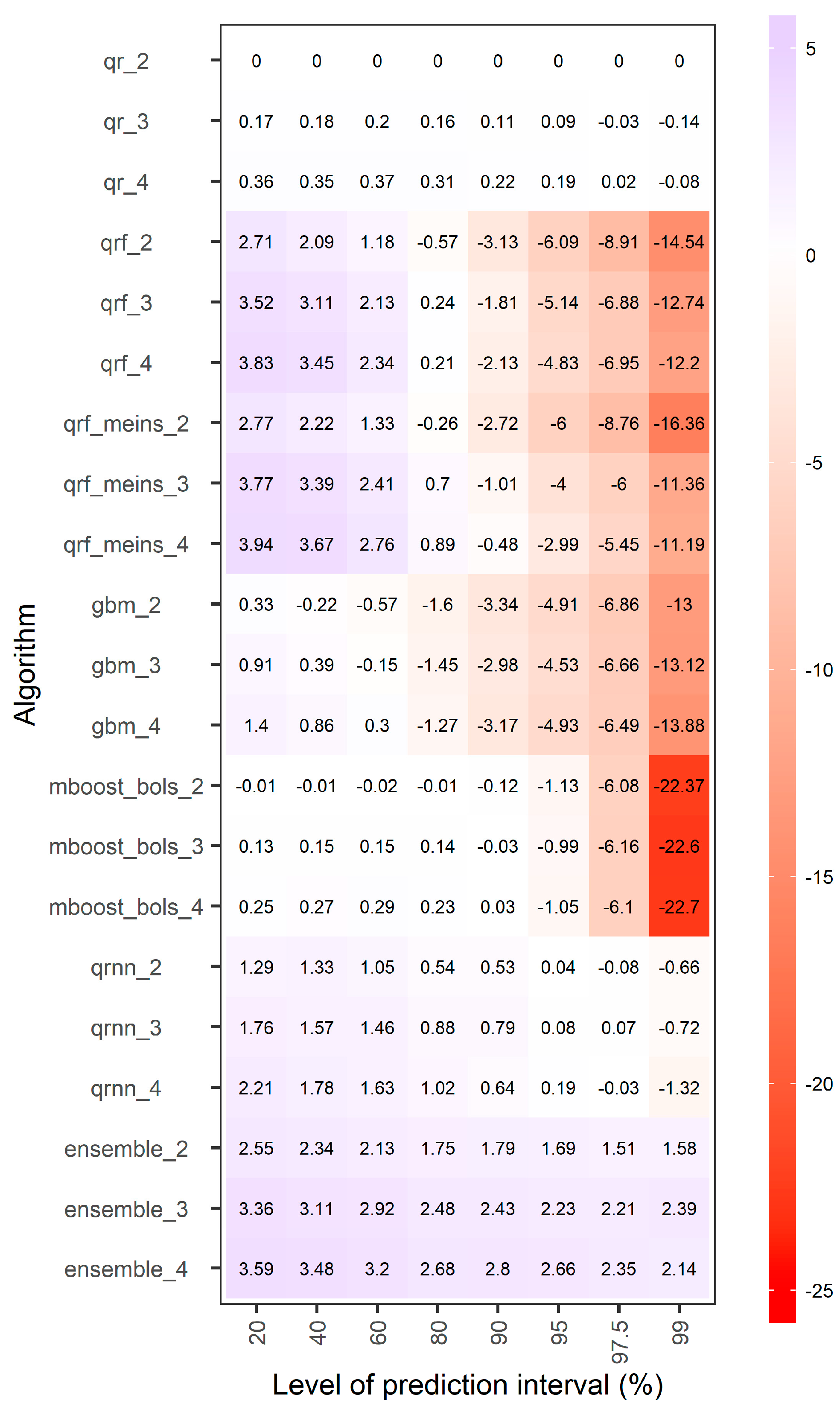
• The overall best performing algorithm is the equal-weight combiner of all algorithms, offering up to approximately 3.5% decrease in terms of both average interval and quantile scores with respect to qr_2.
• For all prediction intervals, qr performs mostly better than mboost_bols, while it is also better than gbm for the 60%, 80%, 90%, 95%, 97.5% and 99% prediction intervals. Only for the predictive quantiles of levels 0.4, 0.5, 0.6, 0.7 and 0.8, gbm performs better than qr. Still, gbm is not the best-performing algorithm either for these quantiles.
• For the 90%, 95%, 97.5% and 99% prediction intervals, qr performs better than most of the remaining algorithms, while the equal-weight combiner is the best. The latter offers decreases from approximately 1.5% to approximately 2.5% with respect to the former in terms of average interval score, and up to approximately 3.5% decrease in terms of average quantile score. The equal-weight combiner is worse than qr only for the two lower levels of predictive quantiles tested herein.
• For the 90%, 95%, 97.5% and 99% prediction intervals, the tree-based methods are performing poorly, probably because they cannot extrapolate beyond the observed values of the training set.
• For the predictive quantiles of levels 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8, and the 20%, 40% and 60% prediction intervals, qrf and qrf_meins are comparable with (or even better performing than) the equal-weight combiner of all algorithms.
• For all tested levels of predictive quantiles except for 0.005 and 0.0125, and the 20%, 40%, 60%, 80% and 90% prediction intervals, qrnn perform better than qr.
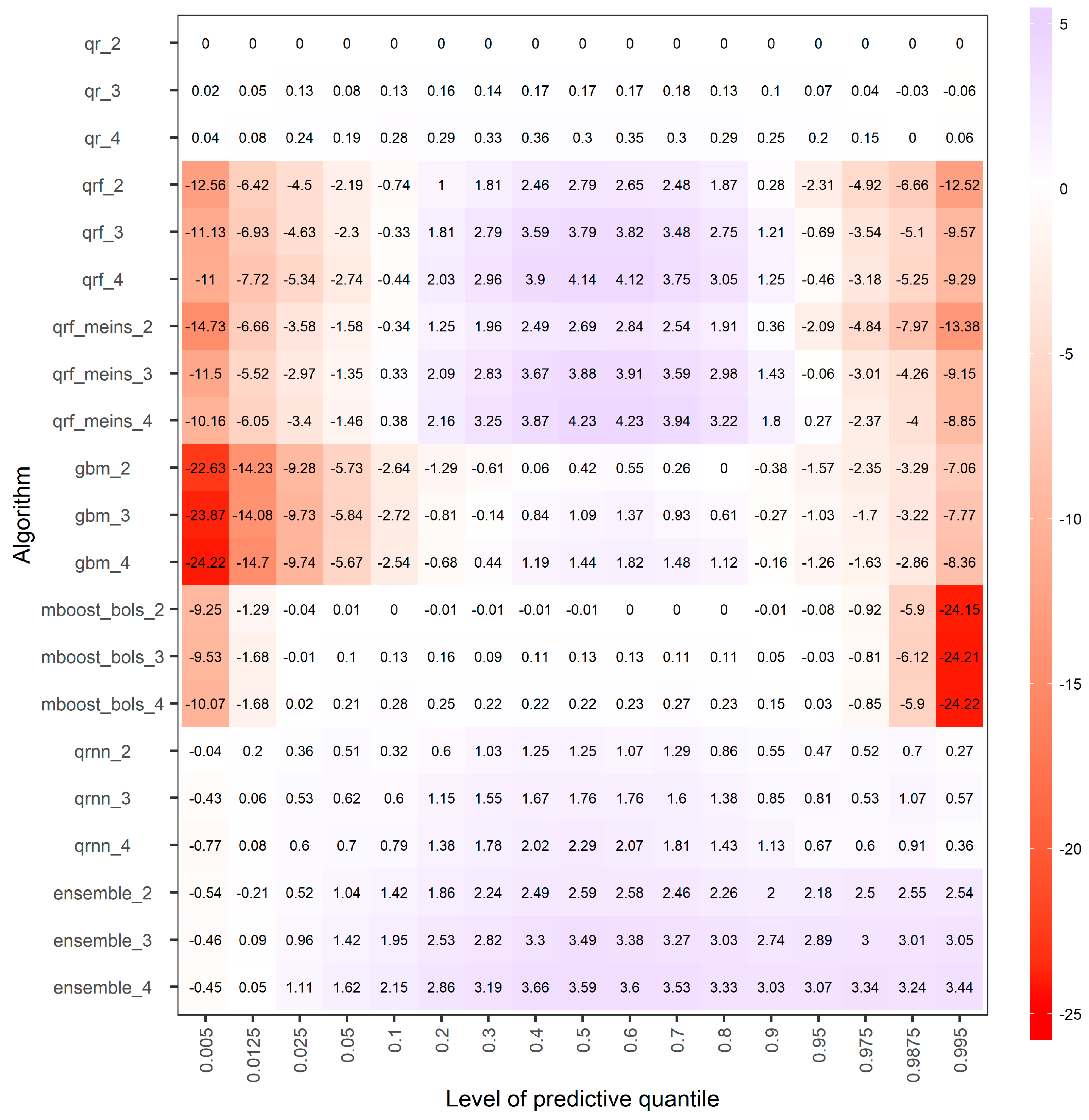
• Different patterns are observed regarding the performance of the algorithms in predicting the targeted quantiles.
• The performance of qrf and qrf_meins could be characterized as symmetric with respect to the predictive quantile of level 0.5, i.e., these machine-learning algorithms show comparably low skill in predicting the upper and lower quantiles that form a specific central prediction interval.
• The same observation does not apply to the remaining machine-learning algorithms. Specifically, gbm is less skilful in predicting the lowest quantiles than the highest ones, probably because of the technical settings of the study, i.e., because we predict the quantiles of the error of the hydrological model and later transform these quantiles to quantiles of daily streamflow.
• The same holds for qrnn and the equal-weight combiner, yet these latter algorithms are more skilful, while mboost_bols is less effective in predicting quantiles of the highest levels.

An important remark to be made, at this point, is that the figures presented both herein and in Papacharalampous et al. [118] could not highlight all the important details extracted from the conducted tests. Notably, the qrnn algorithms were found to produce significant outliers in terms of predictive performance for 10 of the 511 investigated catchments. These outliers largely affect the respective widths of the prediction intervals provided by these algorithms and, thus, can be easily identified using benchmarking by comparing the widths of the prediction intervals provided by qrnn with the widths of the prediction intervals provided by the benchmark (although the realization of the process of interest will be unknown at the time of the prediction). In fact, they result in relative increases of average widths with respect to the qr algorithms in the order of thousands. Their effect is also manifested in the widths of the prediction intervals provided by the ensemble algorithms (yet in a less-pronounced degree), and in the interval and quantile scores computed for both types of algorithms. The median relative decreases in terms of average widths, average interval score and average quantile score (that are presented herein) are not affected by this limitation of qrnn, while the average relative decreases in terms of average widths, average interval score and average quantile score would be.

Lastly, since we are foremost interested in providing information that could be useful within operational contexts, some tangible information on the computational requirements of the algorithms is also essential. In Figure 7, we present the total computational time consumed by each of the assessed machine-learning algorithms within the experiments of the study. The least time-consuming algorithm is by far qr. The remaining algorithms can be ordered from the least to the most time consuming as follows: qrf_meins, qrf, gbm, mboost_bols, qrnn and ensemble. The ensemble algorithm requires more than 10 times the computational time required for qrf to run. Nevertheless, this computational cost may be tolerable in many cases, e.g., when using workstations and/or computer clusters.

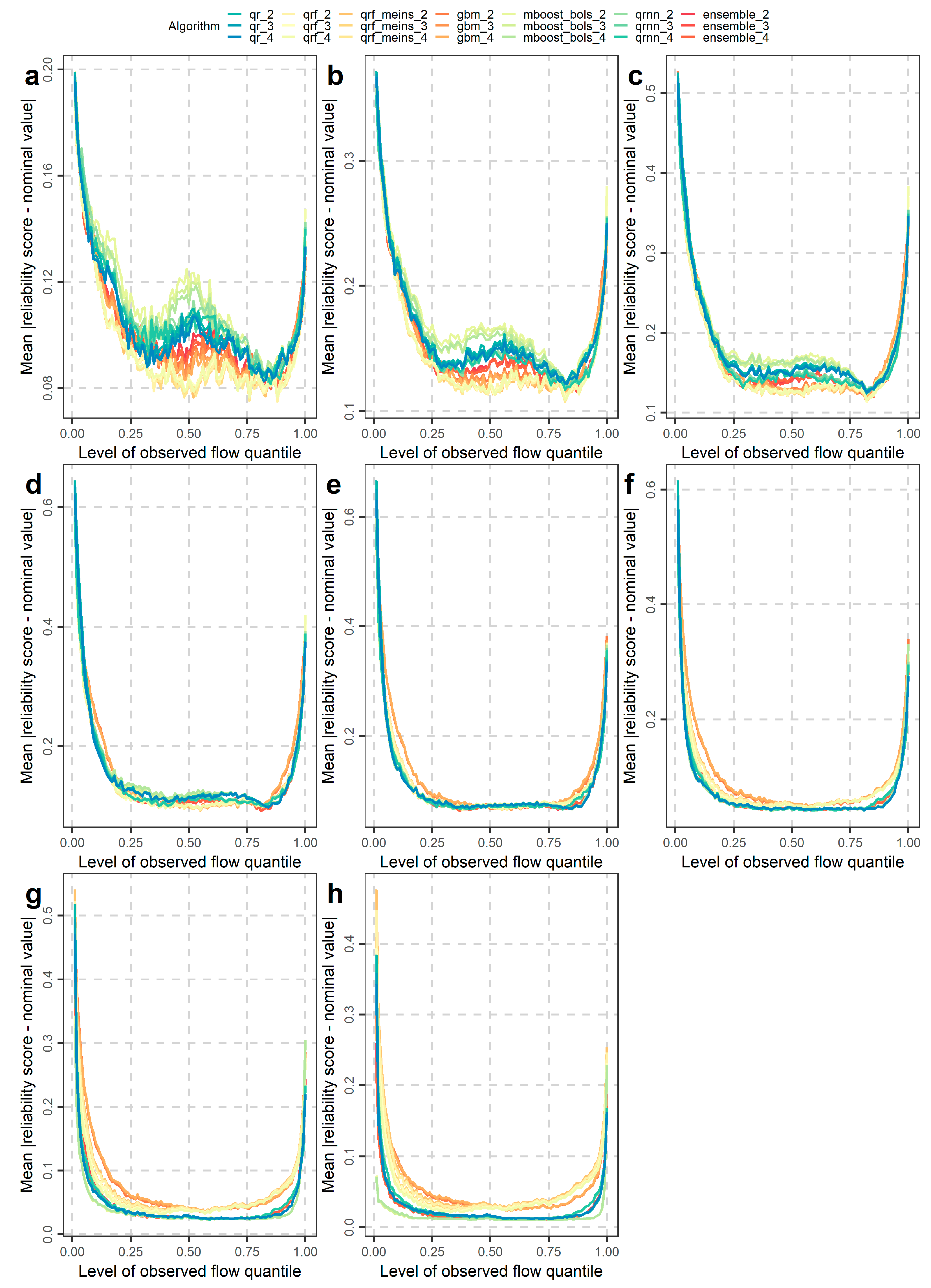
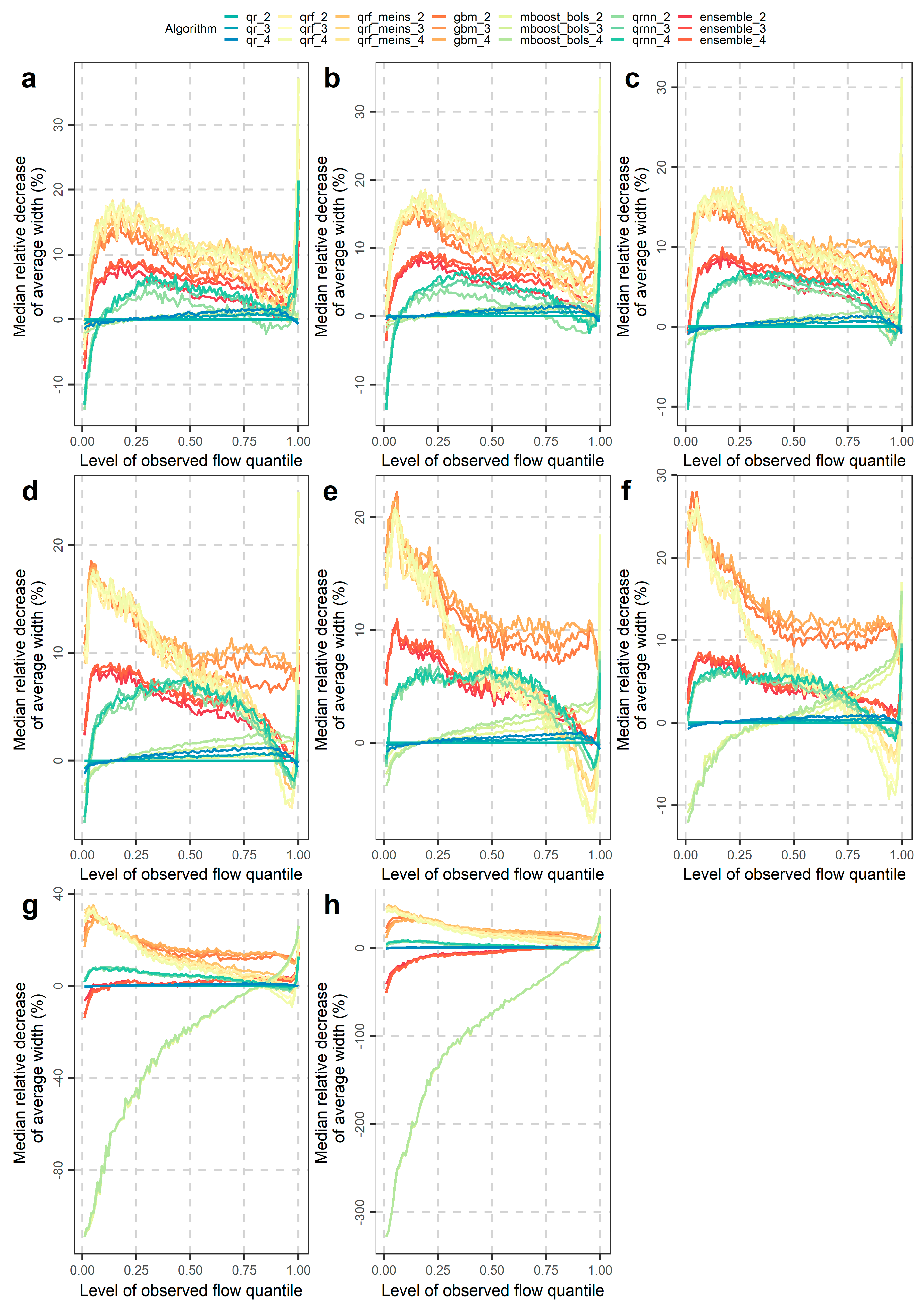
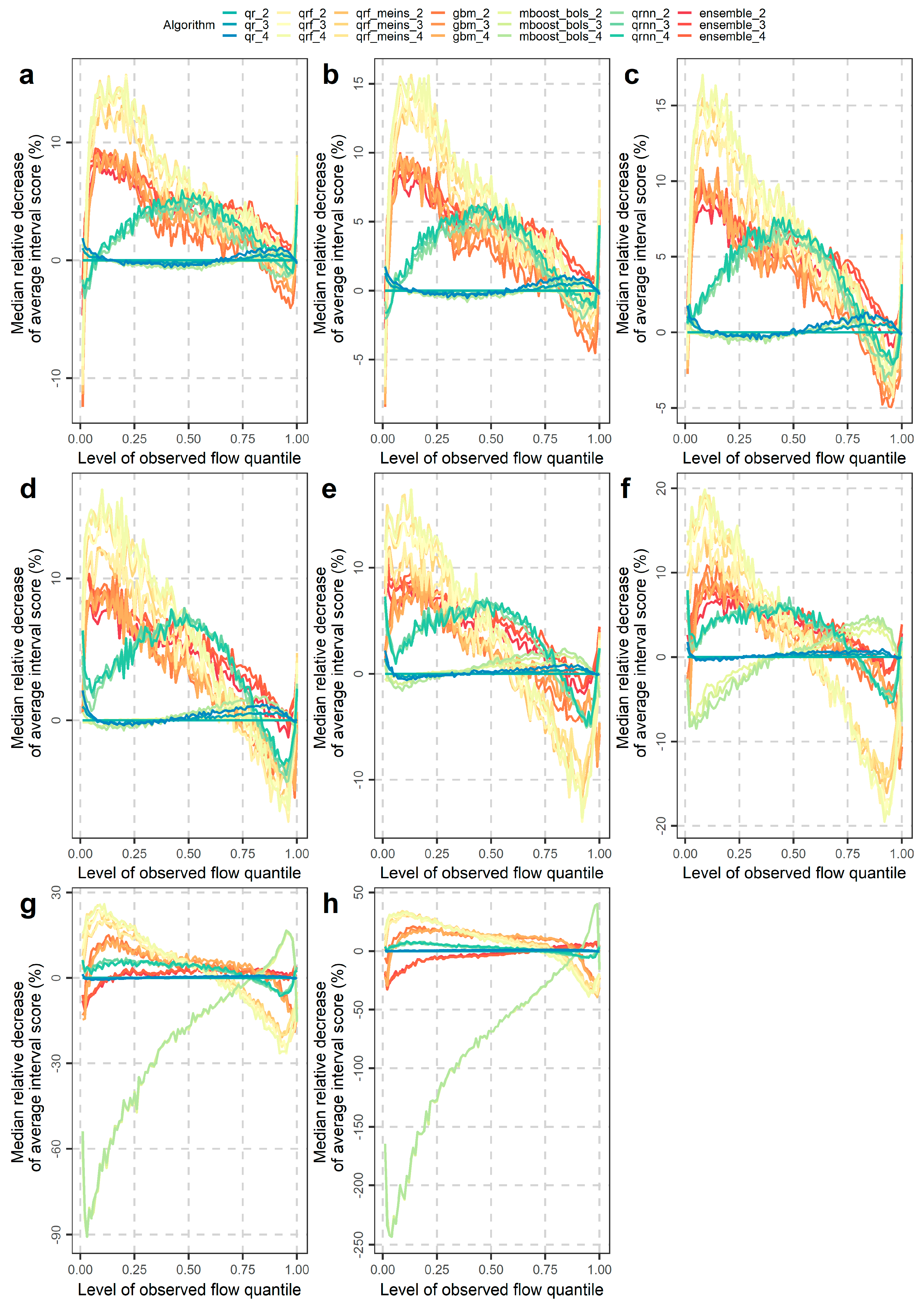
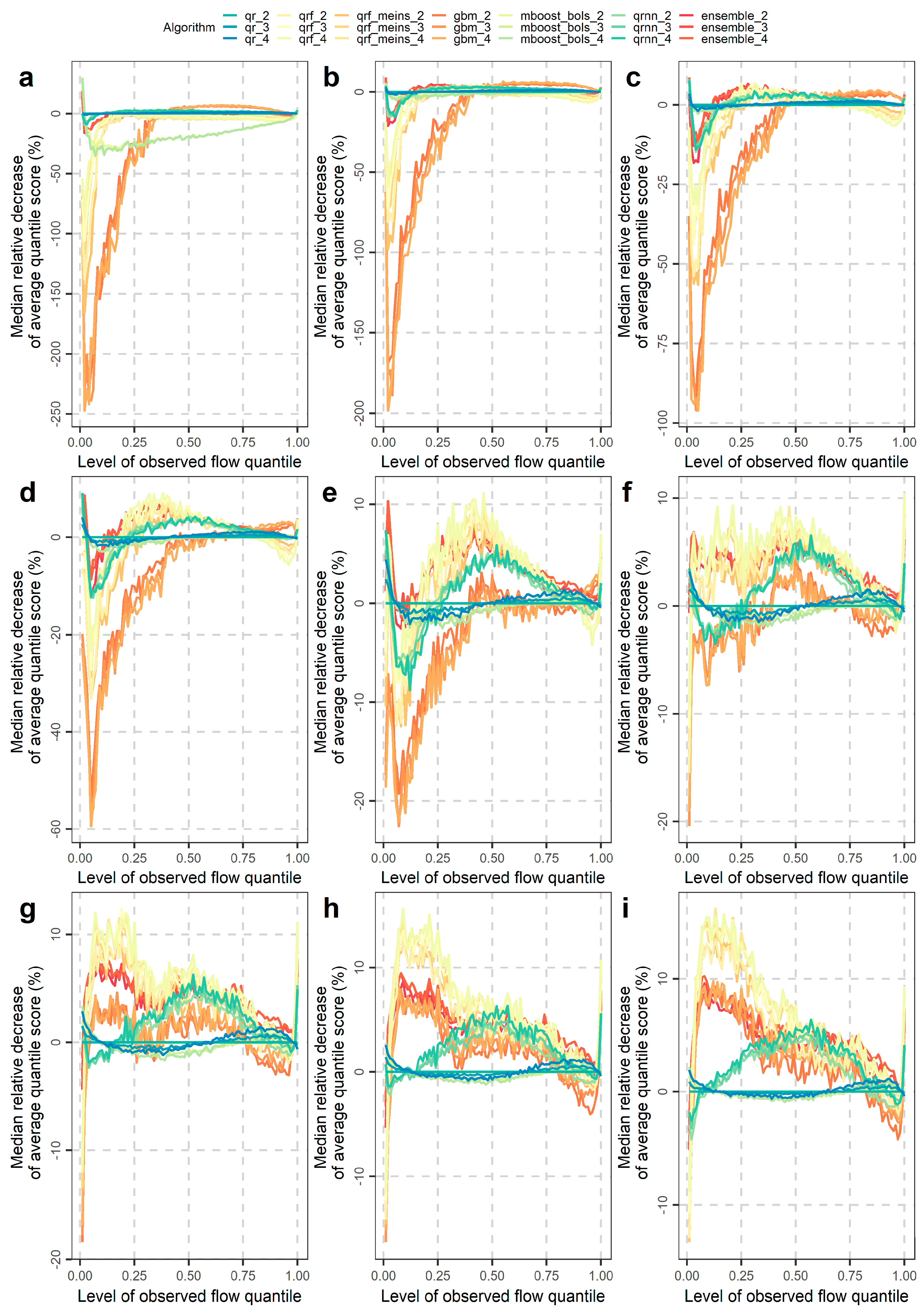
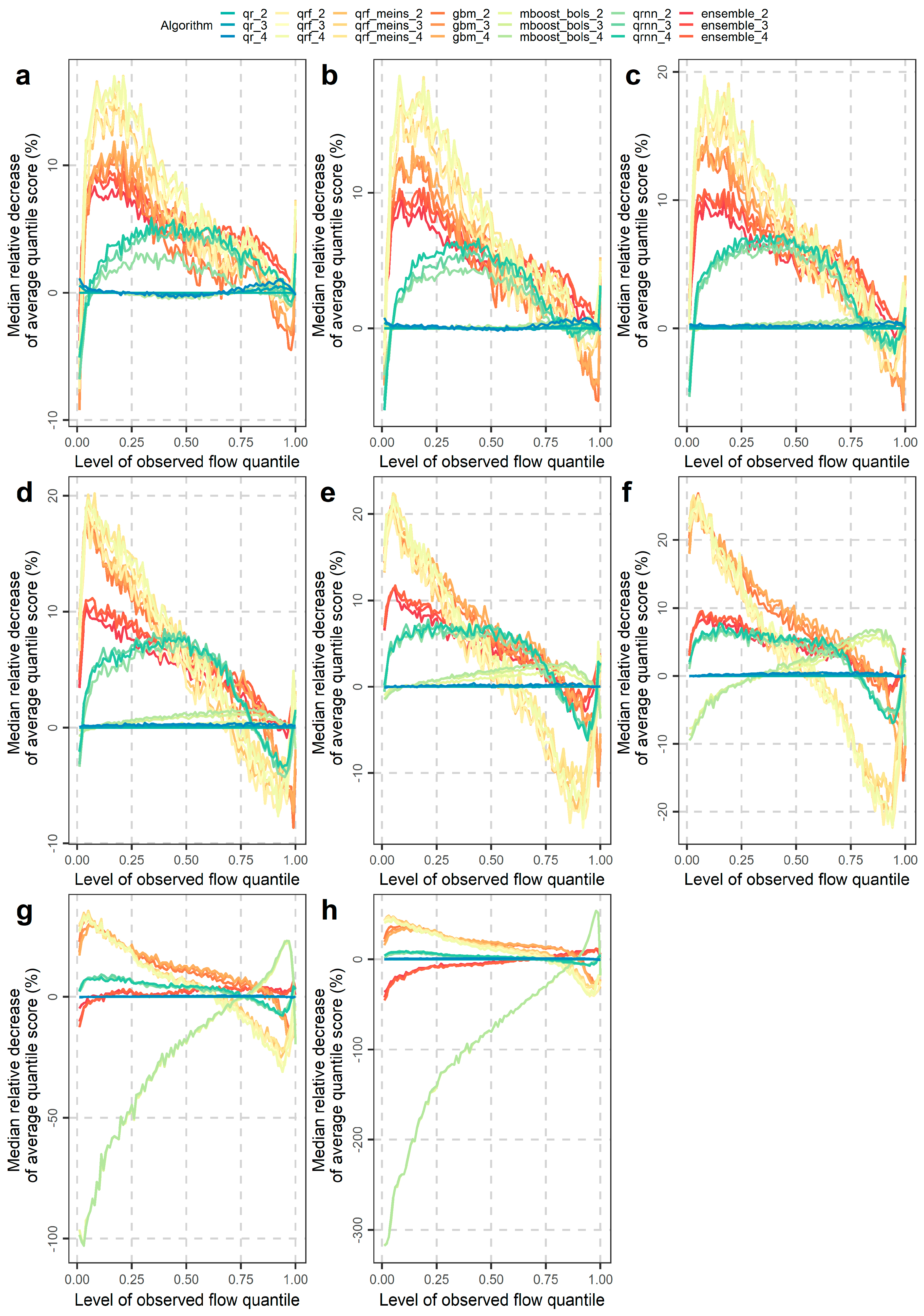
4.2. Investigations for Different Flow Magnitudes

This section is devoted to summarizing the results of the investigations conducted for different flow magnitudes. These investigations complement the overall assessment of the machine-learning algorithms, which is made independently of the flow magnitude, as presented in the preceding section. Due to resolution differences, the results presented in the previous section are not comparable to these in this section.

Figure 8 presents the mean absolute deviations of the reliability scores from their nominal values, computed per level of observed flow quantile and prediction interval. This information can be exploited to comparatively assess the machine-learning algorithms with respect to their average-case reliability for various levels of predictability. In more precise terms, this figure can be interpreted according to the following example: A mean absolute deviation equal to 0.08 for the 20% prediction intervals and the quantile range [0.49, 0.50) means that the absolute deviation of the 511 reliability scores computed for the flow magnitude defined by this quantile range from 0.20 (nominal value for the 20% prediction intervals) is on average equal to 0.08. For all prediction intervals, the algorithms are more reliable for the middle half of the sample quantiles of observed flow, while the delivered probabilistic predictions are quite unreliable for the highest and lowest flows. Regarding this latter point, we also observe that the algorithms are, on average, less reliable for the lowest flows (level of observed flow quantile lower than 0.25) than they are for the highest flows (level of observed flow quantile higher than 0.75), although there is a rough symmetry in the performance of the machine-learning algorithms with respect to the observed flow quantiles of levels close to 0.5. This symmetry is perhaps the most characteristic observed pattern, stemming from limitations implied by the nature of the solved problem (in the sense that low and high flows are less predictable than moderate flows).

For the 20%, 40% and 60% prediction intervals and for the middle half of the sample quantiles of observed flow, the qrf, qrf_meins, gbm and ensemble algorithms mostly produce probabilistic predictions that are in better statistical agreement with the observations than qr, while qrnn is mostly comparable to the same algorithm and mboost_bols is the least reliable. For the same prediction intervals and the outer quantiles (level of observed flow quantile lower than 0.25 or larger than 0.75), the differences between the algorithms are slight. For the 80%, 90% and 95% prediction intervals, the performance of all algorithms is mostly similar, with some significant differences being present for the outer quantiles. The algorithms differentiate more for all quantile levels for the 97.5% and 99% prediction intervals.

Moreover, Figure 9 presents the median relative decreases in terms of average widths provided by the assessed algorithms with respect to qr_2. This information is presented per level of observed flow quantile and prediction interval and, therefore, it can be exploited to comparatively assess the machine-learning algorithms with respect to the median-case sharpness of the delivered prediction intervals for different flow magnitudes. In more precise terms, the presented median relative decreases can be interpreted according to the following example: A median relative decrease in terms of average width equal to ~10%, provided by the gbm_2 algorithm for the 95% prediction intervals and the quantile range [0.49, 0.50), means that, for the flow magnitude defined by this quantile range, the gbm_2 algorithm produces 95% prediction intervals that are, in the median case across the 511 catchments, narrower than the 95% prediction intervals provided by qr_2 by ~10%. In summary, qr produces the wider prediction intervals for all quantiles with some exceptions mostly observed for the lowest and highest flows. Some interesting related patterns should be discussed. The first is related to mboost_bols that produces, on average, much narrower 95% prediction intervals than the benchmark for the lowest half of the observed flows, and 97.5% and 99% prediction intervals for all levels of observed flow quantiles except for the highest (approximately) 10%. The second pattern is related to the ensemble learner, which is largely affected by mboost_bols for 99% prediction intervals. For the latter and for the lowest 75% of observed flow quantiles, the prediction intervals provided by ensemble are, on average, narrower than those provided by the benchmark, but still much wider than those provided by mboost_bols.

To comparatively assess the machine-learning algorithms with respect to both reliability and sharpness for different flow magnitudes, we present, in Figure 10, their relative improvements in terms of average interval score with respect to qr_2, computed per observed flow quantile and prediction interval. These median relative decreases can be interpreted according to the following example: A median relative decrease in terms of average interval score equal to ~5%, provided by the qrnn_2 algorithm for the 95% prediction intervals and the quantile range [0.49, 0.50), means that for the flow magnitude defined by this quantile range the qrnn_2 algorithm produces 95% prediction intervals that are, in the median case across the 511 catchments, better than the 95% prediction intervals delivered by qr_2 by ~5% in terms of average interval score. For the sample quantiles of observed flow of level (mostly) higher than 0.75, qr is mostly the best performing algorithm, while for the lower half of the sample quantiles of observed flow, qrf and qrf_meins are mostly the best performing algorithms. For the middle half of the sample quantiles of observed flow, qrnn is among the best performing algorithms. Moreover, some similar patterns can be observed between Figure 9 and Figure 10. For instance, mboost_bols delivers 95%, 97.5% and 99% prediction intervals that offer negative median-case decreases (median-case deteriorations) in terms of average interval scores. These decreases follow the respective negative decreases presented in Figure 9. Furthermore, qrnn reach their best performance, both in terms of average width and average interval score, for the middle levels of observed flow quantiles, while their performance seems quite symmetric around this highest value for most levels of prediction intervals.

Lastly, in Figure 11 and Figure 12, we present the relative decreases provided by the machine-learning algorithms in terms of average quantile score with respect to qr_2, computed conditional upon the algorithm, the observed flow quantile and the level of predictive quantile. These median relative decreases can be interpreted according to the following example: A median relative decrease in terms of average quantile score equal to ~5%, provided by the qrnn_4 algorithm for the predictive quantiles of level 0.7 and the quantile range [0.49, 0.50), means that for the flow magnitude defined by this quantile range the qrnn_4 algorithm delivers predictive quantiles of level 0.7 that are, in the median case across the 511 catchments, better than the predictive quantiles of level 0.7 delivered by qr_2 by ~5% in terms of average quantile score. As stems from the above, Figure 11 and Figure 12 can provide tangible information about the skill of the algorithms in delivering a predictive quantile of interest for different flow magnitudes. They can also be used to inspect the contribution of the quality of each predictive quantile in the quality of the central prediction intervals, as well as to assess the machine-learning methods in predicting the median of the targeted PDFs per observed flow quantile (see Figure 11i). Regarding this latter task, the relative skills of the machine-learning methods seem to follow a pattern that is similar to the patterns observed, for instance, for the 40% and 60% prediction intervals (see Figure 10b,c).

5. Literature-Driven and Evidence-Based Discussions

5.1. Innovations and Highlights in Light of the Literature

Some key innovations characterizing the present study are the following:

• It is among the very few large-sample studies presently available in both the fields of probabilistic hydrological modelling and hydro-meteorological forecasting (see, e.g., references [45,46,119,120]).
• It includes the largest range of methods ever compared in such concepts and a detailed quantitative assessment, using proper scores, and performing investigations for various prediction intervals and flow magnitudes.
• Three of the assessed machine-learning quantile regression algorithms, specifically generalized regression forests, gradient boosting machine and gradient boosting with linear models as base learners, are implemented for the first time to solve the practical problem of interest.
• It deviates from the mainstream culture of “model overselling” [53] or proving that “my model is better than yours” to “justify model development” [121], since it does not aim at promoting the use of any single algorithm. Instead, it formulates practical recommendations, which highlight the need for making the most of all the assessed algorithms (see the related comments in Sivakumar [121]).
• It is one of the very few studies that aim at attracting attention to ensemble learning post-processing methodologies in probabilistic hydrological modelling and hydro-meteorological forecasting.

It is important to highlight that most of the above-outlined innovations apply beyond hydrology as well. A large-sample regional study by Bakker et al. [122], conducted in a different field and under a different approach, has focused on post-processing solar radiation forecasts at hourly timescale for 30 stations in the Netherlands. The study is, in general, of large scale, since it examines two parametric and five non-parametric machine-learning algorithms, together with a large number of predictor variables; therefore, it provides generalized results for the case of the Netherlands.

5.2. Key Perspectives, Technical Considerations and Suggested Mind-Shifts

5.2.1. Contributions and Challenges from an Uncertainty Reduction Perspective

The challenging character of probabilistic hydrological modelling has been widely acknowledged in the literature (see, e.g., references [6,10,11]). Assumptions are certainly unavoidable when it comes to modelling [6], and probabilistic predictions are not (and should not be expected to be) perfect [11]. What matters the most, from an engineering point of view, is to deliver predictions that are useful. To increase this usefulness (which implies an adequate degree of reliability), one can (i) increase the amount of available information and its quality; and/or (ii) improve its exploitation, i.e., the usefulness of the contributing models, methodologies and frameworks.

These two ways to increase the usefulness of predictions are often collectively referred to under the umbrella term “uncertainty reduction” (or “risk reduction”), while, perhaps, they should be pursued to an extent that is simultaneously feasible, beneficial (e.g., in terms of interval and/or quantile scores that are appropriate for quantifying usefulness) and cost-effective. Point (ii) above can be, in principle, achieved, for example, by (a) reaching a better (physical) understanding of the system to be modelled; (b) (developing or) identifying better models and better predictor variables for each predictive task; (c) developing methodologies that combine different models (and/or algorithms) in an effective manner; and (d) developing unifying frameworks that maximize the benefits from using various methodologies.

By embracing and studying uncertainty, as suggested, for example, in Koutsoyiannis [5], one can also reduce uncertainty. Uncertainty reduction in (probabilistic) hydrological modelling is one of the 23 major unsolved problems in hydrology identified by Blöschl et al. [123] (see also the related discussions in Montanari [9], and Montanari and Koutsoyiannis [6]). Herein, we are explicitly interested in contributing towards point (ii), mostly towards points (b−d), conditional on the available data quantity and quality offered by the CAMELS dataset, and the information provided by the GR4J hydrological model. Hydrological understanding is assumed to be encompassed in the latter, under the justification provided in the following subsection. We believe that the investigations conducted herein and the proposed methodological framework should be accounted as a tangible step towards a new era in (operational) probabilistic hydrological modelling and forecasting.

5.2.2. A Culture-Integrating Approach to Probabilistic Hydrological Modelling

By seeing opportunities (rather than threats) in the integration of process-based and data-driven models within multi-stage probabilistic hydrological post-processing methodologies, new fruitful avenues could open up in the field of hydrological modelling. In the following, we discuss some key benefits stemming from this integration, as understood from an uncertainty reduction point of view. We also discuss the practical advantages exploited by this integrating approach, well supported by the large-scale application made herein.

Hydrological research has been focusing for decades on uncertainty reduction in point hydrological modelling [9]. All the related knowledge and experience gained through the years until today has been encompassed in what is called process-based hydrological modelling [4] (quoting Krzysztofowicz [2]; see, e.g., the review by Efstratiadis and Koutsoyiannis [124]). By incorporating process-based hydrological models into probabilistic hydrological post-processing methodologies, we benefit from this experience (therefore, uncertainty is reduced to some extent) and simultaneously quantify predictive hydrological uncertainty. Moreover, we facilitate the straightforward incorporation and exploitation of any future advancement in the field of process-based hydrological modelling, embedded either within new distributed/lumped hydrological models or within frameworks dedicated to boosting the application of such models, as soon as this advancement is achieved (see the related comments in Montanari and Koutsoyiannis [6]).

To further reduce uncertainty, one has to optimize the statistical modelling part of the probabilistic methodology, which is commonly related to the modelling of the hydrological model errors (see, e.g., references [6,45,61,62,64,65,69]). These errors are known to be heteroscedastic and correlated (see, e.g., references [6,10,87]). Based on the below-discussed properties of machine-learning quantile regression algorithms, we believe that their use for solving the problem of interest could further reduce uncertainty (to some extent) by increasing the amount of information gained from the available historical records. In fact, these algorithms are not only a suitable (of course, not the only suitable), but also a direct and straightforward-to-apply option for modelling hydrological model errors.

From a theoretical point of view, machine-learning quantile regression algorithms are expected to be optimal in offering a satisfactory compromise between reliability and sharpness (targeted in technical applications), since they (most of them) are trained by minimizing the quantile score (see Section 2.3 and Section 3.4). They are also appropriate for modelling heteroscedasticity by perception and construction without requiring multiple fittings (i.e., a different fitting for each season or month), as it would be required for modelling heteroscedasticity using conditional distribution models. Some related technical illustrations on the appropriateness of machine-learning quantile regression algorithms for probabilistic hydrological post-processing can be found in Papacharalampous et al. [69]. Furthermore, additionally to using the hydrological model predictions at time t as predictor variable in the regression setting, one can also use the hydrological model predictions at times t − 1, t − 2, etc. (see, e.g., the implementations herein), and/or precipitation and potential evapotranspiration (or temperature) variables, to increase the amount of exploited information.

To further support our reasoning and rationale behind the selection of machine-learning quantile regression algorithms as statistical post-processing models within methodologies for predictive uncertainty quantification in hydrology, we subsequently discuss some additional practical advantages stemming from their use. First, algorithms from this family are available in open source; therefore, their reproducibility is fully assured. Reproducibility is needed in hydrology, for example, according to Abrahart et al. [125], Ceola et al. [126], and Tyralis et al. [41], while only very few statistical post-processing models by hydrologists are made available in open source (see, e.g., references [127,128]). Moreover, machine-learning algorithms are well-tested (e.g., in forecasting competitions) in solving many practical problems and mostly optimally programmed (by computer scientists). This latter point is particularly important when one is interested in the operational use of the post-processing methodology, since it assures its fast implementation.

Some last, but certainly not least, practical advantages, as identified based on preliminary investigations, are also worth discussing. In contrast to a few parametric (machine-learning) models tried for this study, these algorithms were found (a) to be highly reliable, in the sense that their (satisfactory) fitting was (almost) always possible; and (b) to (mostly) produce reasonable results with respect to the whole picture. Only quantile regression neural networks were found to produce significant outliers in terms of predictive performance, probably due to fitting quality problems. Specifically, this algorithm produced significant outliers for 10 of the 511 investigated catchments in the contiguous United States.

Another sound practical advantage, stemming from point (a) above, is related to what is called “automatic modelling”, i.e., modelling that does not require human intervention during the whole process (see, e.g., references [1,129,130]). In light of this latter point, one could understand that automatic methodologies are the heart of operational hydrology, since they can effectively support large-sample hydrological applications, even at a global level (see, e.g., reference [50]). The preference of these algorithms can indeed facilitate the complete automation of the probabilistic hydrological modelling process and, therefore, can effectively support probabilistic hydrological post-processing “at scale”. An important clarification to be made here is that complete automation is possible even in the case where quantile regression neural networks are exploited, as their rare failures significantly affect the widths of the prediction intervals and, therefore, can be foreseen using benchmarking. However, in such a case, additional attention should be paid, by introducing an extra algorithmic step to detect extreme relative differences (usually relative increases) in terms of average width with respect to a performance stability benchmark (e.g., the quantile regression algorithm used herein). Such detection should be followed by the discard of the respective prediction, and its non-consideration by the equal-weight combiner. This automation has not been applied herein.

In summary, the integration of process-based models and machine-learning quantile regression algorithms is considered highly meaningful, mainly due to the diverse backgrounds and specializations of the experts involved in the model development process for the two mother research fields, and not because these two model categories “simply exist” (see reference [121]). It is also in line with the compromise between process-based and data-driven models proposed by Todini [4]. Inspired by this latter study, one would characterize the related approach to the problem of quantifying predictive hydrological uncertainty as “culture-integrating”.

5.2.3. Value of Ensemble Learning Hydrological Post-Processing Methodologies

A certainly worth-of-attention way to reduce uncertainty in probabilistic hydrological modelling is to (optimally) exploit information provided by different hydrological models and/or different statistical post-processing models. The former type of model combination is more frequently applied and suggested in the literature (see, e.g., the relevant suggestions by Montanari and Koutsoyiannis [6]). A concise and to-the-point presentation of several hydrological model combination approaches, varying in terms of conceptualization and theory-driven reasoning, can be found in Vrugt [131]. Among the methods discussed therein that are appropriate for probabilistic hydrological modelling are PDF combination methods. Simple PDF averaging has been exploited to some degree in hydrological contexts (see, e.g., reference [132]).

In the present study, we have exploited information from different machine-learning quantile regression algorithms through quantile combination approaches. The latter are known to be more convenient in practice than PDF combination approaches (for reasons already reported in the above sub-section) and equally (or even more) useful in terms of predictive performance [76]. To the best of our knowledge, such approaches have only been exploited so far for solving hydrological modelling and forecasting problems in Papacharalampous et al. [45,69] and Tyralis et al. [46], while different machine-learning quantile regression algorithms have been only combined for such purposes in Tyralis et al. [46]. These three papers emphasize the value of ensemble learning in general and equal-weight ensemble learning in particular (see also references [76,77]), which is also well-supported by the large-scale empirical results delivered herein. In fact, the equal-weight combiner of the six machine-learning algorithms of the present study has been found to be an outstanding modelling choice with respect to several criteria.

Further improvements may result by adopting optimally unequal-weight stacked generalization approaches, such as the methodology introduced and validated by Tyralis et al. [46]; see also reference [133] for a similar approach applied within a different context). In Tyralis et al. [46], these improvements (with respect to the equal-weight combiner) have been quantified to be up to 2% in terms of average interval score, when adopting quantile regression and quantile regression forests for probabilistic hydrological post-processing in one-step ahead prediction problems. Such improvements are larger than one would think they are based on comparisons within single-case studies, since a case-specific improvement can be extremely better (or worse) than the average-case and median-case improvements (see the related comments, for instance, in Andréassian et al. [53], Sivakumar [121], and Papacharalampous et al. [44]), and should be pursued, especially for specific categories of applications, for which the cost-effectiveness of the performance-improving methods also applies.

5.2.4. Grounds and Implications of the Proposed Methodological Framework

Understanding how the algorithms behave to improve predictive performance and reduce uncertainty in predictive modelling needs much more than inspecting their regular application and comparison to alternative approaches in some cases [121]. It needs properly conceptualized benchmark experiments (that, in turn, rely on data of adequate quantity and quality; see, e.g., related comments by Andréassian et al. [53] and Todini [4]), while toy experiments can also provide valuable insight into methodologies (see, e.g., references [2,134]). Andréassian et al. [53] reported on a “lack of standardized procedures in model testing” in hydrology, emphasizing the fact that gaining end users’ trust necessarily requires filling this methodological gap. We contribute towards this direction by developing a detailed framework for assessing statistical post-processing models in hydrological contexts. This framework is grounded on key suggestions made, for instance, by Sivakumar [121,135], Andréassian et al. [53] and Todini [4], and on empirical evidence derived from large-scale assessments, as summarized in the following.

The proposed framework produces trustable (or generalized) results. The fundamental role of large datasets in building trust in predictive hydrological modelling (which cannot be completely theory-driven) has been extensively pointed out and exploited by experts in the field (see, e.g., the comments by Andréassian et al. [52] and the model assessment by Perrin et al. [16]). This usefulness of large datasets holds, provided that they also represent a “wide range of climate and catchment conditions” [16]. As emphasized in Andréassian et al. [52], operational hydrologists only trust models that perform well in a wide range of cases. Related comments can be found in Sivakumar [121], who underlines the fact that any model could be proven better than a competitive one in specific cases. This latter fact is consistent with the “no free lunch” theorem by Wolpert [78], which has been first put in a hydrological context in Papacharalampous et al. [44]. This large-sample study and its companions (e.g., references [38,42,50,136]) have empirically proven the validity of the above comment by Sivakumar [121] in hydrological forecasting, when endogenous variables are exclusively used.

Moreover, the proposed framework allows us to find optimized solutions to the following well-posed practical problem: How should we integrate different algorithms (or statistical post-processing models in general) within unifying frameworks or combine different algorithms, aiming at maximizing the benefits and reducing the risks from their use? This research question arises in light of key comments by Sivakumar [121]; see also the related comments by Todini [4]. As pointed out in this latter study, the most useful comparative evaluations are those aimed at revealing the strengths and limitations of the various approaches to facilitate their optimal exploitation by answering research questions such as the above-stated one. It is relevant to highlight that posing research questions of this type requires us to first and foremost embrace the fact that a specific algorithm (or model) can be either useful or useless depending on its intended use [44].

Furthermore, finding reliable answers to such practical questions also requires keeping the scale of our experiments as large as possible in general, i.e., by means besides the exploitation of large datasets as well. In fact, implementing an adequate number of algorithms (and/or models) and contrasting their predictive performance in various modelling situations can help in identifying well-performing algorithms for several prediction tasks that might be of interest. These tasks could be determined, for example, by specific prediction intervals and/or specific ranges of flow magnitudes, which therefore are separately examined within the introduced framework. By only reporting the performance of the algorithms in predicting the entire PDF (e.g., by computing the continuous ranked probability score—CRPS, as made, for example, in Bakker et al. [122], and by relying our practical recommendations on it) and independently of the flow magnitude, a large amount of information (that would be useful in hydrological modelling and forecasting contexts) would remain unrevealed and unstudied.

A single score is mostly enough for properly quantifying the usefulness in performance. In our case, this single score could be the interval or quantile score, depending on the exact application of interest. Nonetheless, a multi-faced presentation of the results is also essential, since it (a) strengthens our understanding on how the various algorithms work by allowing related interpretations; and (b) provides some clues as to how to integrate these algorithms. Such multi-faced presentation is allowed, for instance, by those scores computed in Bourgin et al. [137], Bock et al. [120], Papacharalampous et al. [45,69], and Tyralis et al. [46], and the set of scores proposed herein. For instance, even when we are interested in delivering central prediction intervals, historical quantile scores can guide us towards delivering better probabilistic predictions by facilitating an optimal integration of two algorithms for forming the targeted prediction interval. Within this integration, each algorithm is used to predict quantiles of different level. Finally, we would like to highlight the appropriateness of the proposed framework in facilitating the selection of flow magnitude thresholds for the application of the various algorithms, based on the comparative performance of these algorithms for various flow magnitudes. Sivakumar [135] underlines the role of such thresholds in hydrological modelling and forecasting. As pointed out by Sivakumar [135], a single model should not be expected to model high, medium and low values equally well.

In summary, by applying the framework introduced herein, one can reliably gain insight on (i) which algorithm to select for each prediction task; and/or (ii) how to combine algorithms (also by testing various combinations), to maximize the benefits and minimize the risks from their use, thus facilitating a tangible contribution to the problem of uncertainty reduction. In light of this fact, the introduced framework could be further exploited in the future for:

• identifying the advantages and limitations of more statistical post-processing approaches, utilizing other machine-learning quantile regression algorithms and ensemble learning approaches (implemented with various sets of predictor variables) and/or other hydrological models, provided that these approaches are computationally fast and can be applied in a fully automatic way;
• solving related technical problems at different timescales (e.g., the monthly or seasonal timescales); and
• assessing statistical post-processing approaches in forecasting mode, i.e., by running the hydrological model using forecasts as inputs (instead of using observations).

Some final remarks should be made on our above-expressed suggestion for implementing different hydrological models within the broader methodologies exploited herein. As illustrated in Tyralis et al. [46] (Figure 3), the GR4J hydrological model (implemented herein) successfully “pre-processes” the regression datasets (exploited by the machine-learning quantile regression algorithms in probabilistic hydrological post-processing) by linearizing them. The smaller differences found between the machine-learning algorithms of the present study in predicting the median of daily streamflow compared to those found in Tyralis et al. [138] for point forecasting of daily streamflow by exclusively using machine-learning algorithms could perhaps be attributed to this linearization (which seems to ease the regression problem to be solved). Under this view, the relative differences in the predictive performance of the machine-learning algorithms would perhaps become larger or smaller (to some extent) for potential exploitations of the methodologies of this study with different hydrological models, depending on how well these models perform.

6. Summary and Take-Home Messages

We contribute with large-scale results and best practices to the problem of quantifying predictive uncertainty in hydrology, when the problem is examined from a predictive modelling perspective. We have made a detailed assessment of six machine-learning quantile regression algorithms (i.e., quantile regression, generalized random forests for quantile regression, generalized random forests for quantile regression emulating quantile regression forests, gradient boosting machine, model-based boosting with linear models as base learners and quantile regression neural networks) and their equal-weight combiner in solving probabilistic hydrological modelling problems for 511 catchments in the contiguous United States. The examined catchments represent divergent climatic and catchment characteristics and, therefore, are appropriate for benchmarking purposes. By taking a quick glance at our large-scale results, one can immediately identify which algorithm should be selected (among the assessed ones) for maximizing the benefits and minimizing the risks from their use. The findings can be used in technical applications. The algorithms could be applied as detailed herein or within ensemble learning probabilistic hydrological post-processing methodologies.

In the following, we summarize the practical and methodological contributions of the study in the form of take-home messages and recommendations:

• Preliminary large-sample investigations should focus on identifying a useful set of statistical post-processing models, such as the one composed by the six machine-learning quantile regression algorithms of this study.
• Machine-learning quantile regression algorithms can effectively serve as statistical post-processing models, since they model heteroscedasticity by perception and construction without requiring multiple fittings, i.e., a different fitting for each season, as applying for the case of conditional distribution models.
• These algorithms are also straightforward-to-apply, fully automatic (i.e., their implementation does not require human intervention), available in open source, and computationally convenient and fast, and thus are highly appropriate for large-sample hydrological studies, while machine-learning methods, in general, are known to be ideal for exploiting computers’ brute force.
• Once a useful set of statistical post-processing models is identified, making the most of it, through model integrations and combinations, should be our target.
• Quantifying both the algorithms’ overall performance (independently of the flow magnitude) and the algorithms’ performance conditional upon the flow magnitude is of practical interest.
• Useful results are mostly those presented per level of prediction interval or predictive quantile, while those summarizing the quality of the entire predictive density (e.g., the continuous ranked probability score—CRPS) might also be of interest.
• Although the separate quantification of reliability and sharpness could be useful (mainly for increasing our understanding on how the algorithms work), what is most useful is computing scores that facilitate an objective co-assessment of these two criteria, such as the (rarely used in the literature) interval and quantile scores.
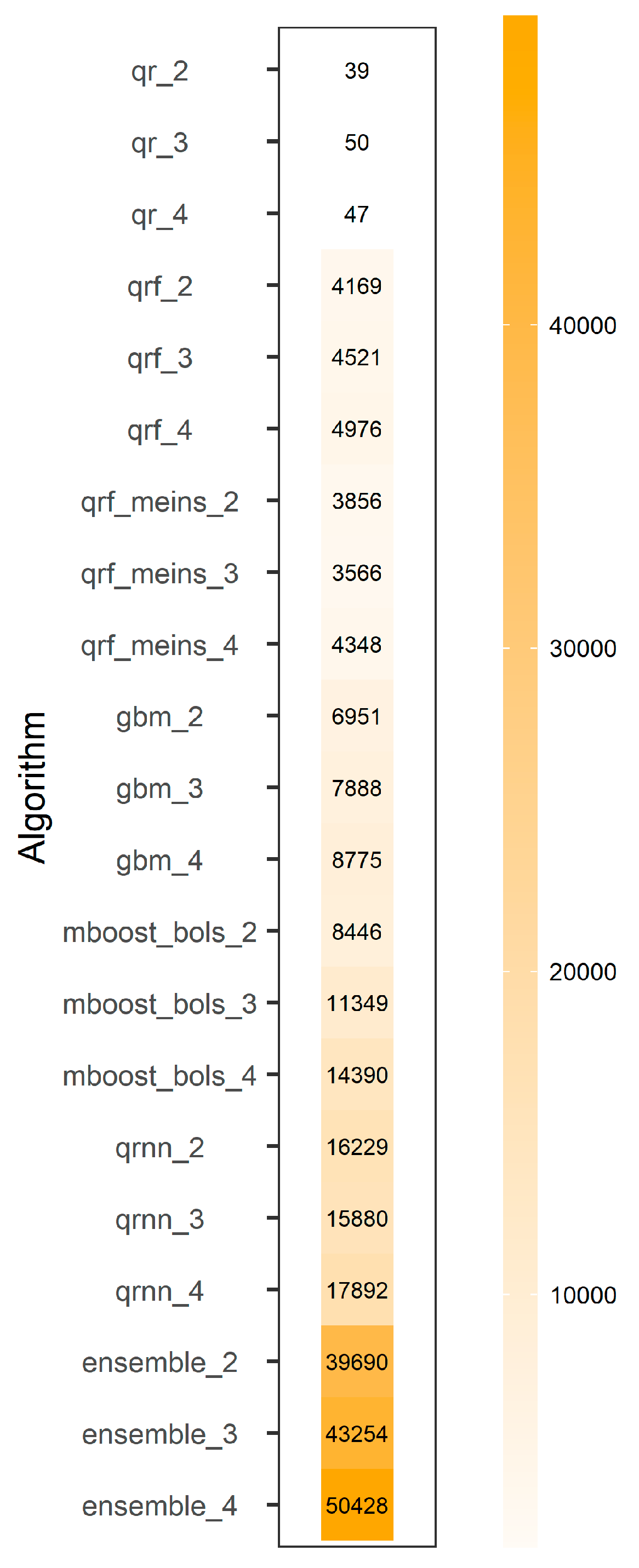
• The computational requirements might also be an important criterion for selecting an algorithm over others.
• In most cases, finding a balance between computational time and predictive performance is required. In any case, the criteria for selecting a statistical post-processing model should be clear.
• If we are foremost interested in obtaining results fast, then we probably should select quantile regression. This selection should be made keeping in mind that this algorithm is up to approximately 3.5% worse in terms of average quantile score than using the equal-weight combiner of all six algorithms of this study.
• The equal-weight combiner of all six algorithms in this study is identified as the best-performing algorithm overall, confirming the value of ensemble learning in general and ensemble learning via simple quantile averaging in particular. This value is well-recognized in the forecasting literature, but has not received much attention yet in the hydrological modelling and hydro-meteorological forecasting literature, in contrast to the popular concepts of ensemble simulation and ensemble prediction (e.g., via Bayesian model averaging) by exploiting information from multiple hydrological models.
• In spite of its outstanding performance, the equal-weight combiner of the six algorithms of this study is, in turn, expected to perform worse than some of the individual algorithms in many modelling situations.
• In general, no algorithm should be expected to be (or presented as) the best performing with respect to every single criterion.
• By using different algorithms for delivering each predictive quantile (or prediction interval), the risk of producing a probabilistic prediction of bad quality is reduced. Related information on the predictive performance of the algorithms was extensively given in Section 4.1, while a summary is given below:

  ✓

  The equal-weight combiner is the best choice or among the best choices in terms of predictive performance for delivering predictive quantiles of level that is higher than 0.0125; however, it is also the most computationally demanding choice.

  ✓

  Quantile regression is the best choice in terms of predictive performance for predicting low-level quantiles (practically predictive quantiles of level lower than 0.0125) and the third-best choice for predicting high-level quantiles (practically predictive quantiles of level higher than 0.9).

  ✓

  Generalized random forests for quantile regression and generalized random forests for quantile regression emulating quantile regression forests are identified as the best choices or among the best choices in terms of predictive performance, when one is interested in delivering predictive quantiles of levels between 0.2 and 0.8. Since they are less computationally intensive than the equal-weight combiner, they would probably be preferred over the latter for relevant modelling applications.

  ✓

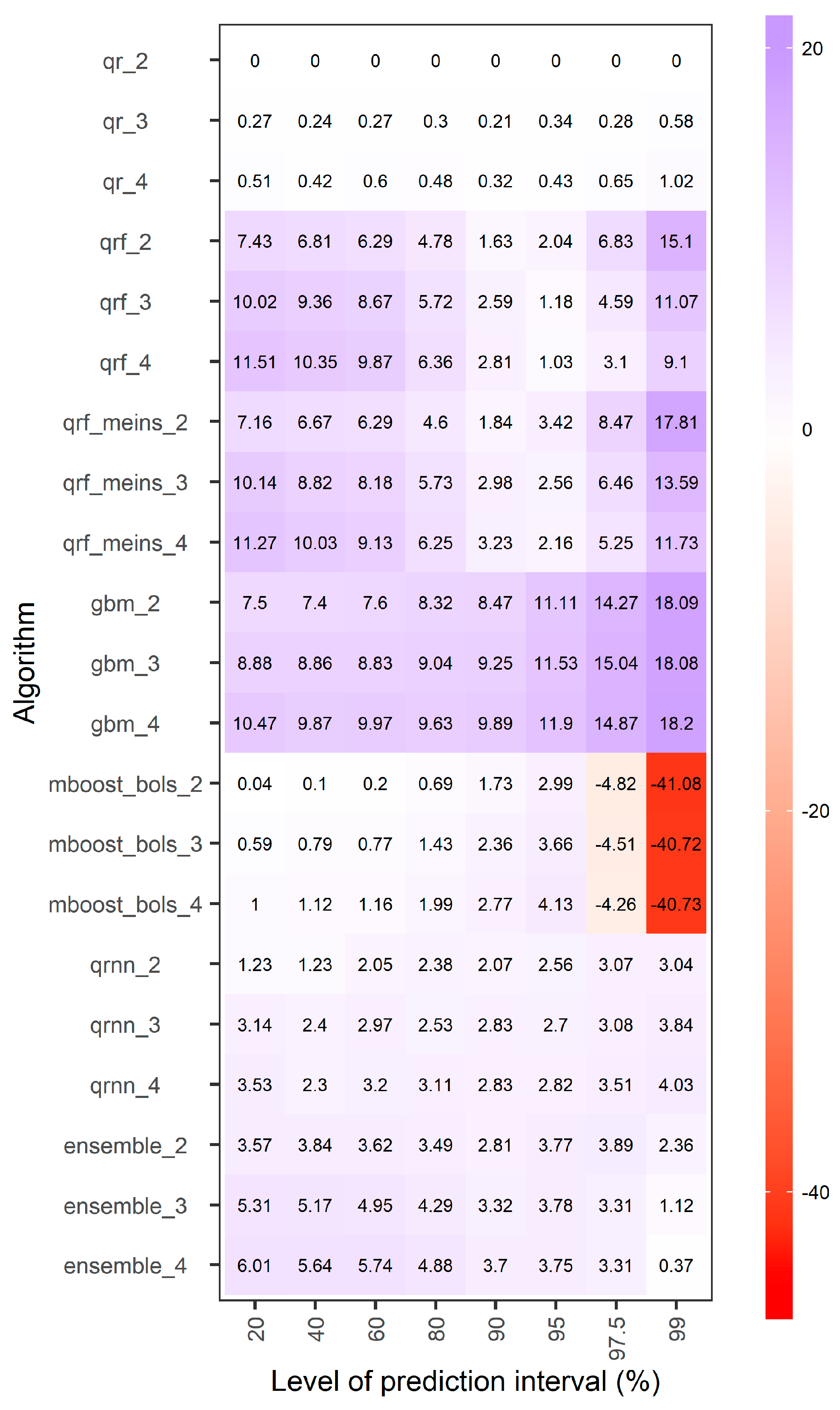
  Improvements up to approximately 1.5% may be achieved for the generalized random forests for quantile regression and the generalized random forests for quantile regression emulating quantile regression forests by using as predictor variables of the regression the hydrological model predictions at times t − 3, t − 2, t − 1 and t instead of using the hydrological model predictions only at times t − 1 and t. By switching from the former set of predictors to the latter one, the improvements for the equal-weight combiner may reach an improvement of approximately 1%.

  ✓

  Quantile regression neural networks is also a well-performing algorithm with respect to the whole picture and less computationally demanding than the equal-weight combiner; nevertheless, it is also the only individual algorithm among the assessed ones that was found to produce significant outliers (for ~2% of the investigated catchments). These performance issues were also manifested in the equal-weight combiner, yet in a less-pronounced degree.

• The overall performance improvements expressed in terms of average interval or quantile score are mostly up to 3%, while only for some extreme cases these improvements may reach up to approximately 20%. These cases concern some predictive quantiles of the lowest and highest levels, for which the tree-based methods, i.e., generalized random forests for quantile regression, generalized random forests for quantile regression emulating quantile regression forests and gradient boosting machine, do not work at their best.
• Unrealistic improvements in the order of 50% and 60%, even up to more than 100%, in terms of overall performance (often appearing in the literature) may result either by chance or by design when using small datasets, while they are highly unlikely to result on a regular basis when using large datasets. Only large-sample studies can produce trustable quantitative results in predictive modelling.
• Conducting large-sample studies is feasible nowadays, due to both the tremendous evolution of personal computers over the past few years and the fact that large datasets (e.g., the CAMELS dataset) are increasingly made available.
• Performance improvements may also be obtained by selecting algorithms according to their skill in predicting low, medium or high flows for the various quantiles (or central prediction intervals). Related information was extensively given in Section 4.2.
• Since we are mostly interested in obtaining results that are useful within operational settings, we have not performed hyperparameter optimization (which would require significantly higher computational time). The results could differ, if such optimization was performed.
• An alternative to hyperparameter optimization is ensemble learning, in the sense that both these procedures aim at improving probabilistic predictions. Here, we have extensively studied this alternative and showed that the improvements achieved are worth-of-attention.

This study is one of the very few large-scale studies in probabilistic hydrological post-processing and the even fewer ones conducted at daily timescale. We hope it will trigger interest and future research on the use of machine-learning quantile regression algorithms in probabilistic hydrological post-processing “at scale” and on ways to maximize the benefits from their use.