Experimental Hydraulic Investigation of Angled Fish Protection Systems—Comparison of Circular Bars and Cables
Abstract
1. Introduction
1.1. General
1.2. Basic Equations
1.3. Literature Values
2. Materials and Methods
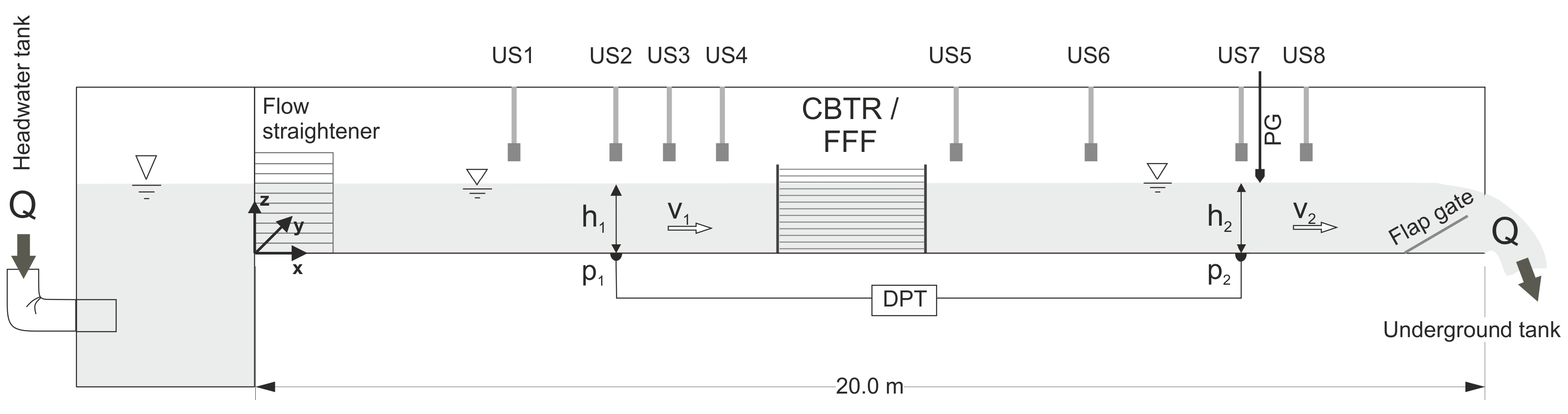
2.1. Experimental Setup
2.2. Measurement
2.3. Investigated Parameters
3. Results
3.1. Overview
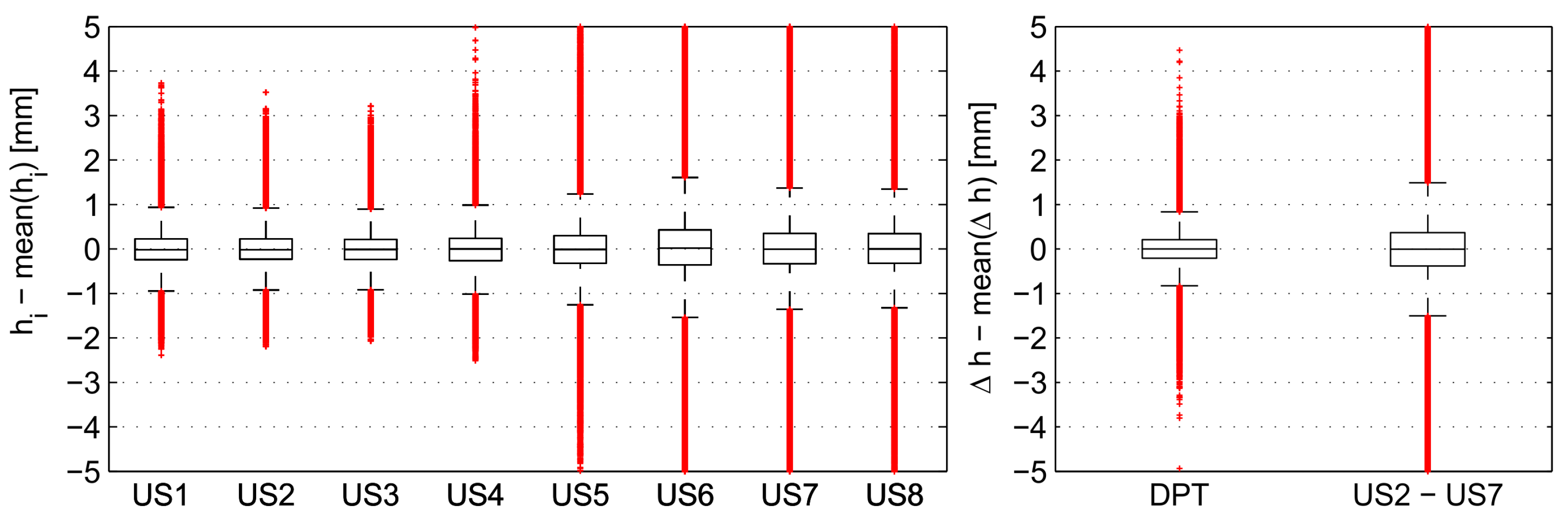
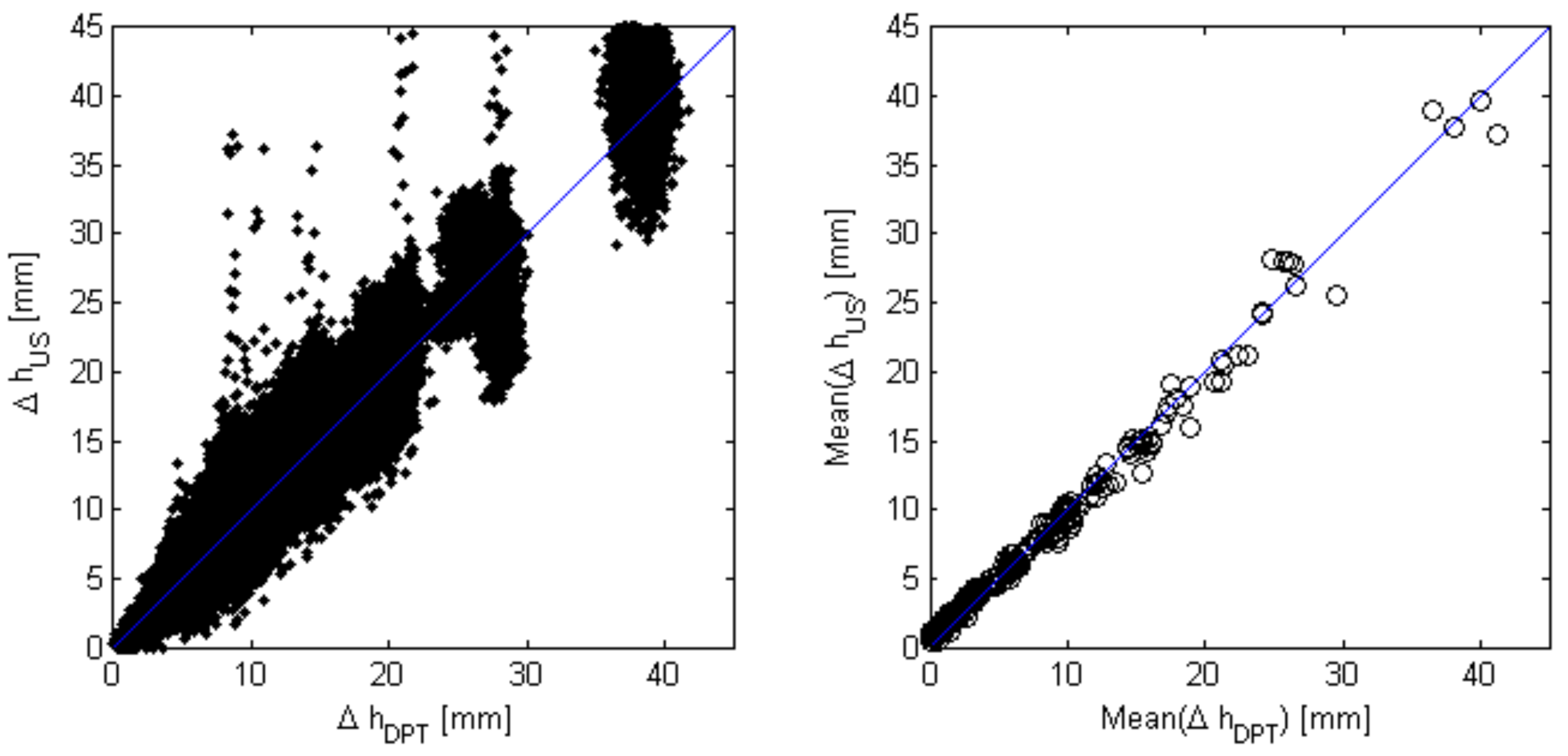
3.2. Measurement Accuracy and Data Verification
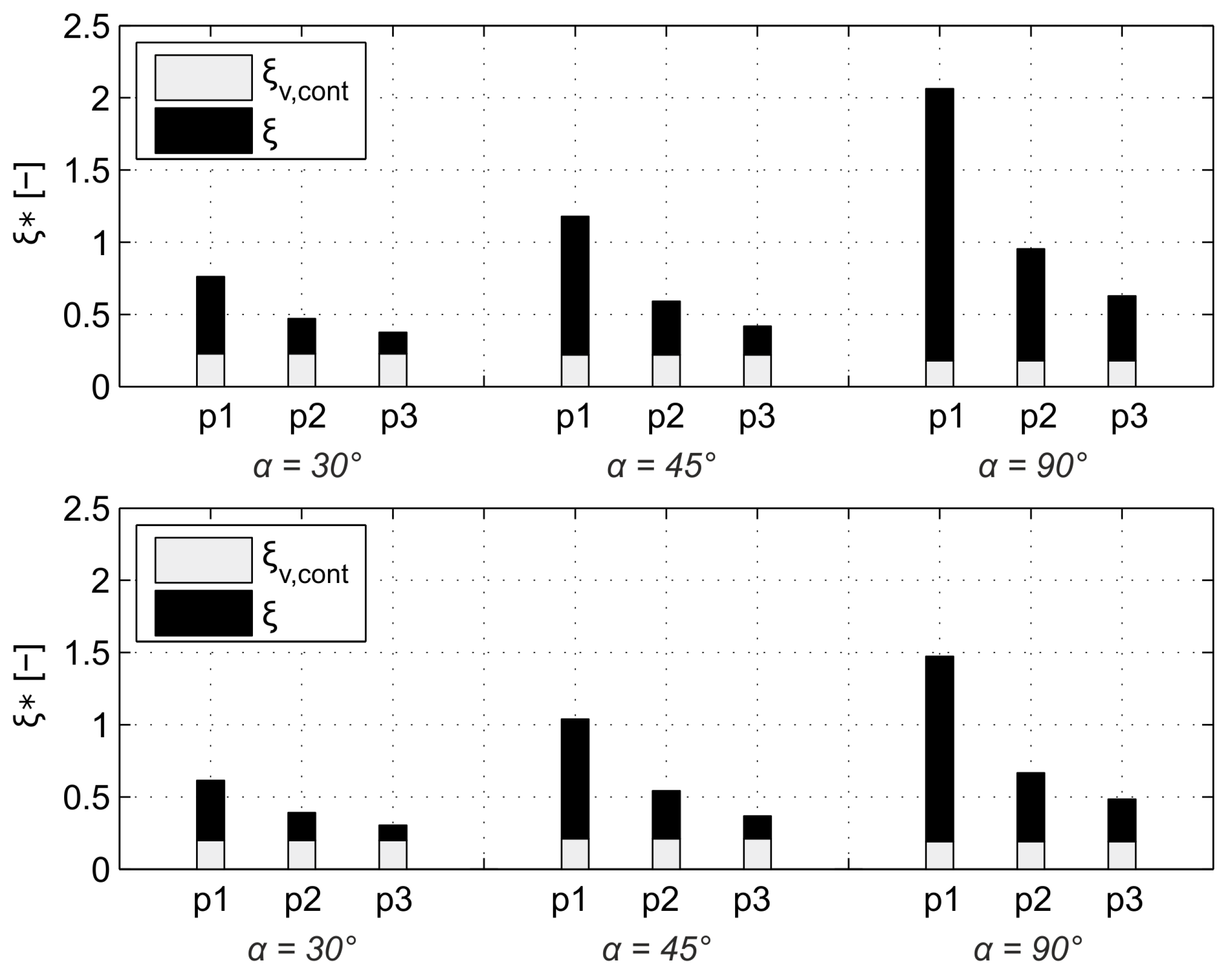
3.3. Head Loss Through Supporting Structures and Surface Friction
3.4. Head Loss Coefficients of the Rack Configurations
3.5. Empirical Relations to Predict Head Loss of Angled Racks
4. Discussion
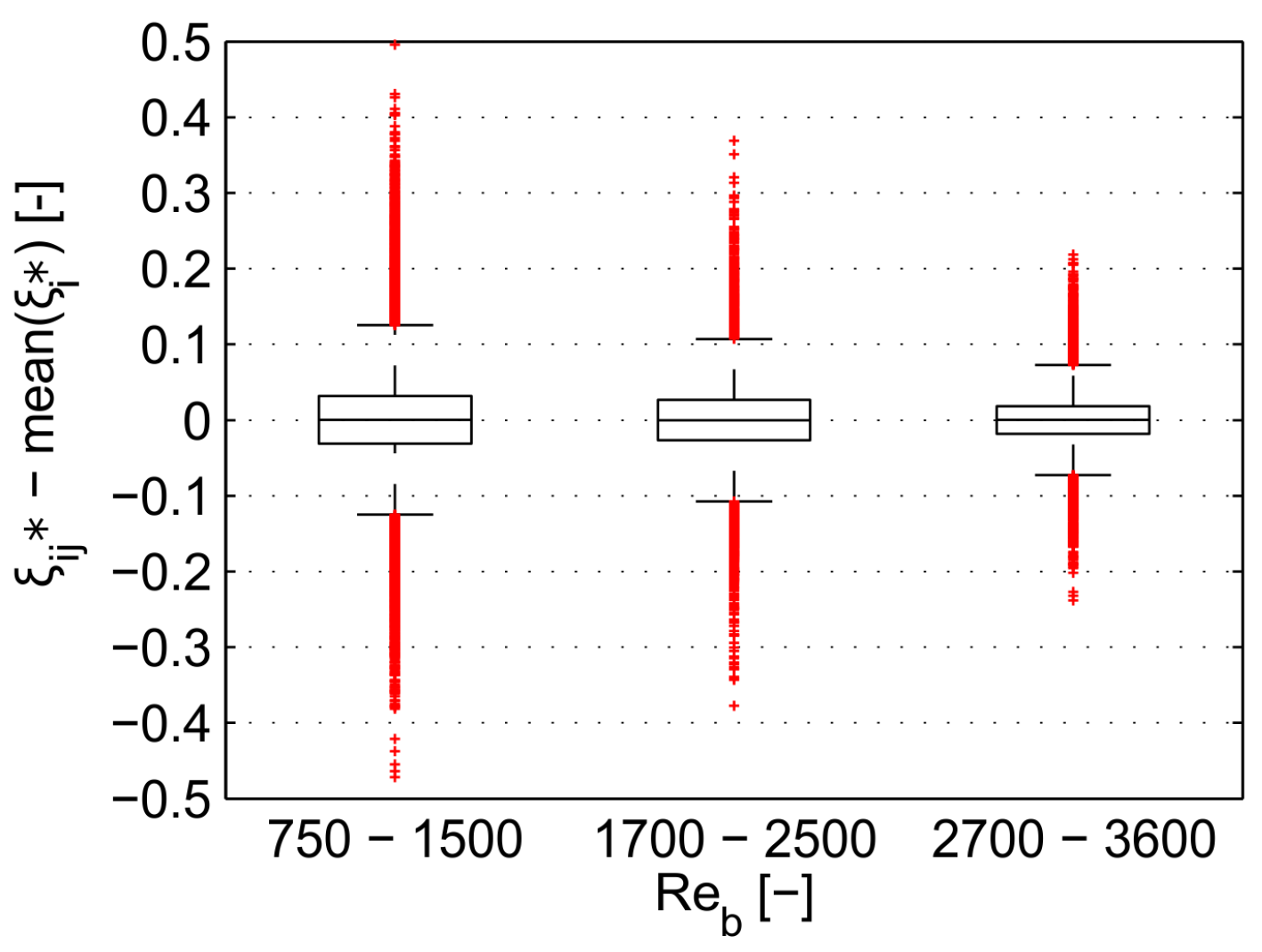
4.1. Accuracy and Scale Effects
4.2. Effect of Blockage and Angle
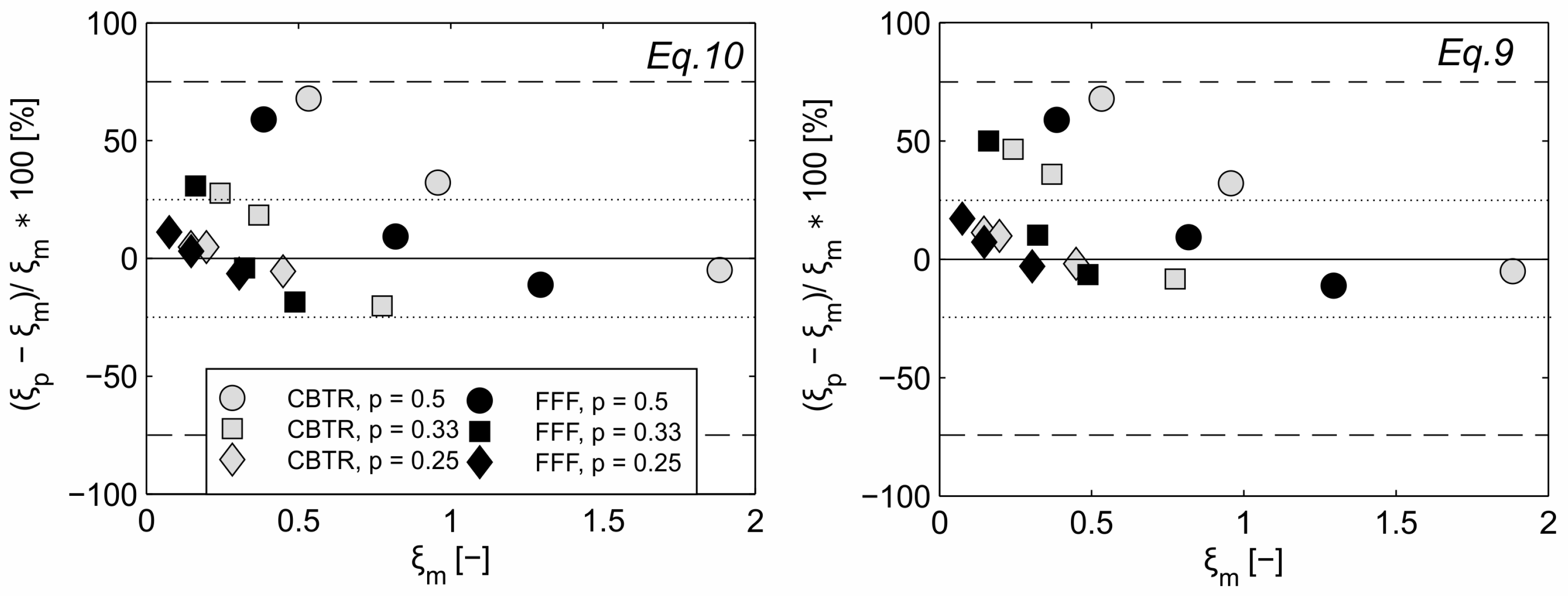
4.3. Prediction of Head Loss Coefficients of Angled Racks with Empirical Equations
4.4. Transferability of the Results to Technical Applications and Outlook
5. Conclusions
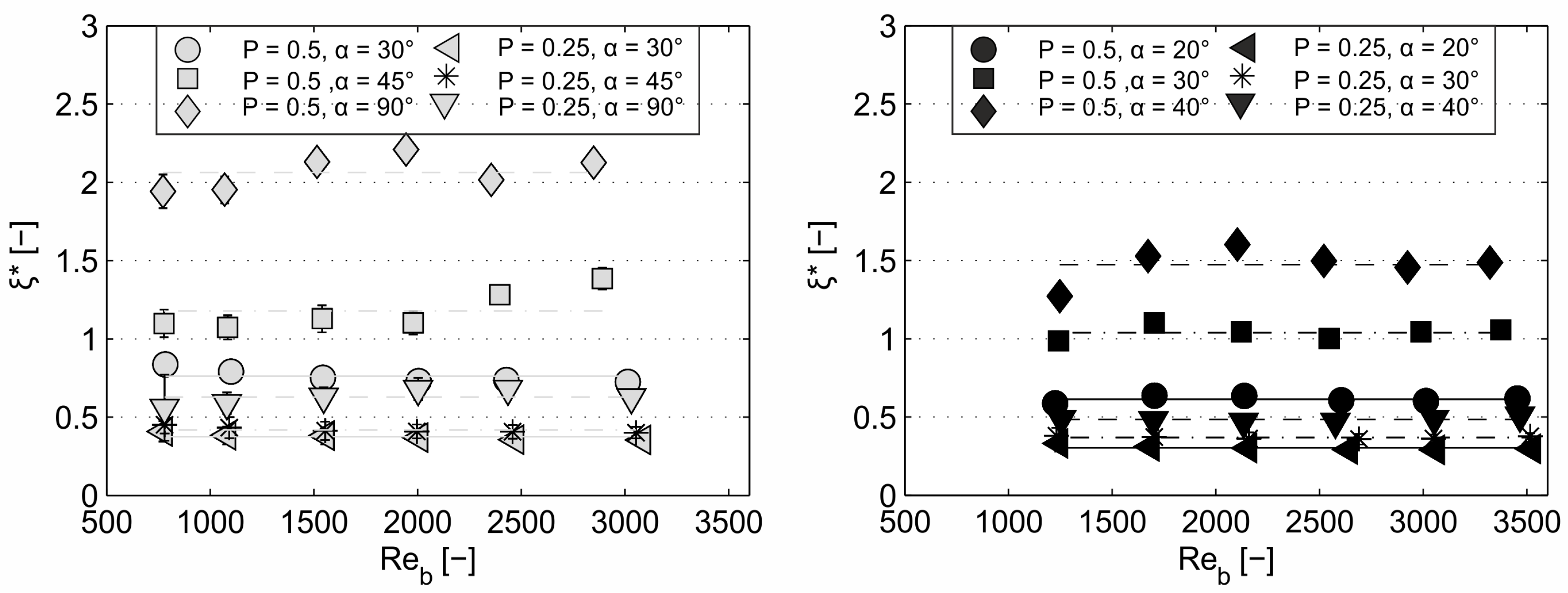
- Head loss coefficient ξ is independent from the Bar–Reynolds number in the studied range of of 750–3500 and scale effects can be neglected.
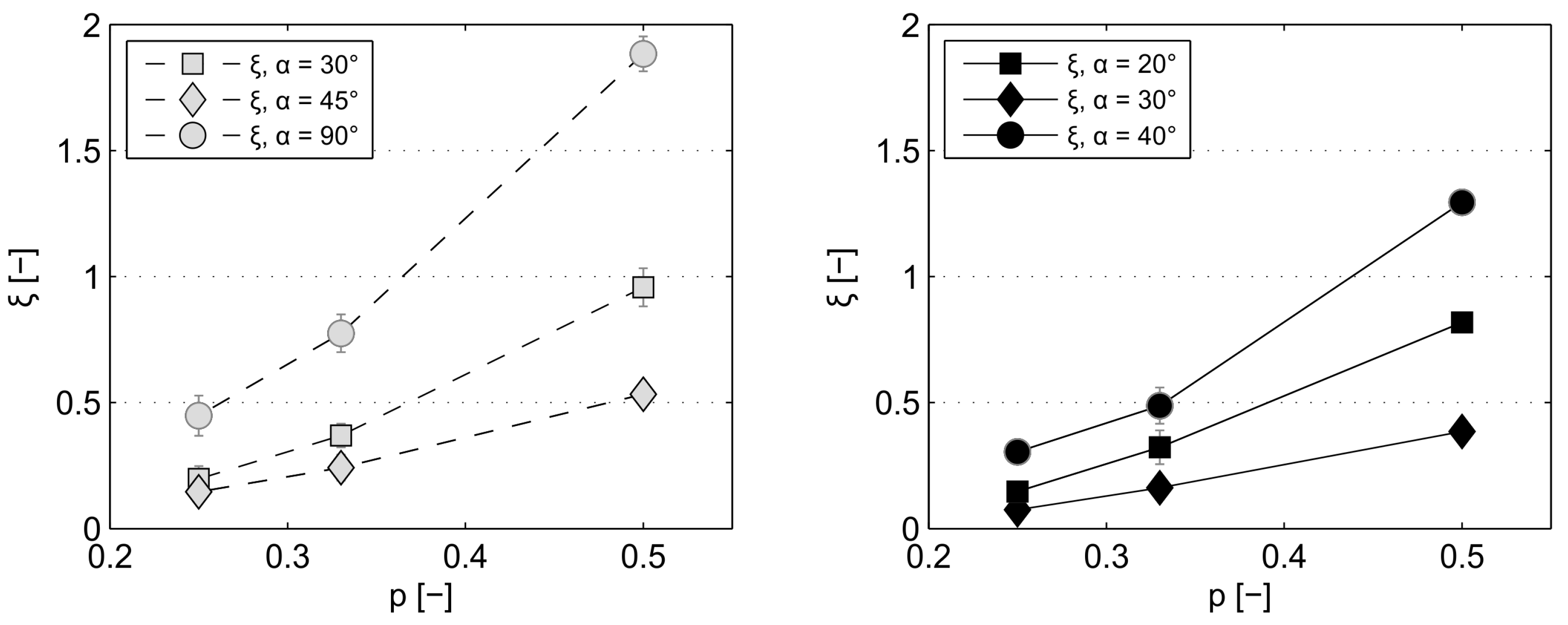
- The coefficient ξ is significantly affected by the blockage ratio and the rack angle (Section 3.4, Table 3). The strong increase of head loss with decreasing bar spacings, which are necessary for fish protection, can be countered by designing lower rack angles (α≤ 45°).
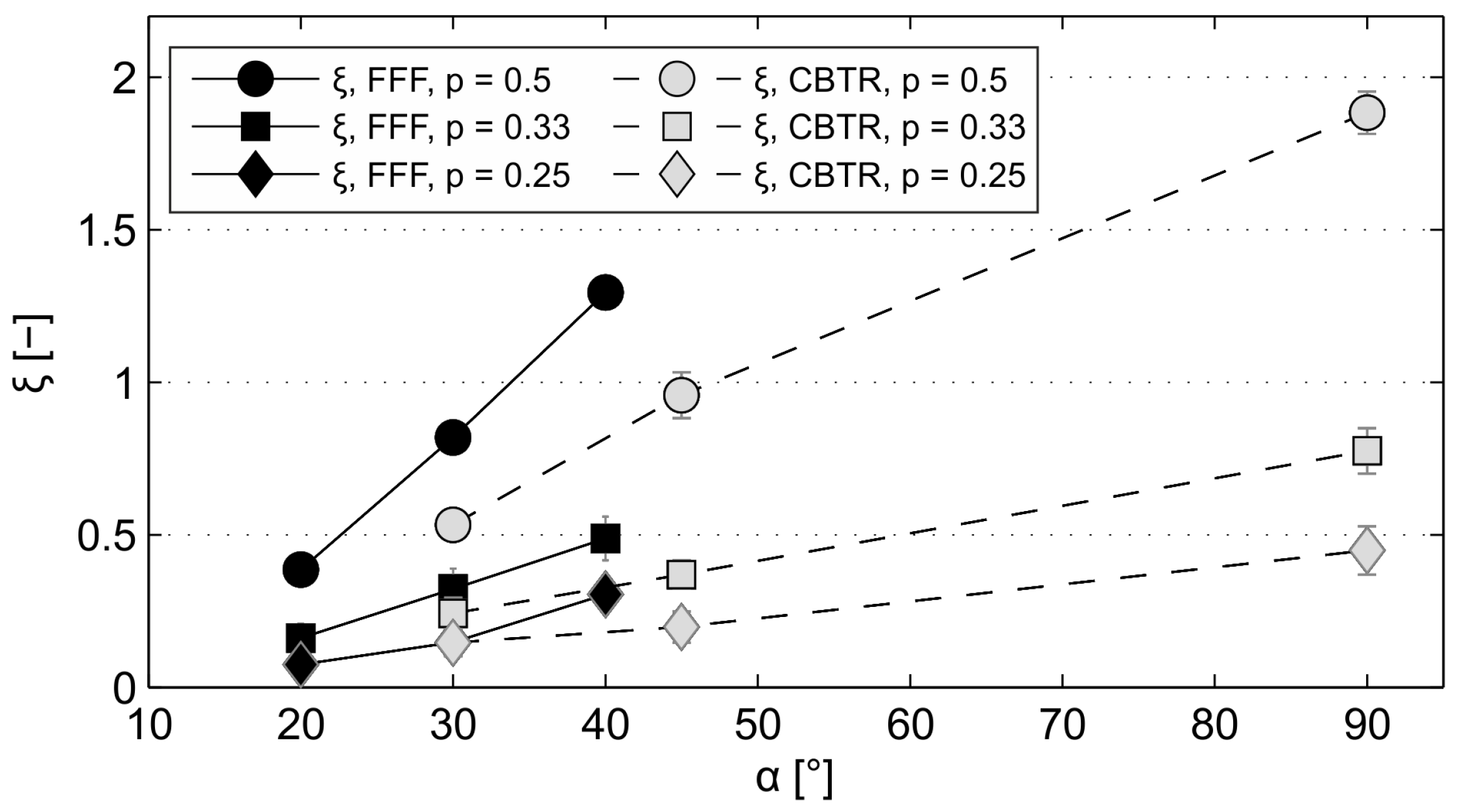
- With increasing blockage ratios, the head loss coefficient at the FFF is up to 53% higher compared to the CBTR. This phenomenon is likely resulting from the effect of flow-induced cable vibrations and hence a further increase of blockage. Since amplitudes and frequencies of the vibrations are depending on parameters such as preload forces, cable length or flow velocity, the transferability to full-scale applications is limited.
- Head loss at the CBTR and FFF can be roughly estimated with a modified version of Equation (10) originally published by Meusburger [18], where the horizontal angle is used instead of the vertical rack inclination. However, the comparison of measured and estimated head loss revealed a systematic bias, which is more pronounced for rack options with low angles and high blockage.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| A | = area (m2) | α | = rack angle in relation to the vertical wall (°) |
| b | = spacing between the bars (m) | β | = rack angle in relation to the ground plane (°) |
| B | = width of the flume (m) | λ | = scale factor (-) |
| F | = Froude number (-) | ρ | = mass density of water ≈ 997 (kg m−3) |
| g | = gravity acceleration (m s−2) | = kinematic viscosity (m2 s−1) | |
| h | = water depth (m) | = head loss coefficient (-) | |
| hv | = head loss (m) | ξ* | = total head loss coefficient (-) |
| = bar shape coefficient (-) | = predicted head loss coefficient | ||
| k | = constant | = measured head loss coefficient | |
| l | = bar length (in cross section) (m) | = ξ due to supports and surface friction (-) | |
| = pressure (Pa) | = differential pressure (Pa) | ||
| p | = blockage ratio (-) | CBTR | circular bar trash rack |
| Q | = discharge (m3 s−1) | DPT | differential pressure transducer |
| = Reynolds Number (-) | FFF | Flexible Fish Fence | |
| = Bar–Reynolds Number (-) | PG | point gauge | |
| s | = diameter of the bar/cable (m) | US | ultrasonic sensor |
| v1,2 | = velocity (m s−1) | ||
| z | = elevation (m) |
References
- Williams, J.G.; Armstrong, G.; Katopodis, C.; Larinier, M.; Travade, F. Thinking like a fish: A key ingredient for development of effective fish passage facilities at river obstructions. River Res. Appl. 2012, 28, 407–417. [Google Scholar] [CrossRef]
- Cada, G.F. The development of advanced hydroelectric turbines to improve fish passage survival. Fisheries 2001, 26, 14–23. [Google Scholar] [CrossRef]
- Schilt, C.R. Developing fish passage and protection at hydropower dams. Appl. Anim. Behav. Sci. 2007, 104, 295–325. [Google Scholar] [CrossRef]
- Larinier, M.; Travade, F. Downstream migration: Problems and facilities. Bulletin Français de la Pêche et de la Pisciculture 2002, 364, 181–207. [Google Scholar] [CrossRef]
- Ebel, G. Fischschutz und Fischabstieg an Wasserkraftanlagen-Handbuch Rechen-und Bypasssysteme. Ingenieurbiologische Grundlagen, Modellierung und Pronose, Bemessung und Gestaltung [Fish Protection and Downstream Passage at Hydro Power Stations-Bioengineering Principles, Modelling and Prediction, Dimensioning and Design], 4th ed.; Mitteilungen aus dem Büro für Gewässerökologie und Fischereibiologie: Halle, Germany, 2018. [Google Scholar]
- Dumont, U. Zum Stand der Technk Einer Ökologisch Angepassten Wasserkraftnutzung [State of the Art about An Ecologically Sustainable Use of Hydro Power]. In Proceedings of the Seminar Gewässer-verträglicher Wasserkraftausbau, Renexpo, Salzburg, Austria, 28 November 2013; RENEXPO INTERHYDRO: Salzburg, Austria, 2013. [Google Scholar]
- Cuchet, M. Fish Protection and Downstream Migration at Hydropower Intakes—Investigation of Fish Behavior under Laboratory Conditions. Ph.D. Thesis, Technical University of Munich (TUM), Munich, Germany, 2014. [Google Scholar]
- Kriewitz-Byun, C.R. Leitrechen an Fischabstiegsanlagen: Hydraulik und fischbiologische Effizienz [Guidance Screens at Fish Protection Facilities—Hydraulics and Fishbiological Efficiency]. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2015. [Google Scholar] [CrossRef]
- Boettcher, H.; Brinkmeier, B.; Aufleger, M. Flexible Fish Fences. In Proceedings of the Norwegian University of Science and Technology 10th International Symposium on Ecohydraulics, Trondheim, Norway, 23–27 June 2014. [Google Scholar]
- Gabl, R.; Innerhofer, D.; Achleitner, S.; Righetti, M.; Aufleger, M. Evaluation criteria for velocity distributions in front of bulb hydro turbines. Renew. Energy 2018, 121, 745–756. [Google Scholar] [CrossRef]
- Umweltbundesamt, Bundesministerium für Umwelt, Naturschutz, Bau und Reaktorschutz, Ecologic Institute. Forum Fischschutz und Fischabstieg—Empfehlungen und Ergebnisse des Forums “Fischschutz und Fischabstieg” [Forum Fish Protection and Downstream Migration—Recommendations and Results]; Umweltforschungsplan des Bundesministeriums für Umwelt, Natuschutz, Bau und Reaktorsicherheit: Bau, Germany, 2015. [Google Scholar]
- Böttcher, H.; Unfer, G.; Zeiringer, B.; Schmutz, S.; Aufleger, M. Fischschutz und Fischabstieg–Kenntnisstand und aktuelle Forschungsprojekte in Österreich [Fish protection and downstream migration: Current state of knowledge and research projects in Austria]. Österreichische Wasser-und Abfallwirtschaft 2015, 67, 299–306. [Google Scholar] [CrossRef]
- Böttcher, H.; Gabl, R.; Ritsch, S.; Aufleger, M. Experimental study of head loss through an angled fish protection system. In Proceedings of the 4th IAHR Europe Congress, Liege, Belgium, 27–29 July 2016; Dewals, B., Ed.; CRC Press: Liege, Belgium, 2016; pp. 637–642. [Google Scholar]
- Unit of Applied Mechanics, University of Innsbruck. Projektbericht—Berechnung der Seilschwingungen beim Seilrechen [Research Project Report—Calculation and Modelling of Cable Vibrations at the Flexible Fish Fence]; University of Innsbruck: Innsbruck, Austrian, 2017. [Google Scholar]
- Gabl, R.; Achleitner, S.; Neuner, J.; Aufleger, M. Accuracy analysis of a physical scale model using the example of an asymmetric orifice. Flow Meas. Instrum. 2014, 36, 36–46. [Google Scholar] [CrossRef]
- Adam, N.J.; De Cesare, G.; Nicolet, C.; Billeter, P.; Angermayr, A.; Valluy, B.; Schleiss, A.J. Design of a Throttled Surge Tank for Refurbishment by Increase of Installed Capacity at a High-Head Power Plant. J. Hydraul. Eng. ASCE 2018, 144, 05017004. [Google Scholar] [CrossRef]
- Gabl, R.; Righetti, M. Design criteria for a type of asymmetric orifice in a surge tank using CFD. Eng. Appl. Comput. Fluid Mech. 2018, 12, 397–410. [Google Scholar] [CrossRef]
- Meusburger, H. Energieverluste an Einlaufrechen Von Flusskraftwerken [Head losses at intakes of run-of-river hydropower plants]. Ph.D. Thesis, Mitteilungen der Versuchsanstalt fur Wasserbau, Hydrologie und Glaziologie an der Eidgenossischen Technischen Hochschule Zürich, Zürich, Switzerland, 2002. [Google Scholar]
- Gabl, R.; Gems, B.; Birkner, F.; Hofer, B.; Aufleger, M. Adaptation of an Existing Intake Structure Caused by Increased Sediment Level. Water 2018, 10, 1066. [Google Scholar] [CrossRef]
- Kirschmer, O. Untersuchungen über den Verlust an Rechen [Study on Head Loss At Trash Racks]; Mitteilungen Hydraulisches Institut München: München, Germany, 1926; Nr. 1. [Google Scholar]
- Zimmermann, J. Widerstand Schräg Angeströmter Rechengitter [Resistance of Trash Racks Caused by Oblique Inflow]; Mitteilungen der Universität Fridericana Karlsruhe, Theodor-Rhebock-Flußbaulaboratorium: Karlsruhe, Germany, 1969; Volume 157. [Google Scholar]
- Spangler, J. Untersuchung über den Verlust an Rechen bei schräger Zuströmung [Study about head Loss at Obliquely Approached Trash Racks]; Mitteilungen des Hydraulischen Instituts der TH München: München, Germany, 1929. [Google Scholar]
- Idelchik, I.E. Handbook of Hydraulic Resistance Coefficients of Local Resistance and of Friction; U.S. Department of Commerce National Technical Information Service (NTIS): Springfield, VA, USA, 1960.
- Clark, S.P.; Tsikata, J.M.; Haresign, M. Experimental study of energy loss through submerged trashracks. J. Hydraul. Res. 2010, 46, 113–118. [Google Scholar] [CrossRef]
- Raynal, S.; Courret, D.; Chatellier, L.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 1. Inclined trashracks. J. Hydraul. Res. 2013, 51, 56–66. [Google Scholar] [CrossRef]
- Raynal, S.; Chatellier, L.; Courret, D.; Larinier, M.; David, L. An experimental study on fish-friendly trashracks—Part 2. Angled trashracks. J. Hydraul. Res. 2013, 51, 67–75. [Google Scholar] [CrossRef]
- Szabo-Meszaros, M.; Navaratnam, C.U.; Aberle, J.; Silva, A.T.; Forseth, T.; Calles, O.; Fjeldstad, H.-P.; Alfredsen, K. Experimental hydraulics on fish-friendly trash-racks: An ecological approach. Ecol. Eng. 2018, 113, 10–20. [Google Scholar] [CrossRef]
- Albayrak, I.; Kriewitz, C.R.; Hager, W.H.; Boes, R.M. An experimental investigation on louvres and angled bar racks. J. Hydraul. Res. 2018, 46, 59–75. [Google Scholar] [CrossRef]
- Berger, C. Rechenverluste und Auslegung von (elektrifizierten) Schrägrechen Anhand Ethohydraulischer Studien [Screen Losses and Design of Inclined (and Electrified) Screens with Horizontal Bars on the Basis of Ethohydraulic Studies]. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2018. [Google Scholar]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Blevins, R.D. Applied Fluid Dynamics Handbook; Van Nostrand Reinhold Company, Inc.: New York, NY, USA, 1984; ISBN 978-1575241821. [Google Scholar]
- Naudascher, E. Hydraulik der Gerinnebauwerke [Hydraulics of Open Channel Flow Structures]; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-3211823668. [Google Scholar]
- Krzyzagorski, S.; Gabl, R.; Seibl, J.; Böttcher, H.; Aufleger, M. Implementierung eines schräg angeströmten Rechens in die 3D-numerische Berechnung mit FLOW-3D [Implementation of an angled trash rack in the 3D-numerical simulation with FLOW-3D]. Österreichische Wasser-und Abfallwirtschaft 2016, 68, 146–153. [Google Scholar] [CrossRef]
- Naudascher, E.; Rockwell, D. Flow-Induced Vibrations: An Engineering Guide; CRC Press: Boca Raton, FL, USA, 1993; ISBN 978-0486442822. [Google Scholar]
- Tanida, Y.; Okajima, A.; Watanabe, Y. Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 1973, 61, 769–784. [Google Scholar] [CrossRef]
- Raynal, S.; Chatellier, L.; Courret, D.; Larinier, M.; David, L. Streamwise bars in fish-friendly angled trashracks. J. Hydraul. Res. 2013, 52, 426–431. [Google Scholar] [CrossRef]

| Parameter | Rods | Cables |
|---|---|---|
| Bar diameter s (mm) | 5 | 5 |
| * Spacing b (mm) | 5, 10, 15 | 5, 10, 15 |
| * Angle α (°) | 90, 45, 30 | 40, 30, 20 |
| * Discharge Q (l s−1) | 50–200 | 80–230 |
| Bar shape coefficient (-) | 1.79 | 1.79 |
| (-) | 0.33, 0.5, 1,0 | 0.33, 0.5, 1.0 |
| Blockage ratio p (-) | 0.25, 0.33, 0.5 | 0.25, 0.33, 0.5 |
| Bar length l (m) | 0.80, 1.24, 1.60 | 1.25, 1.60, 2.34 |
| Approach velocity v (m s−1) | 0.16–0.63 | 0.25–0.72 |
| Bar–Reynolds-No. (-) | 750–3000 | 1250–3500 |
| Reynolds-No. (-) | 31,000–125,000 | 50,000–144,000 |
| Froude F (-) | 0.08–0.3 | 0.13–0.36 |
| US1 | US2 | US3 | US4 | US5 | US6 | US7 | PG | US8 | |
|---|---|---|---|---|---|---|---|---|---|
| x (m) | 5.3 | 6.5 | 7.5 | 8.3 | 11.3 | 13.7 | 16.1 | 17 | 17.3 |
| CBTR | FFF | Difference | |||||
|---|---|---|---|---|---|---|---|
| p (-) | α (°) | (-) | p (-) | α (°) | (-) | (-) | (%) |
| 0.25 | 45 | 0.198 | 0.25 | 20 | 0.075 | - | - |
| 0.33 | 45 | 0.37 | 0.33 | 20 | 0.162 | - | - |
| 0.50 | 45 | 0.957 | 0.50 | 20 | 0.385 | - | - |
| 0.25 | 30 | 0.146 | 0.25 | 30 | 0.148 | 0.002 | 1.4% |
| 0.33 | 30 | 0.242 | 0.33 | 30 | 0.322 | 0.08 | 33.1% |
| 0.50 | 30 | 0.533 | 0.50 | 30 | 0.818 | 0.285 | 53.5% |
| 0.25 | 90 | 0.449 | 0.25 | 40 | 0.305 | - | - |
| 0.33 | 90 | 0.775 | 0.33 | 40 | 0.488 | - | - |
| 0.50 | 90 | 1.884 | 0.50 | 40 | 1.295 | - | - |
| CBTR | 1.80 | 1.3 | 1.7 | 0.9904 | 0.0414 |
| FFF | 3.19 | 1.44 | 1.96 | 0.9861 | 0.0006 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böttcher, H.; Gabl, R.; Aufleger, M. Experimental Hydraulic Investigation of Angled Fish Protection Systems—Comparison of Circular Bars and Cables. Water 2019, 11, 1056. https://doi.org/10.3390/w11051056
Böttcher H, Gabl R, Aufleger M. Experimental Hydraulic Investigation of Angled Fish Protection Systems—Comparison of Circular Bars and Cables. Water. 2019; 11(5):1056. https://doi.org/10.3390/w11051056
Chicago/Turabian StyleBöttcher, Heidi, Roman Gabl, and Markus Aufleger. 2019. "Experimental Hydraulic Investigation of Angled Fish Protection Systems—Comparison of Circular Bars and Cables" Water 11, no. 5: 1056. https://doi.org/10.3390/w11051056
APA StyleBöttcher, H., Gabl, R., & Aufleger, M. (2019). Experimental Hydraulic Investigation of Angled Fish Protection Systems—Comparison of Circular Bars and Cables. Water, 11(5), 1056. https://doi.org/10.3390/w11051056







