Abstract
A hydrological model was integrated with a computational fluid dynamics (CFD) model to determine bacteria levels distributed throughout the Inverness stormwater pond in Calgary, Alberta. The Soil Conservation Service (SCS) curve number model was used as the basis of the hydrological model to generate flow rates from the watershed draining into the pond. These flow rates were then used as input for the CFD model simulations that solved the Reynolds-Averaged Navier-Stokes (RANS) equations with k-ɛ turbulence model. E. coli, the most commonly used fecal indicator bacteria for water quality research, was represented in the model by passive scalars with different decay rates for free bacteria and attached bacteria. Results show good agreement with measured data in each stage of the simulations. The middle of the west wing of the pond was found to be the best spot for extracting water for reuse because it had the lowest level of bacteria both during and after storm events. In addition, only one of the four sediment forebays was found efficient in trapping bacteria.
1. Introduction
In recent decades stormwater has been considered as an alternative water source for reuse, specifically for applications that need less than pristine water quality. Reusing stormwater is more critical in water-scarce regions and regions where rainfall patterns and rainfall frequencies are changing [1]. Several regions are trying to reuse stormwater as a sustainable method of water resources management; thus, prompting research into the feasibility of reusing stormwater from a water quality perspective [2].
Although stormwater ponds are built with the primary objective of reducing runoff quantities in order to protect urban areas against flooding, they also improve the quality of stormwater as well [1]. The stormwater quality within a pond varies both spatially and temporally and is not only a function of the quality of the influent but also a function of local hydrological conditions and on the pond’s design [3,4]. A water quality study of a very large stormwater pond in Calgary, Alberta, Canada, showed that the quality of stormwater in the pond observed over a three year period did meet the irrigation water quality requirements but only under certain circumstances [2]. Thus, stormwater recycling with pond water often requires continuous or intermittent water quality monitoring of the pond water in order to remain compliant with local regulations. Highly distributed water quality sampling in stormwater ponds is often impractical due to the sizes of these ponds and the cost. In addition, most ponds are not designed with reuse in mind and the extraction point is often located in an ad hoc fashion and possibly in a region of the pond which has higher pollution levels relative to the rest of the pond because of local hydrodynamic conditions. If retrofitting a pond with the intent to recycle the water, the municipality could undertake a water quality sampling program that collected samples distributed throughout the pond over a period of time in order to identify the optimum location for extracting the “cleanest” water in the pond (assuming there is no treatment of this water). A more cost-effective alternative is to develop a physical model to estimate the bacteria level in the pond that incorporates the factors leading to bacterial contamination of stormwater in retention ponds.
Water quality is impaired when mobilized sources of contaminants are transported away from their original location by runoff and discharged in aquatic environments [5,6]. Fine particles are either detached from the soil or washed off an impervious surface [7]. Determining levels of pathogenic microorganisms is expensive and difficult due to their large diversity; thus, microbiological water quality monitoring procedures often use fecal indicator bacteria (FIB). FIB are present in feces of human and warm-blooded animals in large numbers and can be easily detected [8]. Total coliforms (TC) and fecal coliforms (FC) were considered the main group of FIB during the twentieth century. However, nowadays, Escherichia coli (E. coli) and intestinal enterococci (IE) are enumerated and considered as FIB because some water-related epidemiological studies have shown that they are better bacterial indicators for predicting sanitary risk [9,10].
The aim of microbiological water quality monitoring of stormwater ponds is primarily to assess the level of fecal contamination in an aquatic system. This contamination varies spatially and temporally throughout the pond and, therefore, very large data sets must be collected to enable an adequate understanding of contamination levels and the processes leading to the degree of pollution in the system. Collecting such a large data set is often intractable, and thus models are often the only feasible approach for gaining greater insight into aquatic ecosystem processes. Two main types of models have been proposed to estimate bacterial levels in aquatic environments: data-driven models, which are also considered black box models, and process-based models [11].
Data-driven models use statistical methods or computational intelligence and machine learning to relate the involved parameters to the state variables (input, internal and output variables) with only a limited number of assumptions about the physical behavior of the system. In contrast, process-based methods predict the FIB concentration based on the mathematical description of sources, sinks, and internal processes influencing FIB levels. The fundamental principle underlying process-based models is conservational equations. The most important factors influencing microorganism fate in the aquatic environment are (i) environmental parameters, and (ii) whether or not they are attached to particles [11]. Few estimates of the percentage of particles with attached bacteria in any collected stormwater sample can be found in the literature. One study found up to 10–28% and 22–30% of fecal coliform and E. coli, respectively, were associated with suspended solids in stormflow samples at the mouth of a canal discharging water to a lake with brackish water [12]. Another study found that 30–55% of both fecal coliform and E. coli were attached to sediment particles in stormwater samples [13].
The fate and transport of bacteria depend heavily on the attachment to suspended solids. Attachment to sediment protects bacteria from some processes that may accelerate death and decay, such as sunlight and predation. Thus, any modelling should use different decay rates for bacteria attached to sediment vs. free-floating bacteria. For example, the decay rate of free-floating E. coli was considered to be twice that of E. coli attached to sediment in a study in the Scheldt drainage network in Belgium [14]. In another study in the Blackstone River watershed in Massachusetts, the ratio of the decay rate of free-floating bacteria to attached bacteria was considered to be 4 [15]. Some studies even assumed that attached pathogens did not decay at all [11].
The fate of bacteria is most commonly modeled by first-order kinetic decay, and this first-order model was used to study the efficiency of waste stabilization ponds. Shilton [16] used a pulse tracer study incorporated with computational fluid dynamics (CFD) to find the retention time of a waste stabilization pond in order to use the first-order kinetic decay based on the retention time [16]. In another study on an anaerobic lagoon, decay was calculated based on the retention time resulting from CFD simulations [17]. In both the study of the waste stabilization pond [16] and the anaerobic lagoon, the objective was only to study the inlet and outlet bacteria concentrations, and they neglected to consider variation within the body. In addition, in both of the studies, the simulation was assumed to be steady-state. Therefore, the retention time, which did not change with time could be an indicator of bacteria concentration. Two other studies on waste stabilization ponds used tracers integrated with CFD simulations to study different configurations of baffles [18,19]. They implemented first-order kinetic decay by a source term in the transport equation of the tracer. All of the abovementioned studies simulated the flow as steady-state and neglected wind. The fluid flow and bacteria fate and transport in stormwater ponds are intrinsically unsteady. Also, the wind cannot be neglected. In addition, the main goal of the present study is to study bacteria concentration within stormwater ponds for the purposes of determining the optimum point at which water may be withdrawn for reuse—the optimum point is that location with the cleanest water and having the lowest level of bacteria concentrations.
In the present study, a comprehensive model was developed that integrates a hydrological model for a catchment draining to a stormwater pond, with a computational fluid dynamics (CFD) model simulating the pond’s hydrodynamics. The results of the hydrological model were used as inputs to the CFD simulation. The model results are validated against data collected at the pond. The overall goal of this paper was to enhance knowledge of bacteria fate and transport in stormwater ponds. Furthermore, the developed modeling approach leading to this enhanced understanding may ultimately be used as a tool to evaluate the capacity for a stormwater pond as a candidate for reuse and/or the need for the modification/retrofit. In addition, it may provide designers and planners with guidance to define standards for stormwater reuse.
2. Materials
2.1. Study Area
The City of Calgary is a semi-arid city in Alberta, Canada, with many stormwater ponds that are being considered as candidate sources of stormwater reuse for irrigating parkland and other public lands during the irrigation season [20]. The Inverness pond is one of the largest stormwater ponds in Calgary and is located in the southeast quadrant of the city. It contains approximately 235,000 m3 of water at the permanent water level. Seven inlets convey stormwater runoff from 415 ha of catchment area into the pond. Figure 1 shows the pond and the locations of the inlets and outlets. All of the inlets are submerged except for I1. Outlet O1 at the west wing of the pond is the main outlet of the pond and is a 1.5 m diameter concrete pipe. I4 inlet, located at the south wing, conveys water from the largest subbasin of the catchment, which is 257.97 ha. The second largest subbasin corresponds to I3 inlet with an area of 89.52 ha. In addition, there are four sediment forebays located in front of I2, I3, I4 and I5 inlets. Table 1 shows the subbasin area and design parameters corresponding to each inlet.
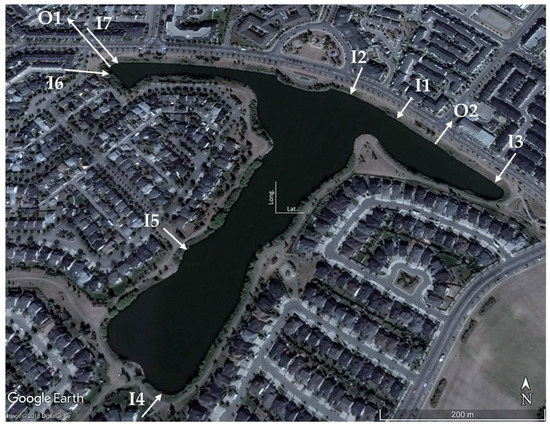
Figure 1.
Arial schematic of Inverness pond showing the location of inlets and outlets (base map from Google Earth (50°54′39.4″ N 113°57′46.2″ W at white cross-hairs at center), arrows and texts added by author).

Table 1.
Inlet and outlet parameters of the Inverness stormwater pond.
2.2. Data Collection
Over a three-year data collection campaign, several data were collected within and around the pond. Water quality and flow rate data collected during several rain events in the 2007 irrigation season were taken at a skimming manhole located just upstream of the I5 inlet. The water quality data included FIB level (E. coli, FC, and total coliform), total suspended solid (TSS), turbidity, pH, and dissolved oxygen (DO) [20]. Rainfall data in 5-min intervals were acquired from the City of Calgary (rain gauge #26 located 1 km north of the study site in McKenzie Towne) and wind data were extracted from the Calgary International Airport. Five rain events documented in 2007 were used in this research. Three of these were lower intensity events leading to moderate flow rates (on 28 May, 26 August and 20 September 2007), while the other two (6 June and 12 September 2007) were high-intensity events leading to large flow rates into the pond. The rain event data are tabulated in Table 2.

Table 2.
Rainfall data of the events in 2007.
An autosampler with 24 pre-sterilized bottles was placed inside the skimming manhole and collected samples for bacteriological analysis once triggered by a rain gauge. The autosampler was programmed to collect 12 samples (two bottles per sample) during long events, and less than 12 samples were analyzed for short duration events. The samples were collected at unequal intervals (3 to 50 min intervals), and much attention was paid to collect samples more frequently in the early stages of the rain event in order to catch the first flush effect. The water samples were recovered right after rain events or very early the next morning in case rain events occurred at night. The samples were packed with ice and analyzed at the Alberta Provincial Laboratory for Public Health by assaying microorganisms using the membrane method [20].
3. Methods
The model is comprised of a hydrological component that simulates stormwater runoff feed into the CFD, which simulates the hydrodynamics and predicts the bacteria levels within a water body. The modeling approach was formulated in a way in which E. coli are primarily discharged into the pond through contaminated stormwater runoff (water fowl droppings from the surface were not considered) and E. coli concentrations were affected by the biological fate of E. coli and pond hydrodynamics, which were in turn affected by meteorology and pond bathymetry. Studies in the literature have revealed that the concentration of bacteria is highly dependent on land use-in particular, the percentage of imperviousness [21]. Developed areas, which have more impervious areas, had elevated increases in E. coli concentrations in runoff [22] as opposed to less developed areas. In order to provide insight into the relationship between land use and bacteria concentration in runoff, bacteria concentrations were measured during storms in different watersheds with different land uses [23]. They demonstrated the variability in fecal coliform concentrations for different land uses. In the present study, the fraction of bacteria in stormflow corresponding to each land use was calculated using the findings of Schoonover and Lockaby [23]. However, here, all of the land uses except for newly graded land and farmland were considered as urban. Thus, by knowing the fraction of bacteria that could be generated from the area draining into inlet I5, the bacteria load of different inlets was estimated based on the measured data of inlet I5.
3.1. Hydrological Model, Calibration and Validation
The Hydrologic Modeling System (HEC-HMS 4.2.1) (Hydrologic Engineering Center, Davis, CA, USA) [24] was used to simulate stormwater runoff generated by each subbasin and drained into the pond in storm events. In the HEC-HMS, the Soil Conservation Service (SCS) curve number (CN) loss method [25], which is a very common and simple method for runoff estimation [26] was adopted. The SCS-CN model considers precipitation excess as a function of cumulative precipitation, soil cover, land use, and antecedent moisture. Precipitation excess was estimated by Equation (1):
where Pe is the accumulated rainfall excess (mm) at time t; P is accumulated rainfall depth (mm) at time t; S is the potential maximum retention (mm); Ia is the initial abstraction (mm), where Ia = 0.2S. Here, S is a function of the CN, which is a function of watershed characteristics, and was calculated by Equation (2) [27]:
The CN number of each subbasin was initially estimated based on the land uses within each subbasin. The time step of the HEC-HMS model was set at 5 min. The runoff at I5, measured in the event on 6 June 2007, was employed to adjust the initial CN of this subbasin aiming to reproduce the runoff well. Accordingly, the CN of other subbasins was modified using the difference between the adjusted CN number for I5 subbasin and its initial CN.
3.2. CFD Simulations
This paper adopted Reynolds averaged Navier Stokes (RANS) equations as follows:
where the velocity decomposed into mean velocity and velocity fluctuation (); T is period of time (s); ρ is density (kg/m3); t is time; p is pressure (pa); is kinematic viscosity (m2/s); is an axis of the Cartesian coordinate system, and i,j = 1,2,3 are indices indicating the three axes in the coordinate system. The term is called Reynold’s stress term [28]. Since the popular k-ɛ turbulence model has been successfully applied to simulate water body flow fields [29,30] in this study the k-ɛ turbulence model [31] was used to calculate the Reynold’s stress terms. The turbulence model is not detailed here. The fundamentals of CFD and turbulence modeling can be found in Versteeg and Malalasekera [32].
Kunkel et al. [33] studied the attachment of E. coli to particles in stormwater. The study showed that E. coli appeared to attach predominantly to fine particles (<4 µm), while a further study on attachment to smaller particles was recommended [33]. Another study on the attachment of E. coli showed that most of them attached to particles smaller than 2 µm [34]. The City of Calgary characterizes the particles in stormwater and suggests the settling velocity of 0.00592 (mm/s) for small particles (<10 µm) [1]. Using Stokes relation for settling velocity [35], the settling velocity of finer particles (<2 µm) can be estimated using:
where ws is settling velocity (m/s); ρp and ρf are particle and fluid density (kg/m3), respectively; dp is particle diameter (m); g is gravitational acceleration (m/s2). This relation is valid for small Reynolds numbers (Re < 1) [36]. With regard to the settling velocity of small particles, this condition was certainly satisfied in the Inverness pond [1]. The calculated settling velocity for the very fine particles (<2 µm) was 0.001 mm/s using the Stokes relation. This suggests that the attached bacteria settle less than 9 cm in 24 h. Therefore, it was assumed that all the bacteria (i.e., free-floating and attached E. coli) remain in the water column during the simulation. Accordingly, bacteria (both attached and free-floating bacteria) were modeled as passive scalars, which are massless particles that do not affect the physical properties of the flow field.
The passive scalar transport equation was solved for the transport of both free-floating and attached E. coli. The transport equation for a passive scalar, is:
where t is time (s); V is volume (m3); A is area (m2); i is the component index; ji is diffusion flux (kg/m2⋅s); is source term (kg/m2⋅s).
The fate of bacteria has been modeled using a negative value for the source term in the passive scalar transport equation in previous studies on waste stabilization ponds [18,19]. This approach is, however, not appropriate for stormwater ponds due to two reasons. Firstly, the flow field and bacteria transport in stormwater ponds are intrinsically unsteady; thus, the location and strength of the sources cannot be determined. Secondly, bacteria concentrations in some spots of stormwater ponds are very low, so a general source, representing decay over the entire domain, might cause negative bacteria concentrations which are not physically feasible. Therefore, in this paper, the transport of bacteria was calculated with Equation (6), while the fate of bacteria was modeled separately.
A finite volume discretization scheme was used to discretize Equations (3) and (6), and the turbulence model equations over the domain to solve the flow field and the concentration of passive scalar. Then, a field function was implemented for the first-order kinetic decay (Equation (7)) for the free-floating portion of bacteria and added the concentrations of both attached and the remaining free-floating bacteria at each computational cell. Characklis et al. [13] found that 30–55% of bacteria attach to sediments in stormwater, whereas the other study [37] applied a higher value in the range (50%). Therefore, in this paper, it was assumed that 50% of bacteria are attached to sediments and do not decay. Decay is calculated using Equation (7).
where N and N0 are the numbers of indicator bacteria at time t and at t = 0, respectively; µ is the decay rate (s−1) [38]. The decay rate of E. coli was calculated with the following relationship that has been used in several studies [14,39] in the literature:
where k20 is the decay rate of E. coli at 20 °C and T is water temperature (°C). A value of 1.25 × 10−5 s−1 was proposed for k20 of E. coli in the water column; average measured data were used for temperature in this paper.
3.2.1. Boundary and Initial Conditions
The effect of wind on the flow field was not negligible considering the size of the study pond. Since the wind vector was not stationary with time, a dynamic boundary condition of wind on the pond surface was defined. The effect of the wind was applied as a velocity vector on the top layer of the pond. The velocity of the top layer of the pond was calculated from the wind velocity based on the experimental data from a study by Banner and Peirson [40], which measured velocity at the top layers of water bodies under windy conditions.
The boundary condition of the inlets was set as the “velocity inlet” with parameters changing with time including velocity and E. coli concentration. A time variable boundary condition was also defined which linearly interpolated the value of bacteria concentration and velocity between the interval that data were collected. “Pressure outlet” and “stationary wall” were set as the boundary conditions for the outlets and the bottom of the pond, respectively.
A steady-state simulation in no storm conditions and with an average wind was simulated and its result (flow field) was used as the initial condition for the main simulations. The main simulation is unsteady. Using the steady simulation’s results also accelerated the convergence. The unsteady simulations started one hour before the storm in order to let the flow field form based on the real wind data before the storm.
3.2.2. Other CFD Settings
The domain of the CFD simulation was sketched based on the bathymetric data of the pond comprised of approximately 33000 GIS points. AutoCAD CIVIL 3D 2018 was used for sketching the domain that includes the water body of the pond and a few meters (10 m on average) of inlet and outlet pipes. A grid was made that is more highly clustered close to the inlets, outlets and water edges. In the CFD simulations, grid dependence was checked by comparing velocity from the simulation with different numbers of grids. An unstructured grid with hexahedral cells and a number of 1.5 million was found sufficiently fine and the corresponding results were presented. Using finite volume discretization, RANS equations with the k-ɛ turbulence model were solved in an unsteady-state with the time step of 0.5 s and 24 inner iterations between each time step. The time step was selected by an approach similar to the grid independence comparison but the number of inner iterations was chosen based on the convergence trend of the solution. The pond was simulated from 1 h before the start of an event until 24 h after the end of the event. The simulations were run on Cedar High-Performance Computer, located at Simon Fraser University, Vancouver, BC, Canada, with 576 GB of memory and 192 computational cores (each core has two CPUs of 2.1 GHz). The CFD simulations were performed by using commercial CFD code STAR-CCM+ 12.04.011 [41].
4. Results and Discussions
4.1. Hydrological Modeling Performance
The hydrological model was manually calibrated with the measured data in inlet I5 on 6 June 2007 and then validated on four other events: 28 May, 26 August, 12 September, and 20 September 2007. During the calibration, the error in the total volume of water between prediction and observation was adopted to evaluate model performance, as the total volume of water entering the pond was considered to be the key factor that determines bacteria loading.
The CN number for the subbasin draining to I5 was calculated to be 11% less than the initially calculated CN value in the calibration of the 6 June 2007 event. Noting this, all other CN numbers were decreased by 11%. Table 3 shows the CN numbers for the different subbasins before and after calibration of the model. Lag time was also calibrated at the same time, and a 30 min lag time was found to be optimal. In addition, an attempt was made to calibrate initial abstraction; however, the default setting (Ia = 0.2S) resulted in the lowest error and was, therefore, left unchanged. Figure 2, Figure 3, Figure 4 and Figure 5 show the modeled and observed hydrographs for the validation events for subbasin I5. The Nash-Sutcliffe model efficiency (NSE), which is a reliable criterion for assessing the goodness of fit of hydrological models [42], and the error in total volume for all events, are tabulated in Table 4. The calibrated CNs (Table 3) were then used to model other subbasins.

Table 3.
Curve numbers of the different subbasins draining to the Inverness pond inlets.
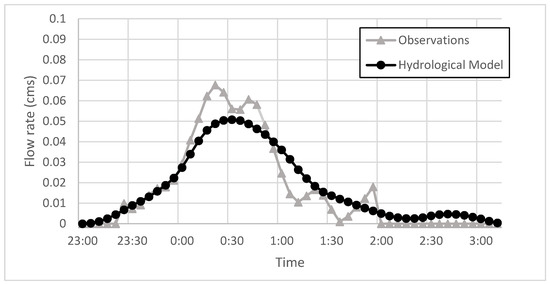
Figure 2.
Modeled and observed hydrographs at I5 inlet of storm event on 28 May 2007.
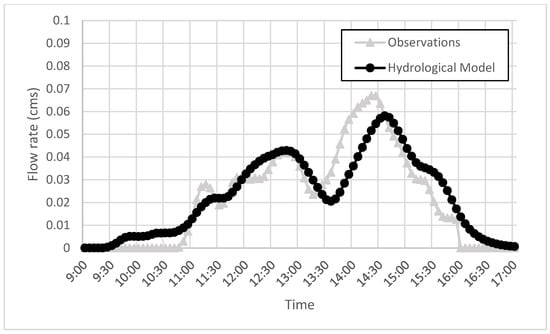
Figure 3.
Modeled and observed hydrographs at I5 inlet of storm event on 26 August 2007.
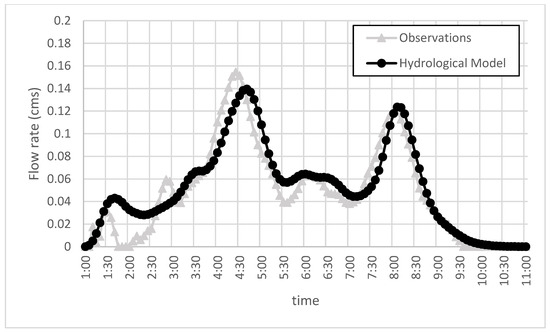
Figure 4.
Modeled and observed hydrographs at I5 inlet of storm event on 12 September 2007.
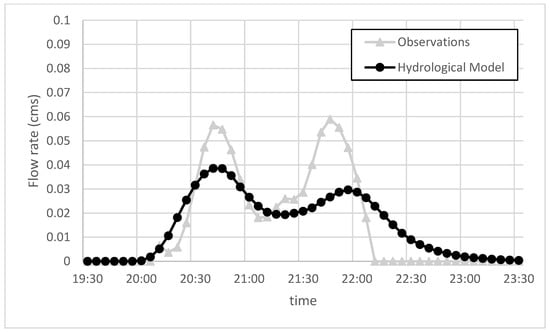
Figure 5.
Modeled and observed hydrographs at I5 inlet of storm event on 20 September 2007.

Table 4.
Model performance in model calibration and validation. The event on 6 June 2007 is the calibration event and all others are validation events.
Results show good agreement between the modeled and measured data. In all of the events except for 20 September 2007, the model slightly overestimated the total volume but the total volume error is less than 10%. The underestimation of the total volume for the event on 20 September 2007 may be due to the excessive moisture in the soil resulting from heavy rains that fell prior to the event; thus, potentially leading to greater runoff generation. However, the Nash-Sutcliffe efficiency in all of the modeled events is reasonable.
4.2. CFD Simulations
The simulation results for the event on 26 August 2007 are detailed and discussed in this section as an example. The concentrations of E. coli on the surface of the pond at different time steps after the rain event are shown in Figure 6. As time passes, bacteria entering from the inlets redistribute in the pond. The flow field was affected by the inlet velocities for the first few hours after the events, but afterwards, the wind was the only parameter affecting the flow field.
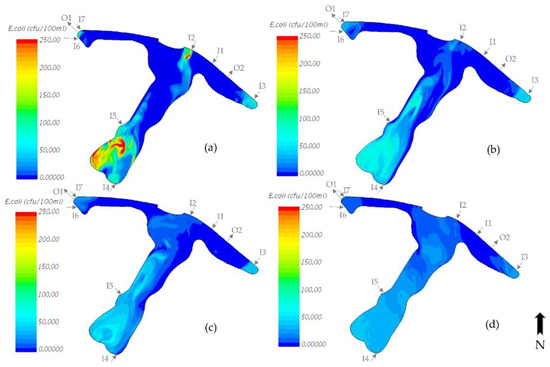
Figure 6.
Contours of E. coli concentration (cfu/100 mL) on the surface of the Inverness pond on (a) 26 August 2007 at 5 p.m., (b) 26 August 2007 at 11 p.m., (c) 27 August 2007 at 5 a.m., and (d) 27 August 2007 at 11 a.m.
The bacteria concentrations in the south wing of the pond were greater as compared with the other two wings (the east and west wings). There are two inlets (I5 and I4) in the south wing. The E. coli concentration is higher in the stormwater runoff entering the pond from inlet I5 than all other inlets; while bacteria loading from I4 is highest as it drains the largest area (Table 1). For example, the E. coli concentration in the storm runoff from I5 on 26 August 2007 at 2 p.m. (during the storm) was 2100 cfu/100mL, while the storm runoff from I4 had a concentration of 1 038 cfu/100 mL. However, the flow rates of the inlets at that time were 0.045 m3/s and 0.39 m3/s for the I5 and I4 inlets, respectively. Therefore, more bacteria mass entered the pond from inlet I4 even though the concentration of bacteria was greater in I5. In addition, a relatively large amount of bacteria entered the pond from inlets I3, I7 and I6, but most of the bacteria that came from I7 and I6 immediately exited the pond through outlet O1, because these two inlets are in proximity to the outlet. Therefore, they do not have a significant effect on the bacteria level in the pond. In general, inlets I4, I3 and I5 had the most significant effect on the bacteria levels in the pond.
Figure 7 shows the vertical profile of E. coli distribution in the pond at 6 h after the end of the storm. It reveals that the bacteria concentration also changes with depth. As illustrated in Figure 7, the maximum concentration of E. coli on the surface barely reached 90 cfu/100 mL. However, the maximum E. coli concentration was more than 120 cfu/100 mL at 2 m depth. In addition, the bacteria in the middle of the pond (where the three wings join) was less distributed at the bottom compared to the surface. The reason is that the direction of the wind had been NE and NNE for the last few hours, so the bacteria escaping from the sediment forebay of inlet I2 could reach the other side where the south wing and the west wing join. In contrast, there was current flow toward the NE and NNE directions at the bottom simply because of mass conservation. This current potentially brought clean water close to the I2 sediment forebay. There was also a downwelling near the bank of the middle of the pond where the south and the west wings join. Generally, the wind causes differences in E. coli distribution in different layers of the water column. E. coli data collected at different depths on five random days between the year 2006 and 2007 [2] reveal that the bacteria concentration changed with depth. However, these data did not show any specific trend, and this is likely an indication of the influence of multiple environmental conditions on the bacteria distribution at various depths.
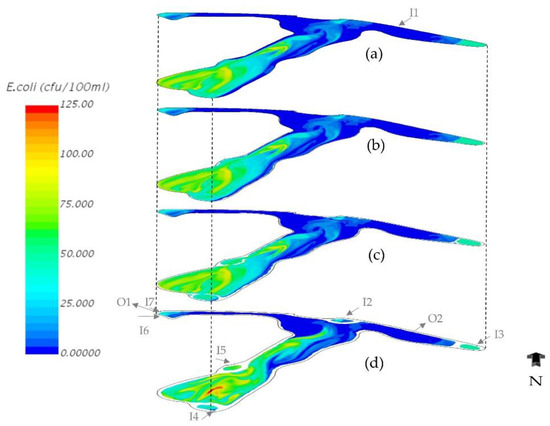
Figure 7.
The vertical profile of E. coli concentration on 26 August 2007 at 11 p.m. (a) on the surface, (b) at 0.5 m below the surface, (c) at 1 m below the surface, and (d) at 2 m below the surface.
The sediment forebay corresponding to I3 was full of bacteria at all depths after the event (Figure 7). The sediment forebay was able to retain bacteria many hours after the event, which resulted in keeping the east wing relatively clean as compared with the south wing. Figure 8 magnifies the contour of E. coli concentration near the sediment forebays at the surface on 27 August 2007 at 2 a.m. It also confirms that the sediment forebay of I3 outperforms the forebay of other inlets. As illustrated in Figure 8, the concentration of E. coli in the sediment forebays of inlets I4 and I5 appears to be similar or even slightly less than that in the region outside the forebays. This reveals that the bacteria entering these forebays during the storm were promptly discharged out of the forebays and consequently increased the E. coli concentration in their nearby regions.
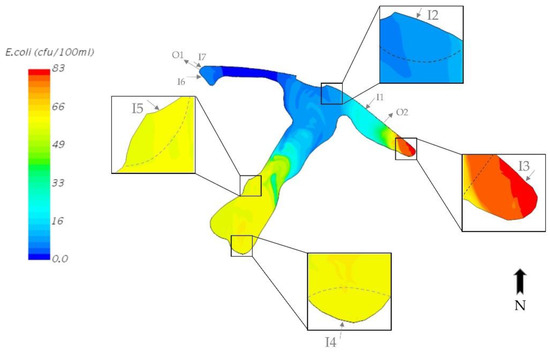
Figure 8.
E. coli distribution on the surface 27 August 2007 at 2 a.m. (9 h after the end of the storm).
The design of sediment forebays, such as their configuration and size, determines their efficiency in trapping bacteria. Figure 9 shows streamlines coming out from the inlets and spreading throughout the pond during the storm. The streamlines from I4 continue straight out of the forebay, which means the bacteria were transported into the pond. One reason is that the size of the forebay was not large enough to fit a circulation proportional to the high flow rate of the I4 inlet. Another reason may be the configuration of the inlet and sediment forebay. The direction of the streamline from I4 and the corresponding sediment forebay were perpendicular to each other (i.e., they were in front of each other), so the water jet coming out of the inlet easily escaped the forebay without circulating. The situation was the same in the sediment forebays corresponding to the inlets I2 and I5. However, their size was proportional to their flow rate. The sediment forebay corresponding to the inlet I3 had the best configuration since the direction of streamlines coming out of the inlet was parallel to the forebay. Thus, the bacteria coming from the inlet had no way but to circulate and in the long term, they die, which kept the east wing relatively clean. In addition, the size of the forebay was large enough to fit two large eddies.
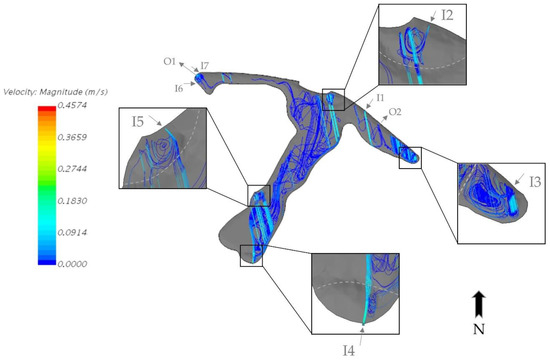
Figure 9.
Velocity streamlines on 26 August 2007 at 3 p.m. (during the storm).
During the data collection campaign, surface grab samples were collected from six different sites at the pond over several days [2]. All of the samples were collected at an average depth of 15 cm. One of the sample collection days was after a day with heavy rain. On 10 September 2005, 68 mm of rain fell and on the next day, water samples were collected from the six sites. Although much greater rain fell on 10 September 2005 than in the simulated events from 2007, it provided an interesting case for validation due to the dominant effect of rain on the bacteria distribution. The initial bacteria level in the pond before an event can influence the final bacteria levels after an event, particularly for small, low rainfall events. However, for high rainfall events, the majority of bacteria is transported into the pond with the storm runoff, and the initial bacteria level is a far smaller proportion of the total bacteria level. In this paper, it was assumed that the initial bacteria level was negligible, and only the effect of the storm was studied. Thus, the modelling results can be compared with the collected data on 10 September 2005. Although it was noted that due to a lack of data it was difficult to validate the process-based FIB methods thoroughly [11], a comparison was done between the different events using a non-dimensional number. The non-dimensional number was computed as the ratio of E. coli concentration at a site to the maximum E. coli concentration among all of the six sites at a certain time. Thus, the non-dimensional number at the site where E. coli concentration was a maximum was one. The number was calculated for the individual modeled events, and then the average was taken for each site. Figure 10 shows the non-dimensional number at the six sites for the measured data and the average of the simulated events with its variation range. Simulation results show a good agreement with the measured data in recognizing hot spots (spots with a high concentration of bacteria) and spots with the lowest level of bacteria. The variation in the non-dimensional number in the east and west wings were higher than that in the south wing and in the middle of the pond. This may be due to a stronger influence from meteorological factors such as wind and rain at the tip of the east wing and the tip of the west wing. On the other hand, the low variation in the calculated data in the south wing and their high values show that the south wing always had the highest bacteria levels in the pond. Therefore, it is not recommended to extract water for reuse from the south wing.
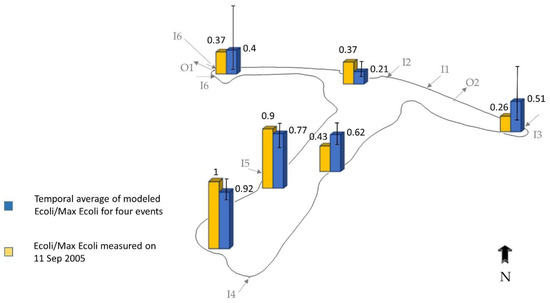
Figure 10.
Non-dimensional E. coli concentration 15 cm below the surface.
In addition, both measured and calculated data show that the middle of the pond, where the three wings join, had the lowest level of bacteria among the six sites; this site was a reliable spot for water extraction due to low concentrations of bacteria and low variability in the calculated data. There were no collected data for the middle of the west wing; however, simulation results show that this spot had the lowest velocity and E. coli concentrations in the pond. In a region with low velocity, fewer bacteria can enter. In addition, even if some bacteria enter a low-velocity region, most of them die due to high retention time in the region, which keep the bacteria concentration relatively low. In addition, the west wing has two inlets and an outlet all located at the tip of the wing. Thus, most of the bacteria that were discharged to the wing by the inlets exited the pond promptly. Therefore, the middle of the west wing can be considered as a potential location for water extraction. However, more data should be collected from the entire pond for a more comprehensive validation. In addition, further modeling studies after rain events are recommended when more data are available. More experimental and modeling studies need to be conducted in order to study the effect of sedimentation on bacteria transport in the pond, which was assumed to be negligible in this paper.
5. Conclusions
An integrated hydrological-CFD model was developed to simulate bacteria concentrations within the Inverness stormwater pond in Calgary, Alberta, in order to locate the best (cleanest) locations within the pond to extract water for potential reuse. The integrated model was calibrated at one inlet with observed flow rate data in order to estimate the flow rates and bacteria levels at other inlets. The flow rate and bacteria concentration at the inlets were implemented as boundary conditions for an unsteady CFD simulation to determine the distribution of bacteria in the pond. The bacteria concentration distribution in Inverness pond was simulated both during and after four rain events using the integrated model. Results showed a good agreement with collected data from six different points in the pond, indicating that the model can be successfully used to model fate and transport of bacteria in stormwater ponds. It was found that the wind plays a crucial role in forming the flow field in the pond, which affects the bacteria distribution. In addition, one of the sediment forebays, located in the east wing of the pond, successfully trapped large amounts of bacteria until death occurred. However, other sediment forebays were found ineffective. The middle of the west wing was found to be the best location for extracting water because it showed the lowest levels of bacteria during the simulation of the pond both in and after the events.
Author Contributions
Conceptualization, modeling, simulation, writing, F.A.; supervision, investigation, reviewing, editing, and fund acquisition, C.V., J.H.; fund acquisition, project administration, and reviewing, N.F.N.
Funding
This research was funded by Alberta Innovates, grant number RES#0030866.
Acknowledgments
The authors would like to thank Mostafa Rahimpour for his comments on CFD modeling and Belaid Moa from WestGrid for his technical support on the parallel computation of the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The City of Calgary Water Resources. Stormwater Management and Design Manual; Urban Development Publications: Calgary, AB, Canada, 2011. [Google Scholar]
- He, J.; Valeo, C.; Chu, A.; Neumann, N.F.; Tn, A. Water Quality Assessment in the Application of Stormwater Reuse for Irrigating Public Lands. Water Qual. Res. J. Can. 2008, 43, 93–107. [Google Scholar] [CrossRef]
- Ahilan, S.; Guan, M.; Wright, N.; Sleigh, A.; Allen, D.; Arthur, S.; Haynes, H.; Krivtsov, V. Modelling the long-term suspended sedimentological effects on stormwater pond performance in an urban catchment. J. Hydrol. 2019, 571, 805–818. [Google Scholar] [CrossRef]
- Clevenot, L.; Carré, C.; Pech, P. A Review of the factors that determine whether stormwater ponds are ecological traps and/or high-quality breeding sites for amphibians. Front. Ecol. Evol. 2018, 6, 40. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Bombardelli, F.A.; Pitton, B.J.L.; Oki, L.R.; Haver, D.L.; Young, T.M. Role of sediments in insecticide runoff from urban surfaces: Analysis and modeling. Int. J. Environ. Res. Public Health 2018, 15, 1464. [Google Scholar] [CrossRef]
- Di Modugno, M.; Gioia, A.; Gorgoglione, A.; Iacobellis, V.; la Forgia, G.; Piccinni, A.; Ranieri, E. Build-up/wash-off monitoring and assessment for sustainable management of first flush in an urban area. Sustainability 2015, 7, 5050–5070. [Google Scholar] [CrossRef]
- St-hilaire, A.; Duchesne, S.; Rousseau, A.N. Canadian Water Resources Journal/Revue canadienne Floods and water quality in Canada: A review of the interactions with urbanization, agriculture and forestry. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2016, 41, 277–291. [Google Scholar]
- Borrego, J.J.; Figueras, M.J. Microbiological quality of natural waters. Microbiologia 1997, 13, 413–426. [Google Scholar]
- Leclerc, H.; Mossel, D.A.A.; Edberg, S.C.; Struijk, C.B. Advances in the bacteriology of the coliform group: Their Suitability as Markers of Microbial Water Safety. Annu. Rev. Microbiol. 2001, 55, 201–234. [Google Scholar] [CrossRef]
- Tallon, P.; Magajna, B.; Lofranco, C.; Leung, K.T. Microbial indicators of faecal contamination in water: A current perspective. Water Air. Soil Pollut. 2005, 166, 139–166. [Google Scholar] [CrossRef]
- De Brauwere, A.; Ouattara, N.K.; Servais, P. Modeling Fecal Indicator Bacteria Concentrations in Natural Surface Waters: A Review. Crit. Rev. Environ. Sci. Technol. 2014, 44, 2380–2453. [Google Scholar] [CrossRef]
- Anna, H.; Jeng, C.; Englande, A.J.; Bakeer, R.M.; Bradford, H.B. Impact of urban stormwater runoff on estuarine environmental quality. Estuar. Coast. Shelf Sci. 2005, 63, 513–526. [Google Scholar]
- Characklis, G.W.; Dilts, M.J.; Simmons, O.D.; Likirdopulos, C.A.; Krometis, L.H.; Sobsey, M.D. Microbial partitioning to settleable particles in stormwater. Water Res. 2005, 39, 1773–1782. [Google Scholar] [CrossRef]
- Ouattara, N.K.; de Brauwere, A.; Billen, G.; Servais, P. Modelling faecal contamination in the Scheldt drainage network. J. Mar. Syst. 2013, 128, 77–88. [Google Scholar] [CrossRef]
- Wu, J.; Rees, P.; Storrer, S.; Alderisio, K.; Dorner, S. Fate and transport modeling of potential pathogens: The contribution from sediments. J. Am. Water Resour. Assoc. 2009, 45, 35–44. [Google Scholar] [CrossRef]
- Shilton, A. Potential application of computational fluid dynamics to pond design. Water Sci. Technol. 2000, 42, 327–334. [Google Scholar] [CrossRef]
- Wu, B.; Chen, Z. An integrated physical and biological model for anaerobic lagoons. Bioresour. Technol. 2011, 102, 5032–5038. [Google Scholar] [CrossRef]
- Shilton, A.; Harrison, J. Integration of coliform decay within a CFD (computational fluid dynamic) model of a waste stabilisation pond. Water Sci. Technol. 2003, 45, 205–210. [Google Scholar] [CrossRef]
- Shilton, A.N.; Mara, D.D. CFD (computational fluid dynamics) modelling of baffles for optimizing tropical waste stabilization pond systems. Water Sci. Technol. 2005, 51, 103–106. [Google Scholar] [CrossRef]
- He, J. Reducing the Vulnerability of Water Supply under a Changing Climate: An Assessment of Stormwater Reuse. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2009. [Google Scholar]
- Mallin, M.A.; Williams, K.E.; Esham, E.C.; Lowe, R.P. Effect of human development on bacteriological water quality in coastal watersheds. Ecol. Appl. 2000, 10, 1047–1056. [Google Scholar] [CrossRef]
- Chen, H.J.; Chang, H. Response of discharge, TSS, and E. coli to raifall events in urban, suburban, and rural watersheds. Environ. Sci. Process. Impacts 2014, 16, 2313–2324. [Google Scholar] [CrossRef]
- Schoonover, J.E.; Lockaby, B.G. Land cover impacts on stream nutrients and fecal coliform in the lower Piedmont of West Georgia. J. Hydrol. 2006, 331, 371–382. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Hydrological Modeling System HEC-HMS User’s Manual: Version 4.2; Hydrologic Engineering Center: Davis, CA, USA, 2016. [Google Scholar]
- Mockus, V. Hydrology. In National Engineering Handbook, 2nd ed.; Natural Resources Conservation Service: Washington, DC, USA, 1972; pp. 21.2–21.49. [Google Scholar]
- Teegavarapu, R.S.V.; Chinatalapudi, S. Incorporating Influences of Shallow Groundwater Conditions in Curve Number-Based Runoff Estimation Methods. Water Resour. Manag. 2018, 32, 4313–4327. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Hydrologic Modeling System HEC-HMS Technical Reference Manual; Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
- Graebel, W.P. Advanced Fluid Mechanics, 1st ed.; Academic Press: Oxford, UK, 2007; pp. 233–250. [Google Scholar]
- Abbasi, A.; Annor, F.O.; van de Giesen, N. Investigation of Temperature Dynamics in Small and Shallow Reservoirs. Case Study: Lake Binaba, Upper East Region of Ghana. Water 2016, 8, 84. [Google Scholar] [CrossRef]
- Shilton, A.; Kreegher, S.; Grigg, N. Comparison of Computation Fluid Dynamics Simulation against Tracer Data from a Scale Model and Full-Sized Waste Stabilization Pond. J. Environ. Eng. 2008, 134, 845–850. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–138. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman Scientific and Technical: New York, NY, USA, 1995. [Google Scholar]
- Kunkel, E.A.; Privette, C.V.; Sawyer, C.B.; Hayes, J.C. Attachment of Escherichia coli to fine sediment particles within construction sediment basins. Adv. Biosci. Biotechnol. 2013, 4, 407–414. [Google Scholar] [CrossRef]
- Muirhead, R.W.; Collins, R.P.; Bremer, P.J. Interaction of Escherichia coli and Soil Particles in Runoff. Appl. Environ. Microbiol. 2006, 72, 3406–3411. [Google Scholar] [CrossRef]
- Stokes, G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Phillosophical Soc. 1851, 9, 8–106. [Google Scholar]
- Gu, L.; Dai, B.; Zhu, D.Z.; Hua, Z.; Liu, X.; van Duin, B. Sediment modelling and design optimization for stormwater ponds. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2017, 42, 70–87. [Google Scholar] [CrossRef]
- Bai, S.; Lung, W.S. Modeling sediment impact on the transport of fecal bacteria. Water Res. 2005, 39, 5232–5240. [Google Scholar] [CrossRef]
- Chick, H. An Investigation of the Laws of Disinfections. J. Hyg. 1908, 8, 92–158. [Google Scholar] [CrossRef]
- De Brauwere, A.; Gourgue, O.; de Brye, B.; Servais, P.; Ouattara, N.K.; Deleersnijder, E. Integrated modelling of faecal contamination in a densely populated river-sea continuum (Scheldt River and Estuary). Sci. Total Environ. 2014, 468–469, 31–45. [Google Scholar] [CrossRef]
- Banner, M.L.; Peirson, W.L. Tangential stress beneath wind-driven air–water interfaces. J. Fluid Mech. 1998, 364, 115–145. [Google Scholar] [CrossRef]
- CD-adapco. STAR-CCM+ 12.04.011 User’s Manual; Siemens Product Lifecycle Management Software Inc.: Melville, NY, USA, 2017. [Google Scholar]
- McCuen, R.H.; Knight, Z.; Cutter, G. Evaluation of the Nash-Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).