Identifying Optimal Irrigation Water Needs at District Scale by Using a Physically Based Agro-Hydrological Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. The FLOWS-HAGES Model
- Soil water contents and pressure potentials in the soil profile;
- Water uptake and actual evapotranspiration (actual water needs);
- Solute (e.g., nitrates, pesticides, salts, heavy metals) concentrations in the soil profile;
- Deep percolation water fluxes (return flow to the groundwater) and their quality in terms of solute (solute fluxes);
- Stress periods for each crop.
- To provide effective water requirement data to be used for optimal management of the irrigation network;
- To facilitate the decision-making process on the quantities of water to be allocated to agricultural users;
- To consider the most profitable cropping patterns given water availability restrictions imposed by the existing hydrological systems, and the potential yields reached in each irrigation district according to its productive characteristics, irrigation efficiency, economic scenario and external factors such as agricultural policies;
- To predict the impact of anticipated climate changes on the irrigation system under the current land use and vegetation cover;
- To predict the impact of human-driven changes in the land use on the irrigation system under current climate conditions;
- To predict the impacts on the irrigation system under mixed conditions 4–5.
2.2. Sector 6 of the Capitanata Irrigation Network
2.3. Soil Characterization in Sector 6
2.4. Crop Distribution and Actual Irrigation Volumes (Year 2016)
2.5. Evaluating Model Simulations by Direct Water Content Measurements
3. Results and Discussion
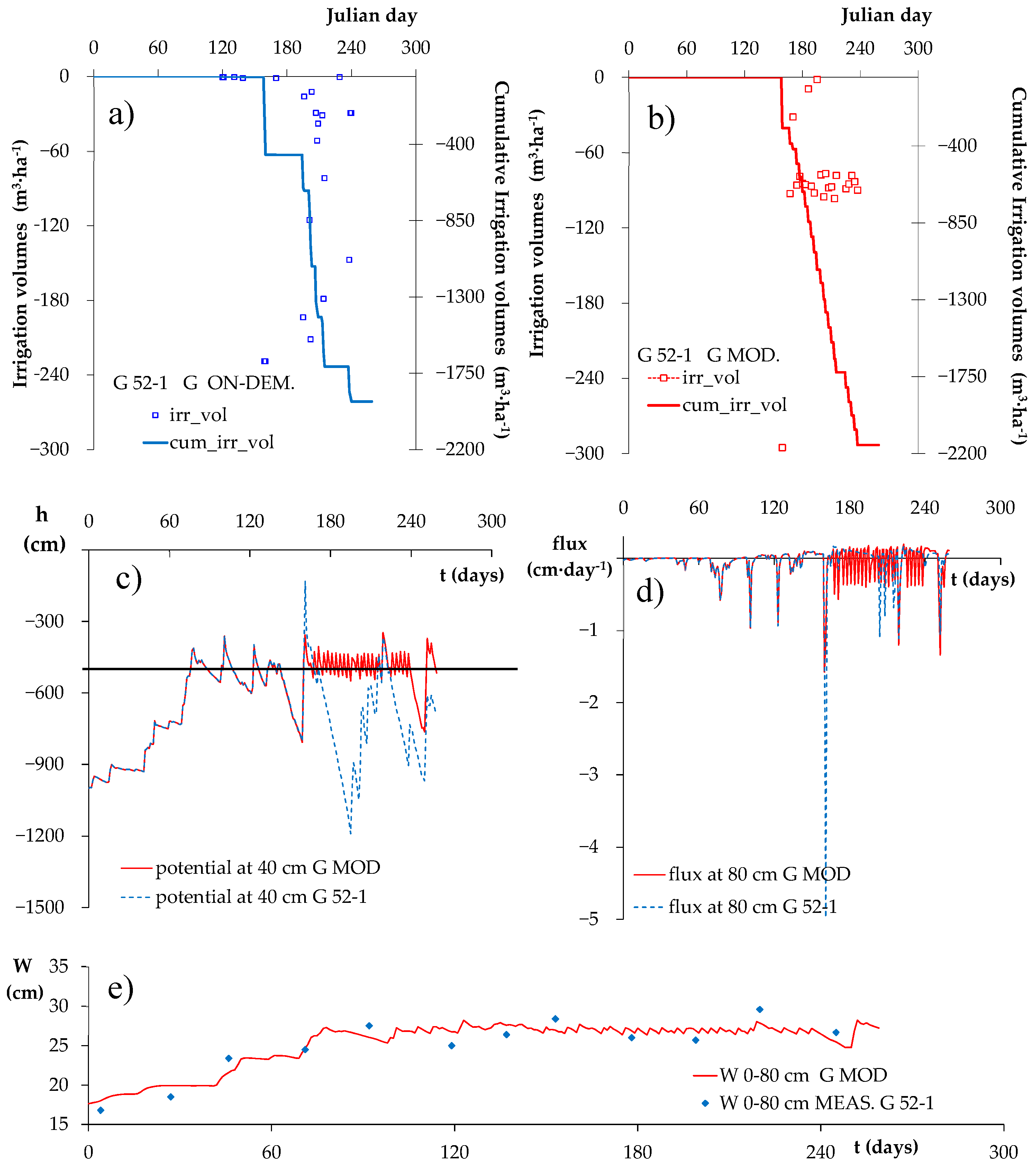
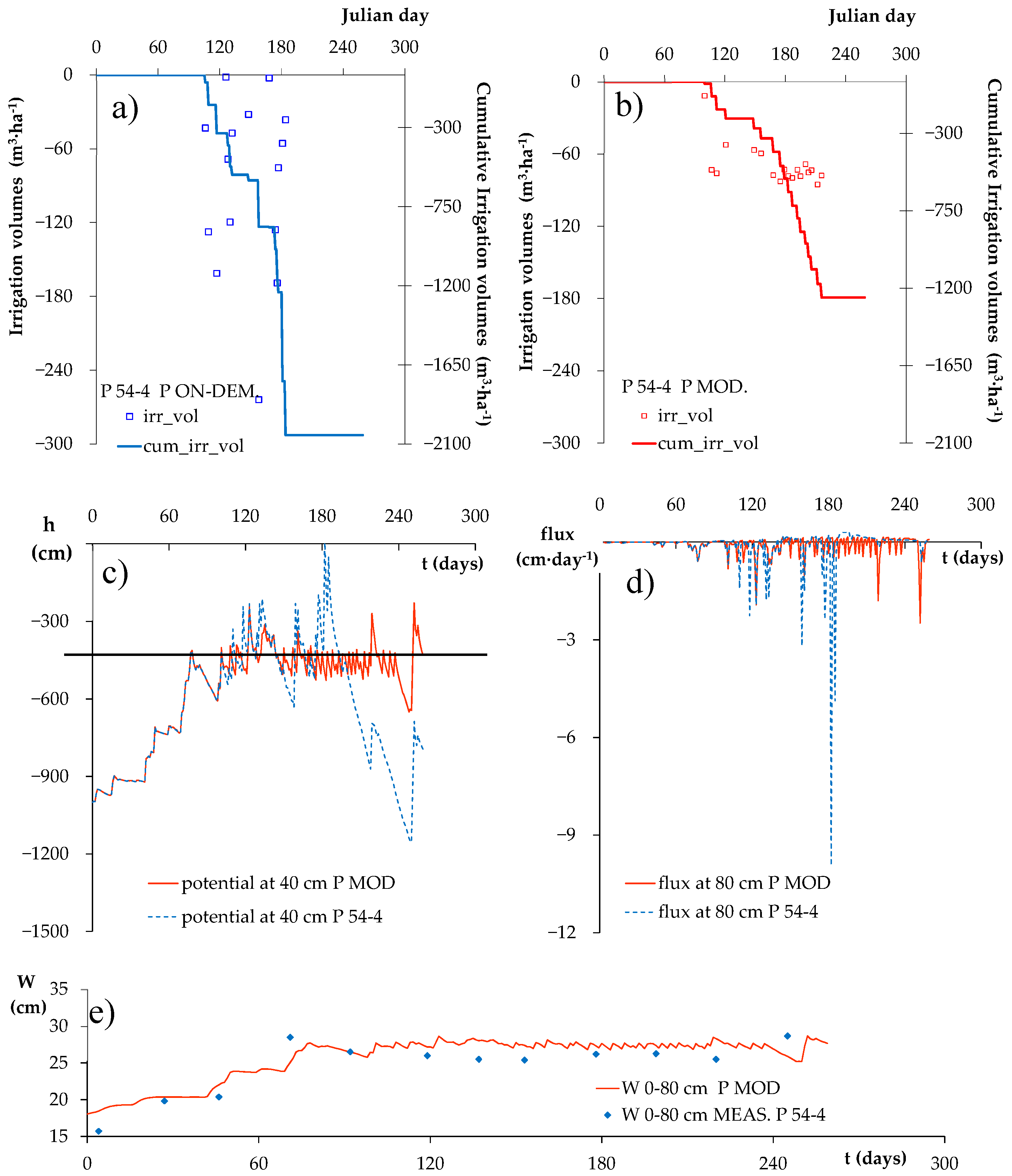
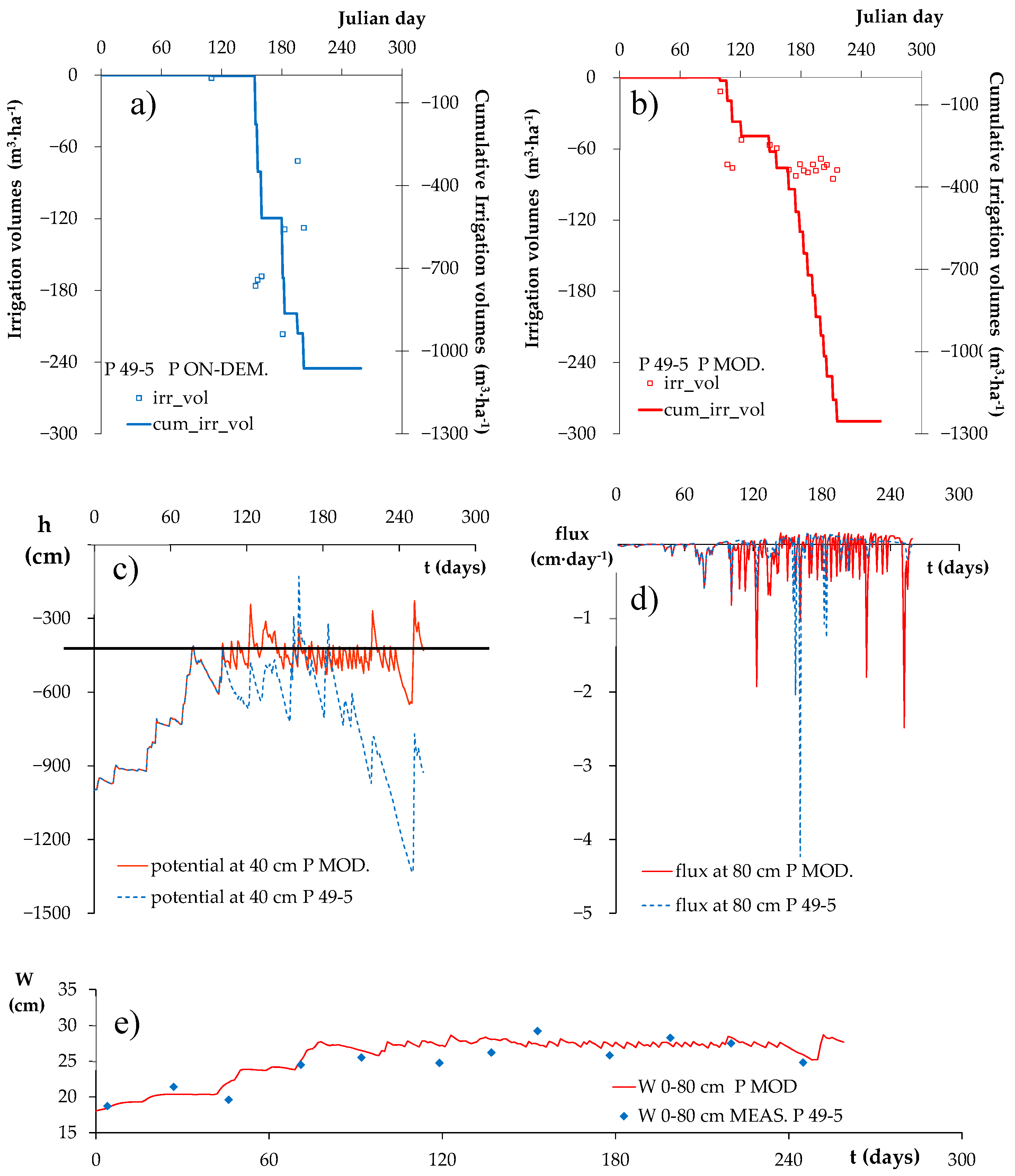
3.1. Irrigation Volumes Measured and Calculated by the Model
3.2. Irrigation Volumes, Pressure Heads in the Root Zone and Deep Percolation Fluxes
3.3. List of Hydrants to be Opened and Efficiency Indices
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. FLOWS-HAGES: Short Model Description
Appendix A.1. Water Flow
Appendix A.2. Solute Transport
Appendix A.3. Hydraulic Properties
Appendix A.4. Root Uptake
Appendix A.5. Calculating the Water Stress Reduction Factor αrw
Appendix A.6. Calculating the Salinity Stress Reduction Factor αrs
Appendix A.7. Combined Water and Salinity Stress
Appendix A.8. Root Density Distribution
Appendix A.9. Solute Sink Term
References
- Blinda, M.; Thivet, G. Ressources et demandes en eau en Méditerranée: Situation et perspectives. Sécheresse 2009, 20, 9–16. [Google Scholar] [CrossRef]
- Hsiao, T.; Steduto, P.; Fereres, E. A systematic and quantitative approach to improve water use efficiency in agriculture. Irrig. Sci. 2007, 25, 209–231. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Sagardoy, J. Performance Analysis of On-Demand Pressurized Irrigation Systems; Food & Agriculture Organization of the United Nations: Rome, Italy, 2000. [Google Scholar] [CrossRef]
- Coppola, A.; Comegna, V.; Basile, A.; Lamaddalena, N.; Severino, G. Darcian preferential water flow and solute transport through bimodal porous systems: Experiments and modelling. J. Contam. Hydrol. 2009, 104, 74–83. [Google Scholar] [CrossRef]
- Coppola, A.; Randazzo, L.A. MatLab code for the transport of water and solutes in unsaturated soils with vegetation. In Tech. Rep. Soil and Contaminant Hydrology Laboratory; University of Basilicata: Potenza, Italy, 2006; Unpublished work. [Google Scholar]
- Coppola, A.; Randazzo, L.; Basile, A.; Fenu, C. FLOWS-HAGES (FLOw of Water and Solutes in Heterogeneous AGri-Environmental Systems): A MatLab Code for the Transport of Water and Solutes in Unsaturated Soils with Vegetation in Heterogenous Systems; D. S. U. o. B. Tech. Rep. Soil and Contaminant Hydrology Laboratory: Potenza, Basilicata, Italy, 2018; in press. [Google Scholar]
- Vogel, T. SWM II-Numerical Model of Two-Dimensional Flow in a Variably Saturated Porous Medium; Wageningen Agricultural University: Wageningen, The Netherlands, 1988. [Google Scholar]
- Gee, G.W.; Or, D. Particle-size analysis. In Methods of soil analysis, Part4. Physical methods. Soil Sci. Soc. Am. Book Ser. 2002, 5, 255–293. [Google Scholar]
- Ankeny, M.; Ahmed, M.; Kaspar, T.; Horton, R. Simple Field Method for Determining Unsaturated Hydraulic Conductivity. Soil Sci. Soc. Am. J. 1991, 55, 467–470. [Google Scholar] [CrossRef]
- Coppola, A.; Basile, A.; Wang, X.; Comegna, V.; Tedeschi, A.; Mele, G.; Comegna, A. Hydrological behaviour of microbiotic crusts on sand dunes: Example from NW China comparing infiltration in crusted and crust-removed soil. Soil Till. Res. 2011, 117, 34–43. [Google Scholar] [CrossRef]
- Basile, A.; Buttafuoco, G.; Mele, G.; Tedeschi, A. Complementary techniques to assess physical properties of a fine soil irrigated with saline water. Environ. Earth Sci. 2012, 66, 1797–1807. [Google Scholar] [CrossRef]
- Lazarovitch, N.; Ben-Gal, A.; Šimůnek, J.; Shani, U. Uniqueness of soil hydraulic parameters determined by a combined Wooding inverse approach. Soil Sci. Soc. Am. J. 2007, 71, 860–865. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Sejna, M. The DISC Computer Software for Analyzing Tension Disc Infiltrometer Data by Parameter Estimation; Version 1.0, US Salinity Laboratory: Riverside, CA, USA, 2000. [Google Scholar]
- Reynolds, D.; Elrick, D. Saturated and field-saturated water flow parameters: Falling head soil core (tank) method. Methods of Soil Analysis, Part 4. Phys. Methods 2002, 5, 809–812. [Google Scholar]
- Dane, J.H.; Hopman, J.W. Water retention and storage. In Methods of Soil Analysis: Part 4—Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 721–738. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Corwin, D.L. Soil electrical conductivity: Effects of soil properties and application to soil salinity appraisal. Commun. Soil Sci. Plant Anal. 1990, 21, 837–860. [Google Scholar] [CrossRef]
- Coppola, A.; Smettem, K.R.; Ajeel, A.; Saeed, A.; Dragonetti, G.; Comegna, A.; Lamaddalena, N.; Vacca, A. Calibration of an electromagnetic induction sensor with time-domain reflectometry data to monitor rootzone electrical conductivity under saline water irrigation. Eur. J. Soil Sci. 2016, 67, 737–748. [Google Scholar] [CrossRef]
- Dragonetti, G.; Comegna, A.; Ajeel, A.; Deidda, G.P.; Lamaddalena, N.; Rodriguez, G.; Vignoli, G.; Coppola, A. Calibrating electromagnetic induction conductivities with time-domain reflectometry measurements. Hydrol. Earth Syst. Sci. 2018, 22, 1509–1523. [Google Scholar] [CrossRef]
- Kachanoski, R.G.; Wesenbeeck, I.V.; Gregorich, E.G. Estimating spatial variations of soil water content using noncontacting electromagnetic inductive methods. Can. J. Soil Sci. 1988, 68, 715–722. [Google Scholar] [CrossRef]
- Kachanoski, R.G.; Wesenbeeck, I.V.; Jong, E.D. Field scale patterns of soil water storage from non-contacting measurements of bulk electrical conductivity. Can. J. Soil Sci. 1990, 70, 537–542. [Google Scholar] [CrossRef]
- Sheets, K.R.; Hendrickx, J.M. Noninvasive soil water content measurement using electromagnetic induction. Water Resour. Res. 1995, 31, 2401–2409. [Google Scholar] [CrossRef]
- Evett, S.R.; Tolk, J.A.; Howell, T.A. Soil profile water content determination. Vadose Zone J. 2006, 5, 894–907. [Google Scholar] [CrossRef]
- Van Dam, J.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.; Groenendijk, P.; Van Diepen, C.A. Theory of SWAP, Version 2.0; Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; Technical Document; Wageningen Agricultural University: Wageningen, The Netherlands, 1998. [Google Scholar]
- Comegna, V.; Coppola, A.; Sommella, A. Nonreactive solute transport in variously structured soil materials as determined by laboratory-based time domain reflectometry (TDR). Geoderma 1999, 92, 167–184. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of Dispersivities for Transport Modeling in Soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Durner, W. Predicting the unsaturated hydraulic conductivity using multi-porosity water retention curves. Indirect Methods Estim. Hydraul. Prop. Unsaturated Soils 1992, 185–202. [Google Scholar]
- Ross, P.J.; Smettem, K.R. Describing soil hydraulic properties with sums of simple functions. Soil Sci. Soc. Am. J. 1993, 57, 26–29. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Priesack, E.; Durner, W. Closed-form expression for the multi-modal unsaturated conductivity function. Vadose Zone J. 2006, 5, 121–124. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, J. Simulation of Field Water Use and Crop Yield; Centre for Agriculture Publishing and Documentation: Wageningen, The Netherland, 1978. [Google Scholar]
- Feddes, R.A.; Raats, P.A.C. Parameterizing the soil–water–plant root system. Unsaturated Zone Model. Prog. Chall. Appl. 2004, 6, 95–141. [Google Scholar]
- Jarvis, N.J. A simple empirical model of root water uptake. J. Hydrol. 1989, 107, 57–72. [Google Scholar] [CrossRef]
- Shouse, P.J.; Ayars, J.E.; Šimůnek, J. Simulating root water uptake from a shallow saline groundwater resource. Agric. Water Manag. 2011, 98, 784–790. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Numerical Model for Water and Solute Movement in and Below the Root Zone; United States Department of Agriculture, Agricultural Research Service U.S. Salinity Laboratory: Riverside, CA, USA, 1987.
- Van Genuchten, M.T.; Hoffman, G.J. Analysis of crop salt tolerance data. In Soil Salinity under Irrigation; Shainberg, I., Shalhevet, J., Eds.; Ecological Studies; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1984; pp. 258–271. [Google Scholar]
- Maas, E.V.; Hoffman, G.J. Crop salt tolerance—Current assessment. J. Irrig. Drain. Div. 1977, 103, 115–134. [Google Scholar]
- Skaggs, T.H.; van Genuchten, M.T.; Shouse, P.J.; Poss, J.A. Macroscopic approaches to root water uptake as a function of water and salinity stress. Agric. Water Manag. 2006, 86, 140–149. [Google Scholar] [CrossRef]
- Homaee, M.; Dirksen, C.; Feddes, R.A. Simulation of root water uptake: I. Non-uniform transient salinity using different macroscopic reduction functions. Agric. Water Manag. 2002, 57, 89–109. [Google Scholar] [CrossRef]
- Homaee, M.; Feddes, R.A.; Dirksen, C. Simulation of root water uptake: II. Non-uniform transient water stress using different reduction functions. Agric. Water Manag. 2002, 57, 111–126. [Google Scholar] [CrossRef]
- Homaee, M.; Feddes, R.A.; Dirksen, C. Simulation of root water uptake: III. Non-uniform transient combined salinity and water stress. Agric. Water Manag. 2002, 57, 127–144. [Google Scholar] [CrossRef]
- Maas, E.V. Salt tolerance of plants. Appl. Agric. Res. 1986, 1, 12–26. [Google Scholar]
- Maas, E.V. Crop salt tolerance. In Agriculture Salinity Assessment and Management; Manuals and Reports on Engineering Practice; American Society Civil Engineers: New York, NY, USA, 1990; pp. 262–334. [Google Scholar]
- Maas, E.V.; Grattan, S.R. Crop yields as affected by salinity. Agronomy 1999, 38, 55–110. [Google Scholar]
- U.S. Salinity Laboratory Staff. Diagnosis and Improvement of Saline and Alkali Soils. USDA Handb.60; U.S. Govenment Printing Office: Washingtin, DC, USA, 1954.
- Wadleigh, C.H. The integrated soil moisture stress upon a root system in a large container of saline soil. Soil Sci. 1946, 61, 219–238. [Google Scholar] [CrossRef]
- Meiri, A.; Shalhevet, J. Crop growth under saline conditions. In Arid Zone Irrigation; Springer: Berlin/Heidelberg, Germany, 1973; pp. 277–290. [Google Scholar]
- Childs, S.W.; Hanks, R.J. Model of Soil Salinity Effects on Crop Growth 1. Soil Sci. Soc. Am. J. 1975, 39, 617–622. [Google Scholar] [CrossRef]
- Du Plessis, H.M. Evapotranspiration of citrus as affected by soil water deficit and soil salinity. Irrig. Sci. 1985, 6, 51–61. [Google Scholar] [CrossRef]
- Bresler, E.; Hoffman, G.J. Irrigation Management for Soil Salinity Control: Theories and Tests 1. Soil Sci. Soc. Am. J. 1986, 50, 1552–1560. [Google Scholar] [CrossRef]
- Shalhevet, J.; Hsiao, T.C. Salinity and drought. Irrig. Sci. 1986, 7, 249–264. [Google Scholar] [CrossRef]
- Prasad, R. A linear root water uptake model. J. Hydrol. 1988, 99, 297–306. [Google Scholar] [CrossRef]
- Raats, P.A.C. Steady Flows of Water and Salt in Uniform Soil Profiles with Plant Roots 1. Soil Sci. Soc. Am. J. 1974, 38, 717–722. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Hopmans, J.W.; Šimunek, J. Calibration of a two-dimensional root water uptake model. Soil Sci. Soc. Am. J. 2001, 65, 1027–1037. [Google Scholar] [CrossRef]
- Coppola, A.; Comegna, A.; Dragonetti, G.; Gerke, H.H.; Basile, A. Simulated preferential water flow and solute transport in shrinking soils. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
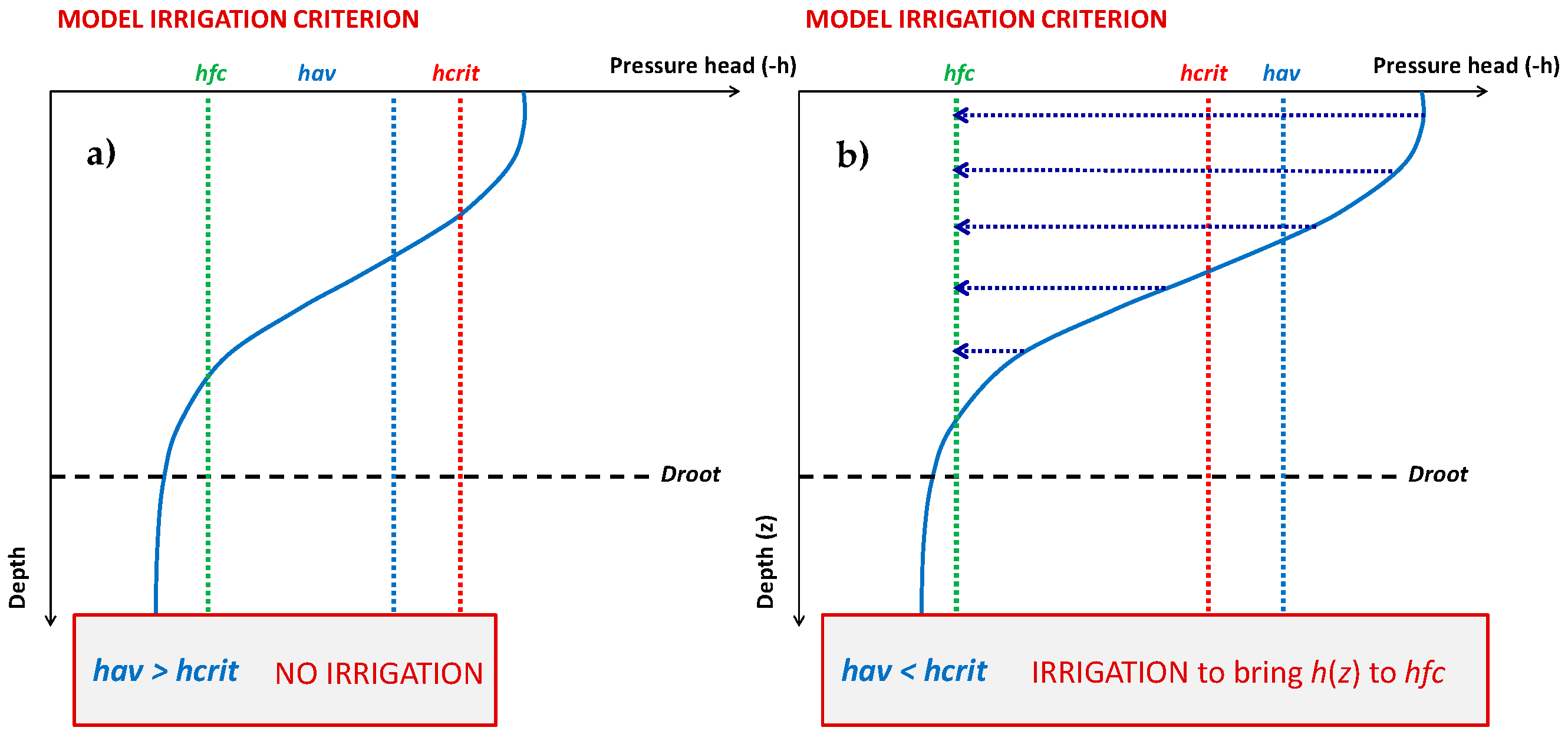
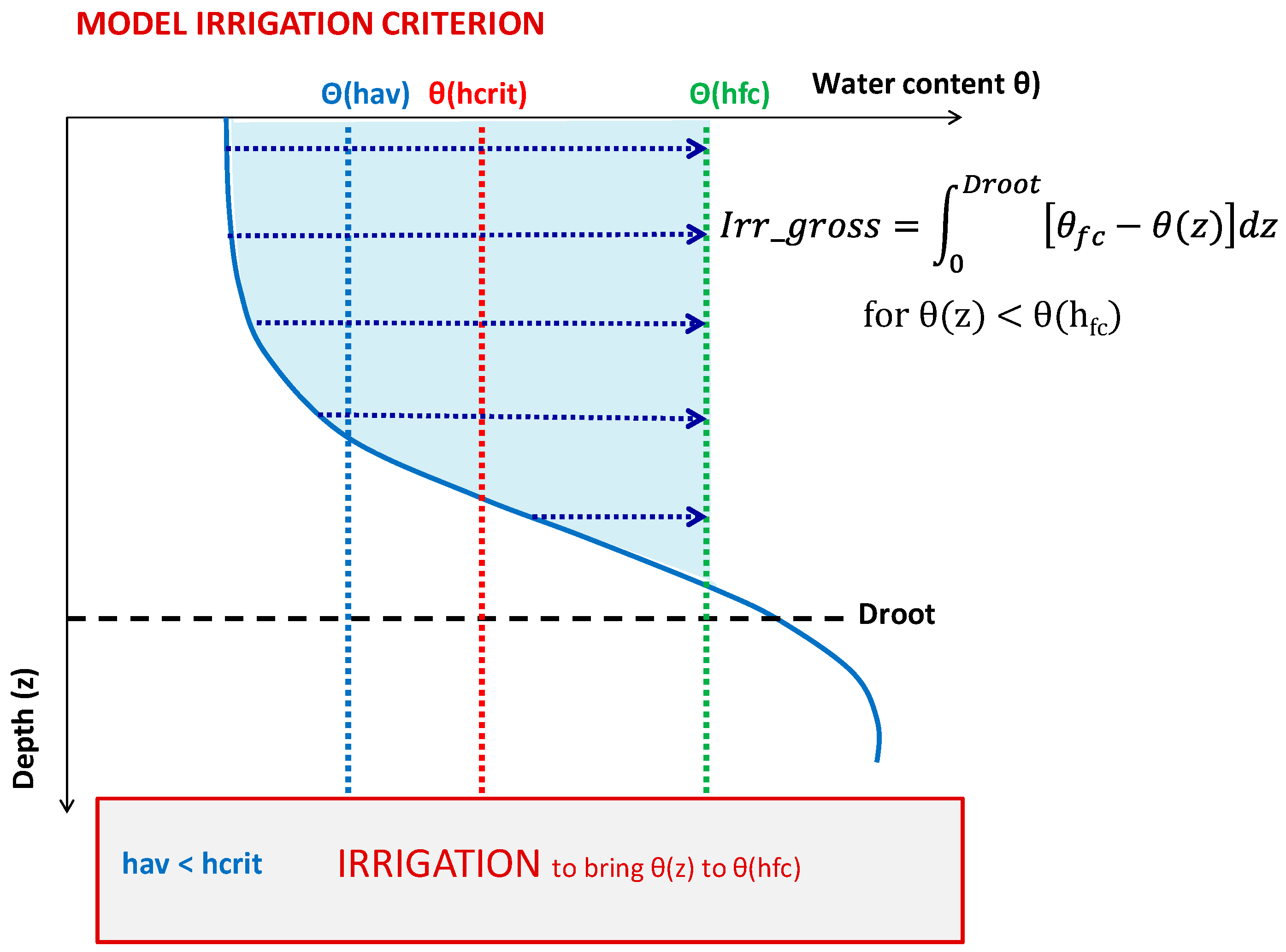
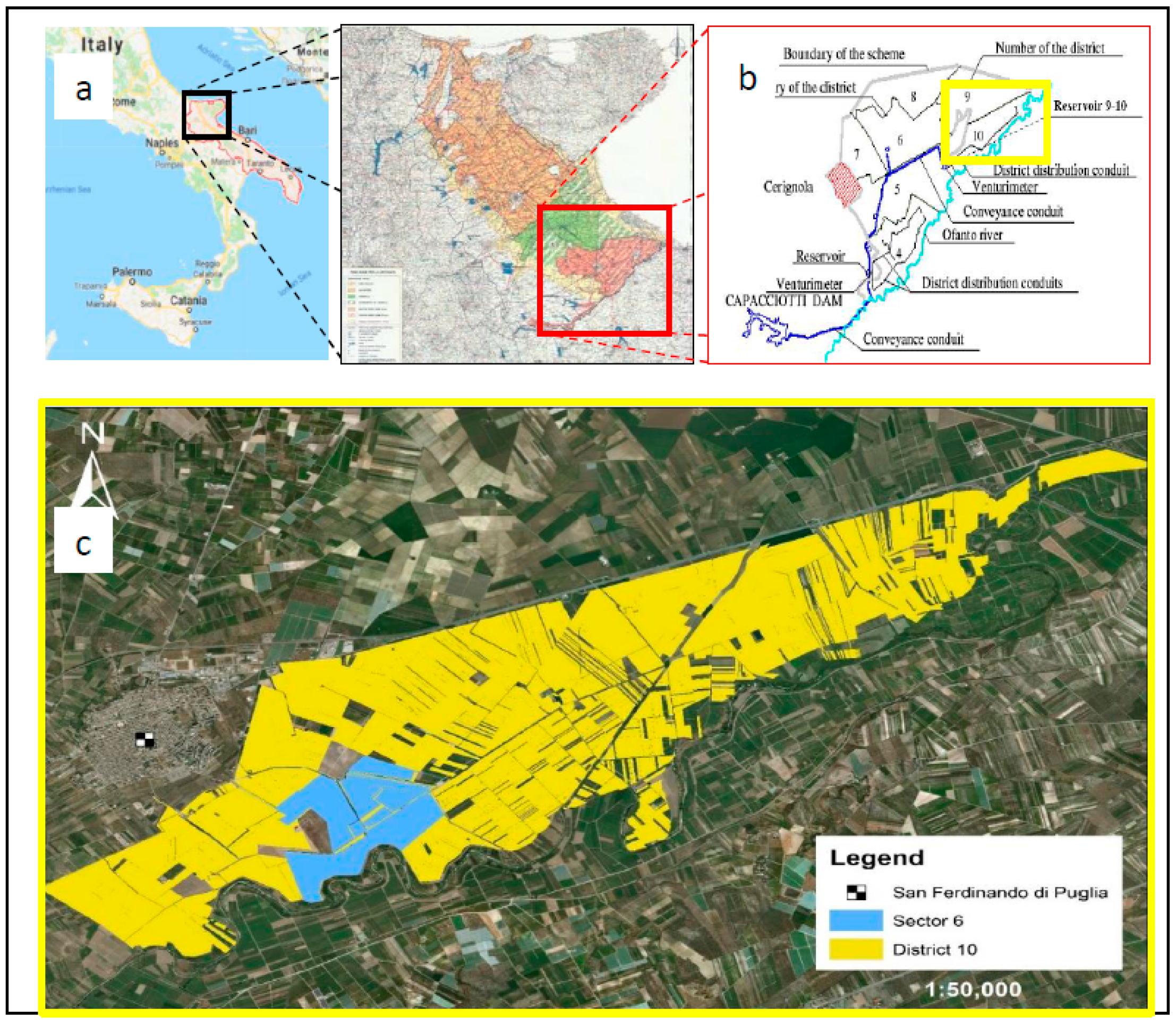

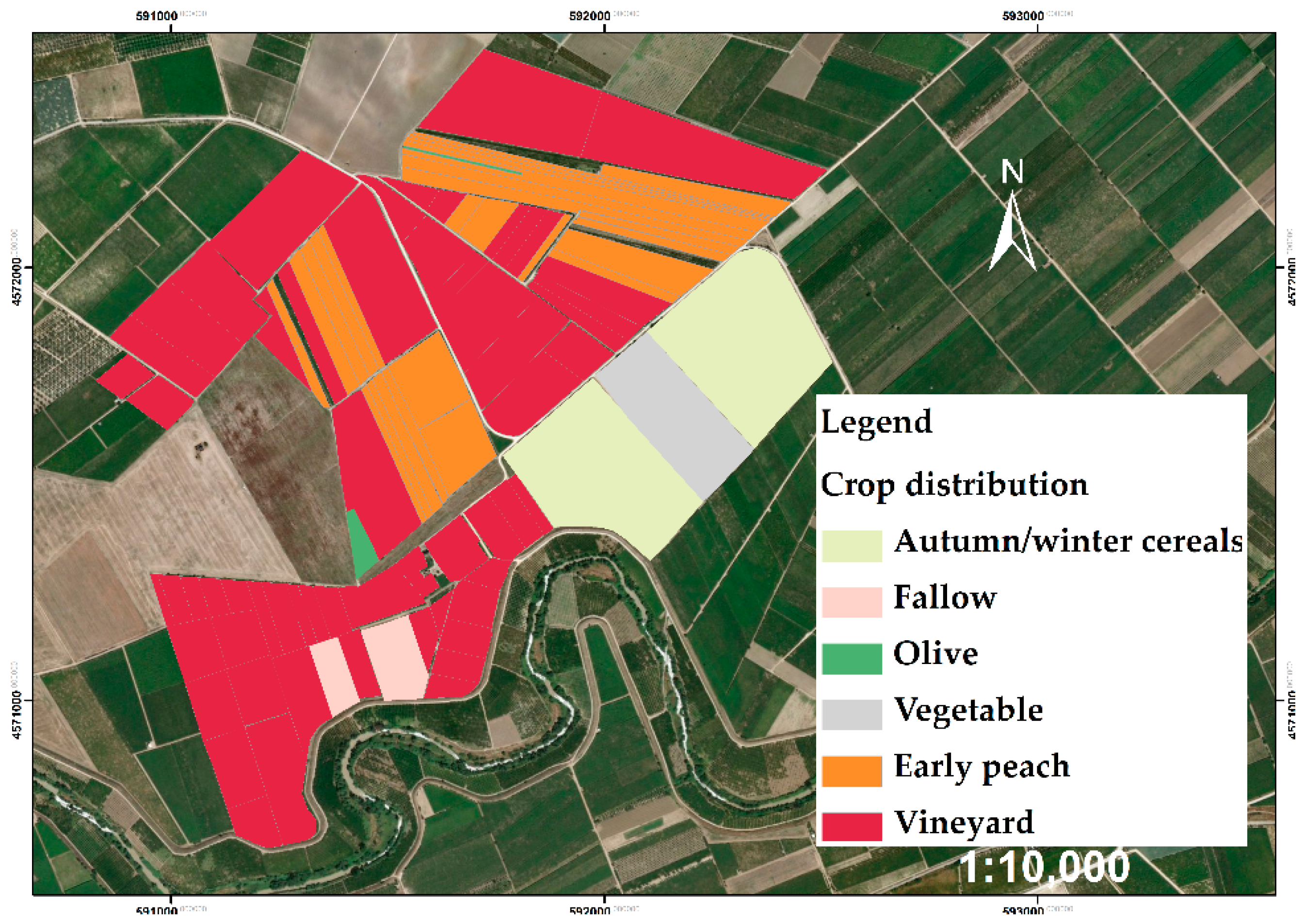


| Profile | Horizon | Texture (%) | Texture Class (USDA) | ||
|---|---|---|---|---|---|
| Sand | Clay | Silt | |||
| P1 | Ap1 | 7.95 | 33.75 | 58.30 | Silty-Clay-Loam |
| Bw1 | 5.25 | 46.25 | 48.50 | Silty-Clay | |
| Bw2 | 5.75 | 38.75 | 55.50 | Silty-Clay-Loam | |
| Bw3 | 6.63 | 41.25 | 52.13 | Silty-Clay | |
| P2 | Ap1 | 27.00 | 18.75 | 54.25 | Silty-Loam |
| Ap2 | 33.48 | 18.75 | 47.78 | Loam | |
| Bw1 | 34.70 | 21.25 | 44.05 | Loam | |
| Bw2 | 34.90 | 21.25 | 43.85 | Loam | |
| P3 | Ap | 20.45 | 26.25 | 53.30 | Silty-Loam |
| Bw1 | 20.00 | 26.25 | 53.75 | Silty-Loam | |
| Bw2 | 19.80 | 31.25 | 48.95 | Silty-Clay-Loam | |
| Bw3 | 14.50 | 31.25 | 54.25 | Silty-Clay-Loam | |
| P4 | Ap | 32.15 | 21.25 | 46.60 | Loam |
| C1 | 35.55 | 18.75 | 45.70 | Loam | |
| C2 | 40.30 | 18.75 | 40.95 | Loam | |
| CK3 | 39.85 | 18.75 | 41.40 | Loam | |
| P5 | Ap | 25.00 | 33.75 | 41.25 | Clay-Loam |
| B/C | 47.25 | 23.75 | 29.00 | Loam | |
| Bw1 | 28.25 | 33.75 | 38.00 | Clay-Loam | |
| Bw2 | 29.70 | 33.75 | 36.55 | Clay-Loam | |
| Crop | Area (ha) | Water Consumption (m3) (Year 2016) | Water Consumption (%) |
|---|---|---|---|
| Vineyard | 64 | 73,640.3 | 60.4 |
| Early peach | 30 | 46,320.7 | 38 |
| Autumn winter cereals | 20 | N/A | N/A |
| Vegetable | 6.5 | N/A | N/A |
| Fallow | 5 | N/A | N/A |
| Table Grape | 1 | 732.3 | 0.6 |
| Apricot | 1 | 1163.7 | 1 |
| Olive | 1 | N/A | N/A |

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coppola, A.; Dragonetti, G.; Sengouga, A.; Lamaddalena, N.; Comegna, A.; Basile, A.; Noviello, N.; Nardella, L. Identifying Optimal Irrigation Water Needs at District Scale by Using a Physically Based Agro-Hydrological Model. Water 2019, 11, 841. https://doi.org/10.3390/w11040841
Coppola A, Dragonetti G, Sengouga A, Lamaddalena N, Comegna A, Basile A, Noviello N, Nardella L. Identifying Optimal Irrigation Water Needs at District Scale by Using a Physically Based Agro-Hydrological Model. Water. 2019; 11(4):841. https://doi.org/10.3390/w11040841
Chicago/Turabian StyleCoppola, Antonio, Giovanna Dragonetti, Asma Sengouga, Nicola Lamaddalena, Alessandro Comegna, Angelo Basile, Nicoletta Noviello, and Luigi Nardella. 2019. "Identifying Optimal Irrigation Water Needs at District Scale by Using a Physically Based Agro-Hydrological Model" Water 11, no. 4: 841. https://doi.org/10.3390/w11040841
APA StyleCoppola, A., Dragonetti, G., Sengouga, A., Lamaddalena, N., Comegna, A., Basile, A., Noviello, N., & Nardella, L. (2019). Identifying Optimal Irrigation Water Needs at District Scale by Using a Physically Based Agro-Hydrological Model. Water, 11(4), 841. https://doi.org/10.3390/w11040841







