Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method
Abstract
:1. Introduction
2. Numerical Methods
2.1. Governing Equations
2.2. Kernel Function
2.3. Gradient Model
2.4. Laplacian Model
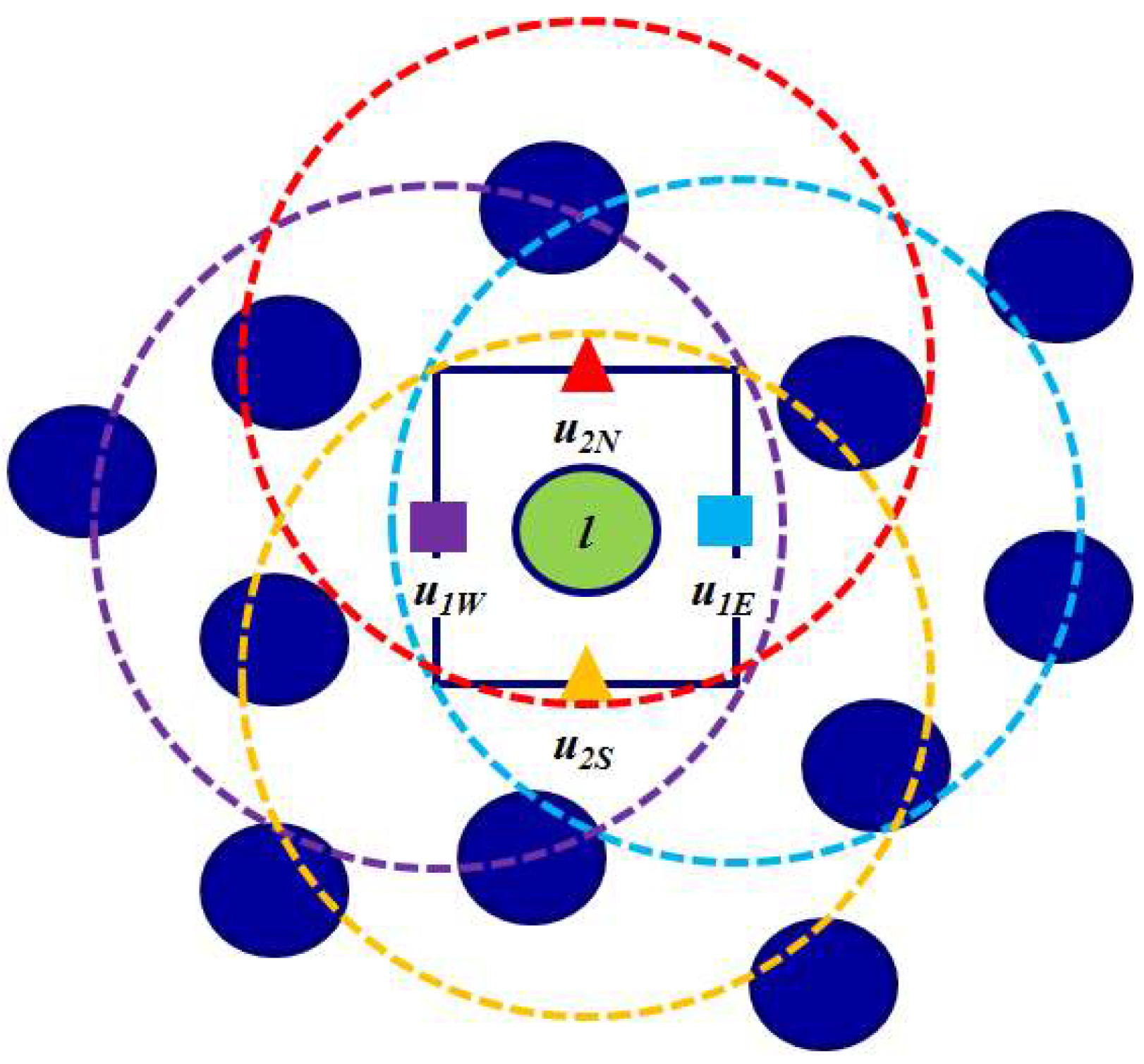
2.5. Incompressibility Model with a Staggered Divergence-Free Model
2.6. Boundary Conditions
2.6.1. Free-Surface Boundary Condition
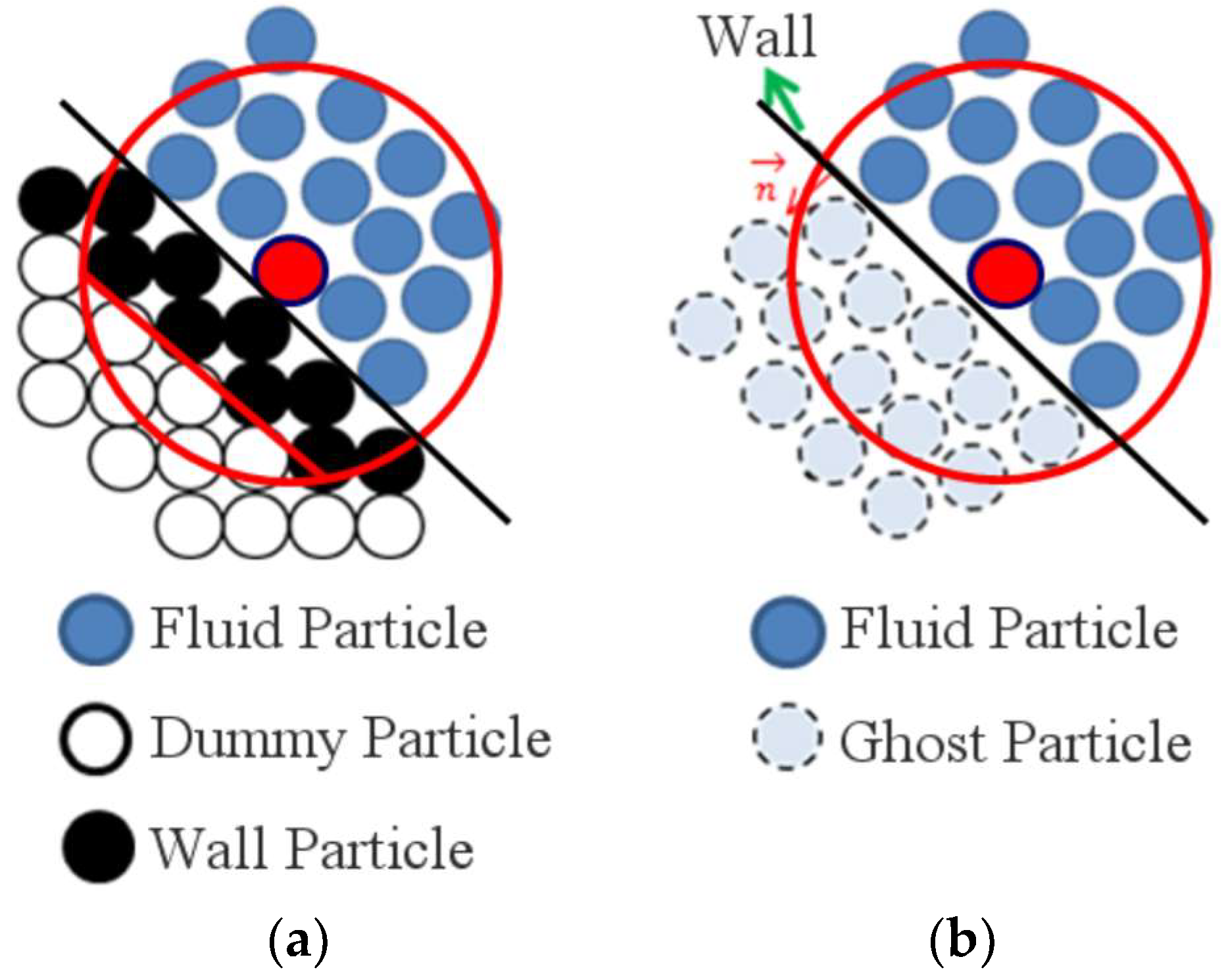
2.6.2. Wall Boundary Condition
2.7. Turbulence Model
3. Numerical Simulations and Discussion
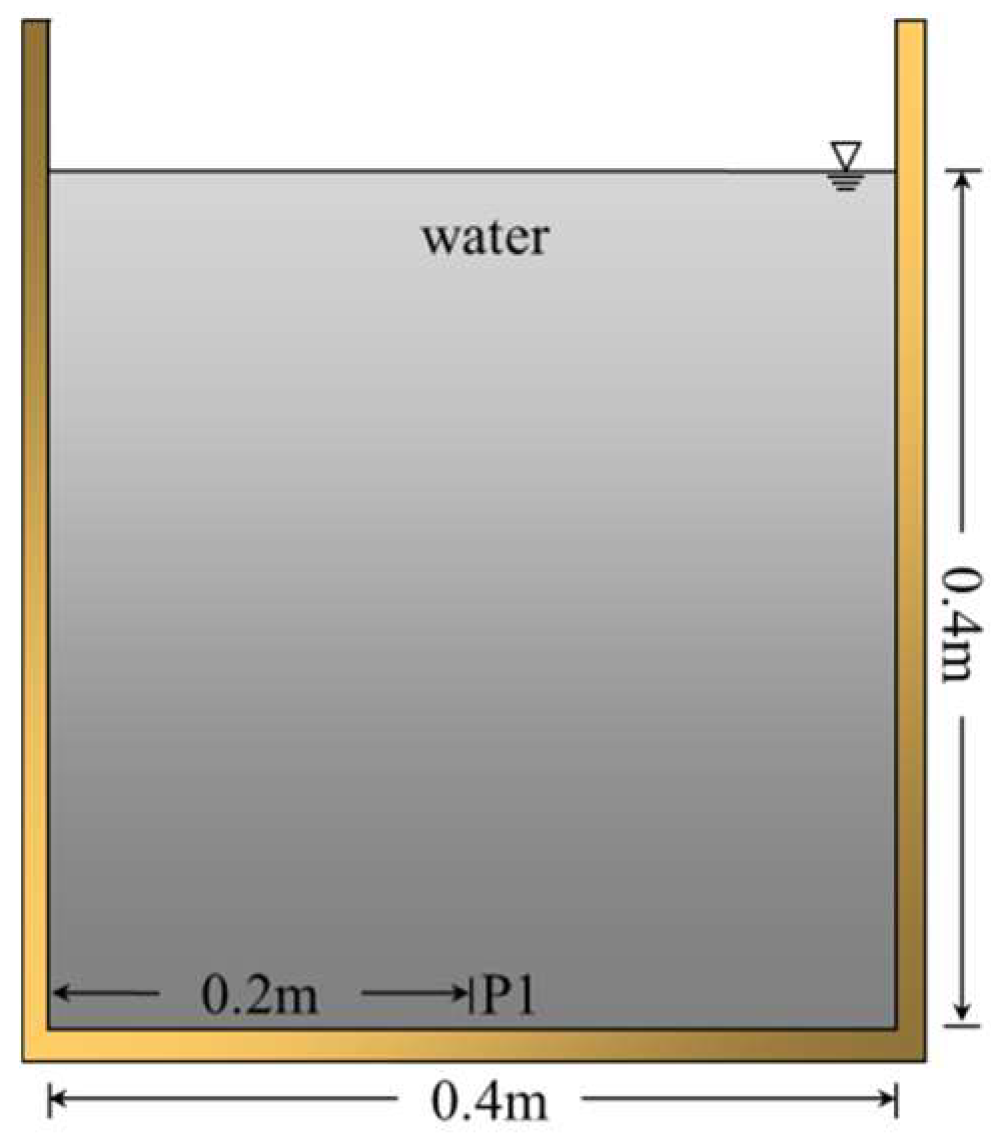
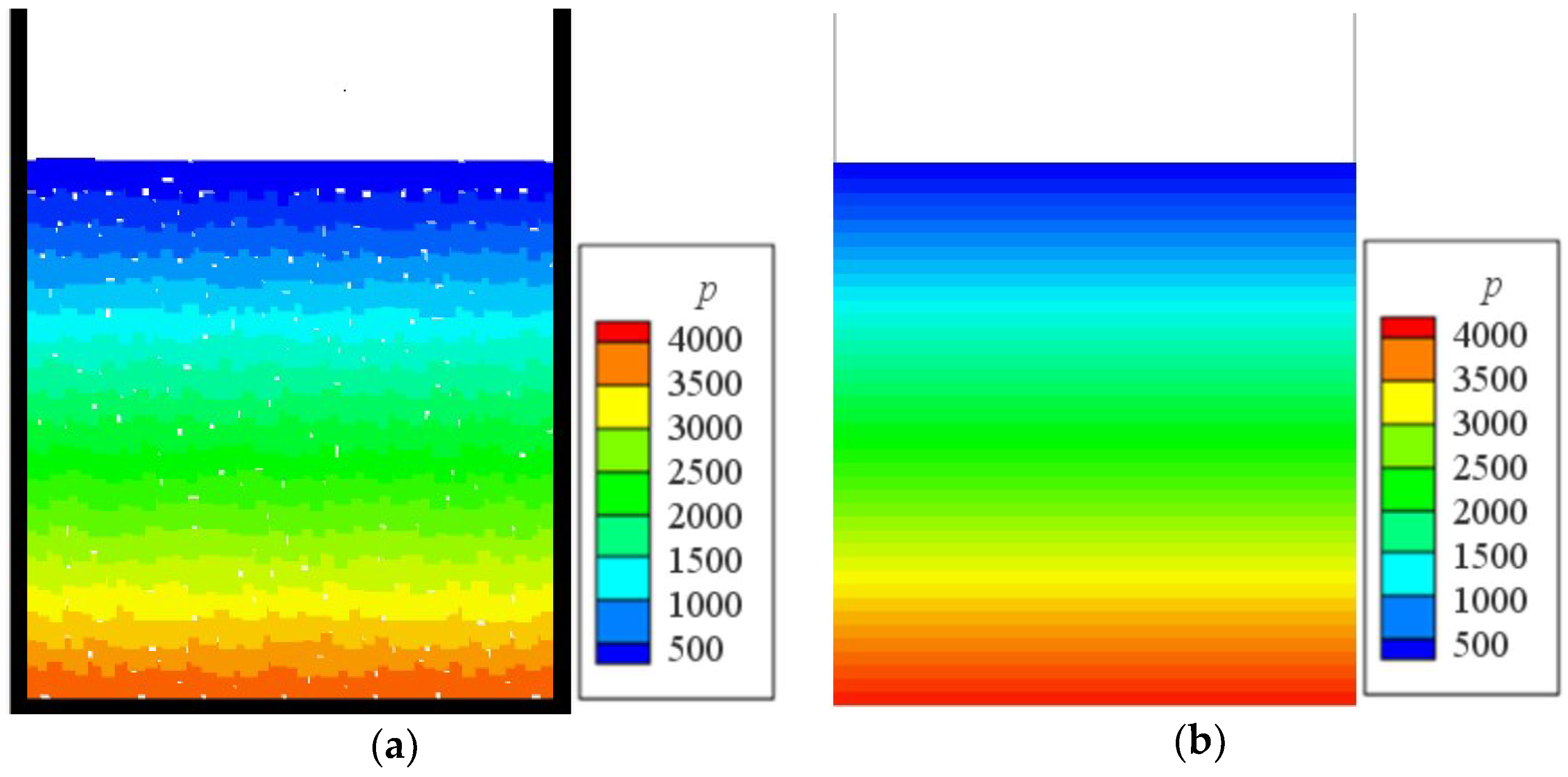
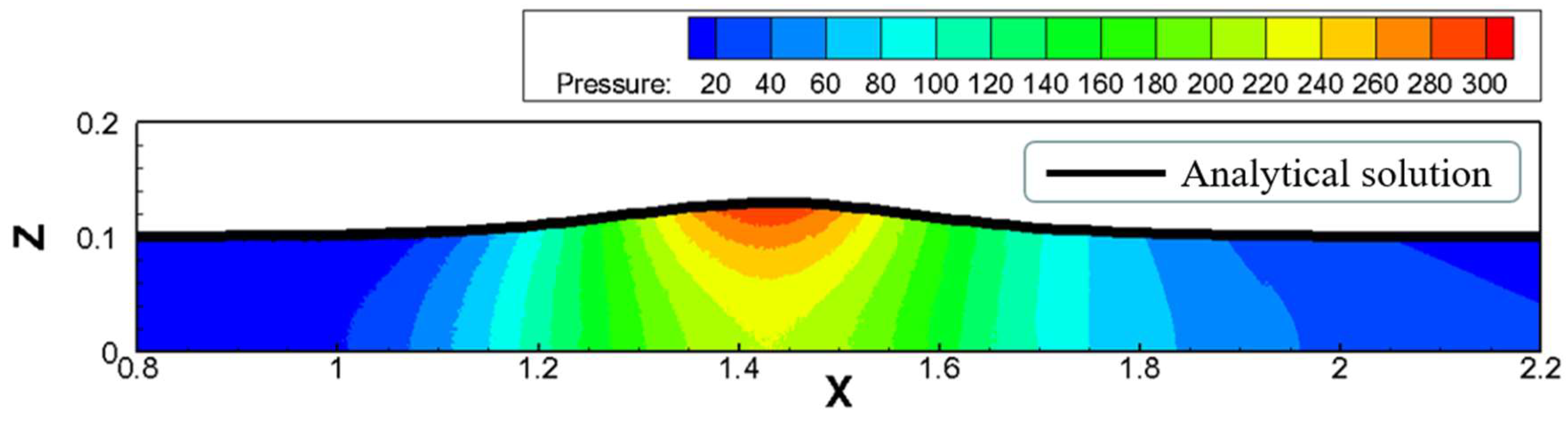
3.1. Hydrostatic Pressure Test
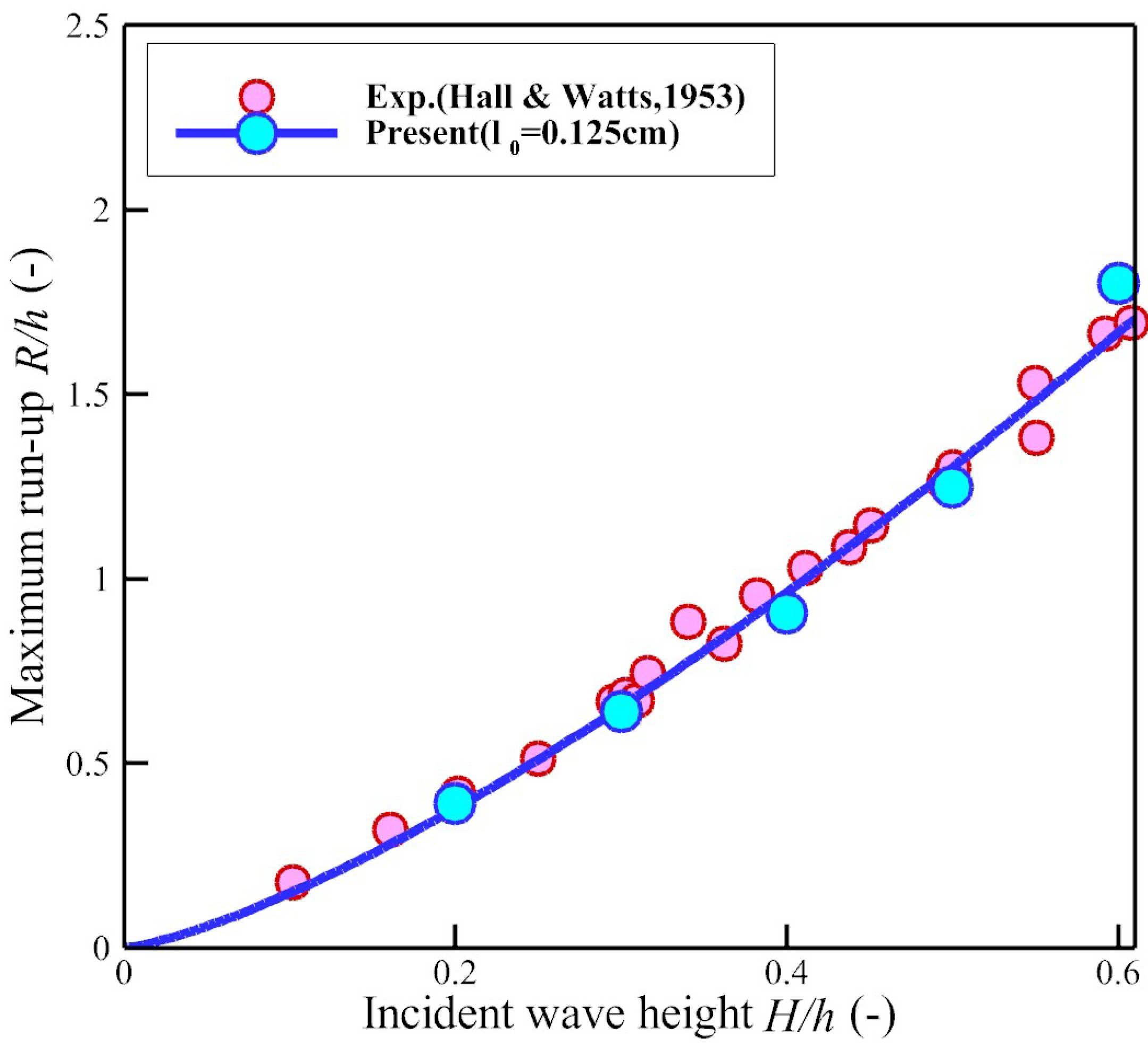
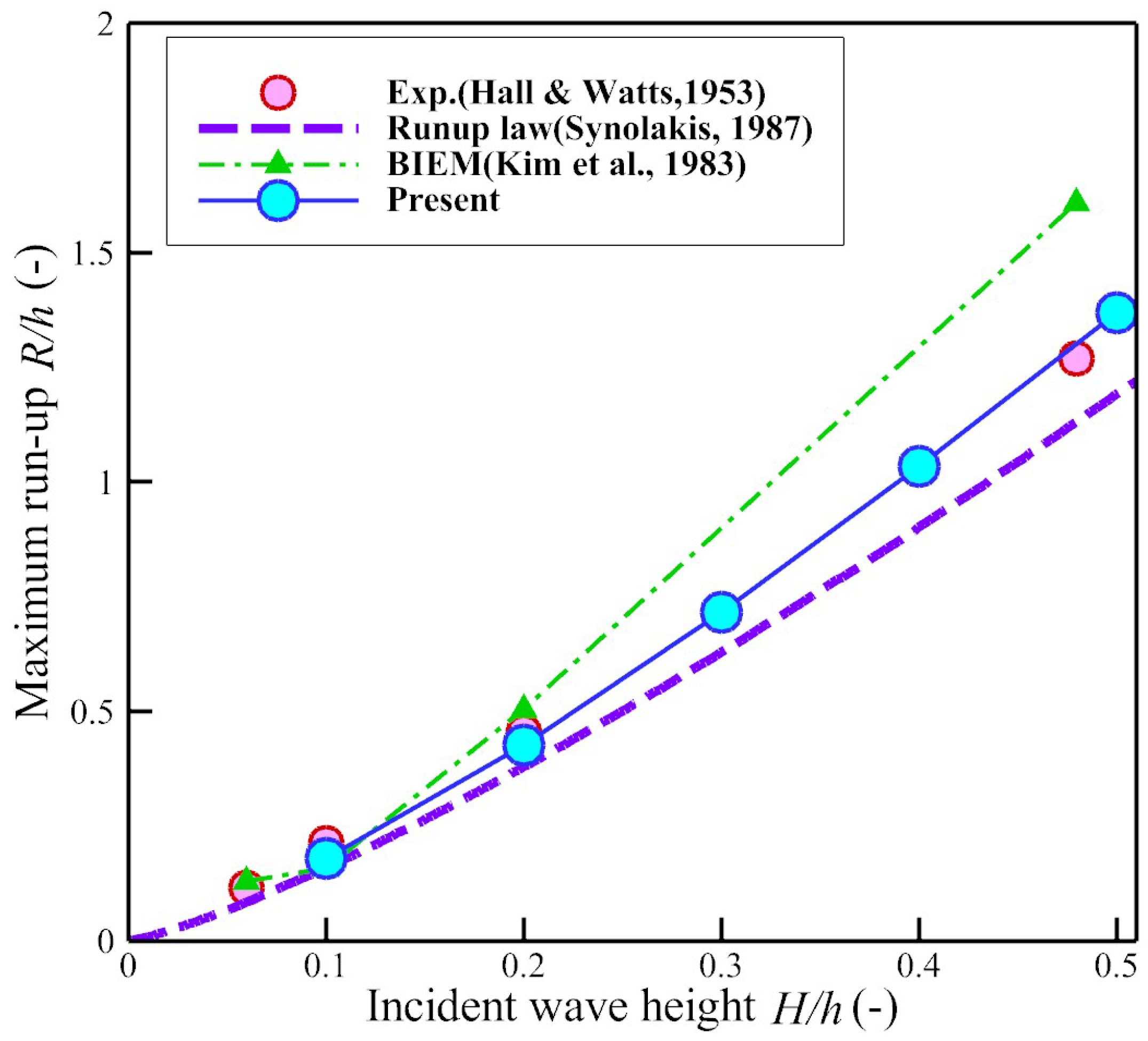
3.2. Solitary Wave Run-Up (Constant Slope Angles)
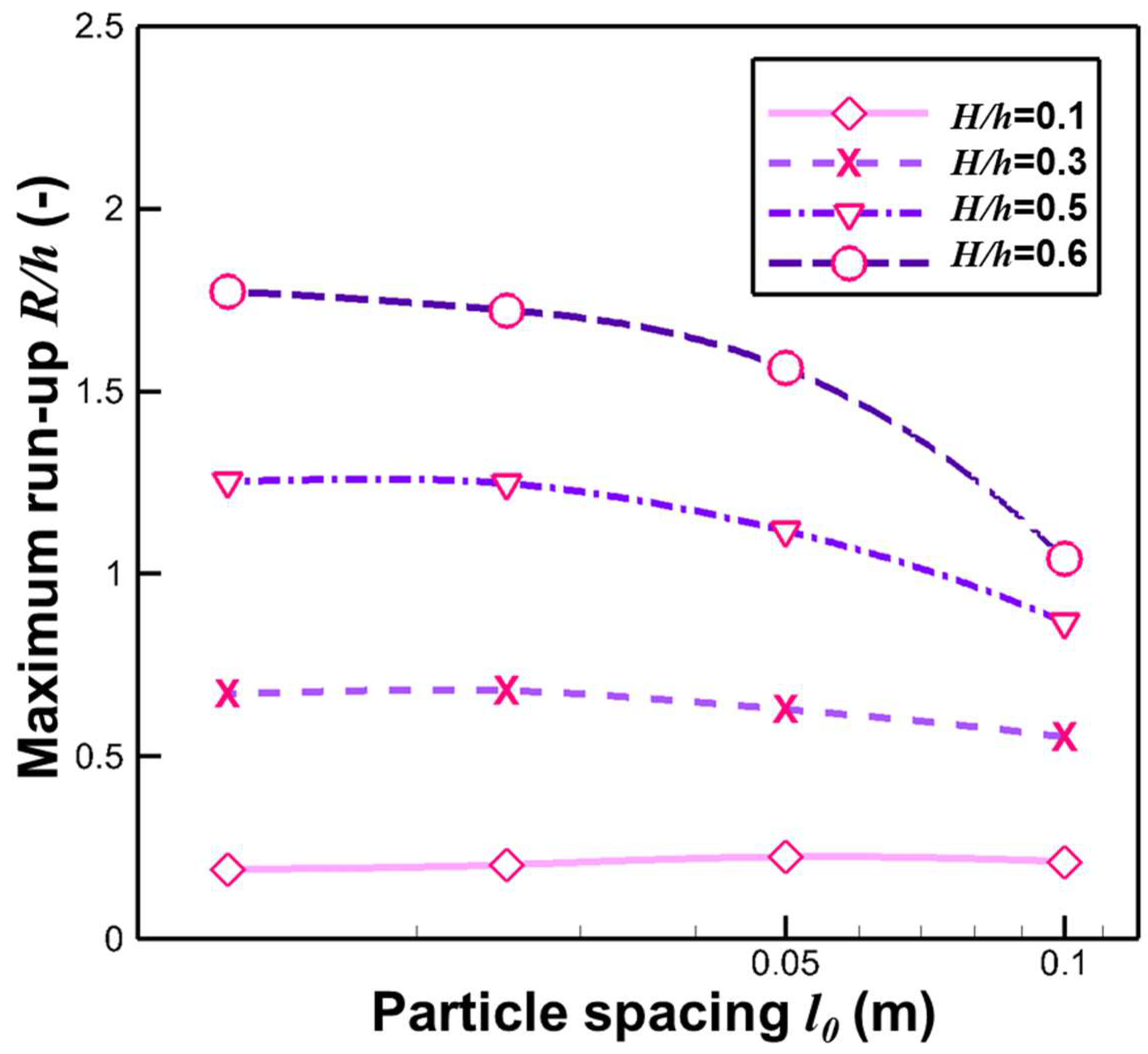
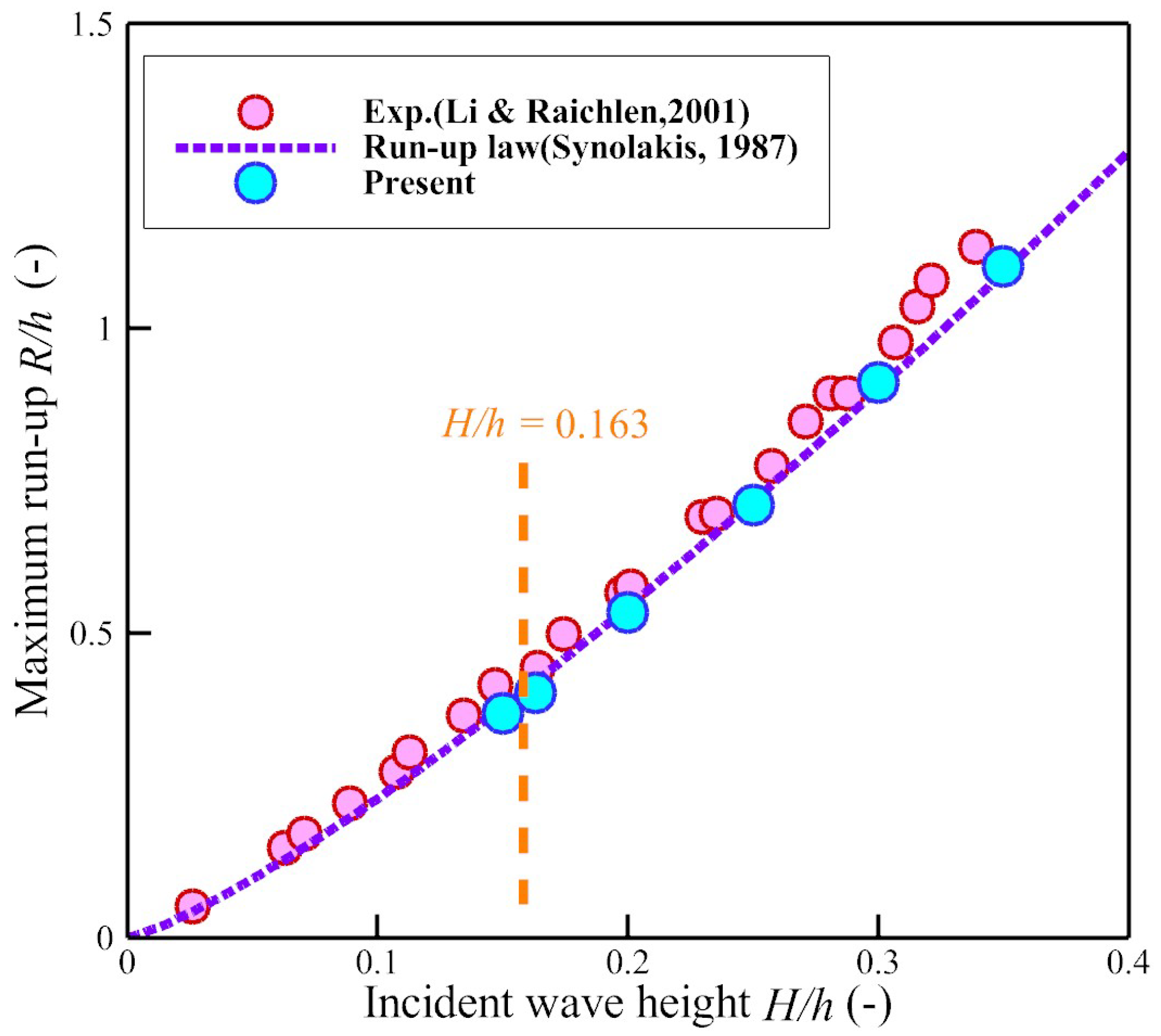
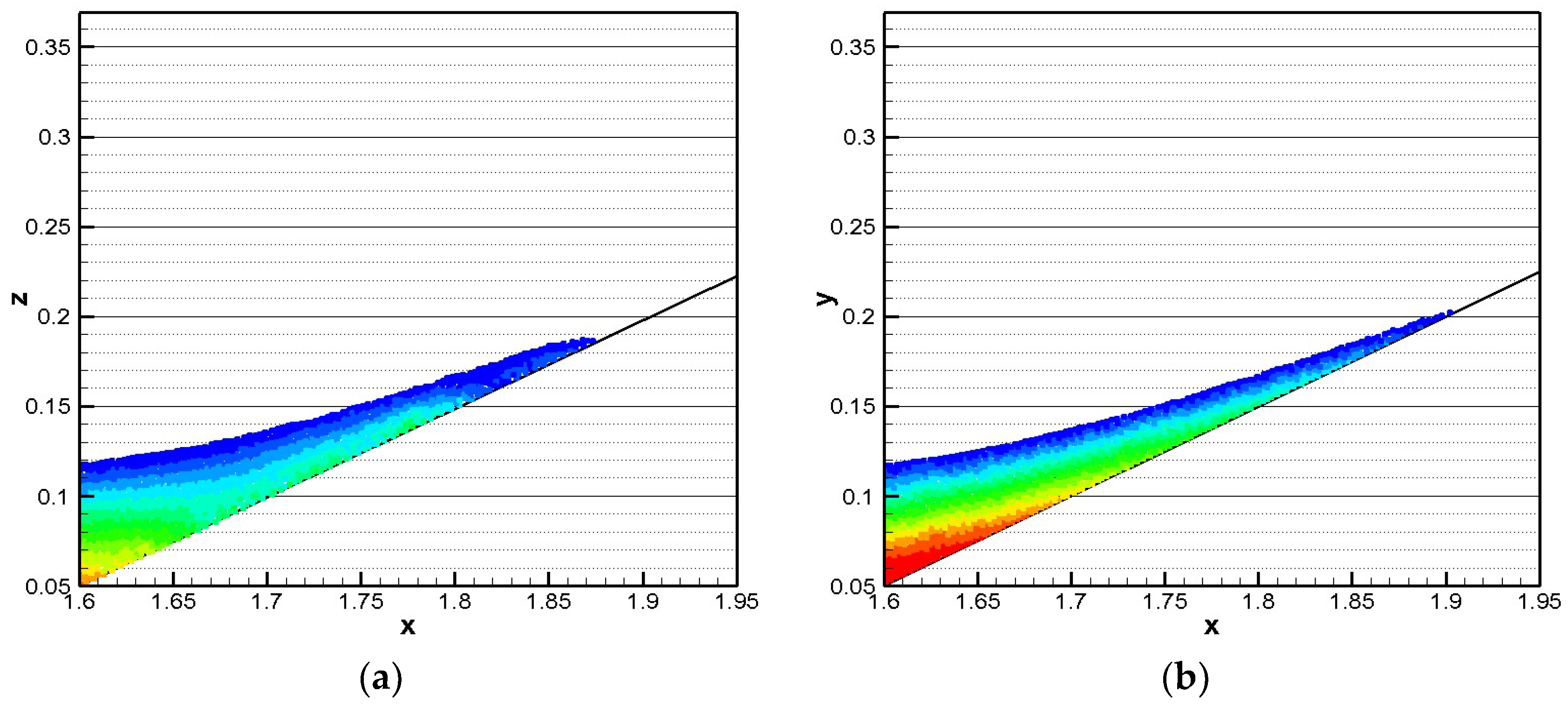
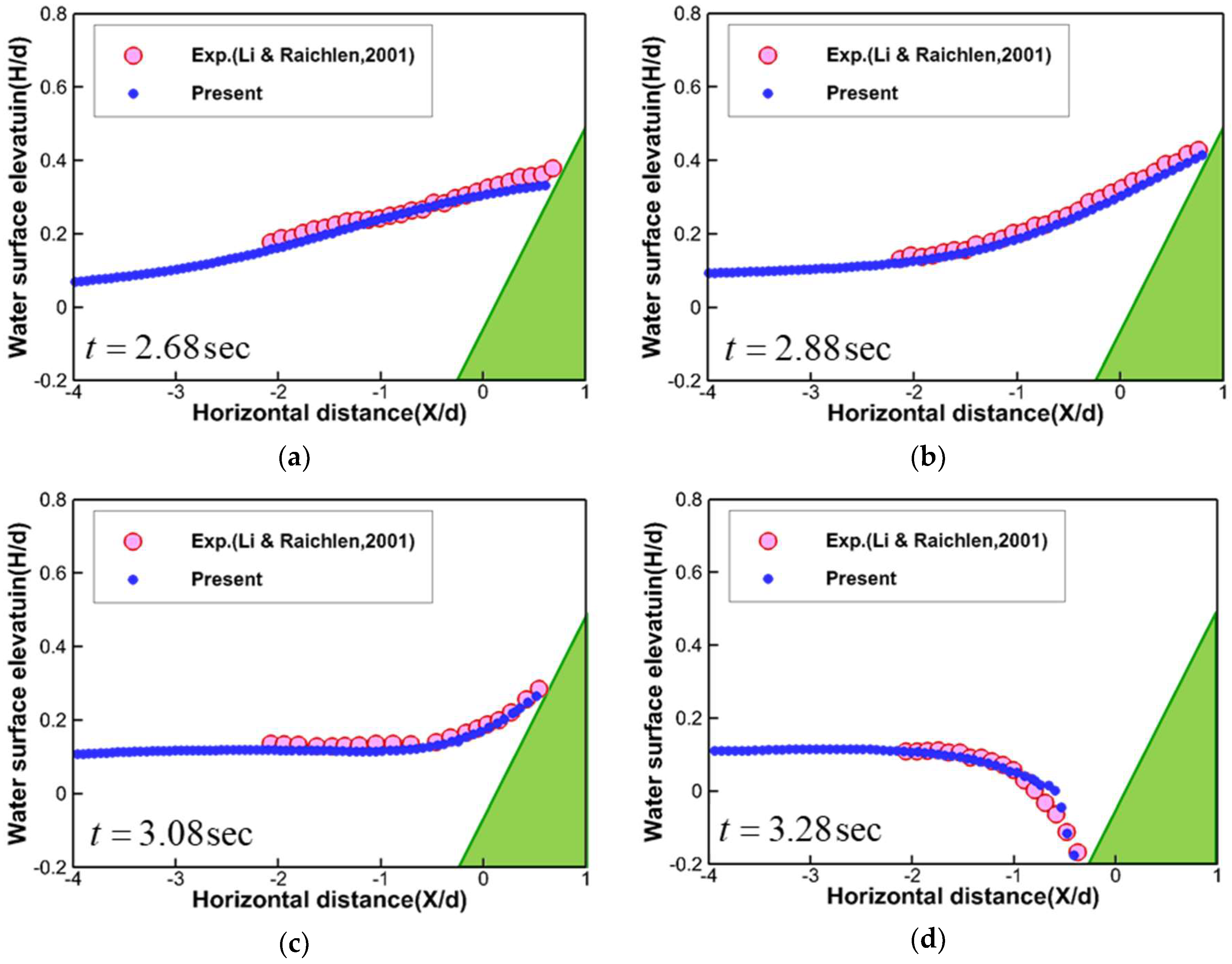
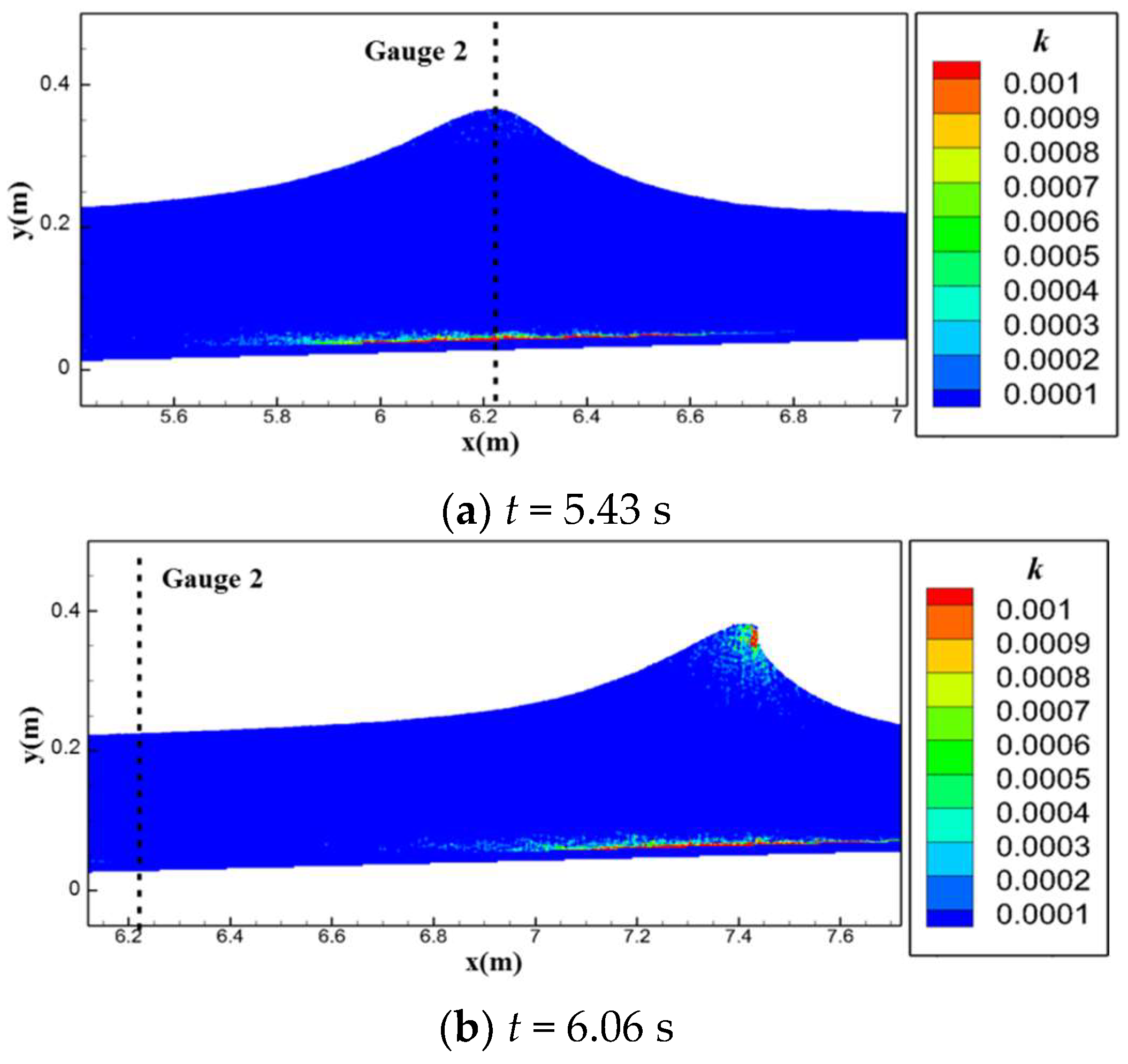
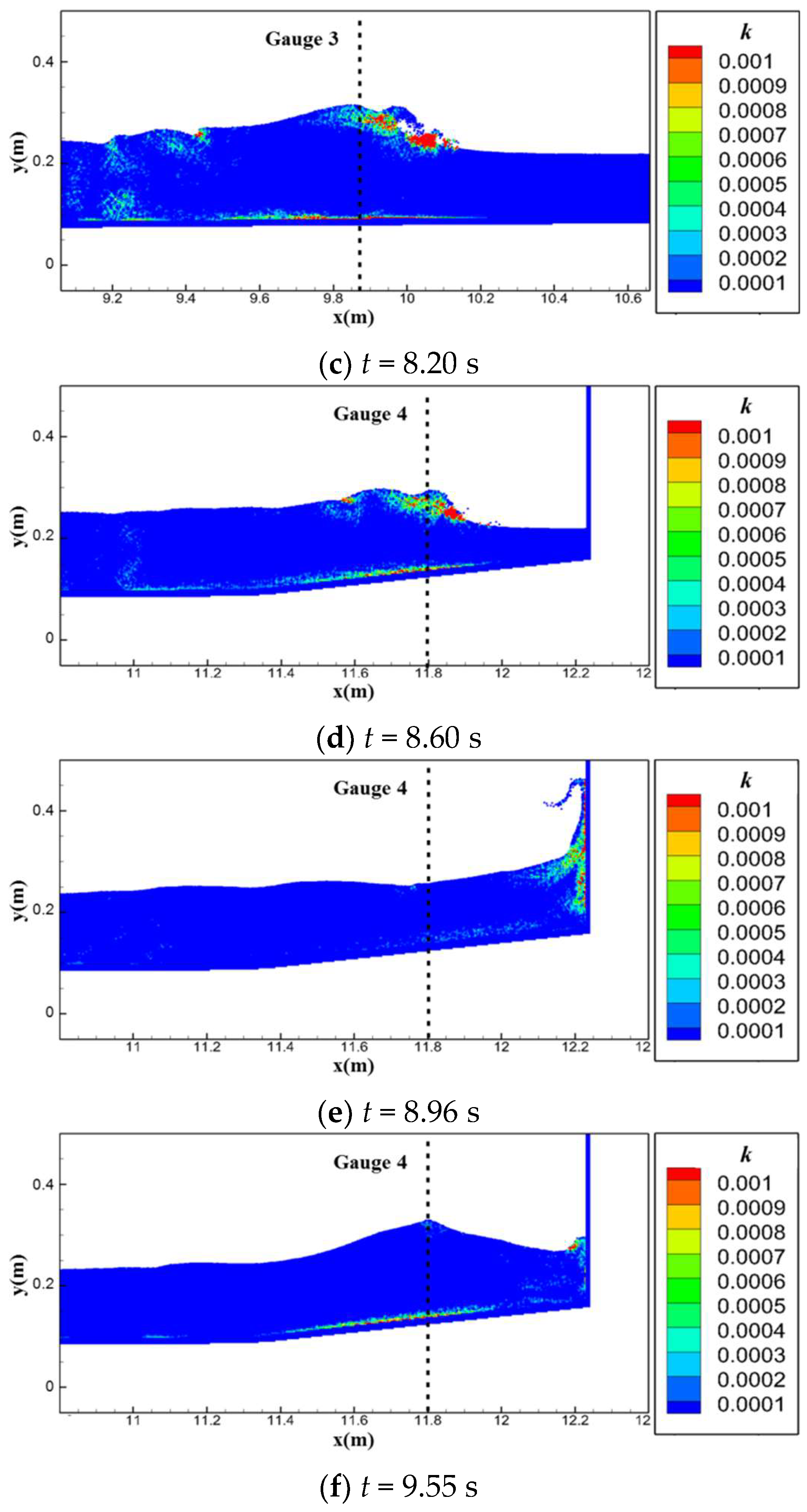
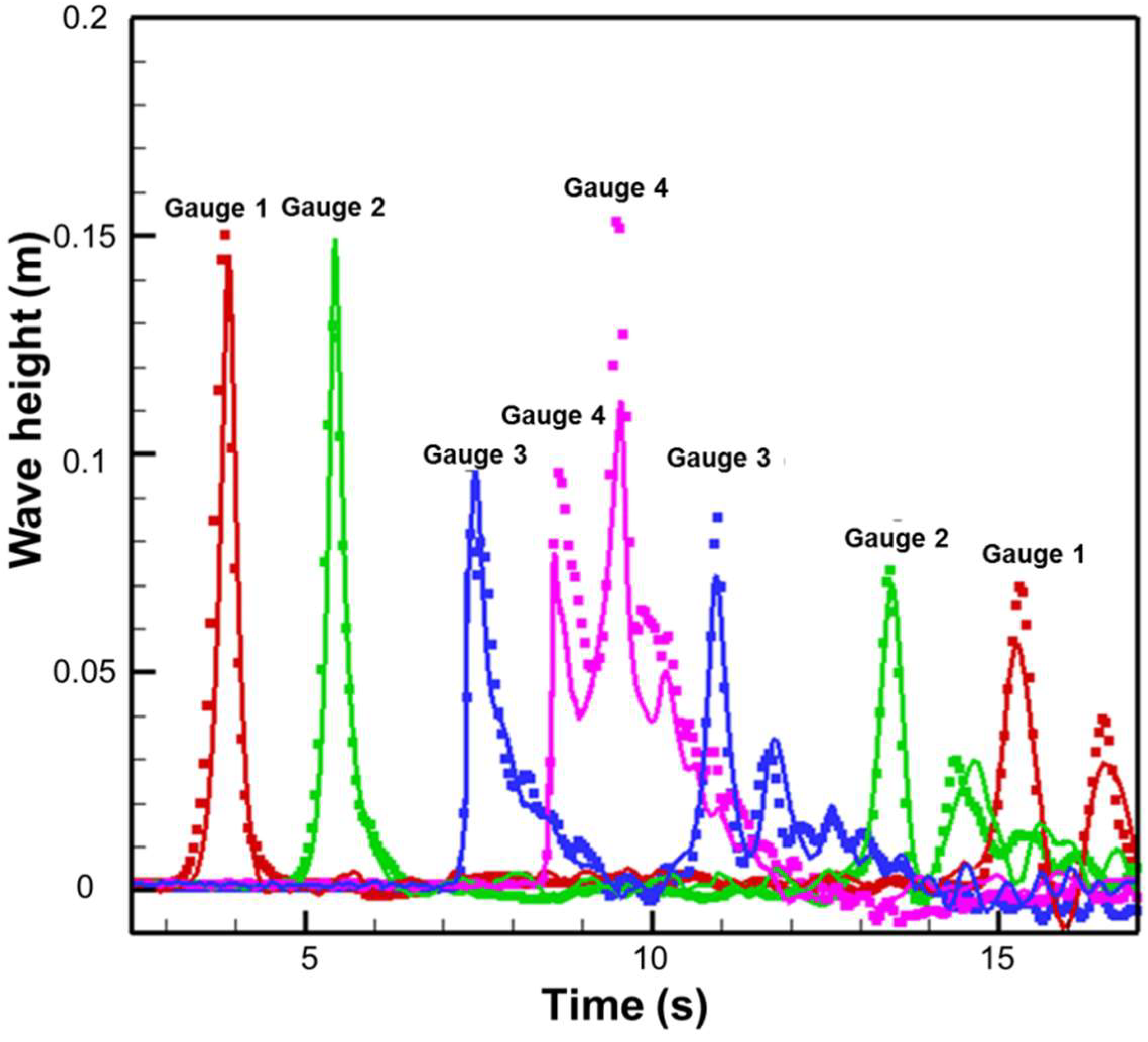
3.3. Solitary Wave Run-Up (Varying Slope Angle)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| , , , | coefficients for making target wave (-) |
| wave-velocity (ms−1) | |
| corrective matrix for gradient model (-) | |
| Smagorinsky constant (-) | |
| number of space dimensions (-) | |
| external force for unit mass (ms−2) | |
| , , , | centers of the east, west, north, and south control surfaces of particle (-) |
| gravitational acceleration (ms−2) | |
| water depth (m) | |
| maximum wave height (m) | |
| -direction component in the Cartesian coordination system (-) | |
| turbulent kinetic energy (m2s−2) | |
| wave-number (m−1) | |
| or | particle index (-) |
| particle size (m) | |
| time step index (-) | |
| fixed particle number density for the incompressibility (-) | |
| particle number density of particle (-) | |
| maximum number of neighboring particles in the initial distribution (-) | |
| number of neighboring particles of particle (-) | |
| pressure (Pa) | |
| position vector between two particles (m) | |
| effective radius for particle interactions (m) | |
| , | position vector of particle and (m) |
| relative position vector between particle and (m) | |
| distance between particle and (m) | |
| wave run-up (m) | |
| strain rate (-) | |
| stroke of wavemaker’s paddle (cm) | |
| time (s) | |
| velocity vector (ms−1) | |
| temporary velocity components of particle (ms−1) | |
| velocity correction of particle (ms−1) | |
| Reynolds stress term for turbulent flows (m2s−2) | |
| statistical volume of particle (-) | |
| speed of wavemaker’s paddle (cms−1) | |
| kernel function (-) | |
| kernel function between particle and (-) | |
| distance between particle and in the x-direction (m) | |
| position of wave-maker at time (m) | |
| distance between particle and in the y-direction (m) | |
| height of wavemaker’s paddle (m) | |
| , | parameters for detecting free surface (-) |
| Kronecker’s delta (-) | |
| particle-to-particle spacing (m) | |
| difference of scalar quantities between particle and (m) | |
| , | scalar quantities at particles and (-) |
| blending parameter for incompressibility model (-) | |
| parameter that makes the increase in variance equal to that of the analytical solution (-) | |
| slope angle of bottom (°) | |
| density (kgm−3) | |
| kinematic viscosity (m2s−1) | |
| eddy viscosity (m2/s−1) |
References
- Mimura, N.; Yasuhara, K.; Kawagoe, S.; Yokoki, H.; Kazama, S. Damage from the Great East Japan Earthquake and Tsunami—A quick report. Mitig. Adapt. Strateg. Glob. Chang. 2011, 16, 809–818. [Google Scholar]
- Camfield, F.E.; Street, R.L. Shoaling of solitary waves on small slopes. J. Waterw. Harb. Div. 1969, 95, 1–22. [Google Scholar]
- Li, Y.; Raichlen, F. Solitary wave runup on plane slopes. J. Waterw. Portcoastaland Ocean Eng. 2001, 127, 33–44. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. JCP 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computation solutions to incompressible two-phase flow. JCP 1981, 114, 272–280. [Google Scholar]
- Miyata, H.; Park, J.C. Chapter 5 wave breaking simulation. In Potential Flow of Fluids; M. Rahman Computational Mechanics Publications; WIT Press/Computational Mechanics: Southampton, UK, 1995; pp. 149–176. [Google Scholar]
- Jeong, S.M.; Hwang, S.C.; Park, J.C. Numerical Simulation of Impact Loads Caused by Sloshing in a Rectangular Tank Using Eulerian and Lagrangian Approaches. Int. J. Offshore Polar Eng. 2014, 24, 174–180. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. Recent results from analysis of flow structures and energy modes induced by viscous wave around a surface-piercing cylinder. Math. Probl. Eng. 2017, 2017, 5875948. [Google Scholar] [CrossRef]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Lee, B.H.; Park, J.C.; Kim, M.H.; Hwang, S.C. Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads. J. Comput. Methods Appl. Mech. Eng. 2011, 200, 1113–1125. [Google Scholar] [CrossRef]
- Zhang, S.; Morita, K.; Fukuda, K.; Shirakawa, N. An improved MPS method for numerical simulations of convective heat transfer problems. Int. J. Numer. Methods Fluids 2006, 51, 31–47. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method. Appl. Ocean Res. 2010, 32, 124–131. [Google Scholar] [CrossRef]
- Tanaka, M.; Masunaga, T. Stabilization and smoothing of pressure in MPS method by Quasi-Compressibility. J. Comput. Phys. 2010, 229, 4279–4290. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. A 3D higher order Laplacian model for enhancement and stabilization of pressure calculation in 3D MPS-based simulations. Appl. Ocean Res. 2012, 37, 120–126. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 2011, 23, 3093–3118. [Google Scholar] [CrossRef]
- Koh, C.; Luo, M.; Gao, M.; Bai, W. Modelling of liquid sloshing with constrained floating baffle. Comput. Struct. 2013, 122, 270–279. [Google Scholar] [CrossRef]
- Lo, E.Y.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Imanian, H.; Kolahdoozan, M.; Zarrati, A.R. Waves simulation in viscous waters using MPS. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks (ICCSN), Xi’an, China, 27–29 May 2011; pp. 264–268. [Google Scholar]
- Dao, M.H.; Xu, H.; Chan, E.S.; Tkalich, P. Modelling of tsunami-like wave run-up, breaking and impact on a vertical wall by SPH method. Nat. Hazards Earth Syst. Sci. 2013, 13, 3457–3467. [Google Scholar] [CrossRef]
- Goto, C.; Ogawa, Y.; Shuto, N.; Imamura, F. Numerical Method of Tsunami Simulation with the Leap-Frog Scheme (IUGG/IOC Time Project); IOC Manual No. 35; UNESCO: Paris, France, 1997. [Google Scholar]
- Wei, Z.; Dalrymple, R.A.; Rustico, E.; Hérault, A.; Bilotta, G. Simulation of Nearshore Tsunami Breaking by Smoothed Particle Hydrodynamics Method. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 05016001. [Google Scholar] [CrossRef]
- Aristodemo, F.; Tripepi, G.; Meringolo, D.D.; Veltri, P. Solitary wave-induced forces on horizontal circular cylinders: Laboratory experiments and SPH simulations. Coast. Eng. 2017, 129, 17–35. [Google Scholar] [CrossRef]
- Ren, Y.; Luo, M.; Lin, P. Consistent Particle Method Simulation of Solitary Wave Interaction with a Submerged Breakwater. Water 2019, 11, 261. [Google Scholar] [CrossRef]
- Gotoh, H.; Shibahara, T.; Sakai, T. Sub-particle-scale turbulence model for the MPS method—Lagrangian flow model for hydraulic engineering. Adv. Methods Comput. Fluid Dyn. 2001, 9, 339–347. [Google Scholar]
- Jeong, S.M.; Nam, J.W.; Hwang, S.C.; Park, J.C.; Kim, M.H. Numerical prediction of oil amount leaked from a damaged tank using two-dimensional moving particle simulation method. Ocean Eng. 2013, 69, 70–78. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Hall, J.V.; Watts, G.M. Laboratory Investigation of the Vertical Rise of Solitary Waves on Impermeable Slopes; Beach Erosion Board; US Army Corps of Engineers: Washington, DC, USA, 1953; Technical Memorandum 33. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993; p. 7. [Google Scholar]
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Kim, S.K.; Liu, P.L.F.; Liggett, J.A. Boundary integral equation solutions for solitary wave generation, propagation and run-up. Coast. Eng. 1983, 7, 299–317. [Google Scholar] [CrossRef]
- Briggs, M.J.; Synolakis, C.E.; Kanoglu, U.; Creen, D.R. Runup of solitary waves on a vertical wall. In Long-Wave Runup Models, Proceedings of the International Workshop, Friday Harbor, USA; World Scientific Pub Co. Inc.: Hackensack, NJ, USA, 1995. [Google Scholar]

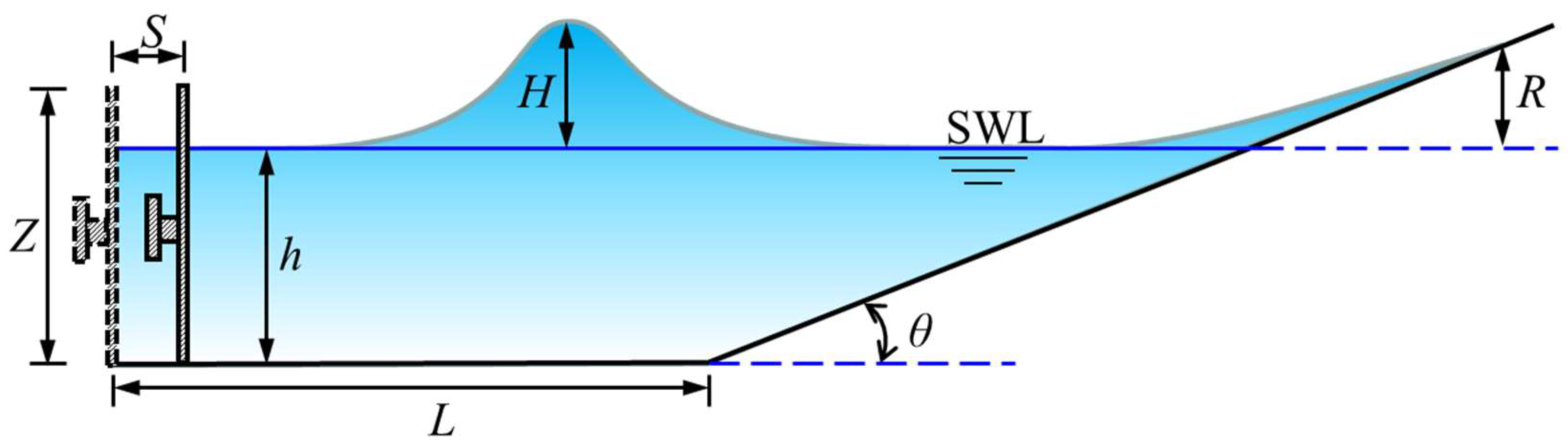
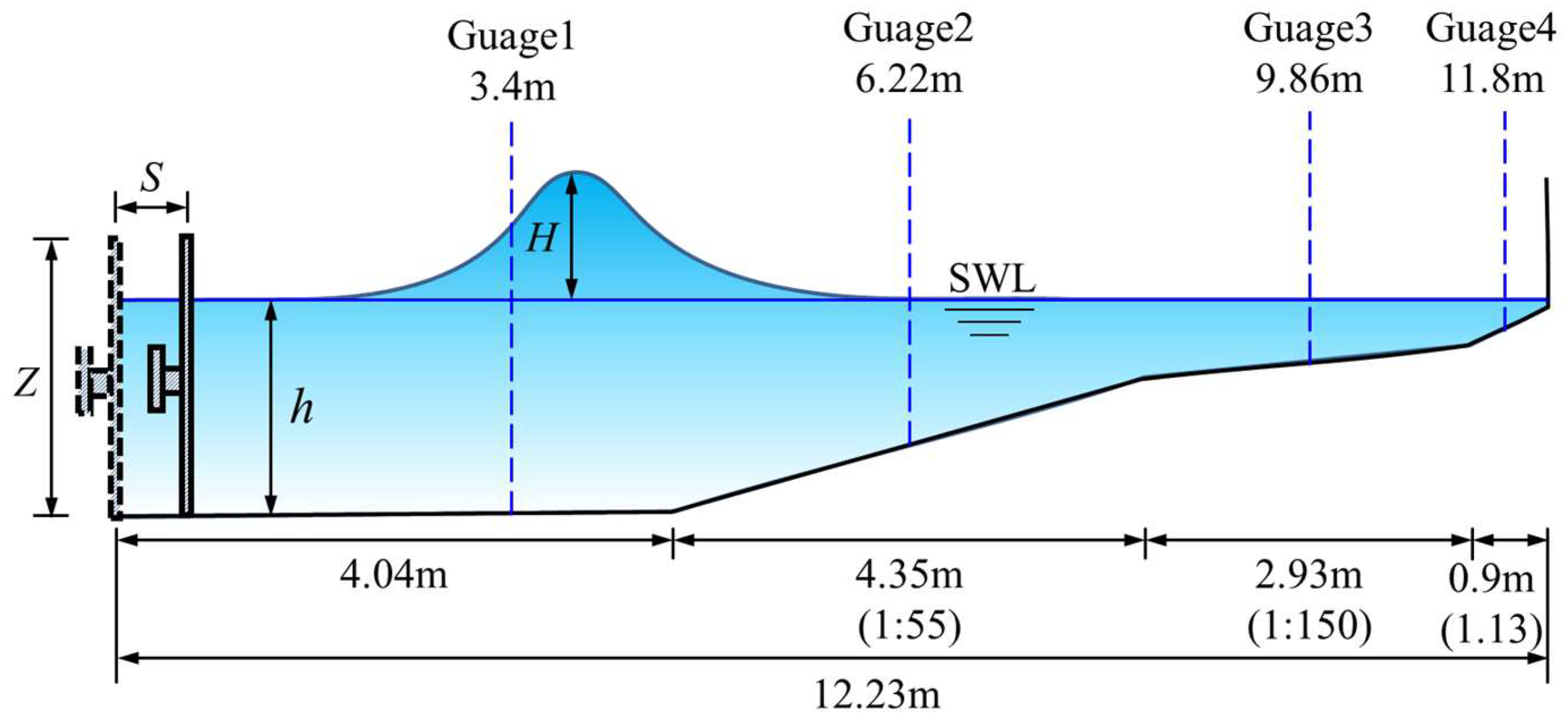
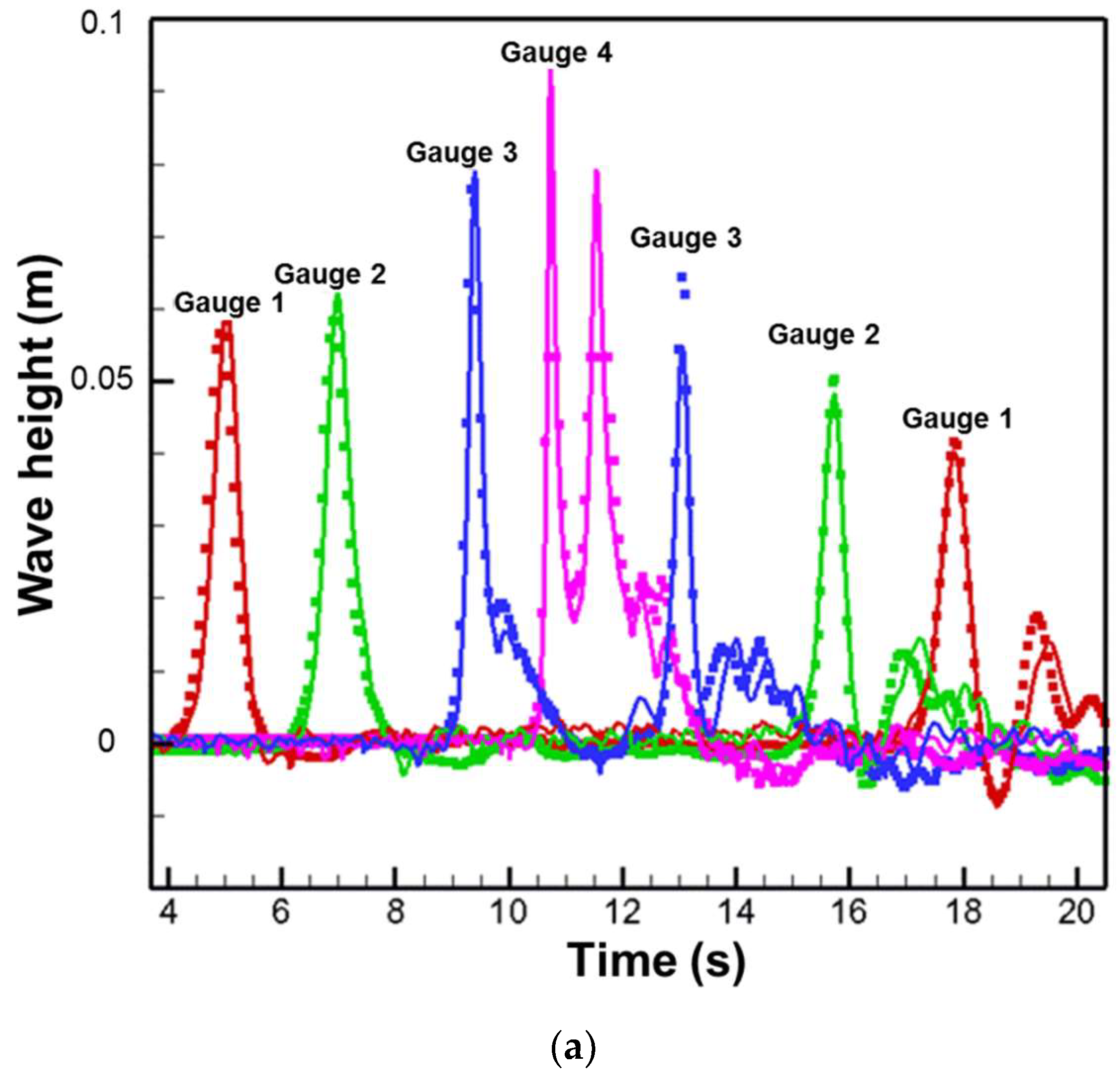
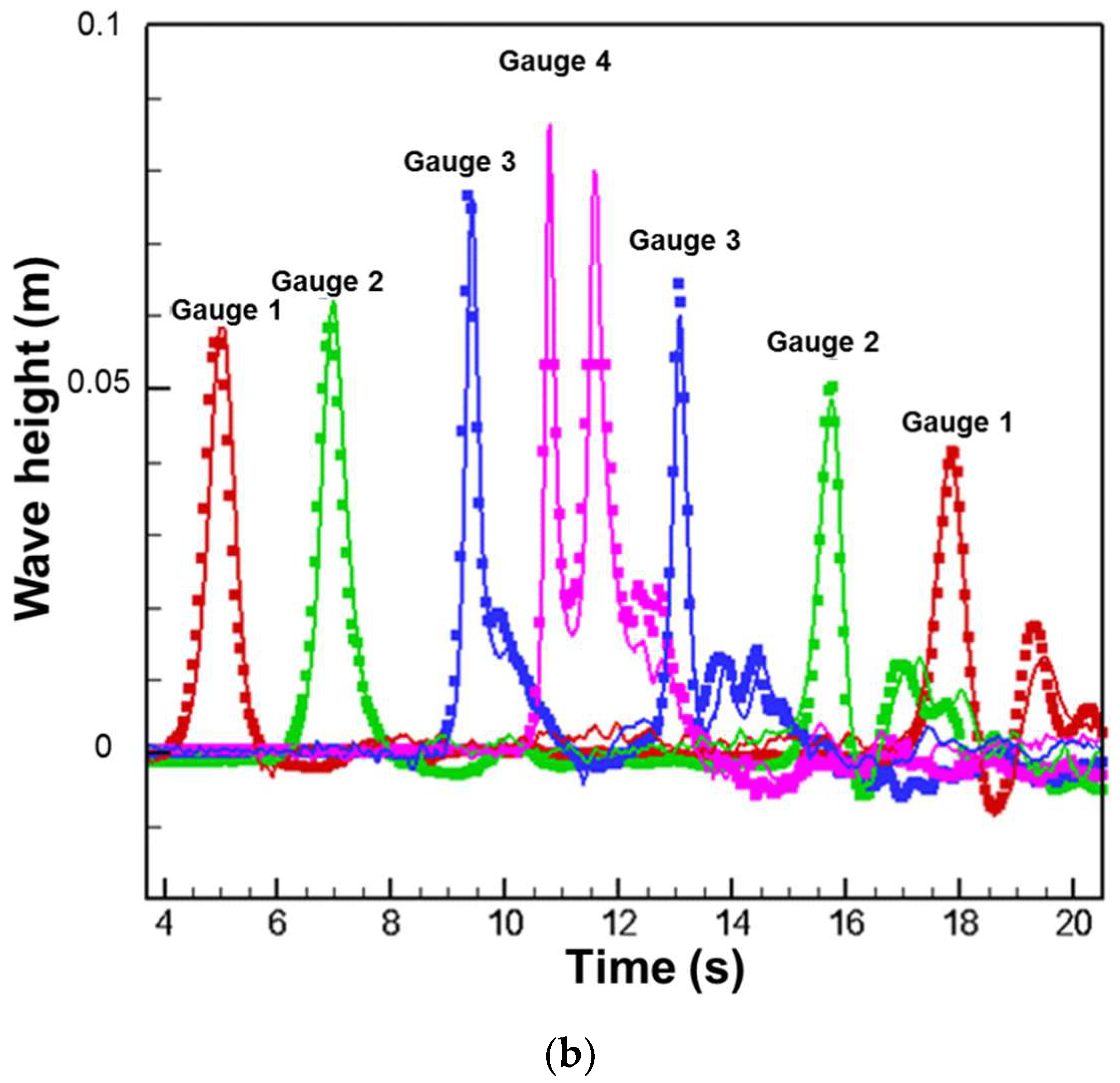
| L (m) | Z (m) | h (m) | θ (°) | l0 (m) | H/h (-) |
|---|---|---|---|---|---|
| 1.5 | 0.3 | 0.1 | 90 | 0.00125, 0.0025, 0.005, 0.010 | 0.1, 0.2, 0.3, 0.4, 0.5,0.6 |
| 45 | 0.0025 | 0.05, 0.1, 0.2, 0.3, 0.4, 0.5 | |||
| 26 | 0.15, 0.163, 0.2, 0.25, 0.3, 0.35 |
| Case | Breaking | Target Wave Height (-) | A1 (-) | A2 (-) | A3 (-) | A4 (-) |
|---|---|---|---|---|---|---|
| 1 | ▲ | 0.3 | 12.85 | 2.93 | 9.42 | −12.85 |
| 2 | O | 0.7 | 19.63 | 4.368 | 12.25 | −19.63 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.-M.; Park, J.-I.; Park, J.-C. Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method. Water 2019, 11, 462. https://doi.org/10.3390/w11030462
Jeong S-M, Park J-I, Park J-C. Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method. Water. 2019; 11(3):462. https://doi.org/10.3390/w11030462
Chicago/Turabian StyleJeong, Se-Min, Ji-In Park, and Jong-Chun Park. 2019. "Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method" Water 11, no. 3: 462. https://doi.org/10.3390/w11030462
APA StyleJeong, S.-M., Park, J.-I., & Park, J.-C. (2019). Numerical Simulation of 2-D Solitary Wave Run-Up over Various Slopes Using a Particle-Based Method. Water, 11(3), 462. https://doi.org/10.3390/w11030462






