Stabilized Formulation for Modeling the Erosion/Deposition Flux of Sediment in Circulation/CFD Models
Abstract
1. Introduction
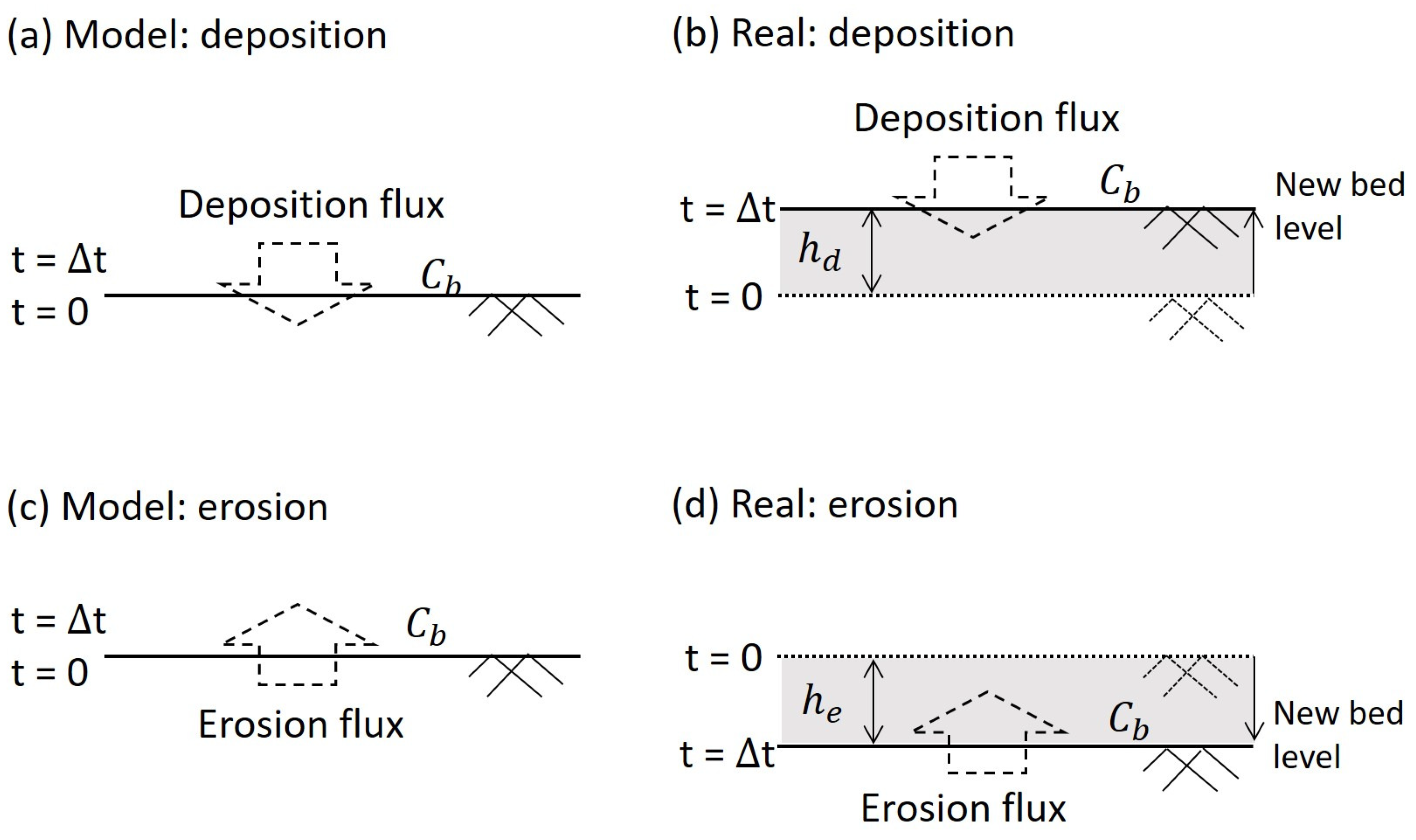
2. Modified Erosion/Deposition Equations Based on Moving-Bottom Formulation
2.1. Deposition
2.2. Erosion
2.3. Modified Erosion/Deposition Formula
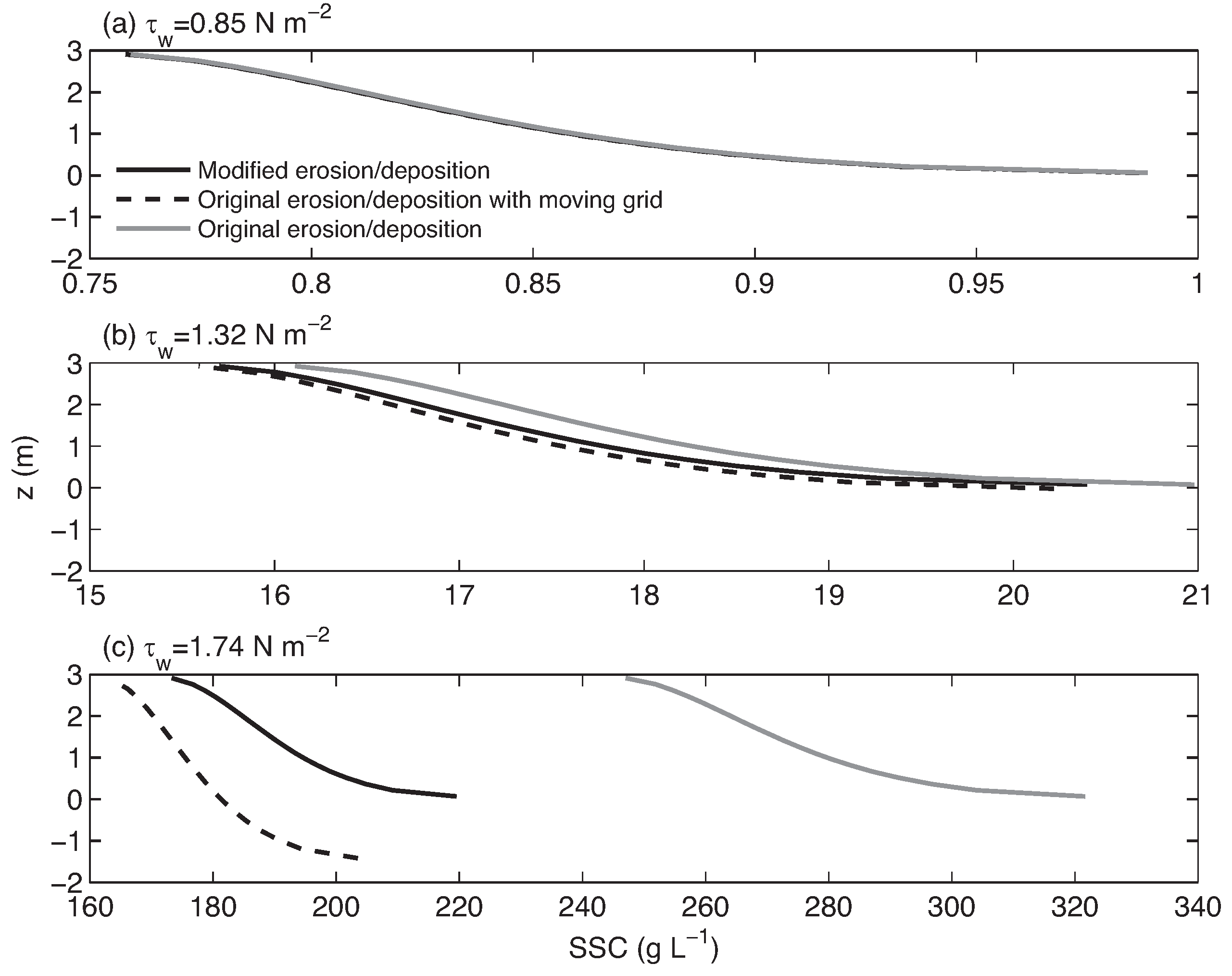
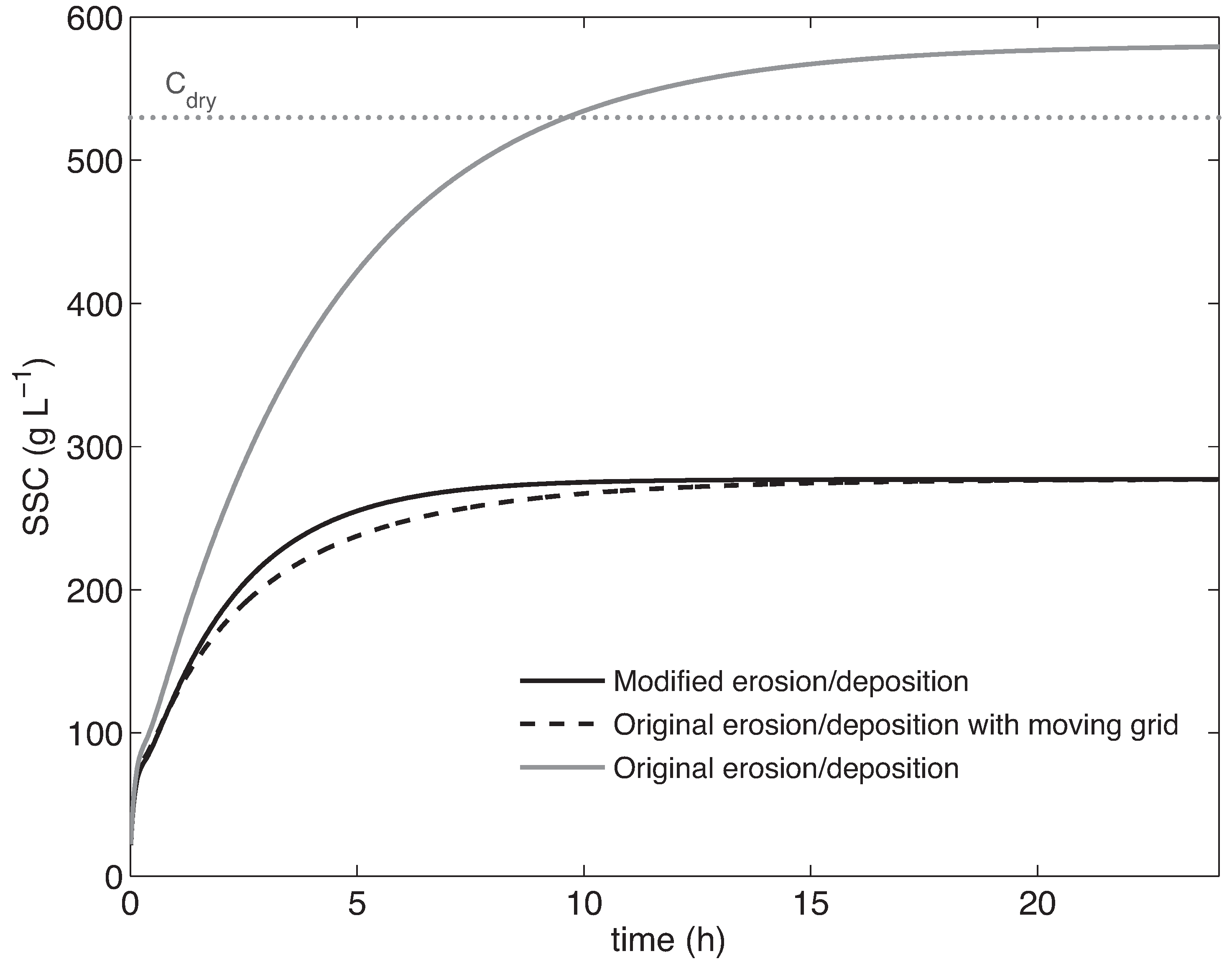
3. Numerical Tests
3.1. 1DV Model
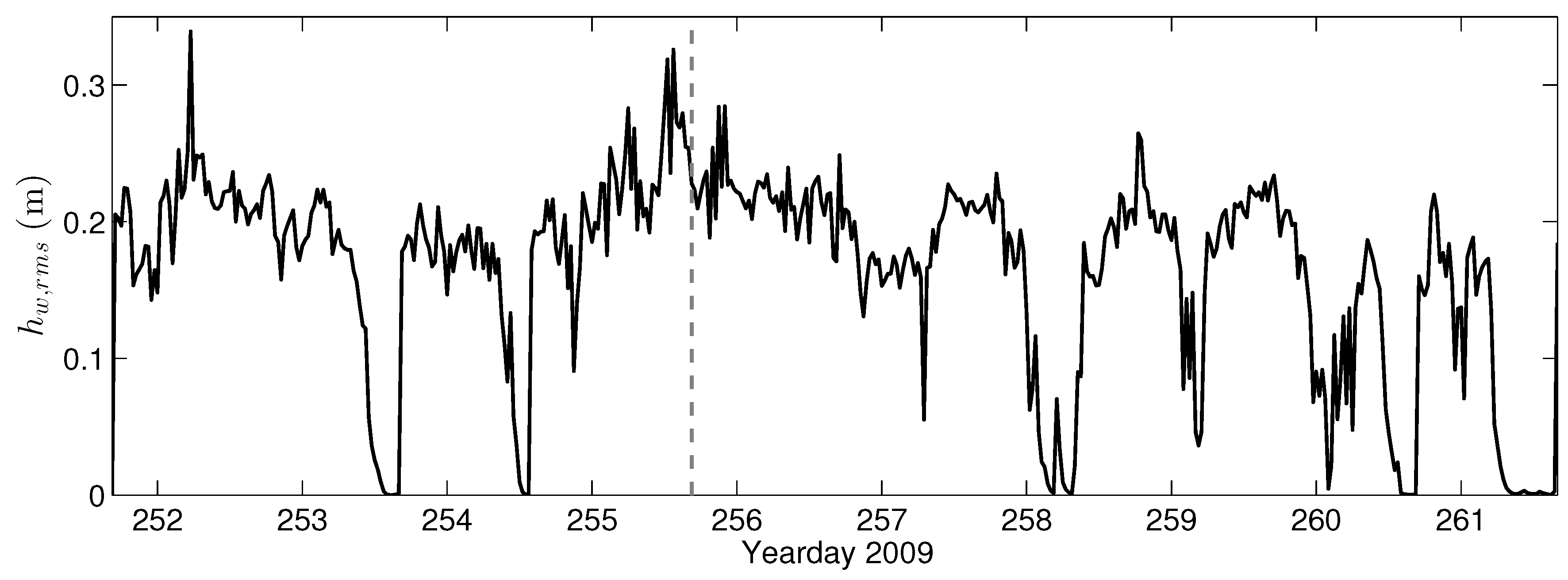
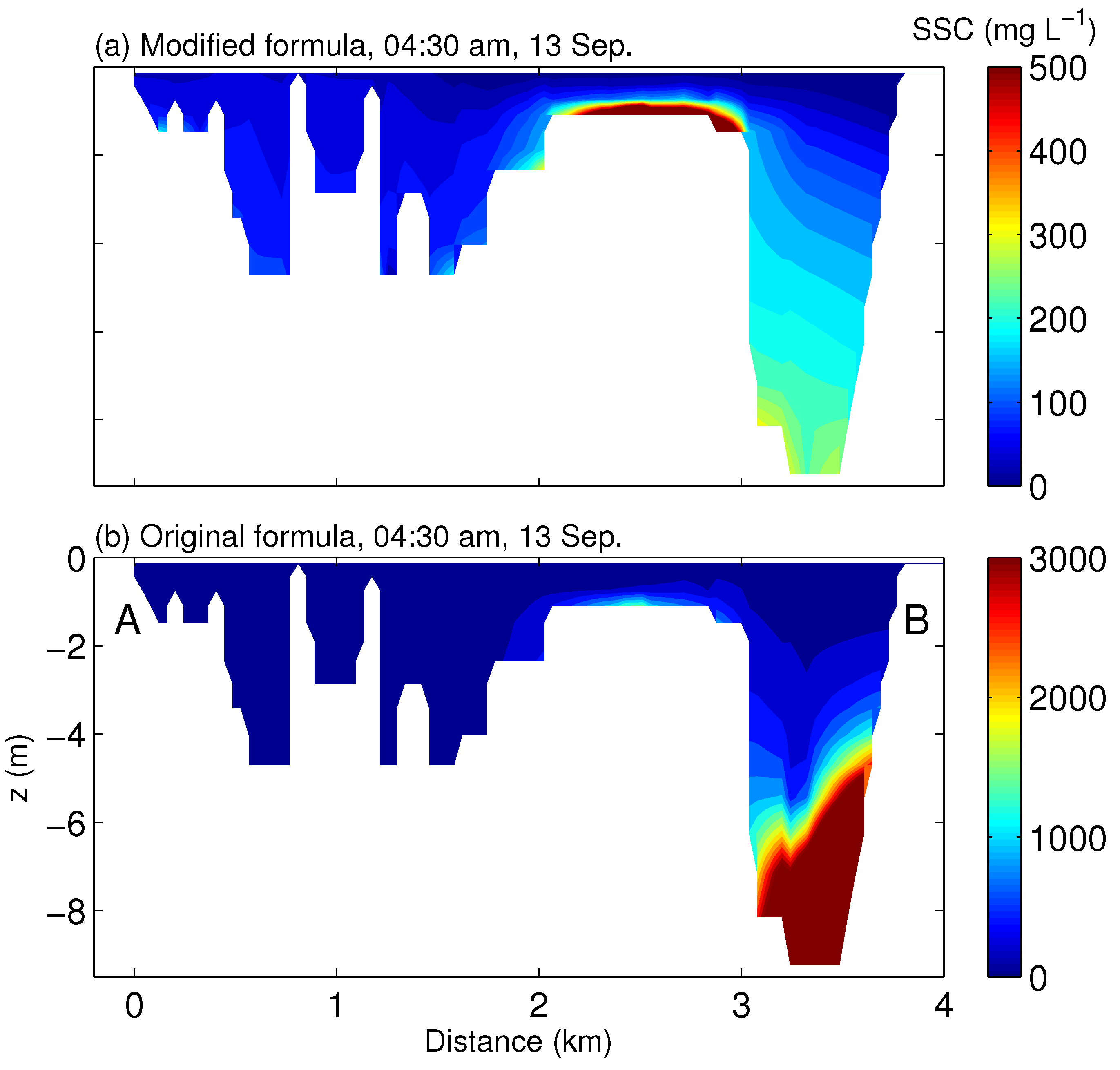
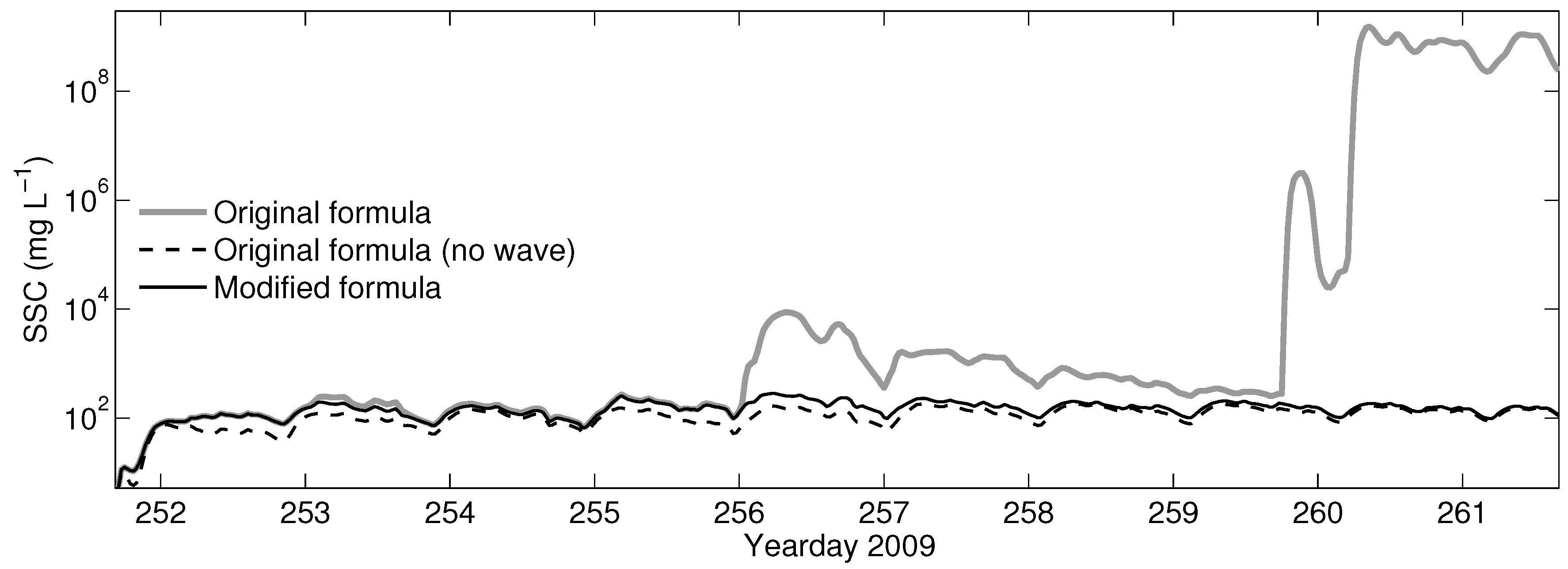
3.2. Three-Dimensional Sediment Transport Modeling of San Francisco Bay, California, USA
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries, and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Meyer-Peter, E.; Mueller, R. Formulas for bed-load transport. In Proceedings of the 2nd Congress of IAHR, Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
- Van Rijn, L.C. Sediment transport, part 2: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1642. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Chou, Y.J.; Nelson, K.S.; Holleman, R.C.; Fringer, O.B.; Stacey, M.T.; Lacy, J.R.; Monismith, S.G.; Koseff, J.R. Three-dimensional modeling of fine sediment transport by waves and currents in a shallow estuary. J. Geophys. Res.-Oceans 2018, 123. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment pick-up functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- Sanford, L.P.; Maa, J.P. A unified erosion formulation for fine sediments. Mar. Geol. 2001, 179, 9–23. [Google Scholar] [CrossRef]
- Parchure, T.M.; Mehta, A.J. Erosion of soft cohesive sediment deposits. J. Hydraul. Eng. 1985, 111, 1308–1326. [Google Scholar] [CrossRef]
- Mehta, A.J. Laboratory studies on cohesive sediment deposition and erosion. In Physical Processes in Estuaries; Dronker, J., van Leussen, W., Eds.; Springer: Berlin, Germany, 1988; pp. 578–584. [Google Scholar]
- Amos, C.L.; Daborn, G.R.; Christian, H.A.; Atkinson, A.; Robertson, A. In situ erosion measurement on fine grained sediments from the Bay of Fundy. Mar. Geol. 1992, 108, 175–196. [Google Scholar] [CrossRef]
- Chapaplain, G.; Sheng, Y.P.; Temperville, A.T. About the specification of erosion flux for soft stratified cohesive sediments. Math. Geol. 1994, 26, 651–676. [Google Scholar] [CrossRef]
- Gust, G.; Morris, M.J. Erosion thresholds and entrainment rates of undisturbed in situ sediments. J. Coast. Res. 1989, 5, 87–100. [Google Scholar]
- Amos, C.L.; Feeney, T.; Sutherland, T.F.; Luternauer, J.L. The stability of fine-grained sediments from the Fraser River delta. Estuar. Coast. Shelf Sci. 1997, 45, 507–524. [Google Scholar] [CrossRef]
- McNeil, S.R.; Taylor, C.; Lick, W. Measurements of erosion of undisturbed bottom sediments with depth. J. Hydraul. Eng. 1996, 122, 316–324. [Google Scholar] [CrossRef]
- Maa, J.P.; Sanford, L.P.; Helka, J.P. Sediment resuspension characteristics in Baltimore Harbot, Maryland. Mar. Geol. 1998, 146, 137–145. [Google Scholar] [CrossRef]
- Lavelle, J.W.; Mofjeld, H.O.; Baker, E.T. An in situ erosion rate for a fine grained marine sediment. J. Geophys. Res. 1984, 89, 6543–6552. [Google Scholar] [CrossRef]
- Lick, W. The transport of contaminants in the great lakes. Ann. Rev. Earth Planet. Sci. 1982, 10, 327–353. [Google Scholar] [CrossRef]
- Ariathurai, R.; Arulanandan, K. Erosion of cohesive soil. J. Hydraul. Div. 1978, 104, 279–283. [Google Scholar]
- Warner, J.C.; Butman, B.; Alexander, P.S. Storm-driven sediment transport in Massachusetts Bay. Continent. Shelf Res. 2008, 28, 257–282. [Google Scholar] [CrossRef]
- Xue, Z.; He, R.; Liu, J.P.; Warner, J.C. Modeling transport and deposition of the Mekong River sediment. Continent. Shelf Res. 2012, 37, 66–78. [Google Scholar] [CrossRef]
- Bian, C.; Jiang, W.; Greatbatch, R.J. An exploratory model study of sediment transport sources and deposits in the Bohai Sea, Yellow Sea, and East China Sea. J. Geophys. Res.-Oceans 2013, 118, 5908–5923. [Google Scholar] [CrossRef]
- Palinkas, C.M.; Halka, J.P.; Li, M.; Sanford, L.P.; Cheng, P. Sediment deposition from tropical storms in the upper Chesapeake Bay: Field observations and model simulations. Continent. Shelf Res. 2014, 86, 6–16. [Google Scholar] [CrossRef]
- Bever, A.J.; Harris, C.K. Storm and fair-weather driven sediment-transport within Poverty Bay, New Zealand, evaluated using coupled numerical models. Continent. Shelf Res. 2014, 86, 34–51. [Google Scholar] [CrossRef]
- Grifoll, M.; Garcia, V.; Aretxabaleta, A.; Guillen, J.; Espino, M.; Warner, J.C. Formation of fine sediment deposit from a flash flood river in the Mediterranean Sea. J. Geophys. Res.-Oceans 2014, 119, 5837–5853. [Google Scholar] [CrossRef]
- Miles, T.; Seroka, G.; Kohut, J.; Schofield, O.; Glenn, S. Glider observation and modeling of sediment transport in Hurricane Sandy. J. Geophys. Res.-Oceans 2015, 120, 1771–1791. [Google Scholar] [CrossRef]
- Moriarty, J.M.; Harris, C.K.; Hadfield, M.G. Event-to-seasonal sediment dispersal on the Waipaoa River Shelf, New Zealand: A numerical modeling study. Continent. Shelf Res. 2015, 110, 108–123. [Google Scholar] [CrossRef]
- Xu, K.; Mickey, R.C.; Chen, Q.; Harris, C.K.; Hetland, R.D.; Hu, K.; Wang, J. Shelf sediment transport during hurricanes Katrina and Rita. Comput. Geosci. 2016, 90, 24–39. [Google Scholar] [CrossRef]
- Bever, A.J.; MacWilliams, M.L. Simulating sediment transport processes in San Pablo Bay using coupled hydrodynamic, wave, and sediment transport models. Mar. Geol. 2013, 345, 235–253. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Q.; Zhang, J.; Tan, F.; Wu, Y.; Zhang, N.; Yang, H.; Pang, Q. An integrated model for three-dimensional cohesive sediment transport in storm event and its application on Lianyungang Harbot, China. Ocean Dyn. 2015, 65, 395–417. [Google Scholar] [CrossRef]
- Ge, J.; Shen, F.; Guo, W.; Chen, C.; Ding, P. Estimation of critical shear stress for erosion in the Changjiang Estuary: A synergy research of observation, OCI sensing and modeling. J. Geophys. Res.-Oceans 2015, 120, 8439–8465. [Google Scholar] [CrossRef]
- DHI. MIKE 21 FLOW MODEL: Mud Transport Module; User Guide; DHI Water and Environment: Hørsholm, Denmark, 2007. [Google Scholar]
- Winterwerp, J.C. Stratification effects by cohesive and noncohesive sediment. J. Geophys. Res. 2001, 106, 22559–22574. [Google Scholar] [CrossRef]
- Chou, Y.; Fringer, O.B. Consistent discretization for simulations of flows with moving generalized curvilinear coordinates. Int. J. Numer. Methods Fluids 2010, 62, 802–826. [Google Scholar] [CrossRef]
- Chou, Y.; Fringer, O.B. A model for the simulation of coupled flow-bed form evolution in turbulent flows. J. Geophys. Res. 2010, 115, 1978–2012. [Google Scholar] [CrossRef]
- Lumborg, U.; Pejrup, M. Modelling of cohesive sediment transport in a tidal lagoon—An annual budget. Mar. Geol. 2005, 218, 1–16. [Google Scholar] [CrossRef]
- Grant, W.D.; Madsen, O.S. The continental-shelf bottom boundary layer. Annu. Rev. Fluid Mech. 1986, 18, 265–305. [Google Scholar] [CrossRef]
- Madsen, O.S.; Poon, Y.K.; Graber, H.C. Spectral wave attenuation by bottom friction: Theory. In Coastal Engineering 1988, Proceedings of the 21th International Conference on Coastal Engineering, Torremolinos, Spain, 20–25 June 1988; ASCE: New York, NY, USA, 1988; pp. 492–504. [Google Scholar]
- McKee, L.J.; Ganju, N.K.; Schoellhamer, D.H. Estimates of suspended sediment entering San Francisco Bay from Sacramento and San Joaquin Delta, San Francisco Bay, California. J. Hydrol. 2006, 323, 335–352. [Google Scholar] [CrossRef]
- Higgins, S.A.; Jaffe, B.E.; Fuller, C.C. Resconstruction sediment age profiles from historical bathymetry changes in San Pable Bay, California. Coast. Shelf Sci. 2007, 73, 165–174. [Google Scholar] [CrossRef]
- Ganju, N.K.; Schoellhamer, D.H.; Jaffe, B.E. Hindcasting of decadal-timescale estuarine bathymetric change with a tidal-timescale model. J. Geophys. Res. 2009, 114, F04019. [Google Scholar] [CrossRef]
- van der Wegen, M.; Dastgheib, A.; Jaffe, B.E.; Roelvink, D. Process-based, morphodynamic hindcast of decadal deposition patterns in San Pablo Bay, California, USA. Ocean Dyn. 2011, 61, 173–186. [Google Scholar] [CrossRef]
- Chua, V.P.; Fringer, O.B. Sensitivity analysis of three-dimensional salinity simulations in North San Francisco Bay using the unstructured-grid SUNTANS model. Ocean Model. 2011, 39, 332–350. [Google Scholar] [CrossRef]
- Chou, Y.J.; Holleman, R.C.; Fringer, O.B.; Stacey, M.T.; Monismith, S.G.; Koseff, J.R. Three-dimensional wave-coupled hydrodynamics modeling in South San Francisco Bay. Comput. Geosci. 2015, 85, 10–21. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Manning, A.J.; Schoellhamer, D.H. Factors Controlling Floc Settling Velocity Along a Longitudinal Estuarine Transect; USGS Publications Warehouse: Virgina, VA, USA, 2013.



| Layer No. | (g m−3) | (N m−2) | (g m−2 s−1) | (g m−2 s−1) | (m) | ||
|---|---|---|---|---|---|---|---|
| 1 | 75,000 | 0.1 | 4.5 | 0.01 | 1 | 0.0002 | 0.1 |
| 2 | 530,000 | 0.4 | 4.5 | 0.01 | 1 | 0.0002 | 0.5 |
| 3 | 1,200,000 | 1.2 | 4.5 | 0.01 | 1 | 0.0002 | 4.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, Y.-J.; Shao, Y.-C.; Sheng, Y.-H.; Cheng, C.-J. Stabilized Formulation for Modeling the Erosion/Deposition Flux of Sediment in Circulation/CFD Models. Water 2019, 11, 197. https://doi.org/10.3390/w11020197
Chou Y-J, Shao Y-C, Sheng Y-H, Cheng C-J. Stabilized Formulation for Modeling the Erosion/Deposition Flux of Sediment in Circulation/CFD Models. Water. 2019; 11(2):197. https://doi.org/10.3390/w11020197
Chicago/Turabian StyleChou, Yi-Ju, Yun-Chuan Shao, Yi-Hao Sheng, and Che-Jung Cheng. 2019. "Stabilized Formulation for Modeling the Erosion/Deposition Flux of Sediment in Circulation/CFD Models" Water 11, no. 2: 197. https://doi.org/10.3390/w11020197
APA StyleChou, Y.-J., Shao, Y.-C., Sheng, Y.-H., & Cheng, C.-J. (2019). Stabilized Formulation for Modeling the Erosion/Deposition Flux of Sediment in Circulation/CFD Models. Water, 11(2), 197. https://doi.org/10.3390/w11020197





