Method for the Calculation of the Underwater Effective Wake Field for Propeller Optimization
Abstract
:1. Introduction
2. Numerical Calculation Method
2.1. Basic Formula
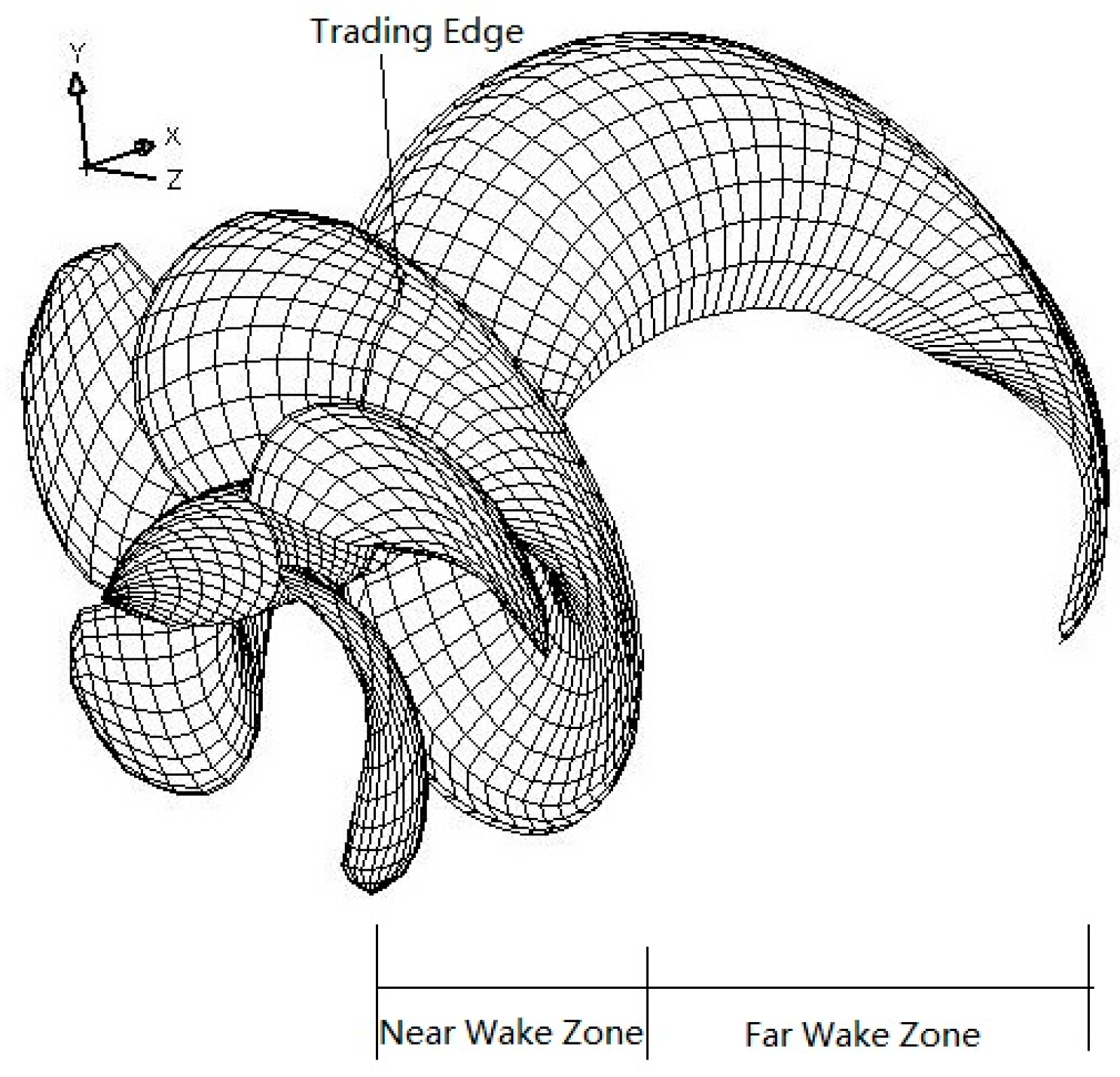
2.2. Numerical Calculation of the Unsteady Propeller-Induced Velocity Field
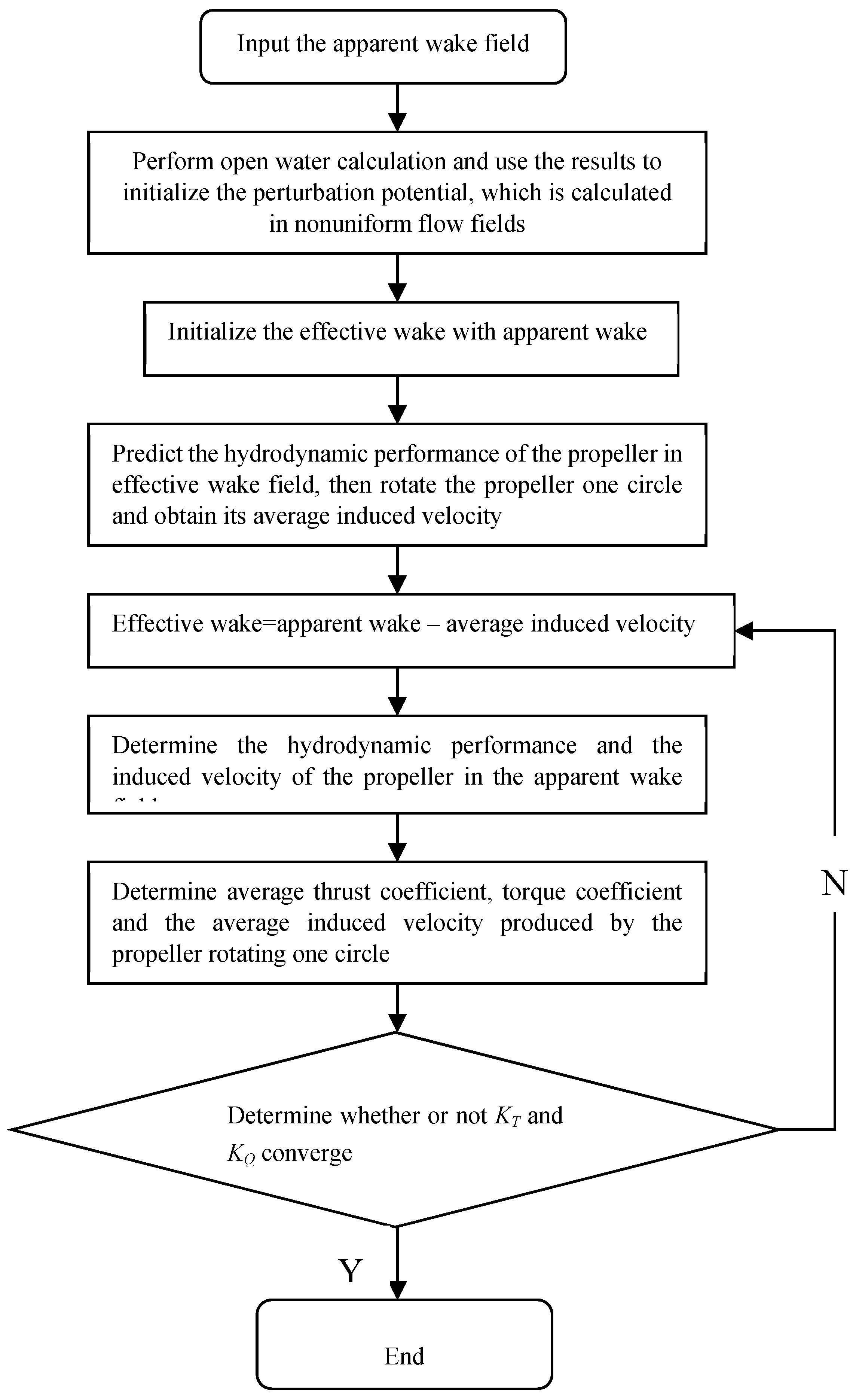
2.3. Iterative Calculation Process
3. Instance Verification
3.1. Model Introduction
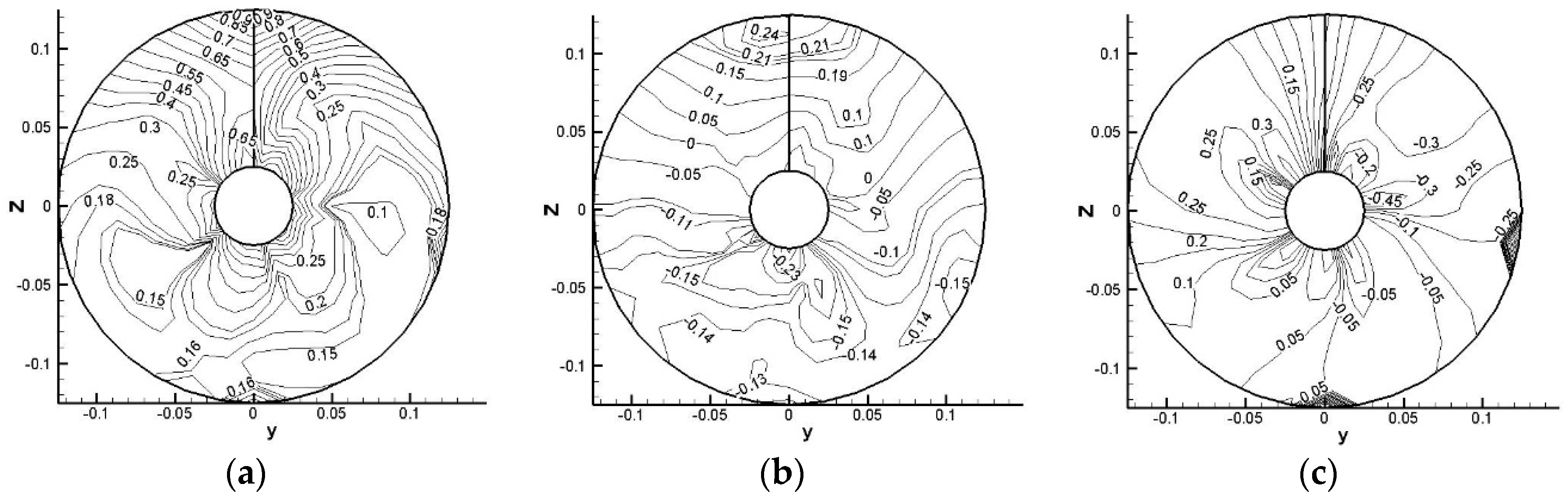
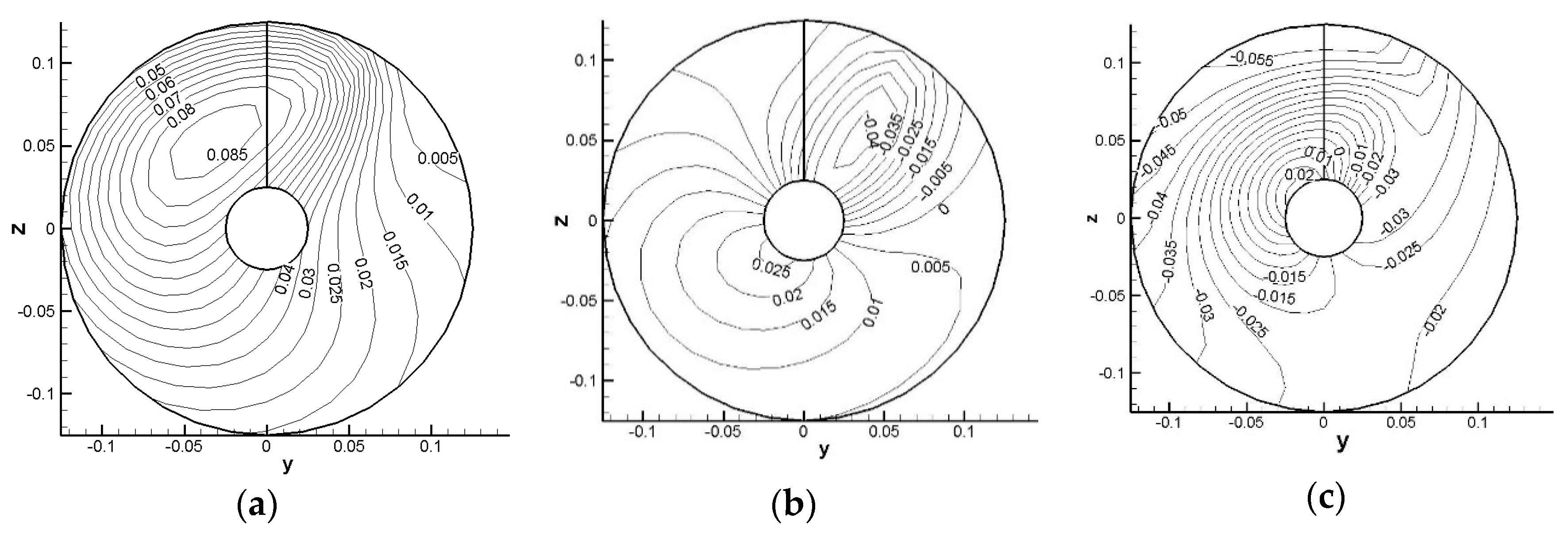
3.2. Effective Wake Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, L.D. Research status of effective wake distribution theoretical prediction. Sh. Mech. Intel. 1982. (In Chinese) [Google Scholar]
- Taylar, T.E. Combined Experimental and Theoretical Determination of Effective for a Marine Propeller. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Kinnas, S.A.; Pyo, S. Cavitating propeller analysis including the effects of wake alignment. J. Ship Res. 1999, 43, 38–47. [Google Scholar]
- Choi, J.K.; Kinnas, S.A. Prediction of non-axissymmetric effective wake by a three-dimension Euler solver. J. Ship Res. 2001, 45, 13–33. [Google Scholar]
- Choi, J.K.; Kinnas, S.A. Prediction of unsteady effective wake by a Euler solver/Vortex-lattice coupled method. J. Ship Res. 2003, 47, 131–144. [Google Scholar]
- Chios, J. Vortex Inflow-Propeller Interaction Using an Unsteady Three-Dimensional Euler Solver. Ph.D. Thesis, Department of Civil Engineering, The University of Texas at Austin, Austin, TX, USA, 2000. [Google Scholar]
- Apurva, G. Numerical Prediction of Flows around Podded Propulsor. Ph.D. Thesis, Department of Civil Engineering, The University of Texas at Austin, Austin, TX, USA, 2004. [Google Scholar]
- Gu, H. Numerical Modeling of Flow around Ducted Propellers. Ph.D. Thesis, Department of Civil Engineering, The University of Texas at Austin, Austin, TX, USA, 2006. [Google Scholar]
- Huang, T.; Wang, H. Propeller/Stern Boundary Layer Interaction on Axisymmetric Bodies: Theory and Experiment; Technical. Report. DTNSRDC 76-0113; Bethesda: Rockville, MD, USA, 1976. [Google Scholar]
- Huang, T.; Groves, N. Effective wake: Theory and experiment. In Proceedings of the 13th Symposium on Naval Hydrodynamic, Tokyo, Japan, 6–10 October 1980. [Google Scholar]
- Wu, J.M. Investigation of the scale effect correction of wake fraction during single paddle ship performance prediction. Ships 1994, 1, 25–30. (In Chinese) [Google Scholar]
- Wang, Y.Y.; Zhang, Z.Y.; Lao, G.S. The conversion method of wake distribution from model to ship wake fields. J. Dali. Univ. Technol. 1982, 21, 59–68. (In Chinese) [Google Scholar]
- Wang, Y.Y.; Dai, H.H. The correlation analysis of wake fields behind ships. Ship Eng. 1987, 3, 12–18. (In Chinese) [Google Scholar]
- Qian, W.H. Effective wake field investigation. Ship Sci. Technol. 1987, 6, 46–47. (In Chinese) [Google Scholar]
- Su, Y.M.; Huang, S.; Ikehata, M.; Kai, H. Numerical calculation of marine propeller hydrodynamic characteristics in unsteady flow by boundary element method. Shipbuild. China 2001, 42, 93–134. [Google Scholar]
- Su, Y.M.; Ikehata, M.; Kai, H. Numerical analysis of the flow field around marine propellers by surface panel method. Ocean Eng. 2002, 20, 44–48. (In Chinese) [Google Scholar]
- Morino, L.; Chen, L.T.; Suciu, E.O. Steady and oscillatory subsonic and supersonic aerodynamics around complex configurations. AIAA J. 1975, 13, 368–374. [Google Scholar]
- Kerwin, J.E.; Leopold, R. Propeller incidence due to blade thickness. JSR 1963, 7, 1–6. [Google Scholar]
- Kerwin, J.E. Computer techniques for propeller blades section design. In Proceedings of the Second Lips Propeller Symposium, Drunen, The Netherlands, 7–31 May 1973. [Google Scholar]
- Kerwin, J.E.; Lee, C.S. Prediction of steady and unsteady marine propeller performance by numerical lifting surface theory. Trans. SNAME 1978, 86, 8. [Google Scholar]
- Kim, J.; Park, I.R.; Van, S.H. RANS computations for KRISO container ship and VLCC tanker using the WAVIS code. In Proceedings of the CFD Workshop Tokyo 2005, Tokyo, Japan, 9–11 March 2005; pp. 598–603. [Google Scholar]
- Tan, T.S. Performance Prediction and Theoretical Design Research on Propeller in Non-Uniform Flow. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2003; pp. 53–54. (In Chinese). [Google Scholar]

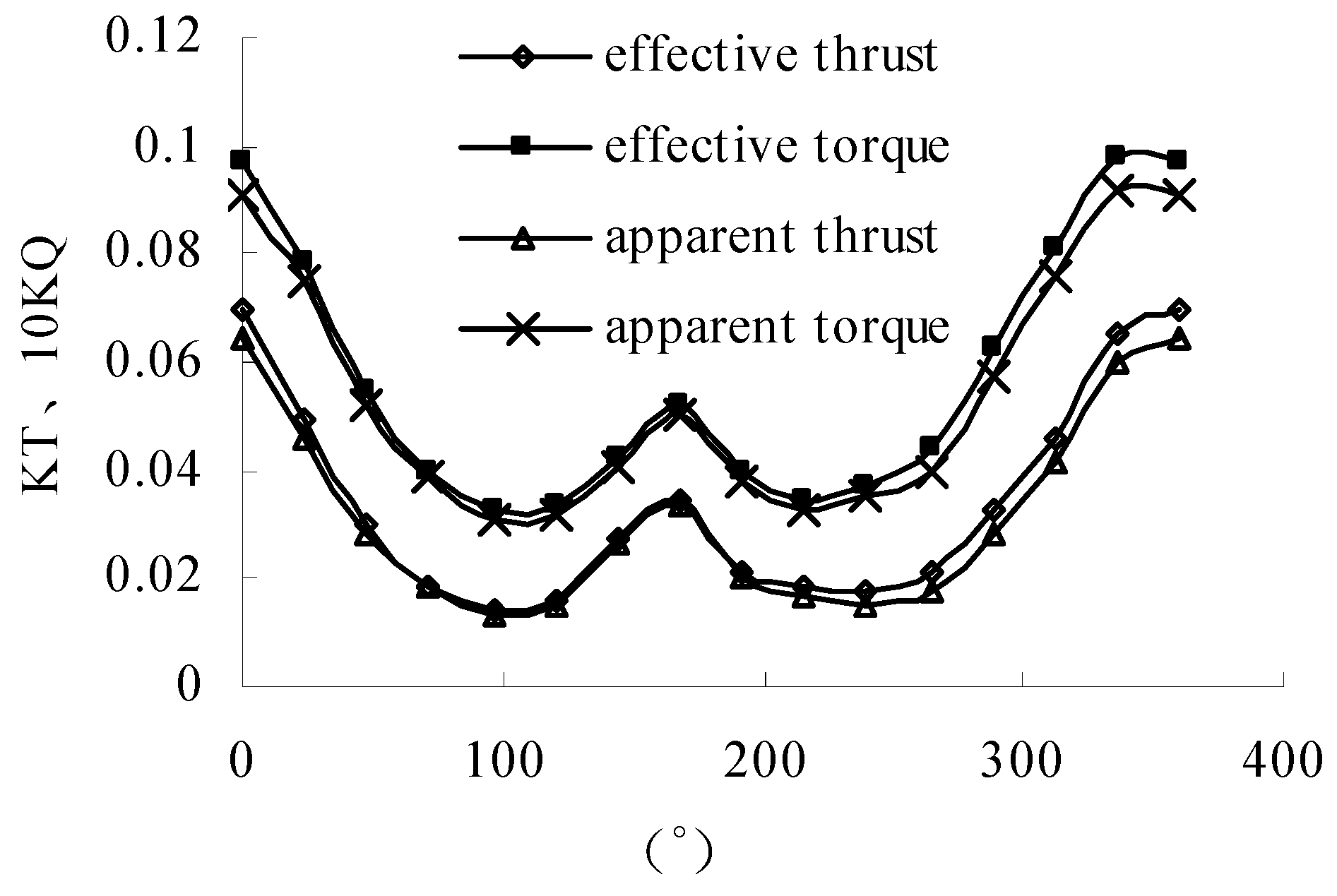
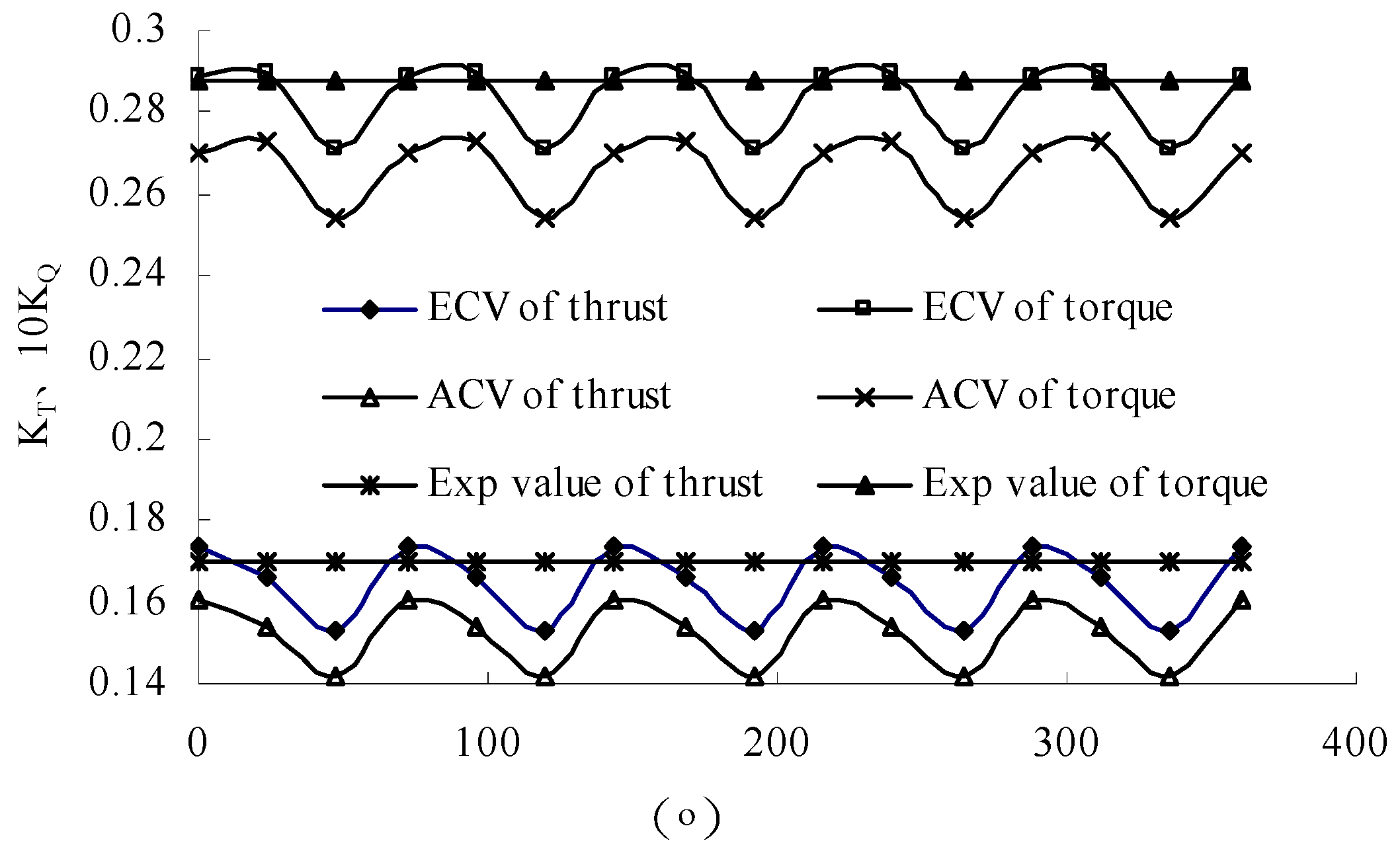
| Length between Perpendiculars (m) | Molded Breadth (m) | Draft (m) | Wetted Surface (m) | Block Coefficient | Advance Coefficient |
|---|---|---|---|---|---|
| 7.2786 | 1.0190 | 0.3418 | 9.438 | 0.65 | 0.925 |
| Number of Blades | Profile Type | Scale Ratio | Propeller Diameter (m) | Boss Ratio |
|---|---|---|---|---|
| 5 | NACA66 + a = 0.8 | 31.599 | 0.25 | 0.18 |
| Calculated Value | Experimental Value | Error | |
|---|---|---|---|
| Hull resistance (N) | 91.8 | 90 | 2% |
| Propeller thrust (N) | 58.5 | 59.9 | 2.34% |
| Propeller torque (N.m) | 2.47 | 2.53 | 2.47% |
| KT | 10KQ | |
|---|---|---|
| ECV | 0.16554 | 0.2828 |
| ACV | 0.14049 | 0.2453 |
| Experimental value | 0.17030 | 0.2880 |
| error of ECV | 2.7% | 1.80% |
| error of ACV | 17.5% | 15.2% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhao, D.; Wang, C.; Sun, S.; Ye, L. Method for the Calculation of the Underwater Effective Wake Field for Propeller Optimization. Water 2019, 11, 165. https://doi.org/10.3390/w11010165
Li J, Zhao D, Wang C, Sun S, Ye L. Method for the Calculation of the Underwater Effective Wake Field for Propeller Optimization. Water. 2019; 11(1):165. https://doi.org/10.3390/w11010165
Chicago/Turabian StyleLi, Jianing, Dagang Zhao, Chao Wang, Shuai Sun, and Liyu Ye. 2019. "Method for the Calculation of the Underwater Effective Wake Field for Propeller Optimization" Water 11, no. 1: 165. https://doi.org/10.3390/w11010165
APA StyleLi, J., Zhao, D., Wang, C., Sun, S., & Ye, L. (2019). Method for the Calculation of the Underwater Effective Wake Field for Propeller Optimization. Water, 11(1), 165. https://doi.org/10.3390/w11010165





