A Spacetime Meshless Method for Modeling Subsurface Flow with a Transient Moving Boundary
Abstract
1. Introduction
2. The Governing Equation
3. The Spacetime Meshless Method Using Trefftz Functions
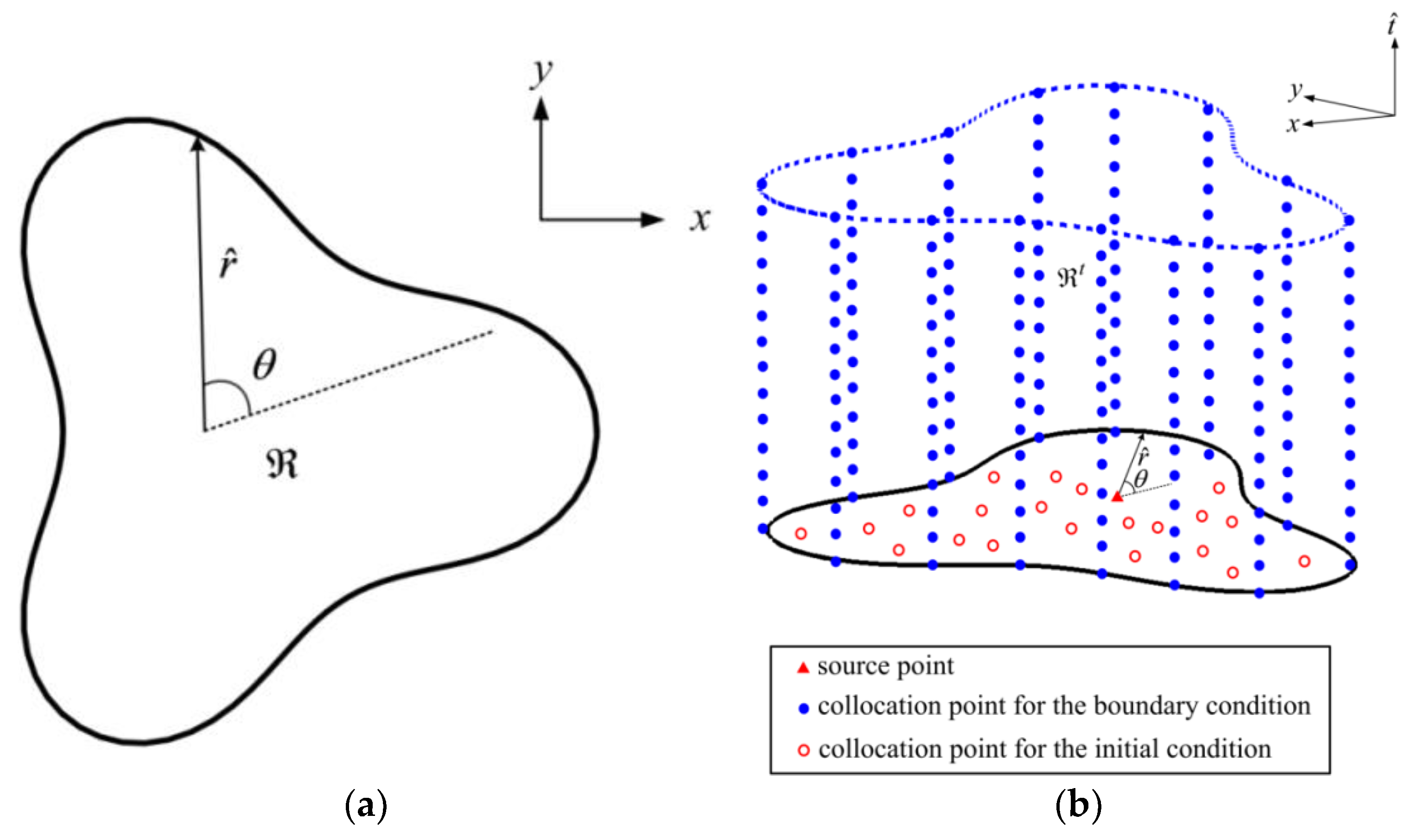
3.1. Trefftz Functions for Transient Moving Boundary Problems
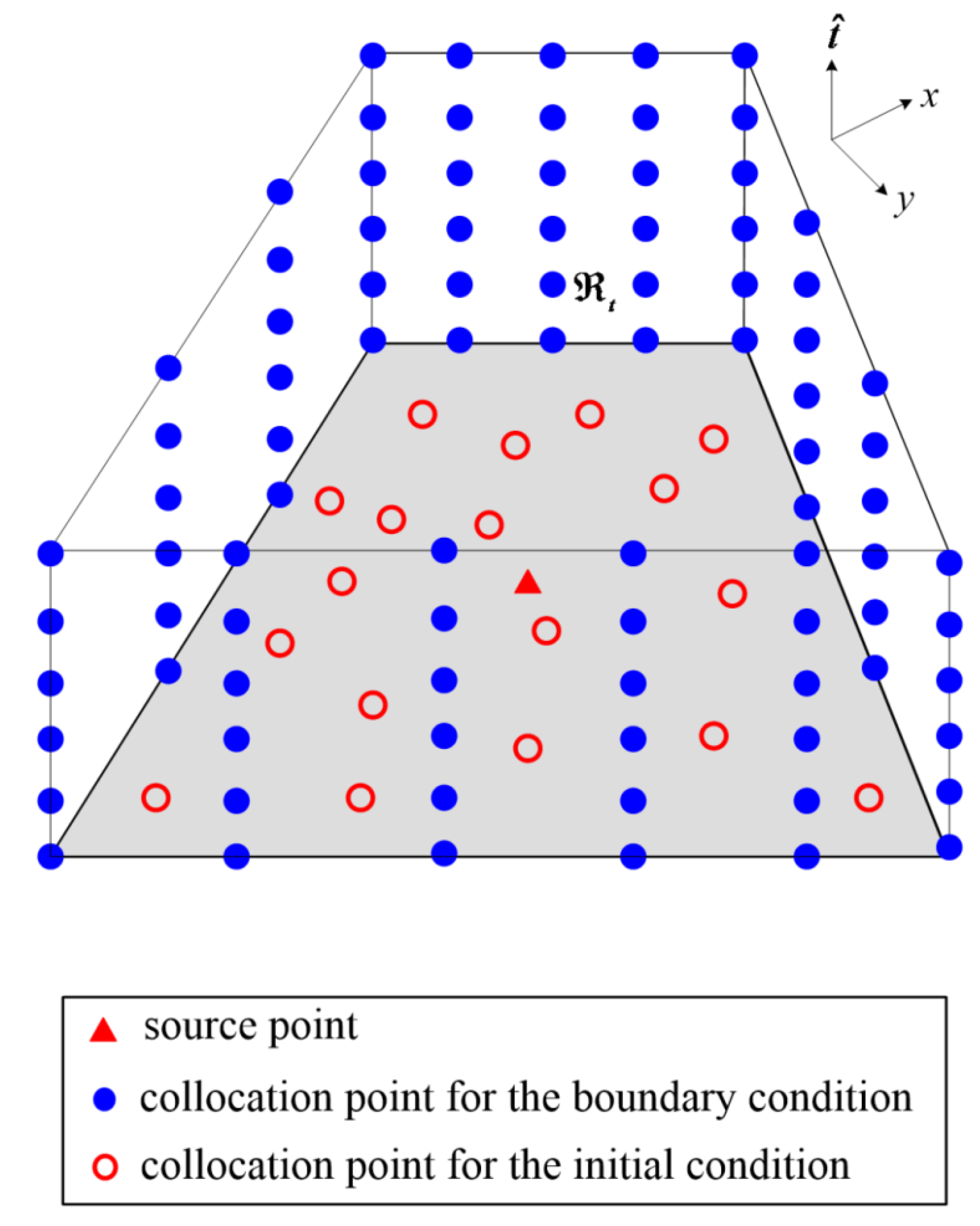
3.2. The Spacetime Collocation Scheme
3.3. The Iterative Scheme for Modeling Transient Moving Boundary
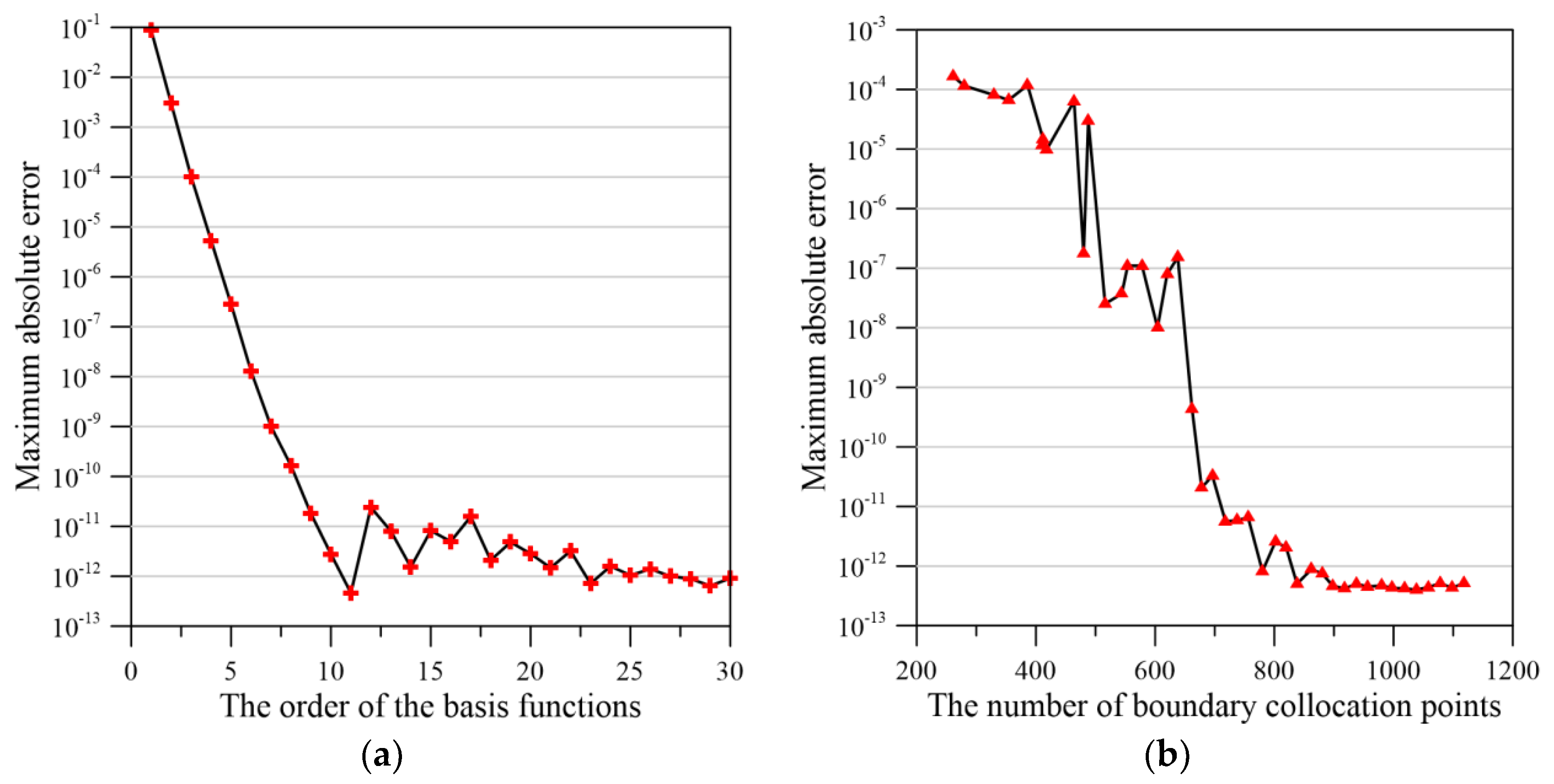
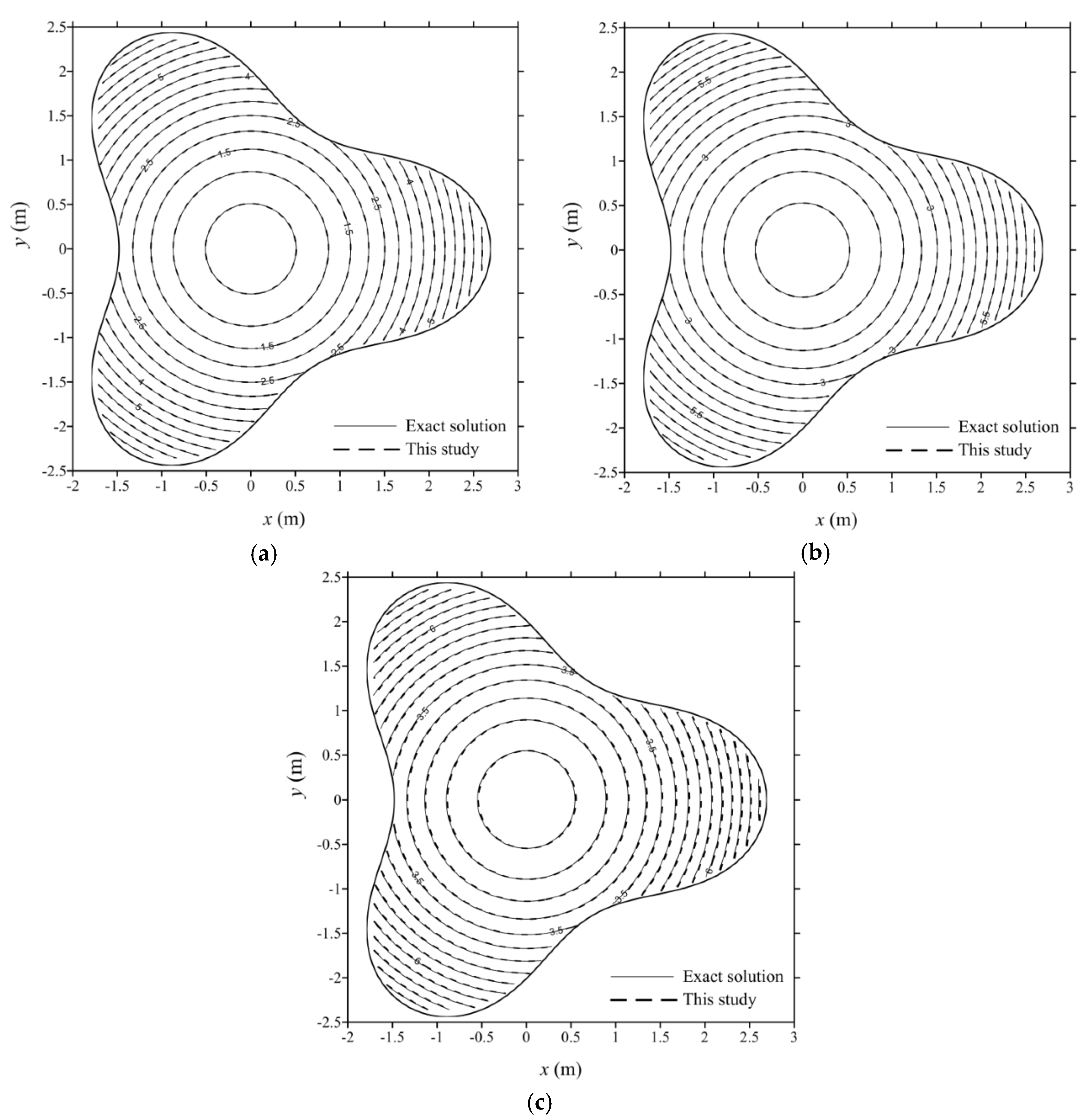
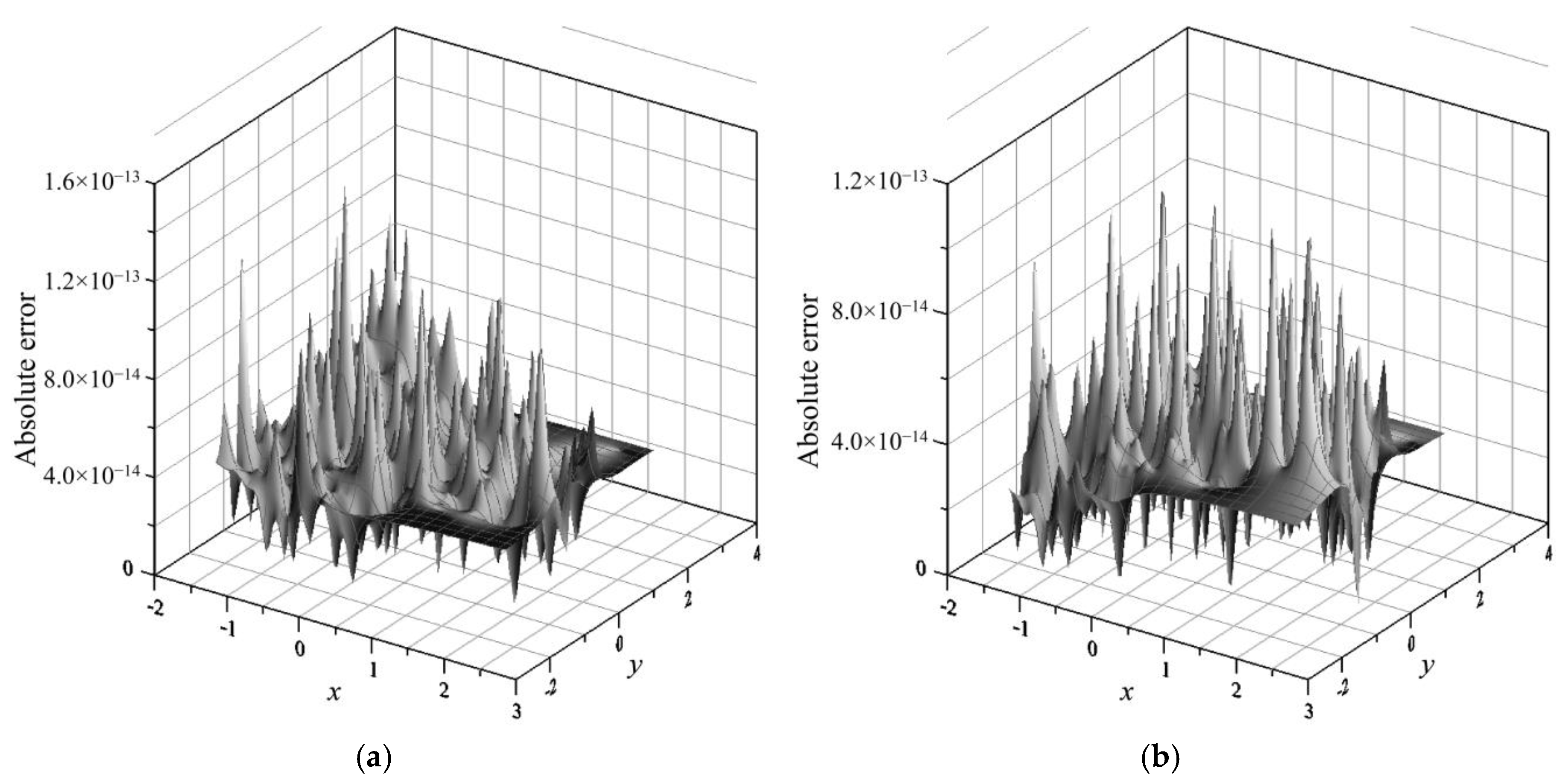
4. Numerical Examples
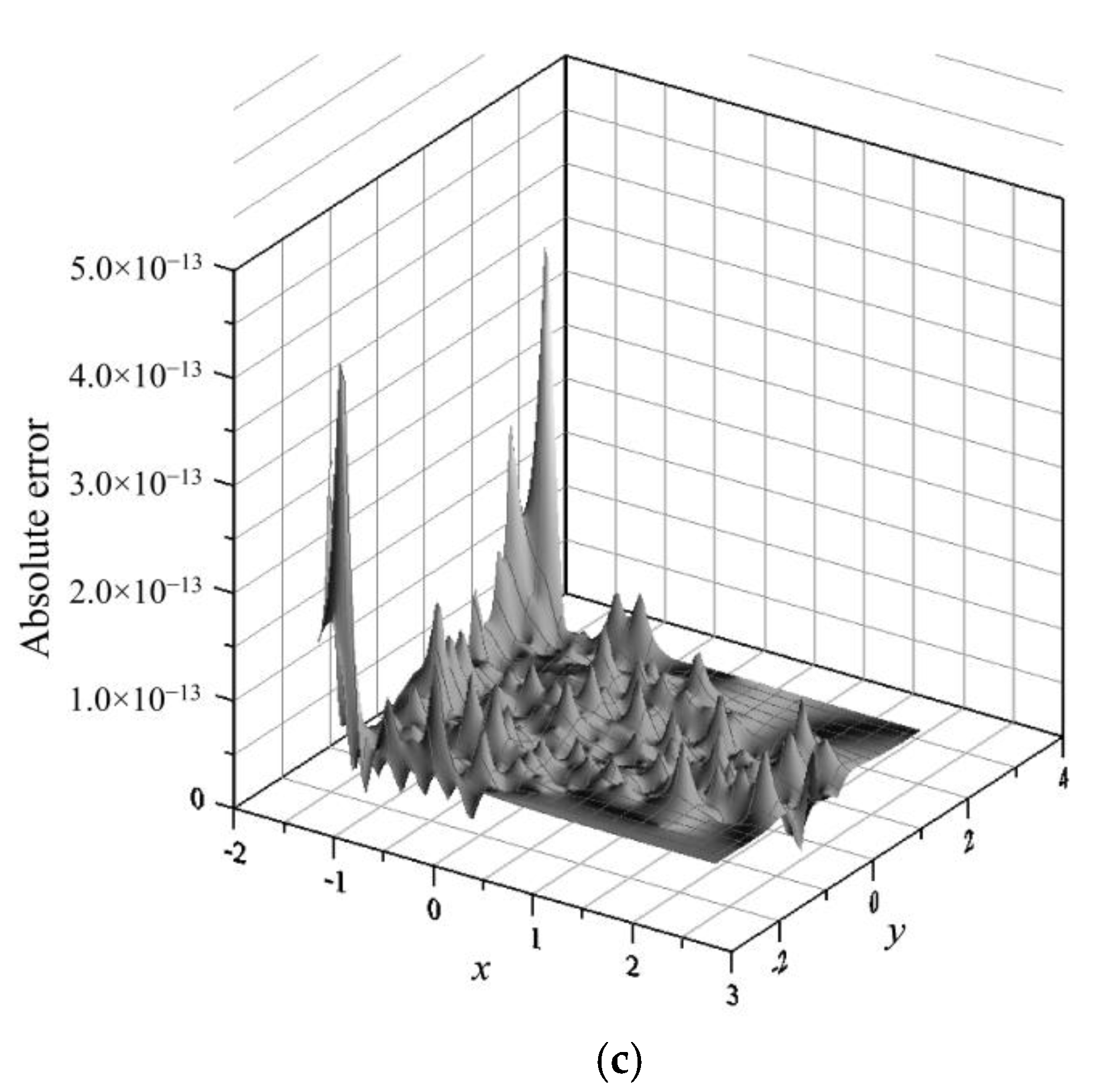
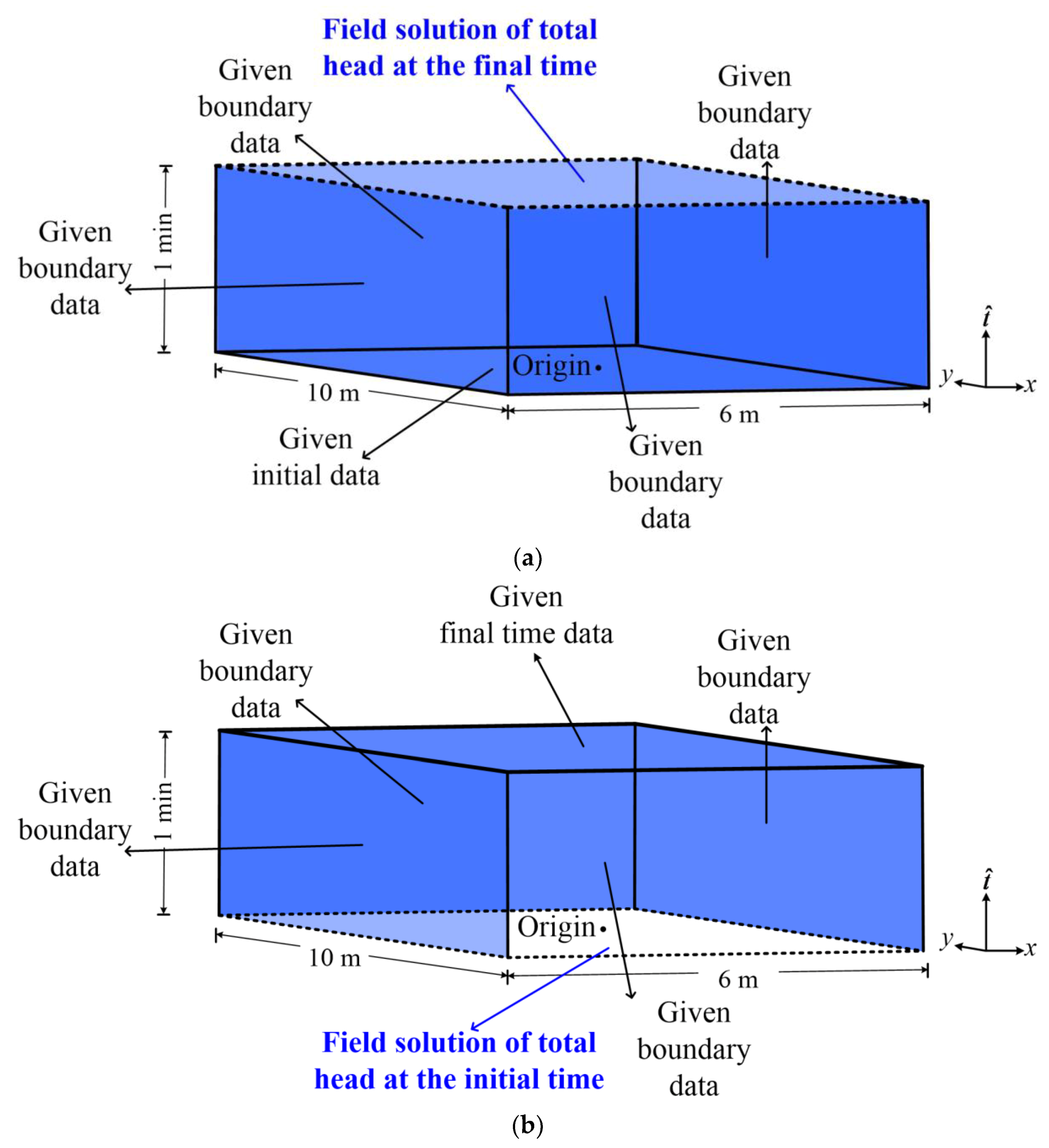
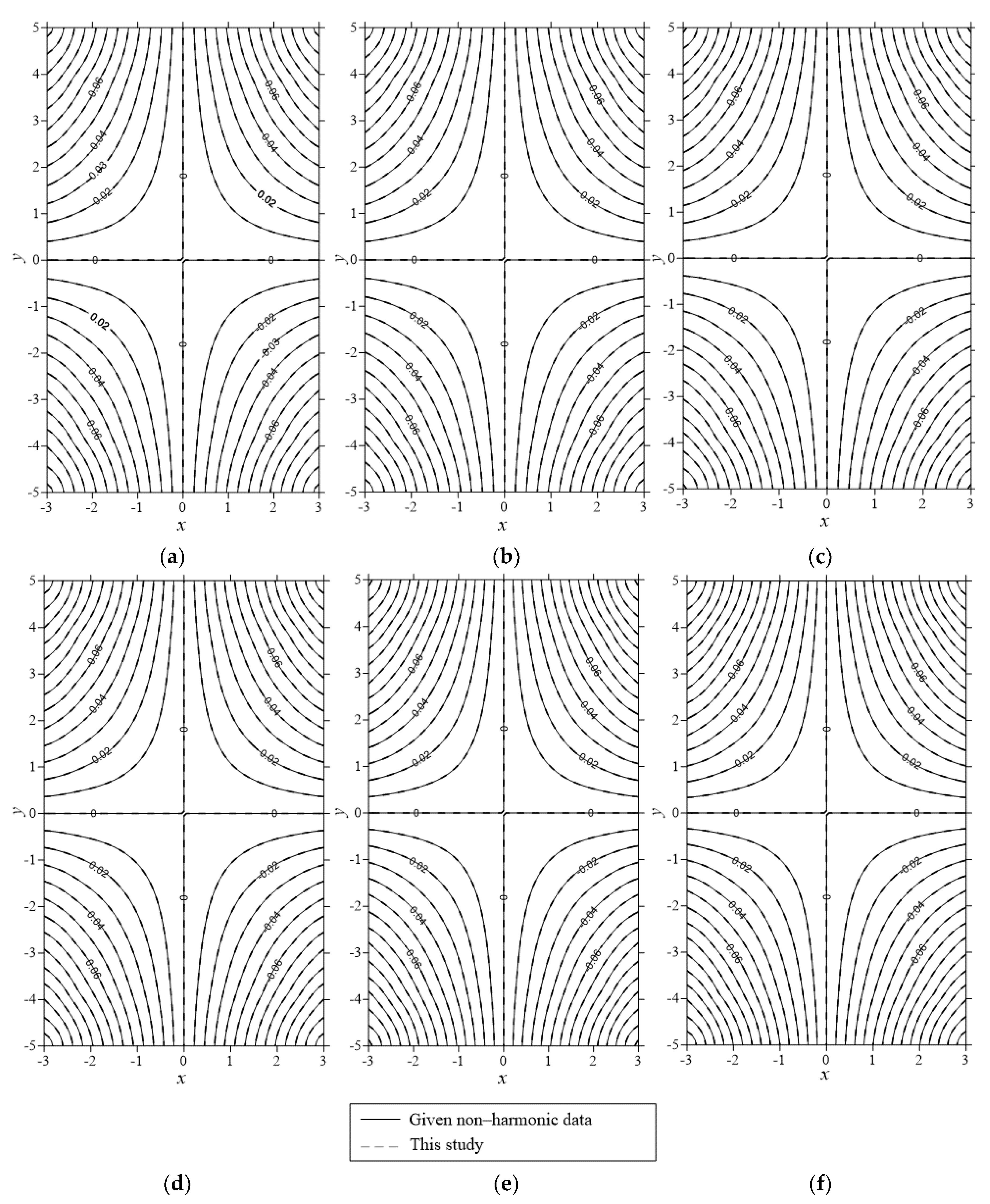
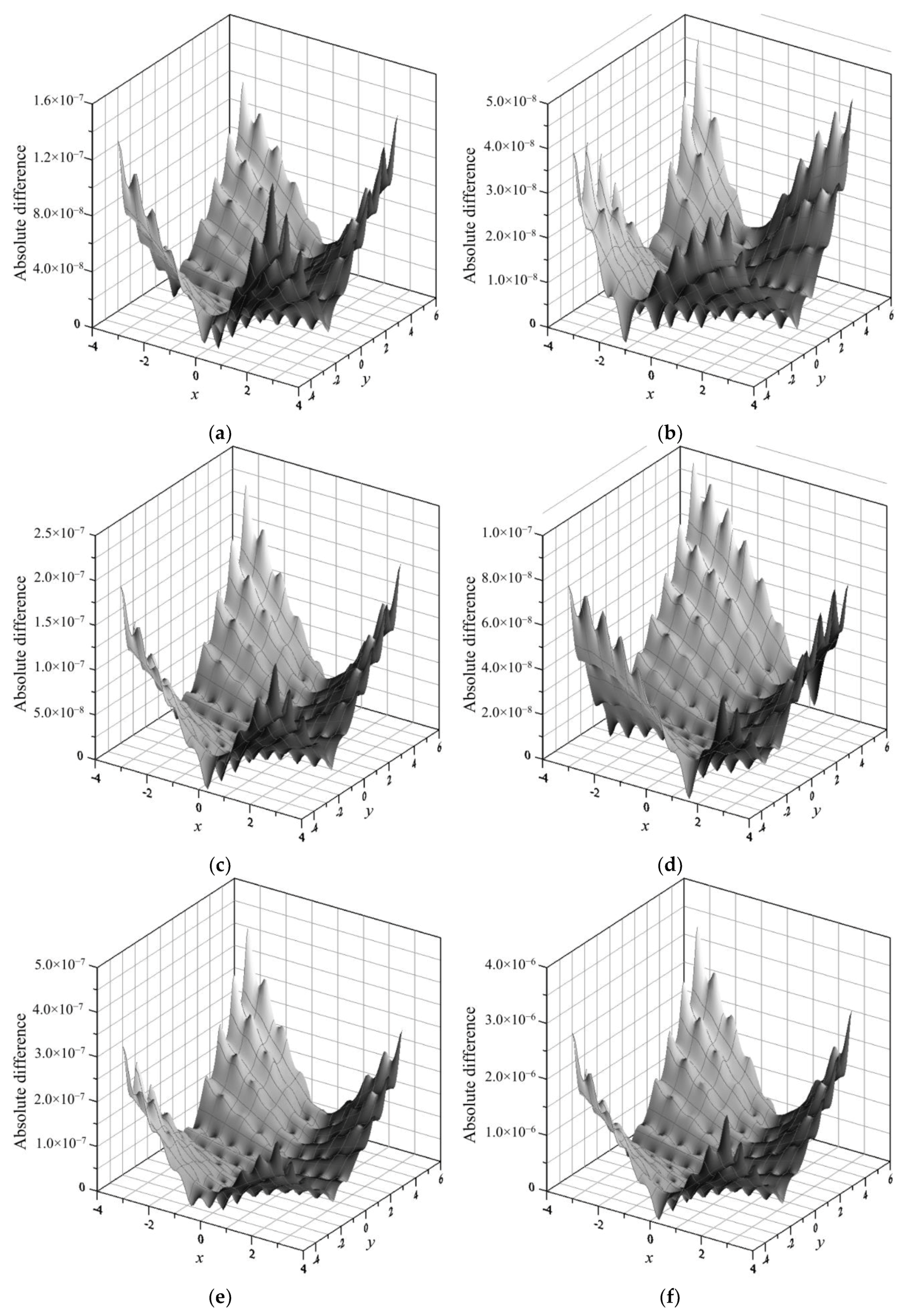
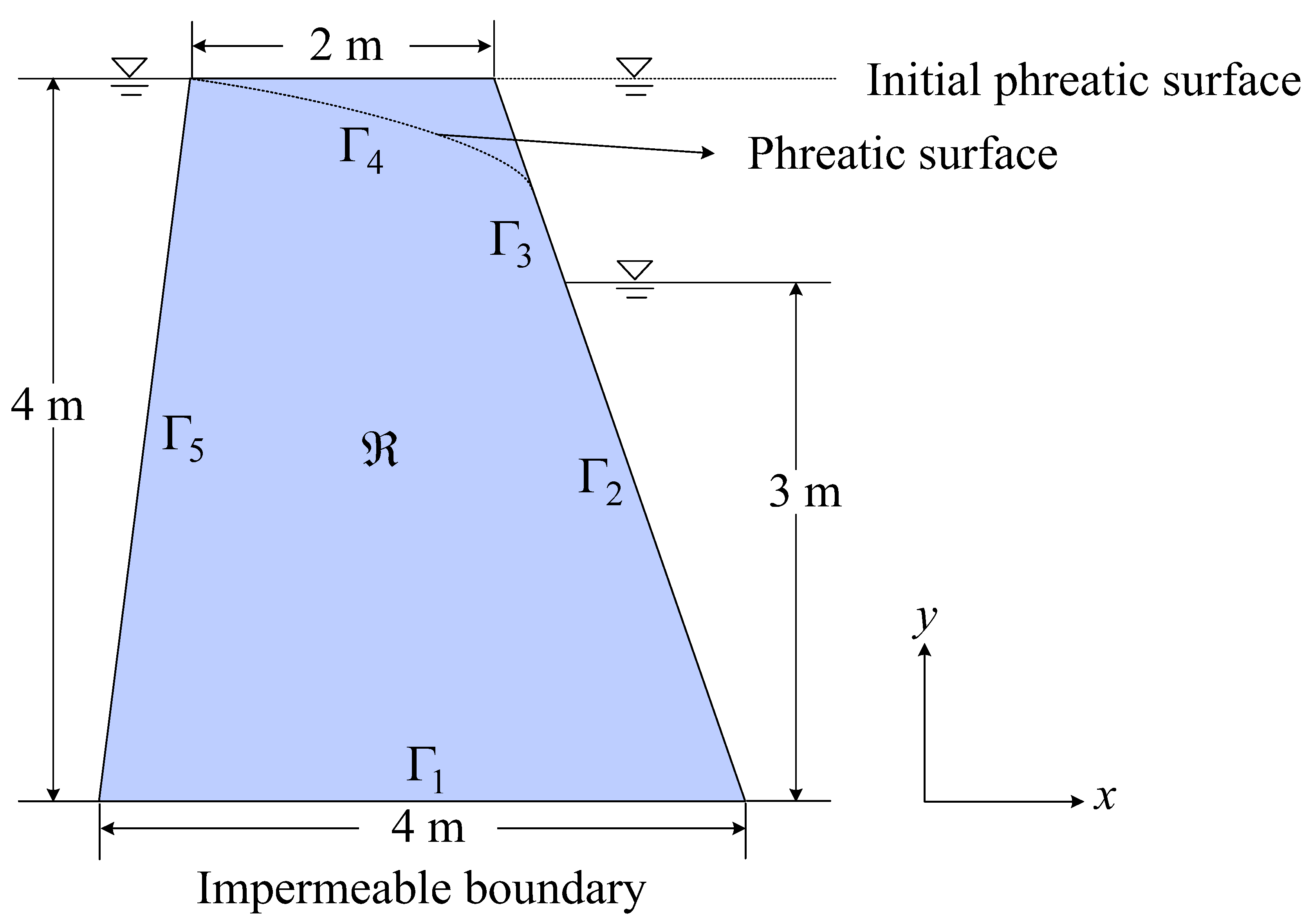
4.1. Numerical Example 1
4.2. Numerical Example 2
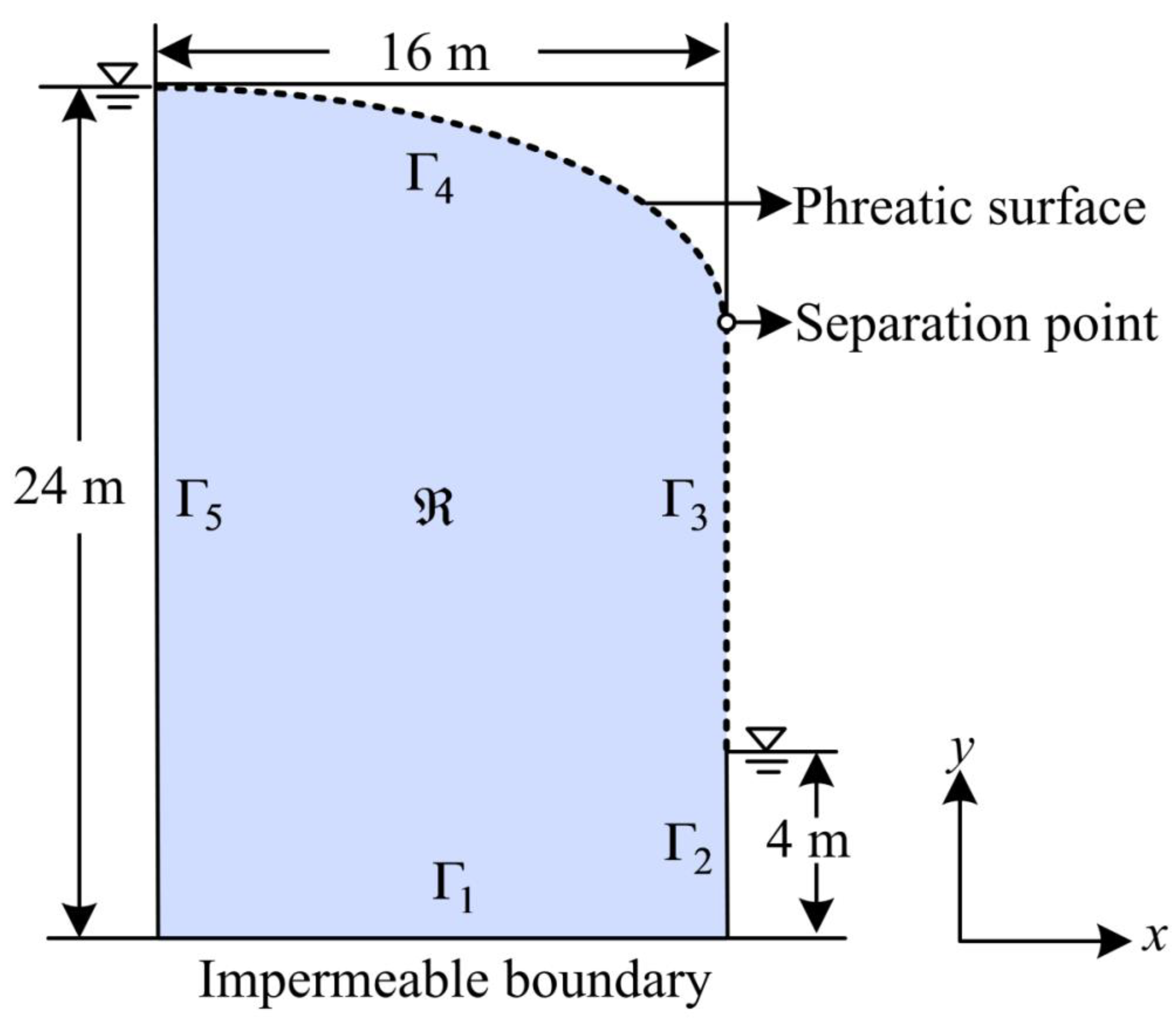
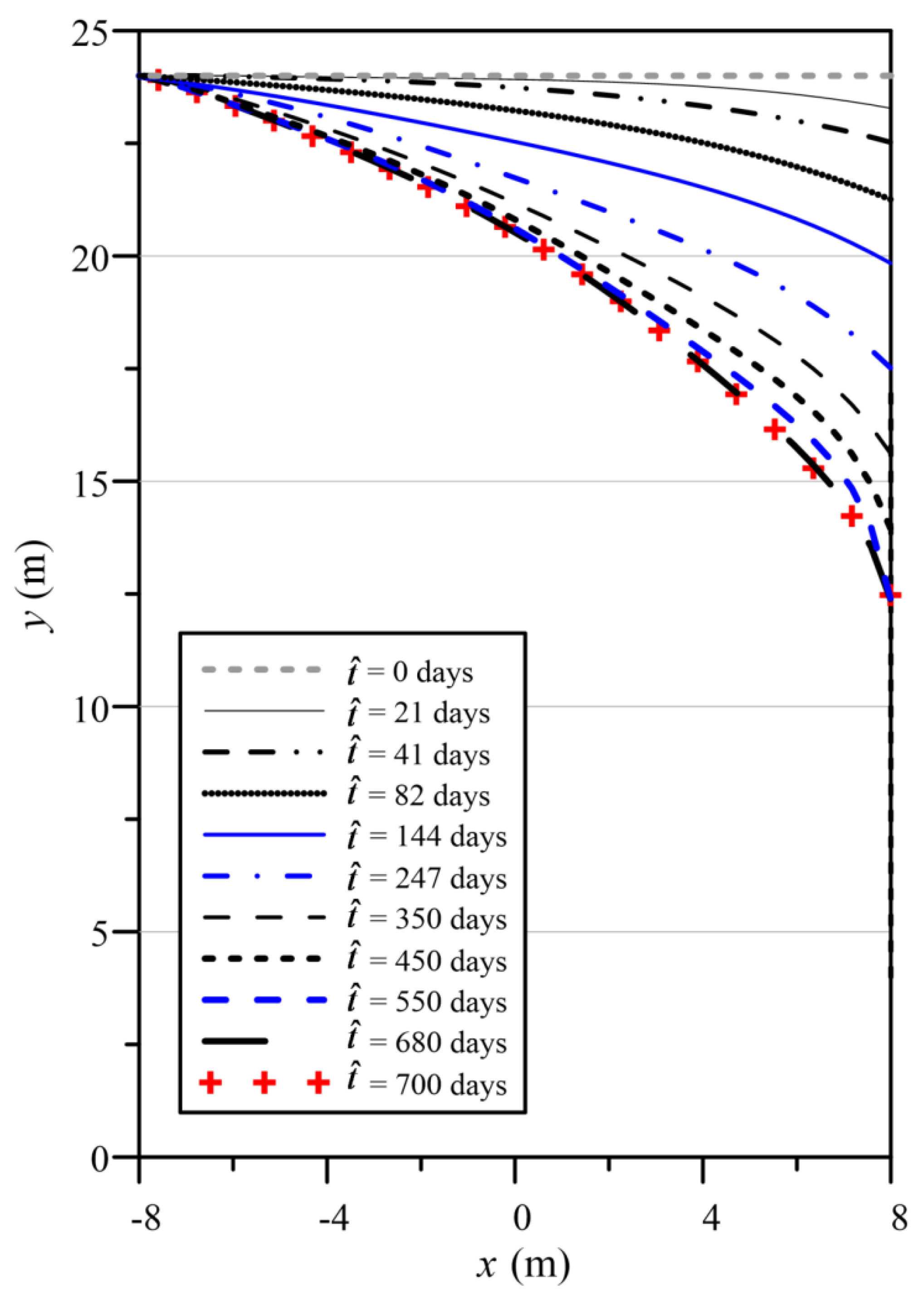
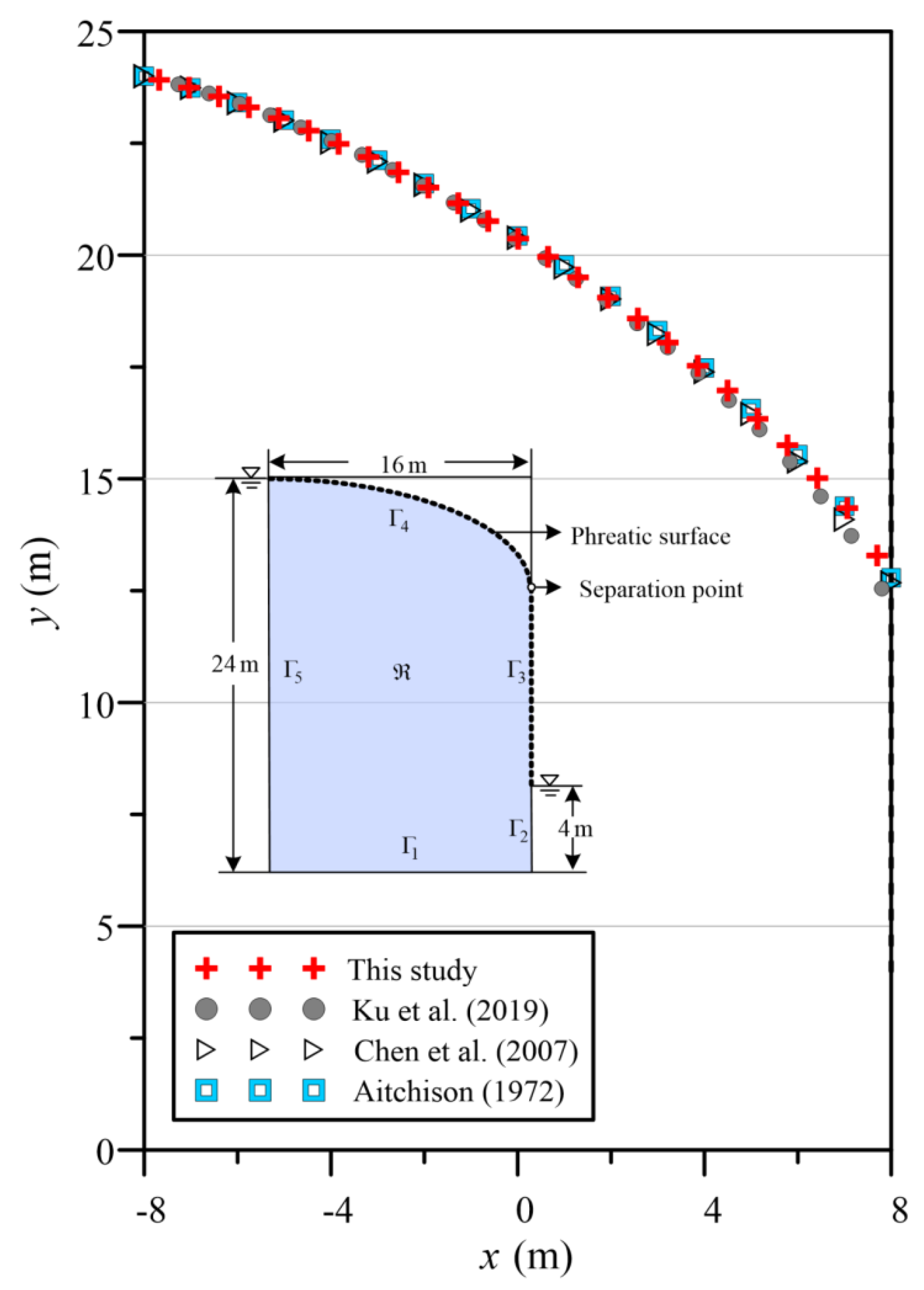
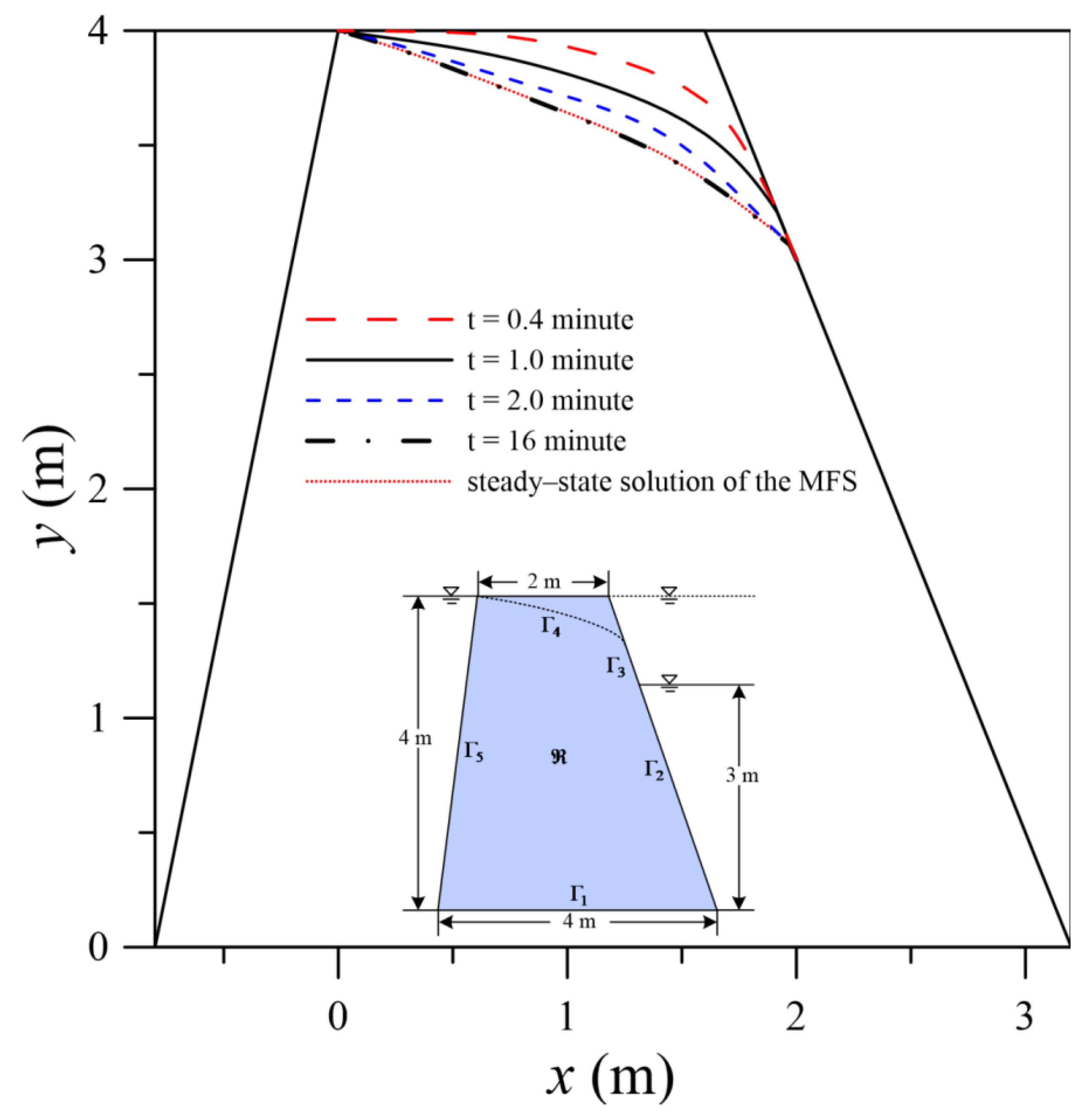
4.3. Numerical Example 3
4.4. Numerical Example 4
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | |||
Appendix B
References
- Ahmed, S.G.; Meshrif, S.A. A new numerical algorithm for 2D moving boundary problems using a boundary element method. Comput. Math. Appl. 2009, 58, 1302–1308. [Google Scholar] [CrossRef]
- Xiao, J.E.; Ku, C.Y.; Liu, C.Y.; Fan, C.M.; Yeih, W. On solving free surface problems in layered soil using the method of fundamental solutions. Eng. Anal. Bound. Elem. 2017, 83, 96–106. [Google Scholar] [CrossRef]
- Wu, C.S. A modified volume-of-fluid/hybrid Cartesian immersed boundary method for simulating free-surface undulation over moving topographies. Comput. Fluids 2019, 179, 91–111. [Google Scholar] [CrossRef]
- Huntul, M.J.; Lesnic, D. Determination of a Time-Dependent Free Boundary in a Two-Dimensional Parabolic Problem. Int. J. Appl. Comput. Math 2019, 5, 118. [Google Scholar] [CrossRef]
- Ku, C.Y.; Xiao, J.E.; Liu, C.Y. The Method of Fundamental Solutions for Three-Dimensional Nonlinear Free Surface Flows Using the Iterative Scheme. Appl. Sci. 2019, 9, 1715. [Google Scholar] [CrossRef]
- Šarler, B. Stefan’s work on solid-liquid phase changes. Eng. Anal. Bound. Elem. 1995, 16, 83–92. [Google Scholar] [CrossRef]
- Yan, Z.L.; Wang, J.J.; Chai, H.J. Influence of water level fluctuation on phreatic line in silty soil model slope. Eng. Geol. 2010, 113, 90–98. [Google Scholar] [CrossRef]
- O’Neill, K. Boundary integral equation solution of moving boundary phase change problems. Int. J. Numer. Methods Eng. 1983, 19, 1825–1850. [Google Scholar] [CrossRef]
- Chen, J.T.; Hsiao, C.C.; Chen, K.H. Study of free surface seepage problems using hypersingular equations. Commun. Numer. Methods Eng. 2007, 23, 755–769. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Tian, H.; Cao, J. Water flow and heat transport including ice/water phase change in porous media: Numerical simulation and application. Cold Reg. Sci. Tech. 2011, 68, 74–84. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, F.; Li, C. Primal mixed solution to unconfined seepage flow in porous media with numerical manifold method. Appl. Math. Model 2015, 39, 794–808. [Google Scholar] [CrossRef]
- Grabski, J.K. A meshless procedure for analysis of fluid flow and heat transfer in an internally finned square duct. Heat Mass Transf. 2019, 1–11. [Google Scholar] [CrossRef]
- Rafiezadeh, K.; Ataie-Ashtiani, B. Transient free-surface seepage in three-dimensional general anisotropic media by BEM. Eng. Anal. Bound. Elem. 2014, 46, 51–66. [Google Scholar] [CrossRef]
- Fukuchi, T. Numerical analyses of steady-state seepage problems using the interpolation finite difference method. Soils Found. 2016, 56, 608–626. [Google Scholar] [CrossRef]
- Sauerland, H.; Fries, T.P. The extended finite element method for two-phase and free-surface flows: A systematic study. J. Comput. Phys. 2011, 230, 3369–3390. [Google Scholar] [CrossRef]
- Darbandi, M.; Torabi, S.O.; Saadat, M.; Daghighi, Y.; Jarrahbashi, D. A moving-mesh finite-volume method to solve free-surface seepage problem in arbitrary geometries. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 1609–1629. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, Z.H.; Hsu, T.W. Using a local radial basis function collocation method to approximate radiation boundary conditions. Ocean Eng. 2015, 105, 231–241. [Google Scholar] [CrossRef]
- Wang, D.; Chen, C.S.; Fan, C.M.; Li, M. The MAPS based on trigonometric basis functions for solving elliptic partial differential equations with variable coefficients and Cauchy–Navier equations. Math. Comput. Simul. 2019, 159, 119–135. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.M.; Qu, W.; Wang, F.; Zhang, C. Localized method of fundamental solutions for three-dimensional inhomogeneous elliptic problems: Theory and MATLAB code. Comput. Mech. 2019, 1–22. [Google Scholar] [CrossRef]
- Li, Z.C.; Lee, M.G.; Huang, H.T.; Chiang, J.Y. Neumann problems of 2D Laplace’s equation by method of fundamental solutions. Appl. Numer. Math. 2017, 119, 126–145. [Google Scholar] [CrossRef]
- Kita, E.; Kamiya, N. Trefftz method: An overview. Adv. Eng. Softw. 1995, 24, 3–12. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, Z.Z.; Hu, H.Y.; Cheng, H.D. Trefftz and Collocation Methods; WIT Press: Southampton/Boston, UK, 2008. [Google Scholar]
- Ku, C.Y.; Xiao, J.E.; Liu, C.Y. On Solving Nonlinear Moving Boundary Problems with Heterogeneity Using the Collocation Meshless Method. Water 2019, 11, 835. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ku, C.Y.; Xiao, J.E.; Yeih, W. A Novel Spacetime Collocation Meshless Method for Solving Two-Dimensional Backward Heat Conduction Problems. Comp. Model. Eng. Sci. 2019, 118, 229–252. [Google Scholar] [CrossRef]
- Trefftz, E. Ein gegenstück zum ritzschen verfahren. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 131–137. [Google Scholar]
- Chen, J.T.; Lee, Y.T.; Shieh, S.C. Revisit of two classical elasticity problems by using the Trefftz method. Eng. Anal. Bound. Elem. 2009, 33, 890–895. [Google Scholar] [CrossRef]
- Grysa, K.; Maciag, A.; Adamczyk-Krasa, J. Trefftz functions applied to direct and inverse non-Fourier heat conduction problems. J. Heat Transf.-Trans. ASME 2014, 136, 091302. [Google Scholar] [CrossRef]
- Li, Z.C.; Young, L.J.; Huang, H.T.; Liu, Y.P.; Cheng, H.D. Comparisons of fundamental solutions and particular solutions for Trefftz methods. Eng. Anal. Bound. Elem. 2010, 34, 248–258. [Google Scholar] [CrossRef]
- Kołodziej, J.A.; Grabski, J.K. Many names of the Trefftz method. Eng. Anal. Bound. Elem. 2018, 96, 169–178. [Google Scholar] [CrossRef]
- Ku, C.Y.; Kuo, C.L.; Fan, C.M.; Liu, C.S.; Guan, P.C. Numerical solution of three-dimensional Laplacian problems using the multiple scale Trefftz method. Eng. Anal. Bound. Elem. 2015, 50, 157–168. [Google Scholar] [CrossRef]
- Aitchison, J. Numerical treatment of a singularity in a free boundary problem. Proc. R. Soc. Lond. 1972, 330, 573–580. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Xiao, J.-E.; Yeih, W.; Fan, C.-M. A Spacetime Meshless Method for Modeling Subsurface Flow with a Transient Moving Boundary. Water 2019, 11, 2595. https://doi.org/10.3390/w11122595
Ku C-Y, Liu C-Y, Xiao J-E, Yeih W, Fan C-M. A Spacetime Meshless Method for Modeling Subsurface Flow with a Transient Moving Boundary. Water. 2019; 11(12):2595. https://doi.org/10.3390/w11122595
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, Jing-En Xiao, Weichung Yeih, and Chia-Ming Fan. 2019. "A Spacetime Meshless Method for Modeling Subsurface Flow with a Transient Moving Boundary" Water 11, no. 12: 2595. https://doi.org/10.3390/w11122595
APA StyleKu, C.-Y., Liu, C.-Y., Xiao, J.-E., Yeih, W., & Fan, C.-M. (2019). A Spacetime Meshless Method for Modeling Subsurface Flow with a Transient Moving Boundary. Water, 11(12), 2595. https://doi.org/10.3390/w11122595








