Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy
Abstract
1. Introduction
2. Materials and Methods
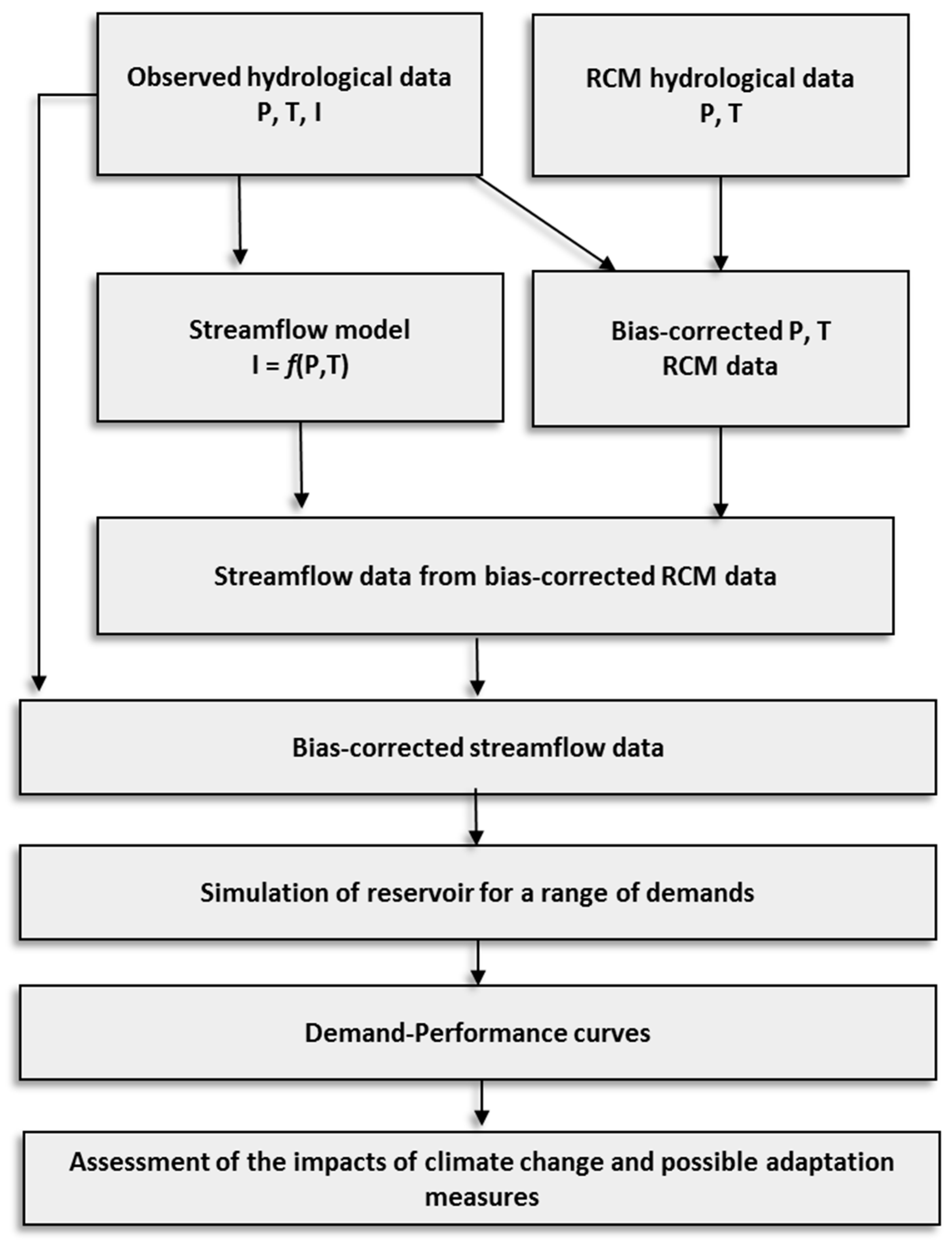
2.1. Overview
2.2. Precipitation and Temperature Data Processing
2.3. Hydrologic Modeling and Correction
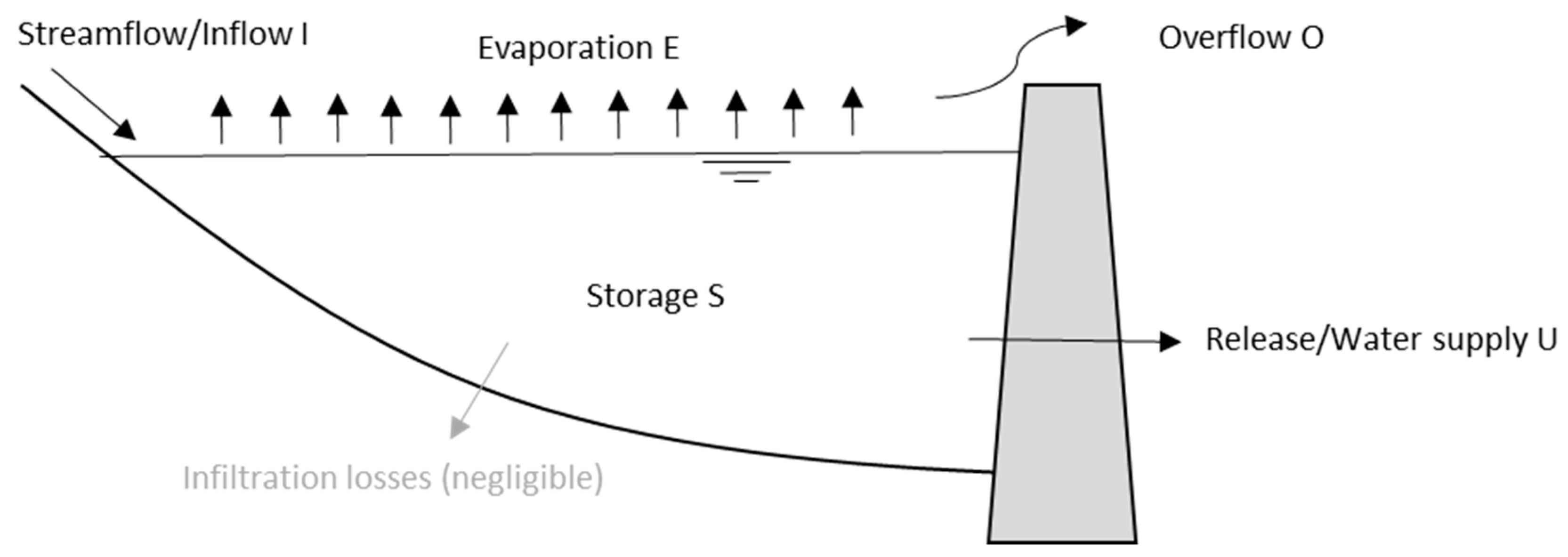
2.4. Reservoir Simulation and Performance Assessment
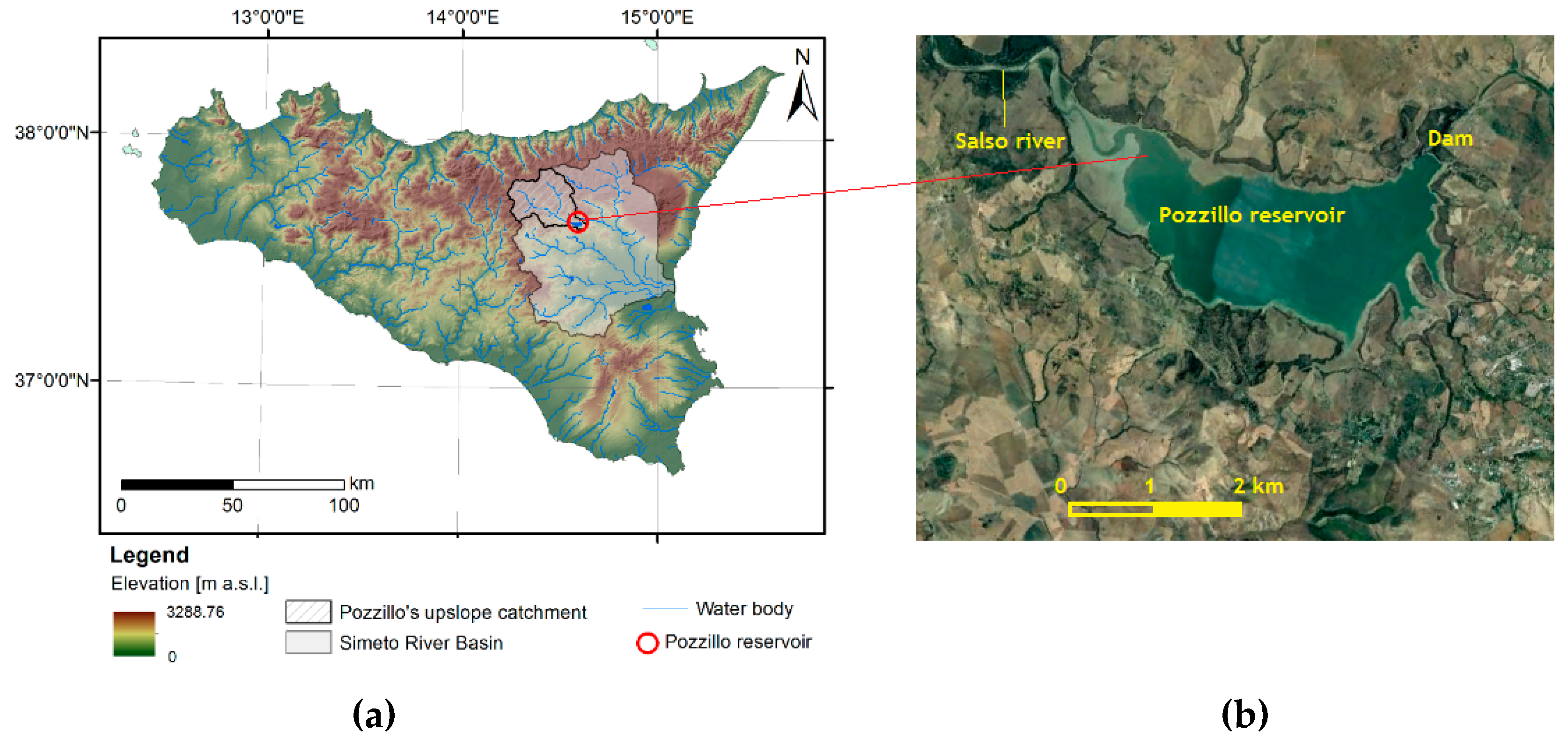
3. Case Study and Data
4. Results
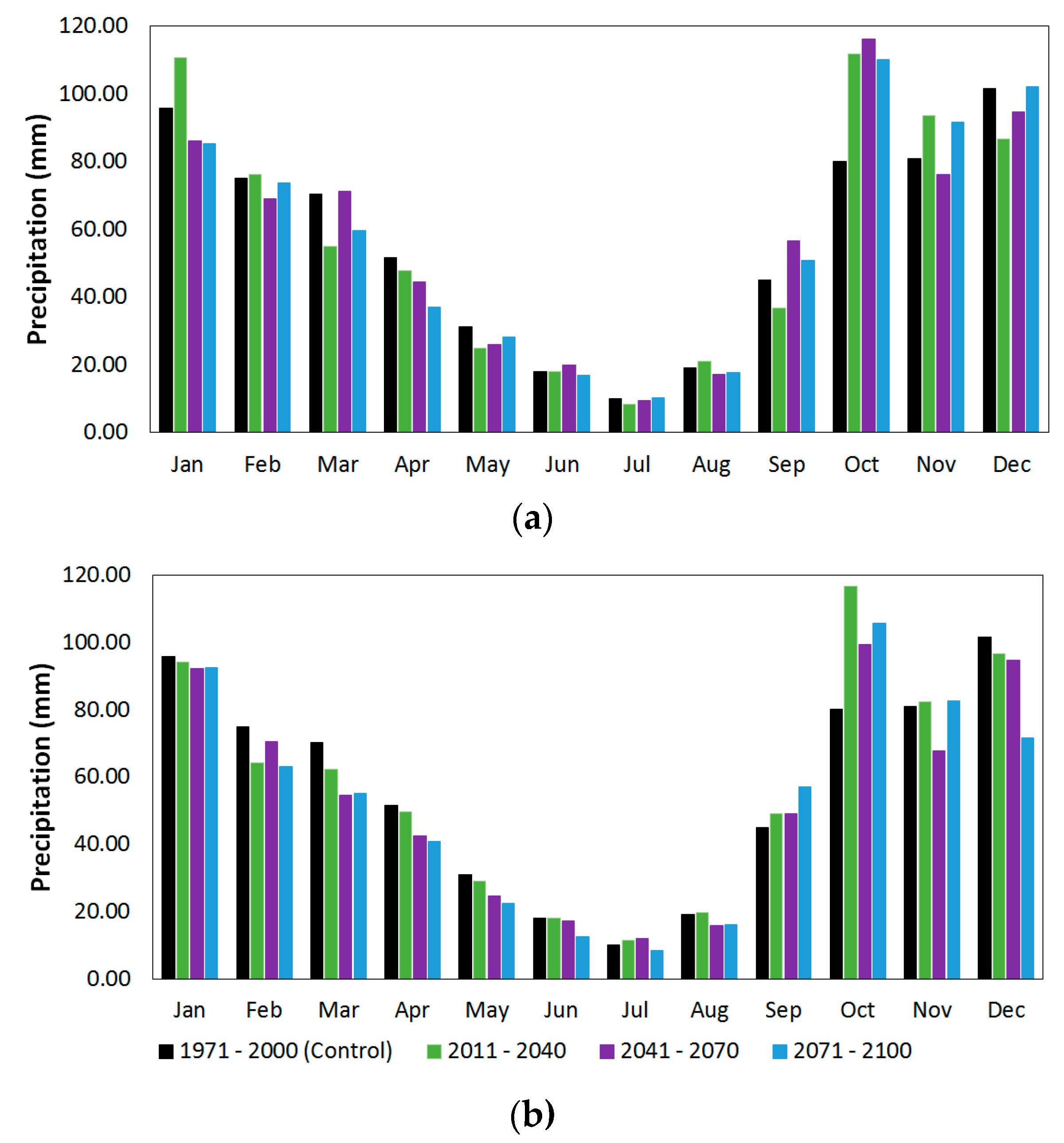
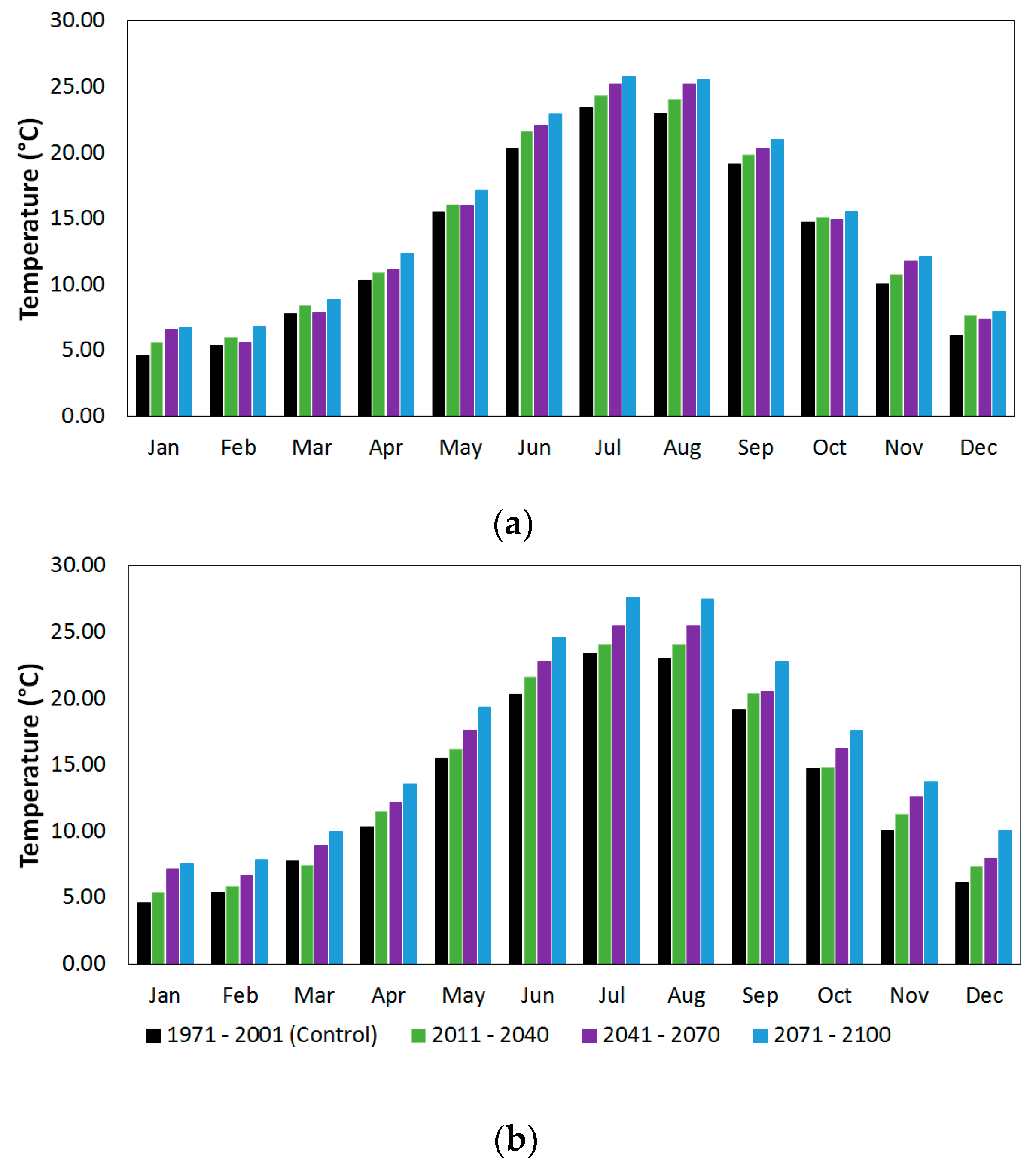
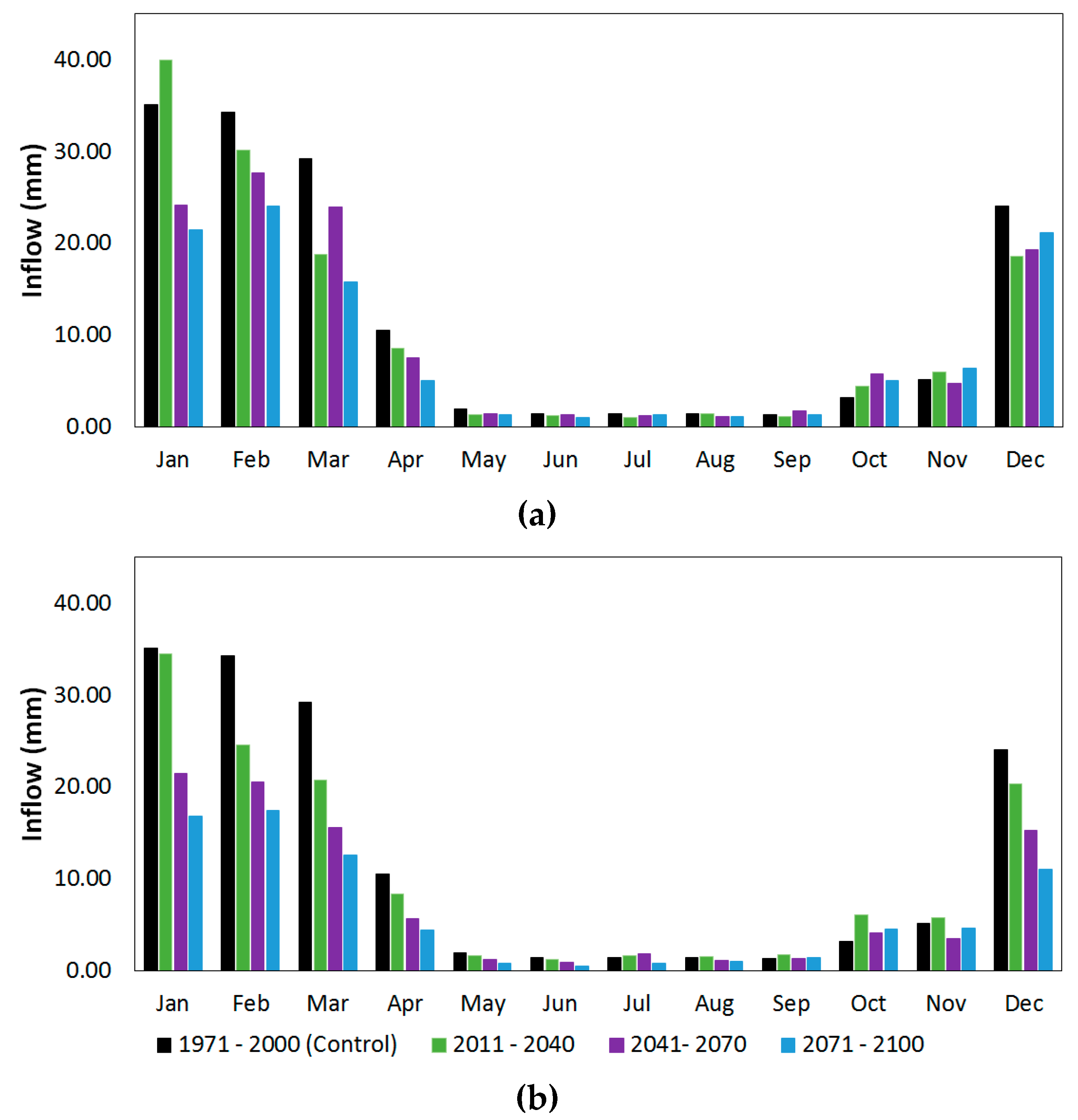
4.1. Impact of Climate Change on Hydrological Variables
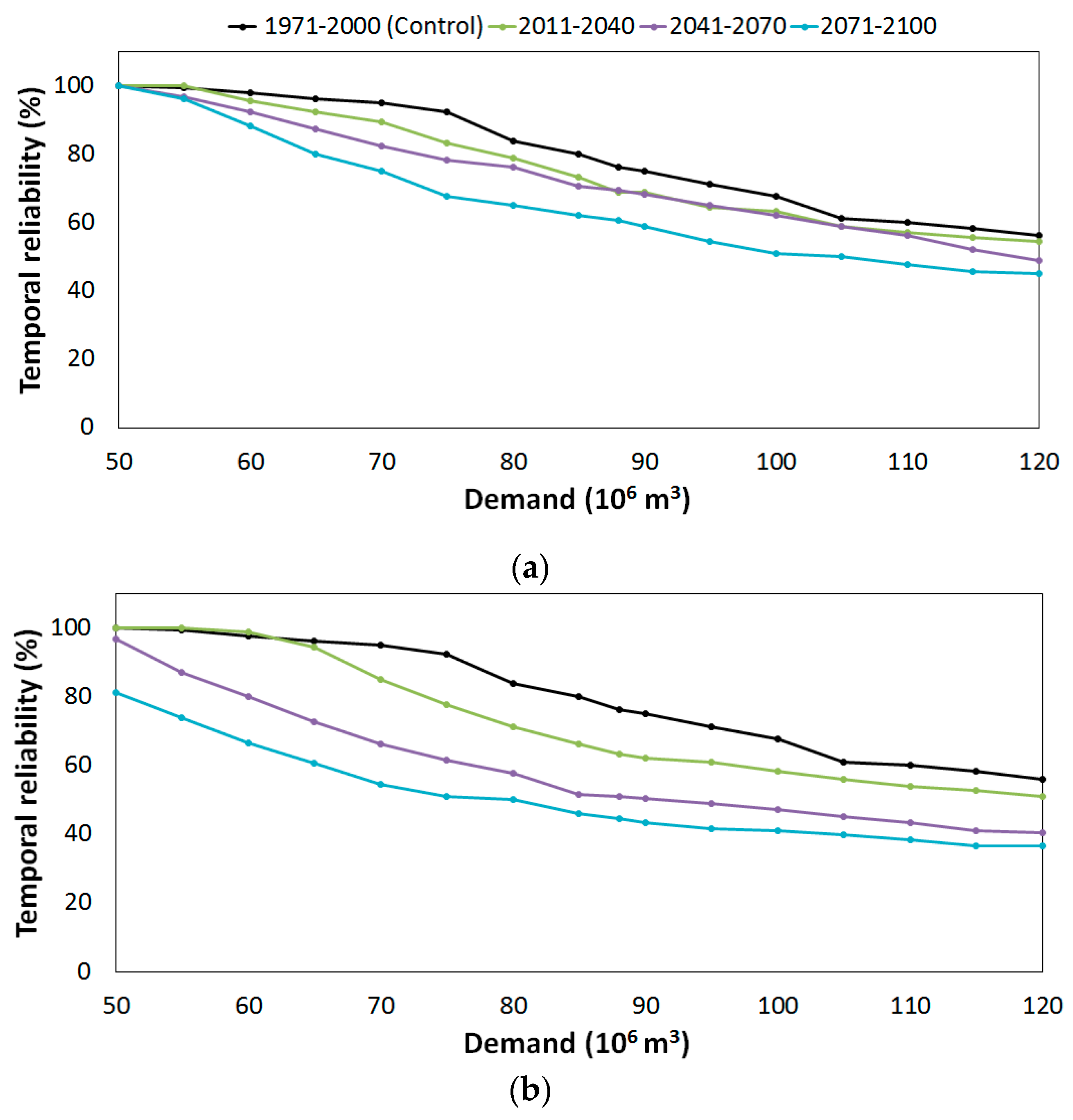
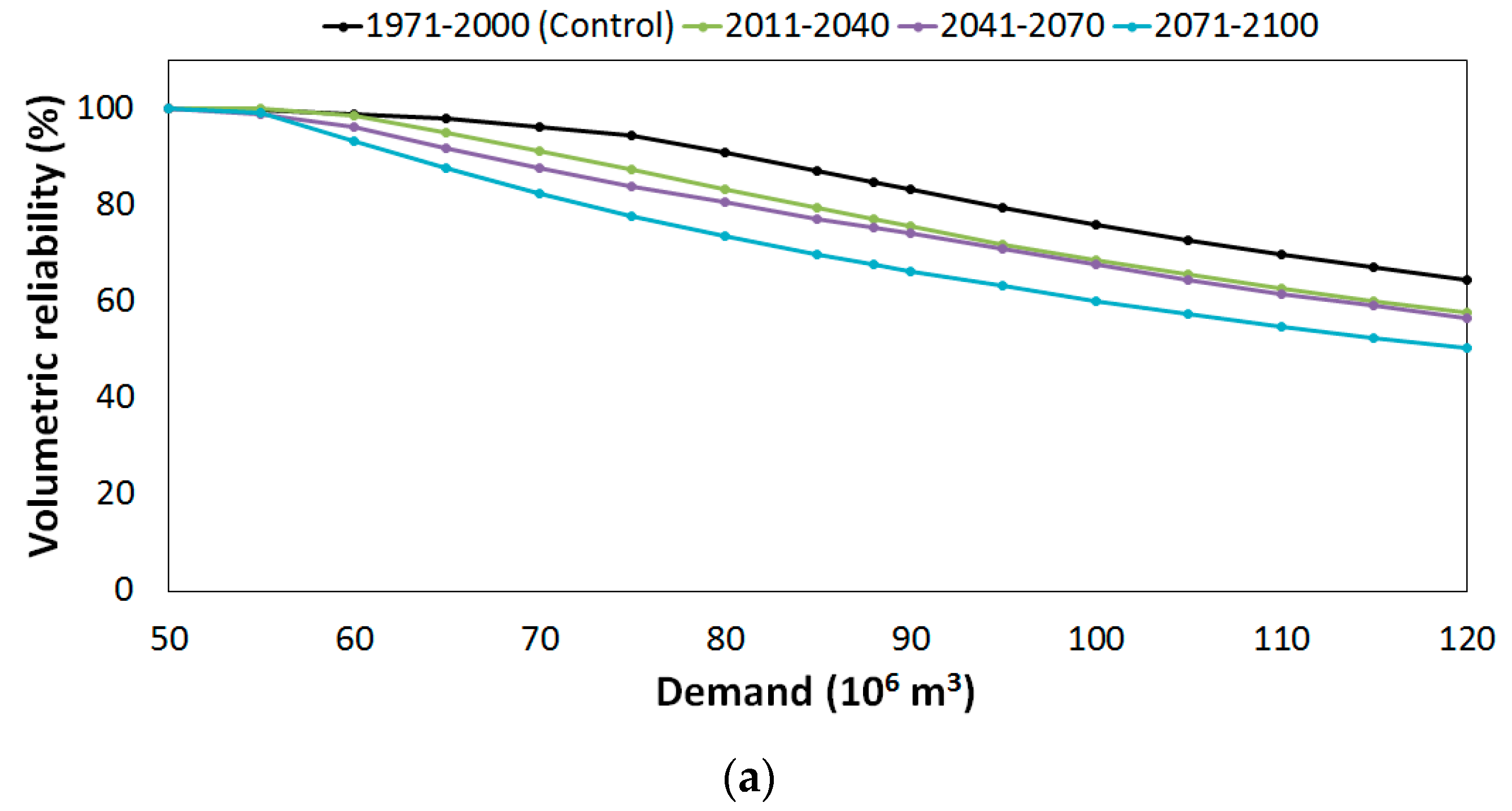
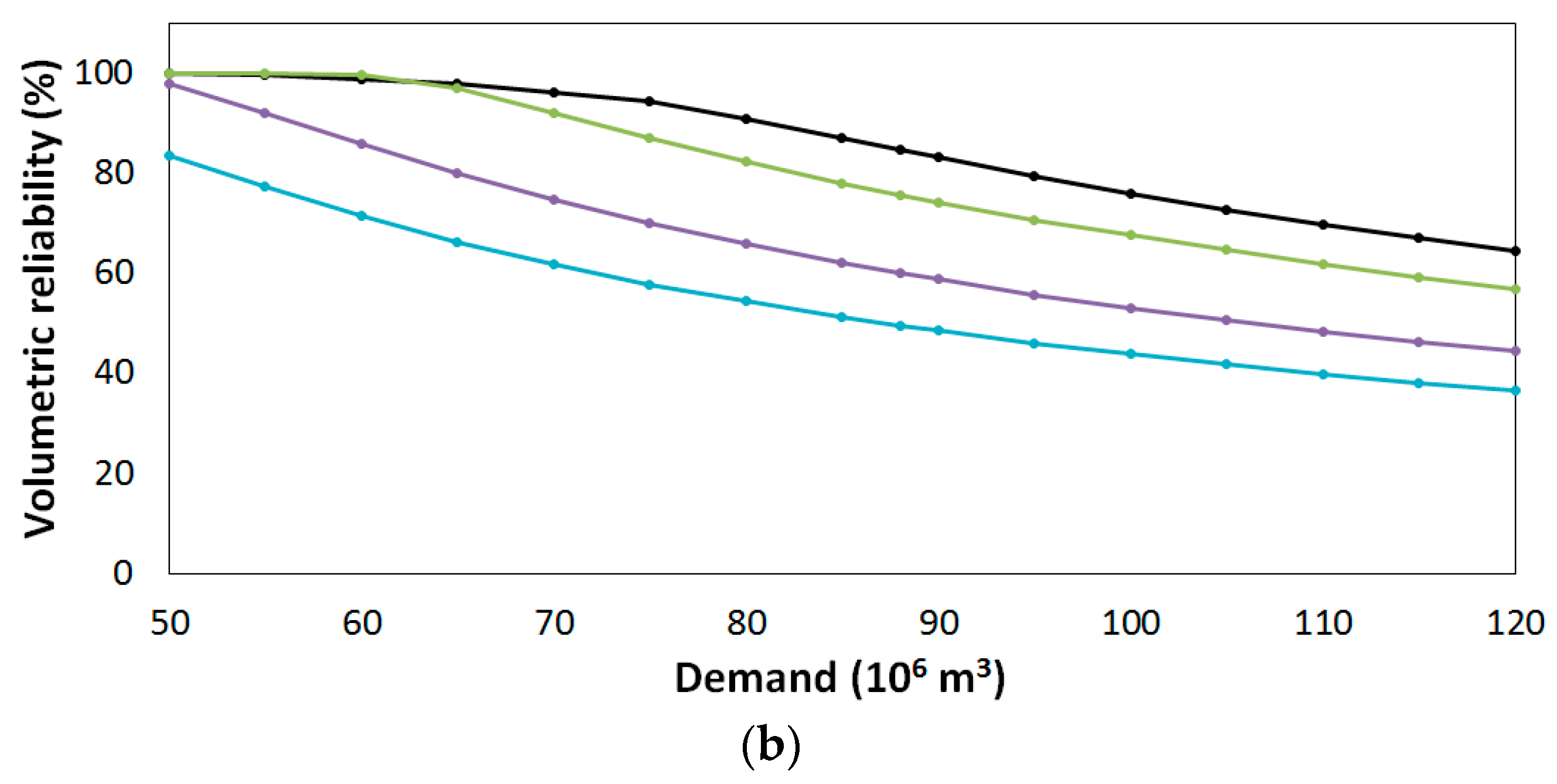
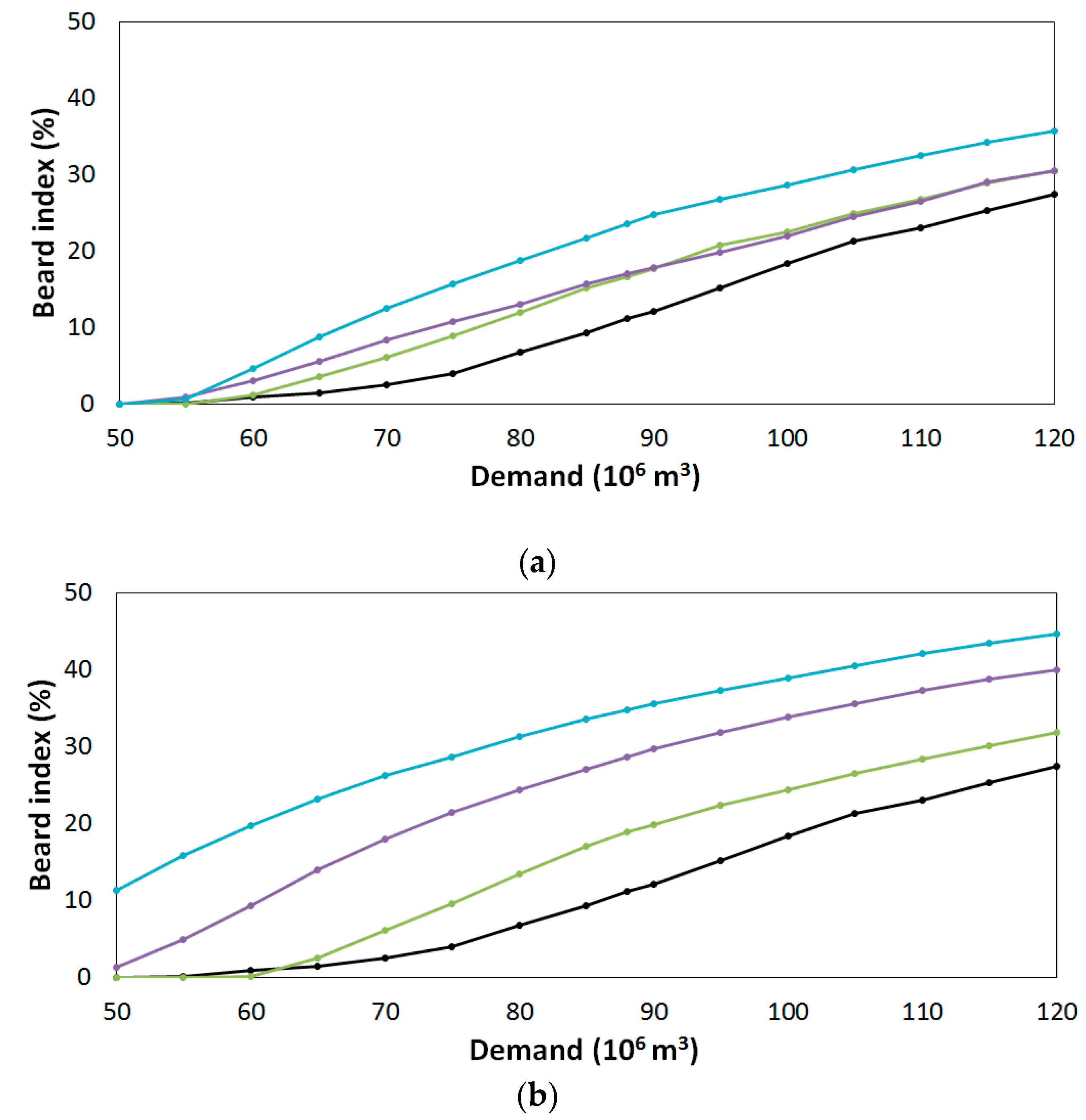
4.2. Impacts of Climate Change on Reservoir Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Field, C.B.; Barros, V.R.; Dokken, D.J.; Mach, K.J.; Mastrandrea, M.D.; Bilir, T.E.; Chatterjee, M.; Ebi, K.L.; Estrada, Y.O.; Genova, R.C.; et al. Climate Change 2014 Impacts, Adaptation and Vulnerability: Part. A: Global and Sectoral Aspects: Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; ISBN 9781107415379. [Google Scholar]
- Quevauviller, P.; Barceló, D.; Beniston, M.; Djordjevic, S.; Harding, R.J.; Iglesias, A.; Ludwig, R.; Navarra, A.; Navarro Ortega, A.; Mark, O.; et al. Integration of research advances in modelling and monitoring in support of WFD river basin management planning in the context of climate change. Sci. Total Environ. 2012, 440, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Garrote, L. Managing Water Resources to Adapt to Climate Change: Facing Uncertainty and Scarcity in a Changing Context. Water Resour. Manag. 2017, 31, 2951–2963. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L.; Flores, F.; Moneo, M. Challenges to Manage the Risk of Water Scarcity and Climate Change in the Mediterranean. Water Resour. Manag. 2007, 21, 775–788. [Google Scholar] [CrossRef]
- Bird, D.N.; Benabdallah, S.; Gouda, N.; Hummel, F.; Koeberl, J.; La Jeunesse, I.; Meyer, S.; Prettenthaler, F.; Soddu, A.; Woess-Gallasch, S. Modelling climate change impacts on and adaptation strategies for agriculture in Sardinia and Tunisia using AquaCrop and value-at-risk. Sci. Total Environ. 2016, 543, 1019–1027. [Google Scholar] [CrossRef]
- Olmstead, S.M. Climate change adaptation and water resource management: A review of the literature. Energy Econ. 2014, 46, 500–509. [Google Scholar] [CrossRef]
- Pahl-Wostl, C. Transitions towards adaptive management of water facing climate and global change. Water Resour. Manag. 2007, 21, 49–62. [Google Scholar] [CrossRef]
- Arnell, N.W.; Delaney, E.K. Adapting to climate change: Public water supply in England and Wales. Clim. Chang. 2006, 78, 227–255. [Google Scholar] [CrossRef]
- Tanaka, S.K.; Zhu, T.; Lund, J.R.; Howitt, R.E.; Jenkins, M.W.; Pulido, M.A.; Tauber, M.; Ritzema, R.S.; Ferreira, I.C. Climate Warming and Water Management Adaptation for California. Clim. Chang. 2006, 76, 361–387. [Google Scholar] [CrossRef]
- Medellín-Azuara, J.; Harou, J.J.; Olivares, M.A.; Madani, K.; Lund, J.R.; Howitt, R.E.; Tanaka, S.K.; Jenkins, M.W.; Zhu, T. Adaptability and adaptations of California’s water supply system to dry climate warming. Clim. Chang. 2008, 87, 75–90. [Google Scholar] [CrossRef]
- Purkey, D.R.; Huber-Lee, A.; Yates, D.N.; Hanemann, M.; Herrod-Julius, S. Integrating a Climate Change Assessment Tool into Stakeholder-Driven Water Management Decision-Making Processes in California. Water Resour. Manag. 2006, 21, 315–329. [Google Scholar] [CrossRef]
- Herrera-Pantoja, M.; Hiscock, K.M. Projected impacts of climate change on water availability indicators in a semi-arid region of central Mexico. Environ. Sci. Policy 2015, 54, 81–89. [Google Scholar] [CrossRef]
- Seager, R.; Ting, M.; Li, C.; Naik, N.; Cook, B.; Nakamura, J.; Liu, H. Projections of declining surface-water availability for the southwestern United States. Nat. Clim. Chang. 2013, 3, 482–486. [Google Scholar] [CrossRef]
- Dlamini, N.S.; Kamal, M.R.; Soom, M.A.B.M.; Mohd, M.S.F.B.; Abdullah, A.F.B.; Hin, L.S. Modeling Potential Impacts of Climate Change on Streamflow Using Projections of the 5th Assessment Report for the Bernam River Basin, Malaysia. Water 2017, 9, 226. [Google Scholar] [CrossRef]
- Mizyed, N. Impacts of Climate Change on Water Resources Availability and Agricultural Water Demand in the West Bank. Water Resour. Manag. 2009, 23, 2015–2029. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S.; Papadopoulou, A.; Cencur Curk, B.; Karleusa, B. Water resources vulnerability assessment in the Adriatic Sea region: The case of Corfu Island. Environ. Sci. Pollut. Res. 2017, 24, 20173–20186. [Google Scholar] [CrossRef]
- Nistor, M.M.; Man, T.C. Water availability variation under climate change in Turkey during 21 St century. Carpathian J. Earth Environ. Sci. 2019, 14, 19–28. [Google Scholar] [CrossRef]
- Rehana, S.; Mujumdar, P.P. Regional impacts of climate change on irrigation water demands. Hydrol. Process. 2013, 27, 2918–2933. [Google Scholar] [CrossRef]
- Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P.; Palmer, R.N. The effects of climate change on the hydrology and water resources of the Colorado River basin. Clim. Chang. 2004, 62, 337–363. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Krau, S.; Leconte, R. Adaptation to Climate Change in the Management of a Canadian Water-Resources System Exploited for Hydropower. Water Resour. Manag. 2009, 23, 2965–2986. [Google Scholar] [CrossRef]
- Adamec, K.; Palmer, R.N.; Polebitski, A.; Ahlfeld, D.; Steinschneider, S.; Pitta, B.; Brown, C. Evaluation of Climate Change Impacts to Reservoir Operations within the Connecticut River Basin. In World Environmental and Water Resources Congress 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 92–100. [Google Scholar]
- Ashofteh, P.S.; Haddad, O.B.; Mariño, M.A. Climate Change Impact on Reservoir Performance Indexes in Agricultural Water Supply. J. Irrig. Drain. Eng. 2013, 139, 85–97. [Google Scholar] [CrossRef]
- Garrote, L.; Iglesias, A.; Granados, A.; Mediero, L.; Martin-Carrasco, F. Quantitative Assessment of Climate Change Vulnerability of Irrigation Demands in Mediterranean Europe. Water Resour. Manag. 2015, 29, 325–338. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Muttiah, R.S.; Felden, F. Incorporation of Climate Change in Water Availability Modeling. J. Hydrol. Eng. 2005, 10, 375–385. [Google Scholar] [CrossRef]
- Raje, D.; Mujumdar, P.P. Reservoir performance under uncertainty in hydrologic impacts of climate change. Adv. Water Resour. 2010, 33, 312–326. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Haddad, O.B.; Loáiciga, H.A. Evaluation of Climatic-Change Impacts on Multiobjective Reservoir Operation with Multiobjective Genetic Programming. J. Water Resour. Plan. Manag. 2015, 141, 04015030. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Peres, D.J.; Cancelliere, A.; Rossi, G. Large Scale Probabilistic Drought Characterization Over Europe. Water Resour. Manag. 2013, 27, 1675–1692. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Peres, D.J.; Castano, A.; Cancelliere, A. SPI-Based Probabilistic Analysis of Drought Areal Extent in Sicily. Water Resour. Manag. 2015, 29, 459–470. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Bordi, I.; Cancelliere, A.; Rossi, G.; Sutera, A. Spatial variability of drought: An analysis of the SPI in Sicily. Water Resour. Manag. 2003, 17, 273–296. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L. Can metric-based approaches really improve multi-model climate projections? The case of summer temperature change in France. Clim. Dyn. 2015, 45, 1913–1928. [Google Scholar] [CrossRef]
- Wilby, R.L. Evaluating climate model outputs for hydrological applications. Hydrol. Sci. J. 2010, 55, 1090–1093. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Johnson, F.; Sharma, A. A nesting model for bias correction of variability at multiple time scales in general circulation model precipitation simulations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mascaro, G.; Viola, F.; Deidda, R. Evaluation of Precipitation From EURO-CORDEX Regional Climate Simulations in a Small-Scale Mediterranean Site. J. Geophys. Res. Atmos. 2018, 123, 1604–1625. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Modeling impacts of climate change on return period of landslide triggering. J. Hydrol. 2018, 567, 420–434. [Google Scholar] [CrossRef]
- Nijssen, B.; Chegwidden, O. Streamflow Bias Correction for Climate Change Impact Studies: Harmless Correction or Wrecking Ball? In American Geophysical Union, Fall Meeting 2017, Abstract #PA41A-0290; American Geophysical Union: Washington, DC, USA, 2017. [Google Scholar]
- WMO. WMO Guidelines on the Calculation of Climate Normals; WMO: Geneva, Switzerland, 2017; pp. 1–29. [Google Scholar]
- Mehan, S.; Gitau, M.; Flanagan, D. Reliable Future Climatic Projections for Sustainable Hydro-Meteorological Assessments in the Western Lake Erie Basin. Water 2019, 11, 581. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Van Deursen, W. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Cutore, P.; Cristaudo, G.; Campisano, A.; Modica, C.; Cancelliere, A.; Rossi, G. Regional Models for the Estimation of Streamflow Series in Ungauged Basins. Water Resour. Manag. 2007, 21, 789–800. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Environmental Flow Assessment Based on Different Metrics of Hydrological Alteration. Water Resour. Manag. 2016, 30, 5799–5817. [Google Scholar] [CrossRef]
- Peres, D.J.; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. Significant wave height record extension by neural networks and reanalysis wind data. Ocean Model. 2015, 94, 128–140. [Google Scholar] [CrossRef]
- Indelicato, S.; Tamburino, V.; Barbagallo, S.; Mazzola, G. Risorse Idriche Nei Grandi Serbatoi Artificiali Siciliani. I Contributo; Quaderno n.; CSEI Catania: Catania, Italy, 1989. (In Italian) [Google Scholar]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Cancelliere, A.; Giuliano, G.; Nicolosi, V.; Rossi, G. Optimal Short-Term Operation of a Multipurpose Reservoir System under Limited Water Supply; IAHS-AISH Publ.: Wallingford, UK, 2003; pp. 200–207. [Google Scholar]
- Cancelliere, A.; Giuliano, G.; Ancarani, A.; Rossi, G. A Neural Networks Approach for Deriving Irrigation Reservoir Operating Rules. Water Resour. Manag. 2002, 16, 71–88. [Google Scholar] [CrossRef]
- Cancelliere, A.; Ancarani, A.; Rossi, G. Susceptibility of Water Supply Reservoirs to Drought Conditions. J. Hydrol. Eng. 1998, 3, 140–148. [Google Scholar] [CrossRef]
- Peres, D.J.; Caruso, M.F.; Cancelliere, A. Assessment of Climate-Change Impacts on Precipitation Based on Selected RCM Projections. European Water 2017, 59, 9–15, E.W. Publications. [Google Scholar]
- Jones, C.G.; Samuelsson, P.; Kjellstr¨Om, E. Regional climate modelling at the Rossby Centre. Tellus A Dyn. Meteorol. Oceanogr. 2011, 63, 1–3. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007. [Google Scholar] [CrossRef]
- CMMC. Piano Nazionale di Adattamento ai Cambiamenti Climatici; CMMC: Lecce, Italy, 2017. (In Italian) [Google Scholar]
- Sykes, M.T. Climate Change Impacts: Vegetation. Encycl. Life Sci. 2009. [Google Scholar] [CrossRef]
- Bachelet, D.; Neilson, R.P.; Lenihan, J.M.; Drapek, R.J. Climate Change Effects on Vegetation Distribution and Carbon Budget in the United States. Ecosystems 2001, 4, 164–185. [Google Scholar] [CrossRef]
- Rungee, J.; Kim, U. Long-term assessment of climate change impacts on Tennessee Valley Authority Reservoir operations: Norris Dam. Water 2017, 9, 649. [Google Scholar] [CrossRef]
- Rossi, G. Policy framework of drought risk mitigation. In Handbook of Drought and Water Scarcity: Management of Drought and Water Scarcity; Eslamian, S., Eslamian, F.A., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 569–588. [Google Scholar]
- Kwakkel, J.H.; Haasnoot, M.; Walker, W.E. Comparing Robust Decision-Making and Dynamic Adaptive Policy Pathways for model-based decision support under deep uncertainty. Environ. Model. Softw. 2016, 86, 168–183. [Google Scholar] [CrossRef]
| May. | Jun. | Jul. | Aug. | Sep. | Oct. |
|---|---|---|---|---|---|
| 3.98% | 13.18% | 27.95% | 28.98% | 19.66% | 6.25% |
| Period | RT (%) | RV (%) | IB (%) | |||
|---|---|---|---|---|---|---|
| RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | |
| 1971–2001 (control) | 76.1 | 76.1 | 84.8 | 84.8 | 11.2 | 11.2 |
| 2011–2040 | 68.9 (−9.5%) | 63.3 (−16.8%) | 77.1 (−9.1%) | 75.7 (−10.7%) | 16.7 (+48.8%) | 18.9 (+69.1%) |
| 2041–2070 | 69.4 (−8.8%) | 51.1 (−32.8%) | 75.3 (−11.2%) | 60.1 (−29.1%) | 17.1 (+52.4%) | 28.7 (+155.8%) |
| 2071–2100 | 60.6 (−20.4%) | 44.4 (−41.6%) | 67.6 (−20.3%) | 49.6 (−41.5%) | 23.6 (+110.7%) | 34.8 (+211.0%) |
| Period | D(RT) (hm3) | D(RV) (hm3) | D(IB) (hm3) | |||
|---|---|---|---|---|---|---|
| RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | RCP4.5 | RCP8.5 | |
| 2011–2040 | 82.5 (−6.3%) | 76.3 (−13.4%) | 78.0 (−11.3%) | 77.4 (−12.0%) | 78.7 (−10.5%) | 77.1 (−12.4%) |
| 2041–2070 | 80.0 (−9.1%) | 62.7 (−28.8%) | 73.8 (−16.2%) | 60.9 (−30.8%) | 75.8 (−13.9%) | 62.0 (−29.5%) |
| 2071–2100 | 68.9 (−21.7%) | 53.5 (−39.2%) | 67.8 (−23.0%) | 49.2 (−44.1%) | 68.2 (−22.4%) | 50.0 (−43.2%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peres, D.J.; Modica, R.; Cancelliere, A. Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy. Water 2019, 11, 2531. https://doi.org/10.3390/w11122531
Peres DJ, Modica R, Cancelliere A. Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy. Water. 2019; 11(12):2531. https://doi.org/10.3390/w11122531
Chicago/Turabian StylePeres, David J., Rosario Modica, and Antonino Cancelliere. 2019. "Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy" Water 11, no. 12: 2531. https://doi.org/10.3390/w11122531
APA StylePeres, D. J., Modica, R., & Cancelliere, A. (2019). Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy. Water, 11(12), 2531. https://doi.org/10.3390/w11122531






