1. Introduction
For a rational and productive irrigation water application, one needs to know well how water infiltrates into the soil, and how the soil moisture profiles evolve. This can be achieved by solving the appropriate Richards’ equation, which is feasible only when major soil hydraulic properties are known, together with the initial and boundary conditions imposed in each case.
To solve the unsaturated flow equation, many procedures have been proposed, e.g., analytical, semi analytical, finite differences, and finite elements. Philip [
1] introduced the flux–concentration (
F(Θ)) relation in order to develop a quasi-analytical technique for solving the unsaturated flow equation. The technique is rather simple and gives a holistic view of the phenomenon [
1,
2].
F(Θ) expresses the relation of soil water flux–density with the normalized volumetric soil water content, and can be used in an attempt to elucidate further the flow phenomena in unsaturated soils, both in the horizontal (absorption, as well as desorption) and in the vertical cases. The form of the
F for the case of horizontal absorption and the normalized volumetric soil water content is given by the following equations:
where
θin is the initial volumetric soil water content of the soil column, considered uniform throughout the column;
θ0 is the volumetric soil water content at the soil surface (
x = 0);
q is the soil water flux density at a position
x where soil water content is
θ; and
q0 is the soil water flux density at
x = 0, the soil surface, where water is absorbed under constant concentration conditions with
θ =
θ0 =
θs (
θs = volumetric soil moisture at saturation) when the soil water pressure head is
H =
H0 = 0 cm column of water.
The values of
F and Θ lie in the range of 0 to 1. A zero value for
F and Θ when q = 0 is far enough from the soil infiltration surface, where
θ =
θin; the value is 1 at the soil surface, where
q =
q0 and
θ =
θ0 [
1]. In general, the
F is a function of
θ,
θin,
θ0, and time (
t) and it is, in most cases, unknown a priori [
3].
For the prediction of the flow regime in porous media, using the flux–concentration relationship, either an iterative procedure should be applied, or accurate estimates of
F(Θ) where feasible are used [
2].
A number of researchers have proposed analytical expressions for the F(Θ) relationship to solve the flow equation for the case of the horizontal absorption under constant pressure head conditions, applied at the soil surface (x = 0).
Smiles et al. [
4] proposed an empirical expression to describe the measured
F(Θ) of a fine sand soil:
Vauclin and Haverkampt [
5] proposed the following simple expression
while Evangelides et al. [
6] proposed the empirical expression
with the value of parameter
m lying in the range 0.718–0.867, and the value
m = 0.8 considered as the most appropriate, which is very close to the mean value.
Recently, Ma et al. [
7] proposed the expression
with the parameter
a2 being a function of the initial soil water saturation and the soil pore structure index that reflects the shape of the soil water retention curve.
From the abovementioned expressions, those where
F is a function of Θ with a parameter for soil properties (Equations (4) and (5)), compared to those where
F is a function of Θ without any parameters (Equations (2) and (3)), are more flexible and can simulate
F(Θ) relationships with higher accuracy for a wide range of texture soils [
7].
Philip [
1] investigated the behavior of
F for two distinct cases of soils, characterized by their
D(
θ) functions—i.e., soils, where their
D(
θ) function is a delta function (the so called Green–Ampt soils, where the moisture profiles advance step-wise), as well as soils whose
D(
θ) function is constant, independent of moisture content
θ (the so called linear soils). In real soils, the
F(Θ) relationship will lie in between the Green–Ampt and linear soils [
1].
Clothier et al. [
8] investigated the possibility of estimating the expression
(Θ), where
is the Boltzmann transformation
for each soil from the experimental data of a horizontal absorption experiment, according to the equation below (Philip [
9],
Table 1, no. 2):
where
λi is the maximum value of
λ(Θ) (i.e., when Θ = 0). Parameter
λi considered to be a characteristic measure of the wetted region in a horizontal absorption experiment, and is influenced only by
θin for every soil [
10,
11,
12];
p is a fitting parameter.
Equation (6) has the advantage of an easy estimation of parameters λi and p; by a log-transformation, Equation (6) becomes linear, with the slope equal to p and transect equal to logλi when the λ(Θ) is described by Equation (6). This procedure appears preferable to least squares fitting.
It is to be mentioned here that previous similar studies [
6] could obtain the
F(Θ) relationship using more complex expressions for it. In the present study, we use a simple, mono-parametric
F(Θ) expression using a mono-parametric
λ(Θ) expression, which adequately describes the experimental data [
8].
In this context, the main objectives of this study are (1) tο test the possibility of the mono-parametric λ(Θ) expression to describe the experimental data, as the equation through the proper selection of a fitting parameter p; and (2) tο investigate whether the experimental F(Θ) relations are described accurately enough from the analytical, mono-parametric function for a wide range of soil types, as well as finding out the physical meaning of the parameter p and the range of its values.
2. Theory
Applying Darcy’s law and the mass conservation principle for the one-dimensional horizontal infiltration case, one easily gets the partial differential equation
where
x is the horizontal axis,
t the time, and
D(θ) the soil water diffusivity. The solution of Equation (7) under the following initial and boundary conditions:
- (a)
t = 0, x > 0, θ = θin
- (b)
t > 0, x = 0, θ = θ0
- (c)
t > 0, x → ∞, θ = θin
could be obtained in terms of the Boltzmann transformation
, considered a function of
θ only as
following the initial and boundary conditions
θ =
θin,
λ → ∞, and
θ =
θ0,
λ = 0.
Introducing the Boltzmann transformation function
in Darcy’s law, one gets
and the combination of Equations (1), (8), and (9) gives the following expression for
FFrom the abovementioned equation, it is obvious that function F, for the case of the horizontal absorption, is independent of time and depends on the values of the volumetric soil water, θ, θin and θ0.
When the
D(
θ) function is a delta function, the flux concentration relationship
F for the horizontal absorption is given by
while for the case where the
D(
θ) function is constant, the flux concentration relationship
F is given by
White et al. [
13] have shown that Equation (12) could be reasonably approximated by the expression
It is obvious from Equations (8) and (10) that the F(Θ) relationship depends on the form of D(θ).
From Equation (6), the soil sorptivity
Sc function could be estimated by analytical expression [
8], since
From the combination of Equations (6), (9), and (10), it could be shown that the
F(Θ) relationship could be estimated analytically, according to the mono-parametrical analytical expression
A similar expression for
F(Θ) was presented by Smiles et al. [
4] in a horizontal absorption experiment in sand, where the parameter
p had a constant value
p = 0.19.
Applying the Bruce and Klute [
14] method, the soil water diffusivity function
D(Θ) can be estimated according to the expression
In this respect, it is rather easy, by introducing the
λ(Θ) expression given in Equation (6), to get an analytical expression for
D(Θ) ([
8]), as
In practice, this means that for soils with a λ(Θ) expression, such as the one given by Equation (6), their diffusivity function D(Θ) should be described analytically by Equation (17), and the flux concentration relationship F(Θ) by Equation (15).
3. Materials and Methods
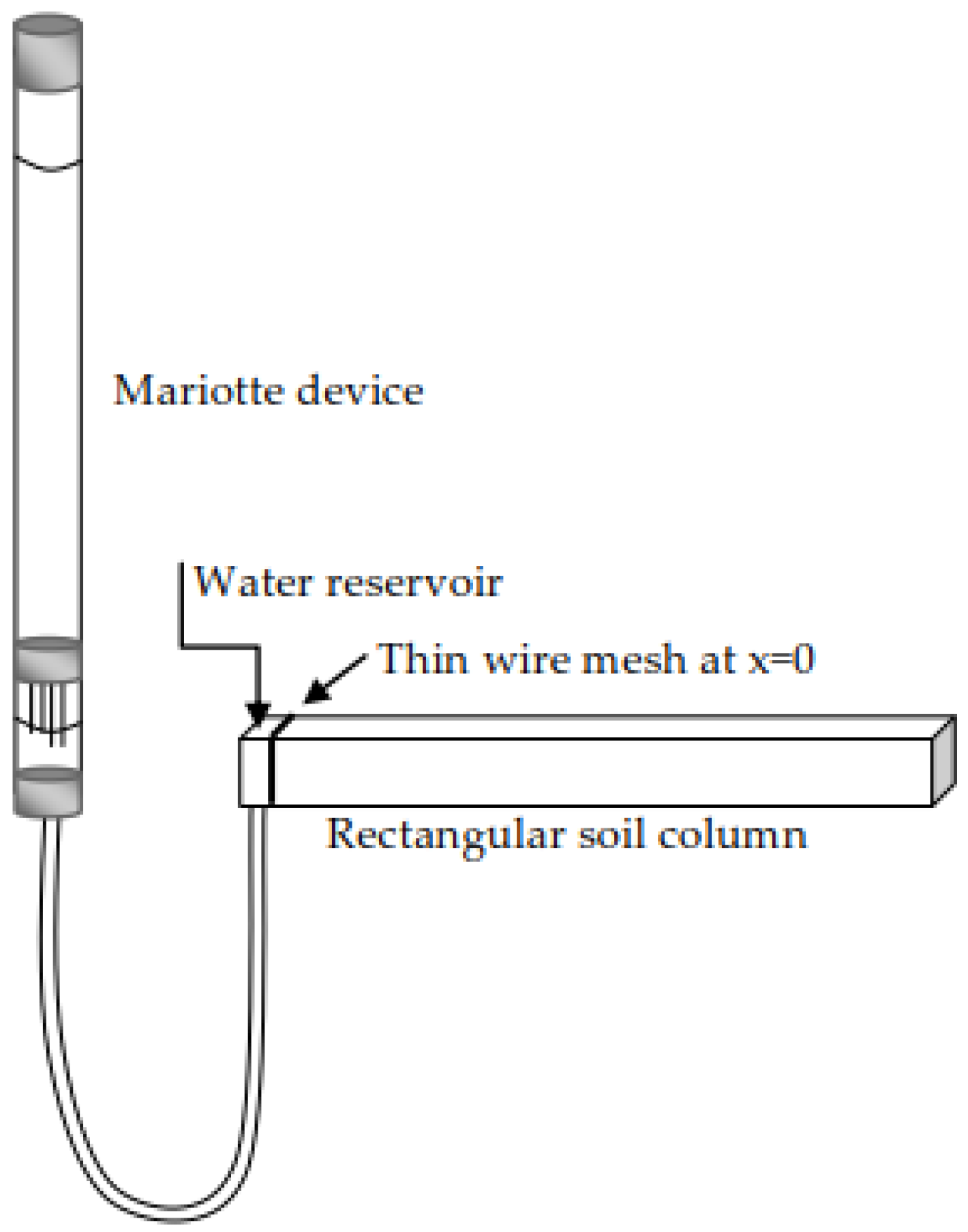
Horizontal infiltration experiments were conducted (
Scheme 1) in three porous media with different soil textures: a sandy loam (SL) (13.2% clay, 8% silt, 78.8% sand), a loam (L) (20% clay, 38% silt, 42% sand), and a silty clay loam (SiCL) (36.5% clay, 52% silt, 11.5% sand). The respective soils were air-dried, ground, and passed through a 2 mm sieve. The soil samples were uniformly packed in a rectangular column 5 cm in width, 2 cm in height, and 50 cm long. The upper soil surface was open to the air, thus securing that the soil air pressure at the soil pores was at atmospheric pressure (
Scheme 1). The experimental data from horizontal absorption experiments conducted in sand (S) by Poulovassilis [
15] were also used.
The volumetric soil water θj(xj, t*) profile, after a time period t* was elapsed from the beginning of the experiment, was determined by cutting, as quickly as possible, the soil column into small rectangular pieces. Specifically, the soil column was sectioned in 0.01 m increments, and the volumetric water content of each rectangular piece θj was determined by using the gravimetric water content and the dry soil bulk density (ρφ). The θj value corresponds to the center of the soil samples, at distance xj from the soil infiltration surface.
The initial values of
θ and
θin were those associated to the air-dry soil, and the condition of the soil infiltration surface was that of a constant pressure head
H value (
H = 0 at
x = 0, with
x = 0 denoting the soil infiltration surface). The zero value of
H was maintained by a Mariotte device (
Scheme 1). A thin wire mesh at
x = 0 was installed to keep the soil at rest, and also provide the least possible resistance to the soil water entry.
The time duration of these experiments varied according to the soil type—i.e., smaller values for coarse-textured soils and larger values for fine-textured soils. For the sand (S), it was 10.4 min [
15], for the SL it was 194 min, for the L it was 251 min, and for the SiCL it was 1630 min. During the experimental process, a continuous monitoring of the water volume entering the column was obtained, thus allowing the cumulative infiltration
I(
t) experimental curve to be determined. The soil sorptivity
S is immediately available from the well-known relationship [
16]
4. Results and Discussion
In
Table 1, some soil characteristics, such as
θ0,
θin,
ρφ,
λi and
S (Equation (18)), together with fitting parameter
p and the value of
Sc (Equation (14)), are shown for each porous media used in this study. It is easily noticeable that the values of
S and
λi depend strongly on the soil type, and they tend to decrease as soils become finer in texture. The same trend for the values
S and
λi for six different soils were presented from McBride and Horton [
10].
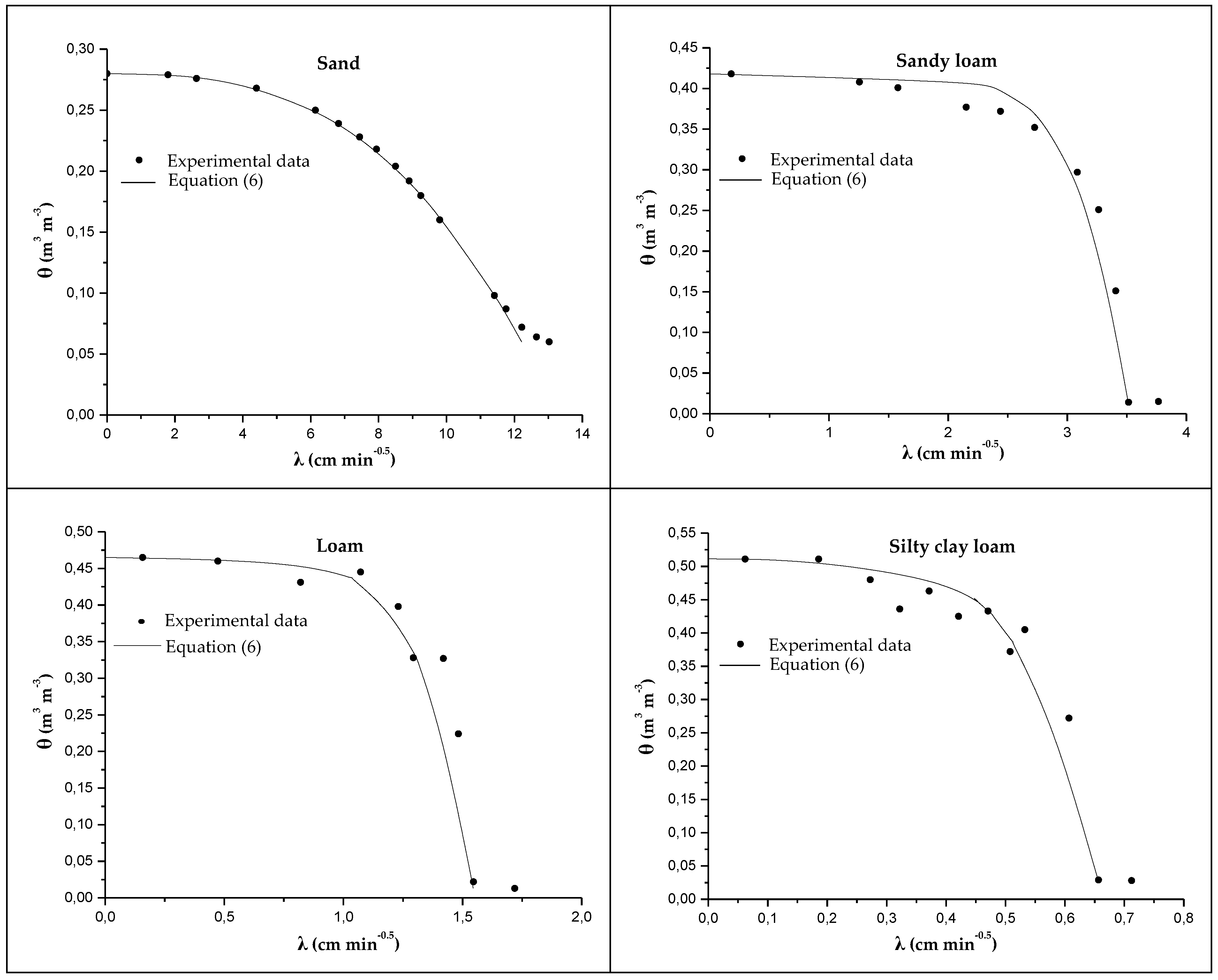
In
Figure 1, the
λ(
θ) profiles are presented, as these were obtained from the experimental
θ(
x,
t) data and the well-known Boltzmann transformation (
), together with the fitted
λ(
θ) relationship (Equation (6)), after the fitting parameter
p was properly selected. From the comparison, it is shown that Equation (6) is suitable for the description of the
λ(
θ) relationships for the horizontal absorption experiments. In each soil, the
p-value was determined as the one where the root mean square error (RMSE) from a series of neighboring
p-values was the least.
One could argue, considering that the
λ(Θ) relationship is unique for each soil, independent of the duration of the experiment, that the two parameters of Equation (6) (
λi and
p) do not represent simple fitting parameters, but are related to the soil’s hydraulic properties. Some researchers insist that parameter
λi may be considered as an index of the soil’s hydraulic properties [
10,
11]. Moreover, Shao and Horton [
11] correlated parameter
p with the parameter
n (
p = 1/
n) of the equation of van Genuchten [
17], which describes the soil moisture retention curve.
In what follows, an investigation of the characteristics of parameter
p will be carried out. According to Equation (14), the ratio
S/
λi(
θ0 –
θin) is equal to (
p + 1)
−1. For the Green–Ampt soils (
D is a Dirac delta-function of
θ), the ratio
S/
λi(
θ0 –
θin) should be unit, thus
p would be zero. Similarly, for the linear soils, the expression (
p + 1)
−1 would be 0.31, and the value of
p will be 2.23 [
8]. Consequently, the values of
p are related to the form of the diffusivity
D(
θ) function. In order to examine this relationship, Equation (6) is rewritten as in Equation (19):
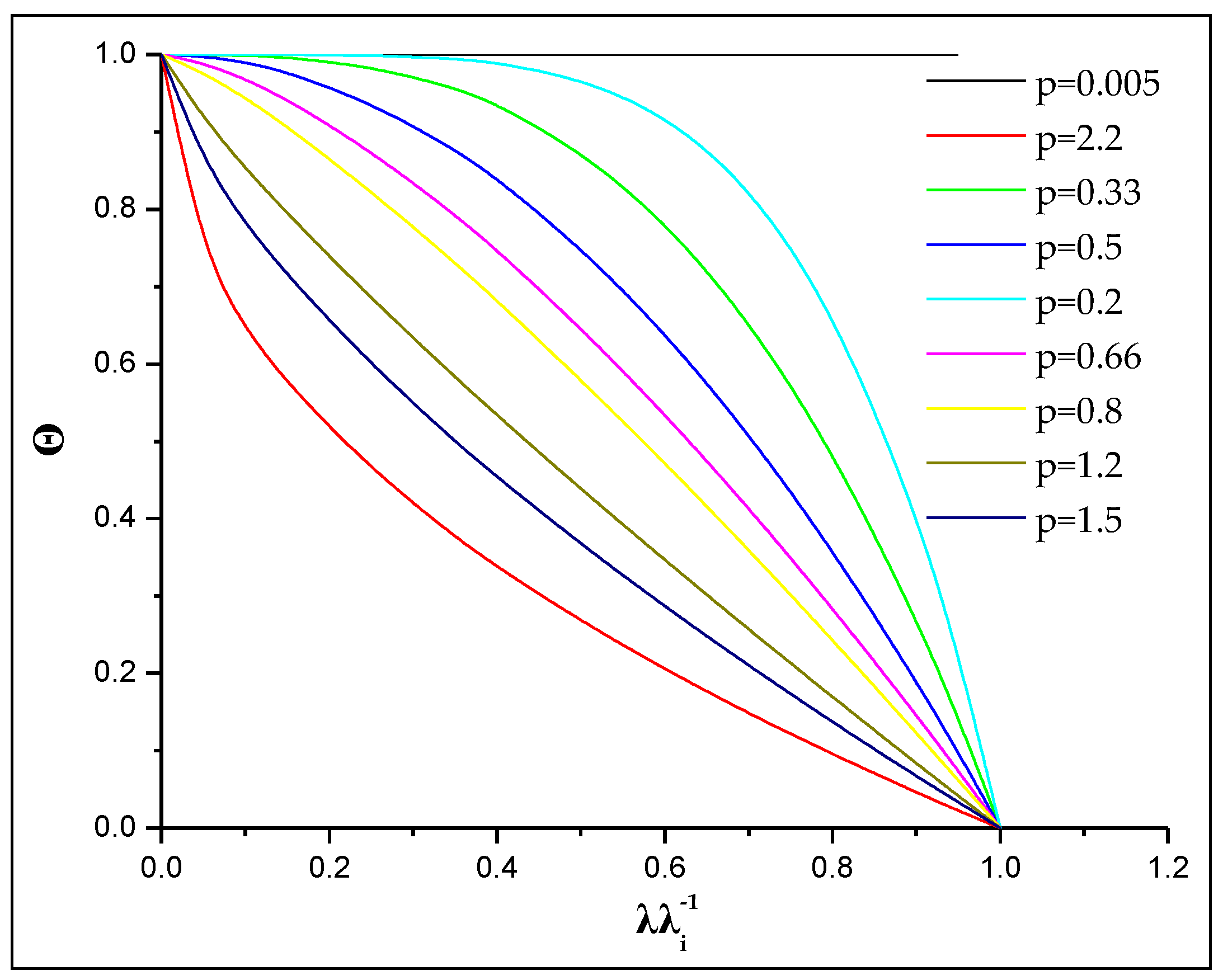
In
Figure 2, the Θ(
λ/
λi) relationship is shown for various values of the parameter
p (0 <
p < 2.23). From
Figure 2, it is shown that all the Θ(
λ/
λi) relations lie in the area with its borders defined by the values of the parameter
p (i.e.,
p ;
D(
θ) Dirac delta function) and
p = 2.23 (
D(
θ) constant). From the investigation of the
λ(
θ) relations in this study, it is found that
p-values fall in the range 0.1 <
p < 0.4. Also, Evangelides et al. [
6] showed that
p-values obtained using data from horizontal infiltration experiments in seven soils fall in the range 0.149 <
p < 0.389. In other words, the range of
p is narrower than the range
.
After the parameter
p selection, using also the
λi,
θ0, and
θin values for each soil, a re-estimation of sorptivity
Sc was performed using Equation (14). From the values of
S and
Sc presented in
Table 1,
Sc values are reasonably close to the experimental values of
S (
S =
I/
t0.5) for three out of the four soils examined (absolute values of RE: 1.55% < RE < 3.08%). The relative error value for the SiCL soil appears to be rather high (13.27%). This could be attributed to the long time duration of the experiment (1630 min) and unavoidable soil water evaporation from the upper soil surface. In any case, the overall differences are small, and therefore one may consider that Equation (14) can lead to a quick and reliable way of estimating
S from a set of horizontal absorption experimental data.
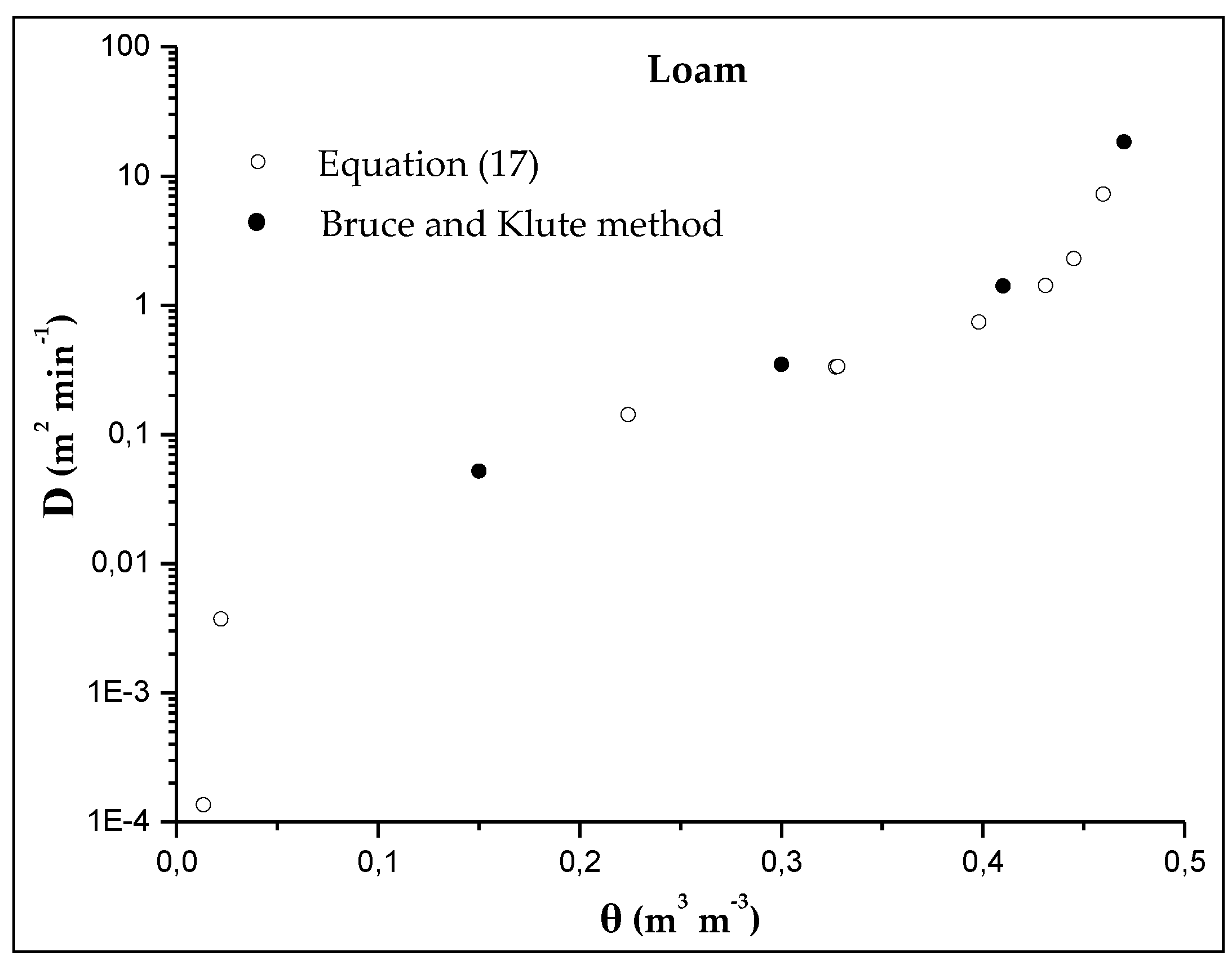
In
Figure 3, the
D(
θ) data for the loamy soil (L) are shown. Closed circles denote data obtained by the Bruce and Klute [
14] method (Equation (16)), while open circles are data obtained from Equation (17). The comparison of the above indicates that Equation (17) could reasonably describe the experimental
D(
θ) data. One should note that by using the analytical expression (Equation (17)), the problem of differentiating the experimental data
in which there is scatter, is overcome. Moreover, the problem of estimating the slope
near saturation, where the
λ(Θ) relationship is almost parallel to the
λ-axis, is overcome by the application of the analytical expression (Equation (17)). Similar results were also obtained for the other soils under present investigation.
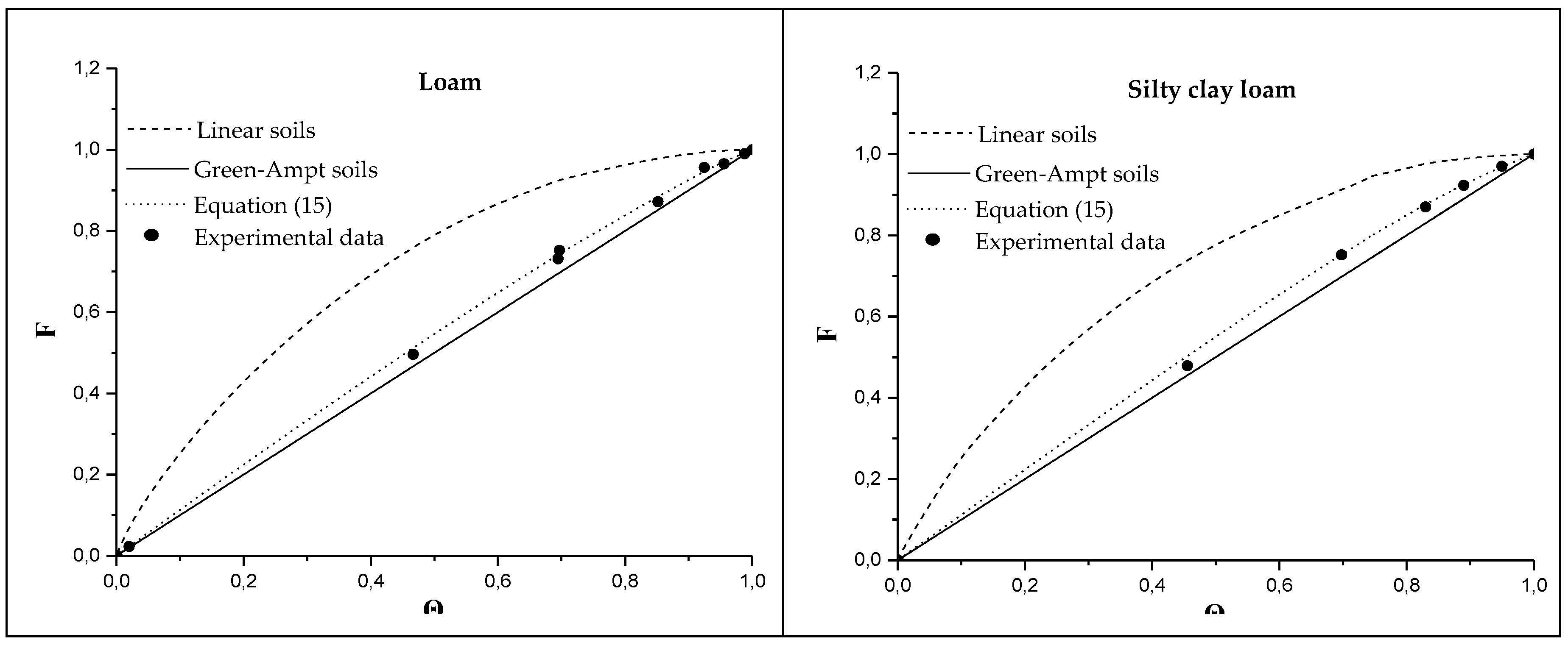
In
Figure 4, the
F(Θ) relationship for the linear Equation (13) and the Green–Ampt soils (Equation (11)) is shown, together with that obtained according to Equation (15) for all soils examined. The experimental
F(Θ) points for all soils were obtained by the application of Equation (10) and the measured value of the sorptivity
S (Equation (18)). From the results, it is shown that the one-parameter Equation (15) gave practically the same values for the
F(Θ) relationships as the ones obtained experimentally, and lies between the two limits (linear and Green–Ampt soils) in all cases that were examined.
It is worth investigating the ability of the equation
F(Θ) = 1 − (1 – Θ)
p+1 to describe the upper and lower theoretical boundaries of F(Θ). As has already mentioned, when
p = 0 the value of
F = Θ—i.e., it converges to the lower limit (
D(
θ) function is a delta function). However, the values of
F for
p = 2.23 (resulted from (
p + 1)
−1 = 0.31 [
8]) differs from the values of
F resulting from Equation (13), which is the upper theoretical limit of
F(Θ). Specifically, it gives higher values of
F(Θ) than the theoretical curve. The fitting of the
F(Θ) = 1 − (1 – Θ)
p+1 equation to the theoretical curve (Equation (13)) showed that the equation
F(Θ) = 1 − (1 – Θ)
2.36 gives very good results of
F(Θ) estimation over the entire range of Θ [
7]. Therefore, the variation range of the parameter
p is between 0 and 1.36, and the resulting shape parameter value for the linear soils ((
p + 1)
−1 = 0.423) is greater than that presented by Clothier et al. [
8].
It can be concluded that F(Θ) = 1 − (1 – Θ)p+1 seems to be appropriate functional form for describing actual flux–saturation curves of general soils, and its parameter p has a physical meaning, i.e., it represents the shape of the soil moisture profile.
Furthermore, one could observe that from the study of Evangelides et al. (Table 2 [
6]), where seven different soils are studied, the fitting parameters
m (Equation (4) [
6]) and
n =
p + 1 (Equation (15)) are strongly linearly related, as
. If one uses
m = 4/5, as Evangelides et al. [
6] proposed, then this leads to
which corresponds to our
p value 0.25. In this respect, Equation (4) [
6], with
m = 0.8, becomes equivalent to Equation (15) in the present study, with
p = 0.25.