Contribution of the Amazon River Discharge to Regional Sea Level in the Tropical Atlantic Ocean

1. Introduction

Global mean sea level rise is one of the most important consequences of the ongoing global warming. Satellite altimetry has revealed a linear increase of 3.1 mm/year since 1993. This global rise is explained by both global ocean warming and freshwater incomes from continental ice melt (mountain glaciers melting and ice-sheets mass loss from Greenland and Antarctica) and land water storage (rivers, lakes, aquifers) [1]. At regional scale, sea level trends present large variations around its global average. In addition to processes explaining the global mean sea level rise, this regional variability is a consequence of temperature and salinity variations, ocean circulation and heat and freshwater air-sea fluxes [2]. If the evolution of the ocean heat content and its contribution to sea level change has been largely investigated for years, the evolution of the salt content and its impact on sea level variations has been poorly considered, mainly because of the lack of in situ salinity data. Since the 2000s, the Argo program provided an unprecedented amount of salinity measurements revealing the importance of salinity contribution to basin scale and regional sea level changes [3,4].

River discharge is one of the causes of regional salinity variability along with precipitation, evaporation and ocean circulation. River discharge can influence sea level through two dynamic responses: First, through the mass input propagation over the global ocean by fast barotropic waves [5]; secondly, through regional density changes caused by modulation of the salt content by the river. This contribution is known as halosteric sea level changes. The discharge results in a low-salinity plume that remains at the ocean surface because of its low density and contributes locally to sea level [6]. The modification of the upper ocean heat content by the plume [7] could also lead to a thermosteric contribution to the regional sea level.

The total world river discharge impacts global sea level through the first process described above (global mass propagation). Its variability is directly linked to world water storage variability. Over 1948–2000, global water storage contribution to global mean sea level change has been investigated with ORCHIDEE Land Surface Model outputs [8]. No significant multi-decadal trend has been detected but a strong interannual variability. The interannual variability of the global water storage explains between −4 to 2 mm in equivalent global mean sea level. This study shows that the interannual variability of global water storage is driven by precipitation principally in the tropics and especially over the south America and northern tropical Africa basins.

Global continental water storage has also been investigated by remote sensing data. Gravity Recovery And Climate Experiment (GRACE) data have been considered over a 7-year time period (i.e., 2002–2009) to investigate global continental water storage from the 33 world’s major river basins. GRACE data confirm the significant contribution of global land water variations to the interannual variability of global mean sea level [9]. This freshwater transfer between the oceans and the continents at interannual time scales is partly due to El Nino Southern Oscillation climate variability.

The contribution of continental waters, based on GRACE data, to global mean sea level trend reaches −0.22 ± 0.05 mm/year for the period 2002–2009 [9] and is largely explained by an evolution of the tropical rivers outflows [10]. However, another study founds a positive contribution of +0.45 ± 0.16 mm/year for the period 1992–2013 [11]. While these different studies highlight the importance of tropical continental river basins, they also shed light on the large trend uncertainties of global continental water storage contribution to the global mean sea level budget [1].

Also, a few studies investigated the regional impact of rivers on sea level, focusing mainly on the coastal impact. Based on tide gauge data, Meade and Emery [12] observed that river discharge explains between 20% and 31% of detrended interannual sea level variance during 1930–1970 along the United States East and Gulf Coasts. Gough and Robinson [13] suggest that discharge from the Churchill River explains 43% of the monthly sea level variance in the Churchill tide gauge records in Hudson Bay (Canada) from 1974 to 1994. Piecuch et al. [14] studied river-discharge effects on United States Atlantic and Gulf coast sea-level changes. They found that sea level rises between 0.01 and 0.08 cm for a 1 km³ annual river-discharge increase, depending on the region. Other studies found no correlation between river discharge and sea level variation, such as Blaha [15] for nonseasonal monthly records in the Chesapeake Bay (from tide gauge) or Han and Webster [16] for interannual sea level variability in the Bay of Bengal (based on simulations). Investigations on the importance of river discharges to coastal sea level variations have been made from hours to seasonal and interannual time scales [17]. Less attention has been brought on open ocean variations caused by river runoffs.

In this study, we will focus on the regional contribution of the Amazon River to regional sea level. The Amazon basin is the largest river in term of volume of freshwater in the world, discharging a mean value of 209,000 m${}^3·$s${}^{-1}$ to the ocean [18], corresponding to 17% of the total world river discharge [19]. Its runoff is almost three times greater during the rainy season (May-June) than during the dry season (December-January) and the standard deviation of its seasonal and interannual time series reach 70,000 m${}^3·$s${}^{-1}$ and 25,000 m${}^3·$s${}^{-1}$, respectively (standard deviation of monthly time series obtained from the hydrological reanalysis ISBA-CTRIP ) [20]. The Amazon river discharges into the Atlantic ocean at 0° N, forming a plume of freshwater whose propagation in the Tropical Atlantic varies seasonally. During boreal winter and spring the plume is transported by the North Brazilian Current (NBC) toward the Caribbean Sea. The remainder of the year, the NBC connects with the North Equatorial Countercurrent (NECC) through a retroflection zone between 5° N and 10° N, transporting the Amazon plume to the east [21,22]. Durand et al. [6] suggest that the impact of the Amazon River discharge on sea level is potentially important at global and regional scales. The authors converted the Amazon discharge into units of equivalent GMSL and show that the standard deviation of its interannual variability is 0.4 mm. Such value is of the same order of magnitude as the interannual standard deviation of 1.0 mm of the GMSL. This confirms the significant contribution of continental water storage and more specifically of tropical rivers basins to interannual variability of global mean sea level.

The impact of river runoff on coastal sea level has received more attention than the impact on open ocean sea level. In the present study, we will focus our investigations on both coastal and open ocean of sea level change to the Amazon freshwater runoff. The main objectives of this analysis are (1) to quantify the Amazon discharge contribution to the mean-state of sea level; (2) to disentangle the processes at play by analyzing changes of temperature and salinity conditions and identifying where and when these changes are generated; (3) to evaluate the impact of the Amazon discharge and variability on regional sea level variability.

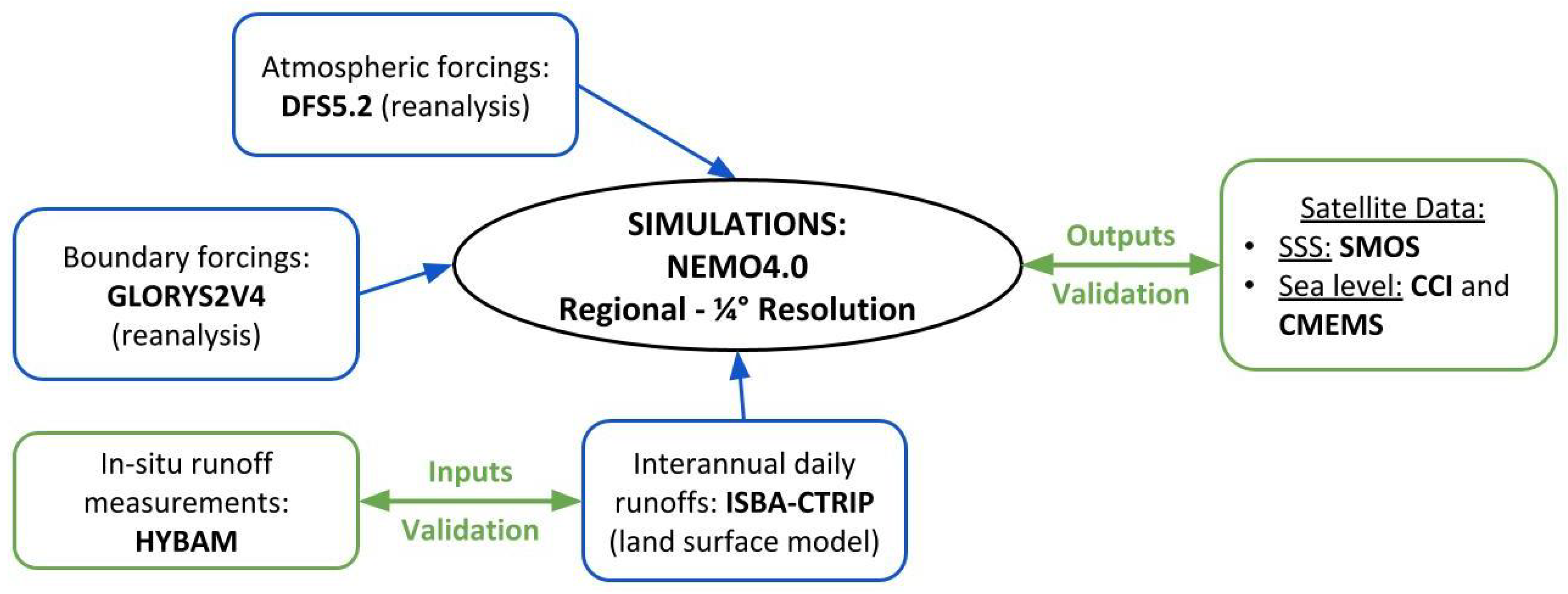
2. Materials and Methods

2.1. Model Configuration

This study relies on dedicated regional simulations of the Tropical Atlantic ocean. They are based on a regional configuration of the ocean model NEMO 4.0 (Nucleus for European Modeling of the Ocean [23]) mainly derived from the configuration described in Reference [24]. The model domain is the tropical Atlantic, from 99° W to 15° E and from 15° S to 34° N. It is discretized on a grid with 1/4° horizontal resolution with 75 levels on the vertical. Temperature and salinity are advected using a Flux Corrected Transport (FCT) scheme with nearly horizontal diffusion parameterized as a Laplacian isopycnal diffusion. For momentum, an energy/enstrophy conserving momentum advection scheme is employed [25] with horizontal bi-Laplacian viscosities applied on model levels. The vertical diffusion coefficients are given by a generic length scale (GLS) scheme configured here as a k minus $ϵ$ turbulent closure. Bottom friction is quadratic with a bottom drag coefficient of 10${}^{-3}$. At lateral walls, partial-slip boundary conditions are assumed. The free surface is solved using a time-splitting technique with the barotropic part of the dynamical equations integrated explicitly.

The model is forced at its boundaries with daily fields from the ocean reanalysis GLORYS2V4 (see Figure 1). At the surface, the air-sea fluxes are computed using bulk formulae [26] and atmospheric variables (winds, air temperature and humidity, shortwave and longwave radiation, precipitation) from DFS5.2 which is a bias-corrected version of ERA interim reanalysis [27].

The model is forced with interannual daily runoffs obtained from the up-to-date ISBA-CTRIP land surface model [20]. For the Amazon river, ISBA-CTRIP (http://www.umr-cnrm.fr/spip.php?article1092&lang=en) daily runoff have been compared to HyBAm in-situ daily measurements from HyBAm (http://www.ore-hybam.org) at Obidos station over the period 1993–2016 (Figure 2). ISBA-CTRIP seasonal cycle is in agreement with observations. However, we note that the model has a higher amplitude compared to the observations. We also find a lag of 1 month for the annual maximum discharge (Figure 2a). The measured runoff at Obidos station is lower than the simulated runoff at the river mouth because the station is located 800 km upstream from the river mouth, with a catchment area amounting for 76% of the total Amazon basin [18,28]. The overall agreement between ISBA-CTRIP and observed Amazon river discharge make the numerical set up suitable to investigate the contribution of the Amazon river runoff to the regional sea level variability.

Four regional simulations were performed with varying Amazon runoff conditions—a reference simulation with interannual Amazon discharge (REF), a simulation without Amazon discharge (NOAMZ), a simulation with constant Amazon discharge (CSTAMZ) and a simulation with a discharge climatology (repetition of the seasonal cycle, CLMAMZ). In the different simulations, the runoff of the remaining rivers is kept interannual. Simulations were integrated from 1970 to 2017. Unless otherwise stated, the analysis focuses on the altimetric period, that is, 1993–2015.

2.2. Data and Products

To evaluate model performance and reliability of the simulations, we make use of several observational products.

Observations for Sea Surface Salinity (hereafter SSS) are from Soil Moisture and Ocean Salinity (SMOS) satellite mission [29]. Data are available for the period 2010–2017 on a regular and global grid with 1/2° horizontal resolution at a monthly basis. Salinity field are corrected from land-sea contamination and latitudinal bias. Systematic errors are reduced and variability is improved compared to previous versions.

For sea level anomalies, the Climate Change Initiative (CCI) product released in 2017 for the period 1993–2015 [30] is used for its accuracy and its homogeneous long-term satellite-based record. The goal of the CCI data product is to provide an accurate and homogeneous long-term altimetry-based sea level record with two main objectives. First, the CCI product considers all available satellite altimeters including the ESA missions (ERS-1/2-Envisat) and the Topex/Poseidon and Jason reference missions. Second, geophysical corrections and all processing steps are applied with coherent data sets over the whole period of the CCI product. This is done to meet the Global Climate Observing Systems requirements. The CCI data set consists of monthly sea level anomalies on a global ¼° grid [30] from January 1993 to December 2015. We are also considering the mean dynamic topography data from CMEMS (http://marine.copernicus.eu/documents/QUID/CMEMS-SL-QUID-008-056-058.pdf) to evaluate its counterpart from the regional NEMO configuration over the period 1993–2018.

2.3. Methods

Based on the hydrostatic equation, barometric-corrected sea level changes can be partitioned between manometric sea level changes (i.e., regional mass changes of the water column, known as barystatic sea level contribution when globally averaged) and steric changes, that is, density changes within the water column [31,32,33]:

$$\underset{\mathrm{sea}\mathrm{level}\mathrm{changes}}{\underbrace{\frac{\partial h}{\partial t}}}=\underset{\mathrm{manometric}\mathrm{changes}}{\underbrace{\frac{1}{{\rho }_{0}g}\frac{\partial P_{bottom}}{\partial t}}}-\underset{\mathrm{steric}\mathrm{changes}}{\underbrace{\frac{1}{{\rho }_0}{\int }_H^h\frac{\partial \rho (T,S,p)}{\partial t}dz}}$$

(1)

with h the ocean surface, ${\rho }_0$ the mean seawater density, $P_{bottom}$ the bottom pressure, g the acceleration of gravity, H the ocean depth, $\rho$, T, S and p respectively the seawater density, temperature, salinity and pressure. Note that ${\rho }_0$ is equal to 1035 kg· m${}^{-3}$ as considered in the NEMO model.

Steric changes can be divided into two parts: Halosteric changes (due to changes in salinity only) and thermosteric changes (due to changes in temperature only). They are calculated as:

$$\frac{\partial h_{halo}}{\partial t}=-\frac{1}{{\rho }_0}{\int }_H^h\frac{\partial \rho (\overline{T},S,p)}{\partial t}dz$$

(2)

$$\frac{\partial h_{thermo}}{\partial t}=-\frac{1}{{\rho }_0}{\int }_H^h\frac{\partial \rho (T,\overline{S},p)}{\partial t}dz$$

(3)

where overbars represent the time-mean salinity or temperature computed as a function of depth over 1993–2015.

In Section 3.1, we compute time-mean differences between the reference simulation (REF) and the simulation without Amazon runoff (NOAMZ). In Section 3.2, we aim to evaluate the contributions of temperature, salinity and mass to the mean-state of sea level. We separate the sea level anomaly into a steric contribution and a manometric contribution. Then, we partition the steric contribution into halosteric and thermosteric sea level contributions in order to evaluate the distinct roles of salinity and temperature, respectively. The difference between mean-states of two simulations is noted hereafter with the symbol $\Delta$. Equation (1) becomes:

$$\Delta h=\Delta h_{manometric}+\Delta h_{steric}$$

(4)

In order to apply and interpret such decomposition in a regional ocean model, some precautions must be taken. NEMO4.0 is a Boussinesq model that conserves volume rather than mass. Therefore, regional mean sea level is not properly resolved by the model [23]. Thus, to overcome this issue, we remove the regional averages of the sea level, mass, steric, halosteric and thermosteric heights and we present spatial anomalies with respect to their regional averages.

Amazon discharge contribution to the time-mean steric, halosteric and thermosteric sea level are calculated as follows:

$$\Delta {\eta }_{steric}=\frac{1}{{\rho }_0}{\int }_{-H}^h\left[\rho (T_{REF},S_{REF},p)-\rho (T_{NOAMZ},S_{NOAMZ},p)\right]dz$$

(5)

$$\Delta {\eta }_{halo}=\frac{1}{{\rho }_0}{\int }_{-H}^h\left[\rho ({\overline{T}}_{NOAMZ},S_{REF},p)-\rho ({\overline{T}}_{NOAMZ},S_{NOAMZ},p)\right]dz$$

(6)

$$\Delta {\eta }_{thermo}=\frac{1}{{\rho }_0}{\int }_{-H}^h\left[\rho (T_{REF},{\overline{S}}_{NOAMZ},p)-\rho (T_{NOAMZ},{\overline{S}}_{NOAMZ},p)\right]dz$$

(7)

Finally, mechanisms controlling salinity changes are investigated by analyzing the main contributors to the salinity budget as a function of depth and time during the spin up period (i.e., 1970–1975). Considering the spin up period allows for a direct identification of the time scales involved to reach the steady state. The salinity budget is calculated as:

$$\frac{\partial S}{\partial t}=\underset{ADV}{\underbrace{-u\frac{\partial S}{\partial x}-v\frac{\partial S}{\partial y}-w\frac{\partial S}{\partial z}}}+\underset{ZDF}{\underbrace{\frac{\partial }{\partial z}\left(K_z\frac{\partial S}{\partial z}\right)}}+\underset{LDF}{\underbrace{D_l(S)}}+\underset{FLX}{\underbrace{E-P-R}}$$

(8)

with S the salinity, (u, v, w) the zonal, meridional and vertical components of the velocity vector, $K_z$ the vertical turbulent diffusion coefficient, $D_l(S)$ the lateral diffusion of salinity, E the evaporation, P the precipitation and R the river runoffs. The left-hand side of Equation (8) represents the salinity tendency. At the right-hand side of Equation (8), ADV is the total salinity advection, ZDF the vertical diffusion, LDF the lateral diffusion and FLX the surface freshwater flux. Monthly averages of the different terms of the budget are computed online at each model grid point in order to provide exact contributions of the non-linear terms.

In Section 3.3, we analyze the seasonal signal and the interannual variability of the Sea Level Anomaly (SLA), defined as the difference between the Absolute Dynamic Topography (time-varying sea level above geoid, hereafter ADT) and the Mean Dynamic Topography (time-mean sea level above geoid, hereafter MDT):

$$SLA=ADT-MDT$$

(9)

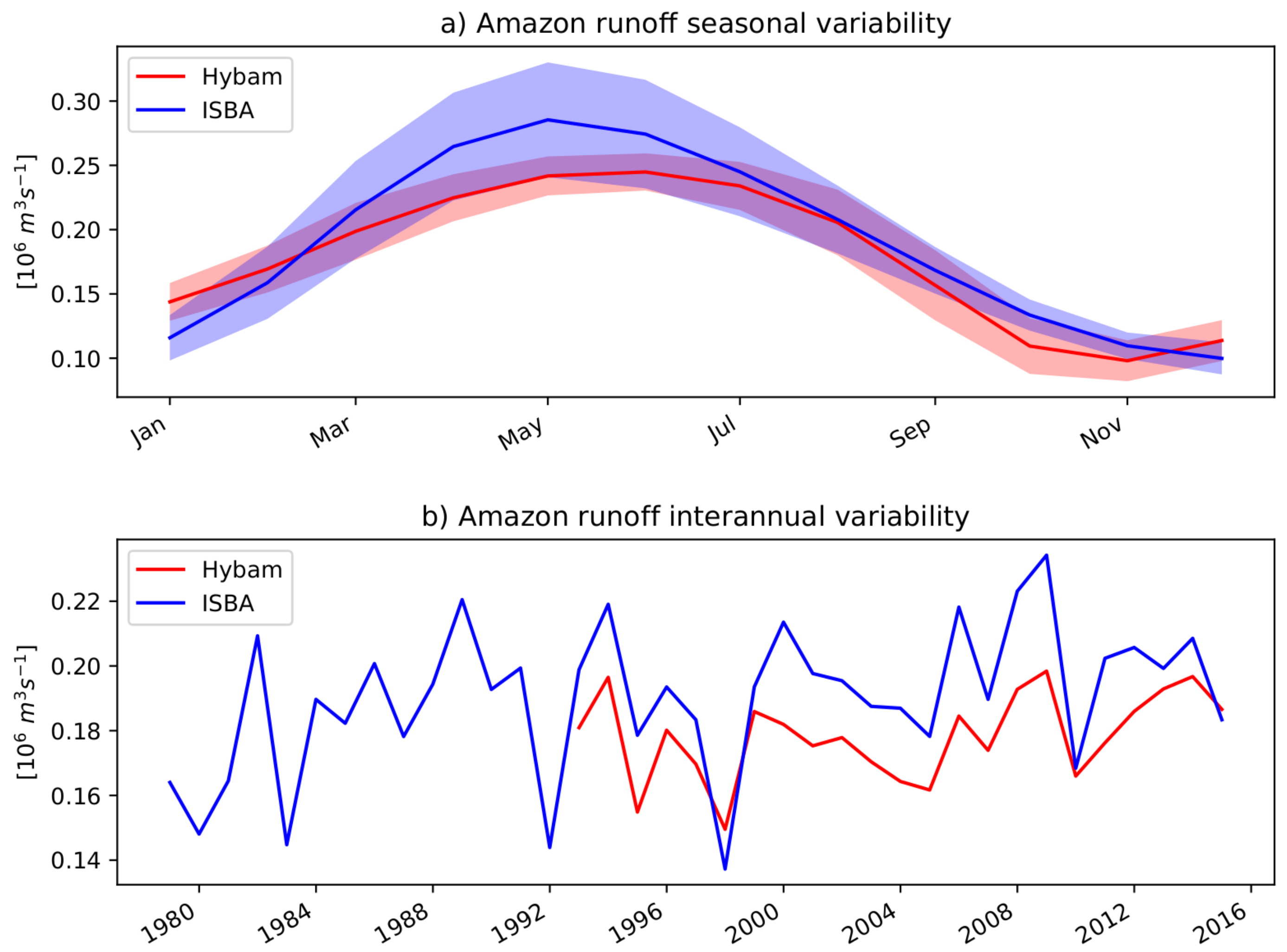
2.4. Model-Observation Comparisons

The validation of the reference simulation is focused on two key metrics of our study: The sea surface salinity and the sea level.

The comparison of SSS from SMOS data and from model outputs is presented in Figure 3. The comparison is not possible along the coast because SMOS data are given on a 1/2° resolution grid with not enough accuracy in coastal areas because of high land-sea emissivity contrasts [29]. The large scale distribution of the mean-state of SSS is well simulated by the model and we clearly identify the Amazon, Congo and Orinoco plumes characterized by low sea surface salinity patterns (Figure 3a,b). The North Atlantic subtropical gyre, characterized by a sea surface salinity maximum between 20° N and 30° N, is reproduced by the model but saltier than the remote sensing observations. For the Gulf of Guinea, sea surface salinity if fresher from the model than from the observations. The Amazon plume is correctly represented by the model, although it is slightly more extended northward. To investigate the time variability, salinity is averaged from 50° W to 74° W and from 11° N to 26° N, that is, over an area of size 2500 km × 1700 km (corresponding to the purple rectangle, Figure 3a,b). We chose this area, since as we will see in Section 3, as the sea level of this region is significantly under influence of the Amazon river runoff.

Model and observation SSS seasonal cycles are close but the model is one month in phase advance with respect to the observations from February to September (Figure 3c). The model properly simulates SSS interannual variability in this area, although it may overestimate some interannual peaks (Figure 3d).

The model sea level is compared to CMEMS Mean Dynamic Topography and CCI sea level anomalies. The model reproduces with accuracy the MDT spatial distribution and magnitude, which demonstrates its capacity to simulate the regional mean circulation (Figure 4a,b). However, sea level gradients are slightly stronger in the model than in the observations in the Caribbean Sea, suggesting a too large transport by the Caribbean Current.

Main features of both seasonal and interannual variabilities are in agreement, despite differences in magnitude (Figure 4c,d). Note that for properly evaluating the interannual variability of regional sea level, we first remove the seasonal cycle and the linear trend at each grid point. Observed sea level presents strong seasonal variations in the north-western part of the studied area, reaching 7 cm in the Gulf of Mexico and around the Gulf Stream (standard deviation of monthly time series). There are two other patterns of high variability east of the Lesser Antilles (60° W–50° W, 10° N–20° N) and north of the equator (40° W–20° W, 0°–10° N). Sea level presents weak seasonal variations in the south hemisphere. The model simulates these seasonal patterns albeit with some differences in terms of amplitude and spatial extent.

The observed interannual variability (yearly averaged) is large in the Gulf of Mexico, in the Caribbean Sea and at the Amazon mouth, with variances exceeding 4 cm (Figure 4e). All these features except the one at the Amazon mouth are represented by the model with smaller amplitudes (Figure 4f). Model resolution might be too low to simulate complex dynamics on the continental shelf near the Amazon mouth. The disagreement found at the mouth of the river might also be due to the tide contribution. Indeed, the tide is not implemented in the current model configuration.

3. Results and Discussions

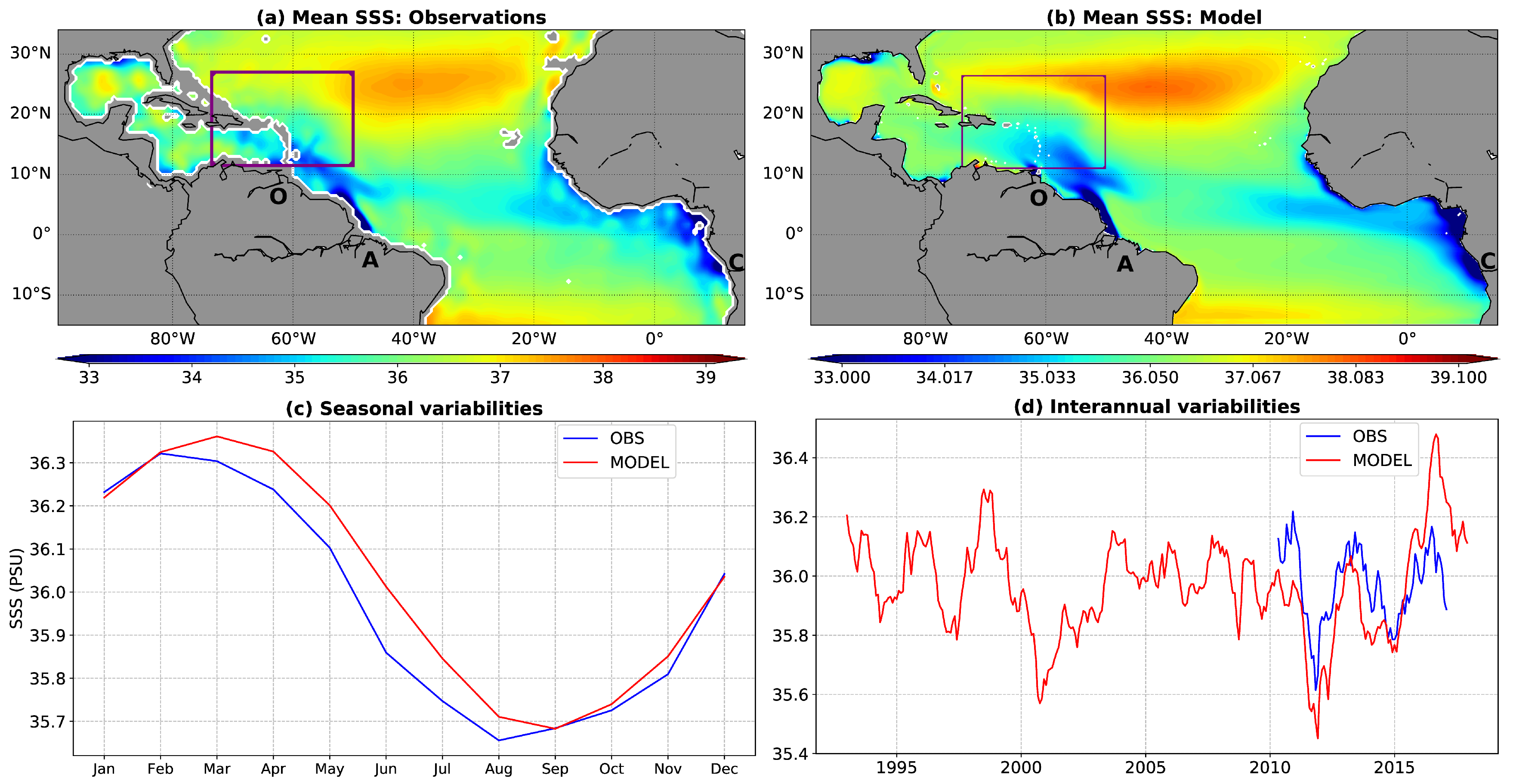
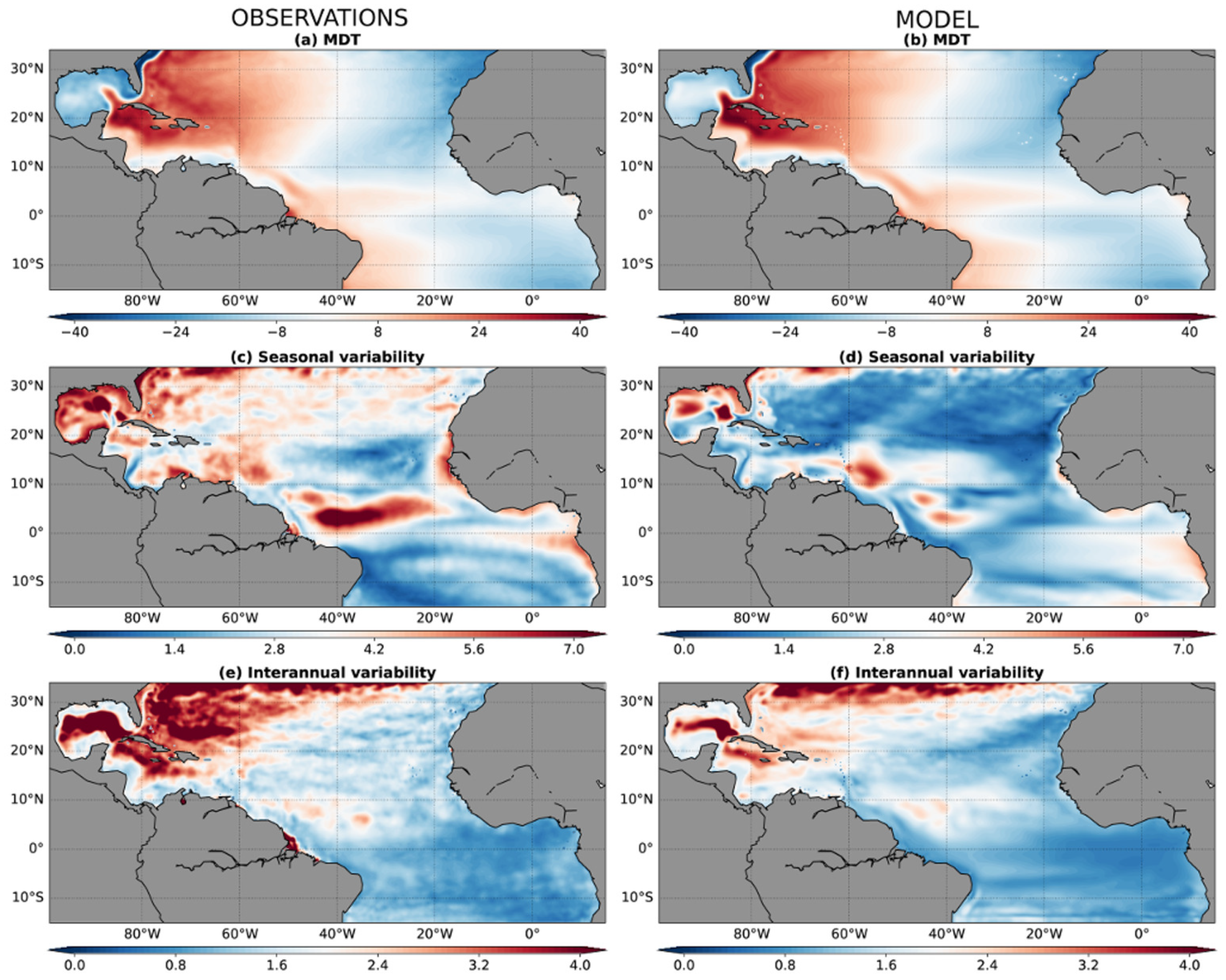
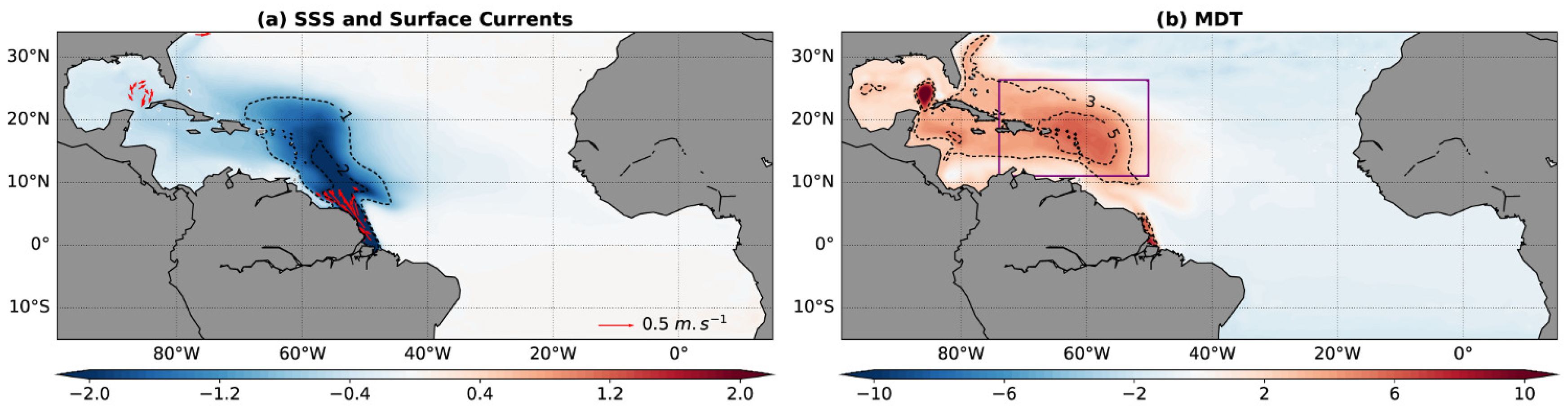
3.1. Mean State of Sea Level

To investigate the contribution of the Amazon River discharge to the mean-state of regional sea level, we compute the difference between the reference simulation and the simulation without Amazon runoff (REF minus NOAMZ) averaged over the period 1993–2015. Anomalies are shown for surface salinity, surface currents and sea level in Figure 5. As expected, the Amazon runoff has a large scale imprint on SSS (Figure 5a). The main SSS anomaly reaches the Caribbean Archipelago with values greater than 1 PSU 3000 km away from its mouth but anomalies are also observed in the Caribbean Sea, in the Gulf of Mexico and in the retroflection area of the NBC. A response of the surface currents is also found, overlapping the low-salinity plume and strengthening the NBC. This increase is strongest in the first 200 km to the north of the river mouth with values exceeding 0.7 m·s${}^{-1}$.

Near the Amazon mouth, the MDT is up to 11 cm greater with the net Amazon runoff than without any runoff (Figure 5b). More interestingly, the discharge impacts the whole Caribbean region with anomalies of 5 cm in a large area including the Lesser Antilles and Puerto Rico and a mean contribution of 3.3 cm in the diagnosis box. The Loop Current (near 85° W, 25° N) presents a large positive signal for the mean-state of sea level. The Loop Current is known to have large variability and to episodically shed eddies towards the Gulf of Mexico. It presents large steric sea level anomalies that have a temperature origin (see Figure 6a,d). Although the Loop Current could integrate the upstream changes in the large scale circulation and heat content, these anomalies could also be a consequence of the stochasticity of the Loop Current system. Therefore, it is difficult to conclude whether the sea level anomaly detected is directly linked to the Amazon runoff. We do think it is not relevant to investigate further from this set of simulations.

It is noteworthy that the SSS pattern is not superimposed to the MDT pattern. This reveals that SSS anomalies do not straightforwardly explain the distribution of the MDT anomaly for the open ocean. Therefore, vertical distributions of salt contents need to be considered and investigated in more details.

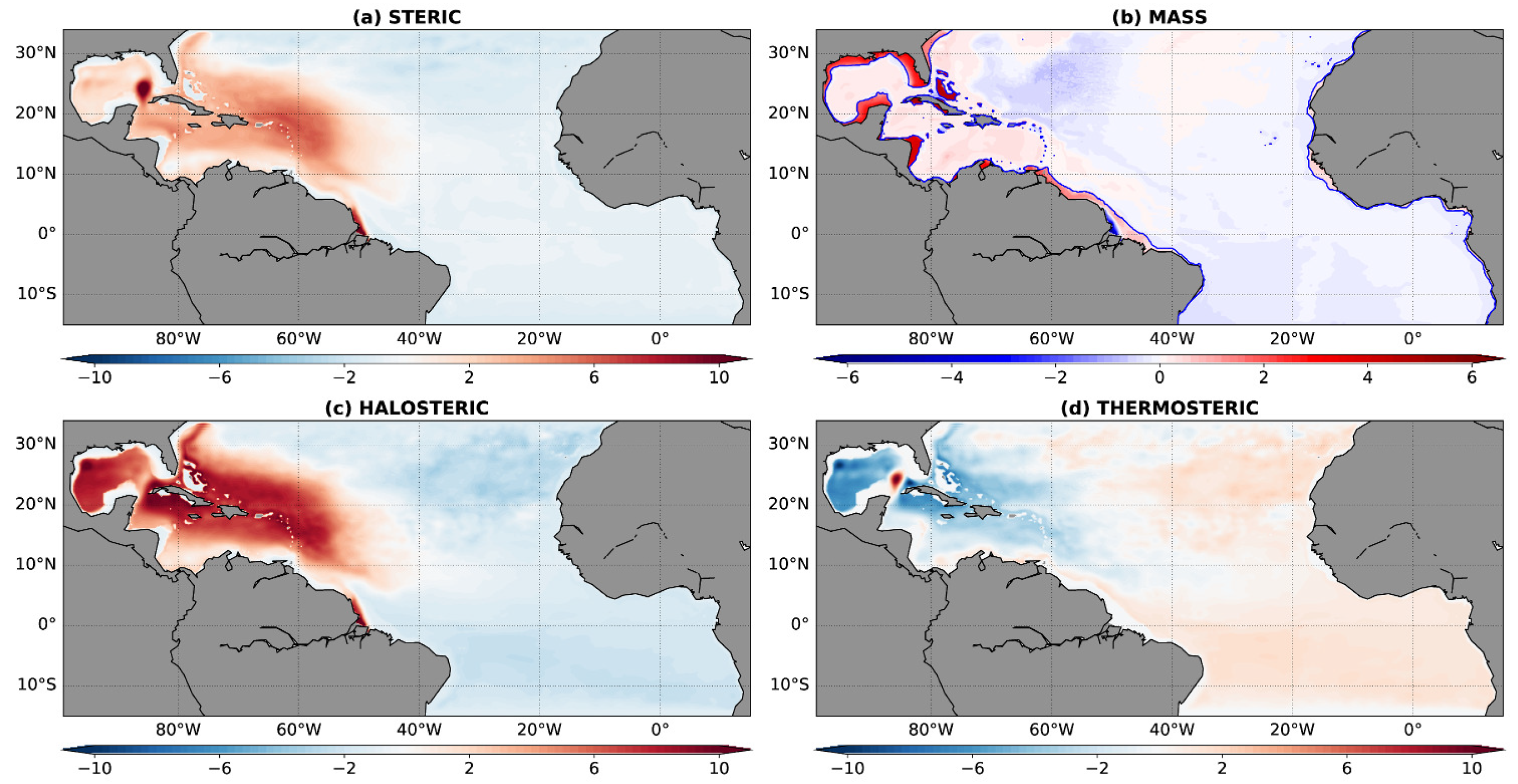
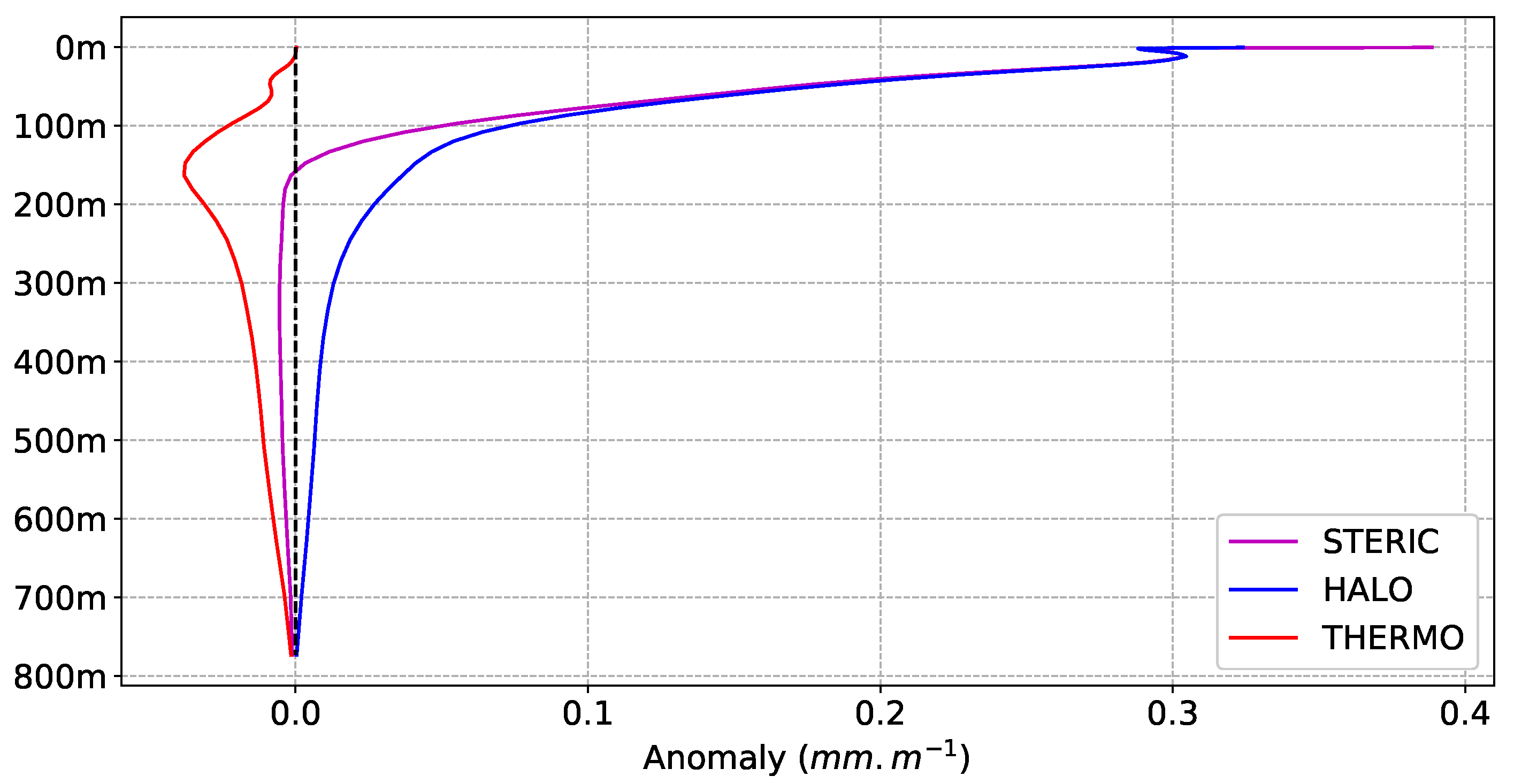
3.2. Temperature, Salinity and Manometric Contributions to Regional Mean-State Sea Level

We use Equation (4) to separate the MDT anomaly into the steric sea level contribution and the manometric sea level contribution and Equations (5)–(7) to partition the steric contribution into halosteric and thermosteric sea level contributions. We find that the steric sea level explains most of the mean-state of sea level (Figure 5b and Figure 6a). We also find regional mass redistributions with a decrease at the river mouth of around 8 cm and positive contributions reaching 4.5 cm mainly on continental shelves (approximately identified by the 100 m bathymetry contour, see Figure 6b). Interestingly, we find that these positive contributions are not only located in the vicinity of the river mouth but also located remotely around the Gulf of Mexico and around the Caribbean archipelago (Figure 6b), 3000 km away from the river mouth. An hypothesis to explain coastal mass increases is that on continental shelves, the shallow water column allows smaller steric expansion than in the open ocean, resulting in a steric gradient between the coast and the open ocean. Mass redistribution is then the fastest way to balance this gradient [34]. This result corroborates former studies in which mass increases caused by thermosteric changes were observed on continental shelves in climate change simulations [35]. We also observe that the steric signal is dominated by halosteric sea level contribution. We remark that halosteric anomalies present similar features than steric anomalies but with stronger magnitude: They are partly counterbalanced by thermosteric anomalies (Figure 6c,d).

We further investigate the steric sea level anomalies and the thermosteric and halosteric sea level contributions around the Caribbean Archipelago by investigating their averages over the area shown in Figure 5b. The vertical distribution of horizontal averaged steric, halosteric and thermosteric contributions to sea level is presented in Figure 7. Contributions are expressed in millimeters of sea level increase per meter of water column. In the first 80 m of the ocean, the halosteric sea level height is large and controls the total steric sea level height. Deeper, the thermosteric height is negative and tends to counterbalance the total steric height. As a result, 95% of the total steric anomaly is located in the first 80 m of the ocean, whereas 250 m of water column are needed to reach 95% of the total halosteric anomaly, indicating that large compensations occur between halosteric and thermosteric contributions. Clearly, the Amazon river discharge contributes to the mean-state of sea level by freshening the upper 250 m of the tropical Atlantic ocean over the Caribbean Archipelago.

The influence of the Amazon on the salt content reaches depths of 250 m (Figure 7), while the plume is only 15 m deep at the river mouth. This suggests a large scale and downward propagation of the salt anomalies. It raises the question of what time scale is needed to transport the Amazon freshwater from the surface to deeper layers. For that purpose, we have investigated distributions of the main contributors of the salinity budget as a function of depth and time (see Equation (8)) during the spin up period (Figure 8). Results show that a strong and stable seasonal cycle rapidly occurs in the upper 30 m of the ocean, with negative values of 1.2 PSU during boreal summer and 0.8 PSU during boreal winter (Figure 8a). This results in alternating positive and negative anomalies of the salinity total tendency (Figure 8b). We observe that salinity anomalies are set up to a depth of 200 m–250 m in about 5 years before reaching a steady state.

Main contributors to salinity differences are the turbulent vertical diffusion, hereafter noted as ZDF, (Figure 8c) and the total advection (sum of horizontal and vertical advections, Figure 8d). The strong vertical mixing between the Amazon freshwater in the top 15 m of the ocean and the saltier underlying layer is accompanied with negative ZDF anomalies at the surface and positive values in the layer 15–30 m. During winter, the plume gets thicker and ZDF spreads the Amazon freshwater to 200–250 m depth. This suggests that winter time convection and mixing are the leading physical processes controlling the freshwater downward propagation. On the other hand, advection tends to balance ZDF anomalies, although this process is very weak under 50 m.

We previously highlighted that changes in surface salinity do not fully explain sea level changes, which evidences the importance of subsurface salinity anomalies (Figure 5 and Figure 7). It results that these subsurface salinity anomalies (we consider here the layer 30–160 m) are located further from the Amazon mouth than the surface salinity anomalies (Figure 5a and Figure 9a). They cover the whole Caribbean Archipelago with values greater than 0.5 PSU. Almost no salinity tendency is observed over the period 1993–2015 (not shown), which was expected considering simulations reached a steady state and considering the trend of the Amazon mean discharge is small [36]. However, the term ZDF shows these salinity anomalies are generated in two areas, the first one at 10° N, with an extension from 47° W to 60° W; and the second one near 23° N, with an extension from 55° W to 63° W (Figure 9). It is interesting to note that vertical mixing is not uniform and occurs in preferential areas, both far from the river mouth. The anomalies generated out of the Caribbean Archipelago most probably propagate westward through advection by the large scale currents.

3.3. Seasonal and Interannual Sea Level Variability

After investigating the mean-state of sea level, we now examine the influence of the seasonal and interannual variability of the Amazon runoff on the time-mean sea level and on sea level variability. For that purpose, we take advantage of the simulations forced with a constant Amazon discharge (CSTAMZ) and a climatological Amazon discharge (CLMAMZ) described in Section 2.3. In the considered area, the MDT is 3.3 cm higher when taking into account the Amazon discharge (difference between REF and NOAMZ simulation, Figure 10a). Noteworthy, the runoff variability has almost no impact on the time-mean sea level (only 2 mm at most, see CLMAMZ and CSTAMZ simulations in Figure 10a).

The seasonal and interannual sea level variability for the four simulations is shown in (Figure 10). Interestingly, we find that considering a constant Amazon runoff already strongly contribute to the sea level variability. Indeed, sea level seasonal and interannual standard deviations are raised by 23% and 11%, respectively, in comparison with the simulation without any Amazon runoff. The Amazon seasonal cycle introduces only 6% and 2% of additional sea level seasonal and interannual variance, compared to the case with constant Amazon. Contrary to what was expected, the Amazon discharge interannual variations have no significant impact on sea level variability in this remote area. The Amazon discharge contributes to 23% and 12% of the seasonal and interannual sea level variances, respectively, almost independently of its variability.

4. Conclusions

This study highlights large river discharges affecting sea level not only at the coasts but also for the open ocean. We find that the sea level influence of the Amazon river is noticeable 3000 km away from the river mouth. For this reason, attention has been given to both remote and coastal sea level changes. We quantified the Amazon contribution to the mean-state of sea level and we shed light on the mechanisms associated with this contribution. We also investigated sea level variability through sensitivity simulations with constant, seasonally varying and inter-annually varying Amazon runoff. Main results are summarized below.

• The Mean Dynamic Topography (MDT) is up to 11 cm higher at the Amazon mouth with Amazon runoff and 3.3 cm higher around the Caribbean Archipelago.
• The MDT anomaly is mostly explained by the halosteric response to freshwater input coming from the Amazon river discharge, located in the upper 250 m of the ocean, while the thermosteric response is weak and tends to counterbalance this effect.
• Regional mass redistributions are observed with a decrease at the river mouth equivalent to 8 cm of mean sea level and increases on continental shelves of the Gulf of Mexico and Caribbean Sea equivalent to 4.5 cm of mean sea level.
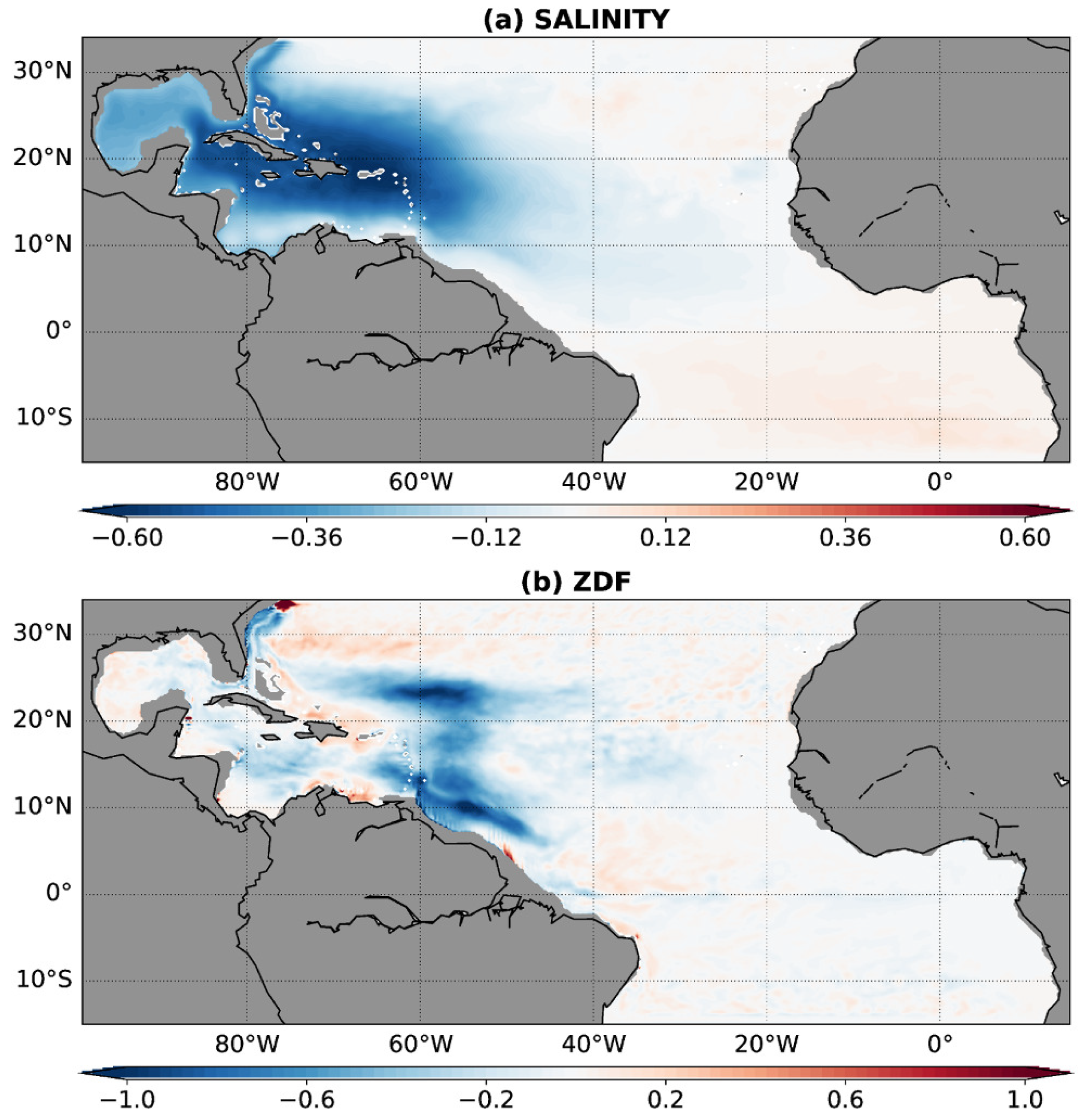
• The Amazon low-salinity plume is mixed with subsurface waters in two remote areas: The first one at (55° W, 10° N); and the second one near (60° W, 23° N). This results in a time-mean salinity anomaly of 0.5 PSU located under 30 m depth over a large region encompassing the Caribbean Archipelago. This subsurface anomaly partly explains the regional sea level anomaly.
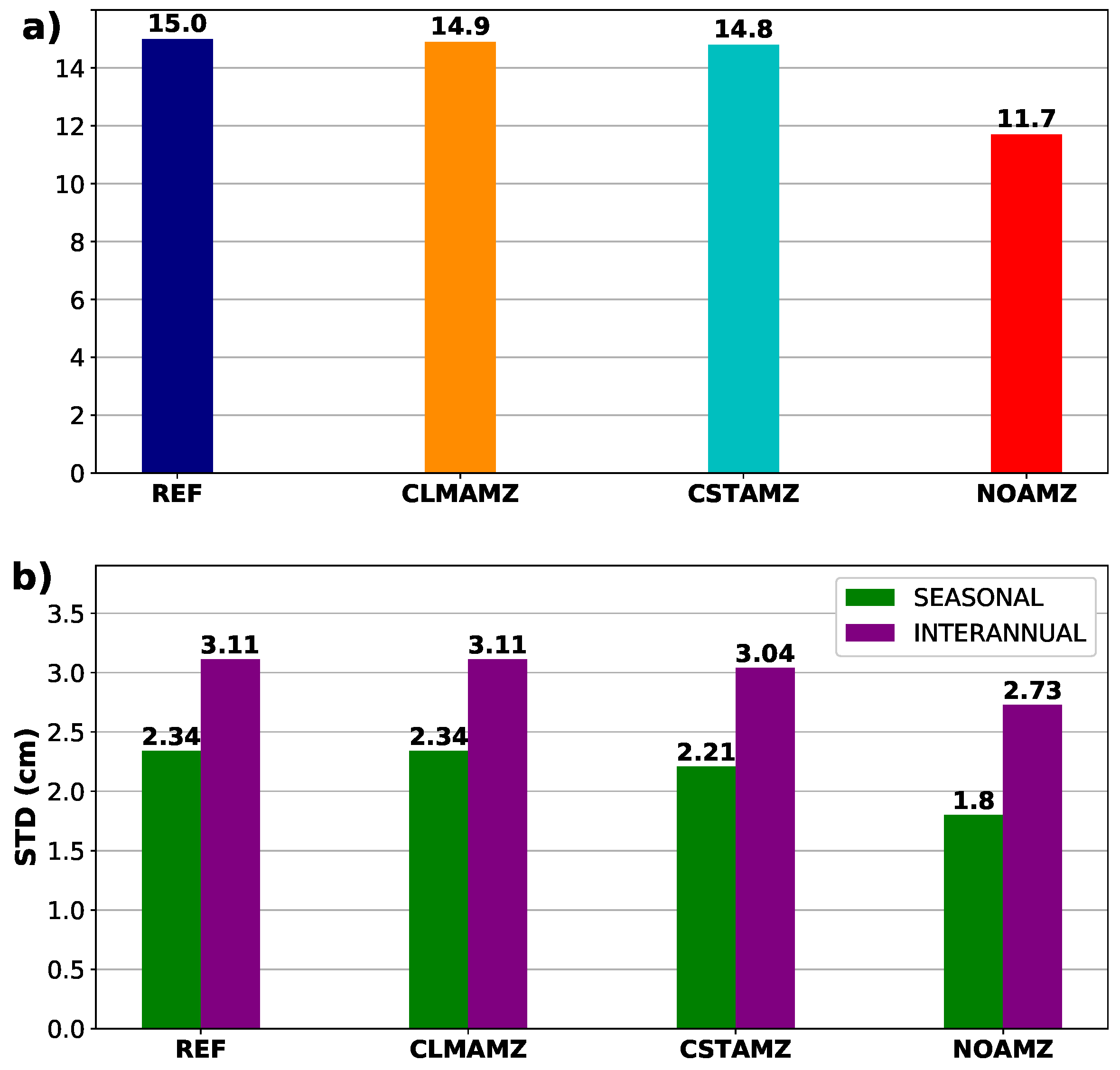
• The Amazon discharge contributes to 23% and 12% of the seasonal and interannual sea level variances in a large area around the Caribbean Archipelago. We showed that the Amazon mean discharge largely explains this sea level variability increase. This suggests that most of the sea level variability associated with the Amazon runoff is the result of the variability of the river plume in response to seasonal and interannual variability of the upper ocean regional circulation. The Amazon seasonal cycle introduces a 6% and 2% additional sea level seasonal and interannual variances, compared to the case with constant Amazon. Finally, interannual variations of the Amazon discharge do not clearly impact sea level variability.

This study highlights the importance of the Amazon river discharge to regional sea level variations in the tropical Atlantic Ocean. Radical changes in river discharge variability and trends are expected due to anthropogenic climate change and modification of the Amazon basin water cycle. Projections indicate that seasonal variability of precipitations in the Amazonia will increase and that extreme weather events like droughts and floods will become more frequent and severe, resulting in an increase in discharge variability and so to a probable increase in sea level variability [2,37]. Also, more than a hundred hydropower dams have already been built over the Amazon tributaries [38] and more than 200 are planned for the next decades [39]. Dams can reduce river discharge as water evaporates in reservoirs or is diverted for irrigation and it decreases seasonal flow variability, mostly by attenuating flood maxima [40]. Therefore, it is difficult to know whether or not river discharge variability will increase. We leave for future investigations the potential anthropogenic contribution of river discharge to regional sea level changes.