1. Introduction
One of the most important challenges in hydrology is to quantify water availability for every climatic scenario and geographic area in order to support socio-economic activities and ecosystem needs [
1].
Simplified models are available to explore water partitioning processes at large temporal and spatial scales [
2,
3,
4]. Considering steady state conditions [
5,
6] and neglecting the variation of water storage [
7,
8,
9], the mean annual precipitation
is balanced by mean annual runoff
and mean annual evapotranspiration
. Under these conditions, Budyko [
10] found a semi-empirical relation between the ratio of mean annual potential evapotranspiration
to
and the ratio of
to
. The first one is called the aridity index (
) and it is an indicator related to the local climatic condition, meaning the higher the aridity index is, the dryer the climate. In the Budyko’s theory,
is constrained by energy and water availability, by net radiation, and by
[
11,
12,
13]. For this reason, the ratio of
, called the evaporative index (
), can vary between 0 and 1 (energy and water limit), differently to the aridity index that could be higher than one and theoretically could reach an infinite value.
The variability of Budyko’s curve could be caused by three main triggers [
14]: (i) climate properties [
15,
16,
17,
18], (ii) catchments physical processes [
19,
20], and (iii) vegetation [
6,
21,
22].
Different authors proposed parametric or analytic expressions to describe the relation between
and the aridity index
[
5,
23,
24,
25,
26,
27]; one of the most well known expressions was obtained by Fu [
28] with only one parameter, commonly indicated as
, describing the rainfall partitioning into
and
. The mathematical expression was as follows:
The higher the Fu’s parameter, the higher
for a given aridity index
. Some authors derived the
value of Budyko’s semi-empirical expression as being equal to 2.6 [
23,
29,
30].
Since Fu’s equation is a representation of Budyko’s curve that, as said before, is responsive to climate, catchment processes, and vegetation,
should comprise and describe the variability in the annual water catchment response [
8,
30,
31,
32,
33].
Different attempts have been done to interpret and model
. Using 270 Australian catchments, Zhang, Hickel, Dawes, Chiew, Western, and Briggs [
9] performed a stepwise regression analysis between
and basin properties (i.e., vegetation cover, precipitation characteristics, catchment slopes, and plant available water capacity), and found that the most significant elements were the average storm, depth, and coefficient of variation in daily precipitation. Similarly, Xu et al. [
34] linked Fu’s parameter with geographic and morphometric catchment properties of a dataset composed by MOPEX “small” basins [
35] and a “large basin” whose data are from different sources (CRU TS 3.20, HYDRO1K, GIMMS). A simple stepwise regression and a more complex artificial neural network analysis were adopted to explain the relationship between the
hydrological defined parameter and morphological basin properties, finding good explanatory capacity of the two developed models for small and large basins (
= 0.53–0.83). Latitude has proved to be the best correlate with Fu’s parameter. As an alternative, Yang et al. [
36] selected non-linear expression for predicting
over 180 non-humid basins in China, which was a function of infiltration capacity, soil water storage, and average terrain slope. The expression was able to predict annual water cycle components (95.2% and 62% of the variance of mean annual evapotranspiration and runoff, respectively) by just using the aforementioned morphological descriptors. Through water-soil-vegetation metrics, Abatzoglou and Ficklin [
2] studied the correlation between
and morphological properties over watersheds in the United States. The relative cumulative moisture surplus (
), the ratio of available soil water holding capacity to precipitation (
), and the topographic slope were integrated in a regression model that demonstrated the ability to simulate the spatial variability of
(81.2%), which was involved in increasing the value of
as Fu’s parameter decreased, whereas
has direct proportionality with
.
In this work, we will trace an original way (i) to further demonstrate and support the idea that climate, basin morphology, and vegetation drive water partitioning within Budyko’s framework and (ii) to establish the value in data-poor condition, providing practitioners and hydrologists with a tool for assessing annual runoff. But, differently from the previous studies, we used in silico experiments. Namely, we ran a simple conceptual lumped model, which preserved the physical description of fundamental hydrological processes acting within a natural basin. The choice of a simple model allowed us to deal with a huge amount of stochastic input data, consider a large range of basin descriptors and vegetation types, and work within reasonable computational time. The model will be forced by stochastic synthetic potential evapotranspiration and precipitation daily timeseries. The climatic input will be generated by a weather generator that roughly epitomizes the climatic variability by using five combinations of seasonal patterns involving potential evapotranspiration and precipitation. The model parameters domain was explored in order to assess how basin morphology and vegetation impact on the water partitioning process and for determining the value. Then we interpreted the model outputs within the Budyko’s framework to unravel the role of climate, basin morphology, and vegetation in multi-years water partitioning rules.
2. Methods
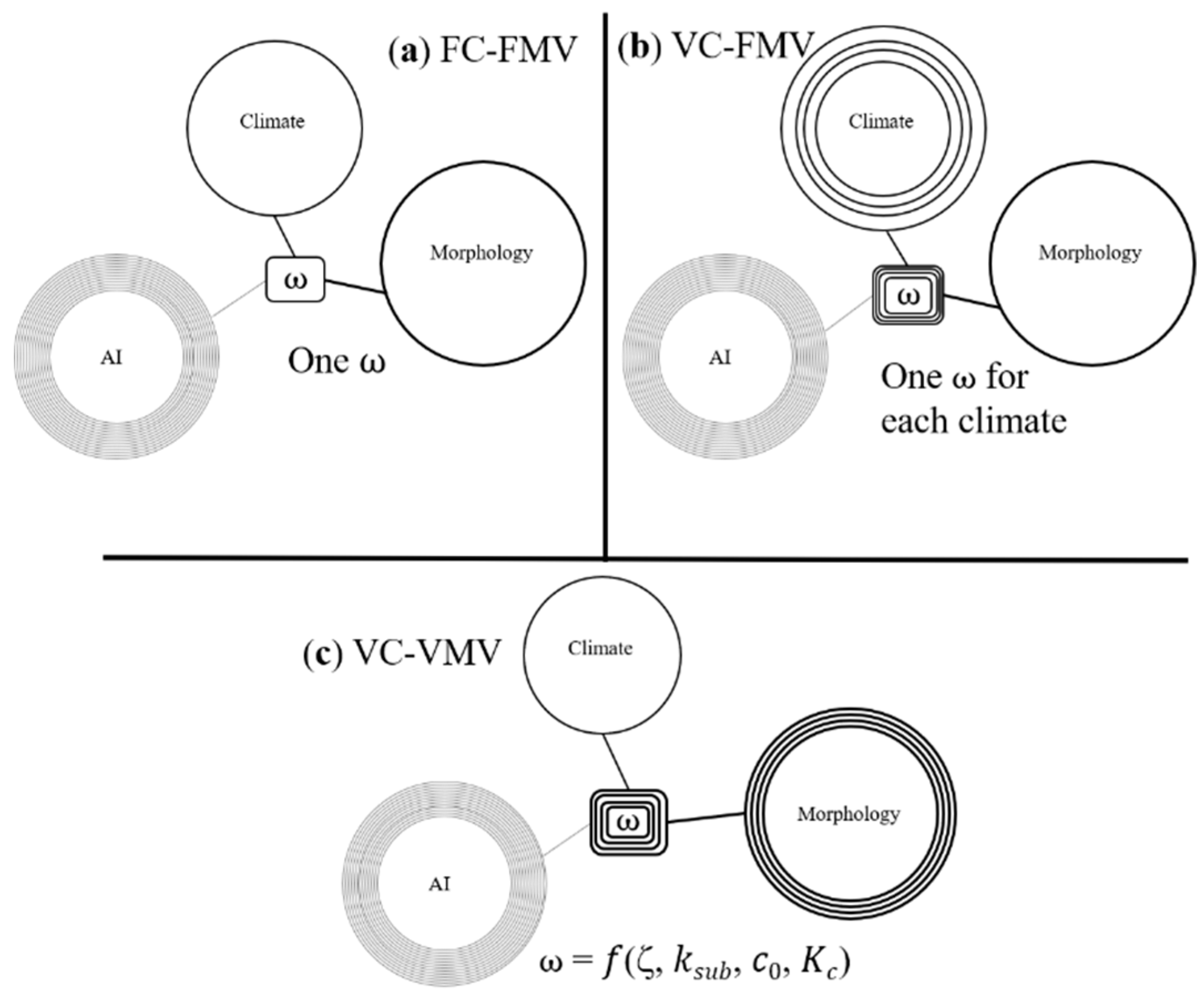
The role of climate, basin morphology, and vegetation in characterizing long term hydrological processes and in determining the
value was explored by three consequent modeling experiments, which are sketched in
Figure 1.
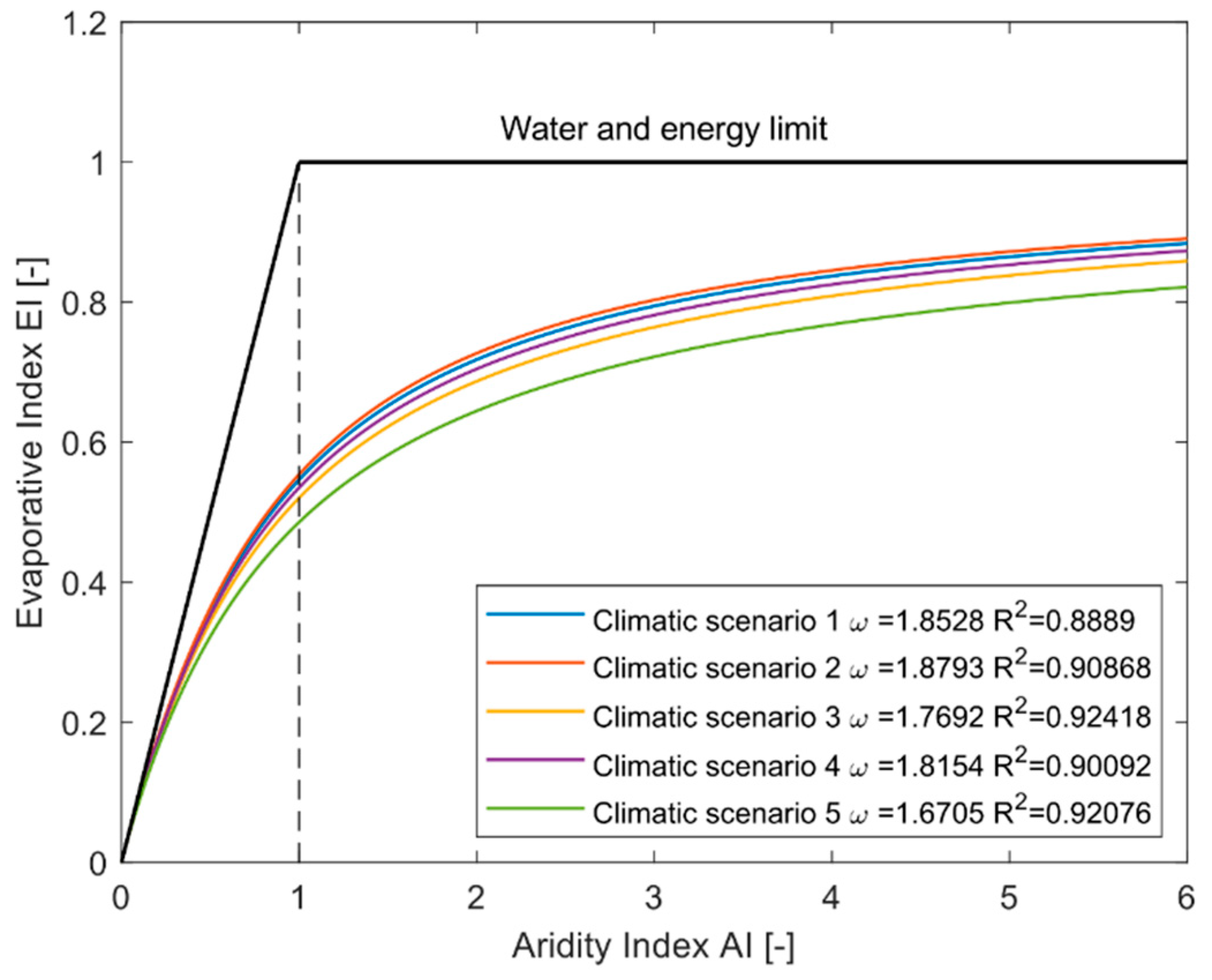
Supposing a particular climate, defined as a characteristic seasonal pattern of potential evapotranspiration and precipitation, once defined the morphological basin and vegetation properties (model parameters), we hypothesize that the hydrological response is only related to the aridity index. In other words, for a given climate condition, notwithstanding that the combinations between mean annual precipitation and potential evapotranspiration are infinite, water partitioning rules are uniquely defined. In the Budyko’s framework and using the Fu’s equation, this means that for different casual couples of
and
, a unique value of
is identifiable (
Figure 1a).
Another cornerstone of this work is to support the idea that the hydrological behavior of a basin is driven by climate, again defined as a seasonal pattern of potential evapotranspiration and precipitation. Namely, the same basin (the same model parameters and then, morphological and vegetation properties), in different geographic areas with different seasonal patterns of climatic variables will result in different partitioning rules as a function of climate (
Figure 1b).
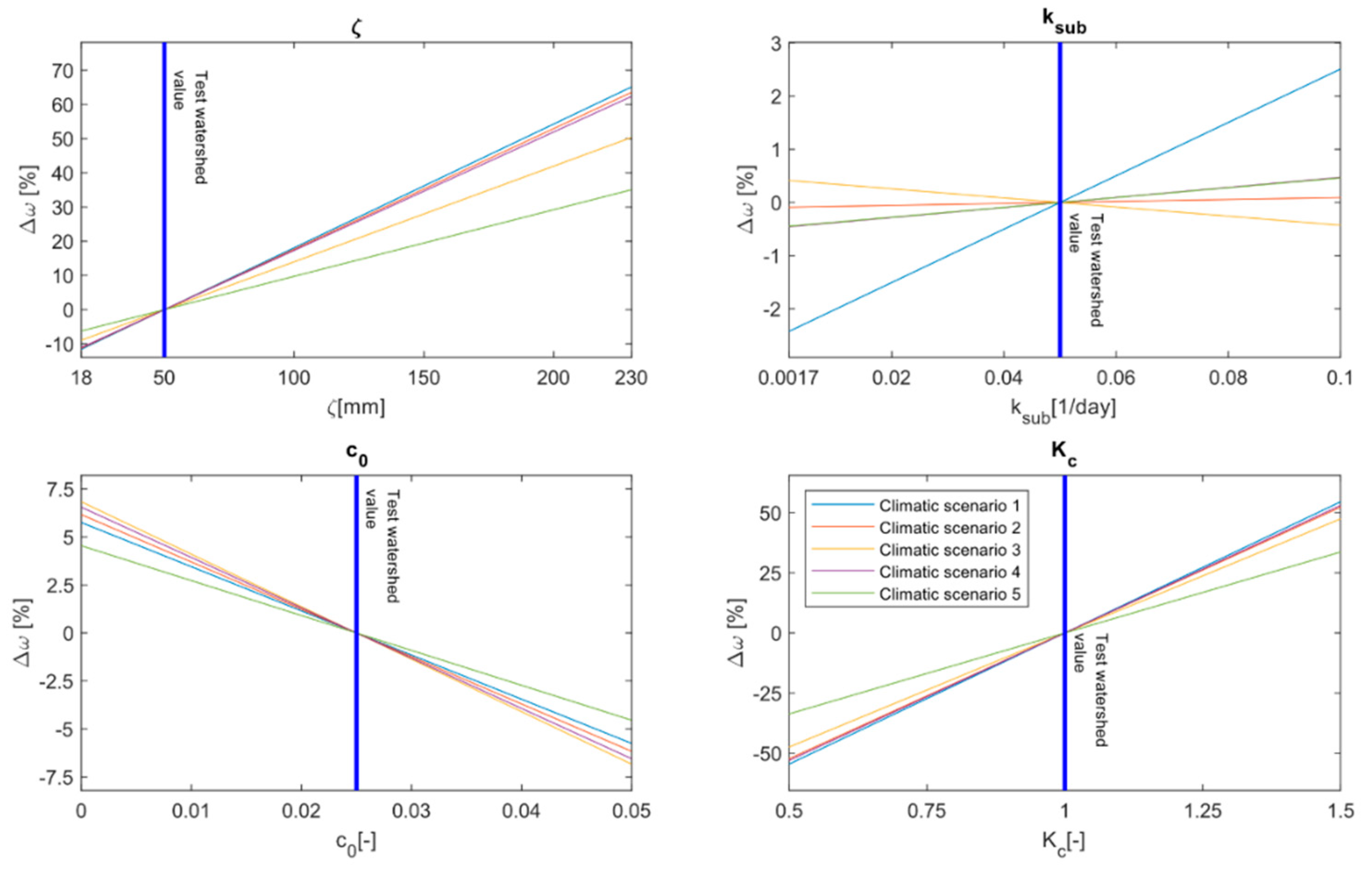
Finally, we support the idea of biunivocal relationship between basin morphometric and vegetation properties and hydrological response (
Figure 1c). Numerical simulations were run for the five climates with different basin morphological and vegetation properties (model parameter combinations). Results were used to create five linear relations (one for each climate type) between model parameters (that are four, representing the role of morphology and vegetation) and
. These relations are aimed to help practitioners and hydrologists in using Fu’s parameter in the case of limited or missing evapotranspiration and runoff data.
2.1. Climatic Scenarios and Weather Generator
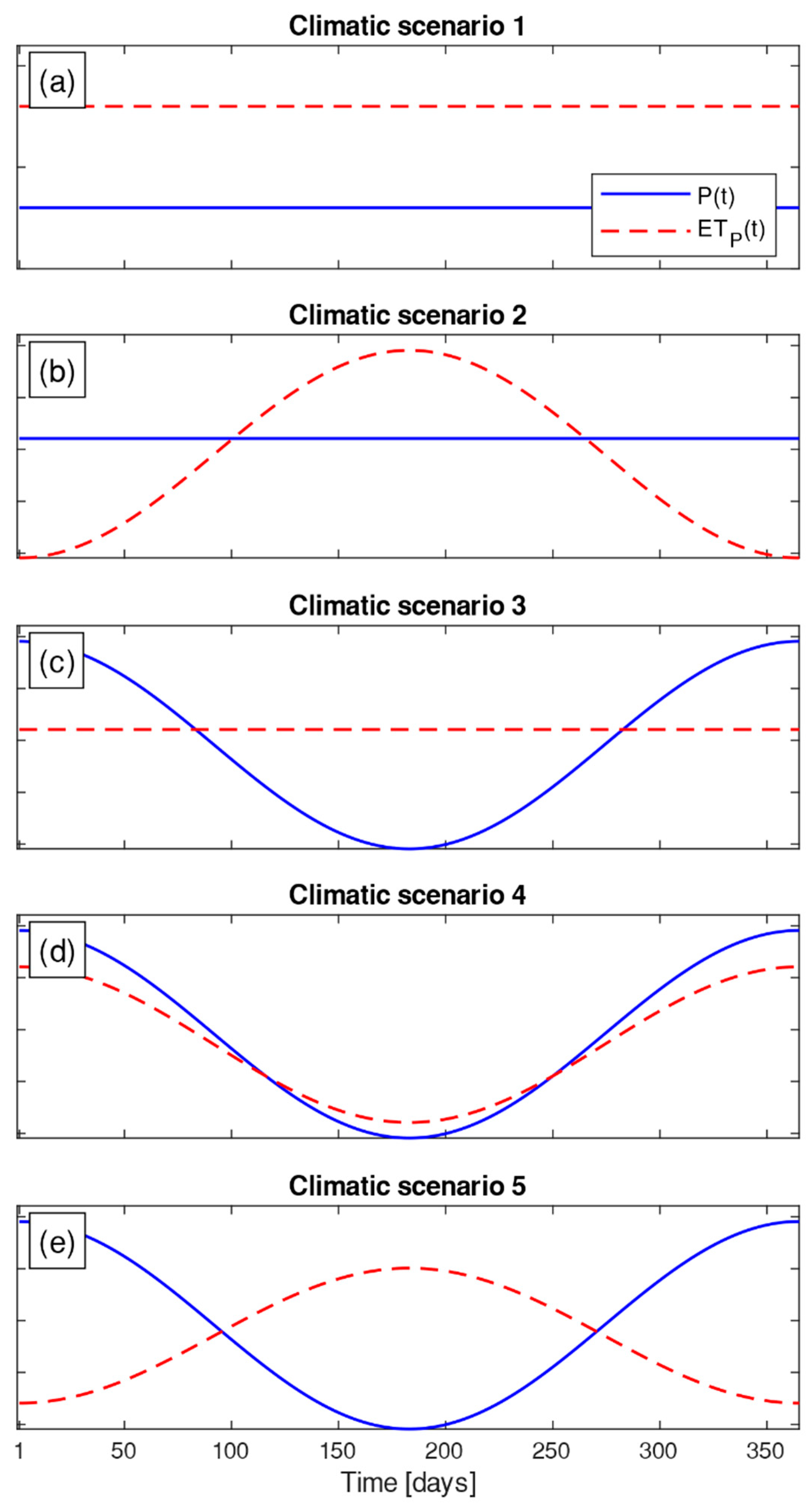
To take into account the role of climate in water partitioning, we considered five climatic scenarios which roughly mimic some of the most frequent climate conditions. As specified before, every climate is characterized here by different seasonal patterns of rain and potential evapotranspiration. Within a given climate, we generated synthetic series of rainfall
and
at daily time scale
using a weather generator. The five climatic scenarios are intended to represent the seasonal variability of rain and potential evapotranspiration time patterns, as illustrated in
Figure 2. The idea of exemplifying climate in such a simple schematization refers to Viola et al. [
37], where it has been used to investigate green roof retention performances. The first climatic scenario (
Figure 2a) represents stationary condition of rain and potential evapotranspiration during the year. This is an ideal situation in which the variance of meteoclimatic variables is zero, being the less realistic seasonal pattern of the five proposed in this work. The second case (
Figure 2b) is typical of oceanic areas with almost constant precipitation during the hydrological year, while potential evapotranspiration has a peak. Climatic scenario 3 (
Figure 2c) is the opposite of the last ones, namely potential evapotranspiration is almost constant and major precipitation values are observed during a specific rain season. This climatic scenario is attributable to a tropical climate with high constant temperatures along the year and a monsoon season with a precipitation peak. The feature of climatic scenario 4 (
Figure 2d) is in-phase climatic forcing: this is a classic case of humid subtropical climates, where the precipitation peak occurs simultaneously with the temperature one. The last case is the opposite of the climatic scenario 4 (
Figure 2e), that is rainfall and potential evapotranspiration are in counter-phase during the hydrological year. Mediterranean climate is well represented by this climatic scenario, because it is well known that rainfall mostly occurs during the winter, while temperature peaks occur in the summer.
In this work the synthetic time series
and
referring to climatic scenarios were created by the weather generator proposed by Viola, Hellies, and Deidda [
37], whose parameters have been calibrated according to main climatic features observed in 10,000 observational sites worldwide. The rain series are intended as daily precipitation arising from a non-stationary and cyclic Poisson point process, characterized by a frequency
(rate of the Poisson process occurrences, (1/days)). The
parameter was modeled as a sinusoidal function of time
(days), with amplitude
, the average interarrival time (days) between two rain events and one-year period, as described in in the following equation:
where
characterizes the ratio of the semi-amplitude of the annual harmonics of
to the annual average, while
is the initial phase of the sinusoidal function. Every day with precipitation different to a zero event
(mm/day), where
i subscript indicates rain days in the
series, is simulated as a random process extracted from an exponential distribution with mean daily value
(mm/day), modeled as follows:
where
is the average amount of rainfall (mm/day),
represents the ratio of the semi-amplitudes of the annual harmonics of
to the annual average, and
is the value of phase when
. Therefore, Equations (1) and (2) allow us to calculate mean interarrival times and mean daily precipitation along the year, which in turns allow us to randomly obtain rain time series.
Similarly, the daily potential evapotranspiration series
(mm/day) are defined as a sinusoidal function with a similar structure to the previous one:
where
is the daily mean evapotranspiration (mm/day),
the ratio of the semi-amplitude of the annual harmonics of
to the annual average, and
is the initial phase.
Each climate is defined by a phase between rain and potential evapotranspiration (as described by
,
and
) and by a specific seasonal variability of rainfall (as described by
and
) and potential evapotranspiration (modeled by
). The values of the semi-amplitude
,
and
have been assessed by Viola, Hellies, and Deidda [
37] as the median of their empirical distributions, as observed in 10,000 worldwide stations. For the five climate scenarios, the parameters of the Equations (2)–(4) are reported in
Table 1.
The climate definition, as given above, may embed wide geographic areas where the seasonal patterns of rainfall and potential evapotranspiration are homogeneous, and are described by the six aforementioned parameters. At the same time, annual precipitation and potential evapotranspiration may vary within a climatic area, for instance following topographic gradients. This kind of variability is reflected in the weather generator by allowing us to obtain different aridity indices (
). Numerically, this is achieved by generating synthetic series with different values of
and
; we suppose that
varies between 3.5–24 (mm/day) and
between 0.3–5.5 (mm/day). These ranges have been selected considering a realistic range of annual precipitation and potential evapotranspiration. For sake of simplicity,
was assumed to be constant, and equal to 4.35 (days) (
Table 1) in all the considered climates. This numerical value has been obtained as the mean of the global interarrival times between rainfall events; indeed, the assumption of a unique value restricts the generality of this approach because it hampers the ability to investigate the influence of this parameter on the annual rainfall partitioning, but it is indeed a common and reasonable assumption [
20]. Under these conditions, the mean annual amount of precipitation
generated and used in this work can vary between 300 and 2000 mm; similarly,
ranges from 100 to 2000 mm.
2.2. EHSM Model
The precipitation
and the potential evapotranspiration
time series have been then used as an input into a conceptual hydrological model, namely a slight simplified version of the Ecohydrological Streamflow Model (EHSM) [
38]. The way the model is used to describe hydrological responses is to represent a basin with two linear reservoirs describing surface and baseflow runoff, and one soil bucket split into two compartments representing the impervious area
and the permeable area (1
). The daily precipitation
that falls in the soil bucket is divided in two parts:
flows directly in the surface linear reservoir and (1 −
)
infiltrates in the permeable soil bucket portion (1 −
) and is accumulated into the soil bucket. Water infiltration and leakage in and from the soil bucket are regulated by 3 parameters: the active soil depth
(mm), which is the product of the soil porosity
(-), the root zone thickness
(mm), the hygroscopic point
(-), and the soil moisture at field capacity
(-). In order to have only a variable that expresses hydrological soil properties, we condensed
,
, and
with the following expression:
where
(mm) is maximum water holding capacity, representative of maximum amount of water that could be stored in the soil.
The soil moisture of soil bucket regulates the partition of (1 − ) in runoff that flows into surface and baseflow linear reservoir. If the soil moisture content exceeds the field capacity, this water volume becomes leakage pulses that feed the linear reservoir which is responsible for baseflow conceptual description. The mean residence time of water within this bucket has been defined as 1/ (1/day), which from a physical point of view is related to groundwater dynamics. When soil moisture overpasses saturation, the excess feeds the surface linear reservoir related to surface runoff production. From the union of the outputs of the two linear reservoirs, the model generated the daily runoff series .
The model allows us to simulate soil moisture dynamics and the influence of vegetation in drying the soil during two consecutive rain events. In order to quantify the evapotranspiration process, we assumed a limitation induced by the soil moisture that is equal to the maximum value calculated as the product between reference evapotranspiration and the coltural coefficient (-).
The model parameters describing the watershed are only four, summarizing the key processes producing, limiting, and delaying runoff at long time scales. Namely, the selected descriptors are:
maximum water holding capacity,
subsurface bucket parameter,
impermeable area, and
coltural coefficient. For all experiments and demonstrations conducted in this work, the model parameters can vary between physically reasonable ranges, reported in
Table 2. It is worth mentioning that
range (less than 5%) is reasonable because Budyko’s framework applies to large watersheds, in which impervious surfaces are often spread over the basin. This physically implies that impervious surfaces away from outlet, still contribute to runoff, because the routing drives water volumes to pervious areas, where infiltration occur; this physical process is not accounted in the model. Then, impervious areas in EHSM should be considered as the ones close to the outlet, therefore, we limited the range of
.
4. Case Study Basins
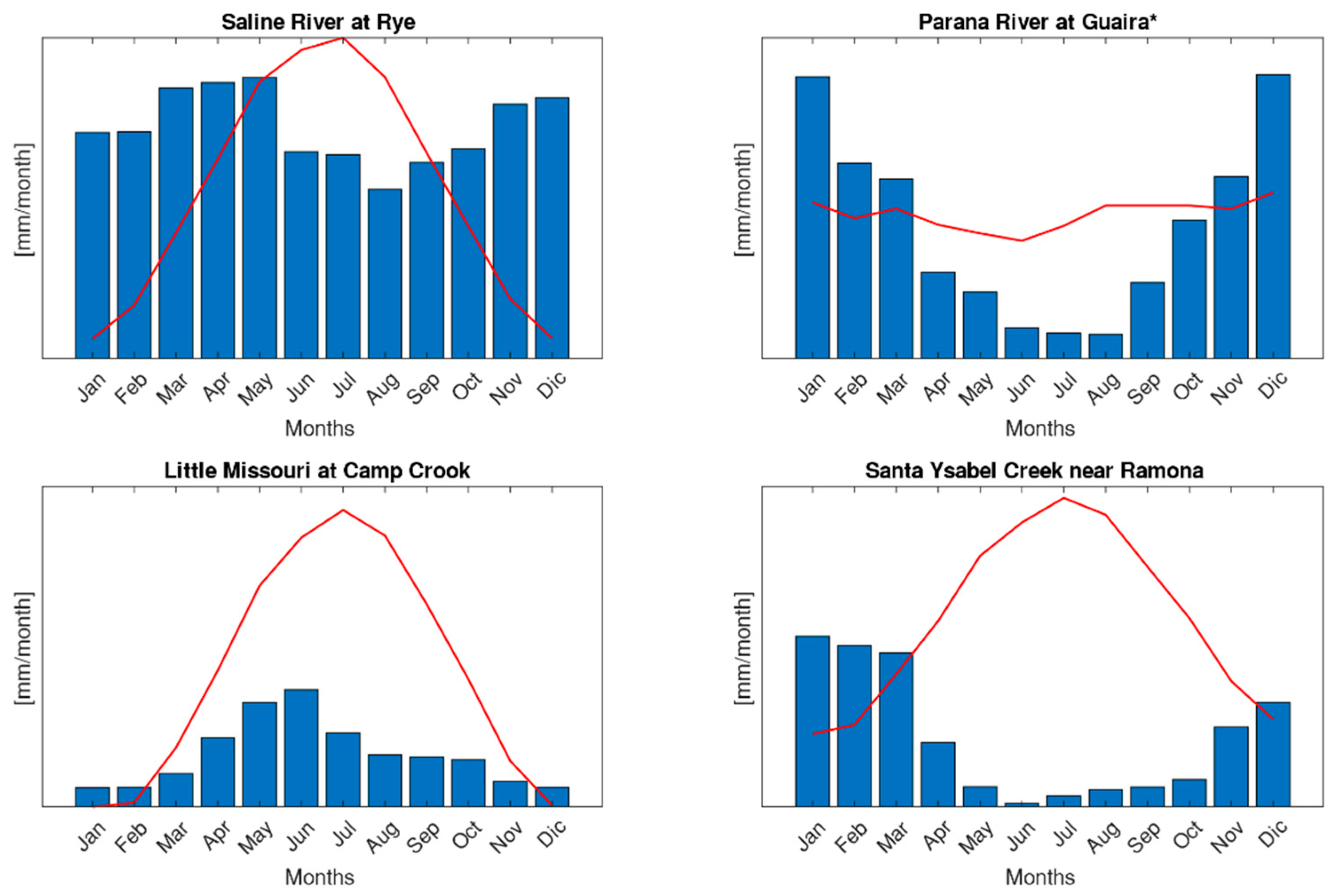
In order to demonstrate the ability of the obtained regression equations to reproduce in different climate in the real world, we used four case study catchments, associated with the last four climatic scenarios considered. The first climatic scenario has been neglected since it is an ideal condition. We compared the values collected from regression equations (in this work called “assessed ”) with the ones calculated by fitting the Fu’s curve to hydrological data (called “hydrological ”).
The first case study is Saline River Basin at Rye, Arkansas (USA) and it is a sub-catchment of Ouachita River with an extension of 2102 km2. The climate is Atlantic-oceanic with constant precipitation during the year and potential evaporation that has a peak in the summer months (June–August). We observed that its climatic condition is associable with climate scenario 2. Mean annual precipitation is 1314 mm with a runoff coefficient of 0.33, while mean annual potential evapotranspiration is 945 mm, close to real evapotranspiration (883.6 mm). Evergreen forest is the most prevalent land use coverage (96%) and the remaining part is urban and built-up areas.
The second case is the Parana River at Guaira, which is in South America and passes through Brazil, with an approximate area of 830,000 km2. The climate is tropical with a constant value of potential evapotranspiration and a precipitation peaks in December, following seasonal pattern of climatic scenario 3. The mean annual precipitation is pretty high (1469.7 mm), as is the mean annual potential evapotranspiration (1368.15 mm); the runoff coefficient is about 0.22, also due to high mean annual evapotranspiration (1144.15 mm). The largest part of the basin is covered by pasture (44%), while annual crop and sugar cane occupy the 27% and 9% of the watershed, respectively; finally, forest is only the 9% of the total of Parana basin.
The third case study is a tributary of the Missouri River and its basin covers three USA states: Montana, North Dakota and South Dakota with a catchment area of 1970 km2. to the climate in this area satisfies climate condition 4, with the most important precipitations in the summer months and a mean annual value of 394.2 mm. Precipitation is in-phase with the potential evapotranspiration that has a maximum in the middle of the year, with a mean annual value of 1022 mm. Runoff coefficient is 0.06 and mean annual evapotranspiration is 372.3 mm. The vegetation consists of permanent wetland (61%) and woody savannah (37%).
The latter case study refers to a watershed in California, namely the Santa Ysabel Creek, with a typical Mediterranean climate, characterized by wet winter/autumn and dry summers, attributable to climatic scenario 5. Santa Ysabel Creek has an extension of 112 km2, is 521.95 mm; only a small fraction of rainfall, namely 6%, is transformed into discharge. The mean potential annual evapotranspiration is 1405.25 mm due to high temperature and only 489.1 mm becomes real evapotranspiration because of soil moisture limitation. Forest and shrubland are the prevalent land cover type (51% and 46%), with a small amount of savannas.
Monthly rainfall and temperature in the four considered case study are represented in
Figure 9. Climatic data are provided by different sources: for the three US watersheds (Saline River Basin at Rye, the tributary of the Missouri River and Santa Ysabel Creek) we used the Model Parameter Estimation Experiment (MOPEX) [
35], while for the Parana at Guaira basin we employed CRU TS version 4.00 [
42], the CGIAR-CSI Global Aridity Index (Global-Aridity), and the Global Potential Evapo-Transpiration (Global-PET) Climate Database [
43,
44]. In order to give a morphological and vegetation characterization of the study cases, different sources of data have been used: for the three US watersheds, the MOPEX [
35] database was used, and for Parana at Guaira basin, the info reported by Melo et al. [
45] and soil maps were utilized.
Starting from the basin morphological and vegetation characteristics, we calculated the four aforementioned model parameters (
,
,
and
). The maximum water holding capacity
was calculated using different soil parameters, according to Equation (5).
,
and
were obtained from soil type information, while
was related to the vegetation type within the considered basin following Yang et al. [
46]. The evaluation of the subsurface parameter
was done using the global maps provided by Beck et al. [
47]. The percentage of impervious area
was obtained from soil use information reported within the mentioned database. The coltural coefficient
was presumed to be related to vegetation type; we set a value of 1.5 for forest, 1.25 for shrubland and savannahs, 1 for cropland and grassland, and 0.5 for bare soil. Then, a weighted average provided a unique value over the considered basins.
Once we had calculated the model parameters, we then calculated
through the regression equations of
Section 3.3 and reported values in the column “Assessed
” in
Table 4. On the other hand, climatic and hydrological data also allowed us to define
and
for each case study, and consequently
could be assessed by making the Fu’s curve pass through those points. A simple comparison has been carried out between the “hydrological” and “assessed”
values, while the relative percentual difference
was assessed and reported in
Table 4. For the considered case study, errors are indeed limited, with only 3% for the Santa Ysabel Creek near Ramona.
The results are encouraging, but it is necessary to underline some limitations of the proposed method. First, the definition of a climatic pattern may be too simplistic in representing seasonal behavior of rainfall and potential evapotranspiration worldwide. In addition, the daily rainfall representation as a Poissonian process, with a constant interarrival time, could result in errors in streamflow estimation. In fact low values of imply elevate soil moisture and more runoff production and vice versa. Thus, a correct characterization of is crucial for a precise description of long-term hydrological dynamics.
5. Conclusions
In this work, we examined the complex relations between climatic, morphological, and vegetation watershed properties and long term water partitioning processes. We provided simple equations for calculating the Fu’s parameter in hydrological data poor conditions. We believe that the proposed tool will help practitioners and hydrologists to assess mean annual runoff, even in ungauged basins.
We used five seasonal patterns of precipitation and potential evapotranspiration and chose four basin morphological and vegetation descriptors (
,
,
and
) to summarize climate and basin characteristics. First, given a climate and a basin, we demonstrated that water partitioning is only related to the aridity index, which is a measure of local climatic conditions. This was based on a different point of view about Budyko’s theory: water partitioning rules for a given basin, in a given climatic scenario, forced by different couples of stochastic
and
, are well described by a Fu’s curve, as stated by the high values of coefficient of determination
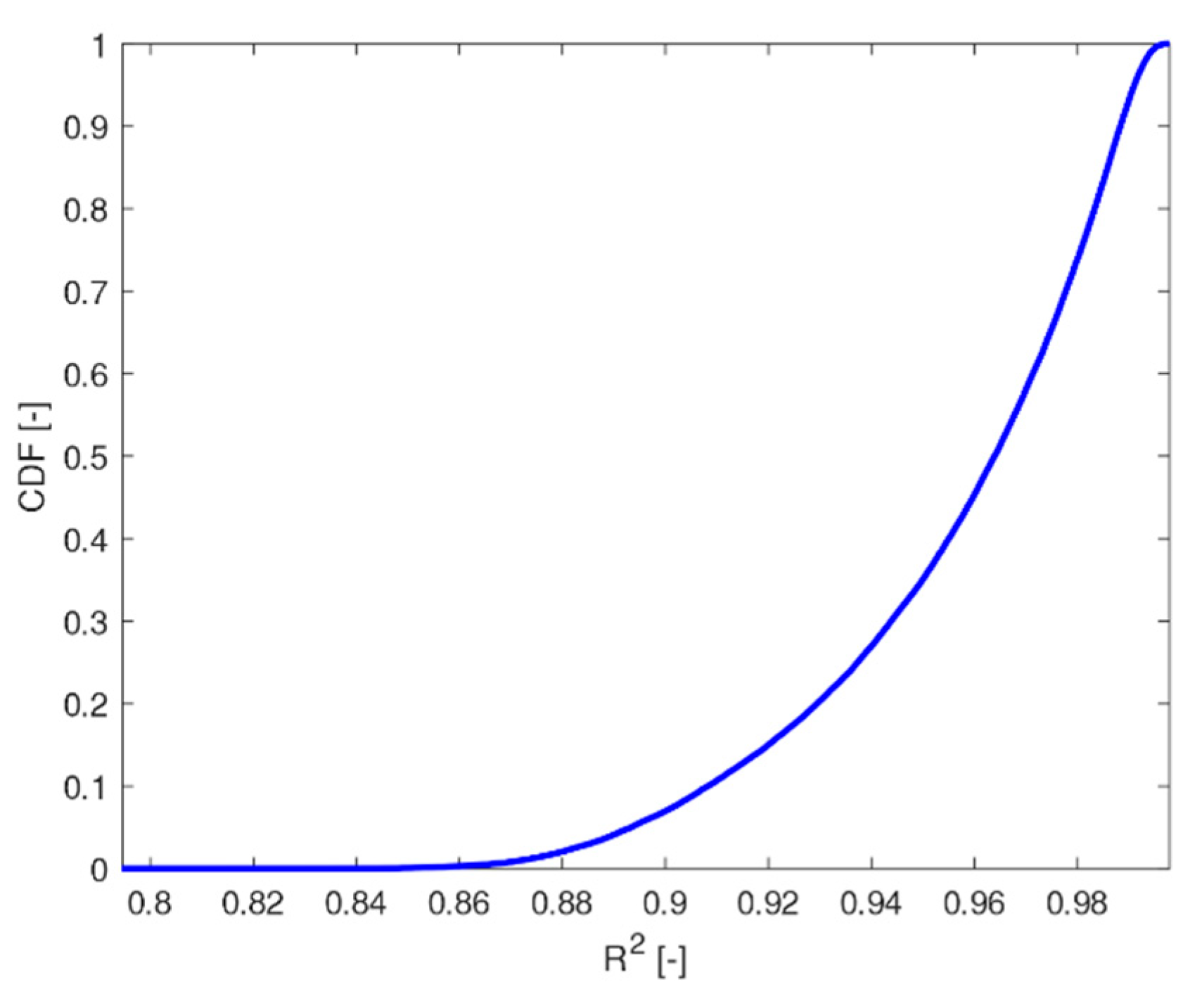
(
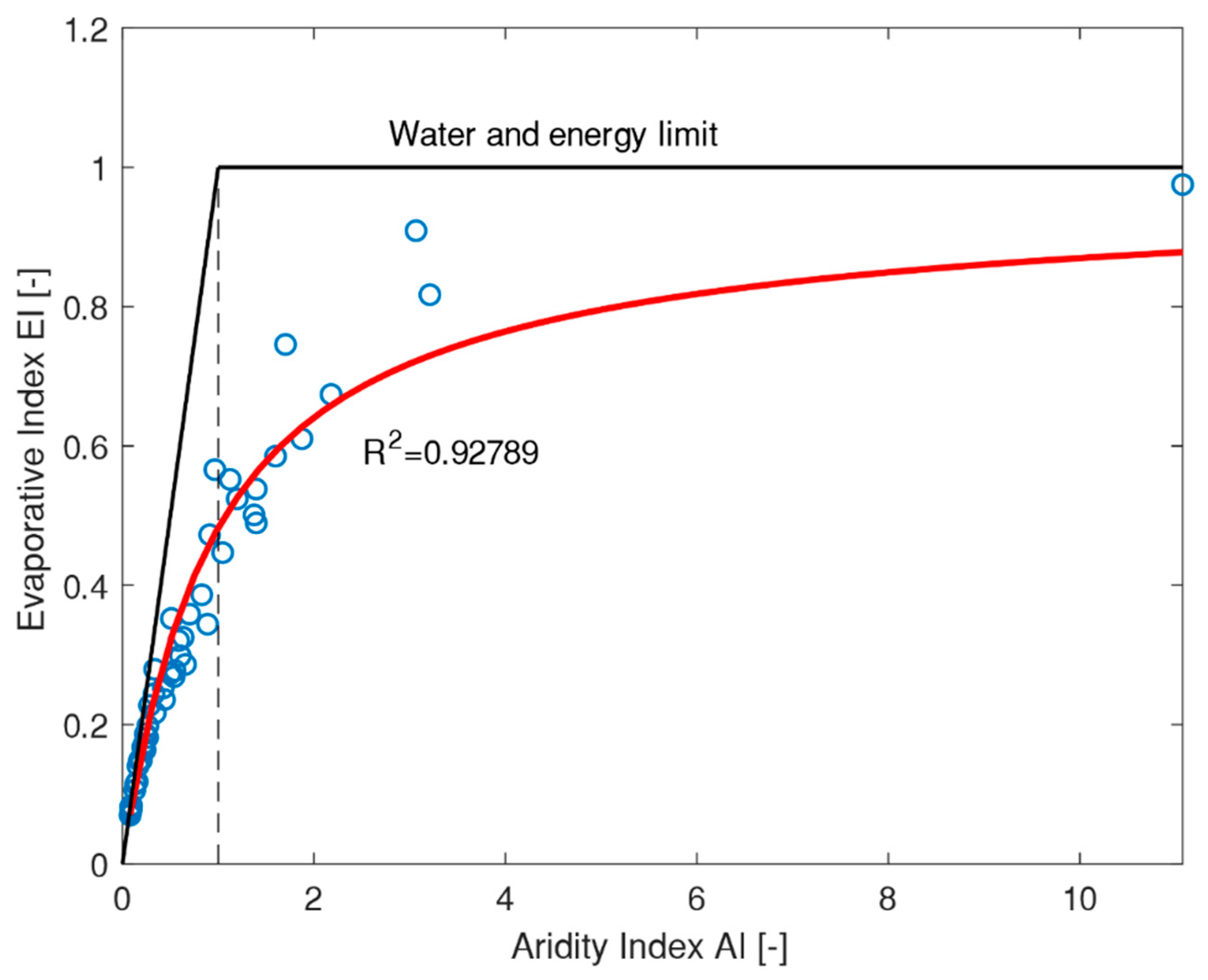
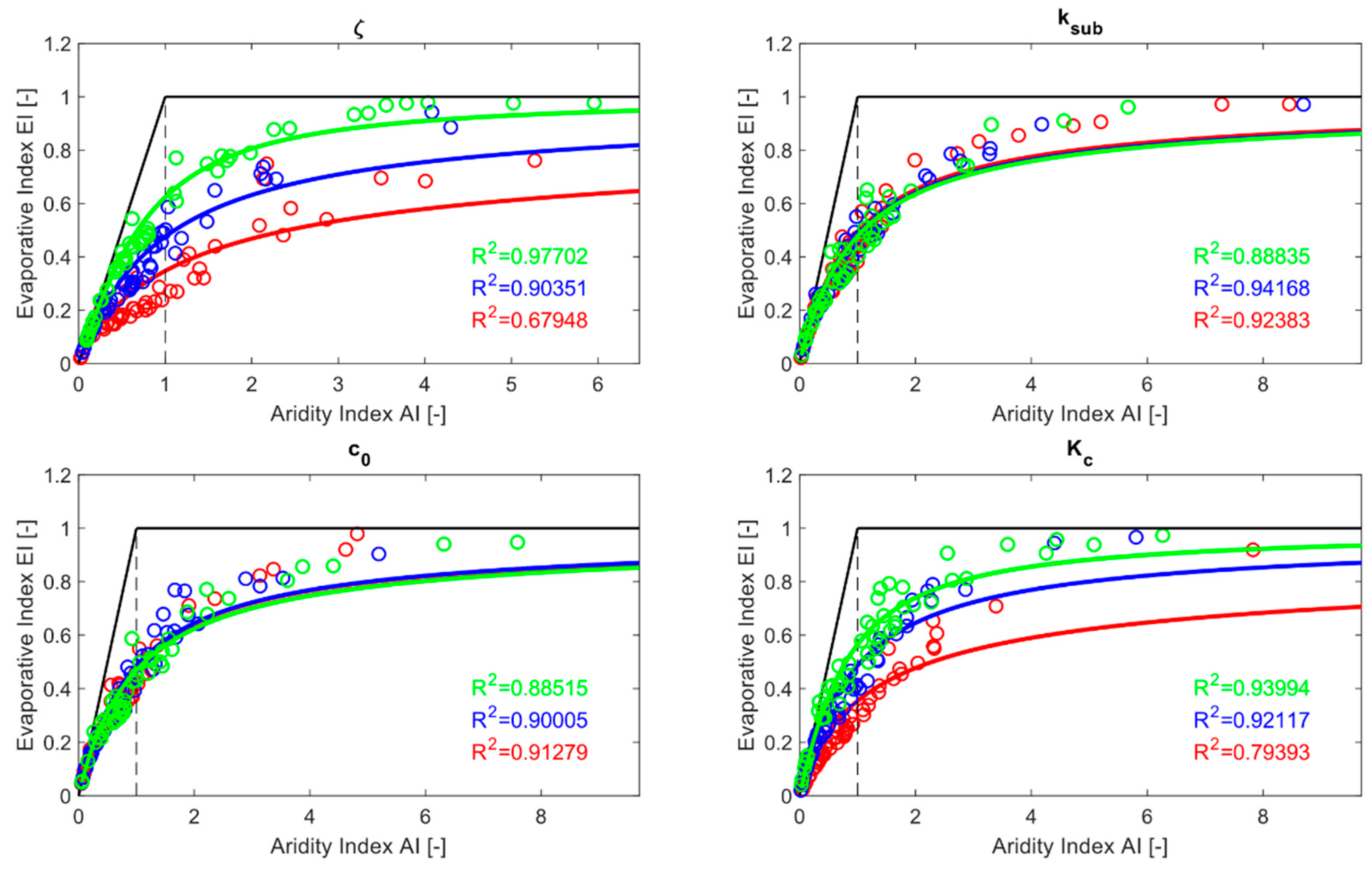
Figure 3,
Figure 4 and
Figure 5).
Second, we conducted an experiment to assess the climate effect in determining ; we simulated hydrological behavior of the same watershed within different climatic scenarios. As expected, water partition is heavily affected by climate: under a Mediterranean climate we observed the highest mean annual runoff Q, while the oceanic climate was the driest among the considered climatic scenarios. This means that seasonal patterns and the phase between precipitation and potential evapotranspiration (temperature) play a non-negligible role in long term water partitioning.
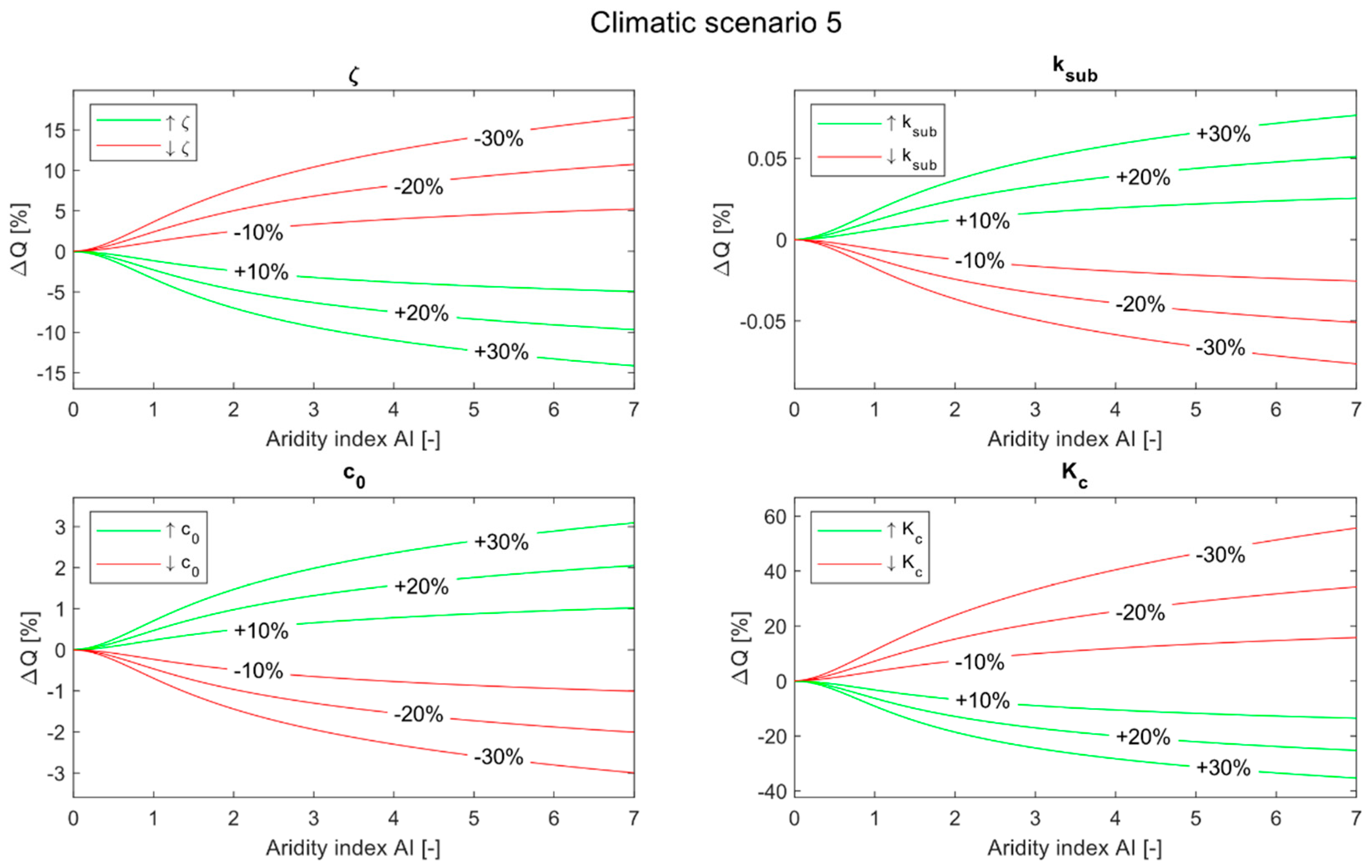
Third, we evaluated how the morphological and vegetation properties influence water partitioning. Then, given different climate and different watersheds, we mathematically described the effect of morphological and vegetation descriptors in water partitioning processes. Five linear regressions between the four model parameters and have been calculated, one for each climatic scenario. We showed that the coltural coefficient and the maximum soil water holding capacity are the most important factors in influencing long term hydrological processes. Finally, we tested the linear regressions performances in four case studies in the US and South America, and obtained encouraging results.
Obviously, the range within which regression equations have been tuned (
Table 2) and the limited number of parameters (
Section 2.2) are a limitation for the presented method, which introduces further approximation within Budyko’s theory. Nevertheless, the regression equations enlarge the feasibility of Fu’s equation, providing a rough assessment of annual runoff in limited data conditions and with low computational effort.