Abstract
Over the years, several studies have been carried out to investigate how the statistics of annual discharge maxima vary with the size of basins, with diverse findings regarding the observed type of scaling (i.e., simple scaling vs. multiscaling), especially in cases where the data originated from regions with significantly different hydroclimatic characteristics. In this context, an important question arises on how one can effectively conclude on an approximate type of statistical scaling of annual discharge maxima with respect to the basin size. The present study aims at addressing this question, using daily discharges from 805 catchments located in different parts of the United Kingdom, with at least 30 years of recordings. To do so, we isolate the effects of the catchment area and the local rainfall climatology, and examine how the statistics of the standardized discharge maxima vary with the basin scale. The obtained results show that: (a) the local rainfall climatology is an important contributor to the observed statistics of peak annual discharges, and (b) when the effects of the local rainfall climatology are properly isolated, the scaling of the standardized annual discharge maxima with the area of the catchment closely follows that commonly met in actual rainfields, deviating significantly from the simple scaling rule. The aforementioned findings explain to a large extent the diverse results obtained by previous studies in the absence of rainfall information, shedding light on the approximate type of scaling of annual discharge maxima with the basin size.
Highlights:
- The statistical scaling of annual discharge maxima with the drainage area A of catchments is revisited in the light of rainfall climatology.
- Neglecting the dependence of annual discharge maxima on rainfall characteristics may lead to diverse findings regarding the observed type of scaling.
- The multiplicative fluctuations of discharge maxima relative to their corresponding means closely follow the scaling properties of actual rainfields.
- For spatial scales below approximately 100 km2, where rainfall deviates from multiflactal scale invariance, a break of scaling is also observed for the multiplicative fluctuations.
1. Introduction
Since the early works of Dalrymple [1] and Benson [2], regional frequency analysis (RFA) has been an important tool to model the spatial variation of hydrologic fluxes, and improve estimation of hydrologic quantities at ungauged locations see e.g., [3,4,5,6,7,8,9,10,11,12].
In general terms, RFA includes the transfer of statistical information of hydrologic quantities between catchments in a homogeneous region (see e.g., the detailed review in Hosking and Wallis [13]), and exhibits a long history with starting point the index flood method initially developed by Dalrymple [1] in 1960, who made a first attempt to standardize the maximum annual discharges measured within a statistically homogeneous geographical region by the corresponding local means, and describe them using a single probability distribution model see e.g., [4,6,7,10,11,14,15]. Soon afterwards, USGS suggested a quantile regression technique where flood quantiles are regressed against catchment characteristics to develop regional flood prediction equations see [2,16], thus creating a shift towards the direction of modeling regional variability of river discharges based on rainfall climatology and catchment physical variables see e.g., [6,17,18,19,20,21,22,23,24,25,26,27].
More than half a century later, river flow prediction in ungauged basins (PUB) still remains an open challenge in hydrology, as it becomes apparent also from the PUB initiative set by the International Association of Hydrological Sciences (IAHS) for the decade 2003–2012 (see https://iahs.info/pub/index.php), with primary aim to reduce uncertainty in hydrological predictions.
In the context of PUB initiative, an attractive approach to model the statistical characteristics of maximum annual discharges at ungauged locations of a river network, is to use scale invariance arguments to link them to the statistical properties of maximum annual discharges measured at gauged locations within the same statistically homogeneous geographical region see e.g., [3,4,8,9,10,14,17,19,20,21,28,29,30,31,32]. More precisely, define to be the annual maximum discharge at gauged location i of a river network that drains area Ai, and to be the annual maximum discharge at an ungauged location j upstream of i that drains area . In the most general case of statistical scale invariance, referred to as stochastic self-similarity, multiscaling, or multifractality see e.g., [3,4,7,8,9,10,11,14,17,19,20,28,30,32,33] one can obtain the statistical properties of as a function of the statistical properties of through (see e.g., the review in Veneziano and Langousis [32] and references therein):
where G is a random function that depends on the ratio and is stochastically independent from , and denotes equality in all finite dimensional distributions. Note that Equation (1) includes self-similarity (also referred to as simple scaling) as a sub-case when G is deterministic. It follows from Equation (1) that the moments of different orders q depend on the catchment size A in a log-linear way see e.g., [3,4,32]:
where is a non-linear (linear) function of q in the multiscaling (simple-scaling) case. Note that Equation (2) is a necessary but not sufficient condition for stochastic self-similarity to hold, as it describes the marginal statistics of as a function of scale A. More precisely, Equation (2) implies that:
where denotes equality in the marginal distributions of (i.e., obtained across independent basins of various areas A), whereas Equation (1) refers to all finite dimensional distributions of the maxima field (i.e., obtained across all sub-catchments of various areas A of a basin). Gupta and Waymire [3] (see also Lovejoy and Schertzer [34]) introduced the term “wide sense multiscaling” for the scaling of the marginals imposed by Equations (2) and (3), and “strict sense multiscaling” for the scaling imposed by Equation (1). In what follows, and since the present study deals with scaling of annual discharge maxima as a function of the drainage area A across geographically distinct basins, we skip the qualification term “wide sense” and refer to the scaling imposed solely by Equations (2) and (3) as multiscaling (simple scaling), in case the function in Equation (2) is a non-linear (linear) function of q.
Based on Equation (2), a convenient way to distinguish between multiscaling and simple scaling (or self-similarity) of annual discharge maxima, is by studying the form of the moment scaling function , defined as:
Where . An alternative way that has been suggested in order to distinguish between these two different types of scaling, is to study the dependence of the coefficient of variation (CV) of as a function of the drainage area A see e.g., [4,6,7,10,11,14,17,19,33]. In the simple scaling case, CV is independent of A, whereas in the case of multiscaling, CV becomes a function of scale see e.g., [4,10,32].
The idea that the catchment area A can serve as the most critical factor in explaining flood variability has a long history, as briefly outlined below. The starting point was in the late 20th century, where new methods were developed to estimate design floods see e.g., [4,6,10,15,28,32,35,36]. For example, NERC [37] argued that with can explain approximately 69% of the sample variability of mean annual floods in Great Britain and Ireland. Cadavid [38] analyzed instantaneous streamflow records from different regions of the United States, pointing towards multiscaling behavior. Smith [14] studied flood records from the Appalachia, showing that varies approximately log-linearly with A, with CV values displaying an ascending trend with A for basins smaller than a critical area , and a descending trend for basins with larger areas.
In a subsequent study, Gupta et al. [4] studied the scaling properties of using daily discharges from 270 drainage basins in central Appalachia, including the 104 catchments studied by Smith [14]. The study concluded that there is a break of scaling for catchment sizes larger than a critical area , characterized by significant uncertainties due to the dispersion of the considered sample. Robinson and Sivapalan [7] used the CV concept outlined above, to analyze the same dataset as Gupta et al. [4]. They concluded that the CV values exhibited significant variability with a slight descending trend for catchments larger than a critical area , and an ascending trend for catchments with .
A moment scaling analysis was also performed by Pandey [8] using streamflow records from 180 stations in Canada. The main conclusion of the study, obtained by studying how the moments of different orders q vary with the catchment area A, was that displays simple-scaling behavior with A. Similar findings on the self-similarity of annual discharge maxima using moment scaling analysis have been reported by Bhatti [39], who studied annual discharge maxima from 2150 unregulated basins from the USGS database, Vogel and Sankarasubramanian [40] who used streamflow records from 1433 river basins across the United States, and Ishak et al. [11] who used streamflow data from 91 catchments from New South Wales (NSW) in Australia. Additionally, Dodov and Foufoula-Georgiou [10] provided further evidence on the self-similar behavior of peak annual discharges, by using 99 daily flow series from the US and showing that exhibits two distinct simple-scaling regimes: for and for .
It follows from the discussion above that while some type of scaling of with A exists, one cannot easily conclude on its precise type. This is primarily due the type of the conducted analysis, and the large dispersion of the analyzed samples. Regarding the first issue, all aforementioned analyses were performed by studying the log-linearity of the moments of against A. Since increases almost proportionally with the drainage area A, the strong log-linear dependence of on A makes statistical interpretation of any type of non-linear behavior almost impossible from data. Regarding the second issue, note that for rainfall-triggered flood events, river discharges increase almost proportionally with both the drainage area A and the rainfall depth Ī. Hence, unless all catchments fall within the same hydrologically homogeneous geographical region (i.e., in terms of rainfall accumulations; see e.g., Gupta et al. [31]), regressing solely against A cannot resolve the variability induced by the different hydroclimatologies and, more importantly, it may produce biased results in favor of a simple scaling rule (see discussion below). This explains to an extent the significant dispersion of the samples analyzed by the aforementioned studies, as well as some of the findings in favor of a simple scaling rule.
More precisely, according to the main assumption of the index flood method see e.g., [1,7], the discharge maxima at different locations within the same statistically homogeneous geographical region exhibit the same probability distribution when standardized by their mean, or some other index discharge. For example, considering that the mean discharge at some location j increases almost proportionally with the annual rainfall depth, thus, being indicative of the local climatology, the index flood method can be written in the form:
where denotes the maximum annual discharge at location j. Assuming proportionality of discharges with rainfall intensity and some power of the drainage area (i.e., generalized rational method; see [15,26,41,42,43,44]), if the mean annual rainfall intensity is assumed constant over the region of interest, then the assumption holds in good approximation, and the index flood approach in Equation (5) reduces to a simple scaling rule of annual discharge maxima with the drainage area A:
Evidently, in the most general case when locations i, j exhibit different hydroclimatic characteristics, as is the case when investigating data originating from different regions, Equation (5) may lead to more complex types of scaling than the simple scaling rule in Equation (6).
It follows from the discussion above that, from a theoretical point of view, any type of moment scaling analysis of with A cannot be conclusive regarding the actual type of scaling of . This is because when regressing the moments of against A, one a priori assumes a constant mean rainfall intensity field over the region of interest (see discussion on the derivation of Equation (6)) and, consequently, a simple scaling rule for the annual discharge maxima.
In this context, an important question arises on how one can effectively conclude on an approximate type of scaling of annual discharge maxima. Here we aim at answering this question, by investigating the effect of rainfall climatology on the spatial scaling of maximum annual floods using daily discharge data from 805 stations located in different parts of the United Kingdom. To the best of our knowledge, no such investigation has been conducted so far. This is done by: (1) studying how the mean value of the standardized discharge maxima depends on the catchment area A and the average precipitation in 30-year climatic periods, hereafter referred to as SAAR (Standard-period Average Annual Rainfall), and (2) studying how the distribution of the ratio , also referred to as index flood ratio (see e.g., Hosking and Wallis [13]) or amplification factor (see e.g., Langousis and Veneziano [45]), scales with the area A, along the lines of the index flood concept in Equation (5).
Section 2 provides necessary information regarding the data used. In Section 3, we start by illustrating the strong linkage between the rainfall characteristics of catchments and the statistics of annual discharge maxima, and then focus on the application of two alternative standardization approaches to study the scaling properties of annual discharge maxima with the size of basins A, while discussing the origins of the observed differences: (a) standardization by the catchment area A, through the ratio (i.e., used in most studies focusing on the scaling of peak discharges; see above), and (b) standardization by the corresponding discharge mean, through the amplification factor (i.e., following the original version of the index flood method in Equation (5)). A comprehensive summary of the main findings of the study, as well as future research directions are presented in Section 4.
2. Data
The hydrologic information used in this study originates from NRFA (National River Flow Archive; see https://nrfa.ceh.ac.uk/), an extensive open access database of flow information and catchment descriptors in the United Kingdom, hosted by the Centre for Ecology and Hydrology (CEH), holding over 60,000 station-years of data. Information used in this paper includes: (a) daily discharges from 805 catchments with at least 30 years of recordings, located in different parts of the United Kingdom, (b) catchment size information, and (c) average annual rainfall in mm for two standard 30-year periods; i.e., 1941–1970 and 1961–1990 referred to as SAAR1 and SAAR2, respectively. Catchment sizes vary from 0.9 to 9948 km2 with a mean value of 359 km2. For the total of 805 stations, the average SAAR value (i.e., SAAR = (SAAR1 + SAAR2)/2), corresponding to the mean annual precipitation in mm for the 60-year period 1941–1990, varies from 558.5 to 2910.5 mm with a mean value of 1059.5 mm. Figure 1 shows the spatial distribution of the average SAAR for the 805 considered catchments across the United Kingdom. SAAR values tend to decrease when moving from the West to the East coast, with lowest values located in the southeastern region of the United Kingdom. The observed rainfall gradient is directly linked to Gulf Stream and the local topography, as moist air masses from the sea move upslope and cool causing precipitation to form see e.g., [44,46].
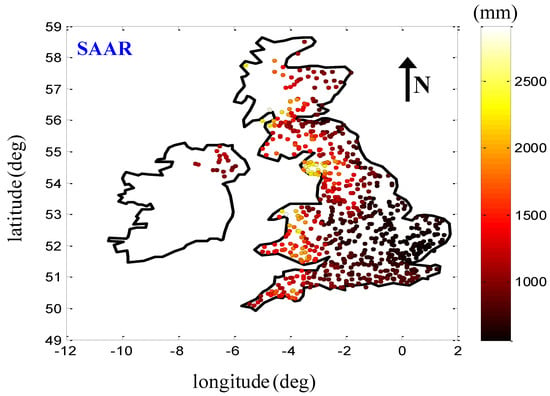
Figure 1.
Spatial distribution of the average SAAR values for the 805 considered catchments across the United Kingdom.
3. Analysis and Results
Figure 2 illustrates how the mean value of the standardized annual discharge maxima varies spatially, following the same pattern as SAAR (see Figure 1), indicating its strong linkage to the local rainfall climatology. The aforementioned linkage can also be observed in Figure 3, where the means of the standardized discharges (Figure 3a), and the means of the standardized annual discharge maxima (Figure 3b) of all considered basins are plotted against their corresponding SAAR values. Standardization of and by the catchment area A is important for the effects of local rainfall climatology to be revealed, as river discharges increase with both the basin size and accumulated rainfall.
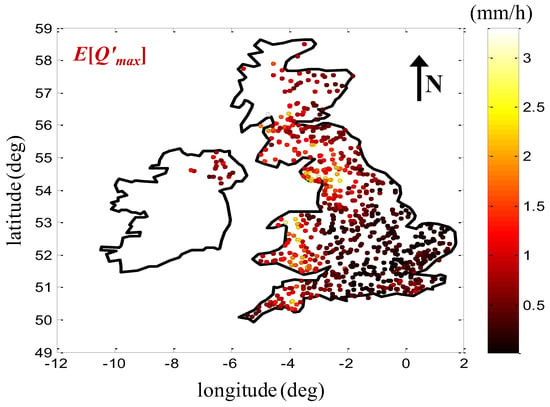
Figure 2.
Spatial distribution of the mean value of the standardized discharge maxima .
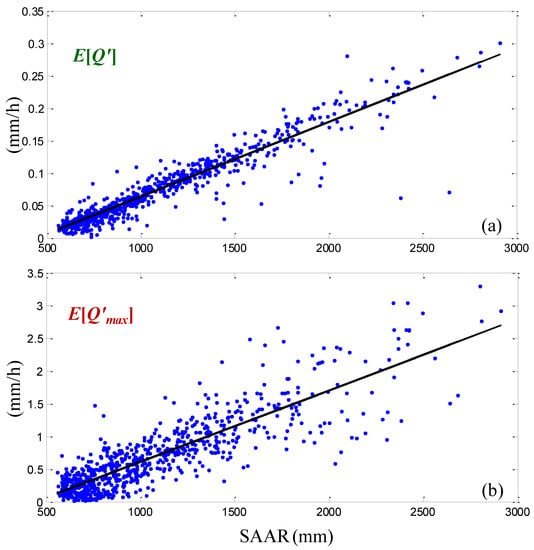
Figure 3.
(a) Scatterplot (points) and linear least-squares (LS) fit (solid line) of the mean values of the standardized discharges for the 805 considered catchments, with respect to their corresponding SAAR values. (b) Same as (a) but for the means of the standardized annual discharge maxima
The strong dependence of the statistics of on the local rainfall climatology explains to a large extent the diverse findings of previous studies see e.g., [8,10,11,28,39,40] for evidence on simple scaling, and [4,14,17] for evidence on multiscaling, when the effects of rainfall signature are not taken into account; see below.
A way to simultaneously isolate the effects of the area of the basin A, and the local rainfall characteristics when studying the scaling properties of annual discharge maxima, it is to follow the exact version of the index flood method in Equation (5) (i.e., without additional assumptions on the functional dependence of on A), standardize the annual discharge maxima at each location j by the corresponding discharge mean , and study the distribution of the amplification factor .
In what follows, we examine how the distributions of: (a) the standardized discharge maxima (i.e., used in most studies focusing on the scaling of peak discharges; see Introduction), and (b) the amplification factor , which removes the variability induced by the different sizes and rainfall characteristics of the considered catchments (see above), vary with the drainage area A of the basin. We do so by: (1) classifying the selected 805 catchments, according to their size, into 10 approximately equally sized groups (i.e., ~80 catchments per group; see Table 1), and (2) studying how the ensemble averages of the initial moments and of different orders q inside each group vary with the average area Ā of the grouped catchments. Similar plots have been used in the literature to study the scaling properties of discharges as a function of the basin size see e.g., [4,8,9,10,11,14,19,28,39,40].

Table 1.
Classification of the selected catchments, according to their size, into 10 approximately equally sized groups.
Figure 4 shows log-log plots of the empirical moments (points) of the standardized discharge maxima inside each group, as a function of the average area Ā of the grouped catchments, for different moment orders . The reason why we limit our analysis to moment orders , is because for highly variable random fields (as is the case of discharge maxima), higher moment orders are underestimated with high probability see e.g., [32,47,48,49,50,51,52,53].
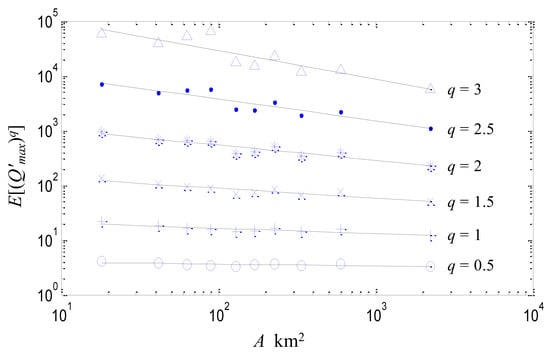
Figure 4.
Log-log plots of the empirical moments of standardized annual discharge maxima , as a function of the catchment area A, for different moment orders . Black solid lines correspond to least-squares (LS) fits.
Similar to the findings of previous studies see e.g., [4,8,9,10,11,14,19,28,40], one sees that for all moment orders considered, the initial moments of the standardized discharge maxima vary log-linearly with the drainage area A (see least-squares (LS) fitted lines), with negative slopes corresponding to the empirical moment scaling function in Equation (4). Clearly, the shape of the function is non-linear (see circles in Figure 5), indicating significant deviations from the simple scaling rule. Since river discharges are the hydrological response of a catchment to the rainfall input, runoff maxima can be seen as the filtered output of a rainfall signal, and therefore any observed type of scaling is expected to be inherited (at least to some extent) from the statistical properties of the input see e.g., [32,54,55,56]. Therefore, the observed deviations from simple scaling can be attributed to the multifractal structure of actual rainfields within finite but practically important ranges of scales: typically from below 1 hour to several days in time and from a few kilometers (say 9 to 10) to more than 100 km in space see e.g., [32,34,51,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86]. For smaller spatial scales, a break of the log-linearity of the initial moments of areal rainfall with the scale of spatial averaging occurs see e.g., [32,50,61,62,73,85,87], with much smaller log-log slopes, indicating a power deficit of high frequency fluctuations. This break of scaling is not observable in Figure 4, as it is smeared out by the considerable variability of the rainfall climatologies of the analyzed basins; see discussion above.
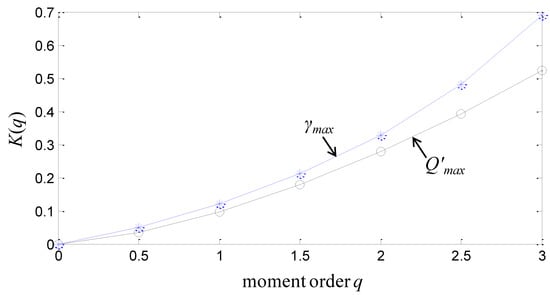
Figure 5.
Empirical moment scaling functions for the standardized discharge maxima (circles), and the amplification factor (stars).
Along these lines, Figure 6 shows log-log plots of the empirical moments (points) of the amplification factors inside each group as a function of the average area Ā of the grouped catchments, for different moments One sees that a break of the log-linearity occurs for spatial scales below approximately 100 km2, with much smaller slopes, which concurs with the observed break of scaling in spatial rainfall (see above). In addition, for spatial scales larger than 100 km2, the empirical moment scaling function in Equation (4) (see stars in Figure 5), estimated as the negative log-log slopes of the LS fitted lines in Figure 6, remains non-linear and close to that of the standardized discharge maxima .
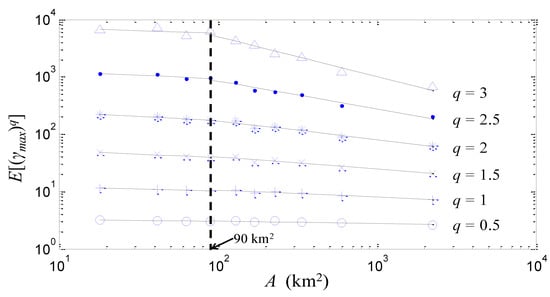
Figure 6.
Log-log plots of the empirical moments of the amplification factor , as a function of the catchment area A, for different moment orders . Black solid lines correspond to least-squares (LS) fits.
Similar findings on the scaling properties of flood annual maxima recorded in Southern Italy have been obtained, also, by Iacobellis et al. [56]. The latter study reported a break of scaling around 100 km2 and, also, showed that although significantly influenced by soil infiltration and abstraction mechanisms, the dependence of the CV of flood annual maxima on the area A of basins is theoretically linked to rainfall scaling. In any case, a definite argument on the origins of the observed scaling cannot be reached in the absence of concurrent rainfall and discharge data at high temporal resolution (i.e., at least hourly).
Based on the aforementioned findings, one may conclude that by neglecting the dependence of the statistics of annual discharge maxima on the rainfall climatology, the dispersion/variability of the analyzed samples increases, with important consequences on the diversity of the corresponding findings, and the accuracy of the assessments made (see Introduction).
4. Conclusions
The present work aimed at investigating the marginal statistics of annual discharge maxima after proper standardization, so that the effects of the catchment area and the local rainfall climatology are effectively isolated. The analysis was conducted using daily discharge data from 805 stations located in different parts of the United Kingdom, with at least 30 years of recordings, by: (a) standardizing the annual discharge maxima at each location j by the corresponding discharge mean , following the exact version of the index flood method in Equation (5) (without additional assumptions on the functional dependence of on A; see discussion on the derivation of Equation (6)), and (b) studying the scaling of the initial moments of the amplification factor with the area A of the basin. Note that corresponds to the multiplicative fluctuations of the annual discharge maxima relative to the discharge mean , with the latter been strongly linked to both the sizes and rainfall characteristics of catchments.
The obtained results show that the regional rainfall climatology significantly affects the mean value of the standardized discharge maxima (see Figure 2 and Figure 3b, and discussion in Section 3) and, therefore, by neglecting the dependence of the statistics of annual discharge maxima on rainfall, the dispersion/variability of the analyzed samples increases, with important consequences on the diversity of the obtained findings, and the accuracy of the assessments made. This explains to a large extent the diverse results of previous studies regarding the observed type of scaling (i.e., simple scaling vs. multiscaling) of peak annual discharges with the catchment area (see Introduction).
When the effects of the local rainfall climatology are properly isolated, through proper standardization of annual discharge maxima by the corresponding discharge means, the resulting multiplicative fluctuations closely follow the scaling properties of actual rainfields, deviating significantly from the simple scaling rule. In addition, for spatial scales below 100 km2 where significant deviations of rainfall from multiflactal scale invariance have been observed see e.g., [32,50,61,62,73,85,87], a break of scaling is also observed for the amplification factor (see Figure 6). This break is not observable when studying the initial moments of (or the ratio ) with A (see Figure 4), as it is smeared out by the considerable variability of the rainfall characteristics of basins.
While the presented analysis and findings shed light on the important role of local rainfall climatology on the statistical scaling of annual discharge maxima, one should not neglect the important influence of catchment properties and runoff routing mechanisms, as well as the space-time rainfall distribution embodied in different precipitation patterns see e.g., [88], especially at small temporal resolutions (below daily) where infiltration and abstraction effects become more influential see e.g., [54,55,56]. The aforementioned topics and, in particular, how the statistical scaling of annual discharge maxima with the size of basins depends on the characteristics of dominant rainfall generating mechanisms, and the scale of temporal averaging (i.e., resolution) of observed discharges, still constitute an open research challenge that remains to be addressed in the context of a large-scale study, when concurrent rainfall and discharge data at high temporal resolution (e.g., at least hourly) become openly available.
Author Contributions
Conceptualization, A.L. and Y.Y.; methodology, A.L.; software, A.P. and A.L.; validation, A.P. and A.L.; formal analysis, A.P.; data curation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, A.L.; visualization, A.P.; supervision, A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The Authors would like to explicitly acknowledge the constructive comments and suggestions by three anonymous Reviewers and the Topical Editor, which helped them to significantly improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dalrymple, T. Flood-frequency analyses. U.S. Geol. Surv. Water Supply Pap. 1960, 1543, 11–51. [Google Scholar]
- Benson, M.A. Factors influencing the occurrence of floods in a humid region of diverse terrain. U.S. Geol. Surv. Water Supply Pap. 1962, 1580, 62. [Google Scholar]
- Gupta, V.K.; Waymire, E.C. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mesa, O.J.; Dawdy, D.R. Multiscaling theory of floods: Regional quantile analysis. Water Resour. Res. 1994, 30, 3405–3421. [Google Scholar] [CrossRef]
- Blöschl, G. Scale and scaling in hydrology (Habilitationsschrift). In Wiener Mitteilungen, Wasser-Abwasser-Gewasser; Technische Universität Wien, Institut für Wasserversorgung, Abwasserreinigung und Gewässerschutz: Wien, Austria, 1996; Volume 132, p. 346. [Google Scholar]
- Blöschl, G.; Sivapalan, M. Process controls on regional flood frequency: Coefficient of variation and basin scale. Water Resour. Res. 1997, 33, 2967–2980. [Google Scholar] [CrossRef]
- Robinson, J.S.; Sivapalan, M. An investigation into the physical causes of scaling and heterogeneity of regional flood frequency. Water Resour. Res. 1997, 33, 1045–1059. [Google Scholar] [CrossRef]
- Pandey, G.R. Assessment of scaling behavior of regional floods. J. Hydrol. Eng. 1998, 3, 169–173. [Google Scholar] [CrossRef]
- Menabde, M.; Sivapalan, M. Linking space-time variability of river runoff and rainfall fields: A dynamic approach. Adv. Water Resour. 2001, 24, 1001–1014. [Google Scholar] [CrossRef]
- Dodov, B.; Foufoula-Georgiou, E. Fluvial processes and streamflow variability: Interplay in the scale-frequency continuum and implications for scaling. Water Resour. Res. 2005, 41, W05005. [Google Scholar] [CrossRef]
- Ishak, E.; Haddad, K.; Zaman, M.; Rahman, A. Scaling property of regional floods in New South Wales Australia. Nat. Hazards 2011, 58, 1155–1167. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Analyzing the effects of excess rainfall properties on the scaling structure of peak discharges: Insights from a mesoscale river basin. Water Resour. Res. 2015, 51, 3900–3921. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, R. Regional Frequency Analysis: An. Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Smith, J.A. Representation of basin scale in flood peak distributions. Water Resour. Res. 1992, 28, 2993–2999. [Google Scholar] [CrossRef]
- Dawdy, D.R.; Griffis, V.W.; Gupta, V.K. Regional flood-frequency analysis: How we got here and where we are going. J. Hydrol. Eng. 2012, 17, 953–959. [Google Scholar] [CrossRef]
- Thomas, D.M.; Benson, M.A. Generalization of streamflow characteristics from drainage basin characteristics. U.S. Geol. Surv. Water Supply 1970, 1975, 55. [Google Scholar]
- Gupta, V.K.; Dawdy, D.R. Physical interpretations of regional variations in the scaling exponents of flood quantiles. Hydrolog. Process. 1995, 9, 347–361. [Google Scholar] [CrossRef]
- Jothityangkoon, C.; Sivapalan, M. Temporal scales of rainfall-runoff processes and spatial scaling of flood peaks: Space-time connection through catchment water balance. Adv. Water Resour. 2001, 24, 1015–1036. [Google Scholar] [CrossRef]
- Morrison, J.E.; Smith, J.A. Scaling properties of flood peaks. Extremes 2001, 4, 5–22. [Google Scholar] [CrossRef]
- Ogden, F.L.; Dawdy, D.R. Peak discharge scaling in small hortonian watershed. J. Hydrol. Eng. 2003, 8, 64–73. [Google Scholar] [CrossRef]
- Furey, P.R.; Gupta, V.K. Effects of excess rainfall on the temporal variability of observed peak-discharge power laws. Adv. Water Resour. 2005, 28, 1240–1253. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A process typology of regional floods. Water Resour. Res. 2003, 39, 1340. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A regional analysis of event runoff coefficients with respect to climate and catchment characteristics in Austria. Water Resour. Res. 2009, 45, 1–19. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Process controls on the statistical flood moments—A data based analysis. Hydrol. Process. 2009, 23, 675–696. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A. Flood peak distributions for the eastern United States. Water Resour. Res. 2010, 46, W06504. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R.; Small, S.J. Exploring the effects of hillslope-channel link dynamics and excess rainfall properties on the scaling structure of peak-discharge. Adv. Water Resour. 2014, 64, 9–20. [Google Scholar] [CrossRef]
- Furey, P.R.; Troutman, B.M.; Gupta, V.K.; Krajewski, W.F. Connecting event-based scaling of flood peaks to regional flood frequency relationships. J. Hydrol. Eng. 2016, 21, 04016037. [Google Scholar] [CrossRef]
- De Michele, C.; Rosso, R. Self-similarity as a physical basis for regionalization of flood probabilities. In Proceedings of the Workshop on the Hydrometeorology, Impacts, and Management of Extreme Floods, Perugia, Italy, 13–17 November 1995. [Google Scholar]
- Gupta, V.K.; Castro, S.L.; Over, T.M. On scaling exponents of spatial peak flows from rainfall and river network geometry. J. Hydrol. Eng. 1996, 187, 81–104. [Google Scholar] [CrossRef]
- Troutman, B.M.; Over, T.M. River flow mass exponents with fractal channel networks and rainfall. Adv. Water Resour. 2001, 24, 967–989. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mantilla, R.; Troutman, B.M.; Dawdy, D.; Krajewski, W.F. Generalizing a nonlinear geophysical flood theory to medium-sized river networks. Geophys. Res. Lett. 2010, 37, L11402. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A. Scaling and fractals in hydrology. In Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; Sivakumar, B., Berndtsson, R., Eds.; World Scientific: Singapore, 2010; pp. 107–243. [Google Scholar]
- Robinson, J.S.; Sivapalan, M. Temporal scales and hydrological regimes: Implications for flood frequency scaling. Water Resour. Res. 1997, 33, 2981–2999. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Multifractals and rain. In New Uncertainty Concepts in Hydrology and Hydrological Modelling; Kundzewicz, A.W., Ed.; Cambridge University Press: Cambridge, UK, 1995; pp. 61–103. [Google Scholar]
- Pandey, G.R.; Lovejoy, S.; Schertzer, D. Multifractal analysis of daily river flows including extremes for basins of five to two million square kilometres, one day to 75 years. J. Hydrol. Eng. 1998, 208, 62–81. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Krajewski, W.F.; Mantilla, R.; Gupta, V.K. Dissecting the effect or rainfall variability on the statistical structure of peak flows. Adv. Water Resour. 2009, 32, 1508–1525. [Google Scholar] [CrossRef]
- Natural Environmental Research Council. Flood Studies Report; NERC Publication: London, UK, 1975. [Google Scholar]
- Cadavid, E. Hydraulic Geometry of Channel Networks: Tests of Scaling Invariance. Master’s Thesis, University of Mississippi, Oxford, MS, USA, 1988. [Google Scholar]
- Bhatti, M.B. Extreme Rainfall, Flood Scaling and Flood Policy Options in the United States. Master’s Thesis, Department of Civil and Environmental Engineering Engineering Systems Division, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Vogel, R.M.; Sankarasubramanian, A. Spatial scaling properties of annual streamflow in the United States. Hydrol. Sci. J. 2000, 45, 465–476. [Google Scholar] [CrossRef]
- O’Connell, P. On the relation of the freshwater floods of rivers to the areas and physical features of their basins and on a method of classifying rivers and streams with reference to the magnitude of their floods. Minutes Proc. Inst. Civ. Eng. 1868, 27, 204–217. [Google Scholar]
- Kuichling, E. The Relation between the Rainfall and the Discharge of Sewers in Populous Districts. Trans. Am. Soc. Civ. Eng. ASCE 1889, 20, 37–40. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Singh, V.P. Elementary Hydrology, 1st ed.; Pearson: London, UK, 1992; ISBN 978-0132493840. [Google Scholar]
- Langousis, A.; Veneziano, D. Long-term rainfall risk from tropical cyclones in coastal areas. Wat. Resour. Res. 2009, 45, W11430. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Langousis, A. Treaties on Water Sciences: Hydrology; Wilderer, P., Uhlenbrook, S., Eds.; Academic Press: Oxford, UK, 2011; pp. 27–78. [Google Scholar]
- Ossiander, M.; Waymire, E.C. Statistical Estimation for Multiplicative Cascades. Annals Stat. 2000, 28, 1533–1560. [Google Scholar]
- Ossiander, M.; Waymire, E.C. On Estimation Theory for Multiplicative Cascades. Sankhyā Ind. J. Stat. Ser. A 2002, 64, 323–343. [Google Scholar]
- Lashermes, B.; Abry, P.; Chainais, P. New Insights into the Estimation of Scaling Exponents. Int. J. Wavelets Multi. 2004, 2, 497–523. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A.; Furcolo, P. Multifractality and rainfall extremes: A review. Water Resour. Res. 2006, 42, W06D15. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D. Intensity–duration–frequency curves from scaling representations of rainfall. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Improved moment scaling estimation for multifractal signals. Nonlinear Process. Geophys. 2009, 16, 641–653. [Google Scholar] [CrossRef][Green Version]
- Langousis, A.; Kaleris, V. Statistical framework to simulate daily rainfall series conditional on upper-air predictor variables. Water Resour. Res. 2014, 50, 3907–3932. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M. Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 2000, 36, 469–482. [Google Scholar] [CrossRef]
- Fiorentino, M.; Iacobellis, V. New insights about the climatic and geologic control on the probability distribution of floods. Water Resour. Res. 2001, 37, 721–730. [Google Scholar] [CrossRef]
- Iacobellis, V.; Claps, P.; Fiorentino, M. Climatic control on the variability of flood distribution. Hydrol. Earth Syst. Sci. 2002, 6, 229–237. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modeling and analysis of rain and clouds by anisotropic scaling of multiplicative processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Fraedrich, K.; Larnder, C. Scaling regimes of composite rainfall time series. Tellus Ser. A 1993, 45, 289–298. [Google Scholar] [CrossRef]
- Olsson, J. Limits and characteristics of the multifractal behavior of a high-resolution rainfall time series. Nonlinear Process. Geophys. 1995, 2, 23–29. [Google Scholar] [CrossRef][Green Version]
- Marsan, D.; Schertzer, D.; Lovejoy, S. Causal space-time multifractal processes: Predictability and forecasting of rain fields. J. Geophys. Res. 1996, 101, 26333–26346. [Google Scholar] [CrossRef]
- Perica, S.; Foufoula-Georgiou, E. Linkage of scaling and thermodynamic parameters of rainfall: Results from midlatitude mesoscale convective systems. J. Geophys. Res. 1996, 101, 7431–7448. [Google Scholar] [CrossRef]
- Perica, S.; Foufoula-Georgiou, E. Model for multiscale disaggregation of spatial rainfall based on coupling meteorological and scaling descriptions. J. Geophys. Res. 1996, 101, 26347–26361. [Google Scholar] [CrossRef]
- Tessier, Y.; Lovejoy, S.; Hubert, P.; Schertzer, D.; Pecknold, S. Multifractal analysis and modelling of rainfall and river flows and scaling, causal transfer functions. J. Geophys. Res. 1996, 101, 26427–26440. [Google Scholar] [CrossRef]
- Over, T.M.; Gupta, V.K. A space-time theory of mesoscale rainfall using random cascades. J. Geophys. Res. 1996, 101, 26319–26331. [Google Scholar] [CrossRef]
- Menabde, M.; Harris, D.; Seed, A.; Austin, G.; Stow, D. Multiscaling properties of rainfall and bounded random cascades. Water Resour. Res. 1997, 33, 2823–2830. [Google Scholar] [CrossRef]
- Schmitt, F.; Vannistem, S.; Barbosa, A. Modeling of rainfall time series using two-state renewal processes and multifractals. J. Geophys. Res. 1998, 103, 23181–23193. [Google Scholar] [CrossRef]
- Olsson, J. Evaluation of a scaling cascade model for temporal rainfall disaggregation. Hydrol. Earth Syst. Sci. 1998, 2, 19–30. [Google Scholar] [CrossRef]
- Hubert, P.; Bendjoudi, H.; Schertzer, D.; Lovejoy, S. A Multifractal Explanation for Rainfall-Intensity-Duration Curves. In Heavy Rain and Flash Floods; Llasat, C., Versace, P., Ferrari, E., Eds.; Natl. Res. Counc., Group of Prev. from Hydrol. Disasters: Consenza, Italy, 1998; pp. 21–28. [Google Scholar]
- Venugopal, V.; Foufoula-Georgiou, E.; Sapozhnikov, V. A space-time downscaling model for rainfall. J. Geophys. Res. 1999, 104, 19705–19721. [Google Scholar] [CrossRef]
- Deidda, R.; Benzi, R.; Siccardi, F. Multifractal modeling of anomalous scaling laws in rainfall. Water Resour. Res. 1999, 35, 1853–1867. [Google Scholar] [CrossRef]
- Deidda, R.; Badas, M.G.; Piga, E. Space-time scaling in high-intensity Tropical Ocean Global Atmosphere Coupled Ocean-Atmosphere Response Experiment (TOGA-COARE) storms. Water Resour. Res. 2004, 40, W02506. [Google Scholar] [CrossRef]
- Deidda, R.; Badas, M.G.; Piga, E. Space-time multifractality of remotely sensed rainfall fields. J. Hydrol. Amsterdam 2006, 322, 2–13. [Google Scholar] [CrossRef]
- Deidda, R. Rainfall downscaling in a space-time multifractal framework. Water Resour. Res. 2000, 36, 1779–1794. [Google Scholar] [CrossRef]
- Güntner, A.; Olsson, J.; Calver, A.; Gannon, B. Cascade-based disaggregation of continuous rainfall time series: The influence of climate. Hydrol. Earth Syst. Sci. 2001, 5, 145–164. [Google Scholar] [CrossRef]
- Carvalho, L.M.V.; Lavallée, D.; Jones, C. Multifractal properties of evolving convective systems over tropical South America. Geophys. Res. Lett. 2002, 29, 33-1–33-4. [Google Scholar] [CrossRef]
- Pathirana, A.; Herath, S. Multifractal modeling and simulation of rain fields exhibiting spatial heterogeneity. Hydrol. Earth Syst. Sci. 2002, 6, 695–708. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and intensity–duration–frequency curves. Water Resour. Res. 2002, 38, 1306–1317. [Google Scholar] [CrossRef]
- Veneziano, D.; Iacobellis, V. Multiscaling pulse representation of temporal rainfall. Water Resour. Res. 2002, 38, 13-1–13-13. [Google Scholar] [CrossRef]
- Pathirana, A.; Herath, S.; Yamada, T. Estimating rainfall distributions at high temporal resolutions using a multifractal model. Hydrol. Eart Syst. Sci. 2003, 7, 668–679. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A. The areal reduction factor a multifractal analysis. Water Resour. Res. 2005, 41, W07008. [Google Scholar] [CrossRef]
- Badas, M.G.; Deidda, R.; Piga, E. Orographic influences in rainfall downscaling. Adv. Geosci. 2005, 2, 285–292. [Google Scholar] [CrossRef]
- Gebremichael, M.; Over, T.M.; Krajewski, W.F. Comparison of the scaling characteristics of rainfall derived from space-based and ground-based radar observations. J. Hydrometeorol. 2006, 7, 1277–1294. [Google Scholar] [CrossRef]
- Venugopal, V.; Roux, S.G.; Foufoula-Georgiou, E.; Arneodo, A. Revisiting multifractality of high-resolution temporal rainfall using a wavelet-based formalism. Water Resour. Res. 2006, 42, W06D14. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D.; Furcolo, P.; Lepore, C. Multifractal rainfall extremes: Theoretical analysis and practical estimation. Chaos Solitons Fractals 2009, 39, 1182–1194. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P.; Iacobellis, V. Imperfect scaling of time and space-time rainfall. J. Hydrol. 2006, 322, 105–119. [Google Scholar] [CrossRef]
- Veneziano, D.; Lepore, C.; Langousis, A.; Furcolo, P. Marginal Methods of Intensity-duration-frequency Estimation in Scaling and Nonscaling Rainfall. Wat. Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Paulson, K.S. Spatial-temporal statistics of rainrate random fields. Radio Sci. 2002, 37, 1–8. [Google Scholar] [CrossRef]
- Tarasova, L.; Merz, R.; Kiss, A.; Basso, S.; Blöschl, G.; Merz, B.; Viglione, A.; Plötner, S.; Guse, B.; Schumann, A.; et al. Causative classification of river flood events. WIREs WATER 2019. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).