Analysis of the Saltwater Wedge in a Coastal Karst Aquifer with a Double Conduit Network, Numerical Simulations and Sensitivity Analysis
Abstract
1. Introduction
2. Methods
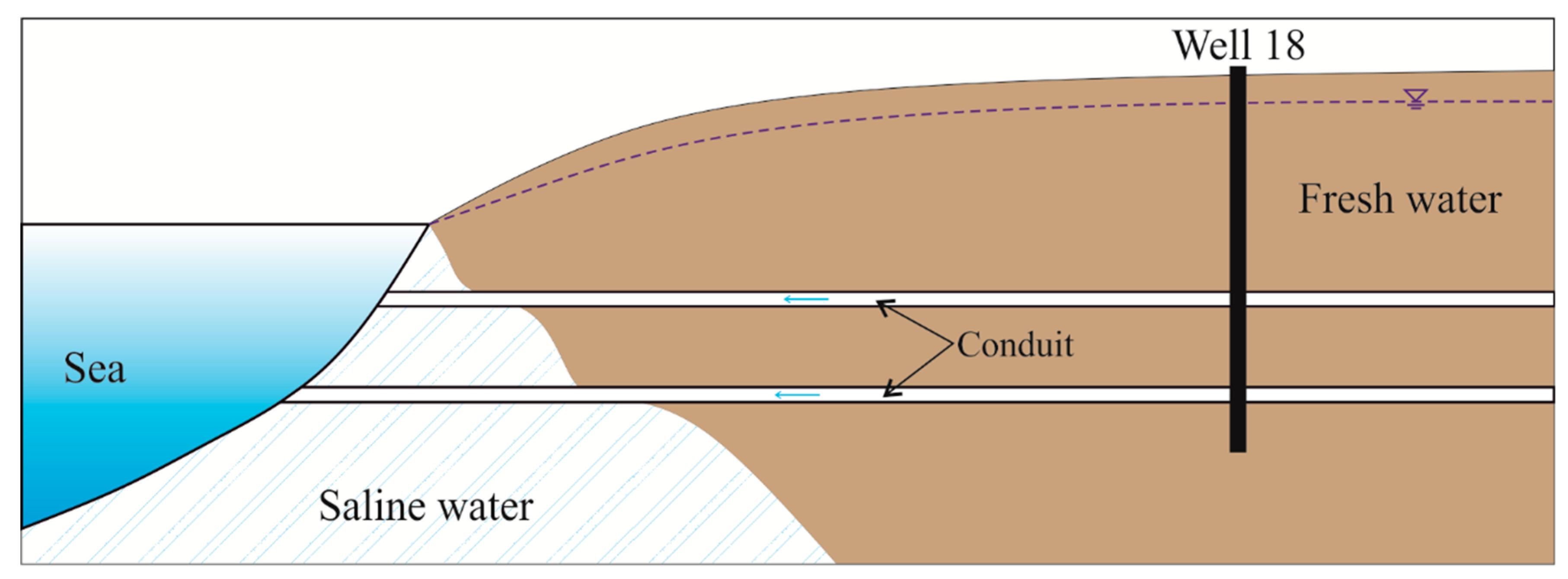
2.1. Study Site
2.2. Hydrological Parameter
3. Results and Discussions
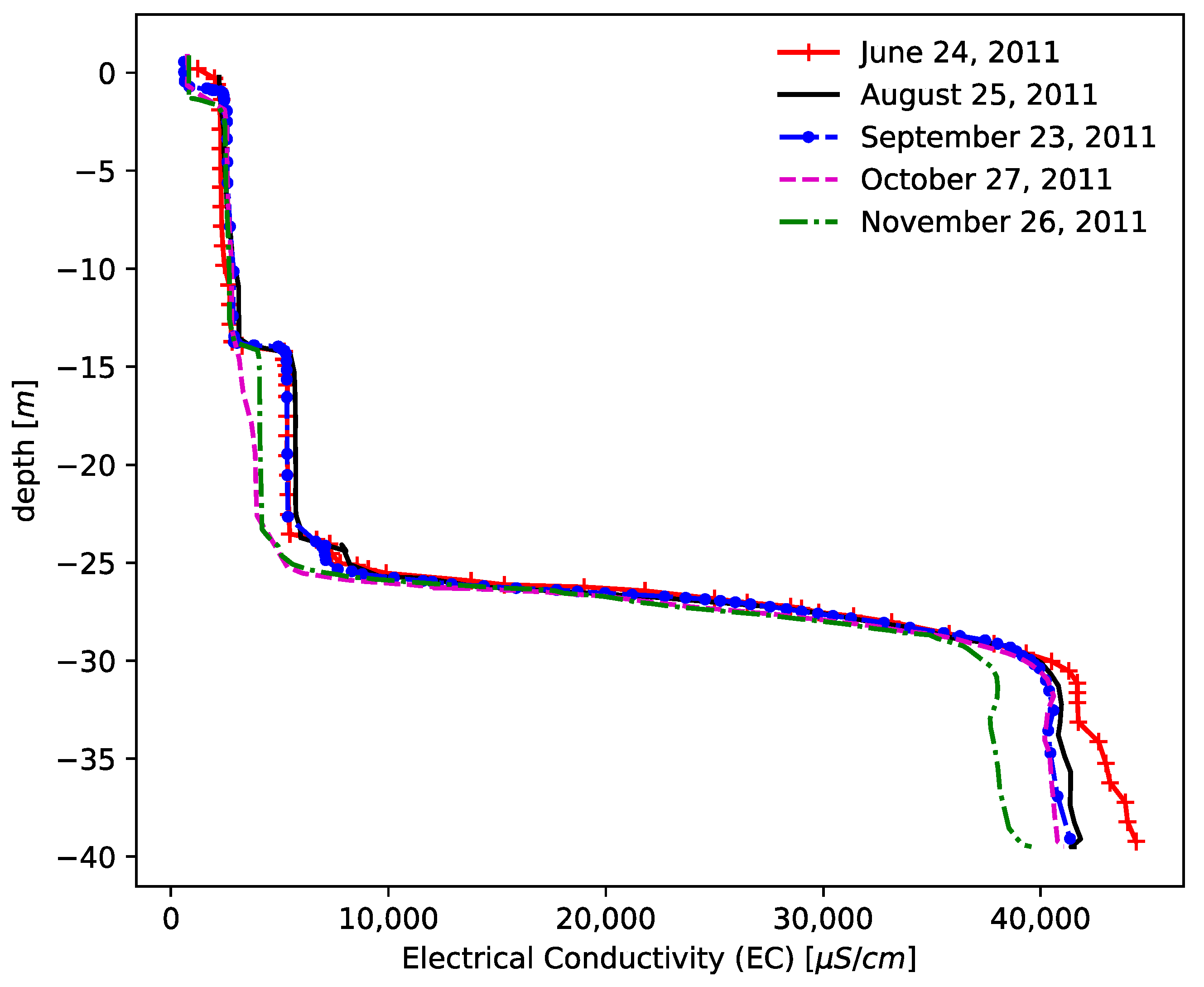
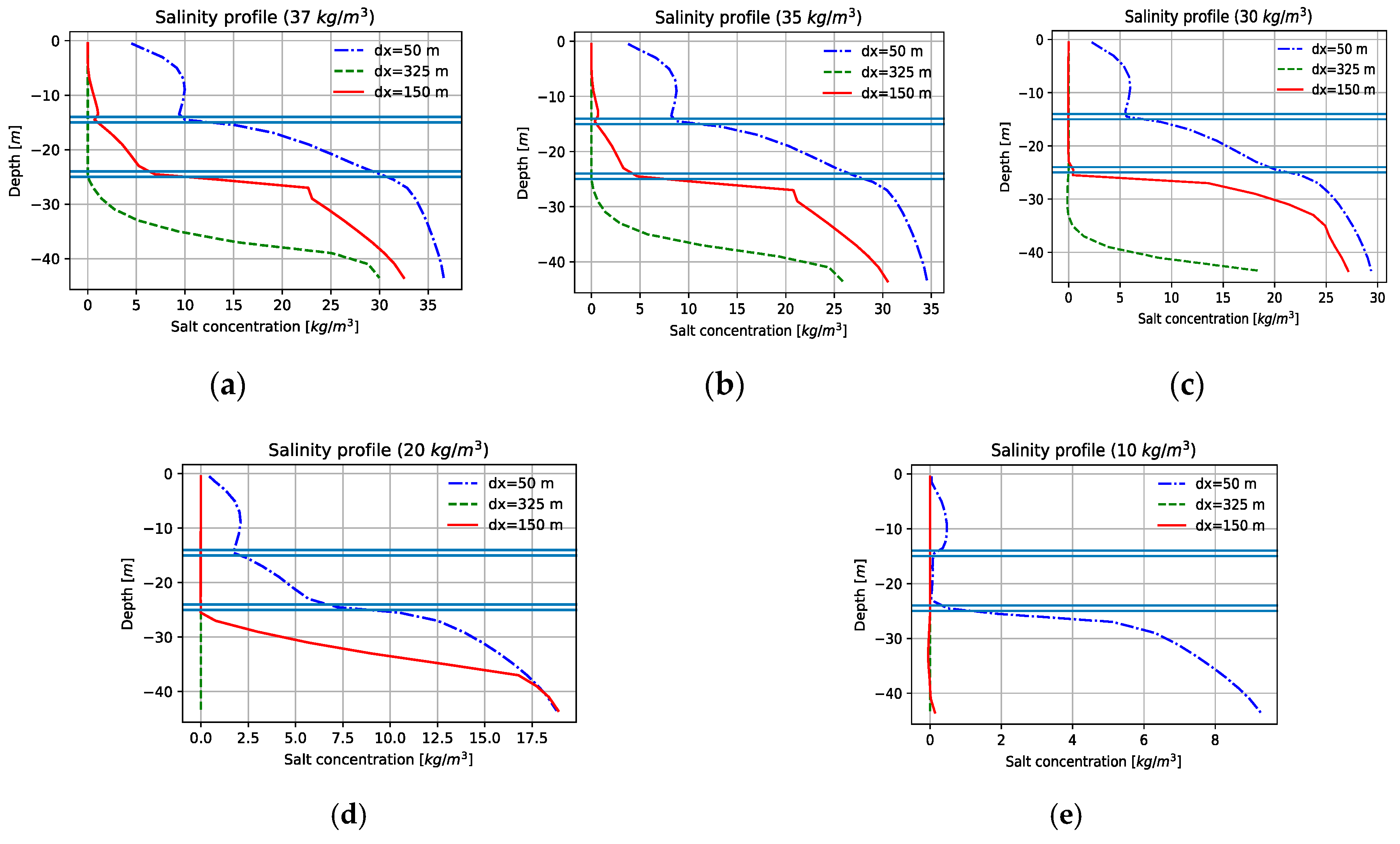
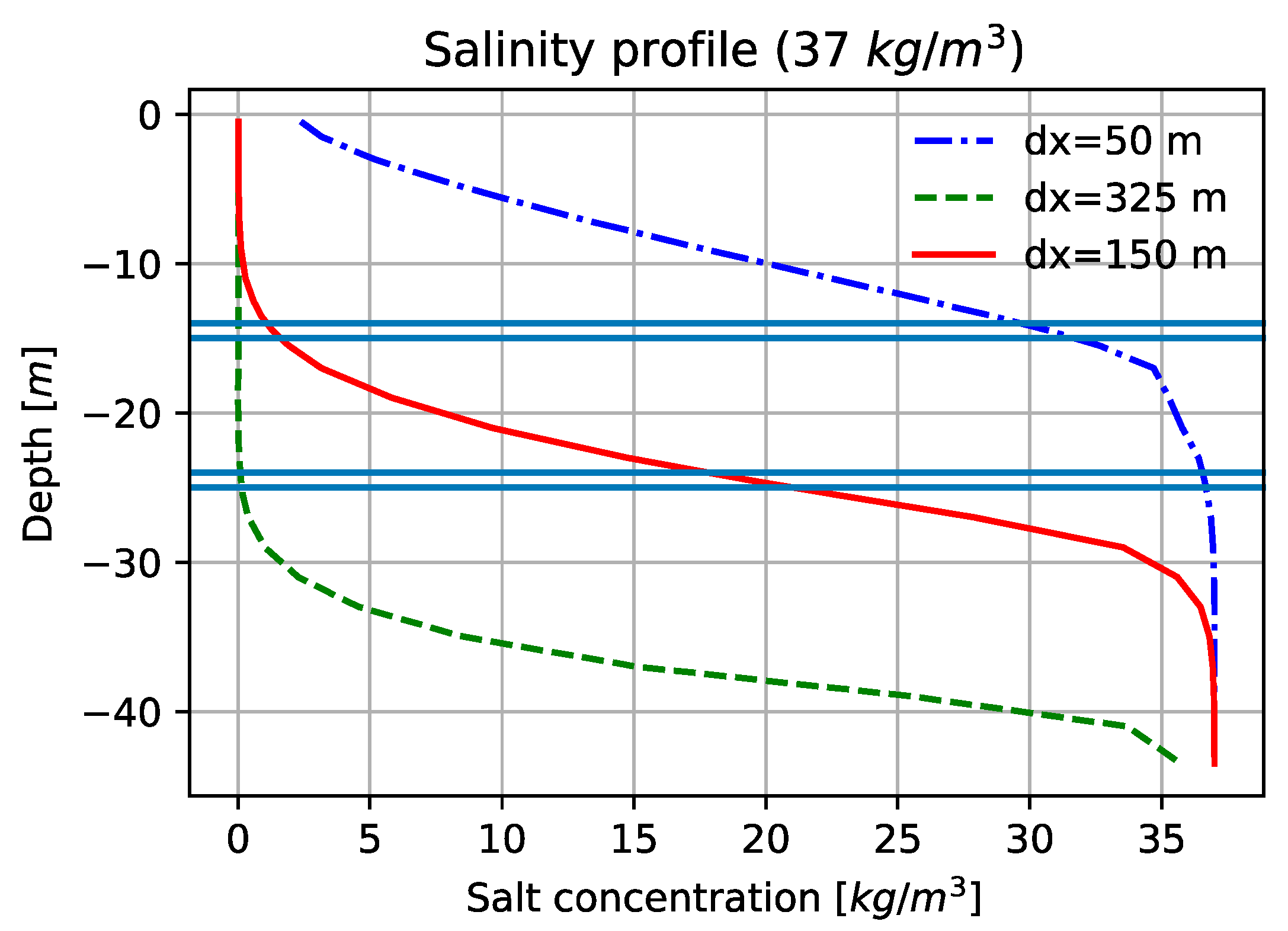
3.1. Spatial and Temporal Discretization
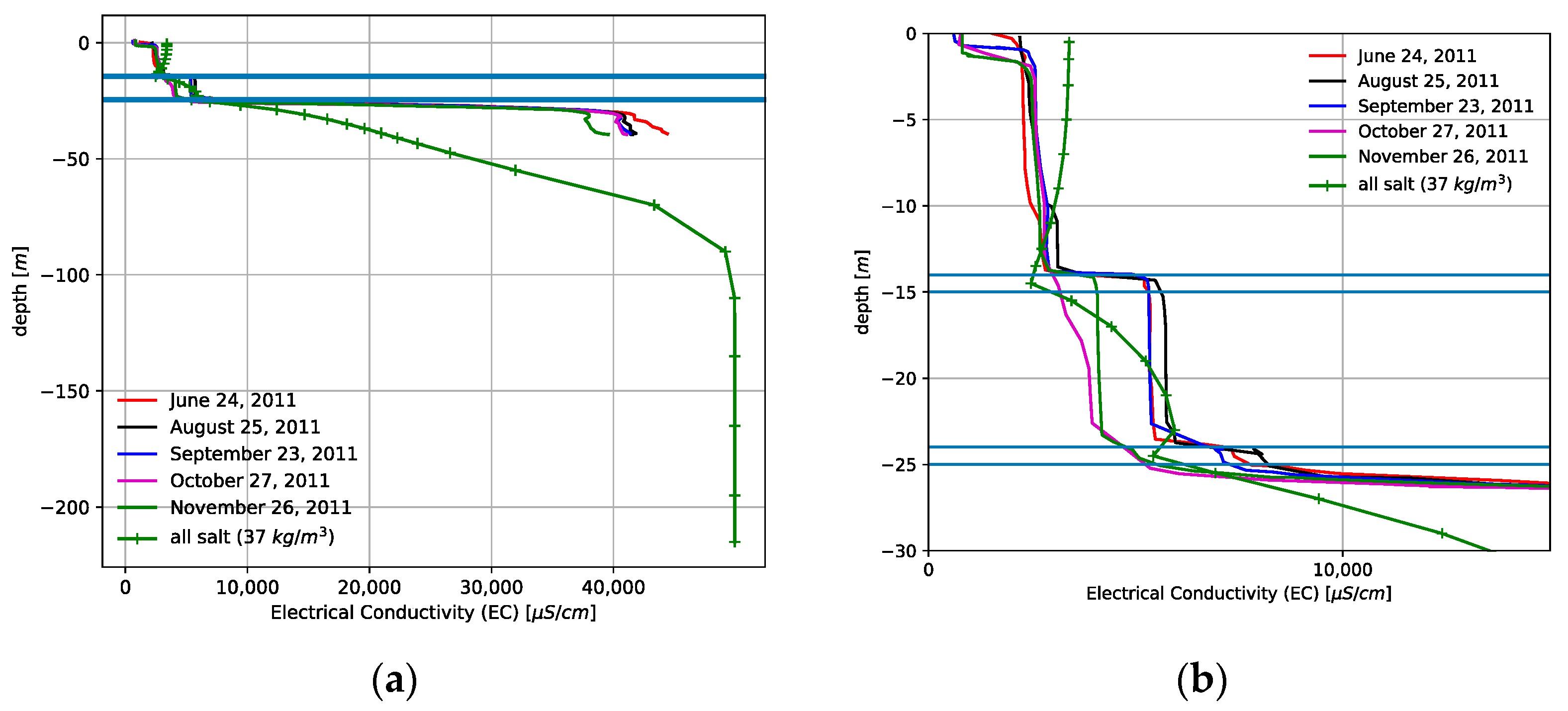
3.2. Initial and Boundary Conditions
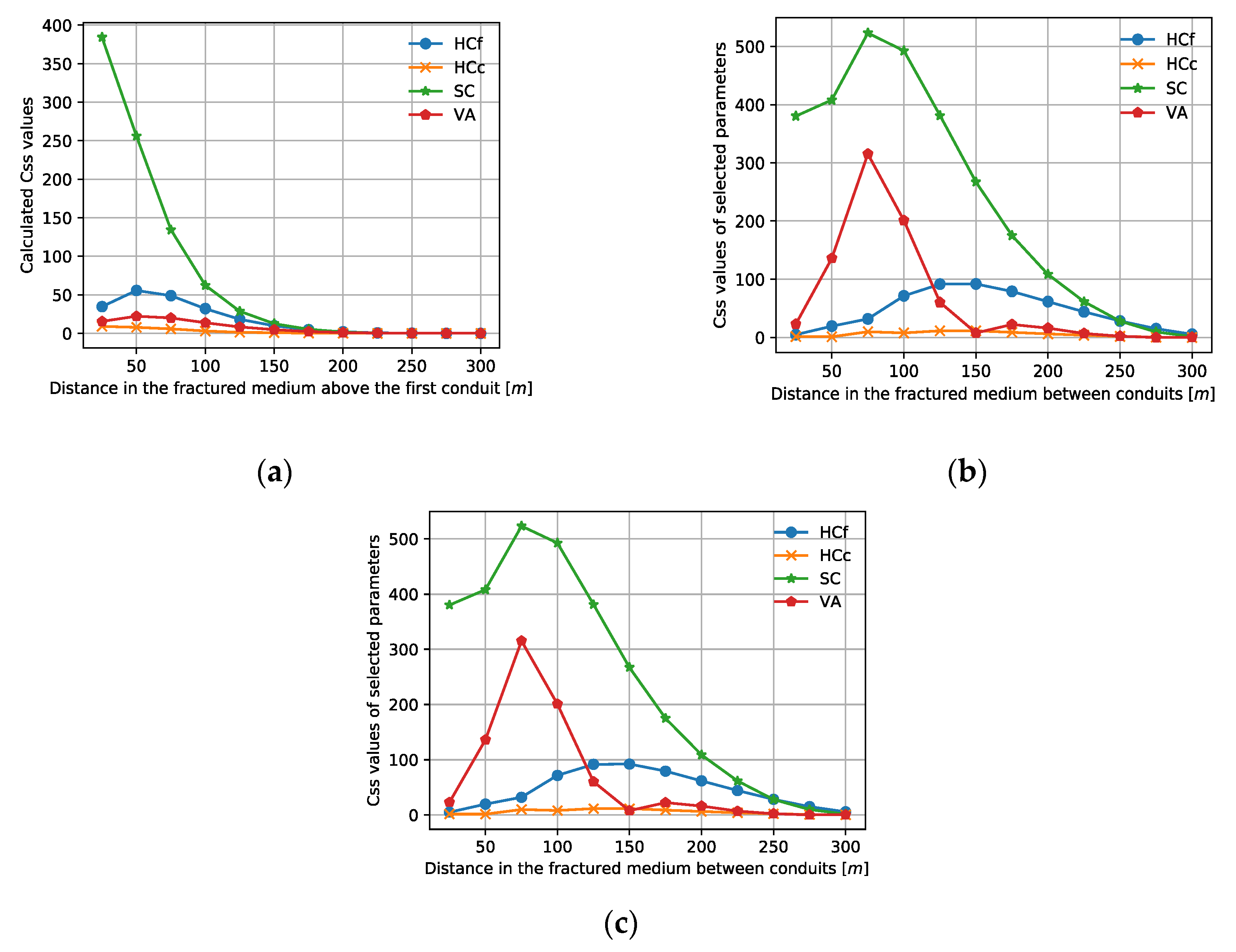
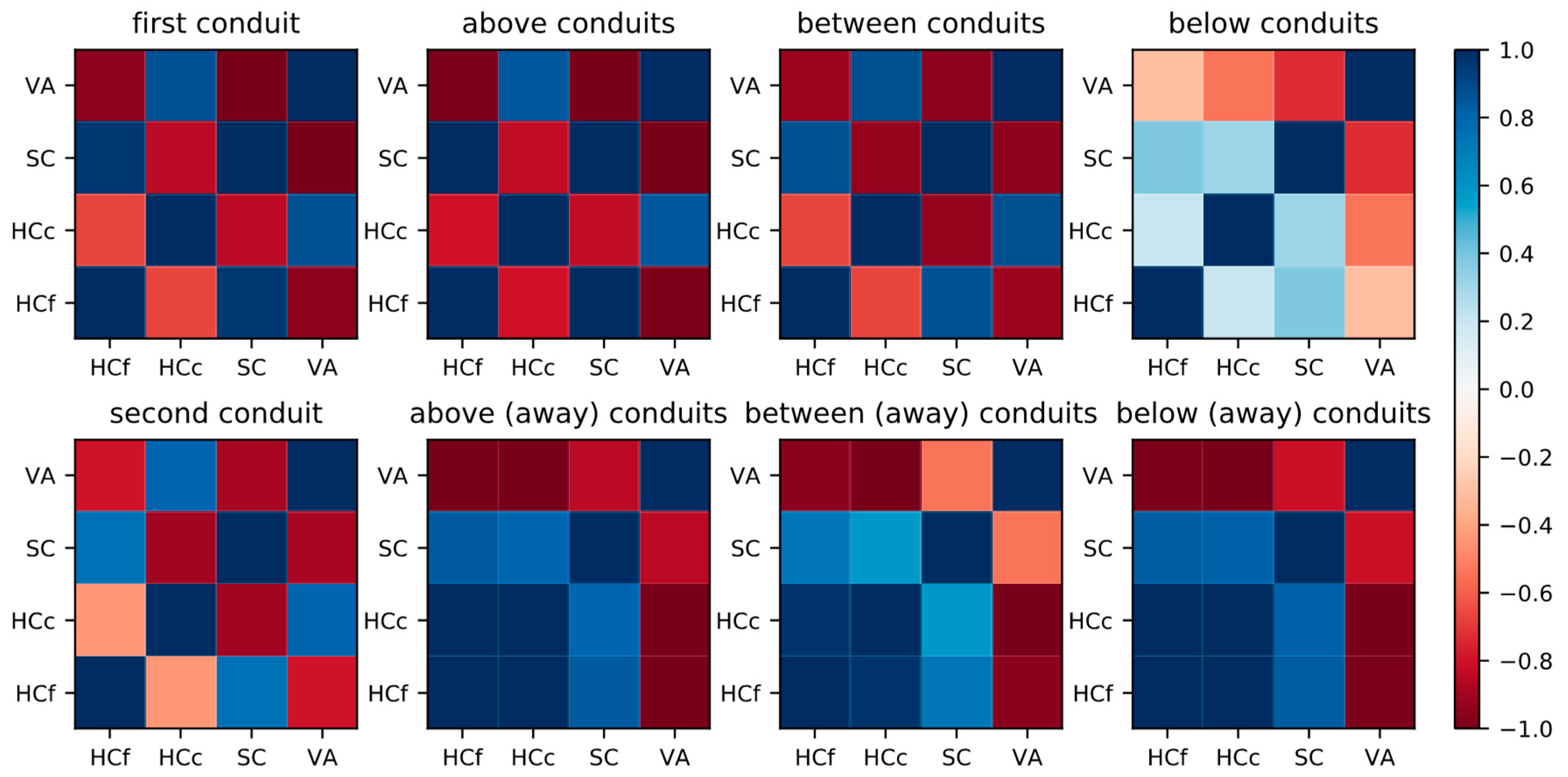
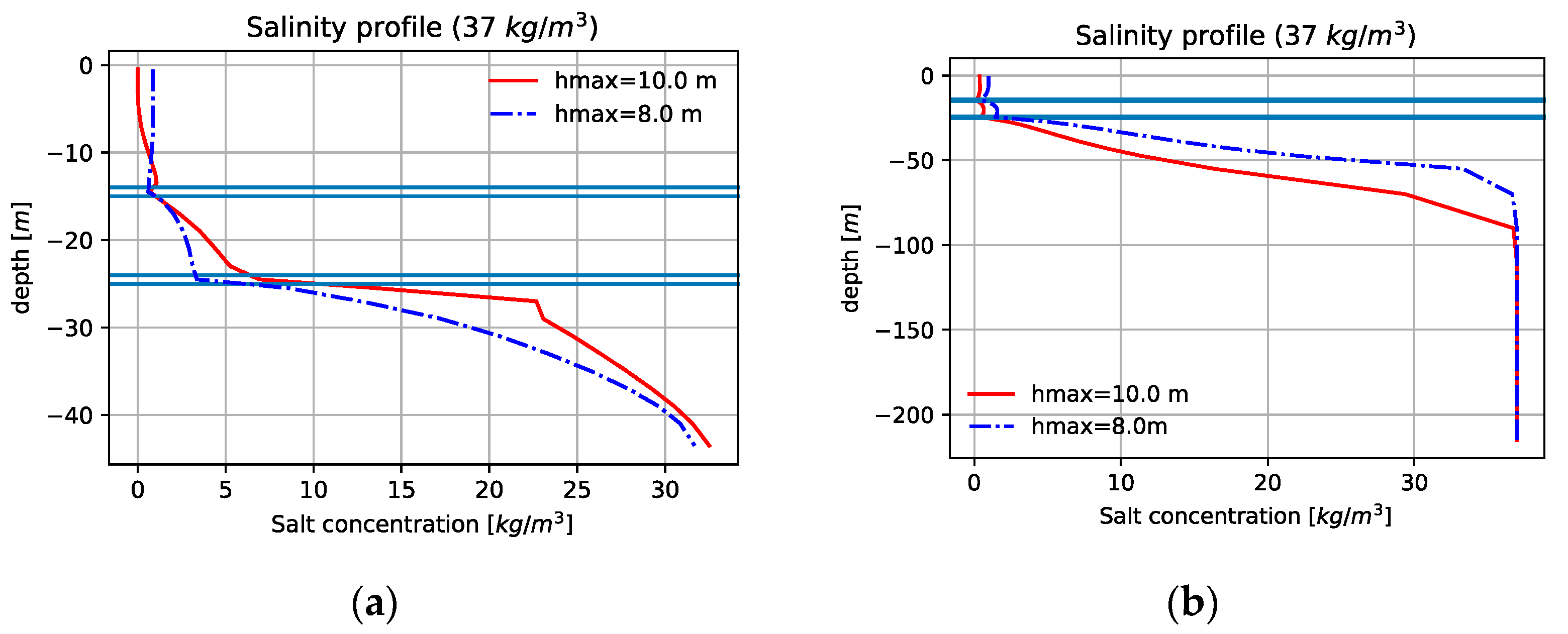
3.3. Sensitivity Analysis
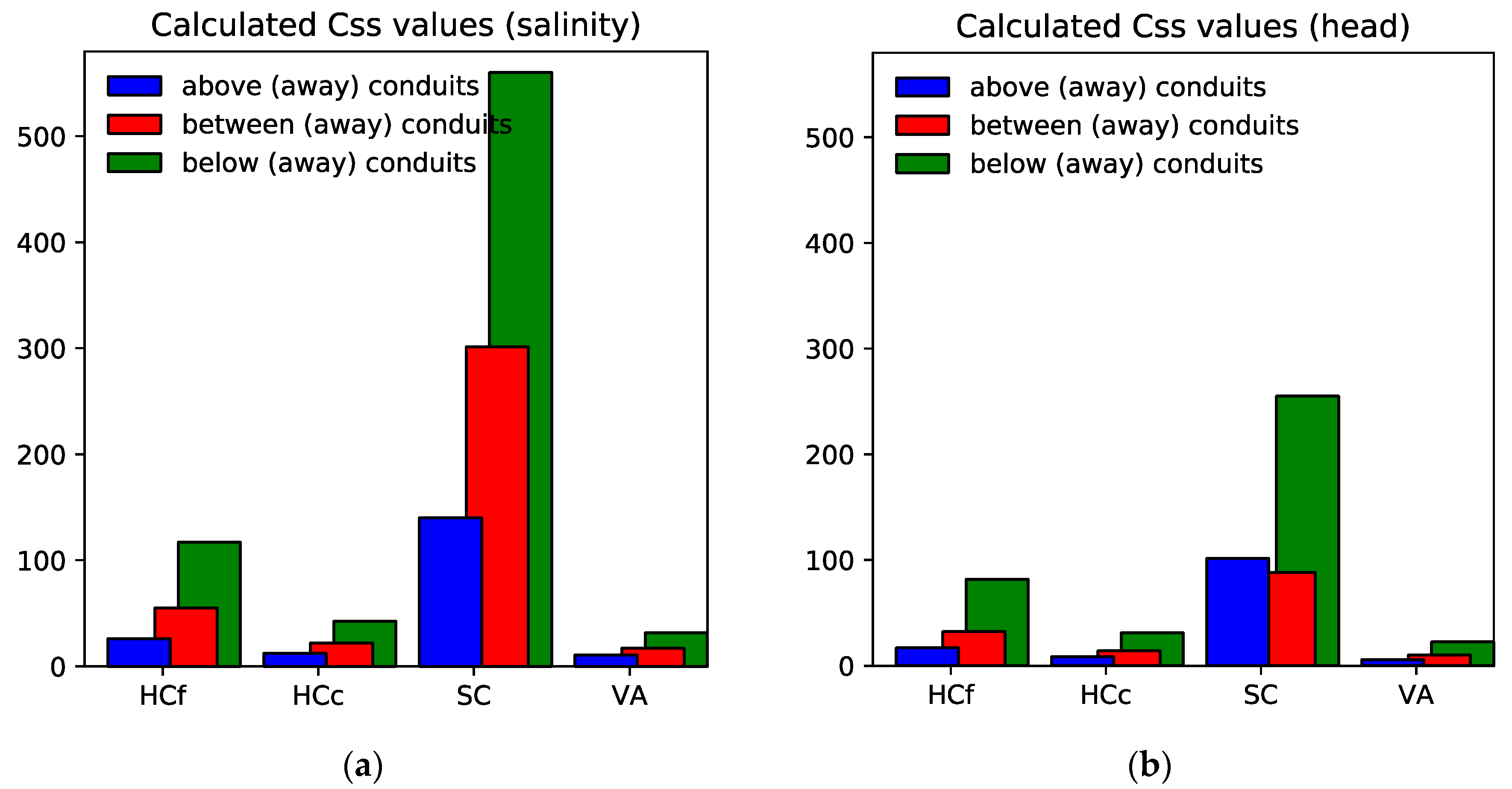
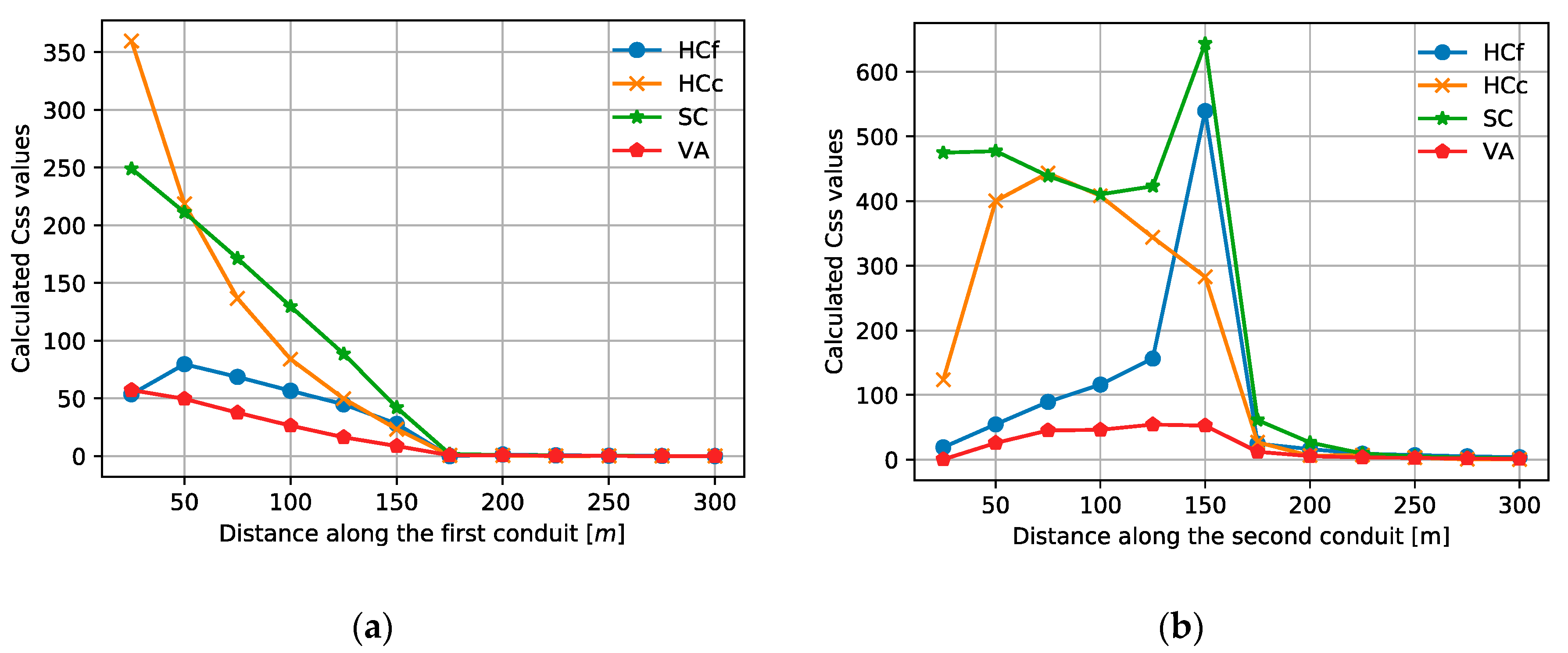
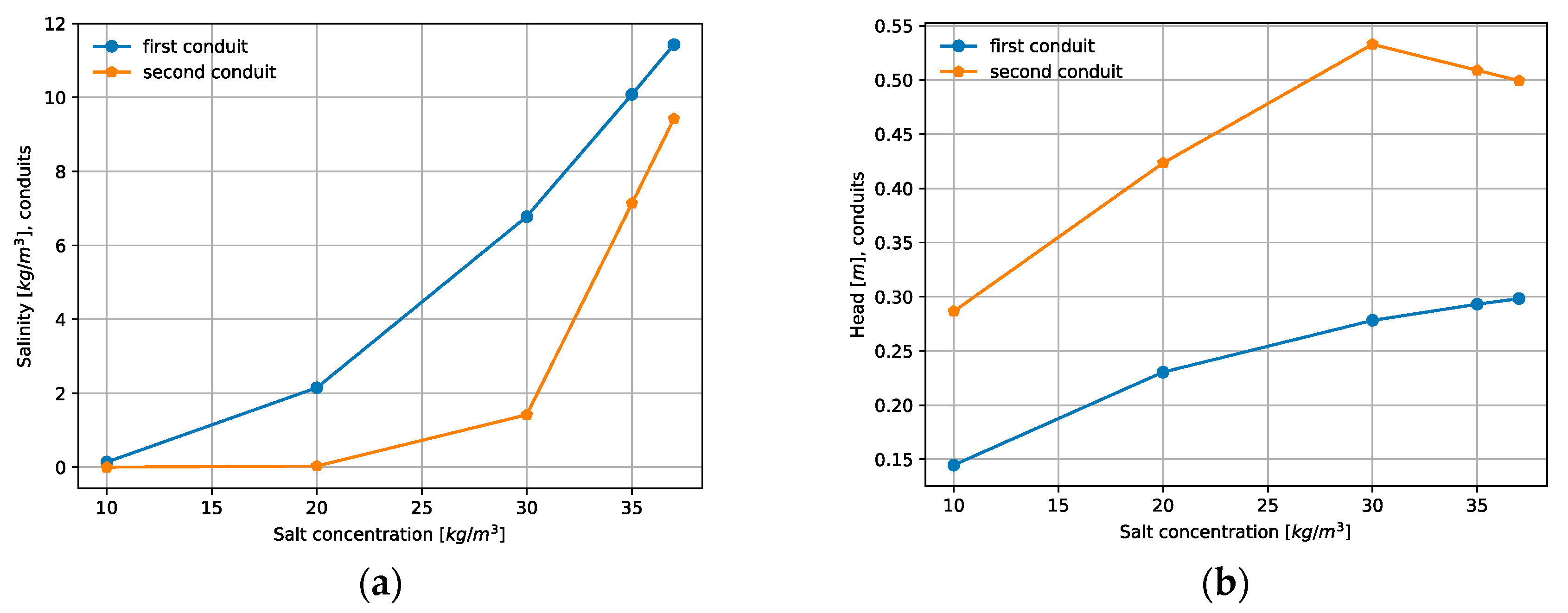
3.3.1. Local Sensitivity Analysis of Numerical Simulations in the Conduits
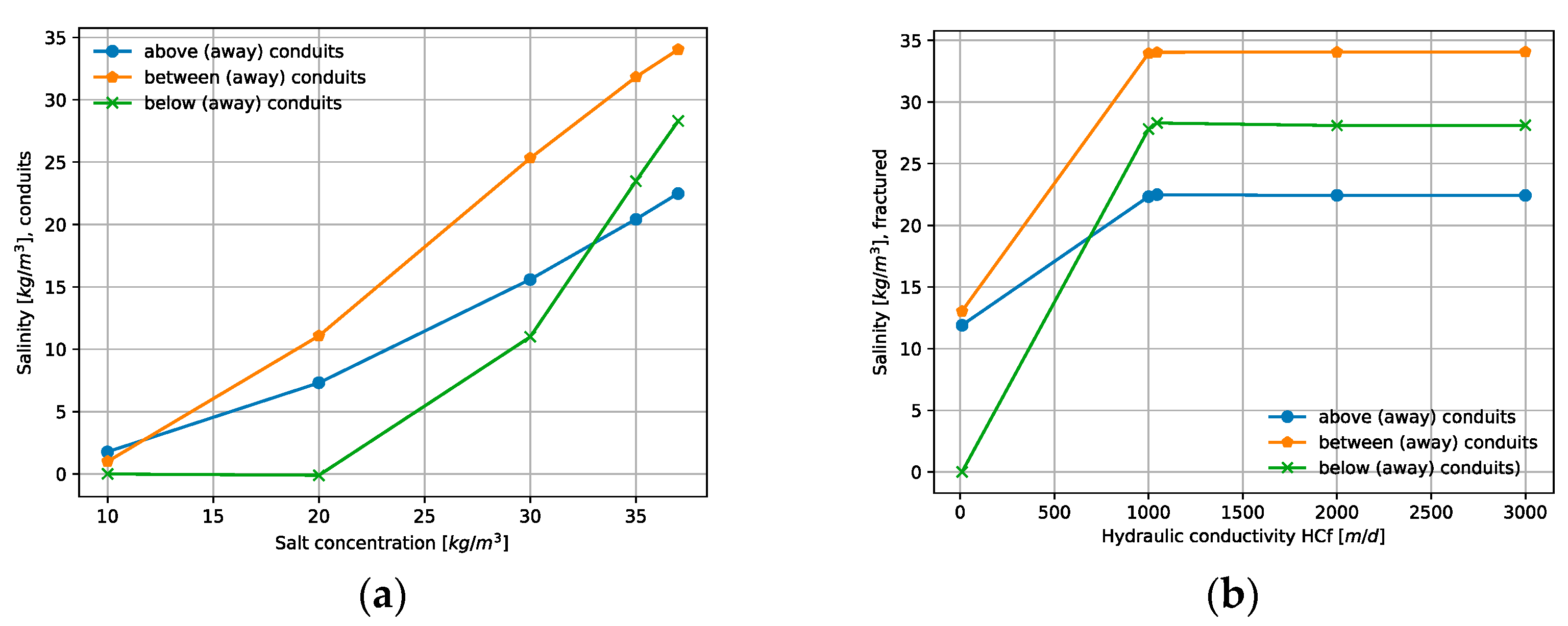
3.3.2. Local Sensitivity Analysis of Numerical Simulations in the Fractured Medium
3.4. Numerical Simulations Results of Seawater Intrusion Scenarios
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fleury, P.; Bakalowicz, M.; de Marsily, G. Submarine springs and coastal karst aquifer: A review. J. Hydrol. 2007, 339, 79–92. [Google Scholar] [CrossRef]
- Bear, J. Seawater Intrusion in Coastal Aquifers; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Werner, C.L.; Bakker, M.; Post, V.E.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigations and management: A recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Voss, C.I.; Souza, W.R. Variable density flow and solute transport simulation of regional aquifers containing a narrow freshwater-saltwater transition zone. Water Resour. Res. 1987, 23, 1851–1866. [Google Scholar] [CrossRef]
- Moore, W.S.; Wilson, A.M. Advective flow through the upper continental shelf driven bt storms, buoyancy, and submarine groundwater discharge. Earth Planet Sci. Lett. 2005, 235, 564–576. [Google Scholar] [CrossRef]
- Voss, C.I.; Provost, A.M. SUTRA, US Geological Survey Water Resources Investigation Reports; 84-4369; USGS: Reston, VA, USA, 1984.
- Diersch, H.J.G. FEFLOW Reference Manual; Institute for Water Resources Planning and Systems Research Ltd.: Berlin, Germany, 2002; p. 278. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water-User Guide to Modularization Concepts and the Ground-Water Flow Process: U.S. Geological Survey Open-File Report 00-92; U.S. Geological Survey: Reston, VA, USA, 2000; p. 121.
- Guo, W.; Langevin, C. Users’ Guide to SEAWAT: A Computer Program for Simulation of Three-Dimensional Variable-Density Ground-Water Flow; Water Resources Investigations Report; United States Geological Survey: Reston, VA, USA, 2002.
- Langevin, C.; Shoemaker, W.B.; Guo, W. MODFLOW-2000, the US Geological Survey Modular Ground-Water Model Documentation of the SEAWAT-2000 Version with the Variable-Density Flow Process (VDF) and the Integrated MT3DMS Transport Process (IMT); US Department of the Interior, US Geological Survey: Reston, VA, USA, 2003.
- Zheng, C.; Wang, P.P. MT3DMS—A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion and Chemical Reactions of Contaminants in Ground-Water Systems; Documentation and User’s Guide: U.S. Army Corps of Engineers Contract Report SERDP-99-1; University of Alabama: Tuscaloosa, AL, USA, 1999. [Google Scholar]
- Zheng, C. MT3DMS v5.2 Supplemental User’s Guide: TECHNICAL Report to the U.S. Army Engineer Research and Development Center, Department of Geological Sciences; University of Alabama: Tuscaloosa, AL, USA, 2006; p. 24. [Google Scholar]
- Davis, J.H. Hydraulic Investigation and Simulation of Groundwater Flow in the Upper Floridan Aquifer of North Central Florida and Southwestern Georgia and Delineation of Contributing Areas for Selected City of Tallahassee, Florida; 95-4296; USGS: Reston, VA, USA, 1966; p. 55.
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a conduit flow process (CFP) for MODFLOW-2005. U.S. Geological Survey. Tech. Methods 2008, 6, 50. [Google Scholar]
- Gallegos, J.J.; Hu, B.X.; Davis, H. Simulating flow in karst aquifers at laboratory and sub-regional scales using MODFLOW-CFP. Hydrogeol. J. 2013, 21, 1749–1760. [Google Scholar] [CrossRef]
- Reimann, T.; Giese, M.; Geyer, T.; Liedl, R.; Maréchal, J.C.; Shoemaker, W.B. Representation of water abstraction from a larst conduit with numerical discrete-continuum models. Hydrol. Earth Syst. Sci. 2014, 18, 227–241. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Cao, J. Simulating long term nitrate-N contamination processes in the Wookville Karst Plain using CFPv2 with UMT3D. J. Hydrol. 2015, 524, 72–88. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Kish, S. Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in a coastal karst aquifer through conduit network using CFPv2. J. Contam. Hydrol. 2015, 182, 131–145. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Xu, Z.; Hu, B.; Ye, M. Numerical modeling and sensitivity analysis of seawater intrusion in a dual permeability coastal karst aquifer with conduit networks. Hydrol. Earth Syst. Sci. 2018, 22, 221–239. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X. Development of a discrete-continuum VDFST-CFP numerical model for simulating seawater intrusion to a coastal karst aquifer with a conduit system. Water Resour. Res. 2017, 53, 688–711. [Google Scholar] [CrossRef]
- Hernandez-Diaz, R.; Petrella, E.; Bucci, A.; Naclerio, G.; Feo, A.; Sferra, G.; Chelli, A.; Zanini, A.; Gonzales-Hernandez, P.; Celico, F. Integrating hydrogeological and microbiological data and modelling to characterize the hydraulic features and behaviour of coastal carbonate aquifers: A case in Western Cuba. Water 2019, 11, 1989. [Google Scholar] [CrossRef]
- Hill, M.; Tiedemann, C. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertaninty; Wiley: Hoboken, NJ, USA, 2006; p. 480. [Google Scholar]
- Hill, M.C. Methods and Guidelines for Effective Model Calibration; Report 98-4005; U.S. Geological Survey Water-Resources Investigations: Reston, VA, USA, 1998.
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity Analysis calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2000, 45, W06427. [Google Scholar] [CrossRef]
- Shoemaker, W.B. Important observations and parameters for a salt water intrusion model. Ground Water 2004, 42, 829–840. [Google Scholar] [PubMed]
- Xu, Z.; Hu, B.; Xu, Z.; Wu, X. Simulating seawater intrusion in a complex coastal karst aquifer using an improved variable-density flow and solute transport-conduit flow process model. Hydrogeol. J. 2019, 27, 1277–1289. [Google Scholar] [CrossRef]
- Fagundo Castillo, J.R.; Gonzales Hernandez, P. Agricultural use and water quality at karstic Cuban western plain. Int. J. Speleol. 1999, 28, 175–185. [Google Scholar] [CrossRef][Green Version]
- Molerio León, L.; Parise, M. Managing environmental problems in Cuban karstic aquifers. Environ. Geol. 2009, 58, 275–283. [Google Scholar] [CrossRef]
- Hernández, R.; Ramírez, R.; López-Portilla, M.; González, P.; Antigüedad, I.; Díaz, S. Seawater Intrusion in the Coastal Aquifer of Guanahacabibes, Pinar del Río, Cuba. In Management of Water Resources in Protected Areas; Farfán González, H., Corvea Porras, J.L., de Bustamante Gutiérrez, I., LaMoreaux, J.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 301–308. [Google Scholar]
- Bucci, A.; Petrella, E.; Celico, F.; Naclerio, G. Use of molecular approaches in hydrogeological studies: The case of carbonate aquifers in southern Italy. Hydrogeol. J. 2017, 25, 1017–1031. [Google Scholar] [CrossRef]
- Petrella, E.; Falasca, A.; Celico, F. Natural-gradient tracer experiment in epikarst: A test study in the Acqua dei Faggi experimental site, southern Italy. Geofluids 2008, 8, 159–166. [Google Scholar] [CrossRef]
- Bakker, M.; Post, V.; Langevin, C.D.; Hughes, J.D.; White, J.T.; Starn, J.J.; Fienen, M.N. Scripting MODFLOW Model Development Using Python and FloPy. Groundwater 2016, 54, 733–739. [Google Scholar] [CrossRef]




| Parameter | Definition | Lower | Upper | Evaluated Value | Units |
|---|---|---|---|---|---|
| HCf | Hydraulic conductivity (fractured medium) | 10.0 | 3000.0 | 1045.0 | ay |
| HCc | Hydraulic conductivity (conduits) | ||||
| VA | Vertical anisotropy | 1.0 | 10.0 | 1.0 | dimensionless |
| POf | Porosity (fractured medium) | 0.1 | dimensionless | ||
| POc | Porosity (conduits) | 1.0 | dimensionless | ||
| LDf | Longitudinal dispersivity (fractured medium) | 10.0 | |||
| LDc | Longitudinal dispersivity (conduits) | 0.3 | |||
| SC | Salinity concentration | 10.0 | 37.0 | 37.0 | |
| SH | Specified head boundary conditions | 8.0 | 10.0 | 10.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feo, A.; Zanini, A.; Petrella, E.; Hernàndez-Diaz, R.; Celico, F. Analysis of the Saltwater Wedge in a Coastal Karst Aquifer with a Double Conduit Network, Numerical Simulations and Sensitivity Analysis. Water 2019, 11, 2311. https://doi.org/10.3390/w11112311
Feo A, Zanini A, Petrella E, Hernàndez-Diaz R, Celico F. Analysis of the Saltwater Wedge in a Coastal Karst Aquifer with a Double Conduit Network, Numerical Simulations and Sensitivity Analysis. Water. 2019; 11(11):2311. https://doi.org/10.3390/w11112311
Chicago/Turabian StyleFeo, Alessandra, Andrea Zanini, Emma Petrella, Rebeca Hernàndez-Diaz, and Fulvio Celico. 2019. "Analysis of the Saltwater Wedge in a Coastal Karst Aquifer with a Double Conduit Network, Numerical Simulations and Sensitivity Analysis" Water 11, no. 11: 2311. https://doi.org/10.3390/w11112311
APA StyleFeo, A., Zanini, A., Petrella, E., Hernàndez-Diaz, R., & Celico, F. (2019). Analysis of the Saltwater Wedge in a Coastal Karst Aquifer with a Double Conduit Network, Numerical Simulations and Sensitivity Analysis. Water, 11(11), 2311. https://doi.org/10.3390/w11112311









