Abstract
Groundwater is an important natural resource in arid and semi-arid environments, where discharge from karst springs is utilized as the principal water supply for human use. The occurrence of karst springs over large areas is often poorly documented, and interpolation strategies are often utilized to map the distribution and discharge potential of springs. This study develops a novel method to delineate karst spring zones on the basis of various hydrogeological factors. A case study of the Bojnourd Region, Iran, where spring discharge measurements are available for 359 sites, is used to demonstrate application of the new approach. Spatial mapping is achieved using ensemble modelling, which is based on certainty factors (CF) and logistic regression (LR). Maps of the CF and LR components of groundwater potential were generated individually, and then, combined to prepare an ensemble map of the study area. The accuracy (A) of the ensemble map was then assessed using area under the receiver operating characteristic curve. Results of this analysis show that LR (A = 78%) outperformed CF (A = 67%) in terms of the comparison between model predictions and known occurrences of karst springs (i.e., calibration data). However, combining the CF and LR results through ensemble modelling produced superior accuracy (A = 85%) in terms of spring potential mapping. By combining CF and LR statistical models through ensemble modelling, weaknesses in CF and LR methods are offset, and therefore, we recommend this ensemble approach for similar karst mapping projects. The methodology developed here offers an efficient method for assessing spring discharge and karst spring potentials over regional scales.
1. Introduction
Groundwater has been considered the most important resource in arid and semi-arid areas. Population increases and economic growth have resulted in water shortages around the globe, especially in developing countries, leading to greater exploitation and reliance on groundwater resources [1,2]. Among the various forms of subsurface freshwater, karst groundwater is a major resource for water supply in many regions, including China, Turkey, Iran, Mexico, and the United States [3,4,5,6,7]. Karst aquifers are relatively high-yielding, heterogeneous systems that are characterized by complex groundwater flow paths [8,9,10]. They store and supply drinking water for approximately 20–25% of the world’s population, while constituting only small areas of the global land surface [11]. The characterization of karst aquifers is hampered by their complex character, and the often limited number of wells available to support hydrogeological observations and geological descriptions [12].
Groundwater models of karst aquifer systems invariably simplify karst features—and the spatial heterogeneity more generally—because it is impossible to acquire sufficient data to properly delineate the main flow features [13]. Additionally, specialized models are required to simulate the conduit flow that occurs within karst aquifers, at least for situations where equivalent porous medium approaches are not valid [14]. However, physically based models of karst aquifers are limited by both data availability and the heavy computational burden of conduit-matrix simulation. Thus, strategies to characterize the hydrogeology of karst aquifers, and in particular, to quantify spring hydrology, are essential precursors to the effective management of groundwater in these systems [15].
Geographical information systems (GIS) and remote sensing (RS) are commonly used to evaluate the hydrogeology of karst aquifers, including the spatial distribution of spring potential [16,17]. Recently, Chen et al. [18] undertook a global-scale project—the World Karst Aquifer Mapping (WOKAM)—to map karst aquifers and carbonate rock settings around the world. Karst springs, wells, caves and other water abstraction structures were also identified, although the large scale of the project meant that many regions have only limited information regarding point features within the landscape.
‘Spring groundwater potential’ was defined as the possibility of spring occurrence (with sufficient water) in an area and helps planners to estimate groundwater productivity [19,20]. There are myriad approaches to groundwater potential mapping using GIS-based statistical models. These include: frequency ratio (FR) [16,21], weight-of-evidence [22], evidential belief function (EBF) [23], logistic regression (LR) [24,25], certainty factor (CF) [26], analytical hierarchy process (AHP) [27], Shannon’s entropy [28], maximum entropy [29], support vector machine (SVM) [30] and boosted regression tree [31]. Groundwater potential mapping highlights the locations of potential groundwater zones including low, moderate and high for the optimal use of resources [32]. In general, multivariate statistical models (e.g., LR) cannot analyze the classes of independent factors (e.g., lithology, land use/land cover, soil, etc.) because they just determine the weight of predictive factors. In addition, bivariate statistical models (e.g., CF) are limited in their capacity to recognize the importance of independent variables [26] because they use a class-based procedure in modelling. To overcome these problems, scientists have developed ensemble statistical approaches [33,34,35,36,37,38,39].
Ensemble modelling is the combination of multiple predictive models that are used conjunctively to provide an evaluation of the same dataset [39]. Ensemble modelling approaches have been widely used in different fields, including groundwater [40,41,42,43,44,45,46,47], flood [40,48,49,50,51,52,53,54,55,56,57], landslide hazard [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87], land/ground subsidence [88,89], gully erosion [90,91], dust storm [92], wildfire [93], sinkhole [94], droughtiness [95,96], earthquake [97,98] and species distribution [99,100,101]. These studies provide clear evidence that the application of ensemble models can potentially result in improved capability (over individual methods) of GIS-based statistical models [102]. However, previous studies aimed at the prediction of karst spring occurrence have not investigated the potential of ensemble models that integrate bivariate and multivariate statistical models to support the construction of spring potential maps [24,25].
The main aim of this study is to explore different statistical models, both single and ensemble, to assess spring groundwater potential in a karst area, namely Bojnourd Region, northeast Iran. Although various researchers have tried to delineate groundwater spring potential zones [30,45,103,104], the evaluation of other modeling approaches is highly necessary. To address this, a new ensembling technique is proposed to improve the accuracy of the statistical models and to identify groundwater potential zones. The novel approach of ensemble certainty factor and logistic regression models has not previously been touched upon in the literature. Therefore, the principal motivation of this study is to use this ensemble model to delineate prone areas to karst springs in Bojnourd region, Khorasan Shomali, Iran. It is anticipated that the outputs of this study will identify the strengths and weaknesses of the applied models, thereby, providing improved insights into model choice in the spatio-temporal analysis of karst springs discharge using statistical models.
2. Study Area
The study area, Bojnourd Region, is located in the north east of Khorasan Shomali province, Iran, between latitudes 37°15′ to 37°35′ N and longitudes 57°03′ to 57°40′ E (Figure 1), with minimum and maximum elevation of 875 and 2968 m, respectively. The mean precipitation is 272 mm/year and temperature ranges between 6.8 to 19.7 °C [105]. There are six main lithological formations in the study area including Aitamir (Cretaceous), Sarcheshmeh (Early Cretaceous), Shurijeh (Jurassic-Cretaceous), Upper-Red (Miocene), Niur (Silurian) and Shemshak (Triassic-Jurassic). Lithological characteristics of these formations are summarized in Table 1. From a geomorphological point of view, the study area is dominated by a mountainous landscape. In addition, there are numerous folds and faults in the study area which cause the occurrence of springs [106]. The major faults are oriented NE-SW and the others NW-SE and N-S. Inceptisols and entisols are dominant soil types of the study area. The depth of soil varies from one to three meters, although there are numerous surficial rocks (lithological outcrops) in steep areas of upstream zones. According to the reports of Iranian Department of Water Resources Management (IDWRM), hydraulic conductivities in this mountainous region range between 10−4 and 10−5 m/s.
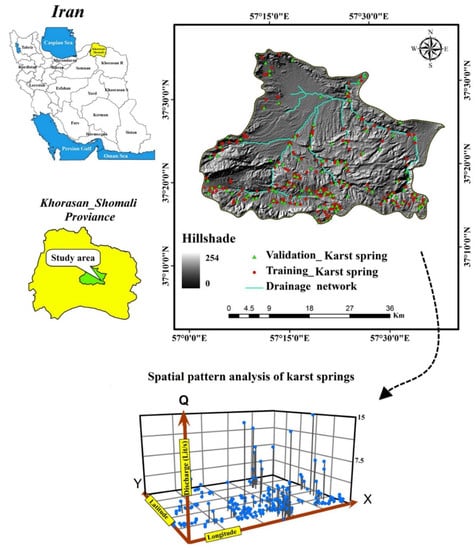
Figure 1.
Karst spring location with hill-shaded map of the study area, Khorasan Shomali, Iran.

Table 1.
Geological formations in the study area.
Nearly 88% of water demand in Khorasan Shomali province is supplied by groundwater resources [107]. Therefore, it has become necessary to predict groundwater potential zone in this region. The discharge of springs ranges between 0.5 and 15.2 SI. The size of karstic areas in this province is over 17,000 km2, which are used as karst water resources to provide drinking water for the Khorasan Shomali and Khorasan Razavi provinces. Furthermore, Khorasan Shomali province covers approximately an area of 248,000 km2, which is inhabited by more than 6 million people and where agriculture is the major activity.
3. Methodology
The adopted methodology (Figure 2) included: preparation of data, construction of models and production of karst spring potential map (KSPM), validation of results and evaluation of their efficiency.
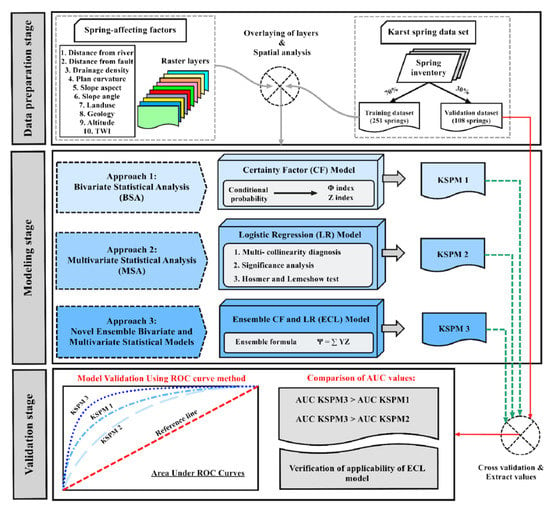
Figure 2.
Methodology flowchart used in the study.
3.1. Data Used
In order to analyze karst spring potential, springs locations and 10 spring-affecting factors were considered as dependent and independent variables, respectively. All data were obtained from the Iranian Department of Water Resources Management (IDWRM).
3.1.1. Karst Spring Inventory
A total of 359 karst springs was identified and recorded by the Iranian Department of Water Resources Management (IDWRM) in the study area, of which 251 (70%) were randomly selected for calibration/training of models and the remaining 108 (30%) for validation purpose. The distribution of training and validation karst springs is shown in Figure 1.
3.1.2. Karst Spring-Affecting Factors
As mentioned by Crozier [108], preparation of corresponding thematic data layers and the selection of factors are important components of any model. In this study, 10 karst spring-affecting factors including distance from fault, land use/land cover, geology, topographic elevation, slope angle, slope aspect, plan curvature, topographic wetness index (TWI), drainage density and distance from river were utilized for producing KSPMs.
Distance from fault
Distance from fault is among those factors that has been widely used as an important groundwater influential factor [109]. The faults were extracted from a geological map of the study area as line features in ArcGIS 10.2 and a map of ‘distance from faults’ was developed using the Euclidean distance tool and classified (Figure 3a).
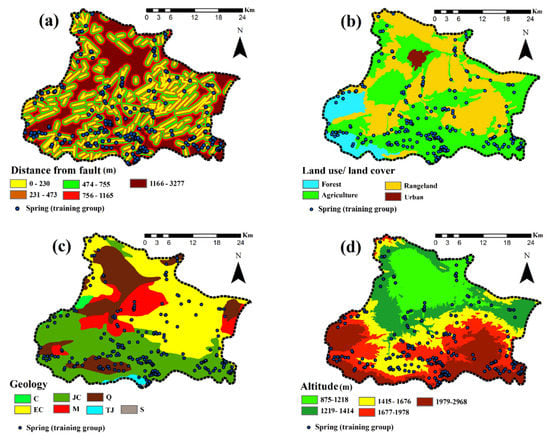
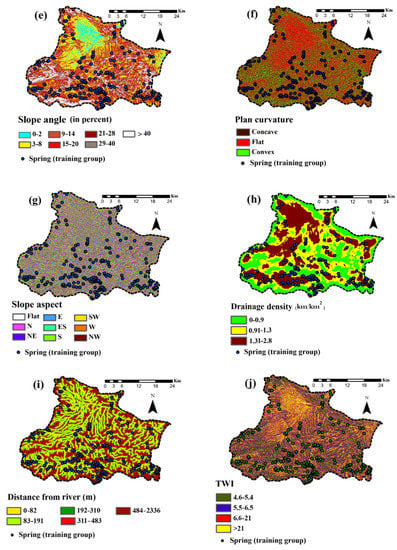
Figure 3.
Karst spring inventory: (a) distance from fault, (b) land use/land cover, (c) geology, (d) topographic elevation, (e) slope angle, (f) plan curvature, (g) slope aspect, (h) drainage density, (i) distance from river and (j) TWI.
Land use/ land cover
Geology
Since the hydraulic conductivity and porosity of soils and rocks are affected by lithological variations, groundwater occurrence is highly influenced by geology [104,111]. In this study, the geologic map of study area with seven lithological groups was extracted from 1:100,000 scale geologic map of Iran (Figure 3c, Table 1).
Topographic factors
Surface topography controls the runoff rate and direction [112,113]. Therefore, topographic elevation has been frequently used by researchers as a controlling parameter for groundwater occurrence [31,114]. The digital elevation model (DEM) map of the study area was obtained from the IDWRM and we classified it using an equal-interval classification scheme (Figure 3d). IDWRM originally produced the DEM from aerial photographs and topographical lines was obtained from the Iranian Department of Water Resources Management (IDWRM) at 20 m cell resolution. Slope angle affects the infiltration, subsurface flow and duration of overland flow [115,116]. Therefore, the groundwater recharge process is strongly controlled by slope angle [117]. According to Magesh et al. [115], due to low infiltration and high run-off in steeper slope, these areas have poor potential to groundwater accumulation. The slope angle map of study area was extracted from the DEM and classified into seven classes based on IDWRM classification (Figure 3e). Plan curvature represents the rate of slope aspect or slope gradient change. Negative and positive values of plan curvatures characterize concavity and convexity in the downslope direction, respectively. Zero curvature also represents flat areas [118]. As mentioned by Lee and Pradhan [118], concave slope probably contains more water. The plan curvature map of study area was produced from DEM in concave, flat and convex classes (Figure 3f). The slope aspect layer was derived from DEM and divided into nine classes including eight main directions (Figure 3g).
3.2. Statistical Methods
A bivariate statistical analysis (certainty factor) and a multivariate statistical analysis (logistic regression) were applied individually and as an ensemble to delineate karst spring potential. Finally, the ensemble map was compared with each individual map using the receiver operating characteristic (ROC) analysis to find if there is any improvement in combining the models.
3.2.1. Certainty Factor Model
Shortliffe and Buchanan [123] proposed and defined certainty factor (CF) as a probability function that was later modified by Heckerman [124]. Different researchers have applied this model in their studies for landslide susceptibility mapping [125] and groundwater potential mapping [26]. The formula to calculate CF is [124]:
where Pa is conditional probability of having a number of karst spring occurrence in class a, Pb is prior probability of having the total number of karst spring occurrence in the study area. The CF value for different attribute classes in each conditioning factor were calculated from their relationship to the spring occurrence. The CF values ranges from −1 to +1. A positive value of CF means that the groundwater potential is higher, while a negative value illustrates a decrease in the certainty of groundwater occurrence [126]. In order to delineate the combination of two different layers of information, which is denoted as Z, the CF values of the spring-affecting factors are pairwise combined using the integration rules as follow [127].
where CFX and CFY are CF values of two different spring-affecting factors.
The pairwise combination is carried out in different iterations until all the spring-affecting layers are added to prepare the KSPM. The final map was categorized into four classes: low, medium, high and very high [29,128].
3.2.2. Logistic Regression Model
LR aims at finding the best-fit model to express the relationship among a binary dependent variable (groundwater occurrence) and some independent variables [129]. This model is helpful to predict the absence or presence of outcome based on predictive variables (Lee 2005). The LR model is widely applied in different fields of geosciences [24,130]. However, it has some limitations to determine the weight of classes of independent variables [131]. Hosmer and Lemeshow [132] and Kleinbaum et al. [133] also explained the detailed information of this technique. The general form of logistic regression is as follows:
where Z is a linear combination function of the explanatory variables, x1, x2, …, xm are independent variables and b1, b2, …, bm are the coefficients of the logistic regression to be estimated [134]. The relationship between the occurrence and its dependency on several variables is defined as:
where P and e are the probability of spring occurrence (varying from 0 to 1) and the Neperian number, respectively [135]. In addition, Z factor was defined above Equation (4). Value of 1 means the presence of a spring, and value 0 indicates the absence of a spring [24]. After creating the KSPM by LR model, we classified it using natural break classification method. As mentioned by Hosmer and Lemeshow [132], independent variables in LR model is sensitive to co-linearity for model fitting, while more than two variables in LR model is often called ‘multi-collinearity’. Multi-collinearity refers to a linear relation among two or more variables [136]. LR model was used to do statistical analysis and determine whether there was a significant effect on spring occurrence. Tolerance (TOL) and the variance inflation factor (VIF) are significant indicators for determining multi-collinearity among the independent variables [137] that were applied (Table 2). Based on this diagnosis method, variables with TOL < 0.1 and/or VIF > 10 shall be excluded from further analysis [138]. Moreover, the overall statistic of the LR model for all 10 independent variables was assessed using χ2 value of the Hosmer–Lemeshow test, Cox and Snell R2, Nagelkerke R2 and pseudo-R2 mesaures.3.2.3. Ensemble model.

Table 2.
Indices of multi-collinearity diagnosis for independent variables used in logistic regression (LR) modelling.
Ensemble modeling is a technical process of synthesizing the results of single models into a single incorporated model for enhancing the prediction [139]. This type of modeling approach tends to overcome their individual disadvantages while keeping their individual advantages [102]. Weighted linear combination technique is proposed here as an ensemble method to combine the result of CF and LR:
where DF is distance from fault, L is land use/ land cover, G is geology, A is topographic elevation, TWI is topographic wetness index, DD is drainage density, DR is distance from river, S is slope angle, AS is slope aspect, PC is plan curvature and the subscripts ‘r’ and ‘w’ indicate ratings and weights for spring-affecting factors, respectively. Ratings are obtained from the CF model (i.e., the weights of classes of a given spring-affecting factor), whereas w was calculated based on the spatial sensitivity analysis (SSA) of LR model. The SSA allows to determine the influence of predictive variables on the model output [16,140]. In this study, this was conducted by excluding each spring-affecting factor and determining w through the relative decrease of AUC values Equation (7) [29]:
where AUCall and AUCi indicate the AUC values obtained from the LR model using all spring-affecting factors and the prediction when the ith spring-affecting factor was excluded, respectively.
3.2.3. Performance Assessment
Performance assessment is required in any predictive analysis [141]. Nampak et al. [128] also stated that there is no merit in modeling with no scientific significance; hence, validity and uncertainty of models need to be assessed. Furthermore, many researchers have validated their results using different models. Naghibi et al. [31], Pourghasemi and Beheshtirad [109] and Rahmati et al. [3] have utilized area under ROC curve (AUC) to assess the accuracy of groundwater potential maps. This method illustrates to what extent the occurrence or non-occurrence of a considered occurrence is correctly predicted [29]. In the ROC curve, false and true positive rates are plotted in X- and Y-axis, respectively. The resultant AUC value ranges from 0.5 (i.e., a random prediction) to 1 (i.e., an excellent prediction) [142].
4. Results
4.1. CF Modelling
CF values of spring-affecting factors are presented in Figure 4. As depicted in the figure, negative and positive relationships between factors and spring occurrence are well illustrated. Obviously, negative relationship exists between spring potential and distance from faults parameter. Areas with more distance from fault have lower potential to spring occurrence. In the case of geology factor, some lithologic formations including Silurian (S), Jurassic-Cretaceous (JC) and Triassic-Jurassic (TJ) had positive influence in spring occurrence with CF values of 0.94, 0.42 and 0.21, respectively.
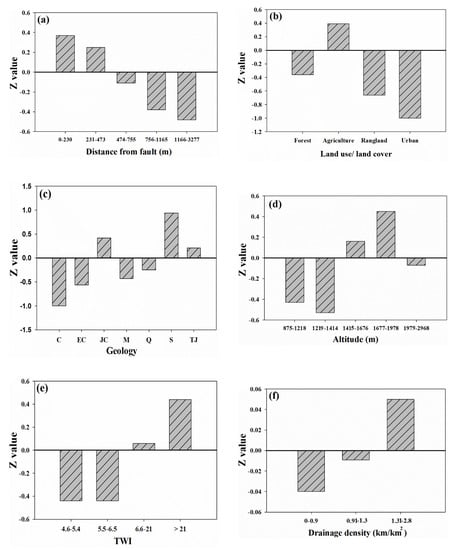
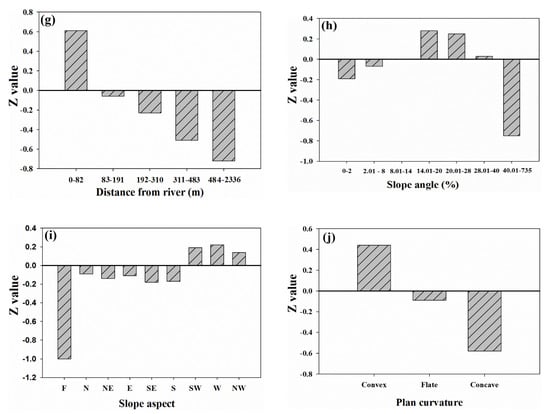
Figure 4.
Results of the certainty factors (CF) modelling per factor class.
In the case of land use/land cover, urban areas and agriculture have the least and most impact on groundwater, respectively. The impervious surface areas in urban areas tend to reduce recharge and hence groundwater availability. As the agriculture areas as a consequence factor need to high water requirement, these areas have a higher potential to groundwater recharge [47]. It was also found that there was no significant correlation between spring occurrence and topographic elevation classes. Areas with elevation ranges of 1676–1978 m and 1414–1676 m have positive influence on spring occurrence probability with CF values of 0.45 and 0.16 which indicate a good karst spring occurrence probability. In another study in this region, Rahmati et al. [44] indicated that spring occurrence probability will reduce as elevation decreases which is in agreement with the results of our study. It is noted that, groundwater is more probable to occur in areas with high TWI values because it is well apparent in Figure 4e that positive correlation exists between increasing spring occurrence and high TWI value.
Conversely, Razandi et al. [26] stated that there is not positive correlation between groundwater occurrence and TWI, which shows a higher groundwater potential over a decreasing TWI value. The reason of this difference between their results and our achievements refer to geomorphological characteristics of study areas (i.e., their study area were plain whereas our study area is a mountainous region). In areas where drainage density ranges from 1.3 to 2.8 km/km2 (CF = 1.82), groundwater potential is higher indicating that springs are more probable in areas with denser drainage density. The assessment of distance from river demonstrated that areas with lower distance from river have more potential for spring occurrence and as this distance increase, the probability to groundwater occurrence decreases. Lee et al. [143] proved these results by indicating that drainage density and distance from the river have positive and negative influence on groundwater yield. Results indicated that the areas with 8–40° slope angles have positive influences with highest value in 14–20° and 20–28° with CF values of 0.28 and 0.25. Manap et al. [21] also mentioned that flat to moderate slopes have higher groundwater probabilities.
In the case of slope aspect, only west (0.22), southwest (0.19) and northwest (0.14) have a positive influence on groundwater occurrence. It is difficult to explain this result, but it might be related to the differences of aspects in terms of vegetation, soil depth and recharge potential. Plan curvature behavior also illustrates that springs are more probable to occur in convex areas. Moghadam et al. [114] also stated that concave areas are more favorable for groundwater compared to the convex slope. Finally, according to the CF value for each influencing factor, karst spring probability map was produced and then categorized into four classes; namely low, medium, high and very high using the natural break classification method (Figure 5), as suggested by Naghibi et al. [31]. Areas with high and very high karst spring potential are seen to be near rivers and faults.
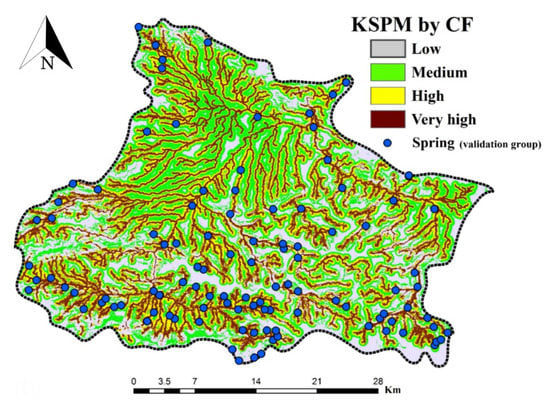
Figure 5.
Karst spring potential map produced by the CF modelling.
4.2. LR Modelling
According to results of TOL and VIF analysis, no severe multi-collinearity was found between independent variables (Table 2).
As shown in Table 3, results indicated that all applied factors have significant effects on spring occurrence (p < 0.05). Similar results can be found in many previous studies [109].

Table 3.
Coefficients of each spring-affecting factors used in logistic regression (LR) model.
Table 4 showed the overall statistic of the LR model for all 10 independent variables. The results indicated that the goodness-of-fit of the equation could be accepted because the significance of χ2 is larger than 0.05 [138]. The values of Cox and Snell R2 and Nagelkerke R2 showed that the independent variables could explain the dependent variables [138,144].

Table 4.
Overall statistics of the LR model with 10 independent variables.
Using the coefficient values obtained from the final output of the LR analysis, the LR equation was obtained, as shown in Equation (8):
where CGeology is the LR coefficient for geology factor, whereas CLand use is the LR coefficient for land use factor. All coefficients of Equation (8) were obtained from Table 3. The final generated map using LR model was then classified into low, medium, high and very high classes using the natural break classification method (Figure 6), as suggested by Naghibi et al. [31]. Areas with high and very high potential to karst springs are located in southwest to southeast of the study area.
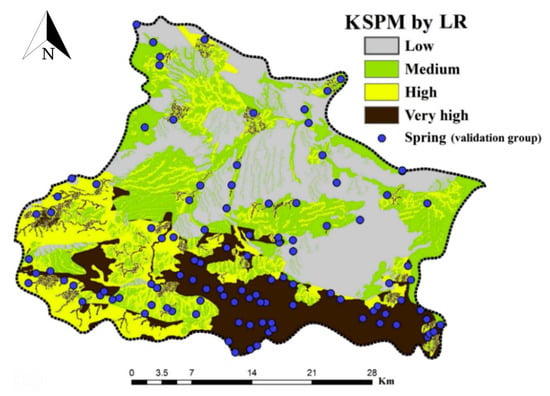
Figure 6.
Karst spring potential map produced by the LR modelling.
4.3. Ensemble Modelling
Although LR was capable to implement multivariate statistical analysis, it had some weakness in analyzing the classes of each occurrences conditioning factor. Conversely, the CF model could evaluate the influence of classes of each spring-affecting factor on an occurrence. However, the relationship between karst spring locations and spring-affecting factors was mostly neglected by LR model. As a result, it can be clearly seen that CF and LR models had some weakness when applied individually. The generated map of ensemble CF and LR (ECL) model was prepared and then classified into low, moderate, high and very high classes using the natural break classification method (Figure 7), as suggested by Naghibi et al. [31].
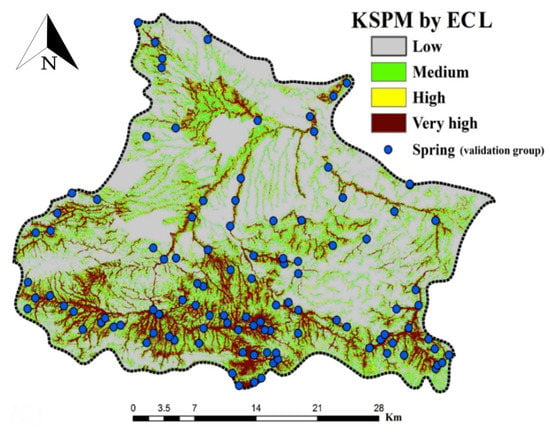
Figure 7.
Karst spring potential map produced by the generated map of ensemble CF and LR (ECL) modelling.
4.4. Validation of Generated KSPMs
The ensemble map was compared to each individual (i.e., CF and LR) map using ROC curve method to find if there was any improvements in combining the individual models. The generated SPMs were overlaid with 30% of spring locations for this phase, which has not been used for model application. According to Figure 8, validation outcomes indicated that LR model could satisfactorily generate groundwater potential map (AUC = 78.4%) and performed better than CF (AUC=66.7%). Moreover, the ECL model had the best performance with an AUC value of 84.7%. It was shown that the ensemble method allowed for a better prediction of groundwater potentiality.
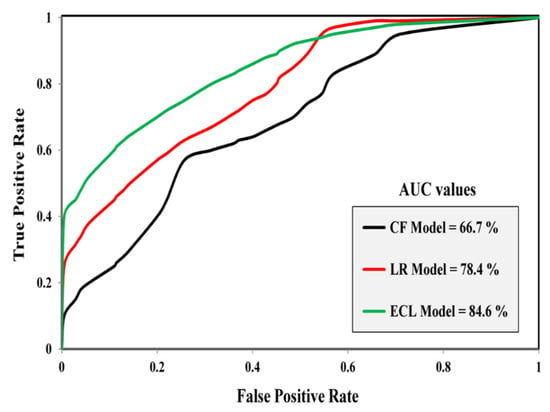
Figure 8.
Receiver operating characteristic (ROC) curves for the karst spring potential maps.
5. Discussion
5.1. Spatial Modeling of Karst Spring Potential
Although several studies have been conducted on construction of karst spring potential maps using statistical models, there are different drawbacks about them, especially defining strict assumptions prior to study. As stated by Dreiseitl and Ohno-Machado [145] and Ozdemir [146], the LR model is usually flexible (especially when it includes only the original covariates) and may be generally desirable. On the other hand, the weak point of bivariate statistical methods such as CF is the neglect of relationship between the groundwater springs and independent variables as observed in this study (i.e., it cannot determine the weight of independent variables). In other word, the CF model just determines the weight of classes of independent variables. Therefore, to overcome these shortcomings, we developed a GIS-based ensemble model that can link the strengths of LR and CF together.
The statistical analysis of LR (Table 3) demonstrated a high contribution of slope aspect (southwest), geology (Cretaceous, Silurian and Jurassic-Cretaceous), land use/land cover (forest) to the modelling process. Prior studies have noted the importance of slope aspect effects on sunshine, air temperature, soil transformation and soil moisture content [147,148]. According to the literature, structural and lithological variations often lead to differences in the permeability and hydraulic properties [8,149,150]. In the case of land use/land cover, it usually influences infiltration and recharge rates as well as the relationship between surface water and groundwater [151]. This is also in agreement with earlier reports, which showed that there is a strong relationship between land use/land cover factor and groundwater recharge [152,153].
5.2. Performance of Ensemble and Individual Models
In Section 4.4, models’ results were analyzed and validated using the validation dataset and the ROC curve method. The results of validation revealed differences between all three approaches, namely including CF (i.e., bivariate statistical model), LR (i.e., multivariate statistical model) and their ensemble.
It should be emphasized that the ensemble model (ECL) provides the best simulation with a good accuracy. This result showed that the accuracy of the prepared KSPM was improved (6.3–17.9%) with the use of the ensemble of bivariate certainty factor and multivariate logistic regression. Therefore, the ensembling process leads to successfully overcome the limitations of LR and CF models. In fact, results shown in this study highlight a remarkable decrease of error through the ensemble approach. This result is in agreement with Arabameri et al. [154] in which the ensemble of LR with evidential belief function (EBF) model can extend an efficient model to reinforce the accuracy of spatial predictions. According to results of this study, the aggregation of multiple prediction of the same variable may lead to better performance, more exact learning and generalization than using a single model prediction. The findings of the current study are consistent with that of Naghibi et al. [30] who found that frequency ratio data mining ensemble model had the best performance among all the single models for groundwater potential mapping. Study in Razandi et al. [26] also compared the performance of different data-mining models and stated that frequency ration (FR) and weight-of-evidence (WOE) could perform better than CF model for groundwater potential mapping in Varamin plain, Iran. This is in line with our finding that the CF model is incapable of analyzing the relation between karst groundwater potential and geo-environmental factors.
6. Conclusions
Springs, as groundwater resources, are important for many sectors, such as domestic consumption and agriculture in arid and semi-arid areas of the world. Sometimes, several families or villages depend heavily on occurrence of a spring; therefore, their spatial modeling is necessary. We designed a new ensemble approach called ECL to deal with this issue. In conclusion, the novel ensemble model gives better predictive performance than could be obtained from any of the constituent models. Therefore, the strength of the proposed methodology is to improve model accuracy by using this novel ensembling technique and to efficiently produce a KSPM for sustainable water recourses management programs. Decision makers and water resources planners can use the proposed approach as an efficient tool to assess the karst spring potential, to establish relationship between karst springs and geo-environmental setting, and to plan and implement effective water resources management in drought condition. Future studies on the current topic are therefore recommended.
Author Contributions
V.-H.N., O.R., F.F., S.S., N.A.-A., H.S., A.S., K.G., H.N. and B.B.A. contributed equally to the work. O.R., F.F. and S.S. collected field data and conducted the groundwater spring potential in karst aquifer and analysis. O.R., F.F., S.S., N.A.-A., H.S., and K.G. wrote the manuscript. V.-H.N., N.A.-A., A.S., K.G., H.N. and B.B.A. provided critical comments in planning this paper and edited the manuscript. All the authors discussed the results and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wada, Y.; Van Beek, L.; Bierkens, M.F. Nonsustainable groundwater sustaining irrigation: A global assessment. Water Resour. Res. 2012, 48, 1–18. [Google Scholar] [CrossRef]
- Gorelick, S.M.; Zheng, C. Global change and the groundwater management challenge. Water Resour. Res. 2015, 51, 3031–3051. [Google Scholar] [CrossRef]
- Rahmati, O.; Samani, A.N.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at kurdistan region of iran using analytic hierarchy process and gis. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C. Gis-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [PubMed]
- White, W.B.; Herman, E.; Rutigliano, M.; Herman, J.; Vesper, D.; Engel, S. Karst groundwater contamination and public health. Leesburg VA Karst Waters Inst. Spec. Publ. 2016, 19, 1–347. [Google Scholar]
- Zhang, L.; Qin, X.; Tang, J.; Liu, W.; Yang, H. Review of arsenic geochemical characteristics and its significance on arsenic pollution studies in karst groundwater, southwest china. Appl. Geochem. 2017, 77, 80–88. [Google Scholar] [CrossRef]
- Yuan, J.; Xu, F.; Deng, G.; Tang, Y. Using stable isotopes and major ions to identify hydrogeochemical characteristics of karst groundwater in xide country, sichuan province. Carbonates Evaporites 2018, 33, 223–234. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Papadopoulou-Vrynioti, K.; Bathrellos, G.D.; Skilodimou, H.D.; Kaviris, G.; Makropoulos, K. Karst collapse susceptibility mapping considering peak ground acceleration in a rapidly growing urban area. Eng. Geol. 2013, 158, 77–88. [Google Scholar] [CrossRef]
- Ebrahimi, O.; Ahmadi, M.; Shahabi, H.; Asgari, S. Evaluation of karst features using principal component analysis (pca): A case from zarneh and kergan, western iran. Carbonates Evaporites 2018, 33, 625–635. [Google Scholar] [CrossRef]
- Andreo, B. Introductory Editorial: Advances in Karst Hydrogeology; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cuchí, J.A.; Chinarro, D.; Villarroel, J.L. Linear system techniques applied to the fuenmayor karst spring, huesca (spain). Environ. Earth Sci. 2014, 71, 1049–1060. [Google Scholar] [CrossRef]
- Fleury, P.; Plagnes, V.; Bakalowicz, M. Modelling of the functioning of karst aquifers with a reservoir model: Application to fontaine de vaucluse (south of france). J. Hydrol. 2007, 345, 38–49. [Google Scholar] [CrossRef]
- Chebud, Y.A.; Melesse, A.M. Numerical modeling of the groundwater flow system of the gumera sub-basin in lake tana basin, ethiopia. Hydrol. Process. Int. J. 2009, 23, 3694–3704. [Google Scholar] [CrossRef]
- Kuniansky, E.L.; Weary, D.J.; Kaufmann, J.E. The current status of mapping karst areas and availability of public sinkhole-risk resources in karst terrains of the united states. Hydrogeol. J. 2016, 24, 613–624. [Google Scholar] [CrossRef]
- Oh, H.-J.; Kim, Y.-S.; Choi, J.-K.; Park, E.; Lee, S. Gis mapping of regional probabilistic groundwater potential in the area of pohang city, korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R. A comparative assessment between three machine learning models and their performance comparison by bivariate and multivariate statistical methods in groundwater potential mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Chen, Z.; Auler, A.S.; Bakalowicz, M.; Drew, D.; Griger, F.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Richts, A.; Stevanovic, Z. The world karst aquifer mapping project: Concept, mapping procedure and map of europe. Hydrogeol. J. 2017, 25, 771–785. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the mt. Modino area (northern apennines, italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Jha, M.K.; Chowdary, V.; Chowdhury, A. Groundwater assessment in salboni block, west bengal (india) using remote sensing, geographical information system and multi-criteria decision analysis techniques. Hydrogeol. J. 2010, 18, 1713–1728. [Google Scholar] [CrossRef]
- Manap, M.A.; Nampak, H.; Pradhan, B.; Lee, S.; Sulaiman, W.N.A.; Ramli, M.F. Application of probabilistic-based frequency ratio model in groundwater potential mapping using remote sensing data and gis. Arab. J. Geosci. 2014, 7, 711–724. [Google Scholar] [CrossRef]
- Sahoo, S.; Munusamy, S.B.; Dhar, A.; Kar, A.; Ram, P. Appraising the accuracy of multi-class frequency ratio and weights of evidence method for delineation of regional groundwater potential zones in canal command system. Water Resour. Manag. 2017, 31, 4399–4413. [Google Scholar] [CrossRef]
- Ghorbani Nejad, S.; Falah, F.; Daneshfar, M.; Haghizadeh, A.; Rahmati, O. Delineation of groundwater potential zones using remote sensing and gis-based data-driven models. Geocarto Int. 2017, 32, 167–187. [Google Scholar] [CrossRef]
- Ozdemir, A. Using a binary logistic regression method and gis for evaluating and mapping the groundwater spring potential in the sultan mountains (aksehir, turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Pourtaghi, Z.S.; Pourghasemi, H.R. Gis-based groundwater spring potential assessment and mapping in the birjand township, southern khorasan province, iran. Hydrogeol. J. 2014, 22, 643–662. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using gis. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Fenta, A.A.; Kifle, A.; Gebreyohannes, T.; Hailu, G. Spatial analysis of groundwater potential using remote sensing and gis-based multi-criteria evaluation in raya valley, northern ethiopia. Hydrogeol. J. 2015, 23, 195–206. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Rezaei, A. Groundwater qanat potential mapping using frequency ratio and shannon’s entropy models in the moghan watershed, iran. Earth Sci. Inform. 2015, 8, 171–186. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of gis-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at mehran region, iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of support vector machine, random forest, and genetic algorithm optimized random forest models in groundwater potential mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. Gis-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Anbazhagan, S.; Jothibasu, A. Geoinformatics in groundwater potential mapping and sustainable development: A case study from southern india. Hydrol. Sci. J. 2016, 61, 1109–1123. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Jebur, M.N.; Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in west sumatera province, indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Jebur, M.N.; El-Harbi, H.M. Landslide susceptibility mapping using ensemble bivariate and multivariate statistical models in fayfa area, saudi arabia. Environ. Earth Sci. 2015, 73, 3745–3761. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (wi) and adaptive neuro-fuzzy inference system (anfis) model at alborz mountains (iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Bui, D.T.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. Gis-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with adaboost, bagging, and multiboost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar]
- Mojaddadi, H.; Pradhan, B.; Nampak, H.; Ahmad, N.; Ghazali, A.H. Ensemble machine-learning-based geospatial approach for flood risk assessment using multi-sensor remote-sensing data and gis. Geomat. Nat. Hazards Risk 2017, 8, 1080–1102. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Bin Ahmad, B. A hybrid computational intelligence approach to groundwater spring potential mapping. Water 2019, 11, 2013. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and uneec methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat. Resour. Res. 2019, 28, 1239–1258. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping groundwater potential using a novel hybrid intelligence approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater spring potential mapping using artificial intelligence approach based on kernel logistic regression, random forest, and alternating decision tree models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2019, 27, 211–224. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (china) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A comparative assessment of flood susceptibility modeling using multi-criteria decision-making analysis and machine learning methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S. Novel hybrid evolutionary algorithms for spatial prediction of floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S. Flood detection and susceptibility mapping using sentinel-1 remote sensing data and a machine learning approach: Hybrid intelligence of bagging ensemble based on k-nearest neighbor classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Khosravi, K.; Melesse, A.M.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hong, H. Flood susceptibility mapping at ningdu catchment, china using bivariate and data mining techniques. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 419–434. [Google Scholar]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.; Panahi, M.; Hong, H. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in cameron highlands, malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, jiangxi province, china. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Ahmad, B.B.; Quoc, N.K.; Lee, S. Landslide susceptibility assessment by novel hybrid machine learning algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Tran, H.T.; Le, T.M.; Van Phong, T.; Khoi, D.K.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modelling using rotation forest ensemble and different base classifiers. Geocarto Int. 2019, 14, 1–25. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using gis. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Hong, H.; Shahabi, H.; Shirzadi, A.; Chen, W.; Chapi, K.; Ahmad, B.B.; Roodposhti, M.S.; Hesar, A.Y.; Tian, Y.; Bui, D.T. Landslide susceptibility assessment at the wuning area, china: A comparison between multi-criteria decision making, bivariate statistical and machine learning methods. Nat. Hazards 2019, 96, 173–212. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, M.; Shahabi, H.; Hagenauer, J. Big data in geohazard; pattern mining and large scale analysis of landslides in iran. Earth Sci. Inform. 2019, 12, 1–17. [Google Scholar] [CrossRef]
- Nguyen, V.V.; Pham, B.T.; Vu, B.T.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.N.; Kumar, R.; Chatterjee, J.M. Hybrid machine learning approaches for landslide susceptibility modeling. Forests 2019, 10, 157. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Tuyen, T.T.; Shirzadi, A.; Pham, B.T.; Shahabi, H.; Omidvar, E.; Amini, A.; Entezami, H.; Prakash, I.; Phong, T.V. Development of a novel hybrid intelligence approach for landslide spatial prediction. Appl. Sci. 2019, 9, 2824. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.J.; Thai Pham, B.; Dou, J.; Talebpour Asl, D.; Bin Ahmad, B. New ensemble models for shallow landslide susceptibility modeling in a semi-arid watershed. Forests 2019, 10, 743. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Shahabi, H.; Shirzadi, A.; Khosravi, K.; Chai, H.; Zhang, S.; Zhang, L.; Ma, J.; Chen, Y. Spatial prediction of landslide susceptibility by combining evidential belief function, logistic regression and logistic model tree. Geocarto Int. 2019, 34, 1177–1201. [Google Scholar] [CrossRef]
- Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. Catena 2019, 178, 172–188. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahamd, B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel gis based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.; Zhang, T.; Zhang, L.; Chai, H. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2018, 34, 1427–1457. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.-X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (china). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy shannon entropy: A hybrid gis-based landslide susceptibility mapping method. Entropy 2016, 18, 343. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and gis-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central zab basin, iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central zab basin, iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using gis-based statistical models and remote sensing data in tropical environment. Sci. Rep. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmad, B.; Khezri, S. Evaluation and comparison of bivariate and multivariate statistical methods for landslide susceptibility mapping (case study: Zab basin). Arab. J. Geosci. 2013, 6, 3885–3907. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef]
- Rahmati, O.; Samadi, M.; Shahabi, H.; Azareh, A.; Rafiei-Sardooi, E.; Alilou, H.; Melesse, A.M.; Pradhan, B.; Chapi, K.; Shirzadi, A. Swpt: An automated gis-based tool for prioritization of sub-watersheds based on morphometric and topo-hydrological factors. Geosci. Front. 2019, 10, 2167–2175. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Omidavr, E.; Pham, B.T.; Talebpour Asl, D.; Khaledian, H.; Pradhan, B.; Panahi, M. A novel ensemble artificial intelligence approach for gully erosion mapping in a semi-arid watershed (iran). Sensors 2019, 19, 2444. [Google Scholar] [CrossRef]
- Rahmati, O.; Panahi, M.; Ghiasi, S.S.; Deo, R.C.; Tiefenbacher, J.P.; Pradhan, B.; Jahani, A.; Goshtasb, H.; Kornejady, A.; Shahabi, H. Hybridized neural fuzzy ensembles for dust source modeling and prediction. Atmos. Environ. 2020, 224, 117320. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Taheri, K.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Gutiérrez, F.; Khosravi, K. Sinkhole susceptibility mapping: A comparison between bayes-based machine learning algorithms. Land Degrad. Dev. 2019, 30, 730–745. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Safarrad, T.; Shahabi, H. Drought sensitivity mapping using two one-class support vector machine algorithms. Atmos. Res. 2017, 193, 73–82. [Google Scholar] [CrossRef]
- Choubin, B.; Soleimani, F.; Pirnia, A.; Sajedi-Hosseini, F.; Alilou, H.; Rahmati, O.; Melesse, A.M.; Singh, V.P.; Shahabi, H. Effects of drought on vegetative cover changes: Investigating spatiotemporal patterns. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 213–222. [Google Scholar]
- Lee, S.; Panahi, M.; Pourghasemi, H.R.; Shahabi, H.; Alizadeh, M.; Shirzadi, A.; Khosravi, K.; Melesse, A.M.; Yekrangnia, M.; Rezaie, F. Sevucas: A novel gis-based machine learning software for seismic vulnerability assessment. Appl. Sci. 2019, 9, 3495. [Google Scholar] [CrossRef]
- Alizadeh, M.; Alizadeh, E.; Asadollahpour Kotenaee, S.; Shahabi, H.; Beiranvand Pour, A.; Panahi, M.; Bin Ahmad, B.; Saro, L. Social vulnerability assessment using artificial neural network (ann) model for earthquake hazard in tabriz city, iran. Sustainability 2018, 10, 3376. [Google Scholar] [CrossRef]
- Araújo, M.B.; New, M. Ensemble forecasting of species distributions. Trends Ecol. Evol. 2007, 22, 42–47. [Google Scholar] [CrossRef]
- Grenouillet, G.; Buisson, L.; Casajus, N.; Lek, S. Ensemble modelling of species distribution: The effects of geographical and environmental ranges. Ecography 2011, 34, 9–17. [Google Scholar] [CrossRef]
- Breiner, F.T.; Nobis, M.P.; Bergamini, A.; Guisan, A. Optimizing ensembles of small models for predicting the distribution of species with few occurrences. Methods Ecol. Evol. 2018, 9, 802–808. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Amini, A.; Shahabi, H.; Al-Ansari, N.; Hamidi, S.; Singh, S.K.; Thai Pham, B.; Ahmad, B.B.; Ghazvinei, P.T. A hybrid intelligence approach to enhance the prediction accuracy of local scour depth at complex bridge piers. Sustainability 2020, 12, 1063. [Google Scholar]
- Chen, W.; Zhao, X.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Wang, X.; Ahmad, B.B. Evaluating the usage of tree-based ensemble methods in groundwater spring potential mapping. J. Hydrol. 2020, 583, 124602. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. Groundwater potential mapping at northeastern wasit and missan governorates, iraq using a data-driven weights of evidence technique in framework of gis. Environ. Earth Sci. 2015, 74, 1109–1124. [Google Scholar] [CrossRef]
- Shamsi, A.; Kazemi, G. A review of research dealing with isotope hydrology in iran and the first iranian meteoric water line. Geopersia 2014, 4, 73–86. [Google Scholar]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Nobre, A.D.; Melesse, A.M. Development of an automated gis tool for reproducing the hand terrain model. Environ. Model. Softw. 2018, 102, 1–12. [Google Scholar] [CrossRef]
- Vali-Khodjeini, A. Human impacts on groundwater resources in iran. IAHS Publ. Ser. Proc. Rep. Intern Assoc Hydrol. Sci. 1995, 230, 141–146. [Google Scholar]
- Crozier, M.J. Landslides: Causes, Consequences & Environment; Taylor & Francis: Abingdon-on-Thames, UK, 1986. [Google Scholar]
- Pourghasemi, H.R.; Beheshtirad, M. Assessment of a data-driven evidential belief function model and gis for groundwater potential mapping in the koohrang watershed, iran. Geocarto Int. 2015, 30, 662–685. [Google Scholar] [CrossRef]
- Gebere, S.B.; Alamirew, T.; Merkel, B.J.; Melesse, A.M. Land use and land cover change impact on groundwater recharge: The case of lake haramaya watershed, ethiopia. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Springer: Berlin/Heidelberg, Germany, 2016; pp. 93–110. [Google Scholar]
- Yalcin, A. Gis-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in ardesen (turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Dai, F.; Xiao, J.; Tan, X.; Yuan, R. Landslide hazard mapping using gis and weight of evidence model in qingshui river watershed of 2008 wenchuan earthquake struck region. J. Earth Sci. 2012, 23, 97–120. [Google Scholar] [CrossRef]
- Moghaddam, D.D.; Rezaei, M.; Pourghasemi, H.; Pourtaghie, Z.; Pradhan, B. Groundwater spring potential mapping using bivariate statistical model and gis in the taleghan watershed, iran. Arab. J. Geosci. 2015, 8, 913–929. [Google Scholar] [CrossRef]
- Magesh, N.; Chandrasekar, N.; Soundranayagam, J.P. Delineation of groundwater potential zones in theni district, tamil nadu, using remote sensing, gis and mif techniques. Geosci. Front. 2012, 3, 189–196. [Google Scholar] [CrossRef]
- Selvam, S.; Magesh, N.; Sivasubramanian, P.; Soundranayagam, J.P.; Manimaran, G.; Seshunarayana, T. Deciphering of groundwater potential zones in tuticorin, tamil nadu, using remote sensing and gis techniques. J. Geol. Soc. India 2014, 84, 597–608. [Google Scholar] [CrossRef]
- Prasad, J. A ground water brochure of jhansi district. Uttar Pradesh 2008, 8, 1–19. [Google Scholar]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the turbolo river catchment (northern calabria, italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Rodhe, A.; Seibert, J. Wetland occurrence in relation to topography: A test of topographic indices as moisture indicators. Agric. For. Meteorol. 1999, 98, 325–340. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Nagarajan, R.; Roy, A.; Kumar, R.V.; Mukherjee, A.; Khire, M. Landslide hazard susceptibility mapping based on terrain and climatic factors for tropical monsoon regions. Bull. Eng. Geol. Environ. 2000, 58, 275–287. [Google Scholar] [CrossRef]
- Shekhar, S.; Pandey, A.C. Delineation of groundwater potential zone in hard rock terrain of india using remote sensing, geographical information system (gis) and analytic hierarchy process (ahp) techniques. Geocarto Int. 2015, 30, 402–421. [Google Scholar] [CrossRef]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Heckerman, D. Probabilistic Interpretation of Mycin’s Certainty Factors w Pracy Kanal ln, Lemmers jf (Eds): Uncertainty in Artificial Intelligence; Elsevier: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 1986. [Google Scholar]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in nepal himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Mohammadi, M.; Moradi, H.R. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at haraz watershed, iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Binaghi, E.; Luzi, L.; Madella, P.; Pergalani, F.; Rampini, A. Slope instability zonation: A comparison between certainty factor and fuzzy dempster–shafer approaches. Nat. Hazards 1998, 17, 77–97. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of gis based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Ohlmacher, G.C.; Davis, J.C. Using multiple logistic regression and gis technology to predict landslide hazard in northeast kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Regmi, A.D.; Devkota, K.C.; Yoshida, K.; Pradhan, B.; Pourghasemi, H.R.; Kumamoto, T.; Akgun, A. Application of frequency ratio, statistical index, and weights-of-evidence models and their comparison in landslide susceptibility mapping in central nepal himalaya. Arab. J. Geosci. 2014, 7, 725–742. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (dt) and a novel ensemble bivariate and multivariate statistical models in gis. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]
- Hosmer, D.; Lemeshow, S. Applied Logistic Regression Second Edition Wiley; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Kleinbaum, D.G.; Dietz, K.; Gail, M.; Klein, M.; Klein, M. Logistic Regression; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Lee, S.; Sambath, T. Landslide susceptibility mapping in the damrei romel area, cambodia using frequency ratio and logistic regression models. Environ. Geol. 2006, 50, 847–855. [Google Scholar] [CrossRef]
- Dai, F.; Lee, C. Landslide characteristics and slope instability modeling using gis, lantau island, hong kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Menard, S. Applied Logistic Regression Analysis; Sage: Newcastle Upon Tyne, UK, 2002; Volume 106. [Google Scholar]
- Bai, S.-B.; Wang, J.; Lü, G.-N.; Zhou, P.-G.; Hou, S.-S.; Xu, S.-N. Gis-based logistic regression for landslide susceptibility mapping of the zhongxian segment in the three gorges area, china. Geomorphology 2010, 115, 23–31. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Park, N.-W. Using maximum entropy modeling for landslide susceptibility mapping with multiple geoenvironmental data sets. Environ. Earth Sci. 2015, 73, 937–949. [Google Scholar] [CrossRef]
- Mancini, F.; Ceppi, C.; Ritrovato, G. GIS and statistical analysis for landslide susceptibility mapping in the daunia area (Italy). Nat. Hazards Earth Syst. Sci. 2010, 10, 1851–1864. [Google Scholar] [CrossRef]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern apennines (reggio emilia province, Italy). Landslides 2010, 7, 433–444. [Google Scholar] [CrossRef]
- Lee, S.; Oh, H.-J. Ensemble-based landslide susceptibility maps in jinbu area, korea. In Terrigenous Mass Movements; Springer: Berlin/Heidelberg, Germany, 2012; pp. 193–220. [Google Scholar]
- Mathew, J.; Jha, V.; Rawat, G. Application of binary logistic regression analysis and its validation for landslide susceptibility mapping in part of garhwal himalaya, india. Int. J. Remote Sens. 2007, 28, 2257–2275. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Ozdemir, A. Gis-based groundwater spring potential mapping in the sultan mountains (konya, turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Bi, H.; Zhang, J.; Zhu, J.; Lin, L.; Guo, C.; Ren, Y.; Yun, L.; Ma, N. Spatial dynamics of soil moisture in a complex terrain in the semi-arid loess plateau region, china 1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 1121–1131. [Google Scholar] [CrossRef]
- Bartholomeus, R.P.; Witte, J.P.M.; Runhaar, J. Drought stress and vegetation characteristics on sites with different slopes and orientations. Ecohydrology 2012, 5, 808–818. [Google Scholar] [CrossRef]
- Worthington, S.R. Diagnostic hydrogeologic characteristics of a karst aquifer (kentucky, USA). Hydrogeol. J. 2009, 17, 1665. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Kazakis, N.; Kougias, I.; Patsialis, T. Assessment of flood hazard areas at a regional scale using an index-based approach and analytical hierarchy process: Application in rhodope–evros region, greece. Sci. Total Environ. 2015, 538, 555–563. [Google Scholar] [CrossRef]
- Ghayoumian, J.; Saravi, M.M.; Feiznia, S.; Nouri, B.; Malekian, A. Application of gis techniques to determine areas most suitable for artificial groundwater recharge in a coastal aquifer in southern iran. J. Asian Earth Sci. 2007, 30, 364–374. [Google Scholar] [CrossRef]
- Ehlers, L.; Herrmann, F.; Blaschek, M.; Duttmann, R.; Wendland, F. Sensitivity of mgrowa-simulated groundwater recharge to changes in soil and land use parameters in a mediterranean environment and conclusions in view of ensemble-based climate impact simulations. Sci. Total Environ. 2016, 543, 937–951. [Google Scholar] [CrossRef] [PubMed]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Yamani, M.; Pourghasemi, H.R.; Lombardo, L. Spatial modelling of gully erosion using evidential belief function, logistic regression, and a new ensemble of evidential belief function–logistic regression algorithm. Land Degrad. Dev. 2018, 29, 4035–4049. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).