Scour around Piers under Waves: Current Status of Research and Its Future Prospect
Abstract
1. Introduction
1.1. Concept of Scour
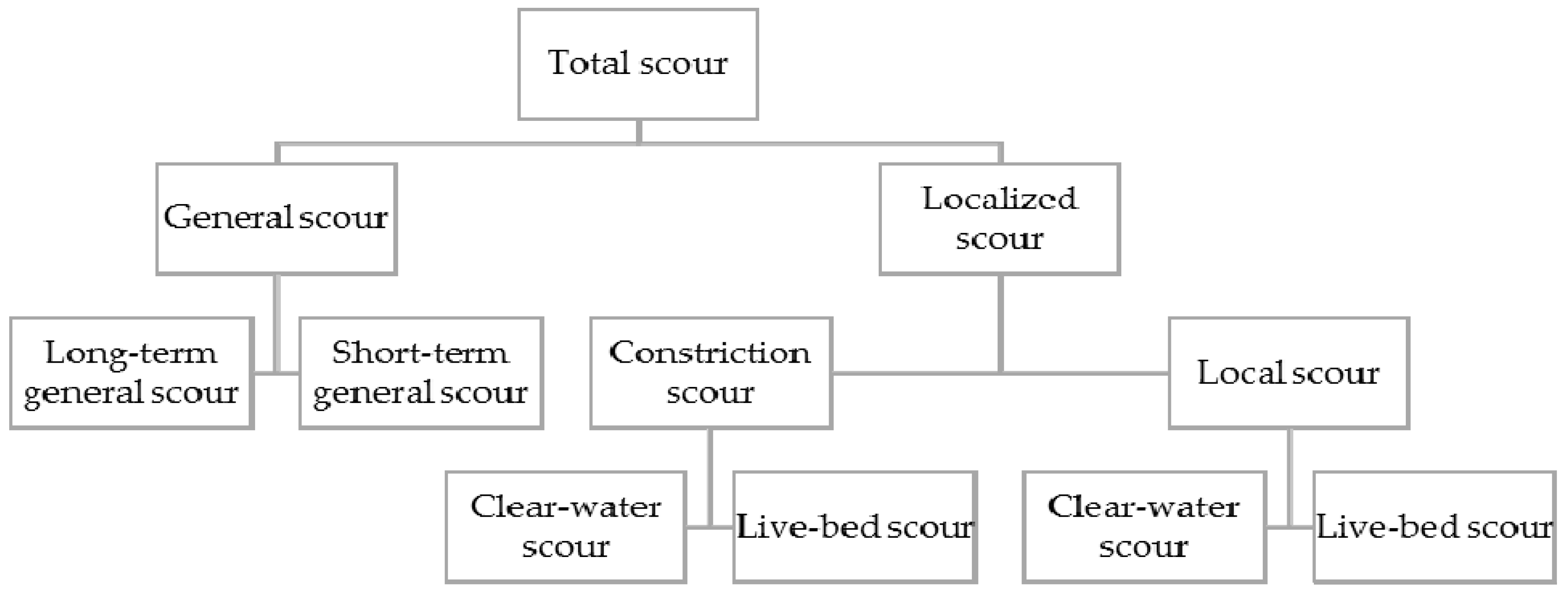
1.2. Types of Scour
1.2.1. General Scour
1.2.2. Localized Scour
1.2.3. Constriction Scour
1.2.4. Local Scour
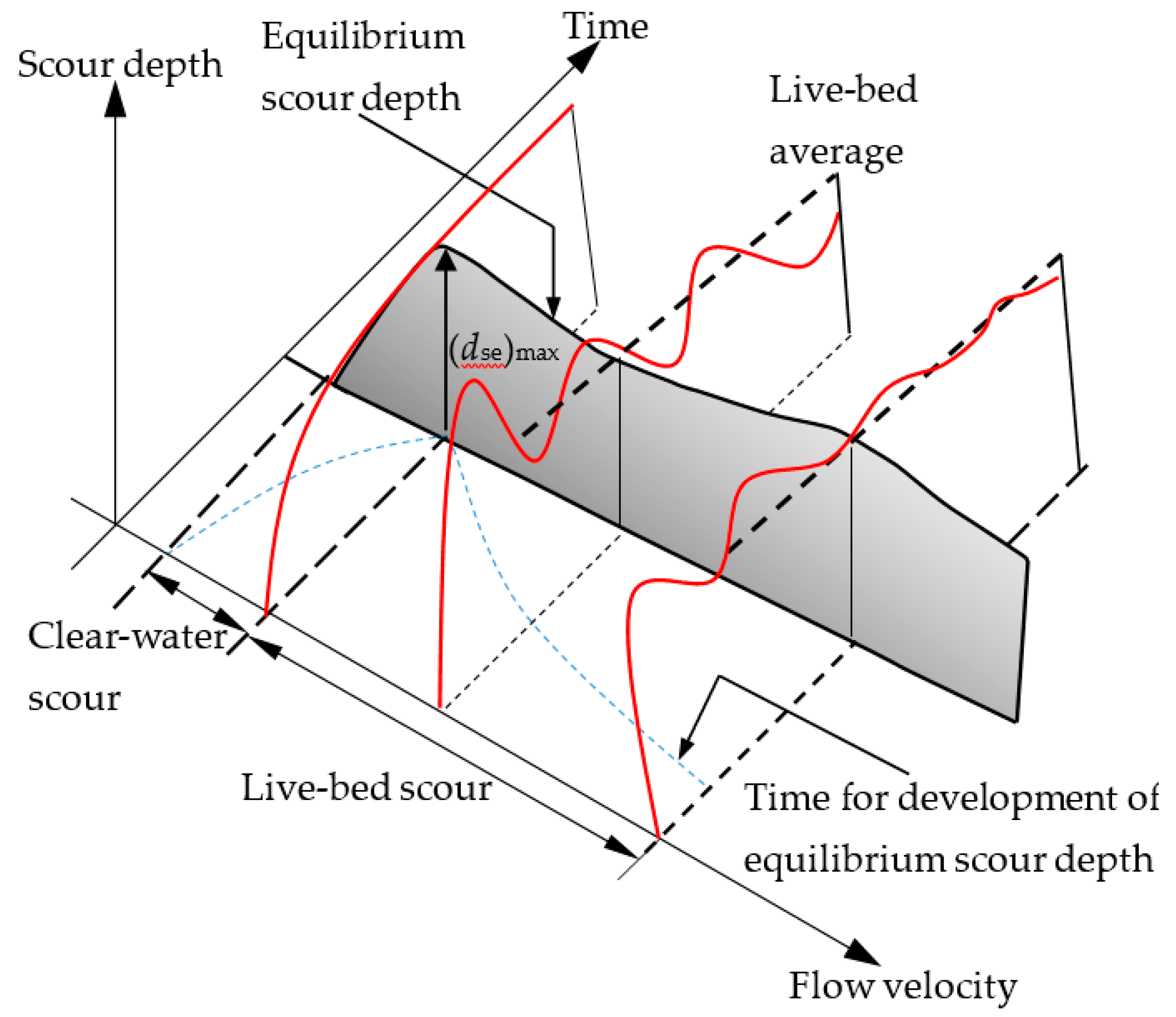
1.2.5. Clear-Water Scour and Live-Bed Scour
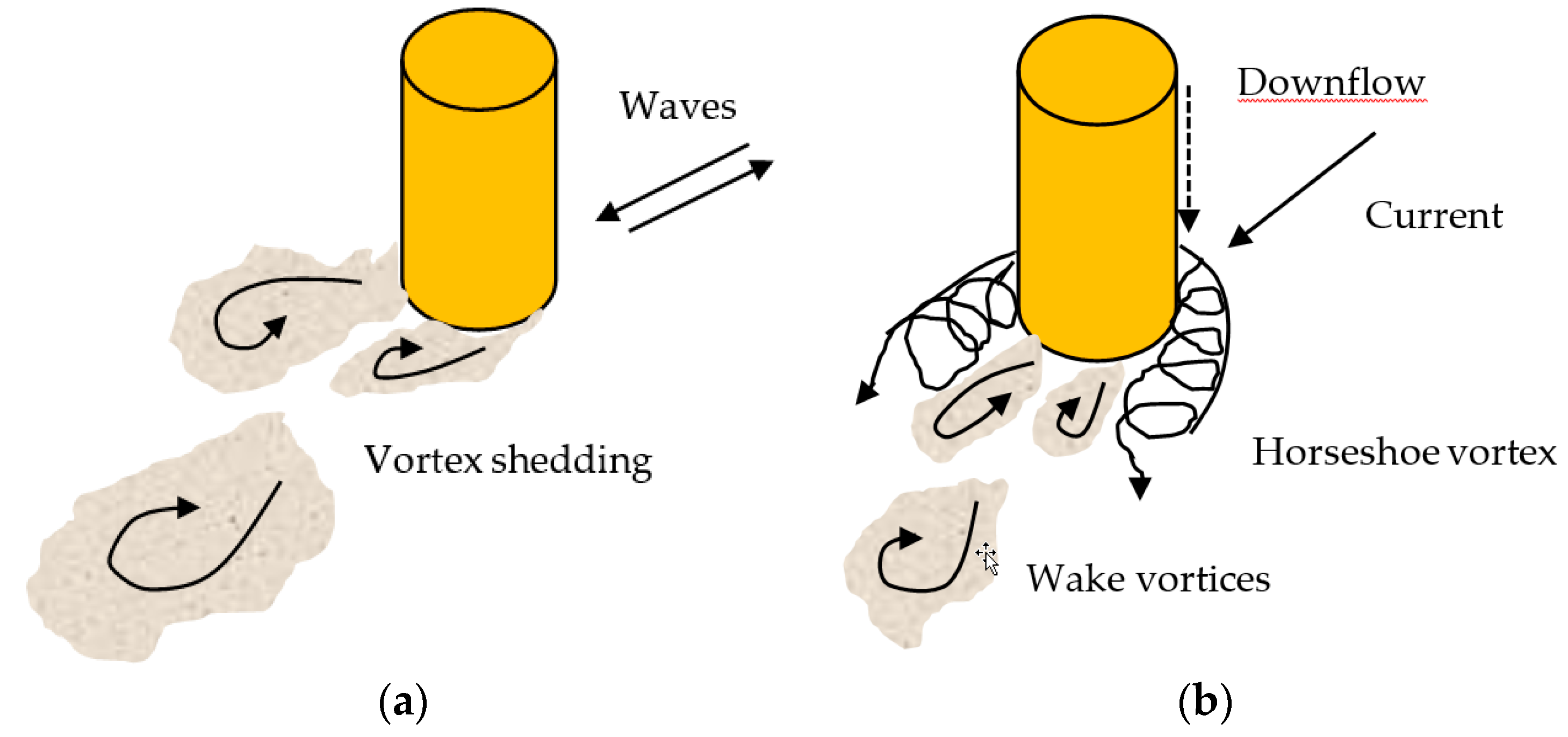
2. Scour under Waves
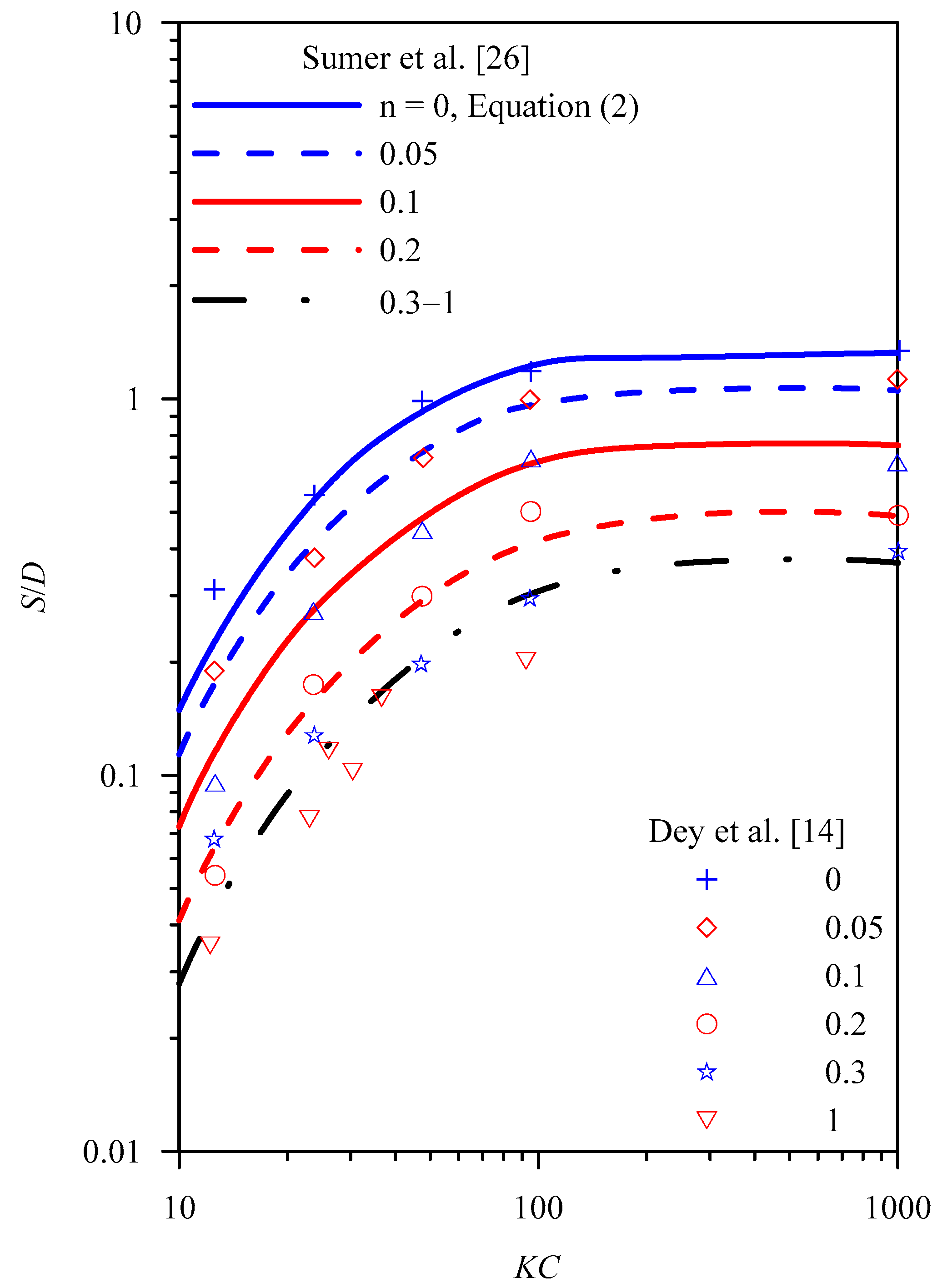
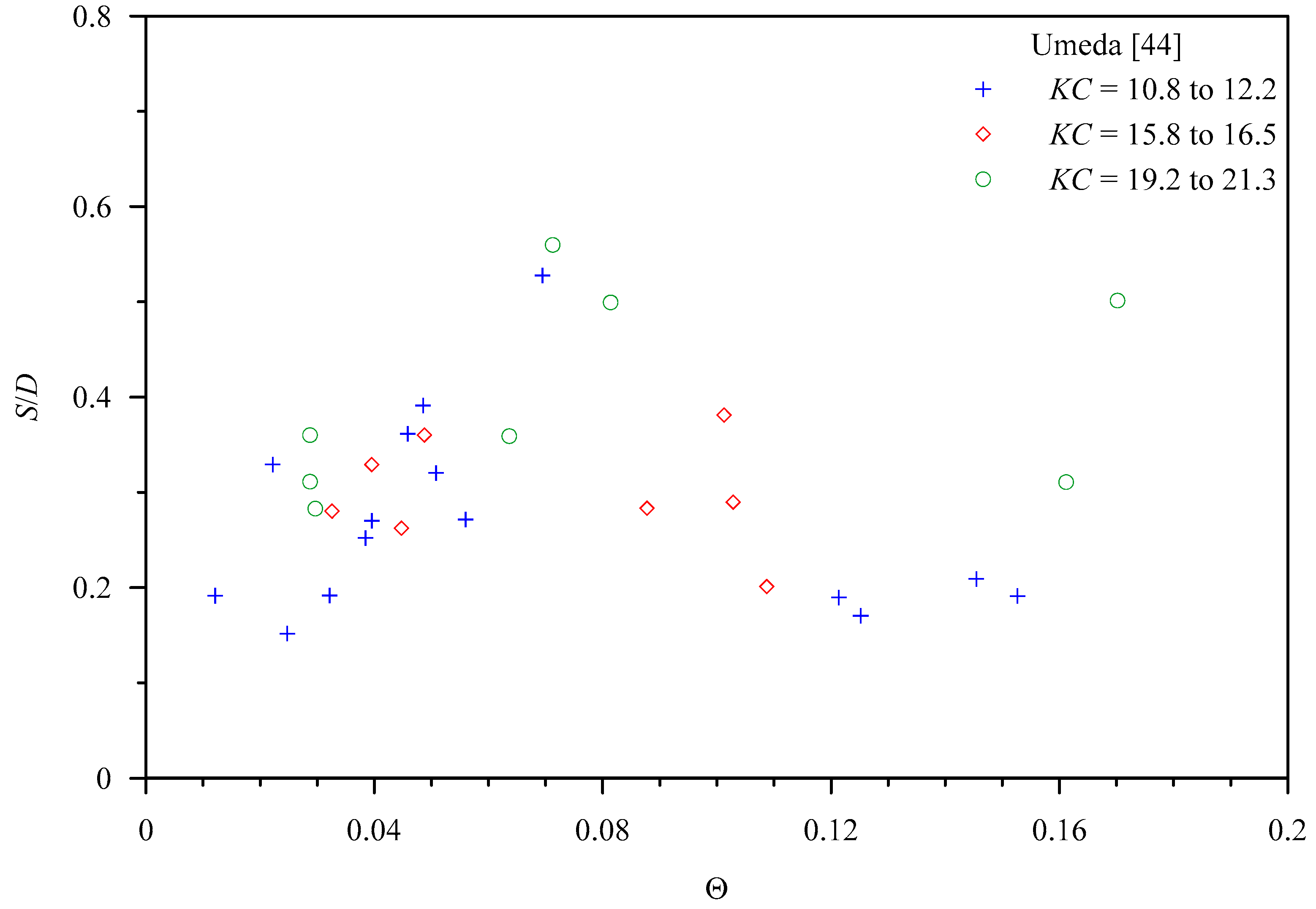
2.1. Scour Depth
2.2. Scour-Hole Shape and Size
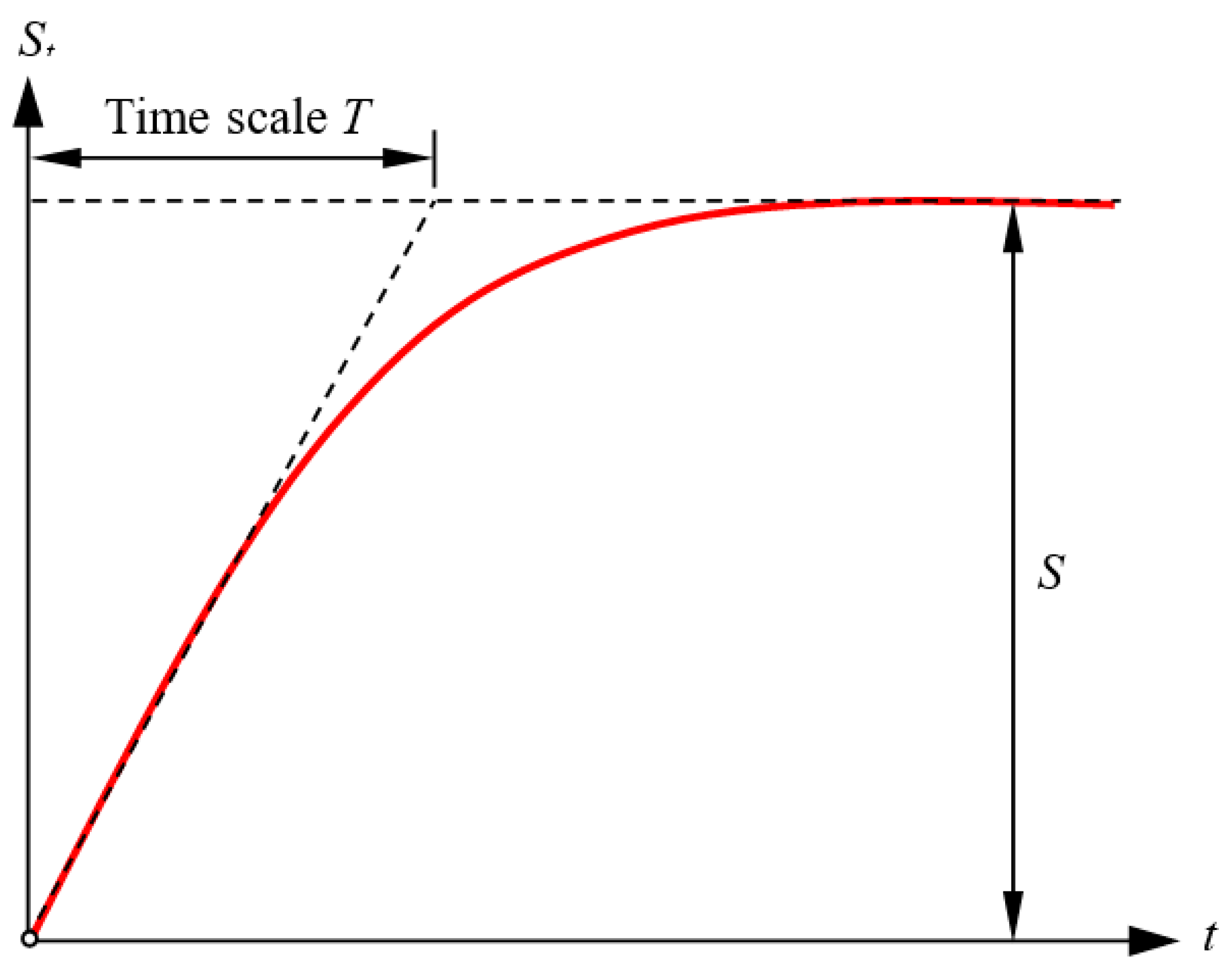
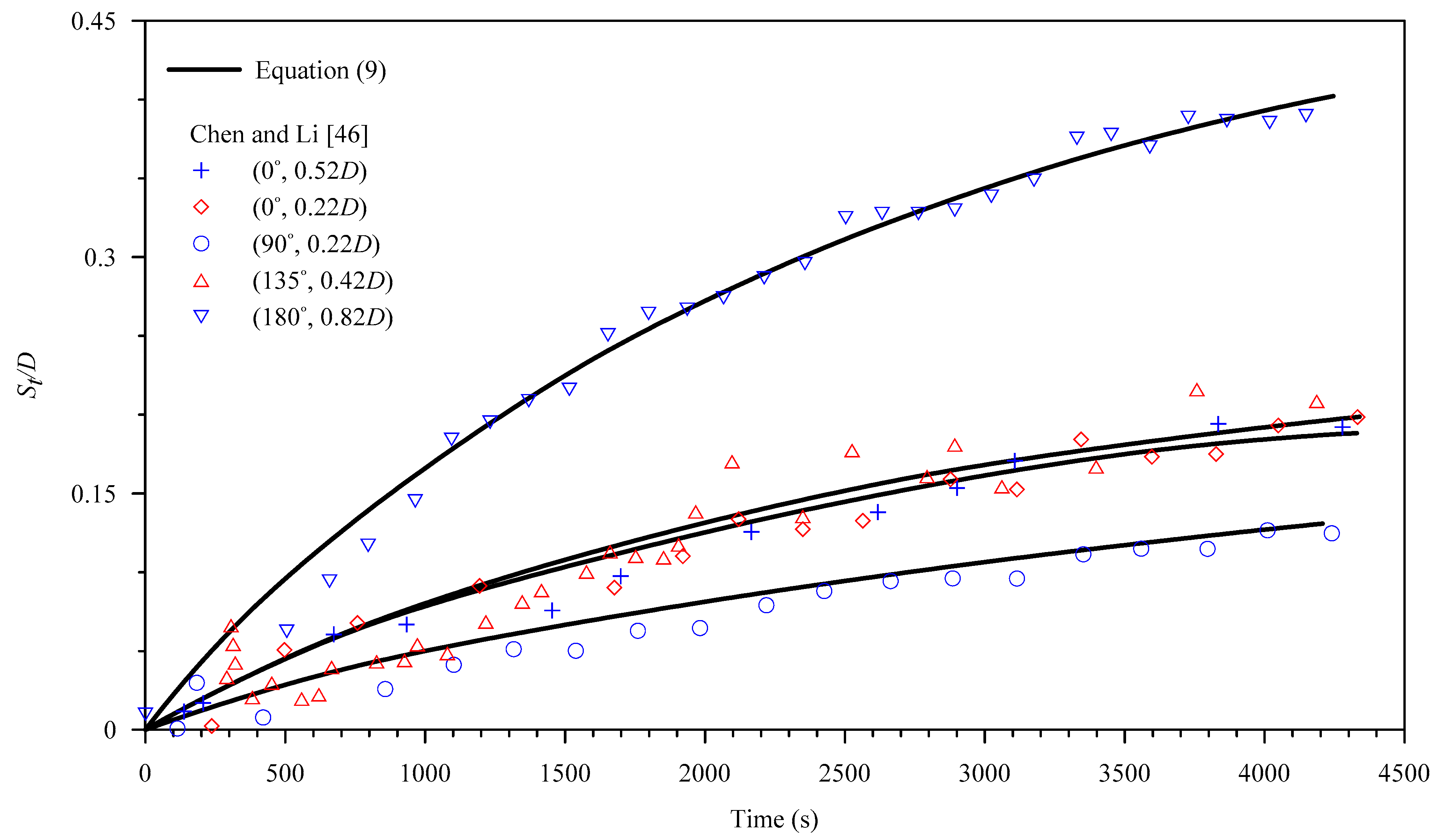
2.3. Timescale
3. Closure and Future Prospects
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lillycrop, W.J.; Hughes, S.A. Scour Hole Problems Experienced by the Corps of Engineers; Data Presentation and Summary; Technical Report; Coastal Engineering Research Center: Vicksburg, MS, USA, 1993. [Google Scholar]
- Smith, D. Bridge failures. Proc. Inst. Civ. Eng. 1976, 60, 367–382. [Google Scholar] [CrossRef]
- Dey, S. Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena; Springer: Berlin, Germany, 2014. [Google Scholar]
- Sumer, B.M. Mathematical modelling of scour: A review. J. Hydraul. Res. 2007, 45, 723–735. [Google Scholar] [CrossRef]
- Kobayashi, T.; Oda, K. Experimental study on developing process of local scour around a vertical cylinder. Coast. Eng. 1995, 1284–1297. [Google Scholar] [CrossRef]
- Whitehouse, R. Scour at Marine Structures: A Manual for Practical Applications; Thomas Telford: London, UK, 1998. [Google Scholar]
- Carreiras, J.; Larroudé, P.; Seabra-Santos, F.; Mory, M. Wave scour around piles. Coast. Eng. 2001, 2, 1860–1870. [Google Scholar]
- Carreiras, J.; do Carmo, J.A.; Seabra-Santos, F. Settlement of vertical piles exposed to waves. Coast. Eng. 2003, 47, 355–365. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J.; Christiansen, N. Scour around vertical pile in waves. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 15–31. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around pile in combined waves and current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Sumer, B.; Fredsøe, J.; Christiansen, N.; Hansen, S. Bed shear stress and scour around coastal structures. Coast. Eng. 1994, 1595–1609. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Time scale of scour around a large vertical cylinder in waves. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; International Society of Offshore and Polar Engineers: Kitakyushu, Japan, 2002. [Google Scholar]
- Dey, S.; Sumer, B.M.; Fredsøe, J. Control of scour at vertical circular piles under waves and current. J. Hydraul. Eng. 2006, 132, 270–279. [Google Scholar] [CrossRef]
- Dey, S.; Helkjær, A.; Mutlu Sumer, B.; Fredsøe, J. Scour at vertical piles in sand-clay mixtures under waves. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 324–331. [Google Scholar] [CrossRef]
- Arabi, M.G.; Sogut, D.V.; Khosronejad, A.; Yalciner, A.C.; Farhadzadeh, A. A numerical and experimental study of local hydrodynamics due to interactions between a solitary wave and an impervious structure. Coast. Eng. 2019, 147, 43–62. [Google Scholar] [CrossRef]
- Sui, T.; Zhang, C.; Guo, Y.; Zheng, J.; Jeng, D.; Zhang, J.; Zhang, W. Three-dimensional numerical model for wave-induced seabed response around mono-pile. Ships. Offshore Struct. 2016, 11, 667–678. [Google Scholar] [CrossRef]
- Sumer, B.M.; Whitehouse, R.J.; Tørum, A. Scour around coastal structures: A summary of recent research. Coast. Eng. 2001, 44, 153–190. [Google Scholar] [CrossRef]
- Richardson, E.; Davies, S. Evaluating Scour at Bridges; HEC18 FHWA NHI-001; Federal Highway Administration, U.S. Department of Transportation: Washington, DC, USA, 2001.
- Cheremisinoff, N.; Cheng, S. Hydraulic Mechanics for Civil. Engineering Practice; Technomic Publishing Company: Lancaster, UK, 1987. [Google Scholar]
- Melville, B.W.; Raudkivi, A.J. Flow characteristics in local scour at bridge piers. J. Hydraul. Res. 1977, 15, 373–380. [Google Scholar] [CrossRef]
- Chiew, Y.; Melville, B. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Melville, B.W. Live-bed scour at bridge piers. J. Hydraul. Eng. 1984, 110, 1234–1247. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Piers. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1975. [Google Scholar]
- Chiew, Y. Local Scour at Bridge Piers; Report No. 355; University of Auckland: Auckland, New Zealand, 1984. [Google Scholar]
- Dargahi, B. The turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Sumer, B.; Christiansen, N.; Fredsøe, J. Time scale of scour around a vertical pile. In Proceedings of the Second International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992; International Society of Offshore and Polar Engineers: San Francisco, CA, USA, 1992; pp. 308–315. [Google Scholar]
- Sumer, B.; Christiansen, N.; Fredsøe, J. Influence of cross section on wave scour around piles. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 477–495. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsøe, J. The horseshoe vortex and vortex shedding around a vertical wall-mounted cylinder exposed to waves. J. Fluid Mech. 1997, 332, 41–70. [Google Scholar] [CrossRef]
- Zanke, U. Kolke am Pfeiler in richtungskonstanter Strömung und unter Welleneinfluß. Mitt. Franzius-Inst. Wasserbau-und Küsteningenieurwesen Univ. Hann. 1982, 54, 381–416. [Google Scholar]
- Das, M. A Literature Review on Bed-Load Transport Due to Wave Action and Localized Scour in Non-Cohesive Sediments; Final Report HEL 21-6; University of California: Berkeley, CA, USA, 1970. [Google Scholar]
- Kawata, Y.; Tsuchiya, Y. Local scour around cylindrical piles due to waves and currents combined. Coast. Eng. 1989, 1310–1322. [Google Scholar] [CrossRef]
- Zyserman, J.; Fredsøe, J. Numerical Simulation of Concentration Profiles of Suspended Sediment. Under Irregular Waves; Progress Report; Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark: Copenhagen, Denmark, 1988. [Google Scholar]
- Sumer, B.M.; Hatipoglu, F.; Fredsøe, J. Wave scour around a pile in sand, medium dense, and dense silt. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 14–27. [Google Scholar] [CrossRef]
- Prepernau, U.; Grüne, J.; Schmidt-Koppenhagen, R.; Wang, Z.; Oumeraci, H. Large-scale model tests on scour around slender monopile under live-bed conditions. In Proceedings of the 2nd International conference on the Application of Physical Modeling to Port and Coastal Protection, Bari, Italy, 2–5 July 2008; pp. 1–8. [Google Scholar]
- Prepernau, U.; Grüne, J.; Sparboom, U.; Schmidt-Koppenhagen, R.; Wang, Z.; Oumeraci, H. Large-scale model study on scour around slender monopiles induced by irregular waves. Coast. Eng. 2009, 2707–2716. [Google Scholar] [CrossRef]
- Zanke, U.C.; Hsu, T.W.; Roland, A.; Link, O.; Diab, R. Equilibrium scour depths around piles in noncohesive sediments under currents and waves. Coast. Eng. 2011, 58, 986–991. [Google Scholar] [CrossRef]
- Myrhaug, D.; Ong, M.C. Effects of sand-clay mixtures on scour around vertical piles due to long-crested and short-crested nonlinear random waves. J. Offshore Mech. Arct. Eng. 2013, 135, 034502. [Google Scholar] [CrossRef]
- Guven, A.; Azamathulla, H.M.; Zakaria, N. Linear genetic programming for prediction of circular pile scour. Ocean Eng. 2009, 36, 985–991. [Google Scholar] [CrossRef]
- Afzal, M.S.; Bihs, H.; Kamath, A.; Arntsen, Ø.A. Three-dimensional numerical modeling of pier scour under current and waves using level-set method. J. Offshore Mech. Arct. Eng. 2015, 137, 032001. [Google Scholar] [CrossRef]
- Ong, M.C.; Myrhaug, D.; Fu, P. Scour around vertical piles due to random waves alone and random waves plus currents on mild slopes. Ocean Syst. Eng. 2016, 6, 161–189. [Google Scholar] [CrossRef]
- Battjes, J.A.; Groenendijk, H.W. Wave height distributions on shallow foreshores. Coast. Eng. 2000, 40, 161–182. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical simulation of scour and backfilling processes around a circular pile in waves. Coast. Eng. 2017, 122, 87–107. [Google Scholar] [CrossRef]
- Chen, B.; Li, S. Experimental Study of Local Scour around a vertical cylinder under wave-only and combined wave-current conditions in a large-scale flume. J. Hydraul. Eng. 2018, 144, 04018058. [Google Scholar] [CrossRef]
- Umeda, S. Scour regime and scour depth around a pile in waves. J. Coast. Res. 2011, 845–849. [Google Scholar]
- Khosronejad, A.; Rennie, C.; Moghimi, S. Application of intelligent system of artificial neural network to predict the scour process in coastal engineering. In Proceedings of the River, Coastal and Estuarine Morphodynamics (RCEM 2007), Enschede, The Netherlands, 17–21 September 2007; pp. 1139–1144. [Google Scholar]
- Chen, B.; Li, S.W. Temporal variation of live-bed pier scour under combined wave-current flow in a large-scale flume. J. Coast. Res. 2019, 35, 348–356. [Google Scholar] [CrossRef]
- Rudolph, D.; Bos, K.J.; Luijendijk, A.; Rietema, K.; Out, J. Scour around offshore structures–analysis of field measurements. In Proceedings of the Second International Conference on Scour and Erosion, Singapore, 14–17 November 2004; pp. 400–407. [Google Scholar]
- Sumer, B.M.; Petersen, T.U.; Locatelli, L.; Fredsøe, J.; Musumeci, R.E.; Foti, E. Backfilling of a scour hole around a pile in waves and current. J. Waterw. Port Coast. Ocean Eng. 2012, 139, 9–23. [Google Scholar] [CrossRef]
- Nishizawa, M.; Sawamoto, M. Local scour around a vertical cylinder under the wave action. In Proceedings of the 6th Congress of APD-IAHR, Kyoto, Japan, 20–22 July 1988; pp. 121–128. [Google Scholar]
- Farooq, R.; Ghumman, A.R. Impact assessment of pier shape and modifications on scouring around bridge pier. Water 2019, 11, 1761. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.M. Time scale for local scour at bridge piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Briaud, J.L.; Ting, F.; Chen, H.; Gudavalli, R.; Kwak, K.; Philogene, B.; Han, S.W.; Perugu, S.; Wei, G.; Nurtjahyo, P. SRICOS: Prediction of Scour Rate at Bridge Piers; Report; Texas Transportation Institute, The Texas A & M University: College Station, TX, USA, 1999. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Littleton, CO, USA, 2000. [Google Scholar]
- Shatanawi, K.M.; Aziz, N.M.; Khan, A.A. Frequency of discharge causing abutment scour in South Carolina. J. Hydraul. Eng. 2008, 134, 1507–1512. [Google Scholar] [CrossRef]
- Dey, S. Experimental study on incipient motion of sediment particles on generalized sloping fluvial beds. Int. J. Sedim. Res. 2001, 16, 391–398. [Google Scholar]
- Engelund, F.; Fredsøe, J. Hydraulic theory of alluvial rivers. Adv. Hydrosci. 1982, 13, 187–215. [Google Scholar]
- Engelund, F.; Fredsøe, J. A sediment transport model for straight alluvial channels. Hydrol. Res. 1976, 7, 293–306. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gazi, A.H.; Afzal, M.S.; Dey, S. Scour around Piers under Waves: Current Status of Research and Its Future Prospect. Water 2019, 11, 2212. https://doi.org/10.3390/w11112212
Gazi AH, Afzal MS, Dey S. Scour around Piers under Waves: Current Status of Research and Its Future Prospect. Water. 2019; 11(11):2212. https://doi.org/10.3390/w11112212
Chicago/Turabian StyleGazi, Ainal Hoque, Mohammad Saud Afzal, and Subhasish Dey. 2019. "Scour around Piers under Waves: Current Status of Research and Its Future Prospect" Water 11, no. 11: 2212. https://doi.org/10.3390/w11112212
APA StyleGazi, A. H., Afzal, M. S., & Dey, S. (2019). Scour around Piers under Waves: Current Status of Research and Its Future Prospect. Water, 11(11), 2212. https://doi.org/10.3390/w11112212






