Predictive Water Virology: Hierarchical Bayesian Modeling for Estimating Virus Inactivation Curve
Abstract
1. Introduction
2. Materials and Methods
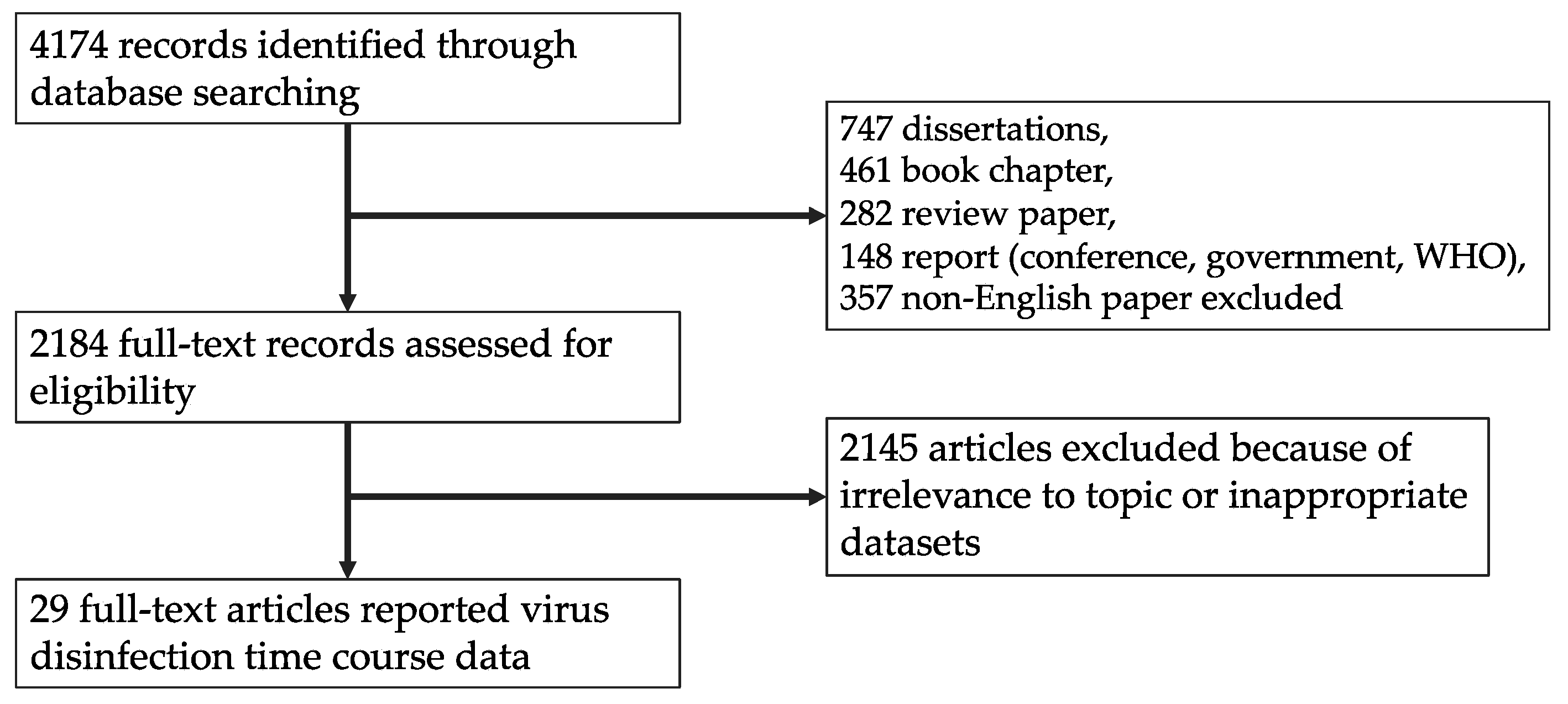
2.1. Systematic Review
2.2. Probability Distribution of Inactivation Model Parameters
2.3. Hierarchical Bayesian Modeling
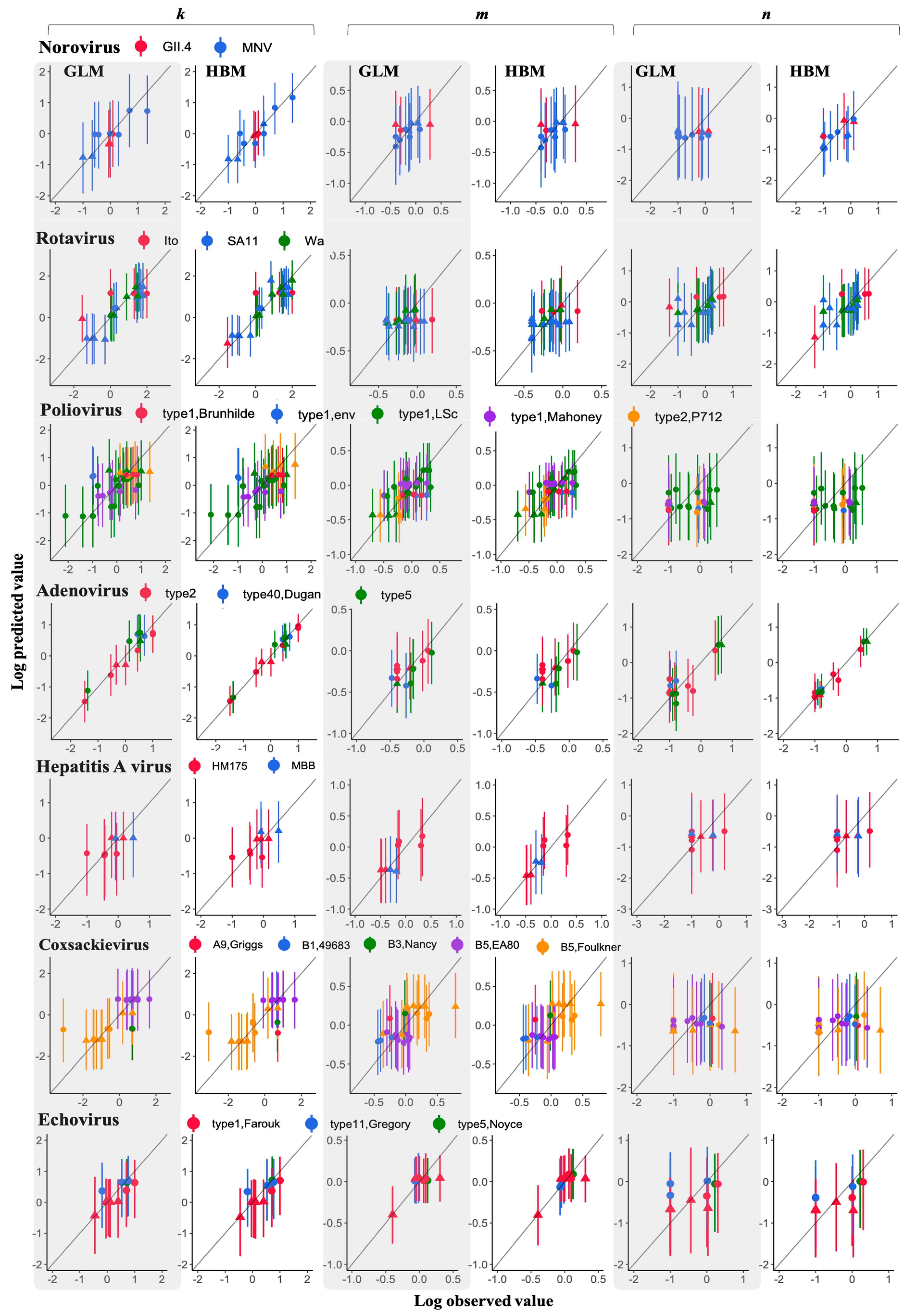
2.4. Model Validation
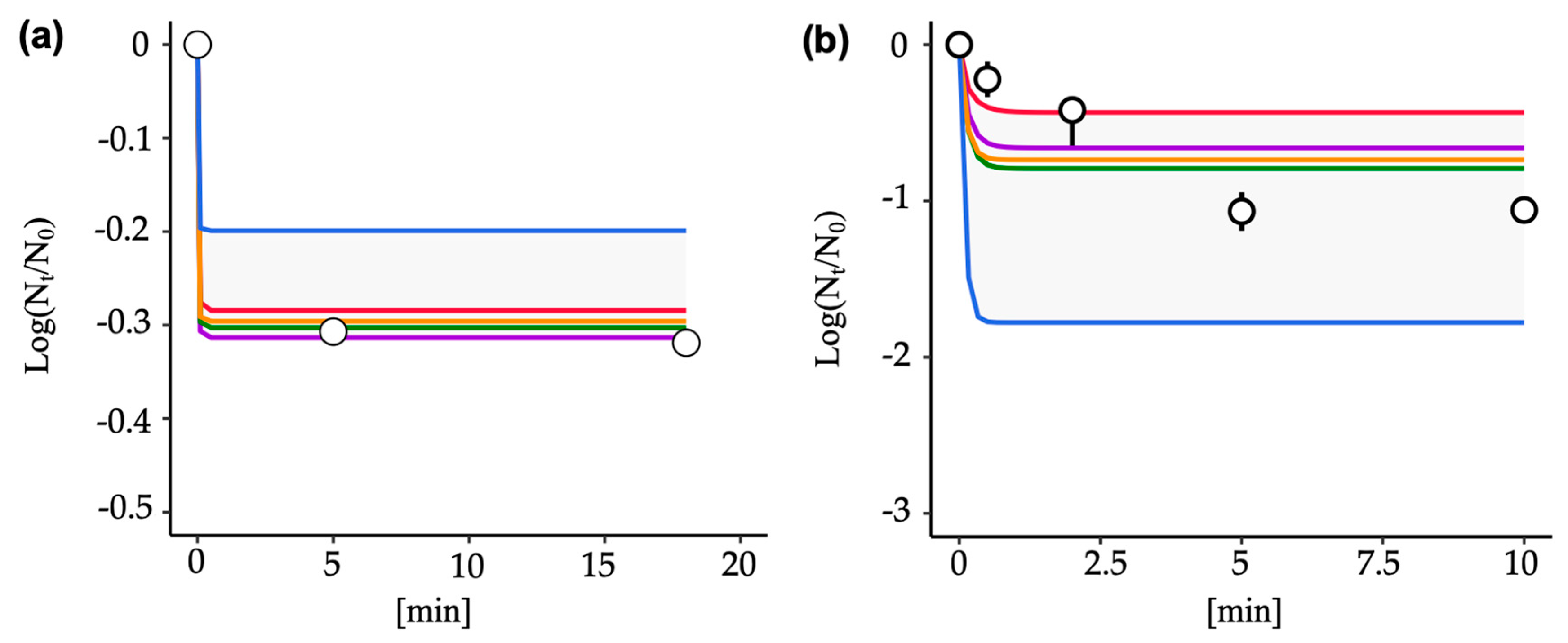
2.4.1. Measurement of Norovirus Concentration in Treated Wastewater
2.4.2. Inactivation Experiment of Rotavirus by Sodium Hypochlorite
2.4.3. Predictive Inactivation Curve
3. Result
3.1. Article Selection and Data Extraction
3.2. Probability Distribution of the Inactivation Model Parameters
3.3. Comparison of a Goodness of Fit between GLM and HBM
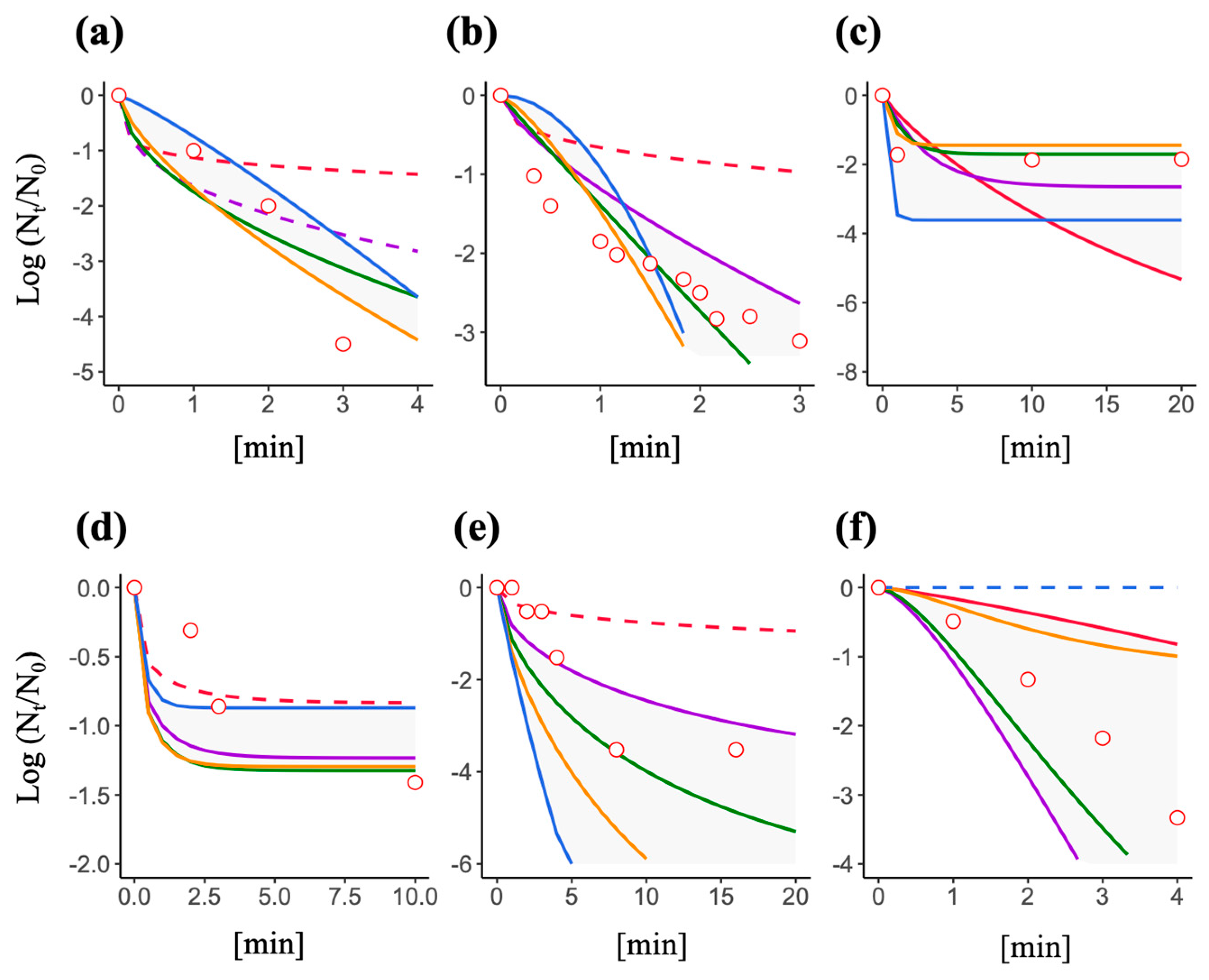
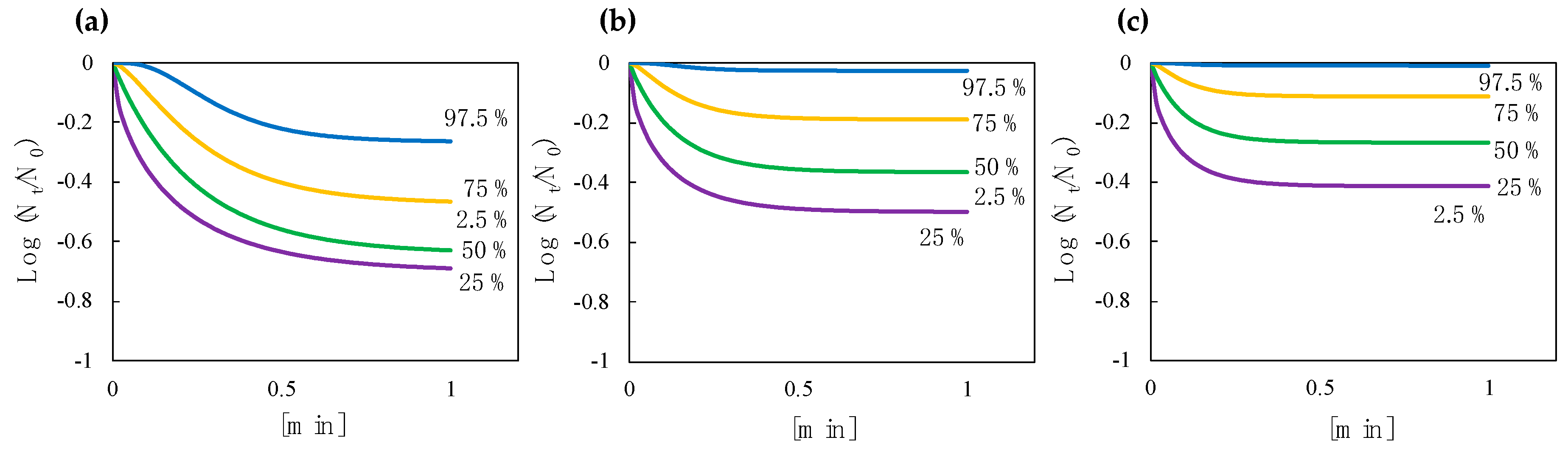
3.4. Predictive Inactivation Curves Based on HBM
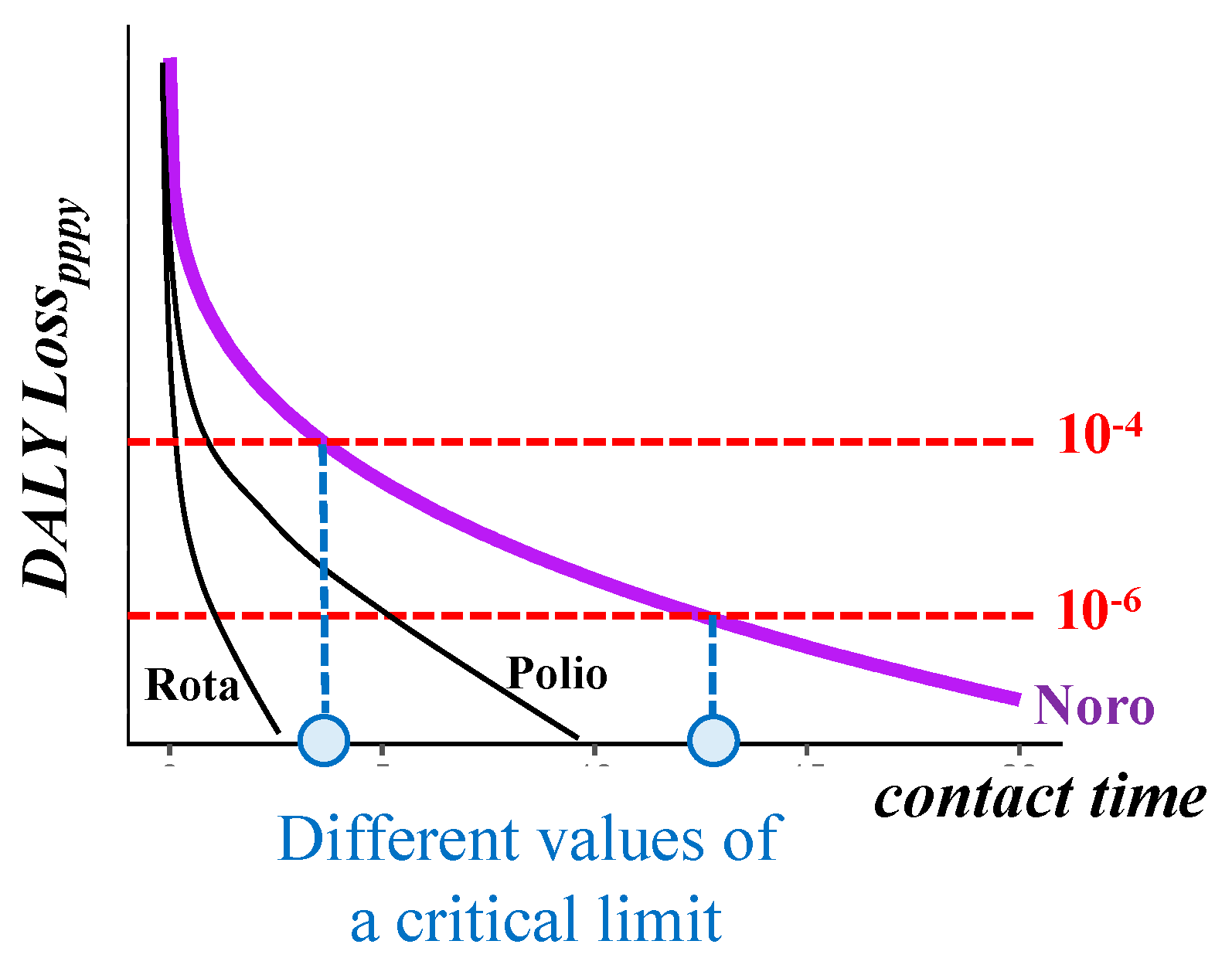
3.5. Effect of a Decay Constant and Efficiency Factor on the Shape of a Predictive Inactivation Curve
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- WHO. Sanitation Safety Planning: Manual for Safe Use and Disposal of Wastewater, Greywater and Excreta; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- WHO. Guidelines for the Safe Use of Wastewater, Excreta and Greywater in Agriculture and Aquaculture, 3rd ed.; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- CAC. Basic texts on Food Hygiene, 4th ed.; Codex Alimentarius Commission: Rome, Italy, 2009. [Google Scholar]
- Bryan, J.J. Hazard analysis and critical control points and their application to the drinking water treatment process. In Proceedings of the AWWA Water Quality Technology Conference, Miami, FL, USA, 7–11 November 1993. [Google Scholar]
- Havellar, H.A. Application of HACCP to drinking water supply. Food Control 1994, 5, 145–152. [Google Scholar] [CrossRef]
- Tsoukalas, D.S.; Tsitsifli, S. A critical evaluation of water safety plans (WSPs) and HACCP implementation in water utilities. Proceedings 2018, 2, 600. [Google Scholar] [CrossRef]
- Ross, T.; McMeekin, T.A. Predictive microbiology. Int. J. Food Microbiol. 1994, 23, 241–264. [Google Scholar] [CrossRef]
- Sharp, D.G.; Leong, J. Inactivation of poliovirus I (Brunhilde) single particles by chlorine in water. Appl. Environ. Microbiol. 1980, 40, 381–385. [Google Scholar] [PubMed]
- Floyd, R.; Sharp, D.G.; Johnson, J.D. Inactivation by chlorine of single poliovirus particles in water. Environ. Sci. Technol. 1979, 13, 438–442. [Google Scholar] [CrossRef]
- Amarasiri, M.; Hashiba, S.; Miura, T.; Nakagomi, T.; Nakagomi, O.; Ishii, S.; Okabe, S.; Sano, D. Bacterial histo-blood group antigens contributing to genotype-dependent removal of human noroviruses with a microfiltration membrane. Water Res. 2016, 95, 383–391. [Google Scholar] [CrossRef] [PubMed]
- Hom, L.W. Kinetics of chlorine disinfection in an ecosystem. J. Sanit. Eng. Div. 1972, 98, 183–193. [Google Scholar]
- Haas, C.N.; Joffe, J. Disinfection under dynamic conditions: Modification of Hom’s model for decay. Environ. Sci. Technol. 1994, 28, 1367–1369. [Google Scholar] [CrossRef]
- Gyurek, L.L.; Finch, G.R. Modeling water treatment chemical disinfection kinetics. J. Environ. Eng. 1998, 124, 783–793. [Google Scholar] [CrossRef]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R package for fitting distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Watanabe, S. Equations of states in singular statistical estimation. Neural Netw. 2010, 23, 20–34. [Google Scholar] [CrossRef]
- Haramoto, E.; Katayama, H.; Ohgaki, S. Detection of noroviruses in tap water in Japan by means of a new method for concentrating enteric viruses in large volumes of freshwater. Appl. Environ. Microbiol. 2004, 70, 2154–2160. [Google Scholar] [CrossRef] [PubMed]
- Kageyama, T.; Kojima, S.; Shinohara, M.; Uchida, K.; Fukushi, S.; Hoshino, F.B.; Takeda, N.; Katayama, K. Broadly reactive and highly sensitive assay for Norwalk-like viruses based on real-time quantitative reverse transcription-PCR. J. Clin. Microbiol. 2003, 29, 934–939. [Google Scholar] [CrossRef] [PubMed]
- Kadoya, S.; Sano, D. Assays for the specific growth rate and cell-binding ability of rotavirus. J. Vis. Exp. 2019, 143, e58821. [Google Scholar] [CrossRef] [PubMed]
- Kahler, A.M.; Cromeans, T.L.; Metcalfe, M.G.; Humphrey, C.D.; Hill, V.R. Aggregation of adenovirus 2 in source water and impacts on disinfection by chlorine. Food Environ. Virol. 2016, 8, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Gall, A.M.; Shisler, J.L.; Marinas, B.J. Analysis of the viral replication cycle of adenovirus serotype 2 after inactivation by free chlorine. Environ. Sci. Technol. 2015, 49, 4584–4590. [Google Scholar] [CrossRef]
- Ma, J.F.; Straub, T.M.; Pepper, I.L.; Gerba, C.P. Cell culture and PCR determination of poliovirus inactivation by disinfectants. Appl. Environ. Microbiol. 1994, 60, 4203–4206. [Google Scholar]
- Tree, J.A.; Adams, M.R.; Lees, D.N. Chlorination of indicator bacteria and viruses in primary sewage effluent. Appl. Environ. Microbiol. 2003, 69, 2038–2043. [Google Scholar] [CrossRef]
- Thurston-Enriquez, J.A.; Haas, C.N.; Jacangelo, J.; Gerba, C.P. Chlorine inactivation of adenovirus type 40 and feline calicivirus. Appl. Environ. Microbiol. 2003, 69, 3979–3985. [Google Scholar] [CrossRef]
- Girones, R.; Carratala, A.; Calgua, B.; Calvo, M.; Rodriguez-Manzano, J.; Emerson, S. Chlorine inactivation of hepatitis E virus and human adenovirus 2 in water. J. Water Health 2014, 12, 436–442. [Google Scholar] [CrossRef]
- Kitajima, M.; Tohya, Y.; Matsubara, K.; Haramoto, E.; Utagawa, E.; Katayama, H. Chlorine inactivation of human norovirus, murine norovirus and poliovirus in drinking water. Lett. Appl. Microbiol. 2010, 51, 119–121. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, P.T.B.; Metcalf, T.G.; Sproul, O.J. Chlorine resistance of poliovirus isolates recovered from drinking water. Appl. Environ. Microbiol. 1980, 40, 1115–1121. [Google Scholar] [PubMed]
- de Abreu Correa, A.; Carratala, A.; Barardi, C.R.M.; calvo, M.; Girones, R.; Bofill-Mas, S. Comparative inactivation of murine norovirus, human adenovirus, and human JC polyomavirus by chlorine in seawater. Appl. Environ. Microbiol. 2012, 78, 6450–6457. [Google Scholar] [CrossRef] [PubMed]
- Engelbrecht, R.S.; Weber, J.M.; Salter, B.L.; Schmidt, C.A. Comparative inactivation of viruses by chlorine. Appl. Environ. Microbiol. 1980, 40, 249–256. [Google Scholar]
- Zhong, Q.; Carratala, A.; Ossola, R.; Bachmann, V.; Kohn, T. Cross-resistance of UV-or chlorine dioxide-resistant echovirus 11 to other disinfectants. Front. Microbiol. 2017, 8, 1928. [Google Scholar] [CrossRef]
- Bates, R.C.; Shaffer, P.T.B.; Sutherland, S.M. Development of poliovirus having increased resistance to chlorine inactivation. Appl. Environ. Microbiol. 1977, 34, 849–853. [Google Scholar]
- Lim, M.Y.; Kim, J.M.; Ko, G.P. Disinfection kinetics of murine norovirus using chlorine and chlorine dioxide. Water Res. 2010, 44, 3243–3251. [Google Scholar] [CrossRef]
- Abad, F.X.; Pinto, R.M.; Diez, J.M.; Bosch, A. Disinfection of human enteric viruses in water by copper and silver in combination with low levels of chlorine. Appl. Environ. Microbiol. 1994, 60, 2377–2383. [Google Scholar]
- Xue, B.; Jin, M.; Yang, D.; Guo, X.; Chen, Z.; Shen, Z.; Wang, X.; Qiu, Z.; Wang, J.; Zhang, B.; et al. Effects of chlorine and chlorine dioxide on human rotavirus infectivity and genome stability. Water Res. 2013, 47, 3329–3338. [Google Scholar] [CrossRef]
- Kahler, A.M.; Cromeans, T.L.; Roberts, J.M.; Hill, V.R. Effects of source water quality on chlorine inactivation of adenovirus, coxsackievirus, echovirus, and murine norovirus. Appl. Environ. Microbiol. 2010, 76, 5159–5164. [Google Scholar] [CrossRef]
- Baxter, C.S.; Hofmann, R.; Templeton, M.R.; Brown, M.; Andrews, R.C. Inactivation of adenovirus type 2. 5. and 41 in drinking water by UV light, free chlorine, and monochloramine. J. Environ. Eng. 2007, 133, 95–103. [Google Scholar] [CrossRef]
- Cromeans, T.L.; Kahler, A.M.; Hill, V.R. Inactivation of adenoviruses, enteroviruses, and murine norovirus in water by free chlorine and monochloramine. Appl. Environ. Microbiol. 2010, 76, 1028–1033. [Google Scholar] [CrossRef] [PubMed]
- Sobsey, M.D.; Fuji, T.; Hall, R.M. Inactivation of cell-associated and dispersed hepatitis A virus in water. J. Am. Water Works Assoc. 1991, 83, 64–67. [Google Scholar] [CrossRef]
- Grabow, W.O.K.; Gauss-Muller, V.; Prozesky, O.W.; Deinhardt, F. Inactivation of hepatitis A virus indicator organisms in water by free chlorine residuals. Appl. Environ. Microbiol. 1983, 46, 619–624. [Google Scholar] [PubMed]
- Grabow, W.O.K.; Coubrough, P.; Hiler, C.; Bateman, B.W. Inactivation of hepatitis A virus, other enteric viurses and indicator organisms in water by chlorination. Water Sci. Technol. 1984, 17, 657–664. [Google Scholar] [CrossRef]
- Vaughn, J.M.; Chen, Y.-S.; Thomas, M.Z. Inactivation of human and simian rotaviruses by chlorine. Appl. Environ. Microbiol. 1986, 51, 391–394. [Google Scholar]
- Harakeh, M.; Butler, M. Inactivation of human rotavirus, SA11 and other enteric viruses in effluent by disinfectants. Epidemiol. Infect. 1984, 93, 157–163. [Google Scholar] [CrossRef]
- Berman, D.; Hoff, J.D. Inactivation of simian rotavirus SA11 by chlorine, chlorine dioxide, and monochloramine. Appl. Environ. Microbiol. 1984, 48, 317–323. [Google Scholar]
- Weidenkopf, S.J. Inactivation of type1 poliomyelitis virus with chlorine. Virology 1958, 5, 56–67. [Google Scholar] [CrossRef]
- Nascimento, M.A.; Magri, M.E.; Schissi, C.D.; Baradi, C.R.M. Recombinant adenovirus as a model to evaluate the efficiency of free chlorine disinfection in filtered water samples. Virol. J. 2015, 12, 30. [Google Scholar] [CrossRef]
- Caballero, S.; Abad, F.X.; Loisy, F.; Le Guyader, F.S.; Cohen, J.; Pinto, R.M.; Bosch, A. Rotavirus virus-like particles as surrogate in environmental persistence and inactivation studies. Appl. Environ. Microbiol. 2004, 70, 3904–3909. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kelly, S.; Sanderson, W.W. The effect of chlorine in water on enteric viruses. Am. J. Public Health Nations Health 1958, 48, 1323–1334. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-S.; Vaughn, J.M. Inactivation of human and simian rotaviruses by chlorine dioxide. Appl. Environ. Microbiol. 1990, 56, 1363–1366. [Google Scholar] [PubMed]
- Sigstam, T.; Gannon, G.; Cascella, M.; Pecson, B.M.; Wigginton, K.R.; Kohn, T. Subtle differences in virus composition affect disinfection kinetics and mechanisms. Appl. Environ. Microbiol. 2013, 79, 3455–3467. [Google Scholar] [CrossRef]
- Rachmadi, A.T.; Kitajima, M.; Watanabe, K.; Yaegashi, S.; Serrana, J.; Nakamura, A.; Nakagomi, T.; Nakagomi, O.; Katayama, K.; Okabe, S.; et al. Free chlorine disinfection as a selection pressure on norovirus. Appl. Environ. Microbiol. 2018, 84, e00244-18. [Google Scholar] [CrossRef]
- Zhong, Q.; Carratala, A.; Nazarov, S.; Guerrero-Ferreira, R.C.; Piccinini, L.; Bachmann, V.; Leiman, P.G.; Kohn, T. Genetic, structural, and phenotypic properties of MS2 coliphage with resistance to ClO2 disinfection. Environ. Sci. Technol. 2016, 50, 13520–13528. [Google Scholar] [CrossRef]
- Zhong, Q.; Carratala, A.; Shim, H.; Bachman, V.; Jensen, J.D.; Kohn, T. Resistance of echovirus 11 to ClO2 is associated with enhanced host receptor use, altered entry routes, and high fitness. Environ. Sci. Technol. 2017, 51, 10746–10755. [Google Scholar] [CrossRef]
- Domingo, E. RNA virus mutations. Annu. Rev. Microbiol. 1997, 51, 151–178. [Google Scholar] [CrossRef]
- Doming, E.; Escarmis, C.; Sevillar, N.; Moya, A.; Elena, S.F.; Quer, J.; Novella, I.S.; Holland, J.J. Basic concepts in RNA virus evolution. FASEB J. 1996, 10, 859–864. [Google Scholar] [CrossRef]
- Jaccard, J.; Wan, C.K.; Turrisi, R. The detection and interpretation of interaction effects between continuous variables in multiple regression. Multivar. Behav. Res. 1990, 25, 467–478. [Google Scholar] [CrossRef]
- Abdul-Wahab, S.A.; Bakheit, C.S.; Al-Alawi, S.M. Principal component and multiple regression analysis in modelling of ground-level ozone and factors affecting its concentrations. Environ. Model. Softw. 2005, 20, 1263–1271. [Google Scholar] [CrossRef]
- Gang, C.E.; Clevenger, T.E.; Banerji, S.K. Modeling chlorine decay in surface water. J. Environ. Inform. 2003, 1, 21–27. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Risk Assessment Guidance for Superfund (RAGS); part A; USEPA: Washington, DC, USA, 1990; Volume III.
- WHO. WHO Methods and Data Sources for Global Burden of Disease Estimates 2000–2015; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
| k | m | n | |
|---|---|---|---|
| Norovirus | Lognormal | →* | → |
| Rotavirus | Lognormal | → | → |
| Poliovirus | Lognormal | Gamma | Lognormal |
| Adenovirus | Lognormal | → | → |
| Hepatitis A virus | Lognormal | → | → |
| Coxsackievirus | Lognormal | → | → |
| Echovirus | Exponential | Lognormal | Lognormal |
| k | m | n | |||||
|---|---|---|---|---|---|---|---|
| Statistics | GLM | HBM | GLM | HBM | GLM | HBM | |
| Norovirus | WAIC | 23.0 | 14.4 | 6.81 | 7.54 | 28.9 | 17.4 |
| RMSE | 0.34 | 0.23 | 0.03 | 0.03 | 0.43 | 0.27 | |
| Rotavirus | WAIC | 54.6 | 45.8 | −7.90 | −11.2 | 43.9 | 35.6 |
| RMSE | 0.45 | 0.41 | 0.16 | 0.14 | 0.20 | 0.14 | |
| Poliovirus | WAIC | 69.5 | 68.8 | 37.9 | 36.3 | 63.9 | 63.3 |
| RMSE | 0.54 | 0.53 | 0.51 | 0.49 | 0.50 | 0.49 | |
| Adenovirus | WAIC | 11.0 | 1.77 | −3.12 | −5.92 | 17.9 | −2.19 |
| RMSE | 0.05 | 0.01 | 0.02 | 0.02 | 0.08 | 0.01 | |
| Hepatitis A virus | WAIC | 19.4 | 11.9 | 4.02 | 2.04 | 18.1 | 18.4 |
| RMSE | 0.29 | 0.27 | 0.17 | 0.15 | 0.16 | 0.15 | |
| Coxsackievirus | WAIC | 67.9 | 65.5 | 2.21 | 3.98 | 48.1 | 47.5 |
| RMSE | 0.70 | 0.68 | 0.20 | 0.19 | 0.51 | 0.49 | |
| Echovirus | WAIC | 50.6 | 48.1 | −9.30 | −8.13 | 18.1 | 13.5 |
| RMSE | 0.24 | 0.23 | 0.10 | 0.09 | 0.46 | 0.41 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadoya, S.-s.; Nishimura, O.; Kato, H.; Sano, D. Predictive Water Virology: Hierarchical Bayesian Modeling for Estimating Virus Inactivation Curve. Water 2019, 11, 2187. https://doi.org/10.3390/w11102187
Kadoya S-s, Nishimura O, Kato H, Sano D. Predictive Water Virology: Hierarchical Bayesian Modeling for Estimating Virus Inactivation Curve. Water. 2019; 11(10):2187. https://doi.org/10.3390/w11102187
Chicago/Turabian StyleKadoya, Syun-suke, Osamu Nishimura, Hiroyuki Kato, and Daisuke Sano. 2019. "Predictive Water Virology: Hierarchical Bayesian Modeling for Estimating Virus Inactivation Curve" Water 11, no. 10: 2187. https://doi.org/10.3390/w11102187
APA StyleKadoya, S.-s., Nishimura, O., Kato, H., & Sano, D. (2019). Predictive Water Virology: Hierarchical Bayesian Modeling for Estimating Virus Inactivation Curve. Water, 11(10), 2187. https://doi.org/10.3390/w11102187




