Abstract
Anthropogenic landscape conversion from forest to agricultural land affects baseflow. Baseflow is a source of potable water and can be used for the irrigation of high value crops. Finding ways to increase base and inter flow (i.e., groundwater flow) is, therefore, essential for the improvement of the livelihood of rural inhabitants. Therefore, the objective is to investigate the effect of landscape interventions on stream discharge and, in particular, on groundwater flow. The Tikur-Wuha experimental watershed in the upper reaches of the Blue Nile was selected because discharge data were available before and after implementation of a suite of land management practices that, among others, enhanced the percolation of water to below the rootzone. The parameter efficient distributed (PED) model was used to separate overland flow from total flow. The groundwater flow index (GWFI), defined as the quotient of the annual groundwater flow to the total stream discharge at the outlet of the watershed, was calculated. Our analysis with the PED model showed that at similar annual rainfall amounts, more baseflow and less surface runoff was generated after the landscape intervention, which promoted deep infiltration of the rainwater. The decrease in surface runoff shortly after the implementation of the land management practices is similar to observations in other watersheds in the Ethiopian highlands.
1. Introduction
Anthropogenic landscape conversion from forest to agricultural land generally increases direct runoff and decreases base and inter flow (together, called groundwater flow) in tropical monsoon climates. Declining groundwater flows in developing countries make it necessary for many women to walk greater distances to obtain water [1,2,3,4,5] and decrease the amount of water that is available for irrigation during the dry monsoon phase [6]. Increasing baseflow by land management practices would be an effective way to increase agricultural and biomass production during the dry phase. Moreover, sufficient groundwater flow is important for the health of rivers’ habitat ecosystem [7,8]. Groundwater flow generally constitutes a large portion of the discharge in most rivers [9,10]. For example, baseflow contributed up to 44% of the annual flow in Yellow River [11]. Similarly, 56% of the streamflow in the Upper Colorado River basin comes from the recession flow [12]. In the lowlands of the Netherlands, the baseflow accounts for 90% of the stream flow [13]. Base and interflow contributed up to 60% of Lake Tana’s total annual inflow [14].
Stream flow can be altered by the implementation of land management practices in a watershed [15,16,17]. We define land management practices here as any practice that attempts to restore the land to its original functioning. These practices may include changes in land use and/or implementation of structural measures such as soil and water conservation practices. Land management together with precipitation affect groundwater flow and surface runoff [3,17,18]. In the Coon Creek and Kickapoo River Watersheds of southwestern Wisconsin, increased precipitation in the 1970s was likely more significant in the increase of baseflow than land management practices [19]. Land management practices in agricultural catchments, consisting of gully treatments and the adoption of conservation tillage, decreased flood peaks and increased baseflow [18]. In the Mississippi river basin, baseflow was increased by land restoration practices that started in the 1940s [16]. In 20 sub-basins in North Carolina, forest cover and baseflow were positively correlated [20]. In addition, a study in south China showed that land management involving land use changes like afforestation increased baseflow [2]. Similarly, in the United States, land use changes impacted the annual water balance by decreasing annual evapotranspiration and increasing both streamflow and base flow [21]. In contrast, the conversion of forests to farmlands increased the baseflow in mountain watershed of China [22].
In the Ethiopian highlands, before the 1950s, shifting cultivation was practiced, streams were mostly free of sediment [23], and land management practices were not needed. When the fallow period decreased, soil organic matter decreased, soil degradation started, and erosion increased [24]. For soils with organic matter less than 3%, aggregates broke up and the soil became finer and the soil particles were more easily dislodged by raindrop impact. The rainwater and sediment water infiltrated the soil and plugged up the pores, resulting in the formation of a hardpan in the top 100 cm of the soil profile. The hardpan in turn reduced percolation and increased direct runoff, thereby greatly increasing sediment loads [24]. Land management practices in the Ethiopian highlands are, therefore, intended to conserve water by restoring deep percolation of surface water and decreasing direct runoff. These management practices consist of stone and earthen bunds with infiltration furrows that are intended to slow down the flow of water, thereby increasing the time that water can percolate downwards [24]. Other practices that are effective are trees and enclosures with deep rooted grasses.
In the semi-arid Ethiopian highlands where potential evaporation exceeds precipitation during the rain phase, land management practices (involving water conservation) decreased direct runoff and increased biomass production by increasing water availability in the valley bottoms [25,26]. In the humid and semi-humid highlands, with more rainfall than evaporation during the rain phase, the effectiveness of land management practices that are intended to conserve rainfall is mixed. Implementation of 50 cm deep contour furrows and bunds decreased direct runoff [17,27,28,29] in the first five years after implementation, however the long-term effectiveness was minimal in the Soil Conservation Research Project (SCRP) watersheds [30]. Research from a paired watershed study near Gondar indicated that a watershed with soil and water conservation structures consisting of stone and earthen bunds significantly had less direct runoff and soil erosion than a watershed without a conservation practice [31]. In the Ene-Chilala watershed in the northcentral highlands, 50 cm deep contour furrows decreased runoff, however runoff overtopped the bunds and caused damage to nearby crops; off-contour furrows increased the overland flow and did not cause damage to the crop [32]. In the Debre Mawi watershed south of Lake Tana, infiltration furrows decreased direct runoff, however sediment concentrations remained initially constant due to active gully formation [17].
Since in the sub-humid and humid highlands the main purpose of conservation practices is to carry off excess rainfall, crop yields per unit area are not affected by these land management interventions [33]. However, overall yield is decreased by the land that is taken out of production [34]. While bunds are planted with multipurpose grasses and trees that could potentially increase overall biomass production [34], these plantings usually do not survive because of consumption by free grazing cattle in the dry phase [35]. Conservation tillage practices can increase yield per unit area [18]. Increased biomass production in the uplands utilizing subsoil moisture via deep rooted plants decreases the overall watershed yield [36], and biomass production decreased during the dry phase in the valley bottom due to the diminished availability of irrigation water [37].
Many computer simulations have been carried out in the Ethiopian highlands to determine the effect of best management practices. However, these simulations were validated only for current conditions and the data are usually not available to validate predicted change [38,39,40,41]. Therefore, simulation models should not be used for evaluating the suitability of implementation. Only experimental studies or validated models can give insight into changes that take place after the implementation of land management practices [17,29,30]. The objective of this study is to experimentally evaluate the effect of landscape interventions on groundwater and surface runoff in the (sub) humid Ethiopian highlands and their indirect effect on the increase in potential biomass production during the dry phase in downstream watersheds. The Tikur-Wuha watershed in the Tana basin was selected for the study, which is in the headwaters of the Blue Nile. The basin is characteristic of many similar watersheds, with significant groundwater flow during the dry monsoon phase.
2. Materials and Methods
2.1. Description of the Study Area
The study was conducted in the 500 ha Tikur-Wuha watershed, in the upper reaches of the Ribb watershed, southeast of Lake Tana (38°05′25′′–38°06′45′′ E–W to 11°48′22′′–11°49′26′′ N–S (Figure 1). The elevation ranged from 2868 to 3302 m above sea level. The average annual rainfall from 2010–2015 was 1518 mm. The rainfall distribution is unimodal: 85% of the rainfall falls from June–September. The mean daily temperature is 15 °C, with a minimum of 10 °C in the coldest month (August) and 22 °C in the warmest month (March). During the rain phase, a perched water table depth ranges from 5 m to 13 m below the surface in the uplands and close to the surface in the valley bottom near the stream [42].
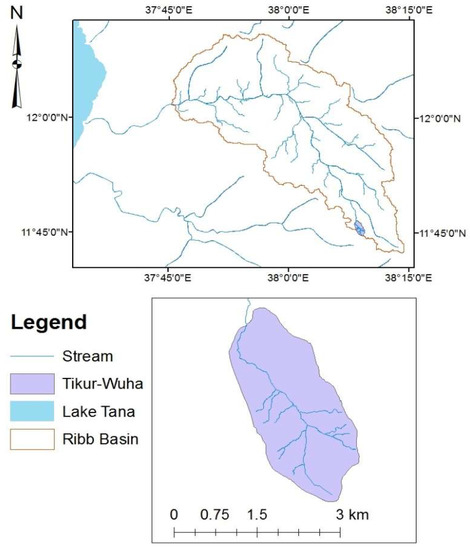
Figure 1.
Map of the Tikur-Wuha watershed in the headwaters of the Ribb, which drains to Lake Tana.
The watershed is underlain by a Tarmabar quaternary basalt that is highly faulted [43]. The faults transmit a portion of the excess rainfall outside the watershed and not necessarily through the gauge. The major soil type is chromic Luvisols [44]. The soil depth of the watershed ranges from 25 cm to 95 cm. The dominant land use is agricultural, which covers 70% of the total land area. The livelihood of the community depends on rain-fed agriculture. Barley, wheat, and potatoes are the major crops.
In 2011 and 2012, soil and water conservation practices were installed in the Tikur-Wuha watershed under the auspices of the Tana-Beles Project, which is aimed at increasing dry season baseflow and reducing the sediment load from the upper catchment. The land management practices included site specific structural conservation techniques such as 50–60 cm deep infiltration furrows with soil bunds downhill (some of which were faced with stones) and stone bunds, waterways, cut off drains, gully rehabilitation with gabions and check dams, hillside terracing, micro basins, and planting of fodder and woodlots on communal lands. In two years, 18% of the Tikur-Wuha watershed was treated with conservation practices. More detailed information is given in [30].
2.2. Data Collection
Temperature: The daily temperature from 2010 to 2015 was collected for the Debra Tabor meteorological station from the Bahir Dar branch of the National Meteorological Agency. The Debra Tabor station is located 18 km from the watershed.
Precipitation: Rainfall was measured using a manual rain gauge that was located in the center of the watershed. In addition, in 2014 and 2015, a tipping bucket rain gauge recorded the 5 min intensity with an accuracy of 0.25 mm.
Infiltration: Soil infiltration rates were measured at 17 sites in the watershed during July and August of 2014 using a single ring infiltrometer [17]. The ring was inserted to a depth of 10 cm, water accumulated inside the ring, and the depth of the infiltrated water was measured using a ruler. Measurement was continued until a steady state was reached.
Discharge: In 2010, a stream gauge station at the outlet of the watershed was established. The stage height was recorded twice a day during base flow conditions and every 30 min during runoff events. The measurements were taken manually. At the same 30 min intervals, the surface flow velocity was measured with a float. The average streamflow velocity was obtained by multiplying surface flow velocity by two thirds and, finally, the discharge was calculated as the product of the wetted cross-section and the average flow velocity. A stage-discharge rating curve was developed by plotting the discharge versus stage height. Additional details can be found in [30].
2.3. Methods
2.3.1. Groundwater Flow Separation
Observed streamflow is the sum of the surface, interflow, and base flow. The portion of each is difficult to identify [45,46]. Mainly two approaches are used in the literature to separate the flow components. These are isotopic and mathematical methods [47]. The applicability of the two approaches varies [13]. Isotope and chemical analysis are expensive and cumbersome to use in developing countries where the instruments are often not in good working condition [48]. Moreover, many factors affect the baseflow calculation such as intra-storm variability of isotopic concentration, elevation effect on the isotopic composition of rain, chemical reactions during runoff formation, and the mixing of components. Calculating the volume of baseflow components using hydrological methods has shown to be an effective alternative to isotope analysis [11,49,50]. The Parameter Efficient Distributed (PED) model was selected for separating baseflow and surface runoff because it needs a minimum input parameter, thereby minimizing equifinality difficulties [51,52]. The PED model was developed for the Ethiopia highlands and outperformed SWAT and HBV in the Lake Tana basin [53].
2.3.2. Hydrological Modeling for Groundwater Flow Separation
The Parameter Efficient Distributed (PED) model was tested and validated in the Ethiopian highlands by a number of researchers [29,52,53,54,55]. We used the model as a mathematical construct to investigate whether the relationship between precipitation, discharge, and groundwater flow has changed due to the implementation of land management practices. Specifically, we used the changes in groundwater flow index (GWFI) to evaluate the effect of land management practices on groundwater flow. The GWFI is the ratio of annual groundwater flow (sum of interflow and baseflow) to the total stream flow.
The Parameter efficient semi-distributed model (PED) is a conceptual water balance model developed by [53] that is based on the saturation excess runoff principle. The model conceptually divides the watershed into three regions consisting of (i) the saturated and (ii) degraded areas, both producing surface runoff (qr1 and qr2), and (iii) the permeable areas upon which rainwater infiltrates and either flows as interflow to the outlet (qi) or recharges the groundwater and eventually produces baseflow (qb). These areas are fractionally represented as A1, A2, and A3 for saturated, degraded, and permeable hillsides, respectively. Areas are degraded when due to hardpan formation, deep percolation is restricted [27]. The other six hydrology parameters that were used in the model are the maximum water storage capacity parameter for the rootzone in each area (Smax1, Smax2, Smax3), the maximum groundwater storage (BSmax), the duration of the interflow (τ*), and the half-life of the aquifer (t½).
The basic water balance for the catchment area for a time step of Δt is:
where P is precipitation, (mm day−1); E is the actual evapotranspiration, (mm day−1), S(t−Δt) is previous time step storage, (mm), R is saturation excess runoff (mm day−1), Perc is percolation to the subsoil (mm day−1), and Δt is the time step. The Thornthwaite-Mather procedure [56] was used for calculating the actual evaporation. Overland flow was simulated as any excess rainfall above the maximum storage Smax1 and Smax2 from areas A1 (periodically saturated) and A2 (degraded). Percolation that becomes recharge was predicted as excess rainfall above the storage at field capacity Smax3 for area A3 (hillside). Since the groundwater was shallow, the time delay between percolation and recharge was minimal and ignored. Finally, the groundwater reservoir was simulated as a linear reservoir with a half-life t½ and the interflow reservoir is a zero-order reservoir with a fixed time after the rainstorm that the interflow stops. More detailed information of the model can be found in [52,53].
The model parameters were manually calibrated by varying parameters to achieve the best goodness of fit between the simulated and observed flow [52]. Then, the ratio of groundwater flow to the total simulated flow was calculated to estimate the groundwater flow index (GWFI) of the watershed. Nash-Sutcliffe Efficiency (NSE) and coefficient of determination (R2) with least square linear regression were applied to evaluate the performance of the model for the calibration periods. The climate inputs to the model consisted of rainfall and potential evaporation. The rainfall was measured and the potential evaporation rate was calculated using the method developed from daily temperature data [57].
3. Results
3.1. Preciptation
The average annual rainfall from 2010 to 2015 of the watersheds was 1518 mm a−1. Most of the rain was recorded in 2011 (1676 mm a−1) and the lowest annual rainfall was in 2015, which was 1176 mm a−1 (Table 1). The maximum 5 min rainfall intensity was 134 mm h−1 in 2014 and 432 mm h−1 in 2015 (Figure 2).

Table 1.
Monthly rainfall amount and observed flow (mm) of the Tikur-Wuha watershed from 2010 to 2015.
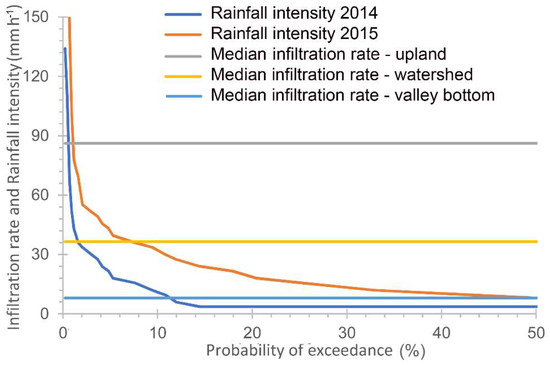
Figure 2.
Rainfall intensity and the infiltration rate of the Tikur-Wuha watershed.
The steady state infiltration rate ranged from 7 mm h−1 for the saturated soils of the valley bottom to 117 mm h−1 upslope (Figure 2). The median infiltration is the most meaningful for the comparison of infiltration with rainfall intensity [58,59]. The steady state median infiltration was 8 mm h−1 for the valley bottom soil, which was lower than the rainfall intensity in 50% of the rainfall events in 2015 and 11% in 2014. Only 0.5% of the rainfall storms had intensities that were greater than the median steady state infiltration rate of 88 mm h−1 of the upland soils in both years. Thus, the likelihood of surface runoff in the saturated valley bottom soils is many times greater than for the uplands (Figure 2).
3.2. Discharge at the Outlet
Most of the discharge at the outlet occurred in the rain phase from late May to September (Table 2). The runoff and the rainfall in the rain phase are obviously related. The precipitation of 500 mm was high in July 2011 and 458 mm in August 2011 (Table 1). These months also had the highest runoff of 110 mm month−1 in July and 125 mm month−1 in August 2011. In 2014, August had more discharge than July, despite the fact that the rainfall was lower because water that was stored in the watershed from July was released as groundwater flow in August (Table 1). During the dry phase, the interflow was negligible and the groundwater flow consists only of base flow without contributions of interflow. It is difficult to discern the effect of land management from the data in Table 1.

Table 2.
Nash Sutcliff coefficient (Nash) and regression coefficient R2 for model calibration of daily discharge in the Tikur-Wuha watershed from 2010 to 2015. Each year was calibrated separately.
3.3. Assessing Changes in the Hydrology Watershed with the Parameter Efficient Distributed Model
The PED model was used as a mathematical construct for characterizing the change in the relationship between precipitation and discharge. The best fit of the rainfall to the daily discharge was obtained for each year (Figure 3). The following rules were followed in fitting the data. The subsurface and the root zone parameters were kept the same because they were not affected by the installation of the management practices; similar to [30], fitting the model to discharge in the Anjeni watershed, we only varied the degraded and hillslope area between the years. The fit between the observed and predicted daily streamflow was good, with Nash Sutcliff values ranging from 0.63 to 0.90 (Table 2) and correlation coefficient values ranging from 0.64 to 0.9 (Table 2, Figure 3 and Figure 4). The fitted parameters for each year are shown in Table 3.
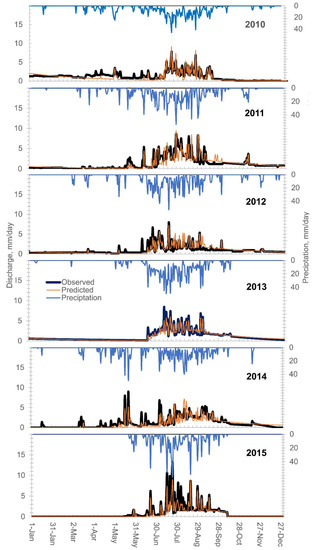
Figure 3.
Daily rainfall observed and predicted runoff of the model hydrograph of the Tikur-Wuha watershed from 2010 to 2015.
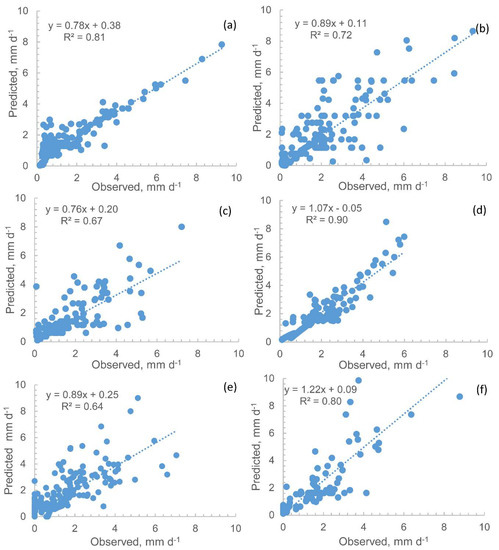
Figure 4.
Observed and PED model predicted daily discharge of the Tikur-Wuha watershed from 2010 to 2015: (a) 2010; (b) 2011; (c) 2012; (d) 2013; (e) 2014; (f) 2015.

Table 3.
Parameter Efficient Distributed (PED) model parameters of the Tikur-Wuha watershed from 2010 to 2015.
The contributing area (i.e., the sum of the saturated, degraded, and hillside areas, Table 3) of the watershed to the gauging station varied between 0.32–0.41. The lowest value was in 2013 when flows were underestimated (Table 3). Consequently, the rain falling on approximately 60% of the watershed area became deep percolation and likely leaved the watershed through quaternary volcanic features, such as faults, which are highly permeable [43]. The flow appears as springs at lower elevations and is not accounted for at the weir at the outlet. Several other watersheds in the region have the same high deep percolation losses, such as the Ribb watershed in which 50%–60% of the flow is unaccounted for at the outlet [54], the Enkula watershed in which only half of the area contributes to the watershed [52], and, finally, the Gomit watershed in which more than 60% is lost as deep percolation, likely to the Takeze basin [60] entering the Nile in Sudan. Almost all watersheds in the uplands show deep percolation losses, but not as large as for the watersheds mentioned above [29].
Before implementation of the land management practices in 2010, the degraded hill slope area comprised 15% of the watershed and this was decreased to less than 10% after practices were installed (Table 3). At the same time, the permeable hillsides portion of the study areas increased from 6% in 2010 to 35% in 2014 and 28% in 2015 (Table 3). These land management practices consisted of infiltration furrows, micro basins, and soil bunds. They improve the recharge to shallow groundwater and decrease surface runoff [30,32]. In the PED model, this is modeled as a decrease in the fraction of degraded hillside lands with limited infiltration capacity in the subsoil [29,52,61]. These former degraded lands become permeable hillsides and hence, the permeable hillside fraction increases because of the installation of management practices.
To illustrate the effect of the land management on the discharge, we used the 2010 and 2013 input values to simulate the cumulative total discharge at the outlet in the other years (Figure 5). Using the hillside fractions of 6% and degraded fractions of 15% (obtained from fitting the 2010 data before the practices were implemented), the PED model overpredicts the observed discharge for the period 2011–2015 (red broken line in Figure 5), indicating that more of the precipitation became discharge during the first year compared with later years. This was likely due to the effect of management practices, which enhance the infiltration of rainfall deeper in the soil profile. In addition, as expected, the data of 2013 with a degraded fraction of 5% and a hillslope fraction of 22% as input to the other years (green line in Figure 5) underpredicts the observed discharge in 2010 before the land management practices were implemented.
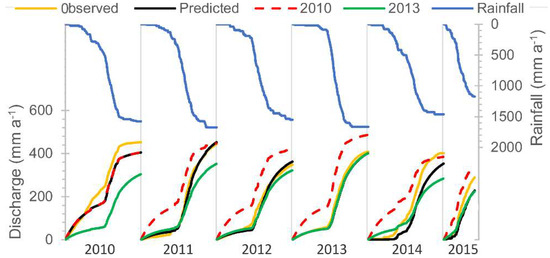
Figure 5.
Cumulative discharge for the Tikur-Wuha watershed for the period of 2010–2015. The blue lines are the observed data. The black lines represent the simulated discharge with the parameter set calibrated for the various periods. The broken red line represents the simulated discharge with the parameters set calibrated for 2010 and the green line indicates 2013. The parameter values are given in Table 3.
3.4. Groundwater Flow Index
The amount of subsurface flow was simulated by the PED model. The model results showed that the outflow could be best explained by a linear reservoir (Table 3) rather than a zero-order model, indicating that major subsurface flow at the outlet was not interflow in the shallow surface layer, but baseflow from an aquifer with relatively little slope. Apparently, most interflow was captured by the faults and all outflow consisted of baseflow. By taking the ratio of the annual subsurface flow and total flow, the groundwater flow index (GWFI) was calculated (Table 4). From the analysis, ground-water contributed up to 69% of the total flow in the Tikur-Wuha watershed (Table 4). The GWFI is increasing with cumulative rainfall both before and after implementation of the land management practices (Figure 6, Table 4). At the same time, for equal rainfall amounts, the GWFI is less (average of 62%) before implementation than after (average 64%) (Figure 6, Table 4). Although many studies in Ethiopian highlands have noted either no change [29] or a decrease in total discharge [17,32,34,62] due to soil and water conservation practices, to the best of our knowledge, there is only one other study that found that soil and water conservation practices increase base flow [63]. Thus, while overall these structural practices do not increase the biomass from the watershed [36], biomass production during the dry phase might potentially increase downstream because more base flow is available for irrigation.

Table 4.
Groundwater flow index (GWFI) for the period 2010–2015 based on hydrological model results of the Tikur-Wuha watershed. Note that the amounts are given as a volume of the contributing area to the gauge divided by the total area of the watershed. In 2015, the data represent the period from 15 May to 22 October.
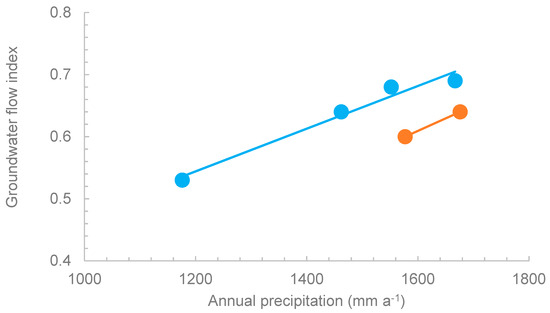
Figure 6.
Groundwater flow index (GWFI) versus the annual precipitation before (2010 and 2011) and after (2012–2015) the implementation of land management.
4. Discussion
The PED model was used to separate groundwater flow from the direct runoff. The PED model has been tested widely and generally is able to predict the discharge with the same or better accuracy than complex models that require more parameters for calibration [53,54]. Unlike the complex models, the PED model is limited to landscapes in which infiltration rates exceeds that of the saturated conductivity of the soil most of the time. Figure 2 shows that for the uplands, this requirement is met 99.5% of the time. However, for the valley bottom lands, in as much as 50% of the rainstorms, the infiltration capacity was exceeded (Figure 2). Since the infiltration measurements were carried out during the rain phase, the low infiltration rate was not caused by a limited saturated conductivity, but soil saturation where the rainwater could not be stored in the soil [17,58,64]. Saturation-excess runoff is the basis on which the PED model provides such good discharge predictions because the complex conductivity field that is needed for predicting infiltration-excess runoff is replaced by a regular water balance that simulates when the soil becomes saturated [57,61,64,65]. It is, therefore, interesting that the greater exceedance of the infiltration rate in 2015 for the valley bottom lands (Figure 2) is clearly reflected in Figure 3, with the much higher discharge peaks in 2015 compared to 2014.
The PED model has two regions (i.e., saturated bottom lands and degraded hillsides) that produce saturated excess runoff. The saturation of the valley bottom lands is caused by more water entering from the sloping uplands than can be transported by lateral flow to the stream. The saturation of the degraded soils is caused by the slowly permeable hardpan preventing deep percolation so that water is mainly removed by evaporation. When precipitation is greater than the evaporation, the soil becomes saturated and saturation excess runoff takes place. Land management practices that improve the percolation through the hardpan will, therefore, lower the direct runoff in favor of deep percolation and baseflow. Besides the direct runoff simulation routine, the groundwater flow is predicted in the Tikur Wuha watershed by collecting the percolation from the permeable hillside in a linear reservoir, which likely consists of several smaller reservoirs that together give the signal of a linear reservoir [66]. Figure 3 shows that the fit with the observed stream discharge during the low flow at the outlet is a good indicator that the assumption of a linear reservoir provides good baseflow predictions.
In fitting the PED model to the observed discharge, we found that 5% of the area was periodically saturated for each year (Table 3). At the same time, the degraded hillside areas decreased from 15% in 2010 to as little as 5% in 2013 due to the implementation of soil and water conservation practices including planting trees, implementing enclosures, and construction of stone and earthen bunds on the contour with 50 cm deep furrows [17,67]. The permeable hillside of the watershed increased from 14% in 2010 to 35% of the watershed areas in 2014 due to the implementation of these practices (Table 2).
The decrease in degraded hillside and the increase in permeable hillside due to land management practices resulted in less direct runoff and more water infiltrated in the rootzone, some of which became available for baseflow. The annual simulated evaporation was more influenced by the duration of the land management practices, since in the rain phase, evaporation was at the potential rate. Table 4 and Figure 5 show that in the years 2013 and 2015 with the shortest rainfall duration, annual evaporation was the least of the five years. In contrast, in 2014 when the rain started early and ended late (Figure 5), annual evaporation for the year was the highest (Table 4).
The groundwater contribution to the total streamflow mainly increased with increasing annual rainfall (Figure 6). In addition, there was a small effect from the installation of land management practices (Figure 6; Table 4) because at the same amount of rainfall, the GWFI before the installation (orange line) was smaller than the GWFI (blue line) after the installation. Several other studies also found that conservation practices decrease direct runoff (improved 10-year data, but few were able to show the effect on inter and baseflow). Finally, it would be desirable to measure discharge at the outlet again at a later date to investigate whether these changes are permanent [17,30].
5. Conclusions
Little is known about the effect of land management practices on surface and groundwater flow at a watershed scale in the Ethiopian highlands where land management practices are widely installed to combat land degradation. To evaluate the effect of these practices, discharge and precipitation were measured in the Tikur-Wuha watershed over a six-year period. During this period, land management practices were installed. They consisted of gully rehabilitation, land enclosures, infiltration furrows with bunds, stone bunds, waterways, planting of trees and fodder plantation, and treatment of degraded lands. The Parameter Efficient Distributed (PED) model was used as a mathematical construct to examine whether the relationship between precipitation, discharge, and groundwater flow was changing due to the effect of the land management practices. We found that over the six-year period, the base flow increased with increasing rainfall and with a number of land management practices installed. Thus, more of the precipitation infiltrated and less surface runoff was generated. The PED model fitted the runoff pattern well and allowed us to tease out the effect of changes in the watershed from the measured discharge.
Author Contributions
A.T.A., S.A.T., M.A.M., and T.S.S. conceived and designed the experiments; A.T.A. performed the experiments; A.T.A., M.A.M., and D.C.D. analyzed the data; A.T.A. and T.S.S. wrote the paper with the aid of S.A.T., D.C.D., and M.A.M.
Funding
Partial funding was provided by The Borlaug LEAP, and Partnerships for Enhanced Engagement in Research (PEER, grant number AID-OAA-A-11-00012) administered by the National Academies of Sciences, Engineering, Medicine of the USA for the fellowship of the first author and research support.
Acknowledgments
Data for this research work was obtained from the Tana-Beles Integrated Water Resources Development Project and onsite data were collected by the researchers. We would like to thank the project team for their time and unwavering support for data compilation, Finally, we thank Marin Cherry for improving our English.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaur, J. Involvement of Women in the Management of Selected Natural Resources in Kandi Area of Punjab; Diss. Punjab Agricultural University: Ludhiana, India, 2016. [Google Scholar]
- Xing, M.A. Response of hydrological processes to land-cover and climate changes in Kejie watershed, south-west China. Hydrol. Proc. Int. J. 2009, 23, 1179–1191. [Google Scholar] [CrossRef]
- Schilling, K.E.; Libra, R.D. Increased baseflow in Iowa over the second half of the 20th century. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 851–860. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Line, D.E.; White, N.M. Effects of development on runoff and pollutant export. Water Environ. Res. 2007, 79, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Worqlul, A.W.; Collick, A.S.; Rossiter, D.G.; Langan, S.; Steenhuis, T.S. Assessment of surface water irrigation potential in the Ethiopian highlands: The Lake Tana Basin. Catena 2015, 129, 76–85. [Google Scholar] [CrossRef]
- Brodie, R.S.; Hostetler, S.; Slatter, E. Comparison of daily percentiles of streamflow and rainfall to investigate stream–aquifer connectivity. J. Hydrol. 2008, 349, 56–67. [Google Scholar] [CrossRef]
- Welderufael, W.A.; Woyessa, Y.E. Stream flow analysis and comparison of methods for base flow separation: Case study of the Modder River basin in central South Africa. Interim Interdiscip. J. 2009, 8, 107–119. [Google Scholar]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Wittenberg, H. Effects of season and man-made changes on baseflow and flow recession: Case studies. Hydrol. Proc. 2003, 17, 2113–2123. [Google Scholar] [CrossRef]
- Liu, D.; Chang, J.; Tian, F.; Huang, Q.; Meng, X. Analysis of baseflow index based hydrological model in Upper Wei River basin on the Loess Plateau in China. Remote Sens. GIS Hydrol. Water Resour. 2015, 368, 403–408. [Google Scholar] [CrossRef][Green Version]
- Miller, M.P.; Buto, S.G.; Susong, D.D.; Rumsey, C.A. The importance of base flow in sustaining surface water flow in the Upper Colorado River Basin. Water Resour. 2016, 52, 3547–3562. [Google Scholar] [CrossRef]
- Gonzales, A.L.; Nonner, J.; Heijkers, J.; Uhlenbrook, S. Comparison of different base flow separation methods in a lowland catchment. Hydrol. Earth Syst. Sci. 2009, 13, 2055–2068. [Google Scholar] [CrossRef]
- Abiy, A.Z.; Demissie, S.S.; MacAlister, C.; Dessu, S.B.; Melesse, A.M. Groundwater Recharge and Contribution to the Tana Sub-basin, Upper Blue Nile Basin, Ethiopia. In Landscape Dynamics, Soils and Hydrological Processes in Varied Climates; Springer: Cham, Switzerland, 2016; pp. 463–481. [Google Scholar] [CrossRef]
- Rittenburg, R.A.; Squires, A.L.; Boll, J.; Brooks, E.S.; Easton, Z.M.; Seenhuis, T.S. Agricultural BMP Effectiveness and Dominant Hydrological Flow Paths: Concepts and a Review. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 305–329. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Schilling, K.E. Increasing streamflow and baseflow in Mississippi River since the 1940s: Effect of land use change. J. Hydrol. 2006, 324, 412–422. [Google Scholar] [CrossRef]
- Dagnew, C.D.; Guzman, C.D.; Zegeye, A.D.; Tebebu, T.Y.; Getaneh, M.; Abate, S.; Zimale, F.A.; Ayana, E.K.; Tilahun, S.A.; Steenhuis, T.S. Impact of conservation practices on runoff and soil loss in the sub-humid Ethiopian Highlands: The Debre Mawi watershed. J. Hydrol. Hydromech. 2015, 63, 210–219. [Google Scholar] [CrossRef]
- Potter, K.W. Hydrological impacts of changing land management practices in a moderate-sized agricultural catchment. Water Resour. Res. 1991, 27, 845–855. [Google Scholar] [CrossRef]
- Juckem, P.F.; Hunt, R.J.; Anderson, M.P.; Robertson, D.M. Effects of climate and land management change on streamflow in the driftless area of Wisconsin. J. Hydrol. 2008, 355, 123–130. [Google Scholar] [CrossRef]
- Price, K.; Jackson, C.R. Effects of forest conversion on baseflow in the southern Appalachians: A cross-landscape comparison of synoptic measurements. In Proceedings of the Georgia Water Resources Conference, Athens, Greece, 27–29 March 2007. [Google Scholar]
- Schilling, K.E.; Jha, M.K.; Zhang, Y.-K.; Gassman, P.W.; Wolter, C.F. Impact of land use and land cover change on the water balance of a large agricultural watershed: Historical effects and future directions. J. Water Resour. 2008, 44. [Google Scholar] [CrossRef]
- Huang, X.D.; Shi, Z.H.; Fang, N.F.; Li, X. Influences of land use change on baseflow in mountainous watersheds. Forests 2016, 7, 16. [Google Scholar] [CrossRef]
- Abate, M.; Nyssen, J.; Moges, M.M.; Enku, T.; Zimale, F.A.; Tilahun, S.A.; Adgo, E.; Steenhuis, T.S. Long-term landscape changes in the lake tana basin as evidenced by delta development and floodplain aggradation, Ethiopia. Land Degrad. Devel. 2016, 28, 1820–1830. [Google Scholar] [CrossRef]
- Tebebu, T.Y.; Bayabil, H.K.; Stoof, C.R.; Giri, S.K.; Gessess, A.A.; Tilahun, S.A.; Steenhuis, T.S. Characterization of degraded soils in the humid Ethiopian highlands. Land Degrad. Devel. 2017, 28, 1891–1901. [Google Scholar] [CrossRef]
- Fenta, A.A.; Yasuda, H.; Shimizu, K.; Haregeweyn, N. Response of streamflow to climate variability and changes in human activities in the semiarid highlands of northern Ethiopia. Reg. Environ. Chang. 2017, 17, 1229–1240. [Google Scholar] [CrossRef]
- Lanckriet, S.; Araya, T.; Cornelis, W.; Verfaillie, E.; Poesen, J.; Govaerts, B.; Bauer, H.; Deckers, J.; Haile, M.; Nyssen, J. Impact of conservation agriculture on catchment runoff and soil loss under changing climate conditions in May Zeg-zeg (Ethiopia). J. Hydrol. 2012, 475, 336–349. [Google Scholar] [CrossRef]
- Tebebu, T.Y.; Steenhuis, T.S.; Dagnew, D.C.; Guzman, C.D.; Bayabil, H.K.; Zegeye, A.D.; Collick, A.S.; Langan, S.; MacAlister, C.; Langendoen, E.J.; et al. Improving efficacy of landscape interventions in the (sub) humid Ethiopian highlands by improved understanding of runoff processes. Front. Earth Sci. 2015, 3, 49. [Google Scholar] [CrossRef]
- Gebreegziabher, T.; Nyssen, J.; Govaerts, B.; Getnet, F.; Behailu, M.; Haile, M.; Deckers, J. Contour furrows for in situ soil and water conservation, Tigray, Northern Ethiopia. Soil Tillage Res. 2009, 103, 257–264. [Google Scholar] [CrossRef]
- Akale, A.; Dagnew, D.; Belete, M.; Tilahun, S.; Mekuria, W.; Steenhuis, T. Impact of soil depth and topography on the effectiveness of conservation practices on discharge and soil loss in the Ethiopian highlands. Land 2017, 6, 78. [Google Scholar] [CrossRef]
- Guzman, C.D.; Zimale, F.A.; Tebebu, T.Y.; Bayabil, H.K.; Tilahun, S.A.; Yitaferu, B.; Rientjes, T.H.; Steenhuis, T.S. Modeling discharge and sediment concentrations after landscape interventions in a humid monsoon climate: The Anjeni watershed in the highlands of Ethiopia. Hydrol. Proc. 2017, 31, 1239–1257. [Google Scholar] [CrossRef]
- Melaku, N.D.; Renschler, C.S.; Flagler, J.; Bayu, W.; Klik, A. Integrated impact assessment of soil and water conservation structures on runoff and sediment yield through measurements and modeling in the Northern Ethiopian highlands. Catena 2018, 169, 140–150. [Google Scholar] [CrossRef]
- Ayele, G.K.; Addisie, M.B.; Langendoen, E.J.; Tegegne, N.H.; Tilahun, S.A.; Moges, M.A.; Nicholson, C.F.; Steenhuis, T.S. Evaluating erosion control practices in an actively gullying watershed in the highlands of Ethiopia. Earth Surf. Proc. Landf. 2018, 43, 2835–2843. [Google Scholar] [CrossRef]
- Adgo, E.; Teshome, A.; Mati, B. Impacts of long-term soil and water conservation on agricultural productivity: The case of Anjenie watershed, Ethiopia. Agric. Water Manag. 2013, 117, 55–61. [Google Scholar] [CrossRef]
- Adimassu, Z.; Langan, S.; Johnston, R.; Mekuria, W.; Amede, T. Impacts of Soil and Water Conservation Practices on Crop Yield, Run-off, Soil Loss and Nutrient Loss in Ethiopia: Review and Synthesis. Environ. Manag. 2017, 59, 87–101. [Google Scholar] [CrossRef] [PubMed]
- Mhiret, D.A.; Dagnew, D.C.; Guzman, C.D.; Alemie, T.C.; Zegeye, A.D.; Tebebu, T.Y.; Langendoen, E.; Zaitchik, B.F.; Tilahun, S.A.; Steenhuis, T.S. The Debre Mawi Watershed: A nine-year study on the benefits and risks of soil and water conservation practices in the humid highlands of Ethiopia. [submitted].
- Mhiret, D.A.; Dagnew, D.C.; Tilahun, S.A.; Zaitchik, B.F.; Steenhuis, T.S. Impact of conservation practices, gullies, and eucalyptus trees on discharge and sediment loss in a degraded watershed in the humid Ethiopian highlands. [submitted].
- Enku, T.; Melesse, A.; Ayana, E.; Tilahun, S.; Abate, M.; Steenhuis, T. Response of Groundwater table to Eucalyptus Plantations in a Tropical Monsoon Climate, Lake Tana Basin, Ethiopia. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2017; Volume 19, p. 4652. [Google Scholar]
- Haregeweyn, N.; Tsunekawa, A.; Tsubo, M.; Meshesha, D.; Adgo, E.; Poesen, J.; Schütt, B. Analyzing the hydrologic effects of region-wide land and water development interventions: A case study of the Upper Blue Nile basin. Reg. Environ. Change 2016, 16, 951–966. [Google Scholar] [CrossRef]
- Addisie, M.B.; Ayele, G.K.; Gessess, A.A.; Tilahun, S.A.; Zegeye, A.D.; Moges, M.M.; Schmitter, P.; Langendoen, E.J.; Steenhuis, T.S. Gully head retreat in the sub-humid Ethiopian highlands: The Ene-Chilala catchment. Land Degrad. Dev. 2017, 28, 1579–1588. [Google Scholar] [CrossRef]
- Lemann, T.; Zeleke, G.; Amsler, C.; Giovanoli, L.; Suter, H.; Roth, V. Modelling the effect of soil and water conservation on discharge and sediment yield in the upper Blue Nile basin, Ethiopia. Appl. Geogr. 2016, 73, 89–101. [Google Scholar] [CrossRef]
- Betrie, G.D.; Mohamed, Y.A.; van Griensven, A.; Srinivasan, R. Sediment management modelling in the Blue Nile Basin using SWAT model. Hydrol. Earth Syst. Sci. 2011, 15, 807. [Google Scholar] [CrossRef]
- Akale, A.T.; Dagnew, D.C.; Giri, S.; Belete, M.A.; Tilahun, S.A.; Mekuria, W.; Steenhuis, T.S. Groundwater quality in an upland agricultural watershed in the sub-humid Ethiopian highlands. J. Water Resour. Prot. 2017, 9, 1199. [Google Scholar] [CrossRef]
- Kebede, S.; Travi, Y.; Alemayehu, T.; Ayenew, T. Groundwater recharge, circulation and geochemical evolution in the source region of the Blue Nile River, Ethiopia. Appl. Geochem. 2005, 20, 1658–1676. [Google Scholar] [CrossRef]
- Amhara Design and Supervision Works Enterprise (ADSWE). Soil Map of Amhara Region, Land Use and Administration Work Process; Amhara Design and Supervision Works Enterprise (ADSWE): Bahir Dar, Ethiopia, 2012. [Google Scholar]
- Partington, D.; Brunner, P.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C. Evaluation of outputs from automated baseflow separation methods against simulated baseflow from a physically based, surface water-groundwater flow model. J. Hydrol. 2012, 458, 28–39. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Q.; Chow, T.L.; Li, S.; Danielescu, S. Baseflow separation in a small watershed in New Brunswick, Canada, using a recursive digital filter calibrated with the conductivity mass balance method. Hydrol. Proc. 2012, 27, 259–2665. [Google Scholar] [CrossRef]
- Ladouche, B.; Probst, A.; Viville, D.; Idir, S.; Baqué, D.; Loubet, M.; Probst, J.L.; Bariac, T. Hydrograph separation using isotopic, chemical and hydrological approaches (Strengbach catchment, France). J. Hydrol. 2001, 242, 255–274. [Google Scholar] [CrossRef]
- Joerin, C.; Beven, K.J.; Iorgulescu, I.; Musy, A. Uncertainty in hydrograph separations based on geochemical mixing models. J. Hydrol. 2002, 255, 90–106. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. An artificial neural network model for generating hydrograph from hydro-meteorological parameters. J. Hydrol. 2005, 315, 236–251. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Proc. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Tilahun, S.A.; Guzman, C.D.; Zegeye, A.D.; Engda, T.A.; Collick, A.S.; Rimmer, A.; Steenhuis, T.S. An efficient semi-distributed hillslope erosion model for the sub-humid Ethiopian Highlands. Hydrol. Earth Syst. Sci. 2013, 17, 1051–1063. [Google Scholar] [CrossRef]
- Moges, M.A.; Schmitter, P.; Tilahun, S.A.; Langan, S.; Dagnew, D.C.; Akale, A.T.; Steenhuis, T.S. Suitability of watershed models to predict distributed hydrologic response in the Awramba watershed in lake Tana basin. Land Degrad. Dev. 2017, 28, 1386–1397. [Google Scholar] [CrossRef]
- Zimale, F.A.; Moges, M.A.; Alemu, M.L.; Ayana, E.K.; Demissie, S.S.; Tilahun, S.A.; Steenhuis, T.S. Budgeting suspended sediment fluxes in tropical monsoonal watersheds with limited data: The Lake Tana basin. Journal of Hydrology and Hydromechanics. J. Hydrol. Hydromech. 2018, 66, 65–78. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; Collick, A.S.; Easton, Z.M.; Leggesse, E.S.; Bayabil, H.K.; White, E.D.; Ahmed, A.A. Predicting discharge and sediment for the Abay (Blue Nile) with a simple model. Hydrol. Proc. 2009, 23, 3728–3737. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; van der Molen, W.H. The Thornthwaite-Mather Procedure as a Simple Engineering Method to Predict Recharge. J. Hydrol. 1986, 84, 221–229. [Google Scholar] [CrossRef]
- Enku, T.; Melesse, A.M. A simple temperature method for the estimation of evapotranspiration. Hydrol. Proc. 2014, 28, 2945–2960. [Google Scholar] [CrossRef]
- Bayabil, H.K.; Tilahun, S.A.; Collick, A.S.; Yitaferu, B.; Steenhuis, T.S. Are runoff processes ecologically or topographically driven in the (sub) humid Ethiopian highlands? The case of the Maybar watershed. J. Ecohydrol. 2010, 3, 457–466. [Google Scholar] [CrossRef]
- Moges, M.A.; Zimale, F.A.; Alemu, M.L.; Ayele, G.K.; Dagnew, D.C.; Tilahun, S.A.; Steenhuis, T.S. Sediment concentration rating curves for a monsoonal climate: Upper Blue Nile Basin. Soil 2016, 2, 337–349. [Google Scholar] [CrossRef]
- Adem, A.A.; Aynalem, D.W.; Addis, G.G.; Tilahun, S.A.; Mekuria, W.; Belete, M.A.; Steenhuis, T.S. Runoff and soil loss of an uphill reforested and a downstream conserved agricultural Ethiopian faulted highland watershed. 2019; [submitted]. [Google Scholar]
- Tesemma, Z.K.; Mohamed, Y.A.; Steenhuis, T.S. Trends in rainfall and runoff in the Blue Nile Basin: 1964–2003. Hydrol. Proc. 2010, 25, 3747–3758. [Google Scholar] [CrossRef]
- Dagnew, D.C.; Guzman, C.D.; Zegeye, A.D.; Akal, A.T.; Moges, M.A.; Tigist, T.Y.; Mekuria, W.; Ayana, E.K.; Tilahun, S.A.; Steenhuis, T.S. Sediment loss patterns in the sub-humid Ethiopian highlands. Land Degrad. Dev. 2016, 28, 1795–1805. [Google Scholar] [CrossRef]
- Opolot, E.; Araya, T.; Nyssen, J.; Al-Barri, B.; Verbist, K.; Cornelis, W.M. Evaluating in Situ Water and Soil Conservation Practices with a Fully Coupled, Surface/Subsurface Process-Based Hydrological Model in Tigray, Ethiopia. Land Degrad. Dev. 2013, 27, 1840–1852. [Google Scholar] [CrossRef]
- Collick, A.S.; Easton, Z.M.; Ashagrie, T.; Biruk, B.; Tilahun, S.; Adgo, E.; Awulachew, S.B.; Zeleke, G.; Steenhuis, T.S. A simple semi-distributed water balance model for the Ethiopian highlands. Hydrol. Proc. 2009, 23, 3718–3727. [Google Scholar] [CrossRef]
- Tilahun, S.A.; Mukundan, R.; Demisse, B.A.; Engda, T.A.; Guzman, C.D.; Tarakegn, B.C.; Easton, Z.M.; Collick, A.S.; Zegeye, A.D.; Schneiderman, E.M.; et al. A saturation excess erosion model. Trans. ASABE 2013, 56, 681–695. [Google Scholar] [CrossRef]
- Malvicini, C.F.; Steenhuis, T.S.; Walter, M.T.; Parlange, J.-Y.; Walter, M.F. Evaluation of spring flow in the uplands of Matalom, Leyte, Philippines. Adv. Water Resour. 2005, 28, 1083–1090. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Tsunekawa, A.; Poesen, J.; Tsubo, M.; Meshesha, D.T.; Fenta, A.A.; Nyssen, J.; Adgo, E. Comprehensive assessment of soil erosion risk for better land use planning in river basins: Case study of the Upper Blue Nile River. Sci. Total Environ. 2017, 574, 95–108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).