1. Introduction
Dams are constructed as water storage to compensate for fluctuations in the catchment area and to generate electricity. Efficient operation of existing water infrastructures is considered important for effective water resources management. However, uncontrollable amounts of discharges released from the dam discharge structure have caused failures of dams [
1]. Accidents due to a high level of energy being stored in the reservoir will give a negative impact on the downstream area and have disastrous effects on environment, society and economy [
2]. Provision of a hydraulically efficient and structurally strong discharge structure is very significant for the safety of the dam, the life and property along the river down below [
3,
4,
5]. It is crucial that these structures are optimized functionally and economically in the individual project. Therefore, understanding how the operation of a newly built reservoir affects the downstream river flow is vital for protecting human life and property downstream.
A study on the flow through the hydraulic structures is usually conducted using physical modeling. Physical modeling is based on the fluid mechanic equations to construct a scaled laboratory model from the prototype. This approach is a safe way to analyze the flow-through or over the hydraulic structures. Boes and Hager [
6] carried out a benchmark experimental study in a large flume for the onset of skimming flows, and they discussed the energy dissipation features of the stepped spillways. Semi-empirical equations have been developed to aid in the design of actual discharge structure and to lessen the need for individual experimental model studies [
7,
8]. Due to high cost of laboratory experiments and confinements of empirical equations, researchers have attempted to adopt numerical simulation to check the working conditions of hydraulic structures [
9,
10,
11]. Li et al. [
12] simulated the joint flood discharge with the surface outlet and bottom outlet of a dam. The energy dissipation rate is enhanced by effective operation rules to stabilize the downstream flow regimes.
Rapidly varied flow having large streamline curvatures exerts non-hydrostatic pressure distribution over the dam discharge structure surface. The enormous three-dimensional (3D) effect of dam discharge flow reveals that two-dimensional (2D) assumptions in solving such problems are inadequate [
13,
14,
15]. 3D numerical simulation comes into sight gradually because it can yield a high-resolution outcome and vividly display the variation of physical parameters in the flow field [
16]. In fact, 3D flood numerical simulation can be used to judge disaster losses in terms of visual experience. More concretely, it can qualitatively and quantitatively assess flood hazards and render visual reference for the development of flood control schemes, providing an important foundation for flood forecasting, dam design, and flood control system application [
17]. The 3D simulation is approximately equivalent to the reality in terms of landform and boundary conditions. Therefore, the results are more accurate and convincing, and it is widely available in practical engineering [
18,
19,
20,
21].
Dam discharge simulation requires an integrated tool that can handle both terrain entities and hydraulic structures. The building information modeling (BIM) method renders an effective approach for the generation of these models. It can provide detailed structure information for spatial objects and manage spatial information in an integrated intelligence way. Nawari et al. [
22] applied the BIM method to construct the hydro-supported structures and improved the design and construction of facilities. Zhong et al. [
23] proposed a proficient BIM workflow for designing hydraulic structures, rendering a theoretical framework for digital modeling. David et al. [
24] assessed the modeling efficiency in construction projects that utilized BIM and suggests that the approach is cost-effective for terrain generation.
Undulating terrain and sophisticated dam structures in river channels could result in complex turbulent flow patterns, including collision, reflection, and vortices [
25]. Discharge at high dams further complicates the flow patterns for high-energy flows pouring down from outlet works and hitting the river channel. An appropriate hydrodynamic model is necessary to capture such a complex flow field. The Reynolds Average Navier-Stokes (RANS) with the RNG k-ε eddy viscosity model for its turbulence closure has been applied widely in flood routing through complex geometries, as well as the Volume of Fluid (VOF) method [
26,
27,
28]. Dai et al. [
29] conducted the high dam discharge simulation with the RNG k-ε turbulence model. The flow motion is calculated by the RANS equations and the VOF is utilized to trace the interface of water and air. They concluded that the integrated application of these three models is applicable to hydraulic engineering research. Zhang et al. [
30] validated the accuracy of RNG k-ε turbulence models for the dam discharge flow and concluded that the RNG turbulence model can perfectly represent the flow at different cross-sections.
The study aims to investigate the hydraulic characteristics of the dam discharge flow and its impact to downstream by coupling uneven terrain and detailed dam structures. The downstream flow field, characterized by the distribution of water depth, pressure, and velocity, is solved to check the dam working conditions under balancing the discharge effects. The objectives of this study are: (1) to explore a novel framework of 3D modeling dam discharge under real terrain and detailed structures, (2) to assess the joint dam discharge energy dissipation rate with surface and bottom outlet under different scenarios, (3) to check the dam operation rules under different water level and conduct the corresponding downstream flood risk assessment.
2. Study Area
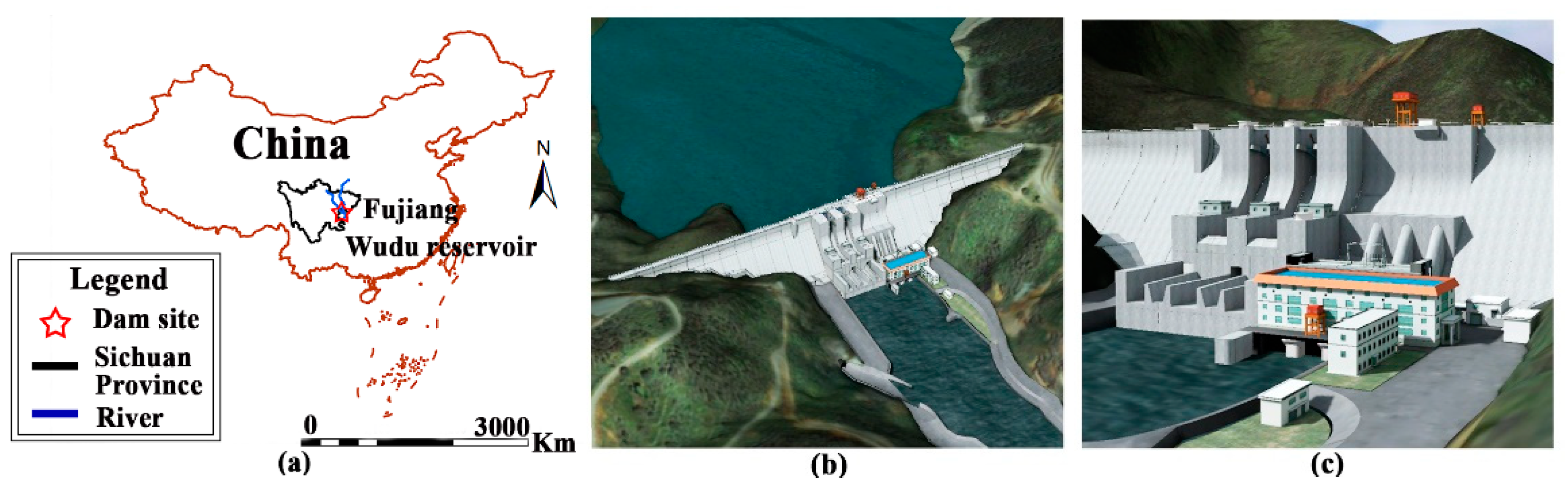
The Wudu reservoir is located on the main stream of the Fujiang River, 4 kilometers upstream of Wudu Town, Sichuan Province, China, as shown in
Figure 1.
To date, the Wudu Reservoir is the largest water control project on the Fujiang River. The hydraulic complex comprises a river dam and a power plant. The surface spillway and the bottom outlet can be utilized to release the surplus flood. The dam is a roller-compacted concrete gravity dam with a maximum height of 120 m, a crest length of 727 m and a reservoir capacity of 572 million m
3. The powerhouse at the dam toe is installed with a capacity of 150,000 KW. The main technical indicators are shown in
Table 1.
3. Materials and Methods
Terrain and hydraulic structures are both indispensable components for numerical simulation. Different approaches are applied to construct these two components. A parametric modeling method is used to build hydraulic structures with regular shapes. Regarding the irregular terrain model, two methods are adopted in the modeling process for the different source data [the surveying control network and digital elevation model (DEM) data]. The difficulty in treating the complex boundaries of the dam structure is overcome by using an unstructured grid to the discrete computational domain. The flow characteristics are calculated based on the RANS equations together with RNG k-ε turbulence model. The RNG k-ε turbulence model, which is suitable for the simulation of complex terrain boundary conditions [
31], is established according to the characteristics of the terrain and structure. The VOF model of the air and water phases can well track the free surface based on the time-dependent simulation.
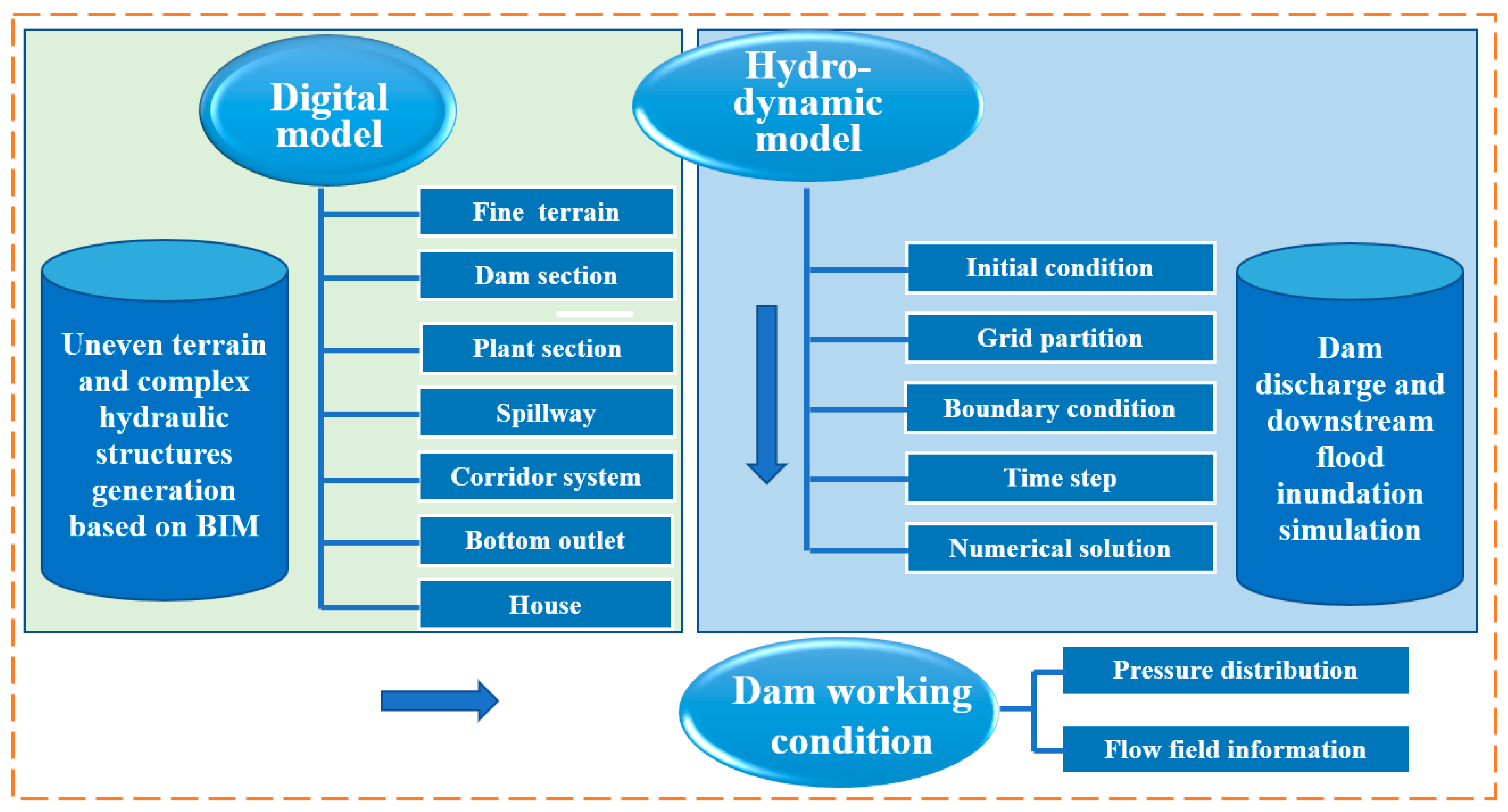
The comprehensive physics-based flood simulation framework has been established, shown in
Figure 2. The digital model is constructed by means of the 3D modeling method, and it comprises the terrain, hydraulic structures, and houses. Then, the high-resolution 3D simulation is conducted and the downstream flow field characteristics are calculated based on the digital model to assess the dam operation rules.
3.1. Hydraulic Structures
As to those hydraulic structures with regular shape, the parametric modeling method is adopted to construct all kinds of parameterized components. The parameterized family is an objective abstraction of models with certain geometric constraints, topological structures, and material partitions. It is a general term for a class of components with geometric similarities, which could be incorporated into a specific component in a project by assigning its variable parameters [
32,
33]. Parameters are divided into two categories: one is the variable dimension parameters, which are used to define the scale of a building, the other is the continuous invariant geometric information, which is used to define the topological constraint relationships between components. The essence of parametric design is that under the action of variable parameters, the system can automatically maintain all the invariant parameters. Therefore, the constraints established in the parametric model could reflect the designer’s intentions. The established parameterized family library such as dam structure, corridors, and radial gates are assembled and integrated into the dam.
3.2. Terrain Generation
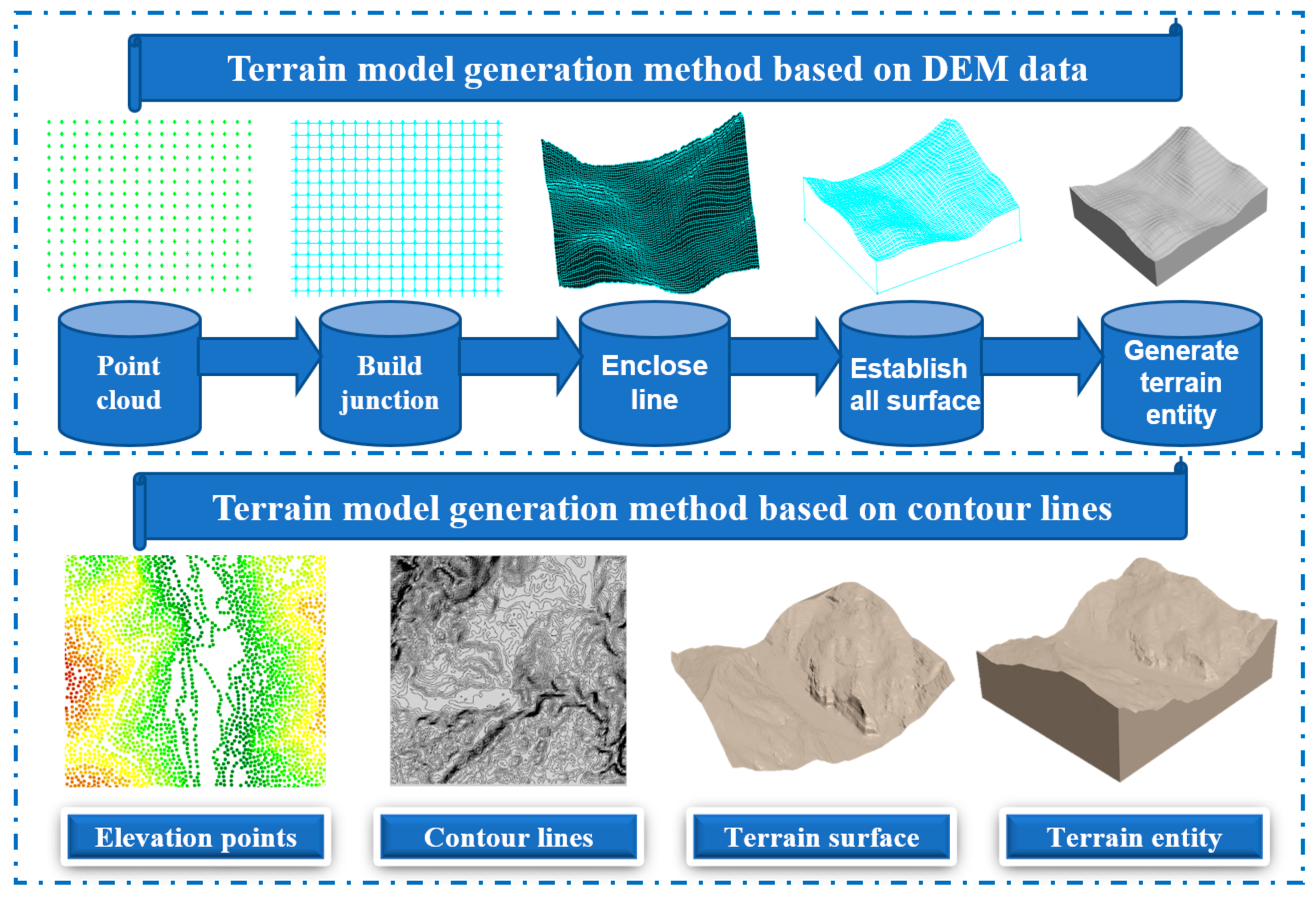
Uneven terrain exerts enormous effect on the flood routing simulation. In this paper, the following two approaches are applied to create the terrain model. After finishing generating the two terrain models, a more accurate terrain entity is selected to complete the flood inundation simulation. Furthermore, the application scope of two terrain modeling methods is discussed.
3.2.1. Terrain Generation Based on DEM Data
To create the terrain with DEM data, the spatial point coordinates should be extracted from the DEM base map by batch processing firstly. The grid points of a fishnet are used as elevation capture points. According to the complexity of the real terrain, the density of the grid point is determined. After extracting the coordinates of the elevation points, we construct points, lines, surfaces, and entities step by step to complete the generation of the terrain. The specific steps are listed as follows: (1) spread the grid points on the DEM layer to extract the coordinates of the points and draw the points in space, (2) connect adjacent points to form the edges, (3) generate the faces with the closed edges, and the units are connected, sharing the common nodes and edges to form the terrain surfaces, (4) vertically offset the four corner points of the terrain surface to a height of 0 m (the thickness of the terrain), then connect adjacent corner points and close each edge to create the side and the bottom surface. At the end, all the surfaces that have been created are enclosed into the geometric entities, and the terrain entities are generated by merging all the units.
3.2.2. Terrain Generation Based on Contour Lines
With the help of contour lines, the absolute coordinates of each control point are extracted from the surveying control network. On this foundation, the 3D contours are generated by the interpolation algorithm to complete the creation of terrain. The specific steps are as follows: (1) obtain terrain data by carrying out on-site measurement and apply Kriging interpolation to get the coordinates and the relative position of each control point of interest, (2) draw 3D contour lines by making use of point data, (3) generate the terrain surface with contour lines, (4) build up a terrain entity using bool operation. A straightforward schematic flow of the two methods is displayed in
Figure 3.
Terrain generation based on DEM data extraction should have a concise data structure so that it could be convenient for program implementation. This paper programs to configure script files to build up terrain models. With MATLAB software, the whole script file can be completed by means of file reading and writing, combined with loop and judgment statements. Each line in the script file corresponds to one instruction to construct a point, edge, face, body, and many other elements.
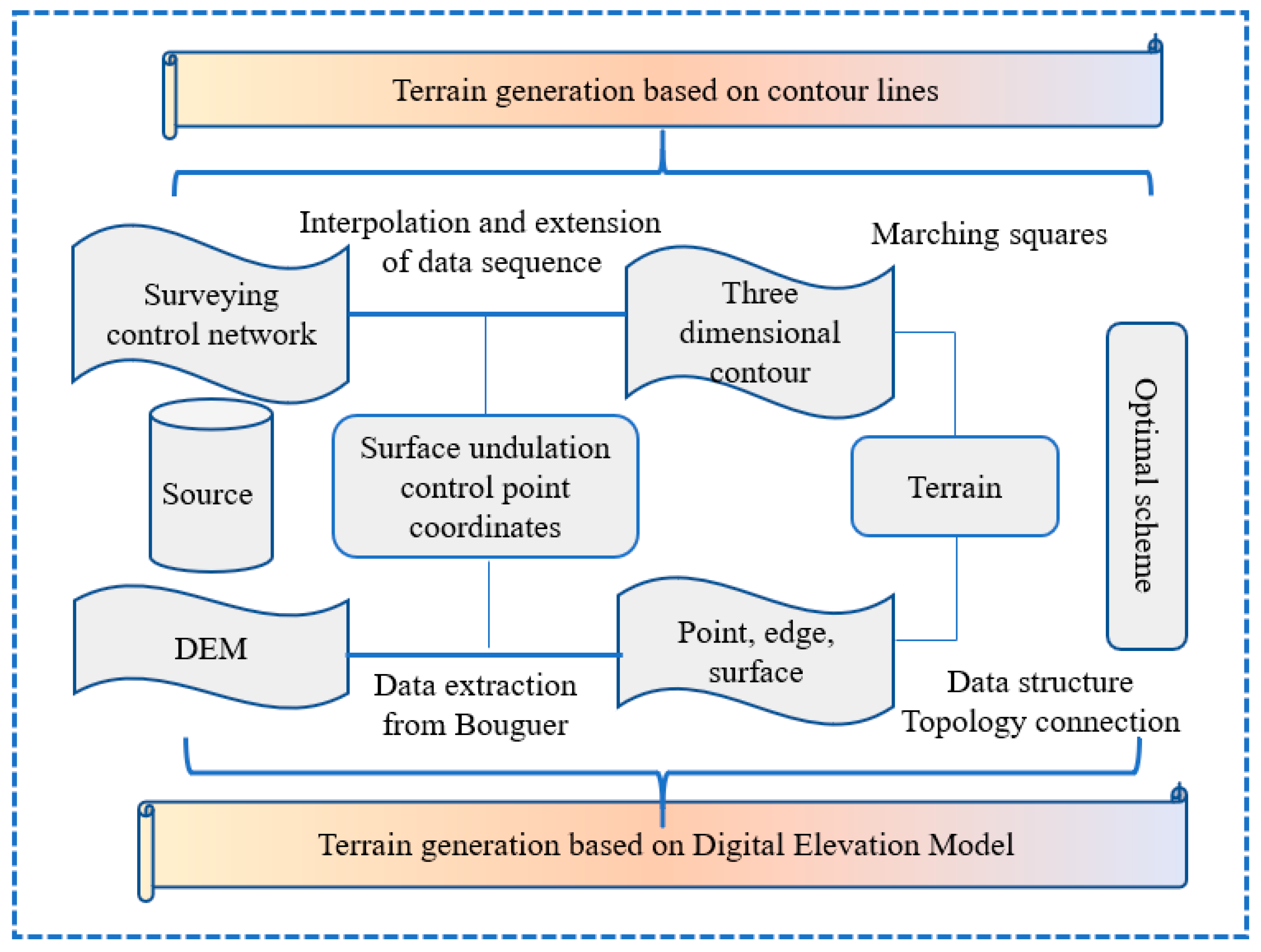
3.2.3. Comparison of the Two Terrain Generation Methods
Both terrain files are constructed in accordance with the coordinates of the space points. For terrain generation based on contour lines, spatial interpolation is required to encrypt the data points. The Marching Squares Algorithm is applied to generate terrain surfaces [
34], while for terrain generation based on DEM data, codes are developed to direct the construction of every component step by step. The processes of these two methods are shown in
Figure 4. The slight distinction in the two terrain generation processes leads to huge discrepancies in the final terrain entities. For terrain generated based on contour lines, the transition between two contour lines is smooth and continuous without mutation, while for the terrain files generated based on DEM data, terrain surfaces are similar to raster data, and each grid cell is connected to generate terrain surfaces. Unreasonable elevation gradient could be seen in the final terrain.
Table 2 illustrates the differences between the two terrain-generation algorithms. Terrain generation based on contour lines seems to have high accuracy, but the field measurement is difficult. With the improvement of the DEM resolution, terrain generation based on DEM data will be applied widely.
3.3. Hydrodynamic Model
Reynolds-Averaged Navier-Stokes (RANS) equations with the RNG
-
eddy viscosity model for its turbulence closure is applied to calculate the dam discharge and flood inundation simulation. The continuity equations [
35] can be expressed in the tensor form as follows:
where
represents mean velocity,
is the coordinate,
represents time,
is pressure,
is the fluid density,
represents the gravitational acceleration,
is the molecular kinematic viscosity and
represents the eddy kinematic viscosity. Turbulence eddy viscosity is computed using turbulent kinetic energy
k and turbulence dissipation rate
as follow:
where
is a constant. A modified
equation with an extra source term is used in the RNG
- model, integrating the renormalization group (RNG) mathematical theory [
36]. In the RNG
- model, the transportation equations for
k and
ε are:
where
is an additional term that is important for sheared turbulence but usually neglected in the standard k-ε model,
G represents the generation-rate of turbulent kinetic energy due to the mean velocity gradients. The coefficients in this model are:
= 0.085,
= 1.42,
= 1.68,
=
= 0.7194,
= 0.012 and
= 4.38.
A true Volume of Flood (VOF) method is utilized for computing free surface motion [
37]. The tracking of the interface between air and water is accomplished by the solution of the continuity equation with the following form:
The variables and properties in any given cell are either purely representative of water or air, or representative of a mixture of them, depending upon the water volume fraction values . The volume fraction of a given cell is constant. As long as the is calculated, the air volume fraction is naturally solved, and the free surface can be traced.
Based on these governing equations, the dam discharge and flood inundation simulation are conducted and the flow field is solved to measure the working condition of the dam. The governing equations are numerically discretized with the finite volume method. Within each control volume, the local mean values of all dependent variables, including pressure (
), fluid fraction (
), density (
), viscosity (
and
), turbulent kinetic energy (
), and dissipation rate (
) are solved. The surface fluxes, surface stresses and body forces of each control volume are computed subsequently in terms of the surrounding variable values to be combined to form approximations for the conservation equations. For the time step, an initial value needs to be specified to start the calculation, and it will be automatically adjusted according to the Courant–Friedrichs–Lewy (CFL) criterion in the following calculation. The CFL condition for the 3D case is the following one:
where C is a dimensionless constant which depends only on the particular equation to be solved. Explicit time marching solver is adopted and the C value is set to 1. As a consequence, the time step must be less than a certain time determined by the CFL criterion, otherwise the simulation may produce incorrect results.
3.4. Model Configuration
The boundary condition and initial condition are used to feature a specific problem. As to the dam discharge simulation, being consistent with the actual operation mode is of vital importance to corresponding with the reality. The water level at the dam site plays a leading role in the transition between the model and the real operation of the reservoir.
3.4.1. Boundary Conditions
Due to the lack of inflow series data, the average flow velocity () at the inlet boundary is solved on the condition that the water level at the dam site is consistent between the model and actual conditions. The flooding process in the Fujiang River generally lasts approximately 2–3 days. Due to the confinement of 3D simulation time, the peak water level period of the reservoir is selected as the simulation period. In fact, there are no dramatic changes in the water level at the dam site in the simulation period, so the inlet boundary condition is configured to guarantee that the water level is constant during the simulation period.
The outlet boundary adopts the free outflow condition, and the upper boundary condition is set as the free surface. As to the other boundaries, they are treated according to the solid wall law, and all nodes are applied to the non-slip boundary condition.
3.4.2. Initial Conditions
The computational domain covers a range of 460 m × 320 m × 120 m. The complexity of dam discharge calculation often requires a grid that will result in a scientifically credible, yet computationally feasible model. The grid should provide a compromise between depicting the physical realities of the hydraulic structures and computational feasibility. Therefore, a sensitivity test on the mesh size is made in order to check if the mesh is fine enough to give a good representation of the flow through the spillway and the bottom outlet. Different mesh resolutions (1 m, 1.5 m, and 2 m) are adopted to carry out the sensitivity analysis. No distinctive discrepancies of the flow velocity and pressure are captured under different mesh resolutions, which means that the simulation results do not rely on mesh size. Therefore, the computational domain mesh is divided into gradient nested structured meshes, with a minimum mesh size of 0.5 m and a global mesh size of 1 m, and the total mesh number is 5.68 million, shown in
Figure 5b. Three probe points are arranged to capture the flow field characteristics (
Figure 5a).
The simulation time must be long enough to capture a relatively stable status of the downstream flow field. Also, it must be short enough to avoid generating too much redundant data. As a consequence, the simulation time is set to 50 s after many attempts. Since the computational time is limited and the water level is nearly constant in the simulation period, the downstream flow field possesses the ability to achieve a relatively stable condition. After that, fluctuations in flow field are not violent. The time step is determined by satisfying the Courant–Friedrichs–Lewy (CFL) condition, which assures the explicit solver of the RANS equations to have stable solutions. Since no observation data are available on the flood plain and for the hydraulic structure, roughness parameters are set to characteristic values commonly cited in the literature [
38].
4. Scenario Analysis
According to the features of the Wudu Reservoir, three characteristic water levels are selected to simulate the dam discharge and one scenario (case 2) is chosen as a validation case. Dam discharge at high water levels would exert a severe effect on downstream river channels. Analysis of different water levels helps in understanding the operational mechanism of the reservoir and in adapting portable and convenient measures dealing with every challenging working condition, as shown in
Table 3.
5. Model Validation
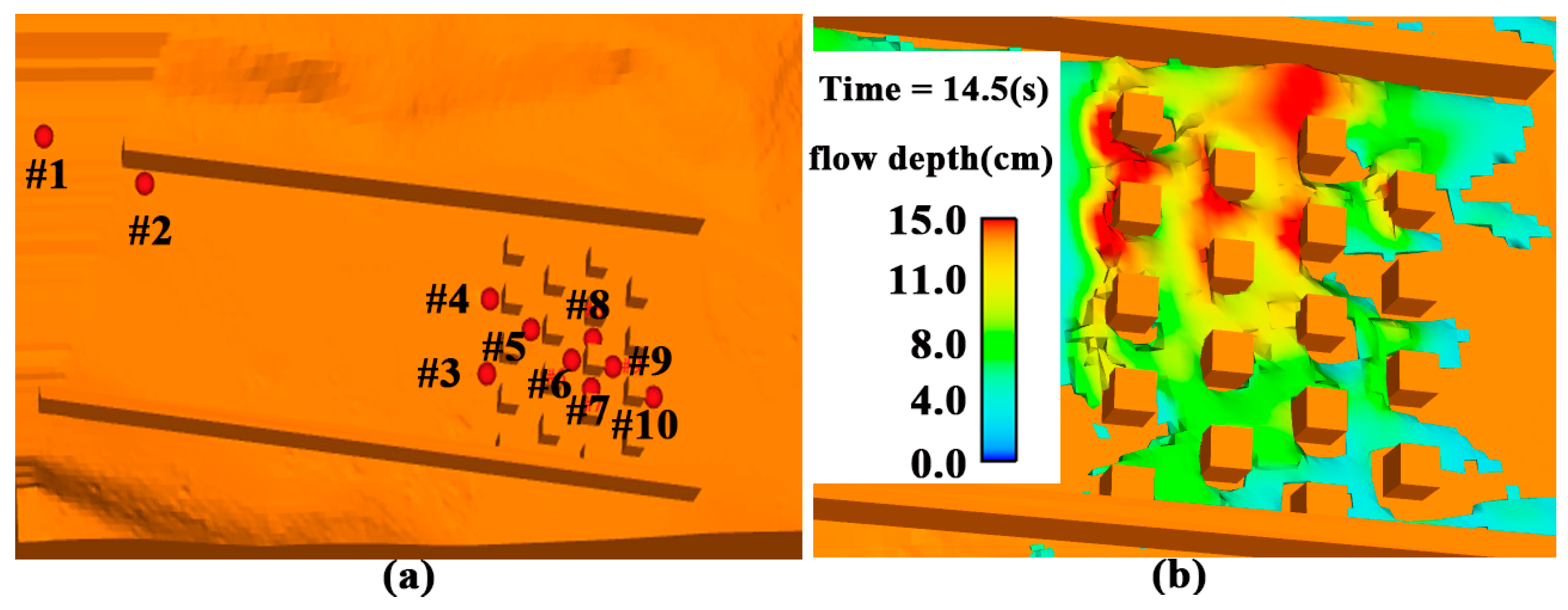
To validate the applicability and accuracy of the hydrodynamic model, a flooding experiment, which has sufficient water depth data at 10 probe points, is constructed with the physics-based flood routing simulation framework. Detailed information could be found in the experiment [
39] and the layout of the experiment is depicted in
Figure 6.
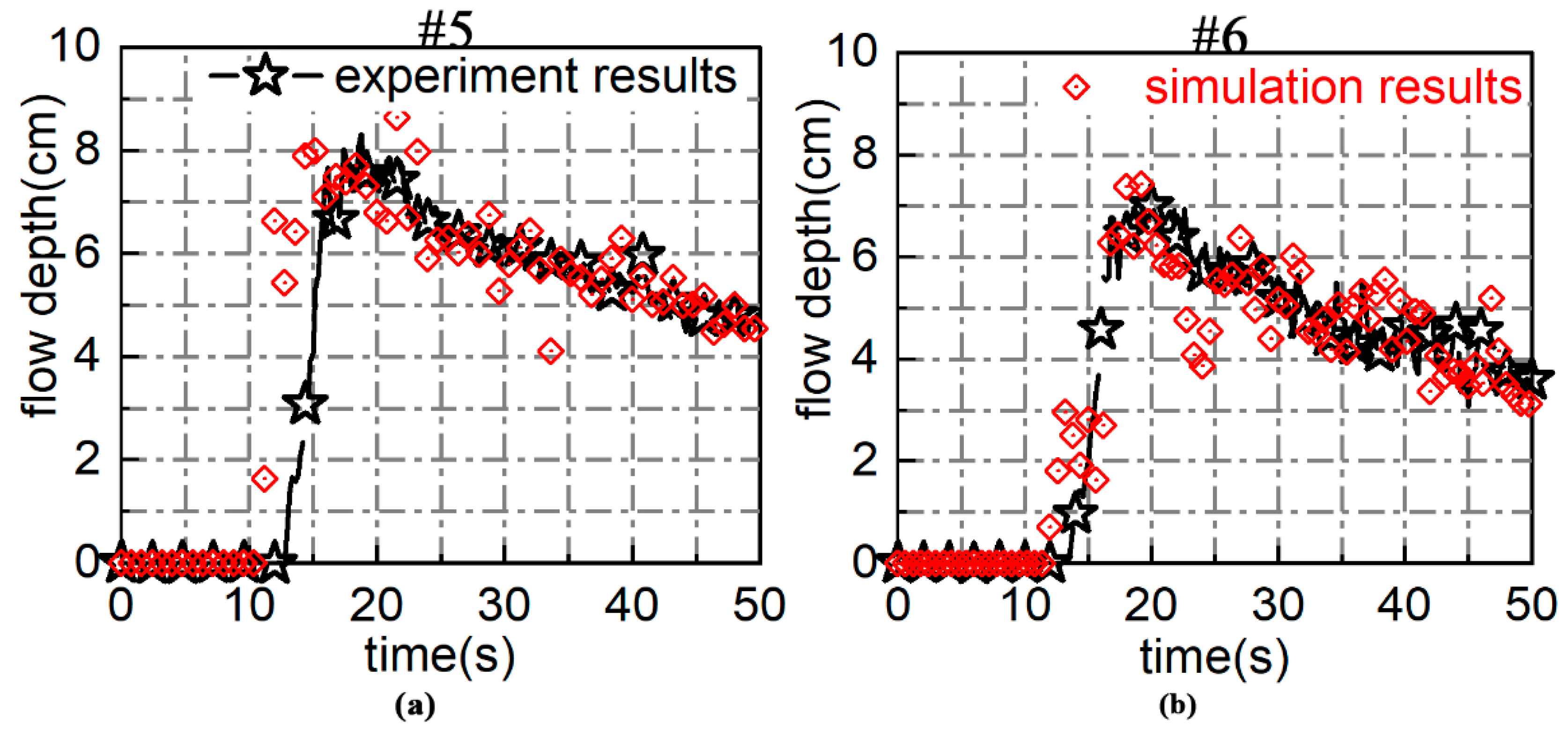
A comparison between the physical experiment and the simulation result regarding the flow depth at all the 10 probe points is performed. The results show that the relative error is rather small, and the Root Mean Squared Error (RMSE) of the flow depth is within 0.5 cm at all the 10 points (
Figure 7). Therefore, the 3D hydrodynamic model established in this paper is applicable to the dam discharge and flood routing simulation.
Moreover, according to the field measurement records in the Wudu reservoir, at 8:00 o’clock on 18 June 2018, the water level is 630 m in the upstream reservoir, and the corresponding water level at a downstream cross-section, 1000 m away from the dam site, is approximately 563.8 m. Since then, the upstream water level time series data are measured as the inlet boundary condition, and the downstream water level time series data from the field measurement and simulation results are compared. The results show that the discrepancies are not enormous, with the RMSE is 0.3 m, indicating that the simulation accuracy can satisfy the demand of engineering application.
6. Results
Based on the uneven terrain and the detailed hydraulic structures, the flow motion is calculated by solving the Reynolds-averaged Navier-Stokes equations with the RNG k-ε turbulence model. The free surface is traced by the VOF model. With the use of an Intel core E5-1603 quad-core processor (@ 2.80 GHz), 32 GB of main memory and a parallel software license code, computation times of approximately 40 h are achieved for each case. Undulating terrain and sophisticated structures in the river channel result in complex 3D turbulent flow patterns, including collision, reflection, and vortices. Hydraulically efficient working conditions of the dam are: discharging capacity, pressures and water surface profiles, energy dissipation arrangement, and downstream flow conditions. The downstream flow field is solved by using Flow 3D software. Taking case 3 as an example, the flow field is depicted to characterize the dam working condition.
6.1. Water Depth
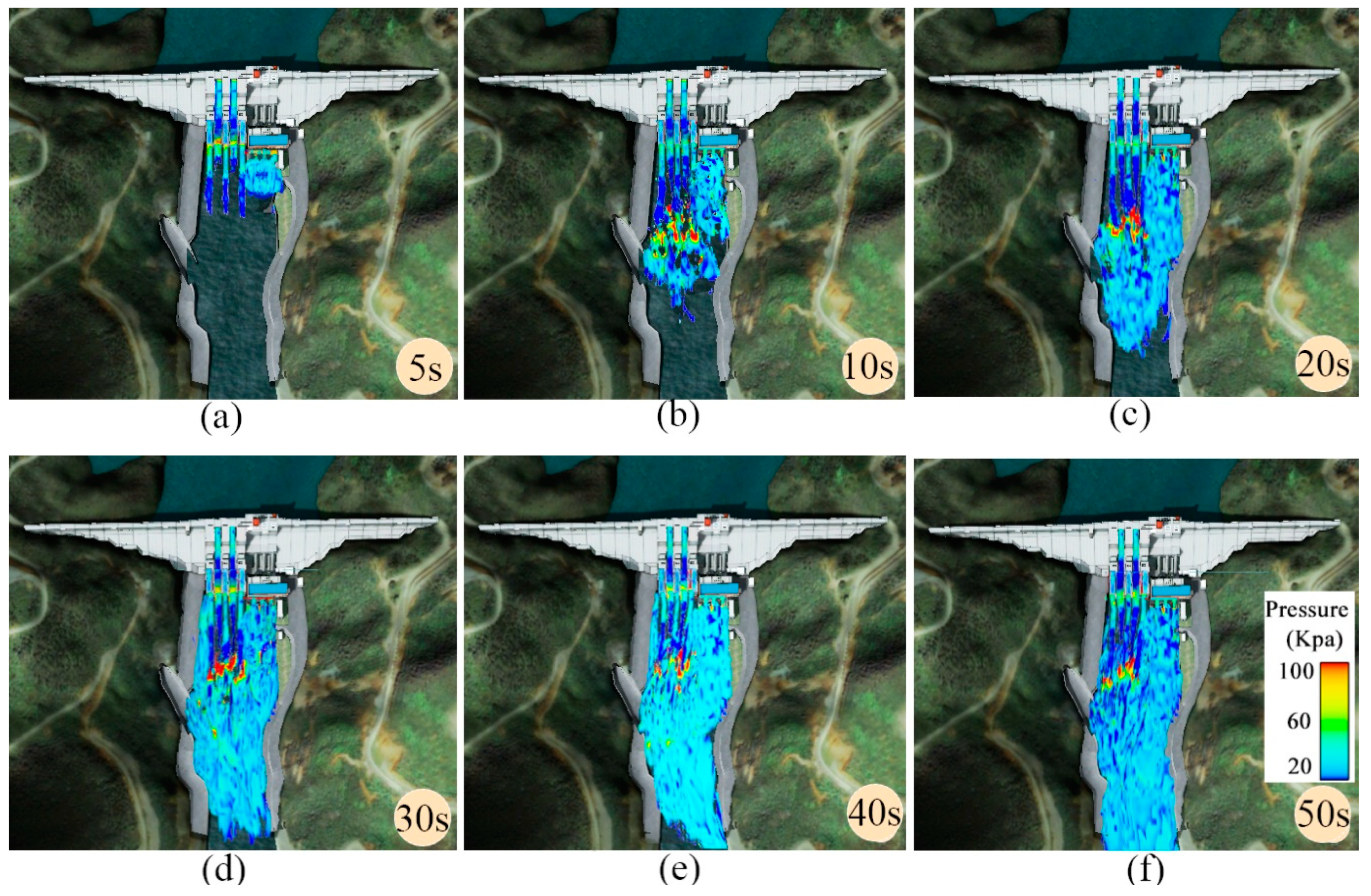
The surface spillway, bottom outlet and the intake of the power plant can be used to release flood under the normal water level. At the early stage of the simulation, the flow spreads linearly in the vicinity of the spillway. As the peak flood approaches, the front of the water body gradually comes across the dam and diffuses around in the forward direction. Due to the distribution of the ground resistance and the adverse steep slope of the riverbed, the flow velocity progressively decreases, and the flow is attenuated from the mainstream to the periphery. The process is accompanied by vortices, and regions of low pressure are consistently detected on the surface. Bubbles are a common phenomenon around the incident points, which are caused by the refraction, reflux, and divergence of the local current.
Multi-horizontal submerged jets with the interval layout of the surface spillway have technical feasibility and are characterized by high energy dissipater ratios, stable flow patterns, and low bottom velocities. Due to the impact of the high-energy jet falling down on the downstream water surface, a circular diffusion region with shallow water depth is formed at the incident points nearby, and the region is contracted laterally and gradually stretched longitudinally. The water depth at the confluence of the two streams, spillway, and bottom outlet jets, is deeper than other positions on both sides of the same cross-section. As water flows through the dam, it rushes along the river channel. When the main stream encounters a bend in the river, it is forced to change direction, resulting in the eventual distribution of the water depth, as is shown in
Figure 8.
Figure 9 shows that during the dam discharge process, high-pressure flow transforms to high-speed flow, hits the flip bucket and then splashes into the air. The maximum discharge capacity reaches to 13,800 m
3/s, and the hydraulic jump is approximately 110 m. Energy is stored in the reservoir is high enough. Under such conditions, both the dam and the downstream environment are facing flood risk challenges. By comparing
Figure 9, it can be seen that the length of the hydraulic jump in the bottom outlet is slightly longer than that in the spillway. Before the jet falls down on the downstream water body, most of the energy exists in the form of impact kinetic energy. After the jets hit the riverbed, energy is consumed by the interaction with the riverbed, which brings about severe riverbed scouring. The downstream flow pattern gradually becomes steadier, indicating that the working condition is fine at normal water level.
The results show that the joint discharge from the surface spillway and bottom outlet could force each flow to laterally offset or collide in the upstream region of the stilling basin, forming an observable vertical vortex and significantly intensifying the mutual shear turbulence that the 2D result is unable to capture. Under the condition of the bottom outlet discharge alone, it is more notable that the running inflow would swiftly transform into a 3D hydraulic jump encountering the sudden expansion section.
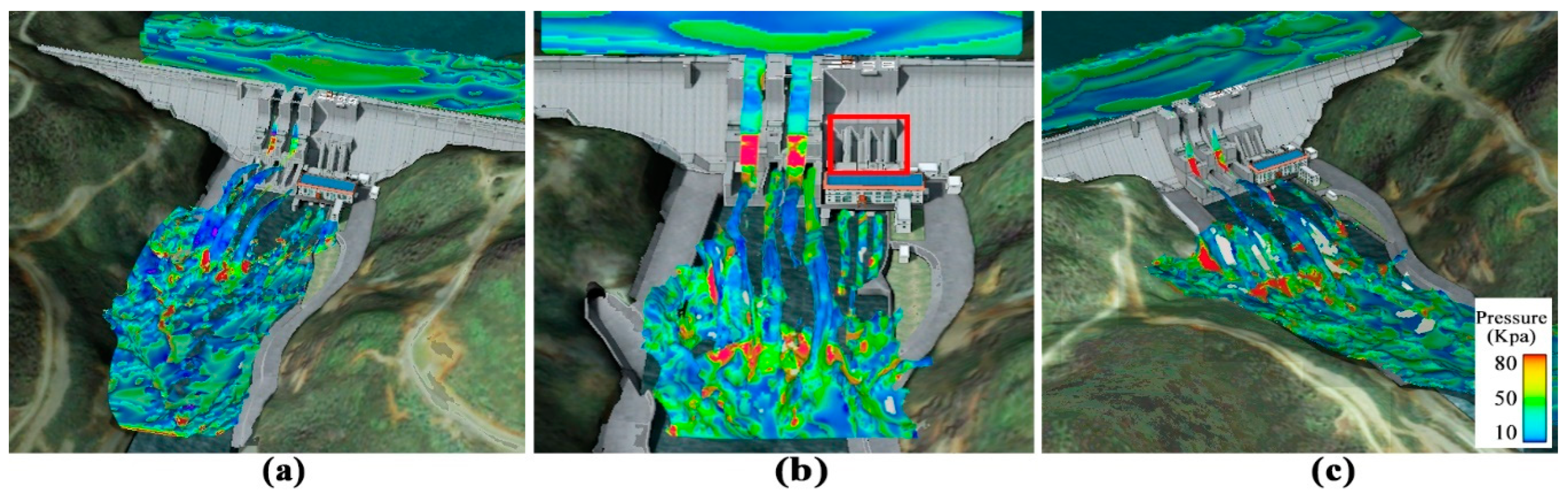
6.2. Dynamic Pressure
When the two jets formed by the spillway and the bottom outlet get past the constraints, the huge impact transfers to the downstream riverbed. At the incident point, the riverbed bears most of the energy of the high-speed flow, causing an abrupt increase in the riverbed pressure. As shown in
Figure 10, the dark red area signifies the location of the incident point. The pressure in the surrounding position is relatively small, the large pressure gradient would gradually destroy the downstream dam foundation, putting the dam safety at risk.
One significant practical value of the joint flood discharge with the surface spillway and the bottom outlet is their highly efficient flow energy dissipation capacity. Collision and energy dissipation occur after the two jets meet, and the deflecting flow consumes a large amount of energy. This could prevent the downstream channel from severe erosion and stabilize the main flow stream in the river management. There is still a great deal of energy directly hitting the riverbed so that it will cause serious partial erosion downstream. Severe erosions at the downstream channel may harm the stability of the hydraulic structures as documented by Dodaro et al. [
40,
41]. Sometimes an abrupt drop is introduced to prevent tailwater effects and to stabilize the jump location. Therefore, the joint dam discharge with surface and bottom outlet has good energy dissipation features and the downstream foundation at the incident point should be paid close attention all the time.
6.3. Instantaneous Flow Field
A complex flow pattern develops due to the presence of the obstacle (dam and ground resistance) as the flow progresses forward. Once the flow reaches the obstacle, a part of the wave is reflected and forms a bore traveling towards the upstream direction while the other part moves up to form the bumps. Turbulence effects are significant, particularly at the reflected wavefront.
Figure 11 shows the transient flow field with streamlines. As the inlet boundary constantly pours water into the model, the water body in the reservoir presents the trend of synchronous propagation towards downstream. However, with the dam’s obstruction, water is forced to accumulate at the outlet works of the dam. The streamlines converge to the surface spillway, bottom outlet and the intake of the power plant, and the water pours down from there instantaneously. The flow gradually accelerates in the spillway due to the conversion of the potential energy. Three main streams, formed by the bottom outlet discharge, are presented. With the spillway discharge, the flow hits the flip bucket, then collides with the bottom outlet and hits on the ground. As for the flood discharges without spillway, huge kinematic energy is dissipated by collision with the downstream ground. In general, the downstream flow field is relatively steady, which suggests that the dam can satisfy the safety demand of the dam under high water level.
6.4. Details of Local Flow
The flood flow through the dam in three ways: surface overflow, bottom outlet, and power plant intake. The joint discharge energy dissipation rate has been proved with the surface spillway and bottom outlet, and the curvilinear inlet pipe of the power plant has an influence on disturbing the movement of the water. The high-pressure flow carries a large amount of impact kinetic energy and is deflected by the pipe, which would be partially broken at the turn of the pipe so that the back pipe of the dam is subjected to great pressure (the part marked by the square in
Figure 12). As a consequence, the inlet pipe of the power plant must be reinforced to avoid damage. The local flow pattern of the overflow dam is shown in
Figure 12.
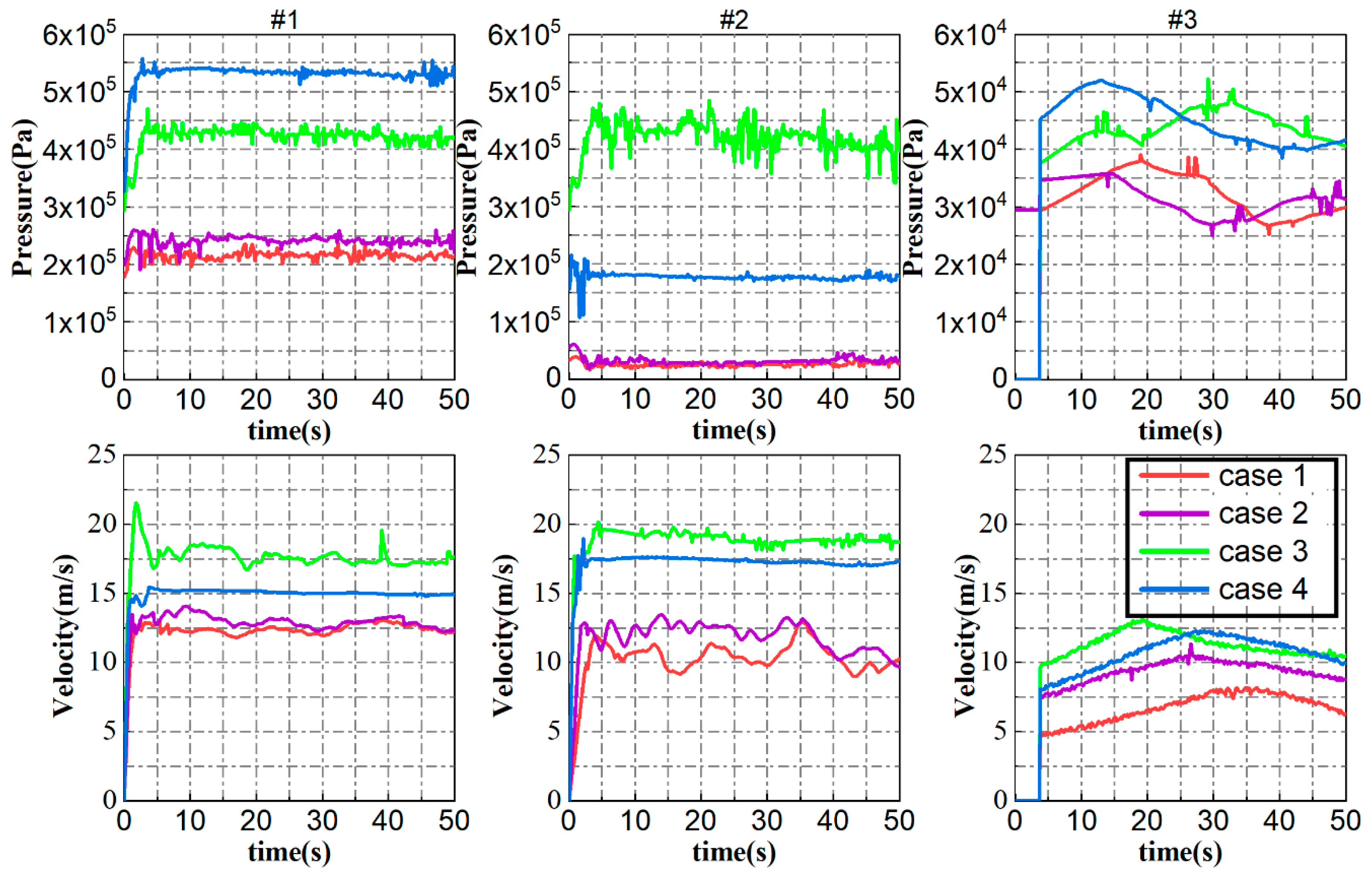
The pressure and flow velocity of 3 probe points [shown in
Figure 5a] in 4 different working conditions (dead water level, the water level at 8:00 o’clock on 18 June 2018, normal water level with spillway discharge and normal water level without spillway outlet) are shown in
Figure 13.
When the water reaches a normal level, a high-energy flood is released through the outlet works, causing the flow to be swift and the flow pattern to be complicated. Slight differences in the water level in the reservoir cause a large change in the flow field. In general, the energy is stored in the reservoir is really high, which can be seen from the pressure and velocity distribution of the upstream probe points. After the high-energy water reaches the downstream, the energy is dissipated. The dam structure and the riverbed have to bear the impact of high-energy flow, putting them in danger. Therefore, the operation rules should take the downstream bearing capacity into consideration to make it a flexible, convenient, and practical rule. With the spillway discharge, the pressure is generally less, and the velocity is usually faster at the downstream #3 probe point. Therefore, we can infer that as long as the bearing capacity of the river channel is strong enough, the dam has better discharge working conditions (low velocity) without spillway discharge under high water level.
6.5. Flood Inundation
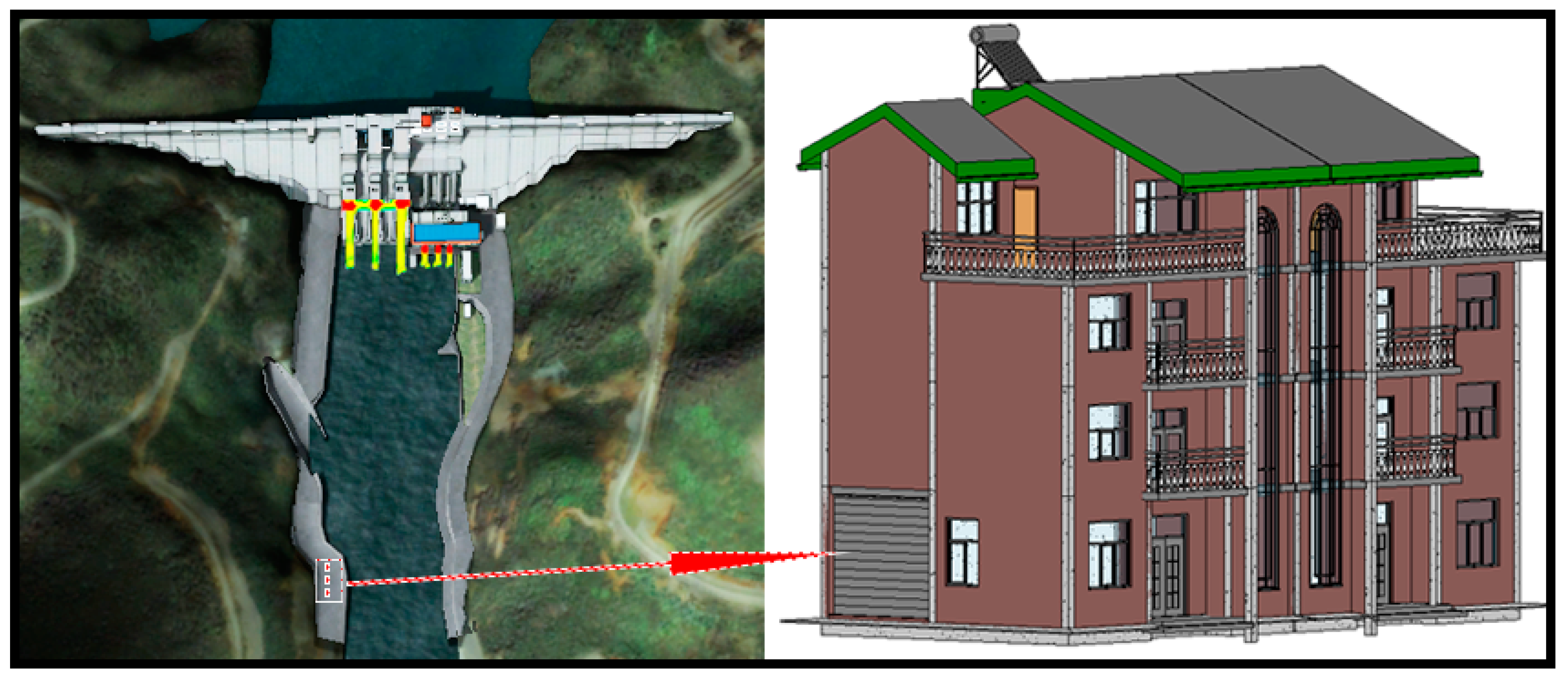
There are some buildings along the bank of the lower reaches of the Wudu Reservoir, which may be threatened by the reservoir flood discharge. We simplified the building area in the computational domain to three residential houses, as shown in
Figure 14. According to the simulation results, houses would be inundated only under normal water levels in all scenarios.
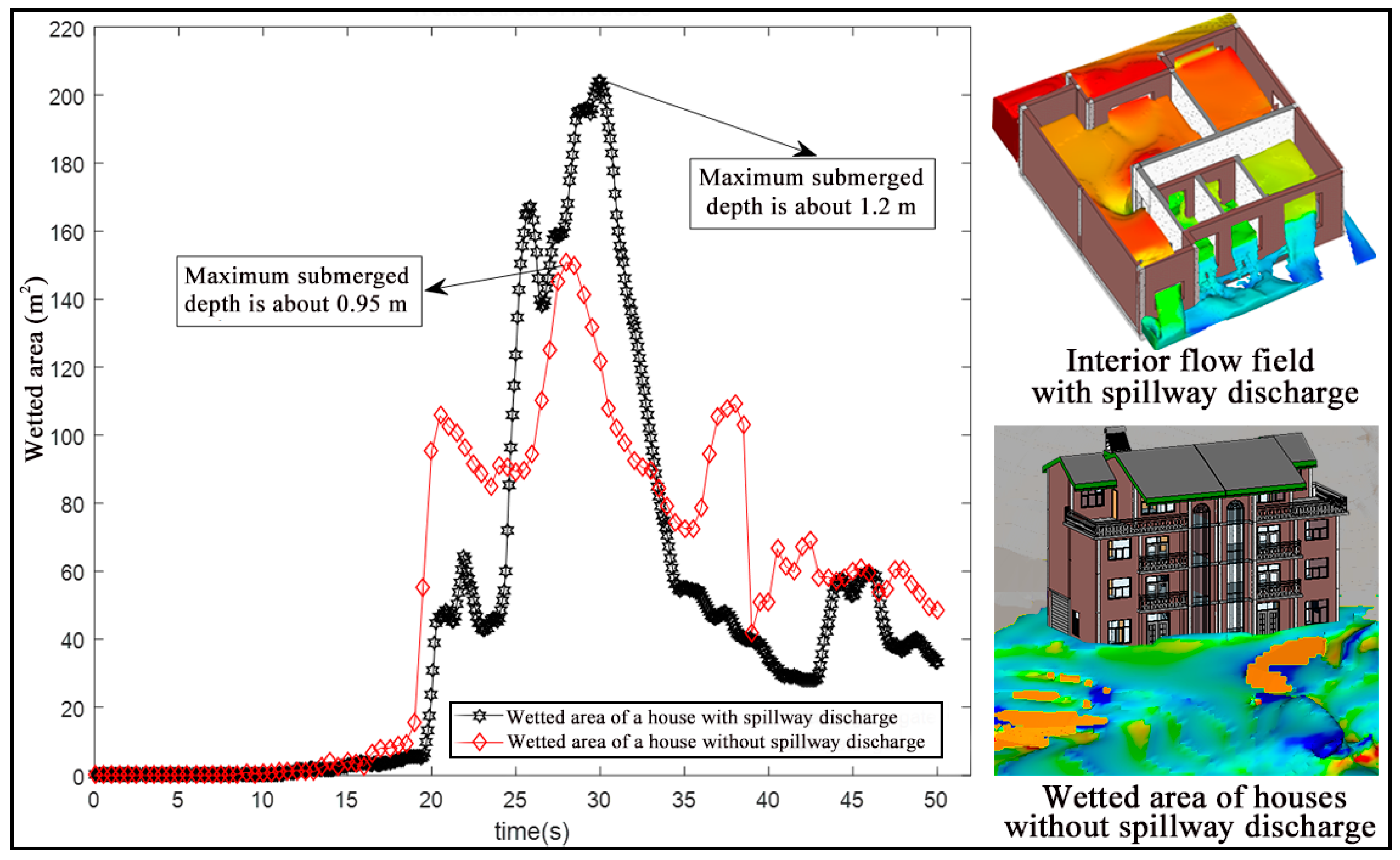
Under a high water level, a large volume of water would rash into the downstream river and the river cannot release the flood in time. Naturally, the downstream water level increases, resulting in a certain inundation of the houses. The maximum submerged area can reach 203 m
2, and the highest water level can drown the house with approximately 1 m of water, as shown in
Figure 15. The house interior flow process is calculated to quantify flood risk. The flooding process into the building’s interior emphasizes the vertical velocity due to the obstacle of the enclosing walls of the building. The complexity and transient characteristics are the primary features of the flow field around the structures. The downstream cities have to deal with the emergency if a long-term dam discharge occurs. In general, even though the dam discharge has high energy dissipater ratios and stable flow patterns, the maximum discharge would bring a disaster to the downstream environment. The dam operation should take all the factors into consideration to draw a reasonable rule.
7. Discussion
The terrain modeling method based on DEM provides a new approach to generate terrain for areas without field measurement data, but the accuracy of the terrain model depends on the precision of DEM data. At present, the accuracy of DEM data is generally 30 m × 30 m, which is insufficiently accurate for high-resolution models, and terrain generation based on contour lines demands an exhausted field measurement. However, an Unmanned Aerial Vehicle can be used to collect data in the study area and obtain high-resolution DEM data by image recognition processing, providing technical support for fast and accurate terrain generation method [
42].
Since the calculation area covers the range of 460 m × 320 m × 120 m, the mesh size is difficult to further refine from the perspective of computational capacity and practical application. Compared with the similar scale-related research [
43,
44] and considered the actual situation, the current mesh size can meet the computational requirements, but if the local details of the flow field are to be captured, the mesh needs to be further subdivided.
The free outflow boundary condition downstream is slightly different from the actual situation. In fact, there is a water-retaining structure approximately 2 km downstream of the Wudu reservoir, which leads to a poor drainage condition. However, the simplified treatment of the downstream still causes the waterfront structures to be submerged. Therefore, the actual flood inundation would be more severe.
There are certain limitations associated with the use of this model. The field observation data is problematic due to the variable nature of the flow field, and generally unable to capture complex flow dynamics. The limited accuracy of field observations, together with the lack of simultaneous physical measurements of overtopping volumes, has hampered the ability to validate flood models. Modeling uncertainties can originate from a wide range of physical processes and at a wide range of space-time scales. Therefore, calibration of the dam discharge and flood routing model is limited. However, the model results are indeed able to provide information to check the operation condition under different scenarios, which indicates that the reservoir has the ability to deal with the surplus flood.
The flood risk assessment is performed by integrating three simplified houses. The physics-based flood routing framework has been proven to get an accurate flow field. A large volume of water would be released from the discharge structures and it would cause a great impact on the downstream environment. A more detailed flood risk assessment should be conducted considering all house distributions of the downstream county. Therefore, the dam operation management could be more reasonable to avoid destroying the downstream environment.
8. Conclusions
In this paper, two terrain generation methods, which have a different application scope, are proposed, and the parametric modeling method is applied to construct complex hydraulic models. Based on the uneven terrain and the detailed hydraulic structures, a physics-based hydrodynamic model is constructed to simulate the dam discharge and flood routing of the Wudu reservoir. A flooding experiment is selected to test and verify the applicability and accuracy of the hydrodynamic model, while the measured downstream water level is used to validate the numerical results. The 3D visualization information of flood routing based on temporal and spatial variation is provided. The model provides detailed information for further understanding the flow movement and analysis of the role of hydraulic structures in the process of dam discharge.
The proposed physics-based dam discharge and flood routing framework can provide not only reasonable results with good accuracy but also more details of the complex flow patterns in three dimensions. Therefore, it has strong power in simulating the complex flow passing through hydraulic engineering. In addition, the use of BIM technology has largely improved structural modeling efficiency in practice.
This paper taking the pressures and water surface profiles, energy dissipation arrangement, and downstream flow conditions into consideration to check the dam operation rules. It can be concluded that the joint discharge with the surface spillway and bottom outlet have a better working condition. The stilling basin which is formed around the incident point helps to dissipate the energy by complex flow patterns, and the dam foundation can be protected to guarantee the safety of the dam. In general, the dam can satisfy the discharge demand under the high water level. The flip bucket of the spillway and the incident point of the discharge flow should be paid close attention, since the pressure and velocity at those positions are relatively high, and they are easily be destroyed.
According to the actual situation and the characteristic water level of the reservoir, the dam discharge process under four different water levels is analyzed. The flow pattern, water depth, flow velocity, and other characteristic information under these four conditions are given, which can provide a reference to guide the actual operation of the reservoir. Improper operation and management of reservoirs may cause serious floods downstream. The waterfront houses are submerged under the normal water level with the maximum discharge capacity. While in other scenarios, the house is safe from inundation. To protect the downstream, the operation rules should be optimized. Once a rare basin flood occurs, the dam had better release the flood in advance. Taking the safety of both the dam and the downstream environment into consideration, drawing a practical operation approach is favorable. Thus, the dam structures are optimized functionally and economically, protecting human life and property downstream.
The complexity and transient characteristics are the primary features of the flow field around the structures. House interior flow process emphasizes the importance of 3D hydrodynamic simulation to assess the dam operation rules. The dam function is to protect the downstream, and the operation management should pay more attention to the downstream environment. In general, the dam discharge and flood routing simulation have confirmed that the stable working condition under different working conditions. The flip bucket at the discharge structures and the incident points should be paid more emphasis to protect the dam, and the maximum discharge at high water level should pay more attention to the downstream environment.
Author Contributions
This manuscript is the result of Y.R., under the supervision of T.Z. and P.F.; L.P. gave the constructive advice. Under the joint efforts of all the authors, this paper has been completed. Conceptualization, Y.R. and L.P; Methodology, T.Z.; Software, L.P.; Validation, T.Z., L.P. and Y.R.; Formal analysis, P.F.; Investigation, T.Z.; Resources, P.F.; Data curation, Y.R.; Writing—original draft preparation, Y.R.; Writing—review and editing, T.Z.; Visualization, Y.R.; Supervision, P.F.; Project administration, P.F; Funding acquisition, T.Z.
Funding
This research was funded by National Natural Science Foundation of China, grant number 51609165 and China Postdoctoral Science Foundation, grant number 2017T100159.
Acknowledgments
The authors are grateful to the editors and anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Soares-Frazao, S.; Zech, Y. Dam-break flow through an idealised city. J. Hydraul. Res. 2008, 46, 648–658. [Google Scholar] [CrossRef]
- Marta-Almeida, M.; Mendes, R.; Amorim, F.N.; Cirano, M.; Dias, J.M. Fundão Dam collapse: Oceanic dispersion of River Doce after the greatest Brazilian environmental accident. Mar. Pollut. Bull. 2016, 112, 359–364. [Google Scholar] [CrossRef] [PubMed]
- Kalinina, A.; Spada, M.; Burgherr, P. Application of a Bayesian hierarchical modeling for risk assessment of accidents at hydropower dams. Saf. Sci. 2018, 110, 164–177. [Google Scholar] [CrossRef]
- Martino, B.; Mauro, B.; Massimo, D.; Carlo, G. Model-based approach for design and performance evaluation of works controlling stony debris flows with an application to a case study at Rovina di Cancia (Venetian Dolomites, Northeast Italy). Sci. Total Environ. 2019, 688, 1373–1388. [Google Scholar]
- Luo, C.; Xu, K.; Zhao, Y. A TVD discretization method for shallow water equations: Numerical simulations of tailing dam break. Int. J. Modeling Simul. Sci. Comput. 2017, 8, 1850001. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydrol. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Miller, D.S. Discharge Characteristics: IAHR Hydraulic Structures Design Manuals 8; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Tullis, B.P.; Young, J.C.; Chandler, M.A. Head-discharge relationships for submerged labyrinth weirs. J. Hydrol. Eng. 2007, 133, 248–254. [Google Scholar] [CrossRef]
- Khatibinia, M.; Chiti, H.; Akbarpour, A.; Naseri, H.R. Reliability–based design optimization of concrete gravity dams using subset simulation. Int. J. Optim. Civ. Eng. 2016, 6, 329–348. [Google Scholar]
- Yazdi, J.; Torshizi, A.D.; Zahraie, B. Risk based optimal design of detention dams considering uncertain inflows. Stoch. Environ. Res. Risk Assess. 2016, 30, 1457–1471. [Google Scholar] [CrossRef]
- van Hooff, T.; Blocken, B.; Tominaga, Y. On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS-VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Nazari, S.; Zamani, M.; Moshizi, S.A. Comparison between two-dimensional and three-dimensional computational fluid dynamics techniques for two straight-bladed vertical-axis wind turbines in inline arrangement. Wind Eng. 2018, 42, 647–664. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling floods in a dense urban area using 2D shallow water equations. J. Hydrol. 2006, 327, 186–199. [Google Scholar] [CrossRef]
- Molinari, D.; De Bruijn, K.M.; Castillo-Rodríguez, J.T.; Aronica, G.T.; Bouwer, L.M. Validation of flood risk models: Current practice and possible improvements. Int. J. Disaster Risk Reduct. 2019, 33, 441–448. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-break flow in the presence of obstacle: Experiment and CFD simulation. Eng. Appl. Comp. Fluid Mech. 2011, 5, 541–552. [Google Scholar] [CrossRef]
- Han, M.; Chen, M. Three-dimension visualization research of flood routing simulation. Comput. Appl. 2005, 25, 1906–1907. [Google Scholar]
- Weng, L.; Cheng, G.; Chang, Na.; Lu, C. Simulation of two-dimensional dam break flow based on finite volume HWENO schemes. Eng. J. Wuhan Univ. 2011, 44, 628–632. [Google Scholar]
- Kim, B.; Sanders, B.F. Dam-break flood model uncertainty assessment: Case study of extreme flooding with multiple dam failures in Gangneung, South Korea. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Zhang, T.; Feng, P.; Maksimovic, C.; Bates, P.D. Application of a three-dimensional unstructured-mesh finite-element flooding model and comparison with two-dimensional approaches. Water Resour. Manag. 2016, 30, 823–841. [Google Scholar] [CrossRef]
- Ortiz, P. Shallow water flows over flooding areas by a flux-corrected finite element method. J. Hydraul. Res. 2014, 52, 241–252. [Google Scholar] [CrossRef]
- Broquetas, M.; Bryde, D.; Volm, J. The project benefits of Building Information Modelling (BIM). Int. J. Proj. Manag. 2013, 31, 971–980. [Google Scholar] [CrossRef]
- Zhong, D.; Li, M.; Liu, J. 3D integrated modeling approach to geo-engineering objects of hydraulic and hydroelectric projects. Sci. China Ser. E Technol. Sci. 2007, 50, 329–342. [Google Scholar] [CrossRef]
- Nawari, N.O. BIM Data Exchange Standard for Hydro-Supported Structures. J. Arch. Eng. 2019, 25. [Google Scholar] [CrossRef]
- Wang, H.R.; Zhao, D.Y.; Jin, Y.F.; Wang, M.J.; You, Z. Unified parametric modeling of origami-based tube. Thin Walled Struct. 2018, 133, 226–234. [Google Scholar] [CrossRef]
- Marsooli, R.; Wu, W. 3-D finite-volume model of dam-break flow over uneven beds based on VOF method. Adv. Water Resour. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Formentin, S.M.; Palma, G.; Contestabile, P.; Vicinanza, D.; Zanuttigh, B. 2DV RANS-VOF numerical modeling of a multi-functional harbour structure. Coast. Eng. Proc. 2016, 1, 3. [Google Scholar] [CrossRef]
- Vashahi, F.; Dafsari, R.A.; Rezaei, S.; Lee, J.K.; Baek, B.J. Assessment of steady VOF RANS turbulence models in rendering the internal flow structure of pressure swirl nozzles. Fluid Dyn. Res. 2019, 51. [Google Scholar] [CrossRef]
- Dai, H.C.; Xu, W.L. Research flood releasing safety of flood discharge structure with high-head & large-discharge. Water Power 2009, 35, 14–17. [Google Scholar]
- De Béjar, L.A. Probability of flood-induced overtopping of barriers in watershed-reservoir-dam systems. J. Hydraul. Eng. 2011, 16, 699–709. [Google Scholar] [CrossRef]
- Kvocka, D.; Falconer, R.A.; Bray, M. Appropriate model use for predicting elevations and inundation extent for extreme flood events. Nat. Hazards 2015, 79, 1791–1808. [Google Scholar] [CrossRef]
- Zhai, X.; Zhai, Q.G.; Wang, J.J.; Fu, X.G. Research on parameterized modeling technology for the bolted joints structure. Appl. Mech. Mater. 2014, 565, 211–216. [Google Scholar] [CrossRef]
- Lin, L.; Song, X.Q.; Huang, M.Y.; Sun, Y.H.; Li, J.; Zhu, Y.; Yang, Z. The creation and exploration of Revit Family based on BIM technology. In Proceedings of the 2016 International Conference on Smart City and Systems Engineering, Hunan, China, 25–26 November 2016; pp. 241–244. [Google Scholar] [CrossRef]
- Mantz, H.; Jacobs, K.; Mecke, K. Utilizing Minkowski functionals for image analysis: A marching square algorithm. J. Stat. Mech. Theory Exp. 2008. [Google Scholar] [CrossRef]
- Yang, C.; Lin, B.; Jiang, C.; Liu, Y. Predicting near-field dam-break flow and impact force using a 3D model. J. Hydraul. Res. 2010, 48, 784–792. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport part III: Bed forms and alluvial roughness. J. Hydraul. Eng. ASCE 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Testa, G.; Zuccala, D.; Alcrudo, F.; Mulet, J.; Soares-Frazao, S. Flash flood flow experiment in a simplified urban district. J. Hydraul. Res. 2007, 45, 37–44. [Google Scholar] [CrossRef]
- Dodaro, G.; Tafarojnoruz, A.; Calomino, F.; Gaudio, R.; Stefanucci, F.; Adduce, C.; Sciortino, G. An experimental and numerical study on the spatial and temporal evolution of a scour hole downstream of a rigid bed. In Proceedings of the International Conference on Fluvial Hydraulics, River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 1415–1422. [Google Scholar]
- Dodaro, G.; Tafarojnoruz, A.; Sciortino, G.; Adduce, C.; Calomino, F.; Gaudio, R. Modified Einstein sediment transport method to simulate the local scour evolution downstream of a rigid bed. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Murtiyoso, A.; Remondino, F.; Rupnik, E.; Nex, F.; Grussenmeyer, P. Oblique aerial photography tool for building inspection and damage assessment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 309–313. [Google Scholar] [CrossRef]
- Chen, J.G.; Zhang, J.M.; Xu, W.L.; Wang, Y.R. Numerical simulation of the energy dissipation characteristics in stilling basin of multi-horizontal submerged jets. J. Hydrodyn. 2010, 22, 732–741. [Google Scholar] [CrossRef]
- Duan, J.G. Mean flow and turbulence around a laboratory spur dike. J. Hydraul. Eng. 2015, 135, 803–811. [Google Scholar] [CrossRef]
Figure 1.
Wudu reservoir. (a) location of Wudu reservoir; (b) layout of the dam structures; (c) perspective view of the dam.
Figure 1.
Wudu reservoir. (a) location of Wudu reservoir; (b) layout of the dam structures; (c) perspective view of the dam.
Figure 2.
The physics-based dam discharge and flood routing simulation framework.
Figure 2.
The physics-based dam discharge and flood routing simulation framework.
Figure 3.
Terrain generation based on DEM and contour lines.
Figure 3.
Terrain generation based on DEM and contour lines.
Figure 4.
Diagram of two terrain modeling methods.
Figure 4.
Diagram of two terrain modeling methods.
Figure 5.
Initial condition configuration. (a) arrangement of probe points; (b) mesh of the partial computational domain.
Figure 5.
Initial condition configuration. (a) arrangement of probe points; (b) mesh of the partial computational domain.
Figure 6.
Numerical validation. (a) arrangement of probe points; (b) flow depth distribution at T = 14.5 s.
Figure 6.
Numerical validation. (a) arrangement of probe points; (b) flow depth distribution at T = 14.5 s.
Figure 7.
Comparison between experiment result and simulation result. (a) water depth at #5 probe point; (b) water depth at #6 probe point.
Figure 7.
Comparison between experiment result and simulation result. (a) water depth at #5 probe point; (b) water depth at #6 probe point.
Figure 8.
Water depth distribution under the normal water level. (a) water depth distribution at T = 5 s; (b)water depth distribution at T = 10 s; (c) water depth distribution at T = 20 s; (d) water depth distribution at T = 30 s; (e) water depth distribution at T = 40 s; (f) water depth distribution at T=50 s.
Figure 8.
Water depth distribution under the normal water level. (a) water depth distribution at T = 5 s; (b)water depth distribution at T = 10 s; (c) water depth distribution at T = 20 s; (d) water depth distribution at T = 30 s; (e) water depth distribution at T = 40 s; (f) water depth distribution at T=50 s.
Figure 9.
Dam discharge flow profile. (a) dam discharge through the surface spillway; (b) dam discharge through the bottom outlet.
Figure 9.
Dam discharge flow profile. (a) dam discharge through the surface spillway; (b) dam discharge through the bottom outlet.
Figure 10.
Pressure distribution under the normal water level. (a) pressure distribution at T = 5 s; (b) pressure distribution at T = 10 s; (c) pressure distribution at T = 20 s; (d) pressure distribution at T = 30 s; (e) pressure distribution at T = 40 s; (f) pressure distribution at T = 50 s.
Figure 10.
Pressure distribution under the normal water level. (a) pressure distribution at T = 5 s; (b) pressure distribution at T = 10 s; (c) pressure distribution at T = 20 s; (d) pressure distribution at T = 30 s; (e) pressure distribution at T = 40 s; (f) pressure distribution at T = 50 s.
Figure 11.
Instantaneous flow field at T = 28 s with/without spillway discharge.
Figure 11.
Instantaneous flow field at T = 28 s with/without spillway discharge.
Figure 12.
Partially enlarged view of local flow pattern under the normal water level. (a) local flow pattern from right-wing view; (b) local flow pattern from top view; (c) local flow pattern from left-wing view.
Figure 12.
Partially enlarged view of local flow pattern under the normal water level. (a) local flow pattern from right-wing view; (b) local flow pattern from top view; (c) local flow pattern from left-wing view.
Figure 13.
Pressure and velocity profiles at each probe point.
Figure 13.
Pressure and velocity profiles at each probe point.
Figure 14.
Location of the house and the house structures.
Figure 14.
Location of the house and the house structures.
Figure 15.
Wetted area of a house and the interior flow process under the normal water level.
Figure 15.
Wetted area of a house and the interior flow process under the normal water level.
Table 1.
Main technical index of the Wudu reservoir.
Table 1.
Main technical index of the Wudu reservoir.
| Main Characteristics | Features |
|---|
| Check flood level | 659.43 m |
| Design flood level | 656.96 m |
| Normal water level | 658.00 m |
| Dead water level | 645.00 m |
| Limited water level of controlling flood | 624.00 m |
| Minimum elevation of building base | 541.00 m |
| Height of the crest of the dam | 660.14 m |
| Maximum height of the dam | 120.00 m |
| Crest length | 727.00 m |
Table 2.
Comparison of two terrain generation methods.
Table 2.
Comparison of two terrain generation methods.
| Method | Terrain Generation Based on Contour Lines | Terrain Generation Based on DEM Data |
|---|
Application
scope | The surveying control point is used as a data source and is suitable for high-resolution scenes. | Point-line-surface-entity modeling process requires simple data structure to develop codes instructing the component generation. |
| Advantage | The elevation gradient is smooth and close to the real terrain, and a more accurate flow field could be solved. | The grid cell is intended to approximate the actual terrain surface Enormous elevation gradient of the terrain departs from reality and high-resolution DEM is required. |
| Disadvantage | Large amount of abundant data makes the terrain files inconvenient for numerical simulation. An exhausted field survey to measure all the feature points is inevitable. | The code cannot satisfy the demand for unstructured terrain mesh generation. Spatial Quadrilateral confines the construction of body-fitted terrain. |
Table 3.
Scenario analysis and corresponding working conditions.
Table 3.
Scenario analysis and corresponding working conditions.
| Case | Scenarios | Working Condition |
|---|
| case 1 | dead water level | bottom outlet and intake of
power plant are fully open |
| case 2 | water level at 8:00 o’clock on
18 June2018 (validation) | bottom outlet and intake of
power plant are fully open |
| case 3 | the normal water level | intake of power plant and bottom outlet
are fully open with spillway discharge |
| case 4 | the normal water level | intake of power plant and bottom outlet
are fully open, without spillway discharge |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).