A Modeling Platform for Landslide Stability: A Hydrological Approach
Abstract
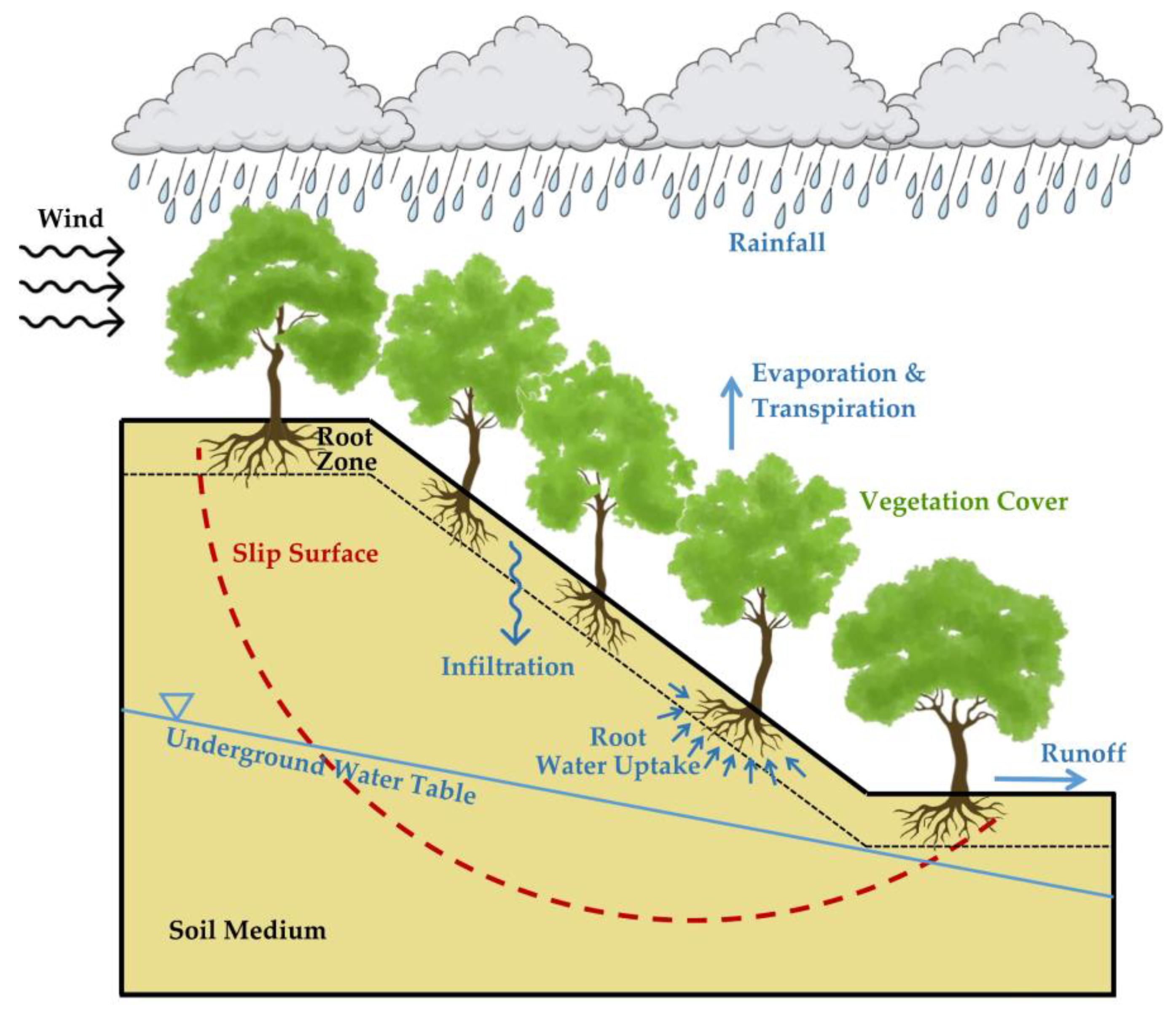
1. Introduction
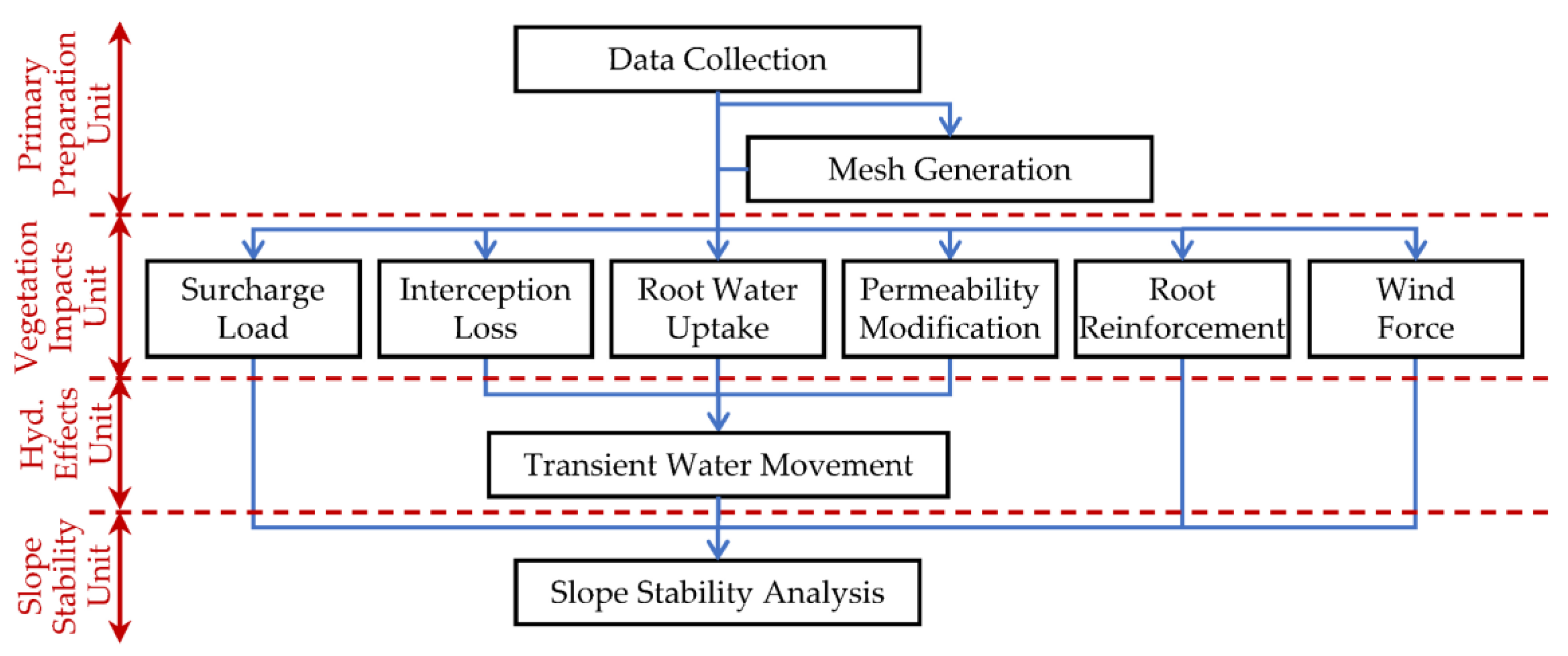
2. Model Structure
2.1. Primary Preparation Unit
2.2. Vegetation Impacts Unit
2.3. Hydrological Effects Unit
2.4. Slope Stability Analysis Unit
3. Mathematical Formulation
3.1. Vegetation Module
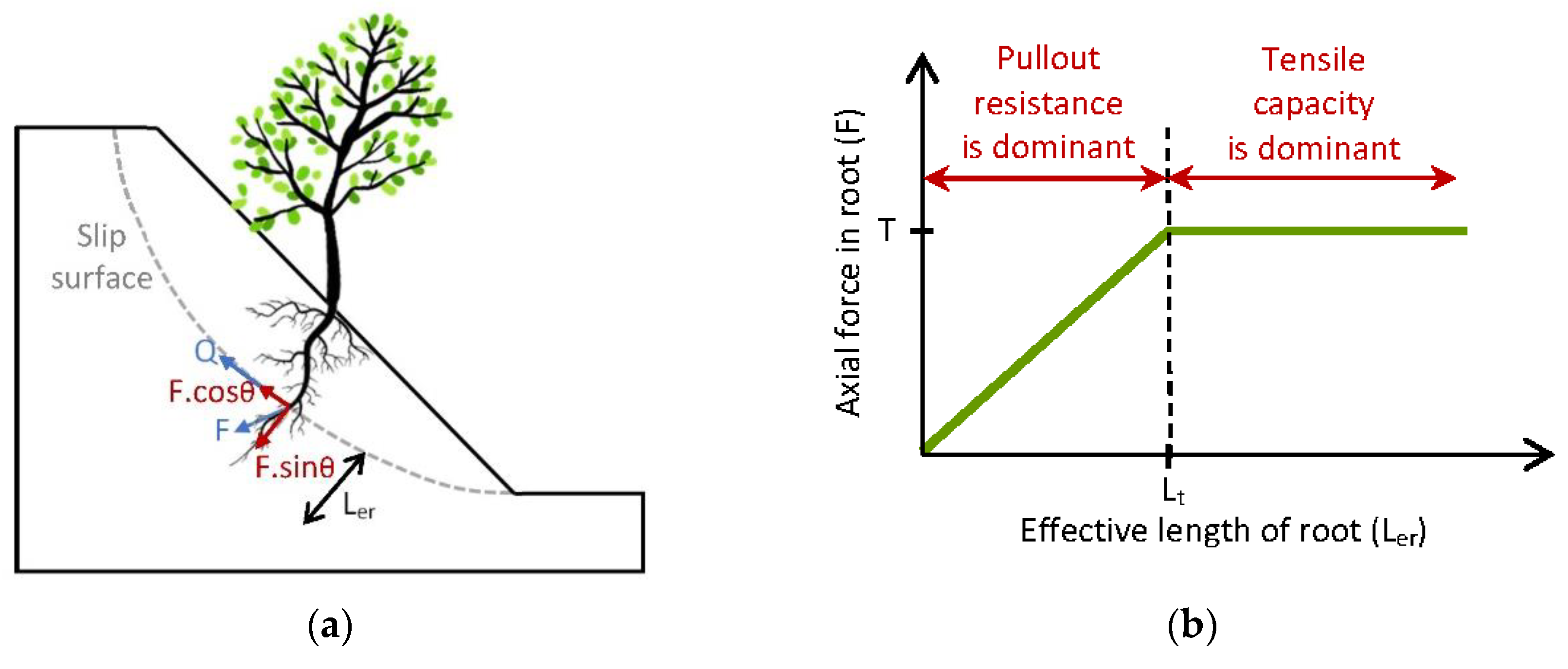
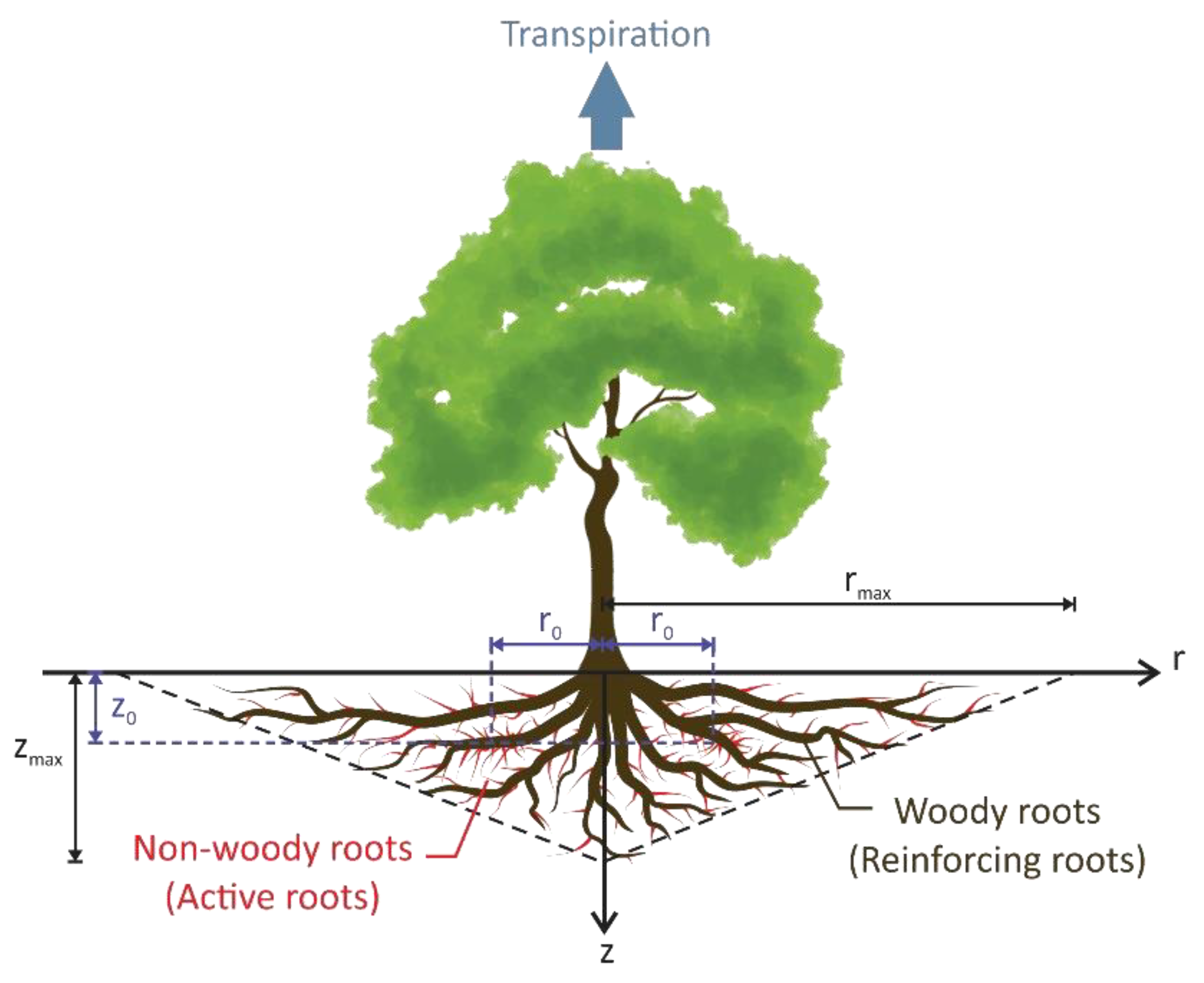
3.1.1. Reinforcement of Soil by Roots
3.1.2. Increasing Permeability
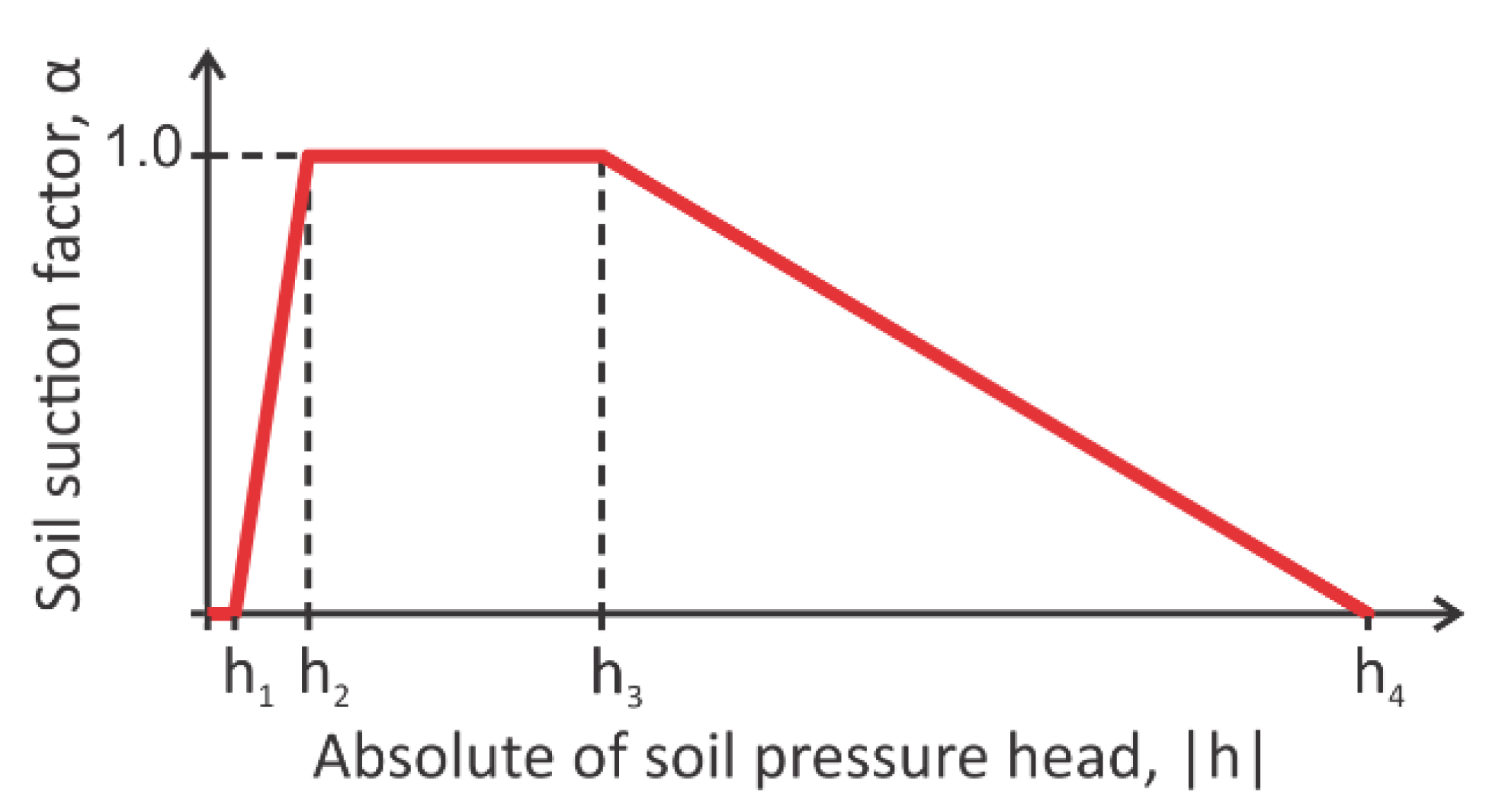
3.1.3. Root Water Uptake
3.1.4. Surcharge Load
3.1.5. Effective Rainfall
3.1.6. Wind Force
3.2. Hydrological Module
3.3. Slope Stability Analysis
3.3.1. Shear Strength in the Saturated and Unsaturated Zone
3.3.2. Simplified Bishop Method
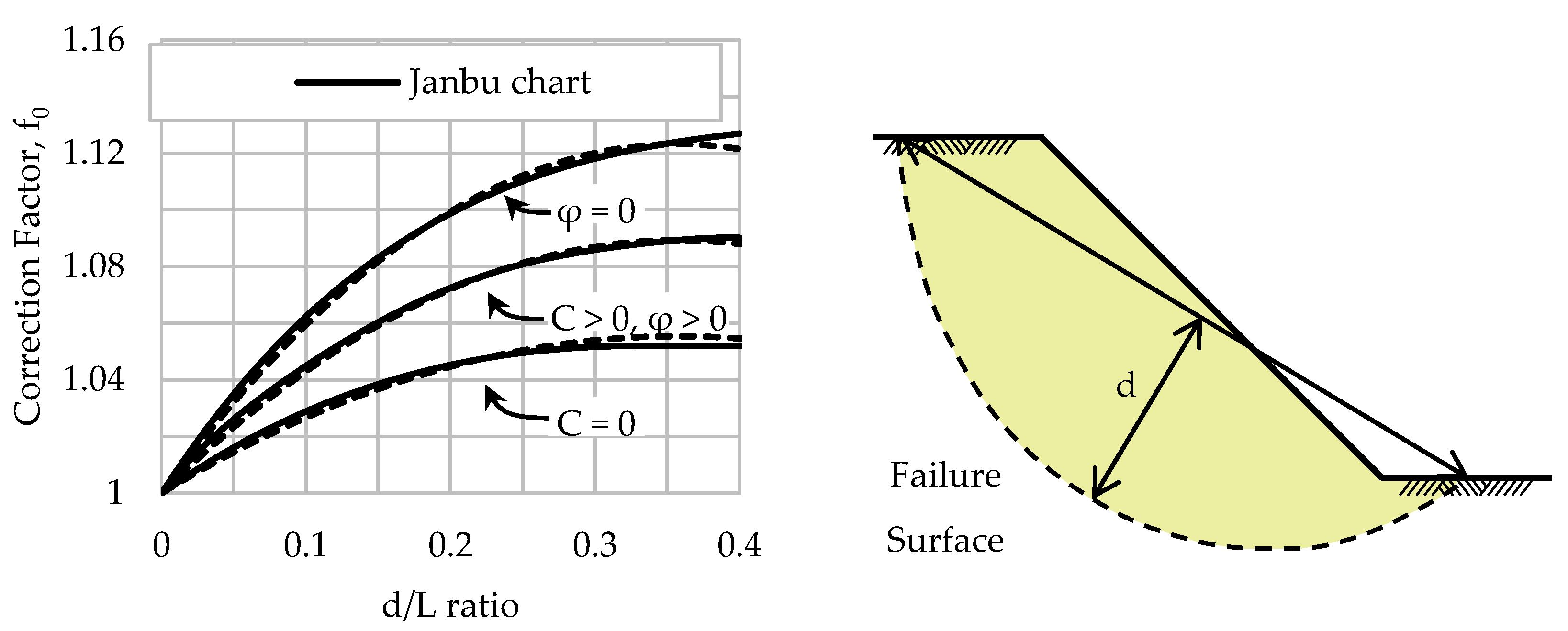
3.3.3. Janbu’s Simplified Method
4. Numerical Formulation
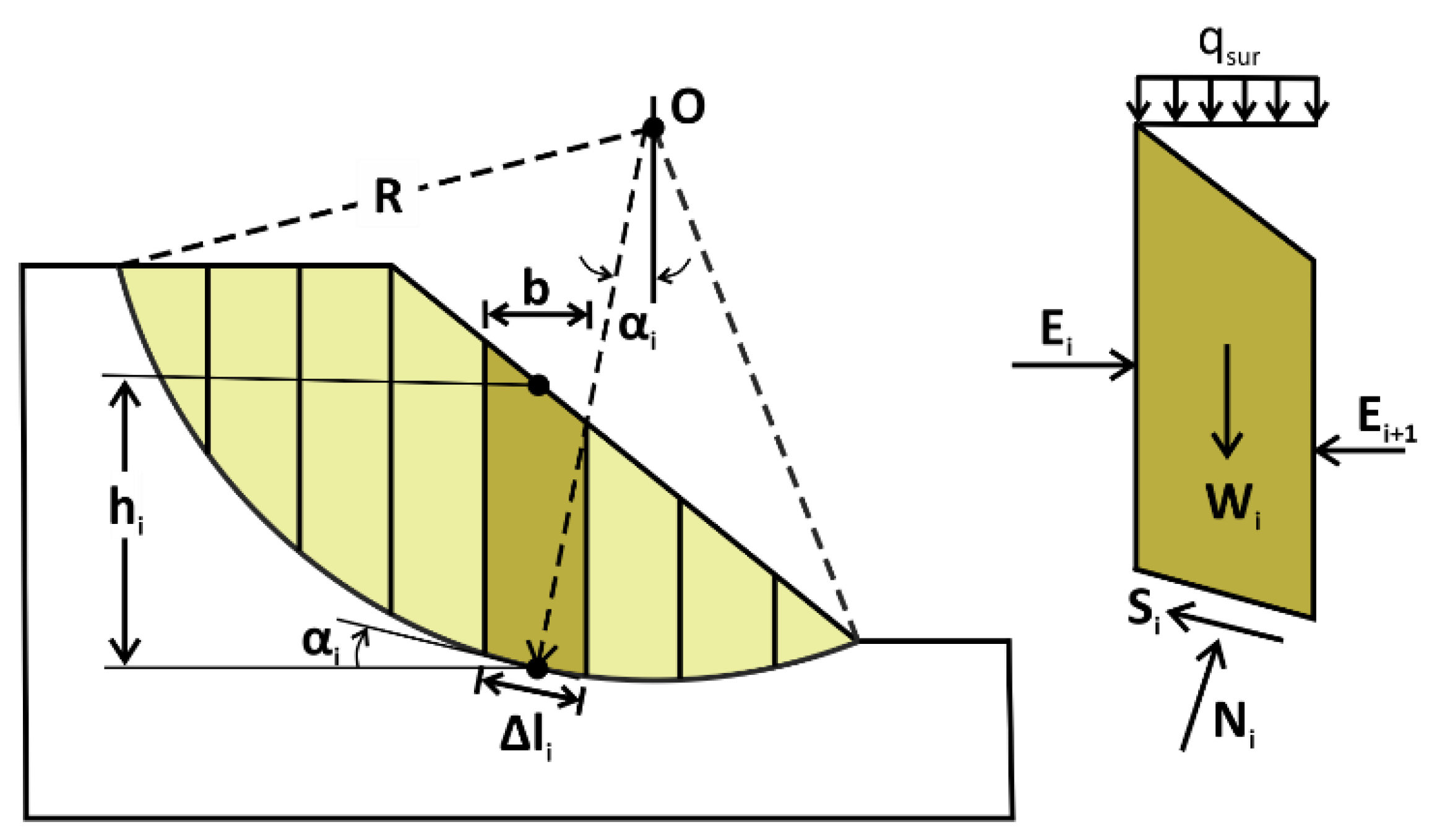
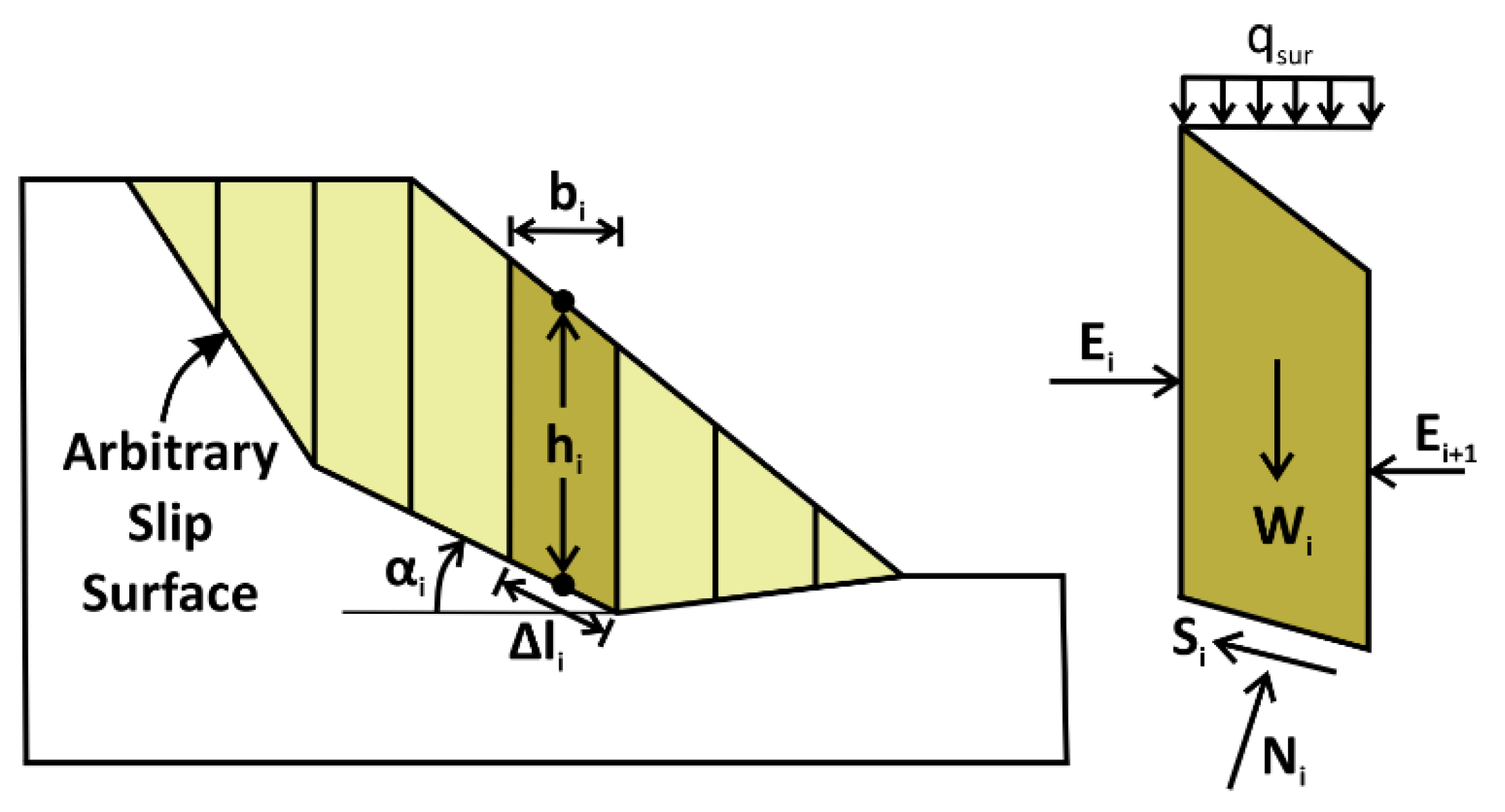
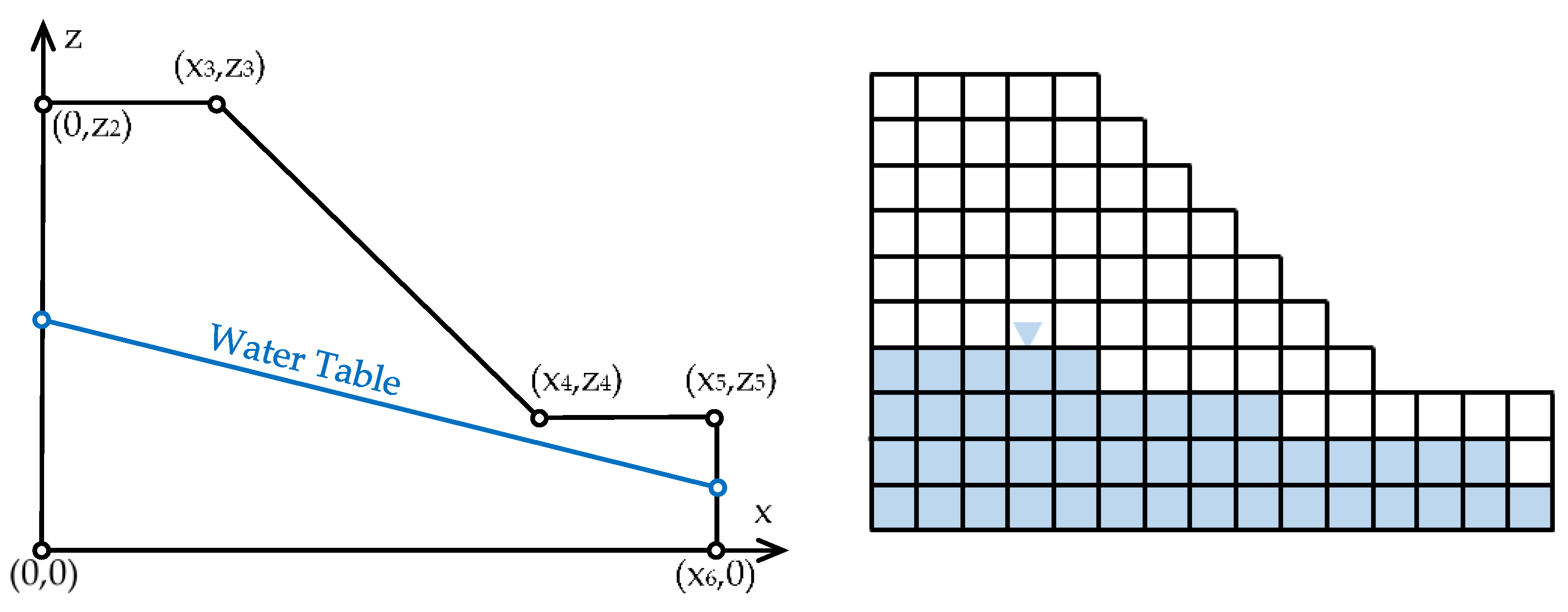
4.1. Geometry Discretization
4.2. Transient Water Infiltration
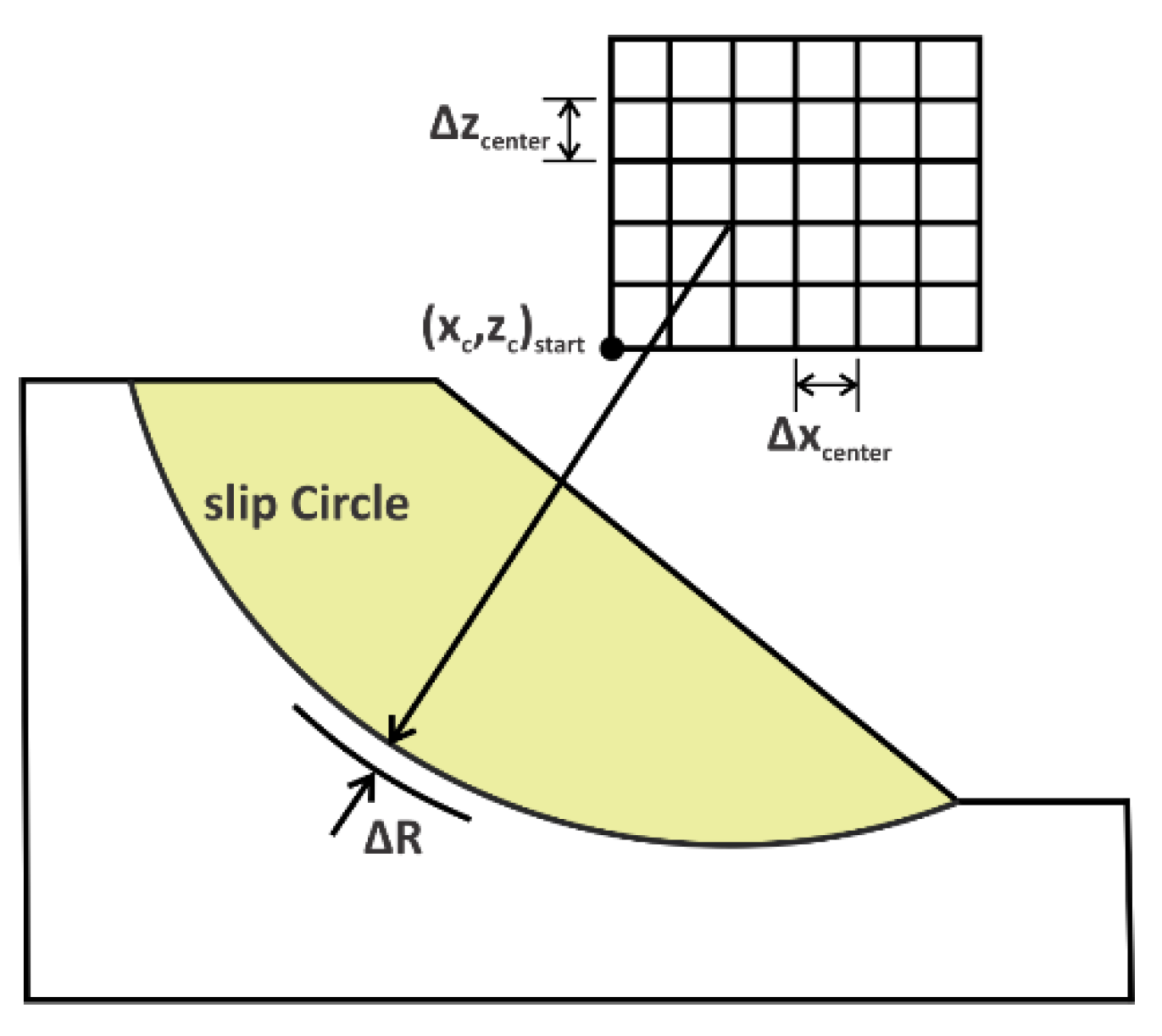
4.3. Slope Stability Analysis
5. Verifications and Results
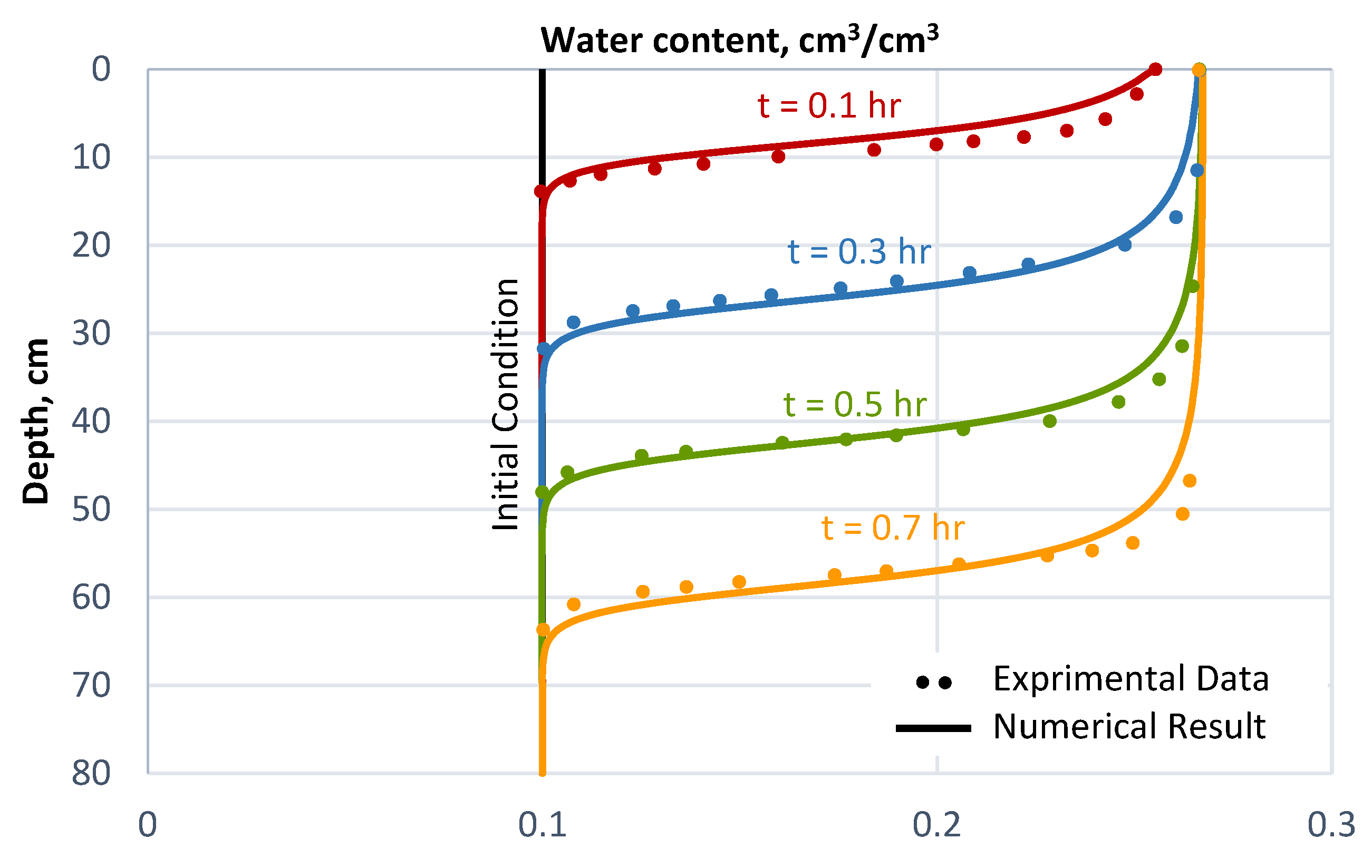
5.1. Example 1: 1-D Infiltration in the Vertical Soil Column
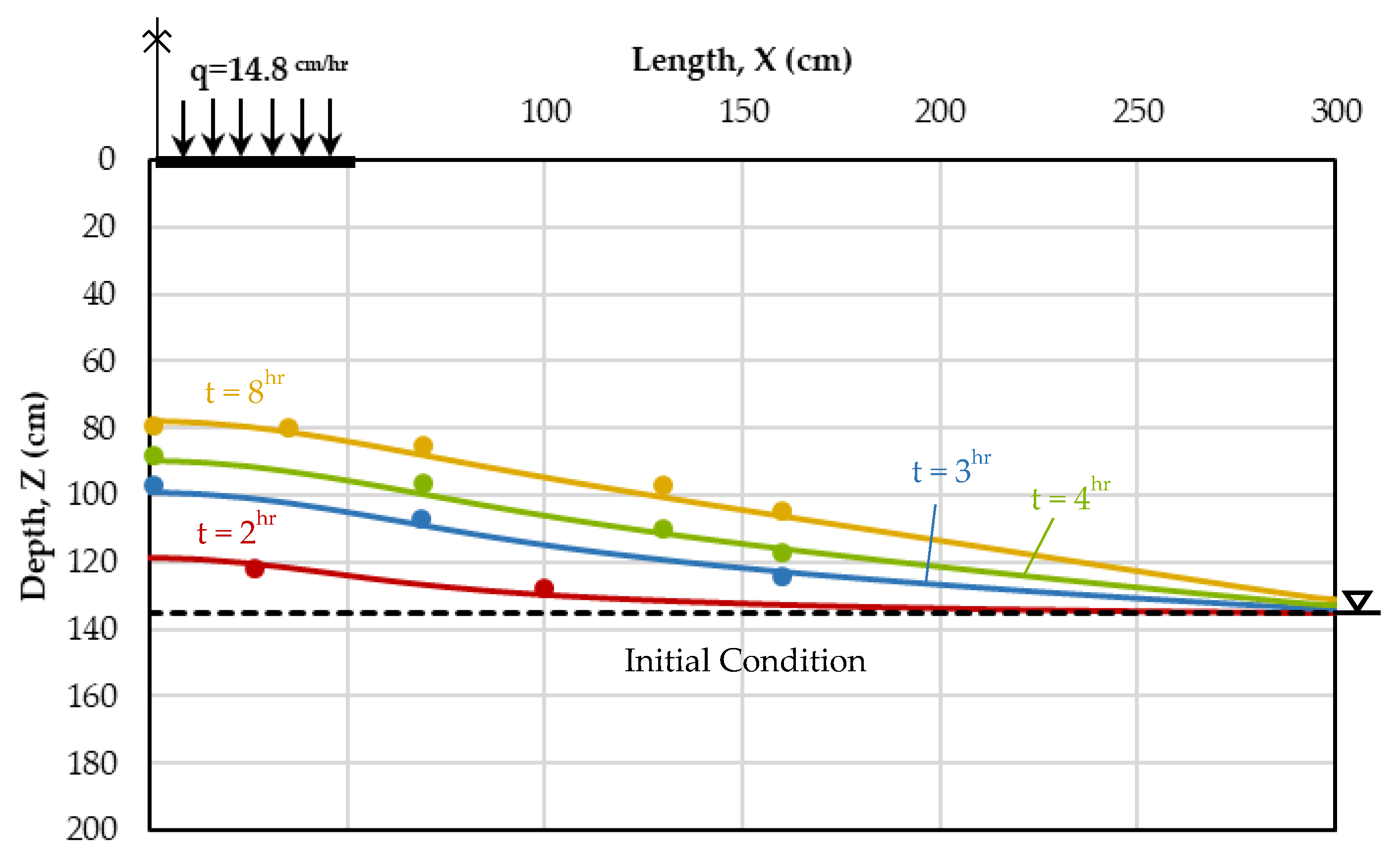
5.2. Example 2: 2-Dimensional Infiltration and Water Table Recharge
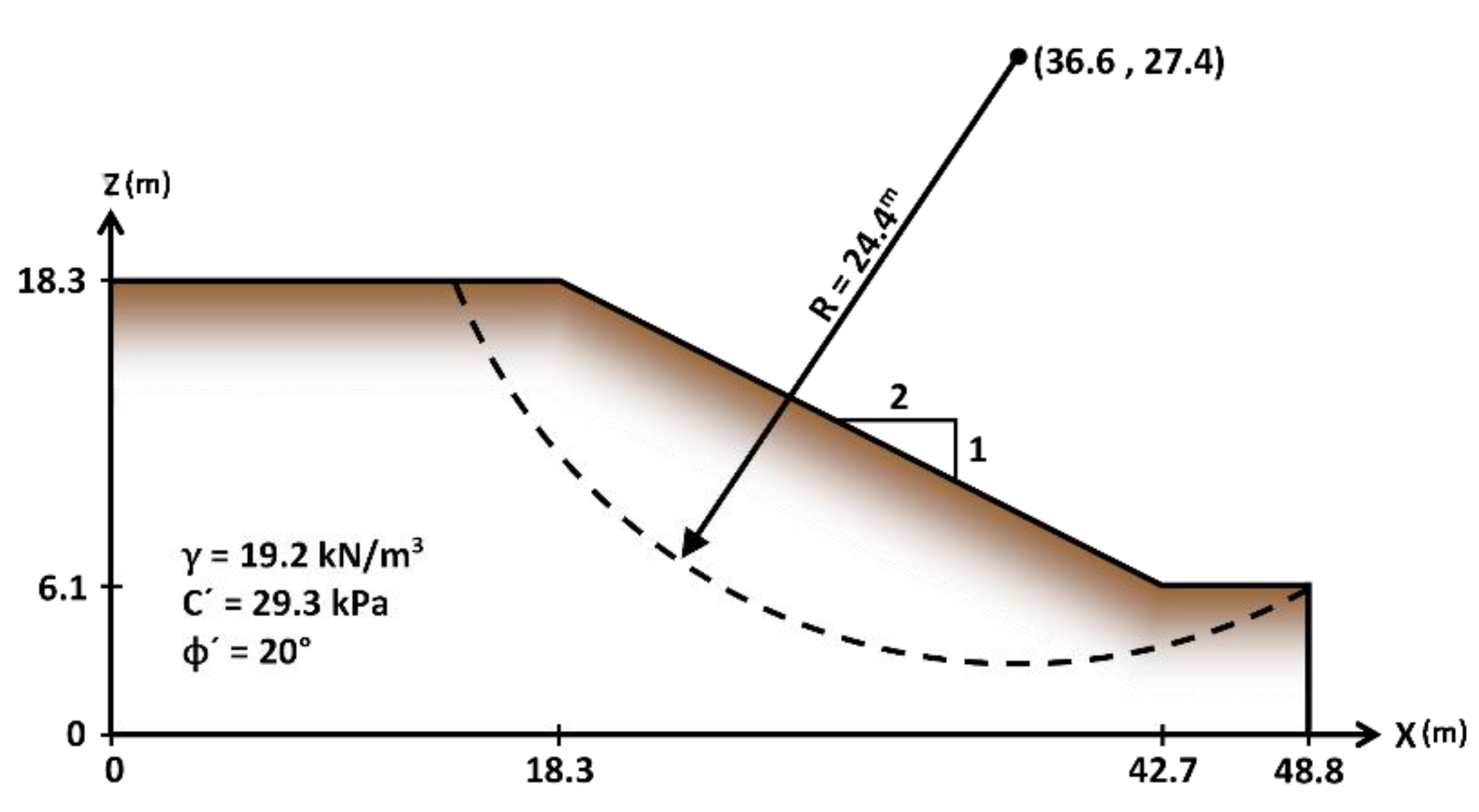
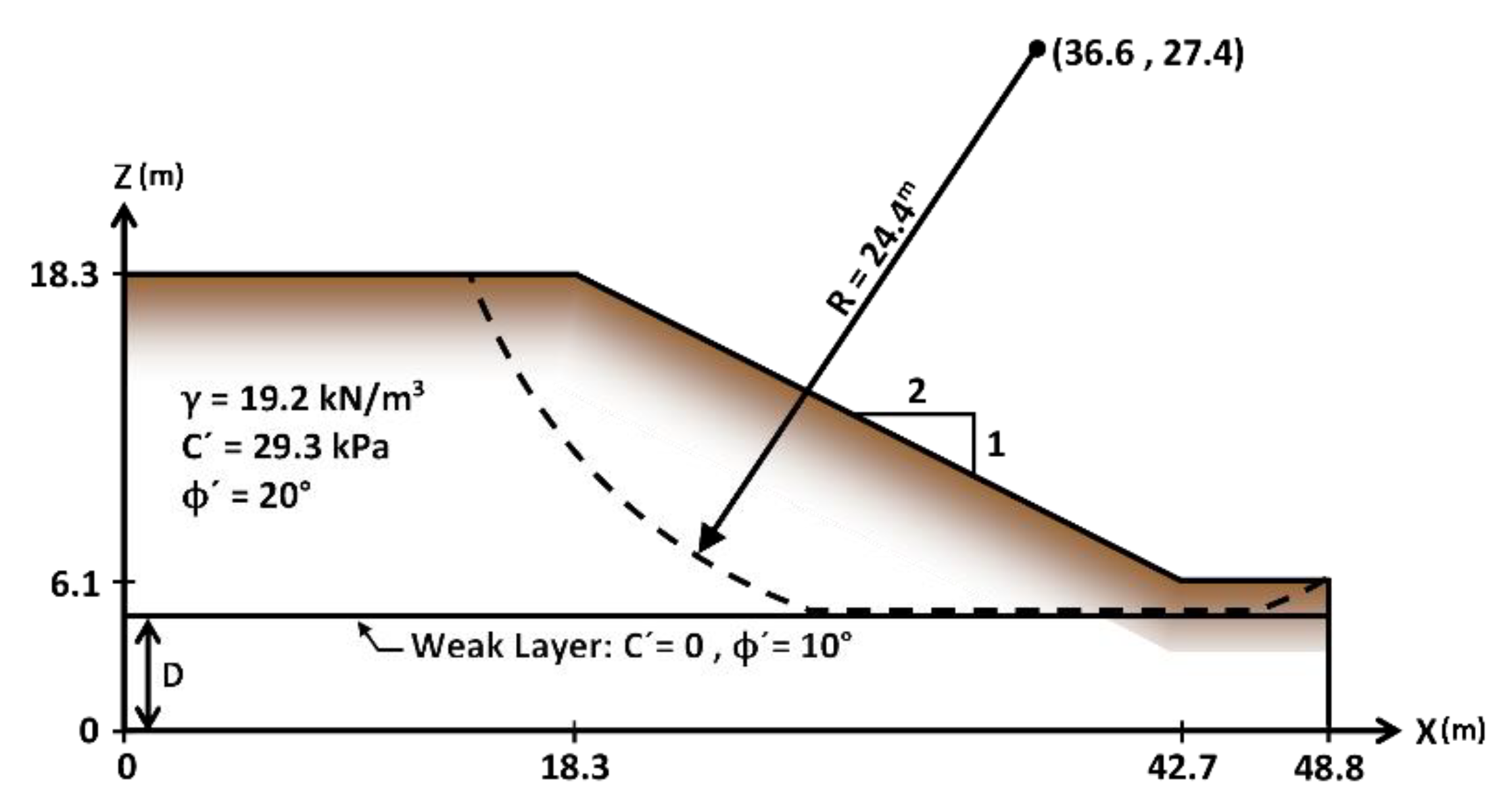
5.3. Example 3: Stability Analysis of a Slope
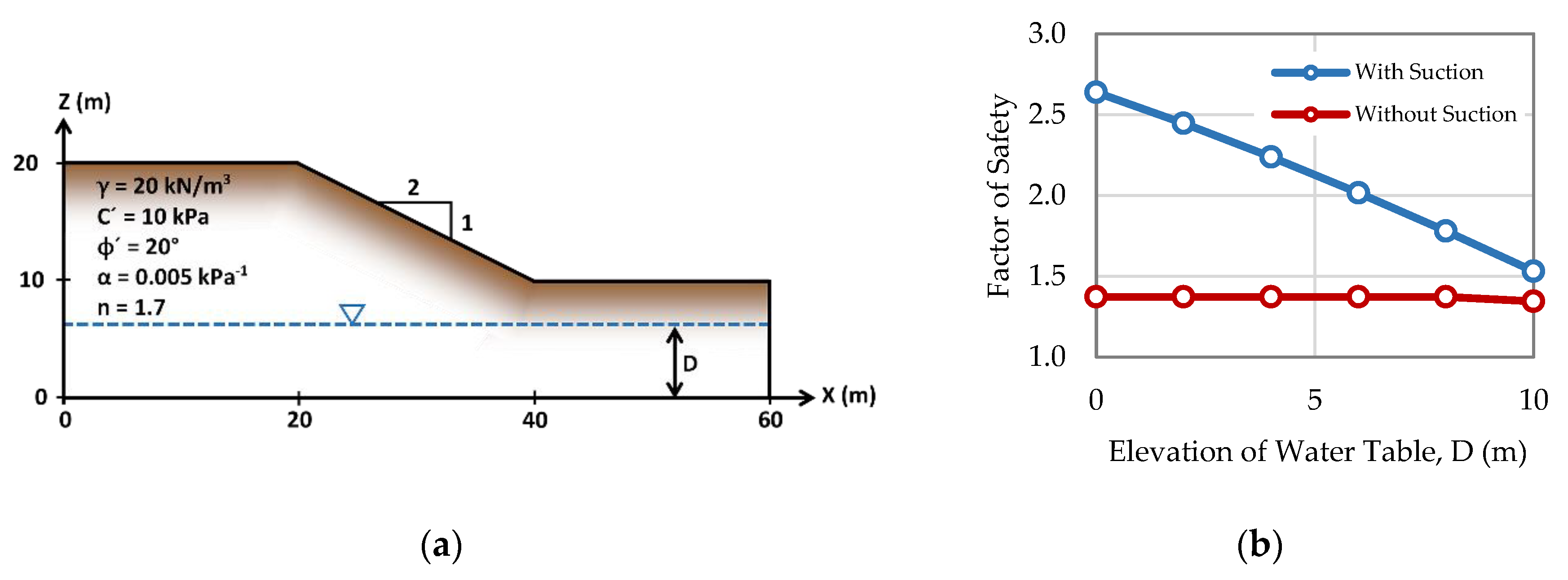
5.4. Example 4: The Effect of Matric Suction on the Stability of a Slope
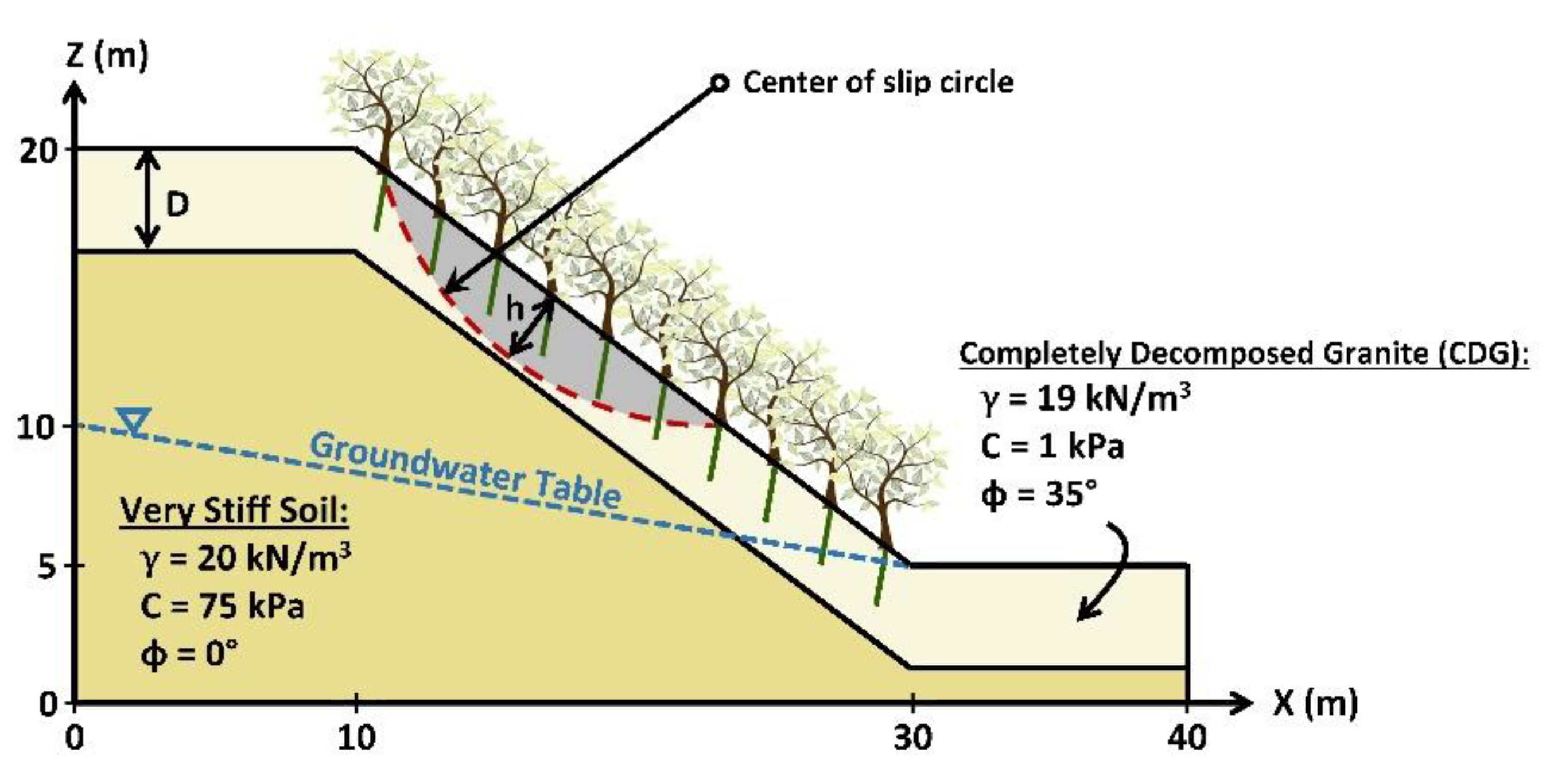
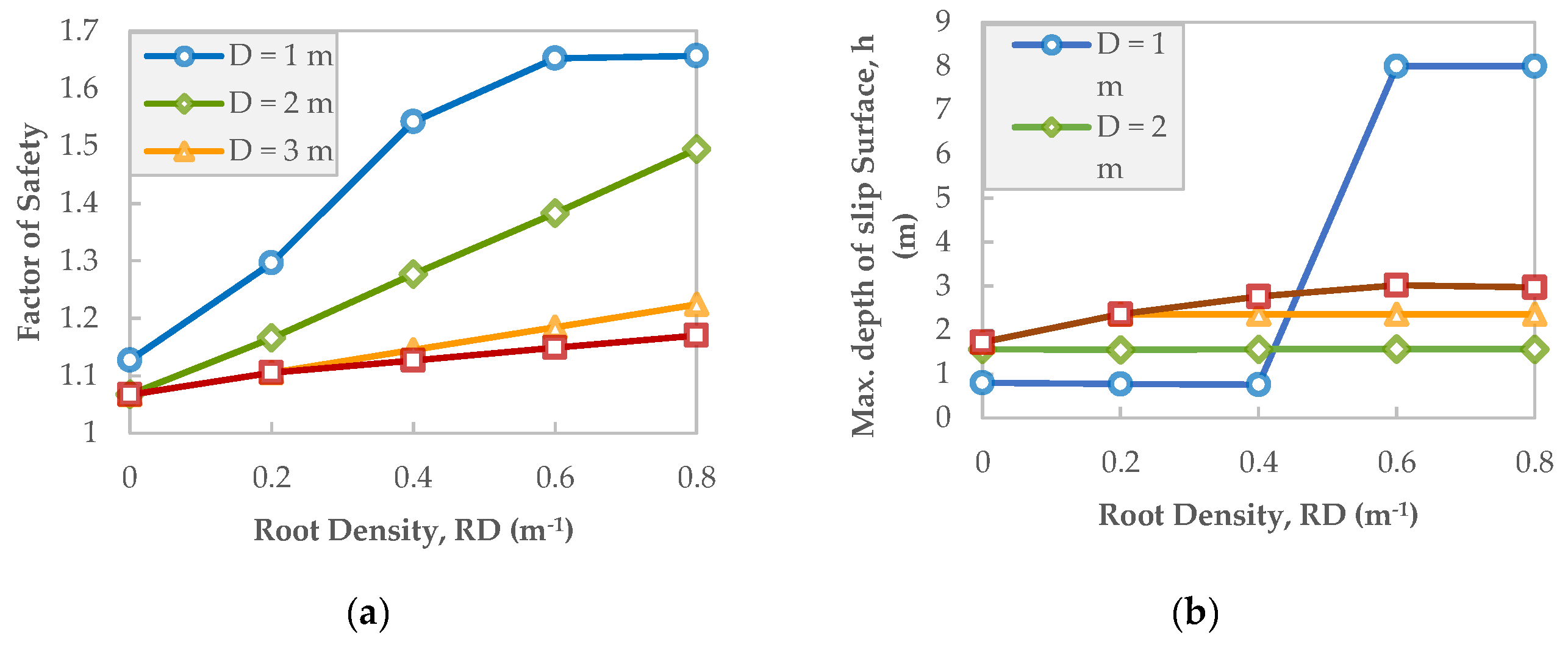
5.5. Example 5: Improvement of Slope Stability by Vegetation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kirschbaum, D.B.; Adler, R.; Hong, Y.; Hill, S.; Lerner-Lam, A. A global landslide catalog for hazard applications: Method, results, and limitations. Nat. Hazards 2010, 52, 561–575. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Haque, U.; Blum, P.; Da Silva, P.F.; Andersen, P.; Pilz, J.; Chalov, S.R.; Malet, J.-P.; Auflič, M.J.; Andres, N.; Poyiadji, E. Fatal landslides in Europe. Landslides 2016, 13, 1545–1554. [Google Scholar] [CrossRef]
- Klose, M.; Maurischat, P.; Damm, B. Landslide impacts in Germany: A historical and socioeconomic perspective. Landslides 2016, 13, 183–199. [Google Scholar] [CrossRef]
- Yavari-Ramshe, S.; Ataie-Ashtiani, B. Numerical modeling of subaerial and submarine landslide-generated tsunami waves—Recent advances and future challenges. Landslides 2016, 13, 1325–1368. [Google Scholar] [CrossRef]
- Panizzo, A.; De Girolamo, P.; Di Risio, M.; Maistri, A.; Petaccia, A. Great landslide events in Italian artificial reservoirs. Nat. Hazards Earth Syst. Sci. 2005, 5, 733–740. [Google Scholar] [CrossRef]
- Dilley, M.; Chen, R.S.; Deichmann, U.; Lerner-Lam, A.L.; Arnold, M. Natural Disaster Hotspots: A Global Risk Analysis; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Sepúlveda, S.A.; Petley, D.N. Regional trends and controlling factors of fatal landslides in Latin America and the Caribbean. Nat. Hazards Earth Syst. Sci. 2015, 15, 1821–1833. [Google Scholar] [CrossRef]
- Wienhöfer, J.; Lindenmaier, F.; Zehe, E. Challenges in Understanding the Hydrologic Controls on the Mobility of Slow-Moving Landslides. Vadose Zone J. 2011, 10, 496–511. [Google Scholar] [CrossRef]
- Strauch, A.M.; MacKenzie, R.A.; Giardina, C.P.; Bruland, G.L. Climate driven changes to rainfall and streamflow patterns in a model tropical island hydrological system. J. Hydrol. 2015, 523, 160–169. [Google Scholar] [CrossRef]
- Forbes, K.; Broadhead, J.; Bischetti, G.; Brardinoni, F.; Dykes, A.; Gray, D.; Imaizumi, F.; Kuriakose, S.; Osman, N.; Petley, D.; et al. Forests and Landslides The Role of Trees and Forests in the Prevention of Landslides and Rehabilitation of Landslide-Affected Areas in Asia; Forbes, K., Broadhead, J., Eds.; FAO Regional Office for Asia and the Pacific: Bangkok, Thailand, 2011. [Google Scholar]
- Meehan, W.R. Influences of Forest and Rangeland Management on Salmonid Fishes and Their Habitats; American Fisheries Society: Bethesda, MD, USA, 1991. [Google Scholar]
- Gaillard, J.; Liamzon, C.; Villanueva, J. ‘Natural’ disaster? A retrospect into the causes of the late-2004 typhoon disaster in Eastern Luzon, Philippines. Environ. Hazards 2007, 7, 257–270. [Google Scholar] [CrossRef]
- Lee, I. A review of vegetative slope stabilization. Hong Kong Inst. Eng. 1985, 13, 9–12. [Google Scholar]
- Greenway, D. Vegetation and slope stability. In Slope Stability: Geotechnical Engineering and Geomorphology; Anderson, M.G., Richards, K.S., Eds.; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Waldron, L.J. The Shear Resistance of Root-Permeated Homogeneous and Stratified Soil1. Soil Sci. Soc. Am. J. 1977, 41, 843. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell Iii, W.P.; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Gardner, W.R. Relation of Root Distribution to Water Uptake and Availability. Agron. J. 1964, 56, 41–45. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.; Kolinska-Malinka, K.; Zaradny, H. Simulation of field water uptake by plants using a soil water dependent root extraction function. J. Hydrol. 1976, 31, 13–26. [Google Scholar] [CrossRef]
- Prasad, R. A linear root water uptake model. J. Hydrol. 1988, 99, 297–306. [Google Scholar] [CrossRef]
- Li, K.Y.; Boisvert, J.B.; Jong, R.D. An exponential root-water-uptake model. Can. J. Soil Sci. 1999, 79, 333–343. [Google Scholar] [CrossRef]
- Rutter, A.J.; Kershaw, K.A.; Robins, P.C.; Morton, A.J. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Rutter, A.J.; Morton, A.J.; Robins, P.C. A Predictive Model of Rainfall Interception in Forests. II. Generalization of the Model and Comparison with Observations in Some Coniferous and Hardwood Stands. J. Appl. Ecol. 1975, 12, 367–380. [Google Scholar] [CrossRef]
- Gash, J. An analytical model of rainfall interception by forests. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Valente, F.; David, J.S.; Gash, J.H.C. Modelling interception loss for two sparse eucalypt and pine forests in central Portugal using reformulated Rutter and Gash analytical models. J. Hydrol. 1997, 190, 141–162. [Google Scholar] [CrossRef]
- Gash, J.H.; Lloyd, C.; Lachaud, G. Estimating sparse forest rainfall interception with an analytical model. J. Hydrol. 1995, 170, 79–86. [Google Scholar] [CrossRef]
- Bishop, A.W. The use of the Slip Circle in the Stability Analysis of Slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Fellenius, W. Calculation of stability of earth dam. In Proceedings of the Transactions: 2nd Congress Large Dams, Washington, DC, USA, 7 September 1936; pp. 445–462. [Google Scholar]
- Janbu, N.; Bjerrum, L.; Kjaernsli, B. Soil Mechanics Applied to Some Engineering Probl Ems; Norwegian Geotechnical Institute: Oslo, Norway, 1956. [Google Scholar]
- Spencer, E. A Method of analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Bishop, A.W. The principle of effective stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Darcy, H.P.G. Les Fontaines Publiques de la Ville de Dijon. Exposition et Application des Principes à Suivre et des Formules à Employer Dans les Questions de Distribution D’eau, Etc; Victor Dalamont: Paris, France, 1856. [Google Scholar]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Anderson, M.; Lloyd, D. Using a combined slope hydrology-stability model to develop cut slope design charts. Proc. Inst. Civ. Eng. Part 2 1991, 91, 705–718. [Google Scholar] [CrossRef]
- Wilkinson, P.L.; Anderson, M.G.; Lloyd, D.M.; Renaud, J.-P. Landslide hazard and bioengineering: Towards providing improved decision support through integrated numerical model development. Environ. Model. Softw. 2002, 17, 333–344. [Google Scholar] [CrossRef]
- Greenwood, J.R. SLIP4EX–A program for routine slope stability analysis to include the effects of vegetation, reinforcement and hydrological changes. Geotech. Geol. Eng. 2006, 24, 449. [Google Scholar] [CrossRef]
- Chok, Y.H. Modelling the Effects of Soil Variability and Vegetation on the Stability of Natural Slopes. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2009. [Google Scholar]
- Anagnostopoulos, G. Hydrological Modelling of Slope Stability; ETH Zurich: Zürich, Switzerland, 2014. [Google Scholar]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins. Landslides 2016, 13, 497–517. [Google Scholar] [CrossRef]
- Pasculli, A.; Calista, M.; Sciarra, N. Variability of local stress states resulting from the application of Monte Carlo and finite difference methods to the stability study of a selected slope. Eng. Geol. 2018, 245, 370–389. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhuang, X.; Nguyen-Thoi, T.; Rabczuk, T. A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv. Eng. Softw. 2016, 100, 19–31. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A.; Collison, A. Advances in assessing the mechanical and hydrologic effects of riparian vegetation on streambank stability. In Riparian Vegetation and Fluvial Geomorphology; American Geophysical Union: Washington, DC, USA, 2004; pp. 125–139. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root-failure Weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W. Hillslope Hydrology and Stability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Mickovski, S.B.; Hallett, P.D.; Bransby, M.F.; Davies, M.C.R.; Sonnenberg, R.; Bengough, A.G. Mechanical Reinforcement of Soil by Willow Roots: Impacts of Root Properties and Root Failure Mechanism. Soil Sci. Soc. Am. J. 2009, 73, 1276. [Google Scholar] [CrossRef]
- Operstein, V.; Frydman, S. The influence of vegetation on soil strength. Proc. Inst. Civ. Eng. Ground Improv. 2000, 4, 81–89. [Google Scholar] [CrossRef]
- Wu, T.H. Root reinforcement of soil: Review of analytical models, test results, and applications to design. Can. Geotech. J. 2013, 50, 259–274. [Google Scholar] [CrossRef]
- Wu, T.H.; Watson, A. In situ shear tests of soil blocks with roots. Can. Geotech. J. 1998, 35, 579–590. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Epis, T.; Morlotti, E. Root cohesion of forest species in the Italian Alps. Plant Soil 2009, 324, 71–89. [Google Scholar] [CrossRef]
- De Baets, S.; Poesen, J.; Reubens, B.; Wemans, K.; De Baerdemaeker, J.; Muys, B. Root tensile strength and root distribution of typical Mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Quantifying root-reinforcement of river bank soils by four Australian tree species. Geomorphology 2008, 100, 401–418. [Google Scholar] [CrossRef]
- Fan, C.-C.; Su, C.-F. Role of roots in the shear strength of root-reinforced soils with high moisture content. Ecol. Eng. 2008, 33, 157–166. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Genet, M.; Mine, F.-X.; Jourdan, C.; Rey, H.; Courbaud, B.; Stokes, A. Engineering ecological protection against landslides in diverse mountain forests: Choosing cohesion models. Ecol. Eng. 2012, 45, 55–69. [Google Scholar] [CrossRef]
- Adhikari, A.R.; Gautam, M.R.; Yu, Z.; Imada, S.; Acharya, K. Estimation of root cohesion for desert shrub species in the Lower Colorado riparian ecosystem and its potential for streambank stabilization. Ecol. Eng. 2013, 51, 33–44. [Google Scholar] [CrossRef]
- Meijer, G.J.; Bengough, A.G.; Knappett, J.A.; Loades, K.W.; Nicoll, B.C. In situ measurement of root reinforcement using corkscrew extraction method. Can. Geotech. J. 2018, 55, 1372–1390. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.M.; Xiao, T.; Li, X.Y. Enhancement of slope stability by vegetation considering uncertainties in root distribution. Comput. Geotech. 2017, 85, 84–89. [Google Scholar] [CrossRef]
- Collison, A.; Anderson, M. Using a combined slope hydrology/stability model to identify suitable conditions for landslide prevention by vegetation in the humid tropics. Earth Surf. Process. Landf. 1996, 21, 737–747. [Google Scholar] [CrossRef]
- Radcliffe, D.; Hayden, T.; Watson, K.; Crowley, P.; Phillips, R. Simulation of Soil Water within the Root Zone of a Corn Crop 1. Agron. J. 1980, 72, 19–24. [Google Scholar] [CrossRef]
- Ali, N. The Influence of Vegetation Induced Moisture Transfer on Unsaturated Soils. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2007. [Google Scholar]
- Rees, S.W.; Ali, N. Seasonal water uptake near trees: A numerical and experimental study. Geomech. Geoengin. 2006, 1, 129–138. [Google Scholar] [CrossRef]
- Kokutse, N.; Fourcaud, T.; Kokou, K.; Neglo, K.; Lac, P. 3D numerical modelling and analysis of the influence of forest structure on hill slopes stability. In Interpraevent; Universal Academy Press: Tokyo, Japan, 2006; pp. 561–567. [Google Scholar]
- Fatahi, B. Modelling of Influence of Matric Suction Induced by Native Vegetation on Sub-Soil Improvement. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2007. [Google Scholar]
- Levin, A.; Shaviv, A.; Indelman, P. Influence of root resistivity on plant water uptake mechanism, part I: Numerical solution. Transp. Porous Media 2007, 70, 63–79. [Google Scholar] [CrossRef]
- Novák, V. Estimation of soil-water extraction patterns by roots. Agric. Water Manag. 1987, 12, 271–278. [Google Scholar] [CrossRef]
- Perrochet, P. Water uptake by plant roots—A simulation model, I. Conceptual model. J. Hydrol. 1987, 95, 55–61. [Google Scholar] [CrossRef]
- Feddes, R.A. Simulation of field water use and crop yield. In Simulation of Plant Growth and Crop Production; Penning de Vries, F.W.T., Laar, H.H.V., Eds.; Pudoc: Wageningen, The Netherlands, 1982; pp. 194–209. [Google Scholar]
- Dobson, M.; Moffat, A. A re-evaluation of objections to tree planting on containment landfills. Waste Manag. Res. 1995, 13, 579–600. [Google Scholar] [CrossRef]
- Landsberg, J. Tree water use and its implications in relation to agroforestry systems. In The Ways Trees Use Water; Landsberg, J., Ed.; Rural Industries Research and Development Corporation (RIRDC): Canberra, Australia, 1999; pp. 1–27. [Google Scholar]
- Fatahi, B.; Khabbaz, H.; Indraratna, B. Bioengineering ground improvement considering root water uptake model. Ecol. Eng. 2010, 36, 222–229. [Google Scholar] [CrossRef]
- Bishop, D.M.; Stevens, M.E. Landslides on Logged Areas in Southeast Alaska; Northern Forest Experiment Station, Forest Service, U.S. Dept. of Agriculture: Alaska, AL, USA, 1964.
- Kokutse, N.K.; Temgoua, A.G.T.; Kavazović, Z. Slope stability and vegetation: Conceptual and numerical investigation of mechanical effects. Ecol. Eng. 2016, 86, 146–153. [Google Scholar] [CrossRef]
- Van Asch, T.W.J.; Deimel, M.S.; Haak, W.J.C.; Simon, J. The viscous creep component in shallow clayey soil and the influence of tree load on creep rates. Earth Surf. Process. Landf. 1989, 14, 557–564. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth Surf. Process. Landf. 2002, 27, 527–546. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. Does the weight of riparian trees destabilize riverbanks? Regul. Rivers Res. Manag. 2000, 16, 565–576. [Google Scholar] [CrossRef]
- Waldron, L.J.; Dakessian, S. Effect of Grass, Legume, and Tree Roots on Soil Shearing Resistance1. Soil Sci. Soc. Am. J. 1982, 46, 894–899. [Google Scholar] [CrossRef]
- Kim, D.; Im, S.; Lee, C.; Woo, C. Modeling the contribution of trees to shallow landslide development in a steep, forested watershed. Ecol. Eng. 2013, 61, 658–668. [Google Scholar] [CrossRef]
- Chiaradia, E.A.; Vergani, C.; Bischetti, G.B. Evaluation of the effects of three European forest types on slope stability by field and probabilistic analyses and their implications for forest management. For. Ecol. Manag. 2016, 370, 114–129. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Bassanelli, C.; Chiaradia, E.A.; Minotta, G.; Vergani, C. The effect of gap openings on soil reinforcement in two conifer stands in northern Italy. For. Ecol. Manag. 2016, 359, 286–299. [Google Scholar] [CrossRef]
- Horton, R.E. Rainfall interception. Mon. Weather Rev. 1919, 47, 603–623. [Google Scholar] [CrossRef]
- Muzylo, A.; Llorens, P.; Valente, F.; Keizer, J.J.; Domingo, F.; Gash, J.H.C. A review of rainfall interception modelling. J. Hydrol. 2009, 370, 191–206. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–28. [Google Scholar]
- Fredlund, D.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Fredlund, D.; Xing, A.; Huang, S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 533–546. [Google Scholar] [CrossRef]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Haverkamp, R.; Vauclin, M.; Touma, J.; Wierenga, P.; Vachaud, G. A comparison of numerical simulation models for one-dimensional infiltration 1. Soil Sci. Soc. Am. J. 1977, 41, 285–294. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Ma, K.-C.; Tan, Y.-C.; Chen, C.-H. The influence of water retention curve hysteresis on the stability of unsaturated soil slopes. Hydrol. Process. 2011, 25, 3563–3574. [Google Scholar] [CrossRef]
- Pasculli, A.; Sciarra, N.; Esposito, L.; Esposito, A.W. Effects of wetting and drying cycles on mechanical properties of pyroclastic soils. CATENA 2017, 156, 113–123. [Google Scholar] [CrossRef]
- Duncan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Janbu, N. Slope stability computations. In Embankment-Dam Engineering; Hirschfeld, R., Poulos, S., Eds.; John Wiley and Sons Inc.: NewYork, NY, USA, 1973. [Google Scholar]
- Fredlund, D.; Krahn, J. Comparison of slope stability methods of analysis. Can. Geotech. J. 1977, 14, 429–439. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943. [Google Scholar]
- Fredlund, D.; Morgenstern, N.R.; Widger, R. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Skempton, A.W. Effective stress in soils, concrete and rocks. In Proceedings of the Conference on Pore Pressure and Suction in Soils, London, UK, 30–31 March 1960; pp. 4–16. [Google Scholar]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of variations in rainfall intensity on slope stability in Singapore. Int. Soil Water Conserv. Res. 2017, 5, 258–264. [Google Scholar] [CrossRef]
- Abramson, L.W.; Lee, T.S.; Sharma, S.; Boyce, G.M. Slope Stability and Stabilization Methods; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Shahraiyni, H.T.; Ataie-Ashtiani, B. Mathematical Forms and Numerical Schemes for the Solution of Unsaturated Flow Equations. J. Irrig. Drain. Eng. 2012, 138, 63–72. [Google Scholar] [CrossRef]
- Srivastava, R.; Guzman-Guzman, A. Analysis of Hydraulic Conductivity Averaging Schemes for One-Dimensional, Steady-State Unsaturated Flow. Ground Water 1995, 33, 946–952. [Google Scholar] [CrossRef]
- Rathfelder, K.; Abriola, L.M. Mass conservative numerical solutions of the head-based Richards equation. Water Resour. Res. 1994, 30, 2579–2586. [Google Scholar] [CrossRef]
- Vogel, T. SWMII-Numerical Model of Two-Dimensional Flow in a Variably Saturated Porous Medium; Wageningen Agricultural University: Wageningen, The Netherlands, 1988. [Google Scholar]
- Vauclin, M.; Khanji, D.; Vachaud, G. Experimental and numerical study of a transient, two-dimensional unsaturated-saturated water table recharge problem. Water Resour. Res. 1979, 15, 1089–1101. [Google Scholar] [CrossRef]
- Clement, T.; Wise, W.R.; Molz, F.J. A physically based, two-dimensional, finite-difference algorithm for modeling variably saturated flow. J. Hydrol. 1994, 161, 71–90. [Google Scholar] [CrossRef]
- Xing, Z. Three-Dimensional Stability Analysis of Concave Slopes in Plan View. J. Geotech. Eng. 1988, 114, 658–671. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Haberfield, C.; Yin, J.-H.; Wang, Y. A three-dimensional slope stability analysis method using the upper bound theorem: Part I: Theory and methods. Int. J. Rock Mech. Min. Sci. 2001, 38, 369–378. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, H.; Zhang, F.; Wang, X. A simplified method for 3D slope stability analysis. Can. Geotech. J. 2003, 40, 675–683. [Google Scholar] [CrossRef]
- Sultan, N.; Gaudin, M.; Berne, S.; Canals, M.; Urgeles, R.; Lafuerza, S. Analysis of slope failures in submarine canyon heads: An example from the Gulf of Lions. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Ge, X.-R. The vector sum method: A new approach to calculating the safety factor of stability against sliding for slope engineering and dam foundation problems. In Advances in Environmental Geotechnics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 99–110. [Google Scholar]
- Sun, G.; Zheng, H.; Jiang, W. A global procedure for evaluating stability of three-dimensional slopes. Nat. Hazards 2011, 61, 1083–1098. [Google Scholar] [CrossRef]
- Liu, G.; Zhuang, X.; Cui, Z. Three-dimensional slope stability analysis using independent cover based numerical manifold and vector method. Eng. Geol. 2017, 225, 83–95. [Google Scholar] [CrossRef]
- Li, K.S.; White, W. Rapid evaluation of the critical slip surface in slope stability problems. Int. J. Numer. Anal. Methods Geomech. 1987, 11, 449–473. [Google Scholar] [CrossRef]
- Hungr, O.; Salgado, F.; Byrne, P. Evaluation of a three-dimensional method of slope stability analysis. Can. Geotech. J. 1989, 26, 679–686. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D. A general limit equilibrium model for three-dimensional slope stability analysis. Can. Geotech. J. 1993, 30, 905–919. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tsai, C.-C. New Method for 3D and Asymmetrical Slope Stability Analysis. J. Geotech. Geoenviron. Eng. 2000, 126, 917–927. [Google Scholar] [CrossRef]
- Kim, J.; Salgado, R.; Lee, J. Stability Analysis of Complex Soil Slopes using Limit Analysis. J. Geotech. Geoenviron. Eng. 2002, 128, 546–557. [Google Scholar] [CrossRef]
- Zheng, H. Eigenvalue Problem from the Stability Analysis of Slopes. J. Geotech. Geoenviron. Eng. 2009, 135, 647–656. [Google Scholar] [CrossRef]
- Zheng, H. A three-dimensional rigorous method for stability analysis of landslides. Eng. Geol. 2012, 145–146, 30–40. [Google Scholar] [CrossRef]
- Griffiths, D.; Lu, N. Unsaturated slope stability analysis with steady infiltration or evaporation using elasto-plastic finite elements. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 249–267. [Google Scholar] [CrossRef]
| Mechanism | Result | Influence |
|---|---|---|
| Root (underground) portion | ||
| Reinforcement and anchorage by root | Increasing soil shear strength | + |
| Root extracts moisture from the soil | Lower pore water pressure | + |
| Increasing hydraulic conductivity | Increased infiltration capacity | − |
| Canopy (aboveground) portion | ||
| Canopy intercepts and evaporates rainfall | Reduce rainfall for infiltration | + |
| Weight of trees surcharges the slope | Increasing normal stress | +/− |
| Vegetation exposed wind forces into the slope | Increasing driving force | − |
| Reference | k″ | Method | Soil | Vegetation |
|---|---|---|---|---|
| Wu and Watson [52] | 0.33 | In-situ shear test | Silty sand | Pinus radiata |
| Operstein and Frydman [50] | 0.21 | In-situ and laboratory tests | Chalky and clay | Alfalfa, Rosemary, Pistacia lentiscus, Cistus |
| Pollen, et al. [44] | 0.34 | Direct shear-box test | Clayey-silt | Riparian vegetation (12 species) |
| Pollen and Simon [45] | Trees: 0.6–0.82 Grass: 0.48 | In comparison with FBM | Silt | trees: Cottonwood, Sycamore, River birch, Pine, Black willow grass: Switchgrass |
| Docker and Hubble [55] | 0.61–0.64 | In-situ shear test | Alluvial (loam and sandy loam) | Casuarina glauca, Eucalyptus amplifolia, Eucalyptus elata, and Acacia floribunda |
| Fan and Su [56] | Peak: 0.325 Residual: 0.35 | In-situ shear test | Sands mixed with silts | Prickly sesban |
| Bischetti, et al. [53] | 0.27–0.83 | Direct shear test | Various (gravel-sand mixture, clayey, silt, …) | European beech, Norway spruce, European larch, Sweet chestnut, European hop-hornbeam |
| Mickovski, et al. [49] | ~0.75 | Direct shear test (laboratory) | Agricultural soil (71% sand, 19% silt, 10% clay) | Willow |
| Mao, et al. [57] | 0.55–1.0 | In comparison with FBM | Various (silt, silty-clay, coarse elements) | Norway spruce, Silver fir, European beech |
| Adhikari, et al. [58] | 0.35–0.56 | In comparison with FBM | Fine sand texture | A. lentiformis, A. occidentialis, L. andersonii, L. tridentata |
| Meijer, et al. [59] | 0.08, 0.225 | Corkscrew test (field and lab.) | Slightly clayey sand, sandy silt | Blackcurrant (shrub), Sitka spruce (tree) |
| Species | Surcharge (kPa) | Size Indicator | Density (tree/ha) | Reference |
|---|---|---|---|---|
| Sitka spruce | Estimated: 5.2 (Used: 3.8) | Avg. height = 6 m | Dense | Wu et al. [19] |
| Sitka spruce | Average: 2.5 | Bishop and Stevens [74] | ||
| Maritime pine | 0.6 | 350 | Kokutse et al. [75] | |
| Conifer forest | up to 2 | Height = up to 80 m | Fully stocked | Greenway [17] |
| Pinus sylvestris | 3.5 | Van Asch et al. [76] | ||
| Riparian vegetation | 1.2 | Avg. height = 18 m | Simon and Collison [77] | |
| Silver wattle | Average tree: 0.81 Large tree: 5.06 | 5000 | Abernethy and Rutherfurd [78] | |
| Pine | 0.228, 0.135 | Age = 52-month | Waldron and Dakessian [79] | |
| Korean pine | 2.94 | Age = 20-year-old | Fully stocked | Kim et al. [80] |
| European beech | 0.309 | Avg. stem dia. = 14–42 cm | 308–2451 | Chiaradia et al. [81] |
| Sweet chestnut | 0.070 | Avg. stem dia. = 13–31 cm | 2268–3764 | |
| Norway spruce | 0.275 | Avg. stem dia. = 22–46 cm | 416–2066 | |
| Mixed conifer forest | 0.275 | Height ≈ 30 m | Bischetti et al. [82] |
| Reference | SWCC | HCF | Parameters |
|---|---|---|---|
| Haverkamp et al. [90] | α, β: Fitting parameters A, B: Fitting parameters | ||
| Van Genuchten [92] | α, n, m: fitting parameters where: | ||
| Fredlund and Xing [87], Fredlund et al. [88] | where: | where: | e: the natural number a, n, m: fitting parameters ψ: matric suction (varied between 0 to 106 kPa) ψr: matric suction corresponding to residual water content C(ψ): correction factor ψaev: matric suction at air entry value y: dummy variable of integration |
| Parameter | Arithmetic Method | Geometric Method | Harmonic Method |
|---|---|---|---|
| Kavg |
| Parameter | Value |
|---|---|
| Soil-Water Characteristic Curve (SWCC) parameters | |
| θS (cm3/cm3) | 0.30 |
| θr (cm3/cm3) | 0 |
| α | 40,000 |
| β | 2.90 |
| Hydraulic conductivity function parameters | |
| Ks (cm/h) (in both horizontal and vertical directions) | 35 |
| A | 2.99 × 106 |
| B | 5.0 |
| Numerical assumption | |
| ∆x (cm) | 10 |
| ∆z (cm) | 5 |
| ∆t (hr) | 0.1 |
| Time stepping method | Automatic |
| Hydraulic conductivity averaging method | Geometric |
| Estimation method of specific moisture capacity | SCS |
| Reference | Analysis Method | SF |
|---|---|---|
| Fredlund and Krahn [97] | Simplified Bishop Method | 2.080 |
| Janbu’s Simplified Method | 2.041 | |
| Xing [109] | Proposed 3D Method | 2.122 |
| Chen et al. [110] | Upper bound method | 2.262 |
| Chen et al. [111] | Proposed 3D Method (STAB-3D) | 2.188 |
| Plain-Strain 3D Method | 2.073 | |
| Sultan et al. [112] | Upper Bound Theorem (SAMU-3D Program) | 2.213 |
| Ge [113] | Vector Sum Method (VSM) | 2.037 |
| Sun et al. [114] | Proposed 3D Method | 2.000 |
| Liu et al. [115] | 3D independent cover-based manifold method (ICMM3D) and vector sum method (VSM). | 2.061 |
| This Study (SSHV-2D) | Simplified Bishop Method | 2.079 |
| Janbu’s Simplified Method | 2.024 |
| Reference | Analysis Method (Program Name) | D (m) | Condition of Weak Layer | SF |
|---|---|---|---|---|
| Fredlund and Krahn [97] | Simplified Bishop Method | 6.1 | Oblique * | 1.377 |
| Janbu’s Simplified Method | 6.1 | Oblique * | 1.448 | |
| Li and White [116] | New Proposed Method | 4 | Horizontal | 1.387 |
| Xing [109] | Proposed 3D Method | 6.1 | Oblique * | 1.548 |
| Hungr et al. [117] | 3D extension of the Bishop’s Simplified method (CLARA) | N/A | N/A | 1.62 |
| Lam and Fredlund [118] | Janbu’s Simplified Method | 5 | Horizontal | 1.558 |
| Huang and Tsai [119] | Modified Bishop Simplified Method | ~4.6 | Horizontal | 1.658 |
| Kim et al. [120] | Lower-Bound Method | 4.6 | Horizontal | 1.25 |
| Upper-Bound Method | 1.37 | |||
| Chen et al. [111] | Proposed 3D Method (STAB-3D) | ~4.6 | Horizontal | 1.64 |
| Plain-Strain 3D Method | 1.384 | |||
| Ge [113] | Vector Sum Method (VSM) | 4.55 | Horizontal | 1.585 |
| Zheng [121] | Proposed 3D Method | 4.55 | Horizontal | 1.707 |
| Sun et al. [114] | Proposed 3D Limit Equilibrium Method | 4.55 | Horizontal | 1.68 |
| Zheng [122] | Spencer’s Method (RMP3D) | 4.55 | Horizontal | 1.735 |
| Corps of Engineers Assumption | 1.766 | |||
| Liu et al. [115] | 3D independent cover-based manifold method (ICMM3D) and vector sum method (VSM). | 4.55 | Horizontal | 1.530 |
| This Study | Janbu’s Simplified Method (SSHV-2D) | 6.1 | Oblique * | 1.391 |
| 5 | Horizontal | 1.446 | ||
| 4.55 | Horizontal | 1.489 |
| Definition | Parameter (Unit) | Value |
|---|---|---|
| Root tensile capacity | T (kN) | 12.5 |
| Root pullout resistance | P (kN/m) | 2.5 |
| Lateral bending strength of the root | Q (kN) | 6.25 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emadi-Tafti, M.; Ataie-Ashtiani, B. A Modeling Platform for Landslide Stability: A Hydrological Approach. Water 2019, 11, 2146. https://doi.org/10.3390/w11102146
Emadi-Tafti M, Ataie-Ashtiani B. A Modeling Platform for Landslide Stability: A Hydrological Approach. Water. 2019; 11(10):2146. https://doi.org/10.3390/w11102146
Chicago/Turabian StyleEmadi-Tafti, Mohsen, and Behzad Ataie-Ashtiani. 2019. "A Modeling Platform for Landslide Stability: A Hydrological Approach" Water 11, no. 10: 2146. https://doi.org/10.3390/w11102146
APA StyleEmadi-Tafti, M., & Ataie-Ashtiani, B. (2019). A Modeling Platform for Landslide Stability: A Hydrological Approach. Water, 11(10), 2146. https://doi.org/10.3390/w11102146