Abstract
Urban flooding as a result of inadequate drainage capacity, failure of flood defenses, etc. is usually featured with highly transient hydrodynamics. Reliable and efficient prediction and forecasting of these urban flash floods is still a great technical challenge. Meanwhile, in urban environments, the flooding hydrodynamics and process may be influenced by flow regulation and flood protection hydraulic infrastructure systems, such as sluice gates, which should be effectively taken into account in an urban flood model. However, direct simulation of hydraulic structures is not a current practice in 2D urban flood modeling. This work aims to develop a robust numerical approach to directly simulate the effects of gate structures in a 2D high-resolution urban flood model. A new modeling component is developed and fully coupled to a finite volume Godunov-type shock-capturing shallow water model, to directly simulate the highly transient flood waves through hydraulic structures. Different coupling approaches, i.e., flux term coupling and source term coupling, are implemented and compared. A numerical experiment conducted for an analytical dam-break test indicates that the flux term coupling approach may lead to more accurate results, with the calculated RMSE against water level 28%–38% less than that produced by the source term coupling approach. The flux term coupling approach is therefore adopted to improve the current urban flood model, and it is further tested by reproducing the laboratory experiments of flood routing in a flume with partially open sluice gates, conducted in the hydraulic laboratory at the Zhejiang Institute of Hydraulics and Estuary, China. The numerical results are compared favorably with experimental measurements, with a maximum RMSE of 0.0851 for all the individual tests. The satisfactory results demonstrate that the flood model implemented with the flux coupling approach is able to accurately simulate the flow through hydraulic structures, with enhanced predictive capability for urban flood modeling.
1. Introduction
Due to climate change and rapid urbanization, extreme floods have been observed to happen more frequently and severely, threatening human lives and causing significant damage to properties [1]. For example, a flash flood caused by an intense rainfall event led to 79 deaths and 1.86 billion USD of economic loss in Beijing, China in July 2012 [2]. A flood disaster in Jakarta, Indonesia caused 44 deaths and substantial economic damage in January 2013 [3]. It is important to develop robust modeling tools to enable computationally efficient simulations to support flood risk assessment and forecasting [4,5]. However, reliable prediction and forecasting of urban flash floods remains a great technical challenge [6].
Canals are one of the key components for certain urban drainage systems. A canal system normally consists of a series of regulation measures, such as sluice gates, dams, and pumping stations, to regulate flows at different locations for different purposes [7,8,9,10,11,12]. In certain cities, severe flood events may occur when there is insufficient time to drain canal systems between a flood peak and high tide [13,14]. The sluice gate may locally change flow patterns and significantly affect the flooding process [15]. Effective operation of sluice gates plays an important role in urban flood risk management [16]. Therefore, it is necessary to develop reliable approaches to represent sluice gates and other hydraulic structures in flood modeling.
For urban flood modeling and prediction, representing flow dynamics and inundation processes in sufficient detail is important for reliable risk assessment and emergency planning [17,18]. Hydrodynamic models based on the numerical solution to the 2D shallow water equations (SWEs) can simulate the dynamic rainfall-runoff and flooding processes over complex urban terrains and have been widely applied in urban flood modeling and risk assessment [19,20,21,22,23,24]. Attempts have been made to represent hydraulic structures in 2D hydrodynamic models for flood modeling. Different coupling approaches for modeling sluice gates, such as flux term coupling [25] and source term coupling [26], have been developed and implemented in SWE models. However, most of the existing approaches and models provide simplified representation of the complex hydraulic boundary conditions resulting from the operation of gate structures [27,28], which may not be adequate to reflect realistic flow dynamics. Furthermore, most of these modeling approaches require excessive model calibration to specify parameter values and are not transferable to different study sites. Few attempts have been made to compare and evaluate different coupling approaches for the simulation of hydraulic structures in flood modeling.
This work implements two coupling approaches to develop new 2D finite volume Godunov-type SWE models for modeling gate structures. Simulation results from the two models are compared to recommend a more accurate approach for wider urban flood modeling.
2. Numerical Model
This section introduces the numerical framework for modeling sluice gates in the context of a 2D finite volume Godunov-type SWE model.
2.1. Finite Volume Godunov-Type SWE Model
Two-dimensional non-linear SWEs, derived by depth-integrating the three-dimensional Reynolds averaged Navier–Stokes equations under the hydrostatic assumption, are widely used to mathematically describe shallow flow hydrodynamics, which may be written in a conservative matrix form as [29]
where t, x, and y are the time and the two horizontal coordinates, respectively; q, f, g, and s represent the vectors containing the flow variables, fluxes in the x- and y-directions, and source terms. Neglecting the Coriolis effect and the surface stresses, which are not significant for flood modeling, the vector terms may be given by [30]
where η represents the water surface elevation above the datum (i.e., water level); u and v are the depth-averaged velocity; and qx and qy are the corresponding unit-width discharges in the x- and y-directions; zb is defined as the bed elevation above the datum; g is the gravity acceleration; r and f represent the rainfall intensity and infiltration rate, respectively; −∂zb/∂x and −∂zb/∂y define the bed slopes in the two Cartesian directions; and cf = gn2/h1/3 is the bed roughness coefficient, with n being the Manning coefficient.
The above SWEs are solved using a finite volume Godunov-type shock-capturing numerical scheme, incorporated with an HLLC (i.e., Harten-Lax-van Leer-Contact) approximated Riemann solver to evaluate the interface fluxes [31,32]. Second-order numerical accuracy in both space and time is achieved using a two-step MUSCL–Hancock method. Detailed implementation of the numerical scheme can be found in Liang and Borthwick [30] and Liang [33]. GPU (Graphics Processing Unit)-based parallelization is implemented via the NVIDIA CUDA framework to improve the computational efficiency [34].
2.2. Gate Model
The flow through the sluice gate can be categorized into free-surface and submerged flow, as shown in Figure 1a,b, respectively. For free-surface flow (Figure 1a), the flow is open to the atmosphere at the downstream side of the gate, and the discharge through the gate can be calculated via an Energy–Momentum (E–M) formula [35]
where e and hu are the gate opening and upstream flow depth, respectively; and ε = hc/e is the contraction coefficient, in which hc is the flow depth at vena contraction.
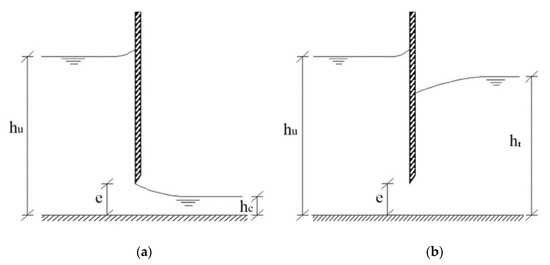
Figure 1.
Flow through a sluice gate: (a) free-surface flow; (b) submerged flow.
For the submerged flow case (Figure 1b), the flow after the sluice gate is covered by a turbulent mass of water and the discharge may be calculated by
where the flow depth H is given by
where ht is the downstream tailwater depth.
2.3. Model Coupling
In order to represent sluice gates in a 2D SWE model, two coupling approaches are considered and implemented in this work, i.e., flux term coupling and source term coupling. In a finite volume SWE model, the Euler scheme may be used to update the flow variables q at cell i
where and are respectively the cell size and the time step, represents the fluxes across the edge k, and is the outward unit vector of edge k.
2.3.1. Flux Term Coupling Approach
In the flux term coupling approach, the gate is idealized as and aligned with a cell interface [35], as shown in Figure 2. Mass and momentum fluxes are considered at both sides of the gate when calculating the fluxes across the cell edge (i.e., gate). In Figure 2, the two bold black lines are used to define an idealized channel and the thinner black line across the channel represents a sluice gate. However, in a grid-based numerical method like the one adopted in this work, the gate is numerically approximated in a stairs-case manner as indicated by the red lines. The flow through the gate at cell i is denoted as , where subscript s marks a cell with its flow depth and momentum affected by the presence of the sluice gate.
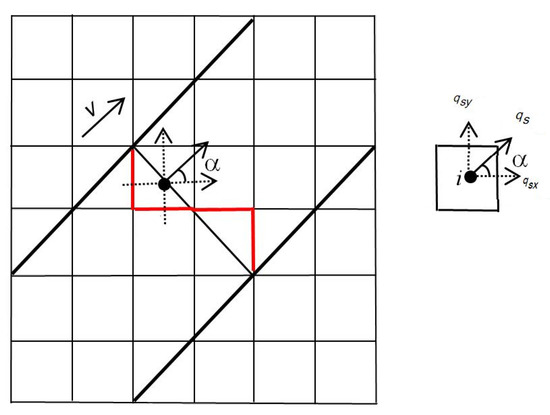
Figure 2.
Calculating fluxes through a sluice gate using the flux term coupling approach.
In the current finite volume Godunov-type scheme, the approximate HLLC Riemann solver is used for calculating the fluxes across cell edges. However, for those cell edges representing a sluice gate, the fluxes need to be calculated differently. For example, for the numerical ‘gate’ as represented by the red lines in Figure 2, cell i is one of the ‘gate’ cells and the ‘gate’ edge is aligned with the y-direction; the fluxes are calculated using the following equations:
- (1)
- Under the free-surface flow condition
- (2)
- Under the submerged flow condition
where the subscript c refers to the flow conditions at the vena contracta; the subscript H indicates the flow variables derived using submerged flow depth H calculated from Equation (5); qsx and qsy are the unit-width discharges in the x- and y-directions calculated from Equations (3) and (4), respectively; uu, uc, and uH are the flow velocities obtained by dividing the discharges defined in Equations (3) and (4) by the corresponding flow depths.
This is the procedure for calculating the fluxes when the gate edge under consideration is aligned with the y-direction. The fluxes across an x-direction gate edge can be calculated similarly by manipulating Equations (7) and (8). When calculating the downstream cell (i.e., the downstream neighbor of cell i), the fluxes across the corresponding edge take the same values but with opposite signs. It should be mentioned that, for the non-orifice flow (i.e., no influence from sluice gate), the gate edge is treated as normal, with fluxes calculated using the HLLC Riemann solver.
2.3.2. Source Term Coupling Approach
When implementing the source term coupling approach, the cell edge representing the sluice gate under consideration is treated as a solid boundary [26]. Momentum exchange between the upstream and the downstream cells of the gate is not taken into account and the mass exchange is quantified using
where nx and ny define the x- and y-direction outward unit vector normal to the edge/boundary under consideration. This is then integrated into the source terms of 2D SWE model as
3. Model Validation
In this section, the SWE models implemented with the two coupling approaches for sluice gates are validated and compared by simulating an analytical and a laboratory test case. The numerical results are respectively compared with analytical solutions and laboratory measurements. In all of the simulations, the time step is controlled by the Courant–Friedrichs–Lewy (CFL) criterion with CFL = 0.5 to ensure numerical stability; g = 9.81 m/s2. The root-mean-squared error (RMSE) defined against water level is calculated to indicate the accuracy of the simulation results, which is defined as
where Si and Oi represent the simulated and analytical/observed data, respectively; and N is the number of observations available for comparison.
3.1. Analytical Tests
Cozzolino et al. [35] presented the analytical solution for a 1D dam-break problem involving a sluice gate. As illustrated in Figure 3, the flume or computational domain was 100 m long, 10 m wide, and 1.2 m deep, with a sluice gate located at x = 50 m, i.e., 50 m away from the upstream boundary. The computational domain was discretized using a 1000 × 100 uniform grid. Four simulations were conducted, with the initial conditions summarized in Table 1 (i.e., upstream water depth hu, downstream water depth hd, and gate opening height e). In all of the simulations, the water was initially at rest, and the gate was rapidly opened to the specified height. The contraction coefficient was set to ε = 0.611.
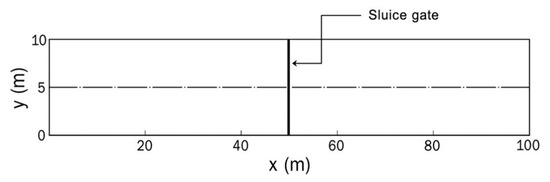
Figure 3.
Plan view of the flume.

Table 1.
Initial conditions of the four numerical tests [33].
After the gate was opened, the water moved from the upstream to the downstream rapidly, and the simulation results are shown in Figure 4. Three types of gate flow conditions were produced, namely, orifice free-surface flow (Figure 4a,b), orifice submerged flow (Figure 4c), and non-orifice flow (Figure 4d). The numerical predictions from the flux term coupling approach (thin solid line) and the source term coupling approach (dashed line) were compared with the analytical solution (hollow circle). It was observed that the results from flux term coupling approach agreed favorably with the analytic solutions in all of the four tests. On the other hand, the numerical predictions from the source term coupling approach failed to accurately capture the flow patterns before and after the gate. This is as expected, because the source term coupling approach only considers mass exchange but neglects the momentum transfer, which will inevitably lead to inaccurate prediction of localized flow dynamics near to the gate.
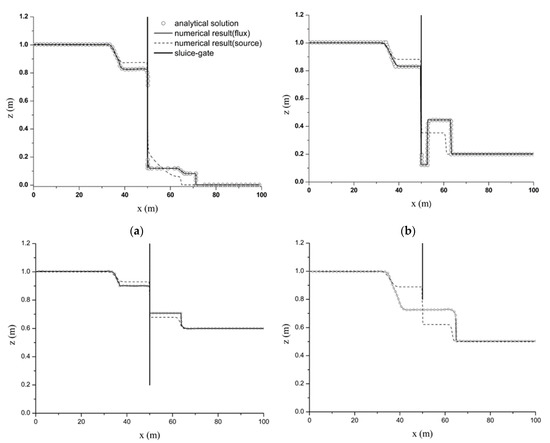
Figure 4.
The numerical and analytical solutions (at t = 5 s) for the four test cases defined in Table 1: (a) Test 1. (b) Test 2. (c) Test 3. (d) Test 4.
To quantitatively compare the simulation results with the analytical solutions, the RMSE defined in Equation (11) was calculated and listed in Table 2. The RMSE resulting from the flux term coupling approach was consistently smaller for all four tests, which was 28%–38% less than that calculated for the source term coupling approach. This confirms that the flux term coupling approach provides better results than the source term coupling approach, with momentum exchange effectively taken into account. As a summary, the source term coupling method does not involve additional flux treatment, and it is straightforward to implement in a numerical scheme. However, the flux coupling approach is demonstrated to better predict the flow states on both sides of the sluice gate, which should be used in wider applications.

Table 2.
RMSE calculated for the four tests.
3.2. Flume Experiments
Bao et al. [36] conducted experiments on partially open sluice gates in the hydraulic laboratory of Zhejiang Institute of Hydraulics and Estuary, China. As shown in Figure 5, the reinforced concrete flume was 20 m long and 10 m wide. Five glass gates were installed in the downstream section of the flume and the net width of sluice hole was 0.2 m. The topography of the flume is shown in Figure 6. Two needle water level gauges with a precision level up to 0.1 mm were placed upstream and downstream of the gate to record the change of water level. The upstream reservoir was filled with initially still water of specified depths through a pump, and a downstream baffle was used to produce the orifice submerged flow. Discharges were measured using an IFS400 electromagnetic flow meter. The gates were rapidly opened to create a gate flow moving from upstream to downstream.
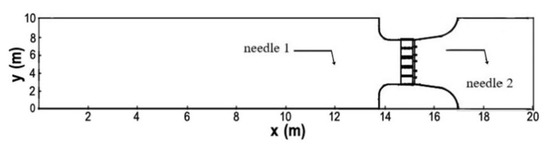
Figure 5.
Plan view of the reinforced concrete flume.
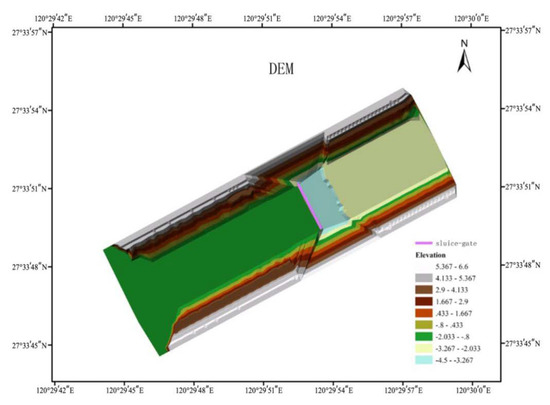
Figure 6.
The topography of the computational domain.
The experiments that produced the orifice free flow and orifice submerged flow were simulated herein using the flux term coupling method. The computational domain was discretized using a uniform grid with square cells of 0.1 m resolution. The Manning coefficient was set to 0.035 for the whole domain to represent the concrete flume surface, and the contraction coefficient was ε = 0.611. The left-hand-side boundary of the computational domain was set to be open with prescribed inflow discharge, which was controlled by pumps during the experiments. The right-hand-side boundary was open to allow free outflow. Close/reflective boundaries were imposed for the two sidewalls. The piers of sluice gates were treated as a rigid boundary and implemented in the corresponding cells.
Figure 7 presents the predicted and measured stage–discharge relationship at the upstream and downstream sides of the sluice gates. For the orifice free flow test, the numerical results reproduce well the stage–discharge relationship as measured in the laboratory. However, when the value of e/hu increases, the discharge simulated by the numerical model is slightly underestimated. This may be because of the existence of the piers of sluice gates, which create localized three-dimensional contraction effects that cannot be captured by the SWE model. Generally, the numerical simulations capture reasonably well the stage–discharge relationships in different flow conditions, which confirms the capability of the current model in predicting the highly transient waves through sluice gates.
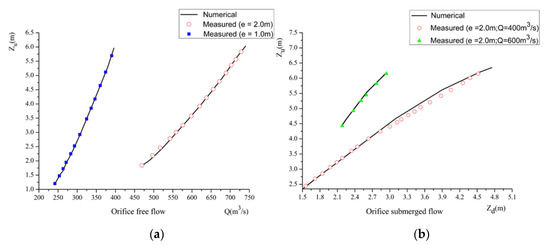
Figure 7.
Comparison between numerical results and experimental measurements at t = 900 s: (a) Orifice free flow; (b) Orifice submerged flow.
In order to quantity the accuracy of simulation results, the RMSE for different tests is calculated and listed in Table 3. The maximum of RMSE is 0.0851, indicating the laboratory tests are all successfully reproduced. The results confirm that the gate modeling approach and resulting flood model can reproduce the laboratory test cases with more complicated settings and are ready for wider applications.

Table 3.
RMSE calculated for the flume experiments.
4. Conclusions
This work develops and compares two different approaches to simulate the effects of sluice gates in a 2D finite volume Godunov-type SWE model for urban flood modeling. The model components are fully coupled to the adopted SWE model, through flux and source terms for predicting highly transient flows through gate structures. The flux term coupling approach considers both the mass and momentum exchanges at both sides of the gate, while the source term coupling approach simply treats gates as a solid boundary and only mass exchange is reinforced when calculating the flow across the sluice gate.
One analytical test case and one more sophisticated experimental case were simulated to validate the coupling approaches and the resulting models. In the analytical test, the simulation results produced by the flux term coupling approach and source term coupling approach were qualitatively and quantitatively compared with the analytical solution. Under four different flow conditions, the results predicted by the flux coupling approach were consistently better than those produced by the source coupling approach. Specifically, the RMSE calculated for the flux coupling approach was 28%–38% less than that calculated for the source term coupling approach. This confirms the more reliable predictive capability of the flux term coupling approach. The flux coupling approach was further verified by reproducing laboratory experiments of flood routing in a flume with partially open sluice gates. Four cases with different experimental settings were simulated and were successfully reproduced, with the maximum of RMSE of the simulation results calculated to be 0.0851. The numerical experiments demonstrate that the SWE-based flood model implemented with the flux term coupling approach can provide a potential tool for predicting urban flash flood dynamics that are locally influenced by sluice gates.
Author Contributions
Conceptualization and supervision, G.W. and Q.L.; methodology, software and validation, Y.C., Q.L. and G.W.; formal analysis, Y.C.; investigation, J.H.; resources, J.H., Y.W.; data curation, Y.W.; writing—original draft preparation, Y.C.; writing—review and editing, Q.L., J.Z. and X.X.; project administration and funding acquisition, Q.L., G.W. and J.H. All authors approved the manuscript.
Funding
This work is partly funded by the National Science and Technology Major Project (2017ZX07603) and UK Natural Environment Research Council (NERC) through the ValBGI project (NE/S00288X/1) and supported by the project of Research and Application of Key Technologies for Urban Flood Simulation in Estuary and Coastal Areas (2017F30013, 2018F10018).
Acknowledgments
The authors thank Jian Zeng and colleagues from the Zhejiang Institute of Hydraulics and Estuary for providing experiment data to validate the new modeling component, Peng Wan from Hohai University for useful discussion on numerical modeling.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Dubash, N.K. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Yin, J.; Yu, D.; Wilby, R. Modelling the impact of land subsidence on urban pluvial flooding: A case study of downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Takagi, H.; Esteban, M.; Mikami, T.; Fujii, D. Projection of coastal floods in 2050 Jakarta. Urban Clim. 2016, 17, 135–145. [Google Scholar] [CrossRef]
- Ward, P.J.; Jongman, B.; Weiland, F.S.; Bouwman, A.; Van Beek, R.; Bierkens, M.F.P.; Ligtvoet, W.; Winsemius, H.C. Assessing flood risk at the global scale: Model setup, results, and sensitivity. Environ. Res. Lett. 2013, 8, 044019. [Google Scholar] [CrossRef]
- Yang, T.H.; Yang, S.C.; Ho, J.Y.; Lin, G.F.; Hwang, G.D.; Lee, C.S. Flash flood warnings using the ensemble precipitation forecasting technique: A case study on forecasting floods in taiwan caused by typhoons. J. Hydrol. 2015, 520, 367–378. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Chan, F.K.S.; Mitchell, G.; Adekola, O.; McDonald, A. Flood risk in Asia’s urban mega-deltas drivers, impacts and response. Environ. Urban. Asia 2012, 3, 41–61. [Google Scholar] [CrossRef]
- Okoye, C.B.; Ojeh, V.N. Mapping of flood prone areas in Surulere, Lagos, Nigeria: A GIS approach. J. Geogr. Inf. Syst. 2015, 7, 158–176. [Google Scholar] [CrossRef]
- Breckpot, M.; Agudelo, O.M.; Meert, P.; Willems, P.; De Moor, B. Flood control of the Demer by using Model Predictive Control. Control Eng. Pract. 2013, 21, 1776–1787. [Google Scholar] [CrossRef]
- Sims, J. The No-Nonsense Guide to Flood Safety; Lulu Books & Beyond the Spectrum Books; Lulu Press: Morrisvill, NC, USA, 2013. [Google Scholar]
- Tingsanchali, T. Urban flood disaster management. Procedia Eng. 2012, 32, 25–37. [Google Scholar] [CrossRef]
- Ogie, R.; Holderness, T.; Dunbar, M.; Turpin, E. Spatio-topological network analysis of hydrological infrastructure as a decision support tool for flood mitigation in coastal mega-cities. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 718–739. [Google Scholar] [CrossRef]
- Ogie, R.; Holderness, T.; Dunn, S.; Turpin, E. Assessing the vulnerability of hydrological infrastructure to flood damage in coastal cities of developing nations. Comput. Environ. Urban Syst. 2018, 68, 97–109. [Google Scholar] [CrossRef]
- Dewan, A. Floods in a Megacity: Geospatial Techniques in Assessing Hazards, Risk and Vulnerability; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Ding, Y.; Wang, S.S. Optimal control of flood diversion in watershed using nonlinear optimization. Adv. Water Resour. 2012, 44, 30–48. [Google Scholar] [CrossRef]
- Munoz, D.H.; Constantinescu, G. A Fully 3-D Numerical Model to Predict Flood Wave Propagation and Assess Efficiency of Flood Protection Measures. Adv. Water Resour. 2018, 122, 148–165. [Google Scholar] [CrossRef]
- Yin, J.; Ye, M.; Yin, Z.; Xu, S. A review of advances in urban flood risk analysis over China. Stoch. Environ. Res. Risk Assess. 2015, 29, 1063–1070. [Google Scholar] [CrossRef]
- Sanders, B.F. Hydrodynamic modeling of urban flood flows and disaster risk reduction. In Oxford Research Encyclopedia of Natural Hazard Science; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Morgan, A.; Olivier, D.; Nathalie, B.; Claire-Marie, D.; Philippe, G. High-resolution Modeling With Bi-dimensional Shallow Water Equations Based Codes—High-Resolution Topographic Data Use for Flood Hazard Assessment Over Urban and Industrial Environments. Procedia Eng. 2016, 154, 853–860. [Google Scholar] [CrossRef]
- Vacondio, R.; Aureli, F.; Ferrari, A.; Mignosa, P.; Dal Palù, A. Simulation of the January 2014 flood on the Secchia River using a fast and high-resolution 2D parallel shallow-water numerical scheme. Nat. Hazards 2016, 80, 103–125. [Google Scholar] [CrossRef]
- Liang, Q.; Smith, L.S. A high-performance integrated hydrodynamic modelling system for urban flood simulations. J. Hydroinform. 2015, 17, 518–533. [Google Scholar] [CrossRef]
- Song, L.; Zhou, J.; Guo, J.; Zou, Q.; Liu, Y. A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 2011, 34, 915–932. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Xing, Y.; Liang, Q.; Wang, G.; Ming, X.; Xia, X. City-scale hydrodynamic modeling of urban flash floods: The issues of scale and resolution. Nat. Hazards 2019, 96, 473–496. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Murillo, J.; García-Navarro, P. The formulation of internal boundary conditions in unsteady 2-D shallow water flows: Application to flood regulation. Water Resour. Res. 2013, 49, 471–487. [Google Scholar] [CrossRef]
- Angeloudis, A.; Falconer, R.; Bray, S. Representation and operation of tidal energy impoundments in a coastal hydrodynamic model. Renew. Energy 2016, 99, 1103–1115. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. A real-time operation optimization model for flood management in river-reservoir systems. Nat. Hazards 2010, 53, 459–482. [Google Scholar] [CrossRef]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: Chichester, UK, 2001. [Google Scholar]
- Liang, Q.; Borthwick, A.G. Adaptive quadtree simulation of shallow flows with wet–dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Toro, E.F.; Garcia-Navarro, P. Godunov-type methods for free-surface shallow flows: A review. J. Hydraul. Res. 2007, 45, 736–751. [Google Scholar] [CrossRef]
- Martins, R.; Kesserwani, G.; Rubinato, M.; Lee, S.; Leandro, J.; Djordjević, S.; Shucksmith, J.D. Validation of 2d shock capturing flood models around a surcharging manhole. Urban Water J. 2017, 14, 1–8. [Google Scholar] [CrossRef]
- Liang, Q. Flood simulation using a well-balanced shallow flow model. Hydraul. Eng. 2010, 136, 669–675. [Google Scholar] [CrossRef]
- Amouzgar, R.; Liang, Q.; Clarke, P.; Yasuda, T.; Mase, H. Computationally Efficient Tsunami Modeling on Graphics Processing Units (GPUs). Int. J. Offshore Polar Eng. 2016, 26, 154–160. [Google Scholar] [CrossRef][Green Version]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Pianese, D.; Della Morte, R. The analytic solution of the Shallow-Water Equations with partially open sluice-gates: The dam-break problem. Adv. Water Resour. 2015, 80, 90–102. [Google Scholar] [CrossRef]
- Bao, Q.; Wang, Y.; Tu, X. Experimental Study on Hydraulic Model of Zhujiazhan Sluice; Water Conservancy Science and Technology in Zhejiang Province: Hangzhou, China, 2013; Volume 41. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).