Analysis of Long-Term Water Level Variations in Qinghai Lake in China
Abstract
1. Introduction
2. Materials and Methods
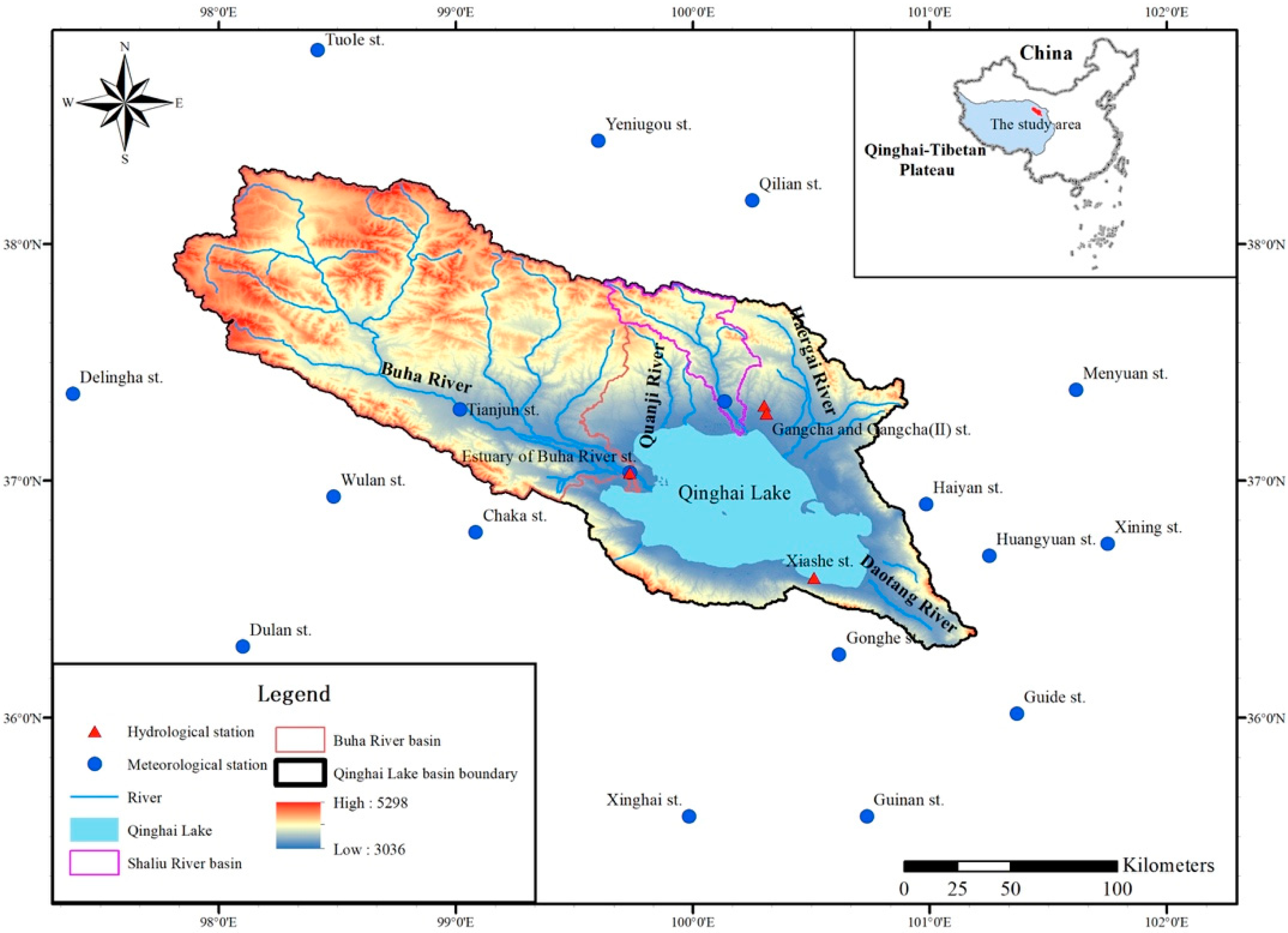
2.1. Study Area and Data Availability
- Daily water levels in Qinghai Lake at Xiashe station (36°35′ N, 100°29′ E) from 1959 to 2016, obtained by the Information Center of Qinghai Hydrographic Bureau, China (ICQHB).
- Daily surface runoff of Buha River and Shaliu River, observed at the estuary of Buha River station (37°18′ N, 99°44′ E, from 1960 to 2016), at Gangcha station (37°17′ N, 100°19′ E, from 1960 to 1975) and at Gangcha II station (36°19′ N, 100°18′ E, from 1976 to 2016, obtained as well by ICQHB.
- Meteorological data:
- Daily meteorological data of 14 national meteorological stations from 1960 to 2016, obtained by the China Meteorological Information Center.
- Monthly meteorological data from 1960 to 2010 at three meteorological stations, obtained by Qinghai Meteorological Bureau in China.
- Daily precipitation data of Buha River rain station from 1962 to 2016 obtained by ICQHB.
- Daily evaporation data from 1984 to 2016 at Xiashe station obtained from ICQHB.
- Environmental and physical details of Qinghai Lake, and these datasets were obtained from ICQHB and the literature [30].
- Land use data from 1980 to 2015, obtained by the Data Center of Resources and Environmental Sciences, Chinese Academy of Sciences.
2.2. Governing Equations
2.2.1. Lake Water Balance Model
2.2.2. Land Use Dynamic Index
2.2.3. Statistical Analysis
2.2.4. Sensitivity Analysis Based on the Budyko Framework
3. Results and Analysis
3.1. Long-Term Variations in Water Levels and the Hydro-Climatic Factors
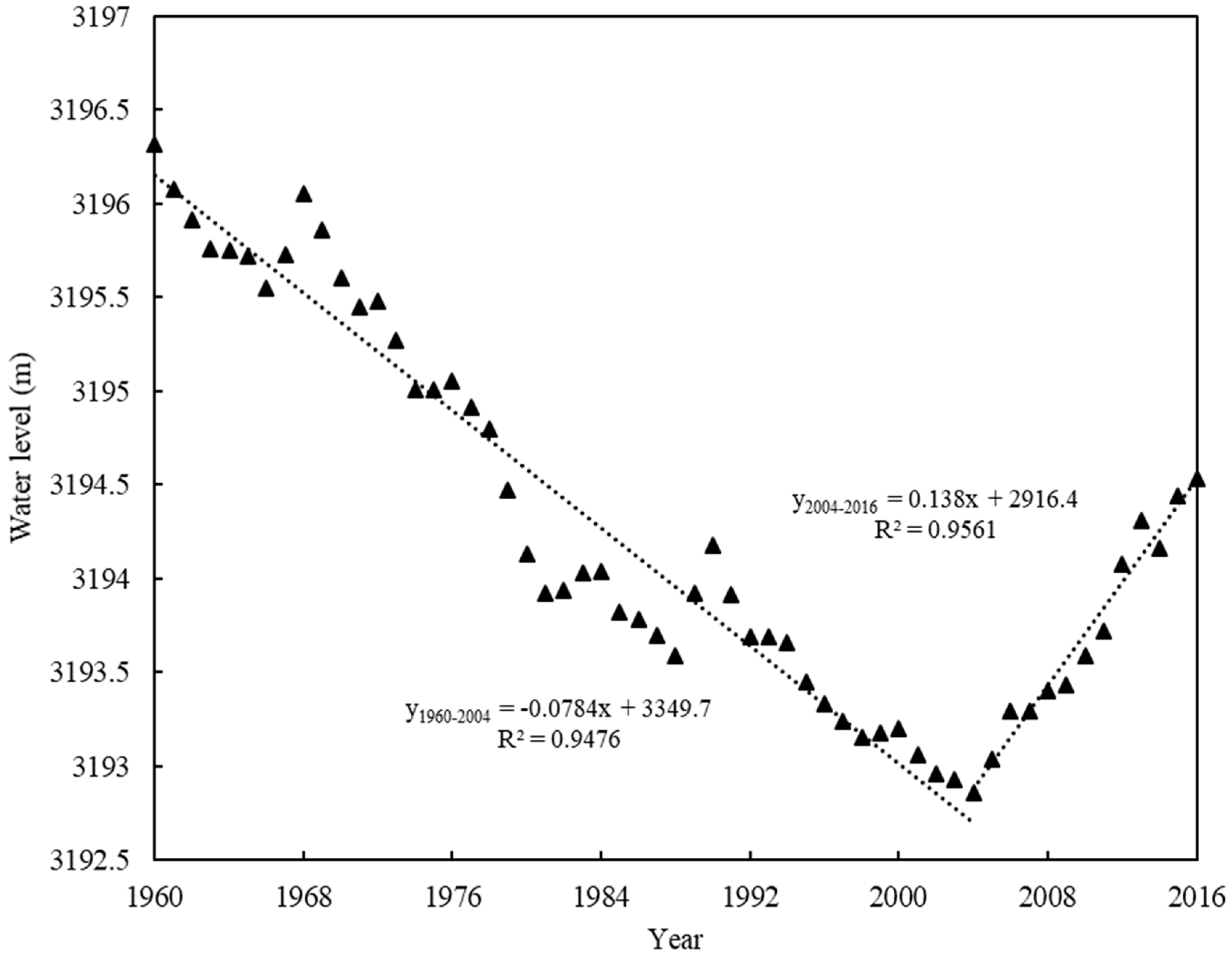
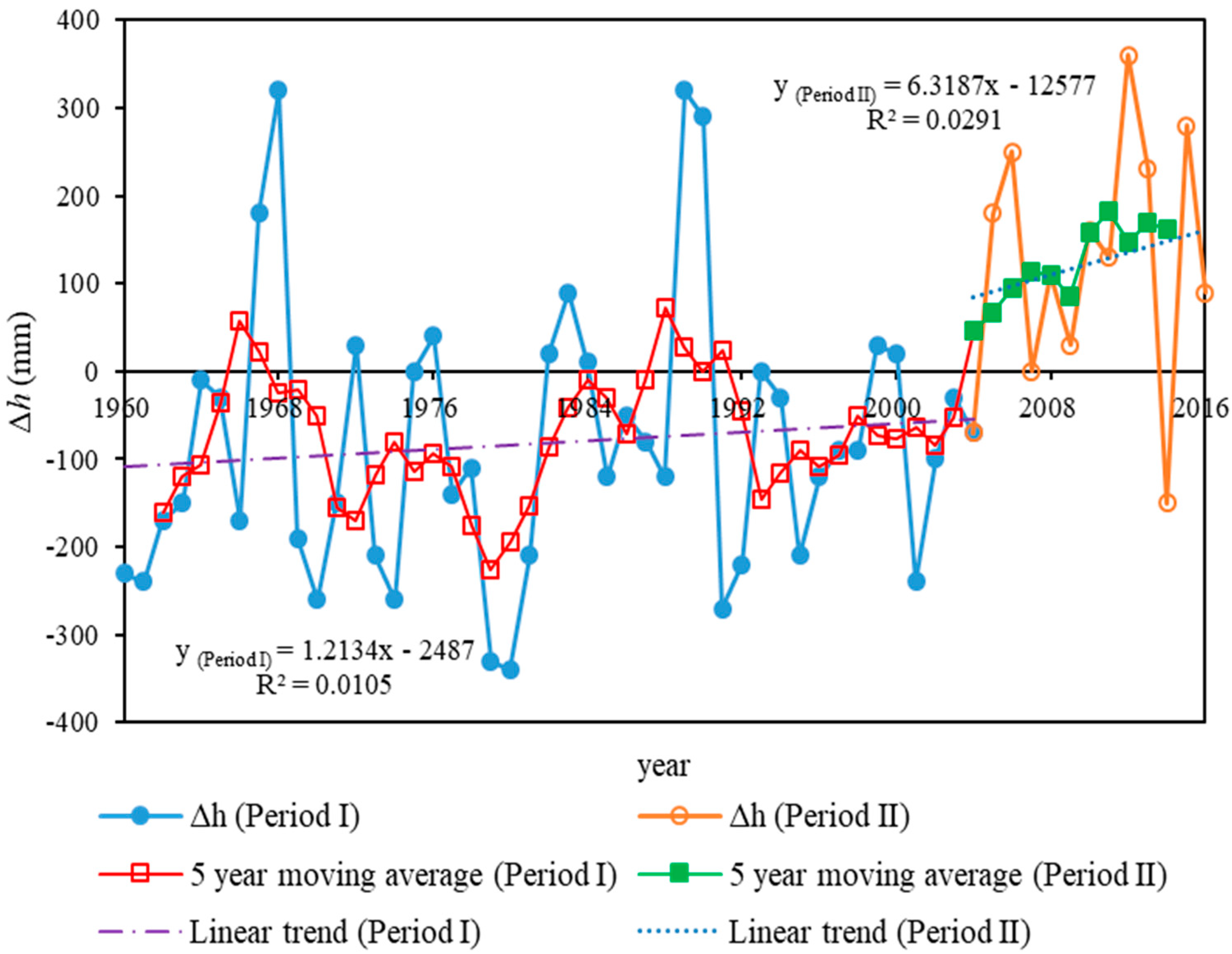
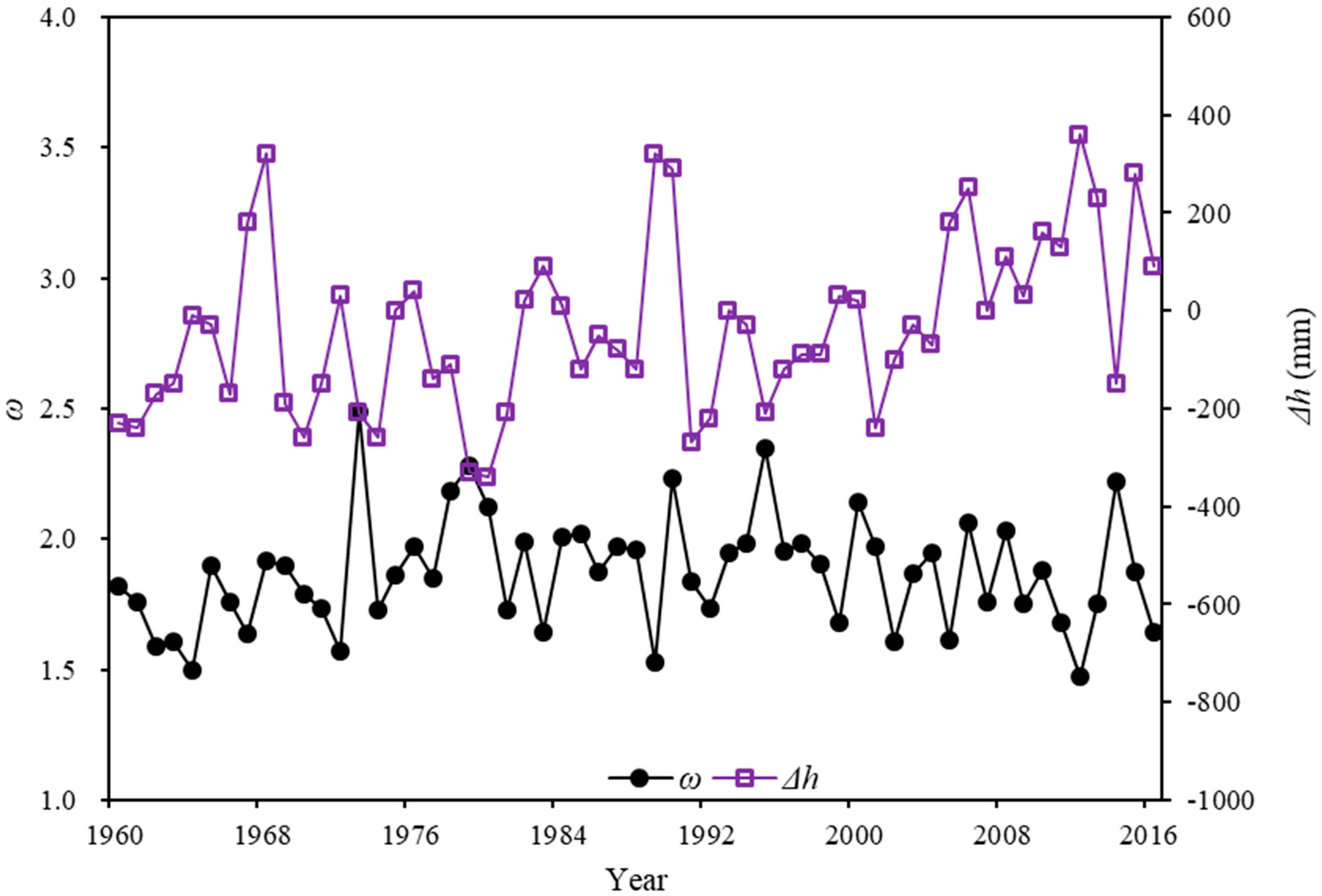
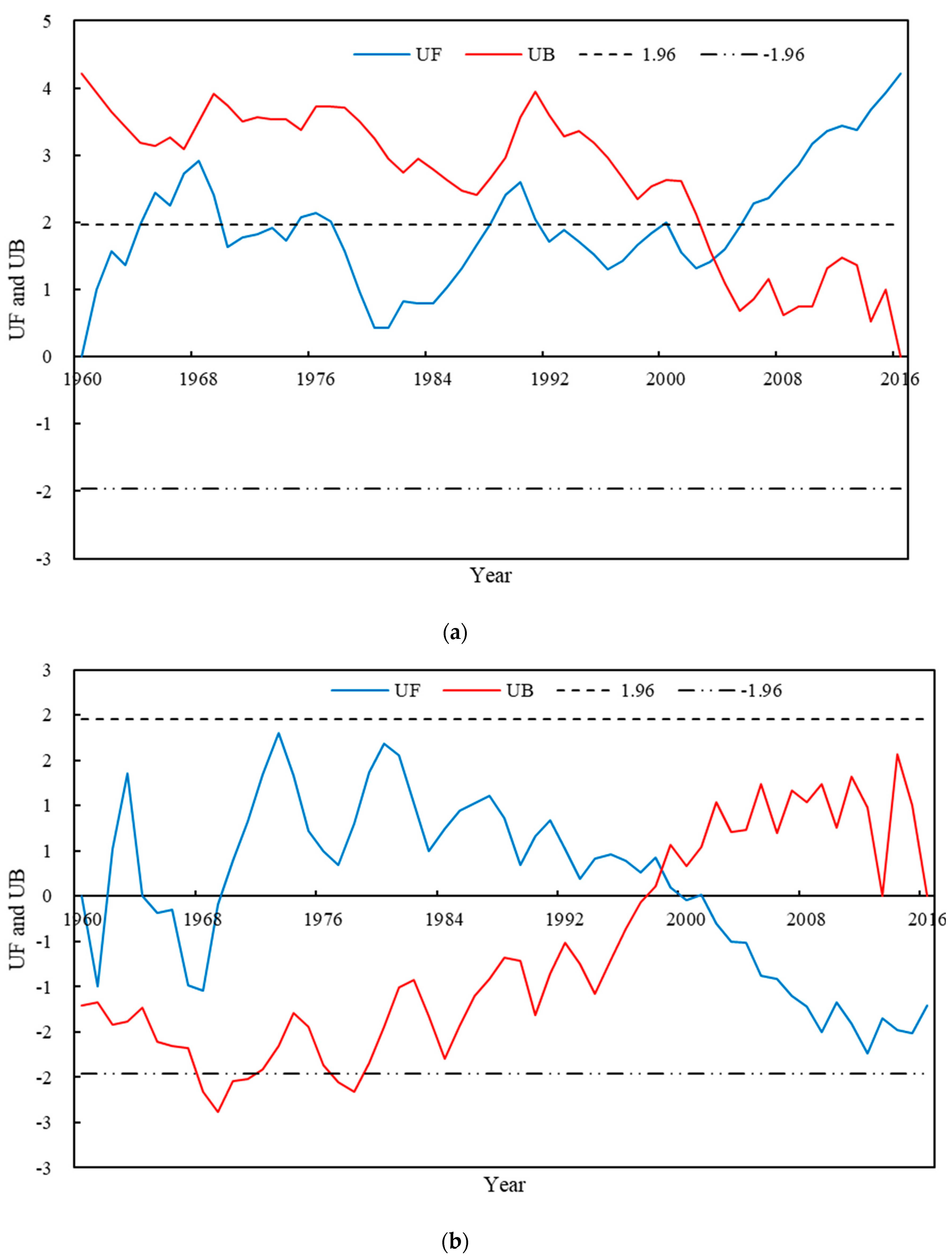
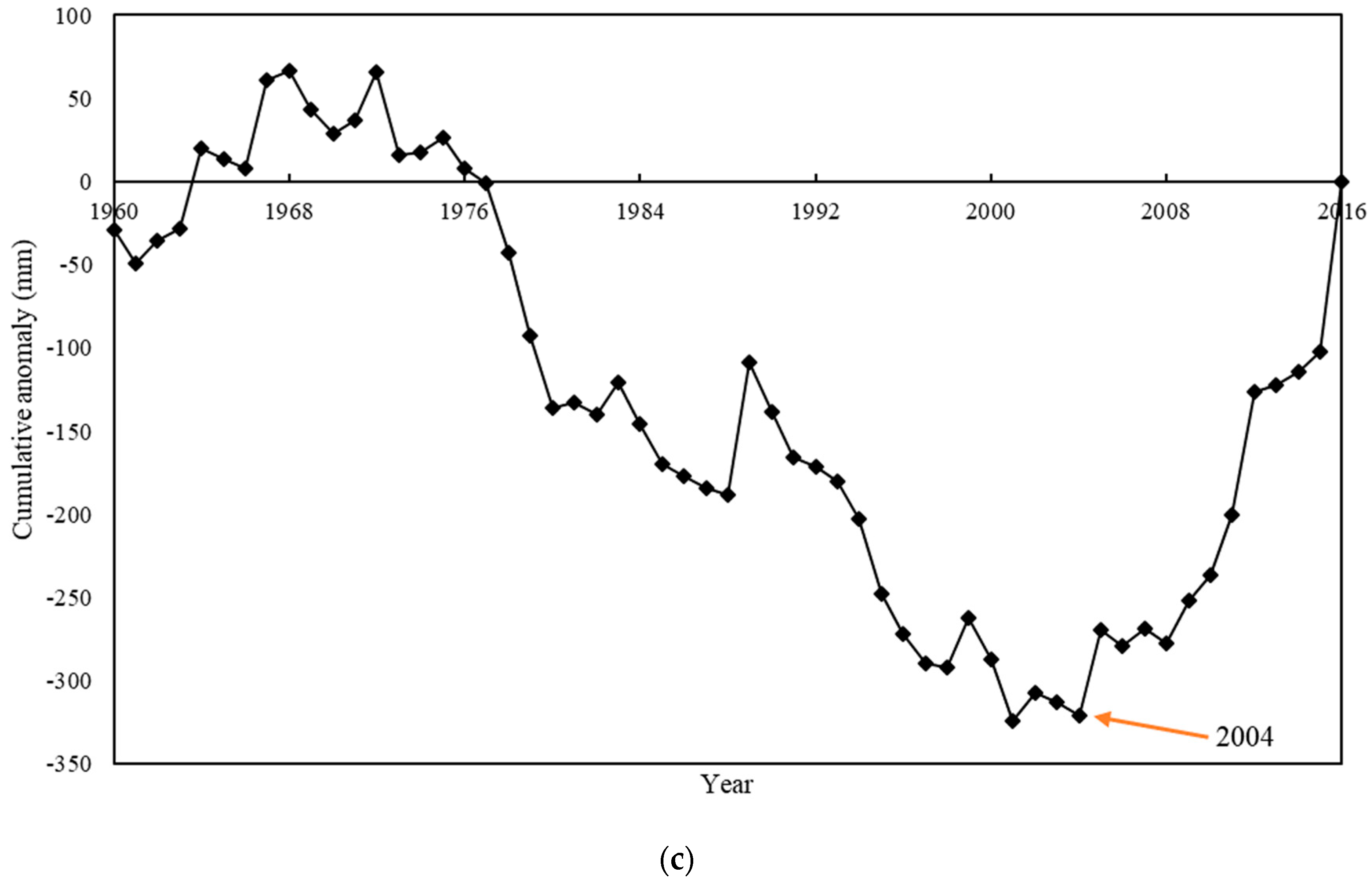
3.1.1. Long-Term Variations in Water Levels
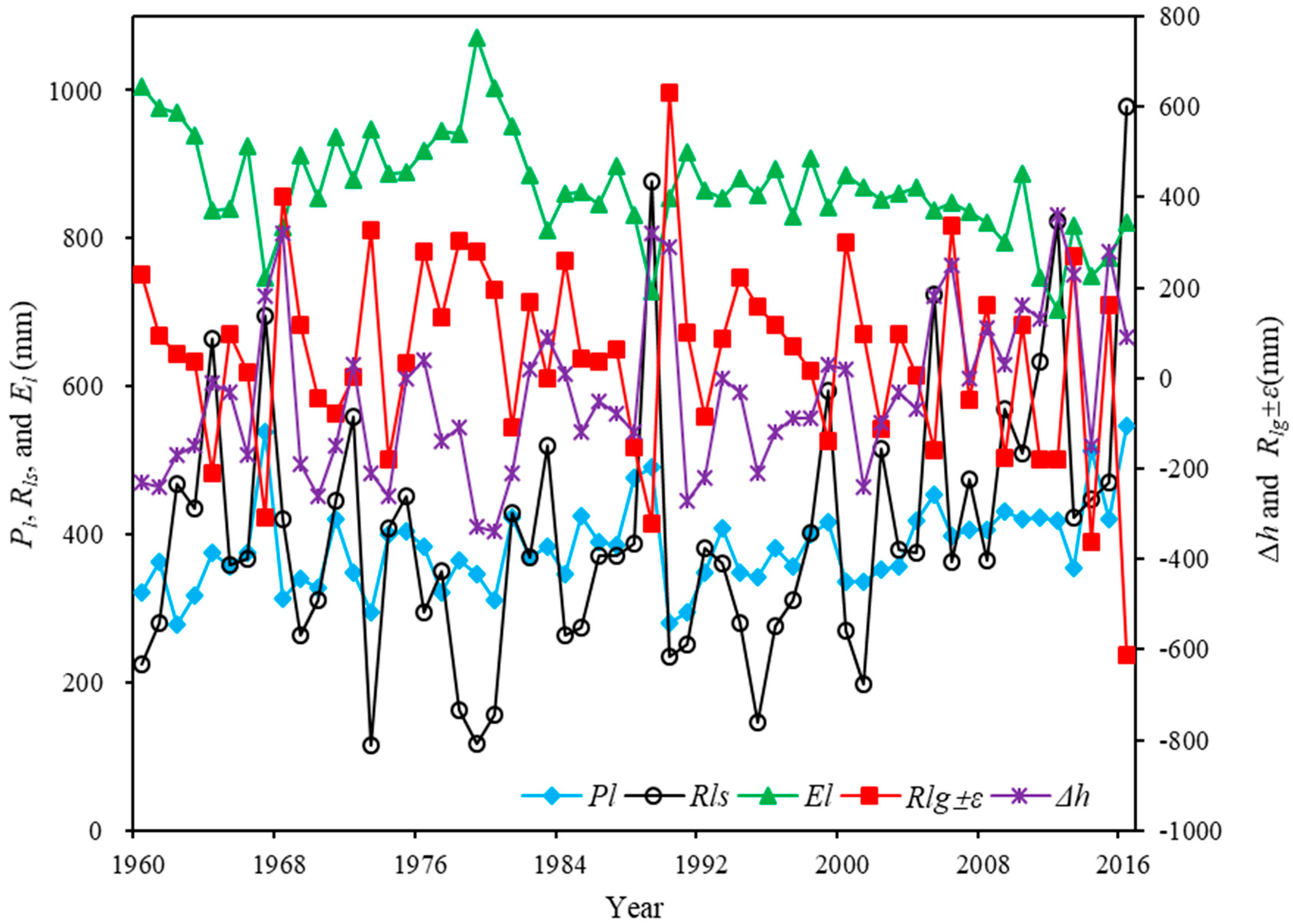
3.1.2. Analysis of Hydro-Climatic Factors Influencing Water Levels
3.2. Causes of Changes in Water Levels of the Lake
3.2.1. Impact of Climate Change on Water Levels
3.2.2. Impact of Human Activities on Catchment Modifications and Consequently on Water Levels
3.2.3. Impact of Climate and Catchment Modifications on the Surface Runoff (Rls)
3.2.4. Impact of Climate and Catchment Modifications on the Underground Runoff (Rlg ± ε)
- water level variation in the lake (x1);
- precipitation on the lake surface area (x2);
- surface runoff of the basin (x3);
- evaporation from the lake surface (x4);
- precipitation across the entire basin area (x5);
- empirical parameter representing land surface characteristics of the basin (x6).
3.2.5. Summary
4. Discussion
4.1. Relationship between the Hydro-Climatic Factors and Lake Water Level Variations
4.2. Relationship between the Catchment Modifications and Water Level Variations
4.3. Uncertainty
5. Conclusions
- (1)
- Qinghai lake experienced severe water level fluctuations in the past 57 years. In period I (1960–2004), the annual water level of the lake declined by 3.46 m at the rate of 7.84 cm/year (P < 0.001), while it rose by 1.49 m at the rate of 13.80 cm/year (P < 0.001) in period II (2005 to 2016). The variation in water level Δh mainly tended to increase during the study period, and the water quantity of the lake increased, passing temporarily from a deficit rate to a surplus one.
- (2)
- The correlation relationships between El, Pl, Rls, Rlg ± ε, ω and Δh followed this order: El (−0.705) > Rls (0.590) > Pl (0.356) > ω (−0.262) > Rlg ± ε (0.143). Overall, the major cause of water level change in Qinghai Lake was the combined effect of evaporation (causing a reduction in water quantities), and precipitation (causing a surface runoff increase).
- (3)
- The contribution rate of multiple factors to the water balance of Qinghai Lake Basin to Δh was quantified and it can be classified as follows: El (−49.34%) > Pl (29.82%) > Rls (16.76%) > Rlg ± ε (4.08%). Among all the factors investigated, El and Pl belong to climate change factors; hence, by combining the contribution rates of climate change and catchment change induced by human activities to Rls, the results obtained were 80.19%, 19.81%, respectively, and those related to Rlg ± ε were 8.44%, −11.56%, respectively. Therefore, the contribution rate for both groups of parameters to Δh was in total 93.13%, 6.87%, respectively. The results showed that climate change was the leading cause of significant changes in water levels in the lake.
- (4)
- The impact of global climate change on the hydrology and environment of the Tibetan Plateau was clear, strongly confirming the high sensitivity of great lakes on the Tibetan Plateau to climate change, and solutions need to be adopted to enable strategies to deal and cope with future climate change scenarios.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; pp. 39–55. [Google Scholar]
- IPCC. Special Report on Global Warming of 1.5 °C (SR15); Cambridge University Press: Cambridge, UK, 2018; pp. 53–68. [Google Scholar]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Jolly, I.; Sophocleous, M.; Zhang, L. Global impacts of conversion from natural to agricultural ecosystem on water resources: Quantity versus quality. Water Resour. Res. 2007, 43, W03437. [Google Scholar] [CrossRef]
- IJmker, J.; Stauch, G.; Pötsch, S.; Diekmann, B.; Wünnemann, B.; Lehmkuhl, F. Dry periods on the NE Tibetan Plateau during the late Quaternary. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2012, 346–347, 108–119. [Google Scholar] [CrossRef]
- Clites, A.H.; Smith, J.P.; Hunter, T.S.; Gronewold, A.D. Visualizing relationships between hydrology, climate, and water level fluctuations on Earth’s largest system of lakes. J. Gt. Lakes Res. 2014, 40, 807–811. [Google Scholar] [CrossRef]
- Assani, A.A.; Landry, R.; Azouaoui, O.; Massicotte, P.; Gratton, D. Comparison of the Characteristics (Frequency and Timing) of Drought and Wetness Indices of Annual Mean Water Levels in the Five North American Great Lakes. Water Resour Manag. 2016, 30, 359–373. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Fortin, V.; Lofgren, B.; Clites, A.; Stow, C.A.; Quinn, F. Coasts, water levels, and climate change: A Great Lakes perspective. Clim. Chang. 2013, 120, 697–711. [Google Scholar] [CrossRef]
- Zhu, W.B.; Jia, S.F.; Lall, U.; Cao, Q.; Mahmood, R. Relative contribution of climate variability and human activities on the water loss of the Chari/Logone River discharge into Lake Chad: A conceptual and statistical approach. J. Hydrol. 2019, 569, 519–531. [Google Scholar] [CrossRef]
- Paillisson, J.; Marion, L. Water level fluctuations for managing excessive plant biomass in shallow lakes. Ecol. Eng. 2011, 37, 241–247. [Google Scholar] [CrossRef]
- Rohling, E.J. Quantitative assessment of glacial fluctuations in the level of Lake Lisan, Dead Sea rift. Quat. Sci. Rev. 2013, 70, 63–72. [Google Scholar] [CrossRef]
- Ye, X.C.; Li, Y.L.; Li, X.H.; Zhang, Q. Factors influencing water level changes in China’s largest freshwater lake, Poyang Lake, in the past 50 years. Water Int. 2014, 39, 983–999. [Google Scholar] [CrossRef]
- Dai, X.; Wan, R.R.; Yang, G.S. Non-stationary water-level fluctuation in China’s Poyang Lake and its interactions with Yangtze River. J. Geogr. Sci. 2015, 25, 274–288. [Google Scholar] [CrossRef]
- Dai, X.; Wan, R.R.; Yang, G.S.; Wang, X.L.; Xu, L.G. Responses of wetland vegetation in Poyang Lake, China to water-level fluctuations. Hydrobiologia 2016, 773, 35–47. [Google Scholar] [CrossRef]
- You, Q.L.; Kang, S.C.; Aguilar, E.; Yan, Y.P. Changes in daily climate extremes in the eastern and central Tibetan Plateau during 1961–2005. J. Geophys. Res. 2008, 113, D07101. [Google Scholar] [CrossRef]
- Chen, S.Y.; Liang, T.G.; Xie, H.J.; Feng, Q.S.; Huang, X.D.; Yu, H. Interrelation among climate factors, snow cover, grassland vegetation, and lake in the Nam co basin of the Tibetan plateau. J. Appl. Remote. Sens. 2014, 8, 084694. [Google Scholar] [CrossRef]
- Ke, L.H.; Song, C.Q. Remotely sensed surface temperature variation of an inland saline lake over the central Qinghai–Tibet Plateau. ISPRS J. Photogramm. Remote Sens. 2014, 98, 157–167. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yao, T.; Xie, H.J.; Zhang, K.; Zhu, F.J. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 24, 3010–3021. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Chang, J.; Xu, C.Y.; Zhou, Y.; Wu, Y.H.; Chen, X.; Jiang, S.S.; Duan, Z. The response of lake area and vegetation cover variations to climate change over the Qinghai-Tibetan Plateau during the past 30 years. Sci. Total Environ. 2018, 635, 443–451. [Google Scholar] [CrossRef]
- Cui, B.L.; Li, X.Y. The impact of climate changes on water level of Qinghai Lake in China over the past 50 years. Hydrol. Res. 2016, 47, 532–542. [Google Scholar] [CrossRef]
- Lu, F.; Li, X. Climate change and tectonic activity during the early Pliocene Warm Period from the ostracod record at Lake Qinghai, northestern Tibetan Plateau. J. Asian Earth Sci. 2017, 138, 446–476. [Google Scholar] [CrossRef]
- Tang, L.; Duan, X.; Kong, F.; Zhang, F.; Zheng, Y.; Li, Z.; Mei, Y.; Zhao, Y.; Hu, S. Influences of climate change on area variation of Qinghai Lake on Qinghai-Tibetan Plateau since 1980s. Sci. Rep. 2018, 8, 7331. [Google Scholar] [CrossRef]
- Karthe, D.; Malsy, M.; Kopp, B.J.; Minderlein, S.; Hülsmann, L. Assessing water availability and drivers in the context of an integrated water resources management (IWRM): A case study from the Kharaa river basin. Mong. Open-File Rep. 2013, 34, 5–26. [Google Scholar]
- Hampton, S.E.; Izmest’Eva, L.R.; Moore, M.V.; Katz, S.L.; Dennis, B.; Silow, E.A. Sixty years of environmental change in the world’s largest freshwater lake-Lake Baikal, Siberia. Glob. Chang. Biol. 2008, 14, 1947–1958. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Robertson, D.M.; Benson, B.J.; Wynne, R.H.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.G.; Card, V.V.; Kuusisto, E.; et al. Historical trends in lake and river ice cover in the Northern Hemisphere. Science 2000, 289, 1743–1746. [Google Scholar] [CrossRef]
- Crapper, P.F.; Fleming, P.M.; Kalma, J.D. Prediction of lake levels using water balance models. Environ. Softw. 1996, 11, 251–258. [Google Scholar] [CrossRef]
- Soja, G.; Züger, J.; Knoflacher, M.; Kinner, P.; Soja, A. Climate impacts on water balance of a shallow steppe lake in Eastern Austria (Lake Neusiedl). J. Hydrol. 2013, 480, 115–124. [Google Scholar] [CrossRef]
- Li, X.Y.; Xu, H.Y.; Sun, Y.L.; Zhang, D.S. Lake-level change and water balance analysis at lake Qinghai, west China during recent decades. Water Resour. Manag. 2007, 21, 1505–1516. [Google Scholar] [CrossRef]
- Qu, Y.G. Water balance and forecasting of water level change in Qinghai Lake. J. Lake Sci. 1994, 6, 298–307. [Google Scholar]
- Ma, F.Y. Reason Analyses and Strategies for the Water Label Drop-Off of the Qinghai Lake; Xi’an University of Technology: Xi’an, China, 2002; pp. 22–27. [Google Scholar]
- Ding, Y.J.; Liu, F.J. Estimating water balance elements in the drainage basin of Qinghai Lake. Arid Land Geogr. J. 1993, 16, 25–30. [Google Scholar]
- Chen, S.P.; Tong, Q.X.; Guo, H.D. Research on the Mechanism of Remote Sensing Information; Science Press: Beijing, China, 1998; pp. 84–113. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 3rd ed.; Hafner Publishing Company: New York, NY, USA, 1962; pp. 92–126. [Google Scholar]
- Mitchell, J.M.; Dzerdzeevskii, B.; Flohn, H.; Hofmeyr, W.L.; Lamb, H.H.; Rao, K.N.; Wallen, C.C. Climatic Change, WMO Technical Note 79; World Meteorological Organization: Geneva, Switzerland, 1966; pp. 1–79. [Google Scholar]
- Liang, L.Q.; Li, L.J.; Liu, Q. Temporal variation of reference evapotranspiration during 1961–2005 in the Taoer River basin of Northeast China. Agric. For. Meteorol. 2010, 150, 298–306. [Google Scholar] [CrossRef]
- Wei, F.Y. Statistical Techniques of Modern Climatic Diagnosis and Forecasting; China Meteorological Press: Beijing, China, 1999; pp. 63–65. [Google Scholar]
- Shang, X.X.; Jiang, X.H.; Jia, R.N.; Chen, W. Land Use and Climate Change Effects on Surface Runoff Variations in the Upper Heihe River Basin. Water 2019, 11, 344. [Google Scholar] [CrossRef]
- Yang, L.S.; Feng, Q.; Yin, Z.L.; Wen, X.H.; Si, J.H.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 1986; pp. 111–137. [Google Scholar]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Plackett, R.L. The discovery of the method of Least Squares. Biometrika 1972, 59, 239–251. [Google Scholar]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, I.W.J. The collinearity problem in linear regression, the partial least squares (PLS) approach to generalized inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Liu, X.M.; Zhang, D.; Luo, Y.Z.; Liu, C.M. Spatial and temporal changes in aridity index in northwest China: 1960 to 2010. Theor. Appl. Climatol. 2013, 112, 307–316. [Google Scholar] [CrossRef]
- Li, B.; Li, L.J.; Qin, Y.C.; Liang, L.Q.; Li, J.Y.; Liu, Y.M. Impact of climate variability on streamflow in the upper and middle reaches of the Taoer River based on the Budyko hypothesis. Resour. Sci. 2011, 33, 70–76. [Google Scholar]
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974; pp. 317–508. [Google Scholar]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. Sin. 1981, 5, 23–31. [Google Scholar]
- Yang, D.W.; Shao, W.W.; Yeh, P.J.F.; Yang, H.B.; Kanae, S.; Oki, T.K. Impact of vegetation coverage on regional water balance in the nonhumid regions of China. Water Resour. Res. 2009, 45, W00A14. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko’s hydrological model. J. Hydrol. 2012, 436–437, 35–50. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Liu, C.M.; Zhang, D. Temporal and spatial change analysis of the sensitivity of potential evapotranspiration to meteorological influencing factors in China. Acta Geogr. Sin. 2011, 66, 579–588. [Google Scholar]
- Zhu, G.F.; He, Y.Q.; Pu, T.; Wang, X.F.; Jia, W.X.; Li, Z.S.; Xin, H.J. Spatial distribution and temporal trends in potential evaporation over Hengduan Mountains Region from 1960 to 2009. Acta Geogr. Sin. 2011, 66, 905–916. [Google Scholar]
- El-Zehairy, A.A.; Lubczynski, M.W.; Gurwin, J. Interactions of artificial lakes with groundwater applying an integrated MODFLOW solution. Hydrogeol. J. 2018, 26, 109–132. [Google Scholar] [CrossRef]
- Michael, L.R.; Graham, D.F. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar]
- Hao, X.N.; Li, Y.T.; Li, B.Y. Variation Characteristics of Pan Evaporation and Its Influence Factor. J. Anhui Agric. Sci. 2011, 39, 19405–19409. [Google Scholar]
- Liu, B.K. Spatial and Temporal Variation Characteristics of Grassland and Lake in Qinghai Lake Basin under Climate Change; Lanzhou University: Lanzhou, China, 2016; pp. 16–19. [Google Scholar]
- Yin, Y.H.; Wu, S.H.; Dai, E.F. Determining factors in potential evapotranspiration changes over China in the period 1971–2008. Chin. Sci Bull. 2010, 55, 2226–2234. [Google Scholar] [CrossRef]
- Song, X.M.; Zhang, J.Y.; Zhan, C.S.; Liu, C.Z. Review for impacts of climate change and human activities on water cycle. J. Hydraul. Eng. 2013, 44, 779–790. [Google Scholar]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Committee of China’s National Assessment Report on Climate Change. China’s National Assessment Report on Climate Change; Science Press: Beijing, China, 2007; pp. 202–211. [Google Scholar]
- Zhao, Y.; Hu, C.H.; Zhang, X.M.; Wang, Y.S.; Cheng, C.; Yin, X.L.; Xie, M. Analysis on runoff and sediment regimes and its causes of the Yellow River in recent 70 years. Trans. Chin. Soc. Agric. Eng. 2018, 34, 112–119. [Google Scholar]
- Wang, H.; Liu, J.F.; Xie, Z.Y.; Ma, L.J. Trend and attribution analysis of runoff in Qinghai Lake basin. Water Resour. Power 2018, 36, 19–21, 32. [Google Scholar]
- Carolina, G.A.; Jackson, C.R. Potential Impacts of Climate Change on Groundwater Supplies to the Doñana Wetland, Spain. Wetlands 2011, 31, 907–920. [Google Scholar]
- Kirshen, P.H. Potential Impacts of Global Warming on Groundwater in Eastern Massachusetts. J. Water Resour. Plan. Manag. 2002, 6, 216–219. [Google Scholar] [CrossRef]
- Wang, X.L.; Liang, T.G.; Xie, H.J.; Huang, X.D.; Lin, H.L. Climate-driven changes in grassland vegetation, snow cover, and lake water of the Qinghai Lake basin. J. Appl. Remote Sens. 2016, 10, 036017. [Google Scholar] [CrossRef]
- Yuan, Y.M. Analysis of temperature, ground temperature and permafrost variation in Qinghai Lake area in recent 30 years. Qinghai Meteorol. 2016, 2, 20–22. [Google Scholar]
- Törnqvist, R.; Jarsjö, J.; Pietroń, J.; Bring, A.; Rogberg, P.; Asokan, S.M.; Destouni, G. Evolution of the hydro-climate system in the Lake Baikal basin. J. Hydrol. 2014, 519, 1953–1962. [Google Scholar] [CrossRef]
- Wang, F.Y.; Duan, K.Q.; Fu, S.Y.; Gou, F.; Liang, W.; Yan, J.W.; Zhang, W.B. Partitioning climate and human contributions to changes in mean annual streamflow based on the Budyko complementary relationship in the Loess Plateau, China. Sci. Total Environ. 2019, 665, 579–590. [Google Scholar] [CrossRef]
| No. | Station Number | Station Name | Latitude (°N) | Longitude (°E) | ASL (m) | Data Collection Frame |
|---|---|---|---|---|---|---|
| 1 | 52,645 | Yeniugou | 38.43 | 99.60 | 3315 | 1960–2016 |
| 2 | 52,842 | Chaka | 36.78 | 99.08 | 3088 | 1960–2016 |
| 3 | 52,633 | Tuole | 38.82 | 98.42 | 3368 | 1960–2016 |
| 4 | 52,833 | Wulan | 36.93 | 98.48 | 2951 | 1960–2016 |
| 5 | 52,836 | Dulan | 36.30 | 98.10 | 3190 | 1960–2016 |
| 6 | 52,737 | Delingha | 37.37 | 97.38 | 2982 | 1960–2016 |
| 7 | 52,868 | Guide | 36.02 | 101.37 | 2274 | 1960–2016 |
| 8 | 52,657 | Qilian | 38.18 | 100.25 | 2788 | 1960–2016 |
| 9 | 52,754 | Gangcha | 37.33 | 100.13 | 3302 | 1960–2016 |
| 10 | 52,856 | Gonghe | 36.27 | 100.62 | 2836 | 1960–2016 |
| 11 | 52,943 | Xinghai | 35.58 | 99.98 | 3324 | 1960–2016 |
| 12 | 52,765 | Menyuan | 37.38 | 101.62 | 2851 | 1960–2016 |
| 13 | 52,866 | Xining | 36.73 | 101.75 | 2296 | 1960–2016 |
| 14 | 52,955 | Guinan | 35.58 | 100.73 | 3121 | 1960–2016 |
| 15 | 52,745 | Tianjun | 37.30 | 99.02 | 3417 | 1961–2010 |
| 16 | 52,855 | Huangyuan | 36.68 | 101.25 | 2675 | 1961–2010 |
| 17 | 52,853 | Haiyan | 36.90 | 100.98 | 3010 | 1961–2010 |
| 18 | 1,329,500 | The estuary of Buha River | 37.03 | 99.73 | 3191 | 1962–2016 |
| Periods | Pl | Rls | Rlg ± ε | El | Δh |
|---|---|---|---|---|---|
| I (1960–2004) | 367.94 (+45.67%) | 364.02 (+45.18%) | 73.68 (+9.15%) | 887.64 (−100%) | −82.00 |
| II (2005–2016) | 432.77 (+43.38%) | 564.93 (+56.62%) | −55.81 (−6.50%) | 802.73 (−93.50%) | +139.17 |
| 1960–2016 | 381.59 (+45.74%) | 406.32 (+48.70%) | 46.42 (+5.56%) | 869.77 (−100.00%) | −35.44 |
| Period | ||||||
|---|---|---|---|---|---|---|
| Period | 1980–1990 | 1190–1995 | 1995–2000 | 2000–2005 | 2005–2010 | 2010–2015 |
| LC (%) | 0.06 | 0.04 | 0.05 | 0.03 | 0.01 | 0.03 |
| Type | Farmland | Forestland | Grassland | Water Area | Constructive Land | Unused Land | Total |
|---|---|---|---|---|---|---|---|
| Farmland | 493 | / | 1 | 1 | 4 | 1 | 500 |
| Forestland | / | 1371 | 10 | 2 | 1 | 1 | 1385 |
| Grassland | 64 | 5 | 17,475 | 30 | 7 | 16 | 17,596 |
| Water area | / | / | 142 | 4842 | / | 157 | 5141 |
| Constructive land | / | / | / | / | 26 | / | 26 |
| Unused land | / | / | 15 | 27 | / | 4975 | 5017 |
| Total | 557 | 1376 | 17,643 | 4901 | 37 | 5149 | 29,664 |
| Variable | Study Period | ||
|---|---|---|---|
| 1960 to 2016 | I | II | |
| Q (mm) | 69.96 | 62.84 | 96.69 |
| P (mm) | 349.13 | 334.65 | 403.42 |
| ET0 (mm) | 1078.55 | 1081.23 | 1068.49 |
| ω | 1.85 | 1.87 | 1.82 |
| ∂Q/∂P | 0.36 | 0.34 | 0.42 |
| ∂Q/∂ET0 | −0.05 | −0.05 | −0.07 |
| ∂Q/∂ω | −115.75 | −106.43 | −146.57 |
| ΔQ | ΔQc | ΔQu | Error | |
|---|---|---|---|---|
| Contribution Amount (mm) | 33.85 | 25.54 | 6.31 | 2.00 |
| Contribution Rate (%) | 100 | 80.19 | 19.81 | 5.91 |
| Correlation Coefficient | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| x1 | 1 | 0.36 ** | 0.51 ** | −0.71 ** | 0.39 ** | −0.26 * |
| x2 | 0.36 ** | 1 | 0.61 ** | −0.56 ** | 0.97 ** | −0.28 * |
| x3 | 0.51 ** | 0.61 ** | 1 | −0.56 ** | 0.64 ** | −0.59 ** |
| x4 | −0.71 ** | −0.56 ** | −0.56 ** | 1 | −0.55 ** | 0.31 * |
| x5 | 0.39 ** | 0.97 ** | 0.64 ** | −0.55 ** | 1 | −0.35 ** |
| x6 | −0.26 * | −0.28 * | −0.59 ** | 0.31 * | −0.35 ** | 1 |
| Incidence Matrix | γ1 | γ2 | γ3 | γ4 | γ5 | γ6 |
|---|---|---|---|---|---|---|
| y | 0.8205 | 0.7683 | 0.7739 | 0.8295 | 0.7609 | 0.8441 |
| Principal Components | The Eigenvalue | Contribution Rate (%) | Cumulative Contribution Rate (%) |
|---|---|---|---|
| F1 | 3.6055 | 60.0919 | 60.0919 |
| F2 | 0.9272 | 15.4527 | 75.5446 |
| F3 | 0.8867 | 14.7779 | 90.3225 |
| F4 | 0.3052 | 5.0872 | 95.4097 |
| F5 | 0.249 | 4.1507 | 99.5604 |
| F6 | 0.0264 | 0.4396 | 100 |
| Principal Components | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| F1 | 0.3589 | −0.5745 | 0.3797 | 0.2533 | 0.5738 | 0.0598 |
| F2 | 0.4464 | 0.5176 | 0.1273 | −0.0852 | 0.119 | 0.7037 |
| F3 | 0.4448 | −0.0788 | −0.2944 | 0.6988 | −0.47 | −0.0069 |
| Contribution Rate | Pl | Rls | El | Rlg ± ε | Δh |
|---|---|---|---|---|---|
| Climate Changes | 100 | 80.19 | 100 | 88.44 | 93.13 |
| Catchment Modifications | 0 | 19.81 | 0 | 11.56 | 6.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Li, G.; Rubinato, M.; Ma, G.; Zhou, J.; Jia, G.; Yu, X.; Wang, H. Analysis of Long-Term Water Level Variations in Qinghai Lake in China. Water 2019, 11, 2136. https://doi.org/10.3390/w11102136
Fang J, Li G, Rubinato M, Ma G, Zhou J, Jia G, Yu X, Wang H. Analysis of Long-Term Water Level Variations in Qinghai Lake in China. Water. 2019; 11(10):2136. https://doi.org/10.3390/w11102136
Chicago/Turabian StyleFang, Jianmei, Guijing Li, Matteo Rubinato, Guoqing Ma, Jinxing Zhou, Guodong Jia, Xinxiao Yu, and Henian Wang. 2019. "Analysis of Long-Term Water Level Variations in Qinghai Lake in China" Water 11, no. 10: 2136. https://doi.org/10.3390/w11102136
APA StyleFang, J., Li, G., Rubinato, M., Ma, G., Zhou, J., Jia, G., Yu, X., & Wang, H. (2019). Analysis of Long-Term Water Level Variations in Qinghai Lake in China. Water, 11(10), 2136. https://doi.org/10.3390/w11102136






