Assessment of Water Resources Management Strategy Under Different Evolutionary Optimization Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Adopted Multi-Objective Optimization Approach
- In a minimization problem, a vector u = (u1, . . . , uM)T is said to dominate another vector v = (v1, . . . , vM)T if ui ≤ vi for i = 1, . . . , M and u ≠ v. This property may be denoted as u ≺v.
- A feasible solution x∈ X is called a Pareto-optimal solution, if there is no alternative solution y∈ X such that F(y) ≺ F(x).
- The Pareto-optimal set, PS, is the union of all Pareto-optimal solutions, and may be defined as PS = {x ∈ X :y ∈ X, F(y) ≺ F(x)}.
- The Pareto-optimal front, PF, is the set comprising the Pareto-optimal solutions in the objective space. It may be expressed as PF = {F(x)|x ∈ PS}.
2.2. Details of Epsilon-Dominance-Driven Self-Adaptive Evolutionary Algorithm (ε-DSEA) Optimization Algorithm
- Diversity expansion to increase decision variables’ search space exploitation
- Self-adaptive operators’ parameters for parameters in process tuning
- Exploration extension for algorithm revival and stagnation coping
- Virtual dominance archive to improve diversity and convergence.
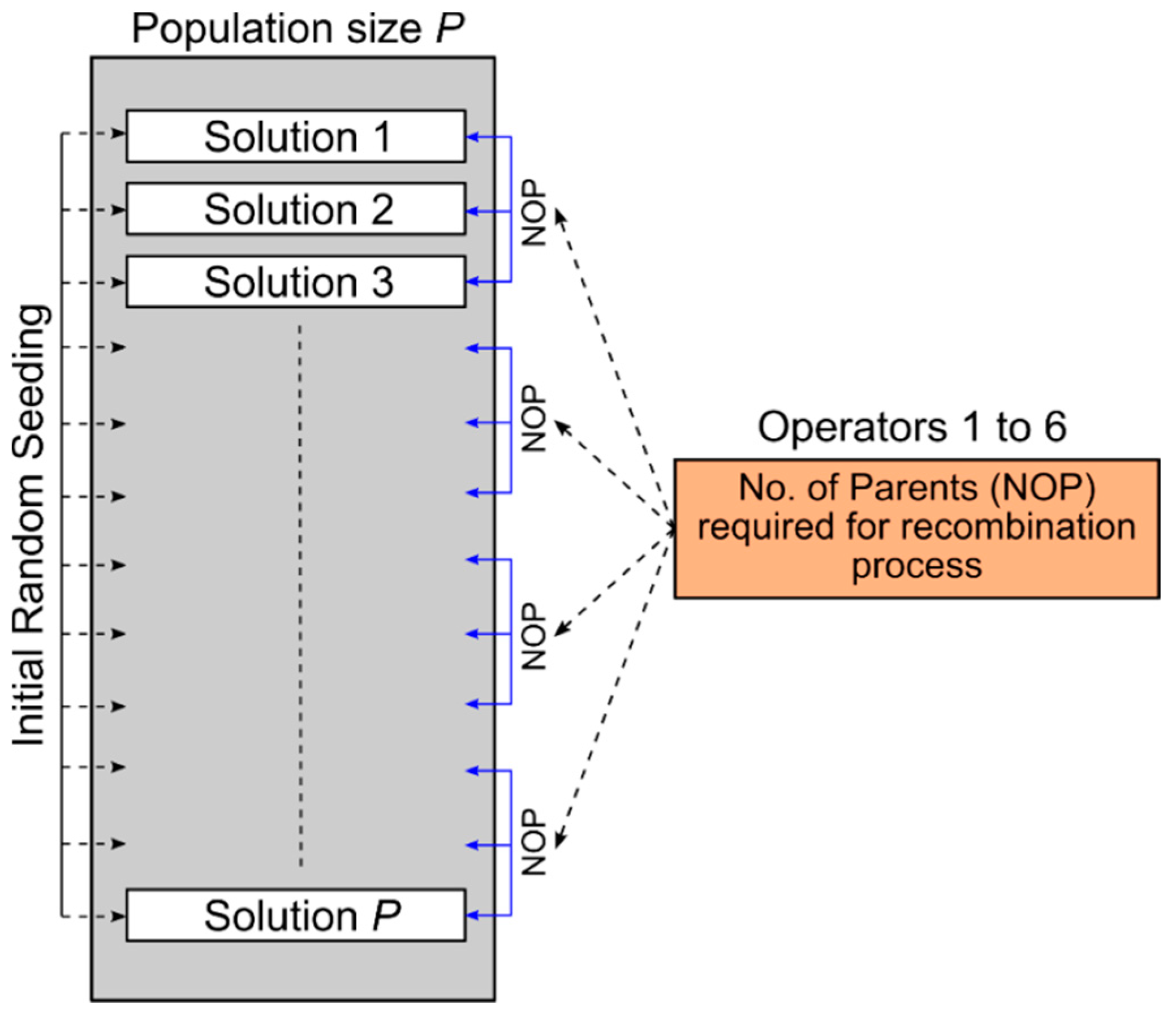
2.2.1. Diversity Expansion
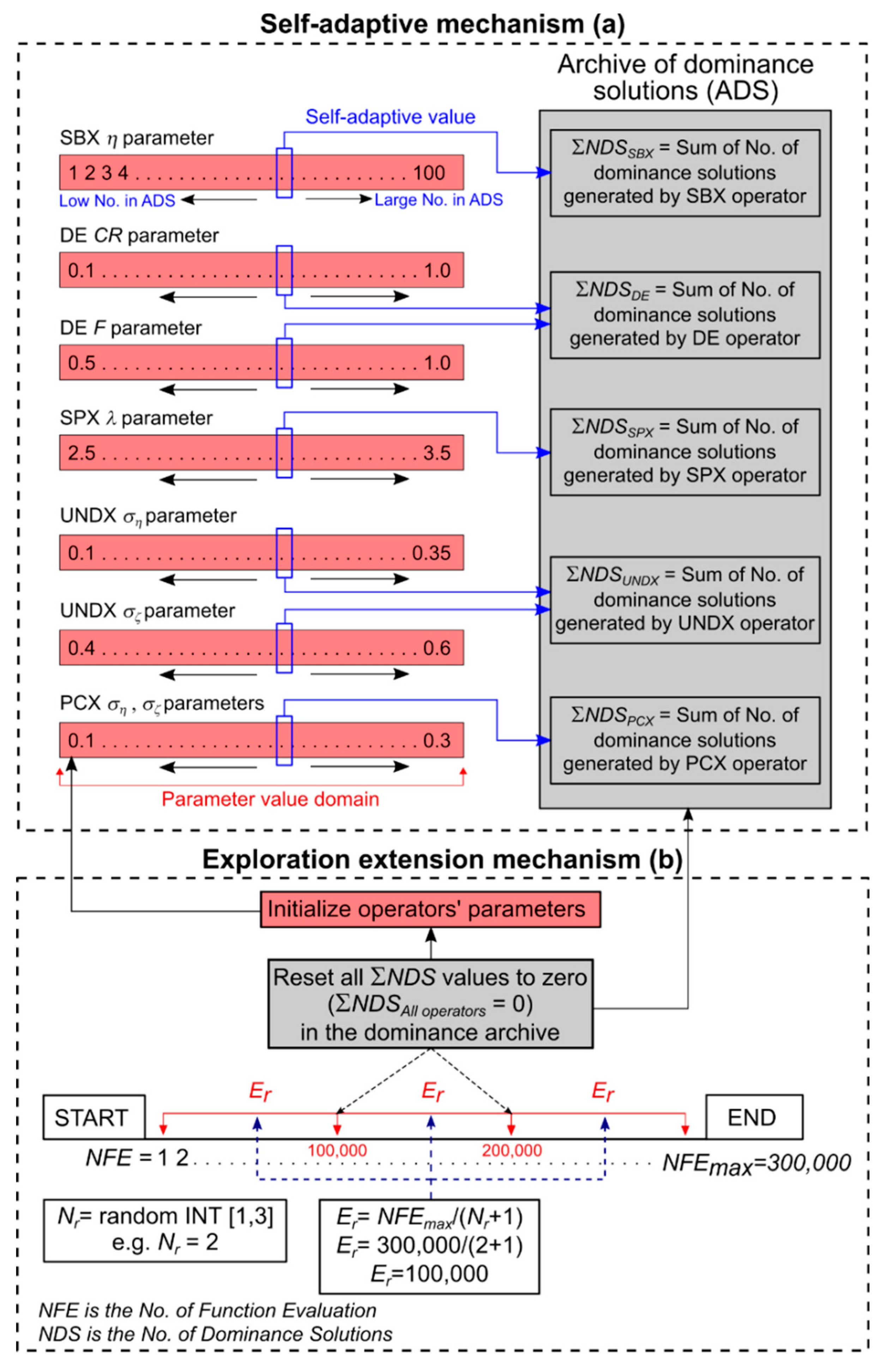
2.2.2. Self-Adaptive Mechanism and Formulae
2.2.3. Exploration Extension Mechanism
2.2.4. Virtual Dominance Archive
2.2.5. Constraint Handling Strategy
2.3. Comparative Paradigms
- If there is no change in the archive size for a certain number of evaluations;
- If there is no improvement indicated by the -progress indicator; and
- If the current population to archive ratio exceeds 1.25×γ
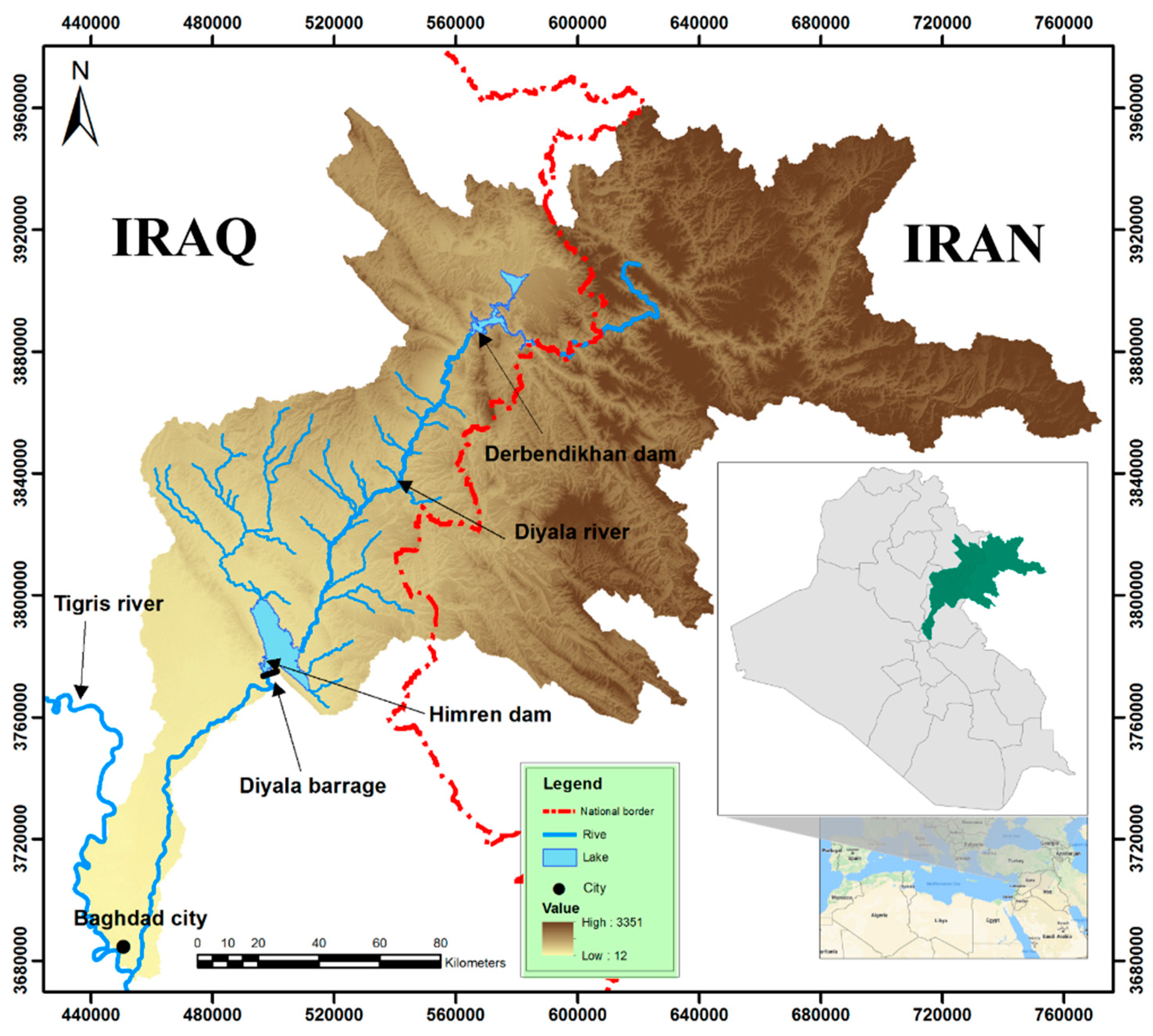
2.4. Identification of a Real-World Experimental Test Problem
2.4.1. Objectives Functions Formulae
2.4.2. Reservoir System Constraints
2.5. Computational Properties
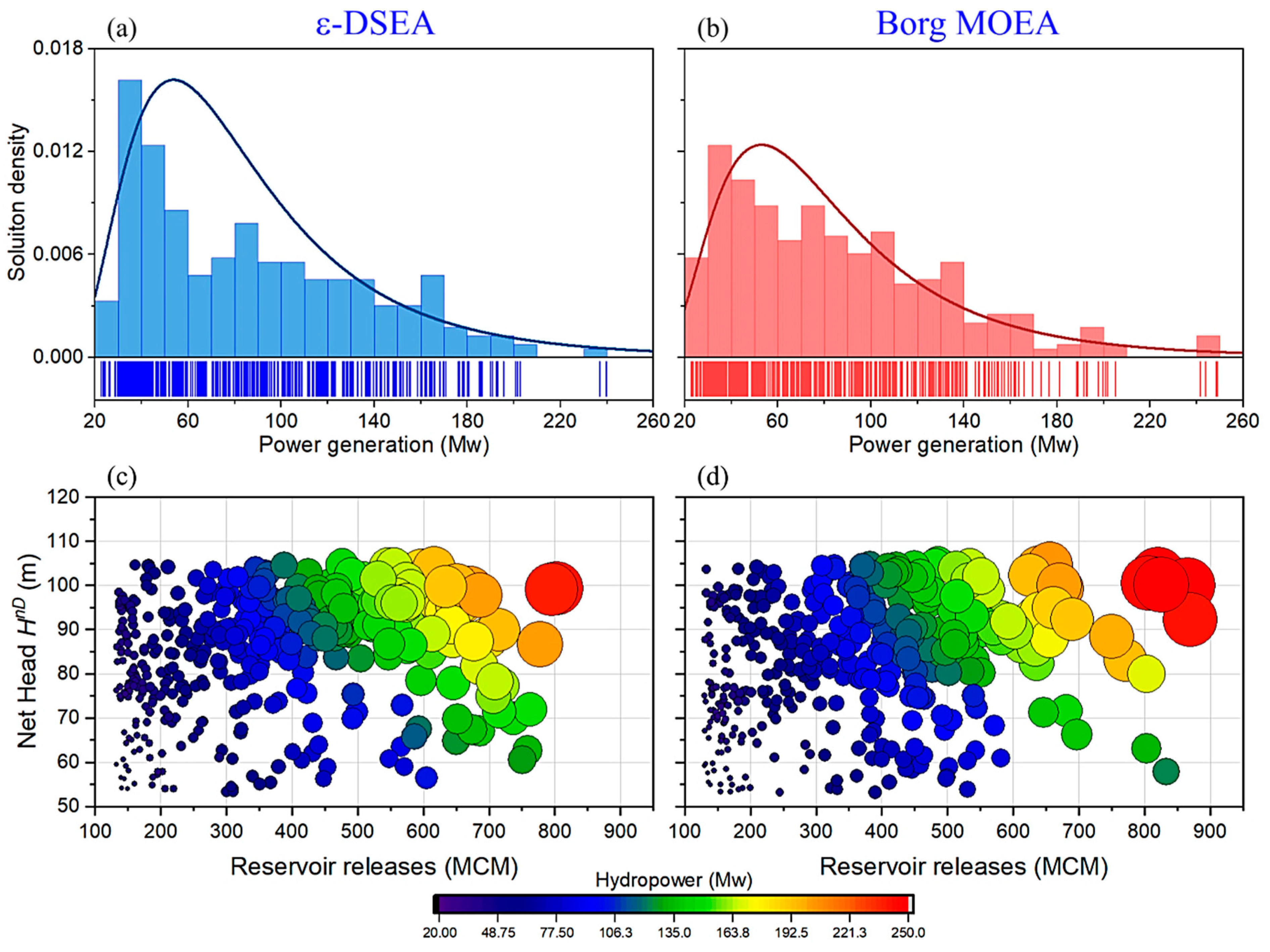
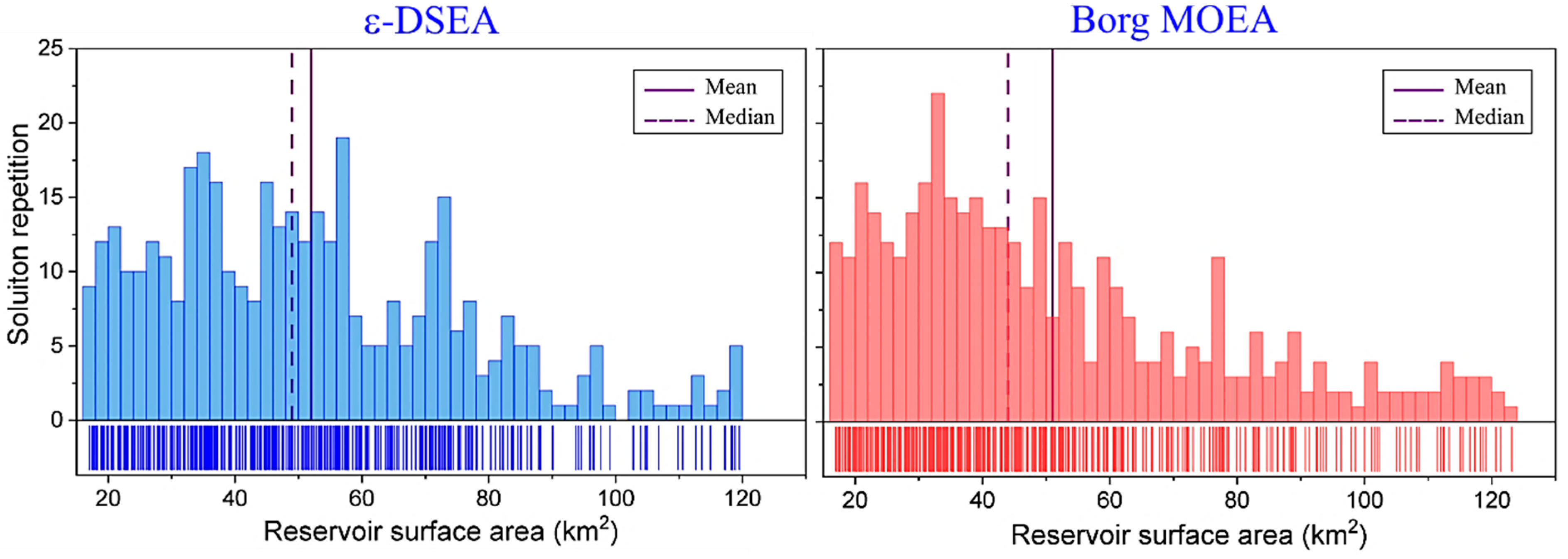
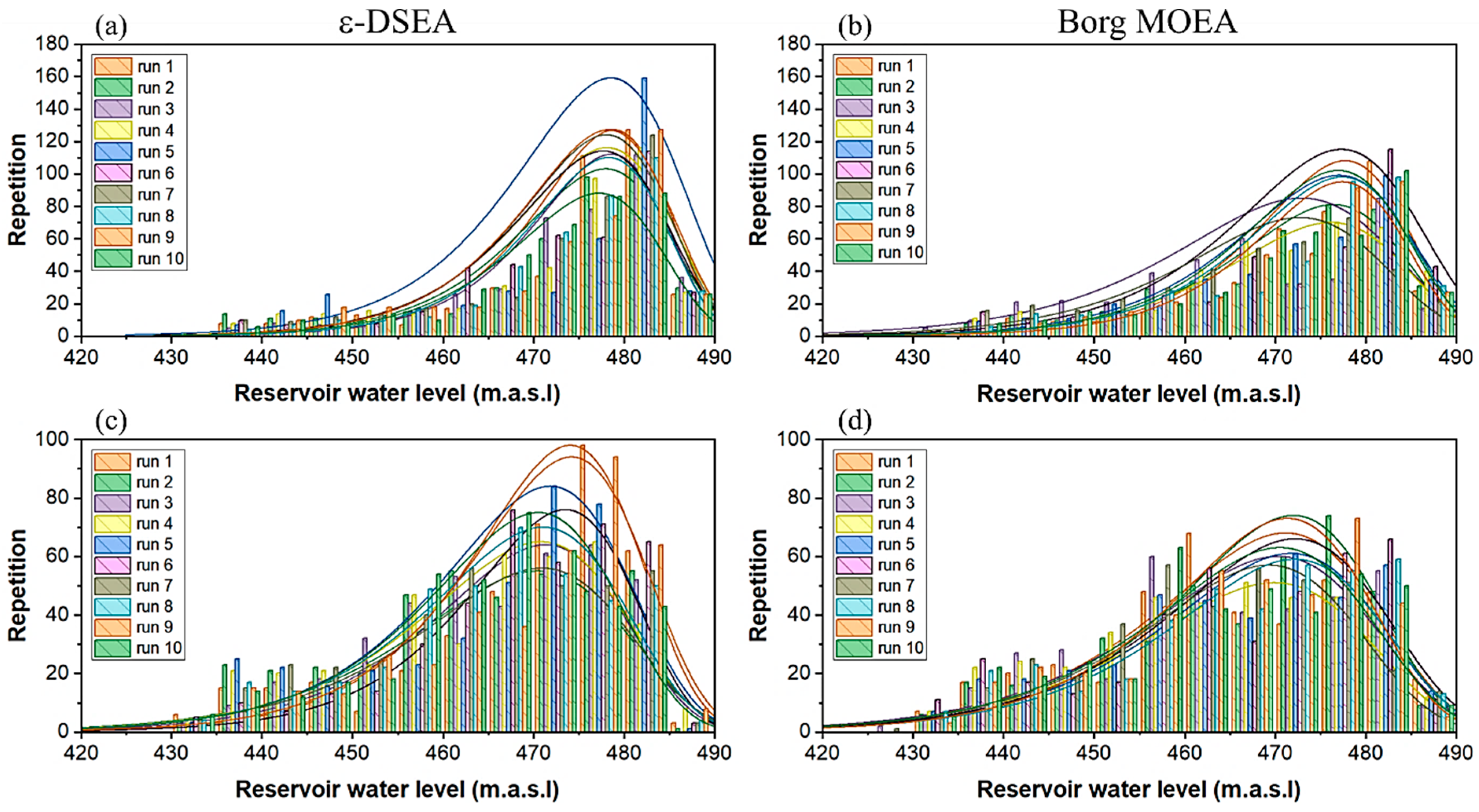
3. Results
3.1. Performance Achievement
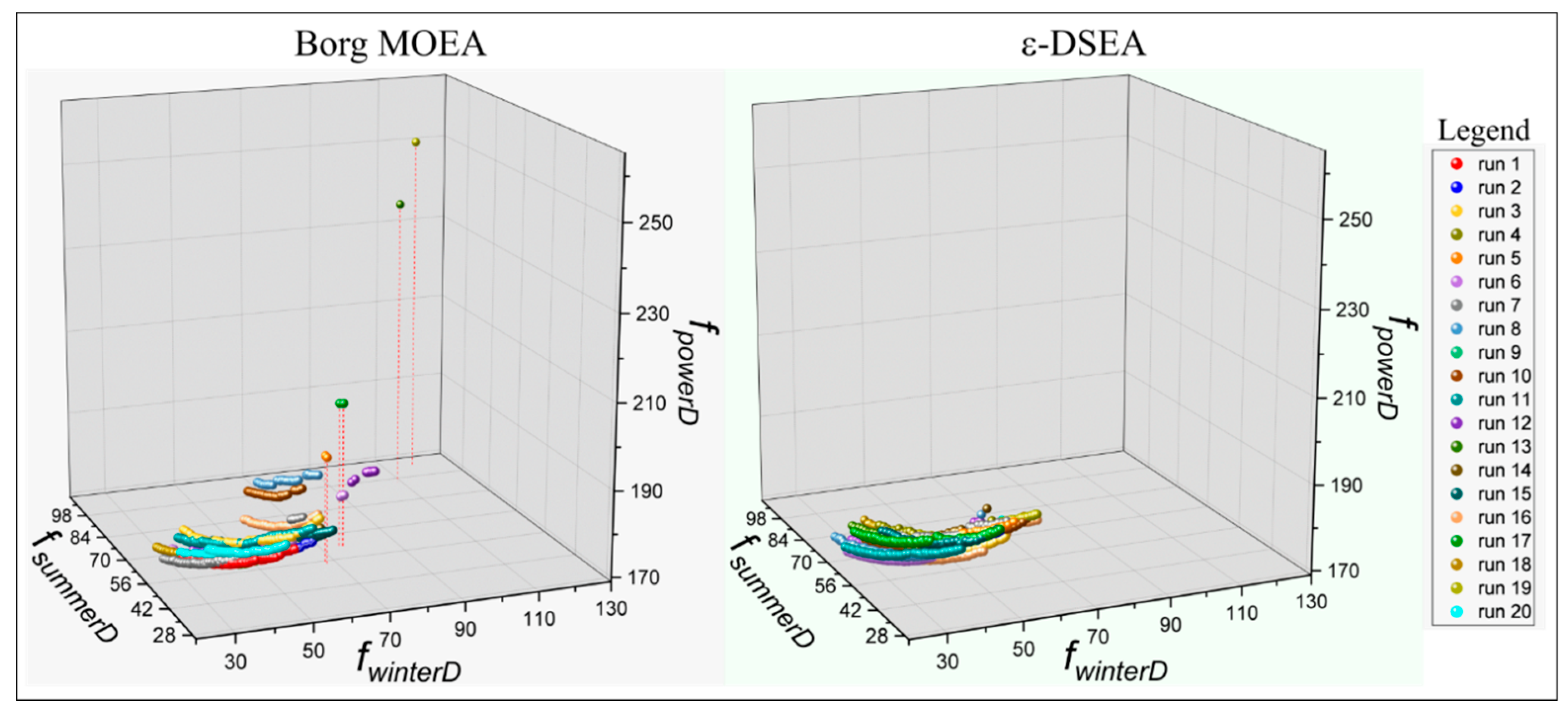
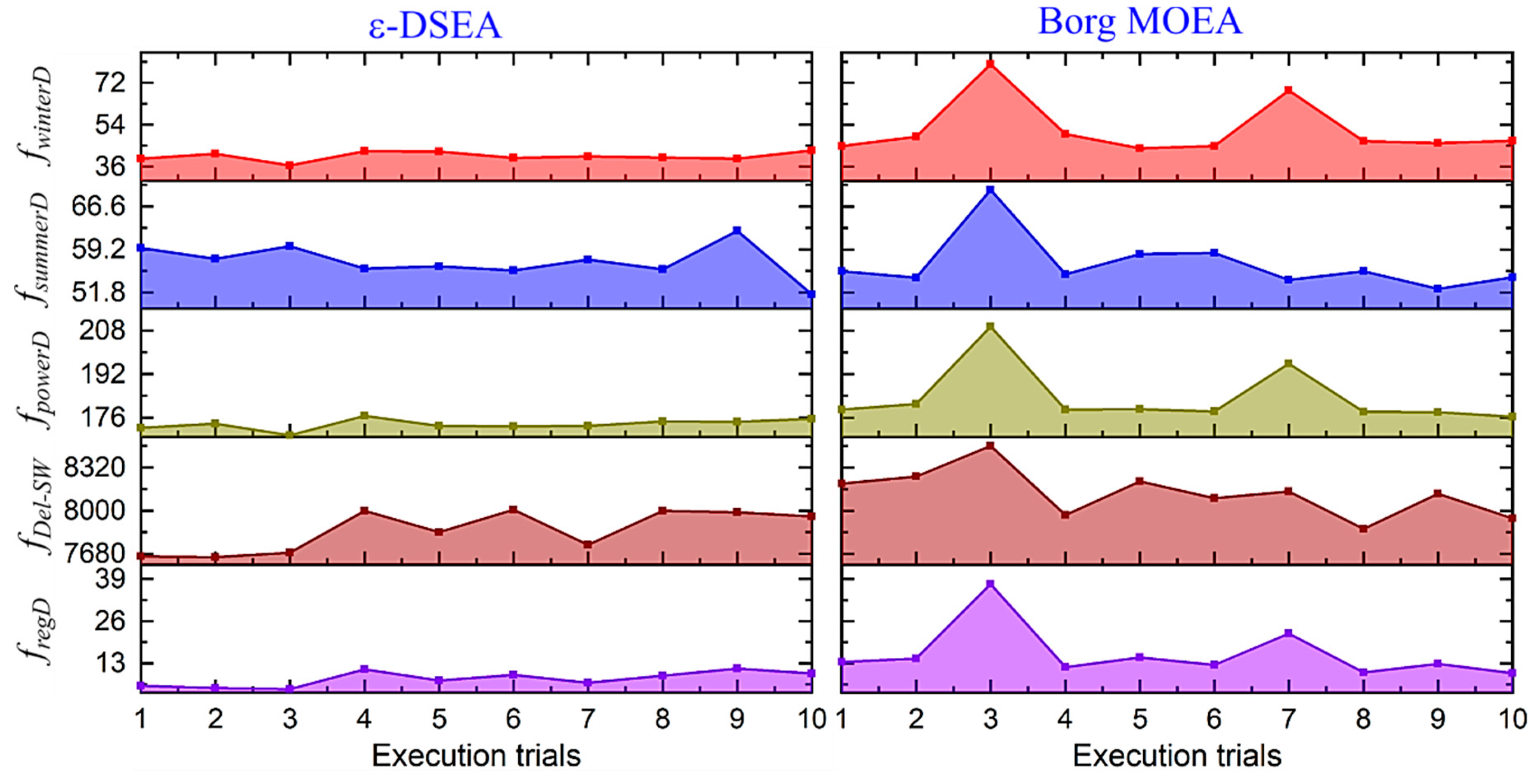
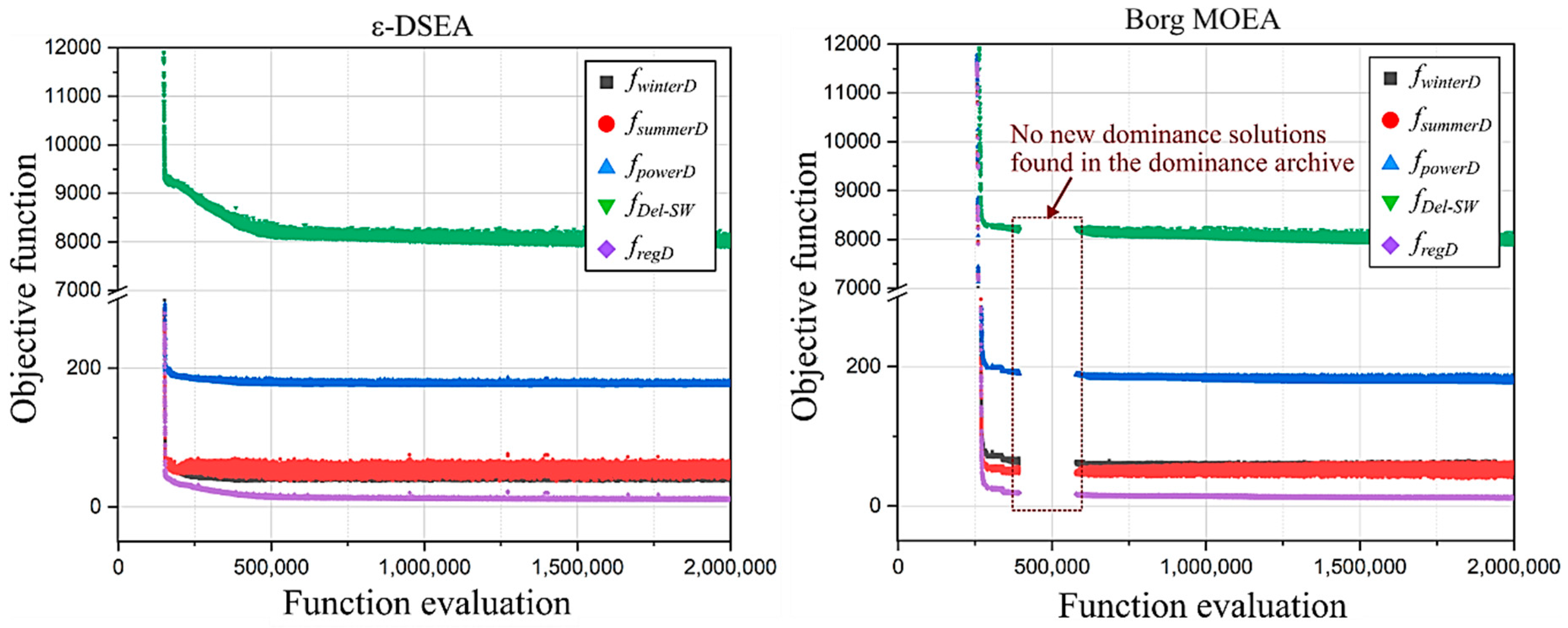
3.1.1. Algorithms’ Reliability
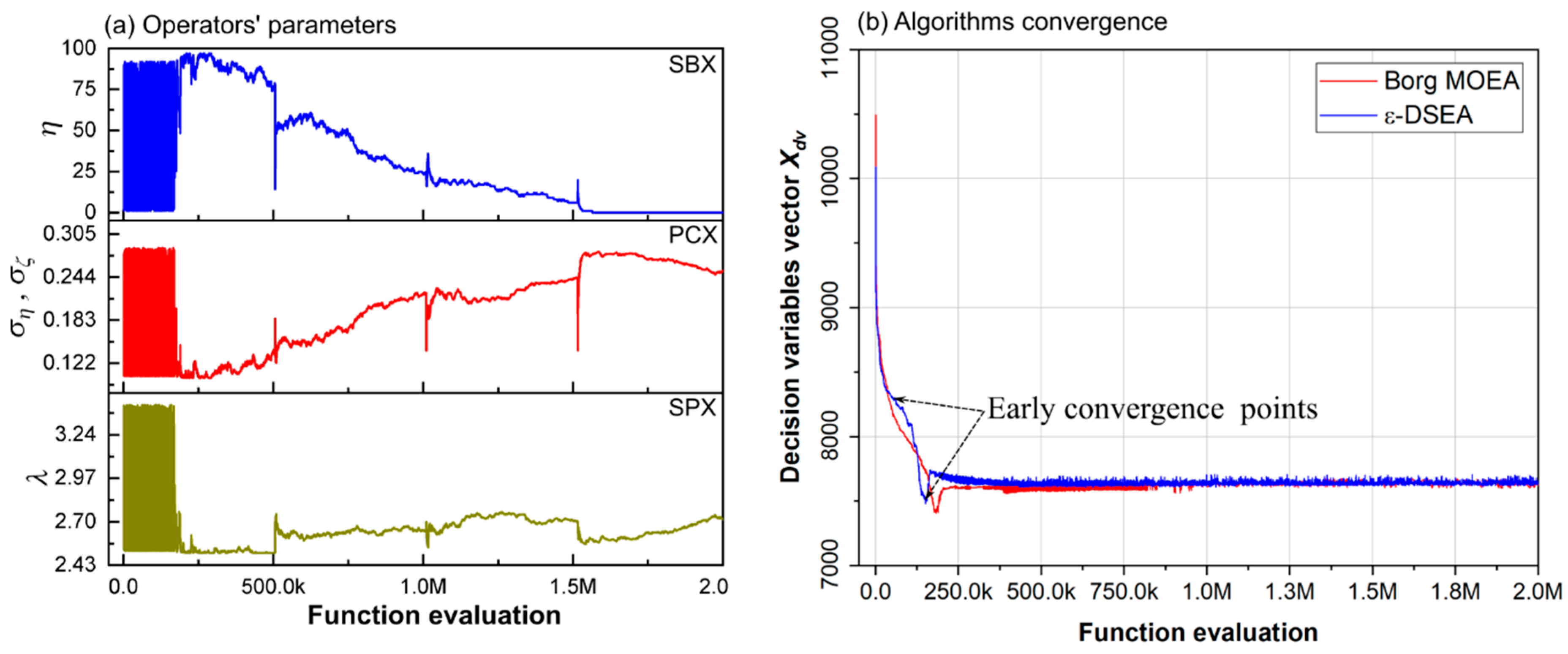
3.1.2. Algorithms’ Robustness and Efficiency
3.1.3. Algorithms’ Effectiveness
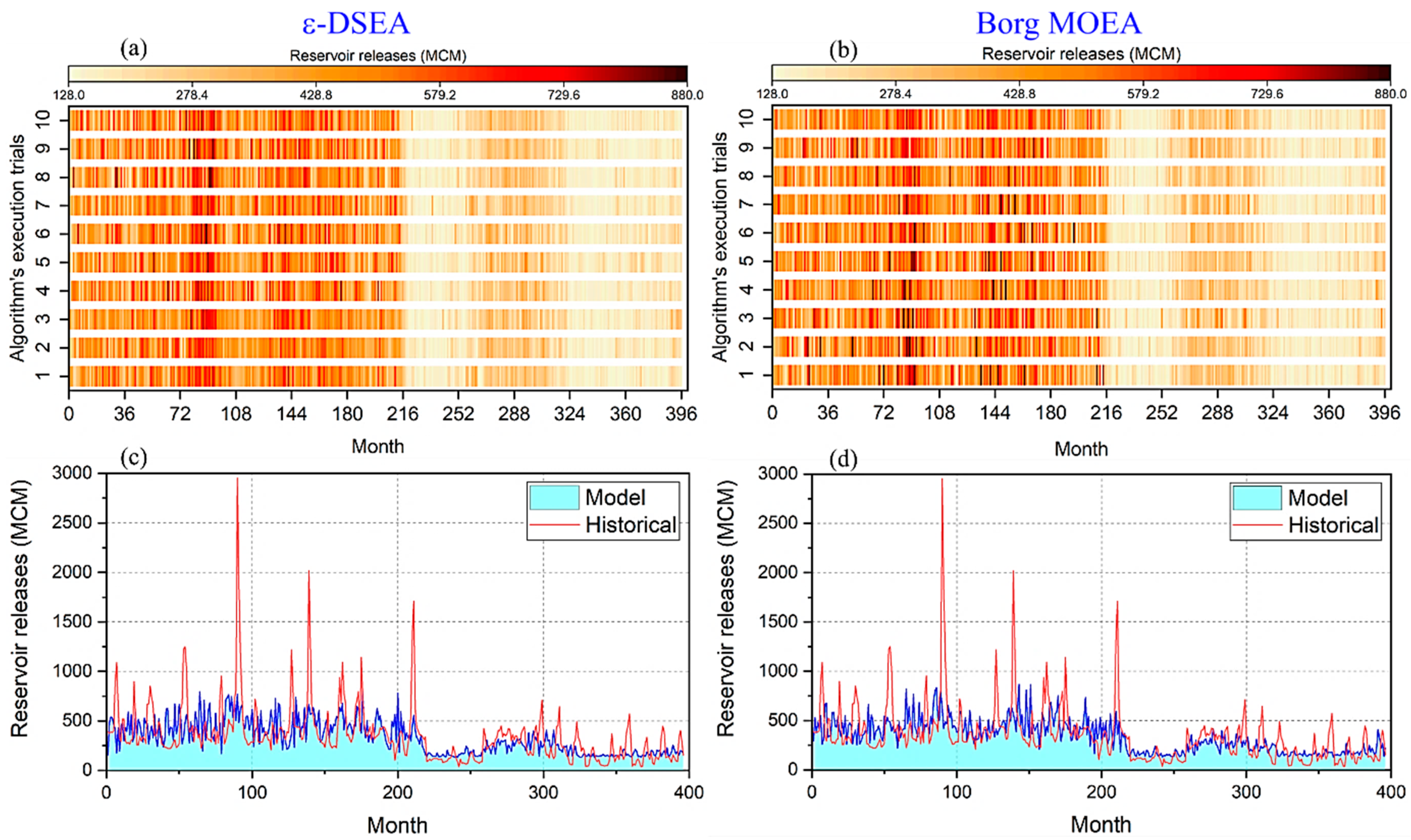
3.2. Strategic Achievement
4. Discussion
4.1. Algorithms’ Optimization Techniques
4.2. Water Resources Management Case Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maier, H.; Kapelan, Z.; Kasprzyk, J.; Matott, L. Thematic issue on Evolutionary Algorithms in Water Resources. Environ. Model. Softw. 2015, 69, 222–225. [Google Scholar] [CrossRef][Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the 1st international Conference on Genetic Algorithms; 1985; pp. 93–100. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-Based Selection in Multiobjective Search. Computer Vision ECCV 2012 2004, 3242, 832–842. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; Bradford Company: Scituate, MA, USA, 2004. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Coello, C.A.C.; Lamont, G.L.; van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Hurford, A.P.; Huskova, I.; Harou, J.J. Using many-objective trade-off analysis to help dams promote economic development, protect the poor and enhance ecological health. Environ. Sci. Policy 2014, 38, 72–86. [Google Scholar] [CrossRef]
- Qi, Y.; Bao, L.; Ma, X.; Miao, Q.; Li, X. Self-adaptive Multi-objective Evolutionary Algorithm based on Decomposition for Large-scale problems: A Case Study on Reservoir Flood Control Operation. Inf. Sci. 2016, 367–368, 529–549. [Google Scholar] [CrossRef]
- Salazar, J.Z.; Reed, P.M.; Quinn, J.D.; Giuliani, M.; Castelletti, A. Balancing exploration, uncertainty and computational demands in many objective reservoir optimization. Adv. Water Resour. 2017, 109, 196–210. [Google Scholar] [CrossRef]
- Al-Jawad, J.Y.S.; Tanyimboh, T.T. Reservoir operation using a robust evolutionary optimization algorithm. J. Environ. Manag. 2017, 197, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Zhang, P.; Wang, Y.; Jiang, D.; Dai, H.; Mao, J.; Wang, M. Multi-objective optimization of cascade reservoirs using NSGA-II: A case study of the Three Gorges-Gezhouba cascade reservoirs in the middle Yangtze River, China. Hum. Ecol. Risk Assess. Int. J. 2017, 23, 1–22. [Google Scholar] [CrossRef]
- Hadka, D.; Reed, P. Diagnostic Assessment of Search Controls and Failure Modes in Many-Objective Evolutionary Optimization. Evol. Comput. 2012, 20, 423–452. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An Evolutionary Many-Objective Optimization Algorithm Based on Dominance and Decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Liu, Z.-Z.; Wang, Y.; Huang, P.-Q. AnD: A many-objective evolutionary algorithm with angle-based selection and shift-based density estimation. Inf. Sci. 2018, 1–20. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Setoguchi, Y.; Masuda, H.; Nojima, Y. Performance of Decomposition-Based Many-Objective Algorithms Strongly Depends on Pareto Front Shapes. IEEE Trans. Evol. Comput. 2017, 21, 1. [Google Scholar] [CrossRef]
- Maier, H.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.; Cunha, M.; Dandy, G.; Gibbs, M.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef]
- Goldberg, D.E. Sizing Populations for Serial and Parallel Genetic Algorithms. In Proceedings of the 3rd International Conference on Genetic Algorithms, San Francisco, CA, USA, 4–7 June 1989; pp. 70–79. [Google Scholar]
- De Jong, K. Parameter Setting in EAs: A 30 Year Perspective. Informatik im Fokus 2007, 54, 1–18. [Google Scholar]
- Karafotias, G.; Hoogendoorn, M.; Eiben, A.E. Parameter Control in Evolutionary Algorithms: Trends and Challenges. IEEE Trans. Evol. Comput. 2015, 19, 167–187. [Google Scholar] [CrossRef]
- Eiben, A.; Hinterding, R.; Michalewicz, Z. Parameter control in evolutionary algorithms. IEEE Trans. Evol. Comput. 1999, 3, 124–141. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Reynoso-Meza, G.; Sanchis, J.; Blasco, X.; Mart´ınez, M. An empirical study on parameter selection for multiobjective optimization algorithms using Differential Evolution. In Proceedings of the 2011 IEEE Symposium on Differential Evolution (SDE), Paris, France, 11–15 April 2011; pp. 1–7. [Google Scholar]
- Stephens, C.R.; Olmedo, I.G.; Mora-Vargas, J.; Waelbroeck, H. Self-Adaptation in Evolving Systems. Artif. Life 1998, 4, 183–201. [Google Scholar] [CrossRef] [PubMed]
- Hadka, D.; Reed, P. Borg: An Auto-Adaptive Many-Objective Evolutionary Computing Framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef] [PubMed]
- Reed, P.; Hadka, D.; Herman, J.; Kasprzyk, J.; Kollat, J.; Reed, P.; Herman, J.; Kasprzyk, J. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Marchi, A.; Dandy, G.; Wilkins, A.; Rohrlach, H. Methodology for Comparing Evolutionary Algorithms for Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 22–31. [Google Scholar] [CrossRef]
- Silver, E.A. An overview of heuristic solution methods. J. Oper. Res. Soc. 2004, 55, 936–956. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Deb, K. Multi-Objective Optimization using Evolutionary Algorithms, 1st ed.; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Stadler, W. A survey of multicriteria optimization or the vector maximum problem, part I: 1776–1960. J. Optim. Theory Appl. 1979, 29, 1–52. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Deb, K.; Joshi, D.; Anand, A. Real-coded evolutionary algorithms with parent-centric recombination. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 61–66. [Google Scholar]
- Kita, H.; Ono, I.; Kobayashi, S. Multi-parental extension of the unimodal normal distribution crossover for real-coded genetic algorithms. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; pp. 1581–1587. [Google Scholar]
- Tsutsui, S.; Yamamura, M.; Higuchi, T. Multi-parent recombination with simplex crossover in real coded genetic algorithms. In Proceedings of the 1999 Genetic and Evolutionary Computation Conference, San Francisco, CA, USA, 13–17 July 1999; pp. 657–664. [Google Scholar]
- Michalewicz, Z.; Logan, T.; Swaminathan, S. Evolutionary operators for continuous convex parameter spaces. In Proceedings of the 3rd Annual Conference on Evolutionary Programming; 1994; pp. 84–97. [Google Scholar]
- Deb, K.; Agrawal, S. A Niched-Penalty Approach for Constraint Handling in Genetic Algorithms. Artif. Neural Nets Genet. Algorithms 1999, 4, 235–243. [Google Scholar]
- Geetha, T.; Mahalakshmi, K.; UmmuSalma, I.; Kumaran, K.M. An Observational Analysis of Genetic Operators. Int. J. Comput. Appl. 2013, 63, 24–34. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining Convergence and Diversity in Evolutionary Multiobjective Optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Manikanth, M.; Shikhar, M. A Fast Multi-Objective Evolutionary Algorithm for Finding Well-Spread Pareto-Optimal Solutions; KanGAL Technical Report No.2003002; IIT: Kanpur, India, 2003. [Google Scholar]
- Kollat, J.; Reed, P. A computational scaling analysis of multiobjective evolutionary algorithms in long-term groundwater monitoring applications. Adv. Water Resour. 2007, 30, 408–419. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Marchi, A.; Nixon, J.B.; Maier, H. Improved understanding of the searching behavior of ant colony optimization algorithms applied to the water distribution design problem. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C.; Maier, H.R.; Feifei, Z. Comparison of the Searching Behavior of NSGA-II, SAMODE, and Borg MOEAs Applied to Water Distribution System Design Problems. J. Water Resour. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Improved evolutionary optimization from genetically adaptive multimethod search. Proc. Natl. Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef]
- Hesser, J.; Männer, R. Towards an optimal mutation probability for genetic algorithms. In Parallel Problem Solving from Nature, Proceedings of 1st Workshop PPSN I Dortmund, FRG, 1–3 October 1990; Schwefel, H.-P., Männer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 23–32. [Google Scholar]
- Aleti, A. An Adaptive Approach to Controlling Parameters of Evolutionary Algorithms. PhD. Thesis, Swinburne University of Technology, Melbourne, Australia, 2012. [Google Scholar]
- Deb, K.; Beyer, H.-G. Self-Adaptive Genetic Algorithms with Simulated Binary Crossover. Evol. Comput. 2001, 9, 197–221. [Google Scholar] [CrossRef] [PubMed]
- Farmani, R.; Wright, J.A. Self-adaptive fitness formulation for constrained optimization. IEEE Trans. Evol. Comput. 2003, 7, 445–455. [Google Scholar] [CrossRef]
- Giger, M.; Keller, D.; Ermanni, P. AORCEA—An adaptive operator rate controlled evolutionary algorithm. Comput. Struct. 2007, 85, 1547–1561. [Google Scholar] [CrossRef]
- Kaveh, A.; Shahrouzi, M. Dynamic selective pressure using hybrid evolutionary and ant system strategies for structural optimization. Int. J. Numer. Methods Eng. 2008, 73, 544–563. [Google Scholar] [CrossRef]
- Vafaee, F.; Nelson, P.C. An explorative and exploitative mutation scheme. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Vrugt, J.A.; Robinson, B.A.; Hyman, J.M. Self-adaptive multimethod search for global optimization in real-parameter spaces. IEEE Trans. Evol. Comput. 2009, 13, 243–259. [Google Scholar] [CrossRef]
- Lwin, K.; Qu, R.; Kendall, G. A learning-guided multi-objective evolutionary algorithm for constrained portfolio optimization. Appl. Soft Comput. 2014, 24, 757–772. [Google Scholar] [CrossRef]
- Bechikh, S.; Datta, R.; Gupta, A. Recent Advances in Evolutionary Multi-objective Optimization, Adaptation, Learning, and Optimization; Springer International Publishing: Cham, Switzerland, 2017; Volume 20. [Google Scholar]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-Objective Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2015, 48, 13:1–13:35. [Google Scholar] [CrossRef]
- Mane, S.U.; Rao, M.R.N. Many-Objective Optimization: Problems and Evolutionary Algorithms—A Short Review. Int. J. Appl. Eng. Res. 2017, 12, 973–4562. [Google Scholar]
- Bechikh, S.; Elarbi, M.; Said, L.B. Many-objective Optimization Using Evolutionary Algorithms: A Survey. In Recent Advances in Evolutionary Multi-objective Optimization; Bechikh, S., Datta, R., Gupta, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 105–137. [Google Scholar]
- Kollat, J.; Reed, P. Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Adv. Water Resour. 2006, 29, 792–807. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Zitzler, E. Evolutionary Algorithms for Multiobjective Optimization: Methods and Applications. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Switzerland, 1999. [Google Scholar]
- Van Veldhuizen, D.A.; Lamont, G.B. Evolutionary Computation and Convergence to a Pareto Front. In Proceedings of the Late Breaking Papers at the Genetic Programming 1998 Conference, Madison, WI, USA, 22–25 July 1998; pp. 221–228. [Google Scholar]
- Hadka, D.; Reed, P.M.; Simpson, T.W. Diagnostic assessment of the borg MOEA for many-objective product family design problems. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–10. [Google Scholar]
- Woodruff, M.J.; Reed, P.M.; Simpson, T.W. Many objective visual analytics: Rethinking the design of complex engineered systems. Struct. Multidiscip. Optim. 2013, 48, 201–219. [Google Scholar] [CrossRef]
- Salazar, J.Z.; Reed, P.M.; Herman, J.D.; Giuliani, M.; Castelletti, A. A diagnostic assessment of evolutionary algorithms for multi-objective surface water reservoir control. Adv. Water Resour. 2016, 92, 172–185. [Google Scholar] [CrossRef]
- Yan, D.; Ludwig, F.; Huang, H.Q.; Werners, S.E. Many-objective robust decision making for water allocation under climate change. Sci. Total Environ. 2017, 607, 294–303. [Google Scholar] [CrossRef]
- GWP (Global Water Partnership). Sharing Knowledge for Equitable, Efficient and Sustainable Water Resources Management; Version 2; Global Water Partnership (GWP): Stockholm, Sweden, 2003. [Google Scholar]
- Cardwell, H.E.; Cole, R.A.; Cartwright, L.A.; Martin, L.A. Integrated Water Resources Management: Definitions and Conceptual Musings. J. Contemp. Water Res. Educ. 2006, 135, 8–18. [Google Scholar] [CrossRef]
- Biswas, A.K. Integrated Water Resources Management: Is It Working? Int. J. Water Resour. Dev. 2008, 24, 5–22. [Google Scholar] [CrossRef]
- Al-Jawad, J.Y.; Alsaffar, H.M.; Bertram, D.; Kalin, R.M. A Comprehensive Optimum Integrated Water Resources Management Approach for Multidisciplinary Water Resources Management Problems. J. Environ. Manag. 2018, in press. [Google Scholar] [CrossRef]
- World Bank. Dokan and Derbendikhan Dam Inspections Report; Consultant Services by SMEC International Pty. Ltd.: Melbourne, Australia, 2006. [Google Scholar]
- Al-Jawad, J.Y.; Alsaffar, H.M.; Bertram, D.; Kalin, R.M. Optimum socio-environmental flows approach for reservoir operation strategy using many-objectives evolutionary optimization algorithm. Sci. Total Environ. 2018, 651, 1877–1891. [Google Scholar] [CrossRef] [PubMed]
| Operator | Parameters | Domain | Adaptation Functions | Comments |
|---|---|---|---|---|
| SBX 1 | [0, 100] | Distribution index | ||
| DE 2 | CR F | [0.1,1.0] [0.5, 1.0] | Crossover probability Step size | |
| SPX 3 | [2.5, 3.5] | Expansion rate | ||
| PCX 4 | [0.1, 0.3] | These parameters (standard deviations) control the spatial distribution of the offspring for PCX and UNDX | ||
| UNDX 4 | [0.4, 0.6] [0.1, 0.35] |
| Parameters | Borg | ε-DSEAa | Parameters | Borg | ε-DSEA |
|---|---|---|---|---|---|
| Initial population size | 100 | 100 | SPX parents | 10 | 3 |
| Tournament selection size | 2 | 2 | SPX offspring | 2 | 2 |
| SBX crossover rate | 1.0 | 1.0 | SPX expansion rate λ | 3 | [2.5, 3.5] |
| SBX distribution index η | 15.0 | [0, 100] | UNDX parents | 10 | 10 |
| DE crossover rate CR | 0.1 | [0.1, 1.0] | UNDX offspring | 2 | 2 |
| DE step size F | 0.5 | [0.5, 1.0] | UNDX σζ | 0.5 | [0.4, 0.6] |
| PCX parents | 10 | 10 | UNDX ση | 0.35/ | [0.1, 0.35]/ |
| PCX offspring | 2 | 2 | UM mutation rate | 1/L | 1/L |
| PCX ση | 0.1 | [0.1, 0.3] | PM mutation rate | 1/L | 1/L |
| PCX σζ | 0.1 | [0.1, 0.3] | PM distribution index ηm | 20 | 20 |
| Borg MOEA | ε-DSEA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area 1 | Head 2 | Power 3 | Storage 4 | Releases 5 | Area | Head | Power | Storage | Releases | |
| 3 Objective problem | ||||||||||
| Min. | 19.18 | 437.79 | 24.50 | 433.55 | 129.94 | 17.32 | 434.73 | 24.83 | 373.82 | 129.75 |
| Max. | 122.79 | 485.97 | 249.00 | 2565.84 | 866.25 | 121.80 | 485.86 | 246.37 | 2551.05 | 877.20 |
| Mean | 74.37 | 474.71 | 94.76 | 1732.33 | 336.06 | 76.39 | 475.53 | 94.77 | 1775.22 | 336.17 |
| Median | 72.03 | 477.12 | 83.00 | 1743.17 | 297.19 | 78.92 | 478.95 | 84.37 | 1867.41 | 316.10 |
| St.7 | 27.19 | 10.11 | 50.88 | 523.86 | 174.84 | 24.99 | 10.42 | 51.88 | 496.30 | 183.22 |
| Gross6 | 37.52 | 686.00 | 133.08 | 37.53 | 702.99 | 133.12 | ||||
| 5 Objective problem | ||||||||||
| Min. | 16.94 | 434.09 | 23.44 | 361.60 | 130.72 | 19.10 | 437.67 | 24.09 | 431.16 | 130.45 |
| Max. | 122.97 | 485.98 | 249.00 | 2568.50 | 866.08 | 123.14 | 486.00 | 249.00 | 2570.98 | 797.97 |
| Mean | 66.09 | 470.67 | 90.46 | 1555.39 | 337.72 | 71.90 | 472.95 | 91.77 | 1672.36 | 334.80 |
| Median | 61.55 | 473.63 | 82.14 | 1540.19 | 316.81 | 71.78 | 477.05 | 82.00 | 1738.53 | 298.79 |
| St. | 29.89 | 12.83 | 45.64 | 597.36 | 162.74 | 28.94 | 12.58 | 47.18 | 583.53 | 169.11 |
| Gross | 35.82 | 615.94 | 133.74 | 36.34 | 662.25 | 132.58 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Y. Al-Jawad, J.; M. Kalin, R. Assessment of Water Resources Management Strategy Under Different Evolutionary Optimization Techniques. Water 2019, 11, 2021. https://doi.org/10.3390/w11102021
Y. Al-Jawad J, M. Kalin R. Assessment of Water Resources Management Strategy Under Different Evolutionary Optimization Techniques. Water. 2019; 11(10):2021. https://doi.org/10.3390/w11102021
Chicago/Turabian StyleY. Al-Jawad, Jafar, and Robert M. Kalin. 2019. "Assessment of Water Resources Management Strategy Under Different Evolutionary Optimization Techniques" Water 11, no. 10: 2021. https://doi.org/10.3390/w11102021
APA StyleY. Al-Jawad, J., & M. Kalin, R. (2019). Assessment of Water Resources Management Strategy Under Different Evolutionary Optimization Techniques. Water, 11(10), 2021. https://doi.org/10.3390/w11102021






