Site-Scale Integrated Decision Support Tool (i-DSTss) for Stormwater Management
Abstract
1. Introduction
2. Overview of Decision Support Tools in Stormwater Management
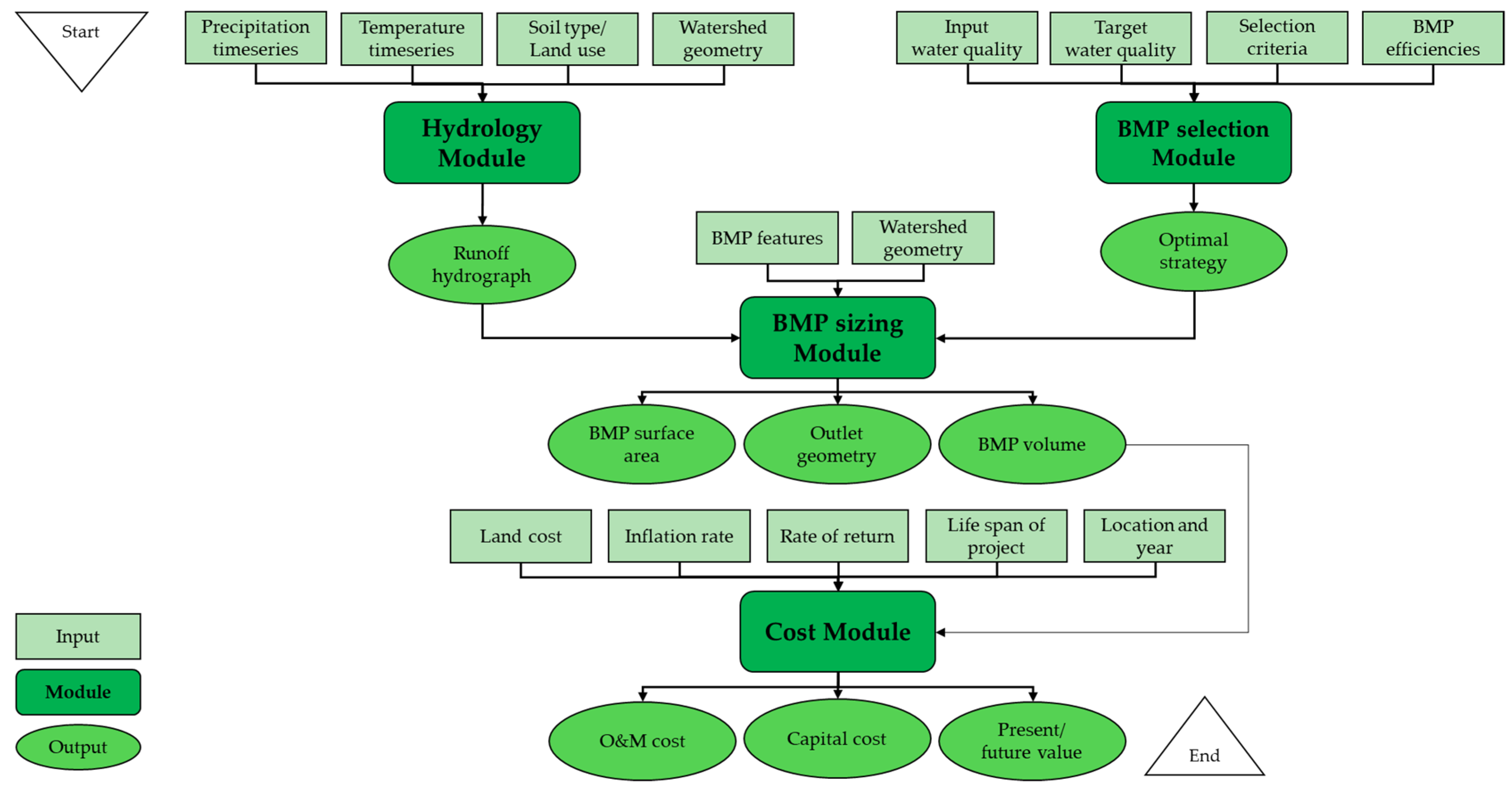
3. Methodology
3.1. Hydrology Module
3.1.1. Selection of the Rainfall-Runoff Model
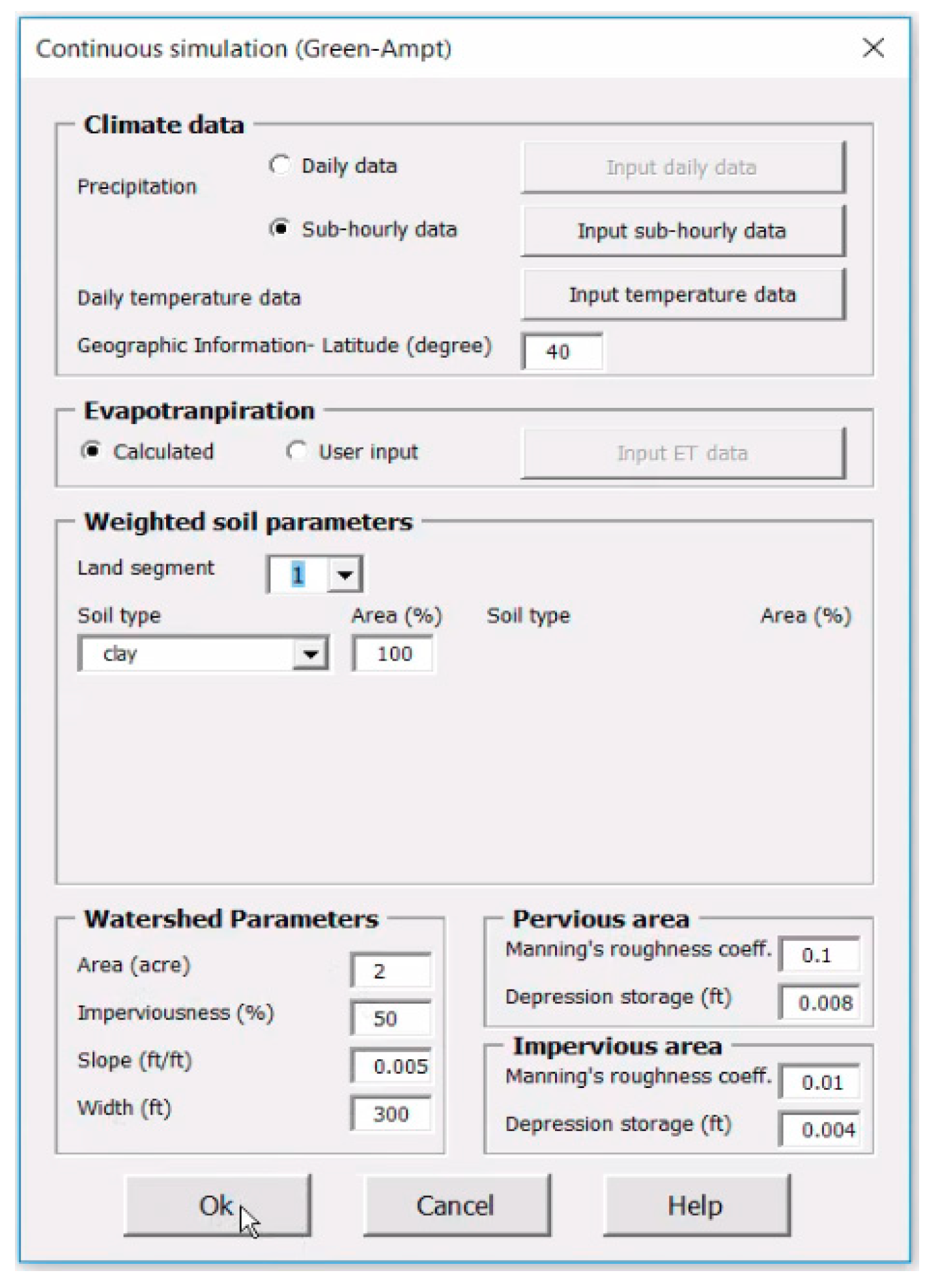
3.1.2. Event-Based and Continuous Simulation
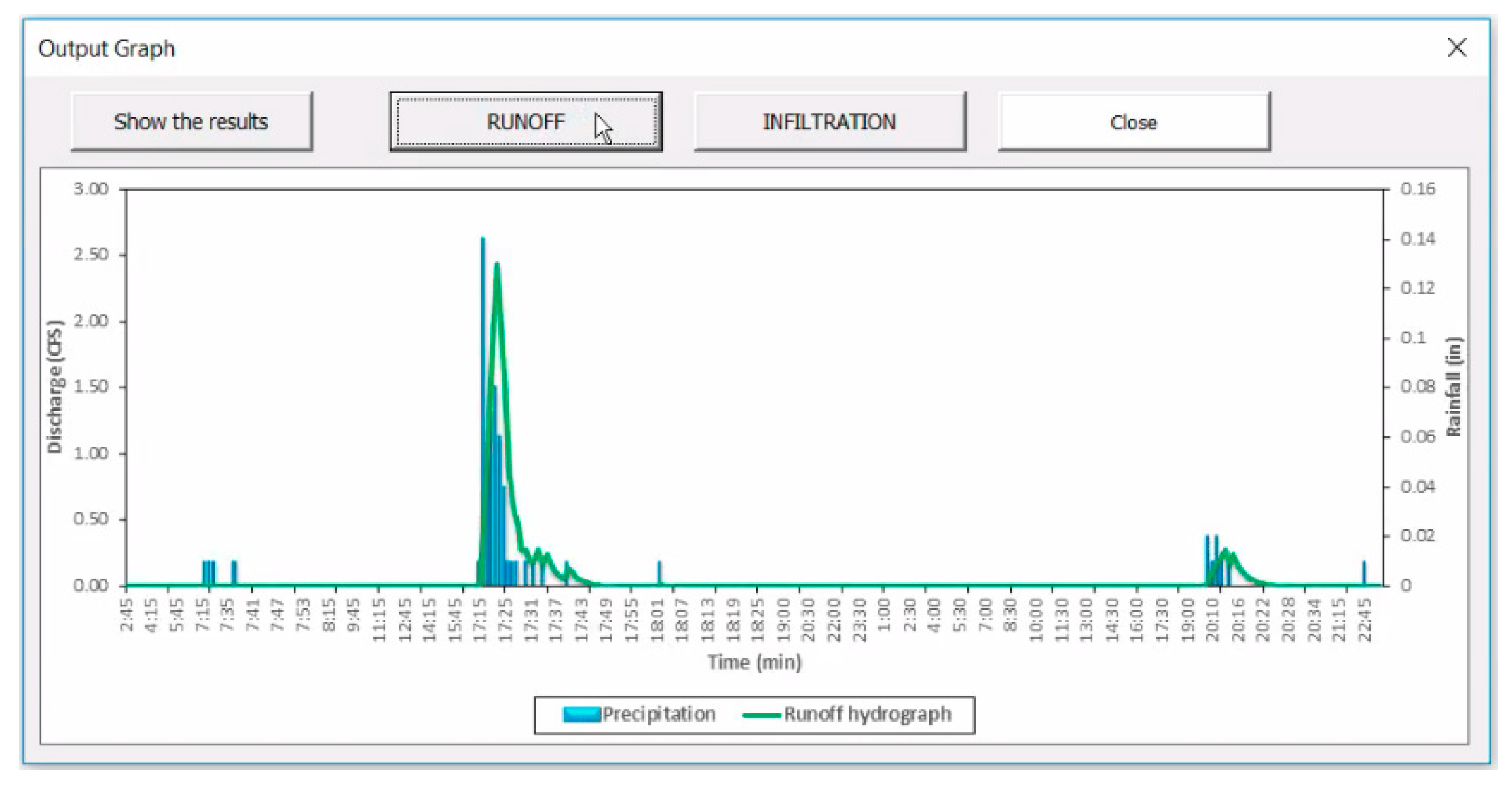
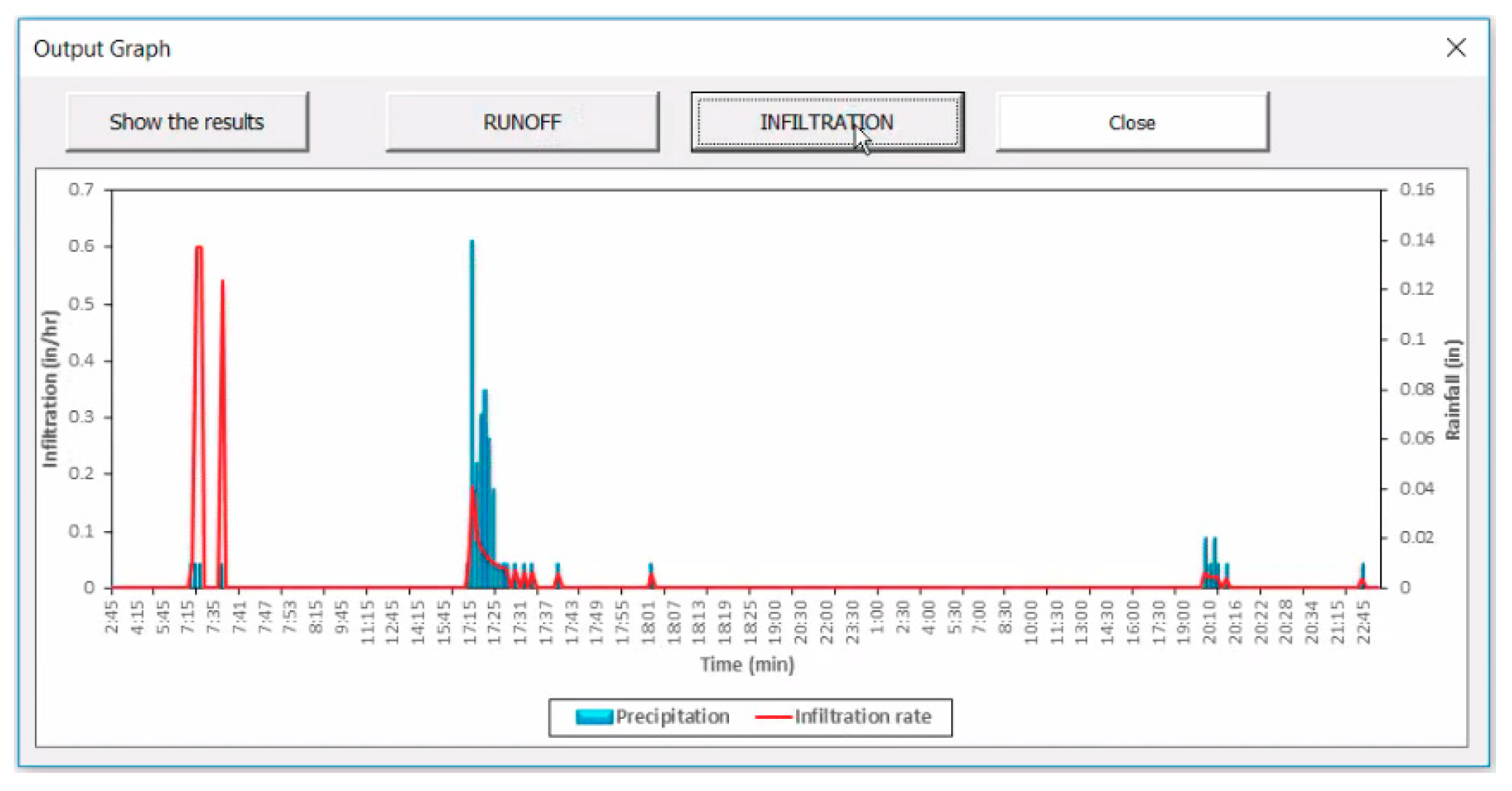
3.1.3. Estimation of Runoff Depth and Hydrograph
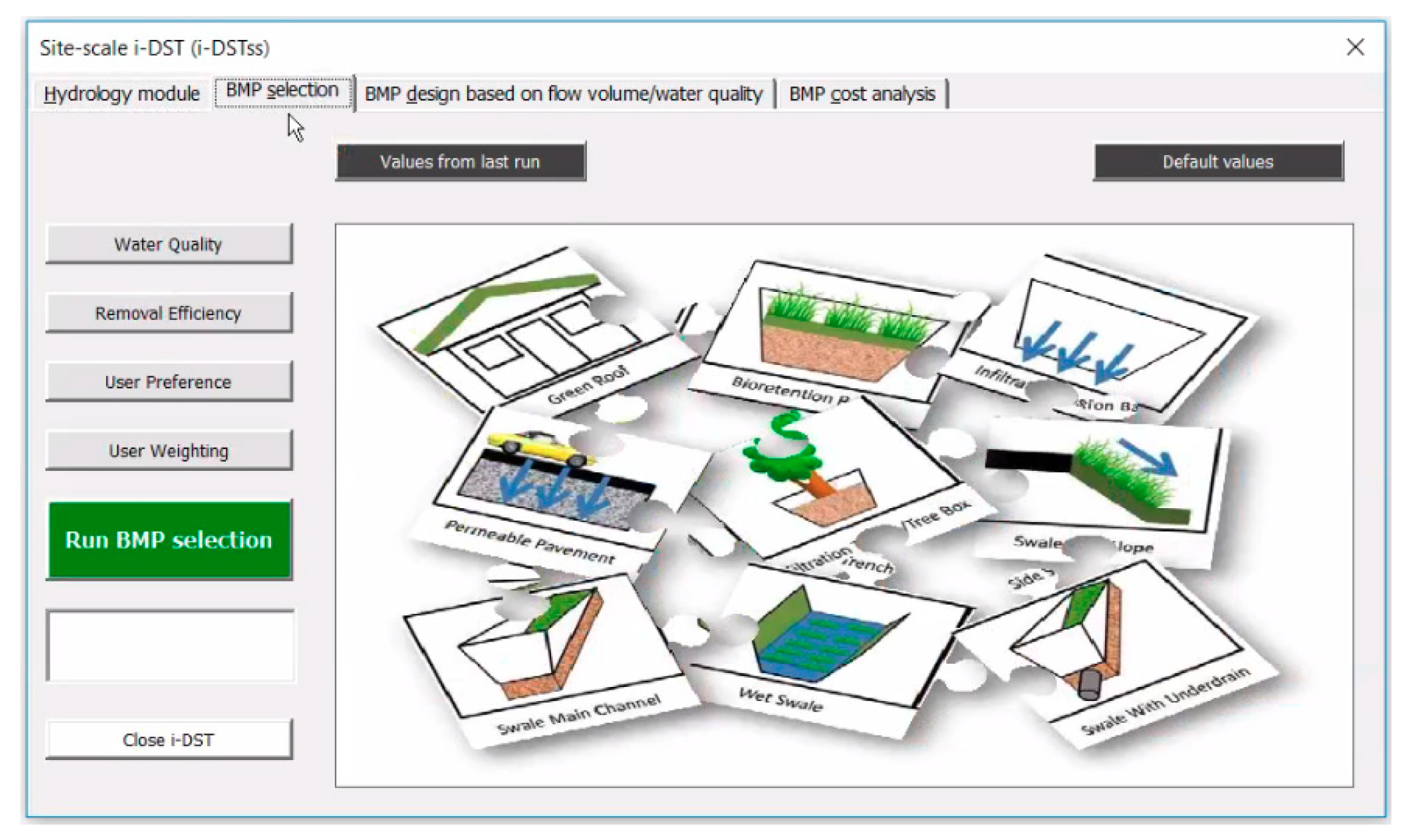
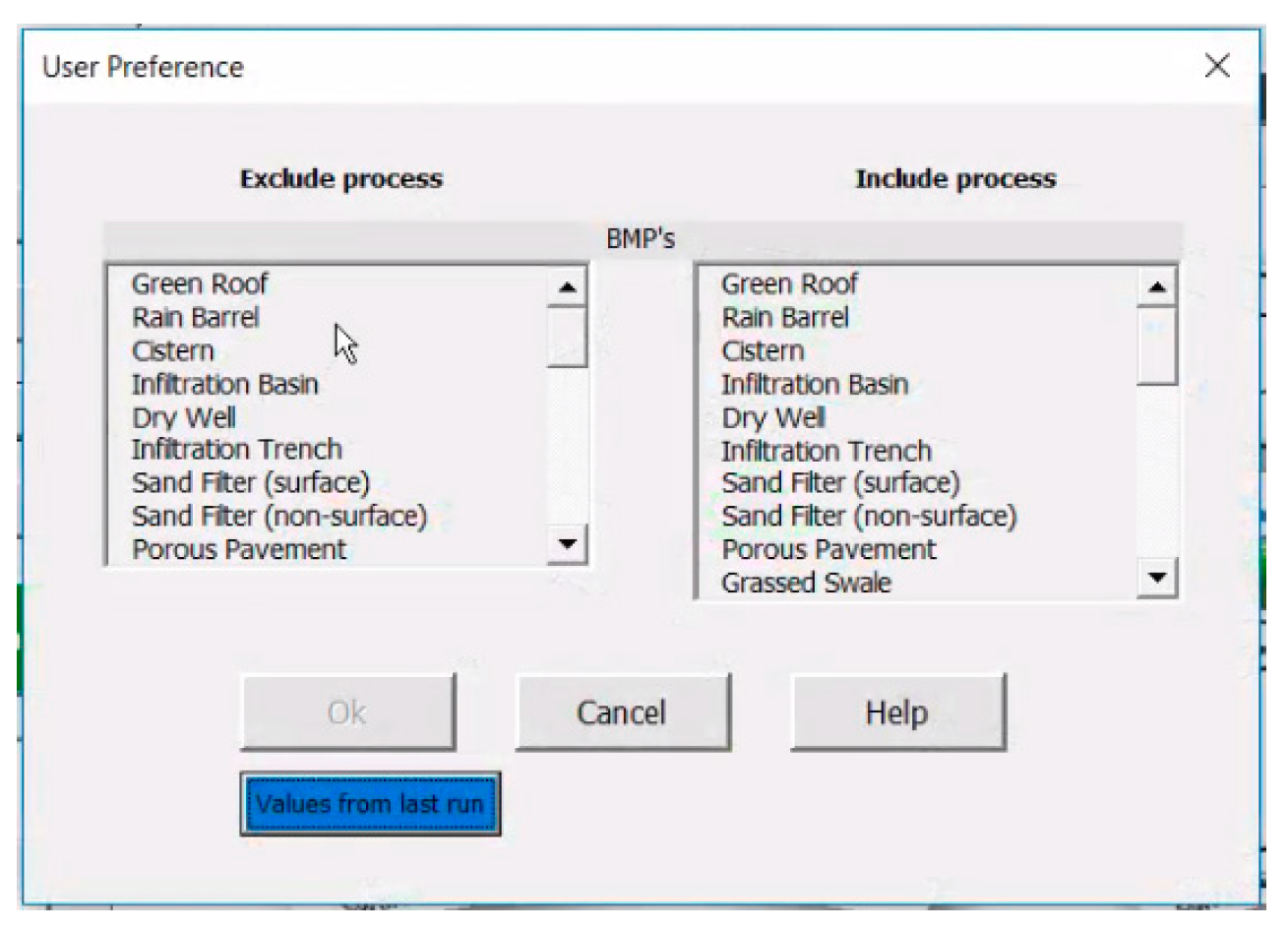
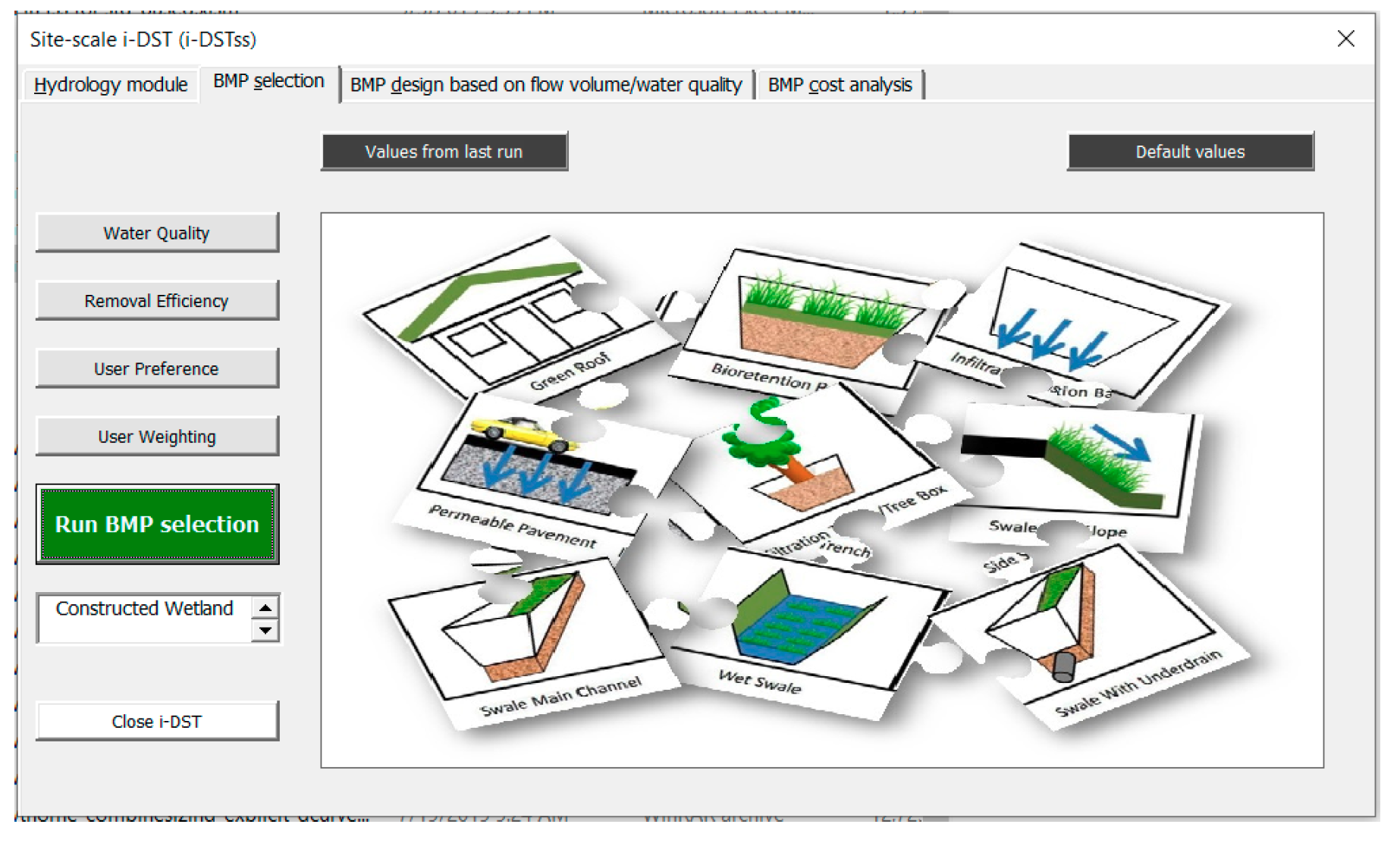
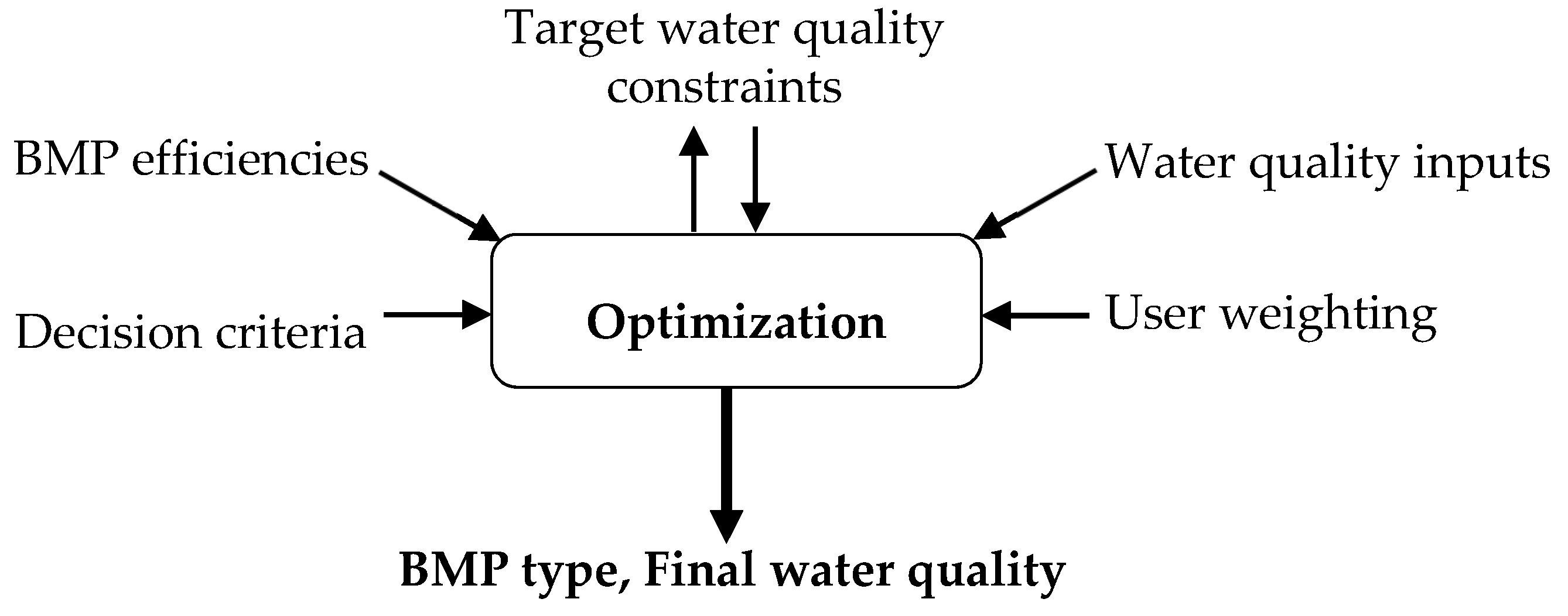
3.2. BMP Selection Module-Optimization Approach
3.2.1. Multi-Objective Optimization (MOO)
3.2.2. The Objective Function
3.2.3. Constraints
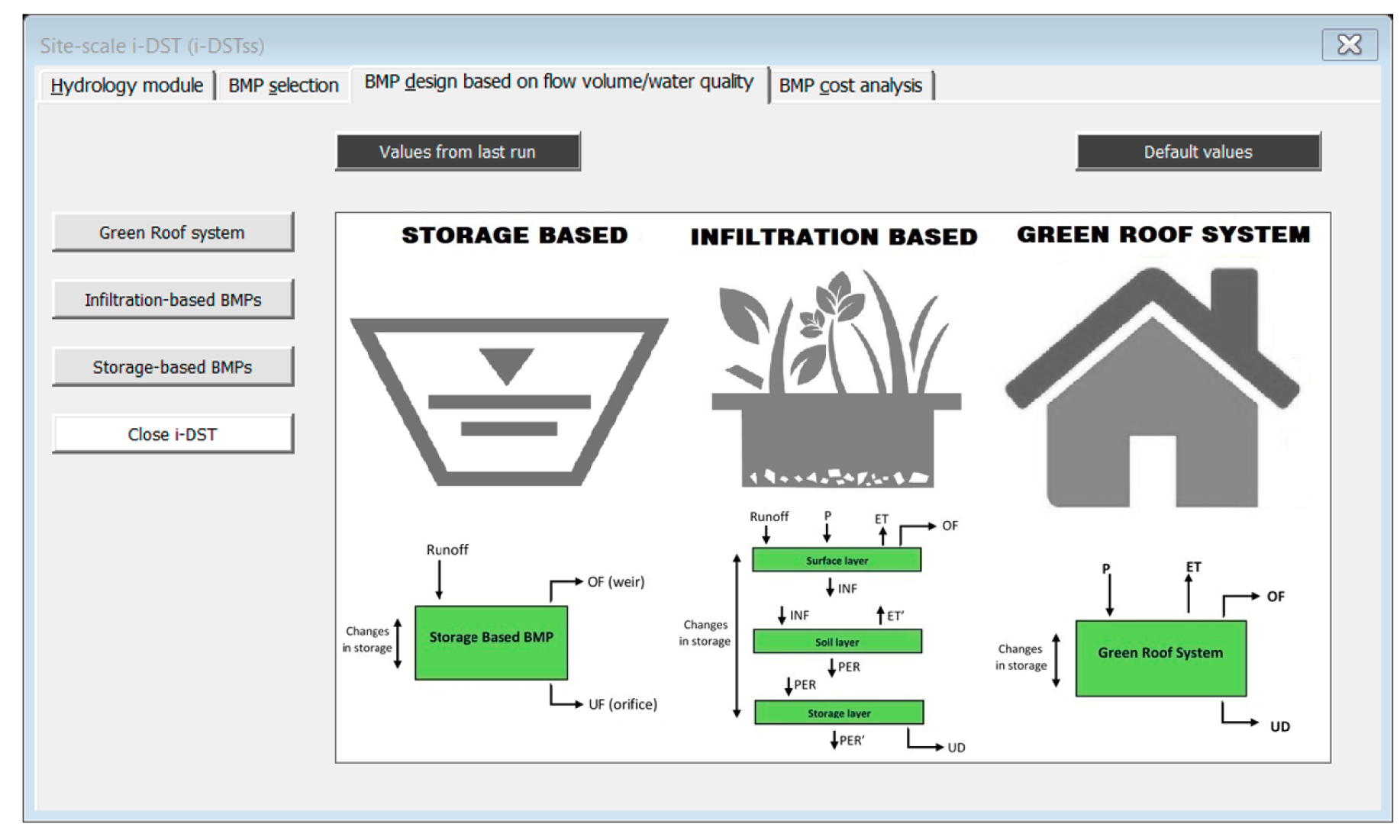
3.3. BMP Sizing Module
3.3.1. Green Roof System
- (a)
- (b)
- (c)
- (d)
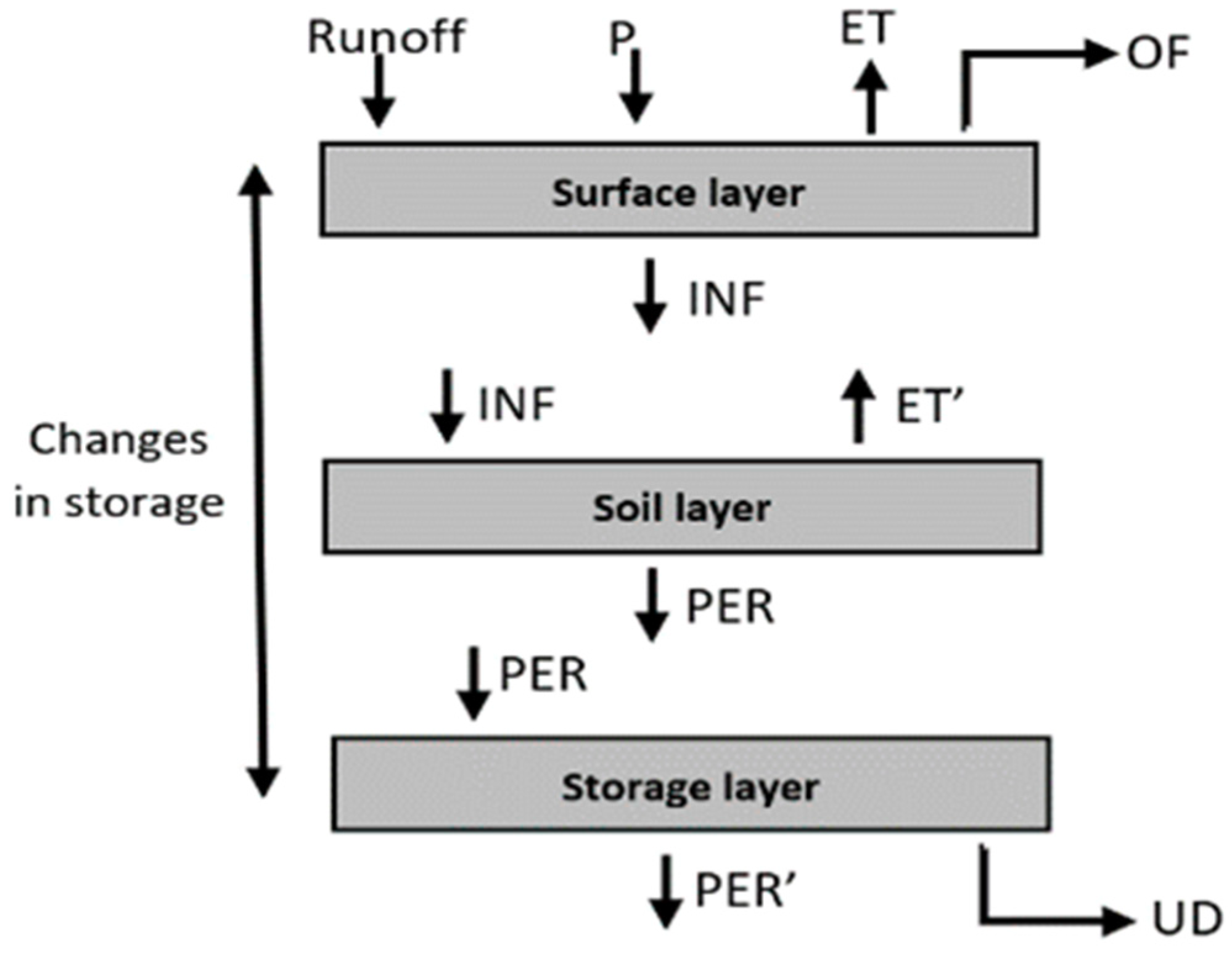
3.3.2. Infiltration-Based BMPs
- (a)
- Infiltration-based BMPs with both soil layer and storage layers: Porous pavement, Grass swale (with surface layer), Bioretention (with surface layer), Sand filter (non-surface);
- (b)
- Infiltration-based BMPs with storage layer but without soil layer: Dry well (with surface layer), Infiltration trench, Sand filter (surface);
- (c)
- Infiltration-based BMPs with soil layer but without storage layer: Vegetated filter strip, Rain garden (with surface layer), Box tree (with surface layer);
- (d)
- Infiltration-based BMPs with neither soil layer nor storage layer: Infiltration basin, wetland (surface/ponding layer only).
3.3.3. Storage-Based BMPs
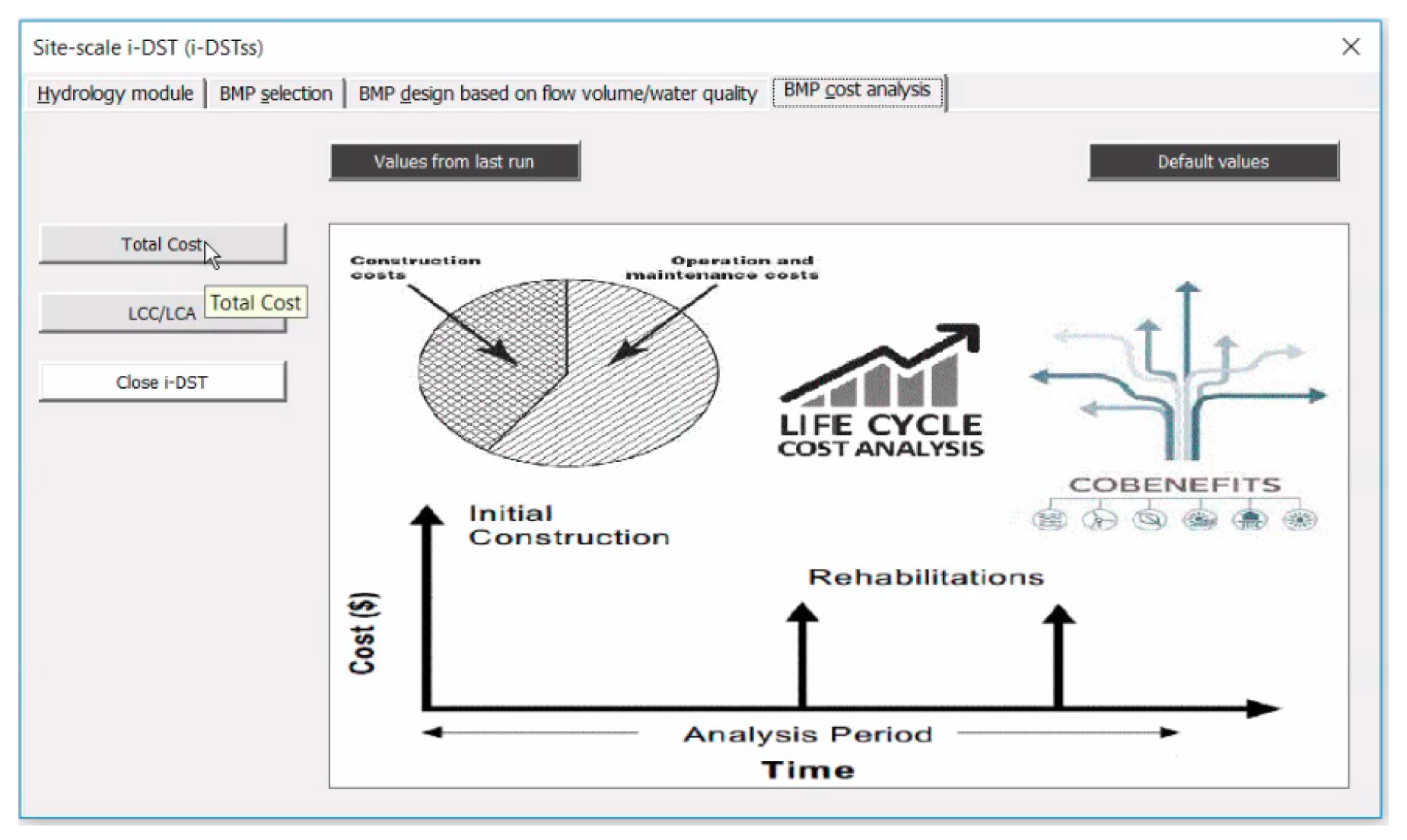
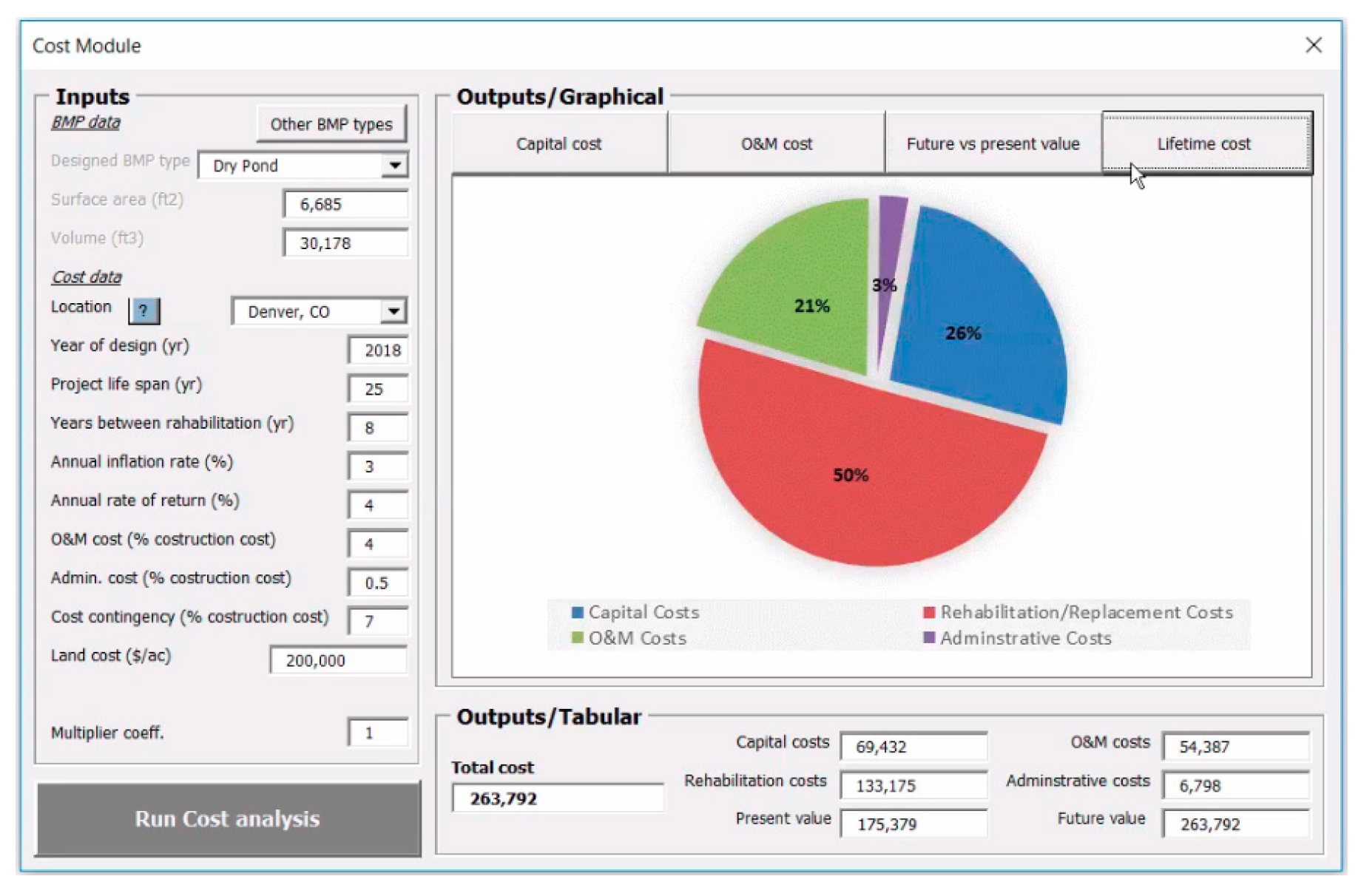
3.4. Cost Module
4. Verification of Component Modules
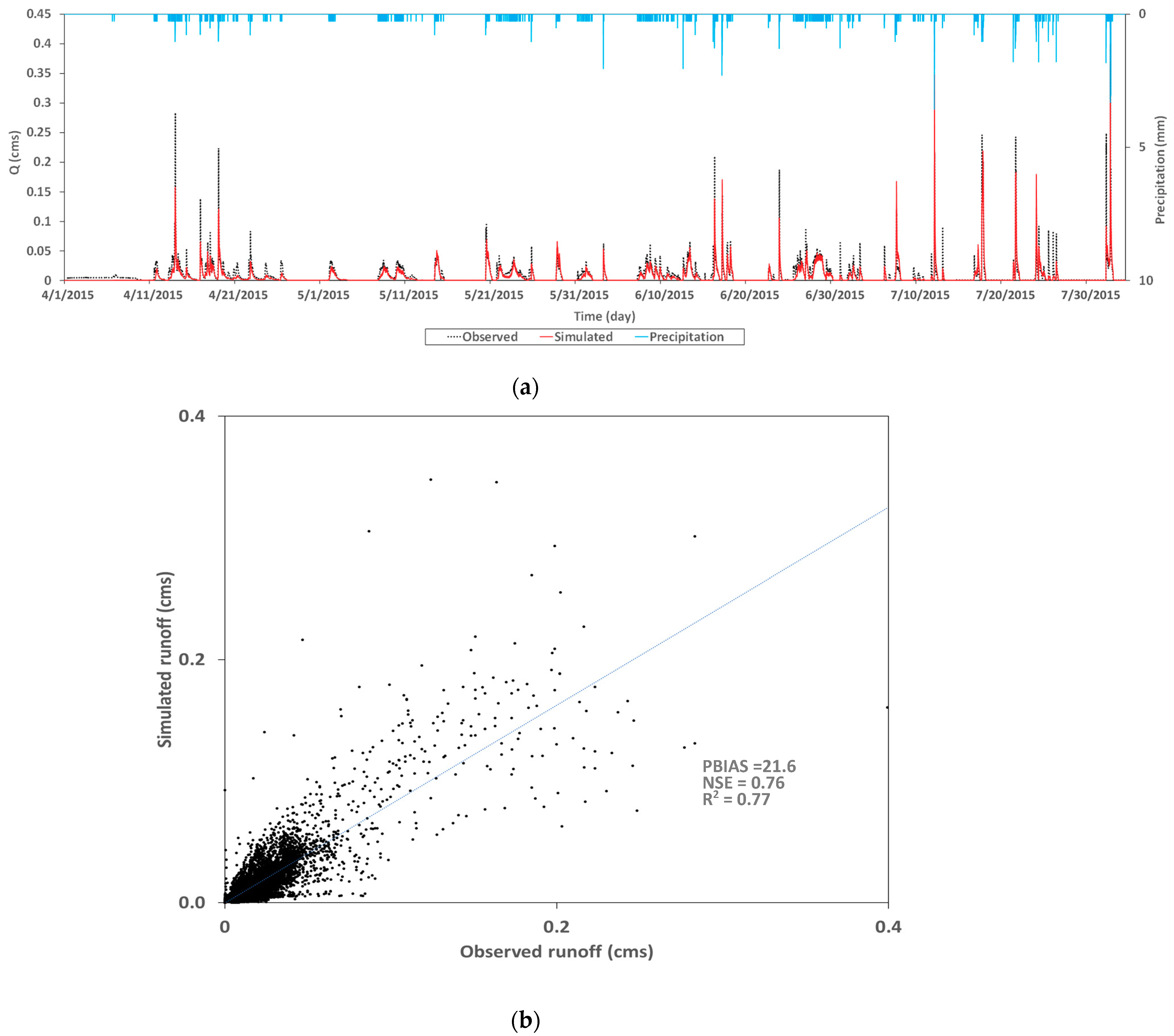
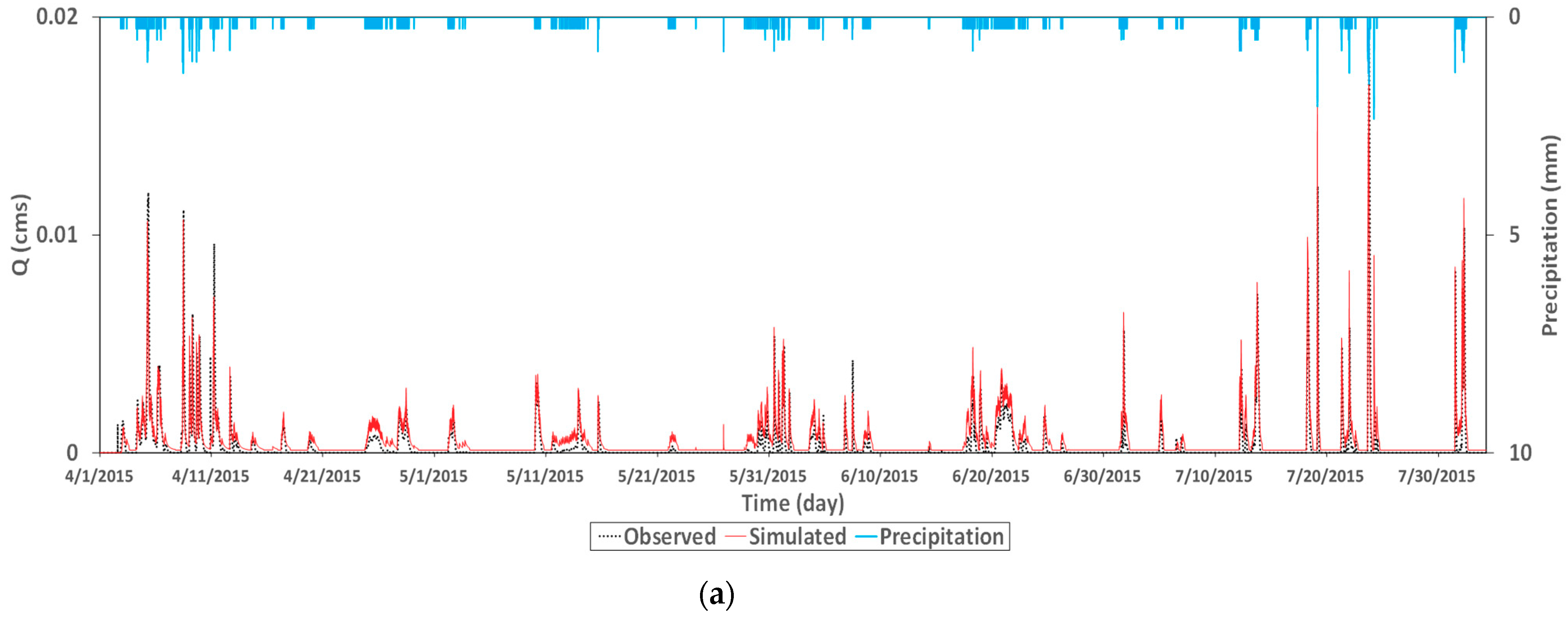
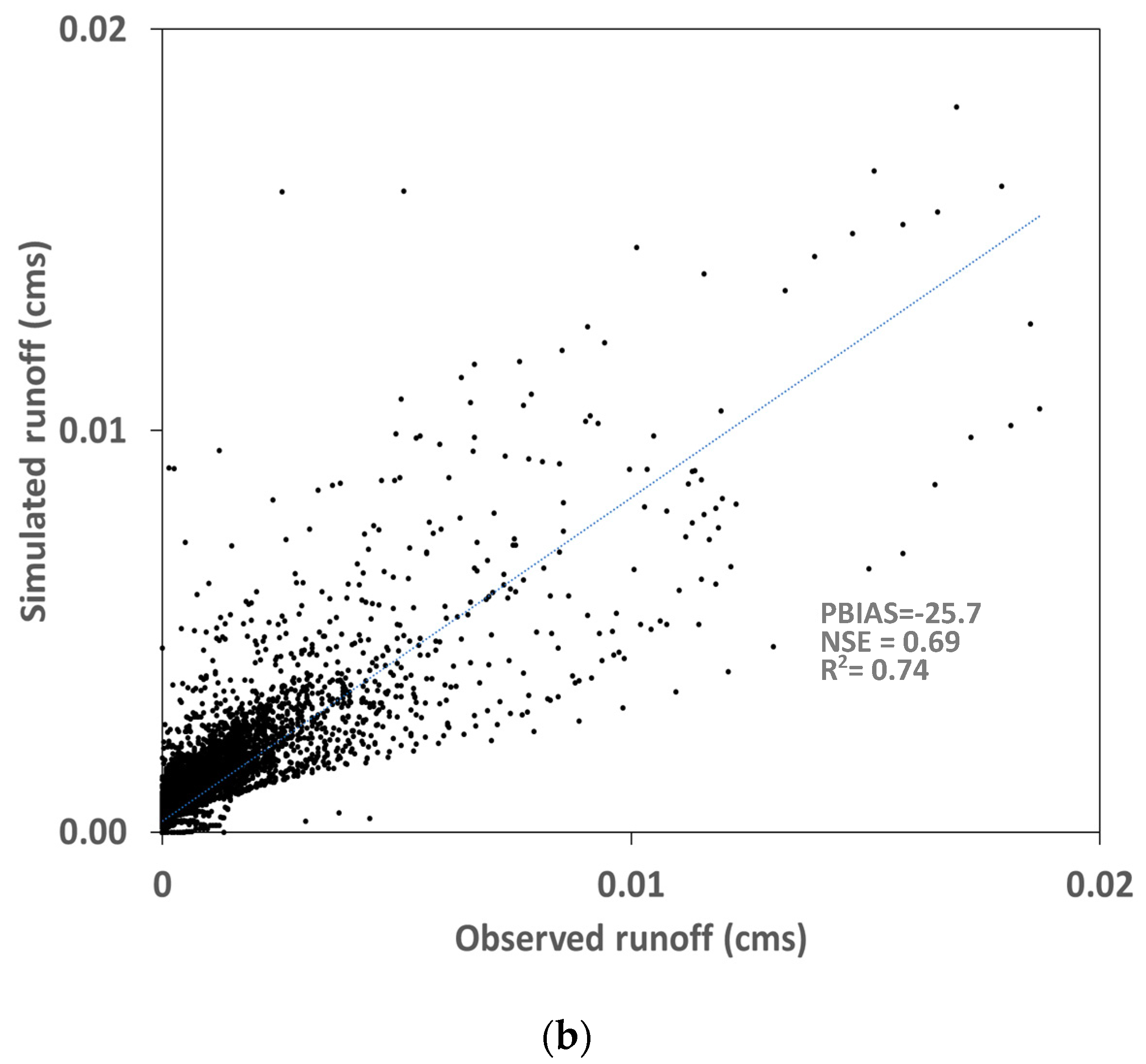
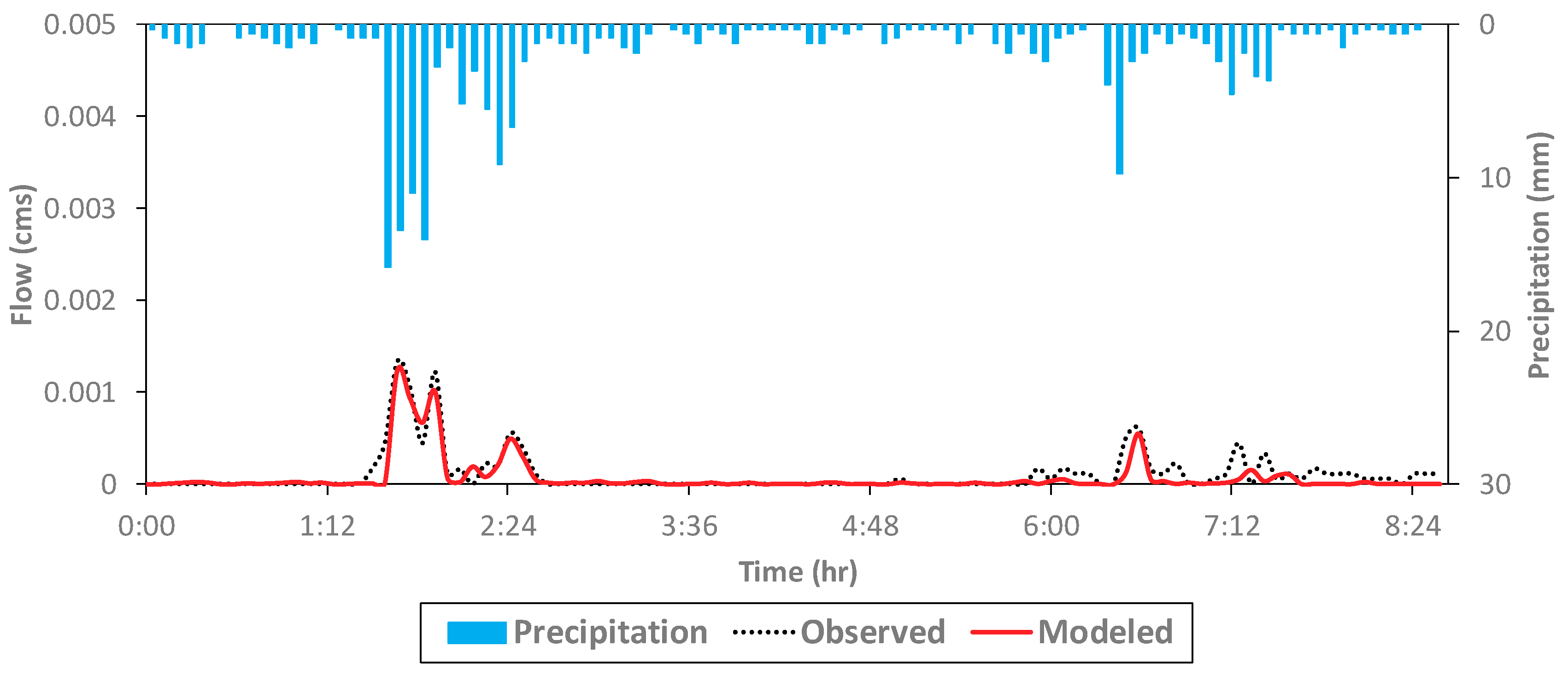
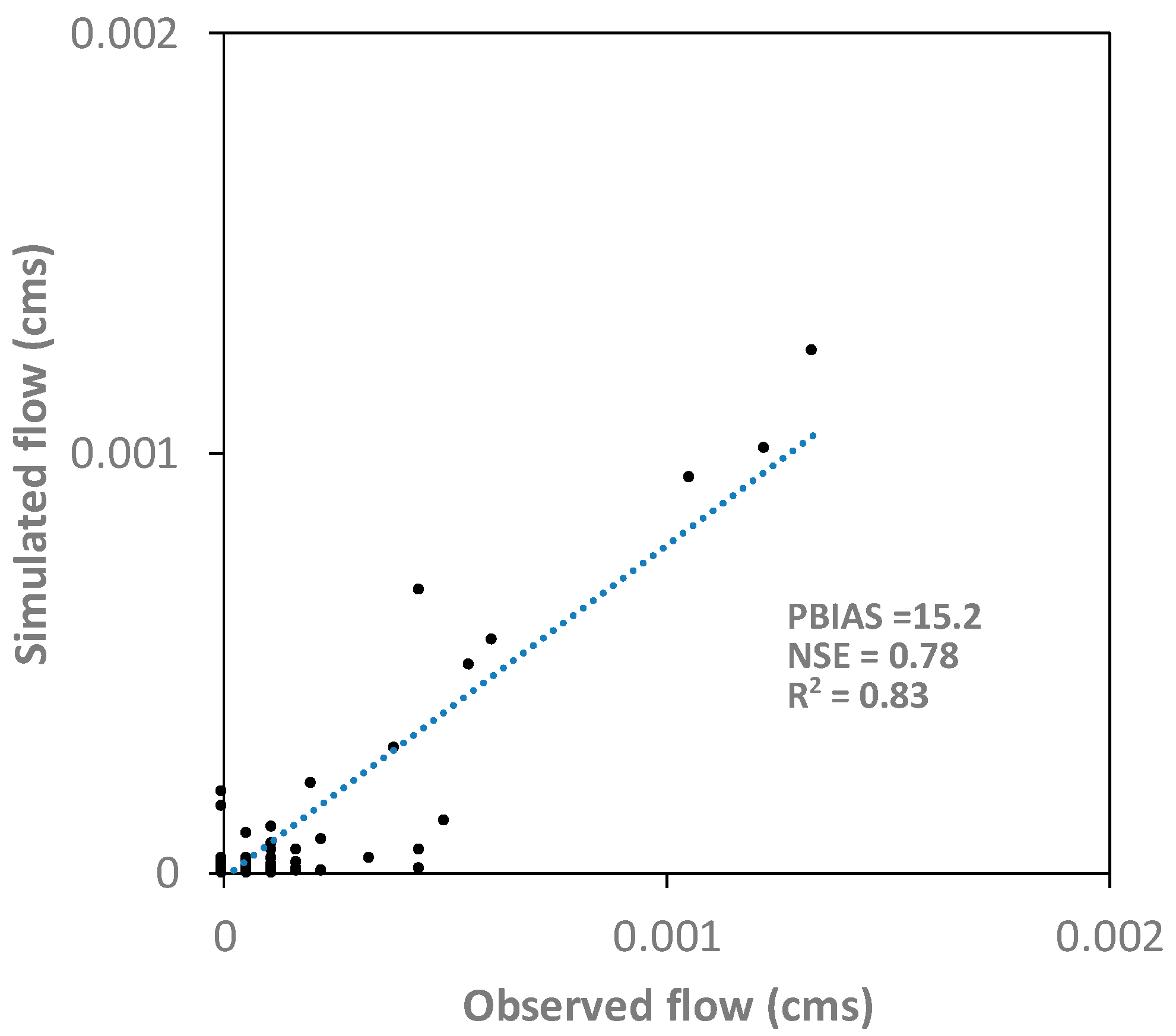
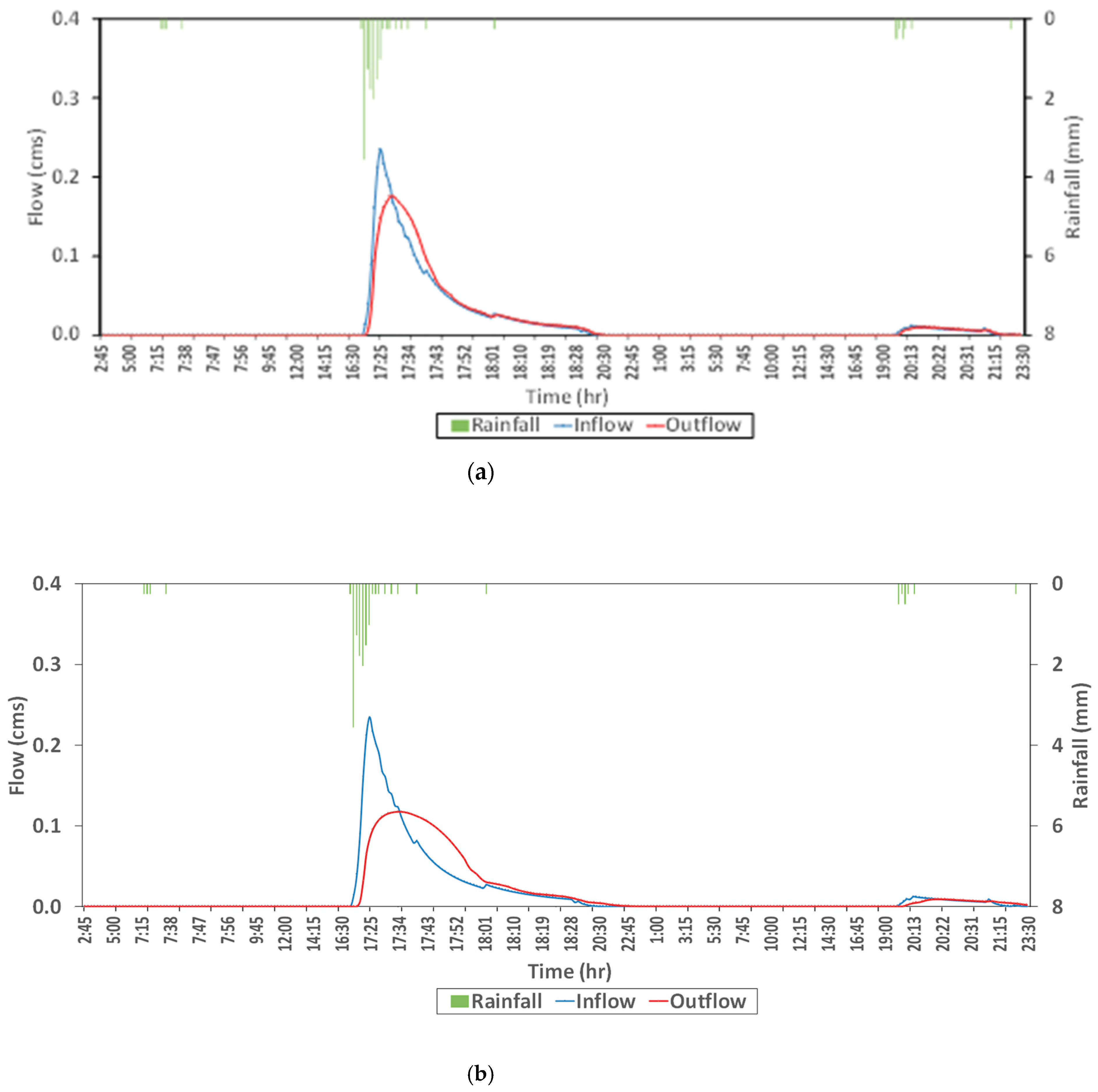
4.1. Hydrology Module
4.2. BMP Selection Scenario Analysis
4.3. BMP Sizing Module
4.3.1. Green Roof System
4.3.2. Infiltration-Based BMPs
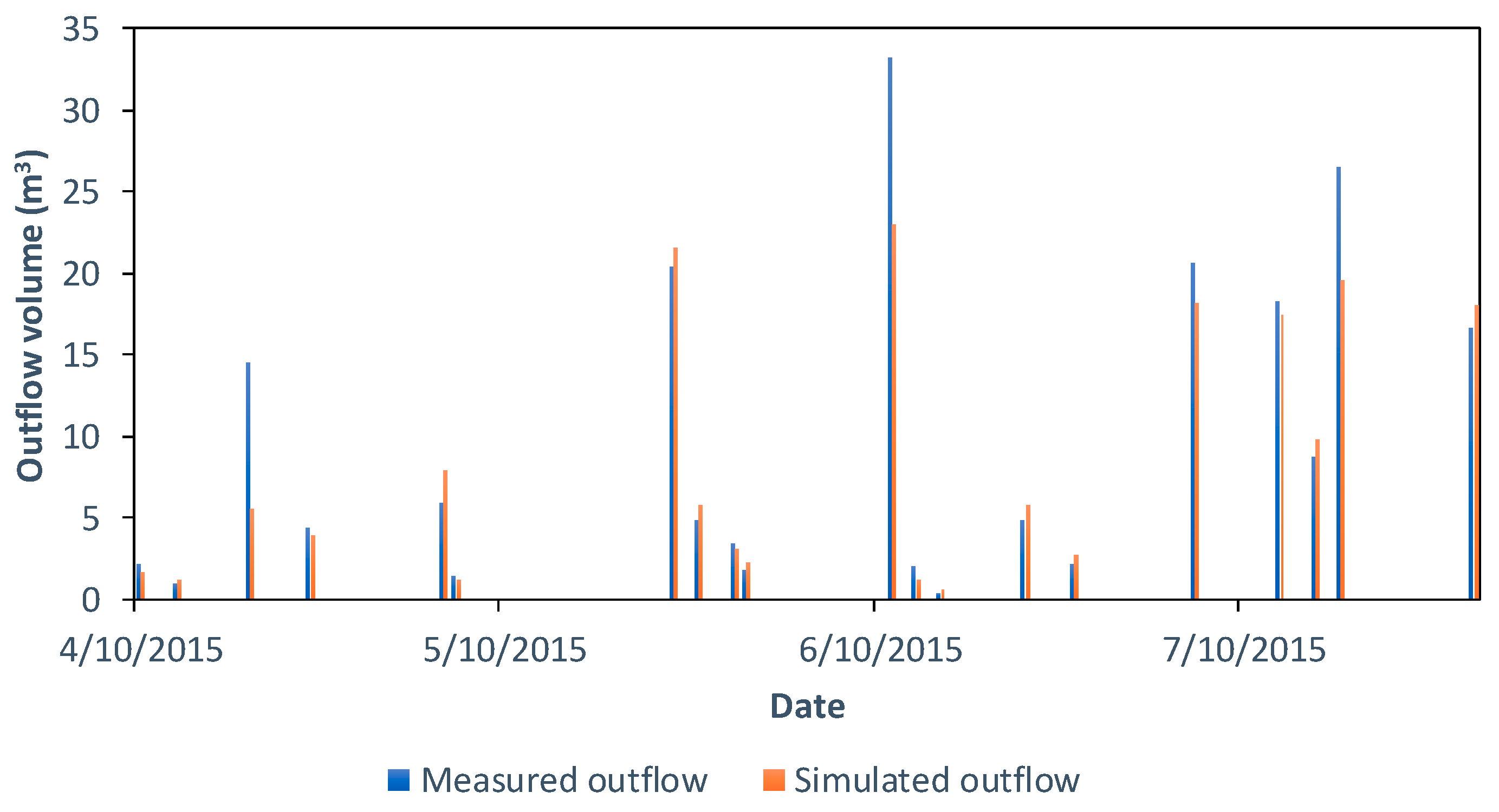
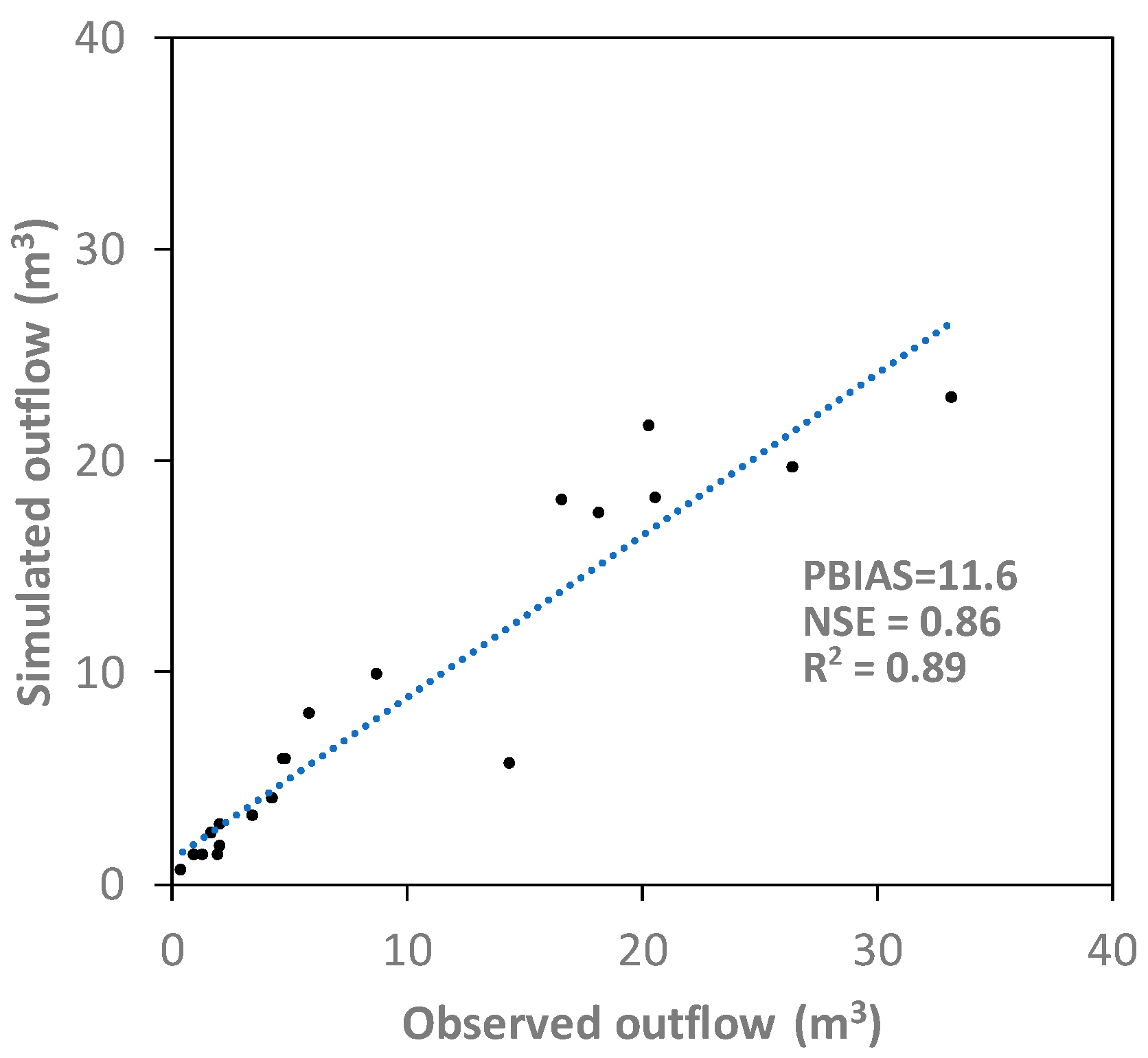
4.3.3. Storage-Based BMPs
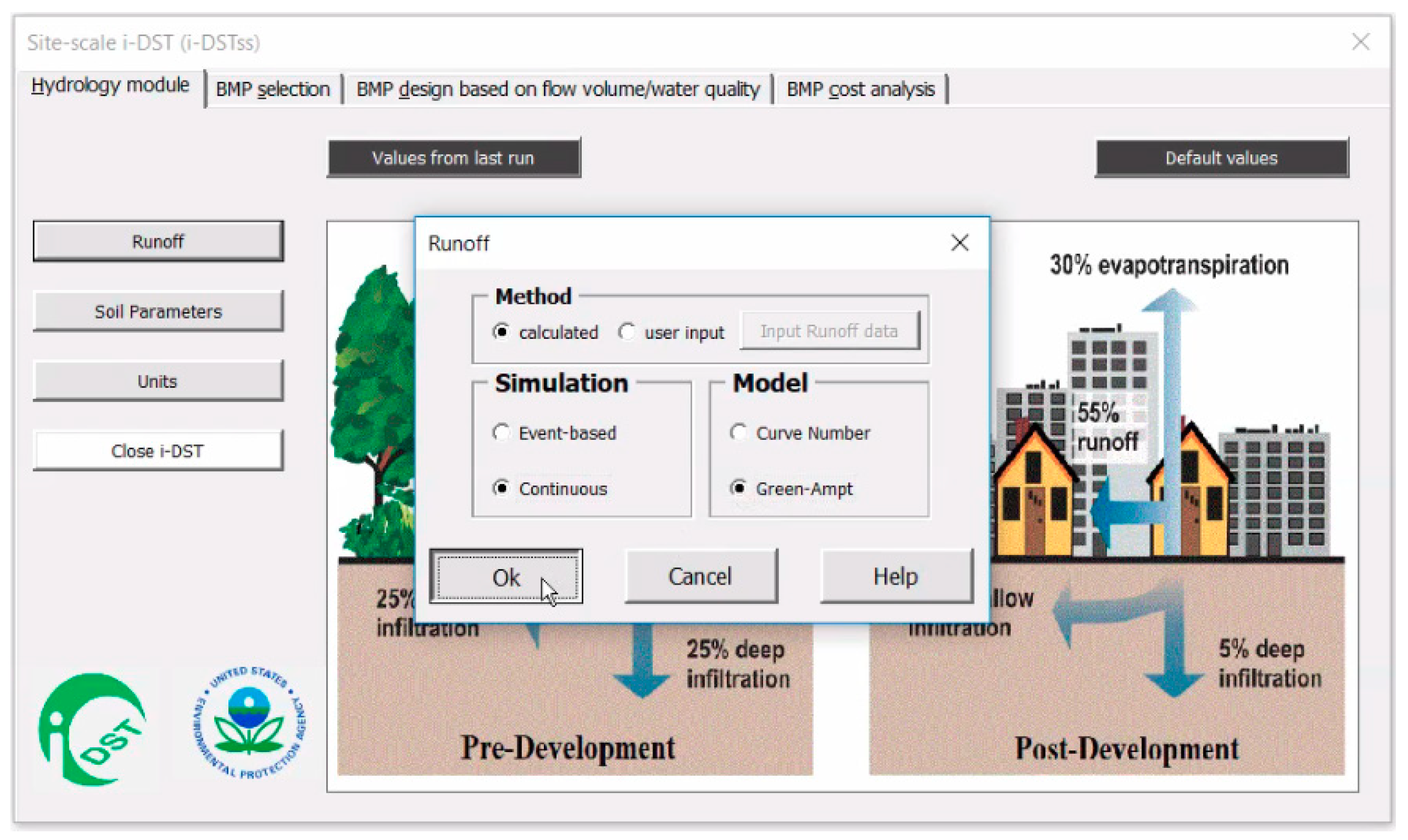
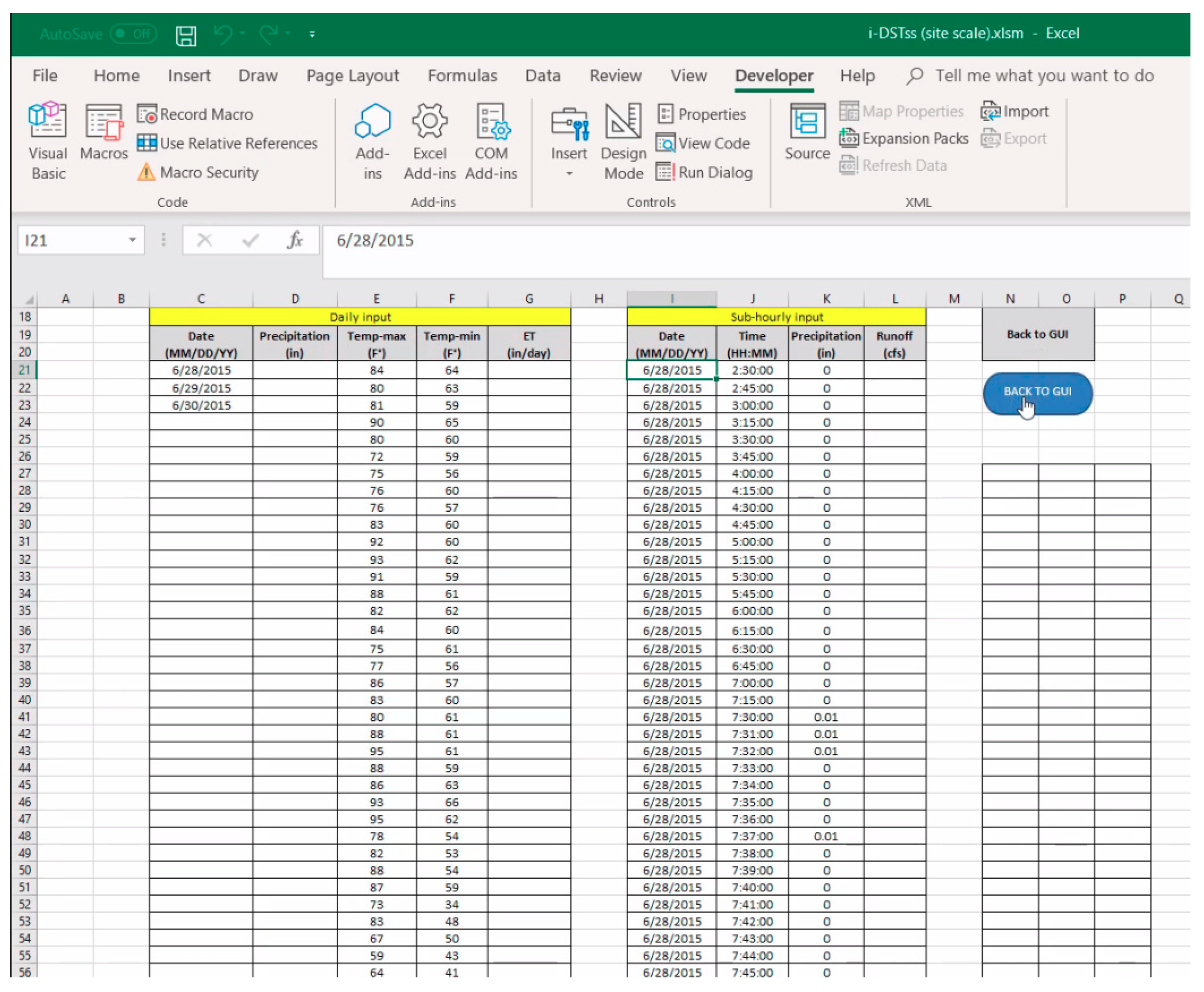
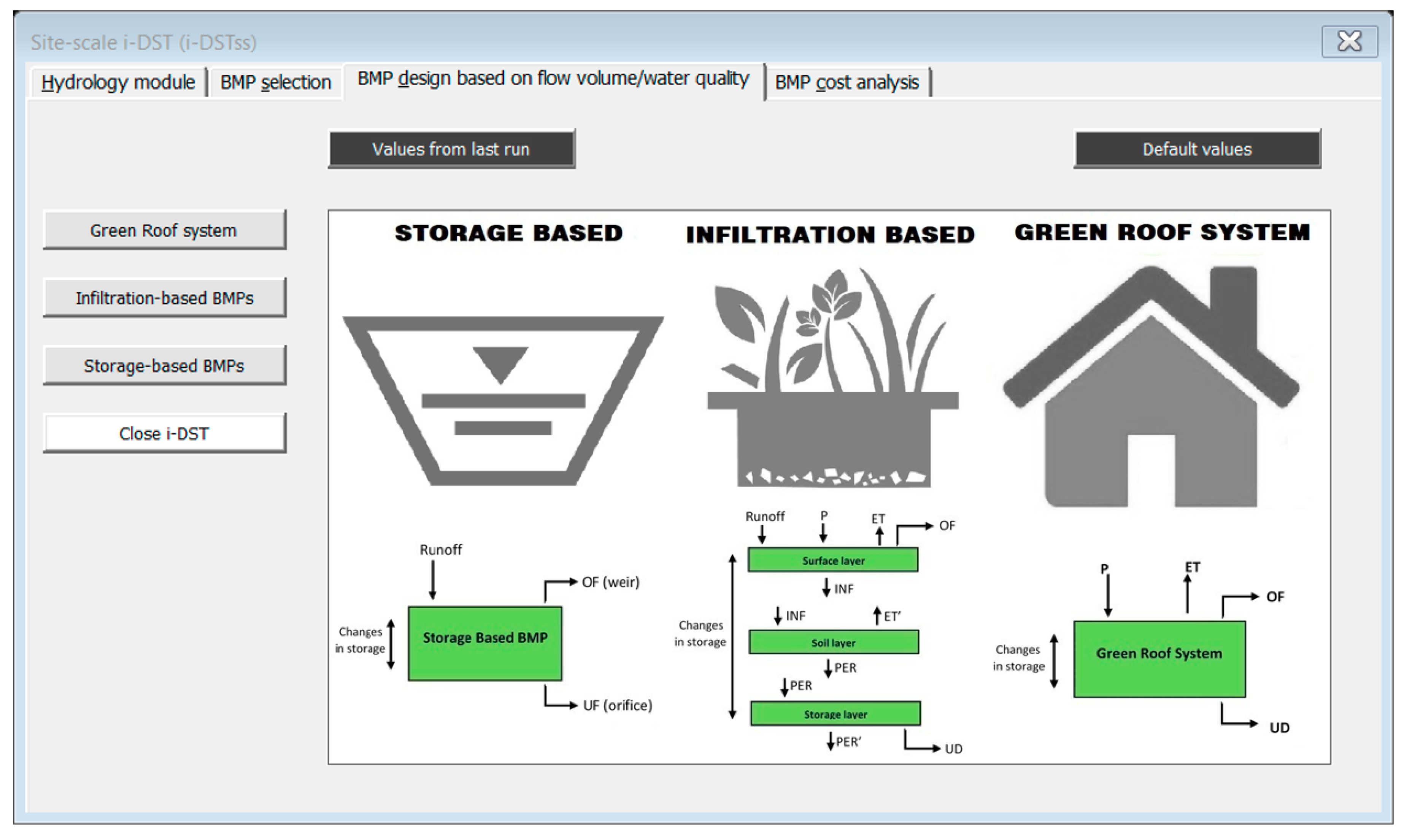
5. The User Interface
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Procedures
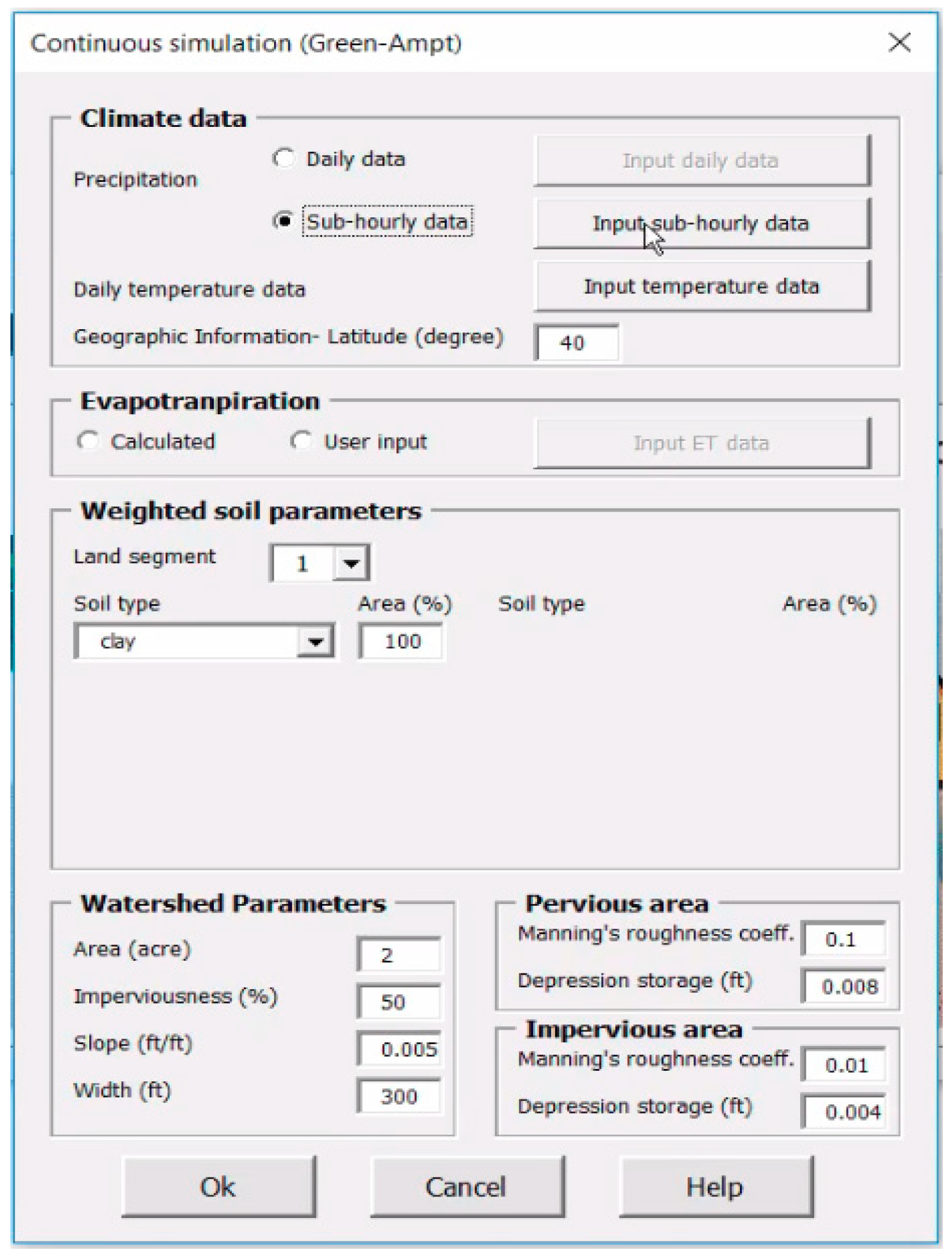
Appendix A1. Hydrology Module
Appendix A1.1. Green-Ampt Method:
- Step 1: Calculate precipitation intensity, i (mm/h)where P (mm) is incremental precipitation, is time step and i (mm/h) is precipitation intensity.
- Step 2: Calculate cumulative infiltration, [37]where , is saturated hydraulic conductivity, (mm) is suction head, IMD is initial soil moisture deficit calculated as:where and are saturated and initial soil water content respectively.
- Step 3: Calculate infiltration rate, [32]
- Step 4: Update soil moisture account [20]
- Case 1: If there is precipitation input (P ≠ 0), the soil moisture deficit (IMD) is updated using Equation (A5) below.where is the soil moisture deficit at the end of a time step and is the soil moisture deficit at beginning of the time step.
- Case 2: If there is no precipitation input (P = 0), then the soil moisture deficit (IMD) is updated using Equation (A6) below.where is residual soil water content, and is moisture deficit recovery constant calculated as: .
- Step 5: Calculate evapotranspiration
- Step 6: Calculate the rainfall excess
- Step 7: Calculate ponding depth [20]
- Step 8: Calculate overland flow/runoff [20]
Appendix A1.2. Curve Number Method:
- Step 1: Calculate precipitation intensity, i (mm/h)
- Step 2: Calculate cumulative infiltration F (mm) [20]where p (mm) is cumulative precipitation and S is retention parameter calculated as [33]:where is composite Curve Number calculated using Equation (A34) below.where , are Curve Number and area for ith segment respectively and n is number of total segments.
- Step 3: Calculate infiltration rate f (mm/h)
- Step 4: Update retention parameter [20]
- Case 1: If there is precipitation input (P ≠ 0), the retention parameter is updated using Equation (A36) below.
- Case 2: If there is no precipitation input (P = 0), then the retention parameter is updated using Equation (A37) below.
Appendix A2. BMP Selection Module
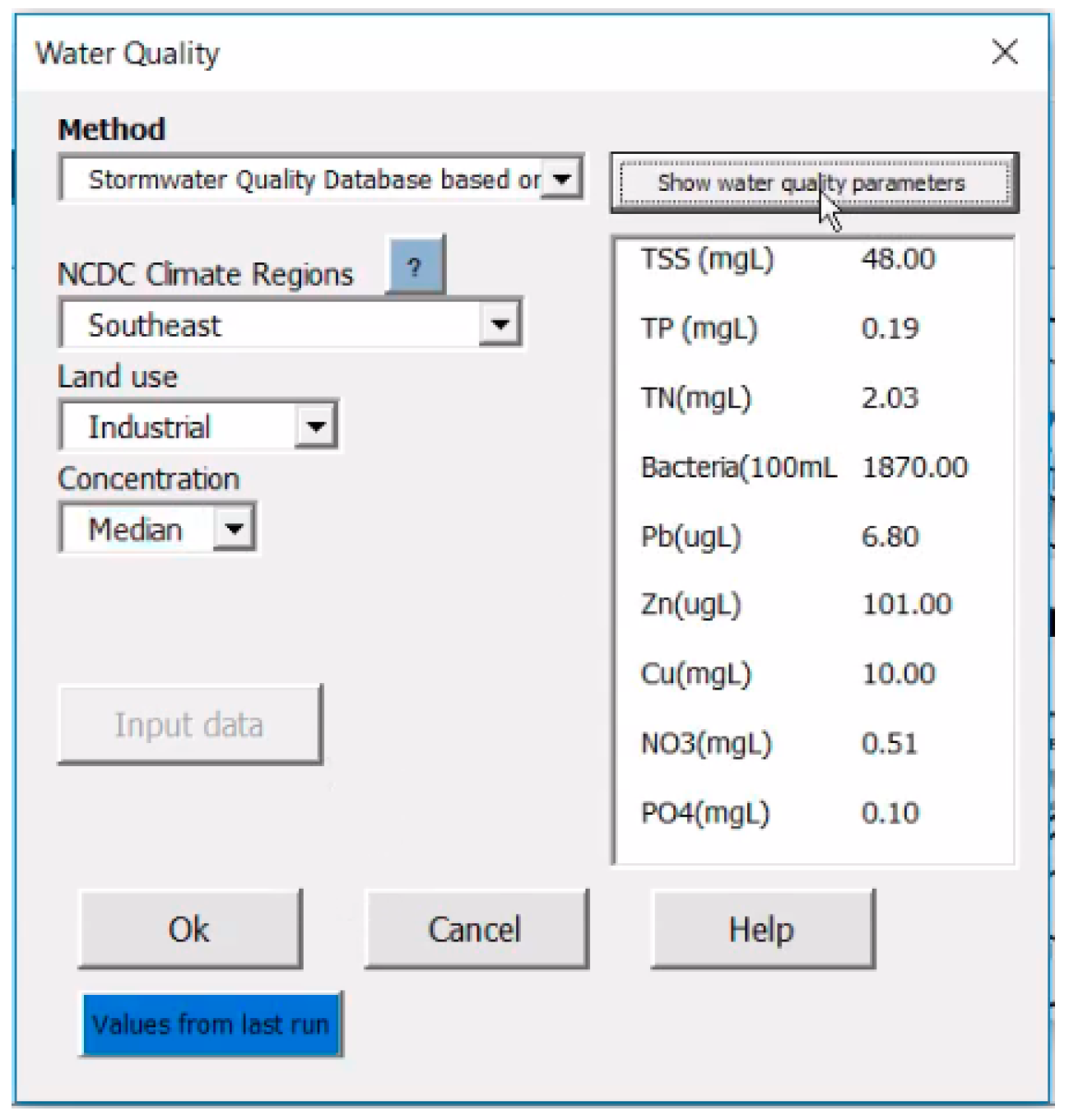
Appendix A2.1. Input Water Quality
Appendix A2.2. Target Water Quality
Appendix A2.3. BMP Removal Efficiency
Appendix A3. BMP Sizing Module
Appendix A3.1. Green-Roof System
Updating water content of media:
Calculate runoff flow from green roof:
Appendix A3.2. Infiltration-Based BMPs
- , this suggest that suction is greater than gravity and water is held tightly with the soil, thus, percolation does not occur.
- where is saturated hydraulic conductivity, is decay constant typically in the range of 5 to 15, is soil moisture content at saturation, is soil moisture content at filed capacity, and is soil moisture content during the time interval [20].
Appendix A3.3. Storage-Based BMPs
Appendix B. Demonstration of Operation of the Tool



- (a)
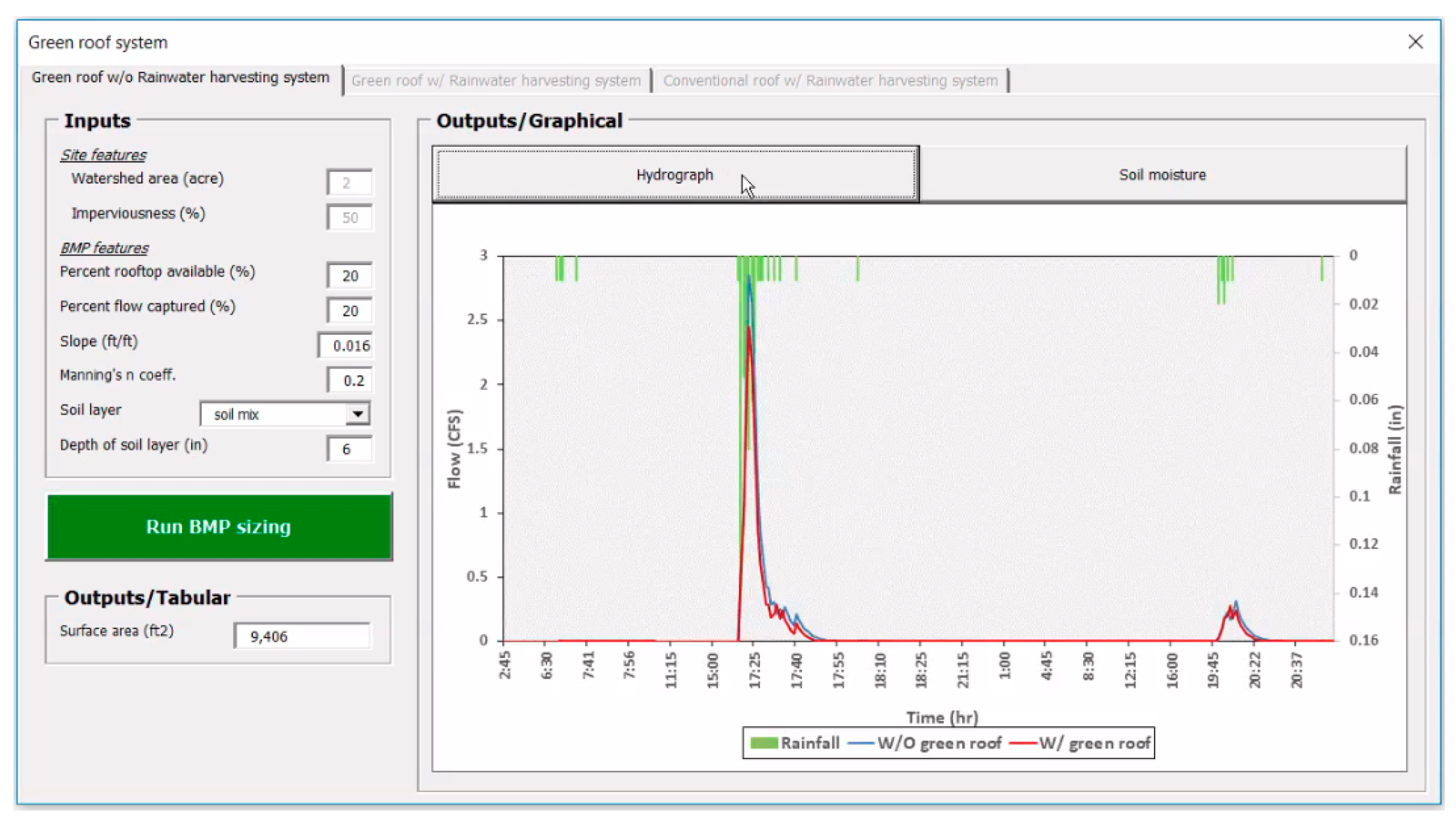
- Green roof system: In the “Green roof system”, the goal is to determine how much area has to be under the green roof to achieve a specific percent flow reduction. The area of the watershed, percent imperviousness and the runoff hydrograph come from the hydrology module. As shown in Figure A16, by running the tool for 20 percent flow reduction, the surface area that has to be under a green roof is calculated. User may also view the hydrographs from the graphical output. In the Figure A16 the blue line shows the hydrograph without green roof and the red line shows the hydrograph with green roof.Figure A16. Output hydrograph for green roof system.
- (b)
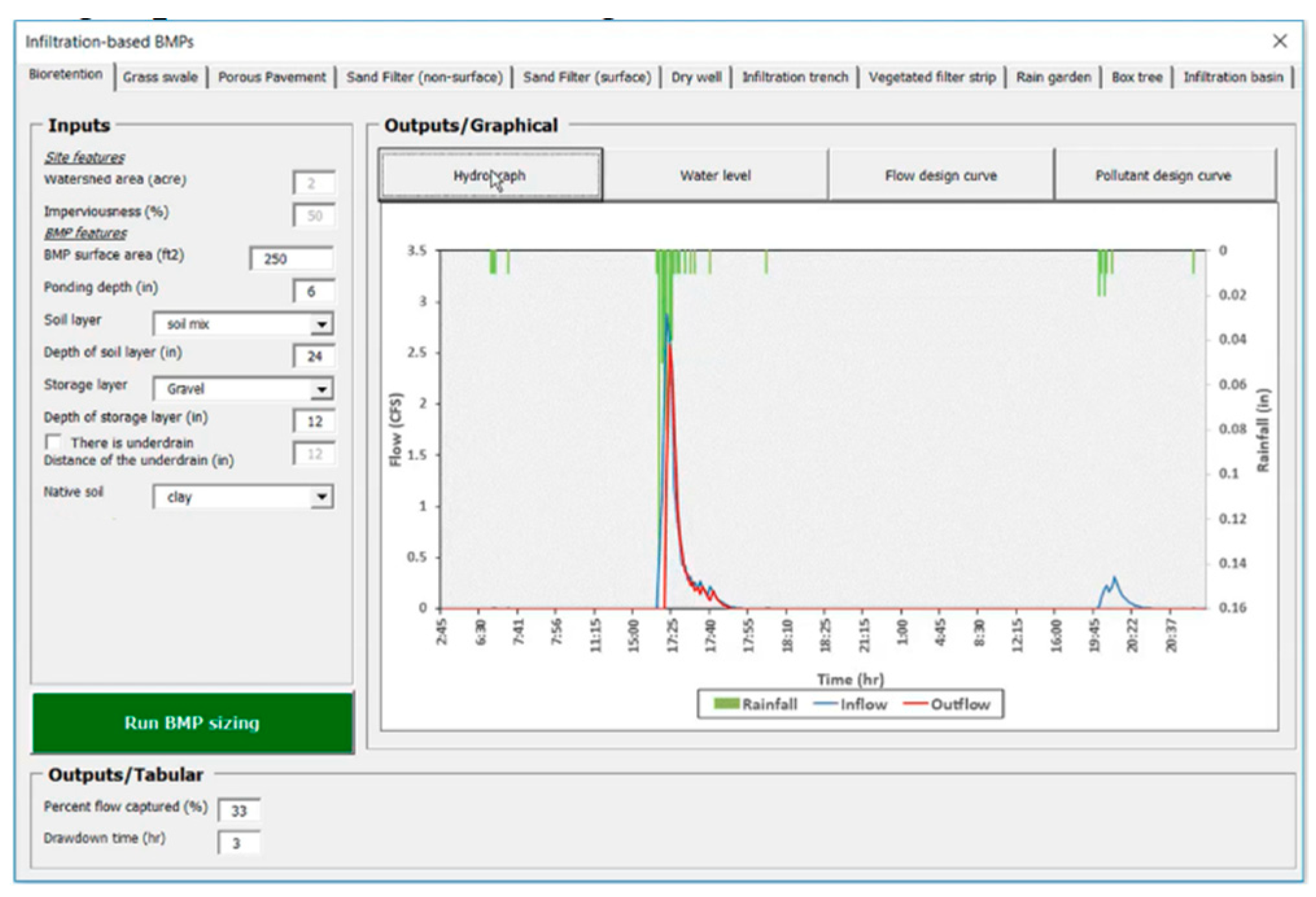
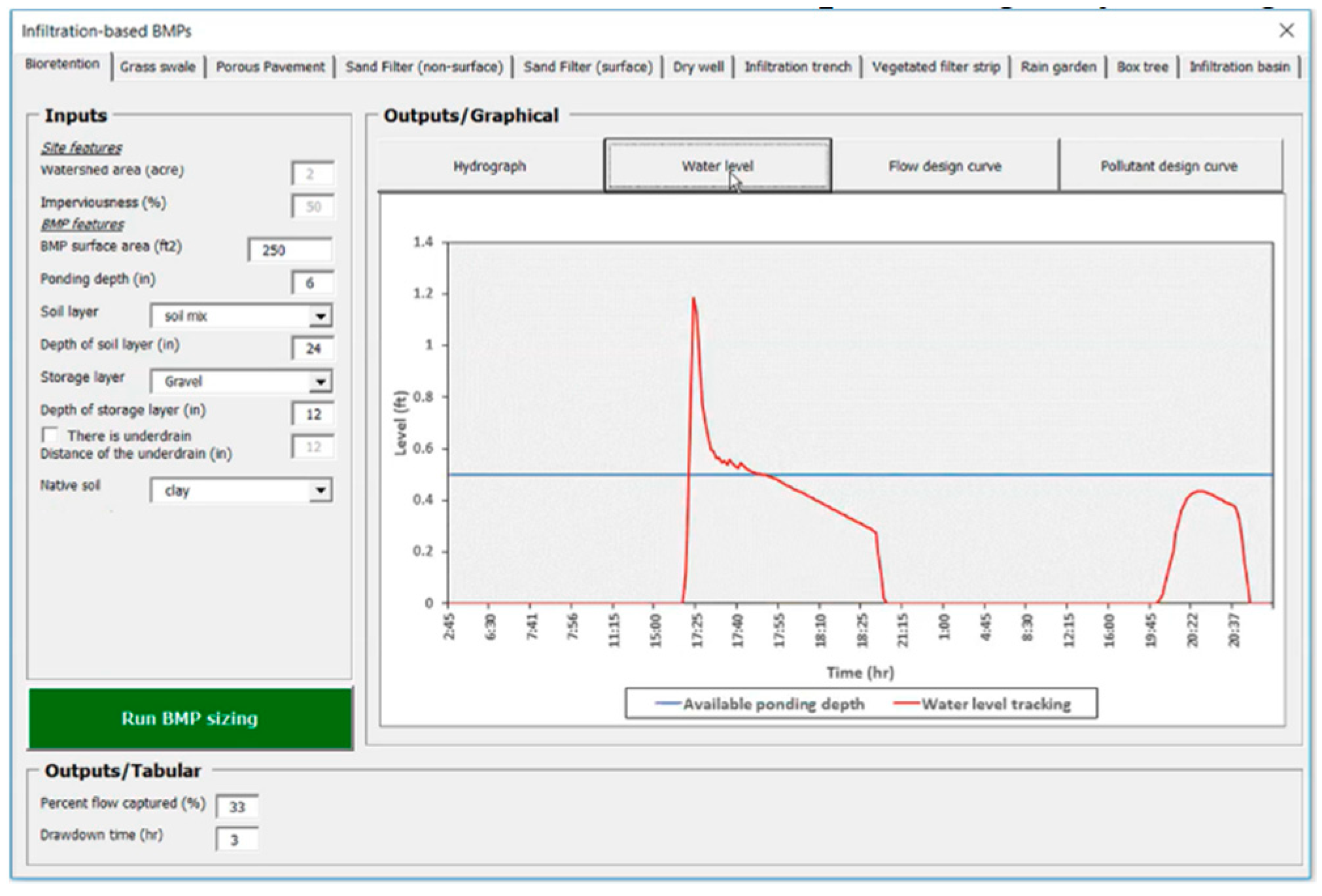
- Infiltration-based BMPs: The next group of BMPs are infiltration-based BMPs. For the infiltration-based BMPs, the user inputs the area of the BMP and the tool will calculate the percent capture and drawdown time. The tool also shows the graphical outputs of inflow and outflow hydrographs as shown in Figure A17.Figure A17. Output hydrograph for infiltration-based BMPs.The tool also tracks the water level inside the surface (ponding) layer (Figure A18).Figure A18. Water level tracking in infiltration-based BMPs.
- (c)
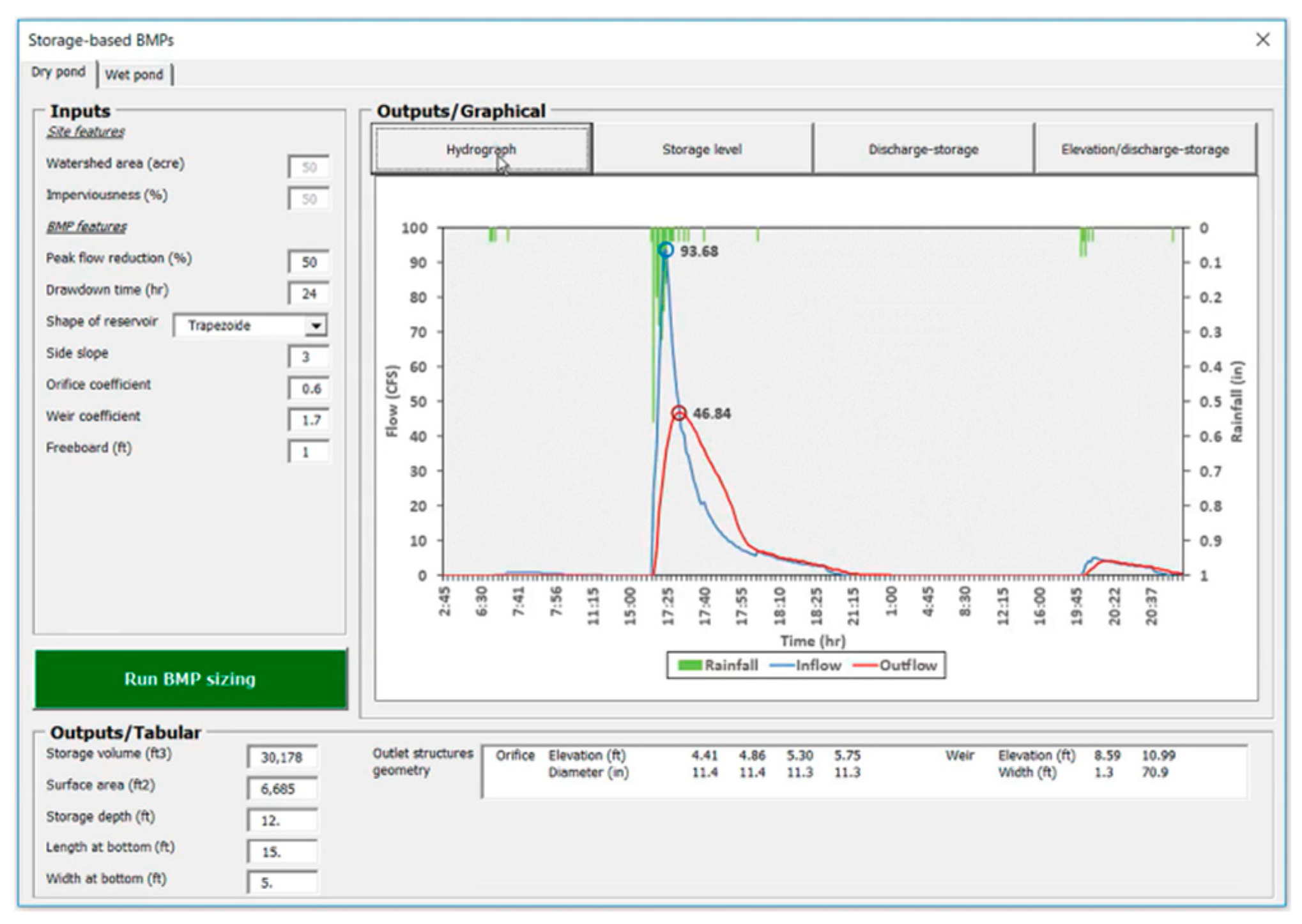
- Storage-based BMPs: The third group of BMPs are storage-based BMPs such as detention pond and retention pond. Since ponds usually are used for stormwater management for bigger area, the area of watershed has been increased in this scenario. The input is percent peak flow reduction and the output is geometry of the pond and geometry of the outlet structures. By inputting 50 percent peak flow reduction and other input parameters, the tool determines optimal size/geometries of pond and outlet structures through an optimization process. By minimizing the size/volume of the pond, the cost will be minimized. Users can view inflow and outflow hydrographs and the peak flow reduction in the graphical output section as shown in Figure A19.Figure A19. Output hydrograph for storage-based BMPs.
References
- Tetra Tech. User’s Guide Spreadsheet Tool for the Estimation of Pollutant Load (STEPL); Tetra Tech, Inc.: Fairfax, VA, USA, 2011. [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Dietz, M.E. Low impact development practices: A review of current research and recommendations for future directions. Water Air Soil Pollut. 2007, 186, 351–363. [Google Scholar] [CrossRef]
- Brabec, E.; Schulte, S.; Richards, P.L. Impervious surfaces and water quality: A review of current literature and its implications for watershed planning. J. Plan. Lit. 2002, 16, 499–514. [Google Scholar] [CrossRef]
- Montgomery, M. United Nations Population Fund: State of world population 2007: Unleashing the potential of urban growth. Popul. Dev. Rev. 2007, 33, 639–641. [Google Scholar]
- Parkinson, J. Drainage and stormwater management strategies for low-income urban communities. Environ. Urban. 2003, 15, 115–126. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L. SUDS, LID, BMPs, WSUD and more–The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Medina, F.M.; Bonnaud, E.; Vidal, E.; Tershy, B.R.; Zavaleta, E.S.; Donlan, C.J.; Keitt, B.S.; le Corre, M.; Horwath, S.V.; Nogales, M. A global review of the impacts of invasive cats on island endangered vertebrates. Glob. Chang. Biol. 2011, 17, 3503–3510. [Google Scholar] [CrossRef]
- Coffman, L.; Cheng, M.S.; Weinstein, N.; Clar, M. Low-Impact Development Hydrologic Analysis and Design. In Water Resources and the Urban Environment; ASCE: New York, NY, USA, 1998. [Google Scholar]
- Dietz, M.E.; Clausen, J.C. Stormwater runoff and export changes with development in a traditional and low impact subdivision. J. Environ. Manag. 2008, 87, 560–566. [Google Scholar] [CrossRef]
- Khader, O.; Montalto, F.A. Development and Calibration of a High Resolution SWMM Model for Simulating the Effects of LID Retrofits on the Outflow Hydrograph of a Dense Urban Watershed. In Low Impact Development for Urban Ecosystem and Habitat Protection; American Society of Civil Engineers: Reston, VA, USA, 2009. [Google Scholar] [CrossRef]
- US Environmental Protection Agency (EPA). Low Impact Development (LID): A Literature Review; US Environmental Protection Agency Office of Water: Washington, DC, USA, 2000. [Google Scholar]
- Montalto, F.; Behr, C.; Alfredo, K.; Wolf, M.; Arye, M.; Walsh, M. Rapid assessment of the cost-effectiveness of low impact development for CSO control. Landsc. Urban Plan. 2007, 82, 117–131. [Google Scholar] [CrossRef]
- Tu, M.C. A New Method to Assess. Best Management Practice Efficiency to Optimize Storm Water Management. Ph.D. Thesis, Texas A & M University, College Station, TX, USA, 2014. Available online: http://hdl.handle.net/1969.1/153810 (accessed on 16 December 2014).
- Connor, T.O.; Sullivan, D.; Clar, M.; Barfield, B. Considerations in the design of treatment best management practices (BMPs) to improve water quality. Proc. Water Environ. Fed. 2003, 2003, 1186–1205. [Google Scholar] [CrossRef]
- Fraley-McNeal, L.; Schueler, T.; Winer, R. National Pollutant Removal Performance Database, Version 3; Center for Watershed Protection: Ellicott City, MD, USA, 2007; pp. 1–10. [Google Scholar]
- Ellis, J. Infiltration systems: A sustainable source—control option for urban stormwater quality management? Water Environ. J. 2000, 14, 27–34. [Google Scholar] [CrossRef]
- Reynolds, S.K.; Pomeroy, C.A.; Rowney, A.C.; Rowney, C.M. Linking Stormwater BMP Systems Water Quality and Quantity Performance to Whole Life Cycle Cost to Improve BMP Selection and Design. In World Environmental and Water Resources Congress 2012: Crossing Boundaries, Albuquerque, NM, USA, 20–24 May 2012; Loucks, E.D., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2012. [Google Scholar]
- Guo, Q.; Correa, C.A. The Impacts of Green Infrastructure on Flood Level Reduction for the Raritan River: Modeling Assessment. In World Environmental and Water Resources Congress 2013: Showcasing the Future, Cincinnati, OH, USA, 19–23 May 2013; Patterson, C.L., Struck, S.D., Murray, D.J., Jr., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- James, W.; Rossman, L.A.; James, W.R.C. User’s Guide to SWMM 5; CHI: Guelph, ON, Canada, 2010. [Google Scholar]
- Pitt, R.; Voorhees, J. SLAMM, the source loading and management model. In Wet-Weather Flow in the Urban Watershed: Technology and Management; CRC Press: Boca raton, FL, USA, 2002; pp. 103–139. [Google Scholar]
- Lai, F.H.; Zhen, J.; Riverson, J.; Alvi, K.; Shoemaker, L. Multiple Watershed Scales Approach for Placement of Best Management Practices in SUSTAIN. In World Environmental and Water Resources Congress 2009: Great Rivers; Kansas City, MO, USA, 17–21 May 2009; Starrett, S., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2009. [Google Scholar]
- Tang, Z.; Engel, B.; Pijanowski, B.; Lim, K. Forecasting land use change and its environmental impact at a watershed scale. J. Environ. Manag. 2005, 76, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.H.; Fletcher, T.D.; Duncan, H.P.; Jenkins, G.A. Modelling urban stormwater treatment—A unified approach. Ecol. Eng. 2006, 27, 58–70. [Google Scholar] [CrossRef]
- Rossman, L.A.; Bernagros, J.T. National Stormwater Calculator User’s Guide–Version 1.2. 0.1; EPA: Washington, DC, USA, 2014. [Google Scholar]
- Minnesota Stormwater Manual, Overview of Minimal Impact Design Standards (MIDS); Minnesota Pollution Control Agency: Rochester, MN, USA, 2016.
- California State University (Sacramento). California Phase II LID Sizing Tool Documentation Manual; California State University: Sacramento, CA, USA, 2019. [Google Scholar]
- Johnson, R.; Sample, D. A semi-distributed model for locating stormwater best management practices in coastal environments. Environ. Model. Softw. 2017, 91, 70–86. [Google Scholar] [CrossRef]
- Alamdari, N.; Sample, D.J. A multiobjective simulation-optimization tool for assisting in urban watershed restoration planning. J. Clean. Prod. 2019, 213, 251–261. [Google Scholar] [CrossRef]
- King, K.W.; Arnold, J.; Bingner, R. Comparison of Green-Ampt and curve number methods on Goodwin Creek watershed using SWAT. Trans. ASAE 1999, 42, 919. [Google Scholar] [CrossRef]
- Doherty, J.; Christensen, S. Use of paired simple and complex models to reduce predictive bias and quantify uncertainty. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Boughton, W. A review of the USDA SCS curve number method. Soil Res. 1989, 27, 511–523. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Fleming, P. A diurnal distribution function for daily evaporation. Water Resour. Res. 1970, 6, 937–942. [Google Scholar] [CrossRef]
- Liu, S.; Graham, W.D.; Jacobs, J.M. Daily potential evapotranspiration and diurnal climate forcings: Influence on the numerical modelling of soil water dynamics and evapotranspiration. J. Hydrol. 2005, 309, 39–52. [Google Scholar] [CrossRef]
- Barry, D.; Parlange, J.Y.; Li, L.; Jeng, D.S.; Crapper, M. Green–Ampt approximations. Adv. Water Resour. 2005, 28, 1003–1009. [Google Scholar] [CrossRef]
- Ali, S.; Islam, A.; Mishra, P.; Sikka, A.K. Green-Ampt approximations: A comprehensive analysis. J. Hydrol. 2016, 535, 340–355. [Google Scholar] [CrossRef]
- Mizumura, K. Analytical Solutions of Nonlinear Kinematic Wave Model. J. Hydrol. Eng. 2006, 11, 539–546. [Google Scholar] [CrossRef]
- Pitt, R.; Maestre, A.; Clary, J. The National Stormwater Quality Database (NSQD, Version 4.02); Department of Civil and Environmental Engineering; University of Alabama: Tuscaloosa, AL, USA, 2018. [Google Scholar]
- International Stormwater BMP Database. Developed by Wright Water Engineers, Inc. and Geosyntec Consultants for the Water Research Foundation (WRF), the American Society of Civil Engineers (ASCE)/Environmental and Water Resources Institute (EWRI), the American Public Works Association (APWA), the Federal Highway Administration (FHWA), and U.S. Environmental Protection Agency (EPA). 2018. Available online: http://www.bmpdatabase.org/download-master.html (accessed on 22 August 2018).
- Ma, G.; Geza, M.; Cath, T.Y.; Drewes, J.E.; Xu, P. iDST: An. integrated decision support tool for treatment and beneficial use of non-traditional water supplies–Part. II. Marcellus and Barnett Shale case studies. J. Water Process Eng. 2018, 25, 258–268. [Google Scholar] [CrossRef]
- Ravindran, A.R.; Warsing, D.P., Jr. Supply Chain Engineering: Models and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kasprzak, E.M.; Lewis, K.E. Pareto analysis in multiobjective optimization using the collinearity theorem and scaling method. Struct. Multi. Optim. 2001, 22, 208–218. [Google Scholar] [CrossRef]
- Feddes, R.; Zaradny, H. Model for simulating soil-water content considering evapotranspiration—Comments. J. Hydrol. 1978, 37, 393–397. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
- Sample, D.J.; Heaney, J.P.; Wright, L.T.; Fan, C.Y.; Lai, F.H.; Field, R. Costs of best management practices and associated land for urban stormwater control. J. Water Resour. Plan. Manag. 2003, 129, 59–68. [Google Scholar] [CrossRef]
- Heaney, J.P.; Sample, D.; Wright, L. Costs of Urban Stormwater Control; US Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 2002.
- California Stormwater Quality Association. California Stormwater BMP Handbook–New Development and Redevelopment; California Stormwater Quality Association: Menlo Park, CA, USA, 2003. [Google Scholar]
- Narayanan, A.; Pitt, R. Costs of Urban Stormwater Control Practices; Citeseer: Forest Grove, OR, USA, 2006. [Google Scholar]
- Selbig, W.R. Evaluation of leaf removal as a means to reduce nutrient concentrations and loads in urban stormwater. Sci. Total Environ. 2016, 571, 124–133. [Google Scholar] [CrossRef]
- Anand, S.; Mankin, K.R.; McVay, K.A.; Janssen, K.A.; Barnes, P.L.; Pierzynski, G.M. Calibration and Validation of ADAPT and SWAT for Field—Scale Runoff Prediction 1. J. Am. Water Resour. Assoc. 2007, 43, 899–910. [Google Scholar] [CrossRef]
- White, K.L.; Chaubey, I. Sensitivity analysis, calibration, and validations for a multisite and multivariable SWAT model 1. J. Am. Water Resour. Assoc. 2005, 41, 1077–1089. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources 1. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chu, T.; Shirmohammadi, A. Evaluation of the SWAT model’s hydrology component in the piedmont physiographic region of Maryland. Trans. ASAE 2004, 47, 1057. [Google Scholar] [CrossRef]
- Geza, M.; Poeter, E.P.; McCray, J.E. Quantifying predictive uncertainty for a mountain-watershed model. J. Hydrol. 2009, 376, 170–181. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Selbig, W.R.; Buer, N. Hydraulic, Water-Quality, and Temperature Performance of Three Types of Permeable Pavement under High Sediment Loading Conditions; US Geological Survey: Menlo Park, CA, USA, 2018.
- Druzdzel, M.J.; Flynn, R.R. Decision Support Systems. Encyclopedia of Library and Information Science. A. Kent; Marcel Dekker, Inc.: New York, NY, USA, 1999; Volume 10, p. 2010. [Google Scholar]
- Flores, X.; Rodríguez-Roda, I.; Poch, M.; Jiménez, L.; Bañares-Alcántara, R. Systematic procedure to handle critical decisions during the conceptual design of activated sludge plants. Ind. Eng. Chem. Res. 2007, 46, 5600–5613. [Google Scholar] [CrossRef]
- Rodriguez-Roda, I.; Poch, M.; Bañares-Alcántara, R. Conceptual design of wastewater treatment plants using a design support system. J. Chem. Technol. Biotechnol.: Int. Res. Process Environ. Clean Technol. 2000, 75, 73–81. [Google Scholar] [CrossRef]
- Gachet, A.; Sprague, R. A Context-Based Approach to the Development of Decision Support Systems. International Workshop on Context Modeling and Decision Support; Paris, France, 2015. Available online: http://citeseerx.ist.psu.edu/viewdoc/similar?doi=10.1.1.143.1230&type=ab (accessed on 28 September 2019).
- Freitas, I.S.; Costa, C.A.; Boaventura, R.A. Conceptual design of industrial wastewater treatment processes: Primary treatment. Comput. Chem. Eng. 2000, 24, 1725–1730. [Google Scholar] [CrossRef]
- Geza, M.; Ma, G.; Kim, H.; Cath, T.Y.; Xu, P. iDST: An. integrated decision support tool for treatment and beneficial use of non-traditional water supplies–Part. I. Methodology. J. Water Process Eng. 2018, 25, 236–246. [Google Scholar] [CrossRef]




| Tool | Capabilities/Features | |||||||
|---|---|---|---|---|---|---|---|---|
| Developing Environment | Runoff Volume | Peak Flow | Pollutant Loads/Concentration 1 | BMP/GI | Cost/LCCA 2 | Integrated Optimization 3 | Water Quality Analysis 4 | |
| WERF SELECT [18] | Excel-VBA | √ | √ | √ | √ | √ | ||
| Green Values [19] | JavaScript | √ | √ | √ | √ | |||
| STEPL [1] | Excel-VBA | √ | √ | √ | √ | |||
| EPA SWMM 5 [20] | C language | √ | √ | √ | √ | √ | ||
| WinSLAMM [21] | Fortran | √ | √ | √ | √ | √ | √ | |
| EPA SUSTAIN [22] | C language | √ | √ | √ | √ | √ | √ | √ |
| L-THIA [23] | Excel-VBA | √ | √ | √ | √ | |||
| MUSIC [24] | Fortran | √ | √ | √ | √ | √ | ||
| LIDRA [13] | Visual studio, C# language | √ | √ | |||||
| Stormwater calculator [25] | C language | √ | √ | √ | ||||
| MIDS calculator [26] | Excel-VBA | √ | √ | √ | √ | |||
| California LID Sizing Tool [27] | Visual basic, JavaScript | √ | √ | √ | ||||
| BMP Checker [28] | Python | √ | √ | √ | √ | √ | √ | |
| RSWMM-Cost [29] | R language | √ | √ | √ | √ | √ | √ | √ |
| i-DSTss | Excel-VBA | √ | √ | √ | √ | √ | √ | |
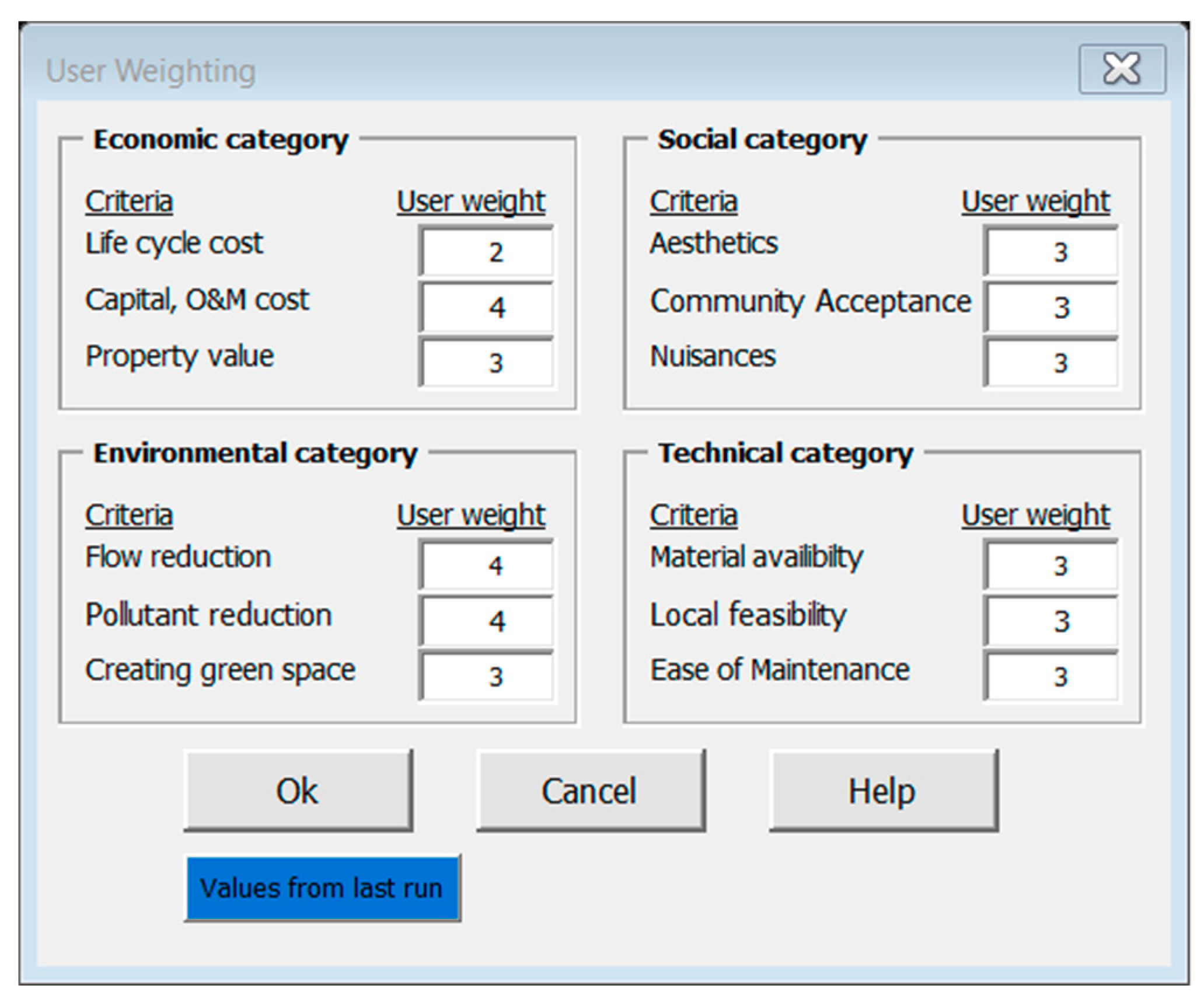
| Category | Criteria | Description |
|---|---|---|
| Economic | LCA | Life cycle cost of a BMP |
| Capital, O&M costs | Cost of installation, operation and maintenance for a BMP | |
| Property value | Land cost and related property value of a BMP | |
| Environmental | Flow reduction | Potential for runoff volume captured or peak flow reduction |
| Pollutant reduction | Pollutant load reduction potential | |
| Green space | Potential for creating green space covered with grass or trees | |
| Social | Aesthetics | Potential for creation of scenic values |
| Community Acceptance | Acceptance by the community, affected populations including local stakeholders and authorities | |
| Nuisances | Creating inconvenience or annoyances | |
| Technical | Material availability | Relative ease of obtaining construction materials |
| Feasibility | Likelihood that projects can be easily implemented | |
| Ease of Maintenance and operation | Relative ease of operation and maintenance if failure occurs due to clogging or other factors |
| Cost Category | Description | |
|---|---|---|
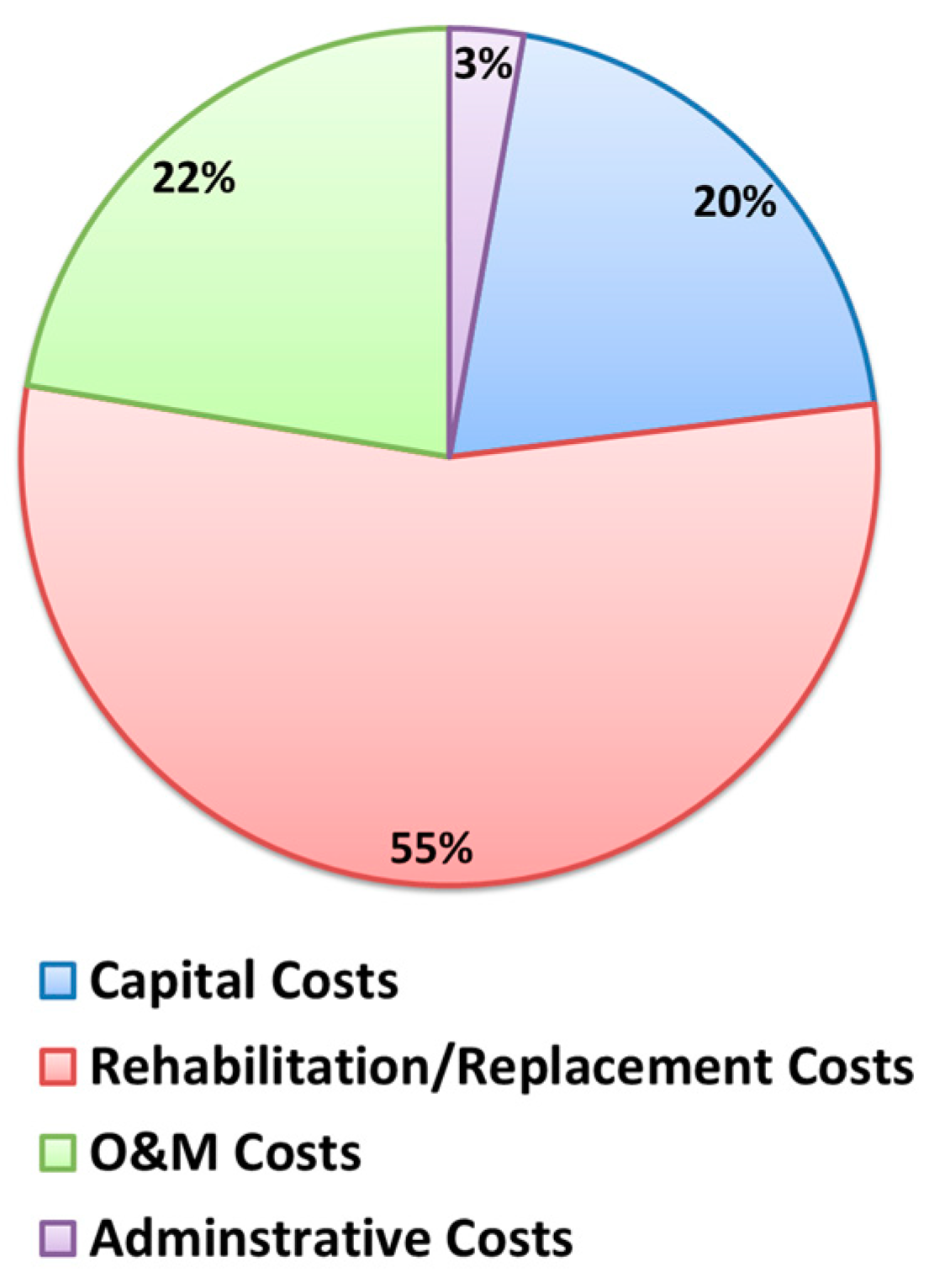
| Capital costs | Construction cost | BMP construction cost |
| Land cost (user input value) | Cost of acquiring the land | |
| Cost contingency, % of construction cost (~7%) | Unexpected cost | |
| O&M costs, % of construction cost (~4%) | Costs incurred each year for maintenance and operation | |
| Rehabilitation costs, % of construction cost (~70%) | Cost for replacing a BMP | |
| Administrative and inspection costs, % of construction cost (~0.5%) | Inspection cost | |
| Land Cover Type | Percent Area |
|---|---|
| Streets | 17% |
| Driveways | 6% |
| Roofs | 17% |
| Sidewalks | 5% |
| Other Impervious | <1% |
| Lawns/Open | 55% |
| Land Use | Water Quality Parameter (unit) | Level of Concentration | ||
|---|---|---|---|---|
| Min | Median | Max | ||
| Residential | TSS (mgL) | 0.25 | 38.00 | 2380.52 |
| TP (mgL) | 0.01 | 0.23 | 21.20 | |
| TN (mgL) | 0.20 | 1.51 | 10.30 | |
| Bacteria (100 mL) | 25.50 | 1870.00 | 48,392.00 | |
| Pb (ugL) | 0.15 | 5.00 | 368.00 | |
| Zn (ugL) | 1.00 | 74.00 | 2077.40 | |
| Cu (mgL) | 0.50 | 10.00 | 7270.00 | |
| NO3 (mgL) | 0.05 | 0.64 | 1.26 | |
| PO4 (mgL) | 0.00 | 0.10 | 6.00 | |
| Optimal BMP | Rain garden | Bioretention | VFS-Bioretention | |
| Land Use | Water Quality Parameter (unit) | Level of Concentration | ||
|---|---|---|---|---|
| Min | Median | Max | ||
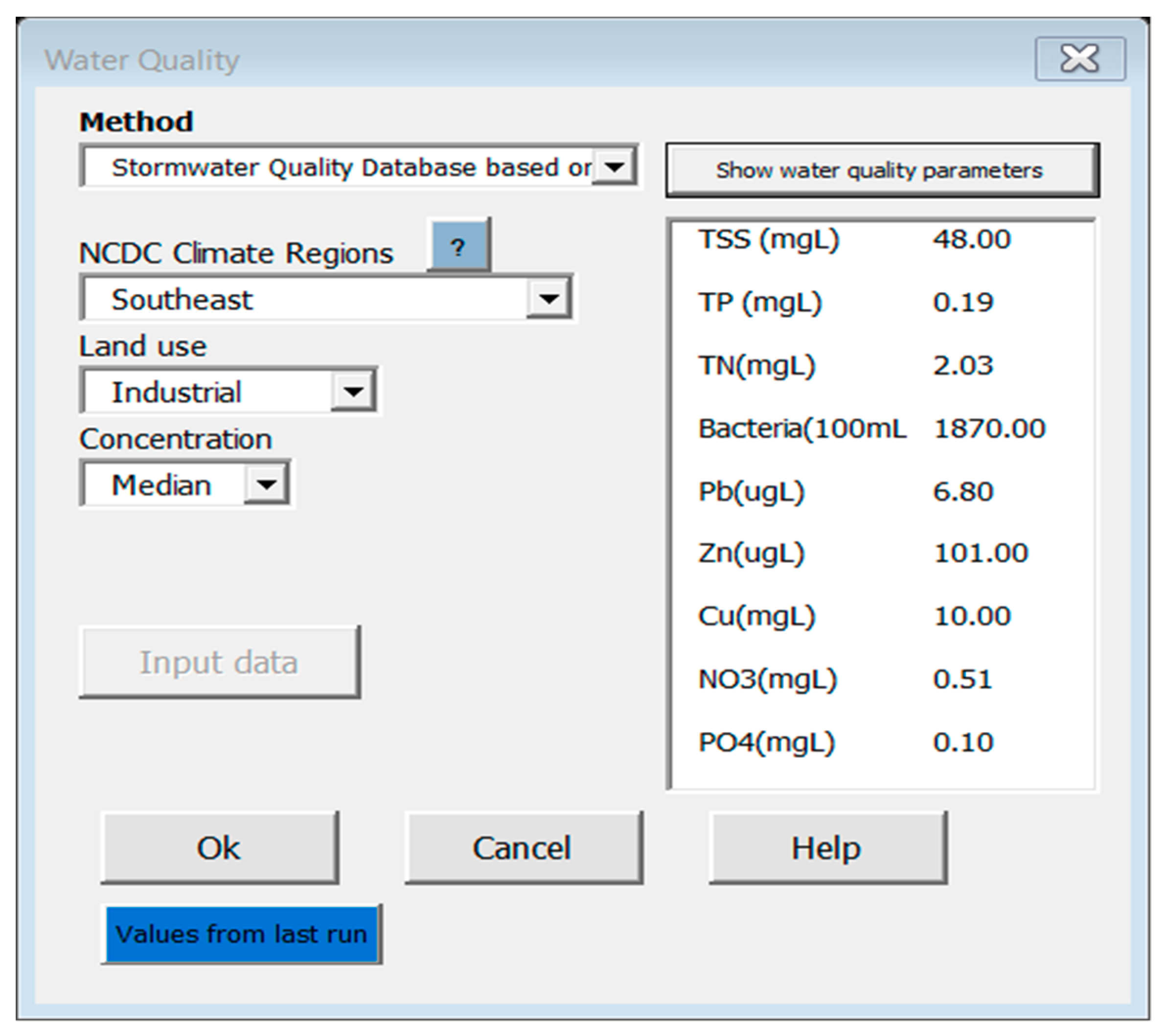
| Industrial | TSS (mgL) | 0.50 | 48.00 | 1130.00 |
| TP (mgL) | 0.01 | 0.19 | 2.14 | |
| TN (mgL) | 0.21 | 2.03 | 8.01 | |
| Bacteria (100 mL) | 25.50 | 1870.00 | 48,392.00 | |
| Pb (ugL) | 0.10 | 6.80 | 370.00 | |
| Zn (ugL) | 1.00 | 101.00 | 7700.00 | |
| Cu (mgL) | 1.00 | 10.00 | 950.00 | |
| NO3 (mgL) | 0.13 | 0.51 | 1.24 | |
| PO4 (mgL) | 0.00 | 0.10 | 6.00 | |
| Optimal BMP | Wetland | Wetland | Forebay-Wetland | |
| Land Use | Water Quality Parameter (unit) | Level of Concentration | ||
|---|---|---|---|---|
| Min | Median | Max | ||
| Freeways | TSS (mgL) | 0.50 | 33.00 | 823.00 |
| TP (mgL) | 0.01 | 0.25 | 3.35 | |
| TN (mgL) | 0.20 | 0.84 | 8.14 | |
| Bacteria (100 mL) | 25.50 | 1870.00 | 48,392.00 | |
| Pb (ugL) | 0.15 | 5.20 | 230.00 | |
| Zn (ugL) | 1.00 | 48.00 | 1000.00 | |
| Cu (mgL) | 1.00 | 6.00 | 122.00 | |
| NO3 (mgL) | 0.03 | 0.51 | 2.20 | |
| PO4 (mgL) | 0.00 | 0.10 | 6.00 | |
| Optimal BMP | Grass swale | Grass swale | Forebay-Grass swale | |
| Peak Flow Reduction (%) | 50 | 25 |
|---|---|---|
| Pond depth (m) | 1.8 | 1.3 |
| Pond storage (m3) | 170 | 64 |
| Pond surface area (m2) | 95 | 49 |
| Length at bottom (m) | 6.1 | 4.2 |
| Width at bottom (m) | 2.0 | 1.4 |
| Total discharge by weir and orifice (cms) | 2.73 | 2.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shojaeizadeh, A.; Geza, M.; McCray, J.; Hogue, T.S. Site-Scale Integrated Decision Support Tool (i-DSTss) for Stormwater Management. Water 2019, 11, 2022. https://doi.org/10.3390/w11102022
Shojaeizadeh A, Geza M, McCray J, Hogue TS. Site-Scale Integrated Decision Support Tool (i-DSTss) for Stormwater Management. Water. 2019; 11(10):2022. https://doi.org/10.3390/w11102022
Chicago/Turabian StyleShojaeizadeh, Ali, Mengistu Geza, John McCray, and Terri S. Hogue. 2019. "Site-Scale Integrated Decision Support Tool (i-DSTss) for Stormwater Management" Water 11, no. 10: 2022. https://doi.org/10.3390/w11102022
APA StyleShojaeizadeh, A., Geza, M., McCray, J., & Hogue, T. S. (2019). Site-Scale Integrated Decision Support Tool (i-DSTss) for Stormwater Management. Water, 11(10), 2022. https://doi.org/10.3390/w11102022