Numerical Analysis on Hydrodynamic Characteristics of Surface Piercing Propellers in Oblique Flow
Abstract
1. Introduction
2. Numerical Method
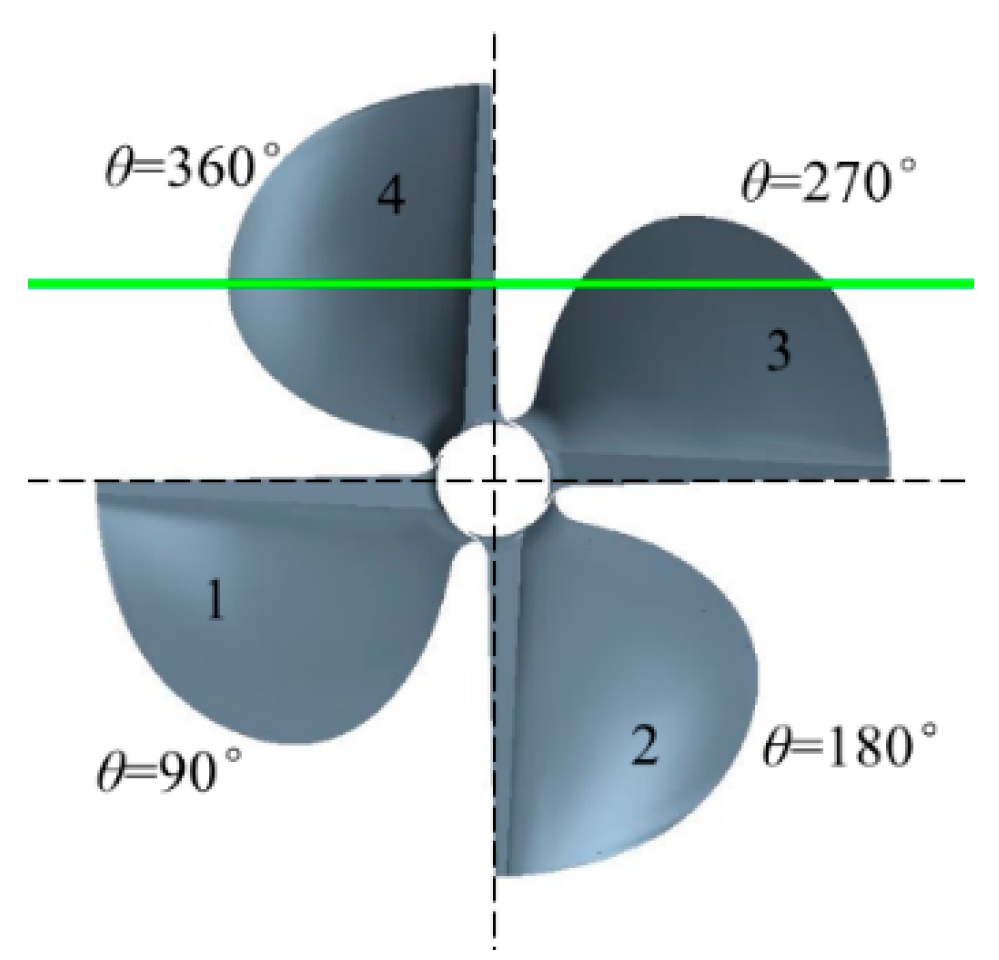
2.1. Geometry Model
2.2. Governing Equations
2.3. Grid Generation
2.4. Boundary and Initial Conditions
3. Verification of Numerical Method
3.1. Grid Independence
3.2. Hydrodynamic Performance
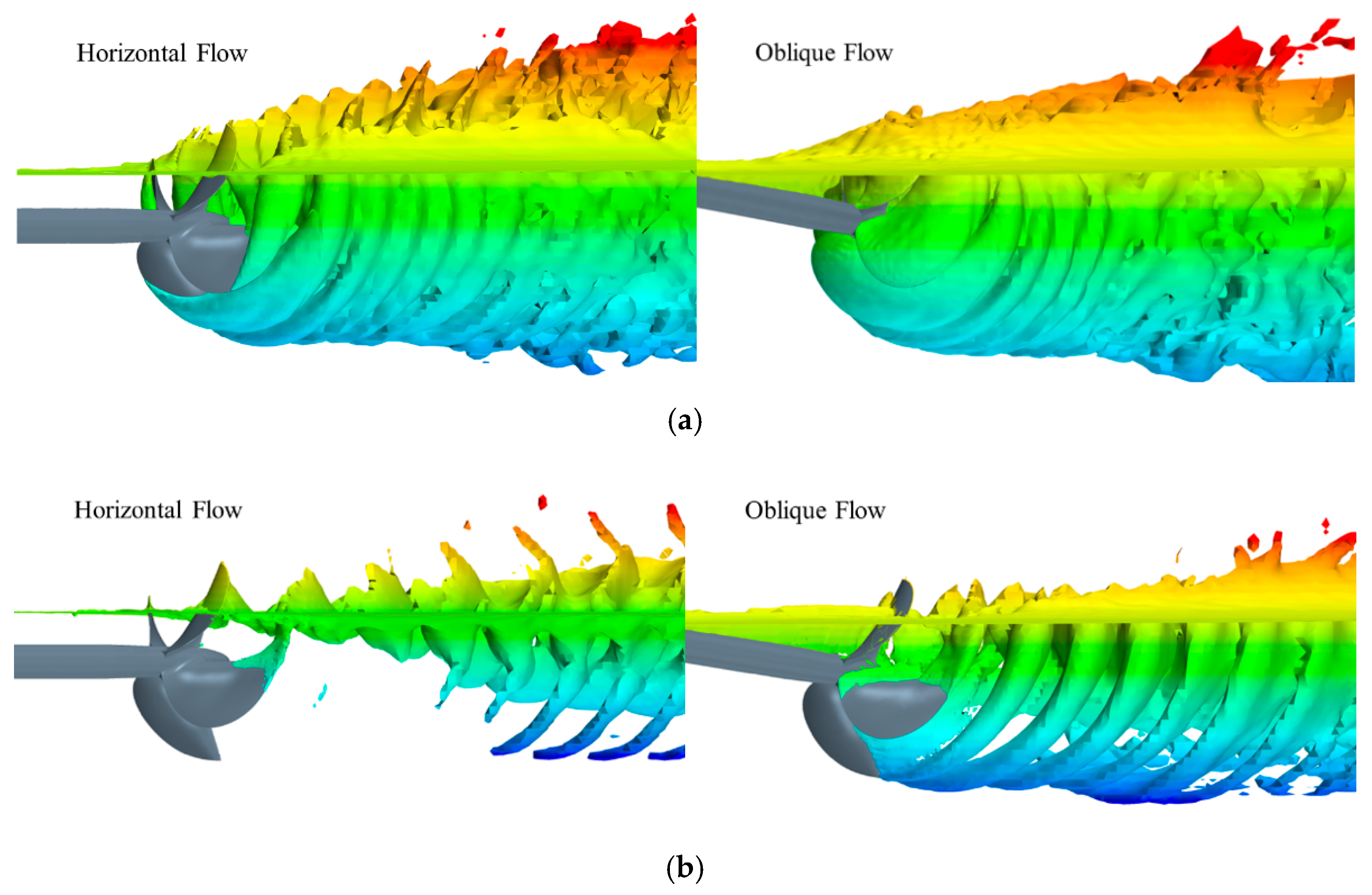
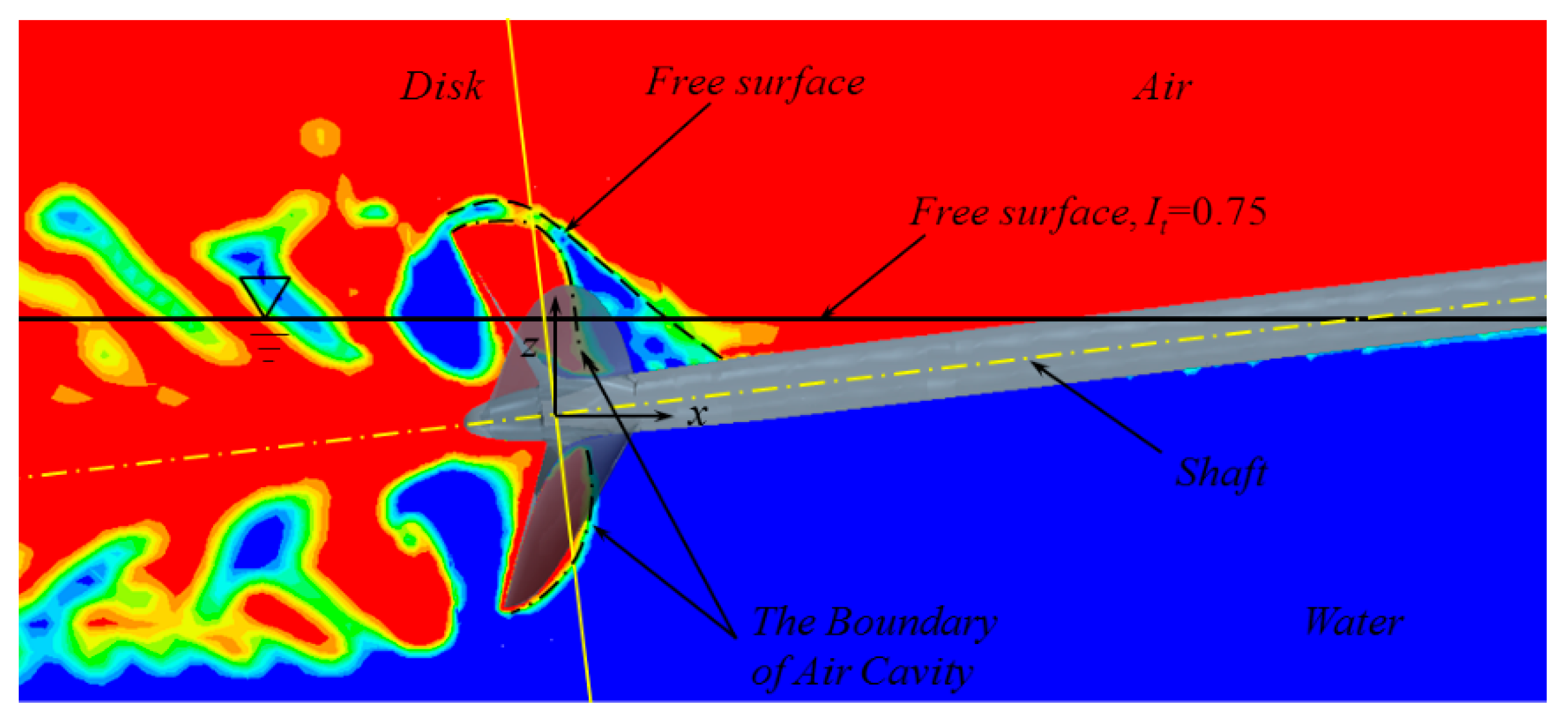
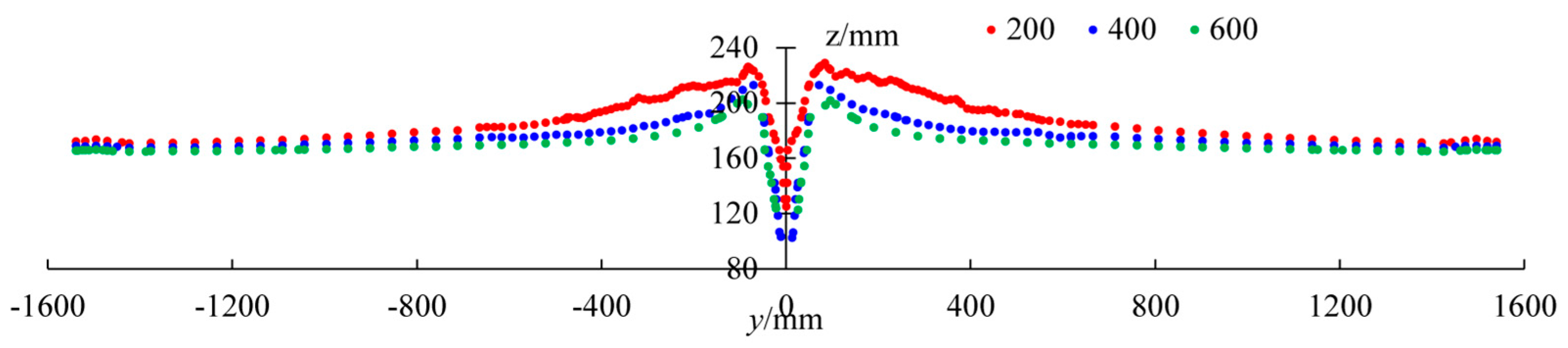
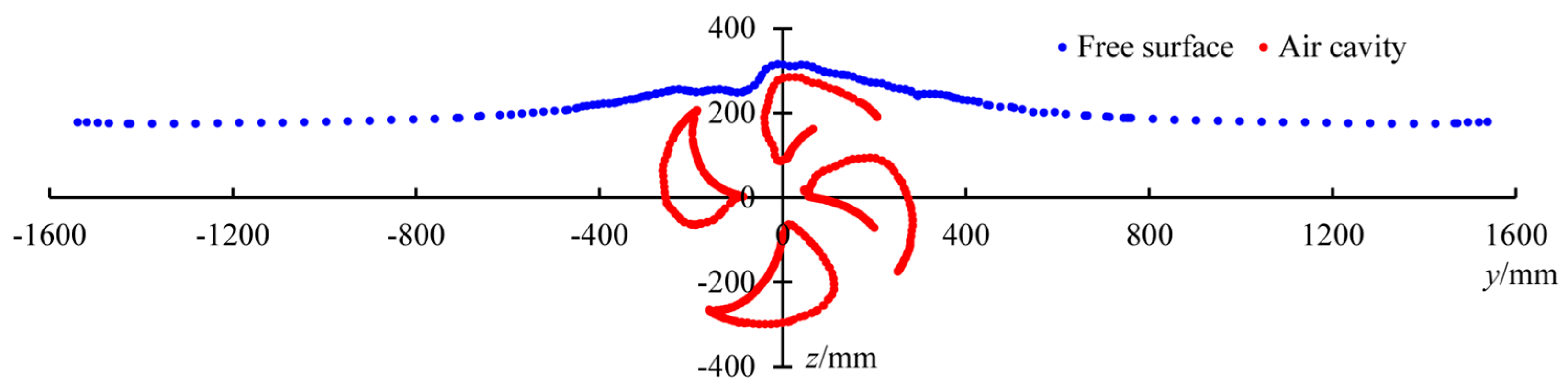
4. Numerical Results and Analysis
4.1. Free Surface
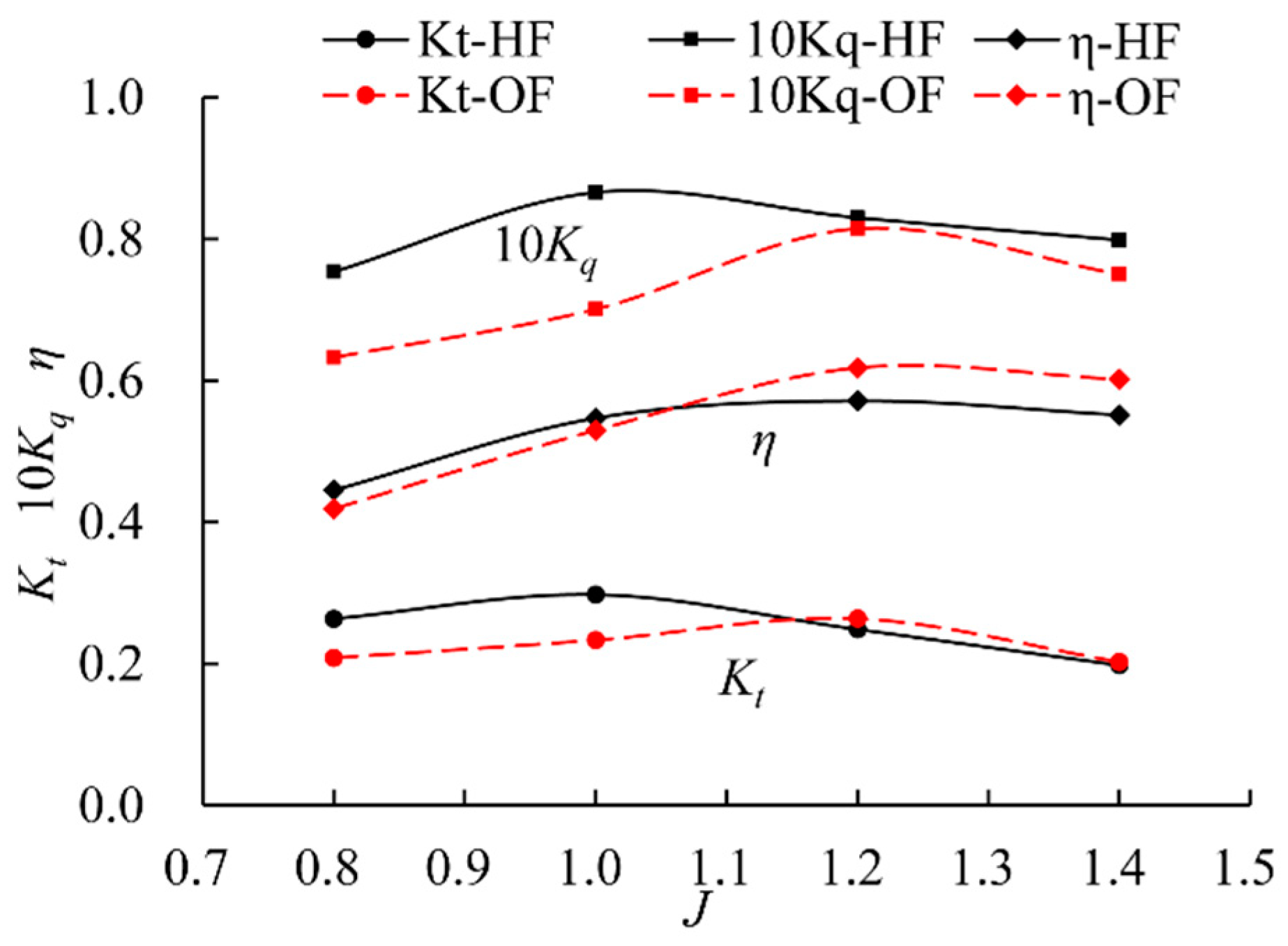
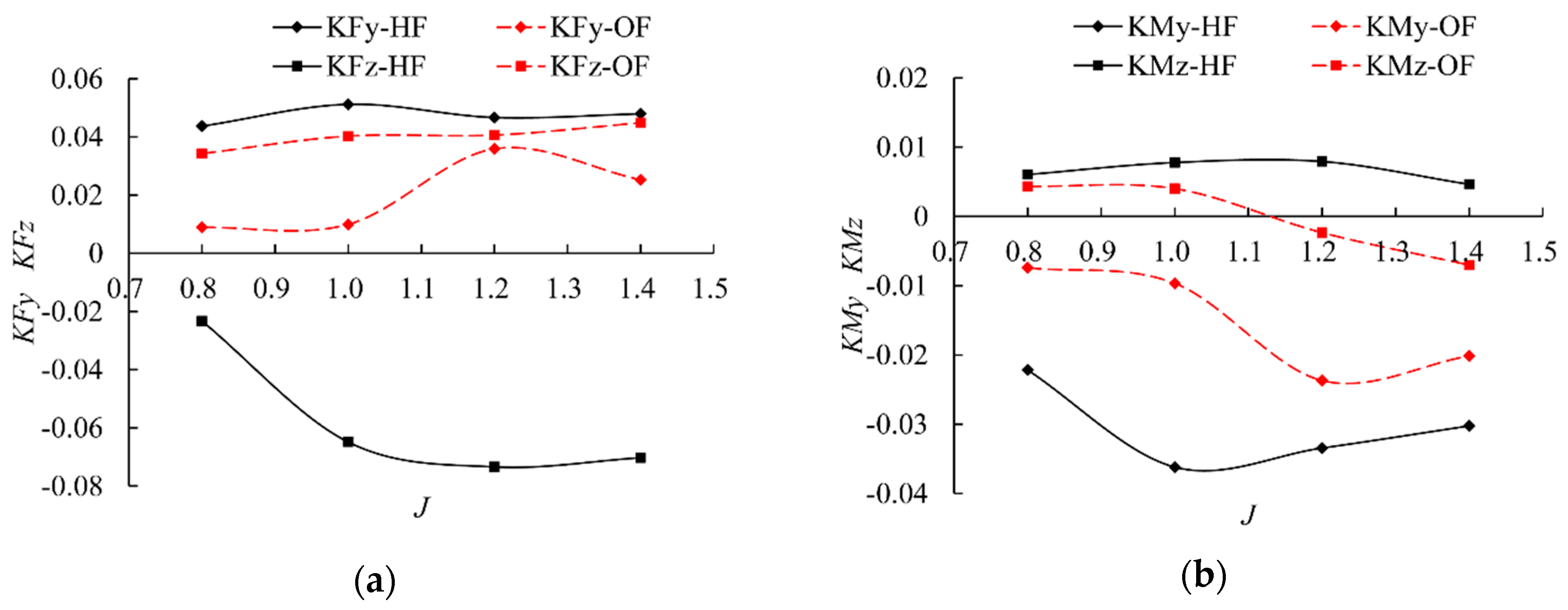
4.2. Hydrodynamic Performance
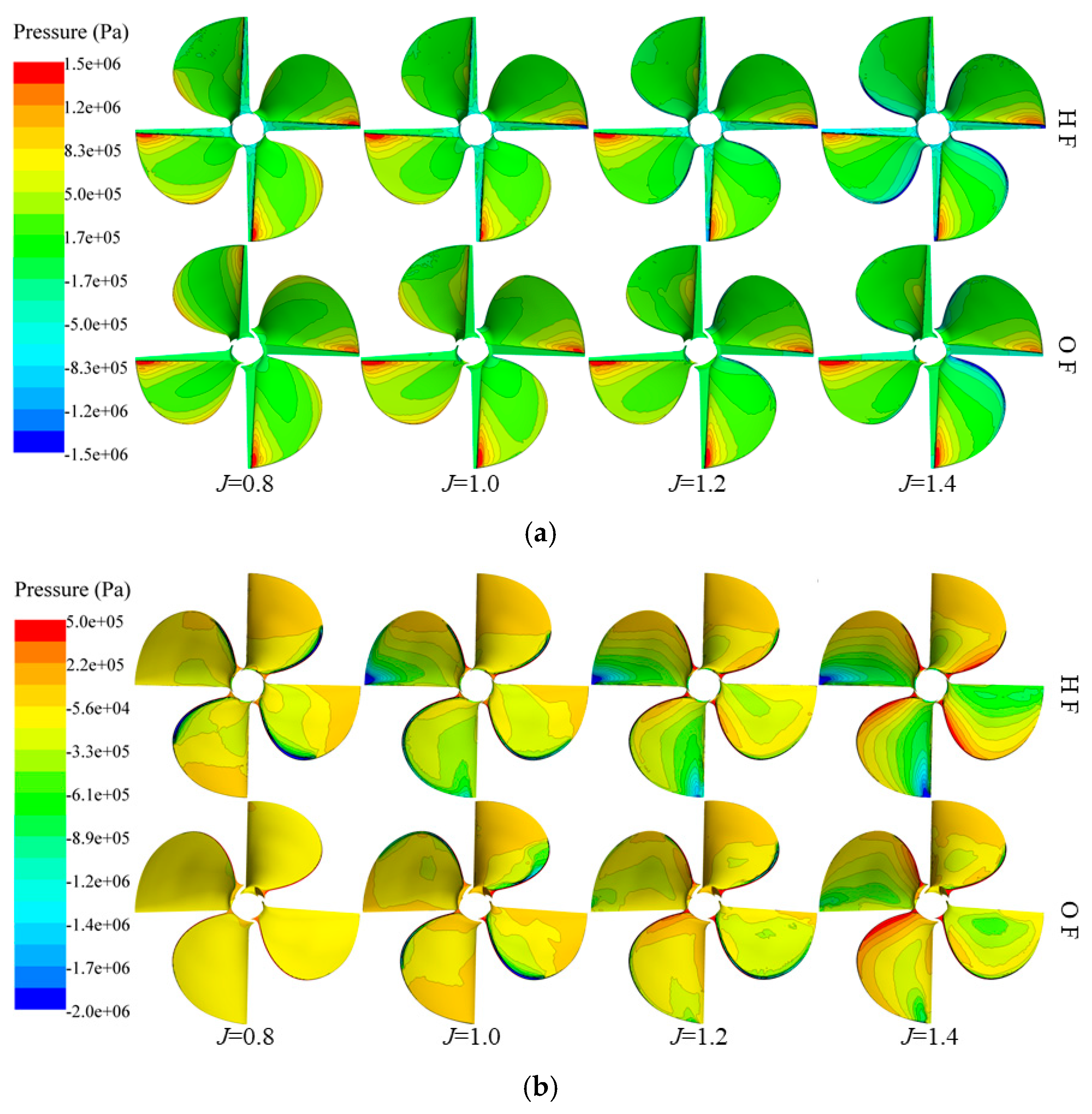
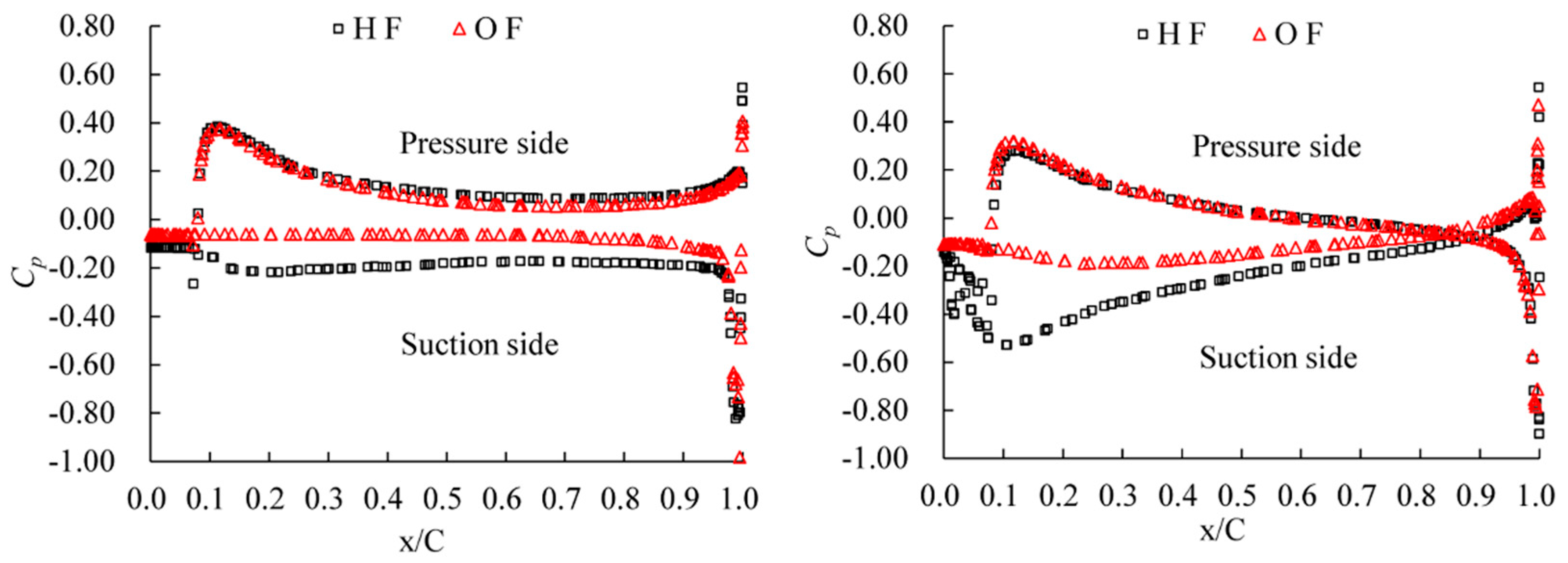
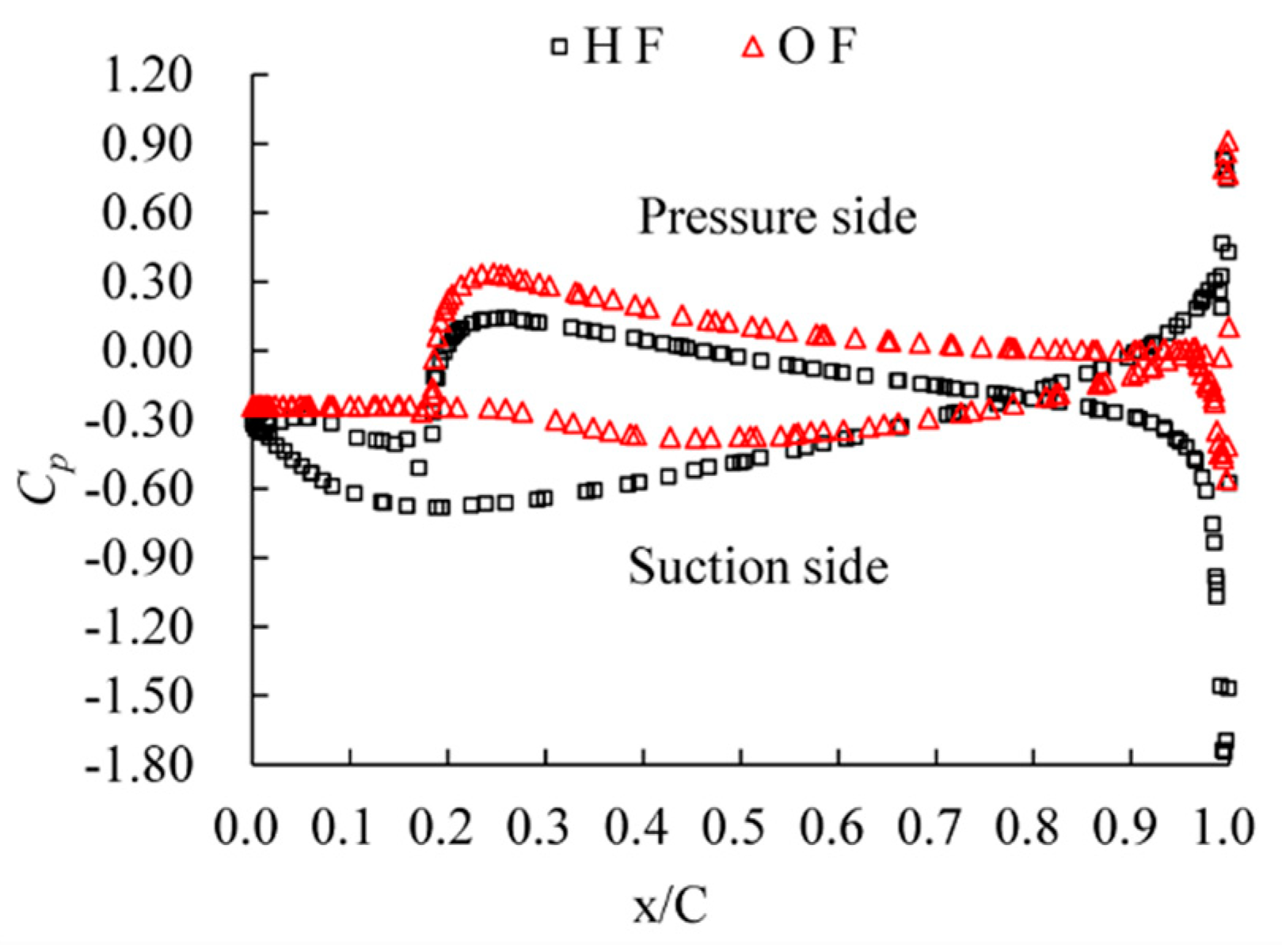
4.3. Pressure on the Blades
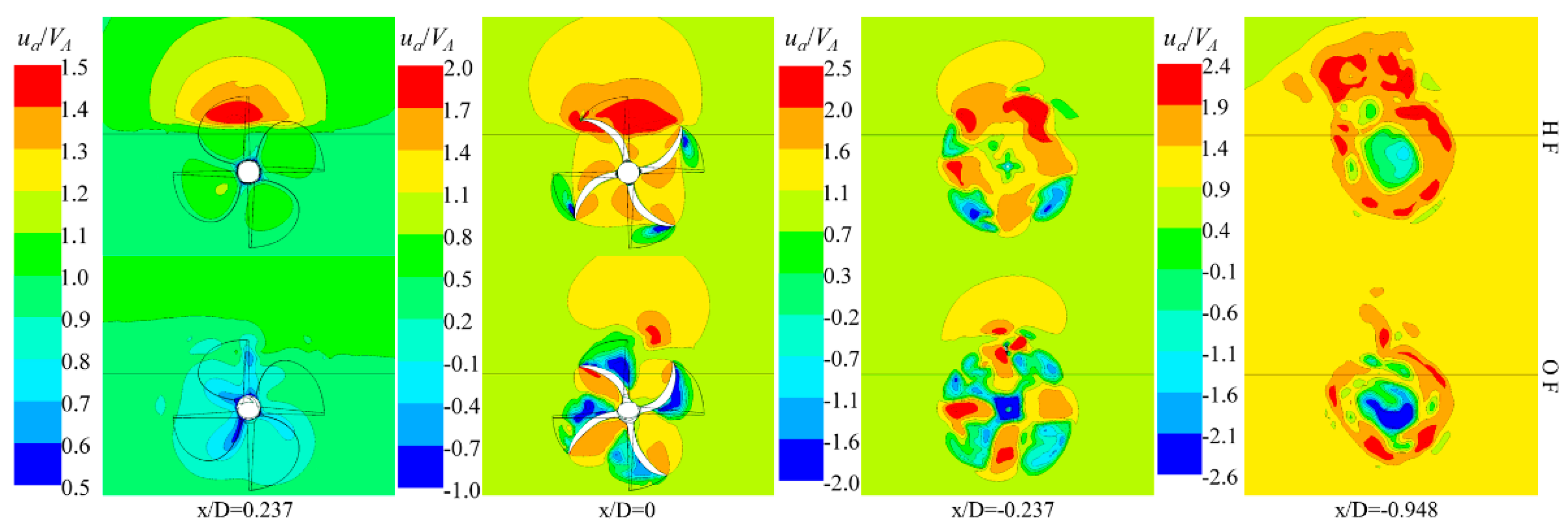
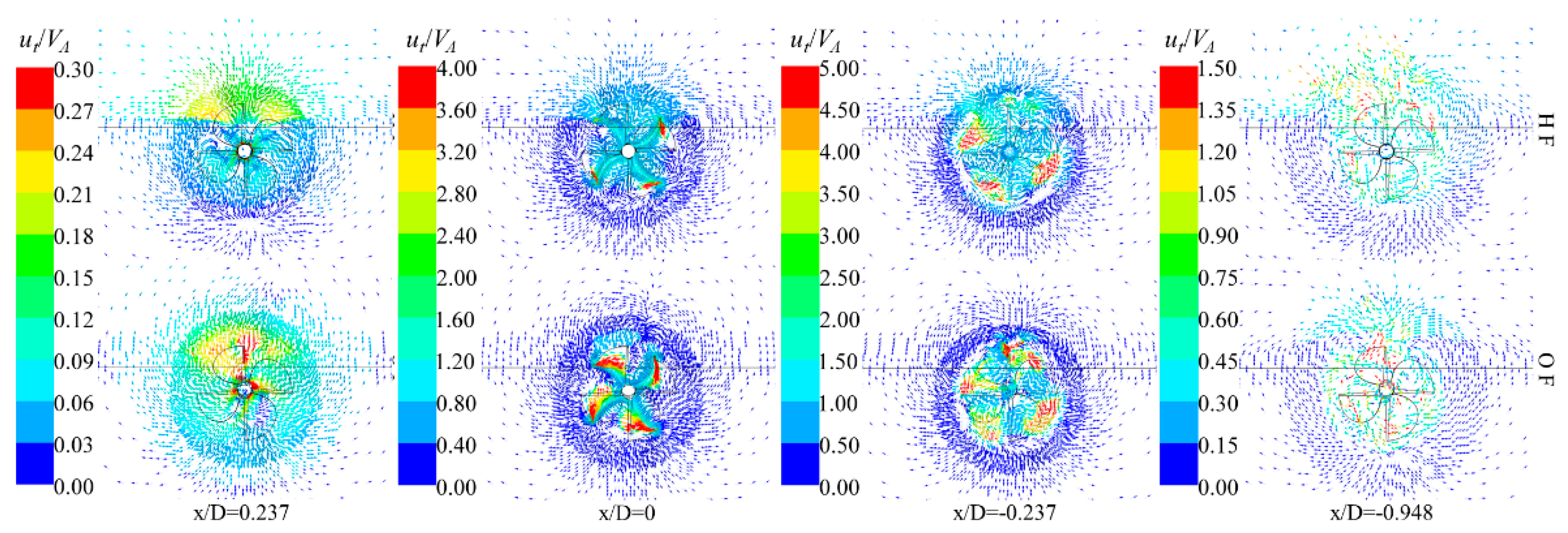
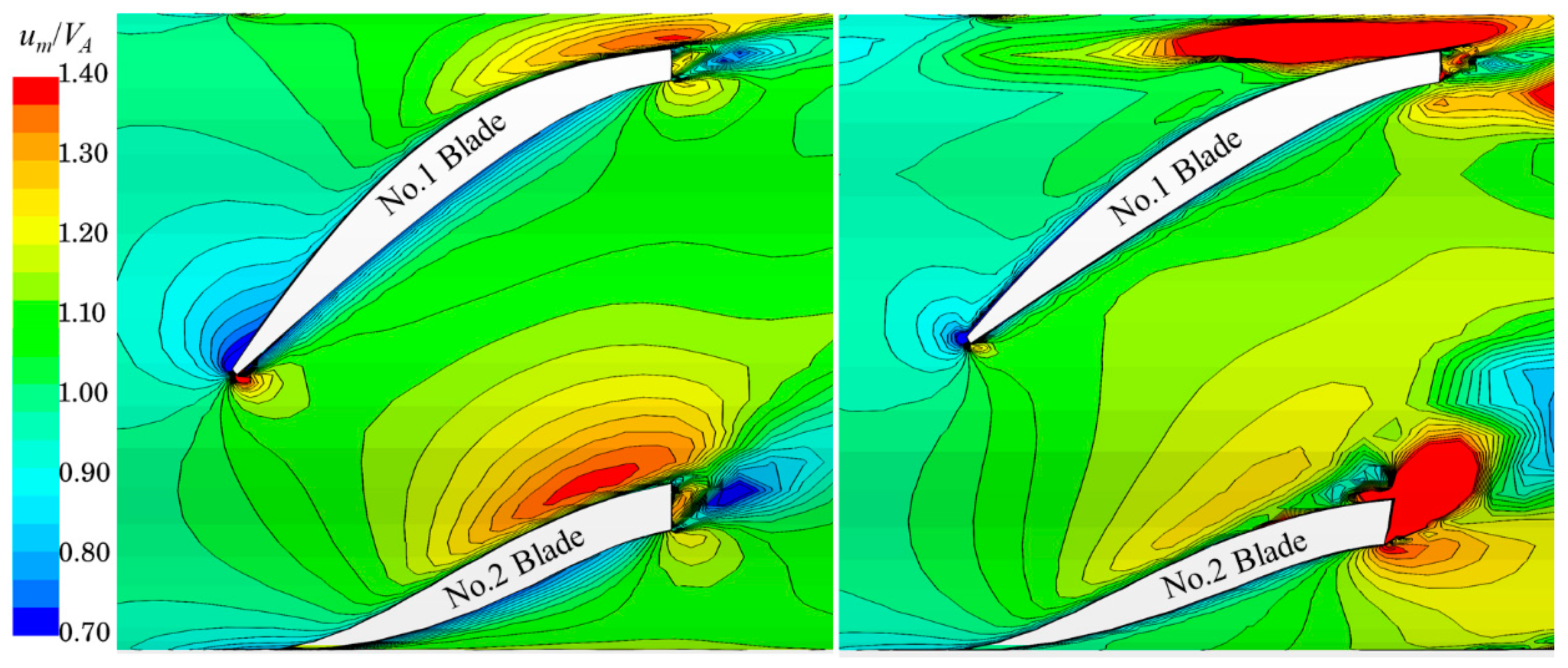
4.4. Wake Field
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferrando, M. Surface piercing propellers: state of the art. Ocean. Eng. Int. 1997, 1, 40–49. [Google Scholar]
- Ding, E.B.; Tang, D.H.; Zhou, W.X. Research review on the semi-submerged propellers. J. Ship Mech. 2002, 6, 75–84. [Google Scholar]
- Hadler, J.B.; Hecker, R. Performance of partially submerged propellers. In Proceedings of the 7th ONR Symposium on Naval Hydrodynamics, Rome, Italy, 25–30 August 1968; pp. 1449–1496. [Google Scholar]
- Misra, S.C.; Gokarn, R.P.; Sha, O.P.; Suryanarayana, C.; Suresh, R.V. Development of a four-bladed surface piercing propellers Series…# 169. Nav. Eng. J. 2012, 124, 111–141. [Google Scholar]
- Ferrando, M.; Panarello, A.; Scamardella, A.; Viviani, M. Model tests and full scale operation with surface piercing propellers. In Proceedings of the Institute of Marine Engineering, Science and Technology. Part B, Journal of Marine Design and Operations; Institute of Marine Engineering, Science and Technology: London, UK, 2003; Volume 3, pp. 21–31. [Google Scholar]
- Chudley, J.; Grieve, D.; Dyson, P.K. Determination of transient loads on surface piercing propellers. R. Inst. Nav. Archit. 2002, 125–141. [Google Scholar]
- Ding, E.B. Study on Test and Design Method of Partially Submerged Propeller. Master’s Thesis, Chinese Ship Scientific Research Center, Wuxi, China, 2002. [Google Scholar]
- Xia, X.; Li, S.C.; Li, H.M. Analysis on surface piercing propellers induced vertical forces. Chin. J. Ship Res. 2006, 1, 68–70. [Google Scholar]
- Furuya, O. A performance-prediction theory for partially submerged ventilated propellers. J. Fluid Mech. 1985, 151, 311–335. [Google Scholar] [CrossRef]
- Young, Y.L.; Kinnas, S.A. Performance prediction of surface-piercing propellers. J. Ship Res. 2004, 48, 288–304. [Google Scholar]
- Young, Y.L. Numerical Modeling of Supercavitating and Surface Piercing Propellers. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2002. [Google Scholar]
- Young, Y.L.; Savander, B.R. Numerical analysis of large-scale surface piercing propellers. Ocean Eng. 2011, 38, 1368–1381. [Google Scholar] [CrossRef]
- Yari, E.; Ghassemi, H. Hydrodynamic analysis of the surface-piercing propeller in unsteady open water condition using boundary element method. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 22–37. [Google Scholar] [CrossRef][Green Version]
- Ghassemi, H.; Shademani, R.; Ardeshir, A. Hydrodynamic characteristics of the surface-piercing propeller for the planing craft. J. Mar. Sci. Appl. 2009, 8, 267–274. [Google Scholar] [CrossRef]
- Caponnetto, M. RANSE simulations of surface piercing propellers. In Proceedings of the 6th Numerical Towing Tank Symposium, Rome, Italy, 29 September–1 October 2003. [Google Scholar] [CrossRef]
- Alimirzazadeh, S.; Roshan, S.Z.; Seif, M.S. Unsteady RANS simulation of a surface piercing propellers in oblique flow. Appl. Ocean Res. 2016, 56, 79–91. [Google Scholar] [CrossRef]
- Yari, E.; Ghassemi, H. Numerical analysis of surface piercing propellers in unsteady conditions and cupped effect on ventilation pattern of blade cross-section. J. Mar. Sci. Technol. 2016, 21, 501–516. [Google Scholar] [CrossRef]
- Himei, K. Numerical analysis of unsteady open water characteristics of surface piercing propellers. In Proceedings of the Third International Symposium on Marine Propulsors SMP, Launceston, Australia, 5–8 May 2013; Volume 13, pp. 292–297. [Google Scholar]
- Shi, Y. Numerical Study of the Hydrodynamic Performance of Surface Piercing Propellers. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. [Google Scholar]
- Yang, D.; Ren, Z.; Guo, Z.; Gao, Z. Numerical analysis on the hydrodynamic performance of an artificially ventilated surface piercing propeller. Water 2018, 10, 1499. [Google Scholar] [CrossRef]
- Olofsson, N. Force and Flow Characteristics of a Partially Submerged Propeller. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 1996. [Google Scholar]
- CD-Adapco Group. STAR-CCM+ User Guide Version 9.06; CD-adapco Group: Melville, NY, USA, 2014. [Google Scholar]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Rogowski, K.; Hansen, M.; Maroński, R.; Lichota, P. Scale adaptive simulation model for the darrieus wind turbine. J. Phys. Conf. Ser. Iop Publ. 2016, 753, 022050. [Google Scholar] [CrossRef]

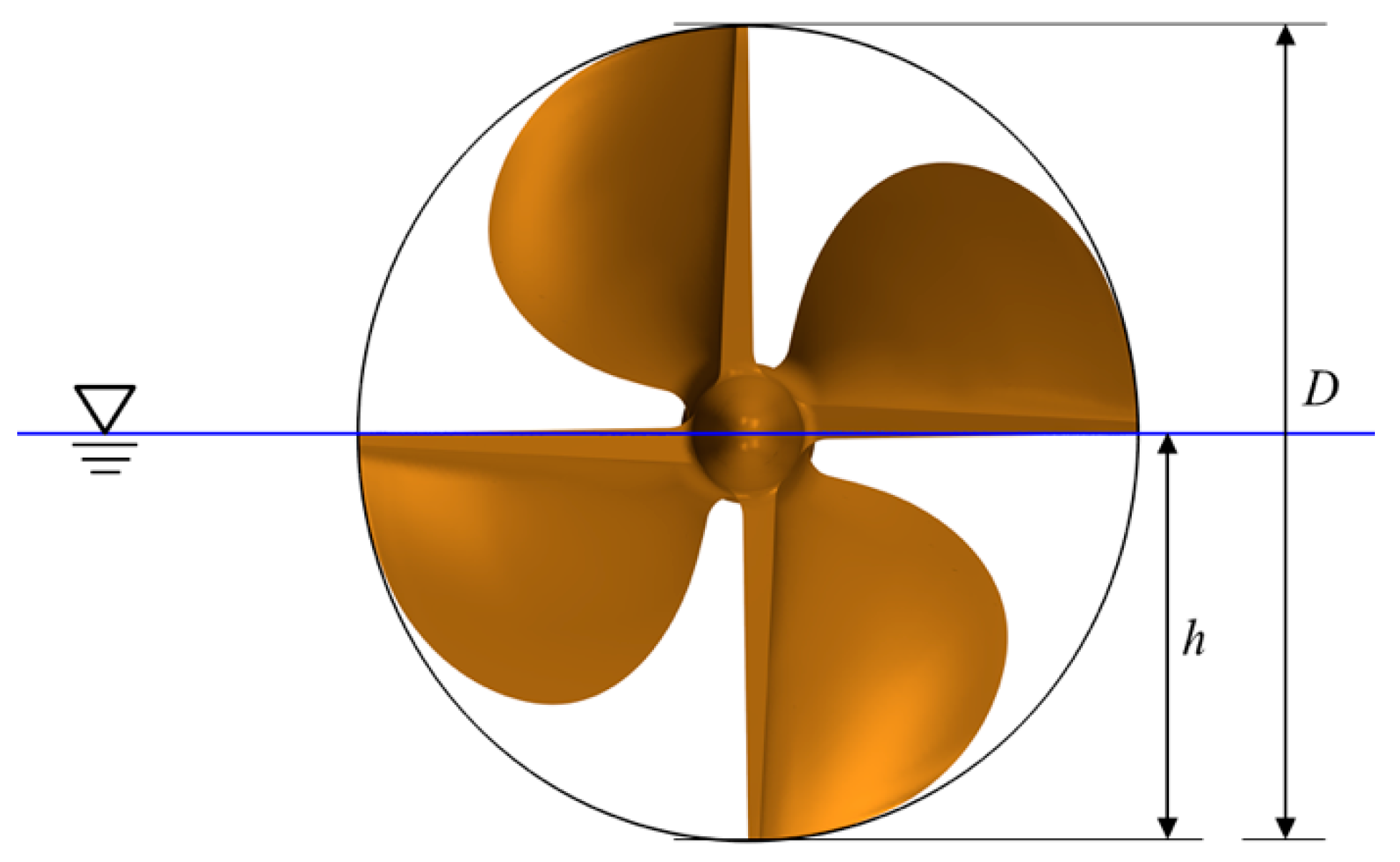
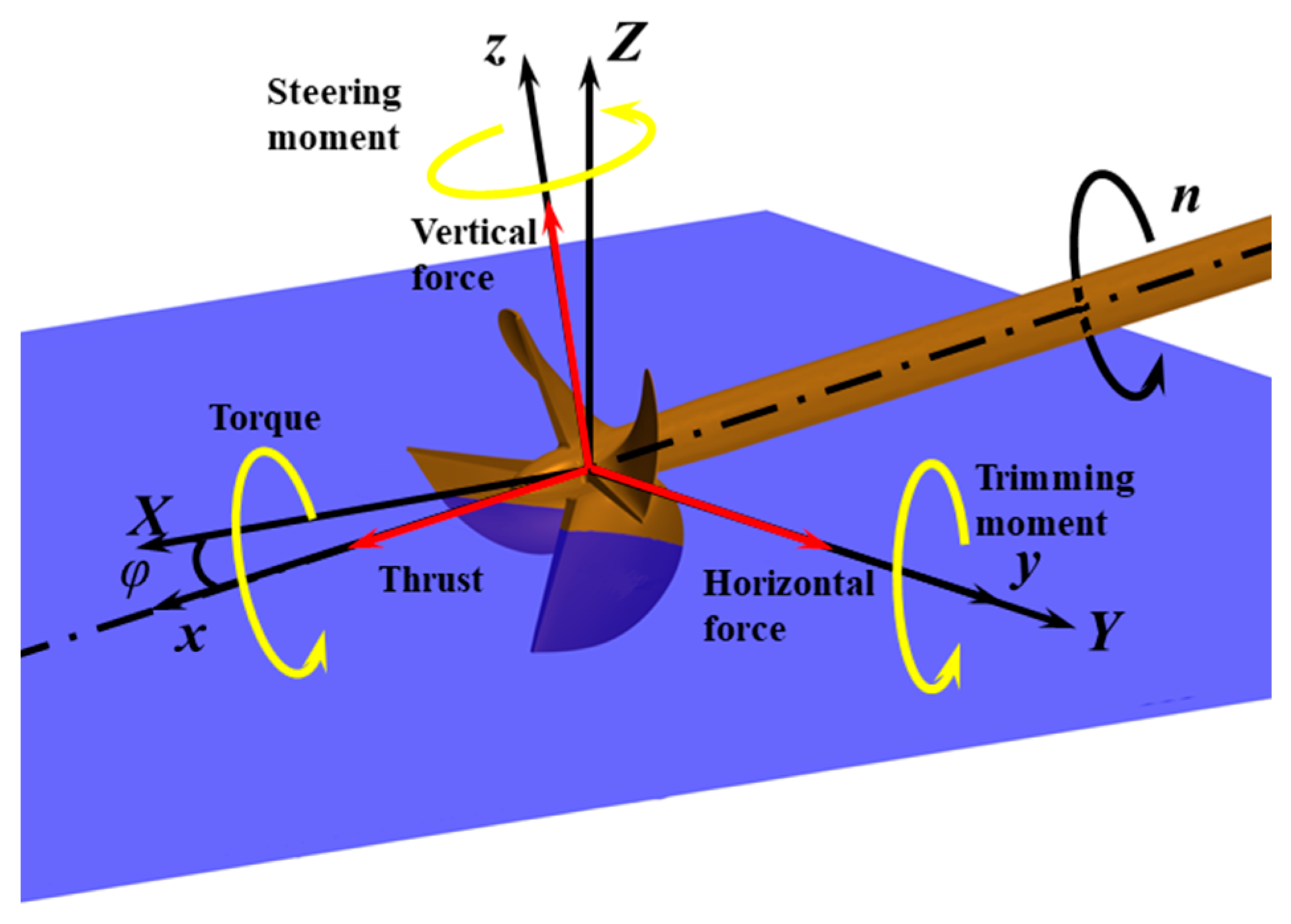
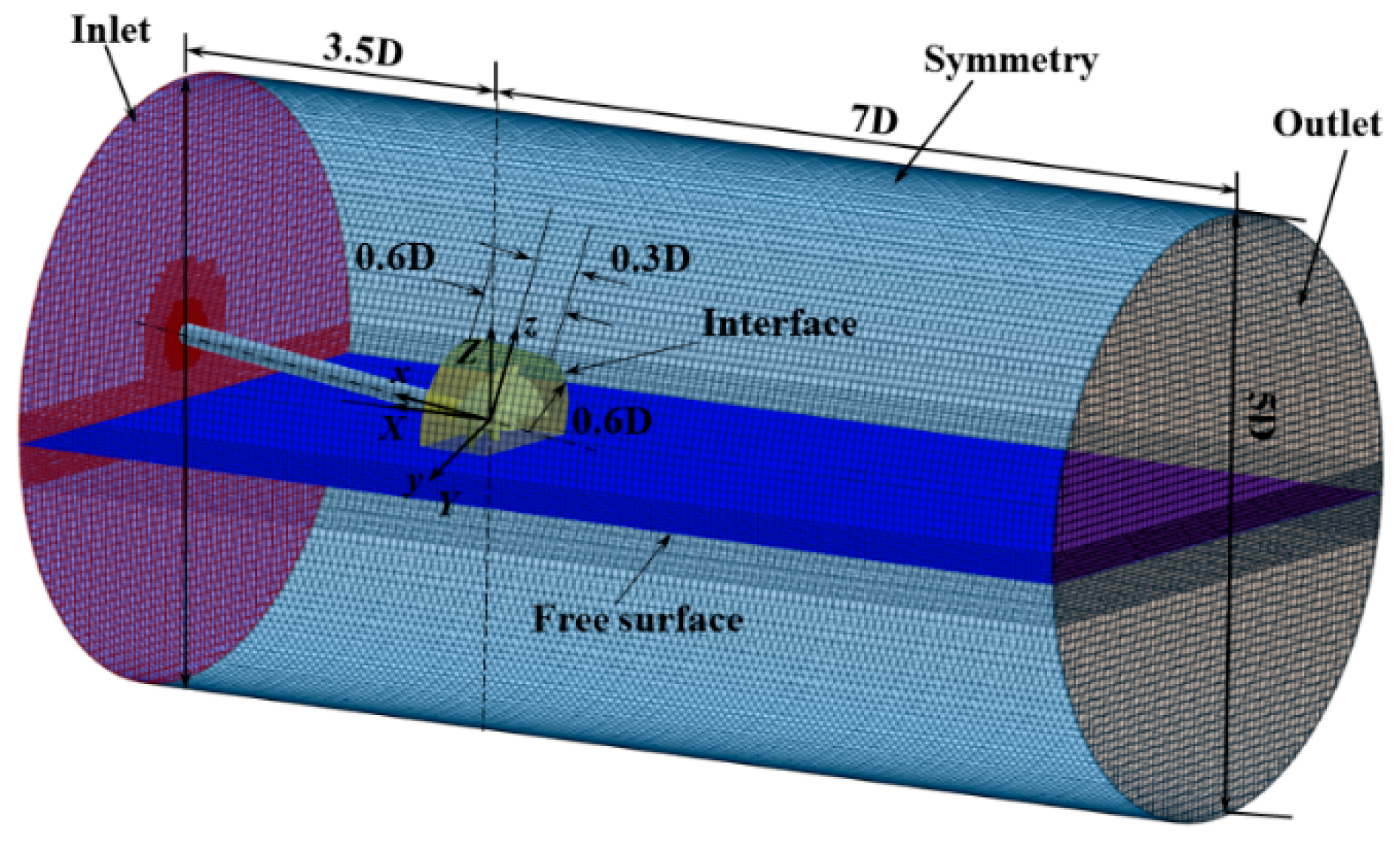


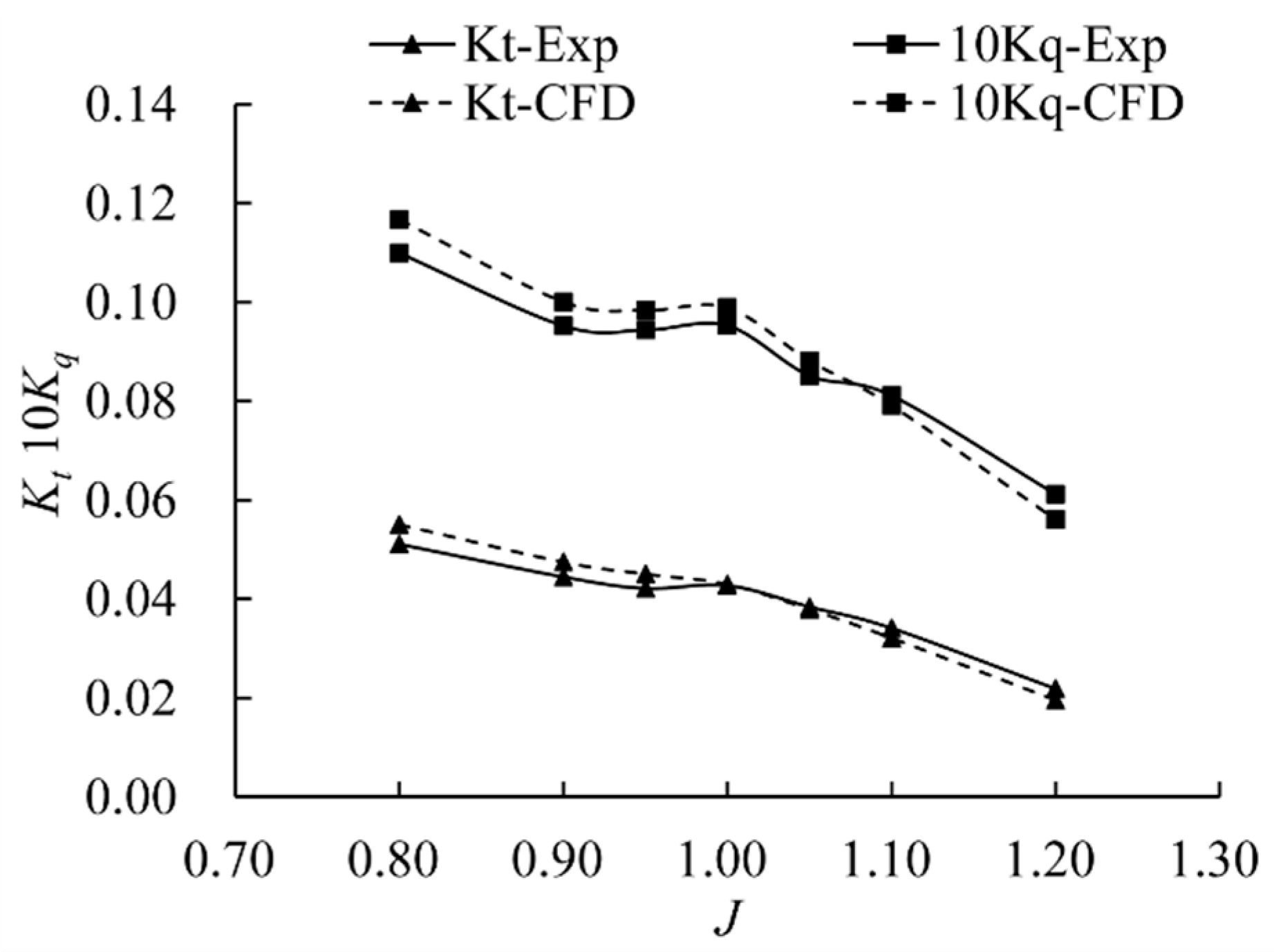

| Parameters | PSP-841B | SPP-1 |
|---|---|---|
| D (mm) | 250 | 633 |
| H/D | 0.34 | 0.15 |
| P/D at 0.7r | 1.24 | 1.60 |
| EAR | 0.58 | 0.83 |
| Blades Number | 4 | 4 |
| Rotation Direction | right | left |
| Grid Number (Million) | Kt | Error | 10 Kq | Error |
|---|---|---|---|---|
| EFD | 0.0511 | 0.1099 | ||
| 1.4 | 0.0572 | 12.1% | 0.1236 | 12.4% |
| 2.6 | 0.0560 | 9.5% | 0.1197 | 9.0% |
| 3.8 | 0.0551 | 7.8% | 0.1167 | 6.1% |
| 5.0 | 0.0546 | 6.9% | 0.1151 | 4.7% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Hua, L.; Ji, P. Numerical Analysis on Hydrodynamic Characteristics of Surface Piercing Propellers in Oblique Flow. Water 2019, 11, 2015. https://doi.org/10.3390/w11102015
Ren Z, Hua L, Ji P. Numerical Analysis on Hydrodynamic Characteristics of Surface Piercing Propellers in Oblique Flow. Water. 2019; 11(10):2015. https://doi.org/10.3390/w11102015
Chicago/Turabian StyleRen, Zhen, Lin Hua, and Penghui Ji. 2019. "Numerical Analysis on Hydrodynamic Characteristics of Surface Piercing Propellers in Oblique Flow" Water 11, no. 10: 2015. https://doi.org/10.3390/w11102015
APA StyleRen, Z., Hua, L., & Ji, P. (2019). Numerical Analysis on Hydrodynamic Characteristics of Surface Piercing Propellers in Oblique Flow. Water, 11(10), 2015. https://doi.org/10.3390/w11102015




