Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Apparatus and Procedures
2.1.1. Flume Characteristics
2.1.2. Experimental Conditions
2.1.3. Non-Dimensional Pi Groups
2.1.4. Description of Energy Dissipation
2.1.5. Delay Time Analysis
3. Results
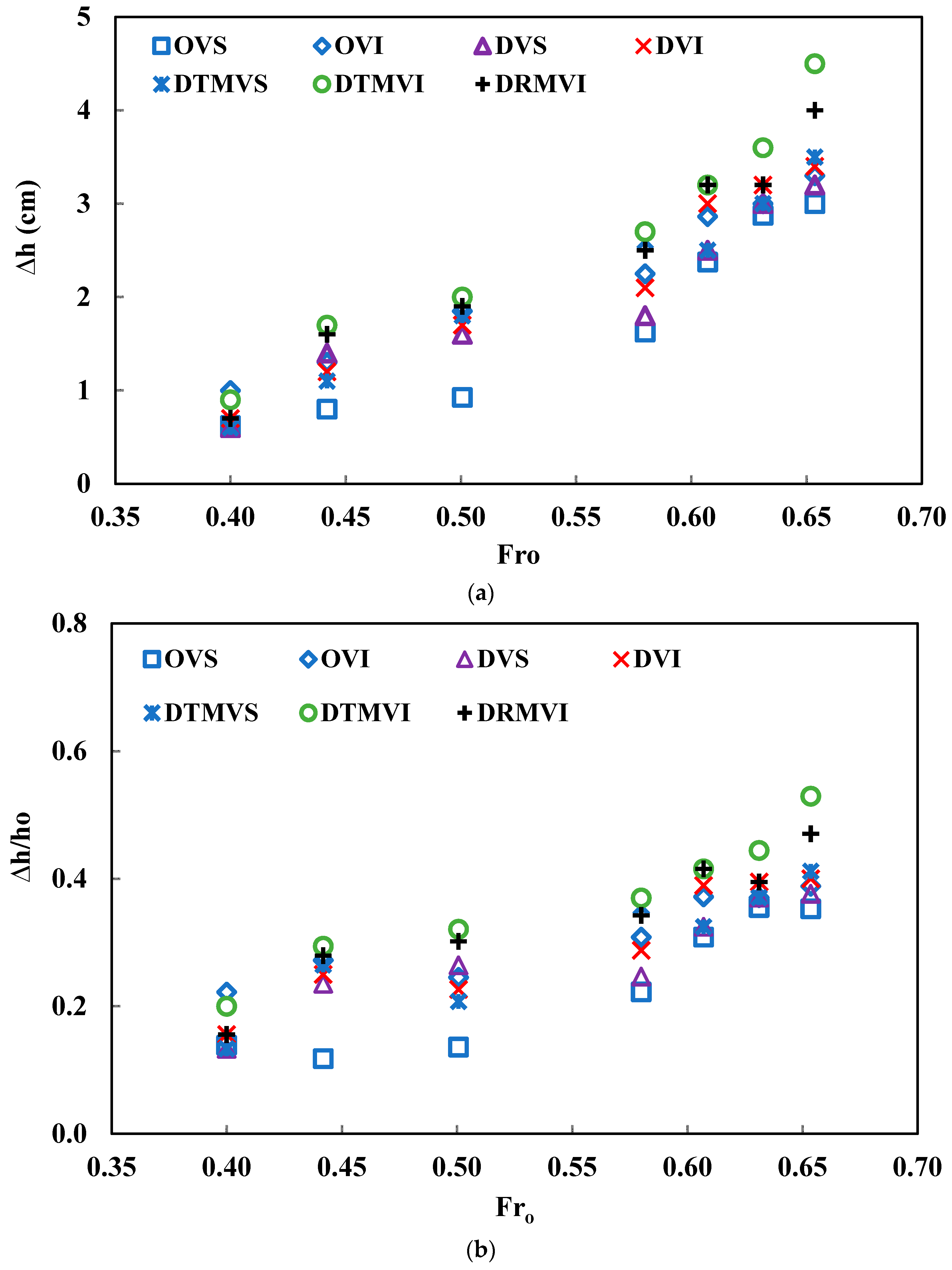
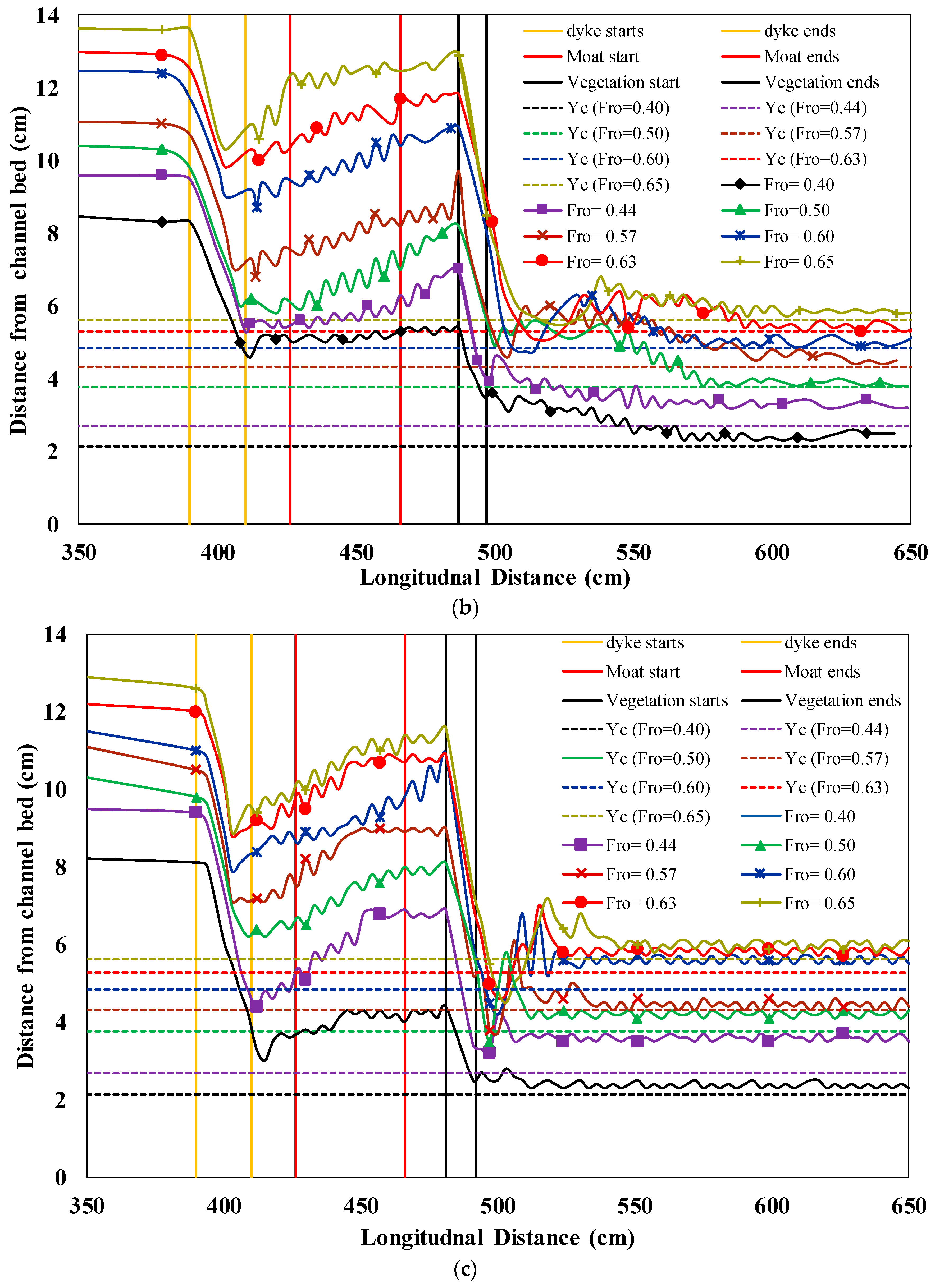
3.1. Backwater Rise
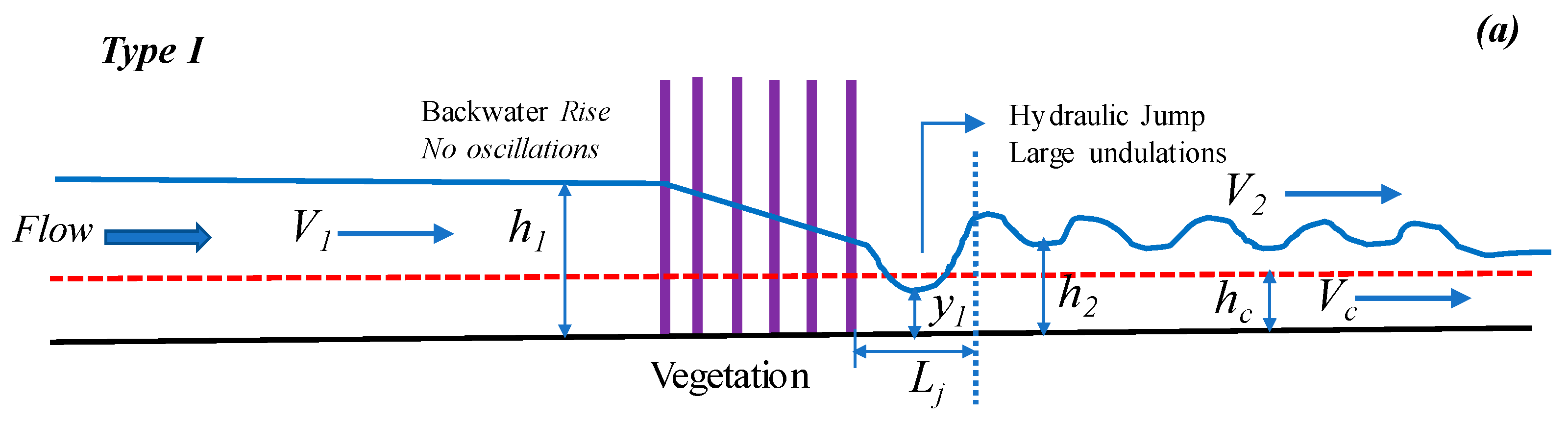
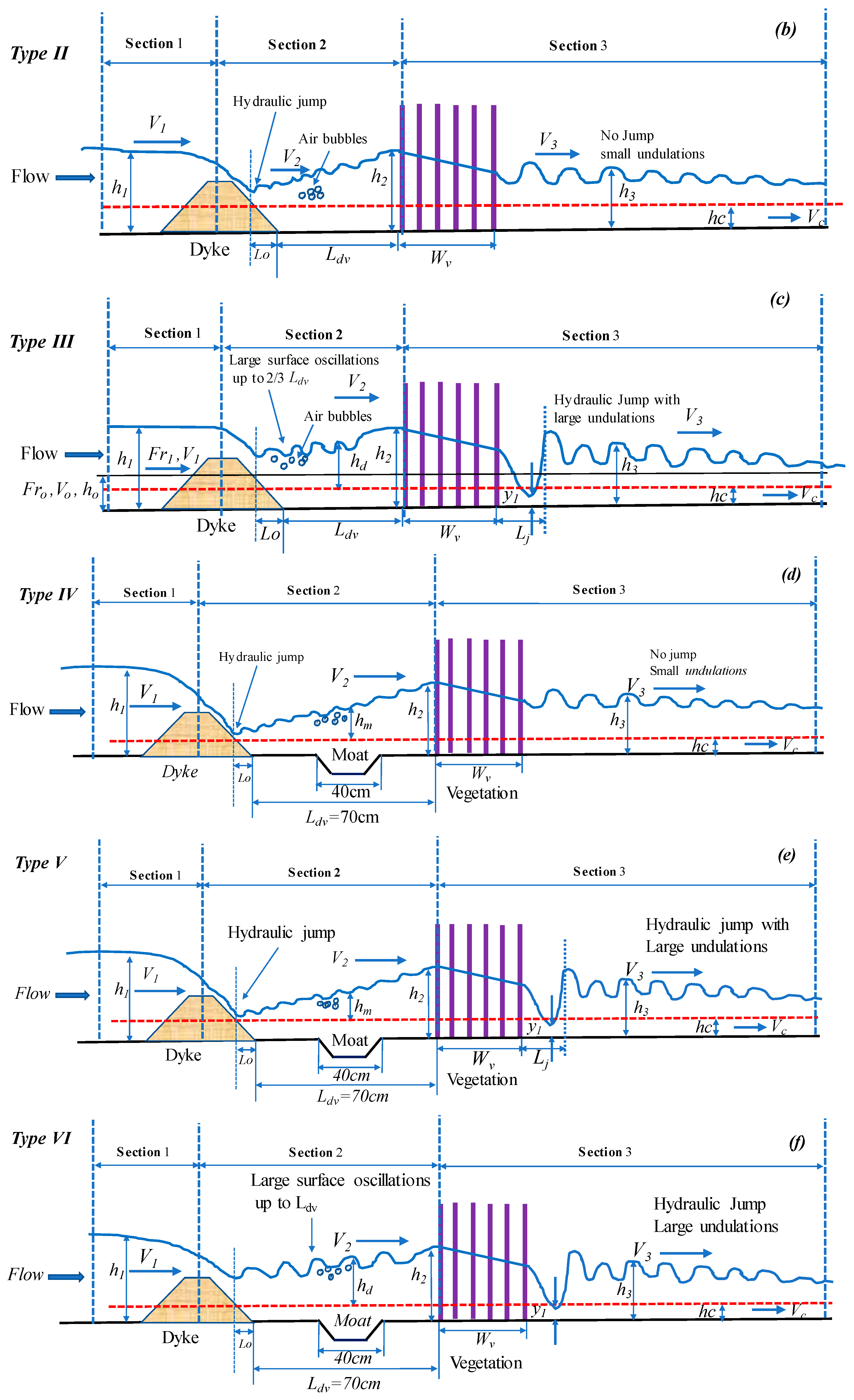
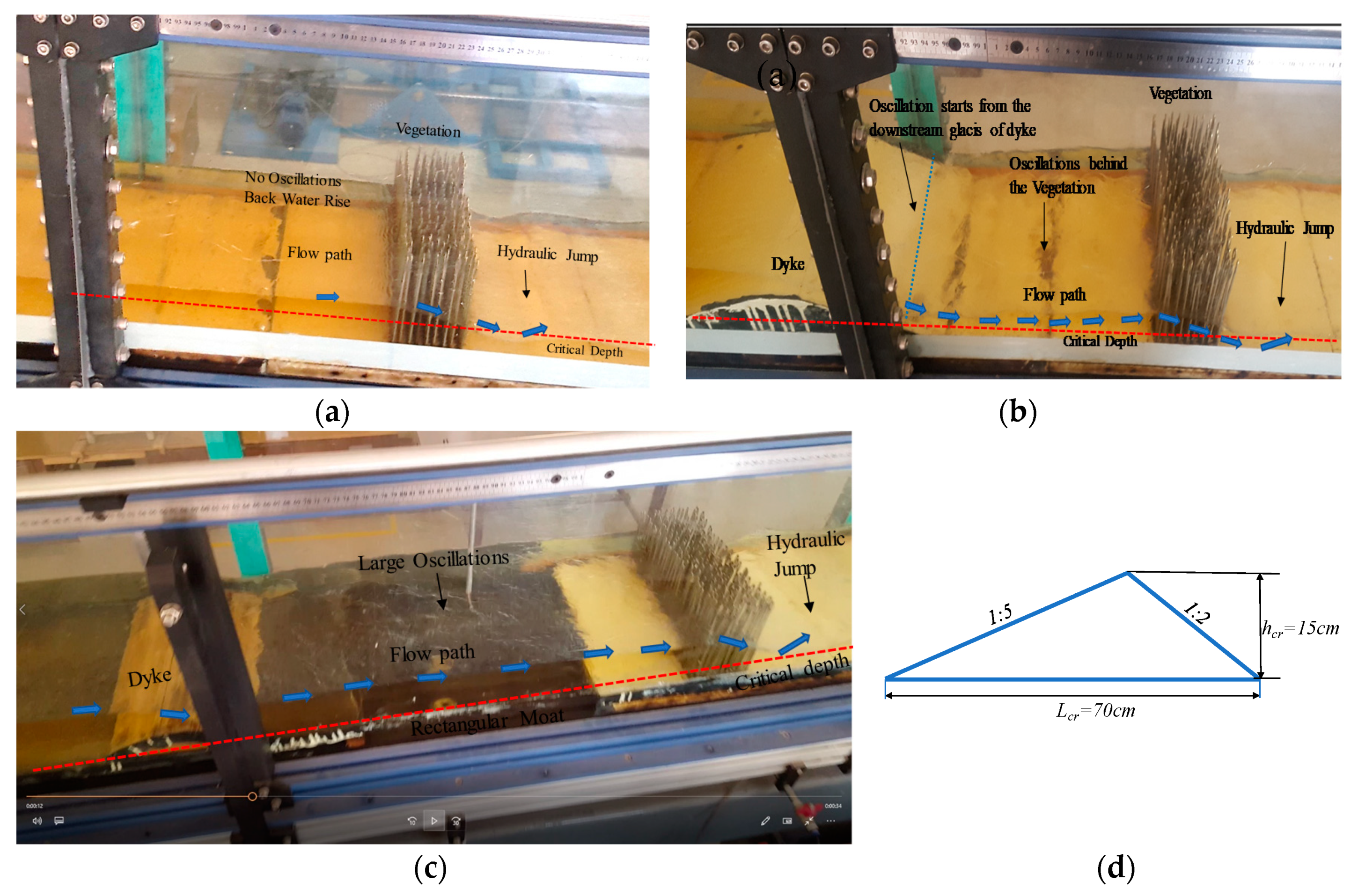
3.2. Hydraulic Jump and Water Surface Profile Classification
3.2.1. Hydraulic Jump Classification in SDS
3.2.2. Hydraulic Jump Classification in HDS
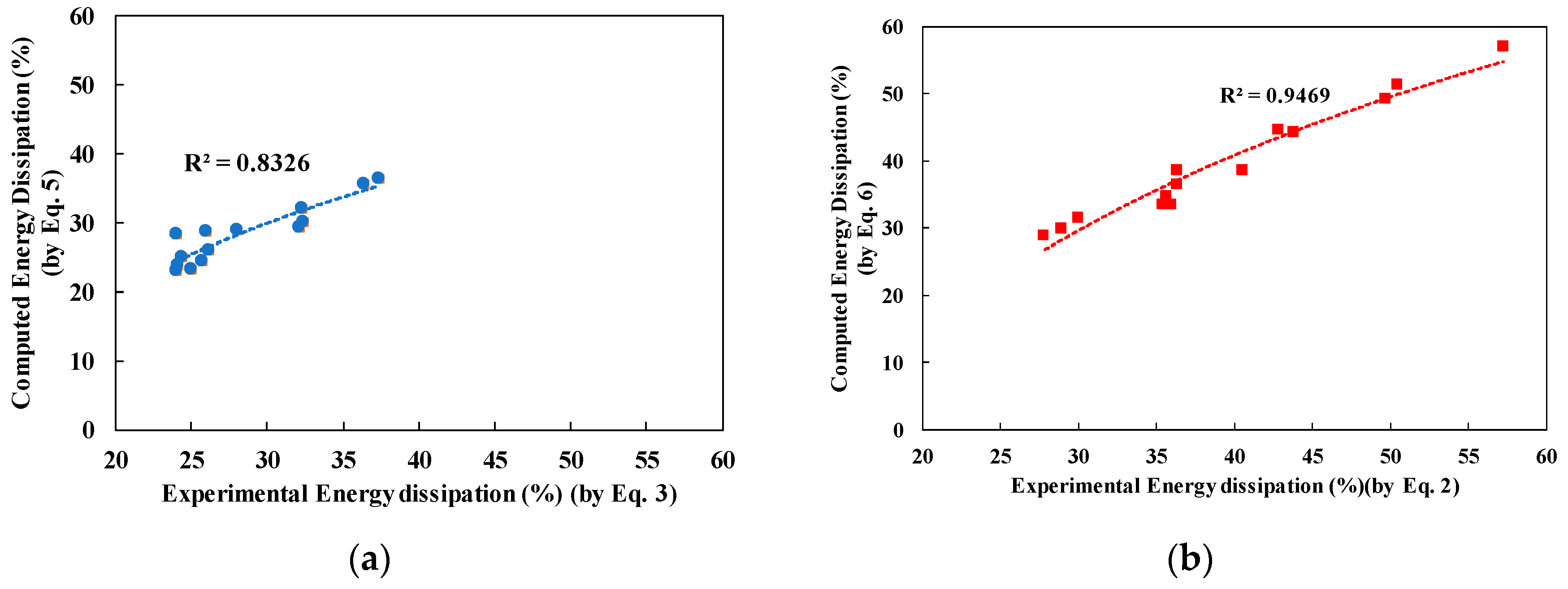
3.3. Evaluation of Energy Dissipation
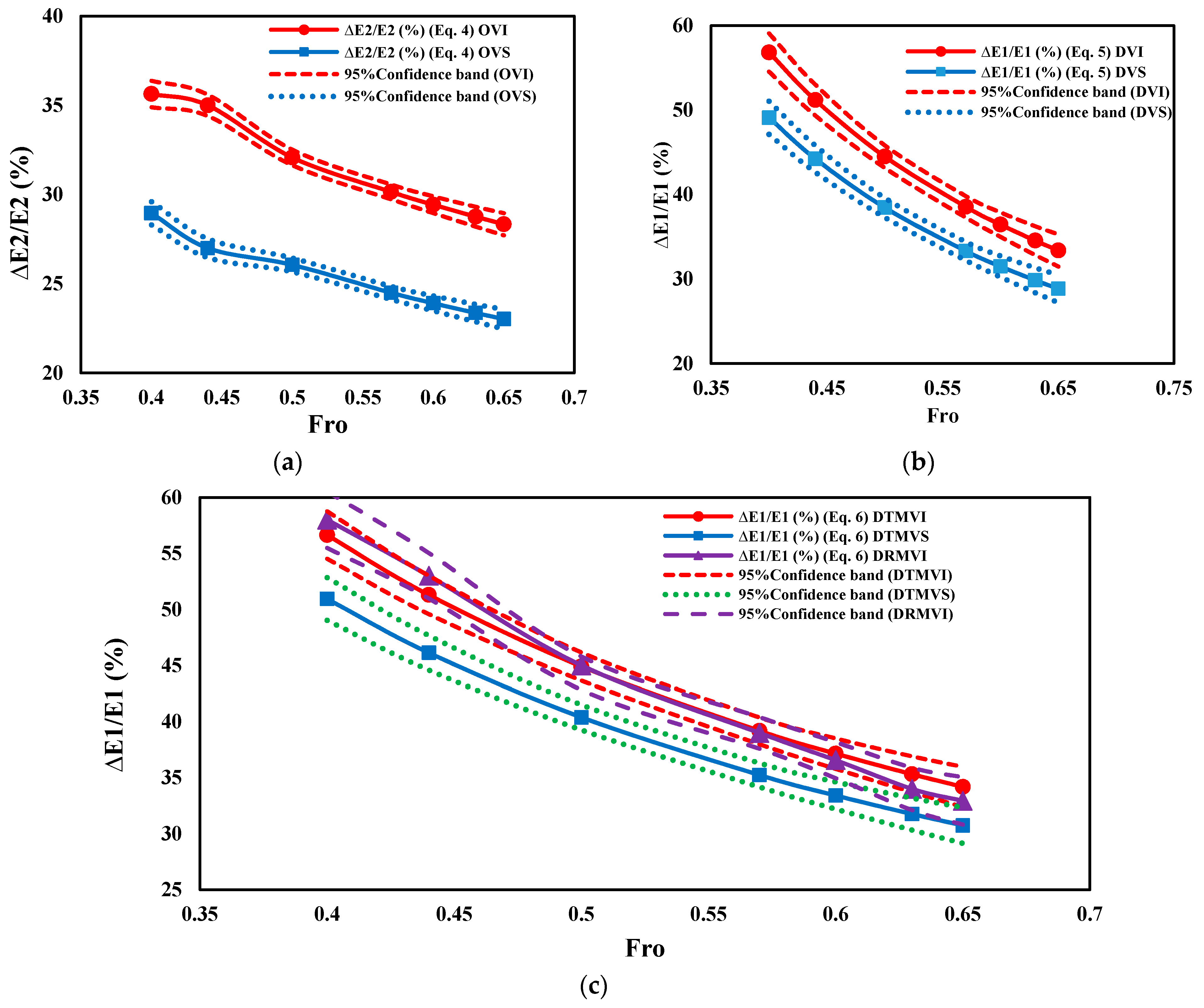
3.3.1. Energy Dissipation in Single Defense System (SDS)
3.3.2. Energy Dissipation in Hybrid Defense System (HDS)
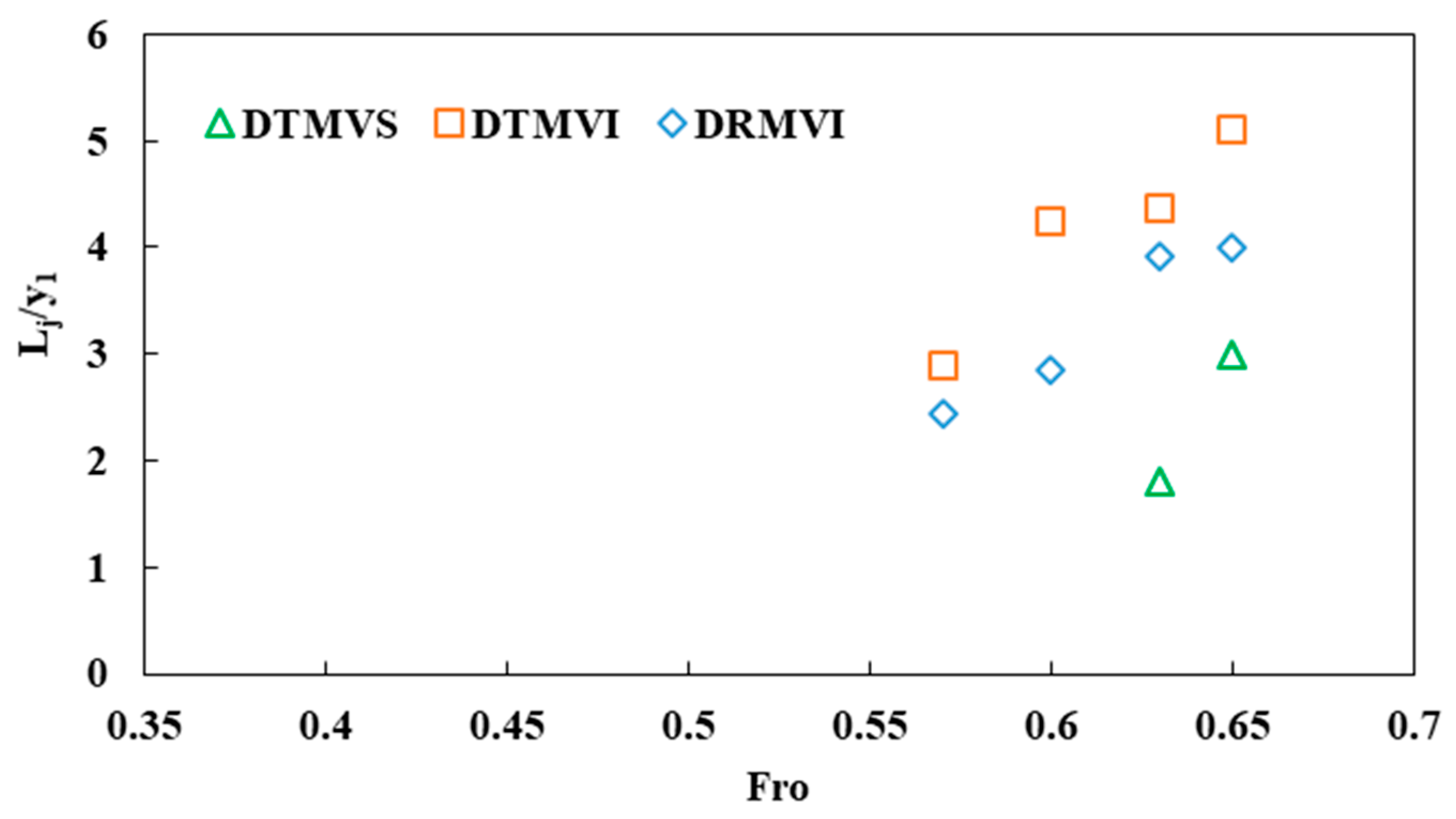
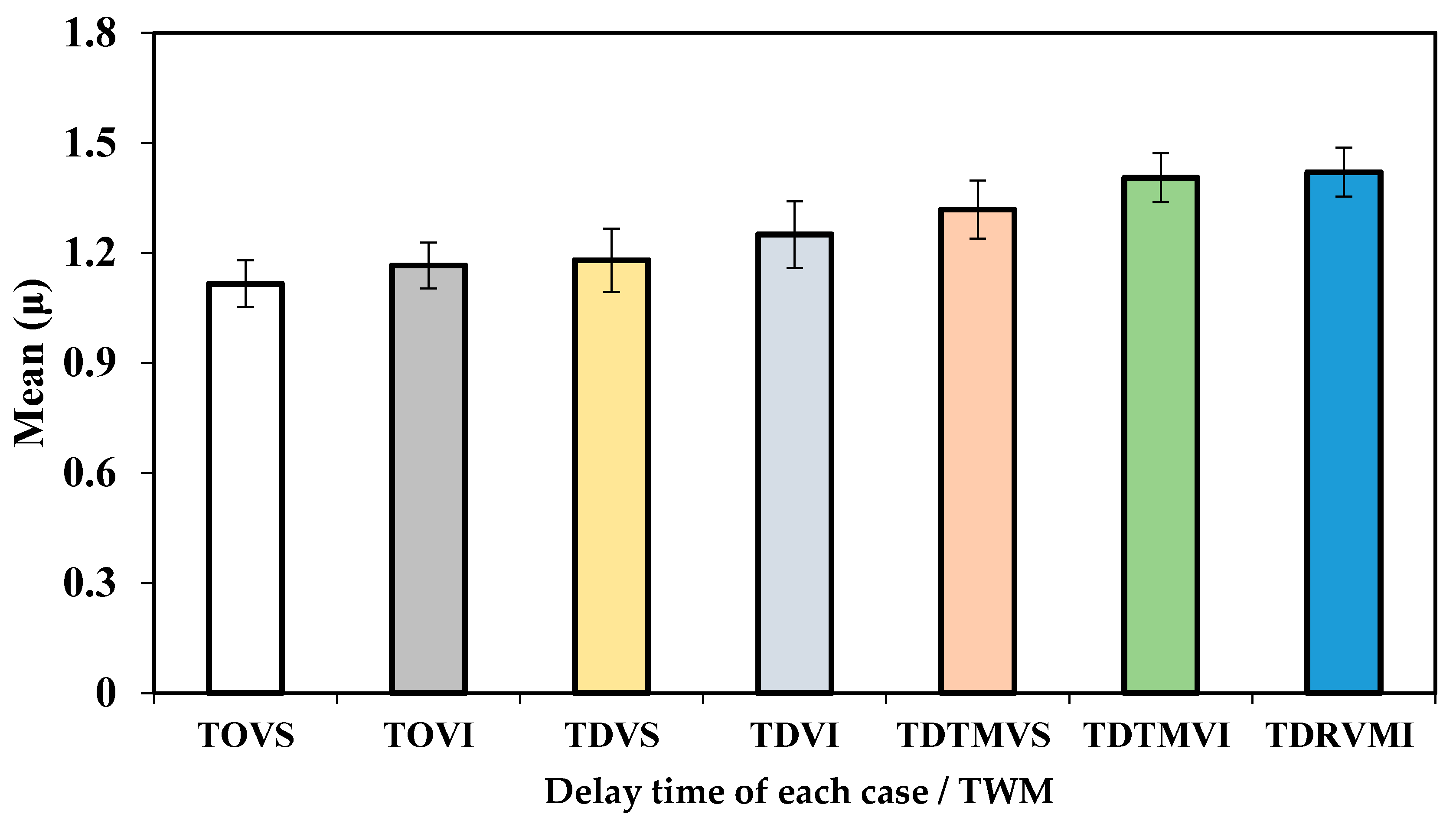
3.3.3. Delay in Floodwater Arrival Time and Water Level Rise
4. Discussion
4.1. Hydraulic Jump Formation and Energy Dissipation in SDS
4.2. Hydraulic Jump Formation and Energy Dissipation in HDS
5. Conclusions
- The backwater rise is maximum for OVI and DTMVI in SDS and HDS, respectively. The backwater rise is directly proportional to the density of vegetation and the value of initial Froude number. The water surface slope also increases by increasing vegetation density. The denser and wider the vegetation, the larger is the total energy dissipation in both SDS and HDS cases.
- In SDS only undulated hydraulic jump was observed in both OVS and OVI, resulting in a significant energy loss. In HDS both weak and undulated hydraulic jumps were formed and in the case of DTMVI, the maximum energy loss due to hydraulic jump formed in between the dike and vegetation was 27% and 4% energy was dissipated due to the formation of jump on the downstream side of vegetation. The maximum total energy reduced in this case was 60% and the average energy reduced was 46%. Similarly, in the case of DRMVI, the maximum value of energy loss due to hydraulic jump between dike and vegetation was 22% and 3% energy was dissipated due to the formation of hydraulic jump on the downstream side of vegetation. The maximum total energy reduction and average energy reduction were 60% and 43.75%, respectively. In all these cases, the rate of energy reduction due to the hydraulic jump decreases by increasing Fro.
- The performance of the DTMVI model to delay the arrival time of floodwater is the highest among all the models investigated in this paper
- The “moat” can serve as floodwater harvesting and increasing the response time of flash floods generated from hill torrents. The shape of the moat affects the reduction of energy in general. However, its trapezoidal shape performs better than rectangular shape.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Group No. | Pairs | µ1–µ2 | Critical Value (LSD) | Remarks | |
|---|---|---|---|---|---|
| 1 | TOVS/TWM | TOVI/TWM | 0.050 | 0.21 | No significant difference |
| 2 | TOVS/TWM | TDVS/TWM | 0.060 | 0.21 | No significant difference |
| 3 | TOVS/TWM | TDVI/TWM | 0.130 | 0.21 | No significant difference |
| 4 | TOVS/TWM | TDTMVS/TWM | 0.202 | 0.21 | No significant difference |
| 5 | TOVS/TWM | TDTMVI/TWM | 0.281 | 0.21 | significant difference |
| 6 | TOVS/TWM | TDRMVI/TWM | 0.281 | 0.21 | significant difference |
| 7 | TOVI/TWM | TDVS/TWM | 0.010 | 0.21 | No significant difference |
| 8 | TOVI/TWM | TDVI/TWM | 0.080 | 0.21 | No significant difference |
| 9 | TOVI/TWM | TDTMVS/TWM | 0.152 | 0.21 | No significant difference |
| 10 | TOVI/TWM | TDTMVI/TWM | 0.239 | 0.21 | significant difference |
| 11 | TOVI/TWM | TDRMVI/TWM | 0.231 | 0.21 | significant difference |
| 12 | TDVS/TWM | TDVI/TWM | 0.069 | 0.21 | No significant difference |
| 13 | TDVS/TWM | TDTMVS/TWM | 0.142 | 0.21 | No significant difference |
| 14 | TDVS/TWM | TDTMVI/TWM | 0.228 | 0.21 | significant difference |
| 15 | TDVS/TWM | TDRMVI/TWM | 0.220 | 0.21 | significant difference |
| 16 | TDVI/TWM | TDTMVS/TWM | 0.072 | 0.21 | No significant difference |
| 17 | TDVI/TWM | TDTMVI/TWM | 0.158 | 0.21 | No significant difference |
| 18 | TDVI/TWM | TDRMVI/TWM | 0.150 | 0.21 | No significant difference |
| 19 | TDTMVS/TWM | TDTMVI/TWM | 0.086 | 0.21 | No significant difference |
| 20 | TDTMVS/TWM | TDRMVI/TWM | 0.078 | 0.21 | No significant difference |
| 21 | TDTMVI/TWM | TDRMVI/TWM | 0.0079 | 0.21 | No significant difference |
References
- Smith, K. Environmental Hazards: Assessing Risk and Reducing Disaster; Routledge: New York, NY, USA, 2003. [Google Scholar]
- Kellens, W.; Terpstra, T.; De Maeyer, P. Perception and communication of flood risks: A systematic review of empirical research. Risk Anal. 2013, 33, 24–49. [Google Scholar] [CrossRef] [PubMed]
- Buijs, J.; Boelens, L.; Bormann, H.; Restemeyer, B.; Terpstra, T.; van der Voorn, T. Adaptive planning for flood resilient areas: Dealing with complexity in decision-making about multilayered flood risk management. In Proceedings of the 16th Meeting: Adaptive Planning for Spatial Transformation, Groningen, The Netherlands, 23–25 May 2018. [Google Scholar]
- Ali Hasan Muhammad, R.; Tanaka, N. Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences 2019, 9, 247. [Google Scholar] [CrossRef]
- Suppasri, A.; Shuto, N.; Imamura, F.; Koshimura, S.; Mas, E.; Yalciner, A.C. Lessons learned from the 2011 Great East Japan tsunami: Performance of tsunami countermeasures, coastal buildings, and tsunami evacuation in Japan. Pure Appl. Geophys. 2013, 170, 993–1018. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Sasaki, Y.; Tanaka, N. Modeling field observations of the 2011 Great East Japan tsunami: Efficacy of artificial and natural structures on tsunami mitigation. Coast. Eng. 2012, 67, 1–13. [Google Scholar] [CrossRef]
- Pakoksung, K.; Suppasri, A.; Imamura, F. Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City. Geosciences 2018, 8, 173. [Google Scholar] [CrossRef]
- Abbas, A.; Amjath-Babu, T.S.; Kächele, H.; Müller, K. Non-structural flood risk mitigation under developing country conditions: An analysis on the determinants of willingness to pay for flood insurance in rural Pakistan. Nat. Hazards 2015, 75, 2119–2135. [Google Scholar] [CrossRef]
- Houze, R.A., Jr.; McMurdie, L.A.; Rasmussen, K.L.; Kumar, A.; Chaplin, M.M. Multiscale aspects of the storm producing the June 2013 flooding in Uttarakhand, India. Mon. Weather Rev. 2017, 145, 4447–4466. [Google Scholar] [CrossRef]
- Van Oldenborgh, G.J.; Otto, F.E.L.; Haustein, K.; AchutaRao, K. The heavy precipitation event of December 2015 in Chennai, India. Bull. Am. Meteorol. Soc. 2016, 97, S87–S91. [Google Scholar] [CrossRef]
- Philip, S.; Sparrow, S.; Kew, S.; Van Der Weil, K.; Wanders, N.; Singh, R.; Hassan, A.; Mohammed, K.; Javid, H.; Haustein, K.; et al. Attributing the 2017 Bangladesh floods from meteorological and hydrological perspectives. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 1409–1429. [Google Scholar] [CrossRef]
- Marfai, M.A.; Hizbaron, D.R. Community’s adaptive capacity due to coastal flooding in Semarang coastal city, Indonesia. Int. J. Ser. Geogr. Ann. Univ. Oradea 2011, 21, 2011. [Google Scholar]
- Marfai, M.A.; King, L. Potential vulnerability implications of coastal inundation due to sea level rise for the coastal zone of Semarang city, Indonesia. Environ. Geol. 2008, 54, 1235–1245. [Google Scholar] [CrossRef]
- Zhao, G.; Ren, Y.; Visser, P.J.; Uijttewaal, W.S.J. Flow Process of the Embankment Breaching. In Proceedings of the 2013 IAHR World Congress, Chengdu, China, 8–13 September 2013. [Google Scholar]
- Evangelista, S. Experiments and numerical simulations of dike erosion due to a wave impact. Water 2015, 7, 5831–5848. [Google Scholar] [CrossRef]
- Greco, M.; Iervolino, M.; Leopardi, A.; Vacca, A. A two-phase model for fast geomorphic shallow flows. Int. J. Sediment Res. 2012, 27, 409–425. [Google Scholar] [CrossRef]
- Dewals, B.; Rulot, F.; Erpicum, S.; Archambeau, P.; Pirotto, M. Advanced Topics in Sediment Transport Modelling: Non-alluvial Beds and Hyperconcentrated Flows. In Sediment Transport; InTech: London, UK, 2012. [Google Scholar]
- Tanaka, N. Vegetation bioshields for tsunami mitigation: Review of effectiveness, limitations, construction, and sustainable management. Landsc. Ecol. Eng. 2009, 5, 71–79. [Google Scholar] [CrossRef]
- Peruzzo, P.; de Serio, F.; Defina, A.; Mossa, M. Wave height attenuation and flow resistance due to emergent or near-emergent vegetation. Water 2018, 10, 402. [Google Scholar] [CrossRef]
- Sanjou, M.; Okamoto, T.; Nezu, I. Experimental study on fluid energy reduction through a flood protection forest. J. Flood Risk Manag. 2018, 11, e12339. [Google Scholar] [CrossRef]
- Anjum, N.; Ghani, U.; Pasha, G.A.; Latif, A.; Sultan, T.; Ali, S. To investigate the flow structure of discontinuous vegetation patches of two vertically different layers in an open channel. Water 2018, 10, 75. [Google Scholar] [CrossRef]
- Mulahasan, S.; Stoesser, T. Flow resistance of in-line vegetation in open channel flow. Int. J. River Basin Manag. 2017, 15, 329–334. [Google Scholar] [CrossRef]
- Thuy, N.B.; Tanimoto, K.; Tanaka, N. Flow and potential force due to runup tsunami around a coastal forest with a gap–experiments and numerical simulations. Sci. Tsunami Hazards 2010, 29, 43–69. [Google Scholar]
- Liu, J.; Zang, C.; Tian, S.; Liu, J.; Yang, H.; Jia, S.; You, L.; Liu, B.; Zhang, M. Water conservancy projects in China: Achievements, challenges and way forward. Glob. Environ. Chang. 2013, 23, 633–643. [Google Scholar] [CrossRef]
- Dalimunthe, S.A. Who manages space? Eco-DRR and the local community. Sustainability 2018, 10, 1705. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J.; Aberle, J. Characteristic reference areas for estimating flow resistance of natural foliated vegetation. J. Hydrol. 2013, 492, 49–60. [Google Scholar] [CrossRef]
- McDonald, T.; Gann, G.; Jonson, J.; Dixon, K. International Standards for the Practice of Ecological Restoration—Including Principles and Key Concepts; Society for Ecological Restoration: Washington, DC, USA, 2016. [Google Scholar]
- Pasha, G.A.; Tanaka, N.; Yagisawa, J.; Achmad, F.N. Tsunami mitigation by combination of coastal vegetation and a backward-facing step. Coast. Eng. J. 2018, 60, 1–22. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro-Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Fadly, U.; Murakami, K. Study on reducing tsunami inundation energy by the modification of topography based on local wisdom. J. Jpn. Soc. Civ. Eng. Ser. B3 2012, 68, I_66–I_71. [Google Scholar] [CrossRef]
- Tanaka, N.; Igarashi, Y. Multiple defense for tsunami inundation by two embankment system and prevention of oscillation by trees on embankment. In Proceedings of the 20th Congress of IAHR APD Congress, Colombo, Sri Lanka, 28–31 August 2016; pp. 1–8. [Google Scholar]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume experiments on optimal arrangement of hybrid defense system comprising an embankment, moat, and emergent vegetation to mitigate inundating tsunami current. Ocean Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Aslam, M. Flood Management Current State, Challenges and Prospects in Pakistan: A Review. Mehran Univ. Res. J. Eng. Technol. 2018, 37, 297–314. [Google Scholar] [CrossRef]
- Tanvir, M.A.; Siddiqui, M.T.; Shah, A.H. Growth and price trend of Eucalyptus camaldulensis in Central Punjab. Int. J. Agric. Biol. 2002, 4, 344–346. [Google Scholar]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Huai, W.; Wang, W.; Hu, Y.; Zeng, Y.; Yang, Z. Analytical model of the mean velocity distribution in an open channel with double-layered rigid vegetation. Adv. Water Resour. 2014, 69, 106–113. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Critical Resistance Affecting Sub- to Super-Critical Transition Flow by Vegetation. J. Earthq. Tsunami 2019, 13, 1950004. [Google Scholar] [CrossRef]
- Pavlin, Ž.; Kuspilić, N. Reference water levels for the design of dykes and earthfill dams. Građevinar 2018, 70, 225–233. [Google Scholar]
- Ali, S. Flow over Weir-Like Obstacles; TU Delft: Delft, The Netherlands, 2013. [Google Scholar]
- Mahtabi, G.; Arvanaghi, H. Experimental and numerical analysis of flow over a rectangular full-width sharp-crested weir. Water Sci. Eng. 2018, 11, 75–80. [Google Scholar] [CrossRef]
- Al-hashimi, S.A.M.; Madhloom, H.M.; Nahi, T.N.; Al-ansari, N. Channel Slope Effect on Energy Dissipation of Flow over Broad Crested Weirs. Engineering 2016, 8, 837–851. [Google Scholar] [CrossRef][Green Version]
- Tuyen, N.B. Influences of the oblique Obstacles to the flow. In Proceedings of the Japan-Vietnam Estuary Workshop, Hochiminh, Vitenam, 20–24 August 2007. [Google Scholar]
- kabiri, S.A.R. Analytical Approach for Flow over an Oblique Weir. Sci. Iran. 2010, 17, 107–117. [Google Scholar]
- Kabiri-Samani, A.; Ansari, A.; Borghei, S.M. Hydraulic behaviour of flow over an oblique weir. J. Hydraul. Res. 2010, 48, 669–673. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J. Flow structures and sedimentation characteristics around clump-type vegetation. J. Hydro-Environ. Res. 2010, 4, 15–25. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Chanson, H. Minimum specific energy and transcritical flow in unsteady open-channel flow. J. Irrig. Drain. Eng. 2015, 142, 04015030. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Hager, W.H. B-jump in sloping channel. J. Hydraul. Res. 1988, 26, 539–558. [Google Scholar] [CrossRef]
- Jesudhas, V.; Murzyn, F.; Balachandar, R. IDDES Evaluation of Oscillating Hydraulic Jumps. E3S Web Conf. 2018, 40, 05067. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D.K. What is the proper way to apply the multiple comparison test? Korean J. Anesthesiol. 2018, 71, 353. [Google Scholar] [CrossRef] [PubMed]
- Fritz, H.M.; Hager, W.H. Hydraulics of Embankment Weirs. J. Hydraul. Eng. 1998, 124, 963–971. [Google Scholar] [CrossRef]
- Valyrakis, M.; Liu, D.; Mcgann, N.; Turker, U.; Yagci, O. Characterrising the effect of increasing river bank vegetation on the flow field across the channel. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherland, 28 June–3 July 2015. [Google Scholar]
- Darcy, H.P.G.; Bazin, H. Recherches Hydrauliques; Imprimerie Impériales: Paris, France, 1865. [Google Scholar]
- Montes, J.S. A study of the undular jump profile. In Proceedings of the 9th Australasian Fluid Mechanics Conference AFMC, Auckland, New Zealand, 8–12 December 1986; pp. 148–151. [Google Scholar]
- Ryabenko, A.A. Conditions favorable to the existence of an undulating jump. Hydrotech. Constr. 1990, 24, 762–770. [Google Scholar] [CrossRef]
- Chanson, H. Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. Eur. J. Mech. 2009, 28, 191–210. [Google Scholar] [CrossRef]
- Aichel, O.G. Abflusszahlen fuer schiefe Wehre. Discharge ratios for oblique weirs. Z. VDI 1953, 95, 26–27. [Google Scholar]
- De Vries, M. Scheef Aangestrooomde Overlaten; WL-Delft Hydraul: Delft, The Netherlands, 1959. [Google Scholar]
- Keramaris, E.; Pechlivanidis, G.; Kasiteropoulou, D.; Michalolias, N.; Liakopoulos, A. Experimental and Numerical Study of Turbulent Flow in Open Channels with Impermeable and Porous Bed. Procedia Eng. 2016, 162, 381–387. [Google Scholar] [CrossRef][Green Version]
- Wols, B.A. Undular hydraulic jumps. Master’s Thesis, Delft University of Technology, Delft, The Netherland, 2005. [Google Scholar]
- Ali, S.; Uijttewaal, W.S.J. The form drag due to vegetated weir-like obstacles interpreted as expansion losses. In Proceedings of the Water engineering for sustainable environment: 33rd IAHR congress, Vancouver, BC, Canada, 9–14 August 2009. [Google Scholar]
- Kawata, Y.; Benson, B.C.; Borrero, J.C.; Borrero, J.L.; Davies, H.L.; de Lange, W.P.; Imamura, F.; Letz, H.; Nott, J.; Synolakis, C.E. Tsunami in Papua New Guinea was as intense as first thought. Eos Trans. Am. Geophys. Union 1999, 80, 101–105. [Google Scholar] [CrossRef]
- Spiske, M.; Weiss, R.; Bahlburg, H.; Roskosch, J.; Amijaya, H. The TsuSedMod inversion model applied to the deposits of the 2004 Sumatra and 2006 Java tsunami and implications for estimating flow parameters of palaeo-tsunami. Sediment. Geol. 2010, 224, 29–37. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J.; Yasuda, S. Breaking pattern and critical breaking condition of Japanese pine trees on coastal sand dunes in huge tsunami caused by Great East Japan Earthquake. Nat. Hazards 2013, 65, 423–442. [Google Scholar] [CrossRef]
- Luoching, R. Hydraulic jump- The state of the art hydrodynamic characteristics of fixed and moveable beds. Int. J. Appl. Eng. Technol. 2015, 5, 1–11. [Google Scholar]
- Pasha, G.A.; Tanaka, N. Effectiveness of Finite Length Inland Forest in Trapping Tsunami-Borne Wood Debris. J. Earthq. Tsunami 2016, 10, 1650008. [Google Scholar] [CrossRef]
- Streeter, V.L.; Wylie, E.B. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Smith, B. The Role of Vegetation in Catastrophic Floods: A Spatial Analysis. Bachelor’s Thesis, University of Wollongong, Wollongong, Australia, 2013. [Google Scholar]

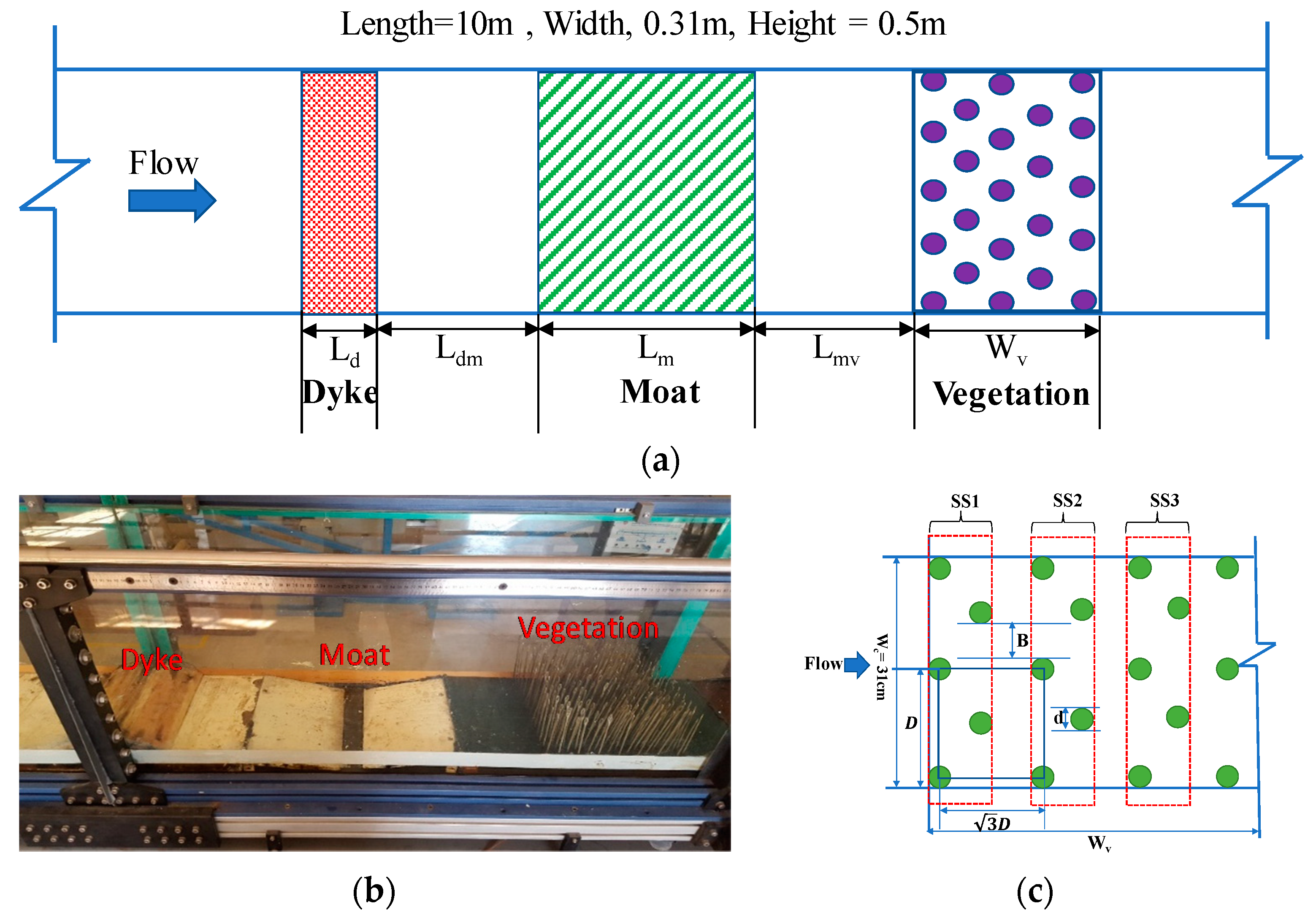
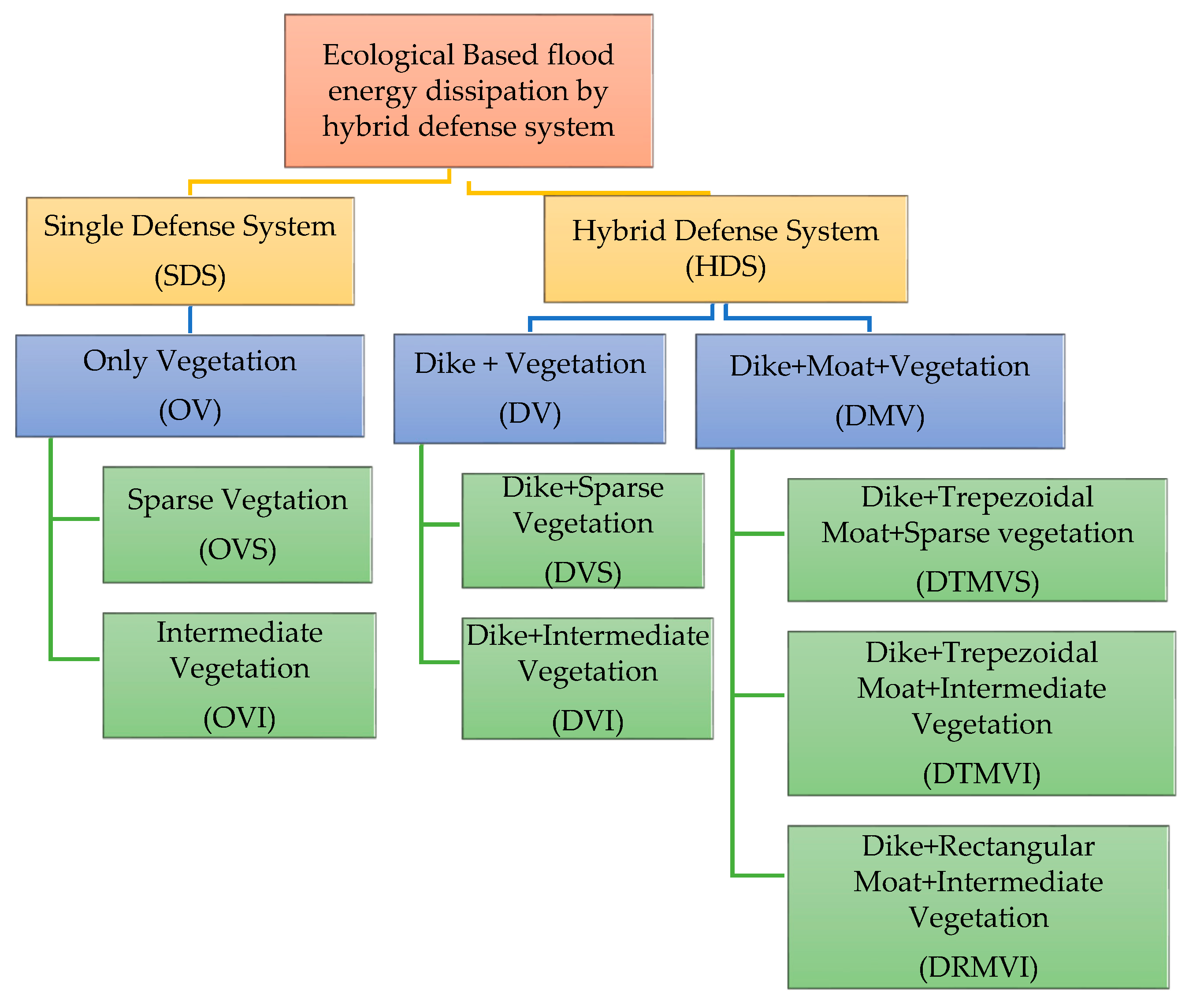
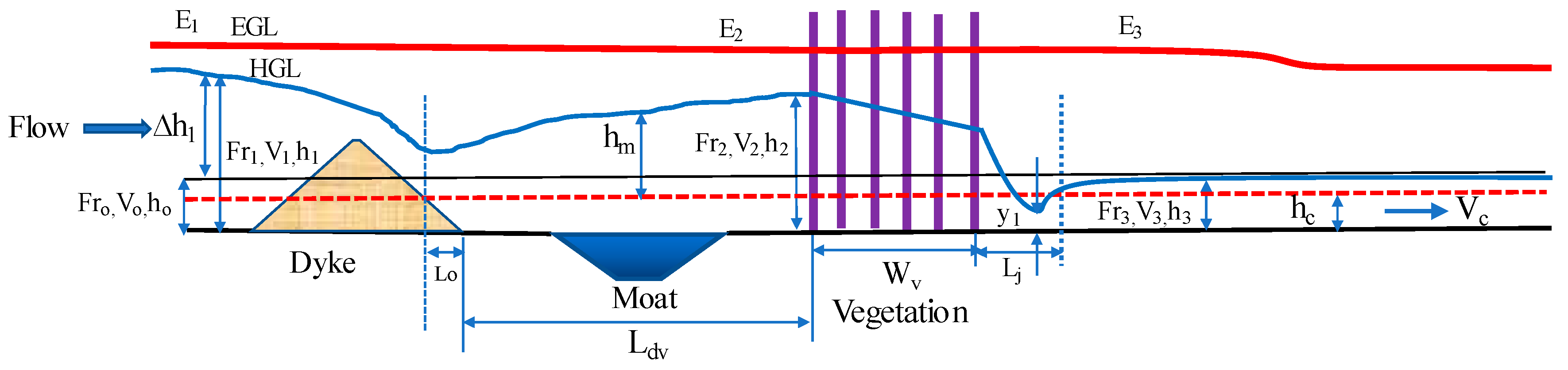


| Case ID | Initial Froude No. (Fro) | Dike | Moat | Vegetation Density (B/d) | D (cm) | Wv (cm) | * Vegetation Thickness “dn” (No.cm) | Vegetation Type |
|---|---|---|---|---|---|---|---|---|
| OVS | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | No dike | No moat | 2.13 | 1.88 | 18.36 | 181.67 | Sparse |
| OVI | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | No dike | No moat | 1.09 | 1.254 | 8.17 | 198.31 | Intermediate |
| DVS | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 |  | No moat | 2.13 | 1.88 | 18.36 | 181.67 | Sparse |
| DVI | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 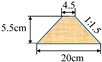 | No moat | 1.09 | 1.254 | 8.17 | 198.31 | Intermediate |
| DTMVS | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 |  | 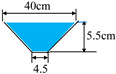 | 2.13 | 1.88 | 18.36 | 181.67 | Sparse |
| DTMVI | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 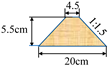 | 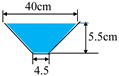 | 1.09 | 1.254 | 8.17 | 198.31 | Intermediate |
| DRMVI | 0.40, 0.44, 0.50, 0.57, 0.60, 0.63, 0.65 | 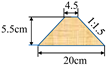 | 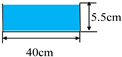 | 1.09 | 1.254 | 8.17 | 198.31 | Intermediate |
| Classification of Hydraulic Jump | |||||||
|---|---|---|---|---|---|---|---|
| Froude Numbers | |||||||
| Case ID | 0.40 | 0.44 | 0.50 | 0.57 | 0.60 | 0.63 | 0.65 |
| OVS | NJ | NJ | NJ | NJ | NJ | UJ, Type I | UJ, Type I |
| OVI | NJ | NJ | NJ | NJ | UJ, Type I | UJ, Type I | UJ, Type I |
| DVS | WJ, Type II | WJ, Type II | UJ, Type II | UJ, Type III | UJ, Type III | UJ, Type III | UJ, Type III |
| DVI | WJ, Type II | WJ, Type II | UJ, Type II | UJ, Type II | UJ, Type III | UJ, Type III | UJ, Type III |
| DTMVS | UJ, Type IV | UJ, Type IV | NJ | NJ | NJ | UJ, Type VI | UJ, Type VI |
| DTMVI | WJ, Type IV | UJ, Type IV | UJ, Type IV | UJ, Type V | UJ, Type VI | UJ, Type VI | UJ, Type VI |
| DRMVI | WJ, Type IV | UJ, Type IV | UJ, Type IV | UJ, Type V | UJ, Type VI | UJ, Type VI | UJ, Type VI |
| Case ID | Energy Loss Due to Hydraulic Jump | Average Energy Loss (%) | Maximum Energy Loss (%) | |
|---|---|---|---|---|
| ΔEj2 (%) | ΔEj3 (%) | |||
| DTMVS | 24 | 2.84 | 38.52 | 53.26 |
| DTMVI | 27 | 4 | 46 | 60 |
| DRMVI | 22 | 3 | 43.75 | 60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Ghumman, A.R. Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System. Water 2019, 11, 1971. https://doi.org/10.3390/w11101971
Ahmed A, Ghumman AR. Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System. Water. 2019; 11(10):1971. https://doi.org/10.3390/w11101971
Chicago/Turabian StyleAhmed, Afzal, and Abdul Razzaq Ghumman. 2019. "Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System" Water 11, no. 10: 1971. https://doi.org/10.3390/w11101971
APA StyleAhmed, A., & Ghumman, A. R. (2019). Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System. Water, 11(10), 1971. https://doi.org/10.3390/w11101971





